Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

Abstract

By combining a detailed computation of the Lyα scattering cross-section with a standard Λ-cold dark matter cosmology, we investigate the accurate intergalactic absorption profiles of neutral hydrogen. Various Lyα absorption systems in the spectra of distant quasars provide crucial measurements of the physical environment of the intergalactic medium. Recent high-redshift observations and cosmological hydrodynamic simulations consistently indicate that the universe has been reionized at z ∼ 6, where a significant flux drop around the Lyα absorption is detected. Since the Lyα opacity is highly sensitive to the presence of atomic hydrogen, the line centre is easily saturated with a tiny neutral fraction (nHi/nH ∼ 10−4). Furthermore, the column density of neutral hydrogen is expected to exceed NHi ∼ 1021 cm−2 through the reionization epoch, which implies that contributions of the off-centre scattering also become important. In order to accurately describe radiative damping phenomena, we consider a fully quantum mechanical scattering cross-section based on the second-order time-dependent perturbation theory. We quantitatively compare our scattering scheme with classical scattering theories, such as the Lorentzian function and the two-level approximation introduced by Peebles. Neglecting contributions of all possible intermediate states, the two-level approximation seriously underestimates scattering probabilities for non-resonant scattering. Adopting the recent concordance cosmology, the Gunn–Peterson absorption profiles are calculated. We find that when the neutral column density reaches NHi ∼ 1021 cm−2, the Peebles approximation yields about 10 per cent overestimation of the transmitted flux and about 5 per cent narrower half-width at half-maximum. For practical applications, we also introduce an analytic function that corrects the classical approximations with an excellent accuracy.

line: profiles, scattering, galaxies: high-redshift, intergalactic medium, cosmology: theory, dark ages, reionization, first stars

1 INTRODUCTION

The neutrality of the intergalactic hydrogen contains invaluable information about the evolution of the universe. Detailed physical processes about the first-generation objects which played the main role in the transition from neutral to ionized universe are carved therein. It is the fundamental challenge to interpret the seriously blended and distorted lights from the first luminous sources. The Lyα and the 21 cm radio wave are two major messengers of the history of the baryonic intergalactic medium (IGM). With the high line strength, redshift coverage, and resolving power, the Lyα absorption has a comparative advantage over the 21 cm emission among the surveys of the early universe (Wolfe, Gawiser & Prochaska 2005). Thus, the importance of having a reliable description of the Lyα scattering processes cannot be overstated.

Recent cosmological observations and theories consistently suggest that the IGM underwent several distinct phases: hot plasma before recombination (z > 1100), dominantly neutral through cosmic dark age (20 < z < 1100), partly ionized during the epoch of reionization, and mostly ionized after the end of reionization (z < 6, Loeb & Barkana 2001; Fan, Carilli & Keating 2006a). The cosmic microwave background indicates that the baryonic pre-galactic medium became dominantly neutral after recombination. On the other hand, high-resolution spectroscopy of the distant quasars reveals that the IGM is mostly ionized until z ∼ 6. This implies that there is a transition epoch where the universe changed from initially neutral to mostly ionized. At the end of the cosmic dark age (z ∼ 20), the first luminous sources started to emit ionizing photons, and the IGM became partly ionized until H ii bubbles completely overlapped with one another (Loeb & Barkana 2001; Ciardi & Ferrara 2005). A series of the Lyα clouds such as the Lyα forests, the Lyman-limit systems (LLSs), and the damped Lyα systems (DLAs) strengthen the idea that they are the remainder that survived after cosmic reionization (Valageas & Silk 1999). Moreover, recent numerical simulations based on the standard Λ-cold dark matter (Λ-CDM) cosmology successfully reproduced large-scale structure (Gnedin & Ostriker 1997; Gnedin & Fan 2006).

During the last two decades, various candidates of the first luminous source, providing the first constraints on the physical processes of reionization, have been discussed: the first stars (Haiman, & Loeb 1997), the first quasars and AGNs (Haiman, & Loeb 1998; Valageas & Silk 1999), protogalaxies (Gnedin 2000; Cen 2003b), the first supermassive black holes (Jiang et al. 2010), afterglows of gamma-ray bursts (Lazzati et al. 2000; Kawai et al. 2006; Robertson & Ellis 2012), and supernova-driven winds (Tegmark, Silk & Evrard 1993). In general, the first-generation objects are a direct consequence of the growth of initial density fluctuations. Therefore, the study of the formation of the first objects provides an important connection from large-scale to small-scale structure. Numerous theoretical models of cosmic reionization have been established throughout analytical studies (Madau, Haardt & Rees 1999; Miralda-Escudé, Haehnelt & Rees 2000; Wyithe & Loeb 2003; Cen 2003a) and numerical simulations (Gnedin 2000; Razoumov et al. 2002; Sokasian, Abel & Hernquist 2002; Ciardi, Stoehr & White 2003; Iliev et al. 2006; Ahn et al. 2012; Iliev et al. 2014). Comprehensive reviews (Loeb & Barkana 2001; Ciardi & Ferrara 2005; Fan et al. 2006a; Morales & Wyithe 2010; Bromm & Yoshida 2011; Fan 2012) provide also extensive discussions on the cosmic reionization.

The presence of atomic hydrogen during the reionization epoch causes a severe suppression of spectra bluewards of the Lyα. This effect is the Gunn–Peterson (GP) trough (Gunn & Peterson 1965; Scheuer 1965), crucial evidence of cosmic reionization. UV radiation from the first objects scatters off intervening hydrogen atoms, and even a small amount of neutral fraction (∼10−4) can produce a considerable Lyα opacity (Becker et al. 2001; Loeb & Barkana 2001; Fan et al. 2006a). In previous theoretical works of the GP models (Miralda-Escudé 1998; Loeb & Rybicki 1999; Madau & Rees 2000), transfer problems have been analysed with a classical approximation assuming a two-level atom (Peebles 1993). Neglecting all possible intermediate p-states, the Peebles approximation seriously underestimates scattering probabilities for low-energy photons. As a result, it yields a considerable overestimation of the transmitted flux. Especially, the column density of neutral hydrogen is extremely high through the reionization epoch, in a way that the off-centre scattering also has non-negligible effects. In order to describe the radiation damping phenomenon accurately, a more accurate description of scattering is required.

In this paper, we present a detailed description of the radiative damping wings incorporating the second-order perturbation theory. First, an accurate scattering cross-section around Lyα is quantitatively compared with the classical approximations (Section 2.1). Then, the intergalactic absorption profiles are examined in the context of the standard cosmology (Section 3). In addition, an analytic function that corrects the classical approximation is also incorporated in Section 2.2.

2 SCATTERING CROSS-SECTION

2.1 Resonance and radiation damping

The interaction between photons and particles is the most fundamental process in the universe. Generally, this interaction is understood in terms of scattering theory of radiation. In the classical theory, natural line broadening is described by the damped harmonic oscillator with the periodic dipole driven force. Then, the angular integration of the time-averaged intensity yields the scattering cross-section
(1)
where the classical damping constant |$\gamma = 2 e^2 \omega _0^2 / 3 m_{\rm e} c^3$|⁠. This classical dispersion relation is known as the Rayleigh scattering. In the case of off-centre scattering (γ ≪ ω), the damping term (γ2ω2) can be safely neglected. For a strongly bound case (ω ≪ ω0), it presents the well-known ω4 – dependence of the Rayleigh scattering. For a free electron (ω0 → 0), it yields the Thomson scattering cross-section |$\sigma _{\!\rm T}= 8 \pi r_{\rm e}^2 /3$| with the classical radius of electron re = e2/(mec2) = 2.82 × 10−13 cm. By applying quantum mechanical correspondence (Γij = γfij) and oscillator strength fij (Weisskopf 1933), the Lyα cross-section has the form of
(2)
where the damping constant Γ2p = 6.262 × 108 s−1 and the line strength f12 = 0.4162. Especially, in the vicinity of resonance (ω ∼ ω0), equation (2) becomes the well-known Lorentzian function
(3)
which provides an excellent approximation for resonance scattering. The Lorentzian has an extremely narrow width (FWHM Γ = Δλ = 0.6 × 10−4 Å) around the resonance frequency. It is an exact solution of the first-order time-dependent perturbation theory, which leads to a good description of the natural line width (Γ), transition lifetime (1/Γ) and atomic decay rate (∼e−Γt) of the excited state (Weisskopf & Wigner 1930). Because of the slow damping rate (∼1/ω2), however, it cannot reproduce accurate scattering probabilities for low-energy photons, and therefore radiation damping cannot be properly prescribed with the linear perturbation theory.
Absorption lines of high-redshift systems are characterized by the broad damped profiles due to the extremely high column density of neutral medium in the Hubble flow. In order to describe the broad damped profile of the Lyα clouds at high redshift, Peebles (1993) introduced an analytic solution based on the two-level approximation
(4)
In their qualitative analysis, the line profile of resonance scattering (the Lorentzian) is gently connected to off-centre region with the ω4 – dependence of the classical Rayleigh scattering. However, as it was remarked explicitly in their work, equation (4) results in considerable underestimation of the transition probability, since contributions of all possible intermediate states are neglected.
The time-dependent energy perturbation theory in second order provides a better understanding of the interaction between photons and atomic electrons. In early quantum electrodynamics, the correspondence principle related to the classical dispersion theory was introduced by Kramers & Heisenberg (1925). In the second-order theory, scattering can be illustrated as two kinds of time-ordered events: the creation of a photon after absorption or the annihilation after emission (Sakurai 1967). Consequently, infinitely many intermediate states (both bound discrete and continuum p-states) will participate in the interaction. Then, the transition probability can be derived by summing all the contributions from participating intermediate states. The resultant differential cross-section known as the Kramers and Heisenberg formula is represented by
(5)
where |$({\boldsymbol {x}}\cdot {\boldsymbol\epsilon} ^{(\alpha ^{\prime })})_{1n}$| denotes the matrix element of the position operator between the ground 1s state and excited np state, and (⁠|${\boldsymbol\epsilon} ^{(\alpha )}, {\boldsymbol\epsilon} ^{(\alpha ^{\prime })}$|⁠) the polarization state vector of the incident and the outgoing photon, respectively. In equation (5), summation (integration) stands for all intermediate bound np states (and continuum n′p states) with eigenenergy En = −1/2n2 (⁠|$E_n^{\prime } = 1/2{n^{\prime }}^2$|⁠) and angular frequency |$\omega _{n1} = \displaystyle\frac{1}{2}(1-1/n^2)$| (⁠|$\omega _{n^{\prime }1} = \displaystyle\frac{1}{2}(1+1/n^{\prime 2})$|⁠). If the energy of the incident photon is much higher than the atomic binding energy (i.e. ω → ∞), then equation (5) is reduced to |${{\rm d}\sigma /{\rm d}\Omega } = {r_{\rm e}}^2 | {\boldsymbol\epsilon} ^{(\alpha )} \cdot {\boldsymbol\epsilon} ^{(\alpha ^{\prime })} |^2$|⁠, that is, the classical Thomson scattering cross-section. In cases of lower energy photons (ω ≪ ω0), the completeness condition of all intermediate states also leads to |${{\rm d}\sigma /{\rm d}\Omega } \sim (r_{\rm e}^2 m_{\rm e}^2 /\hbar ^2) \, \omega ^4$|⁠, which corresponds to the classical Rayleigh scattering (Sakurai 1967). For n = 2, the first term inside the summation in equation (5) becomes
(6)
where ω21 is the resonance frequency of Lyα and Δω = ω − ω21. For n ≥ 3, it gives
(7)
Similarly, for n ≥ 2, the second term can be written as
(8)
Correspondingly, similar relations can also be applied to the integration of continuum states.
Using the recurrence relations of the confluent hypergeometric function, the matrix element of the dipole operator is explicitly obtainable (see Heitler 1954; Bethe & Salpeter 1957; Karzas & Latter 1961; Berestetskii, Lifshitz & Pitaevskii 1971). The matrix element of the dipole operator 〈x〉n1 and |${\left\langle x\right\rangle }_{n^{\prime }1}$| are given by
(9)
and
(10)
respectively (Condon & Shortley 1951; Saslow & Mills 1969). Here, a0 is the Bohr radius (a0 = ℏ2/me2). Now, equation (5) can be expanded to
(11)
Detailed derivation of equation (11) is also introduced in previous work by Lee (2003). In principle, we also considered non-coherent scattering where the quantum state of stimulated emission differs from that of incident photon. However, since only small phase space is available for outgoing photon, this inelastic scattering has negligible effect in the Lyα transition. Therefore, the Raman effect becomes unimportant in this monatomic case.

Radiation damping is the fundamental consequence of the photon–atom interaction which causes line broadening, peak asymmetry and phase shift. In Fig. 1, the fully quantum mechanical cross-section has been compared with the classical approximations around the Lyα. The solid line denotes the Kramers–Heisenberg cross-section (σKH), and the classical approximations (σR, σL, σP) correspond to the classical Rayleigh scattering, the Lorentzian function, and the Peebles formula, respectively. By definition, the Lorentzian approximates well resonance scattering. In Fig. 2, relative errors (Δσ/σKH) of two classical approximations (σL, σP) are illustrated near the resonance region. It is notable that the Lorentzian (dash–dotted) underestimates the cross-section in the wavelength region (λ0 < λ < 1353 Å). The largest deviation in this interval is around 3.5 per cent underestimation at λ ∼ 1274 Å. This behaviour may cause an asymmetry problem in identifying line profiles of the DLAs (Lee 2003, 2013). Due to its asymptotic behaviours and asymmetry features, the Lorentzian cannot provide a proper solution of radiation damping for extremely high dense systems.

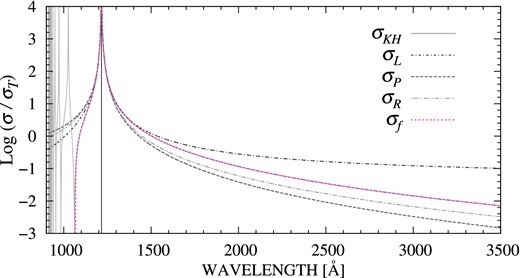
The scattering cross-section around Lyα. The Kramers–Heisenberg dispersion relation, σKH (solid line) is compared to the classical approximations, such as the Lorentzian function σL (dash–dotted), the Rayleigh scattering σR (double-dot–dashed), and the two-level approximation σP by Peebles (1993, dashed). The Lorentzian gives an excellent approximation at the line centre, but its slow damping rate causes a significant overestimation of the off-centre scattering. In the case of the Peebles approximation, resonance scattering is gently connected to the low energy scattering of the classical Rayleigh scattering (ω4 – dependence). This two-level assumption leads to a considerable underestimation of the transition probability by neglecting all possible intermediate states. The dotted line represents the cross-section (σf) based on the fitting function (see Section 2.2) that corrects the classical approximations.
Figure 1.

The scattering cross-section around Lyα. The Kramers–Heisenberg dispersion relation, σKH (solid line) is compared to the classical approximations, such as the Lorentzian function σL (dash–dotted), the Rayleigh scattering σR (double-dot–dashed), and the two-level approximation σP by Peebles (1993, dashed). The Lorentzian gives an excellent approximation at the line centre, but its slow damping rate causes a significant overestimation of the off-centre scattering. In the case of the Peebles approximation, resonance scattering is gently connected to the low energy scattering of the classical Rayleigh scattering (ω4 – dependence). This two-level assumption leads to a considerable underestimation of the transition probability by neglecting all possible intermediate states. The dotted line represents the cross-section (σf) based on the fitting function (see Section 2.2) that corrects the classical approximations.

Open in new tabDownload slide
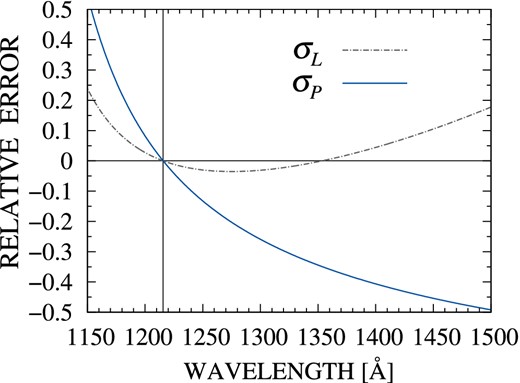
Relative errors of the classical approximations of the Lyα scattering. The relative errors (Δσ/σKH) of the Lorentzian (dash–dotted) and the Peebles approximation (solid line) have been presented. The vertical line denotes the Lyα resonance wavelength. With the extremely narrow width, the Lorentzian well approximates resonance scattering (ω → ω0). However, owing to the slow damping rate, it seriously overestimates scattering probability for low-energy photons (ω ≪ ω0). It is notable that the Lorentzian underestimates in wavelength region (λ0 < λ < 1353 Å), which may cause an asymmetry problem in identifying line profiles of the dense Lyα clouds. The largest deviation in this interval is around 3.5 per cent underestimation at λ ∼ 1274 Å. Owing to assumption of a two-level atom, the Peebles formula significantly underestimates scattering cross-section in the damping wings.
Figure 2.

Relative errors of the classical approximations of the Lyα scattering. The relative errors (Δσ/σKH) of the Lorentzian (dash–dotted) and the Peebles approximation (solid line) have been presented. The vertical line denotes the Lyα resonance wavelength. With the extremely narrow width, the Lorentzian well approximates resonance scattering (ω → ω0). However, owing to the slow damping rate, it seriously overestimates scattering probability for low-energy photons (ω ≪ ω0). It is notable that the Lorentzian underestimates in wavelength region (λ0 < λ < 1353 Å), which may cause an asymmetry problem in identifying line profiles of the dense Lyα clouds. The largest deviation in this interval is around 3.5 per cent underestimation at λ ∼ 1274 Å. Owing to assumption of a two-level atom, the Peebles formula significantly underestimates scattering cross-section in the damping wings.

Open in new tabDownload slide
In their qualitative analysis, Peebles (1993) provides an elegant relation between resonance and off-centre scattering. However, the two-level assumption results in a significant underestimation of transition probabilities in the whole damping region. The oscillator strength is a good measure of the contribution of each individual excited state. Consequently, for low-energy photons (ω < ω0), the contribution of the 2p state is comparable to that of all the remaining states. High-energy photons (ω > ω0) are also affected by the Lyβ scattering with strength f13 = 0.0791. Therefore, the intrinsic scattering cross-section itself has an asymmetric shape, and the classical approximations does not account for contributions of the remaining states. Through an analytic series expansion of the matrix elements, the classical approximations have been quantitatively compared with the intrinsic scattering cross-section in the vicinity of the Lyα (Lee 2013). In their work, the expansion series of the scattering cross-section is derived as
(12)
In equation (12), the zeroth-order term is the Lorentzian function without damping factor, then the first-order coefficient represents the relative difference with respect to the Lorentzian. Near resonance, the Kramers–Heisenberg cross-section has the first-order coefficient, A1 = −1.792. However, the Peebles formula is expanded with the coefficient A1 = 4, which implies that its relative difference differs from that of the Kramers–Heisenberg formula by a factor of 2 with the opposite sign.

2.2 Correction function for the Lyα damping profile

In the majority of spectral line, resonance scattering is dominant, and the Lorentzian function provides an excellent approximation. However, when the number of absorbers increases, the line centre is easily saturated and radiation damping wing also becomes important. The well-constructed scattering theory of the time-dependent second-order energy perturbation already has been given (Kramers & Heisenberg 1925), but the completeness condition makes it difficult to apply to practical problems. For practical applications, we have investigated an analytic function that corrects the classical approximations. In this section, an analytic function which practically covers the whole range of the Lyα scattering is introduced.

We consider an analytic function applicable to off-centre scattering as well as resonance. In order to obtain a correction factor of the classical approximations, a deviation function f(ω) is defined as
(13)
Then, the cross-section can be expressed in terms of the classical Rayleigh scattering
(14)
Meanwhile, neglecting the damping term in equation (2), the Rayleigh cross-section can be related to the Lorentzian function
(15)
Substituting equation (15) into (14), the cross-section can also be expressed in terms of the Lorentzian function
(16)
For a reliable correction which covers the whole practical domain, a deviation function f(ω) should have two asymptotic properties: it should behave like the Lorentzian (i.e. f(ω) → 0) at resonance (ω → ω0), and it should properly compensate damping wings as a low-energy limit. Moreover, it also has to correct the σL near the line centre (λα < λ < 1353 Å) where the Lorentzian underestimates scattering probabilities. In addition, it should cover the blue part profile as well as the red part with an acceptable accuracy.
Employing a non-linear exponential quadratic regression, an analytic form of the correction function and its coefficients have been numerically determined. Our fitting function for the Lyα is determined to be
(17)
with the coefficient set
(18)
where x = 1 − (ω/ω0). This expression is in excellent agreement with the fully quantum mechanical result (Fig. 1). The deviation function and the numerical fit are presented in Fig. 3. For the long wavelength limit of the Lyα scattering, our fitting relation properly corrects the classical Rayleigh scattering (<0.5 per cent error). Moreover, it is also available for the blue part of Lyα with an excellent accuracies (<1 per cent error).
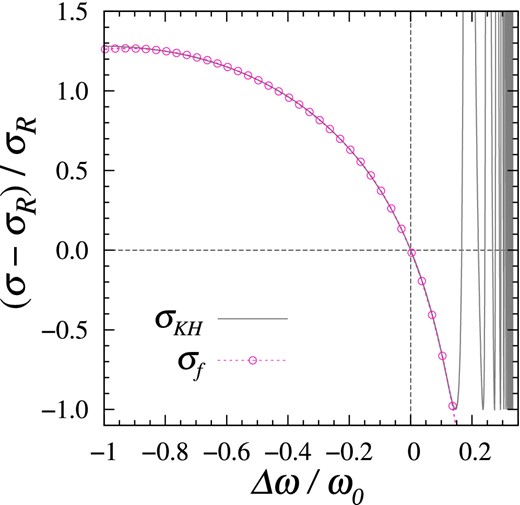
Deviation between the Rayleigh cross-section and the Kramers–Heisenberg relation. The deviation (solid) defined by equation (13) and its fitting relation (dot-circle) have been presented. The analytic function and its coefficients have been numerically determined. It is available for the wavelength region (λ ≥ 1100 Å), which practically covers radiative damping wings of the Lyα within 1 per cent error.
Figure 3.

Deviation between the Rayleigh cross-section and the Kramers–Heisenberg relation. The deviation (solid) defined by equation (13) and its fitting relation (dot-circle) have been presented. The analytic function and its coefficients have been numerically determined. It is available for the wavelength region (λ ≥ 1100 Å), which practically covers radiative damping wings of the Lyα within 1 per cent error.

Open in new tabDownload slide
In previous studies, Gavrila (1967) introduced matrix elements and an analytic expression for low-energy elastic scattering with a threshold frequency. In their quantal computation, the matrix element was derived by the Fourier transformation of the Green's function based on the Schwinger's integral representation. With Gavrila's result, Ferland & Hazy (2001) introduced a power-law fit in his photoionization code ‘cloudy’. Their fitting polynomial for radiative damping wings of the Lyα is given by
(19)
It is available for longer wavelength than the threshold (λ > 1410 Å) with around 4 per cent occasional errors. More previously, Baschek & Scholz (1982) also provided a similar expression in the wavelength region (λ > 2000 Å). However, their simple polynomial fit is not smoothly connected to resonance scattering, i.e. the Lorentzian.

3 THE GP ABSORPTION PROFILES

The presence of neutral medium of high redshift is characterized by the significant suppression bluewards of Lyα and the broad red damping wing. This serious flux drop by neutral IGM was predicted by Gunn & Peterson (1965) and independently by Scheuer (1965). It is a strong evidence that neutral IGM after recombination (z ∼ 1100) has been ionized again by the emission of the first luminous sources. Recent studies of the highest redshift quasars (z > 6) indicate that the IGM is partly ionized, as GP troughs have been detected in their spectra (Fan et al. 2006b; Mortlock et al. 2011). Owing to the high oscillator strength, a small amount of neutral hydrogen can produce a considerable Lyα opacity, and consequently, the GP absorption trough can be present (Fan et al. 2006a). The GP optical depth is defined as
(20)

High-resolution spectroscopy of distant quasars has revealed that various classes of clumpy Lyα absorbers are queueing along the redshift: the Lyα-forest (⁠|$N_{\rm H\,\small {I}} \le 10^{17.2}{\rm \ cm^{-2}}$|⁠), the LLSs (⁠|$10^{17.2} \le N_{\rm H\,\small {I}} \le 10^{19} {\rm \ cm^{-2}}$|⁠), and the sub-DLAs (⁠|$10^{19} \le N_{\rm H\,\small {I}} \le 10^{20.3} {\rm \ cm^{-2}}$|⁠) (Peroux et al. 2005; Rhee et al. 2013; Zafar et al. 2013). Especially, in case of DLAs around z ∼ 3, the column density reaches |$N_{\rm H\,\small {I}} = 2 \times 10^{20}{\rm \ cm^{-2}}$| or higher that is comparable to the typical surface density of disc galaxies (Wolfe et al. 2005). More recently, extremely strong DLAs (⁠|$N_{\rm H\,\small {I}} \ge 0.5 \times 10^{22}{\rm \ cm^{-2}}$|⁠) also have been detected in the redshift range (3 ≤ z ≤ 5) (Noterdaeme et al. 2014). These various Lyα clouds as vestiges of the hierarchical structure formation contain information about the physical processes and the evolutionary history of the IGM (Valageas & Silk 1999; Valageas, Silk & Schaeffer 2001). Moreover, the recent measurement of the cross-correlation between DLAs and Lyα forests from the Baryon Oscillation Spectroscopic Survey (BOSS; Font-Ribera et al. 2012) strengthens the idea that these Lyα clouds are the redshift snapshots of the gravitational evolution during structure formation. In their statistical analysis, the large-scale cross-correlation is in good agreement with linear theory of the standard Λ-CDM cosmology. Therefore, the accurate determination of column densities and redshifts is a crucial issue in probing structure formation of the early universe.

The high number of absorbers of the high-redshift Lyα systems suggest that contribution of the off–centre scattering has non-negligible effect in identifying significantly saturated damping profiles. For an accurate description of the radiation damping, a detailed computation of transition probabilities considering all possible intermediate states is required. In the previous section, the Kramers–Heisenberg dispersion formula based on the time-dependent theory in second-order energy perturbation has been introduced. Incorporating scattering theory of quantum radiation, the GP absorption profiles have been examined within the standard cosmological frames.

Assuming a uniformly expanding universe, we adopt the Friedmann–Robertson–Walker cosmological model
(21)
In a homogeneous universe, a smoothly distributed IGM can be described in terms of comoving density defined by
(22)
Then, the GP optical depth due to intervening neutral hydrogen between the redshift interval [zr, zs] is
(23)
where zs denotes the redshift of the ionization front (IF) near source, zr the end of reionization epoch, dl the proper line element, λobs the observed wavelength, and the present-day Hubble constant H0 = 100 h km s−1 Mpc−1, respectively. From equations (21) and (23), the GP optical depth can be written as
(24)
where the characteristic mean column density of atomic hydrogen is defined as
(25)
For an evolving IGM, density fields can be treated with the differential column density distribution as a function of redshift introduced by Tytler (1981). The differential column density distribution is defined as
(26)
During the last decade, numerous studies of reionization history have been discussed by using analytic calculations (Madau et al. 1999; Miralda-Escudé et al. 2000; Wyithe & Loeb 2003), and numerical simulations (Gnedin 2000; Razoumov et al. 2002; Sokasian et al. 2002; Ciardi et al. 2003; Iliev et al. 2006). The IGM underwent a dramatic change in its chemical states (ionization, metal enrichment) and topological phases (H ii bubble) through the whole epoch of reionization (Loeb & Barkana 2001; Fan et al. 2006a). Therefore, the GP tests are highly sensitive to the line of sight. Moreover, recently measured H i column densities from sub-DLAs and DLAs observations indicate that the universe is highly inhomogeneous in the redshift range (1 ≤ z ≤ 5; Noterdaeme et al. 2012; Zafar et al. 2013; Sobacchi & Mesinger 2014). Indeed, the GP profiles can be affected by inhomogeneous distribution of neutral medium, or by a complex geometry of IFs of the H ii bubbles. If the Lyα emitter is embedded in a mostly neutral IGM, the GP profile will give a substantial information of the density distribution near the source. In order to distinguish the cumulative effect of neutral medium from the density distribution of the IF, the intrinsic Lyα damping profile should be defined. In this work, we focus on the intrinsic GP absorption profile assuming a uniform density fields.
In general, the neutral fraction of hydrogen is determined by the local density of the IGM. The local distribution of atomic hydrogen can be measured by detecting the transmission coefficient
(27)
Then, the broad red damping wing of the GP profile can be resolved in rest-wavelength
(28)
where λ0 is the Lyα resonance in rest frame, and Δλrest = λrest − λ0, respectively. In principle, when the red wing of the Lyβ and the blue wing of the Lyα overlap with their half-width, the complete GP trough is present (Haiman, & Loeb 1999). Consequently, these GP absorption profiles show one broad damping wing in their redward spectra. Defining the half-width at half-maximum (HWHM) as the difference (≡Δλrest) between resonance and the wavelength at which the transmitted flux is reduced to the half (or τ = ln 2 ∼ 0.7), the line width can be evaluated. Due to the degeneracy in redshift and density in highly saturated cases, accurate determination of the line width still is a crucial problem (Miralda-Escudé 1998). Moreover, peculiar velocities of the clumpy IGM and dust extinction complicate even further interpretation of the spectra (Fan 2012). In order to discriminate between physical parameters, a prior knowledge of the accurate radiative damping profile is essential.
Assuming a standard cosmology, recent concordance values based on the 5-yr WMAP data (Hinshaw et al. 2009)
(29)
has been adopted throughout this work. First, the GP absorption profiles have been examined by changing cross-section schemes (σKH, σL, σP). In Fig. 4, transmitted flux (top panel) and relative errors of the classical approximations (bottom) are presented in the redshift range (zr, zs) = (6, 9). In previous studies (Miralda-Escudé 1998; Loeb & Rybicki 1999; Madau & Rees 2000), the GP absorption profiles have been calculated based on the Peebles approximation (equation 4). Because of the assumption of a two-level atom, it underestimates the scattering probabilities, which directly leads to overestimation of the transmitted flux. For a neutral hydrogen column density of (⁠|$N_{{\rm H\,\small {I}}\;\!0}= 5 \times 10^{21} \,{\rm \ cm^{-2}}$|⁠), the corresponding HWHM is Δλ ∼ 15.15 Å and the Peebles approximation results in about 11 per cent overestimation of fractional transmission even at the HWHM. Rather, the Lorentzian gives a better approximation (1 per cent overestimation) than the Peebles approximation, since near-resonance scattering is still dominant. However, owing to its asymptotic behaviours, the Lorentzian cannot provide a proper continuum level. Furthermore, it cannot resolve the cumulative effects of a train of clumpy absorbers in front of the source. Relative errors of the classical approximations to the intrinsic cross-section will grow with respect to the column density of the neutral medium. Basically, the optical depth is affected by the number of absorbers, scattering cross-section and path length. Therefore, the inaccuracies in the cross-section is directly related to uncertainties in estimation of the local density distribution of the neutral IGM.
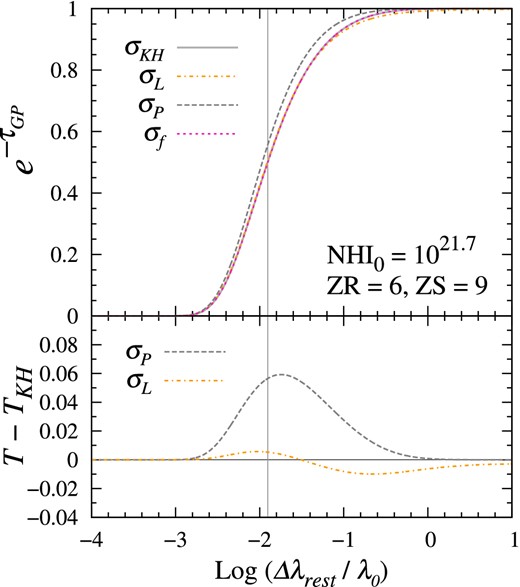
The GP absorption profiles and relative errors of the classical approximations. With the neutral hydrogen column density $N_{{\rm H\,\small {I}}\;\!0}$ = 5 × 1021 cm−2 and the redshift interval (zr, zs) = (6, 9), the GP fractional transmission, $T \equiv {\rm e}^{-\tau _{{\rm GP}}}$ (top) and their differences ΔT = T − TKH (bottom) are illustrated in rest-wavelength. (σKH, σL, σP, σf) denotes the Kramers–Heisenberg relation (solid), the Lorentzian function (dash–dotted), the two-level approximation by Peebles (1993), and the fitting function (red dotted), respectively. It is notable that the σP results in around 11 per cent overestimation of transmitted flux. Owing to the asymptotic behaviours, the Lorentzian cannot resolve the cumulative effects by a train of clumpy absorbers in the line of sight.
Figure 4.

The GP absorption profiles and relative errors of the classical approximations. With the neutral hydrogen column density |$N_{{\rm H\,\small {I}}\;\!0}$| = 5 × 1021 cm−2 and the redshift interval (zr, zs) = (6, 9), the GP fractional transmission, |$T \equiv {\rm e}^{-\tau _{{\rm GP}}}$| (top) and their differences ΔT = T − TKH (bottom) are illustrated in rest-wavelength. (σKH, σL, σP, σf) denotes the Kramers–Heisenberg relation (solid), the Lorentzian function (dash–dotted), the two-level approximation by Peebles (1993), and the fitting function (red dotted), respectively. It is notable that the σP results in around 11 per cent overestimation of transmitted flux. Owing to the asymptotic behaviours, the Lorentzian cannot resolve the cumulative effects by a train of clumpy absorbers in the line of sight.

Open in new tabDownload slide
Considering a uniformly distributed IGM, the comoving mean absorption coefficient can be defined as
(30)
which is a function of frequency and redshift interval. From equations (26) and (23), the GP optical depth is also defined as
(31)
In Fig. 5, the comoving mean absorption coefficient is presented with the same cosmological parameters. For the optical depth τ ∼ 1, the column density is |$N_{\rm H\,\small {I}} \sim 1/\left\langle \, \sigma _{ \nu } \right\rangle$|⁠, so that the effective width can be related to density distribution.
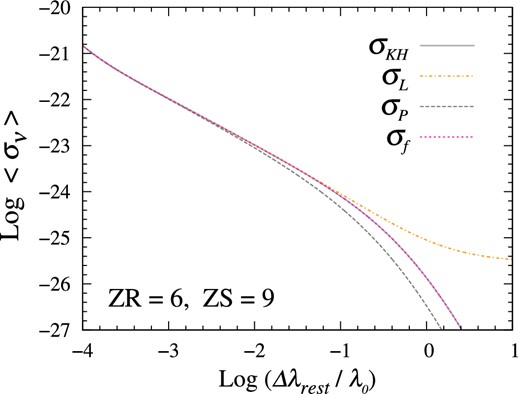
Comoving mean absorption coefficients of the uniformly distributed IGM.
Figure 5.

Comoving mean absorption coefficients of the uniformly distributed IGM.

Open in new tabDownload slide

For a highly saturated absorption profile, the line width of the broad damping wing is an important measurable quantity. Especially, the complete GP troughs are characterized by only one red damping wing, so that the effective line width can be identified with the HWHM (≡Δλrest). Under the same cosmological configurations, we compare various approximation schemes for the Lyα scattering cross-section by adjusting the characteristic number density. In Fig. 6, the theoretical HWHM of the absorption line (top) and the relative errors of the classical approximations (bottom) are presented. For a column density with |$\log N_{{\rm H\,\small {I}}\;\!0}< 20$|⁠, the classical approximations are in good agreement (within 1 per cent error). However, as the number of absorbers increases, the Peebles approximation estimates a narrower HWHM than the intrinsic one. In the case of higher column densities (⁠|$\log N_{{\rm H\,\small {I}}\;\!0}= 21$|⁠) where the intrinsic HWHM (Δλrest) = 3.07 Å, the Peebles approximation results in 5 per cent narrower width with the value of HWHM (Δλrest) = 2.92 Å. When the column density reaches |$\log N_{{\rm H\,\small {I}}\;\!0}= 22$|⁠, the Peebles approximation yields a half-width that is smaller by 20 per cent. On the other hand, the Lorentzian model well approximates the intrinsic HWHM within 1 per cent of error until the column density of |$\log N_{{\rm H\,\small {I}}\;\!0}= 22$|⁠, but it deviates steeply for higher densities. As Miralda-Escudé (1998) discussed, there is a degeneracy problem in determining density and redshift in the presence of absorption systems. Moreover, the evolved IGM seems to be distributed inhomogeneously near the end of reionization epoch. Therefore, an accurate cross-section scheme can invoke the accurate determination of the line centre and the column density distribution.

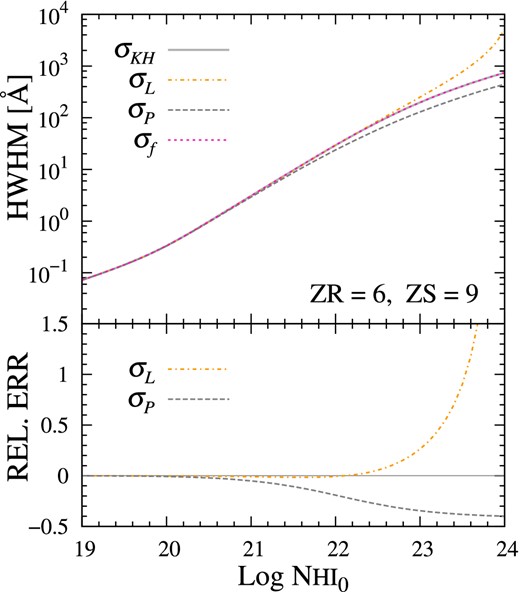
The line width of the GP troughs. Owing to one broad red wing, the complete GP troughs can be evaluated by the HWHM (half-width at half-maximum). For each cross-section scheme, the HWHM (top) and their relative errors (bottom) have been illustrated. When the neutral column density reaches $N_{{\rm H\,\small {I}}\;\!0}\sim 10^{21} {\rm \ cm^{-2}}$, the Peebles approximation results in 5 per cent underestimation of the half line width. Until $N_{{\rm H\,\small {I}}\;\!0}\sim 10^{22} {\rm \ cm^{-2}}$, the Lorentzian provides a good approximation within 1 per cent errors. For a higher column density, it deviates steeply.
Figure 6.

The line width of the GP troughs. Owing to one broad red wing, the complete GP troughs can be evaluated by the HWHM (half-width at half-maximum). For each cross-section scheme, the HWHM (top) and their relative errors (bottom) have been illustrated. When the neutral column density reaches |$N_{{\rm H\,\small {I}}\;\!0}\sim 10^{21} {\rm \ cm^{-2}}$|⁠, the Peebles approximation results in 5 per cent underestimation of the half line width. Until |$N_{{\rm H\,\small {I}}\;\!0}\sim 10^{22} {\rm \ cm^{-2}}$|⁠, the Lorentzian provides a good approximation within 1 per cent errors. For a higher column density, it deviates steeply.

Open in new tabDownload slide

Due to the high line strength of the Lyα transition, the GP absorption profiles are seriously saturated. Consequently, the GP test is sensitive at the end of the reionization where the IGM is mostly ionized (Fan et al. 2006a). However, well-defined damping profiles can give a better interpretation of the shape and width of the GP absorption. Considering a reliable scattering theory, our model of the GP trough provides a better understanding of the epoch of cosmic reionization.

Considering the Kramers–Heisenberg cross-section and recent concordance cosmology, a set of the GP absorption profiles has been computed. Our model grids consist of column densities
(32)
and redshift (zs = 8, 10, 12, and 14). Throughout our calculation, the end of reionization epoch is fixed to be zr = 6. In a previous work (Madau et al. 1999), the characteristic GP optical depth τGP was introduced as
(33)
as a function of the source environment at zs. Relations between physical parameters of absorbers are summarized in Table 1. The group of GP absorption profiles is presented in Fig. 7. With the fixed column number density (⁠|$\log N_{{\rm H\,\small {I}}\;\!0}= 21.3$|⁠), fractional transmissions are illustrated in the rest-wavelength (top panel). In the bottom panel of Fig. 7, curves of growth are presented by increasing number densities of neutral hydrogen in the fixed interval [zr, zs] = [6, 9].
The GP transmission. Considering the Kramers–Heisenberg cross-section (σKH) and recent cosmological parameters ($\Omega _\Lambda$, ΩM, h) = (0.72, 0.23, 0.71), the theoretical absorption profiles have been calculated. By adjusting the redshift of the source (top) and the column number density (bottom), a set of the GP absorption profiles has been calculated.
Figure 7.

The GP transmission. Considering the Kramers–Heisenberg cross-section (σKH) and recent cosmological parameters (⁠|$\Omega _\Lambda$|⁠, ΩM, h) = (0.72, 0.23, 0.71), the theoretical absorption profiles have been calculated. By adjusting the redshift of the source (top) and the column number density (bottom), a set of the GP absorption profiles has been calculated.

Open in new tabDownload slide
Table 1.
Open in new tab

Physical parameters in the GP model grids. The characteristic column number density of atomic hydrogen |$N_{{\rm H\,\small {I}}\;\!0}$|⁠, the comoving number density n0, the characteristic GP optical depth τ0, and the red HWHM (Δλ) in the rest frame are presented.

zs|$\log N_{{\rm H\,\small {I}}\;\!0}$|n0τ0HWHM (Å)
821.301.55 × 10−74.64 × 1055.210
1021.301.55 × 10−76.27 × 1057.061
1221.301.55 × 10−78.06 × 1059.065
1421.301.55 × 10−79.99 × 10511.213
920.301.55 × 10−85.43 × 1040.618
20.804.91 × 10−81.72 × 1051.941
21.301.55 × 10−75.43 × 1056.116
21.804.91 × 10−71.72 × 10618.931
22.301.55 × 10−65.43 × 10655.174
zs|$\log N_{{\rm H\,\small {I}}\;\!0}$|n0τ0HWHM (Å)
821.301.55 × 10−74.64 × 1055.210
1021.301.55 × 10−76.27 × 1057.061
1221.301.55 × 10−78.06 × 1059.065
1421.301.55 × 10−79.99 × 10511.213
920.301.55 × 10−85.43 × 1040.618
20.804.91 × 10−81.72 × 1051.941
21.301.55 × 10−75.43 × 1056.116
21.804.91 × 10−71.72 × 10618.931
22.301.55 × 10−65.43 × 10655.174
Table 1.
Open in new tab

Physical parameters in the GP model grids. The characteristic column number density of atomic hydrogen |$N_{{\rm H\,\small {I}}\;\!0}$|⁠, the comoving number density n0, the characteristic GP optical depth τ0, and the red HWHM (Δλ) in the rest frame are presented.

zs|$\log N_{{\rm H\,\small {I}}\;\!0}$|n0τ0HWHM (Å)
821.301.55 × 10−74.64 × 1055.210
1021.301.55 × 10−76.27 × 1057.061
1221.301.55 × 10−78.06 × 1059.065
1421.301.55 × 10−79.99 × 10511.213
920.301.55 × 10−85.43 × 1040.618
20.804.91 × 10−81.72 × 1051.941
21.301.55 × 10−75.43 × 1056.116
21.804.91 × 10−71.72 × 10618.931
22.301.55 × 10−65.43 × 10655.174
zs|$\log N_{{\rm H\,\small {I}}\;\!0}$|n0τ0HWHM (Å)
821.301.55 × 10−74.64 × 1055.210
1021.301.55 × 10−76.27 × 1057.061
1221.301.55 × 10−78.06 × 1059.065
1421.301.55 × 10−79.99 × 10511.213
920.301.55 × 10−85.43 × 1040.618
20.804.91 × 10−81.72 × 1051.941
21.301.55 × 10−75.43 × 1056.116
21.804.91 × 10−71.72 × 10618.931
22.301.55 × 10−65.43 × 10655.174

4 SUMMARY AND DISCUSSION

The highest redshift Lyα systems are crucial evidence of the small-scale evolution of the IGM. The GP test provides a firm diagnosis of neutrality of baryonic matter during the late phase of cosmic reionization. The ultimate goal of this paper is to provide a reliable constraint of the GP absorption profiles adopting quantum theory of radiation. Considering all possible intermediate transitions, our derivation of the Kramers–Heisenberg dispersion relation has been compared with the classical approximations such as the Rayleigh scattering, the Lorentzian function, and the two-level approximation by Peebles (1993). Near the line centre, the Lorentzian provides a good approximation for optically thin medium where the resonance scattering is still dominant. In the case of high column density systems, however, off-centre scattering also becomes important, and the broad damping wing is a distinguishable measurement in high-resolution spectroscopy. Especially, when the column density reaches |$N_{\rm H\,\small {I}} = 10^{22} {\rm \ cm^{-2}}$|⁠, the GP models based on the classical scattering theories cannot give a proper estimation of the transmitted flux and the line width. Therefore, a detailed cross-section theory is considered in identifying highly saturated absorption lines.

In practice, the pure damped absorption profile cannot be directly detected without accompanying Lyα absorption systems that reside along the line of sight. In order to determine the intrinsic absorption profiles of the damped absorption systems, a superposed absorption by Lyα clouds should be subtracted from them. In principle, the large-scale correlations of DLAs and Lyα forests are accurately predicted by linear theory of the standard Λ-CDM cosmology. Especially, recent statistical analysis of BOSS data (Font-Ribera et al. 2012) has successfully measured the cross-correlation between DLAs and Lyα forests. From similarity of the Lyα clouds on large scale, the intrinsic damped profiles can be elicited.

Recent observations detected extremely strong DLAs (⁠|$N_{\rm H\,\small {I}} \ge 0.5 \times 10^{22}{\rm \ cm^{-2}}$|⁠) in the redshift range 3 ≤ z ≤ 5 (Noterdaeme et al. 2014). The spectra of the highest redshift quasars indicate that the Lyα optical depth increases with τ ∝ (1 + z)4.3 until z < 5.5 (Fan et al. 2006a). Following the growth of the neutral fraction of hydrogen (≥0.1), the optical depth rapidly increases τ ∝ (1 + z)10 around the end of the reionization epoch (z > 5.5) (Fan 2012). Since the IGM evolves dramatically during cosmic reionization, a more realistic model of density distribution has been considered in the GP model (Mesinger & Haiman 2004; Bolton & Haehnelt 2007). Specifically, the transmitted flux of a recently detected quasar (z ∼ 7.1) exhibits a qualitatively different shape and width from the simple GP absorption profiles (Mortlock et al. 2011). As discussed in their work, this discrepancy seems to be affected by inhomogeneity of neutral medium, or by a complex geometry of IFs of the Strömgren sphere. If the Lyα emitters are embedded in a mostly neutral region, the GP absorption profile will give a substantial information of the density distribution near the ionizing fronts. However, with the Lyα absorption, it is not easy to interpret the cumulative effect of the intervening |${{\rm H}\,\small {ii}}$| bubbles which may exist along the line of sight. During the last decade, the size distribution of the ionized bubbles and the corresponding 21 cm signal have been studied by theoretical models (Furlanetto, Zaldarriaga & Hernquist 2004; Iliev et al. 2006; McQuinn et al. 2006; Trac & Cen 2007; Wyithe & Loeb 2007; Choudhury, Haehnelt & Regan 2009). Future observations of the 21 cm line will provide deeper understanding of the density distribution and the reionization processes.

In general, the observed spectrum is affected by the density, temperature, and velocity of the gas located along the line of sight. The Voigt function has been successfully applied to high redshift absorption systems with a wide range of H i column densities. At column density smaller than |$N_{{\rm H\,\small {I}}}\sim 10^{22} {\rm \ cm^{-2}}$|⁠, the Lorentzian function as natural line broadening can be marginally applicable within 1 per cent error. In order to describe line asymmetry of the Lyα forest spectra, Outram, Carswell & Theuns (2000) suggested a statistical method to detect departure from the Voigt profile using non-Gaussian velocity distributions. For denser systems, a detailed treatment of radiation damping also should be included in the Voigt fitting.

We thank the anonymous referee for the constructive suggestions and comments. We are grateful to Roger Blandford, Evangelia Tremou, and Camilla Pacifici for invaluable suggestions and discussions. This research was supported by the Basic Science Research Programme through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (NRF-2010-0024990). KB gratefully acknowledges financial support by the Basic Science Research Programme (NRF-2014-11-1019) and the BK 21 Plus Research Programme (21A-2013-15-00002).

REFERENCES

Ahn
K.
Iliev
I. T.
Shapiro
P. R.
Mellema
G.
Koda
J.
Mao
Y.
, 
ApJ
,
2012
, vol.
756
pg.
L16
Crossref
Search ADS
 
Baschek
B.
Scholz
M.
, 
Astronomy and Astrophysics, Stars and Star Clusters Vol. 2b
,
1982
Berlin
Springer-Verlag

Google Scholar

OpenURL Placeholder Text

 
Becker
R. H.
et al. , 
AJ
,
2001
, vol.
122
pg.
2580
Crossref
Search ADS
 
Berestetskii
V. B.
Lifshitz
E. M.
Pitaevskii
L. P.
, 
Relativistic Quantum Theory
,
1971
Oxford
Pergamon Press

Google Scholar

OpenURL Placeholder Text

 
Bethe
H. A.
Salpeter
E. E.
, 
Quantum Mechanics of One and Two Electron Atoms
,
1957
New York
Academic Press

Google Scholar

OpenURL Placeholder Text

 
Bolton
J. S.
Haehnelt
M. G.
, 
MNRAS
,
2007
, vol.
374
pg.
493
Crossref
Search ADS
 
Bromm
V.
Yoshida
N.
, 
ARA&A
,
2011
, vol.
49
pg.
373
Crossref
Search ADS
 
Cen
R.
, 
ApJ
,
2003a
, vol.
591
pg.
12
Crossref
Search ADS
 
Cen
R.
, 
ApJ
,
2003b
, vol.
597
pg.
L13
Crossref
Search ADS
 
Choudhury
T. R.
Haehnelt
M. G.
Regan
J.
, 
MNRAS
,
2009
, vol.
394
pg.
960
Crossref
Search ADS
 
Ciardi
B.
Ferrara
A.
, 
Space Sci. Rev.
,
2005
, vol.
116
pg.
625
Crossref
Search ADS
 
Ciardi
B.
Stoehr
F.
White
D. M.
, 
MNRAS
,
2003
, vol.
343
pg.
1101
Crossref
Search ADS
 
Condon
E. U.
Shortley
G. H.
, 
The Theory of Atomic Spectra
,
1951
Cambridge
Cambridge Univ. Press

Google Scholar

OpenURL Placeholder Text

 
Fan
X.
, 
Res. Astron. Astrophys.
,
2012
, vol.
12
pg.
865
Crossref
Search ADS
 
Fan
X.
Carilli
C. L.
Keating
B.
, 
ARA&A
,
2006a
, vol.
44
pg.
415
Crossref
Search ADS
 
Fan
X.
et al. , 
AJ
,
2006b
, vol.
131
pg.
1203
Crossref
Search ADS
 
Ferland
G.
Hazy
A.
, 
Brief Introduction to Cloudy 94.00
,
2001
Lexington
Univ. Kentucky

Google Scholar

OpenURL Placeholder Text

 
Font-Ribera
A.
et al. , 
J. Cosmol. Astropart. Phys.
,
2012
, vol.
11
pg.
59
Crossref
Search ADS
 
Furlanetto
S. R.
Zaldarriaga
M.
and Hernquist
L.
, 
ApJ
,
2004
, vol.
613
pg.
16
Crossref
Search ADS
 
Gavrila
M.
, 
Phys. Rev.
,
1967
, vol.
163
pg.
147
Crossref
Search ADS
 
Gnedin
N. Y.
, 
ApJ
,
2000
, vol.
535
pg.
530
Crossref
Search ADS
 
Gnedin
N. Y.
Fan
X.
, 
ApJ
,
2006
, vol.
648
pg.
1
Crossref
Search ADS
 
Gnedin
N. Y.
Kaurov
A. A.
, 
ApJ
,
2014
, vol.
793
pg.
30
Crossref
Search ADS
 
Gnedin
N. Y.
Ostriker
J. P.
, 
ApJ
,
1997
, vol.
486
pg.
581
Crossref
Search ADS
 
Gunn
J. E.
Peterson
B. A.
, 
ApJ
,
1965
, vol.
142
pg.
1633
Crossref
Search ADS
 
Haiman
Z.
Loeb
A.
, 
ApJ
,
1997
, vol.
483
pg.
21
Crossref
Search ADS
 
Haiman
Z.
Loeb
A.
, 
ApJ
,
1998
, vol.
503
pg.
505
Crossref
Search ADS
 
Haiman
Z.
Loeb
A.
, 
ApJ
,
1999
, vol.
519
pg.
497
Crossref
Search ADS
 
Heitler
W.
, 
Quantum Theory of Radiation
,
1954
Oxford
Oxford Univ. Press

Google Scholar

OpenURL Placeholder Text

 
Hinshaw
G.
et al. , 
ApJS
,
2009
, vol.
180
pg.
225
Crossref
Search ADS
 
Iliev
I. T.
Mellema
G.
Pen
U.-L.
Merz
H.
Shapiro
P. R.
Alvarez
M. A.
, 
MNRAS
,
2006
, vol.
369
pg.
1625
Crossref
Search ADS
 
Iliev
I. T.
Mellema
G.
Ahn
K.
Shapiro
P. R.
Mao
Yi
Pen
U.-L
, 
MNRAS
,
2014
, vol.
439
pg.
725
Crossref
Search ADS
 
Jiang
L.
et al. , 
Nature
,
2010
, vol.
464
pg.
380
Crossref
Search ADS
PubMed
 
Karzas
W. J.
Latter
R.
, 
ApJS
,
1961
, vol.
6
pg.
167
Crossref
Search ADS
 
Kawai
N.
et al. , 
Nature
,
2006
, vol.
440
pg.
184
Crossref
Search ADS
PubMed
 
Kramers
H. A.
Heisenberg
W.
, 
Z. Phys.
,
1925
, vol.
31
pg.
681
Crossref
Search ADS
 
Lazzati
D.
Ghisellini
G.
Celotti
A.
Rees
M. J.
, 
ApJ
,
2000
, vol.
529
pg.
17
Crossref
Search ADS
 
Lee
H.-W.
, 
ApJ
,
2003
, vol.
594
pg.
637
Crossref
Search ADS
 
Lee
H.-W.
, 
ApJ
,
2013
, vol.
772
pg.
123
Crossref
Search ADS
 
Loeb
A.
Barkana
R.
, 
ARA&A
,
2001
, vol.
39
pg.
19
Crossref
Search ADS
 
Loeb
A.
Rybicki
G. B.
, 
ApJ
,
1999
, vol.
524
pg.
L527
Crossref
Search ADS
 
McQuinn
M.
Furlanetto
S. R.
Hernquist
L.
Zahn
O.
Zaldarriaga
M.
, 
ApJ
,
2006
, vol.
653
pg.
815
Crossref
Search ADS
 
Madau
P.
Rees
M. J.
, 
ApJ
,
2000
, vol.
542
pg.
L69
Crossref
Search ADS
 
Madau
P.
Haardt
F.
Rees
M. J.
, 
ApJ
,
1999
, vol.
514
pg.
648
Crossref
Search ADS
 
Mesinger
A.
Haiman
Z.
, 
ApJ
,
2004
, vol.
611
pg.
L69
Crossref
Search ADS
 
Miralda-Escudé
J.
, 
ApJ
,
1998
, vol.
501
pg.
15
Crossref
Search ADS
 
Miralda-Escudé
J.
Haehnelt
M.
Rees
M. J.
, 
ApJ
,
2000
, vol.
530
pg.
1
Crossref
Search ADS
 
Morales
M. F.
Wyithe
S.
, 
ARA&A
,
2010
, vol.
48
pg.
127
Crossref
Search ADS
 
Mortlock
D. J.
et al. , 
Nature
,
2011
, vol.
474
pg.
616
Crossref
Search ADS
PubMed
 
Noterdaeme
P.
et al. , 
A&A
,
2012
, vol.
547
pg.
L1
Crossref
Search ADS
 
Noterdaeme
P.
Petitjean
P.
Paris
I.
Cai
Z.
Finley
H.
Ge
J.
Pieri
M. M.
York
D. G.
, 
A&A
,
2014
, vol.
566
pg.
24
Crossref
Search ADS
 
Outram
P. J.
Carswell
R. F.
Theuns
T.
, 
ApJ
,
2000
, vol.
529
pg.
L73
Crossref
Search ADS
 
Peebles
P. J. E.
, 
Principles of Physical Cosmology
,
1993
Princeton, NJ
Princeton Univ. Press

Google Scholar

OpenURL Placeholder Text

 
Peroux
C.
Dessauges-Zavadsky
M.
D'Odorico
S.
Sun
K. T.
McMahon
R. G.
, 
MNRAS
,
2005
, vol.
363
pg.
479
Crossref
Search ADS
 
Razoumov
A. O.
Norman
M. L.
Abel
T.
Scott
D.
, 
ApJ
,
2002
, vol.
572
pg.
695
Crossref
Search ADS
 
Rhee
J.
Zwaan
M. A.
Briggs
F. H.
Chengalur
J. N.
Lah
P.
Oosterloo
T.
van der Hulst
T.
, 
MNRAS
,
2013
, vol.
435
pg.
2693
Crossref
Search ADS
 
Robertson
B. E.
Ellis
R. S.
, 
ApJ
,
2012
, vol.
744
pg.
95
Crossref
Search ADS
 
Sakurai
J. J.
, 
Advanced Quantum Mechanics
,
1967
Reading, MA
Addison-Wesley

Google Scholar

OpenURL Placeholder Text

 
Saslow
W. M.
Mills
D. L.
, 
ApJ
,
1969
, vol.
187
pg.
1025
 
Scheuer
P. A. G.
, 
Nature
,
1965
, vol.
207
pg.
963
Crossref
Search ADS
 
Sobacchi
E.
Mesinger
A.
, 
MNRAS
,
2014
, vol.
440
pg.
1662
Crossref
Search ADS
 
Sokasian
A.
Abel
T.
Hernquist
L.
, 
MNRAS
,
2002
, vol.
332
pg.
601
Crossref
Search ADS
 
Tegmark
M.
Silk
J.
Evrard
A.
, 
ApJ
,
1993
, vol.
417
pg.
54
Crossref
Search ADS
 
Trac
H.
Cen
R.
, 
ApJ
,
2007
, vol.
671
pg.
1
Crossref
Search ADS
 
Tytler
D.
, 
Nature
,
1981
, vol.
291
pg.
289
Crossref
Search ADS
 
Valageas
P.
Silk
J.
, 
A&A
,
1999
, vol.
347
pg.
1
 
Valageas
P.
Silk
J.
Schaeffer
R.
, 
A&A
,
2001
, vol.
366
pg.
363
Crossref
Search ADS
 
Weisskopf
V. F. I.
, 
Observatory
,
1933
, vol.
56
pg.
291
 
Weisskopf
V. F. I.
Wigner
E.
, 
Z. Phys.
,
1930
, vol.
63
pg.
54
Crossref
Search ADS
 
Wolfe
A. M.
Gawiser
E.
Prochaska
J. X.
, 
ARA&A
,
2005
, vol.
43
pg.
861
Crossref
Search ADS
 
Wyithe
S.
Loeb
A.
, 
ApJ
,
2003
, vol.
586
pg.
693
Crossref
Search ADS
 
Wyithe
J. S. B.
Loeb
A.
, 
MNRAS
,
2007
, vol.
375
pg.
1034
Crossref
Search ADS
 
Zafar
T.
Péroux
C.
Popping
A.
Milliard
B.
Deharveng
J.-M.
Frank
S.
, 
A&A
,
2013
, vol.
556
pg.
141
Crossref
Search ADS
 
© 2014 The Authors Published by Oxford University Press on behalf of the Royal Astronomical Society
Issue Section:
Article
Download all slides