-
PDF
- Split View
-
Views
-
Cite
Cite
Christopher E. Moody, Aaron J. Romanowsky, Thomas J. Cox, G. S. Novak, Joel R. Primack, Simulating multiple merger pathways to the central kinematics of early-type galaxies, Monthly Notices of the Royal Astronomical Society, Volume 444, Issue 2, 21 October 2014, Pages 1475–1485, https://doi.org/10.1093/mnras/stu1444
Close - Share Icon Share
Two-dimensional integral field surveys such as ATLAS3D are producing rich observational data sets yielding insights into galaxy formation. These new kinematic observations have highlighted the need to understand the evolutionary mechanisms leading to a spectrum of fast rotators and slow rotators in early-type galaxies. We address the formation of slow and fast rotators through a series of controlled, comprehensive hydrodynamical simulations, sampling idealized galaxy merger scenarios constructed from model spiral galaxies. Idealized and controlled simulations of this sort complement the more ‘realistic’ cosmological simulations by isolating and analysing the effects of specific parameters, as we do in this paper. We recreate minor and major binary mergers, binary merger trees with multiple progenitors, and multiple sequential mergers. Within each of these categories of formation history, we correlate progenitor gas fraction, mass ratio, orbital pericentre, orbital ellipticity, and spin with remnant kinematic properties. We create kinematic profiles of these 95 simulations comparable to ATLAS3D data. By constructing remnant profiles of the projected specific angular momentum (|$\lambda _R= \langle R|V|\rangle / \langle R \sqrt{V^2+\sigma ^2}\rangle$|), triaxiality, and measuring the incidences of kinematic twists and kinematically decoupled cores, we distinguish between varying formation scenarios. We find that binary mergers nearly always form fast rotators. Slow rotators can be formed from zero initial angular momentum configurations and gas-poor mergers, but are not as round as the ATLAS3D galaxies. Remnants of binary merger trees are triaxial slow rotators. Sequential mergers form round slow rotators that most resemble the ATLAS3D rotators.
1 INTRODUCTION
Measurements of the kinematics of early-type galaxies (ETGs, ellipticals and lenticulars) have revealed novel properties otherwise undetected by photometry. The earliest kinematic measurements of ETGs hinted towards a new classification: some galaxies rotated slowly and supported their flattened shapes by anisotropy in the velocity dispersion tensor, whereas others were supported by more rapid rotation (Illingworth 1977; Davies et al. 1983; Binney 1985, 2005). These dynamical differences were found to correlate with photometric properties such as isophote shape (boxy or discy), central luminosity profile (cored or coreless), and total luminosity (Bender 1988; Bender, Doebereiner & Moellenhoff 1988; Kormendy & Bender 1996; Faber et al. 1997). It was therefore suggested that ETGs consisted of two fundamentally different classes of object, with distinct formation mechanisms.
This emerging picture of ETGs was codified with the advent of the SAURON integral-field spectrograph (Bacon et al. 2001) and its eventual application to a large, volume-limited sample of nearby galaxies, ATLAS3D (Cappellari et al. 2011). This work has focused on robust quantification of the stellar specific angular momentum within an effective radius (Re, enclosing half of the projected light), and has shown that ETGs separate cleanly into two populations: the ‘fast’ and ‘slow’ rotators (Emsellem et al. 2007, 2011). Fast rotators are by far the most common overall (86 per舁cent of the sample) and tend to have regular velocity fields indicative of disc-like, oblate-axisymmetric structure (Krajnovic et al. 2011). Slow rotators are dominant among the most luminous ETGs, while hosting kinematically distinct regions, counter rotating cores, and generally more complex velocity fields that imply a somewhat triaxial structure with all three axes unequal.
The fast–slow rotator dichotomy has been proposed as a replacement for traditional morphology-based classifications of ETGs (Emsellem et al. 2011), raising concerns that focusing on the central data provides a biased view (Foster et al. 2013; Arnold et al. 2014). Nonetheless, it is now a key goal to decipher the formational pathways for the different kinematical subtypes, and to connect them with the overall quest to understand the assembly of the red sequence of galaxies (e.g. De Lucia et al. 2006; Faber et al. 2007; Khochfar et al. 2011).
The vast majority of theoretical work on ETG kinematics has focused on the classic framework of binary major mergers: the collision of two comparable-mass spiral galaxies. Violent relaxation in the merger leads to spheroidal structure in the remnant, along with destruction of the initial kinematic patterns. However, significant rotation can be retained – from residual disc structure, from orbital angular momentum transfer, and from re-formation of a disc out of any lingering cold gas. It is thus relatively easy to simulate the formation of major-merger remnants resembling fast rotators (Naab, Burkert & Hernquist 1999; Bendo & Barnes 2000; Cox et al. 2006b), with the merger parameters potentially being diagnosed through more detailed kinematic information (Cretton et al. 2001; Naab & Burkert 2001; González-García, Balcells & Olshevsky 2006; Bournaud, Jog & Combes 2007; Hoffman et al. 2009).
Slow rotators, on the other hand, have been much more challenging to reproduce in simulations. With gas-poor (‘dry’) conditions and near-head-on collisions, it is possible to end up with little net rotation, but such remnants are also more elongated, discy, and internally anisotropic than the observed slow rotators (Naab & Burkert 2003; Cox et al. 2006b; Jesseit et al. 2009; Burkert et al. 2008; Bois et al. 2011; Naab et al. 2014). In cosmological contexts, simulations of dry mergers in groups predominantly yield slowly rotating (v/σ < 0.1) and flattened (ϵ > 0.2) remnants (Taranu, Dubinski & Yee 2013).
An encouraging alternative to the major-merger dead-end has recently emerged from hydrodynamical simulations of galaxy formation in a full cosmological context (Naab et al. 2007). These simulations formed massive spheroidal galaxies through multiple mergers, particularly with very uneven mass ratios (minor mergers). This scenario is now widely considered as the most likely route to forming the most massive ellipticals, owing in particular to size evolution considerations (Bezanson et al. 2009; Naab, Johansson & Ostriker 2009; Oser et al. 2012). Remarkably, the Naab et al. simulations naturally reproduce the detailed central properties of slow rotators – not only in their kinematics but also in their round, isotropic structure (Burkert et al. 2008, with similar hints in González-García et al. 2009). This outcome is presumably linked to random infall directions for the multiple mergers (Vitvitska et al. 2002; Hetznecker & Burkert 2006; Romanowsky & Fall 2012), but the driving mechanisms have not actually been isolated, for example with an understanding of the relative impacts of major and minor mergers. Also, although there is a rich history of dedicated simulations of multiple and minor mergers (e.g. Barnes 1985; Weil & Hernquist 1996; Bekki 2001; Bournaud et al. 2007), none of them has directly engaged with the recent observational constraints on slow, round rotators.
Our paper fills in these missing links by carrying out a suite of controlled merger simulations that is unprecedented in scope, including both major and minor mergers, in both binary and multiple configurations. By comparing the merger remnant properties to observational trends from ATLAS3D, we hope to systematically identify plausible pathways to forming both fast- and slow-rotating ETGs.
The outline of this paper is as follows. Section 2 describes the merger simulations, including their initial conditions and parameter space setup. Section 3 presents the analysis methodology, keeping in mind direct comparisons to observational efforts. Section 4 presents correlations with the initial conditions, including orbital parameters and progenitor properties, to their locations on the λR–ϵ and λR–T diagrams. Section 5 makes a similar set of analyses, but instead of correlating to λR–ϵ we attempt to find specific initial conditions leading to kinematically decoupled cores (KDCs) and kinematic twists (KTs). In Section 6, we summarize our findings.
2 MERGER SIMULATIONS
Our analysis will focus on 95 simulated remnants of galactic mergers, covering a wide variety of initial conditions as will be discussed below. Many aspects of the simulations and the remnants were detailed in Cox et al. (2004, 2006b, 2008), with the novelties here including an extension to multiple merger histories (initially discussed in Novak 2008) and an expanded kinematics analysis.
In brief, the simulations use the numerical N-body/smoothed particle hydrodynamics (SPH) code gadget (Springel, Yoshida & White 2001) with entropy conservation enabled. Star and dark matter particles are collisionless and subject only to gravitational forces, while gas particles also experience hydrodynamical forces. The gravitational softening lengths for stars and dark matter are 100 and 400 pc, respectively, while for the gas, the SPH smoothing length is required to be greater than 50 pc. Gas particles are transformed into star particles following the observed rates between gas and star formation rate surface densities. The gas has a ‘stiff’ equation of state where the pressure is proportional to the square of the density. The star formation begins above a density threshold of 0.0171 M⊙ pc−3 with an efficiency of 3 per cent. Feedback from supernovae is also included, and acts to pressurize the interstellar medium and regulate star formation; it is implemented as a gradual transfer of turbulent energy to thermal pressure support on 8 Myr time-scales. The details of these recipes can be found in Cox et al. (2006a, table 1 in particular). An active galactic nucleus is not included.
Simulations of binary mergers under a variety of initial conditions have not generally found a prescription to create slow and round rotators. As a result, we experiment with two types of multiple merger histories. These simulations are not designed to have realistic merger histories, in contrast to formation histories that semi-analytic models or cosmological simulations might produce. Instead, these cases are idealized, featuring progenitors modelled after local galaxies but with varying initial positions. Progenitor spin orientations are randomly chosen over the unit sphere, and eccentricities are chosen between 1.0 and 0.95. Binary merger trees feature progenitors that build mass exclusively in repeated, equal-mass mergers. While binary merger tree simulations test a formation history of extended major merging, sequential mergers remnants are formed from decreasing mass ratio mergers. Sequential mergers start with an initial merger equal in mass, but as the remnant builds up mass, subsequent identical mergers become increasingly more minor. Both scenarios are simulated with three initial pericentres of 1.5, 3.0, and 6.0舁kpc, keeping in mind that higher pericentres correspond to increased initial orbital angular momentum. While the magnitude of the orbital angular momentum is systemically varied, the progenitors’ angular momenta orientations are randomized, and thus the relation between the internal angular momentum and the initial angular momentum is obscured. Instead, we focus on the effect of increasing the number of progenitors and varying the merging scheme.
In all of our simulations, we use 12 unique spiral galaxies as the building blocks and construct varying formation histories. Each progenitor galaxy is composed of a disc of stars and gas, a stellar bulge, and a dark matter halo. We base the galaxies on isolated low-redshift systems, rather than attempting to evolve them from initial cosmological conditions. Table 1 summarizes the progenitor properties. ‘G’ series galaxies are designed to replicate the properties of observed local galaxies in the Sloan Digital Sky survey, and cover a range of masses, gas fractions, and bulge-to-disc ratios. ‘Sbc’ series galaxies are modelled after local Sbc-type spirals with small bulges and high gas fractions, and cover less variation in galaxy parameters than the G series, but a larger variety of orbits. The number of collisionless particles per galaxy ranges from 40 000 (G0) to 190 000 (G3), and the dark matter particle masses range from 1.7 × 106 to 9.7 × 106舁M⊙, and the star particle masses from 2 × 104 to 1.3 × 106舁M⊙. There are 10 000–50 000 gas particles per galaxy, with particle masses from 6 × 104 to 1.8 × 106舁M⊙.
Progenitor galaxy properties, grouped by series. Mtot represents the total gas, stellar, and dark matter mass. Mbaryon is the sum of gas and stellar masses. fgas is the mass of stars divided by the total baryon mass. B/D is the initial stellar bulge-to-disc ratio. R1/2 is half-mass radius of the progenitor galaxy.
| Type . | Mtot . | Mbaryon . | fgas . | B/D . | R1/2 . |
|---|---|---|---|---|---|
| . | (1010舁M⊙) . | (1010舁M⊙) . | . | . | (kpc) . |
| Sbc series | |||||
| Sbc | 91 | 10.28 | 0.52 | 0.26 | 7.15 |
| G series | |||||
| G0 | 5 | 0.44 | 0.38 | 0.02 | 1.84 |
| G1 | 20 | 0.70 | 0.29 | 0.06 | 2.33 |
| G2 | 51 | 2.00 | 0.23 | 0.11 | 2.90 |
| G3 | 116 | 6.20 | 0.20 | 0.22 | 3.90 |
| G3 gas fraction series | |||||
| G3gf1 | 116 | 3.09 | 0.43 | 0.32 | 3.49 |
| G3gf2 | 116 | 4.18 | 0.58 | 0.52 | 2.89 |
| G3gf3 | 116 | 5.40 | 0.76 | 1.34 | 1.77 |
| G3gf4 | 116 | 0.68 | 0.10 | 0.20 | 3.96 |
| Type . | Mtot . | Mbaryon . | fgas . | B/D . | R1/2 . |
|---|---|---|---|---|---|
| . | (1010舁M⊙) . | (1010舁M⊙) . | . | . | (kpc) . |
| Sbc series | |||||
| Sbc | 91 | 10.28 | 0.52 | 0.26 | 7.15 |
| G series | |||||
| G0 | 5 | 0.44 | 0.38 | 0.02 | 1.84 |
| G1 | 20 | 0.70 | 0.29 | 0.06 | 2.33 |
| G2 | 51 | 2.00 | 0.23 | 0.11 | 2.90 |
| G3 | 116 | 6.20 | 0.20 | 0.22 | 3.90 |
| G3 gas fraction series | |||||
| G3gf1 | 116 | 3.09 | 0.43 | 0.32 | 3.49 |
| G3gf2 | 116 | 4.18 | 0.58 | 0.52 | 2.89 |
| G3gf3 | 116 | 5.40 | 0.76 | 1.34 | 1.77 |
| G3gf4 | 116 | 0.68 | 0.10 | 0.20 | 3.96 |
Progenitor galaxy properties, grouped by series. Mtot represents the total gas, stellar, and dark matter mass. Mbaryon is the sum of gas and stellar masses. fgas is the mass of stars divided by the total baryon mass. B/D is the initial stellar bulge-to-disc ratio. R1/2 is half-mass radius of the progenitor galaxy.
| Type . | Mtot . | Mbaryon . | fgas . | B/D . | R1/2 . |
|---|---|---|---|---|---|
| . | (1010舁M⊙) . | (1010舁M⊙) . | . | . | (kpc) . |
| Sbc series | |||||
| Sbc | 91 | 10.28 | 0.52 | 0.26 | 7.15 |
| G series | |||||
| G0 | 5 | 0.44 | 0.38 | 0.02 | 1.84 |
| G1 | 20 | 0.70 | 0.29 | 0.06 | 2.33 |
| G2 | 51 | 2.00 | 0.23 | 0.11 | 2.90 |
| G3 | 116 | 6.20 | 0.20 | 0.22 | 3.90 |
| G3 gas fraction series | |||||
| G3gf1 | 116 | 3.09 | 0.43 | 0.32 | 3.49 |
| G3gf2 | 116 | 4.18 | 0.58 | 0.52 | 2.89 |
| G3gf3 | 116 | 5.40 | 0.76 | 1.34 | 1.77 |
| G3gf4 | 116 | 0.68 | 0.10 | 0.20 | 3.96 |
| Type . | Mtot . | Mbaryon . | fgas . | B/D . | R1/2 . |
|---|---|---|---|---|---|
| . | (1010舁M⊙) . | (1010舁M⊙) . | . | . | (kpc) . |
| Sbc series | |||||
| Sbc | 91 | 10.28 | 0.52 | 0.26 | 7.15 |
| G series | |||||
| G0 | 5 | 0.44 | 0.38 | 0.02 | 1.84 |
| G1 | 20 | 0.70 | 0.29 | 0.06 | 2.33 |
| G2 | 51 | 2.00 | 0.23 | 0.11 | 2.90 |
| G3 | 116 | 6.20 | 0.20 | 0.22 | 3.90 |
| G3 gas fraction series | |||||
| G3gf1 | 116 | 3.09 | 0.43 | 0.32 | 3.49 |
| G3gf2 | 116 | 4.18 | 0.58 | 0.52 | 2.89 |
| G3gf3 | 116 | 5.40 | 0.76 | 1.34 | 1.77 |
| G3gf4 | 116 | 0.68 | 0.10 | 0.20 | 3.96 |
Using the library of model progenitors, we construct binary and multiple mergers. The binary mergers have a range of stellar mass ratios of 1.6–8.9 (total mass ratios of 2.3–10.2). We define major and minor mergers as those with stellar mass ratios less than and greater than 3.0, respectively. By varying the orbital eccentricity, pericentre, and orbital orientations, we generate multiple initial conditions for each pair of identical galaxies. These parameters are presented in more detail in table 2 of Covington (2008); they are motivated by orbits in a cosmological context (Khochfar & Burkert 2006) but are not designed to be a statistical ensemble.
We label each merger case according to the progenitor type, followed by a string identifying the unique initial conditions for the simulation. For example, G3G1R is a binary minor merger between the most massive G3 galaxy and the third-most massive galaxy G1, with the minor galaxy having a retrograde spin. ‘Sbc’ galaxy simulations are always equal-mass mergers with two identical Sbc galaxies, and so for brevity we drop the second ‘Sbc’ from the label.
We define major mergers as approximately equal-mass mergers of identical progenitor galaxies, and minor mergers as being between any two distinct galaxies with a mass ratio of more than 3:1.
sequential histories that grow by mergers of four or eight identical progenitors,
binary merger tree histories that grow by successive 1:1 mergers. This models the growth of a galaxy exclusively through multiple major mergers.
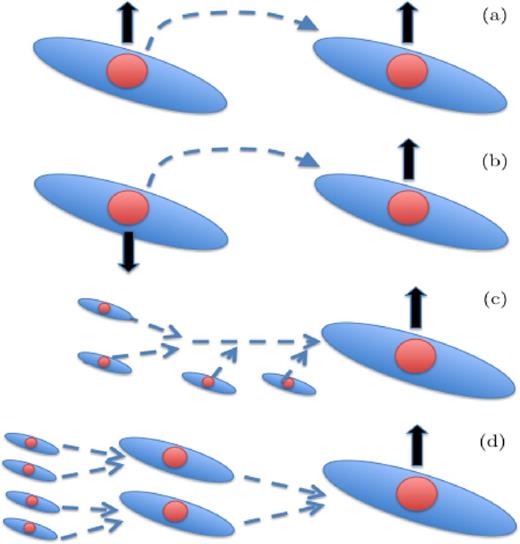
A schematic of the varying orbital orientations and initial conditions of the merger simulations. In all cases, the orbital angular momentum is oriented such that it points upwards. Shown are (a) a prograde–prograde binary merger with the spin of both galaxies aligned, (b) a prograde–retrograde binary merger, (c) a series of sequential mergers, and (d) a binary merger tree simulation with each generation of galaxies equal in mass.
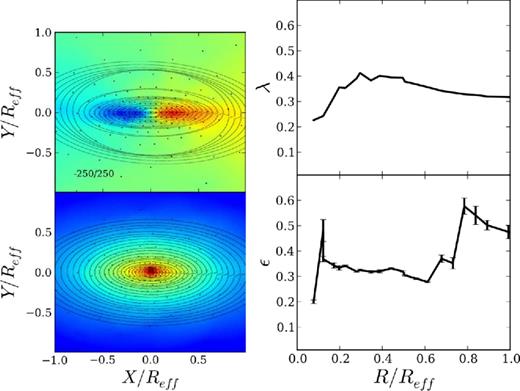
The edge-on (top left) LOS velocity and (bottom left) density of the fiducial remnant, SbcPP. The λR parameter versus radius is shown in the top right and the ellipticity of the kinemetric ellipses is shown in the bottom right. Black dots are the Voronoi centroids that ensure a minimum signal-to-noise ratio. As an example, the kinemetric and photometric best-fitting ellipses are overlaid.
The multiple mergers are always constructed from a set of initially identical galaxies, so the labelling (Table 2) simply indicates the number and initial orientations. In such a case, G2-8s-1 indicates that eight G2 galaxies merged sequentially with pericentres of 1.0 kpc. In all cases, the progenitors accrete isotropically and at a regular time interval on to the larger galaxy.
| Name . | Pericentre . | Number of . | Number of . |
|---|---|---|---|
| . | (kpc) . | G2 progenitors . | G1 progenitors . |
| Sequential series | |||
| G1-8s | 3.0 | 0 | 8 |
| G1-8s-1 | 1.5 | 0 | 8 |
| G1-8s-3 | 6.0 | 0 | 8 |
| G2-4s | 3.0 | 4 | 0 |
| G2-4s-1 | 1.5 | 4 | 0 |
| G2-4s-3 | 6.0 | 4 | 0 |
| Binary merger tree series | |||
| G1-8b | 3.0 | 0 | 8 |
| G1-8b-1 | 1.5 | 0 | 8 |
| G1-8b-3 | 6.0 | 0 | 8 |
| G2-4b | 3.0 | 4 | 0 |
| G2-4b-1 | 1.5 | 4 | 0 |
| G2-4b-3 | 6.0 | 4 | 0 |
| Name . | Pericentre . | Number of . | Number of . |
|---|---|---|---|
| . | (kpc) . | G2 progenitors . | G1 progenitors . |
| Sequential series | |||
| G1-8s | 3.0 | 0 | 8 |
| G1-8s-1 | 1.5 | 0 | 8 |
| G1-8s-3 | 6.0 | 0 | 8 |
| G2-4s | 3.0 | 4 | 0 |
| G2-4s-1 | 1.5 | 4 | 0 |
| G2-4s-3 | 6.0 | 4 | 0 |
| Binary merger tree series | |||
| G1-8b | 3.0 | 0 | 8 |
| G1-8b-1 | 1.5 | 0 | 8 |
| G1-8b-3 | 6.0 | 0 | 8 |
| G2-4b | 3.0 | 4 | 0 |
| G2-4b-1 | 1.5 | 4 | 0 |
| G2-4b-3 | 6.0 | 4 | 0 |
| Name . | Pericentre . | Number of . | Number of . |
|---|---|---|---|
| . | (kpc) . | G2 progenitors . | G1 progenitors . |
| Sequential series | |||
| G1-8s | 3.0 | 0 | 8 |
| G1-8s-1 | 1.5 | 0 | 8 |
| G1-8s-3 | 6.0 | 0 | 8 |
| G2-4s | 3.0 | 4 | 0 |
| G2-4s-1 | 1.5 | 4 | 0 |
| G2-4s-3 | 6.0 | 4 | 0 |
| Binary merger tree series | |||
| G1-8b | 3.0 | 0 | 8 |
| G1-8b-1 | 1.5 | 0 | 8 |
| G1-8b-3 | 6.0 | 0 | 8 |
| G2-4b | 3.0 | 4 | 0 |
| G2-4b-1 | 1.5 | 4 | 0 |
| G2-4b-3 | 6.0 | 4 | 0 |
| Name . | Pericentre . | Number of . | Number of . |
|---|---|---|---|
| . | (kpc) . | G2 progenitors . | G1 progenitors . |
| Sequential series | |||
| G1-8s | 3.0 | 0 | 8 |
| G1-8s-1 | 1.5 | 0 | 8 |
| G1-8s-3 | 6.0 | 0 | 8 |
| G2-4s | 3.0 | 4 | 0 |
| G2-4s-1 | 1.5 | 4 | 0 |
| G2-4s-3 | 6.0 | 4 | 0 |
| Binary merger tree series | |||
| G1-8b | 3.0 | 0 | 8 |
| G1-8b-1 | 1.5 | 0 | 8 |
| G1-8b-3 | 6.0 | 0 | 8 |
| G2-4b | 3.0 | 4 | 0 |
| G2-4b-1 | 1.5 | 4 | 0 |
| G2-4b-3 | 6.0 | 4 | 0 |
3 MERGER REMNANT ANALYSIS
The lower limit for this angular momentum metric is λR = 0, which could correspond to a purely-pressure-supported system with no rotation, or to a system where the angular momentum vector is exactly along the LOS so the rotation is not observable. The upper limit is λR = 1 for pure rotation in a dynamically cold disc. The rough boundary between slow and fast rotators is λR ∼ 0.1, with a more precise diagnostic to be discussed in Section 4.
As the first step in calculating λR, for every merger remnant we project the stellar component, including both the initial stars and those formed during the course of the simulation. We use 128 viewing angles randomly chosen on a sphere. Once projected, we bin particles in two spatial dimensions with sides of ≈0.03Re. We then use an adaptive Voronoi binning software to ensure that a minimum of |$\sqrt{N}\ge 20$| particles are enclosed in each bin (Cappellari & Copin 2003). This binning scheme combines nearby bins with few particles to create an aggregate bin with a higher signal-to-noise ratio, while keeping the region as compact and as uniform as possible. This adaptive binning is particularly useful beyond 0.5Re, where the number of particles per bin falls quickly. The centroid of each Voronoi bin is then assigned values of Mi, Vi, and σi. We assume that these quantities are Poisson distributed, and assign uncertainties proportional to the enclosed number of particles, |$\sqrt{N}$|.
Given these Voronoi bins, we could proceed to calculate λR as in equation (1). However, there is a complication that estimates of λR can be biased high from small-scale fluctuations in numerical simulations, since only the absolute value of V contributes to the calculation. As emphasized by Bois et al. (2010), this problem can lead to slow rotators being misclassified as fast rotators. We address this problem by calculating λR from smoothed kinematic fields, whose construction will be discussed below. We find that with standard resolution, noise fluctuations do indeed drive up the values of λR by ≈0.1 (which would make slow–fast distinctions very problematic) while high-resolution cases are biased by only ≈0.01. Fortunately, the smoothed standard-resolution case turns out to have λR comparable to the high-resolution case, and we conclude that we can reliably identify slow rotators if present among our merger remnants.
We calculate multiple best-fitting ellipses for every projected density and velocity map, constraining the long axis of each ellipse to 25 logarithmically spaced values from 0 to 1.5Re, and fixing the centroid for each ellipse. From these ellipses we can calculate the position angle (PA) and ellipticity, ϵ, as a function of the projected ellipse radius. The ellipticity is defined as ϵ = 1 − b/a, so that a circle has ϵ = 0 and 1 is an infinitely elongated ellipse. The misalignment angle, Ψ is calculated as the difference between the photometric and kinematic ellipses, sin舁Ψ = |sin舁(PAkin − PAphot)|.
The λR–radius profile for a typical edge-on ETG starts at nearly zero at the centre where it is dispersion supported. As the dispersion support falls off with increasing radius, λ climbs roughly in proportion to V/σ, and ultimately plateaus (see Fig. 2), largely reflecting the rising rotation curve at larger radii. Barring KDCs, KTs, misalignments or other phenomena discussed later, face-on projections tend to show little rotational support and so have λR values closer to zero.
In Section 5, we discuss the correlation of triaxiality and projected ellipticities with λR. To quantify the shapes of merger remnants, we iteratively diagonalize the moment of inertia tensor using an ellipsoidal window (Novak et al. 2006). The eigenvectors of the tensor yield the ellipsoid axes which in turn can be used to calculate the three-dimensional triaxiality T = 1.0 − (a2 − b2)/(a2 − c2). Ellipsoids are oblate, triaxial, or prolate if T > 0.75, 0.25 ≤ T ≤ 0.75, or T < 0.25, respectively.
The majority of the kinematic maps are dominated by regular rotation, where |$\overline{k_5/k_1}$| tends to be smaller than 0.04. For the rest of the maps, we adopt the kinematic classification scheme of Krajnovic et al. (2011) and find the rate of KTs and KDCs in each LOS velocity map. KTs are defined to smoothly change by at least 10° in PAkin over the whole map. KDCs are defined by abrupt changes in PAkin of at least 30° in a region of zero velocity.
4 PARAMETER STUDY OF REMNANT PROPERTIES
The second diagnostic is based on the galaxies’ observed non-uniform occupancy of the λR–ϵ plane (see first panel of Fig. 3). The fast rotators occupy a characteristic quasi-diagonal region that is understood to trace a relatively homologous family of near-oblate rotators at random viewing angles. We will not discuss this distribution in further detail since fast rotators are not the primary focus of this paper. The slow rotators are generally very round, with almost all of them having ϵ ≲ 0.35. This is a fundamental and challenging constraint for formation models of these galaxies, which may be better called ‘round slow rotators’.

Diagnostic plot of central specific angular momentum versus ellipticity for ETGs, where the dashed curve separates fast and slow rotators. The top panel shows the observations from ATLAS3D. The bottom panel shows simulated merger remnants where each point represents a different case (generally classified according to the legend). The point location is given by the median λR over many projection angles, and the corresponding ellipticity, ϵ for that point. All classes of binary mergers are generally consistent with the observed family of fast rotators, while only the sequential, multiple mergers match the observed round, slow rotators.
Here, it is important to recognize that it is not enough for the simulations to produce an occasional object with the right apparent properties, since for example, this can happen for a fast rotator viewed nearly face-on. The goal is for the ensemble of projections for a given set of merger simulations to resemble the ensemble of observations of slow rotators.
We now carry out a series of parameter studies, where we investigate systemically the effects of each parameter (among the progenitor properties and orbital variations) on the merger remnant in the λR–ϵ plane (other remnant properties will be discussed in the next section). A preview summary of the results is shown in the second panel of Fig. 3, where the median λR and the corresponding ϵ of each type of remnant has been evaluated over all projection angles and coloured by category of initial conditions. Many of the remnants reproduce broadly the properties of the fast rotators, while only a very limited subset match the observed round slow rotators.
We focus on quantifying and separating fast from slow rotators by making extensive use of the λR–ϵ diagnostic diagram. Tests of merger remnants show that λR is a robust indicator of the angular momentum content and that the confusion rate between a face-on fast rotator and a true slow rotator is small (Jesseit et al. 2009).
We begin with binary mergers, where our first parameter study is of the initial gas fraction fgas, using the G3 series of progenitors. Our fiducial case has fgas = 20 per舁cent, and we cover a range of 10–76 per舁cent. We also try a bulgeless version of G3, which is effectively a dry merger (fgas ∼ 0 per舁cent), with most of the available gas converted into stars before the merger even begins: although this case is not realistic, it provides a bracketing limit for isolating the effects of gas. The results are shown in Fig. 4, where each curved line encloses all projected values for a given simulation (colour coded as in the legend). We see that each remnant populates a characteristic diagonal region upwards to the right in λR–ϵ space. This is because a flattened, rotating system seen edge-on shows the maximum rotation and elongation, while more face-on projections reduce both observed quantities in a correlated fashion.
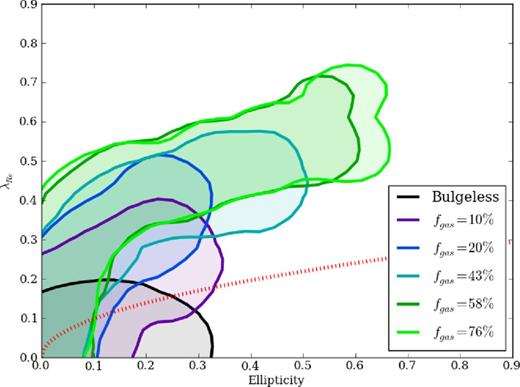
Central specific angular momentum versus ellipticity for simulated major-merger remnants, for a series of varying gas fraction. Here, each curve outlines all projections for a given simulation, colour coded as in the legend. Increasing the gas fraction yields faster rotators. In the simulation lacking a bulge, star formation in the progenitor is much higher than in the fiducial case prior to the merger event. The bulgeless case has an effective gas fraction of less than 10 per舁cent. Averaged over all viewing angles, the bulgeless case is rotating marginally faster than the ATLAS3D relation.
Marginalizing out the projection effects, we see that there is a systematic trend for remnants of increasing gas fractions to be faster and more elongated rotators. We conclude that the extra gas has the effect of funnelling angular momentum to inside the half-mass radius, increasing rotational support in the interior, and shrinking the semimajor axis of the remnant – which mirrors the results of Cox et al. (2006a). We note however that this effect could be weakened or even reversed if the gas were treated as clumpy and turbulent, and with earlier star formation, so that the merger became effectively collisionless (cf. Teyssier, Chapon & Bournaud 2010; Bournaud et al. 2011). The bulgeless case has 〈λR〉 = 0.15 and 〈ϵ〉 = 0.10, placing it marginally above the slow-rotator criterion. Therefore, the remnant is rotating just quickly enough to not be a slow rotator.
Next, we consider lower eccentricities of the merger orbits (e = 0.8 and 0.9 versus 1.0 for the fiducial case), at fixed pericentric distance, using SbcPP progenitors. The more circular orbits increase the initially available angular momentum and result in a more rapid merger, with less time for initial gas consumption and for the dark matter halo to absorb angular momentum. All of these effects (detailed in Cox et al. 2006b) lead to higher rotational support of the remnant, as shown in Fig. 5.
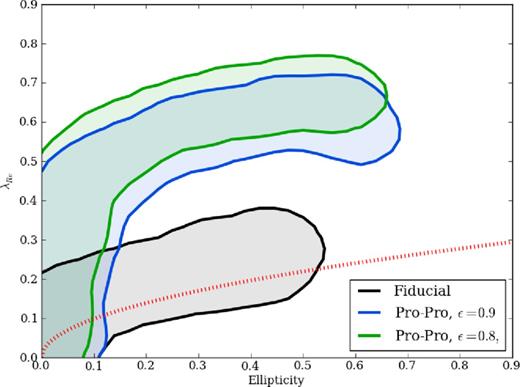
Same as Fig. 4, but with variations of the merger orbits to lower eccentricities. These lead to faster rotating remnants.
Next, we consider variations in initial disc spin directions, using Sbc progenitors. The fiducial case has all three angular momenta (orbital momenta, and the two progenitors’ spins) aligned. ‘Polar’ has both progenitors’ axes perpendicular to the orbital angular momentum. The ‘Polar−’ (‘Polar+’) case has a single progenitor rotated 90° such that angular momentum spin axis points away (towards) from the other progenitor. The results are shown in Fig. 6. The ‘Polar−’ case is of interest because its initial orbital and spin angular momenta are approximately equal, which yields a rounder and slower rotating remnant than the fiducial case. However, it is still too flattened and fast rotating (ϵ ≈ 0.3, 〈λR〉 ≈ 0.2) to match the observed slow rotators.
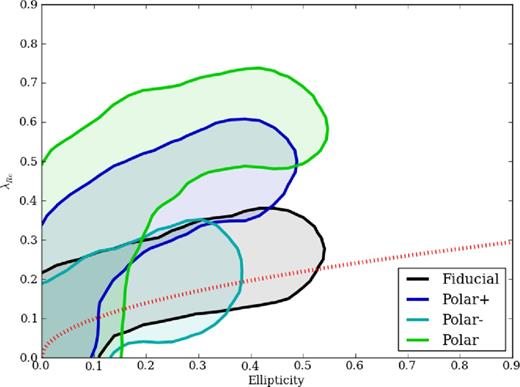
Same as Fig. 4, but showing varying polar orbits in Sbc-type galaxies. Polar orbits vary the orientation of the galactic angular momentum with respect to the orbital angular momentum axis. The ‘Polar−’ case minimizes by construction the angular momentum in any one axis. While some polar orbits do yield remnants that can be significantly as slowly rotating as the fiducial, these remnants are still far more elliptical than ATLAS3D slow rotators.
Variations in the initial orbital angular momentum case are shown in Fig. 7. The fiducial case labelled ‘r’ has the standard pericentre distance of 11 kpc for SbcPP, a prograde–prograde merger. This fiducial case is compared to a merger where the orbital angular momentum is fixed to negate the progenitor galaxies’ spin (labelled ‘L=0’), thereby constructing a system with nearly zero initial angular momentum. Compared to the fiducial case, the average λR of the ‘L=0’ remnant is halved, yielding a reduced λR of about 0.1. Evidently, a zero net initial orbital angular momentum leads to a rotator supported less by rotation than by dispersion. Averaged over all projections, the zero-angular-momentum case nominally qualifies as a slow rotator. However, the remnant is still highly elliptical (ϵ ≈ 0.4) and thus not a suitable analogue of ATLAS3D slow rotators. As the radial pericentre is increased, so the orbital angular momentum rises (L舁∝舁R2), and so does the amount of rotation in the final remnant. This increased rotation flattens the remnant slightly, with our example simulations increasing from maximum ϵ = 0.45 in the zero-angular-momentum case to a maximum ϵ = 0.55 in the fastest rotating remnant. The magnitude of the initial angular momentum does not appear to affect the ellipticity of the remnant significantly, a finding shared by Cox et al. (2006b) and Bois et al. (2010). So while the rotation of the remnant can certainly be reduced, a baseline flattening due to a dispersion anisotropy remains unchanged.

Same as Fig. 4, but showing initial conditions with varying total angular momenta (orbit + spin). As the initial orbital angular momentum is decreased, the rotational support of the remnant is similarly reduced. However, in all cases, the remnant is not as round as ATLAS3D slow rotators.
This last issue is the overall obstacle to forming the family of slow, round rotators with binary major mergers. Various effects can modify the rotation (or λR), where we note additionally that the coarse gas treatment in our simulations (stiff equation of state, and minimum resolution of 50 pc) could lead to an overprediction of the rotation (see Bois et al. 2010). However, none of these merger variations have been shown to produce galaxies that are round enough on average.
As it is more difficult for minor mergers to disrupt the properties of the larger progenitors, the variation in remnants of individual minor merging is much smaller and less dramatic than in major majors. The mergers shown in Fig. 8 are all retrograde, thereby containing less global angular momentum than the fiducial prograde case. As the merger ratio increases, the minor progenitor negates more of the available initial angular momentum. Since the rotation of the remnant depends on the merger ratio, with more massive progenitors (with smaller mass ratios) leading to higher λR and slightly more flattening. The effect is not dramatic, with λR, max varying from 0.5 to 0.7, and ϵ ranging from 0.4 to 0.6.

Same as Fig. 4, but showing binary minor-merger simulations varying both progenitor masses. Evidently, a single minor merger does not create a slow rotator. The merger ratios presented here range from 1:1.7, G1G0R in black, to 1:10, G3G2R in orange.
Fig. 9 shows the remnants of binary merger tree simulations, ranging from four progenitors merged in two rounds, to eight progenitors merged in three rounds of major merging. The remnants of all four-progenitor binary merger tree simulations are fast rotators, with most projections having |$\lambda _R>0.31\sqrt{\epsilon }$| and significant flattening. Increasing the number of progenitors to eight and thereby adding another round of merging yields remnants with largely the same λR but lower ϵ than remnants formed from two rounds of merging.
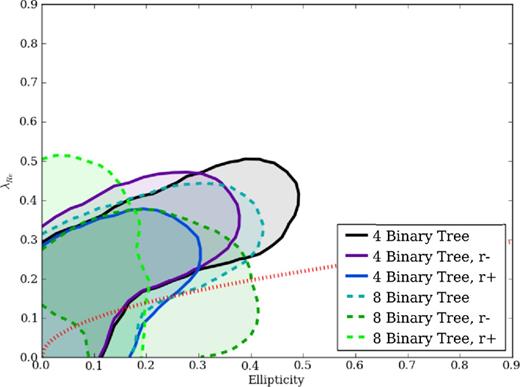
Same as Fig. 4, but showing binary merger tree simulations with either four or eight identical G1 or G2 progenitors. Simulations with four progenitors are shown in solid lines, otherwise eight-progenitor simulations are shown in dashed lines. Binary merger tree simulations of four (eight) progenitors occur in two (three) generations of binary equal-mass mergers. Increasing the number of progenitors in sequential simulations from four to eight yields still rounder and slower remnants, albeit not as slow and round as sequential merger remnants (see Fig. 10).
Using the Millenium Simulation and semi-analytic models, De Lucia et al. (2006) found that systems with stellar mass M* < 1011舁M⊙ formed from fewer than two massive progenitors, but rising to five progenitors for the most massive systems. In the ATLAS3D sample, these most massive systems are predominantly slow rotators, suggesting that multiple mergers may give rise to slow rotators. Simulations of multiple minor mergers demonstrate that a transformation from a spiral progenitor into an elliptical galaxy takes place when the cumulative mass added exceeds 30–40 per舁cent (Bournaud et al. 2007). With increasing numbers of mergers, the overall V/σ dropped and remnant systems became progressively more round. Nevertheless, remnants comparable to the ATLAS3D slow rotators were not found, and in this paper we test whether further merging would create a suitably slow remnant.
Fig. 10 shows the remnants of the sequential merging of four progenitors. Four-progenitor simulations yield remnants that are more slowly rotating than any binary merger in our suite. For this series, the mean λR varies from 0.03 to 0.12, with the mean ellipticity ranging from 0.1 to 0.2. Remnants of sequential merging are slower and rounder than those produced in binary tree merging. As in the binary merger tree case, doubling the number of progenitors does not decrease the ellipticity but does decrease the rotational support (i.e. the mean λR).

Same as Fig. 9, but showing multiple sequential merger simulations with either four or eight identical G1 or G2 progenitors. Sequential simulations begin with four or eight progenitors, and have a staggered formation history. In contrast to the binary merger tree simulations, the merger ratio decreases from the initial 1:1 value to 1:3 (1:7) in the four (eight) progenitor case. Increasing the number of progenitors in sequential simulations from four to eight yields still rounder and slower remnants. Remnants formed via sequential merging form slow and round rotators representative of the slow rotators found in the ATLAS3D observations.
In summary, compared with multiple mergers, binary mergers have fast rotator remnants with higher ellipticities and in general fall on the top right of the diagram. Individual minor-merger events keep much of the progenitor structure intact and preserve the high rotational velocities, and as a result are the fastest rotators in our sample. Remnants of major mergers have slightly less rotational support when compared to minor-merger remnants, and form the second-fastest rotators of our sample. Varying the gas fraction in progenitors does not produce any slow rotators, but does yield the largest range of both λR and ϵ values of any other category of mergers studied here. The poorest gas fraction simulation produces remnants with low λR and low ϵ, which is similar to simulations of dissipationless binary mergers (Cox et al. 2006b). The most gas-poor mergers result in slowly rotating but highly elongated systems. Variations in the pericentre distance or orbital ellipticities do not generate slow rotators, but does produce a spread of photometric ellipticities. Finally, multiple mergers lead to the slowest, roundest rotators. Binary merger tree simulations with either four or eight progenitors produce remnants that, while quite round, are much faster than sequential mergers. In the majority of projections, these remnants are above |$\lambda _R=0.31\sqrt{\epsilon }$| and thus classified as fast rotators.
Sequential mergers with eight progenitors produce slower and rounder remnants than four progenitors, which agrees with the current conventional wisdom that multiple minor mergers are the most likely mechanism for producing this class of galaxies (e.g., Khochfar et al. 2011). We note that our merging sequences do not extend fully into the minor-dominated merger regime that may be typical for massive galaxies in dense environments: our eight-progenitor merger mass ratio (both number weighted and mass weighted) is 1:2.7, while cosmological simulations suggest ∼ 1:10 (mass weighted) or ∼ 1:40 (number weighted) may be typical for this class of galaxies (Naab et al. 2014). Given the general trends from our controlled experiments, we expect that such mergers, if fairly isotropic, could produce even better agreement with the observed class of round, slow rotators – with our experiments perhaps representative of the first stages of their formation.
5 TRIAXIALITY AND TWISTS
In a series of simulations, Jesseit et al. (2009) showed that fast rotators tend to have lower triaxialities, and slow rotators have higher triaxialities. We revisit this question with knowledge of the initial merger conditions (see Figs 11 and 12). Binary mergers yield fast rotating but non-triaxial remnants. As demonstrated by Cox et al. (2006b), the triaxiality depends strongly on the initial orbital parameters of the progenitor disc galaxies, which leads to the scatter in triaxiality from 0.0–0.1 in our binary merger remnants. The two lowest gas fraction initial conditions are the only two binary merger remnants to attain high triaxialities. Sequential merger simulations on the other hand are generally triaxial and much more slowly rotating. Binary merger tree simulations yield mildly triaxial galaxies with T ranging from 0.1 to 0.3 for four progenitors and climbing to 0.2 to 0.5 for eight progenitors. Remnants of four sequential mergers have higher triaxiality than the binary tree mergers, and doubling the number does not appear to influence the shape of the remnant dramatically, while still decreasing the overall rotation.
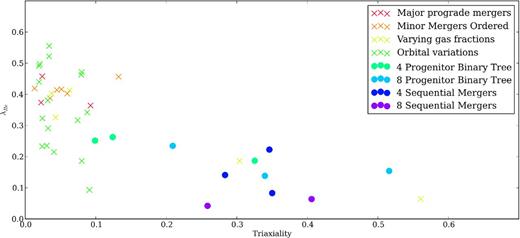
λR versus the triaxiality evaluated at 1.0 Re, and averaged over each projection of a simulation. As in Fig. 3, filled circles represent multiple merger simulations, and cross marks are binary major mergers. Multiple mergers tend to produce triaxial slow rotators while binary mergers lead to largely fast rotators with little triaxiality.
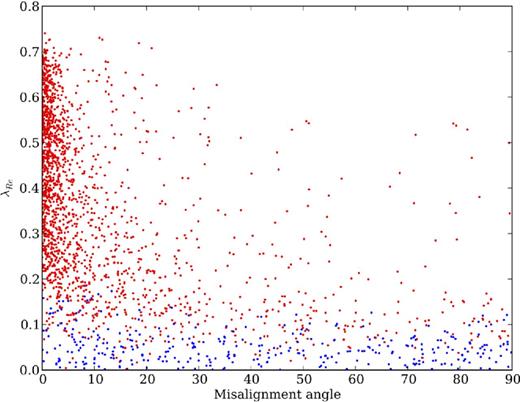
|$\lambda _{R_{\rm e}}$| and the kinematic misalignment evaluated at 1.0 Re shown for each projection for all simulations. Fast rotators, shown in red, satisfy |$\lambda _{R_{\rm e}} \ge 0.31\sqrt{\epsilon }$|; slow rotators are shown in blue. For readability, only 10 per舁cent of points are shown. Fast rotators tend to have highly coupled kinematic and photometric axes with misalignments typically less than 10°. Below λR = 0.1, most projections are slow rotators with no alignment between the kinematic and photometric axes, and hence have misalignments ranging from 0°to 90°.
In this section, we report the incidence of KTs and KDCs for various classes of mergers. While the majority of the projected LOS quantities display regular rotation characterized by a rotational velocity that climbs smoothly with radius, many kinematic maps have distorted features. To study how these features arise, we correlate the incidence of KTs and KDCs with the formation histories of the merger remnants.
Fig. 13 demonstrates that binary mergers typically have KTs in 10–20 per舁cent of projections, while multiple mergers produce higher probabilities of KTs. There are two exceptional binary mergers where the probability of finding a KT is ≈60 per舁cent. The first is a polar orbit where the angular momenta of the two progenitors are nearly equal in magnitude but perpendicular in direction, which yields a fast rotator with high incidence of KTs. Out of the full set of polar orbit set of simulations, this simulation maximizes the initial misalignment in orbital angular momenta, and has the maximum incidence of KTs in the remnant. The second binary merger with a high incidence of KTs occurs in a unique orbital variation where the orbits are initialized with a net angular momentum of zero. By construction, this forms a slowly rotating remnant with high incidence of KTs.
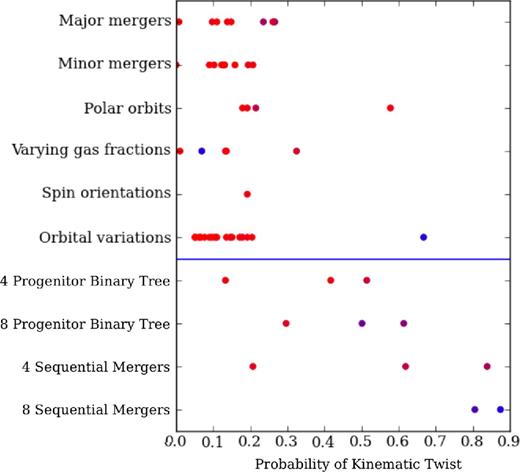
KTs are defined as a gradual change in the kinematic angle that changes by at least 10° over all radii. Points represent the probability of observing a KT in various categories of merger scenarios. Blue dots are shown for simulations which are predominantly slow rotators, while red are fast rotators. Roughly speaking, binary mergers typically have a 15 per舁cent chance of finding a KT. The two slow rotators formed in the binary mergers have dramatically different behaviours. The gas-poor slow rotator forms almost no KTs but the slow rotator formed with an orbital variation of zero initial angular momentum has a high (70 per舁cent) probability of finding a KT. Multiple merger simulations generally host KTs with much greater frequency than binary merger simulations, with sequential mergers with eight progenitors having 80–90 per舁cent chance of finding a KT in any single projection.
The incidence of KTs in multiple mergers is in general much higher and spans a larger range than in binary mergers. Binary merger tree simulations have KT incidences spanning 15–60 per舁cent, while sequential mergers are much more likely to be slower rotators with more KTs. In the most extreme case, eight sequential mergers yields a twist in nearly 90 per舁cent of all projections. In both binary merger tree and sequential simulations, doubling the number of progenitors increases the likelihood of finding a KT. Unlike binary mergers, the likelihood of finding a slow rotator appears to scale with the chance of finding a KT.
Fig. 14 shows that binary merger remnants rarely host KDCs, with KDCs occurring only in 1–5 per舁cent of projections. Slowly rotating binary remnants feature KDCs, with somewhat increased frequency when compared to fast rotators. Binary merger tree simulations have similarly low incidences of KDCs, although the most slowly rotating remnants do not appear to have an increased incidence of decoupled cores. Sequential mergers have the highest rate of decoupled cores. The slow-rotator remnants of eight sequential mergers are more likely to feature a KDC than any binary merger remnant in our sample.
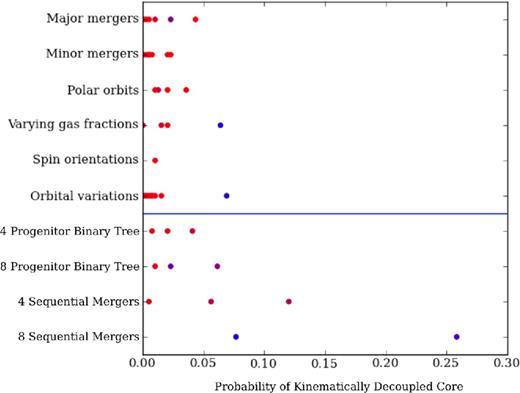
Same as Fig. 13 but with the incidence of KDCs. To be labelled a KDC, the kinematic moment must undergo at least a change of 30° in the orientation of the kinematic moment in a single radial bin. Above the blue line are binary mergers and below are multiple merger simulations. KDCs are more commonly found in sequential merger simulations than in binary mergers. Within any single category of simulations, slowly rotating remnants are the more likely to host a KDC than fast rotators.
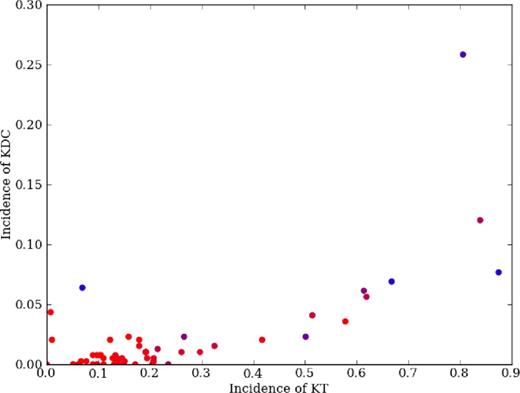
For all simulations, the probability of finding a KT is compared to the probability of finding a KDC in the same simulation. Slow rotators are coloured blue, fast rotators red. For simulations with KT rates above 50 per舁cent, which are predominantly multiple merger simulations, KTs correlate with KDCs, suggesting that these two phenomena are linked and that KDCs are extreme forms of KTs.
Simulations featuring KTs in 0-30 per舁cent of projections have a constant rate of KDCs (see Fig. 15). Once the majority of projections feature a twist, the rate of decoupled cores also scales with the KT rate. However, there are only two binary merger simulations with twisting rates higher than 50 per舁cent, so the trend could be the result of differences between multiple and binary mergers instead of an intrinsic correlation between KTs and KDCs.
6 SUMMARY
In this paper, we present a kinematic analysis and kinematic classification of 95 simulated remnants spanning a range of initial conditions. Our simulated binary merger remnants vary in mass ratio, orbital pericentre, orbital ellipticity, spin, and gas fraction. We also include multiple merger simulations where the remnant is grown exclusively through major merging or where the progenitor grows through sequential and increasingly more minor merging.
Nearly all of our binary merger remnants resemble ATLAS3D fast rotators. These simulations have a small chance of being observed as a slow rotator (≈5 per舁cent of projections). λR rises steadily with ϵ, the mean photometric–kinematic moments are aligned to within 5 per舁cent, and the stellar components are well described by an oblate ellipsoid. We find that a single major or minor merger does not yield a slowly rotating and spherical remnant. However, low gas fractions of ≈10 per舁cent lead to merger remnants that are slowly rotating but elongated, a result qualitatively similar to simulations of dissipationless systems (Cox et al. 2006b). Simulations where the progenitors’ initial angular momenta and orbital angular momentum sums to zero also lead to remnants that are slow rotators but are nevertheless still highly elliptical. Thus, even in binary mergers simulations that lead to the formation of slowly rotating remnants, the remnants are highly elongated and largely incompatible with the slow rotators as found by ATLAS3D.
In contrast to binary merger simulations, remnants of multiple mergers resemble observed slow rotators. We study two classes of multiple merger histories, both having progenitors identical in number and properties, but differ in the order that they are merged. ‘Binary merger tree simulations’ form a remnant exclusively through generations of binary major merging, and ‘sequential’ multiple mergers form a remnant by multiple, largely non-overlapping, increasingly minor mergers. Broadly speaking, both binary tree merger remnants and sequential merging remnants were rounder and slower than binary merger remnants. Thus, we find that the merger history is an important ingredient to forming slow or fast rotators (see also Navarro-González et al. 2013). Despite having identical progenitors as binary merger tree simulations, the sequential merger remnants were more likely to be round slow rotators. For both the binary merger tree and sequential multiple merger simulations, increasing the number of progenitors from four to eight yielded remnants that were rounder and more slowly rotating. Our results suggest that multiple mergers that grow exclusively through generations of major merging yield predominantly fast rotators, but growth through minor merging largely yields slow mergers.
KTs are found (∼10–20 per舁cent of projections) in our binary mergers, but are much more common (∼30–80 per舁cent) in remnants of multiple mergers. KDCs are found infrequently in binary mergers (≈5 per舁cent) but multiple merger remnants commonly host KDCs (5–30 per舁cent). Kinematically distinct cores are overall less prevalent than KTs, but again are most commonly found in multiple merger remnants, particularly in sequential multiple merging. Overall, we find that the incidence of KTs holds regardless of whether in a given projection the remnant is a slow or fast rotator.
In conclusion, our controlled experiments support the emerging framework that massive, round, slow-rotating ellipticals can be formed only through the accumulation of many minor mergers, while fast rotators may be formed through a variety of pathways. More work is now needed to connect the infall patterns of galaxies in a full cosmological context with their rotational outcomes. Further clues to the specific merging conditions for both fast and slow rotators could come through more detailed analyses of their kinematics, including in the outer regions (e.g. Arnold et al. 2014; Raskutti, Greene & Murphy 2014; Schauer et al. 2014; Wu et al. 2014).
We thank Frederic Bournaud for a helpful report, and Michele Cappellari, Duncan Forbes, and Dan Taranu for comments. This work was supported by National Science Foundation grant AST-0909237 and by computing resources at the NASA Ames Research Center. GSN was supported by the Department of Energy Computational Science Graduate Fellowship administered by the Krell Institute and by the ERC European Research Council under the Advanced Grant Program number 267399-Momentum.
REFERENCES



