-
PDF
- Split View
-
Views
-
Cite
Cite
Martina Falco, Steen H. Hansen, Radoslaw Wojtak, Thejs Brinckmann, Mikkel Lindholmer, Stefania Pandolfi, A new method to measure the mass of galaxy clusters, Monthly Notices of the Royal Astronomical Society, Volume 442, Issue 2, 1 August 2014, Pages 1887–1896, https://doi.org/10.1093/mnras/stu971
Close - Share Icon Share
Abstract
The mass measurement of galaxy clusters is an important tool for the determination of cosmological parameters describing the matter and energy content of the Universe. However, the standard methods rely on various assumptions about the shape or the level of equilibrium of the cluster. We present a novel method of measuring cluster masses. It is complementary to most of the other methods, since it only uses kinematical information from outside the virialized cluster. Our method identifies objects, as galaxy sheets or filaments, in the cluster outer region, and infers the cluster mass by modelling how the massive cluster perturbs the motion of the structures from the Hubble flow. At the same time, this technique allows to constrain the three-dimensional orientation of the detected structures with a good accuracy. We use a cosmological numerical simulation to test the method. We then apply the method to the Coma cluster, where we find two galaxy sheets, and measure the mass of Coma to be Mvir = (9.2 ± 2.4) × 1014 M⊙, in good agreement with previous measurements obtained with the standard methods.
1 INTRODUCTION
The picture of the large-scale structures reveals that matter in the Universe forms an intricate and complex system, referred to as ‘cosmic web’ (Zeldovich, Einasto & Shandarin 1982; Shandarin & Zeldovich 1983; Einasto et al. 1984; Bond, Kofman & Pogosyan 1996; Aragón-Calvo et al. 2010).
First attempts of mapping the three-dimensional (3D) spatial distribution of galaxies in the Universe (Gregory, Thompson & Tifft 1978; de Lapparent, Geller & Huchra 1986; Geller & Huchra 1989; Shectman et al. 1996), as well as more recent large galaxy surveys (Colless et al. 2003; Tegmark et al. 2004; Huchra et al. 2005), display a strongly anisotropic morphology. The galactic mass distribution seems to form a rich cosmos containing clumpy structures, such as clusters, sheets and filaments, surrounded by large voids (van de Weygaert & Bond 2008). A similar cosmic network has emerged from cosmological N-body simulations of the dark matter (DM) distribution (Bond et al. 1996; Aragón-Calvo et al. 2007; Hahn et al. 2007).
The large-scale structures are expected to span a range of scales that goes from a few up to hundreds of megaparsec. Despite the many well-established methods to identify clusters and voids, there is not yet a clear characterization of filaments and sheets. Because of their complex shape, there is not a common agreement on the definition and the internal properties of these objects (Bond, Strauss & Cen 2010). Moreover, their detection in observations is extremely difficult due to projection effects. Nevertheless, several automated algorithms for filament and sheet finding, both in 3D and two-dimensional (2D), have been developed (Novikov, Colombi & Doré 2006; Aragón-Calvo et al. 2007; Sousbie et al. 2008; Bond et al. 2010). Several galaxy filaments have been detected by eye (Colberg, Krughoff & Connolly 2005; Porter et al. 2008) and DM filaments have also been detected from their weak gravitational lensing signal (Dietrich et al. 2012). Powerful methods for the cosmic web classification are based on the study of the Hessian of the gravitational potential and the shear of the velocity field (Hahn et al. 2007; Hoffman et al. 2012).
From the qualitative point of view, several elaborate theories have been proposed. The cosmic web nature is intimately connected with the gravitational formation process. In the standard model of hierarchical structure formation, the cosmic structure has emerged from the growth of small initial density fluctuations in the early Universe (Peebles 1980; Davis et al. 1985; White & Frenk 1991). The accretion process involves the matter flowing out of the voids, collapsing into sheets and filaments and merging into massive clusters. Thus, galaxy clusters are located at the intersection of filaments and sheets, which operate as channels for the matter to flow into them (van Haarlem & van de Weygaert 1993; Colberg et al. 1999). The innermost part of clusters tends to eventually reach the virial equilibrium.
As result of this gravitational collapse (the so-called bottom-up scenario), clusters of galaxies are the most recent structures in the Universe. For this reason, they are possibly the easiest large-scale systems to study. Mass measurement of galaxy clusters is of great interest for understanding the large-scale physical processes and the evolution of structures in the Universe (White, Cohn & Smit 2010). Moreover, the abundance of galaxy clusters as function of their mass is crucial for constraining cosmological models: the cluster mass function is an important tool for the determination of the amount of DM in the Universe and for studying the nature and evolution of dark energy (Haiman, Mohr & Holder 2001; Cunha, Huterer & Frieman 2009; Allen, Evrard & Mantz 2011). The oldest method for the cluster mass determination is based on the application of the virial theorem to positions and velocities of the cluster members (Zwicky 1933). This method suffers from the main limitation that the estimated mass is significantly biased when the cluster is far from virialization. More recent and sophisticated techniques also rely strongly on the assumption of hydrostatic or dynamical equilibrium. The cluster mass profile can be estimated, for example, from observations of density and temperature of the hot X-ray gas, through the application of the hydrostatic equilibrium equation (Ettori et al. 2002; Borgani et al. 2004; Zappacosta et al. 2006; Schmidt & Allen 2007; Host & Hansen 2011). Another approach is based on the dynamical analysis of cluster member galaxies and involves the application of the Jeans equations for steady-state spherical system (Girardi et al. 1998; Łokas & Mamon 2003; Łokas et al. 2006; Mamon & Boué 2010). Additional cluster mass estimators have been proposed, which are independent of the cluster dynamical state. A measurement of the total cluster mass can be achieved by studying the distortion of background galaxies due to gravitational lensing (Mandelbaum et al. 2010; Lombriser 2011). The lensing technique is very sensitive to the instrument resolution and the projection effects. The caustic method has been proposed by Diaferio (1999). This method requires very large galaxy surveys, in order to determine the caustic curve accurately. Therefore, the development of new techniques and the combination of different independent methods is extremely useful for providing a more accurate cluster mass measurement.
The Coma cluster of galaxies (Abell 1656) is one of the most extensively studied system of galaxies (Biviano 1998), as the most regular, richest and best-observed in our neighbourhood. The X-ray observations have provided several mass estimates (Hughes 1989; Watt et al. 1992), obtained by assuming hydrostatic equilibrium. Dynamical mass measurements with different methods, based on the assumption of dynamical equilibrium, are reported in The & White (1986) and Łokas & Mamon (2003). Geller, Diaferio & Kurtz (1999) perform a dynamical measurement of the Coma cluster, using the caustic method, and weak lensing mass estimates of Coma have been carried on by Kubo et al. (2007) and Gavazzi et al. (2009).
In the present paper we propose a new method for estimating the mass of clusters. We intend to infer total cluster mass from the knowledge of the kinematics in the outskirts, where the matter has not yet reached equilibrium. The key of our method is the analysis of filamentary and sheet-like structures flowing outside the cluster. We apply our method for the total virial mass estimate to the Coma cluster, and we compare our result with some of the previous ones in the literature. Our method also provides an estimation of the orientation of the structures we find, in the 3D space. This can be useful to identify a major merging plane, if a sufficient number of structures are detected and at least three of them are on the same plane.
The paper is organized as follows. In Section 2 we derive the relation between the velocity profile of galaxies in the outer region of clusters and the virial cluster mass. In Section 3 we propose a method to detect filaments or sheets by looking at the observed velocity field. In Section 4 we test the method to a cosmological simulated cluster-size halo and we present the result on the mass measurement. In Section 5 we present the structures we find around the Coma cluster and the Coma virial mass determination.
2 MASS ESTIMATE FROM THE RADIAL VELOCITY PROFILE
Therefore, once we know the relation between |$\overline{v}_{\rm p}$| and Mv, equation (5) can be used to infer the virial mass of clusters.
In the next section, we will derive the equation that connects the peculiar velocity of galaxies |$\overline{v}_{\rm p}$| with the virial mass of the cluster Mv.
2.1 Radial infall velocity profile
Simulations have shown a quite universal trend for the radial mean velocity profile of cluster-size haloes, when normalized to their virial velocities (Prada et al. 2006; Cuesta et al. 2008). This feature can be seen, for example, in Fig. 1, where the median radial velocity profile for three samples of simulated haloes is displayed. The units in the plot are the virial velocity Vv and virial radius rv. The mean virial masses in the samples are Mv = 0.8 × 1014 M⊙ (blue, triple-dot dashed line), Mv = 1.1 × 1014 M⊙ (green dot dashed line) and Mv = 4.7 × 1014 M⊙ (red dashed line). The cosmological N-body simulation we used is described in Section 4.
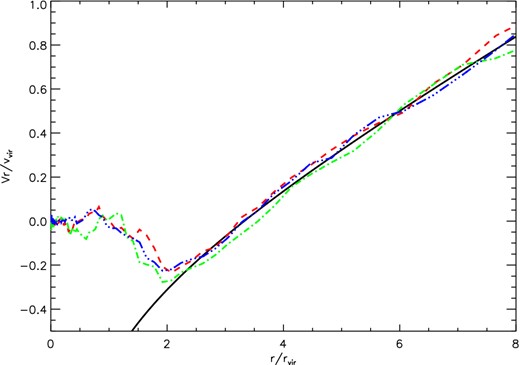
Median radial velocity profile for three samples of simulated haloes. The virial masses for the samples are Mv = 0.8 × 1014 M⊙ (blue, triple-dot dashed line), Mv = 1.1 × 1014 M⊙ (green dot dashed line) and Mv = 4.7 × 1014 M⊙ (red dashed line). The black solid line is our simultaneous fit to the three profiles.
In order to derive an approximation for the mean velocity profile, the spherical collapse model has been assumed in several works (Peirani & de Freitas Pacheco 2006, 2008; Karachentsev & Nasonova (Kashibadze) 2010; Nasonova, de Freitas Pacheco & Karachentsev 2011). In Zu & Weinberg (2013), they instead develop an analytical model for the galaxy infall kinematic profiles around cluster mass haloes, from the measurement of the redshift-space cluster–galaxy correlation function. Their model is a combination of geometry and phenomenological fits and they do not assume equilibrium of the cluster.
Here we make a quite conservative choice. We parametrize the infall profile using only the information that it must reach zero at large distances from the halo centre, and then we fit the universal shape of the simulated haloes profiles. Therefore, we do not assume the spherical infall model.
We fit equation (6) to the three profiles in Fig. 1 simultaneously, with a and b as free parameters. The fit is performed in the range r = 3–8 rv. The best fit is the black solid line, corresponding to parameters: a = 0.8 ± 0.2 and b = 0.42 ± 0.16.
This allows us to fix a universal shape for the mean velocity of the infalling matter, as function of the virial velocity, i.e. the virial mass, in the outer region of clusters. In the following analysis, we therefore assume that the best fit shown in Fig. 1 provides a good approximation for the infall profile of any cluster-size halo. Such a model for the infall is based on the hypothesis of spherical symmetry. However, the median radial velocity profile of the samples might slightly differ from the real velocity profile of each individual non-spherical halo. In a future paper, we hope to quantify how the departure of the cluster shape from sphericity affects the infall velocity profile. The parameters a and b in equation (6) can also change when restricting ourselves to special regions around a halo. In Section 4.2, we estimate the intrinsic scatter of the simulated infall velocity profiles. Our estimate of this inaccuracy yields 50 per cent for the virial mass.
One should also expect the simulated infall profile, and therefore our fit values, to be dependent on the cosmology adopted in the simulation. However, we leave a quantification of this effect to future studies.
3 FILAMENTS AND SHEETS AROUND GALAXY CLUSTERS
The method we propose for measuring the virial cluster mass, consists in using only observed velocities and distances of galaxies, which are outside the virialized part of the cluster, but whose motion is still affected by the mass of the cluster. Given the dependence of the infall velocity on the virial mass, we wish to estimate Mv by fitting the measured velocity of galaxies moving around the cluster with equations (5) and (6).
To this end, we need to select galaxies which are sitting, on average, in the transition region of the mean radial velocity profile. For the fit to be accurate, the galaxies should be spread over several megaparsec in radius.
Observations give the 2D map of clusters and their surroundings, namely the projected radius of galaxies on the sky R, and the component of the galaxy velocities along the line of sight vlos. The reconstruction of the radial velocity profile would require the knowledge of the radial position of the galaxies, i.e. the radius r. The velocity profile that we infer from observations is also affected by the projection effects. If the galaxies were randomly located around clusters, the projected velocities would be quite uniformly distributed, beyond the standard redshift-space distortions (Kaiser 1987). The strong anisotropy of the matter distribution allows us to see signatures of the radial velocity profile in the redshift space. At several megaparsec away from the cluster centre, we will select collections of galaxies bound into systems, as filaments or sheets. The presence of such objects can break the spatial degeneracy in the velocity space.
In Sections 3.1 and 3.2, we explain in details how such objects can be identified as filamentary structures in the projected velocity space.
3.1 Line of sight velocity profile
In order to apply the universal velocity profile (6) to observations, we need to transform the 3D radial equation (4) to a 2D projected equation. We thus need to compute the line of sight velocity profile vlos as function of the projected radius R.
Let us consider a filamentary structure forming an angle α between the 3D radial position of galaxy members r and the 2D projected radius R. Alternatively, let us consider a sheet in the 3D space lying on a plan with inclination α with respect to the plan of the sky (see the schematic Fig. 2).
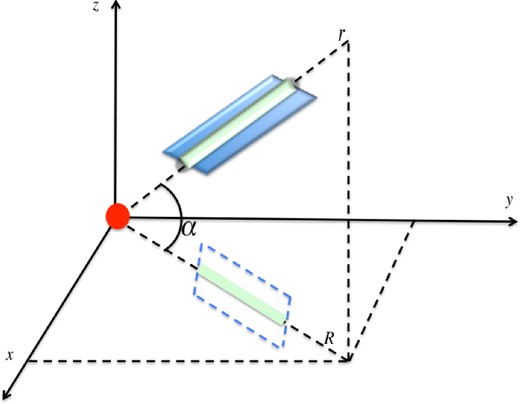
Schematic drawing of a filament or a sheet in 3D with inclination α between the radial distance r and the projected radius R. The cluster is represented by the red circle in the centre of the frame. The z-axis corresponds to the observer line of sight.
3.2 Linear structures in the velocity field
Our interest here is thus in finding groups of galaxies outside clusters that form a bound system with a relatively small dispersion in velocity, and that lie on a preferential direction in the 3D space. In particular, we are interested in such objects when they are far enough from the cluster, to follow a nearly linear radial pattern in the velocity space, corresponding to a decelerated Hubble flow.
We expect these objects to form filament-like structures in the projected velocity space. In fact, if we apply the formula in equation (9) to galaxies with the same orientation angle α within a small scatter, the radial velocity shape given by equation (5) is preserved. Thus, these galaxies can be identified as they are collected on a line in the observed velocity space.
Nevertheless, we can look at the structure in the 2D map [the (x, y) plane in Fig. 2]. If all the selected galaxies lie on a line, within a small scatter, also in the (x, y) plane, they can be defined as a filament. If they are confined in a region within a small angular aperture, they might form a sheet (see Fig. 2). Complementary papers will analyse properties of such sheets (Brinckmann et al., in preparation; Wadekar & Hansen, in preparation).
We want to point out here that Fig. 2 describes the ideal configuration for filaments and sheets to have a quasi-linear shape in the observed velocity plane. Therefore, not all the filaments and sheets will satisfy this requirement, i.e. not all the structures outside clusters can be detected by looking at the velocity field.
Our method for identifying these objects is optimized towards structures which are narrow in velocity space, while still containing many galaxies, and therefore which are closer to face-on than edge-on. It consists in selecting a region in the sky, and looking for a possible presence of an overdensity in the corresponding velocity space. We will describe the method in details in the next section.
4 TESTING THE METHOD ON COSMOLOGICAL SIMULATION
As a test of our method, we apply it to a cluster-size haloes from a cosmological N-body simulation of pure DM.
The N-body simulation is based on the 3-year Wilkinson Microwave Anisotropy Probe (WMAP3) cosmology. The cosmological parameters are ΩM = 0.24 and ΩΛ = 0.76, and the reduced Hubble parameter is h = 0.73. The particles are confined in a box of size 160 h−1 Mpc. The particle mass is 3.5 × 108 M⊙, thus there are 10243 particles in the box. The evolution is followed from the initial redshift z = 30, using the mpi version of the art code (Kravtsov, Klypin & Khokhlov 1997; Gottloeber & Klypin 2008). The algorithm used to identify clusters is the hierarchical friends-of-friends (FOF) with a linking length of 0.17 times the mean interparticle distance. The cluster centres correspond to the positions of the most massive substructures found at the linking length eight times shorter than the mean interparticle distance. We define the virial radius of haloes as the radius containing an overdensity of Δ = 93.8 relative to the critical density of the Universe. More details on the simulation can be found in Wojtak et al. (2008).
As an example, we first apply the procedure to one simulated halo. In Section 4.3 we will show the analysis on 20 haloes. We select, at redshift z = 0, a halo of virial quantities Mv = 4.75 × 1014 M⊙, rv = 2.0 Mpc and Vv = 1007.3 km s−1.
We treat the DM particles in the halo as galaxies from observations. The first step is to project the 3D halo as we would see it on the sky. We consider three directions as possible lines of sight. For each projection, we include in our analysis the galaxies in the box x = [−20, 20] Mpc and y = [−20, 20] Mpc, where x, y are the two directions perpendicular to the line of sight. We down-sample the DM particles in the above-mentioned box around the halo, in order to use a space galaxy density comparable with the best observations. In particular, we take roughly ≈9000 particles, i.e. the same number of galaxies as in the Sloan Digital Sky Survey (SDSS) sample of the Coma cluster that includes galaxies within 18° from the Coma centre, which we will analyse in Section 5. We assume that there is no velocity bias, i.e. that the infall profile for DM particles is the same as the infall profile for galaxies. We justify such assumption in Section 5.
The method described in the next section is applied to all the three projections.
4.1 Identification of filaments and sheets from the velocity field
Our goal is to find structures confined in a relatively small area in the (x, y) plane. To this end, we split the spatial distribution into eight 2D wedges (e.g. in Fig. 3 the orange points represent one of the wedges) and we look at each of them in the (R, vlos) space (e.g. in Fig. 4 we look at the orange wedge in Fig. 3, in the velocity space), where we aim to look for overdensities.
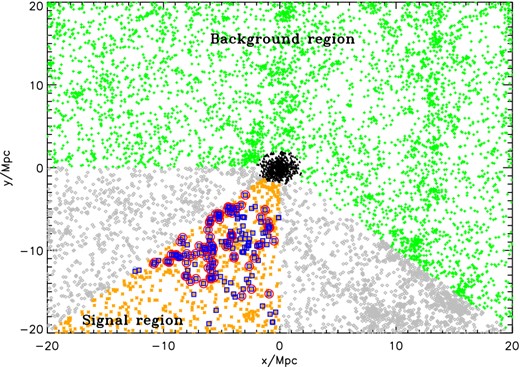
2D projection of the simulation box, centred on the selected simulated halo. The black triangles represent the particles inside the virial radius of the halo. The orange points belong to one of the eight wedges we select in the (x, y) plane. The background for the selected wedge is given by the green crosses. The two wedges adjacent to the selected wedge, grey diamonds, are excluded from the analysis. In the selected wedge, we identify a sheet that is represented by the red circles. The blue squares correspond to the total overdensity we find in the wedge, with the method described in the text.
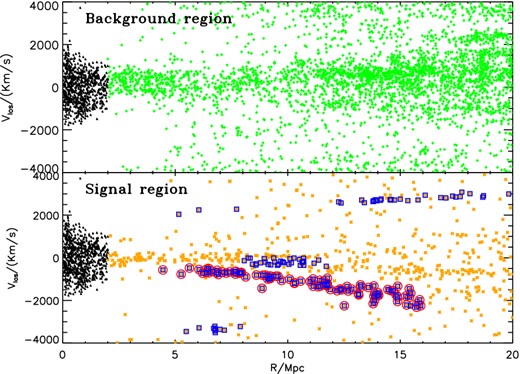
Line of sight velocity vlos as function of the projected distance R from the centre of the simulated halo. Upper panel: the background in the analysis is represented by the green crosses. The black triangles are all the particles within the virial radius. Bottom panel: the orange points represent our signal, i.e. the selected wedge. The blue points correspond to the overdensity in the wedge. The only almost straight inclined line is shown in red circles. We identify this filamentary-like structure as a sheet.
We confine the velocity field to the box: vlos = [−4000, 4000] km s−1 and R = [4, 20] Mpc, and we divide the box into 50 cells, 4 Mpc large and 400 km s−1 high.
For each of the selected wedges, we want to compare the galaxy number density ni in each cell i, with the same quantity calculated for the rest of the wedges in the same cell. More precisely, in each cell, we calculate the mean of the galaxy number density of all the wedges but the selected one. This quantity acts as background for the selected wedge, and we refer to it as |$n^{{\rm bg}}_{i}$|.
In Fig. 3, the wedge under analysis is represented by the orange points, and the background by the green points. We exclude from the background the two wedges adjacent to the selected one (grey points in Fig. 3). We need this step because, if any structure is sitting in the selected wedge, it might stretch to the closest wedges.
This method leaves us with only one structure inside the wedge in Fig. 3 (red points). It is a sheet, as it appears as a 2D object on the sky, opposed to a filament which should appear one-dimensional (1D). We see such sheet only in one of the three projections we analyse. The bottom panel of Fig. 4 shows the velocity–distance plot corresponding to all the galaxies belonging to the selected wedge (orange points), while the selected strips of galaxies are shown as blue points. The desired sheet (red points) is an almost straight inclined line crossing zero velocity roughly near 5–10 Mpc and contains 88 particles. The background wedges are displayed in the upper panel of Fig. 4.
4.2 Analysis and result
We run one chain of 5000 combinations of parameters and then we remove the burn-in points.
In Fig. 5 we show the scatter plot on the plane of the two parameters, and the 1D probability distribution functions of the virial mass and the orientation angle. The mean value for the virial mass is Mvir = (4.3 ± 2.2) × 1014 M⊙, which is comparable to the true halo virial mass Mvir = 4.75 × 1014 M⊙. The mean value for the cosine of the angle between R and r is cos(α) = 0.48 ± 0.02, corresponding to α = −1.07 ± 0.02 rad. In Fig. 6 we show the sheet in the 3D space (blue points). The best fit for the plane where the sheet is laying is shown as the green plane, and the corresponding angle is α = −1.05 rad, giving cos(α) = 0.5. Our estimation is thus consistent, within the statistical error, with the true orientation of the sheet in 3D.
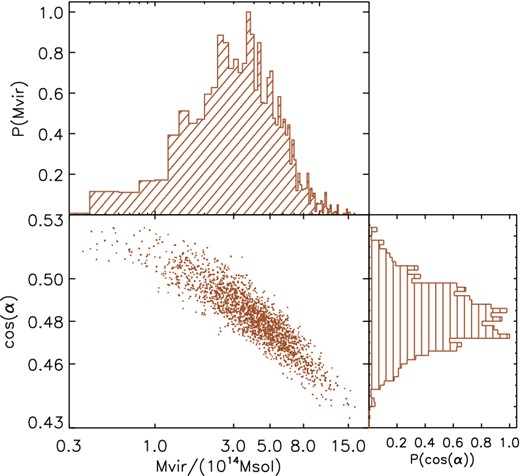
Result of the MCMC applied to the sheet found outside the simulated halo. Central panel: scatter plot of the two free parameters (cos(α), Mvir) obtained by the MCMC chain. Upper panel: probability density function of the virial mass. Left-hand panel: probability density function of the viewing angle. The initial number of points is 5000 and we remove the points of burn-in. The mean value for the virial mass and the cosine of the angle are Mvir = (4.3 ± 2.2) × 1014 M⊙ and cos(α) = 0.48 ± 0.02, which are comparable to the true halo virial mass Mvir = 4.75 × 1014 M⊙ and angle cos(α) = 0.5.
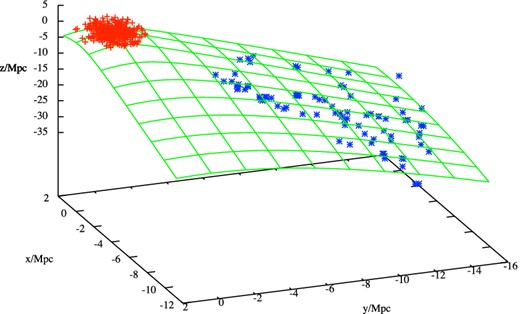
The sheet we found outside the simulated halo in the 3D space. The z-axis corresponds to the line of sight direction. The blue points represent the particles belonging to the sheet, and the green plane is the best fit for the sheet's plane, corresponding to α = −1.05 (cos(α) = 0.5) rad. The red points represent the particles within the virial radius of the halo.
Our method provides the correct halo mass and orientation angle within the errors.
The main source of uncertainties resides in the assumption of universality of the infall velocity profile. As discussed in Section 2.1, we expect the radial velocity profile to have a non-negligible halo to halo variance. We estimate this inaccuracy by replacing, in the analysis, the median radial velocity of the three samples with the corresponding quartiles. Thereby we estimate a systematic error of 50 per cent for the virial mass and 2.5 per cent for the angle. In particular, we determine this error in the specific case of the halo under analysis. The bottom panel of Fig. 7 represents our result of the sheet analysis, when using a fit to the real mean radial velocity of the halo, which is shown in the upper panel. The best-fitting parameters to the radial velocity profile of the halo, with equation (6), are a = 1.5 and b = 0.89. In Fig. 7, the black solid line is the fit to the halo velocity profile (red dashed line) and the green dot–dashed line is the universal velocity profile used in the previous analysis. The two profiles overlap in the range ≈3–5 rv, but they slightly differ for larger distances, where our sheet is actually sitting. Replacing the universal radial velocity profile with the true one, eliminates the small off set caused by the departure of the two profiles. In the new analysis, the mean value for the virial mass is Mvir = (4.67 ± 1.9) × 1014 M⊙, while the mean value for the cosine of the angle between R and r is cos(α) = 0.5 ± 0.01. They are in very good agreement with the true values of the parameters Mvir = 4.7 × 1014 M⊙ and cos(α) = 0.5.
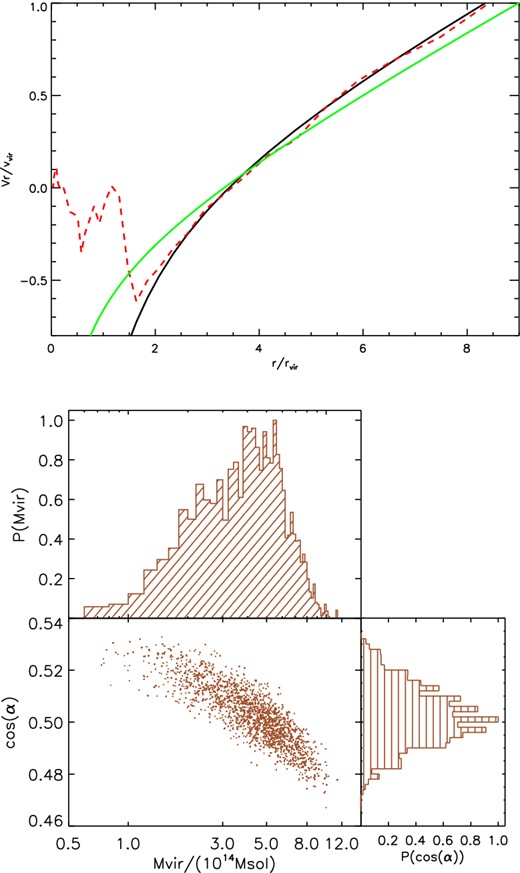
The top figure shows the median radial velocity profile for the simulated halo (red dashed line). The black solid line is our fit to the profile. The green dot–dashed line is the universal radial profile showed in Fig. 1. The bottom figure shows the result of the MCMC applied on the sheet found around the simulated halo, using the fit to the mean velocity profile of the halo (top figure). Central panel: scatter plot of the two free parameters (cos(α), Mvir) obtained by the MCMC chain. Upper panel: probability density function of the virial mass. Left-hand panel: probability density function of the viewing angle. The initial number of points is 5000 and we remove the points of burn-in. The mean value for the virial mass is Mvir = (4.67 ± 1.9) × 1014 M⊙, which is very close to the true halo virial mass Mvir = 4.75 × 1014 M⊙. The mean value for the cosine of the angle is cos(α) = 0.5 ± 0.01, in agreement with the real value cos(α) = 0.5.
4.3 Statistical test of the method
We analysed 20 of the most isolated haloes extracted from the cosmological simulation at redshift z = 0. The halo masses vary within the range Mvir ≈ [2, 20] × 1014 M⊙. We consider one random projection of every halo, and apply our method for the sheet detection and the mass estimation. We identify seven sheets that each leads to a mass measurement in agreement with the true virial halo mass within 2σ. Therefore, our method detected a structure in ≈30 per cent of the cases.
In Fig. 8 we show three representative structures we find outside three different haloes, both in the x–y plane and in the phase space. The probability distributions of the virial mass obtained by the analysis of the sheets are shown in Fig. 9, for all the seven sheets.
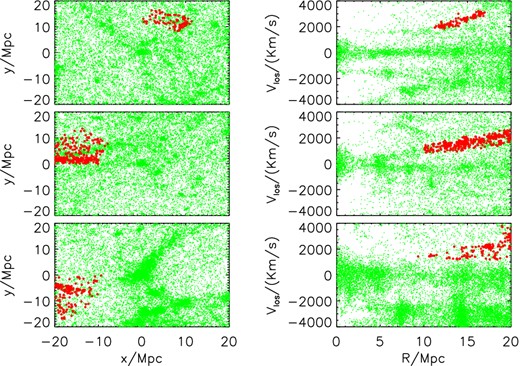
Three sheets we found outside three haloes of virial masses: Mvir = 2.3 × 1014 M⊙ (top panels), Mvir = 2.5 × 1014 M⊙ (middle panels) and Mvir = 11 × 1014 M⊙ (bottom panel). The panels on the left correspond to the 2D projection of the simulation box, centred on the selected simulated haloes. The panels on the right represent the line of sight velocity vlos as function of the projected distance R from the centre of the simulated haloes. The detected sheets are represented by the red circles.
![Probability distribution functions of the virial mass, derived through the sheet technique. The different distributions correspond to seven sheets found outside seven different simulated haloes. The mass of the haloes varies within the range Mvir ≈ [2, 20] × 1014 M⊙. The distributions corresponding to the three sheets in Fig. 8 are, starting from the top one, the number 2, 3 and 5. The panel in the bottom right shows the value of Mvir/Mtrue with the corresponding 2σ error bars for the seven sheets.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/442/2/10.1093_mnras_stu971/1/m_stu971fig9.jpeg?Expires=1749887371&Signature=V6Cdz5SrgBWJS4TAzG-e~U8YJ8lB~drKRvPGqGhkcOlTWXPrMajTO8mBjtNy3MXtryDkIleNX~q6SwXHtbGVUOONX8c6Ah-VWrI~SdMhS7ZIUSOLgdvy5SeZ3GaRkHErtKGnDcJFTLUDxYbY~Qzb~2VoH8NvbNAe-e-AoUqqUeMA8ZCNHPs8zYovCCJwGlX2Ol8OIdXFaWhgFN9eMi7zhBlNlgQw9nN0Gej21tFNYA5WWNi3xMvkTbI~Ggl7a6EtXwE6daOEboy~TcFfiqK~zutLZsvIFbLAKzSWaR~JiOYj~9PRmsAFpZ4kKN2wiOfwPgKIrvE5Kirzgrz~ueNslg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Probability distribution functions of the virial mass, derived through the sheet technique. The different distributions correspond to seven sheets found outside seven different simulated haloes. The mass of the haloes varies within the range Mvir ≈ [2, 20] × 1014 M⊙. The distributions corresponding to the three sheets in Fig. 8 are, starting from the top one, the number 2, 3 and 5. The panel in the bottom right shows the value of Mvir/Mtrue with the corresponding 2σ error bars for the seven sheets.
The result confirms that, once a structure is found, our kinematical analysis is efficient in measuring the virial halo mass.
We also recover the orientation angle of the sheets with good accuracy. We point out here that our method seems to be more sensitive to sheets which are inclined with an angle not bigger than α ≈ 2/3π with respect to the sky plane, i.e. closer to be faced-on.
The low statistic in the number of structures we find can be significantly increased by improving the detection procedure. In Sacchi et al. (in preparation), we are developing a more sophisticated method to identify filaments and sheets in the redshift space. In the approach we use in this paper, we split the phase space in small cells, look for overdensities in each cell, and finally select the overdense regions that form elongated structures. The new technique is also based on the identification of overdensities, but it filters a priori towards long quasi-linear structures. This allows us to identify structures that might not clearly appear within the overdense regions.
5 RESULT ON COMA CLUSTER
In this section, we will apply our method to real data of the Coma cluster.
We search for data in and around the Coma cluster in the SDSS data base (Abazajian et al. 2009). We take the galaxy NGC 4874 as the centre of the Coma cluster (Kent & Gunn 1982), which has coordinates RA = 12h59m35|${^{\rm s}_{.}}$|7, Dec. = +27°57′33″. We select galaxies within 18° from the position of the Coma centre and with velocities between 3000 and 11 000 km s−1. The sample contains 9000 galaxies.
We apply the method for the identification of structures outside clusters to the Coma data. We detect two galactic sheets in the environment of Coma. We denote our sheets as sheet 1 and sheet 2.
Fig. 10 shows the Coma cluster and its environment up to 18° from the cluster centre. The number of galaxies with spectroscopically measured redshifts within 2.5 Mpc, which is roughly the virial radius of Coma, is 748. These galaxies are indicated as black triangles. The sheets are the red circles. The upper panel refers to the sheet 1, which contains 51 galaxies. The bottom panel refers to the sheet 2, which is more extended and contains 228 galaxies. In Fig. 11 we show the sheets in the velocity space. They both appear as inclined straight lines. The sheet 1 goes from ≈7 to ≈14 Mpc. As the velocities are negative, the sheet is between us and Coma. The sheet 2 goes from ≈11 to ≈22 Mpc. As the velocities are positive, the sheet is beyond Coma.
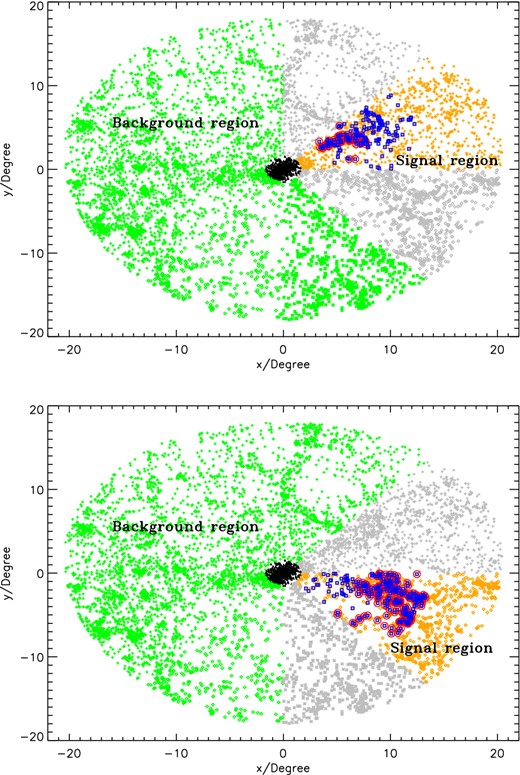
Sky map of the Coma cluster. The top figure shows the sheet 1 and the bottom figure shows the sheet 2. The black triangles represent the particles inside the virial radius of Coma. The orange points belong to one of the eight wedges we select in the (x, y) plane. The background for the selected wedge is given by the green crosses. The two wedges adjacent to the selected wedge, grey diamonds, are excluded from the analysis. In the selected wedge, we identify a sheet that is represented by the red circles. The blue squares correspond to the total overdensity we find in the wedge, with the method described in the text.
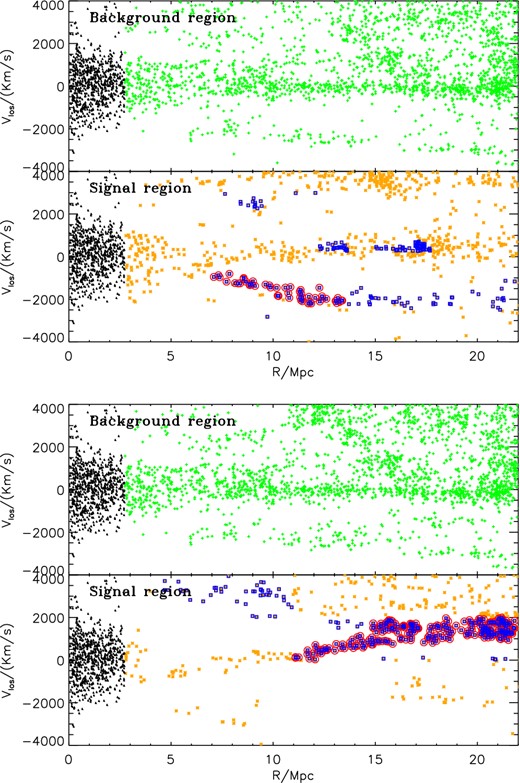
Line of sight velocity vlos as function of the projected distance R from the centre of Coma. The velocities are scaled by the velocity of Coma vComa = 4000 km s−1. The top figure shows the sheet 1 and the bottom figure shows the sheet 2. Upper panels: the background in the analysis is represented by the green crosses. The black triangles are all the galaxies within r = 2.5 Mpc. Bottom panel: the orange points represent the signal, i.e. the selected wedge. The blue points correspond to the overdensity. The almost straight inclined lines are shown in red circles. We identify these filamentary-like structures as sheets.
As we did for the cosmological simulation, we have removed the collections of galaxies which are horizontal groups in (R, vlos) space by hand. For example, in the case of the sheet 1 in the upper panel of Fig. 11, we define the sheet only by including the inclined pattern and, therefore, by excluding the horizontal part of the strip.
We then fit the line of sight velocity profiles of the two sheets with equation (10). We set Δ = 93.8 and H0 = 73 km s−1 Mpc−1, as for the cosmological simulation.
In Fig. 12 we show the scatter plot on the plane of the two parameters (cos(α), Mvir), and the 1D probability distribution functions of the virial mass and the orientation angle, for both the sheets. The angle α can be very different for different sheets, as it only depends on the position of the structure in 3D. Instead, we expect the result on the cluster mass Mvir to be identical, as it refers to the same cluster.
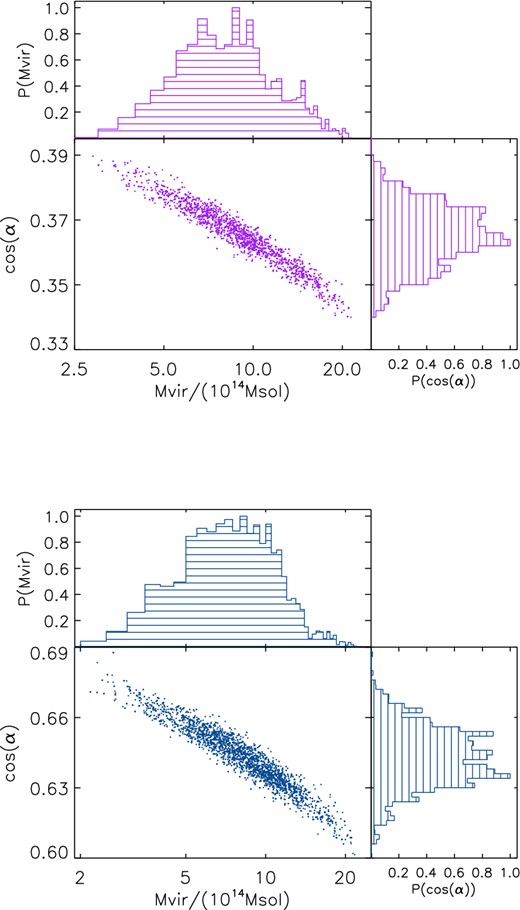
Result of the MCMC applied to the two sheets found outside the Coma cluster. The top figure refers to the sheet 1 and the bottom figure refers to the sheet 2. Central panels: scatter plot of the two free parameters (cos(α), Mvir) obtained by the MCMC chain. Upper panels: probability density function of the virial mass. Right-hand panels: probability density function of the viewing angle. The initial number of points is 5000 and we remove the points of burn-in.
In Fig. 13 we overplot the probability distributions for the virial mass of Coma, from the analysis of the two sheets. The two probability distributions are very similar. The mean value of the virial mass is Mvir = (9.7 ± 3.6) × 1014 M⊙ for the sheet 1 and Mvir = (8.7 ± 3.3) × 1014 M⊙ for the sheet 2. When applying equation (1), these values give a virial radius of rvir = 2.5 and 2.4 Mpc, respectively. The best mass estimate based on the combination of these measurements is Mvir = (9.2 ± 2.4) × 1014 M⊙.
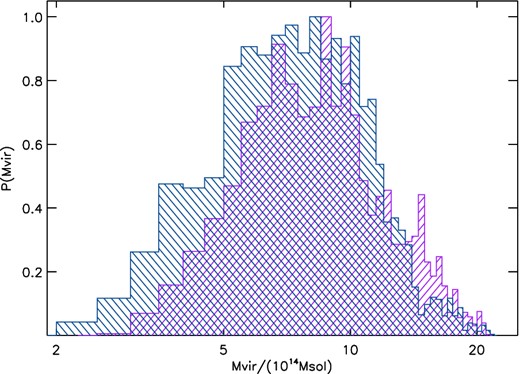
The probability density function of the Coma virial mass, derived through the sheet technique. The distribution coming from the sheet 2 is the blue one, slightly to the left. The violet slightly narrower distribution corresponds to the sheet 1. The best mass estimate based on these measurement is Mvir = (9.2 ± 2.4) × 1014 M⊙.
Our result is in good agreement with previous estimates of the Coma cluster mass. In Hughes (1989), they obtain a virial mass Mvir = (13 ± 2) × 1014 M⊙ from their X-ray study. From the galaxy kinematic analysis, Łokas & Mamon (2003) report a virial mass M100 = (15 ± 4.5) × 1014 M⊙, corresponding to a density contrast Δ = 100, which is very close to our value. Geller et al. (1999) find a mass M200 = 15 × 1014 M⊙, corresponding to a density contrast Δ = 200. The weak lensing mass estimate in Kubo et al. (2007) gives |$M_{200} = 2.7^{+3.6}_{-1.9}\times 10^{15}\,\rm{M}_{{\odot }}$|.
The mean value for cosine of the orientation angle is cos(α) = 0.36 ± 0.01, corresponding to α = −1.2 ± 0.01 rad, for the sheet 1 and cos(α) = 0.64 ± 0.02, corresponding to α = 0.87 ± 0.02 rad, for the sheet 2. These results are affected by a statistical error of 50 per cent for the mass and 2.5 per cent for the angle, as discussed in Section 4.2.
When applying the universal infall profile obtained from simulations to galaxy clusters, we assume that galaxies follow DM particles. The departure of the galaxy velocity from the DM velocity profile might cause a corresponding bias in the recovered cluster mass. However, we do not expect this bias to be significant. In Evrard et al. (2008) they report a summary of different studies on the velocity bias bv, i.e. the ratio of the galaxy velocity dispersion to that of the DM in cosmological simulations. The main conclusion is that the velocity bias is likely to be very small (bv ≈ 1). Moreover, we expect it to be even smaller in our work, since we analyse regions very far from the halo centre.
The value obtained for the orientation α of a sheet corresponds to the mean angle of all the galaxies belonging to the sheet. By knowing α, we can calculate the corresponding coordinate along the line of sight for all the galaxies, and therefore, we reconstruct the 3D map of the two structures, as shown in Fig. 14. The sheets we find are lying on two different planes.
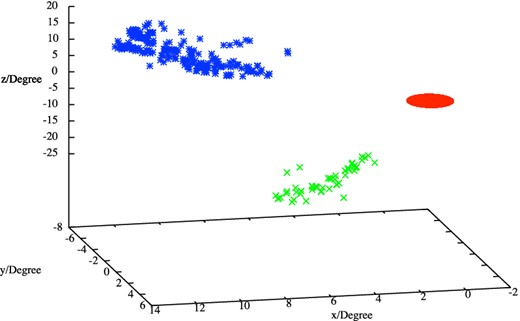
The sheets we found outside the Coma cluster in the 3D space. The blue and the green points represent the particles belonging to the sheet 1 and the sheet 2, respectively. The Coma cluster is indicated as a red sphere centred at (x, y, z) = (0, 0, 0).
6 SUMMARY AND CONCLUSION
The main purpose of this paper is to propose and test a new method for the mass estimation of clusters within the virial radius. The idea is to infer it only from the kinematical data of structures in the cluster outskirts.
In the hierarchical scenario of structure formation, galaxy clusters are located at the intersection of filaments and sheets. The motion of such non-virialized structures is thus affected by the presence of the nearest massive cluster.
We found that modelling the kinematic data of these objects leads to an estimation of the neighbour cluster mass. The gravitational effect of the cluster mass is to perturb the pure Hubble motion, leading to a deceleration. Therefore, the measured departure from the Hubble flow of those structures allows us to infer the virial mass of the cluster. We have developed a technique to detect the presence of structures outside galaxy clusters, by looking at the velocity space. We underline that the proposed technique does not aim to map all the objects around clusters, but it is limited to finding those structures that are suitable for the virial cluster mass estimation.
Our mass estimation method does not require the dynamical analysis of the virialized region of the cluster, therefore, it is not based on the dynamical equilibrium hypothesis. However, our method relies on the assumption of spherical symmetry of the system. In fact, we assume a radial velocity profile. Moreover, the method is biased by fixing the phenomenological fit to the radial infall velocity profile of simulation, as universal infall profile. From the practical point of view, this technique requires gathering galaxy positions and velocities in the outskirts of galaxy clusters, very far away from the cluster centre. A quite dense sample of redshifts is needed, in order to identify the possible presence of structures over the background. Once the structures are detected, the fit to their line of sight velocity profiles has to be performed. The fitting procedure involves only two free parameters: the virial mass of the cluster and the orientation angle of the structure in 3D. This makes the estimation of the virial cluster mass quite easy to obtain.
We have analysed cosmological simulations first, in order to test both the technique to identify structures outside clusters and the method to extract the cluster mass. We find one sheet outside the selected simulated halo, and we infer the correct halo mass and sheet orientation angle, within the errors.
We performed a statistical analysis on 20 simulated haloes. The result shows that the method we propose is fairly accurate in the determination of the virial mass. However, the low statistic in the structure finding suggests that the detection procedure can be significantly improved. The approach used in this paper can be seen more as a science demonstration case that can be used for further development.
We then applied our method to the Coma cluster. We have analysed the SDSS data of projected distances and velocities, up to 20 Mpc far from the Coma centre. Our work led to the detection of two galactic sheets in the environment of the Coma cluster. The estimation of the Coma cluster mass through the analysis of the two sheets gives Mvir = (9.2 ± 2.4) × 1014 M⊙. This value is in agreement with previous results from the standard methods. We note however that our method tends to underestimate the Coma virial mass, compared with previous measurements, which either assume equilibrium or sphericity.
In the near future, we plan to optimize our method of structure selection. We also aim to apply our technique to other surveys, where redshifts at very large distances from the clusters centre are available. If a large number of sheets and filaments will be found, our method could also represent a tool to deproject the spatial distribution of galaxies outside galaxy clusters into the 3D space.
The authors thank Stefan Gottloeber, who kindly agreed for one of the CLUES simulations (http://www.clues-project.org/simulations.html) to be used in the paper, and the referee for comments which improved the paper. The simulation has been performed at the Leibniz Rechenzentrum (LRZ), Munich. The Dark Cosmology Centre is funded by the Danish National Research Foundation.



