-
PDF
- Split View
-
Views
-
Cite
Cite
Ivan Debono, Dark energy model selection with current and future data, Monthly Notices of the Royal Astronomical Society, Volume 442, Issue 2, 1 August 2014, Pages 1619–1627, https://doi.org/10.1093/mnras/stu980
Close - Share Icon Share
Abstract
The main goal of the next generation of weak-lensing probes is to constrain cosmological parameters by measuring the mass distribution and geometry of the low-redshift Universe and thus to test the concordance model of cosmology. A future all-sky tomographic cosmic shear survey with design properties similar to Euclid has the potential to provide the statistical accuracy required to distinguish between different dark energy models. In order to assess the model selection capability of such a probe, we consider the dark energy equation-of-state parameter w0. We forecast the Bayes factor of future observations, in the light of current information from Planck, by computing the predictive posterior odds distribution. We find that Euclid is unlikely to overturn current model selection results, and that the future data are likely to be compatible with a cosmological constant model. This result holds for a wide range of priors.
1 INTRODUCTION
There is no shortage of data in modern cosmology, and information from various experiments has allowed us to measure the parameters in our cosmological model with increasing precision. These data include cosmic microwave background (CMB) measurements (e.g. Hinshaw et al. 2013, WMAP; Planck Collaboration 2013a, Planck), supernovae compilations (e.g. Goldhaber 2009, SCP), large-scale structure maps (e.g. Ahn et al. 2014, SDSS), and weak-lensing observations (e.g. Parker et al. 2007; Schrabback et al. 2010). The next generation of experiments (e.g. Amendola et al. 2013, Euclid; Blake et al. 2004, SKA) should provide even better precision.
The Λ cold dark matter (ΛCDM) concordance model can fit current astrophysical data with only six parameters describing the mass–energy content of the Universe (baryons, CDM and dark energy) and the initial conditions. However, this is not a statement on whether the model is correct. It merely implies that deviations from ΛCDM are too small compared to the current observational uncertainties to be inferred from cosmological data alone. One obvious example is the addition of hot dark matter (HDM) to the model, i.e. parameters for the physical neutrino density and the number of massive neutrino species (see e.g. Abazajian et al. 2011; Audren et al. 2013; Basse et al. 2014). Although massive neutrinos are not required by current cosmological observations, neutrino oscillation observations have shown that neutrinos have a non-zero mass.
The fundamental questions facing cosmologists are not simply about parameter estimation, but about the possibility of new physics, therefore about model selection. In addition to estimating the values of the parameters in the model, this involves decisions on which parameters to include or exclude. In some cases, the inclusion of parameters is possible only by invoking new physical models.
This is the case with the dark energy problem (Albrecht et al. 2006; Peacock et al. 2006). There is firm observational evidence suggesting that the Universe entered a recent stage of accelerated expansion. The physical mechanism driving this expansion rate remains unclear and there exist several potential models. In the framework of General Relativity applied to a homogeneous and isotropic universe, the acceleration could be produced either by an additional term in the gravitational field equations or by a new isotropic comoving perfect fluid with negative pressure, called dark energy (see e.g. Peebles & Ratra 2003; Johri & Rath 2007; Polarski 2013).
The main science goal of the next generation of cosmological probes is to test the concordance model of cosmology. In the case of dark energy, the objective is to measure the expansion history of the Universe and the growth of structure (see Weinberg et al. 2013 for a comprehensive review). In this work, we will consider cosmic shear from a future all-sky survey similar to the European Space Agency mission Euclid, due for launch in 2020 (see Amendola et al. 2013). The main scientific objective of Euclid is to understand the origin of the accelerated expansion of the Universe by probing the nature of dark energy using weak-lensing and galaxy-clustering observations. It could potentially test for departures from the current concordance model (see e.g. Heavens, Kitching & Verde 2007; Jain & Khoury 2010; Zhao et al. 2012). In a previous paper (Debono 2014), we studied the ability of Euclid weak lensing to distinguish between dark energy models. This time, we go a step further by addressing the following question: Based on current data, what model will we select using future weak-lensing data from Euclid? What is the probability that these data could favour ΛCDM?
Cosmologists are faced with the task of constructing valid physical models based on incomplete information. In this relation between data and theory, Bayesian inference provides a quantitative framework for plausible conclusions (see e.g. Robert, Chopin & Rousseau 2009; Hobson et al. 2010; Jenkins & Peacock 2011 for a discussion) and can be understood as operating on three levels:
Parameter inference (estimation): we assume that a model M is true, and we select a prior for the parameters |$p(\boldsymbol {\theta }| M)$|, where p is some probability distribution and |$\boldsymbol {\theta }$| is the set of model parameters.
Model selection or comparison: there are several possible models Mi. We find the relative plausibility of each in the light of the data D.
Model averaging: there is no clear evidence for a best model. We find the inference on the parameters which accounts for the model uncertainty.
The dark energy question is a model comparison or model averaging problem. In this work, we will confine ourselves to model selection.
In order to produce an accelerated expansion at the present epoch, the dark energy equation-of-state parameter should satisfy the conservative bound wDE = pDE/ρDE < −0.5. Observations suggest a lower value, close to −1. If the data are compatible with this value, then in model selection terms it means that they are compatible with ΛCDM. However, ΛCDM is not merely a special case of some more general model where wDE = −1. It contains a smaller number of free parameters, and if it fits the data, it is favoured by the Occam razor effect because it is more predictive. In the cosmological context, the question is whether there is evidence that we need to expand our cosmological model beyond ΛCDM to fit these data (see e.g. Liddle 2004; March et al. 2011).
Consider a result from an experiment quoted in terms of a mean value μ, and a confidence interval σ. This is a parameter estimation result. In the frequentist interpretation, a confidence interval of 68.3 per cent means that if we were to repeat the experiment an infinite number of times and obtain a 1σ distribution for the mean, the true value would lie inside the intervals thus obtained 68.3 per cent of the time. This is not the same as saying that the probability of μ lying within a given interval is 68.3 per cent. The latter is a statement on model selection, and it only follows if we use Bayesian techniques.
In simple terms, how do we know if a given accuracy on a certain mean value is enough to falsify a model? If it falsifies a model, what does it verify? It is therefore clear that model selection calculations must include information on the alternatives under consideration. We cannot reject a hypothesis unless an alternative hypothesis is available that fits the facts better.
In the context of the dark energy problem, it means that a claim such as ‘ΛCDM is false’ is not enough. We need an alternative model, for we would know at least the number of free parameters and their allowed ranges, before the data come along. This is the model prior. Intuitively, we know that the prior affects the model selection outcome. We know wDE to be within range of values around −1, but for a cosmological constant, the prior width is zero. Statistically, we will measure wDE to be a different value each time, so we take some average. It is the average that is compatible with theory that we understand to be the value of the cosmological constant.
The question is therefore to know which range of measured values leads us to choose ΛCDM, and which values lead us to discard it. In terms of model selection, we need to quantify the degree of compatibility with ΛCDM of a measured value of wDE that is xσ away from −1.
One important point to note is that in constructing models, we are seeking to find that model which will best predict future data. We can always include all possible parameters and obtain a perfect fit to the current data, but we also want our model to be predictive. Thus, the model that explains the past data best may not be the most predictive model. Bayesian evidence quantifies this trade-off between goodness of fit and predictivity or model simplicity.
We are interested in forecasting the result of a future model comparison, by predicting the distribution of future data. In this work, we assess the potential of Euclid to address model comparison questions, based on current information. We derive a predictive distribution for the dark energy equation-of-state parameter for a cosmic shear survey with the Euclid probe using the predictive posterior odds distribution (PPOD) method developed by Trotta (2007b). We also study the dependence of our results on the prior width.
This paper is organized as follows. In Section 2, we describe the Bayesian framework. The PPOD method is described in Section 3. Our cosmological and weak-lensing formalism for Euclid, together with the current and future data are described in Section 4. We apply the PPOD to Euclid in Section 5, and present our conclusions in Section 6.
2 BAYESIAN MODEL COMPARISON
The details of Bayesian model comparison and the derivation of the Savage–Dickey density ratio (SDDR) are given in a companion paper (Debono 2014). Here we give a brief overview.
We use the Jeffreys scale to interpret the logarithm of the Bayes factor in terms of the strength of evidence. We adopt a slightly more conservative version of the convention used by Jeffreys (1961) and Trotta (2007a). This is shown in Table 1.
Jeffreys's scale for the strength of evidence when comparing two models M0 (restricted) against M1 (extended), interpreted here as the evidence for the extended model. The probability is the posterior probability of the favoured model, assuming non-committal priors on the two models, and assuming that the two models fill all the model space. Negative evidence for the extended model is equivalent to evidence for the simpler model. Note that the labels attached to the Jeffreys scale are empirical, and their interpretation depends to a large extent on the problem being modelled. An experiment for which |ln B| < 1 is usually deemed inconclusive.
| ln B01 . | Probability . | Evidence . |
|---|---|---|
| >0 | <0.5 | Negative |
| −2.5 to 0 | 0.5 to 0.923 | Positive |
| −5 to −2.5 | 0.923 to 0.993 | Moderate |
| <−5 | >0.993 | Strong |
| ln B01 . | Probability . | Evidence . |
|---|---|---|
| >0 | <0.5 | Negative |
| −2.5 to 0 | 0.5 to 0.923 | Positive |
| −5 to −2.5 | 0.923 to 0.993 | Moderate |
| <−5 | >0.993 | Strong |
Jeffreys's scale for the strength of evidence when comparing two models M0 (restricted) against M1 (extended), interpreted here as the evidence for the extended model. The probability is the posterior probability of the favoured model, assuming non-committal priors on the two models, and assuming that the two models fill all the model space. Negative evidence for the extended model is equivalent to evidence for the simpler model. Note that the labels attached to the Jeffreys scale are empirical, and their interpretation depends to a large extent on the problem being modelled. An experiment for which |ln B| < 1 is usually deemed inconclusive.
| ln B01 . | Probability . | Evidence . |
|---|---|---|
| >0 | <0.5 | Negative |
| −2.5 to 0 | 0.5 to 0.923 | Positive |
| −5 to −2.5 | 0.923 to 0.993 | Moderate |
| <−5 | >0.993 | Strong |
| ln B01 . | Probability . | Evidence . |
|---|---|---|
| >0 | <0.5 | Negative |
| −2.5 to 0 | 0.5 to 0.923 | Positive |
| −5 to −2.5 | 0.923 to 0.993 | Moderate |
| <−5 | >0.993 | Strong |
Inconclusive evidence for one model means that the alternative model cannot be distinguished from the null hypothesis. This occurs when |ln B01| < 1. A positive Bayes factor ln B01 > 0 favours model M0 over M1 with odds of B01 against 1.
3 THE PPOD
In a companion paper (Debono 2014), we examined the ability of Euclid cosmic shear measurements to distinguish between different dark energy models. Our current knowledge is included in the calculations in two ways: through our choice of fiducial model, and through the prior ranges. Implicit in the former is the assumption that the future maximum likelihoods for the cosmological parameters common to all models under consideration will be roughly the same as the current likelihoods. However, we do not include information on the position of the current maximum likelihood of the extra parameters (in this case, the dark energy equation-of-state parameters). In other words, we do not take into account the present posterior distribution.
One way of including this information is through the PPOD developed by Trotta (2007b). This extends the idea of posterior odds forecasting introduced by Trotta (2007a) and also Pahud et al. (2006, 2007), which is based on the concept of predictive probability. This uses present knowledge and uncertainty to predict what a future measurement will find, with corresponding probability. The predictive probability is therefore the future likelihood weighted by the present posterior.
The PPOD is a hybrid technique, combining a Fisher matrix analysis (Fisher 1935, 1936) with the SDDR. It gives us the probability distribution for the model comparison result of a future measurement. It is conditional on our present knowledge, and gives us the probability distribution for the Bayes factor of a future observation. In other words, it allows us to quantify the probability with which a future experiment will be able to confirm or reject the null hypothesis.
The PPOD showed its usefulness in predicting the outcome of the Planck experiment. Trotta (2007b) found that Planck had over 90 per cent probability of obtaining model selection result favouring a scale-dependent primordial power spectrum, with only a small probability that it would find evidence in favour of a scale-invariant spectrum. This result was confirmed by actual data a few years later, when Planck temperature anisotropy measurements combined with the Wilkinson Microwave Anisotropy Probe (WMAP) large-angle polarization found a value of ns = 0.96 ± 0.0073, ruling out scale invariance at over 5σ (Planck Collaboration 2013b).
In this paper, we apply the PPOD technique to the dark energy equation-of-state parameter, comparing the evidence for ΛCDM against a dynamical dark energy model wCDM. From the current posterior, we can produce a PPOD for the Euclid satellite. In this section, we review the formalism of the PPOD.
Let us consider the case of nested models, with |${\boldsymbol {\theta }=(\boldsymbol {\psi },\boldsymbol {\omega })}$| as defined previously. It is reasonable to assume that the current and future likelihoods for the data considered in this paper are both Gaussian. For future data, this assumption is implicit in our use of Fisher matrix analysis to forecast the future covariance matrix |$\bf{C}$|. We make the further assumption that the covariance matrix does not depend on the fiducial values chosen for the common parameters |$\boldsymbol {\psi }$|. Then, we can marginalize over the common parameters, and compare a one-dimensional model M1 with a model M0 with no free parameters.
The priors on the extra parameter are taken to be Gaussian, centred on zero, with a prior width equal to unity. The current likelihood is also assumed to be Gaussian, centred on ω = μ of width σ. The Gaussian mean and width are expressed in units of the prior width and are therefore dimensionless. Likewise, the predicted likelihood is assumed to have a Gaussian distribution, with mean ω = ν and constant standard deviation τ. The latter is the forecast error |$\tau =\sqrt{\mathbb {C}_{11}}$| obtained from a Fisher matrix calculation. It is assumed to be independent of ω, which is a reasonable assumption, since the marginalized errors are very stable to a change in the fiducial values of the model parameters over the region of interest (see Debono 2014 for the variation of the dark energy Figure of Merit in the w0-wa parameter space).
Note that in the equation above, |$p(M_0)=p(M_1)=\frac{1}{2}$|. At present, there is no evidence which justifies assigning a higher probability to a particular model. This is a statement on our prior knowledge, which is based on the accumulation of information from a multitude of experiments (see Brewer & Francis 2009). In this paper, we justify assigning equal probabilities to each model because we are testing two at a time.
4 FORECASTS FOR EUCLID
We apply the PPOD technique to assess the potential of the Euclid mission in terms of model selection, taking into account the information from current data. Our current information is taken from Planck results, while we forecast our future cosmic shear data from Euclid.
4.1 The future data
We forecast the errors for future Euclid cosmic shear data using the Fisher matrix technique. The restricted fiducial cosmological model used for our forecast contains parameters describing baryonic matter, CDM, massive neutrinos (or HDM) and dark energy. We drop the requirement for flat spatial geometry by including a dark energy density parameter ΩDE together with the total matter density Ωm.
We choose fiducial parameter values based on the Planck 2013 best-fitting values (Planck Collaboration 2013a):
Total matter density: Ωm = 0.31 (which includes baryonic matter, HDM and CDM),
Baryonic matter density: Ωb = 0.048,
Neutrinos (HDM): mν = 0.25 eV (total mass); Nν = 3 (number of massive neutrino species),
Dark energy density: ΩDE = 0.69,
Hubble parameter: h = 0.67(100 km−1 Mpc−1) and
Primordial power spectrum parameters: σ8 = 0.82 (amplitude); ns = 0.9603 (scalar spectral index); α = 0 (its running).
We assume a total of three neutrino species, with degenerate masses for the most massive eigenstates. The temperature of the relativistic neutrinos is assumed to be equal to (4/11)1/3 of the photon temperature. We model Nν, the number of massive neutrino species, by a continuous variable.
CMB anisotropy observations from the Planck probe suggest caution in employing an overly simple parametrization of the primordial power spectrum (Planck Collaboration 2013a,b). For this reason, we allow for possible departures from a scale-invariant primordial power spectrum.
For simplicity, we shall refer to this fiducial model as ΛCDM. Note that our work implicitly assumes that future best-fitting values for the restricted model will not deviate significantly from the current ones. This assumption must be used carefully (see Starkman, Trotta & Vaudrevange 2010) but it is a reasonable one when studying the question of nested models. In this case, the model doubt really only concerns the need for the additional parameters in the extended model (see Starkman, Trotta & Vaudrevange 2008; March et al. 2011).
We use the numerical Boltzmann code camb (Lewis, Challinor & Lasenby 2000) to calculate the linear matter power spectrum. This includes the contribution of baryonic matter, CDM, dark energy and massive neutrino oscillations. We use the Smith et al. (2003) halofit fitting formula to calculate the non-linear power spectrum, with the modification by Bird, Viel & Haehnelt (2012). The power spectrum is normalized using σ8, the root-mean-square amplitude of the density contrast inside an 8 h−1 Mpc sphere.
To calculate future errors, we use forecasts for an all-sky tomographic weak-lensing survey similar to Euclid (Laureijs et al. 2011; Amendola et al. 2013), using the method described in Debono (2014).
We calculate the measurement errors based on two configurations of the Euclid-type survey, referred to as the ‘requirements’ and ‘goals’ in the Euclid Definition Study Report (Laureijs et al. 2011). The experiment is defined by the following parameters: the survey area As, median redshift of the density distribution of galaxies zmedian, the observed number density of galaxies ng, the photometric redshift errors σz(z), and the intrinsic noise in the observed ellipticity of galaxies σϵ, such that |$\sigma _\epsilon ^2=\sigma _\gamma ^2$|, where σγ is the variance in the shear per galaxy. These parameters are shown in Table 2.
Fiducial parameters for the Euclid-type all-sky weak-lensing survey used for our future data.
| Survey property . | Requirements . | Goals . |
|---|---|---|
| As/deg2 | 15 000 | 20 000 |
| zmedian | 0.9 | 0.9 |
| ng/arcmin2 | 30 | 40 |
| σz(z)/(1 + z) | 0.05 | 0.03 |
| σϵ | 0.25 | 0.25 |
| Survey property . | Requirements . | Goals . |
|---|---|---|
| As/deg2 | 15 000 | 20 000 |
| zmedian | 0.9 | 0.9 |
| ng/arcmin2 | 30 | 40 |
| σz(z)/(1 + z) | 0.05 | 0.03 |
| σϵ | 0.25 | 0.25 |
Fiducial parameters for the Euclid-type all-sky weak-lensing survey used for our future data.
| Survey property . | Requirements . | Goals . |
|---|---|---|
| As/deg2 | 15 000 | 20 000 |
| zmedian | 0.9 | 0.9 |
| ng/arcmin2 | 30 | 40 |
| σz(z)/(1 + z) | 0.05 | 0.03 |
| σϵ | 0.25 | 0.25 |
| Survey property . | Requirements . | Goals . |
|---|---|---|
| As/deg2 | 15 000 | 20 000 |
| zmedian | 0.9 | 0.9 |
| ng/arcmin2 | 30 | 40 |
| σz(z)/(1 + z) | 0.05 | 0.03 |
| σϵ | 0.25 | 0.25 |
4.2 Dark energy parametrization
This paper examines the question of whether dark energy is Λ or whether there is evidence for dynamical dark energy. Specifically, we ask how well the future Euclid probe will be able to answer this in the light of the current model selection outcome.
We include dark energy perturbations in all our calculations by using the parametrized post-Friedmann framework (Hu & Sawicki 2007; Hu 2008) as implemented in camb (Fang, Hu & Lewis 2008; Fang et al. 2008).
As stated previously, we assume uncorrelated priors for the parameters in the restricted cosmological model and the extra parameter. The joint prior of (w0, ψ) is simply the product of the individual priors of w0 and ψ. This allows us to use the SDDR (equation 5) to find the Bayes factor. Strictly speaking, this is not the case (ψ includes wa, for instance), but our assumption is justified if we consider the form of the prior to be the space of possible choices, and not the space of actual observed data. In calculating the SDDR, we assume total ignorance of the possible values of the parameters in ψ. In other words, we take ‘ignorance’ to be consistent with ‘independence’.
4.3 The current data
As our current posterior, we use the results from four Planck data sets used by the Planck Collaboration (2013a) to estimate the values of cosmological parameters. In these parameter-estimation calculations, the Planck temperature power spectrum is combined with a WMAP polarization low-multipole likelihood and with four other data sets, as detailed below:
Planck+WP+BAO: Planck and WMAP, combined with baryon acoustic oscillation measurements;
Planck+WP+Union 2.1: Planck and WMAP, combined with an updated Union2.1 supernova compilation by Suzuki et al. (2012);
Planck+WP+SNLS: Planck and WMAP, combined with the Supernova Legacy Survey compilation by Conley et al. (2011); and
Planck+WP+H0: Planck and WMAP, combined with the Riess et al. (2011) H0 measurements.
Model selection results with four current data sets including Planck, assuming a Gaussian prior centred on w0 = −1 with a prior width of 0.5. Most of the data favour ΛCDM. A combination of Planck, WP and H0 data shows positive evidence for dynamical dark energy. Note that this calculation uses a rather restrictive prior. This model of dynamical dark energy would have an equation-of-state parameter in the range −1.5 < w0 < −0.5.
| Current data . | w0 . | σ . | ln B01 . | Evidence . |
|---|---|---|---|---|
| Planck+WP+BAO | −1.13 | 0.120 | 0.900 | Positive for ΛCDM |
| Planck+WP+Union2.1 | −1.09 | 0.085 | 1.241 | Positive for ΛCDM |
| Planck+WP+SNLS | −1.13 | 0.065 | 0.082 | Inconclusive to weak for ΛCDM |
| Planck+WP+H0 | −1.24 | 0.090 | −1.713 | Positive for wCDM |
| Current data . | w0 . | σ . | ln B01 . | Evidence . |
|---|---|---|---|---|
| Planck+WP+BAO | −1.13 | 0.120 | 0.900 | Positive for ΛCDM |
| Planck+WP+Union2.1 | −1.09 | 0.085 | 1.241 | Positive for ΛCDM |
| Planck+WP+SNLS | −1.13 | 0.065 | 0.082 | Inconclusive to weak for ΛCDM |
| Planck+WP+H0 | −1.24 | 0.090 | −1.713 | Positive for wCDM |
Model selection results with four current data sets including Planck, assuming a Gaussian prior centred on w0 = −1 with a prior width of 0.5. Most of the data favour ΛCDM. A combination of Planck, WP and H0 data shows positive evidence for dynamical dark energy. Note that this calculation uses a rather restrictive prior. This model of dynamical dark energy would have an equation-of-state parameter in the range −1.5 < w0 < −0.5.
| Current data . | w0 . | σ . | ln B01 . | Evidence . |
|---|---|---|---|---|
| Planck+WP+BAO | −1.13 | 0.120 | 0.900 | Positive for ΛCDM |
| Planck+WP+Union2.1 | −1.09 | 0.085 | 1.241 | Positive for ΛCDM |
| Planck+WP+SNLS | −1.13 | 0.065 | 0.082 | Inconclusive to weak for ΛCDM |
| Planck+WP+H0 | −1.24 | 0.090 | −1.713 | Positive for wCDM |
| Current data . | w0 . | σ . | ln B01 . | Evidence . |
|---|---|---|---|---|
| Planck+WP+BAO | −1.13 | 0.120 | 0.900 | Positive for ΛCDM |
| Planck+WP+Union2.1 | −1.09 | 0.085 | 1.241 | Positive for ΛCDM |
| Planck+WP+SNLS | −1.13 | 0.065 | 0.082 | Inconclusive to weak for ΛCDM |
| Planck+WP+H0 | −1.24 | 0.090 | −1.713 | Positive for wCDM |
The Bayesian evidence for ΛCDM against a dynamical dark energy model wCDM with −1.5 < w0 < −0.5 is given in the fourth column of Table 3. Our model selection results qualitatively confirm general conclusions of the Planck parameter estimation results (Planck Collaboration 2013a), where a wider prior range is used. In the Planck paper, the BAO and Union2.1 data sets were found to be compatible with a cosmological constant, SNLS data weakly favour the phantom domain, while H0 data are in tension with w = −1.
From our results, we conclude that most of the current Planck data favour a cosmological constant. Next, we turn to the question of whether future data from the Euclid probe can overturn these results.
5 THE PPOD APPLIED TO THE DARK ENERGY QUESTION
We produce a PPOD forecast for Euclid following the method described in Section 3. The physical question we study is the choice of dark energy model. We therefore focus on the dark energy equation-of-state parameter w0, comparing a cosmological constant model (ΛCDM) with w0 = −1 against a dynamical dark energy model (wCDM) with a Gaussian prior of width Δw0 = 0.5. We calculate the PPOD for two configurations of the Euclid survey, based on the present knowledge from the four data sets described earlier. The constant future and current errors, τ and σ respectively, are expressed in units of the prior width Δw0 = 0.5. Thus, the current errors are τ = 0.0551/Δw0 = 0.1102 and τ = 0.0382/Δw0 = 0.0764 for the requirement and goal survey, respectively. Likewise, we express the current mean μ and future mean ν in units of the prior width.
5.1 PPOD forecasts
The predictive distribution for Euclid using current knowledge from Planck is shown in Fig. 1. For the Planck+BAO+supernova data, the peak of the distribution is located at w0 = −1. This is a consequence of the fact that the errors around the current mean with these data sets are too large to exclude w0 = −1. For the Planck+WP+H0 data set, the most probable models are located around w0 = −1.24.
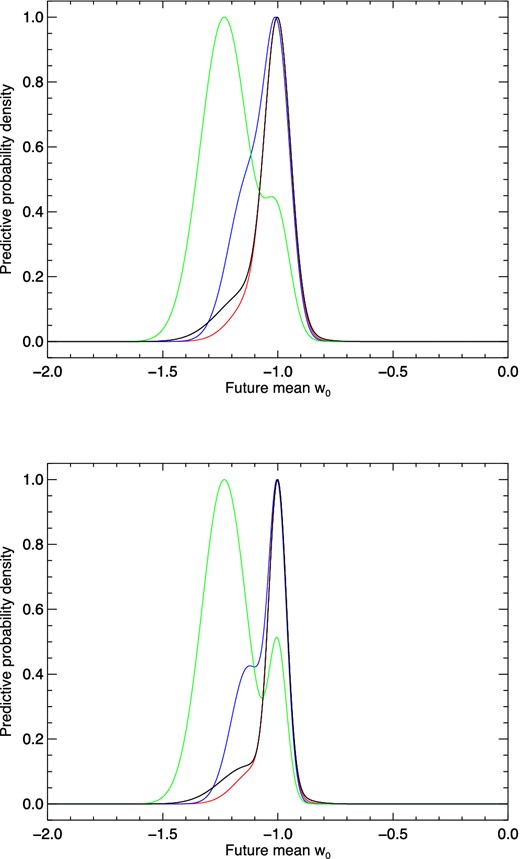
The predictive data distribution for Euclid cosmic shear, conditional on current knowledge. The probability distribution (normalized to the peak) is that of future measurements of the dark energy equation-of-state parameter w0. The peaks centred on w0 = −1 correspond to ΛCDM. We use Euclid ‘requirement’ and ‘goal’ survey parameters in the top and bottom panel, respectively. In each panel, we plot p(D|d) for four current data sets: Planck+WP+BAO (black), Planck+WP+Union 2.1 (red), Planck+WP+SNLS (blue) and Planck+WP+H0 (green).
The PPOD results obtained from the predictive distribution are shown in Table 4. The main result is that Euclid has a low probability of finding high-odds evidence [i.e. p(ln B < −5)] for wCDM for the Planck data sets using BAO and supernova data. If the current mean is given by the Planck+WP+H0 data set, then this probability increases to more than 50 per cent. This is consistent with the model selection results for Planck given in Table 3. It means that Euclid is not likely to overturn the current model selection results for this choice of prior.
Probability of future model selection results for the two survey configurations of the Euclid mission described in the test, using cosmic shear data, conditional on present knowledge from four Planck data sets. The probability that Euclid will favour ΛCDM is shown in the last column. The third to fifth columns give the probability that Euclid will provide strong, moderate and positive evidence for wCDM, respectively.
| Dark energy: w0 = −1 versus −1.5 ≤ w0 ≤ −0.5 (Gaussian) . | |||||
|---|---|---|---|---|---|
| Future data . | Current data . | p(ln B < −5) . | p(−5 < ln B < −2.5) . | p(−2.5 < ln B < 0) . | p(ln B > 0) . |
| Euclid requirement survey | |||||
| Planck+WP+BAO | 0.150 | 0.160 | 0.337 | 0.353 | |
| Planck+WP+Union2.1 | 0.108 | 0.156 | 0.356 | 0.380 | |
| Planck+WP+SNLS | 0.252 | 0.225 | 0.278 | 0.245 | |
| Planck+WP+H0 | 0.531 | 0.200 | 0.160 | 0.109 | |
| Euclid goal survey | |||||
| Planck+WP+BAO | 0.163 | 0.135 | 0.309 | 0.393 | |
| Planck+WP+Union2.1 | 0.125 | 0.137 | 0.323 | 0.414 | |
| Planck+WP+SNLS | 0.286 | 0.185 | 0.253 | 0.276 | |
| Planck+WP+H0 | 0.621 | 0.119 | 0.132 | 0.128 | |
| Dark energy: w0 = −1 versus −1.5 ≤ w0 ≤ −0.5 (Gaussian) . | |||||
|---|---|---|---|---|---|
| Future data . | Current data . | p(ln B < −5) . | p(−5 < ln B < −2.5) . | p(−2.5 < ln B < 0) . | p(ln B > 0) . |
| Euclid requirement survey | |||||
| Planck+WP+BAO | 0.150 | 0.160 | 0.337 | 0.353 | |
| Planck+WP+Union2.1 | 0.108 | 0.156 | 0.356 | 0.380 | |
| Planck+WP+SNLS | 0.252 | 0.225 | 0.278 | 0.245 | |
| Planck+WP+H0 | 0.531 | 0.200 | 0.160 | 0.109 | |
| Euclid goal survey | |||||
| Planck+WP+BAO | 0.163 | 0.135 | 0.309 | 0.393 | |
| Planck+WP+Union2.1 | 0.125 | 0.137 | 0.323 | 0.414 | |
| Planck+WP+SNLS | 0.286 | 0.185 | 0.253 | 0.276 | |
| Planck+WP+H0 | 0.621 | 0.119 | 0.132 | 0.128 | |
Probability of future model selection results for the two survey configurations of the Euclid mission described in the test, using cosmic shear data, conditional on present knowledge from four Planck data sets. The probability that Euclid will favour ΛCDM is shown in the last column. The third to fifth columns give the probability that Euclid will provide strong, moderate and positive evidence for wCDM, respectively.
| Dark energy: w0 = −1 versus −1.5 ≤ w0 ≤ −0.5 (Gaussian) . | |||||
|---|---|---|---|---|---|
| Future data . | Current data . | p(ln B < −5) . | p(−5 < ln B < −2.5) . | p(−2.5 < ln B < 0) . | p(ln B > 0) . |
| Euclid requirement survey | |||||
| Planck+WP+BAO | 0.150 | 0.160 | 0.337 | 0.353 | |
| Planck+WP+Union2.1 | 0.108 | 0.156 | 0.356 | 0.380 | |
| Planck+WP+SNLS | 0.252 | 0.225 | 0.278 | 0.245 | |
| Planck+WP+H0 | 0.531 | 0.200 | 0.160 | 0.109 | |
| Euclid goal survey | |||||
| Planck+WP+BAO | 0.163 | 0.135 | 0.309 | 0.393 | |
| Planck+WP+Union2.1 | 0.125 | 0.137 | 0.323 | 0.414 | |
| Planck+WP+SNLS | 0.286 | 0.185 | 0.253 | 0.276 | |
| Planck+WP+H0 | 0.621 | 0.119 | 0.132 | 0.128 | |
| Dark energy: w0 = −1 versus −1.5 ≤ w0 ≤ −0.5 (Gaussian) . | |||||
|---|---|---|---|---|---|
| Future data . | Current data . | p(ln B < −5) . | p(−5 < ln B < −2.5) . | p(−2.5 < ln B < 0) . | p(ln B > 0) . |
| Euclid requirement survey | |||||
| Planck+WP+BAO | 0.150 | 0.160 | 0.337 | 0.353 | |
| Planck+WP+Union2.1 | 0.108 | 0.156 | 0.356 | 0.380 | |
| Planck+WP+SNLS | 0.252 | 0.225 | 0.278 | 0.245 | |
| Planck+WP+H0 | 0.531 | 0.200 | 0.160 | 0.109 | |
| Euclid goal survey | |||||
| Planck+WP+BAO | 0.163 | 0.135 | 0.309 | 0.393 | |
| Planck+WP+Union2.1 | 0.125 | 0.137 | 0.323 | 0.414 | |
| Planck+WP+SNLS | 0.286 | 0.185 | 0.253 | 0.276 | |
| Planck+WP+H0 | 0.621 | 0.119 | 0.132 | 0.128 | |
There are two points to note about the PPOD results given here. First, the Gaussian approximation used in the PPOD breaks down in the tails of the distribution. Secondly, the intervals for ln B used in the Jeffreys scale are arbitrary. Furthermore, the interpretation given to each region has an empirical origin in betting odds and depends to some extent on the nature of the model selection question (see Kass & Raftery 1995; Efron & Gous 2001; Nesseris & García-Bellido 2013). For these reasons, the results given here should be interpreted as a rough guide to the model selection outcome. A more general result can be obtained at the expense of computational speed by dropping the assumption of Gaussianity of the current and future likelihoods and sampling from both using Markov chain Monte Carlo techniques.
It should be noted that the future data set considered here is the weak-lensing part of the Euclid mission, and our results only apply to these data. Euclid has two primary probes of dark energy, which are weak lensing and galaxy clustering. With weak lensing alone, using the goal survey parameters, we obtain a dark energy Figure of Merit (as defined in Albrecht et al. 2006) of 102 (Debono 2014). The addition of galaxy-clustering data improves the Figure of Merit by a factor of ∼4, and would provide decisive Bayesian evidence in favour of a cosmological constant if the data are consistent with this model (Laureijs et al. 2011).
However, if there is some tension between the current maximum likelihood result and a cosmological constant, then an improvement in dark energy parameter precision will not result in a substantial improvement in the odds in favour of a cosmological constant. This is the case with the Planck+WP+H0 data. If we use the Euclid Red Book joint weak-lensing and galaxy-clustering predicted precision of Δw0 = 0.015 (Laureijs et al. 2011), we obtain p(ln B > 0) = 0.142, which is only a slight improvement on the probability of 0.128 using the Euclid goal survey, shown in Table 4, where we only consider weak-lensing future data.
On the other hand, using Planck+WP+BAO as current data, with joint weak lensing and galaxy clustering as future data, we obtain a probability of 0.497 for Bayesian evidence in favour of the ΛCDM model, which is a significant improvement on the lensing-only result. The point here is that an improvement in parameter precision decreases the error around the current estimated parameter value, and accumulates more evidence around the peak of the current distribution. If the current value of the peak is in tension with ΛCDM, then improved parameter precision is unlikely to overturn the current Bayesian evidence result. For the current Bayesian evidence result to be overturned, there would have to be a systematic shift in the position of the peak of the likelihood in future data. We know this to be the case intuitively.
In our calculations for parameter errors from future data, we include statistical uncertainties, but not systematic effects, which reduce the precision and introduce bias (see e.g. Massey et al. 2013 for a review). We expect a weak-lensing survey such as the one described here to be affected by various systematics including measurement systematics from point spread function effects (Kaiser, Squires & Broadhurst 1995; Hoekstra 2004; Mandelbaum et al. 2014), redshift distribution systematics (Hu & Tegmark 1999; Ma, Hu & Huterer 2006; Amara & Réfrégier 2007; Cardone et al. 2014), theoretical uncertainties on the matter power spectrum, especially in the non-linear regime (Huterer & Takada 2005; Hilbert et al. 2009; Teyssier et al. 2009; Beynon et al. 2012) and intrinsic correlations (King & Schneider 2003; Bridle & King 2007; Joachimi & Schneider 2009).
Cosmic shear surveys are especially affected by intrinsic alignment signal contamination. A perfect knowledge of the intrinsic alignment signal would allow us to produce unbiased measurements. There is a wide variation in the impact on the degradation of the dark energy parameter errors, depending on the intrinsic alignment model (Kirk et al. 2012; Heymans et al. 2013). The dark energy Figure of Merit can be degraded by 20–50 per cent depending on the intrinsic–intrinsic and galaxy–intrinsic correlation model chosen (Bridle & King 2007). These correlations, to a certain extent, can be mitigated by using a sufficient number of redshift bins. Laszlo et al. (2012) find that the inclusion of intrinsic alignments can change the dark energy equation-of-state Figure of Merit by a factor of ∼4, but that the constraints can be recovered by combining CMB data with shear data. Provided the intrinsic alignment model is accurate enough, galaxy–intrinsic correlations themselves can be used as a cosmological probe, and the inclusion of this effect can actually enhance constraints on dark energy (Kitching & Taylor 2011).
Precise calculation of the errors on any parameter achievable with a weak-lensing survey is therefore highly dependent on a host of nuisance parameters and physical models. The PPOD technique only requires knowledge of the statistical properties of the parameters of interest, which means that the model selection part of the technique is independent of the parameter estimation algorithm. The parameter of interest in this work is w0. The error forecasts for w0 presented here are the best that can be achieved for the survey design described, using weak lensing only.
5.2 The dependence on the prior
The dependence of model selection conclusions on the prior range is an important aspect of modern cosmology (see e.g. Kunz, Trotta & Parkinson 2006). The prior width determines the strength of the Occam's razor effect, since a larger prior favours the simpler model. While the prior range should be large enough to contain most of the likelihood volume, an arbitrarily large prior can result in an arbitrarily small evidence for the extended model. For a discussion on the dependence of evidence on the choice of prior see e.g. Kunz et al. (2006), Trotta (2007a) and Brewer & Francis (2009). In Section 5, we used a fixed prior width of 0.5. We now examine the impact of a change of prior on our PPOD results.
In Fig. 2, we show the dependence on the prior width of the probabilities for Euclid weak lensing to obtain different levels of evidence for a dynamical dark energy model wCDM against a cosmological constant model ΛCDM. As current data, we use the Planck+WP+BAO data set. Our results hold for a wide range of priors. We note that the probability of evidence for ΛCDM approaches 75 per cent while the probability of strong evidence for wCDM falls below 10 per cent as the prior is widened beyond Δw0 = 1. The prior would have to be narrowed to less than 0.2 for the model selection conclusion to be reversed, namely, for the probability of strong evidence for wCDM to be greater than the evidence for ΛCDM. For any reasonable choice of prior, and for both Euclid survey configurations, there is at most 25 probability of strong evidence for wCDM.
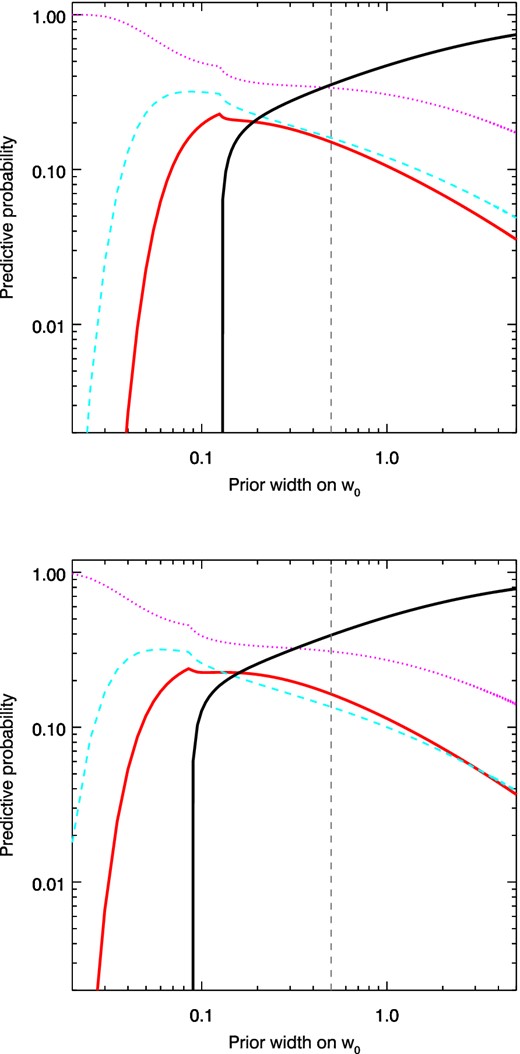
The PPOD dependence on the prior width of w0, using Planck+WP+BAO as the current data, and forecasts for Euclid with a requirement survey configuration. The vertical dotted line shows the prior width of 0.5 used to calculate P(D|d) in the previous figure. The lines show the future probability of evidence for wCDM according to the Jeffreys scale for Bayesian evidence: positive (magenta dots), moderate (cyan dashes), strong (thick red line) and negative (thick black line). Negative evidence for the extended model is equivalent to evidence for the restricted model ΛCDM. In order to obtain a larger probability for moderate evidence for wCDM, one would have to use a prior width smaller than about 0.4. With a prior width smaller than about 0.2, when the evidence for ΛCDM drops sharply, the bulk of the data will provide only positive evidence for wCDM, falling short of strong or even moderate evidence. In Jeffreys's terminology, the evidence is in the inconclusive regime. The probability of strong evidence for wCDM with this prior width is below 20 per cent.
These results show the important role of the prior in the dark energy question. The narrower the prior, the greater the precision on w0 that is required to provide evidence for the extended model. The prior width defines the model predictivity space. When we seek some significant evidence for ΛCDM, we are in fact finding the space of models that can be significantly disfavoured with respect to w0 = −1 at a given accuracy. This point is highlighted in Trotta (2006). For an extended model with small departures from ΛCDM, it is evident that the required accuracy needs to be higher than if we were testing an extended model with large departures from ΛCDM.
6 CONCLUSIONS
We have applied the PPOD technique to produce forecasts for the Bayes factor using weak lensing from the future Euclid probe. We carry out our calculations for the dark energy equation-of-state parameter w0, which is a central parameter in the dark energy model selection question.
We have shown that there is a high probability that cosmic shear data from Euclid will confirm current Planck model selection results, where the evidence for ΛCDM is positive but not overwhelming. The most important result is that for three out of four current data sets, using a prior range of −1.5 < w0 < −0.5, future data have less than 29 per cent probability of providing strong evidence for w0 ≠ −1. For a wider prior range, compatible with the theoretical priors of dynamical dark energy models, the probability of evidence for ΛCDM rises to above 75 per cent while the probability of strong evidence for w0 ≠ −1 falls to less than 5 per cent.
These conclusions qualitatively support the results in Debono (2014), in which we find that Euclid cosmic shear data forecasts return an undecided Bayesian evidence result if the true values of w0 and wa are close to their ΛCDM fixed values of −1 and 0. Furthermore, this work shows that ΛCDM is still well supported by the forecasts if we include current information, since the inclusion of the extra parameter w0 is not required by Bayesian evidence, even if the alternative model has a relatively narrow prior range (Δw0 = 0.5). As we widen the prior range, the probability of evidence for ΛCDM becomes overwhelming.
Improving the parameter precision by going from a requirement to a goal-survey configuration increases the probability of evidence in favour of ΛCDM. This result holds for all prior ranges considered in this paper. The addition of galaxy-clustering data improves the parameter precision and the probability even further. Our results highlight the essential role of both parameter precision and prior width in deciding model selection questions.
The author is supported by a European Space Agency International Research Fellowship.



