-
PDF
- Split View
-
Views
-
Cite
Cite
Kai Hoffmann, Susana Planelles, Enrique Gaztañaga, Alexander Knebe, Frazer R. Pearce, Hanni Lux, Julian Onions, Stuart I. Muldrew, Pascal Elahi, Peter Behroozi, Yago Ascasibar, Jiaxin Han, Michal Maciejewski, Manuel E. Merchan, Mark Neyrinck, Andrés N. Ruiz, Mario A. Sgro, Subhaloes gone Notts: subhaloes as tracers of the dark matter halo shape, Monthly Notices of the Royal Astronomical Society, Volume 442, Issue 2, 1 August 2014, Pages 1197–1210, https://doi.org/10.1093/mnras/stu933
Close - Share Icon Share
Abstract
We study the shapes of subhalo distributions from four dark-matter-only simulations of Milky Way-type haloes. Comparing the shapes derived from the subhalo distributions at high resolution to those of the underlying dark matter fields, we find the former to be more triaxial if the analysis is restricted to massive subhaloes. For three of the four analysed haloes, the increased triaxiality of the distributions of massive subhaloes can be explained by a systematic effect caused by the low number of objects. Subhaloes of the fourth halo show indications for anisotropic accretion via their strong triaxial distribution and orbit alignment with respect to the dark matter field. These results are independent of the employed subhalo finder. Comparing the shape of the observed Milky Way satellite distribution to those of high-resolution subhalo samples from simulations, we find agreement for samples of bright satellites, but significant deviations if faint satellites are included in the analysis. These deviations might result from observational incompleteness.
1 INTRODUCTION
The modelling of how galaxies trace the underlying matter field is one of the biggest uncertainties in observational cosmology. Understanding the relation between the distributions of galaxies and matter at small scales, such as those of galaxy groups and clusters, turns out to be difficult due to the non-linear evolution of matter density fluctuations and the complex processes involved in galaxy formation. However, it is worth addressing this challenge as modelling the galaxy distribution at these scales increases the statistical power of cosmological surveys. Furthermore, it opens the possibility of comparing model predictions to the well-observed properties of our local Universe.
The host haloes of galaxy groups and clusters can be characterized by their radial density profiles and their triaxiality. In this study, we are interested in the latter property as we analyse the relation between the shape of dark matter (DM) haloes obtained from high-resolution simulations and their subhalo populations. The relation between these shapes is relevant for the Halo Occupation Distribution models, which are used to predict and interpret observational data. In these models, satellite galaxies are distributed in host haloes with an assumed ellipticity. This ellipticity has an impact on the correlation functions derived from these models (e.g. Smith & Watts 2005; Smith, Watts & Sheth 2006; van Daalen, Angulo & White 2012).
Observations of the local Universe suggest that the shapes of host haloes and those of their satellite populations are not necessarily the same since the satellites are found to be distributed along thin discs. During recent years, the discs of satellite galaxies around the Milky Way (MW; Demers & Kunkel 1976; Lynden-Bell 1976) and the Andromeda galaxies (M31; Koch & Grebel 2006; Metz, Kroupa & Jerjen 2007, 2009; Pawlowski et al. 2012; Conn et al. 2013) are discussed in the literature with focus on whether or not such flat satellite distributions around MW-like host haloes are expected in the standard, spatially flat Λ cold dark matter model with cosmological constant (ΛCDM; Blumenthal et al. 1984).
Within this hierarchical model of structure formation, haloes accrete matter from preferential directions of the surrounding sheets and filaments. As a consequence, the substructure distribution in haloes is not expected to be spherical until the orbits of the accreted matter components are completely randomized (Knebe et al. 2004; Libeskind et al. 2005; Zentner et al. 2005). Such an anisotropic accretion of substructures was first observed in simulations by Tormen (1997, see Lovell et al. 2011; Vera-Ciro et al. 2011; Libeskind et al. 2012 for recent studies). Indeed, flat satellite systems are also found in CDM N-body simulations, albeit those are unlikely to be as flat as the satellite systems of the MW and M31 (see e.g. Wang, Frenk & Cooper 2013, who also take into account possible obscuration effects from the galactic disc). However, ΛCDM simulations of the local Universe with constrained initial conditions are able to reproduce the galaxy distribution in our neighbourhood. Analysing a set of such simulations, Libeskind et al. (2011) found that the local satellite distribution probably results from anisotropic accretion of matter.
Light was shed from a different angle on the anisotropic accretion scenario by Danovich et al. (2012). Simulating DM together with gas in hydrodynamical simulations these authors find that, at high redshifts, a large fraction of the baryonic mass of massive haloes is accreted from a few narrow streams of cold gas which tend to lie in the same sheets of the DM distribution. This effect leads to thin discs of satellites (Goerdt & Burkert 2013) and might explain why planar subhalo distributions as thin as the MW and M31 are unlikely to be found in DM-only simulations.
However, discrepancies between the discs of satellites in ΛCDM simulations and observations of the Local Group as well as the missing satellite problem (e.g. Weinmann et al. 2006) motivate the exploration of alternative formation scenarios, within which the discs of satellites could originate from tidal arms developed during an encounter of a young MW with another galaxy (e.g. Pawlowski et al. 2012 suggested M31 for the Large Magellanic Cloud). Such events are observed (e.g. Weilbacher, Duc & Fritze-v. Alvensleben 2003) and can be also seen in simulations (e.g. Bournaud, Duc & Emsellem 2008) without requiring the assumption of CDM.
In this study, we aim to improve the understanding of why massive subhaloes in ΛCDM simulations are distributed anisotropically around the centre of their host halo. We therefore examine the shape of the DM subhalo populations in four MW-like host haloes from the Aquarius simulation to disentangle systematic effects from anisotropic accretion as possible explanation for the flat distribution of the most massive subhaloes. Two possible systematics are studied:
Substructures in DM haloes are not well-defined objects. After accretion, DM particles can move away from the subhalo, as the latter orbits under the action of the complex gravitational field of its host. The question if a given DM particle is still associated with the subhalo within which it entered the host can be answered differently by different subhalo finders. The resulting uncertainty of subhalo properties (e.g. mass) causes the problem that subhalo samples, defined by these properties, can consist of different objects, depending on the employed subhalo finder. Uncertainties of subhalo properties can therefore propagate into uncertainties in the shape of their distribution if, for instance, the N most massive subhaloes are analysed.
Besides the detection of subhaloes in simulations, the small number of massive (observationally speaking, the most luminous) subhaloes complicates the shape measurement of their distribution. Ensembles with low numbers of objects are more likely to appear aligned, which can cause an apparent, non-physical flattening of subhalo distributions.
Looking for indications of anisotropic infall, we also investigate the orbit orientation of subhaloes, given by the direction of their angular momenta, with respect to the DM field of the corresponding host haloes.
Finally, after investigating possible reasons for the flatness of the Aquarius subhalo populations, we compare the shape of these populations to results computed from the observed MW satellite distribution.
This paper is organized as follows: in Section 2, we describe the simulations analysed in this work together with the different subhalo finders participating in this study; in Section 3, we introduce the method used to derive halo shapes. Shape measurements of haloes and their subhalo population are presented in Section 4 together with an analysis on subhalo orbit orientation with respect to the DM field and a comparison with shapes of the observed MW satellite distribution. Finally, our findings are summarized and discussed in Section 5. In the appendix, we study the accuracy and precision of our shape measurements and present the observational data.
2 SIMULATIONS
We study subhalo populations from four simulated MW-sized host haloes. These haloes are part of the Aquarius simulation project (Springel et al. 2008) – a suite of high-resolution N-body simulations performed using the cosmological smoothed particle hydrodynamics code gadget-3 (based on gadget-2; Springel 2005). The simulated haloes were selected from the larger cosmological ΛCDM simulation Millennium-II (Boylan-Kolchin et al. 2009) and then re-simulated at higher resolution with the cosmological parameters Ωm = 0.25, ΩΛ = 0.75, σ8 = 0.9, ns = 1 and H0 = 100 h km s-1 Mpc-1 = 73 km s−1 Mpc-1.
The four Aquarius haloes analysed in this work, labelled from Aq-A to Aq-D, have final masses of ∼1012 M⊙ and were chosen to be relatively isolated at redshift z = 0. Each halo has been re-simulated at five resolution levels, labelled as 5, for the lowest, to 1, for the highest resolution level, respectively. The mass per particle varies from mp = 2.94 × 106 h−1 M⊙ in level 5 to mp = 1.25 × 103 h−1 M⊙ in the highest resolution run, resolving a given halo with approximately half-million up to 1.5-billion particles within the virial radius for level 5 and 1, respectively. In our analysis we focus on subhaloes detected at the second highest level of resolution 2 at z = 0. Those are compared to the DM field at the second lowest level of resolution 4 (DM data from higher resolution runs was not available for this analysis). The particle masses of these haloes are shown in Table 1. More information on the haloes is given by Springel et al. (2008).
Haloes from the Aquarius simulation analysed in this work. The left-hand column shows the simulation name, encoding the halo (A to D), and the resolution level (2 and 4); the corresponding particle masses are shown in the right-hand column, where h = 0.73.
| Halo . | Particle mass (h−1 M⊙) . |
|---|---|
| Aq-A-2 | 1.877 × 104 |
| Aq-A-4 | 5.382 × 105 |
| Aq-B-2 | 8.832 × 103 |
| Aq-B-4 | 3.071 × 105 |
| Aq-C-2 | 1.916 × 104 |
| Aq-C-4 | 4.401 × 105 |
| Aq-D-2 | 1.914 × 104 |
| Aq-D-4 | 3.667 × 105 |
| Halo . | Particle mass (h−1 M⊙) . |
|---|---|
| Aq-A-2 | 1.877 × 104 |
| Aq-A-4 | 5.382 × 105 |
| Aq-B-2 | 8.832 × 103 |
| Aq-B-4 | 3.071 × 105 |
| Aq-C-2 | 1.916 × 104 |
| Aq-C-4 | 4.401 × 105 |
| Aq-D-2 | 1.914 × 104 |
| Aq-D-4 | 3.667 × 105 |
Haloes from the Aquarius simulation analysed in this work. The left-hand column shows the simulation name, encoding the halo (A to D), and the resolution level (2 and 4); the corresponding particle masses are shown in the right-hand column, where h = 0.73.
| Halo . | Particle mass (h−1 M⊙) . |
|---|---|
| Aq-A-2 | 1.877 × 104 |
| Aq-A-4 | 5.382 × 105 |
| Aq-B-2 | 8.832 × 103 |
| Aq-B-4 | 3.071 × 105 |
| Aq-C-2 | 1.916 × 104 |
| Aq-C-4 | 4.401 × 105 |
| Aq-D-2 | 1.914 × 104 |
| Aq-D-4 | 3.667 × 105 |
| Halo . | Particle mass (h−1 M⊙) . |
|---|---|
| Aq-A-2 | 1.877 × 104 |
| Aq-A-4 | 5.382 × 105 |
| Aq-B-2 | 8.832 × 103 |
| Aq-B-4 | 3.071 × 105 |
| Aq-C-2 | 1.916 × 104 |
| Aq-C-4 | 4.401 × 105 |
| Aq-D-2 | 1.914 × 104 |
| Aq-D-4 | 3.667 × 105 |
2.1 Subhalo finders
Several subhalo finders have been applied on the Aquarius haloes. Each of them delivers a different subhalo catalogue, due to their specific numerical techniques. In order to minimize differences when comparing subhalo samples from different finders, a common post-processing pipeline has been applied. A detailed analysis of these subhalo catalogues can be found in Onions et al. (2012), whereas additional studies of the same data have been published in several recent papers resulting from the ‘Subhalo Finder Comparison Project’ (e.g. Elahi et al. 2013; Knebe et al. 2013; Onions et al. 2013; Pujol et al. 2014).
11 subhalo finders participated in the comparison project. However, we present only results for the Amiga Halo Finder (ahf; Knollmann & Knebe 2009), subfind (Springel et al. 2001), rockstar (Behroozi, Wechsler & Wu 2013), and the STructure Finder (stf, also known as velociraptor; Elahi, Thacker & Widrow 2011), since only those where run at high resolution on all four Aquarius haloes, analysed in this work, due to their computational efficiency. For further details of the different halo-finding algorithms, we refer the reader to the corresponding code papers.
3 SHAPE MEASUREMENT
The subhalo masses are set to unity to be unaffected by uncertainties in their determination and to simplify the comparison with observations. Assuming ellipsoidal distributions, the square root of the largest, intermediate and smallest eigenvalue corresponds to the absolute value of the major, intermediate and minor axis, respectively, that is, |$(a, b, c) = \sqrt{(\lambda _1,\lambda _2,\lambda _3)}$|, with λ3 ≤ λ2 ≤ λ1.
Contrary to what is often done, we do not measure shapes iteratively. In the iterative shape measurement particles that reside within the fitted ellipsoid are used to remeasure the shape, while for the initial measurement all particles are taken into account. This procedure is repeated until the shape parameters converge. We do not employ this method because during the iteration objects are excluded from the analysis which complicates the interpretation of shape measurements of, for instance, the N most massive subhaloes. Furthermore, we found that q and s sometimes converge to zero during the iteration, when only a few particles are analysed. Bailin & Steinmetz (2005) showed that, if shape measurement is performed without iteration, selecting particles in a sphere biases the measured shape parameters towards spherical results. We have verified these results using the Aq-A DM field. However, in this study we are not interested in the exact values of the shape parameters, but more in how the shapes of the subhalo populations are related to those of their hosts.
Besides the method for deriving the axial ratios, shape measurements can depend on the definition of the halo centre. A possible offset between the centre of mass of the host halo and the one of the full matter distribution, caused by massive substructure, can introduce an artificial triaxiality, especially when shapes are measured within the central part of a halo. Moreover, an offset can indicate an unrelaxed condition of the halo according to results of Power, Knebe & Knollmann (2012), who found that the distance between the most bound particle and the centre of mass is correlated with the virial ratio of the halo. To find the centre of the host halo, we apply the following procedure: (i) particles within the distance R/n around the centre of mass are selected to recalculate a new centre of mass, where n is initially set to unity and R is the largest particle distance to the centre of mass at the highest resolution level. (ii) Step (i) is repeated n = 100 times, while n is increased by one in every iteration step. Visual inspection confirmed that the centre determined by this procedure corresponds to the centre of the host halo. We use the host halo centre for the shape measurement of both – the DM field, as well as the subhalo population. This approach is chosen because it is easily applicable to observational data sets, assuming that the most luminous galaxy (e.g. the MW) resides in the centre of the host halo (see e.g. Vale & Ostriker 2004). This latter assumption might be wrong in some cases (see e.g. Skibba et al. 2011; Trujillo-Gomez et al. 2011).
4 RESULTS
In this section, we present our shape measurements of the Aquarius subhalo populations and compare them to the shape of the underlying DM field as well as to observational data.
In the whole analysis, we quantify subhalo masses with the values of the current maximum rotational velocity vmax with which DM particles orbit around the subhalo centre. Kravtsov, Gnedin & Klypin (2004) found that these vmax values are correlated with the subhalo masses, even during tidal stripping. Onions et al. (2012) demonstrated that when vmax is used as mass proxy the mass function of subhaloes obtained from different halo finders are in better agreement with each other than for M200. This might be explained by vmax measurements being less dependent on uncertain definitions, such as the subhalo boundaries.
4.1 Distribution of subhalo populations identified by different finders
To gain a visual impression of how subhaloes are distributed around the centre of their host halo, we display the Aq-A DM field together with its subhalo population in Fig. 1. The halo is rotated so that the intermediate axis of the ellipsoid approximating the DM isodensity contours stands perpendicular to the plane of the figure. This ellipsoid is fitted to the DM distribution within a 250 h−1 kpc sphere around the halo centre. The coloured area denotes the normalized projected density of the DM particles at the second lowest level of resolution (level 4) within a 100 h−1 kpc slice through the halo centre and parallel to the intermediate axis. The full DM field at different resolution levels was not available for our analysis, whereas we do not expect this limitation to affect our conclusions as discussed in Section 4.2. The black-rimmed green dots denote the positions of the 13 and 50 highest vmax subhaloes1 (top and bottom panels, respectively), identified by the subhalo finders ahf, subfind, rockstar and stf at the second highest level of resolution (level 2).
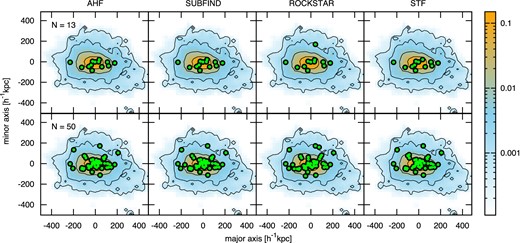
Matter distribution of the Aq-A halo together with the population of the 13 (upper panels) and the 50 (bottom panels) subhaloes with the highest vmax values. Colours shown on the right bar denote the normalized density of DM at the resolution level 4 in a 100 h− 1 kpc slice through the halo centre perpendicular to the intermediate axis measured at 250 h− 1 kpc. The black-rimmed green dots denote positions of the NAq-A subhaloes with the highest vmax values within a sphere of 250 h− 1 kpc identified by the subhalo finders ahf, subfind, rockstar and stf at resolution level 2. Note that in the case of rockstar and stf only 12 of the 13 highest vmax subhaloes are visible since one is obscured by other subhaloes.
We find that the subhalo distributions identified by the different halo finders differ only by a few objects. Especially the results of ahf and subfind agree very well with each other. We also find that the 13 Aq-A subhaloes with the highest vmax values are roughly aligned with the major axis of the DM field, while their distribution is flatter. An alignment in the same direction is also apparent for the 50 subhaloes with the highest vmax values, while the shape of their distribution is more isotropic and, therefore, in better agreement with the shape of the underlying DM field.
A physical explanation for the flattening of the massive subhalo population might be that massive objects maintain information about their infall direction for a longer time due to their large moment of inertia, while the orbits of low-mass subhaloes randomize faster after infall. If subhaloes are accreted anisotropically, the triaxiality of a given subhalo distribution might therefore increase the more massive objects are contained in the samples. Furthermore, tidal forces can strip of material from subhaloes, while they orbit around the centre of their host. This might introduce an additional correlation between the subhalo mass and its orbit orientation with respect to the infall direction. Another reason might be that dynamical friction causes massive subhaloes to sink faster to the host centre. For this reason, they might more prone to be totally disrupted before developing circular orbits, as suggested by Gill et al. (2004). However, due to the small number of massive subhaloes the flatness of their distribution might be an effect of random sampling. We attempt to disentangle such a systematic effect from anisotropic accretion as reasons for the flatness in Section 4.2.
4.2 Flatness of the subhalo population
Focusing the analysis on the flattening of the massive subhalo population with respect to the DM field, we measure their shapes using results from the four haloes Aq-(A-D). To quantify shapes, we follow the procedure described in Section 3 by determining the largest, intermediate and smallest eigenvalues of the reduced moment of inertia (a, b, c, respectively). The latter is constructed from objects (either DM particles or subhaloes) that reside within a 250 h−1 kpc sphere around the halo centre. The shape can then be quantified by the shape parameters q = b/a and s = c/a which correspond to the axial ratios of ellipsoids approximating the DM and subhalo distributions. Note that according to this definition, the extreme cases q = s = 1, s ≪ q = 1 and q = a ≪ 1 correspond, respectively, to a sphere, a disc and a filament.
4.2.1 Systematic bias in shape measurements from small numbers of tracers
A systematic bias in the shape measurement towards triaxiality from low numbers of shape tracing points (in our case subhaloes) is expected since any discreteness noise will produce a non-zero ellipticity even from a perfectly spherical object. In the extreme cases of two and three tracer points, any density field will be classified as a filament and disc, respectively. This known effect (e.g. Paz, Lambas, Padilla & Merchán 2006; van Daalen et al. 2012; Joachimi et al. 2013) might be the reason why we measure smaller values of the shape parameters q and s for the distribution of the most massive subhaloes than for larger sets including less massive subhaloes or the DM field.
We show in Fig. 2 the values of q and s measured from the distributions of the N most massive Aq-(A-D) subhaloes using vmax as a proxy for mass. Different coloured line types stand for the results of the subhalo samples obtained from the four halo finders that were run at the resolution level 2 on all haloes. The shape parameters show a Δq ≃ Δs ≃ 0.1 scatter when roughly more than 100 subhaloes are used for the measurement. For smaller numbers of subhaloes results from different finders show a stronger scatter of around Δq ≃ Δs ≃ 0.2. A more detailed analysis based on results from 10 subhalo finders, run at all five resolution levels of the Aq-A halo, revealed a stronger scatter for a larger variety of finders, which tends to increase at low resolution. At the lowest resolution level 5, we find a scatter of roughly Δq ≃ Δs ≃ 0.4 for samples consisting of the 13 highest vmax subhaloes, partly because of the larger number of finders run at low resolution. This finding suggests that the shapes of subhalo populations consisting of the highest vmax objects in MW-like host haloes, measured in currently high-resolution cosmological simulations, strongly depend on the subhalo finder employed to identify substructures.
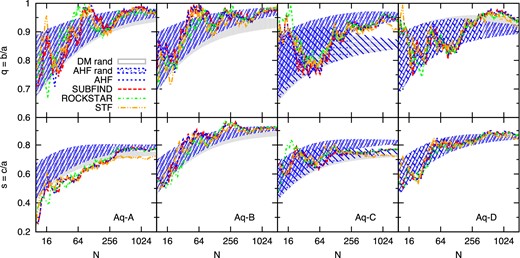
Shape parameters q (upper panels) and s (bottom panels) of Aq-(A-D) subhalo populations (panels from left to right) at the resolution level 2 for the N subhaloes with the highest vmax values within 250 h−1 kpc around the halo centre. The blue hatched (grey) areas result from random selections of N subhaloes (DM particles at the resolution level 4) regardless of their mass. They denote 68 per cent confidence levels derived from 1000 realizations of such random selections. As explained in Section 4.2.1, the wide blue hatched area in the panel for the Aq-C halo results from a validation test to explain the difference between shapes from DM and subhalo random samples.
As indicated by the visual impression from Fig. 1, the shape parameters increase (shapes become more spherical) if more subhaloes with lower mass (lower vmax values) are used for the shape measurement. This effect is apparent for all four haloes Aq-(A-D), while the measurements also show strong fluctuations for different numbers of most massive subhaloes. We mentioned Section 4.1 that the decrease of shape parameters for the N most massive subhaloes might be caused by physical effects, such as anisotropic infall, but also by a systematic effect resulting from small numbers of subhaloes in these samples.
To distinguish between the two possible reasons for the flatness, we generate random samples of Nahf subhaloes that are randomly selected from all detected subhaloes within a given halo, independently of their vmax value. If the shape parameters of the distribution of the N most massive subhaloes are significantly smaller than the values obtained from many random samples, then this would indicate a physical reason for the flatness. Systematics from small numbers of subhaloes should not cause differences between shapes from the two types of samples, since both consist of the of the same number of objects. We generate 1000 random samples, each with Nahf subhaloes, from which we obtain median values of the shape parameters and 68 per cent probability regions as indicator for the scatter. The latter is shown as a blue hatched region in Fig. 2. We find that the shape parameters q and s of the distributions of the N most massive subhaloes roughly lie within the central 68 per cent region of q and s measurements derived from random samples. We have tested that randomly sampling subhaloes identified by different subhalo finders leads to the same result. In most cases, the increased triaxiality (smaller shape parameters) of the N most massive subhaloes with respect to the DM field can therefore be explained by a systematic bias in the shape measurement due to small numbers of objects. An exception of this result is the s parameter of Aq-A, which is significantly smaller for samples of the N most massive subhaloes than the expected value from random sampling. We will discuss this finding in Section 4.2.2 in more detail.
The results in Fig. 2 also show that the variation between shape measurements for subhalo populations at level 2 from different finders is smaller than the noise in the measurement, expected from random sampling. The aforementioned scatter at low resolution is comparable to the noise from random sampling.
When the number of considered shape tracers is above 1000 the shape measurements start to converge to certain values of q and s. Studying the shapes of artificial haloes, we find that the convergence of the shape parameters for large numbers of tracer particles depends on the halo shape. The number of particles necessary to reach a certain precision in the shape measurement increases the closer a halo is to spherical symmetry, while in that case roughly 1000 tracer particles are needed for a 10 per cent precision (see Fig. A1 in Appendix A). Note that this result might depend on the exact method used for the shape measurement. Although similar results are reported by authors using different definitions of the moment of inertia (e.g. Joachimi et al. 2013), further study might be worthwhile to explore how heavily different shape measurements are affected by discreteness noise.
Comparing the shapes of the distributions of the N most massive subhaloes with the DM halo shape, taking into account the bias in the measurements from low numbers of objects, we also generate 1000 samples of N randomly selected DM particles from each Aquarius halo at the resolution level 4, instead of using subhaloes. As mentioned before, only the resolution level 4 was available for this analysis. Vera-Ciro et al. (2011) demonstrated that their Aq-A DM halo shape parameters at the five resolution levels differ by less than 4 per cent from each other, when the measurement is performed at radii as large as those used in our study (250 h−1 kpc). Their shape parameters measured from DM particles within 250 h−1 kpc around the halo centre are smaller than ours, in part because we measure shapes without iteration. We are able to roughly reproduce their results if we measure the DM shapes iteratively as well. Moreover, the difference between our measurement of the shape parameter s derived with and without iteration is consistent with results reported by Bailin & Steinmetz (2005).
Besides measuring DM shapes without iteration a further difference to the measurements of Vera-Ciro et al. (2011) is that we do not exclude particles that are members of subhaloes from the analysis. We do not follow this approach, as the relation between the shape of the subhalo population and the full DM shape is closer to observational information, as DM halo shapes might be traced for example by X-ray or lensing signals, which result from the full mass distribution. The 68 per cent probability regions of the 1000 shape measurements are shown as grey regions in the same figure.
If the random samples of subhaloes and DM particles consist only of a few objects, both types of random samples show similar distributions of the shape parameters. However, for larger numbers of objects, the shape parameters of subhalo and DM random samples do not converge to the same values. We can explain this result if we bear in mind that each substructure is represented by just one single object (the subhalo) in case of the subhalo random samples, but as several objects (the DM particles of the subhalo) in case of the DM random samples. This feature might introduce an artificial anisotropy in the DM moment of inertia which is reflected by smaller shape parameters. In this sense, the fact that the difference between shape measurements from random subhalo and DM particle samples is stronger for the Aq-C halo might be related to the fact that this halo has more high-mass substructures, as it can be seen in fig. 3 from Springel et al. (2008).
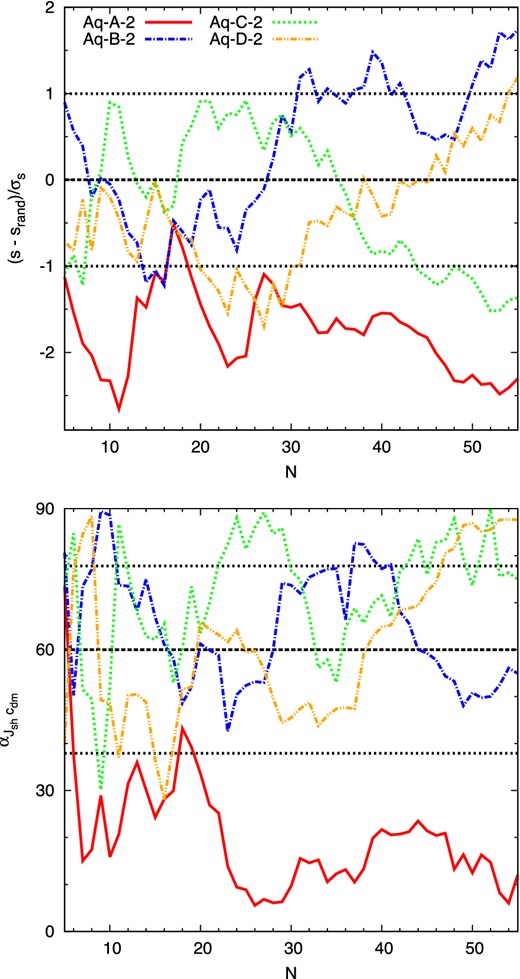
Top panel: difference between the shape parameter s calculated from the N most highest vmaxahf subhaloes and the median value of 1000 shape measurements from N randomly selected ahf subhaloes (srand) divided by the 1σ errors, shown as a hatched area in Fig. 2. Bottom panel: angle between the total angular momentum of the subhalo population (with subhalo masses set to unity) and the minor axis of the DM field. The dashed and dotted lines indicate the mean angles ±1σ deviations from an isotropic distribution, respectively.
To gain a better understanding of this effect, we perform a simple test that consists in giving more weight to the massive subhaloes during the random selection. For this purpose, we simply write subhaloes with large values of vmax (vmax > 100 km s−1) 2000 times in the subhalo catalogue and repeat the shape measurement from random samples. Following this simple approach, we can roughly reproduce the results from the DM random sampling, as shown by the additional wide blue hatched area included in the panel for the Aq-C halo in Fig. 2. For the sake of clarity, we only show the result of this test for the Aq-C halo, although we have checked that we obtain similar results for the rest of Aquarius haloes.
This same effect could have been tested by excluding DM particles in subhaloes from the measurement.
4.2.2 Anisotropic infall
We found in the previous section that the value of s measured from the N most massive Aq-A subhaloes is significantly below the expected value from randomly sampling subhaloes (Fig. 2). It is therefore unlikely that the flatness of the Aq-A population of massive subhaloes can be explained by random sampling. Since this effect is independent of the employed subhalo finder we show, for the sake of clarity, here and in the following analysis only results derived from ahf subhalo populations. We have tested that our conclusions do not change when employing different finders.
Focusing the analysis on the flatness of the massive Aq-A subhaloes we show in the top panel of Fig. 3 the significance of the deviation between the shape parameter s of the N most massive Aq-(A-D) subhaloes and the median values obtained from randomly sampling subhaloes. We define this significance as the ratio of the deviation and the error obtained from randomly sampling subhaloes, shown as blue hatched areas in Fig. 2. Again, we see that the Aq-A subhalo population is significantly flatter than expected from random sampling, while the flatness of massive subhalo populations in the other haloes lies within the expected range.
In order to understand this particular result, we study, in the following, anisotropic infall as an additional source of flattening. A proper way to study anisotropic infall would be to follow the subhalo positions through different time steps of the simulation, for example such as Libeskind et al. (2005). However, since these data are not available within the present comparison project, we investigate the orbit orientation of subhaloes given by the direction of their angular momenta with respect to the DM field of the corresponding host haloes. This approach is motivated by the following consideration: if the N highest vmax subhaloes do not accidentally lie in a plane, then also their orbits should lie within the same plane, possibly because they entered the host halo from a similar direction. The angular momentum |$\boldsymbol {J}$| of this subhalo population should therefore be aligned with the minor axis of the ellipsoid fitted to the DM halo, if the orbital plane is contained within the plane defined by the major and intermediate axes of the DM ellipsoid (hereafter referred to as the major plane).
In the bottom panel of Fig. 3, we show the angle between the minor axis of the DM field of each host halo Aq-(A-D) and the total angular momentum of the corresponding subhalo populations when we take samples consisting of the N highest vmax subhaloes. We find that this angle is smaller for Aq-A than for the other haloes, indicating a stronger alignment between the subhalo populations angular momentum and the DM minor axis. If we associate this stronger alignment with the effects of anisotropic infall, this result suggests that anisotropic infall can slightly increase the flattening of the subhalo populations, while the main reason for the flattening is the bias in the shape measurement due to small numbers of objects.
Note that the individual subhaloes do not contribute equally to the total angular momentum, since they are weighted by their distance and velocity with respect to the halo centre. Consequently, few objects with high velocities, large distances to the centre, or both can dominate the measurement. We therefore study in the following the flattening of subhalo populations and their rotational support with quantities that are defined for individual objects.
We start with a complementary method to study the degree of flattening of the subhalo population which consists in analysing the distribution of distances of the individual subhaloes to the major plane of the DM ellipsoid. From the subhalo distances to the DM major plane, dc we derive the mean over the whole subhalo population, dc, mean. We show the mean relative distance dc/dc, mean as computed in bins of 11 subhaloes with the highest vmax values in the top panel of Fig. 4. For each bin we also show error bars that enclose the 68 per cent of the values around the mean of the distribution. In general, we find that the subhaloes of Aq-(B-D) with the highest vmax values do not lie significantly closer to the major plane of the DM field than the mean over the whole population. The situation is slightly different for Aq-A, whose most massive subhaloes seem to be closer to the major plane, indicating therefore a flatter distribution. This result is consistent with those from shape measurements shown in Fig. 3, where we derived cumulative instead of differential values of subhalo populations with the highest vmax values.
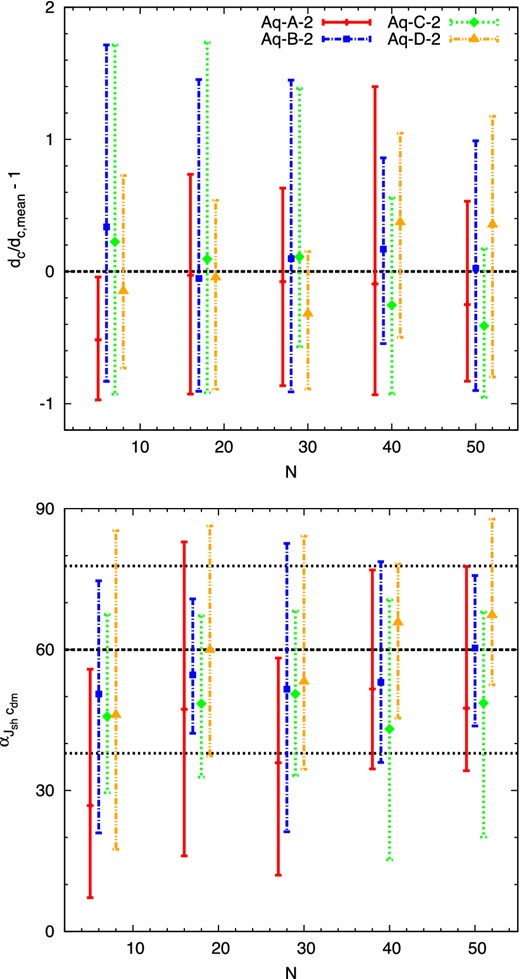
Top panel: distance, dc, of each subhalo to the plane spanned by the major and the intermediate axis of the DM moment of inertia in units relative to the mean distance to the same plane computed over the whole subhalo population. Symbols show the mean dc/dc, mean − 1 over N ± 5 ahf subhaloes with the highest vmax values. Error bars enclose the central 68 per cent of the distribution in each bin. Bottom panel: angle between angular momentum of each subhalo and the minor axis of the DM moment of inertia. Binning and error bars are calculated in the same way as in the top panel. The dashed and dotted lines indicate the mean angles ±1σ deviations from an isotropic distribution, respectively.
In order to verify rotational support, we measure for each subhalo separately the angle between the angular momentum and the minor axis of the ellipsoid fitted to the DM field as |$\alpha _n = \arccos (\hat{J}_n \cdot \hat{c}_{dm})$|. Using the same bins of 11 subhaloes sorted by vmax as in the top panel of Fig. 4, we now show, in the bottom panel of the same figure, the mean values of αn in each bin together with the error bars which enclose the central 68 per cent of the distribution. In agreement with our previous results, we find that the Aq-A subhalo population, which is significantly flattened, is also stronger aligned with the minor axis of the DM ellipsoid than it is the case for the other haloes. These findings point towards a scenario in which the flatness of the Aq-A subhalo population can be partially explained by the effects of anisotropic infall.
Results of Vera-Ciro et al. (2011) also support this scenario (see their fig. 8). These authors show that material falling into the Aq-A halo has a strong dipole component between 11 and 8 Gyr lookback time, indicating filamentary accretion. The dipole components that they find for the other haloes are smaller, as material was accreted more isotropically. This result also confirms the reports by Lovell et al. (2011) who also found indications for anisotropic accretion by studying the alignment between the angular momenta of Aquarius subhaloes (as detected by subfind) and their DM host halo. More specifically, Lovell et al. (2011) found that the distribution of angular momentum directions of subhaloes with the 11 largest progenitors had the strongest dipolarity in the case of Aq-A.
4.3 Comparing shapes of simulated subhalo populations with those of MW satellites
In this section, we compare the shapes of the Aquarius subhalo populations to those of the MW satellite population consisting of up to 27 objects within 250 h−1 kpc around the galactic centre. As we have ranked subhaloes by their vmax values, we now use V-band luminosities to rank the satellite galaxies. Our comparison with MW data is therefore based on the assumption that the satellite galaxies with the brightest V-band magnitudes (MV) live in the subhaloes with the highest vmax values. As we use vmax as a proxy for the total subhalo mass, MV can be used to quantify the stellar mass of a satellite galaxy (Baraffe et al. 1998). A weak correlation between the stellar mass of satellite galaxies in MW like haloes and their vmax values can be found in simulations (Zolotov et al. 2012; Reddick et al. 2013; Rodríguez-Puebla, Avila-Reese & Drory 2013; Brooks & Zolotov 2014). On the contrary, Libeskind et al. (2005) found that the stellar masses of semi-analytical model satellites are not correlated with the corresponding total subhalo mass at z = 0, but with the total mass of the main progenitor, as suggested by Conroy, Wechsler & Kravtsov (2006). However, their employed model does not include tidal stripping of the stellar mass component. Despite the existing uncertainties, we assume that vmax is a convenient property for comparing results of the most massive subhaloes to those derived from the observed most luminous MW satellites. Note that all masses are set to unity in the definition of the moment of inertia from which we measure the shapes. The positions and V-band luminosities of the 27 MW satellites, taken from McConnachie (2012), are shown in Appendix C.
The shape parameters measured from satellite populations consisting of the N brightest objects are shown as black lines in the left-hand panel of Fig. 5. We also show the shape measurements of the Aq-(A-D) subhalo populations, consisting of the N objects with highest vmax values. We find that the absolute values of the shape parameters q measured from the satellite populations are similar to the results from simulations for samples that consist of the roughly twelve or less most massive objects. When fainter satellites are included in the measurement we find a decrease of q while the Aquarius results remain roughly constant, resulting in lower values for q in observations than in simulations. The increase of the q from Aq-(A-D) with the number of objects, which we have seen for large numbers in Fig. 2, is not apparent when the analysis is restricted to the 27 highest vmax subhaloes. In the case of the s parameter we find that the observational values tend to be below the results from simulations except for samples of the highest mass Aq-A subhaloes. Our values of s for the population of the twelve most luminous satellites is in rough agreement with those reported by Starkenburg et al. (2013). The s measurements for the 12 highest vmax subhaloes roughly agree with results that these authors obtain from randomly sampling satellites with MV < −8.5 from semi-analytic models of galaxy formation imposed on the Aquarius simulation.
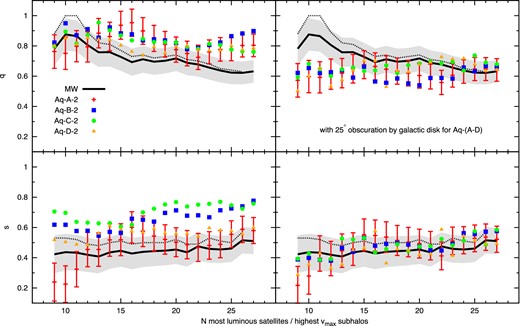
Shape parameters of the MW satellite distribution consisting of the N objects with highest V-band luminosities (black lines). These shapes are compared to those of Aquarius subhalo populations consisting in the N objects with highest vmax values identified by the ahf subhalo finder. The left-hand panel shows results for the highest vmax subhaloes in the full sky. The right-hand panel shows results for selecting subhaloes in a light cone with 130° opening angle, assuming 25° obscuration by the galactic disc. The coloured symbols denote the median values from 1000 realizations with randomly oriented light cones. The grey area and the error bars show the standard deviations estimated as described in Appendix B. Black dashed lines show shape parameters from the MW data measured with a method that decreases systematic bias from low numbers of tracers, as described in Appendix A.
The stronger discrepancies between the shape parameters from observed satellite and simulated subhalo populations for larger samples might be explained by an angular selection effect, which has a stronger impact on faint objects. We expect selection effects to be twofold. On the one hand, galactic obscuration prevents us from detecting objects that lie close to the galactic plane. On the other hand, the sky is observed with an inhomogeneous intensity, due to the limited area of surveys. Both types of selection effects should affect stronger faint, as opposed to bright, objects. To study the effect of angular selection on the shape measurement, we follow the procedure described by Wang et al. (2013) by measuring the shapes of the highest vmaxAq-(A-D) subhalo population residing within a light cone with an opening angle of α = 180 − 2αobs, where αobs is the angle of obscuration with respect to the galactic plane. Assuming that the orientation of this synthetic galactic plane is arbitrary, we conduct 1000 shape measurements with randomly oriented galactic planes. Orienting the galactic plane randomly is motivated by reports on the weak alignment of observed blue late-type galaxies and disc galaxies from hydrodynamic simulations with their surrounding matter distribution at large scales (Hahn, Teyssier & Carollo 2010; Sales et al. 2012; Joachimi et al. 2013; Zhang et al. 2013). The mean results of these 1000 shape measurements are shown in the right-hand panel of Fig. 5. We find that both q and s are decreased when galactic obscuration is taken into account. Using an obscuration angle of αobs = 25°, we find that, for the population of all 27 satellites, the observational results for the shape parameters agree with those from simulations. If the analysis is restricted to the 12 brightest satellites, the observed shape parameters are higher than those from simulations. This indicates that faint samples are strongly affected by obscuration, as we have initially guessed. However, angular selection effects are probably more complicated than in our model. The obscuration angle of αobs = 25° is larger than commonly reported for the MW. In Fig. C1, we see that the majority of satellites resides outside of this zone. This might be explained by a smaller obscuration angle together with the angular limitation of the SDSS (both shown in Metz et al. 2009), which result in a larger effective obscuration angle.
The black dashed lines in Fig. 5 show the shape parameters of satellite populations measured with a method that decreases the bias in the shape measurement from low numbers of shape tracing objects. This method is described in Appendix A.
5 SUMMARY AND CONCLUSIONS
We have analysed four high-resolution simulations of DM haloes with MW-like masses from the Aquarius project, Aq-(A-D), to measure the shapes of their subhalo populations and compared them to those of the underlying DM distributions. Throughout the analysis, we used the vmax values of the subhaloes as a proxy for the subhalo mass.
We find that the shapes of subhalo populations, consisting of the objects with the highest vmax values, show only a weak dependence on the employed subhalo finder when the subhaloes are analysed at high-mass resolution. This result changes for small samples at lower mass resolutions since shape measurements for smaller subhalo samples are highly sensitive to changes of a few members. We therefore expect that similar measurements, performed in currently high-resolution cosmological simulations (e.g. Millennium-II), strongly depend on the subhalo finder used to identify substructures.
Our shapes measured from subhalo populations consisting of the N subhaloes with the highest vmax values show that the subhalo distributions are more triaxial when only objects with highest vmax values are considered. This trend is apparent for all four halo finders run at the resolution level 2 and all four Aquarius haloes. Interpreting these results in terms of anisotropic accretion is delicate due to the fact that triaxiallity is likely to increase for samples with a few subhaloes. As a null test, we conducted the same shape measurement for N randomly selected subhaloes and DM particles. In all cases, we found a decrease of the shape parameters for small numbers of objects. In three of the four analysed haloes, the decrease of the shape parameters for the subhaloes with the highest vmax values is consistent with results from random samples. For Aq-A, the shape parameter s is up to 40 per cent smaller than the median value from random sampling. This difference roughly corresponds to a 2σ deviation and indicates a flattening of the population of high vmax subhaloes due to anisotropic infall.
To further verify if the flattening of the high vmax subhalo populations is not caused by random sampling, we studied the alignment of the angular momenta of the subhalo populations with the ellipsoid of the DM field. We found that the highest vmaxAq-A subhaloes are stronger aligned with the minor axis of the DM ellipsoid than the Aq-(B-D) subhalo populations. This finding indicates that the orbits of the high vmaxAq-A subhaloes tend to reside in the plane spanned by the major and intermediate axis of the DM moment of inertia, which is in agreement with subhalo accretion along the host halo major axis. Such an interpretation is consistent with the findings of Vera-Ciro et al. (2011), who showed that the matter accreted by the Aq-A halo has a dipole component – a signal of filamentary infall. Also Lovell et al. (2011) report indications for anisotropic accretion by studying the alignment between the angular momenta of Aquarius subhaloes and the DM field of their host halo.
After having analysed possible reasons for the increased triaxiallity of the highest vmax Aquarius subhaloes, we compare the shape of their distributions with those of observed MW satellites. In this regard, we found that the shape parameters derived for the distribution of the twelve satellites with the brightest V-band magnitudes lie within the range expected from the four Aquarius haloes when using the same number of subhaloes with the highest vmax values. However, for larger samples including fainter satellites and lower vmax subhaloes the shape parameters are below the results from simulations, especially the major to intermediate axial ratio q. This discrepancy can be decreased by assuming an overly strong galactic obscuration of 25°, while in that case the shape parameters for the high vmax samples lie below the results from bright satellites samples. This demonstrates that the geometry of our observational window, defined by the zone obscured by the galactic disc, and the geometry of the surveys mapping the sky can affect the shape measurements of the satellite distribution, while we expect a stronger impact on samples including faint satellites.
Within the ΛCDM context, the strong triaxiality of the MW satellite distribution with respect to our results from simulations can be interpreted as an result of anisotropic accretion, which would agree with the findings of Libeskind et al. (2011). A further reason for the strong flatness of the observed satellite distribution might be that the assumption that the most luminous satellites live in the subhaloes with the highest mass at redshift zero (using the maximum rotational velocity as mass proxy) might be inadequate to mimic the results of galaxy formation (Boylan-Kolchin, Bullock & Kaplinghat 2011). Simulations and observations suggest that the subhalo mass after infall and their stellar mass are not or just weakly correlated, while we assume a monotonic relation for our comparison with MW data (Libeskind et al. 2005; Rodríguez-Puebla et al. 2013; Brooks & Zolotov 2014). It might be necessary to simulate the evolution of DM together with the baryonic physics to produce thinner satellite discs (Danovich et al. 2012).
Our analysis of systematic effects on the shape measurement revealed that hundreds of tracers are needed for obtaining reliable results. We conclude that even if subhaloes, as potential hosts of satellite galaxies, follow the DM field of their host, they are too few for a reliable shape measurement of the MW DM halo. The expected increase of the number of known satellites in future surveys (Simon & Geha 2007) will probably not be sufficient to solve this problem. However, we also found that the shapes of subhalo populations in three of the four MW-like host haloes are consistent with the shapes of the DM field, if bias from the small number of tracers in the shape measurement is taken into account. The assumption that subhaloes trace the DM field of their host is therefore in reasonable agreement with our results.
A similar analysis performed on larger host haloes with more massive subhaloes at different redshifts would allow for an improved comparison with larger observational data sets from cosmological surveys.
This paper was initiated at the Subhaloes going Notts workshop in Dovedale, UK, which was funded by the European Commissions Framework Programme 7, through the Marie Curie Initial Training Network Cosmo- Comp (PITN-GA-2009-238356). We wish to thank the Virgo Consortium for allowing the use of the Aquarius data set and Adrian Jenkins for assisting with the data.
KH is supported by beca FI from Generalitat de Catalunya. He acknowledges Noam Libeskind for a fruitful discussion. SP and HL acknowledge a fellowship from the European Commission's Framework Programme 7, through the Marie Curie Initial Training Network CosmoComp (PITN-GA-2009-238356). SP also acknowledges support by the PRIN-INAF09 project ‘Towards an Italian Network for Computational Cosmology’ and by Spanish Ministerio de Ciencia e Innovación (MICINN) (grants AYA2010-21322-C03-02 and CONSOLIDER2007-00050). EG and KH acknowledge the Spanish Ministerio de Ciencia e Innovación (MICINN) project AYA2009-13936, Consolider-Ingenio CSD2007- 00060, AK is supported by the Ministerio de Economía y Competitividad (MINECO) in Spain through grant AYA2012-31101 as well as the Consolider-Ingenio 2010 Programme of the Spanish Ministerio de Ciencia e Innovación (MICINN) under grant MultiDark CSD2009-00064. He also acknowledges support from the Australian Research Council (ARC) grants DP130100117 and DP140100198. He further thanks Felt for penelope tree. SIM acknowledges the support of the STFC Studentship Enhancement Program (STEP). YA receives financial support from project AYA2010-21887-C04-03 from the former Ministerio de Ciencia e Innovación (MICINN, Spain), as well as the Ramón y Cajal programme (RyC-2011-09461), now managed by the Ministerio de Economía y Competitividad (fiercely cutting back on the Spanish scientific infrastructure). PSB is supported by a Giacconi Fellowship through the Space Telescope Science Institute, which is supported through NASA contract NAS5-26555. MN thanks the Sir John Templeton Foundation for support through a New Frontiers and Astronomy and Cosmology grant.
The authors contributed in the following ways to this paper: KH and SP undertook this project. KH performed the analysis presented and wrote the paper together with SP. KH is a PhD student supervised by EG. FRP, AK, EG, HL, JO and SIM contributed with useful discussions and with the organization of the workshop at which this study was initiated. They designed the comparison study and planned and organized the data. The other authors provided data and had the opportunity to proof, read and comment on the paper.
The selection of the 13 highest vmax subhaloes is motivated by the set of 13 MW satellites that are brighter than MV = −8.5, listed in Table C1. This set of satellites consists mostly of objects detected before the SDSS analysis (the ‘classical’ satellites). The number of highest vmax subhaloes in the larger sample corresponds to the 50 MW satellites, predicted by Simon & Geha (2007) for a completely observed sky.
REFERENCES
APPENDIX A: IMPROVED SHAPE MEASUREMENT
To study in detail the bias induced in the shape measurement due to low numbers of tracer points, we perform the following test. We build mock DM haloes by generating particle distributions characterized by a given ellipticity and density profile. Using 10 000 random realizations of such artificial haloes formed by N tracers (representing subhaloes or DM particles), we measure the mean shape parameters q and s and the corresponding standard deviations for different sets of input shapes as a function of N. The results of this analysis, shown in Fig. A1, reveal that around 1000 tracer particles are required to ensure that the measured shape parameters deviate by less than 10 per cent from the true (input) values. The bias in the shape measurement due to low tracer points is stronger if the shape parameters of the artificial haloes are close to unity, while results are almost unbiased if the shape parameters are below 0.2.
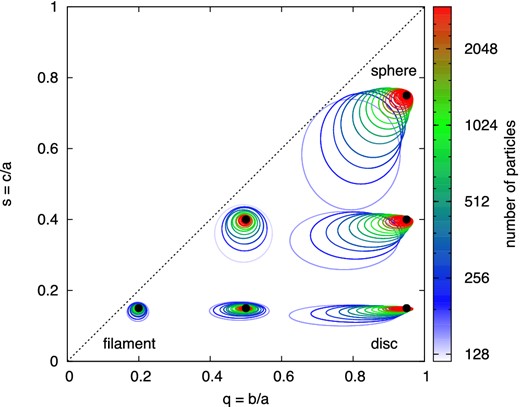
Measured shape parameters of artificial particle distributions with given input shapes, marked by black dots. The centre of the ellipses are the mean measurements of q and s derived from 10 000 random realizations of the particle distributions. The major and minor axes denote the standard deviation of q and s measurements, respectively. The colour of the ellipses denotes the number of random particles used in each of the 10 000 realizations.
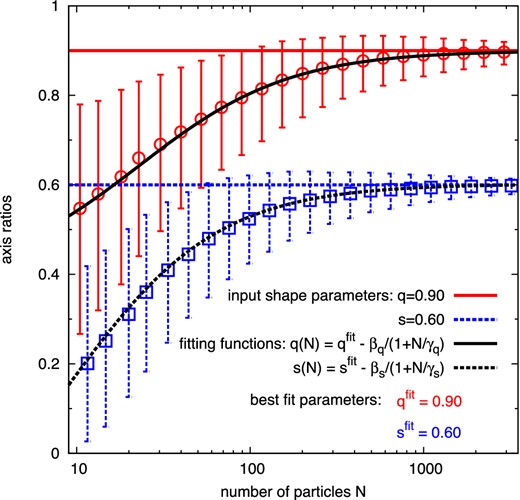
Shape parameters of artificial particle distributions (mimicking a halo with q = 0.9 and s = 0.6) as a function of the number of tracer particles N. The shape parameters, used to generate the particle distributions, are shown as the coloured horizontal lines. The symbols show the median and central 68 per cent values obtained from 10 000 random realizations. Solid and dashed black lines show fits of equation (A1) to the measurements of q and s, respectively.
These fitting functions open the possibility of decreasing the bias in the shape measurement from low number counts using the following procedure. If we consider the case of the subhalo populations, we randomly sample groups of subhaloes, as much as possible, without replacement. These samples are drawn from the N highest vmax subhaloes, since in real life only the most massive (or luminous) satellite galaxies are observed. The mean shape parameters of such groups are then measured as a function of the number of group members, Nrand. By fitting equation (A1) to the measured q(Nrand) and s(Nrand), we can derive the parameters qfit and sfit as shown in Fig. A3.
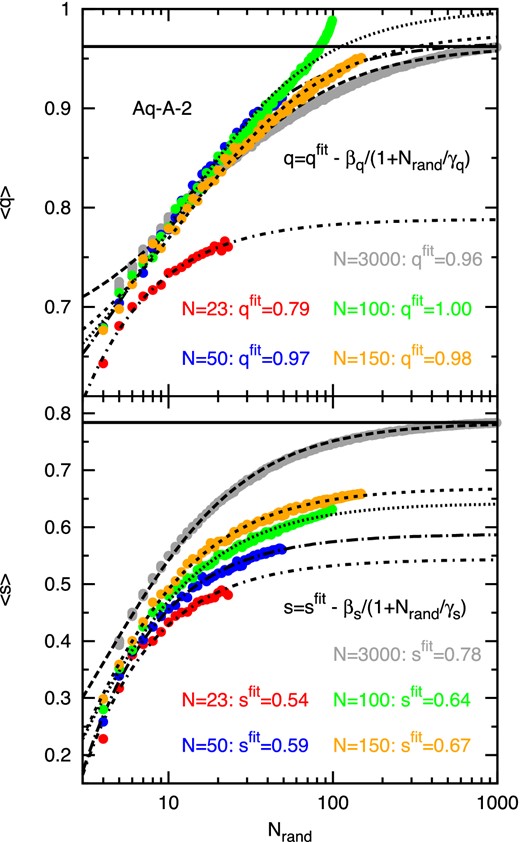
Mean shape parameters derived from 1000 random samples consisting of Nrand subhaloes (coloured symbols). The samples are drawn from the NAq-A subhaloes with the highest vmax values without replacement. The black dashed lines show the fitting function given by equation (A1) with the best-fitting values for qfit and sfit displayed in the figure. The best-fitting values derived from the N = 3000 highest vmax subhaloes are shown as black solid lines.
These fitting parameters tend to lie closer to the shape parameters derived from the 3000 subhaloes with the highest vmax values than the shape parameters measured using the N < 3000 most massive subhaloes. Indeed, as it is shown in Fig. A4, for the 23 highest vmax subhaloes in Aq-(A-D), the difference between q(N) and q(3000) decreases by about 5 per cent, whereas in the case of s(N) the deviation from s(3000) is about 10 per cent smaller if this correction procedure is applied.
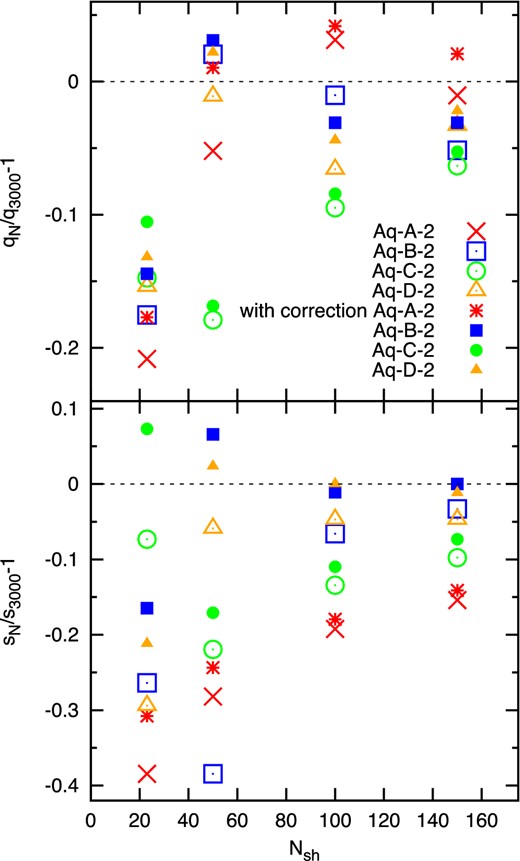
Relative difference between the shape parameters q and s measured from the Nsh and 3000 Aq-(A-D) subhaloes with the highest vmax values. Open symbols show direct q and s measurements, whereas closed symbols represent measurements corrected as described in the text and demonstrated in Fig. A3.
APPENDIX B: ERROR ESTIMATIONS FOR THE SHAPE MEASUREMENT
We estimate the error of the shape measurements from the observational data and highest vmaxAq-A subhaloes shown in Fig. 5 using the results from random sampling Aquarius subhaloes independently of their vmax values. The standard deviation derived from sampling Nahf subhaloes 10 000 times are shown in Fig. A5. We find that these results can be approximated by a power law shown in the same figure. The error estimate applied to the observational data is the same power law that describes the standard deviation from the Aq-A results.
APPENDIX C: MW SATELLITES
For comparing the shapes of the Aquarius subhalo distributions to MW data, we use the positions and absolute V-band magnitudes of 27 satellite galaxies from McConnachie (2012), presented in Table C1. The distribution of these satellites around the centre of the MW is shown in Fig. C1.
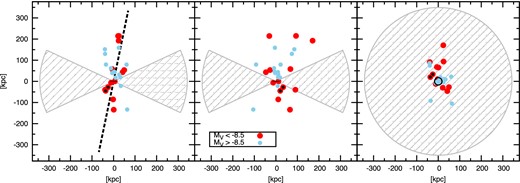
Distribution of satellites from Table C1 around the MW centre. Left and central panel show edge on views on the galactic disc. Coordinates are rotated, so that the best-fitting plane, spanned by the major and intermediate axis of the ellipsoid fitted to all 27 objects, is edge on in the left-hand panel. The central panel shows the same distribution while the perspective is rotated by 90° around the galactic pole. The right-hand panel shows a face-on view on the galactic disc. Red and blue dots denote, respectively, satellites with V-band magnitudes brighter and fainter than MV = −8.5. The shaded area is the assumed galactic obscuration zone used to calculate the shapes for Aquarius subhalo samples shown in the right-hand panel of Fig. 5. Its radial size of 250 h−1 kpc, with h = 0.73 corresponds to the size of the spherical window within which we select Aquarius subhaloes for the analysis. The obscuration angle of 25° is about twice as large as the value usually assumed. Metz et al. (2009) show a similar figure with a smaller galactic obscuration zone together with the projected SDSS light cone, which encloses all faint satellites. The extension of the galactic disc is roughly indicated by black bars in the left and central panel and an open circle in the right-hand panel. Small and Large Magellanic Clouds are marked by black dots for orientation.
MW satellite galaxies used in this work sorted by the absolute V-band magnitude MV. This list is based on the table given by McConnachie (2012), where l and b are angles in heliocentric galactic coordinates, r⊙ is the distance to the sun, x, y, z are Cartesian coordinates with the centre of the Galaxy in the origin, and rGC is the distance to the galactic centre.
| Nr. . | Satellite . | l (deg) . | b (deg) . | r⊙(kpc) . | x(kpc ) . | y(kpc) . | z(kpc) . | rGC(kpc) . | MV . |
|---|---|---|---|---|---|---|---|---|---|
| 1 | LMC | 280.5 | −32.9 | 51 | −0.50 | −42.10 | −27.70 | 50.40 | −18.1 |
| 2 | SMC | 302.8 | −44.3 | 64 | 16.51 | −38.50 | −44.70 | 61.26 | −16.8 |
| 3 | Canis Major | 240.0 | −0.8 | 7 | −11.80 | −6.06 | −0.098 | 13.27 | −14.4 |
| 4 | Sagittarius | 5.6 | −14.2 | 26 | 16.79 | 2.46 | −6.378 | 18.12 | −13.5 |
| 5 | Fornax | 237.1 | −65.7 | 147 | −41.16 | −50.79 | −133.98 | 149.08 | −13.4 |
| 6 | LeoI | 226.0 | 49.1 | 254 | −123.83 | −119.63 | 191.99 | 257.88 | −12.0 |
| 7 | Sculptor | 287.5 | −83.2 | 86 | −5.24 | −9.71 | −85.40 | 86.11 | −11.1 |
| 8 | LeoII | 220.2 | 67.2 | 233 | −77.26 | −58.28 | 214.79 | 235.59 | −9.8 |
| 9 | Sextans | 243.5 | 42.3 | 86 | −36.68 | −56.93 | 57.88 | 89.08 | −9.3 |
| 10 | Carina | 260.1 | −22.2 | 105 | −25.01 | −95.77 | −39.67 | 106.64 | −9.1 |
| 11 | Draco | 86.4 | 34.7 | 76 | −4.38 | 62.36 | 43.27 | 76.03 | −8.8 |
| 12 | Ursa Minor | 105.0 | 44.8 | 76 | −22.36 | 52.09 | 53.55 | 77.95 | −8.8 |
| 13 | CVn I | 74.3 | 79.8 | 218 | 2.15 | 37.16 | 214.56 | 217.76 | −8.6 |
| 14 | Hercules | 28.7 | 36.9 | 132 | 84.29 | 50.69 | 79.27 | 126.32 | −6.6 |
| 15 | Bootes I | 358.1 | 69.6 | 66 | 14.69 | −0.76 | 61.86 | 63.59 | −6.3 |
| 16 | LeoIV | 265.4 | 57.4 | 154 | −14.95 | −82.70 | 129.74 | 154.58 | −5.8 |
| 17 | Bootes III | 35.4 | 75.4 | 47 | 1.36 | 6.86 | 45.48 | 46.02 | −5.8 |
| 18 | Ursa Major I | 159.43 | 54.4 | 97 | −61.17 | 19.84 | 78.87 | 101.76 | −5.5 |
| 19 | LeoV | 261.9 | 58.5 | 178 | −21.40 | −92.08 | 151.77 | 178.80 | −5.2 |
| 20 | PscII | 79.2 | −47.1 | 182 | 14.91 | 121.70 | −133.32 | 181.13 | −5.0 |
| 21 | CVn II | 113.6 | 82.7 | 160 | −16.44 | 18.63 | 158.70 | 160.64 | −4.9 |
| 22 | Ursa Major II | 152.5 | 37.4 | 32 | −30.85 | 11.74 | 19.44 | 38.30 | −4.2 |
| 23 | Coma Berenices | 241.9 | 83.6 | 44 | −10.61 | −4.33 | 43.73 | 45.20 | −4.1 |
| 24 | Bootes II | 353.7 | 68.9 | 42 | 6.73 | −1.66 | 39.18 | 39.79 | −2.7 |
| 25 | Wilkman I | 158.6 | 56.8 | 38 | −27.67 | 7.59 | 31.80 | 42.83 | −2.7 |
| 26 | Segue II | 149.4 | −38.1 | 35 | −32.01 | 14.02 | −21.60 | 41.08 | −2.5 |
| 27 | Segue I | 220.5 | 50.4 | 23 | −19.45 | −9.52 | 17.72 | 27.98 | −1.5 |
| Nr. . | Satellite . | l (deg) . | b (deg) . | r⊙(kpc) . | x(kpc ) . | y(kpc) . | z(kpc) . | rGC(kpc) . | MV . |
|---|---|---|---|---|---|---|---|---|---|
| 1 | LMC | 280.5 | −32.9 | 51 | −0.50 | −42.10 | −27.70 | 50.40 | −18.1 |
| 2 | SMC | 302.8 | −44.3 | 64 | 16.51 | −38.50 | −44.70 | 61.26 | −16.8 |
| 3 | Canis Major | 240.0 | −0.8 | 7 | −11.80 | −6.06 | −0.098 | 13.27 | −14.4 |
| 4 | Sagittarius | 5.6 | −14.2 | 26 | 16.79 | 2.46 | −6.378 | 18.12 | −13.5 |
| 5 | Fornax | 237.1 | −65.7 | 147 | −41.16 | −50.79 | −133.98 | 149.08 | −13.4 |
| 6 | LeoI | 226.0 | 49.1 | 254 | −123.83 | −119.63 | 191.99 | 257.88 | −12.0 |
| 7 | Sculptor | 287.5 | −83.2 | 86 | −5.24 | −9.71 | −85.40 | 86.11 | −11.1 |
| 8 | LeoII | 220.2 | 67.2 | 233 | −77.26 | −58.28 | 214.79 | 235.59 | −9.8 |
| 9 | Sextans | 243.5 | 42.3 | 86 | −36.68 | −56.93 | 57.88 | 89.08 | −9.3 |
| 10 | Carina | 260.1 | −22.2 | 105 | −25.01 | −95.77 | −39.67 | 106.64 | −9.1 |
| 11 | Draco | 86.4 | 34.7 | 76 | −4.38 | 62.36 | 43.27 | 76.03 | −8.8 |
| 12 | Ursa Minor | 105.0 | 44.8 | 76 | −22.36 | 52.09 | 53.55 | 77.95 | −8.8 |
| 13 | CVn I | 74.3 | 79.8 | 218 | 2.15 | 37.16 | 214.56 | 217.76 | −8.6 |
| 14 | Hercules | 28.7 | 36.9 | 132 | 84.29 | 50.69 | 79.27 | 126.32 | −6.6 |
| 15 | Bootes I | 358.1 | 69.6 | 66 | 14.69 | −0.76 | 61.86 | 63.59 | −6.3 |
| 16 | LeoIV | 265.4 | 57.4 | 154 | −14.95 | −82.70 | 129.74 | 154.58 | −5.8 |
| 17 | Bootes III | 35.4 | 75.4 | 47 | 1.36 | 6.86 | 45.48 | 46.02 | −5.8 |
| 18 | Ursa Major I | 159.43 | 54.4 | 97 | −61.17 | 19.84 | 78.87 | 101.76 | −5.5 |
| 19 | LeoV | 261.9 | 58.5 | 178 | −21.40 | −92.08 | 151.77 | 178.80 | −5.2 |
| 20 | PscII | 79.2 | −47.1 | 182 | 14.91 | 121.70 | −133.32 | 181.13 | −5.0 |
| 21 | CVn II | 113.6 | 82.7 | 160 | −16.44 | 18.63 | 158.70 | 160.64 | −4.9 |
| 22 | Ursa Major II | 152.5 | 37.4 | 32 | −30.85 | 11.74 | 19.44 | 38.30 | −4.2 |
| 23 | Coma Berenices | 241.9 | 83.6 | 44 | −10.61 | −4.33 | 43.73 | 45.20 | −4.1 |
| 24 | Bootes II | 353.7 | 68.9 | 42 | 6.73 | −1.66 | 39.18 | 39.79 | −2.7 |
| 25 | Wilkman I | 158.6 | 56.8 | 38 | −27.67 | 7.59 | 31.80 | 42.83 | −2.7 |
| 26 | Segue II | 149.4 | −38.1 | 35 | −32.01 | 14.02 | −21.60 | 41.08 | −2.5 |
| 27 | Segue I | 220.5 | 50.4 | 23 | −19.45 | −9.52 | 17.72 | 27.98 | −1.5 |
MW satellite galaxies used in this work sorted by the absolute V-band magnitude MV. This list is based on the table given by McConnachie (2012), where l and b are angles in heliocentric galactic coordinates, r⊙ is the distance to the sun, x, y, z are Cartesian coordinates with the centre of the Galaxy in the origin, and rGC is the distance to the galactic centre.
| Nr. . | Satellite . | l (deg) . | b (deg) . | r⊙(kpc) . | x(kpc ) . | y(kpc) . | z(kpc) . | rGC(kpc) . | MV . |
|---|---|---|---|---|---|---|---|---|---|
| 1 | LMC | 280.5 | −32.9 | 51 | −0.50 | −42.10 | −27.70 | 50.40 | −18.1 |
| 2 | SMC | 302.8 | −44.3 | 64 | 16.51 | −38.50 | −44.70 | 61.26 | −16.8 |
| 3 | Canis Major | 240.0 | −0.8 | 7 | −11.80 | −6.06 | −0.098 | 13.27 | −14.4 |
| 4 | Sagittarius | 5.6 | −14.2 | 26 | 16.79 | 2.46 | −6.378 | 18.12 | −13.5 |
| 5 | Fornax | 237.1 | −65.7 | 147 | −41.16 | −50.79 | −133.98 | 149.08 | −13.4 |
| 6 | LeoI | 226.0 | 49.1 | 254 | −123.83 | −119.63 | 191.99 | 257.88 | −12.0 |
| 7 | Sculptor | 287.5 | −83.2 | 86 | −5.24 | −9.71 | −85.40 | 86.11 | −11.1 |
| 8 | LeoII | 220.2 | 67.2 | 233 | −77.26 | −58.28 | 214.79 | 235.59 | −9.8 |
| 9 | Sextans | 243.5 | 42.3 | 86 | −36.68 | −56.93 | 57.88 | 89.08 | −9.3 |
| 10 | Carina | 260.1 | −22.2 | 105 | −25.01 | −95.77 | −39.67 | 106.64 | −9.1 |
| 11 | Draco | 86.4 | 34.7 | 76 | −4.38 | 62.36 | 43.27 | 76.03 | −8.8 |
| 12 | Ursa Minor | 105.0 | 44.8 | 76 | −22.36 | 52.09 | 53.55 | 77.95 | −8.8 |
| 13 | CVn I | 74.3 | 79.8 | 218 | 2.15 | 37.16 | 214.56 | 217.76 | −8.6 |
| 14 | Hercules | 28.7 | 36.9 | 132 | 84.29 | 50.69 | 79.27 | 126.32 | −6.6 |
| 15 | Bootes I | 358.1 | 69.6 | 66 | 14.69 | −0.76 | 61.86 | 63.59 | −6.3 |
| 16 | LeoIV | 265.4 | 57.4 | 154 | −14.95 | −82.70 | 129.74 | 154.58 | −5.8 |
| 17 | Bootes III | 35.4 | 75.4 | 47 | 1.36 | 6.86 | 45.48 | 46.02 | −5.8 |
| 18 | Ursa Major I | 159.43 | 54.4 | 97 | −61.17 | 19.84 | 78.87 | 101.76 | −5.5 |
| 19 | LeoV | 261.9 | 58.5 | 178 | −21.40 | −92.08 | 151.77 | 178.80 | −5.2 |
| 20 | PscII | 79.2 | −47.1 | 182 | 14.91 | 121.70 | −133.32 | 181.13 | −5.0 |
| 21 | CVn II | 113.6 | 82.7 | 160 | −16.44 | 18.63 | 158.70 | 160.64 | −4.9 |
| 22 | Ursa Major II | 152.5 | 37.4 | 32 | −30.85 | 11.74 | 19.44 | 38.30 | −4.2 |
| 23 | Coma Berenices | 241.9 | 83.6 | 44 | −10.61 | −4.33 | 43.73 | 45.20 | −4.1 |
| 24 | Bootes II | 353.7 | 68.9 | 42 | 6.73 | −1.66 | 39.18 | 39.79 | −2.7 |
| 25 | Wilkman I | 158.6 | 56.8 | 38 | −27.67 | 7.59 | 31.80 | 42.83 | −2.7 |
| 26 | Segue II | 149.4 | −38.1 | 35 | −32.01 | 14.02 | −21.60 | 41.08 | −2.5 |
| 27 | Segue I | 220.5 | 50.4 | 23 | −19.45 | −9.52 | 17.72 | 27.98 | −1.5 |
| Nr. . | Satellite . | l (deg) . | b (deg) . | r⊙(kpc) . | x(kpc ) . | y(kpc) . | z(kpc) . | rGC(kpc) . | MV . |
|---|---|---|---|---|---|---|---|---|---|
| 1 | LMC | 280.5 | −32.9 | 51 | −0.50 | −42.10 | −27.70 | 50.40 | −18.1 |
| 2 | SMC | 302.8 | −44.3 | 64 | 16.51 | −38.50 | −44.70 | 61.26 | −16.8 |
| 3 | Canis Major | 240.0 | −0.8 | 7 | −11.80 | −6.06 | −0.098 | 13.27 | −14.4 |
| 4 | Sagittarius | 5.6 | −14.2 | 26 | 16.79 | 2.46 | −6.378 | 18.12 | −13.5 |
| 5 | Fornax | 237.1 | −65.7 | 147 | −41.16 | −50.79 | −133.98 | 149.08 | −13.4 |
| 6 | LeoI | 226.0 | 49.1 | 254 | −123.83 | −119.63 | 191.99 | 257.88 | −12.0 |
| 7 | Sculptor | 287.5 | −83.2 | 86 | −5.24 | −9.71 | −85.40 | 86.11 | −11.1 |
| 8 | LeoII | 220.2 | 67.2 | 233 | −77.26 | −58.28 | 214.79 | 235.59 | −9.8 |
| 9 | Sextans | 243.5 | 42.3 | 86 | −36.68 | −56.93 | 57.88 | 89.08 | −9.3 |
| 10 | Carina | 260.1 | −22.2 | 105 | −25.01 | −95.77 | −39.67 | 106.64 | −9.1 |
| 11 | Draco | 86.4 | 34.7 | 76 | −4.38 | 62.36 | 43.27 | 76.03 | −8.8 |
| 12 | Ursa Minor | 105.0 | 44.8 | 76 | −22.36 | 52.09 | 53.55 | 77.95 | −8.8 |
| 13 | CVn I | 74.3 | 79.8 | 218 | 2.15 | 37.16 | 214.56 | 217.76 | −8.6 |
| 14 | Hercules | 28.7 | 36.9 | 132 | 84.29 | 50.69 | 79.27 | 126.32 | −6.6 |
| 15 | Bootes I | 358.1 | 69.6 | 66 | 14.69 | −0.76 | 61.86 | 63.59 | −6.3 |
| 16 | LeoIV | 265.4 | 57.4 | 154 | −14.95 | −82.70 | 129.74 | 154.58 | −5.8 |
| 17 | Bootes III | 35.4 | 75.4 | 47 | 1.36 | 6.86 | 45.48 | 46.02 | −5.8 |
| 18 | Ursa Major I | 159.43 | 54.4 | 97 | −61.17 | 19.84 | 78.87 | 101.76 | −5.5 |
| 19 | LeoV | 261.9 | 58.5 | 178 | −21.40 | −92.08 | 151.77 | 178.80 | −5.2 |
| 20 | PscII | 79.2 | −47.1 | 182 | 14.91 | 121.70 | −133.32 | 181.13 | −5.0 |
| 21 | CVn II | 113.6 | 82.7 | 160 | −16.44 | 18.63 | 158.70 | 160.64 | −4.9 |
| 22 | Ursa Major II | 152.5 | 37.4 | 32 | −30.85 | 11.74 | 19.44 | 38.30 | −4.2 |
| 23 | Coma Berenices | 241.9 | 83.6 | 44 | −10.61 | −4.33 | 43.73 | 45.20 | −4.1 |
| 24 | Bootes II | 353.7 | 68.9 | 42 | 6.73 | −1.66 | 39.18 | 39.79 | −2.7 |
| 25 | Wilkman I | 158.6 | 56.8 | 38 | −27.67 | 7.59 | 31.80 | 42.83 | −2.7 |
| 26 | Segue II | 149.4 | −38.1 | 35 | −32.01 | 14.02 | −21.60 | 41.08 | −2.5 |
| 27 | Segue I | 220.5 | 50.4 | 23 | −19.45 | −9.52 | 17.72 | 27.98 | −1.5 |




