-
PDF
- Split View
-
Views
-
Cite
Cite
Regner Trampedach, Robert F. Stein, Jørgen Christensen-Dalsgaard, Åke Nordlund, Martin Asplund, Improvements to stellar structure models, based on a grid of 3D convection simulations – I. T(τ) relations, Monthly Notices of the Royal Astronomical Society, Volume 442, Issue 1, 21 July 2014, Pages 805–820, https://doi.org/10.1093/mnras/stu889
Close - Share Icon Share
Abstract
Relations between temperature, T, and optical depth, τ, are often used for describing the photospheric transition from optically thick to optically thin in stellar structure models. We show that this is well justified, but also that currently used T(τ) relations are often inconsistent with their implementation. As an outer boundary condition on the system of stellar structure equations, T(τ) relations have an undue effect on the overall structure of stars. In this age of precision asteroseismology, we need to re-assess both the method for computing and for implementing T(τ) relations, and the assumptions they rest on. We develop a formulation for proper and consistent evaluation of T(τ) relations from arbitrary 1D or 3D stellar atmospheres, and for their implementation in stellar structure and evolution models. We extract radiative T(τ) relations, as described by our new formulation, from 3D simulations of convection in deep stellar atmospheres of late-type stars from dwarfs to giants. These simulations employ realistic opacities and equation of state, and account for line blanketing. For comparison, we also extract T(τ) relations from 1Dmarcsmodel atmospheres using the same formulation. T(τ) relations from our grid of 3D convection simulations display a larger range of behaviours with surface gravity, compared with those of conventional theoretical 1D hydrostatic atmosphere models based on the mixing-length theory for convection. The 1D atmospheres show little dependence on gravity. 1D atmospheres of main-sequence stars also show an abrupt transition to the diffusion approximation at τ ≃ 2.5, whereas the 3D simulations exhibit smooth transitions that occur at the same depth for M ≃ 0.8 M⊙, and higher in the atmosphere for both more and less massive main-sequence stars. Based on these results, we recommend no longer using scaled solar T(τ) relations. Files with T(τ) relations for our grid of simulations are made available to the community, together with routines for interpolating in this irregular grid. We also provide matching tables of atmospheric opacity, for consistent implementation in stellar structure models.
1 INTRODUCTION
The complexity of stellar atmospheres is due to the highly complicated behaviour of opacity with wavelength and thermodynamic state, coupled with the non-local nature of radiative transfer in the photospheric transition from optically thick to optically thin. To treat this region properly, present-day stellar atmosphere codes solve the radiative transfer for hundreds of thousands of wavelength points, including tens of millions of spectral lines. Further ‘non-classical’ complications arise when deviations from local thermodynamic equilibrium (LTE) need to be accounted for, when the absence of convection allows for chemical stratification, or when strong magnetic fields or rapid rotation affect the atmospheric structure. Thus, although stellar evolution modelling requires non-trivial boundary conditions at the stellar surface, these complications obviously render impractical the direct calculation of realistic atmospheres in stellar structure models.
A solution to this problem is to use pre-computed results of stellar atmosphere modelling (semi-empirical or fully theoretical) as upper boundary conditions for stellar structure models. Knowing pressure (equation-of-state, EOS) and Rosseland opacity as functions of ϱ and T, and assuming hydrostatic equilibrium, the system of equations can be closed by the T(τ) relation without having to solve the frequency-dependent radiative transfer – i.e. the stratification of the detailed atmosphere calculation can be recovered with a mean opacity, as we show in Section 2. Note that the Rosseland opacity is not used for performing radiative transfer in the atmosphere of the structure model – it is merely used to reconstitute the detailed atmosphere model, which has been condensed into the T(τ) relation. The resulting atmosphere is therefore not grey, unless the grey T(τ) relation has been used (see e.g. Fig. 3).
Since this method was implemented by, e.g., Böhm-Vitense (1958), this outer boundary has received relatively little attention. Indeed, T(τ) relations from that period are still in widespread use in stellar structure models – despite these T(τ) relations having little resemblance with current atmosphere models.
Chabrier & Baraffe (1997) investigated the effect of T(τ) relations on stellar evolution for solar-composition low-mass stars. The authors were rightly concerned about the proper implementation and interpretation of T(τ) relations in the transition between radiative and convective zones – an issue which is often overlooked. VandenBerg et al. (2008) performed a similar analysis of stellar models using marcs stellar atmosphere models (Gustafsson et al. 2008) as outer boundaries, as well as the often used grey and Krishna Swamy (1966, see Section 5) atmospheres. They were likewise concerned about how and where to merge the two formulations, and the inconsistencies and discontinuities arising there. The fundamental problem is that the transition should ideally take place in the optically deep layers, where the diffusion approximation applies, and above the top of the convection zone to avoid inconsistencies due to differing formulations of convection. It is often assumed that optically deep means τ ≳ 1 in which case it is barely possible to have this separation in one-dimensional (1D) models. Morel et al. (1994) show, however, that the diffusion approximation is not fulfilled unless τ ≳ 10 (as we confirm). Furthermore, in more realistic 3D simulations of convective atmospheres, even τ = 1 overlaps with convection. The problems plaguing the outer boundary conditions are recognized, yet there has been little theoretical progress on the issue. We address these problems with our new self-consistent formulation, discussed in Section 2, which also eliminates the extra parameters introduced by the above-mentioned prescriptions.
A helioseismic analysis of various commonly used prescriptions for the outer boundary of solar models was carried out by Morel et al. (1994). They found sizeable effects that show up as part of the so-called surface effect: a systematic and frequency-dependent shift of frequencies (Christensen-Dalsgaard & Thompson 1997). They also show how the classic calibration of solar models to the present Sun (Gough & Weiss 1976) tightly couples the outer boundary condition to the mixing length of convection.
Since the solar T(τ) relation can in principle be inferred from limb-darkening observations (e.g. Mitchell 1959), the use of semi-empirical models based on such observations has often been considered the safest choice. The observations and corresponding T(τ) relations can only be performed monochromatically, however, which is of little use to stellar modellers. Connecting to the more useful Rosseland optical depth scale requires pan-chromatic knowledge of opacities, which is the exact weakness of fully theoretical models that semi-empirical models seek to circumvent. At the time there were indications, though, that the Rosseland opacity was little affected by spectral lines, in which case the 5000 Å monochromatic opacity (which is straightforward to compute, since only few and well-known sources contribute to that opacity) was a good proxy in late-type stars. This justified the use of semi-empirical models, as a largely model-independent alternative to fully theoretical models. Subsequent work has shown that spectral lines can have a large influence on the Rosseland opacity, in our case adding 20–40 per cent to the opacity in stellar atmospheres. Since the Rosseland mean is a harmonic mean, it heavily weights the lowest opacity, that is, the continuum. When the spectral density of lines becomes so high that lines overlap, a pseudo-continuum is formed, which raises the Rosseland mean (Rogers & Iglesias 1994, for analysis of interior opacities). The result is that semi-empirical models depend almost as much on opacities (and other atomic physics) as do the fully theoretical solar model atmosphere.
Theoretical T(τ) relations from 1D stellar atmosphere models have been published in connection with, e.g., the atlas (Kurucz 1992c, 1996; Castelli & Kurucz 2003), the marcs (Gustafsson et al. 1975; Asplund et al. 1997; Gustafsson et al. 2008), the NextGen (Hauschildt, Allard & Baron 1999a; Hauschildt et al. 1999b; Short et al. 2012) and the MAFAGS-OS (Grupp 2004; Grupp, Kurucz & Tan 2009) grids of stellar atmospheres. These are grids in effective temperature, surface gravity and metallicity, and the grids are dense enough that simple interpolation is safe. The level of sophistication is very impressive, but detailed comparisons with solar spectra still reveal many lines unaccounted for (e.g. Kurucz 2009). Plez (2011) compares the first three grids for late-type stars and find good agreement between their atmospheric structures (see also Gustafsson et al. 2008), but significant differences between their spectra.
In late-type stars, however, the treatment of convection is the weakest point in the modelling of atmospheres. Not only are they not one-dimensional, but the convective fluctuations are also well outside the regime of linear perturbations. So far, the only way to deal with the combined problem of radiation and convection in stellar photospheres is to perform realistic radiation-coupled hydrodynamic (RHD) simulations. There are now a couple of grids of such simulations in development or available: the CIFIST grid (Ludwig et al. 2009) of co5bold simulations (Wedemeyer et al. 2004; Freytag et al. 2012) and the stagger grid (Collet, Magic & Asplund 2011; Magic et al. 2013) of stagger-code simulations (Nordlund & Galsgaard 1995; Stein et al. 2009). T(τ) relations were briefly discussed by Ludwig, Freytag & Steffen (1999) for an earlier grid, using a 2D version of the predecessor of the co5bold code. They used mostly grey radiative transfer in the simulations and a fit to the grey atmosphere in the structure models, with no details on their implementation of the latter. The few T(τ) relations they did evaluate from non-grey simulations were not published. Magic, Weiss & Asplund (2014) used 1D atmosphere models corresponding to the simulations of their stagger grid, as their T(τ) relations, also not published. Tanner, Basu & Demarque (2014) carried out 3D simulations that use the Eddington approximation to the grey atmosphere, instead of solving the radiative transfer, and explored effects of metallicity. This approach neatly isolates the effect of adiabatic cooling by convective overshooting (Nordlund & Stein 1991; Asplund et al. 1999; Collet, Asplund & Trampedach 2007), since they ignore line blanketing (Chandrasekhar 1935) which would normally interfere with this effect. It does, however, not describe a realistic atmosphere, since the defining radiative transfer has been ignored.
We base our present work on the grid of solar-metallicity, deep convective atmospheres by Trampedach et al. (2013), which used the Stein & Nordlund (1998) code. We describe the most pertinent features of these convection simulations in Section 3 and derive a consistent formulation of T(τ) relations that also works with 3D radiative transfer in Section 2.4. The T(τ) relations of the simulations are presented in Section 4, and in Section 5 we make a more detailed analysis of our solar simulation and compare with semi-empirical and theoretical T(τ) relations from the literature. The general variation of our T(τ) relations with stellar parameters is explored in Section 6, by means of interpolation routines readily employed in stellar structure calculations.
This paper is the first in a series dedicated to the improvement of stellar structure and evolution calculations. These improvements are based on lessons learnt from 3D radiation-coupled hydrodynamical simulations of convection in the atmospheres of late-type stars (F-K). Here we present results on the radiative part of the mean stratification of the simulations in the form of T(τ) relations, to be used as outer boundary conditions for stellar structure models. Paper II (Trampedach et al. 2014) deals with the convective part of the mean stratification by calibrating the mixing length and presenting the results in a form easy to implement in stellar structure codes. The radiative and the convective parts of the problem are strongly interdependent, as discussed in this paper and in Paper II, but we also show that separating the two parts is possible and that such a separation is relevant for stellar structure models. Paper II also examines the coupling between T(τ) relations and the mixing length of convection. A future paper will address the consequences of applying the above improvements to stellar evolution calculations.
2 THE BASIS FOR T(τ) RELATIONS
A T(τ) relation is needed for describing the photospheric transition between optically thick (diffusion approximation) and optically thin (the free-streaming approximation) layers. In late-type stars, this transition is affected by the large temperature fluctuations caused by convection, but it is in principle separable from the issue of how large a fraction of the flux is transported by convection. We first need to formalize these statements and establish the theoretical foundation for a consistent definition and use of T(τ) relations.
The 3D simulations are all performed with uniform gravity, which corresponds to the plane-parallel approximation in 1D. We keep the following derivations in that approximation. This should be valid even for our lowest gravity simulations (nos. 1 and 2 in Table 1, with log g = 2.2), since Plez, Brett & Nordlund (1992) found a maximum sphericity effect of a mere −20 K for a 3800 K, log g = 1.0, 1 M⊙ giant, at log τ = −4.5, using marcs 1D model atmospheres. The sphericity effect will obviously be smaller for larger g as in our case.
| sim . | MK class . | Teff (K) . | log g . | M (M⊙) . | Star . |
|---|---|---|---|---|---|
| 1 | K3 | 4681 ± 19 | 2.200 | 3.694 | |
| 2 | K2 | 4962 ± 21 | 2.200 | 4.805 | |
| 3 | K5 | 4301 ± 17 | 2.420 | 0.400 | |
| 4 | K6 | 4250 ± 11 | 3.000 | 0.189 | |
| 5 | K3 | 4665 ± 16 | 3.000 | 0.852 | |
| 6 | K1 | 4994 ± 15 | 2.930 | 2.440 | ξ Hya |
| 7 | G8 | 5552 ± 17 | 3.000 | 2.756 | |
| 8 | K3 | 4718 ± 15 | 3.500 | 0.721 | |
| 9 | K0 | 5187 ± 17 | 3.500 | 1.786 | |
| 10 | K0 | 5288 ± 20 | 3.421 | 1.923 | ν Ind |
| 11 | F9 | 6105 ± 25 | 3.500 | 1.875 | |
| 12 | K6 | 4205 ± 8 | 4.000 | 0.601 | |
| 13 | K4 | 4494 ± 9 | 4.000 | 0.684 | |
| 14 | K3 | 4674 ± 8 | 4.000 | 0.738 | |
| 15 | K2 | 4986 ± 13 | 4.000 | 0.836 | |
| 16 | G6 | 5674 ± 16 | 3.943 | 1.130 | β Hyi |
| 17 | F9 | 6137 ± 14 | 4.040 | 1.222 | |
| 18 | F4 | 6582 ± 26 | 3.966 | 1.567 | Procyon |
| 19 | F4 | 6617 ± 33 | 4.000 | 1.542 | |
| 20 | K4 | 4604 ± 8 | 4.300 | 0.568 | |
| 21 | K1 | 4996 ± 17 | 4.300 | 0.694 | |
| 22 | K1 | 5069 ± 11 | 4.300 | 0.719 | |
| 23 | K0 | 5323 ± 16 | 4.300 | 0.810 | |
| 24 | G1 | 5926 ± 18 | 4.295 | 1.056 | α Cen A |
| 25 | F5 | 6418 ± 26 | 4.300 | 1.261 | |
| 26 | F2 | 6901 ± 29 | 4.292 | 1.433 | |
| 27 | K4 | 4500 ± 4 | 4.500 | 0.565 | |
| 28 | K3 | 4813 ± 8 | 4.500 | 0.664 | |
| 29 | K0 | 5232 ± 12 | 4.500 | 0.812 | |
| 30 | G5 | 5774 ± 17 | 4.438 | 1.002 | The Sun |
| 31 | F7 | 6287 ± 15 | 4.500 | 1.246 | |
| 32 | F4 | 6569 ± 17 | 4.450 | 1.329 | |
| 33 | K1 | 5021 ± 11 | 4.550 | 0.772 | |
| 34 | G9 | 5485 ± 14 | 4.557 | 0.949 | α Cen B |
| 35 | G1 | 5905 ± 15 | 4.550 | 1.114 | |
| 36 | K6 | 4185 ± 3 | 4.740 | 0.649 | |
| 37 | K4 | 4531 ± 10 | 4.740 | 0.742 |
| sim . | MK class . | Teff (K) . | log g . | M (M⊙) . | Star . |
|---|---|---|---|---|---|
| 1 | K3 | 4681 ± 19 | 2.200 | 3.694 | |
| 2 | K2 | 4962 ± 21 | 2.200 | 4.805 | |
| 3 | K5 | 4301 ± 17 | 2.420 | 0.400 | |
| 4 | K6 | 4250 ± 11 | 3.000 | 0.189 | |
| 5 | K3 | 4665 ± 16 | 3.000 | 0.852 | |
| 6 | K1 | 4994 ± 15 | 2.930 | 2.440 | ξ Hya |
| 7 | G8 | 5552 ± 17 | 3.000 | 2.756 | |
| 8 | K3 | 4718 ± 15 | 3.500 | 0.721 | |
| 9 | K0 | 5187 ± 17 | 3.500 | 1.786 | |
| 10 | K0 | 5288 ± 20 | 3.421 | 1.923 | ν Ind |
| 11 | F9 | 6105 ± 25 | 3.500 | 1.875 | |
| 12 | K6 | 4205 ± 8 | 4.000 | 0.601 | |
| 13 | K4 | 4494 ± 9 | 4.000 | 0.684 | |
| 14 | K3 | 4674 ± 8 | 4.000 | 0.738 | |
| 15 | K2 | 4986 ± 13 | 4.000 | 0.836 | |
| 16 | G6 | 5674 ± 16 | 3.943 | 1.130 | β Hyi |
| 17 | F9 | 6137 ± 14 | 4.040 | 1.222 | |
| 18 | F4 | 6582 ± 26 | 3.966 | 1.567 | Procyon |
| 19 | F4 | 6617 ± 33 | 4.000 | 1.542 | |
| 20 | K4 | 4604 ± 8 | 4.300 | 0.568 | |
| 21 | K1 | 4996 ± 17 | 4.300 | 0.694 | |
| 22 | K1 | 5069 ± 11 | 4.300 | 0.719 | |
| 23 | K0 | 5323 ± 16 | 4.300 | 0.810 | |
| 24 | G1 | 5926 ± 18 | 4.295 | 1.056 | α Cen A |
| 25 | F5 | 6418 ± 26 | 4.300 | 1.261 | |
| 26 | F2 | 6901 ± 29 | 4.292 | 1.433 | |
| 27 | K4 | 4500 ± 4 | 4.500 | 0.565 | |
| 28 | K3 | 4813 ± 8 | 4.500 | 0.664 | |
| 29 | K0 | 5232 ± 12 | 4.500 | 0.812 | |
| 30 | G5 | 5774 ± 17 | 4.438 | 1.002 | The Sun |
| 31 | F7 | 6287 ± 15 | 4.500 | 1.246 | |
| 32 | F4 | 6569 ± 17 | 4.450 | 1.329 | |
| 33 | K1 | 5021 ± 11 | 4.550 | 0.772 | |
| 34 | G9 | 5485 ± 14 | 4.557 | 0.949 | α Cen B |
| 35 | G1 | 5905 ± 15 | 4.550 | 1.114 | |
| 36 | K6 | 4185 ± 3 | 4.740 | 0.649 | |
| 37 | K4 | 4531 ± 10 | 4.740 | 0.742 |
| sim . | MK class . | Teff (K) . | log g . | M (M⊙) . | Star . |
|---|---|---|---|---|---|
| 1 | K3 | 4681 ± 19 | 2.200 | 3.694 | |
| 2 | K2 | 4962 ± 21 | 2.200 | 4.805 | |
| 3 | K5 | 4301 ± 17 | 2.420 | 0.400 | |
| 4 | K6 | 4250 ± 11 | 3.000 | 0.189 | |
| 5 | K3 | 4665 ± 16 | 3.000 | 0.852 | |
| 6 | K1 | 4994 ± 15 | 2.930 | 2.440 | ξ Hya |
| 7 | G8 | 5552 ± 17 | 3.000 | 2.756 | |
| 8 | K3 | 4718 ± 15 | 3.500 | 0.721 | |
| 9 | K0 | 5187 ± 17 | 3.500 | 1.786 | |
| 10 | K0 | 5288 ± 20 | 3.421 | 1.923 | ν Ind |
| 11 | F9 | 6105 ± 25 | 3.500 | 1.875 | |
| 12 | K6 | 4205 ± 8 | 4.000 | 0.601 | |
| 13 | K4 | 4494 ± 9 | 4.000 | 0.684 | |
| 14 | K3 | 4674 ± 8 | 4.000 | 0.738 | |
| 15 | K2 | 4986 ± 13 | 4.000 | 0.836 | |
| 16 | G6 | 5674 ± 16 | 3.943 | 1.130 | β Hyi |
| 17 | F9 | 6137 ± 14 | 4.040 | 1.222 | |
| 18 | F4 | 6582 ± 26 | 3.966 | 1.567 | Procyon |
| 19 | F4 | 6617 ± 33 | 4.000 | 1.542 | |
| 20 | K4 | 4604 ± 8 | 4.300 | 0.568 | |
| 21 | K1 | 4996 ± 17 | 4.300 | 0.694 | |
| 22 | K1 | 5069 ± 11 | 4.300 | 0.719 | |
| 23 | K0 | 5323 ± 16 | 4.300 | 0.810 | |
| 24 | G1 | 5926 ± 18 | 4.295 | 1.056 | α Cen A |
| 25 | F5 | 6418 ± 26 | 4.300 | 1.261 | |
| 26 | F2 | 6901 ± 29 | 4.292 | 1.433 | |
| 27 | K4 | 4500 ± 4 | 4.500 | 0.565 | |
| 28 | K3 | 4813 ± 8 | 4.500 | 0.664 | |
| 29 | K0 | 5232 ± 12 | 4.500 | 0.812 | |
| 30 | G5 | 5774 ± 17 | 4.438 | 1.002 | The Sun |
| 31 | F7 | 6287 ± 15 | 4.500 | 1.246 | |
| 32 | F4 | 6569 ± 17 | 4.450 | 1.329 | |
| 33 | K1 | 5021 ± 11 | 4.550 | 0.772 | |
| 34 | G9 | 5485 ± 14 | 4.557 | 0.949 | α Cen B |
| 35 | G1 | 5905 ± 15 | 4.550 | 1.114 | |
| 36 | K6 | 4185 ± 3 | 4.740 | 0.649 | |
| 37 | K4 | 4531 ± 10 | 4.740 | 0.742 |
| sim . | MK class . | Teff (K) . | log g . | M (M⊙) . | Star . |
|---|---|---|---|---|---|
| 1 | K3 | 4681 ± 19 | 2.200 | 3.694 | |
| 2 | K2 | 4962 ± 21 | 2.200 | 4.805 | |
| 3 | K5 | 4301 ± 17 | 2.420 | 0.400 | |
| 4 | K6 | 4250 ± 11 | 3.000 | 0.189 | |
| 5 | K3 | 4665 ± 16 | 3.000 | 0.852 | |
| 6 | K1 | 4994 ± 15 | 2.930 | 2.440 | ξ Hya |
| 7 | G8 | 5552 ± 17 | 3.000 | 2.756 | |
| 8 | K3 | 4718 ± 15 | 3.500 | 0.721 | |
| 9 | K0 | 5187 ± 17 | 3.500 | 1.786 | |
| 10 | K0 | 5288 ± 20 | 3.421 | 1.923 | ν Ind |
| 11 | F9 | 6105 ± 25 | 3.500 | 1.875 | |
| 12 | K6 | 4205 ± 8 | 4.000 | 0.601 | |
| 13 | K4 | 4494 ± 9 | 4.000 | 0.684 | |
| 14 | K3 | 4674 ± 8 | 4.000 | 0.738 | |
| 15 | K2 | 4986 ± 13 | 4.000 | 0.836 | |
| 16 | G6 | 5674 ± 16 | 3.943 | 1.130 | β Hyi |
| 17 | F9 | 6137 ± 14 | 4.040 | 1.222 | |
| 18 | F4 | 6582 ± 26 | 3.966 | 1.567 | Procyon |
| 19 | F4 | 6617 ± 33 | 4.000 | 1.542 | |
| 20 | K4 | 4604 ± 8 | 4.300 | 0.568 | |
| 21 | K1 | 4996 ± 17 | 4.300 | 0.694 | |
| 22 | K1 | 5069 ± 11 | 4.300 | 0.719 | |
| 23 | K0 | 5323 ± 16 | 4.300 | 0.810 | |
| 24 | G1 | 5926 ± 18 | 4.295 | 1.056 | α Cen A |
| 25 | F5 | 6418 ± 26 | 4.300 | 1.261 | |
| 26 | F2 | 6901 ± 29 | 4.292 | 1.433 | |
| 27 | K4 | 4500 ± 4 | 4.500 | 0.565 | |
| 28 | K3 | 4813 ± 8 | 4.500 | 0.664 | |
| 29 | K0 | 5232 ± 12 | 4.500 | 0.812 | |
| 30 | G5 | 5774 ± 17 | 4.438 | 1.002 | The Sun |
| 31 | F7 | 6287 ± 15 | 4.500 | 1.246 | |
| 32 | F4 | 6569 ± 17 | 4.450 | 1.329 | |
| 33 | K1 | 5021 ± 11 | 4.550 | 0.772 | |
| 34 | G9 | 5485 ± 14 | 4.557 | 0.949 | α Cen B |
| 35 | G1 | 5905 ± 15 | 4.550 | 1.114 | |
| 36 | K6 | 4185 ± 3 | 4.740 | 0.649 | |
| 37 | K4 | 4531 ± 10 | 4.740 | 0.742 |
2.1 Convective versus radiative T(τ) relations
The temperature as a function of optical depth, T(τ), is trivial to extract from any atmosphere model, be it 1D or a 3D simulation. The T(τ) relation, however, is greatly affected by the presence of convection, having a much smaller gradient in convective regions (see Fig. 3). When applying T(τ) relations to stellar structure calculations, the convective fluxes will most likely differ between the atmosphere model and the 1D structure model, which renders the T(τ) relation inappropriate for the structure model. Using the T(τ) relation from even the most sophisticated 3D simulation of a convective atmosphere in a 1D model would be both inconsistent and unphysical if the convective flux differs between the two cases. Unfortunately, we do not yet have a way of directly incorporating the convection of the 3D simulations into the 1D models in any consistent or even physically meaningful way. To rectify this is obviously a long-term goal of ours.
The first-order effect of convection on T(τ) relations is due to the radiative flux not being constant. If we can somehow express the T(τ) relation with an explicit appearance of the radiative flux, it should be possible to isolate this first-order effect and calculate a radiativeT(τ) relation (i.e. reduced to the radiative equilibrium case with Qrad = 0 and therefore Frad = const). When used in stellar structure calculations, the first-order convective effect can be added back in, as appropriate for that particular model (see Section 2.5). From here on we will call temperatures from T(τ) relations with this first-order convective effect subtracted Trad(τ) – the radiative T(τ) relation.
The original, unaltered T(τ) relation of the atmosphere models, which includes the transition to convective transport of the flux, will be referred to as partially convective T(τ) relations.
Another effect of a varying H is the finite difference between source function and mean intensity, Δ = J − S, giving rise to the radiative heating or flux divergence of equation (4). In radiative equilibrium Δ converges, Δ → 0, with optical depth, but not in the transition to a convection zone. The relative difference, Δ/S, is small, however. The largest values are found in the cooling peak at the top of convective envelopes, where |Δ|/S ≲ 1×10− 3, or in a heating bump above the photosphere of the coolest dwarf stars, with |Δ|/S ≲ 5×10− 3. Estimating the effect on temperature as |Δ|/S ≃ 4ΔT, we get |ΔT| ≲ 1 K and |ΔT| ≲ 4 K, respectively, and we have therefore chosen to ignore this effect. Since it is equally ignored in the 1D models used here, this in practice means that we assume the same Δ in the atmosphere model as in the 1D structure model. The actual error thus committed is therefore much smaller.
It follows that in order to make self-consistent 1D stellar models, we need to remove the first-order effect from the 3D T(τ) relation: the transition from convective to radiative transport of energy in the photosphere. All higher order convective effects arising from, e.g., the mean stratification differing from the 1D model, cooling by convective overshooting (cf. Section 6), the large convective fluctuations in the photosphere and the correlations between them will, however, be retained in Trad(τ). And this is plenty motivation for continuing this exercise, as will be shown in the comparisons between 1D and 3D T(τ) relations in Section 4.
2.2 T(τ) relations from grey atmospheres
In order to isolate the first-order convective effect on the T(τ) relation, we seek an expression containing H, and to simplify the problem we begin with the grey case (by simply dropping the λ subscripts), and generalize afterwards.
The choice of formulation rests on the choice of quantity that will be assumed invariant under convection, i.e. unchanged whether convection carries flux or not. The invariant should contain quantities from equations (5) and (6) which can be used to reconstruct the Planck function, B = σT4/π. Reasonable choices are K/B, K/J, dK/dB or dK/dJ, which all can be shown to converge to 1/3 for τ → ∞ (Mihalas 1978; Rutten 2003). These ratios can all be used in a similar way as the variable Eddington factor, K/J (Auer & Mihalas 1970). We choose fdB(τ) ≡ dK/dB for the relative simplicity of the temperature reconstruction. We effectively distil the whole stellar atmosphere calculation down to one quantity: fdB as a function of depth. This is the essence of the elaborate atmosphere calculation that we want to transfer to the stellar structure calculation, regardless of how convection differs between the two cases.
Such a temperature perturbation, from different treatments of convection, would cause differences in fdB if it were to be computed anew from radiative transfer on the perturbed structure. So by keeping fdB invariant, we impose on the structure model the radiative transfer result from the full atmosphere calculation based on the latter's temperature structure. This counts amongst the second-order effects of convection on the radiative transfer (variation of fdB is indeed quadratic in small temperature perturbations, but also sizeable at relevant amplitudes).
The main thrust in this paper is the utility of 3D atmosphere simulations in setting outer boundary conditions for stellar structure models. Our method can also be used with 1D stellar atmospheres, however, e.g. using different formulations or parameters for convection than the interior models, but with a seamless combination of the two (see Section 2.5).
The radiative Hopf function (which assumes an atmosphere in radiative equilibrium) is convergent, qrad(τ) → q∞ for τ → ∞, and thus recovers the diffusion approximation at depth. Equivalently, we describe a (partly) convective stratification, T(τ), by qconv(τ). With part of the flux transported by convection, the temperature is decoupled from the optical depth and there is no convergence with depth. The Schwarzschild criterion (e.g. Kippenhahn & Weigert 1990) for convective instability tells us that at any depth the energy transport mechanism with the smallest temperature gradient is the relevant one. The temperature in a partly convective stratification will therefore be lower than that in a corresponding radiative one, and from equation (9) we see that qconv(τ) will diverge to large negative values.
The use for T(τ) relations in the grey case is widely appreciated, but we have now included convective effects and put the whole formulation on a firmer footing. The final step is to ensure that they can be used in the general non-grey case and therefore provide a valid and useful description of real stellar atmospheres.
2.3 T(τ) relations from non-grey atmospheres
From this analysis, we conclude that T(τ) relations are perfectly suited for describing real stellar atmospheres. Since the formulation does not rely on S = B, except in the optically deep layers, this formulation will also be valid for non-LTE atmospheres, whether they just include continuum scattering or a thorough implementation of non-LTE effects. The choice of κRoss as the standard opacity is merely to ensure proper convergence with depth and as a convenience to stellar modellers. This does not limit the scope of the formulation in the photosphere and above. It is often asserted that the use of T(τ) relations with a Rosseland opacity amounts to using the grey approximation. We hope that we have demonstrated this to be far from the case and that T(τ) relations can describe arbitrarily realistic and complex atmospheres. The use of a Rosseland opacity to reconstitute the atmosphere in structure models says nothing about the level of complexity that went into the original atmosphere calculation from which the T(τ) relation was derived. Reconstituting the T(τ) relation with the Rosseland opacity results in the structure of the original atmosphere, but without the need to perform the computationally expensive radiative transfer calculation.
2.4 T(τ) relations in 3D
In 1D there is no ambiguity about the meaning of a certain quantity, e.g. τ and T, and they depend in simple ways on the height in the atmosphere, z. In 3D, on the other hand, there is a whole range of temperatures and optical depths at a particular height, and different averaging methods will give rather different results. This is illustrated in Fig. 1 where we compare three different averaging methods for our solar simulation (no. 30 in Table 1). We plot temperatures averaged over the undulated surfaces of equal optical depth (τ-average) in case (a). In case (b) we plot a straight horizontal average of the temperature as a function of a straight horizontal average of the optical depth, 〈…〉z. For the temporal averaging of these, we map the horizontal averages to a fixed column mass scale. We refer to these as pseudo (since we use the average, not the local column mass) Lagrangian averages, denoted by 〈…〉L. This filters out the main effect of the p modes that are excited in the simulations. Finally, in case (c) we show the horizontally averaged temperature as a function of an optical depth integrated from the opacity of the horizontally averaged density and temperature.
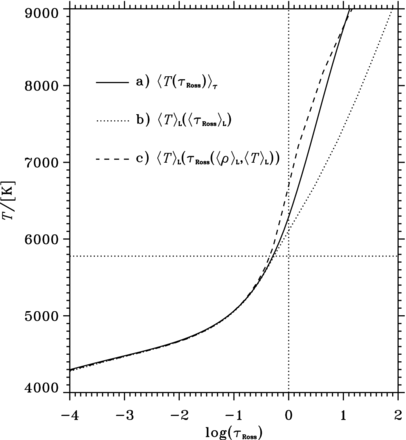
The effect of various averaging techniques applied to a solar simulation (see the text for details). Notice how cases (a) and (b) follow closely in the atmosphere down to 〈T〉 = Teff, at log τ ≃ −0.3. The horizontal dotted line indicates Teff and the vertical, unity optical depth. The solar T(τ) relations in this plot include the first-order convective effect.
Not unexpectedly, these three different methods diverge in the region where the temperature fluctuations are the largest, from the photosphere down to 1 Mm below (at τRoss ∼ 105). There the convective fluctuations, in mainly the temperature, are so large that the opacity and the EOS (e.g. gas pressure, pg) are non-linear on the scale of the fluctuations. This has the consequence that 〈pg〉 ≠ pg(〈ϱ〉, 〈T〉). In other words, the average gas pressure is, in general, not related to the average density and temperature through the EOS. The relative difference amounts to about 5 per cent in the solar photosphere. This effect is much larger for the opacity where the relative difference reaches more than 90 per cent in the solar photosphere. Well above the photosphere, the averaging methods converge, as the temperature fluctuations decrease and, more importantly, as the opacity varies less steeply.
The large differences between the methods around the photosphere mean that great care is needed in choosing the appropriate form of averaging. Intuitively, quantities having to do with radiative transfer would be best represented as τ-averages, case (a) above. This choice was also advocated by Ludwig et al. (1999), who used τ-averaged temperatures of their 2D convection simulations as T(τ) relations for corresponding 1D envelope models. These then formed the basis for a calibration of the mixing length, similar to what we present in Paper II.
The τH-scale defined by equation (23) is a bit awkward, since it demands knowledge of the complete radiative transfer solution – something we explicitly are trying to avoid with our approach. We therefore want to rephrase q in terms of the ‘universal’ Rosseland opacity, which depends only on the local thermodynamic state.
Unfortunately, what would normally be interpreted as the average Rosseland opacity does not converge to the flux averaged opacity, 〈ϱκH〉z, as defined by equation (23). On the other hand, q(τH) depends on this definition in order to fulfil the constraints of converging |$f^z_{{\rm d}B}$| and qrad(τH) and the ability of qconv(τH) to reproduce the temperature stratification of the simulations.
In and above the photosphere the two opacities diverge, as the diffusion approximation no longer holds, κH being the larger of the two (since the flux spectrum is largely determined at the photosphere and the temperature there, whereas dBλ/dτλ is entirely set by the local temperature. This redshifts the Rosseland weighting function towards the lower opacity of the H− bump, away from the crowded lines and metallic absorption edges in the UV). This means qRoss > qH, and in the optically deep layers they are merely offset by a constant. It is also worth noting that the 1D form of equation (28) is identical to the conventional form, leaving our formulation consistent with previous 1D work.
2.5 Implementation of the T(τ) relation in stellar structure models
We proved above that T(τ) relations can describe real stellar atmospheres and therefore have the potential to provide the outer boundary conditions of stellar structure models. In this section, we will show in detail how this is carried out, in particular how convective effects are reintroduced in a consistent manner. The reason for this elimination and subsequent reintroduction of convection to the T(τ) relation is the resulting independence of convection treatment between the atmosphere models (providing the T(τ) relation) and the stellar structure models (employing the T(τ) relation). Thus, the models can be internally self-consistent, despite differing greatly in their convection treatment – in our case 3D convection simulations and 1D with the mixing-length theory (MLT; Böhm-Vitense 1958) formulation of convection.
From here on, we will use the abbreviation |$q=q_{\rm Ross}^{\rm rad}$|, and a Rosseland mean is implied for both opacity and optical depth, unless explicitly stated otherwise. All quantities in this section pertain to the structure model implementing the T(τ) relation, except for q(τ) which, of course, is computed from the atmosphere model.
The right-hand side is the complete T(τ) relation of the structure model, including the transition to (1D) convection, and qrad(τ) + τ is the radiative T(τ) relation from the detailed atmosphere model, converging properly for τ → ∞. The change of |$\tau \rightarrow \hat{\tau }$| on the left-hand side is solely responsible for recovering the partially convective T(τ) relation from a radiative Hopf function. Due to the simple behaviour of the first-order effect of convection on the temperature stratification (a consequence of equation 6), the radiative equilibrium stratification and the actual stratification can be described by the same Hopf function, merely by a simple change to the argument.
With these relations, the T(τ) relation can be used throughout the stellar envelope model, without the (common) artificial transition between atmosphere and interior. A somewhat similar, but less rigorous, approach was used by Henyey, Vardya & Bodenheimer (1965) to ensure a smooth transition between the atmosphere and interior of stellar models.
2.6 Summary of procedures
As derived above, there are two separate steps involved. First, the calculation of the T(τ) relation, in the form of a generalized Hopf function q(τ), from an atmosphere model which explicitly solves the radiative transfer equation. Secondly, the implementation of T(τ) relations in 1D stellar structure models.
The purely radiative Hopf function, q(τ), is computed from 1D stellar atmospheres from equation (11) and the invariant fdB of equation (18), both based on the Rosseland opacity.
For 3D atmospheres, the procedure is slightly more complicated, although it reduces properly to the 1D case above. In 3D the invariant, fdB, is computed from equation (20) and applied in equation (25) for the radiative Hopf function. The horizontally averaged Rosseland opacity, 〈ϱκRoss〉z, needs to be slightly redefined, so that the wavelength integrals of the opacity and of the normalization factor are averaged separately, as specified by equation (28).
The implementation of the T(τ) relation is accomplished through modifications of the radiative, ∇rad, and actual temperature gradients, ∇, equations (35) and (36), respectively. The actual gradient involves the radiative Hopf function evaluated at a modified τ-scale, |$q(\hat{\tau })$|, constructed to account for the first-order convective effect on the stratification, due to departure from radiative equilibrium. This modification is defined by equation (38).
We have provided electronic tables of q(τ) for our grid of simulations, and of the [Fe/H] = 0.0 Rosseland opacity, as well as code for reading and interpolating in these tables.
3 THE 3D CONVECTION SIMULATIONS
The fully compressible, transmitting-boundary, radiation-coupled hydrodynamic (RHD) simulations that we rely on here are described by Trampedach et al. (2013). A recent and thorough review of applications of such 3D stellar convection simulations can be found in Nordlund, Stein & Asplund (2009).
The EOS and the opacities were originally supplied by the so-called Uppsala package by Gustafsson (1973) which forms the atomic-physics basis for the original marcs atmosphere models (Gustafsson et al. 1975, greatly improved and updated in the present marcs models by Gustafsson et al. 2008). Since the matching to 1D envelopes (employed in the mixing-length calibration of Paper II) requires a high degree of consistency between the simulations and the envelopes, we found it necessary to bring the microphysics of the 3D simulations up to the same level as that of the 1D envelopes. The ever stronger constraints from improving observations also demanded an upgrade to more realistic atomic physics.
We therefore implemented the realistic Mihalas–Hummer–Däppen (MHD) EOS (Däppen et al. 1988; Hummer & Mihalas 1988). This EOS treats hundreds of bound levels explicitly for every ionization level of every included element. The hydrogen molecules H2 and H|$_2^+$| are included as the only molecules, and non-ideal interactions leading to pressure ionization are treated in detail, as are degenerate electrons. Furthermore, thermodynamic consistency (that the Maxwell relations are obeyed) is ensured by the use of the free energy minimization procedure (Däppen 1980), which was also a motivation for the EOS update. The EOS tables were custom calculated for a 15-element mixture (as opposed to the normal 6), to correspond to what is included in the Uppsala package.
Improvements to the continuum opacities are described in Section 3.1. Line opacity is supplied by the opacity distribution functions (ODFs) of Kurucz (1992a,b), and line blanketing is included in the radiative transfer by means of opacity binning (Nordlund 1982). The spectrum is divided into four bins according to the strength of opacity at each wavelength, and the source function is summed-up for each bin, as described in detail by Trampedach (1997) and Trampedach et al. (2013). Radiative transfer in the simulations is then calculated for just these four bins, reducing the problem by more than three orders of magnitude and making it tractable in 3D. This binning scheme does not benefit from increasing the number of bins beyond 4. From comparisons with the full monochromatic radiative transfer, we estimate that the temperature error due to this binning is less than 40 K for the solar case, in the range of −4 < log τ < 0. For each bin, the transfer equation, equation (3), is solved for the vertical ray and four slanted, μ = 1/3 rays, equally spaced in azimuthal angle (giving a total of five rays). The azimuthal dimension is of course degenerate in 1D, but adds another dimension to the 3D problem. The bin assignment is based on a full monochromatic radiative transfer calculation for the temporally and horizontally averaged simulation, and therefore varies between the simulations. Detailed radiative transfer is computed for all horizontal layers that have a minimum Rosseland optical depth min (τ) < 300, and the diffusion approximation is used below.
Our radiative transfer is performed in strict LTE where S = B. We minimize the effects of that approximation by excluding scattering cross-sections from the free-streaming, intensity-weighted opacity above the photosphere, and including it as absorption in the Rosseland mean below. Hayek et al. (2010) found from a consistent treatment of scattering that this is a good approximation, at least for solar-metallicity atmospheres.
We have performed simulations for 37 sets of atmospheric parameters, all with solar abundances (discussed below), as listed in Table 1. This table is ordered in ascending gravity and, for similar gravities, ascending in effective temperature – the same order as in table 2 of Trampedach et al. (2013). The spectral class is rather approximate, as is the mass which is based on estimates of intersections with evolutionary tracks. Neither of these two quantities is used in this work, but is merely included for the reader's convenience. Some of the simulations correspond to actual stars, as indicated in the rightmost column, but with the caveat that all the simulations have solar composition.
Sample of the online table of Hopf functions as functions of log τ (rows) and atmospheric parameters, Teff and log g (columns).
| Sim. no. . | 18 . | 30 . | 28 . | 17 . | 26 . | 3 . | 16 . | 24 . | ⋅⋅⋅ . |
|---|---|---|---|---|---|---|---|---|---|
| Teff (K) | 6582.301 | 5774.501 | 4813.199 | 6137.301 | 6901.799 | 4301.201 | 5674.800 | 5926.601 | ⋅⋅⋅ |
| log g | 3.966 | 4.438 | 4.500 | 4.040 | 4.292 | 2.420 | 3.943 | 4.295 | ⋅⋅⋅ |
| [Fe/H] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ⋅⋅⋅ |
| MLT alpha | 1.648 100 97 | 1.767 387 99 | 1.760 032 06 | 1.696 580 05 | 1.677 181 01 | 1.764 937 04 | 1.757 174 97 | 1.753 844 02 | ⋅⋅⋅ |
| sig alpha | 0.029 251 00 | 0.030 499 00 | 0.021 746 00 | 0.025 264 00 | 0.038 257 00 | 0.021 235 00 | 0.034 484 00 | 0.028 779 00 | ⋅⋅⋅ |
| −4.50000000 | 0.371 563 89 | 0.383 302 16 | 0.368 646 82 | 0.384 669 47 | 0.364 006 30 | 0.398 519 32 | 0.386 380 91 | 0.383 715 88 | ⋅⋅⋅ |
| −4.41975307 | 0.376 204 99 | 0.387 974 57 | 0.373 356 18 | 0.388 954 23 | 0.368 983 50 | 0.404 105 61 | 0.391 587 57 | 0.388 082 86 | ⋅⋅⋅ |
| −4.33950615 | 0.380 910 88 | 0.392 815 06 | 0.378 165 40 | 0.393 375 89 | 0.373 985 17 | 0.409 728 24 | 0.396 948 69 | 0.392 584 15 | ⋅⋅⋅ |
| −4.25925922 | 0.385 652 36 | 0.397 799 05 | 0.383 055 31 | 0.397 953 61 | 0.379 007 28 | 0.415 373 87 | 0.402 404 68 | 0.397 233 57 | ⋅⋅⋅ |
| −4.17901230 | 0.390 435 54 | 0.402 904 39 | 0.387 918 91 | 0.402 688 37 | 0.384 051 11 | 0.421 022 08 | 0.407 893 70 | 0.402 015 36 | ⋅⋅⋅ |
| −4.09876537 | 0.395 290 22 | 0.408 120 81 | 0.392 838 12 | 0.407 568 58 | 0.389 098 73 | 0.426 663 48 | 0.413 416 77 | 0.406 937 03 | ⋅⋅⋅ |
| −4.01851845 | 0.400 233 93 | 0.413 430 65 | 0.397 905 01 | 0.412 588 76 | 0.394 171 38 | 0.432 303 24 | 0.418 975 63 | 0.411 987 29 | ⋅⋅⋅ |
| ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ |
| Sim. no. . | 18 . | 30 . | 28 . | 17 . | 26 . | 3 . | 16 . | 24 . | ⋅⋅⋅ . |
|---|---|---|---|---|---|---|---|---|---|
| Teff (K) | 6582.301 | 5774.501 | 4813.199 | 6137.301 | 6901.799 | 4301.201 | 5674.800 | 5926.601 | ⋅⋅⋅ |
| log g | 3.966 | 4.438 | 4.500 | 4.040 | 4.292 | 2.420 | 3.943 | 4.295 | ⋅⋅⋅ |
| [Fe/H] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ⋅⋅⋅ |
| MLT alpha | 1.648 100 97 | 1.767 387 99 | 1.760 032 06 | 1.696 580 05 | 1.677 181 01 | 1.764 937 04 | 1.757 174 97 | 1.753 844 02 | ⋅⋅⋅ |
| sig alpha | 0.029 251 00 | 0.030 499 00 | 0.021 746 00 | 0.025 264 00 | 0.038 257 00 | 0.021 235 00 | 0.034 484 00 | 0.028 779 00 | ⋅⋅⋅ |
| −4.50000000 | 0.371 563 89 | 0.383 302 16 | 0.368 646 82 | 0.384 669 47 | 0.364 006 30 | 0.398 519 32 | 0.386 380 91 | 0.383 715 88 | ⋅⋅⋅ |
| −4.41975307 | 0.376 204 99 | 0.387 974 57 | 0.373 356 18 | 0.388 954 23 | 0.368 983 50 | 0.404 105 61 | 0.391 587 57 | 0.388 082 86 | ⋅⋅⋅ |
| −4.33950615 | 0.380 910 88 | 0.392 815 06 | 0.378 165 40 | 0.393 375 89 | 0.373 985 17 | 0.409 728 24 | 0.396 948 69 | 0.392 584 15 | ⋅⋅⋅ |
| −4.25925922 | 0.385 652 36 | 0.397 799 05 | 0.383 055 31 | 0.397 953 61 | 0.379 007 28 | 0.415 373 87 | 0.402 404 68 | 0.397 233 57 | ⋅⋅⋅ |
| −4.17901230 | 0.390 435 54 | 0.402 904 39 | 0.387 918 91 | 0.402 688 37 | 0.384 051 11 | 0.421 022 08 | 0.407 893 70 | 0.402 015 36 | ⋅⋅⋅ |
| −4.09876537 | 0.395 290 22 | 0.408 120 81 | 0.392 838 12 | 0.407 568 58 | 0.389 098 73 | 0.426 663 48 | 0.413 416 77 | 0.406 937 03 | ⋅⋅⋅ |
| −4.01851845 | 0.400 233 93 | 0.413 430 65 | 0.397 905 01 | 0.412 588 76 | 0.394 171 38 | 0.432 303 24 | 0.418 975 63 | 0.411 987 29 | ⋅⋅⋅ |
| ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ |
Sample of the online table of Hopf functions as functions of log τ (rows) and atmospheric parameters, Teff and log g (columns).
| Sim. no. . | 18 . | 30 . | 28 . | 17 . | 26 . | 3 . | 16 . | 24 . | ⋅⋅⋅ . |
|---|---|---|---|---|---|---|---|---|---|
| Teff (K) | 6582.301 | 5774.501 | 4813.199 | 6137.301 | 6901.799 | 4301.201 | 5674.800 | 5926.601 | ⋅⋅⋅ |
| log g | 3.966 | 4.438 | 4.500 | 4.040 | 4.292 | 2.420 | 3.943 | 4.295 | ⋅⋅⋅ |
| [Fe/H] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ⋅⋅⋅ |
| MLT alpha | 1.648 100 97 | 1.767 387 99 | 1.760 032 06 | 1.696 580 05 | 1.677 181 01 | 1.764 937 04 | 1.757 174 97 | 1.753 844 02 | ⋅⋅⋅ |
| sig alpha | 0.029 251 00 | 0.030 499 00 | 0.021 746 00 | 0.025 264 00 | 0.038 257 00 | 0.021 235 00 | 0.034 484 00 | 0.028 779 00 | ⋅⋅⋅ |
| −4.50000000 | 0.371 563 89 | 0.383 302 16 | 0.368 646 82 | 0.384 669 47 | 0.364 006 30 | 0.398 519 32 | 0.386 380 91 | 0.383 715 88 | ⋅⋅⋅ |
| −4.41975307 | 0.376 204 99 | 0.387 974 57 | 0.373 356 18 | 0.388 954 23 | 0.368 983 50 | 0.404 105 61 | 0.391 587 57 | 0.388 082 86 | ⋅⋅⋅ |
| −4.33950615 | 0.380 910 88 | 0.392 815 06 | 0.378 165 40 | 0.393 375 89 | 0.373 985 17 | 0.409 728 24 | 0.396 948 69 | 0.392 584 15 | ⋅⋅⋅ |
| −4.25925922 | 0.385 652 36 | 0.397 799 05 | 0.383 055 31 | 0.397 953 61 | 0.379 007 28 | 0.415 373 87 | 0.402 404 68 | 0.397 233 57 | ⋅⋅⋅ |
| −4.17901230 | 0.390 435 54 | 0.402 904 39 | 0.387 918 91 | 0.402 688 37 | 0.384 051 11 | 0.421 022 08 | 0.407 893 70 | 0.402 015 36 | ⋅⋅⋅ |
| −4.09876537 | 0.395 290 22 | 0.408 120 81 | 0.392 838 12 | 0.407 568 58 | 0.389 098 73 | 0.426 663 48 | 0.413 416 77 | 0.406 937 03 | ⋅⋅⋅ |
| −4.01851845 | 0.400 233 93 | 0.413 430 65 | 0.397 905 01 | 0.412 588 76 | 0.394 171 38 | 0.432 303 24 | 0.418 975 63 | 0.411 987 29 | ⋅⋅⋅ |
| ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ |
| Sim. no. . | 18 . | 30 . | 28 . | 17 . | 26 . | 3 . | 16 . | 24 . | ⋅⋅⋅ . |
|---|---|---|---|---|---|---|---|---|---|
| Teff (K) | 6582.301 | 5774.501 | 4813.199 | 6137.301 | 6901.799 | 4301.201 | 5674.800 | 5926.601 | ⋅⋅⋅ |
| log g | 3.966 | 4.438 | 4.500 | 4.040 | 4.292 | 2.420 | 3.943 | 4.295 | ⋅⋅⋅ |
| [Fe/H] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ⋅⋅⋅ |
| MLT alpha | 1.648 100 97 | 1.767 387 99 | 1.760 032 06 | 1.696 580 05 | 1.677 181 01 | 1.764 937 04 | 1.757 174 97 | 1.753 844 02 | ⋅⋅⋅ |
| sig alpha | 0.029 251 00 | 0.030 499 00 | 0.021 746 00 | 0.025 264 00 | 0.038 257 00 | 0.021 235 00 | 0.034 484 00 | 0.028 779 00 | ⋅⋅⋅ |
| −4.50000000 | 0.371 563 89 | 0.383 302 16 | 0.368 646 82 | 0.384 669 47 | 0.364 006 30 | 0.398 519 32 | 0.386 380 91 | 0.383 715 88 | ⋅⋅⋅ |
| −4.41975307 | 0.376 204 99 | 0.387 974 57 | 0.373 356 18 | 0.388 954 23 | 0.368 983 50 | 0.404 105 61 | 0.391 587 57 | 0.388 082 86 | ⋅⋅⋅ |
| −4.33950615 | 0.380 910 88 | 0.392 815 06 | 0.378 165 40 | 0.393 375 89 | 0.373 985 17 | 0.409 728 24 | 0.396 948 69 | 0.392 584 15 | ⋅⋅⋅ |
| −4.25925922 | 0.385 652 36 | 0.397 799 05 | 0.383 055 31 | 0.397 953 61 | 0.379 007 28 | 0.415 373 87 | 0.402 404 68 | 0.397 233 57 | ⋅⋅⋅ |
| −4.17901230 | 0.390 435 54 | 0.402 904 39 | 0.387 918 91 | 0.402 688 37 | 0.384 051 11 | 0.421 022 08 | 0.407 893 70 | 0.402 015 36 | ⋅⋅⋅ |
| −4.09876537 | 0.395 290 22 | 0.408 120 81 | 0.392 838 12 | 0.407 568 58 | 0.389 098 73 | 0.426 663 48 | 0.413 416 77 | 0.406 937 03 | ⋅⋅⋅ |
| −4.01851845 | 0.400 233 93 | 0.413 430 65 | 0.397 905 01 | 0.412 588 76 | 0.394 171 38 | 0.432 303 24 | 0.418 975 63 | 0.411 987 29 | ⋅⋅⋅ |
| ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ |
This set of simulations is the beginning of a grid of stellar convection simulations, aimed at augmenting the existing grids of 1D stellar atmosphere models. Other aspects and applications of the grid will be presented in forthcoming papers.
For the solar composition, we have chosen a helium mass fraction, Y⊙ = 0.245, according to helioseismic determinations (Basu & Antia 1995), and a metal-to-hydrogen ratio (by mass) of Z⊙/X⊙ = 0.0245 in agreement with Grevesse & Noels (1993). This ratio results in the hydrogen mass fraction X = 0.736 945 and the helium–hydrogen number ratio N(He)/N(H) = 0.083 70, instead of the historically assumed value of ≃ 0.1. Our metal mixture is constrained by that of the available ODF tables (Kurucz 1992a) that were constructed for Anders & Grevesse (1989) abundances. Additional tables for different He and Fe abundances meant that we could interpolate between tables to the He abundance above, A(He/H) = 10.92 and A(Fe/H) = 7.50 from Grevesse & Noels (1993), where A denotes logarithmic number abundances, normalized to A(H) = 12.
The above solar composition has been challenged over the last decade by abundance analyses performed on 3D convection simulations using the same code and atomic physics as used for the simulations in this paper. The result is a general lowering of the metal abundances as detailed by Asplund, Grevesse & Sauval (2005, and references therein). Such a lower metal abundance ruins the otherwise good agreement with helioseismic inversions, as pointed out by Antia & Basu (2005) and Bahcall et al. (2005). This controversy highlights the fact that our own star, the Sun, is less well known than often assumed and stresses the need for improved modelling efforts as pursued with, e.g., this work, and improved atomic-physics calculations (Rogers & Nayfonov 2002; Badnell et al. 2005). The re-evaluation of the solar abundances by Asplund et al. (2009), based on a new solar simulation, has increased the overall metallicity by about 10 per cent and reduces the disagreement with helioseismology to about 2/3 of the former (Serenelli et al. 2009). The new simulation has improved radiative transfer and opacities (Trampedach et al., in preparation) and agrees very well with observations of limb darkening, flux distribution and strong hydrogen lines (Pereira et al. 2013).
Due to the lingering controversy, and since the change in abundances will have a rather small effect on stellar atmospheres, we did not feel compelled to re-compute the, at that time, mostly finished grid of simulations to adopt the new abundances.
Each of the simulations was performed on a 150$ × $150$ × $82-point grid (equidistant horizontally and non-uniform vertically, optimized to resolve the large photospheric gradients). This resolution is adequate for our purposes and is guided by the study of resolution effects by Asplund et al. (2000a). The simulation domain covers about 10 major granules horizontally and 13 pressure scaleheights vertically, with about 20 per cent (in height) being above 〈T〉 = Teff. We ensured that Rosseland optical depths as low as log τ = −4.5 were completely contained in each of the simulations. The area and depth of the solar simulation is 6$ × $6$ × $3.6 Mm and the size of the other simulations is mainly scaled by g−1. After relaxation to a quasi-stationary state, we calculated mean models as described in Section 2.4. The relaxation involves a damping of radial p modes which efficiently extracts surplus energy from the simulations. This damping is turned off again for the production runs, on which our work is based.
3.1 Opacities
We have revised most of the continuum opacity sources and added a few more sources as follows: H− bound–free (bf; Broad & Reinhardt 1976; Wishart 1979), free–free (ff; Bell & Berrington 1987), H|$_2^+$| bf+ff (Stancil 1994), H|$_2^-$| ff (Bell 1980) and OH/CH photodissociation (Kurucz, van Dishoeck & Tarafdar 1987). The most important levels of He i, C i, N i, O i, Na i, Mg i, Mg ii, Al i, Si i, Ca i, Ca ii and Fe i were included as simple analytical fits as listed by Mathisen (1984). The usual Thomson scattering by free electrons is included, together with Rayleigh scattering by H i (Gavrila 1967), He i (Langhoff, Sims & Corcoran 1974) and H2 (Victor & Dalgarno 1969). These changes were described in more detail by Trampedach (1997).
We have generated Rosseland opacity tables with these absorption sources, for a rectangular grid of (X, Z) compositions with 8 values of X ∈ [0; 0.9] and 13 values of Z ∈ [0; 0.1]. We have not merely scaled the contribution of each opacity source by the change in abundance (i.e. assuming the EOS to be linear in composition), but have rather re-computed the EOS for each of the 104 sets of compositions to use as a basis for the summation of opacities.
These tables have in turn been assembled into one global opacity table that can be interpolated in density, log ϱ, temperature, log T and composition, X, Y. These atmospheric, low-temperature tables (log T ∈ [3; 4.5]) have furthermore been merged differentiably with interior opacities from the Opacity Project (OP; Badnell et al. 2005). The combined opacities can be accessed by stellar structure codes through the interpolation package, opint, by Houdek & Rogl (1996), currently at version 11.
We show our atmospheric opacities in Fig. 2 together with the interior OP opacities. We note that the two sets of opacities show good agreement in the temperature range where we bridge between the two. In Fig. 2, we also compare with the atmospheric opacities of Ferguson et al. (2005), which also include water molecules (contributing for log T ≲ 3.5) and dust particles (the two bumps for log T ≲ 3.2). None of our simulations enter the dusty regime, but our coolest simulations would be affected by absorption by water.
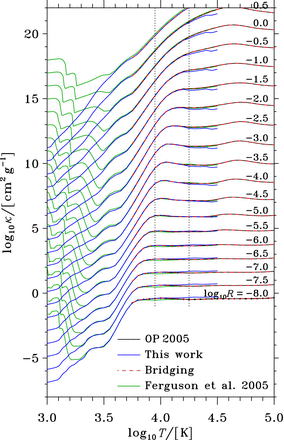
Opacities per mass as a function of log T. The 19 sets of curves are for log R = log ϱ − 3$ × $(log T − 6) as indicated, each offset by 1.0 from the previous, with no offset for log R = −8. The black curves show the interior OP (Badnell et al. 2005) opacities for log T ≥ 3.75. The blue curves show the present calculation of atmospheric opacities, compared with the Ferguson et al. (2005) opacities in green. The atmospheric are bridged with the interior opacities between the two vertical dotted lines.
4 T(τ) RELATIONS OF THE SIMULATIONS
The T(τ) relations of six of the simulations (nos. 2, 3, 11, 4, 26 and 36 of Table 1) are compared with 1D marcs stellar atmospheres in Fig. 3. The thick solid lines show the partially convective T(τ) relations of the simulations, and the thick dashed lines show the radiative T(τ) relations, where the first-order convective effect has been removed.
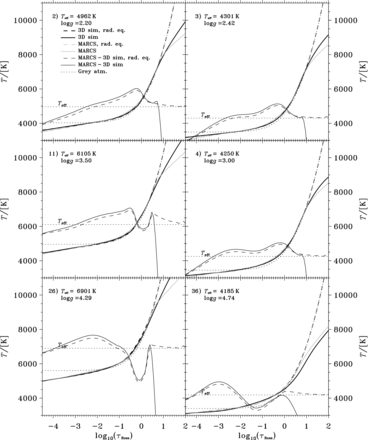
Comparison of T(τ) relations for six of the simulations with corresponding 1D atmosphere models. Solid lines show full T(τ) relations, including the first-order convective effect, and dashed lines show radiative T(τ) relations without this first-order convective effect. The black thick lines show results for the 3D simulations and the thin grey lines show 1D atmospheres interpolated in the marcs (Gustafsson et al. 2008) grid. The solution to the grey atmosphere is shown with dotted lines. The horizontal dotted lines show Teff. The differences between the 1D marcs models and the 3D simulations are shown around the T = Teff line with thin black lines (dashed for the radiative T(τ) relations), and exaggerated by a factor of 10. The atmospheric parameters and index in Table 1 are given in each panel.
The light grey lines show the marcs 1D models by Gustafsson et al. (2008), with the dashed grey lines showing the radiative T(τ) relations, as calculated from equations (10) and (18). The 1D marcs models are interpolated to the same atmospheric parameters as the simulations. The corresponding 1D atlas9 models are very similar to the marcs models, with only minor differences below the photosphere due to different choices for the parameters of the standard MLT formulation (Böhm-Vitense 1958) of convection [see Ludwig et al. (1999, appendix A) for a comparison of the form factors of the various flavours of MLT].
The plots of Fig. 3 are ordered with Teff decreasing to the right and log g decreasing towards the top. This ordering also means that the most efficient convection occurs in the right-side plots, and the least efficient on the left side. Low efficiency of convection means that it takes larger velocities to transport the required flux, resulting in the turbulent pressure contributing more to the hydrostatic equilibrium (sub-photospheric maxima of the pturb/ptot-ratios of 27 per cent for our warmest dwarf, no. 26, versus 3.9 per cent for our coolest dwarf, no. 36, of Table 1), expanding the atmosphere (Trampedach et al. 2013). It is also accompanied by larger temperature fluctuations, not the least due to the large temperature sensitivity of the opacity. The higher opacities in the warm upflows mean that they stay adiabatic until (spatially) very close to the photosphere. These are the bright granules. In the cooler downflows, the photosphere lies much deeper with the overturning plasma radiating away energy all the way. The net effect is higher temperatures below the photosphere, compared with a corresponding 1D model. This effect is also known as convective back-warming (Trampedach 2003), and expands the atmosphere by about as much as the turbulent pressure (as higher temperatures cause larger pressure scaleheights).
From Fig. 3, we clearly see the first-order effect of convection (due to a non-constant radiative flux), as the differences between solid and dashed lines. This shows the onset of convection and the sets of lines converge above the convection zone.
The difference between the 1D atmospheres (dotted and short dashed lines) and the grey atmospheres (solid grey lines) in the photosphere and above shows the effect of line blanketing. The line absorption evidently affects the cooler atmospheres the most, although they all show the signature of strong lines, by having a temperature gradient even at the uppermost point of the model.
The radiative T(τ) relations of the simulations (dashed lines) converge to the grey atmospheres (grey lines) with depth, as expected. In the photosphere and above, the deviations show the effects of lines and higher order convective effects. In this region, the differences between the 1D models and the 3D simulations mainly show the higher order convective effects. This comparison can be most cleanly carried out with the atlas9 models since we have employed the same line opacity data for our 3D simulations. The higher order convective effects are clearly significant and depend in a non-trivial way on the atmospheric parameters.
5 THE SOLAR CASE
Simulation no. 30, presented in Table 1, is constructed to correspond to the Sun.
It has an effective temperature of Teff = 5 774 ± 17 K and a (nominal) surface gravitational acceleration of 27 395.9 cm s−2.
We compare the resulting T(τ) relations with various 1D models in Fig. 4, using both the optical depth τRoss defined with the Rosseland mean opacity κRoss and the monochromatic optical depth τ5000 corresponding to the opacity at 5000 Å. This plot compares the full T(τ) relations including convection, employing flavours of MLT in the 1D theoretical models. Panel (a) shows temperature differences on the τRoss-scale and panel (b) is for the τ5000-scale. The vertically hatched area around the zero-line (in both panels) shows the temporal rms scatter of the T(τ) relation of the simulation, indicating which differences are statistically significant. Panel (a) also shows the difference between the temperature measured on the two τ-scales for the simulation (dot–dashed curve), the sign of which means that we can see deeper into the Sun at 5000 Å than on (a Rosseland) average, as a consequence of the fact that the Rosseland opacity is larger than the 5000 Å opacity.
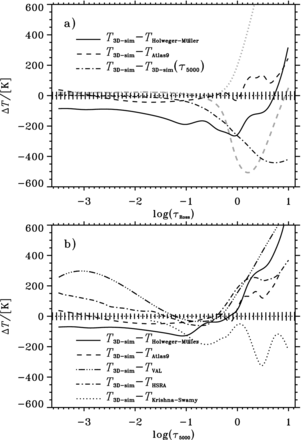
Comparison of the full τ-averaged temperature structure, 〈T〉τ, from the solar simulation, with some often used solar T(τ) relations. (a) The difference in Rosseland T(τ) relations between the simulation and the semi-empirical model by Holweger & Müller (1974, solid line), and an atlas9 atmosphere model (Kurucz 1993; Castelli, Gratton & Kurucz 1997, dashed line). Here we also show the difference between the two τ-scales (dot–dashed line) as T(τRoss = x) − T(τ5000 = x), as well as comparisons with the averaging methods of Fig. 1 in grey: dotted for case (b) 〈T〉L(〈τRoss〉L) and dashed for case (c) 〈T〉L(τRoss(〈ϱ〉L, 〈T〉L)). (b) Differences, on a τ5000-scale, between the simulation and an atlas9 model, and four semi-empirical atmosphere models: the model by Holweger & Müller (1974), the classical fit by Krishna Swamy (1966), the HSRA model (Gingerich, Noyes & Kalkofen 1971) and the average, quiet-Sun, VAL model (Vernazza et al. 1981, see the text).
The past two decades of work on compiling and computing line data for atoms and molecules has added a lot of line opacity in the UV, which has increased the Rosseland opacity with respect to the 5000 Å opacity (Kurucz 1992b; Trampedach 1997; Castelli & Kurucz 2003; Gustafsson et al. 2008). This in turn has increased the difference between τRoss and τ5000, which is clearly expressed in the 200 K difference at |$\tau \simeq \frac{2}{3}$|. This difference is twice as large as the corresponding differences amongst modern atmosphere models (cf. Fig. 4b), so it is no longer justified to assume the two τ-scales to be equal. For stellar structure calculations, it has been common practice to use a T–τ5000 relation combined with a Rosseland opacity. With the current opacities and today's demand for accuracy, this no longer seems a valid approximation and we recommend against using it.
The semi-empirical Holweger & Müller (1974) model (solid line in Fig. 4) is given on both the 5000 Å and the Rosseland τ-scales. We have used their original data and have made no attempt to update the Rosseland scale with modern opacities. Above the photosphere, the Holweger & Müller (1974) model is about 100 K warmer than the simulation, on both τ-scales. For this model, the T difference between the two τ-scales is less than 60 K, so in layers deeper than τ ≃ 0.5 the behaviour in the two panels is dominated by the (τRoss − τ5000) difference for the simulation. In the photosphere, the Holweger–Müller model is hotter than the simulation by up to 300 K on the τRoss-scale, but on the τ5000-scale they are very similar. On both τ-scales, the Holweger–Müller model becomes increasingly cooler with depth, compared with the 3D solar simulation, indicating a faster transition to convective transport of the whole flux.
For the theoretical atlas9 atmosphere models (Kurucz 1993), both monochromatic and Rosseland T(τ) relations are available, illustrated as the dashed line in both panels of Fig. 4. The peculiar wiggles in these curves are features from the atlas9 model. Using the ‘overshoot’ option, later disfavoured by Castelli et al. (1997), these wiggles combine to a larger but smoother dip, compared with the simulation. The rather close agreement in the radiative part of the atmosphere is expected, since the same line opacities were used, and since the convective fluctuations have only a small effect on the averaged T(τ) relation above the convection zone (i.e. all averaging methods give the same results, cf. Fig. 1). This is not necessarily the case for other stars where there will be a different balance between the expansion cooling of the overshooting flows and the radiative heating/cooling by spectral lines (see Section 6; Asplund et al. 1999; Collet et al. 2007) – a balance that does not exist in 1D models due to a lack of physical models of overshooting.
The two other semi-empirical atmosphere models presented in Fig. 4, the component averaged VAL model for the quiet Sun (Vernazza, Avrett & Loeser 1981) and the Harvard–Smithsonian solar reference atmosphere (HSRA; Gingerich et al. 1971), differ significantly and essentially in the same way from the simulation results. We used an average of the VAL model over its six components, with quiet-Sun weights as specified in their table 7. This structure is close to the often used C component, but is warmer by 2 K around the photosphere, rising to 27 K at log τ5000 = −2.25. Most of the differences between VAL-C and the average VAL model stay below the rms fluctuations of our solar simulation.
High in the atmosphere, the situation is a bit less clear. This plot covers up to 0.5 Mm above the photosphere, although the simulation reaches up to 0.8 Mm above. The solar temperature minimum occurs around 0.5 Mm before the sudden rise to chromospheric temperatures at an average height of about 2 Mm. In the VAL C model, the temperature minimum occurs at log τ5000 ≃ −3.5, but there is no sign of temperature minima in any of our simulations. This is not surprising, considering the lack of non-LTE effects or magnetic fields in our simulations, and their implications in chromospheric and coronal heating (e.g. Gudiksen & Nordlund 2005; van Ballegooijen et al. 2011).
The last T(τ) relation presented in Fig. 4 is the one by Krishna Swamy (1966, dotted line, only defined for τ = 0.02–10), which is still used as an upper boundary in some stellar model codes (e.g. Straniero, Chieffi & Limongi 1997; Chaboyer et al. 2001; Pietrinferni et al. 2004; Demarque et al. 2008). It is interesting to note that the behaviour below the photosphere is opposite that of the more modern T(τ) relations.
At intermediate optical depths, from log τ ≃ −1 down to 〈T〉 = Teff, the agreement between the simulation and both theoretical and semi-empirical atmospheres is rather good, as expected. Differences are also smaller than the difference between the 5000 Å and the Rosseland T(τ) relation from the simulation.
The agreement with semi-empirical models in this region is encouraging, as convective fluctuations are smaller here, damped by radiative losses. It is, however, not in itself a validation of the convection simulations. Such a validation has to be performed much closer to the actual observations, in order to avoid all the theoretical biases that go into, e.g., semi-empirical models. Semi-empirical atmospheres have too often been assumed equivalent to observations, and we argue that the considerable differences between the VAL, HSRA and Holweger–Müller models speak against that practice. The actual limb darkening, spectral energy distribution and line profiles are the benchmarks with which all atmosphere models should be compared. Solar and stellar 3D simulations presented here perform very well against observational diagnostics, including detailed line profiles (Asplund et al. 2000b; Prieto et al. 2002), and the solar continuum limb darkening (Pereira, Asplund & Trampedach 2008; Pereira et al. 2013).
As convection becomes the dominant mode of energy transport, the T(τ) relations in Fig. 4 diverge, with the various theoretical 1D models, sharing the MLT formulation of convection, all differing from the simulation in more or less the same manner. The semi-empirical models do not account for convection. Below 〈T〉 = Teff, 3D effects become important and the turbulent pressure contributes up to 14 per cent of the total pressure, rendering the simulation the better choice for an atmosphere model.
6 VARIATION WITH STELLAR ATMOSPHERIC PARAMETERS
Having evaluated T(τ) relations for our grid of simulations, we can now proceed to give an overview of the behaviour with atmospheric parameters, Teff and log g.
The q surfaces as a function of stellar parameters are shown at three optical depths in Fig. 5. The edge towards the reader is populated by main-sequence stars and the far-right corner, by red giants. The offset between the three surfaces is the real difference between the Hopf functions at the three τRoss-levels. The bottom level in the plot (highest point included in the atmosphere) shows fairly little variation. At the mid-level, there is an increase of q towards the cool dwarfs and a slow increase towards the giants. In the optical deep part, q → q∞ is dominated by a broad bump at medium-temperature dwarfs that extends towards the cool giants, and an upturn on the main sequence for both hot and cool dwarfs. The location of the solar simulation is indicated with ⊙ and lies near the maximum of the bump in q∞, which means q changes little in the immediate neighbourhood of the Sun.
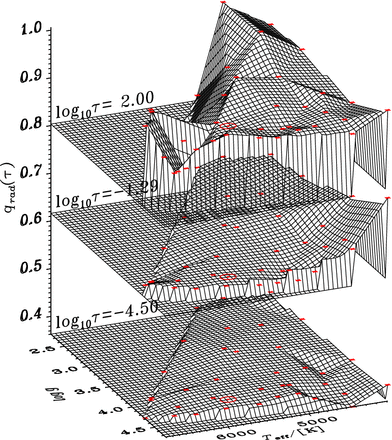
The dependence of the radiative Hopf function, q as a function of optical depth and atmospheric parameters, Teff and log g. The locations of the simulations are indicated with red asterisks, and the solar simulation is indicated by a red ⊙.
In Fig. 6, we present the variation of q with stellar mass on the zero-age main sequence (ZAMS). The atmospheric parameters for the ZAMS were derived from the stellar evolution models computed with the mesa code (Paxton et al. 2011), using MLT α and initial helium abundance Y0 calibrated to the present Sun. The radiative Hopf functions were interpolated linearly on the Thiessen triangles of the irregular grid. For comparison, we also plot q derived from 1D marcs atmospheres (grey dashed lines in Fig. 6), through equations (10) and (18). The simulations have a smooth transition to the asymptotic value in the diffusion approximation, q∞, contrary to the behaviour of the M > 0.8 M⊙ 1D marcs models, which exhibit a deeper and rather abrupt transition to q∞ and the medium-mass models also display a marked plateau around the photosphere. We suspected second-order effects from the onset of MLT convection, but this feature in qrad(τ) does not seem to be correlated with the Fconv/Ftot-ratio of the models. The optically deep values, q∞, are lower for the 3D simulations than their 1D counterparts for high and low masses and opposite around 1 M⊙. The 3D T(τ) relations above the photosphere are generally seen to have a larger range of behaviour compared with those of the 1D models. The 3D case is shallower in the high atmosphere and steeper at intermediate τ. The low-mass simulations converge to q∞ strikingly high in the atmosphere. This is not caused by interpolation between the simulations, as the parameters of the zero-age, 0.6 M⊙ star are very close to simulation no. 36 of Table 1, which displays a similar behaviour.
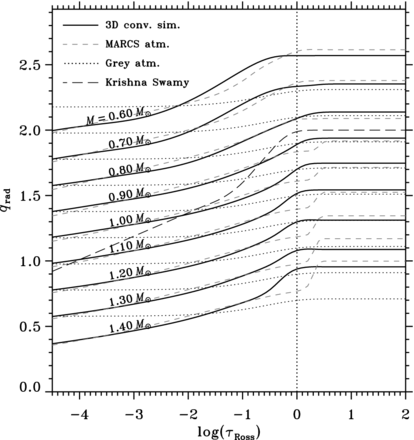
The change of the radiative Hopf function q with stellar mass, on the zero-age main sequence. The mass is indicated to the right, and each set of curves is offset by 0.2 with respect to the next mass, with the M = 1.40 M⊙ curve having no offset. The solid lines show the simulations interpolated to the parameters of the zero-age main sequence, and the dashed grey curves show the corresponding 1D marcs models (Gustafsson et al. 2008). The dotted curves indicate the grey atmosphere, crossing their corresponding line-blanketed atmospheres between log τRoss = −2 and −1.5. The long-dashed curve shows the often applied Krishna Swamy (1966) relation, offset by the same amount as the 1.00 M⊙ curves. The vertical dotted line indicates optical depth unity.
Fig. 7 illustrates the gravity dependence of the T(τ) relations. Going to lower gravity, the T(τ) relation gets steeper in the photosphere and shallower just above, developing a kink right in the photosphere of the lowest gravity case. This feature is also not a result of the interpolation between the simulations, since simulation no. 2 is very close to the log g = 2.25 case plotted, and exhibits the same kink. The qs from the 1D models are generally steeper in the high atmosphere, and show very little overall variation with gravity, compared with the 3D simulations.
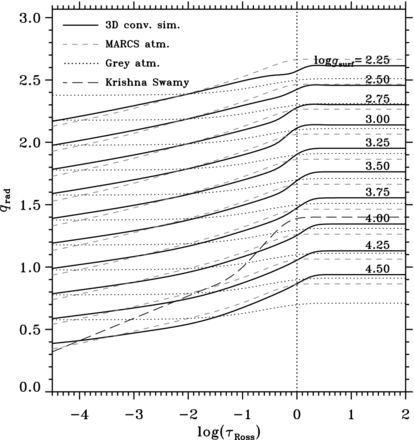
As Fig. 6, but showing the change of q with gravity, for a fixed Teff = 5000 K. This Teff is chosen for the grid of simulations having the largest extent in gravity here. The offset between each set of curves is 0.2, and the log g = 4.5 curves have no offset. The Krishna Swamy (1966) atmosphere has no offset either.
The opacities in the atlas9 models and the 3D simulations are nearly identical, and Gustafsson et al. (2008) found that the differences between marcs and atlas9 models in this region amount to less than 20 K throughout the atmospheres, −5 ≤ log τ ≤ 2. This means that the differences we see here, between 1D atmospheres and 3D convection simulations, must be mainly due to the more realistic treatment of convection in our simulations.
One of the major differences between hydrodynamic simulations and the MLT formulation is the presence of overshooting from the top of the convection zone and into the stably stratified part of the atmosphere. As a result, we see significant velocity fields throughout the atmospheres of our simulations. As pointed out by Asplund et al. (1999), the radiative heating and cooling therefore have competition from the expansion cooling of rising plasma, expanding due to the large density gradient in the atmosphere. The adiabatic stratification is typically more than 1000 K cooler than the radiative equilibrium solution. A stratification in between these two extremes will therefore experience radiative heating and expansion cooling, and obtain equilibrium at a lower temperature than the purely radiative atmosphere. This convective cooling from overshooting is one of the higher order convective effects visible in Figs 6 and 7. And the process occurs outside the convection zone, in a region where convection carries no flux – or rather, the convective flux is less than a per cent of the total and it is negative. This effect is rather small for solar-metallicity stars, as the large opacity will establish an equilibrium close to the radiative one. For metal-poor stars, the effect can be of the order of 103 K (Asplund et al. 1999; Collet et al. 2007).
In Figs 6 and 7, we also show the grey atmosphere (King 1956; Mihalas 1978) with dotted lines. It is obvious that the grey approximation is insufficient in all cases.
7 CONCLUSION
We have confirmed that the use of T(τ) relations is indeed a good and consistent method for incorporating the effects of full radiative transfer in stellar structure computations – even in the non-grey case, as shown in Section 2. It is often remarked that T(τ) relations imply grey radiative transfer since they are used with the grey Rosseland opacity. That is only the case, however, when the grey Hopf function is used. When a generalized Hopf function is used, any physical effects can be included in the atmosphere, and with the T(τ) relation and a Rosseland opacity the stratification can be reconstituted without the need for detailed radiative transfer. With our formulation, the T(τ) relations can be based on any realistic atmosphere calculation, be it 1D, 3D or non-LTE, without the stellar structure code implementing them needing any information about such complications. We also developed a more general formulation to deal with T(τ) relations in 3D, which reduces properly to the simpler 1D case.
Based on that we proceeded to compute T(τ) relations for a number of 3D simulations of radiation-coupled convective stellar atmospheres, the results of which are displayed in Sections 4 and 5. Comparisons with 1D models reveal differences of the order of 100 K in the shape of the T(τ) relations (see Fig. 3). In Figs 6 and 7, the differences are put in the context of stellar evolution, by displaying cuts in the Hertzsprung-Russell (HR) diagram. These differences are again significant and smooth but not monotonic in atmospheric parameters, with the 3D simulations displaying a larger range of behaviours – especially with varying gravity and fixed Teff. The warmer 1D marcs atmospheres show a curiously sharp transition to the constant Hopf function of the diffusion approximation.
The simulations populate the Teff/g plane densely enough for interpolation between the simulations to be safe. Routines for interpolating irregularly gridded data are publicly available (Renka 1984) and make for straightforward implementation in stellar structure and evolution codes.
To separate, in stellar structure models, the effects of convection from those of the radiative transition in the photosphere, and to avoid unnecessary systematic effects, we recommend that the T(τ) relations be reduced to radiative equilibrium, as defined in Section 2, and that convection is reintroduced into the interior structure model, as described in Section 2.5 .
As the precision and scope of modern observations of stars steadily improve, and as we find ourselves in the age of detailed asteroseismic inferences, higher demands are placed on the modelling of stars. With improved understanding and treatment of the interplay between radiation and convection, it will be possible to isolate other effects that so far have been shrouded in the uncertainty of the atmospheric part of stellar models. With improved outer boundary conditions, combined with the mixing-length calibration in Paper II, we can have more confidence in predictions about the depth of convective envelopes. This, in turn, will allow the study of other mixing processes, such as convective overshoot at the base of the convection zone, rotational and gravity-wave mixing, etc., and comparisons with observations of chemical enrichment from dredge-ups and the destruction of volatile elements such as Li and B.
Data Retrieval: A file with the q(τ) data and Fortran 77 routines for reading and interpolating the data can be downloaded from http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/MNRAS/. A few entries from the online file are shown in Table 2. The data file contains both the radiative Hopf functions, q(τRoss), and the calibrated mixing-length parameter, α, as found in Paper II, as functions of atmospheric parameters, Teff and log g. The URL also contains the routines necessary for setting up and interpolating in the triangulation of the irregular grid of simulations (Renka 1984). Finally, we also supply a simple user-level function to include in stellar structure codes, which does not require any knowledge of the data or the details of the triangulation.
The opint opacity interpolation package can be downloaded from http://phys.au.dk/∼hg62/OPINT, together with the atmospheric opacities from our calculation, merged with interior OP opacities (cf. Section 3.1).
The helpful comments and suggestions by the anonymous referee have improved the paper and are much appreciated. We are grateful to R. L. Kurucz for providing access to his data base of opacity distribution functions, and we are also grateful to W. Däppen for access to the code and data tables for the MHD equation of state. RT acknowledges funding from the Australian Research Council (grants DP 0342613 and DP 0558836) and NASA grants NNX08AI57G and NNX11AJ36G. RFS acknowledges NSF grant AGS-1141921 and NASA grant and NNX12AH49G. Funding for the Stellar Astrophysics Centre is provided by the Danish National Research Foundation (Grant DNRF106). The research is supported by the ASTERISK project (ASTERoseismic Investigations with SONG and Kepler) funded by the European Research Council (grant agreement no.: 267864). The work of MA has been supported through a Laureate Fellowship from the Australian Research Council (FL110100012). The simulations were run at the Australian Partnership for Advanced Computations (APAC). This research has made extensive use of NASA's Astrophysics Data System.
REFERENCES
SUPPORTING INFORMATION
Additional Supporting Information may be found in the online version of this article:
Table 2. Sample of the online table of Hopf functions as functions of log τ (rows) and atmospheric parameters, Teff and log g (columns) (Supplementary Data).
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the paper.



