-
PDF
- Split View
-
Views
-
Cite
Cite
Kanti M. Aggarwal, Francis P. Keenan, Energy levels, radiative rates and electron impact excitation rates for transitions in Si ii, Monthly Notices of the Royal Astronomical Society, Volume 442, Issue 1, 21 July 2014, Pages 388–400, https://doi.org/10.1093/mnras/stu883
Close - Share Icon Share
Abstract
Energies for the lowest 56 levels, belonging to the 3s2 3p, 3s 3p2, 3p3, 3s2 3d, 3s 3p 3d, 3s2 4ℓ and 3s2 5ℓ configurations of Si ii, are calculated using the General-purpose Relativistic Atomic Structure Package (grasp) code. Analogous calculations have also been performed (for up to 175 levels) using the Flexible Atomic Code (fac). Furthermore, radiative rates are calculated for all E1, E2, M1 and M2 transitions. Extensive comparisons are made with available theoretical and experimental energy levels, and the accuracy of the present results is assessed to be better than 0.1 Ryd. Similarly, the accuracy for radiative rates (and subsequently lifetimes) is estimated to be better than 20 per cent for most of the (strong) transitions. Electron impact excitation collision strengths are also calculated, with the Dirac Atomic R-matrix Code (darc), over a wide energy range up to 13 Ryd. Finally, to determine effective collision strengths, resonances are resolved in a fine energy mesh in the thresholds region. These collision strengths are averaged over a Maxwellian velocity distribution and results listed over a wide range of temperatures, up to 105.5 K. Our data are compared with earlier R-matrix calculations and differences noted, up to a factor of 2, for several transitions. Although scope remains for improvement, the accuracy for our results of collision strengths and effective collision strengths is assessed to be about 20 per cent for a majority of transitions.
1 INTRODUCTION
Emission lines of Si ii have been observed at optical and ultraviolet (UV) wavelengths in a variety of plasmas, such as planetary nebulae, quasars and the interstellar medium (see e.g. Judge, Carpenter & Harper 1991). Particularly useful for diagnostic purposes are the multiplets 3s2 3p 2Po–3s 3p2 4P and 3s2 3p 2Po–3s 3p2 2D at around 2340 and 1810 Å, respectively. Similarly, Hubrig & González (2007) have detected two emission lines (∼7849 Å) in the magnetic Bp star a Centauri (HD 125823). Recently, Shaltout et al. (2013) have determined the silicon abundance in the solar atmosphere, based on lines of Si ions, including those of Si ii. Many lines of Si ii in the 750–6680 Å wavelength range are listed in the CHIANTI data base at http://www.chiantidatabase.org/ and the Atomic Line List (v2.04) of Peter van Hoof at http://www.pa.uky.edu/peter/atomic/. Silicon ions, including Si ii, are also important for the studies of fusion plasmas, particularly because amorphous silicon is used for coating the first wall of the devices, such as Tokamak Experiment for Technology Oriented Research (TEXTOR). Huber et al. (2003) have measured intensities of several Si ii lines in the TEXTOR tokamak in the 290–640 Å wavelength range, belonging to the n ≤ 5 levels. The importance of data for Si ions has further increased with the developing International Thermonuclear Experimental Reactor (ITER) project.
For plasma diagnostics and modelling, atomic data are required for a range of parameters, particularly energy levels, radiative rates (A values) and excitation rates (or equivalently the effective collision strengths ϒ). Measured values of energy levels have been compiled by the National Institute of Standards and Technology (NIST) team (Kramida et al. 2013) and are available at their website http://www.nist.gov/pml/data/asd.cfm. Theoretical energy levels have been determined by several authors, and the most notable results are those of Tayal (2007) and Bautista et al. (2009). Both these workers have also listed the A values.
Results for collision strengths (Ω) and effective collision strengths (ϒ) are also available. Dufton & Kingston (1991) have reported ϒ data for transitions among the lowest seven levels of the 3s2 3p and 3s 3p2 configurations and from the 3s2 3p 2P|$^o_{1/2,3/2}$| ground state levels to higher excited ones, up to 15 (see Table 1). These limited results are based on the R-matrix method and are primarily in LS coupling (Russell–Saunders or spin–orbit coupling), but corresponding data for fine-structure transitions were determined through algebraic transformation. Although calculations for Ω were performed up to an energy of 10 Ryd, which is fully sufficient to determine ϒ up to Te = 104.6 K, the range of partial waves adopted by them (J ≤ 6) was too limited to obtain convergence of Ω, not only for the allowed but also the forbidden transitions. Furthermore, Judge et al. (1991) analysed several observations using their data and noted discrepancies with theory by up to a factor of 2 for several lines. On the other hand, Baldwin et al. (1996) studied broad emission lines of high-luminosity quasi-stellar objects (QSOs), including some of Si ii, particularly λ ∼ 1263 Å (3s2 3p 2Po–3s2 3d 2D), 1307 Å (3s2 3p 2Po–3s 3p22S) and 1814 Å (3s2 3p 2Po–3s 3p22D). For the 1814 Å line there was a satisfactory agreement between prediction and observation, but the discrepancies for the other two lines were over an order of magnitude. Therefore, there was a clear need to re-examine the theoretical atomic data.
Subsequently, Tayal (2008) made significant improvements over the atomic data of Dufton & Kingston (1991), mainly by extending the range of partial waves up to angular momentum J = 36. Furthermore, he performed calculations in the Breit–Pauli B-spline R-matrix (BSRM) approach and reported ϒ not only over a wider temperature range (up to log Te = 5.4 K) but also for all transitions among 31 levels of the 3s2 3p, 3s 3p2, 3s 3p 3d, 3s2 4ℓ, 3s2 5s/p/d/f and 3s2 6s/p configurations. As a result of these improvements the differences between his values of ϒ and those of Dufton & Kingston (1991) were significant for some transitions, in both magnitude and behaviour, particularly the allowed ones, such as 1–12 (3s2 3p 2P|$^o_{1/2}$|–3s2 3d 2D3/2) and 2–13 (3s2 3p 2P|$^o_{3/2}$|–3s2 3d 2D5/2), as shown in his fig. 6. However, Tayal included only two levels (2D|$^o_{3/2,5/2}$|) of the 3s 3p 3d configuration, whereas it generates 23 in total (see Table 1), and some of these lie in between those of the 3s2 4ℓ and 3s2 5ℓ configurations, included in his calculations. The omission of these levels affects the resonance structure of Ω and subsequently calculations of ϒ. Therefore, there is a scope for improvement as well as confirmation of accuracy of the Tayal results, so that data can be confidently applied to plasma studies.
Bautista et al. (2009) performed another calculation adopting the Breit–Pauli R-matrix code of Berrington, Eissner & Norrington (1995). Although a large number of (43) LS terms were included in the collisional calculations, they reported values of ϒ only at three temperatures and for eight transitions from the ground level. More importantly, discrepancies with the corresponding results of Dufton & Kingston (1991) as well as Tayal (2008) are up to 50 per cent for several transitions. In general, there is poor agreement among the three R-matrix calculations. Bautista et al. (2009) speculated that differences with the calculations of Tayal (2008) could be because of the non-orthogonal orbitals adopted by him. However, Dufton & Kingston (1991) adopted orthogonal orbitals, as did Bautista et al. (2009), but differences between the two sets of ϒ are still up to 50 per cent at all temperatures between 5000 and 20 000 K. A closer examination of the collision strengths shown by Tayal (2008) and Bautista et al. (2009) for three transitions, namely 1–2 (3s2 3p 2P|$^o_{1/2}$|–3s2 3p 2P|$^o_{3/2}$|), 2–4 (3s2 3p 2P|$^o_{3/2}$|–3s 3p24P1/2) and 2–7 (3s2 3p 2P|$^o_{3/2}$|–3s 3p22D5/2), reveals that background values of ΩB are lower in the latter's calculations, particularly at energies below 0.8 Ryd (equivalent to ∼1.25 × 105 K). These differences clearly lead to the lowest values of ϒ reported by Bautista et al. (2009) for all transitions and at all temperatures.
Bautista et al. (2009) included a larger range of partial waves (L ≤ 16) in comparison to those of Dufton & Kingston (1991), who included only L ≤ 8, and yet their values of ϒ are the lowest, not only for the allowed (such as 1–3, 4 and 6) but also the forbidden (1–2 and 1–5) transitions. Therefore, neither the range of partial waves nor the use of (non)-orthogonal orbitals appears to be a convincing cause of the discrepancies in ϒ. For this reason we have performed another calculation for the important Si ii ion and report a complete set of results for energy levels, A values and ϒ for all transitions among 56 levels of the 3s2 3p, 3s 3p2, 3p3, 3s2 3d, 3s 3p 3d, 3s2 4ℓ and 3s2 5ℓ configurations.
2 ENERGY LEVELS
To calculate energy levels and A values we have employed the multiconfiguration Dirac–Fock (mcdf) code, developed by Grant et al. (1980). It is a fully relativistic code, based on the jj coupling scheme, and includes higher order relativistic corrections arising from the Breit (magnetic) interaction and quantum electrodynamics (QED) effects (vacuum polarization and Lamb shift). This code has undergone several revisions by the names General-purpose Relativistic Atomic Structure Package (grasp), grasp92 and grasp2K, revised by Dyall et al. (1989), Parpia et al. (1989) and Jönsson et al. (2007, 2013), respectively. However, the version adopted here has been revised by one of its authors (Dr P. H. Norrington) is known as grasp0 and is freely available at the website http://web.am.qub.ac.uk/DARC/. This provides comparable results with other revised versions and has been extensively applied by ourselves and other workers to a wide range of ions. Furthermore, as in our earlier work, the option of extended average level (EAL) has been adopted in which a weighted (proportional to 2j+1) trace of the Hamiltonian matrix is minimized. We note that results obtained for energy levels and A values are comparable to other options, such as average level (AL), as demonstrated by Aggarwal, Keenan & Lawson (2008) for Kr ions.
For the determination of atomic structure we have included 14 configurations, namely (1s2 2s2 2p6) 3s2 3p, 3s 3p2, 3p3, 3s2 3d, 3s 3p 3d, 3s2 4ℓ and 3s2 5ℓ, which generate 56 levels listed in Table 1. Our calculated level energies, obtained with the inclusion of Breit and QED effects, are given in Table 1 along with the NIST compilations of experimental energies and those of Tayal (2008) who adopted the multiconfiguration Hartree–Fock (mchf) code of Zatsarinny & Fischer (1999). Since Si ii is only moderately heavy, the contributions of Breit and QED effects are negligible. However, differences with the NIST listings are up to ∼0.1 Ryd for some of the levels, particularly 3s 3p22P1/2, 3/2 (14 and 15). Additionally, the orderings are also slightly different in a few instances – see for example levels 17–22. We note here that for some species, such as Al-like Ti X (Aggarwal & Keenan 2013), it is not possible to unambiguously identify the levels, because of strong mixing. However, that is not the case for Si ii. The energies obtained by Tayal (2008) are in closer agreement with those of NIST for all levels, because he has used non-orthogonal orbitals. However, his energy level ordering differs with that of NIST in a few instances, such as for 6–7 and 21–22. Furthermore, using the similar non-orthogonal orbitals, in his earlier calculations (Tayal 2007) the energy obtained for the 3s2 3p 2P|$^o_{3/2}$| level is lower by 13 per cent. Nevertheless, a clear advantage of this approach is that orbitals can be independently optimized on individual states/levels and thus a higher accuracy can be achieved by minimizing the differences with the measured results. However, this approach can only be successfully applied if experimental energies are already available, which is the case for Si ii, but not for all levels, because several are missing from the NIST compilations as seen in Table 1. Since Tayal (2008) performed collisional calculations among experimentally determined levels only, he could apply the approach of non-orthogonal orbitals. Nevertheless, most of the scattering codes, including the one adopted here and discussed in Section 5, do not have a provision of this option.
Energy levels of Si ii, their threshold energies (in Ryd) and lifetimes (s) (a ± b ≡ a ×10±b).
| Index . | Configuration . | Level . | NIST . | SST . | grasp . | fac1 . | fac2 . | fac3 . | τ (s) . |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 3s2 3p | 2P|$^o _{1/2}$| | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | .......... |
| 2 | 3s2 3p | 2P|$^o _{3/2}$| | 0.00262 | 0.00262 | 0.00233 | 0.00224 | 0.00194 | 0.00195 | 6.693+03 |
| 3 | 3s 3p2 | 4P1/2 | 0.39024 | 0.38056 | 0.35314 | 0.36774 | 0.35294 | 0.35373 | 2.510−04 |
| 4 | 3s 3p2 | 4P3/2 | 0.39123 | 0.38139 | 0.35411 | 0.36828 | 0.35370 | 0.35449 | 8.004−03 |
| 5 | 3s 3p2 | 4P5/2 | 0.39283 | 0.38275 | 0.35569 | 0.36996 | 0.35494 | 0.35573 | 3.391−03 |
| 6 | 3s 3p2 | 2D3/2 | 0.50402 | 0.50142 | 0.52570 | 0.53233 | 0.48520 | 0.48597 | 5.629−06 |
| 7 | 3s 3p2 | 2D5/2 | 0.50416 | 0.50159 | 0.52583 | 0.53252 | 0.48541 | 0.48618 | 4.254−06 |
| 8 | 3s2 4s | 2S1/2 | 0.59688 | 0.59763 | 0.64329 | 0.66222 | 0.64309 | 0.64347 | 6.705−10 |
| 9 | 3s 3p2 | 2S1/2 | 0.69863 | 0.70229 | 0.76675 | 0.75842 | 0.75351 | 0.75421 | 7.363−10 |
| 10 | 3s2 4p | 2P|$^o _{1/2}$| | 0.73987 | 0.72724 | 0.77820 | 0.79569 | 0.78195 | 0.78164 | 8.891−09 |
| 11 | 3s2 4p | 2P|$^o _{3/2}$| | 0.74042 | 0.73769 | 0.77871 | 0.79597 | 0.78211 | 0.78182 | 8.835−09 |
| 12 | 3s2 3d | 2D3/2 | 0.72299 | 0.72889 | 0.79914 | 0.80484 | 0.73396 | 0.73261 | 3.078−10 |
| 13 | 3s2 3d | 2D5/2 | 0.72314 | 0.72905 | 0.79931 | 0.80501 | 0.73406 | 0.73271 | 3.092−10 |
| 14 | 3s 3p2 | 2P1/2 | 0.76366 | 0.77039 | 0.89104 | 0.87977 | 0.82156 | 0.82235 | 1.850−10 |
| 15 | 3s 3p2 | 2P3/2 | 0.76550 | 0.77468 | 0.89273 | 0.88128 | 0.82280 | 0.82359 | 1.847−10 |
| 16 | 3s2 5s | 2S1/2 | 0.89279 | 0.89164 | 0.92186 | 0.92866 | 0.91463 | 0.91452 | 1.865−09 |
| 17 | 3s 3p(3P)3d | 2D|$^o _{3/2}$| | 0.99126 | 0.98377 | 0.95559 | 0.98332 | 0.93831 | 0.93910 | 4.397−07 |
| 18 | 3s 3p(3P)3d | 2D|$^o _{5/2}$| | 0.99165 | 0.98421 | 0.95604 | 0.98356 | 0.93869 | 0.93947 | 4.319−07 |
| 19 | 3s2 4d | 2D3/2 | 0.92059 | 0.92128 | 0.96139 | 0.96016 | 0.94787 | 0.94554 | 6.419−10 |
| 20 | 3s2 4d | 2D5/2 | 0.92060 | 0.92131 | 0.96141 | 0.96016 | 0.94784 | 0.94552 | 6.456−10 |
| 21 | 3s2 4f | 2F|$^o _{7/2}$| | 0.94367 | 0.94370 | 0.96650 | 0.97091 | 0.95576 | 0.95654 | 3.881−09 |
| 22 | 3s2 4f | 2F|$^o _{5/2}$| | 0.94367 | 0.94370 | 0.96650 | 0.97091 | 0.95576 | 0.95655 | 3.886−09 |
| 23 | 3s2 5p | 2P|$^o _{1/2}$| | 0.94645 | 0.94287 | 0.97479 | 0.98940 | 0.97822 | 0.97662 | 1.596−08 |
| 24 | 3s2 5p | 2P|$^o _{3/2}$| | 0.94667 | 0.94305 | 0.97500 | 0.98957 | 0.97824 | 0.97672 | 1.597−08 |
| 25 | 3s 3p(3P)3d | 4F|$^o _{3/2}$| | 1.04127 | 1.00875 | 1.02983 | 0.98646 | 0.98725 | 7.061−06 | |
| 26 | 3s 3p(3P)3d | 4F|$^o _{5/2}$| | 1.04183 | 1.00932 | 1.03366 | 0.98694 | 0.98773 | 3.746−06 | |
| 27 | 3s 3p(3P) 3d | 4F|$^o _{7/2}$| | 1.04262 | 1.01013 | 1.03593 | 0.98761 | 0.98840 | 3.601−06 | |
| 28 | 3s 3p(3P) 3d | 4F|$^o _{9/2}$| | 1.04367 | 1.01119 | 1.03355 | 0.98849 | 0.98928 | 2.129+01 | |
| 29 | 3s2 5d | 2D3/2 | 1.02421 | 1.02377 | 1.05396 | 1.05700 | 1.05998 | 1.04788 | 2.146−09 |
| 30 | 3s2 5d | 2D5/2 | 1.02422 | 1.02378 | 1.05396 | 1.05697 | 1.05987 | 1.04784 | 2.157−09 |
| 31 | 3s2 5f | 2F|$^o _{7/2}$| | 1.03666 | 1.03511 | 1.05837 | 1.07196 | 1.05601 | 1.05678 | 9.149−09 |
| 32 | 3s2 5f | 2F|$^o _{5/2}$| | 1.03666 | 1.03511 | 1.05837 | 1.07197 | 1.05602 | 1.05678 | 9.164−09 |
| 33 | 3s2 5g | 2G7/2 | 1.04046 | 1.06176 | 1.06279 | 1.04711 | 1.04790 | 1.397−08 | |
| 34 | 3s2 5g | 2G9/2 | 1.04046 | 1.06176 | 1.06279 | 1.04711 | 1.04790 | 1.397−08 | |
| 35 | 3s 3p(3P)3d | 4P|$^o _{5/2}$| | 1.09742 | 1.11565 | 1.08685 | 1.08763 | 4.540−10 | ||
| 36 | 3s 3p(3P)3d | 4P|$^o _{3/2}$| | 1.09836 | 1.11493 | 1.08768 | 1.08847 | 4.520−10 | ||
| 37 | 3s 3p(3P)3d | 4P|$^o _{1/2}$| | 1.09900 | 1.11657 | 1.08824 | 1.08903 | 4.545−10 | ||
| 38 | 3s 3p(3P)3d | 4D|$^o _{1/2}$| | 1.10612 | 1.12194 | 1.09802 | 1.09881 | 2.465−10 | ||
| 39 | 3s 3p(3P)3d | 4D|$^o _{3/2}$| | 1.10640 | 1.12361 | 1.09820 | 1.09899 | 2.477−10 | ||
| 40 | 3s 3p(3P)3d | 4D|$^o _{5/2}$| | 1.10672 | 1.12461 | 1.09844 | 1.09923 | 2.479−10 | ||
| 41 | 3s 3p(3P)3d | 4D|$^o _{7/2}$| | 1.10700 | 1.12303 | 1.09866 | 1.09945 | 2.465−10 | ||
| 42 | 3p3 | 4S|$^o _{3/2}$| | 1.10799 | 1.12719 | 1.10455 | 1.10534 | 1.973−10 | ||
| 43 | 3s 3p(3P)3d | 2P|$^o _{3/2}$| | 1.15102 | 1.16203 | 1.15549 | 1.15765 | 1.404−09 | ||
| 44 | 3s 3p(3P)3d | 2P|$^o _{1/2}$| | 1.15184 | 1.16236 | 1.15602 | 1.15819 | 1.394−09 | ||
| 45 | 3s 3p(3P)3d | 2F|$^o _{5/2}$| | 1.21481 | 1.22215 | 1.22773 | 1.22857 | 4.865−10 | ||
| 46 | 3s 3p(3P)3d | 2F|$^o _{7/2}$| | 1.21707 | 1.22420 | 1.22969 | 1.23053 | 4.828−10 | ||
| 47 | 3p3 | 2D|$^o _{5/2}$| | 1.28531 | 1.29345 | 1.25126 | 1.25204 | 2.109−10 | ||
| 48 | 3p3 | 2D|$^o _{3/2}$| | 1.28548 | 1.29386 | 1.25138 | 1.25217 | 2.109−10 | ||
| 49 | 3p3 | 2P|$^o _{1/2}$| | 1.41958 | 1.41436 | 1.42672 | 1.42754 | 2.334−10 | ||
| 50 | 3p3 | 2P|$^o _{3/2}$| | 1.41960 | 1.41475 | 1.42678 | 1.42759 | 2.330−10 | ||
| 51 | 3s 3p(1P)3d | 2F|$^o _{7/2}$| | 1.47195 | 1.47076 | 1.43957 | 1.44241 | 1.843−10 | ||
| 52 | 3s 3p(1P)3d | 2F|$^o _{5/2}$| | 1.47258 | 1.47138 | 1.44027 | 1.44310 | 1.836−10 | ||
| 53 | 3s 3p(1P)3d | 2D|$^o _{3/2}$| | 1.56391 | 1.55317 | 1.54933 | 1.55012 | 1.376−10 | ||
| 54 | 3s 3p(1P)3d | 2D|$^o _{5/2}$| | 1.56428 | 1.55328 | 1.54973 | 1.55052 | 1.377−10 | ||
| 55 | 3s 3p(1P)3d | 2P|$^o _{1/2}$| | 1.60151 | 1.58768 | 1.55439 | 1.55520 | 9.231−11 | ||
| 56 | 3s 3p(1P)3d | 2P|$^o _{3/2}$| | 1.60159 | 1.58734 | 1.55438 | 1.55519 | 9.246−11 |
| Index . | Configuration . | Level . | NIST . | SST . | grasp . | fac1 . | fac2 . | fac3 . | τ (s) . |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 3s2 3p | 2P|$^o _{1/2}$| | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | .......... |
| 2 | 3s2 3p | 2P|$^o _{3/2}$| | 0.00262 | 0.00262 | 0.00233 | 0.00224 | 0.00194 | 0.00195 | 6.693+03 |
| 3 | 3s 3p2 | 4P1/2 | 0.39024 | 0.38056 | 0.35314 | 0.36774 | 0.35294 | 0.35373 | 2.510−04 |
| 4 | 3s 3p2 | 4P3/2 | 0.39123 | 0.38139 | 0.35411 | 0.36828 | 0.35370 | 0.35449 | 8.004−03 |
| 5 | 3s 3p2 | 4P5/2 | 0.39283 | 0.38275 | 0.35569 | 0.36996 | 0.35494 | 0.35573 | 3.391−03 |
| 6 | 3s 3p2 | 2D3/2 | 0.50402 | 0.50142 | 0.52570 | 0.53233 | 0.48520 | 0.48597 | 5.629−06 |
| 7 | 3s 3p2 | 2D5/2 | 0.50416 | 0.50159 | 0.52583 | 0.53252 | 0.48541 | 0.48618 | 4.254−06 |
| 8 | 3s2 4s | 2S1/2 | 0.59688 | 0.59763 | 0.64329 | 0.66222 | 0.64309 | 0.64347 | 6.705−10 |
| 9 | 3s 3p2 | 2S1/2 | 0.69863 | 0.70229 | 0.76675 | 0.75842 | 0.75351 | 0.75421 | 7.363−10 |
| 10 | 3s2 4p | 2P|$^o _{1/2}$| | 0.73987 | 0.72724 | 0.77820 | 0.79569 | 0.78195 | 0.78164 | 8.891−09 |
| 11 | 3s2 4p | 2P|$^o _{3/2}$| | 0.74042 | 0.73769 | 0.77871 | 0.79597 | 0.78211 | 0.78182 | 8.835−09 |
| 12 | 3s2 3d | 2D3/2 | 0.72299 | 0.72889 | 0.79914 | 0.80484 | 0.73396 | 0.73261 | 3.078−10 |
| 13 | 3s2 3d | 2D5/2 | 0.72314 | 0.72905 | 0.79931 | 0.80501 | 0.73406 | 0.73271 | 3.092−10 |
| 14 | 3s 3p2 | 2P1/2 | 0.76366 | 0.77039 | 0.89104 | 0.87977 | 0.82156 | 0.82235 | 1.850−10 |
| 15 | 3s 3p2 | 2P3/2 | 0.76550 | 0.77468 | 0.89273 | 0.88128 | 0.82280 | 0.82359 | 1.847−10 |
| 16 | 3s2 5s | 2S1/2 | 0.89279 | 0.89164 | 0.92186 | 0.92866 | 0.91463 | 0.91452 | 1.865−09 |
| 17 | 3s 3p(3P)3d | 2D|$^o _{3/2}$| | 0.99126 | 0.98377 | 0.95559 | 0.98332 | 0.93831 | 0.93910 | 4.397−07 |
| 18 | 3s 3p(3P)3d | 2D|$^o _{5/2}$| | 0.99165 | 0.98421 | 0.95604 | 0.98356 | 0.93869 | 0.93947 | 4.319−07 |
| 19 | 3s2 4d | 2D3/2 | 0.92059 | 0.92128 | 0.96139 | 0.96016 | 0.94787 | 0.94554 | 6.419−10 |
| 20 | 3s2 4d | 2D5/2 | 0.92060 | 0.92131 | 0.96141 | 0.96016 | 0.94784 | 0.94552 | 6.456−10 |
| 21 | 3s2 4f | 2F|$^o _{7/2}$| | 0.94367 | 0.94370 | 0.96650 | 0.97091 | 0.95576 | 0.95654 | 3.881−09 |
| 22 | 3s2 4f | 2F|$^o _{5/2}$| | 0.94367 | 0.94370 | 0.96650 | 0.97091 | 0.95576 | 0.95655 | 3.886−09 |
| 23 | 3s2 5p | 2P|$^o _{1/2}$| | 0.94645 | 0.94287 | 0.97479 | 0.98940 | 0.97822 | 0.97662 | 1.596−08 |
| 24 | 3s2 5p | 2P|$^o _{3/2}$| | 0.94667 | 0.94305 | 0.97500 | 0.98957 | 0.97824 | 0.97672 | 1.597−08 |
| 25 | 3s 3p(3P)3d | 4F|$^o _{3/2}$| | 1.04127 | 1.00875 | 1.02983 | 0.98646 | 0.98725 | 7.061−06 | |
| 26 | 3s 3p(3P)3d | 4F|$^o _{5/2}$| | 1.04183 | 1.00932 | 1.03366 | 0.98694 | 0.98773 | 3.746−06 | |
| 27 | 3s 3p(3P) 3d | 4F|$^o _{7/2}$| | 1.04262 | 1.01013 | 1.03593 | 0.98761 | 0.98840 | 3.601−06 | |
| 28 | 3s 3p(3P) 3d | 4F|$^o _{9/2}$| | 1.04367 | 1.01119 | 1.03355 | 0.98849 | 0.98928 | 2.129+01 | |
| 29 | 3s2 5d | 2D3/2 | 1.02421 | 1.02377 | 1.05396 | 1.05700 | 1.05998 | 1.04788 | 2.146−09 |
| 30 | 3s2 5d | 2D5/2 | 1.02422 | 1.02378 | 1.05396 | 1.05697 | 1.05987 | 1.04784 | 2.157−09 |
| 31 | 3s2 5f | 2F|$^o _{7/2}$| | 1.03666 | 1.03511 | 1.05837 | 1.07196 | 1.05601 | 1.05678 | 9.149−09 |
| 32 | 3s2 5f | 2F|$^o _{5/2}$| | 1.03666 | 1.03511 | 1.05837 | 1.07197 | 1.05602 | 1.05678 | 9.164−09 |
| 33 | 3s2 5g | 2G7/2 | 1.04046 | 1.06176 | 1.06279 | 1.04711 | 1.04790 | 1.397−08 | |
| 34 | 3s2 5g | 2G9/2 | 1.04046 | 1.06176 | 1.06279 | 1.04711 | 1.04790 | 1.397−08 | |
| 35 | 3s 3p(3P)3d | 4P|$^o _{5/2}$| | 1.09742 | 1.11565 | 1.08685 | 1.08763 | 4.540−10 | ||
| 36 | 3s 3p(3P)3d | 4P|$^o _{3/2}$| | 1.09836 | 1.11493 | 1.08768 | 1.08847 | 4.520−10 | ||
| 37 | 3s 3p(3P)3d | 4P|$^o _{1/2}$| | 1.09900 | 1.11657 | 1.08824 | 1.08903 | 4.545−10 | ||
| 38 | 3s 3p(3P)3d | 4D|$^o _{1/2}$| | 1.10612 | 1.12194 | 1.09802 | 1.09881 | 2.465−10 | ||
| 39 | 3s 3p(3P)3d | 4D|$^o _{3/2}$| | 1.10640 | 1.12361 | 1.09820 | 1.09899 | 2.477−10 | ||
| 40 | 3s 3p(3P)3d | 4D|$^o _{5/2}$| | 1.10672 | 1.12461 | 1.09844 | 1.09923 | 2.479−10 | ||
| 41 | 3s 3p(3P)3d | 4D|$^o _{7/2}$| | 1.10700 | 1.12303 | 1.09866 | 1.09945 | 2.465−10 | ||
| 42 | 3p3 | 4S|$^o _{3/2}$| | 1.10799 | 1.12719 | 1.10455 | 1.10534 | 1.973−10 | ||
| 43 | 3s 3p(3P)3d | 2P|$^o _{3/2}$| | 1.15102 | 1.16203 | 1.15549 | 1.15765 | 1.404−09 | ||
| 44 | 3s 3p(3P)3d | 2P|$^o _{1/2}$| | 1.15184 | 1.16236 | 1.15602 | 1.15819 | 1.394−09 | ||
| 45 | 3s 3p(3P)3d | 2F|$^o _{5/2}$| | 1.21481 | 1.22215 | 1.22773 | 1.22857 | 4.865−10 | ||
| 46 | 3s 3p(3P)3d | 2F|$^o _{7/2}$| | 1.21707 | 1.22420 | 1.22969 | 1.23053 | 4.828−10 | ||
| 47 | 3p3 | 2D|$^o _{5/2}$| | 1.28531 | 1.29345 | 1.25126 | 1.25204 | 2.109−10 | ||
| 48 | 3p3 | 2D|$^o _{3/2}$| | 1.28548 | 1.29386 | 1.25138 | 1.25217 | 2.109−10 | ||
| 49 | 3p3 | 2P|$^o _{1/2}$| | 1.41958 | 1.41436 | 1.42672 | 1.42754 | 2.334−10 | ||
| 50 | 3p3 | 2P|$^o _{3/2}$| | 1.41960 | 1.41475 | 1.42678 | 1.42759 | 2.330−10 | ||
| 51 | 3s 3p(1P)3d | 2F|$^o _{7/2}$| | 1.47195 | 1.47076 | 1.43957 | 1.44241 | 1.843−10 | ||
| 52 | 3s 3p(1P)3d | 2F|$^o _{5/2}$| | 1.47258 | 1.47138 | 1.44027 | 1.44310 | 1.836−10 | ||
| 53 | 3s 3p(1P)3d | 2D|$^o _{3/2}$| | 1.56391 | 1.55317 | 1.54933 | 1.55012 | 1.376−10 | ||
| 54 | 3s 3p(1P)3d | 2D|$^o _{5/2}$| | 1.56428 | 1.55328 | 1.54973 | 1.55052 | 1.377−10 | ||
| 55 | 3s 3p(1P)3d | 2P|$^o _{1/2}$| | 1.60151 | 1.58768 | 1.55439 | 1.55520 | 9.231−11 | ||
| 56 | 3s 3p(1P)3d | 2P|$^o _{3/2}$| | 1.60159 | 1.58734 | 1.55438 | 1.55519 | 9.246−11 |
Note. NIST: http://www.nist.gov/pml/data/asd.cfm; SST: Tayal (2008); grasp: present results including the QED effects; fac1: present results with 56 levels; fac2: present results with 164 levels; fac3: present results with 175 levels.
Energy levels of Si ii, their threshold energies (in Ryd) and lifetimes (s) (a ± b ≡ a ×10±b).
| Index . | Configuration . | Level . | NIST . | SST . | grasp . | fac1 . | fac2 . | fac3 . | τ (s) . |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 3s2 3p | 2P|$^o _{1/2}$| | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | .......... |
| 2 | 3s2 3p | 2P|$^o _{3/2}$| | 0.00262 | 0.00262 | 0.00233 | 0.00224 | 0.00194 | 0.00195 | 6.693+03 |
| 3 | 3s 3p2 | 4P1/2 | 0.39024 | 0.38056 | 0.35314 | 0.36774 | 0.35294 | 0.35373 | 2.510−04 |
| 4 | 3s 3p2 | 4P3/2 | 0.39123 | 0.38139 | 0.35411 | 0.36828 | 0.35370 | 0.35449 | 8.004−03 |
| 5 | 3s 3p2 | 4P5/2 | 0.39283 | 0.38275 | 0.35569 | 0.36996 | 0.35494 | 0.35573 | 3.391−03 |
| 6 | 3s 3p2 | 2D3/2 | 0.50402 | 0.50142 | 0.52570 | 0.53233 | 0.48520 | 0.48597 | 5.629−06 |
| 7 | 3s 3p2 | 2D5/2 | 0.50416 | 0.50159 | 0.52583 | 0.53252 | 0.48541 | 0.48618 | 4.254−06 |
| 8 | 3s2 4s | 2S1/2 | 0.59688 | 0.59763 | 0.64329 | 0.66222 | 0.64309 | 0.64347 | 6.705−10 |
| 9 | 3s 3p2 | 2S1/2 | 0.69863 | 0.70229 | 0.76675 | 0.75842 | 0.75351 | 0.75421 | 7.363−10 |
| 10 | 3s2 4p | 2P|$^o _{1/2}$| | 0.73987 | 0.72724 | 0.77820 | 0.79569 | 0.78195 | 0.78164 | 8.891−09 |
| 11 | 3s2 4p | 2P|$^o _{3/2}$| | 0.74042 | 0.73769 | 0.77871 | 0.79597 | 0.78211 | 0.78182 | 8.835−09 |
| 12 | 3s2 3d | 2D3/2 | 0.72299 | 0.72889 | 0.79914 | 0.80484 | 0.73396 | 0.73261 | 3.078−10 |
| 13 | 3s2 3d | 2D5/2 | 0.72314 | 0.72905 | 0.79931 | 0.80501 | 0.73406 | 0.73271 | 3.092−10 |
| 14 | 3s 3p2 | 2P1/2 | 0.76366 | 0.77039 | 0.89104 | 0.87977 | 0.82156 | 0.82235 | 1.850−10 |
| 15 | 3s 3p2 | 2P3/2 | 0.76550 | 0.77468 | 0.89273 | 0.88128 | 0.82280 | 0.82359 | 1.847−10 |
| 16 | 3s2 5s | 2S1/2 | 0.89279 | 0.89164 | 0.92186 | 0.92866 | 0.91463 | 0.91452 | 1.865−09 |
| 17 | 3s 3p(3P)3d | 2D|$^o _{3/2}$| | 0.99126 | 0.98377 | 0.95559 | 0.98332 | 0.93831 | 0.93910 | 4.397−07 |
| 18 | 3s 3p(3P)3d | 2D|$^o _{5/2}$| | 0.99165 | 0.98421 | 0.95604 | 0.98356 | 0.93869 | 0.93947 | 4.319−07 |
| 19 | 3s2 4d | 2D3/2 | 0.92059 | 0.92128 | 0.96139 | 0.96016 | 0.94787 | 0.94554 | 6.419−10 |
| 20 | 3s2 4d | 2D5/2 | 0.92060 | 0.92131 | 0.96141 | 0.96016 | 0.94784 | 0.94552 | 6.456−10 |
| 21 | 3s2 4f | 2F|$^o _{7/2}$| | 0.94367 | 0.94370 | 0.96650 | 0.97091 | 0.95576 | 0.95654 | 3.881−09 |
| 22 | 3s2 4f | 2F|$^o _{5/2}$| | 0.94367 | 0.94370 | 0.96650 | 0.97091 | 0.95576 | 0.95655 | 3.886−09 |
| 23 | 3s2 5p | 2P|$^o _{1/2}$| | 0.94645 | 0.94287 | 0.97479 | 0.98940 | 0.97822 | 0.97662 | 1.596−08 |
| 24 | 3s2 5p | 2P|$^o _{3/2}$| | 0.94667 | 0.94305 | 0.97500 | 0.98957 | 0.97824 | 0.97672 | 1.597−08 |
| 25 | 3s 3p(3P)3d | 4F|$^o _{3/2}$| | 1.04127 | 1.00875 | 1.02983 | 0.98646 | 0.98725 | 7.061−06 | |
| 26 | 3s 3p(3P)3d | 4F|$^o _{5/2}$| | 1.04183 | 1.00932 | 1.03366 | 0.98694 | 0.98773 | 3.746−06 | |
| 27 | 3s 3p(3P) 3d | 4F|$^o _{7/2}$| | 1.04262 | 1.01013 | 1.03593 | 0.98761 | 0.98840 | 3.601−06 | |
| 28 | 3s 3p(3P) 3d | 4F|$^o _{9/2}$| | 1.04367 | 1.01119 | 1.03355 | 0.98849 | 0.98928 | 2.129+01 | |
| 29 | 3s2 5d | 2D3/2 | 1.02421 | 1.02377 | 1.05396 | 1.05700 | 1.05998 | 1.04788 | 2.146−09 |
| 30 | 3s2 5d | 2D5/2 | 1.02422 | 1.02378 | 1.05396 | 1.05697 | 1.05987 | 1.04784 | 2.157−09 |
| 31 | 3s2 5f | 2F|$^o _{7/2}$| | 1.03666 | 1.03511 | 1.05837 | 1.07196 | 1.05601 | 1.05678 | 9.149−09 |
| 32 | 3s2 5f | 2F|$^o _{5/2}$| | 1.03666 | 1.03511 | 1.05837 | 1.07197 | 1.05602 | 1.05678 | 9.164−09 |
| 33 | 3s2 5g | 2G7/2 | 1.04046 | 1.06176 | 1.06279 | 1.04711 | 1.04790 | 1.397−08 | |
| 34 | 3s2 5g | 2G9/2 | 1.04046 | 1.06176 | 1.06279 | 1.04711 | 1.04790 | 1.397−08 | |
| 35 | 3s 3p(3P)3d | 4P|$^o _{5/2}$| | 1.09742 | 1.11565 | 1.08685 | 1.08763 | 4.540−10 | ||
| 36 | 3s 3p(3P)3d | 4P|$^o _{3/2}$| | 1.09836 | 1.11493 | 1.08768 | 1.08847 | 4.520−10 | ||
| 37 | 3s 3p(3P)3d | 4P|$^o _{1/2}$| | 1.09900 | 1.11657 | 1.08824 | 1.08903 | 4.545−10 | ||
| 38 | 3s 3p(3P)3d | 4D|$^o _{1/2}$| | 1.10612 | 1.12194 | 1.09802 | 1.09881 | 2.465−10 | ||
| 39 | 3s 3p(3P)3d | 4D|$^o _{3/2}$| | 1.10640 | 1.12361 | 1.09820 | 1.09899 | 2.477−10 | ||
| 40 | 3s 3p(3P)3d | 4D|$^o _{5/2}$| | 1.10672 | 1.12461 | 1.09844 | 1.09923 | 2.479−10 | ||
| 41 | 3s 3p(3P)3d | 4D|$^o _{7/2}$| | 1.10700 | 1.12303 | 1.09866 | 1.09945 | 2.465−10 | ||
| 42 | 3p3 | 4S|$^o _{3/2}$| | 1.10799 | 1.12719 | 1.10455 | 1.10534 | 1.973−10 | ||
| 43 | 3s 3p(3P)3d | 2P|$^o _{3/2}$| | 1.15102 | 1.16203 | 1.15549 | 1.15765 | 1.404−09 | ||
| 44 | 3s 3p(3P)3d | 2P|$^o _{1/2}$| | 1.15184 | 1.16236 | 1.15602 | 1.15819 | 1.394−09 | ||
| 45 | 3s 3p(3P)3d | 2F|$^o _{5/2}$| | 1.21481 | 1.22215 | 1.22773 | 1.22857 | 4.865−10 | ||
| 46 | 3s 3p(3P)3d | 2F|$^o _{7/2}$| | 1.21707 | 1.22420 | 1.22969 | 1.23053 | 4.828−10 | ||
| 47 | 3p3 | 2D|$^o _{5/2}$| | 1.28531 | 1.29345 | 1.25126 | 1.25204 | 2.109−10 | ||
| 48 | 3p3 | 2D|$^o _{3/2}$| | 1.28548 | 1.29386 | 1.25138 | 1.25217 | 2.109−10 | ||
| 49 | 3p3 | 2P|$^o _{1/2}$| | 1.41958 | 1.41436 | 1.42672 | 1.42754 | 2.334−10 | ||
| 50 | 3p3 | 2P|$^o _{3/2}$| | 1.41960 | 1.41475 | 1.42678 | 1.42759 | 2.330−10 | ||
| 51 | 3s 3p(1P)3d | 2F|$^o _{7/2}$| | 1.47195 | 1.47076 | 1.43957 | 1.44241 | 1.843−10 | ||
| 52 | 3s 3p(1P)3d | 2F|$^o _{5/2}$| | 1.47258 | 1.47138 | 1.44027 | 1.44310 | 1.836−10 | ||
| 53 | 3s 3p(1P)3d | 2D|$^o _{3/2}$| | 1.56391 | 1.55317 | 1.54933 | 1.55012 | 1.376−10 | ||
| 54 | 3s 3p(1P)3d | 2D|$^o _{5/2}$| | 1.56428 | 1.55328 | 1.54973 | 1.55052 | 1.377−10 | ||
| 55 | 3s 3p(1P)3d | 2P|$^o _{1/2}$| | 1.60151 | 1.58768 | 1.55439 | 1.55520 | 9.231−11 | ||
| 56 | 3s 3p(1P)3d | 2P|$^o _{3/2}$| | 1.60159 | 1.58734 | 1.55438 | 1.55519 | 9.246−11 |
| Index . | Configuration . | Level . | NIST . | SST . | grasp . | fac1 . | fac2 . | fac3 . | τ (s) . |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 3s2 3p | 2P|$^o _{1/2}$| | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | .......... |
| 2 | 3s2 3p | 2P|$^o _{3/2}$| | 0.00262 | 0.00262 | 0.00233 | 0.00224 | 0.00194 | 0.00195 | 6.693+03 |
| 3 | 3s 3p2 | 4P1/2 | 0.39024 | 0.38056 | 0.35314 | 0.36774 | 0.35294 | 0.35373 | 2.510−04 |
| 4 | 3s 3p2 | 4P3/2 | 0.39123 | 0.38139 | 0.35411 | 0.36828 | 0.35370 | 0.35449 | 8.004−03 |
| 5 | 3s 3p2 | 4P5/2 | 0.39283 | 0.38275 | 0.35569 | 0.36996 | 0.35494 | 0.35573 | 3.391−03 |
| 6 | 3s 3p2 | 2D3/2 | 0.50402 | 0.50142 | 0.52570 | 0.53233 | 0.48520 | 0.48597 | 5.629−06 |
| 7 | 3s 3p2 | 2D5/2 | 0.50416 | 0.50159 | 0.52583 | 0.53252 | 0.48541 | 0.48618 | 4.254−06 |
| 8 | 3s2 4s | 2S1/2 | 0.59688 | 0.59763 | 0.64329 | 0.66222 | 0.64309 | 0.64347 | 6.705−10 |
| 9 | 3s 3p2 | 2S1/2 | 0.69863 | 0.70229 | 0.76675 | 0.75842 | 0.75351 | 0.75421 | 7.363−10 |
| 10 | 3s2 4p | 2P|$^o _{1/2}$| | 0.73987 | 0.72724 | 0.77820 | 0.79569 | 0.78195 | 0.78164 | 8.891−09 |
| 11 | 3s2 4p | 2P|$^o _{3/2}$| | 0.74042 | 0.73769 | 0.77871 | 0.79597 | 0.78211 | 0.78182 | 8.835−09 |
| 12 | 3s2 3d | 2D3/2 | 0.72299 | 0.72889 | 0.79914 | 0.80484 | 0.73396 | 0.73261 | 3.078−10 |
| 13 | 3s2 3d | 2D5/2 | 0.72314 | 0.72905 | 0.79931 | 0.80501 | 0.73406 | 0.73271 | 3.092−10 |
| 14 | 3s 3p2 | 2P1/2 | 0.76366 | 0.77039 | 0.89104 | 0.87977 | 0.82156 | 0.82235 | 1.850−10 |
| 15 | 3s 3p2 | 2P3/2 | 0.76550 | 0.77468 | 0.89273 | 0.88128 | 0.82280 | 0.82359 | 1.847−10 |
| 16 | 3s2 5s | 2S1/2 | 0.89279 | 0.89164 | 0.92186 | 0.92866 | 0.91463 | 0.91452 | 1.865−09 |
| 17 | 3s 3p(3P)3d | 2D|$^o _{3/2}$| | 0.99126 | 0.98377 | 0.95559 | 0.98332 | 0.93831 | 0.93910 | 4.397−07 |
| 18 | 3s 3p(3P)3d | 2D|$^o _{5/2}$| | 0.99165 | 0.98421 | 0.95604 | 0.98356 | 0.93869 | 0.93947 | 4.319−07 |
| 19 | 3s2 4d | 2D3/2 | 0.92059 | 0.92128 | 0.96139 | 0.96016 | 0.94787 | 0.94554 | 6.419−10 |
| 20 | 3s2 4d | 2D5/2 | 0.92060 | 0.92131 | 0.96141 | 0.96016 | 0.94784 | 0.94552 | 6.456−10 |
| 21 | 3s2 4f | 2F|$^o _{7/2}$| | 0.94367 | 0.94370 | 0.96650 | 0.97091 | 0.95576 | 0.95654 | 3.881−09 |
| 22 | 3s2 4f | 2F|$^o _{5/2}$| | 0.94367 | 0.94370 | 0.96650 | 0.97091 | 0.95576 | 0.95655 | 3.886−09 |
| 23 | 3s2 5p | 2P|$^o _{1/2}$| | 0.94645 | 0.94287 | 0.97479 | 0.98940 | 0.97822 | 0.97662 | 1.596−08 |
| 24 | 3s2 5p | 2P|$^o _{3/2}$| | 0.94667 | 0.94305 | 0.97500 | 0.98957 | 0.97824 | 0.97672 | 1.597−08 |
| 25 | 3s 3p(3P)3d | 4F|$^o _{3/2}$| | 1.04127 | 1.00875 | 1.02983 | 0.98646 | 0.98725 | 7.061−06 | |
| 26 | 3s 3p(3P)3d | 4F|$^o _{5/2}$| | 1.04183 | 1.00932 | 1.03366 | 0.98694 | 0.98773 | 3.746−06 | |
| 27 | 3s 3p(3P) 3d | 4F|$^o _{7/2}$| | 1.04262 | 1.01013 | 1.03593 | 0.98761 | 0.98840 | 3.601−06 | |
| 28 | 3s 3p(3P) 3d | 4F|$^o _{9/2}$| | 1.04367 | 1.01119 | 1.03355 | 0.98849 | 0.98928 | 2.129+01 | |
| 29 | 3s2 5d | 2D3/2 | 1.02421 | 1.02377 | 1.05396 | 1.05700 | 1.05998 | 1.04788 | 2.146−09 |
| 30 | 3s2 5d | 2D5/2 | 1.02422 | 1.02378 | 1.05396 | 1.05697 | 1.05987 | 1.04784 | 2.157−09 |
| 31 | 3s2 5f | 2F|$^o _{7/2}$| | 1.03666 | 1.03511 | 1.05837 | 1.07196 | 1.05601 | 1.05678 | 9.149−09 |
| 32 | 3s2 5f | 2F|$^o _{5/2}$| | 1.03666 | 1.03511 | 1.05837 | 1.07197 | 1.05602 | 1.05678 | 9.164−09 |
| 33 | 3s2 5g | 2G7/2 | 1.04046 | 1.06176 | 1.06279 | 1.04711 | 1.04790 | 1.397−08 | |
| 34 | 3s2 5g | 2G9/2 | 1.04046 | 1.06176 | 1.06279 | 1.04711 | 1.04790 | 1.397−08 | |
| 35 | 3s 3p(3P)3d | 4P|$^o _{5/2}$| | 1.09742 | 1.11565 | 1.08685 | 1.08763 | 4.540−10 | ||
| 36 | 3s 3p(3P)3d | 4P|$^o _{3/2}$| | 1.09836 | 1.11493 | 1.08768 | 1.08847 | 4.520−10 | ||
| 37 | 3s 3p(3P)3d | 4P|$^o _{1/2}$| | 1.09900 | 1.11657 | 1.08824 | 1.08903 | 4.545−10 | ||
| 38 | 3s 3p(3P)3d | 4D|$^o _{1/2}$| | 1.10612 | 1.12194 | 1.09802 | 1.09881 | 2.465−10 | ||
| 39 | 3s 3p(3P)3d | 4D|$^o _{3/2}$| | 1.10640 | 1.12361 | 1.09820 | 1.09899 | 2.477−10 | ||
| 40 | 3s 3p(3P)3d | 4D|$^o _{5/2}$| | 1.10672 | 1.12461 | 1.09844 | 1.09923 | 2.479−10 | ||
| 41 | 3s 3p(3P)3d | 4D|$^o _{7/2}$| | 1.10700 | 1.12303 | 1.09866 | 1.09945 | 2.465−10 | ||
| 42 | 3p3 | 4S|$^o _{3/2}$| | 1.10799 | 1.12719 | 1.10455 | 1.10534 | 1.973−10 | ||
| 43 | 3s 3p(3P)3d | 2P|$^o _{3/2}$| | 1.15102 | 1.16203 | 1.15549 | 1.15765 | 1.404−09 | ||
| 44 | 3s 3p(3P)3d | 2P|$^o _{1/2}$| | 1.15184 | 1.16236 | 1.15602 | 1.15819 | 1.394−09 | ||
| 45 | 3s 3p(3P)3d | 2F|$^o _{5/2}$| | 1.21481 | 1.22215 | 1.22773 | 1.22857 | 4.865−10 | ||
| 46 | 3s 3p(3P)3d | 2F|$^o _{7/2}$| | 1.21707 | 1.22420 | 1.22969 | 1.23053 | 4.828−10 | ||
| 47 | 3p3 | 2D|$^o _{5/2}$| | 1.28531 | 1.29345 | 1.25126 | 1.25204 | 2.109−10 | ||
| 48 | 3p3 | 2D|$^o _{3/2}$| | 1.28548 | 1.29386 | 1.25138 | 1.25217 | 2.109−10 | ||
| 49 | 3p3 | 2P|$^o _{1/2}$| | 1.41958 | 1.41436 | 1.42672 | 1.42754 | 2.334−10 | ||
| 50 | 3p3 | 2P|$^o _{3/2}$| | 1.41960 | 1.41475 | 1.42678 | 1.42759 | 2.330−10 | ||
| 51 | 3s 3p(1P)3d | 2F|$^o _{7/2}$| | 1.47195 | 1.47076 | 1.43957 | 1.44241 | 1.843−10 | ||
| 52 | 3s 3p(1P)3d | 2F|$^o _{5/2}$| | 1.47258 | 1.47138 | 1.44027 | 1.44310 | 1.836−10 | ||
| 53 | 3s 3p(1P)3d | 2D|$^o _{3/2}$| | 1.56391 | 1.55317 | 1.54933 | 1.55012 | 1.376−10 | ||
| 54 | 3s 3p(1P)3d | 2D|$^o _{5/2}$| | 1.56428 | 1.55328 | 1.54973 | 1.55052 | 1.377−10 | ||
| 55 | 3s 3p(1P)3d | 2P|$^o _{1/2}$| | 1.60151 | 1.58768 | 1.55439 | 1.55520 | 9.231−11 | ||
| 56 | 3s 3p(1P)3d | 2P|$^o _{3/2}$| | 1.60159 | 1.58734 | 1.55438 | 1.55519 | 9.246−11 |
Note. NIST: http://www.nist.gov/pml/data/asd.cfm; SST: Tayal (2008); grasp: present results including the QED effects; fac1: present results with 56 levels; fac2: present results with 164 levels; fac3: present results with 175 levels.
A most commonly and widely used methodology for an accurate determination of energy levels (and hence subsequent other parameters) is the inclusion of configuration interaction (CI). This approach has been extensively applied to a wide range of ions by many workers, including ourselves for other Si ions (Aggarwal & Keenan 2010). Therefore, to assess the effect of additional CI we have performed further calculations with the Flexible Atomic Code (fac) of Gu (2008). This code, apart from being highly efficient, provides results for energy levels and A values of comparable accuracy with other atomic structure codes, such as configuration interaction version 3 (civ3) of Hibbert (1975) and grasp, as shown by Aggarwal et al. (2007) for three Mg-like ions.
We have performed three calculations with the fac code with increasing amount of CI, namely (i) fac1, which includes the same configurations/levels as in grasp; (ii) fac2, which includes all possible combinations of the 3ℓ orbitals (3*3) plus 3s2 4ℓ and 3s2 5ℓ, generating 164 levels in total and finally (iii) fac3, which includes a further 11 levels of 3s2 6ℓ, because some of these intermix with those of fac2. Energies obtained from these three calculations are listed in Table 1 for comparison with other results.
Our fac1 energies agree closely with those from grasp (within 0.03 Ryd) and the ordering is also similar, although a few differ slightly, such as levels 17–22. We also note that small discrepancies in the grasp and fac energies mainly arise due to the different ways the calculations of central potential for radial orbitals and recoupling schemes of angular parts are performed – see the detailed discussion in the fac manual (http://sprg.ssl.berkeley.edu/∼mfgu/fac/). Such small differences have also been noted for several other ions. Inclusion of larger CI in fac2 lowers the energies, by up to 0.07 Ryd, for some of the levels, such as 12–15, but differences with the NIST compilations remain of up to ∼0.1 Ryd. Finally, energies obtained in fac3 are comparable (within 0.01 Ryd) to those from fac2 indicating that the inclusion of the 3s2 6ℓ configuration has little effect on the energy levels of Table 1. Furthermore, the energy for level 2 (3s2 3p 2P|$^o_{3/2}$|) has become worse than in fac1 or grasp, and hence there in no overall advantage of including more CI than that already considered in grasp. We discuss this further below.
Bautista et al. (2009) have performed a series of calculations with the atomic structure (as) code of Badnell (1997). Apart from adopting different optimization procedures (including the minimization with observed energies) they have included extensive CI with up to n = 5 orbitals in 44 configurations. They have also opened the n = 2 shell (frozen in our work with grasp and fac) to account for the core–valence correlation. However, none of their nine calculations yielded accurate energies for the lowest 15 levels. Differences with the measurements for all sets of energies are over 15 per cent for some levels or others, as shown in their table 2. It is clear that inclusion of a large amount of CI is not helpful for the accurate determination of Si ii energy levels.
Apart from the inclusion of CI, another possibility of improving the accuracy of wave functions is to add correlation effects through pseudo-orbitals, i.e. all orbitals need not be spectroscopic as has been the case in the calculations described above with the grasp, fac and as codes. This is a normal practice in standard R-matrix calculations for Ω, for which input wave functions are generated through the civ3 code, but all orbitals are orthogonal. Therefore, Dufton et al. (1983) adopted this approach but their energy levels still differ by up to 6 per cent with the measurements. Additionally, a disadvantage of this approach is the presence of unphysical pseudo-resonances, because the corresponding eigenstates are not included in the calculations of Ω (see e.g. fig. 1 of Aggarwal & Hibbert 1991). If these pseudo-resonances are not properly removed then the subsequent results for ϒ may be significantly overestimated (see e.g. figs 1–6 of Aggarwal et al. 2000). Therefore, scope remains for improvement over our energy levels listed in Table 1, but keeping in mind our further calculations for more important parameters (Ω and ϒ), the accuracy achieved should be satisfactory for a majority of the levels.

Partial collision strengths at three energies of 2 Ryd (circles), 6 Ryd (triangles) and 12 Ryd (stars) for three transitions of Si ii, namely (a) 1–12 (3s2 3p 2P|$^o_{1/2}$|–3s2 3d 2D3/2), (b) 2–13 (3s2 3p 2P|$^o_{3/2}$|–3s2 3d 2D5/2) and (c) 2–15 (3s2 3p 2P|$^o_{3/2}$|–3s 3p22P3/2).
3 RADIATIVE RATES
In Table 2 we list transition (energies) wavelengths (λ, in Å), radiative rates (Aji, in s−1), oscillator strengths (fij, dimensionless) and line strengths (S, in a.u.) for all 460 electric dipole (E1) transitions among the 56 levels of Si ii. The A, f and S values have been calculated in both Babushkin and Coulomb gauges, i.e. the length and velocity forms in the widely used non-relativistic nomenclature. However, in Table 2 results are listed in the length form alone, because the velocity form is generally considered to be comparatively less accurate. Nevertheless, we will discuss later the velocity/length form ratio, as this provides some assessment of the accuracy of the results. Also note that the indices used to represent the lower and upper levels of a transition correspond to those in Table 1. Apart from the above E1 transitions, there are 733 electric quadrupole (E2), 567 magnetic dipole (M1) and 574 magnetic quadrupole (M2) transitions among the same 56 levels. However, for these only the A values are listed in Table 2, because these are the ones required for plasma modelling. The corresponding results for f values can be easily obtained through equation (1). Similarly, if required, corresponding S values can be obtained through equations (2)–(5) of Aggarwal & Keenan (2012).
Transition wavelengths (λij in Å), radiative rates (Aji in s−1), oscillator strengths (fij, dimensionless) and line strengths (S, in atomic units) for electric dipole (E1), and Aji for E2, M1 and M2 transitions in Si ii (a ± b ≡ a ×10±b). (For complete table see Supporting Information.)
| i . | j . | λij . | |$A^{{\rm E1}}_{ji}$| . | |$f^{{\rm E1}}_{ij}$| . | SE1 . | |$A^{{\rm E2}}_{ji}$| . | |$A^{{\rm M1}}_{ji}$| . | |$A^{{\rm M2}}_{ji}$| . |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3.919+05 | 0.000+00 | 0.000+00 | 0.000+00 | 1.082−09 | 1.494−04 | 0.000+00 |
| 1 | 3 | 2.580+03 | 1.703+03 | 1.700−06 | 2.889−05 | 0.000+00 | 0.000+00 | 0.000+00 |
| 1 | 4 | 2.573+03 | 8.227+00 | 1.634−08 | 2.768−07 | 0.000+00 | 0.000+00 | 2.818−03 |
| 1 | 5 | 2.562+03 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 1.103−03 |
| 1 | 6 | 1.734+03 | 1.167+05 | 1.051−04 | 1.200−03 | 0.000+00 | 0.000+00 | 3.553−07 |
| 1 | 7 | 1.733+03 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 2.256−02 |
| 1 | 8 | 1.417+03 | 4.996+08 | 1.503−01 | 1.402+00 | 0.000+00 | 0.000+00 | 0.000+00 |
| 1 | 9 | 1.188+03 | 4.781+08 | 1.012−01 | 7.923−01 | 0.000+00 | 0.000+00 | 0.000+00 |
| 1 | 10 | 1.171+03 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 8.890−06 | 0.000+00 |
| . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . |
| i . | j . | λij . | |$A^{{\rm E1}}_{ji}$| . | |$f^{{\rm E1}}_{ij}$| . | SE1 . | |$A^{{\rm E2}}_{ji}$| . | |$A^{{\rm M1}}_{ji}$| . | |$A^{{\rm M2}}_{ji}$| . |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3.919+05 | 0.000+00 | 0.000+00 | 0.000+00 | 1.082−09 | 1.494−04 | 0.000+00 |
| 1 | 3 | 2.580+03 | 1.703+03 | 1.700−06 | 2.889−05 | 0.000+00 | 0.000+00 | 0.000+00 |
| 1 | 4 | 2.573+03 | 8.227+00 | 1.634−08 | 2.768−07 | 0.000+00 | 0.000+00 | 2.818−03 |
| 1 | 5 | 2.562+03 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 1.103−03 |
| 1 | 6 | 1.734+03 | 1.167+05 | 1.051−04 | 1.200−03 | 0.000+00 | 0.000+00 | 3.553−07 |
| 1 | 7 | 1.733+03 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 2.256−02 |
| 1 | 8 | 1.417+03 | 4.996+08 | 1.503−01 | 1.402+00 | 0.000+00 | 0.000+00 | 0.000+00 |
| 1 | 9 | 1.188+03 | 4.781+08 | 1.012−01 | 7.923−01 | 0.000+00 | 0.000+00 | 0.000+00 |
| 1 | 10 | 1.171+03 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 8.890−06 | 0.000+00 |
| . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . |
Transition wavelengths (λij in Å), radiative rates (Aji in s−1), oscillator strengths (fij, dimensionless) and line strengths (S, in atomic units) for electric dipole (E1), and Aji for E2, M1 and M2 transitions in Si ii (a ± b ≡ a ×10±b). (For complete table see Supporting Information.)
| i . | j . | λij . | |$A^{{\rm E1}}_{ji}$| . | |$f^{{\rm E1}}_{ij}$| . | SE1 . | |$A^{{\rm E2}}_{ji}$| . | |$A^{{\rm M1}}_{ji}$| . | |$A^{{\rm M2}}_{ji}$| . |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3.919+05 | 0.000+00 | 0.000+00 | 0.000+00 | 1.082−09 | 1.494−04 | 0.000+00 |
| 1 | 3 | 2.580+03 | 1.703+03 | 1.700−06 | 2.889−05 | 0.000+00 | 0.000+00 | 0.000+00 |
| 1 | 4 | 2.573+03 | 8.227+00 | 1.634−08 | 2.768−07 | 0.000+00 | 0.000+00 | 2.818−03 |
| 1 | 5 | 2.562+03 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 1.103−03 |
| 1 | 6 | 1.734+03 | 1.167+05 | 1.051−04 | 1.200−03 | 0.000+00 | 0.000+00 | 3.553−07 |
| 1 | 7 | 1.733+03 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 2.256−02 |
| 1 | 8 | 1.417+03 | 4.996+08 | 1.503−01 | 1.402+00 | 0.000+00 | 0.000+00 | 0.000+00 |
| 1 | 9 | 1.188+03 | 4.781+08 | 1.012−01 | 7.923−01 | 0.000+00 | 0.000+00 | 0.000+00 |
| 1 | 10 | 1.171+03 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 8.890−06 | 0.000+00 |
| . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . |
| i . | j . | λij . | |$A^{{\rm E1}}_{ji}$| . | |$f^{{\rm E1}}_{ij}$| . | SE1 . | |$A^{{\rm E2}}_{ji}$| . | |$A^{{\rm M1}}_{ji}$| . | |$A^{{\rm M2}}_{ji}$| . |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3.919+05 | 0.000+00 | 0.000+00 | 0.000+00 | 1.082−09 | 1.494−04 | 0.000+00 |
| 1 | 3 | 2.580+03 | 1.703+03 | 1.700−06 | 2.889−05 | 0.000+00 | 0.000+00 | 0.000+00 |
| 1 | 4 | 2.573+03 | 8.227+00 | 1.634−08 | 2.768−07 | 0.000+00 | 0.000+00 | 2.818−03 |
| 1 | 5 | 2.562+03 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 1.103−03 |
| 1 | 6 | 1.734+03 | 1.167+05 | 1.051−04 | 1.200−03 | 0.000+00 | 0.000+00 | 3.553−07 |
| 1 | 7 | 1.733+03 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 2.256−02 |
| 1 | 8 | 1.417+03 | 4.996+08 | 1.503−01 | 1.402+00 | 0.000+00 | 0.000+00 | 0.000+00 |
| 1 | 9 | 1.188+03 | 4.781+08 | 1.012−01 | 7.923−01 | 0.000+00 | 0.000+00 | 0.000+00 |
| 1 | 10 | 1.171+03 | 0.000+00 | 0.000+00 | 0.000+00 | 0.000+00 | 8.890−06 | 0.000+00 |
| . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . |
In Table 3 we compare our f values from grasp with those of Tayal (2007) and Bautista et al. (2009) for transitions among the lowest 30 levels of Table 1. Bautista et al. (2009) have listed several sets of f values, but those included in Table 3 correspond to their ‘recommended’ results, which are based on the averages of a variety of theoretical and experimental (to be discussed later) values. These authors reported f values only for transitions among the lowest 15 levels, but many are missing from the work of Tayal (2007). Most of the missing transitions are weak (i.e. f ∼ 10−5 or even less), but some are rather strong, such as 6–22 (f = 0.125), 7–21 (f = 0.120) and 12–22 (f = 0.734). This is because he included the 3s2 4f (21–22) levels in his calculations for collisional data (Tayal 2008), but not for the radiative rates. Nevertheless, the absence of f (or A) values for these transitions may affect the modelling of plasmas.
Comparison of oscillator strengths (f values) for transitions among the lowest 30 levels of Si ii (a ± b ≡ a ×10±b).
| I . | J . | grasp . | mchf . | as . | R . | I . | J . | grasp . | mchf . | as . | R . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 1.700−6 | ......... | 4.500−6 | 1.8−1 | 9 | 23 | 1.715−4 | ......... | ......... | 2.5+0 |
| 1 | 4 | 1.634−8 | ......... | 2.000−9 | 4.5+0 | 9 | 24 | 3.588−4 | ......... | ......... | 2.5+0 |
| 1 | 6 | 1.051−4 | 2.500−3 | 2.400−3 | 3.2+1 | 9 | 25 | 7.61−10 | ......... | ......... | 1.3+0 |
| 1 | 8 | 1.503−1 | 1.310−1 | 1.400−1 | 5.6−1 | 10 | 12 | 9.477−2 | 1.680−2 | ......... | 4.6−1 |
| 1 | 9 | 1.012−1 | 9.210−2 | 9.100−2 | 7.8−1 | 10 | 14 | 2.559−4 | ......... | ......... | 2.3+0 |
| 1 | 12 | 1.063+0 | 1.180+0 | 1.200+0 | 8.6−1 | 10 | 15 | 2.730−4 | ......... | ......... | 1.8+0 |
| 1 | 14 | 5.616−1 | 5.780−1 | 5.400−1 | 8.7−1 | 10 | 16 | 2.392−1 | 2.370−1 | ......... | 9.3−1 |
| 1 | 15 | 2.789−1 | 2.850−1 | 2.600−1 | 8.7−1 | 10 | 19 | 8.121−1 | 9.090−1 | ......... | 1.0+0 |
| 1 | 16 | 1.942−2 | 1.490−2 | ......... | 5.5−1 | 10 | 29 | 1.665−1 | 1.060−1 | ......... | 9.9−1 |
| 1 | 19 | 3.184−1 | 1.700−1 | ......... | 6.7−1 | 11 | 12 | 9.264−3 | 3.500−3 | ......... | 4.7−1 |
| 1 | 29 | 6.900−2 | 4.170−2 | ......... | 1.0+0 | 11 | 13 | 8.404−2 | 2.070−2 | ......... | 4.7−1 |
| 2 | 3 | 1.154−6 | ......... | 1.700−6 | 2.0−1 | 11 | 14 | 1.764−5 | ......... | ......... | 5.2+0 |
| 2 | 4 | 1.174−7 | ......... | 1.000−6 | 2.1−1 | 11 | 15 | 1.661−4 | ......... | ......... | 3.2+0 |
| 2 | 5 | 4.410−7 | ......... | 2.600−6 | 1.2+0 | 11 | 16 | 2.406−1 | 2.380−1 | ......... | 9.3−1 |
| 2 | 6 | 2.771−5 | 1.700−4 | 1.800−4 | 9.9+0 | 11 | 19 | 8.158−2 | 9.110−2 | ......... | 1.0+0 |
| 2 | 7 | 1.602−4 | 1.970−3 | 1.700−3 | 1.7+1 | 11 | 20 | 7.333−1 | 8.190−1 | ......... | 1.0+0 |
| 2 | 8 | 1.503−1 | 1.300−1 | 1.300−1 | 5.6−1 | 11 | 29 | 1.663−2 | 1.040−2 | ......... | 9.9−1 |
| 2 | 9 | 9.374−2 | 8.090−2 | 8.100−2 | 7.8−1 | 11 | 30 | 1.496−1 | 9.340−2 | ......... | 9.9−1 |
| 2 | 12 | 1.025−1 | 1.110−1 | 1.000−1 | 8.6−1 | 12 | 17 | 1.447−5 | ......... | ......... | 8.4+0 |
| 2 | 13 | 9.506−1 | 1.050+0 | 1.000+0 | 8.6−1 | 12 | 18 | 8.911−6 | ......... | ......... | 8.5+0 |
| 2 | 14 | 1.437−1 | 1.510−1 | 1.400−1 | 8.7−1 | 12 | 22 | 7.344−1 | ......... | ......... | 7.6−1 |
| 2 | 15 | 7.100−1 | 7.390−1 | 4.800−1 | 8.7−1 | 12 | 23 | 2.702−2 | 6.890−3 | ......... | 2.2−1 |
| 2 | 16 | 2.097−2 | 1.520−2 | ......... | 5.6−1 | 12 | 24 | 5.313−3 | 8.140−3 | ......... | 2.2−1 |
| 2 | 19 | 3.310−2 | 1.750−2 | ......... | 6.7−1 | 12 | 25 | 1.631−8 | ......... | ......... | 1.8+1 |
| 2 | 20 | 2.878−1 | 1.520−1 | ......... | 6.7−1 | 12 | 26 | 1.204−5 | ......... | ......... | 8.7−1 |
| 2 | 29 | 7.024−3 | 4.180−3 | ......... | 1.0+0 | 13 | 17 | 4.734−9 | ......... | ......... | 7.2+3 |
| 2 | 30 | 6.214−2 | 3.740−2 | ......... | 1.0+0 | 13 | 18 | 2.262−5 | ......... | ......... | 5.3+0 |
| 3 | 10 | 1.382−7 | ......... | ......... | 4.8−1 | 13 | 21 | 6.992−1 | ......... | ......... | 7.6−1 |
| 3 | 11 | 1.885−7 | ......... | 1.500−7 | 4.4−1 | 13 | 22 | 3.495−2 | ......... | ......... | 7.6−1 |
| 3 | 17 | 4.348−6 | ......... | ......... | 8.3−1 | 13 | 24 | 3.210−2 | ......... | ......... | 2.2−1 |
| 3 | 23 | 1.774−7 | ......... | ......... | 2.9−1 | 13 | 25 | 7.97−10 | ......... | ......... | 1.8+1 |
| 3 | 24 | 8.658−8 | ......... | ......... | 9.2−2 | 13 | 26 | 4.425−7 | ......... | ......... | 2.7+0 |
| 3 | 25 | 3.017−5 | ......... | ......... | 7.2−1 | 13 | 27 | 1.509−5 | ......... | ......... | 9.5−1 |
| 4 | 10 | 1.220−7 | ......... | 3.000−7 | 2.5−1 | 14 | 17 | 7.666−5 | ......... | ......... | 1.9+1 |
| 4 | 11 | 3.396−9 | ......... | 2.900−8 | 2.0−2 | 14 | 23 | 8.043−8 | ......... | ......... | 2.0+1 |
| 4 | 17 | 7.207−7 | ......... | ......... | 9.9−1 | 14 | 24 | 8.815−5 | ......... | ......... | 2.3−1 |
| 4 | 18 | 9.915−6 | ......... | ......... | 8.2−1 | 14 | 25 | 1.628−7 | ......... | ......... | 7.2+0 |
| 4 | 22 | 6.561−7 | ......... | ......... | 9.5−1 | 15 | 17 | 5.351−6 | ......... | ......... | 6.4+0 |
| 4 | 23 | 6.962−8 | ......... | ......... | 2.7−2 | 15 | 18 | 7.031−5 | ......... | ......... | 1.5+1 |
| 4 | 24 | 4.594−8 | ......... | ......... | 1.3+0 | 15 | 22 | 4.104−5 | ......... | ......... | 9.3−1 |
| 4 | 25 | 1.898−5 | ......... | ......... | 7.2−1 | 15 | 23 | 1.158−6 | ......... | ......... | 2.3+0 |
| 4 | 26 | 7.766−5 | ......... | ......... | 7.2−1 | 15 | 24 | 4.258−5 | ......... | ......... | 1.7−1 |
| 5 | 11 | 7.569−7 | ......... | 1.800−6 | 2.1−1 | 15 | 25 | 1.861−8 | ......... | ......... | 4.0+0 |
| 5 | 17 | 1.576−9 | ......... | ......... | 4.2−3 | 15 | 26 | 5.387−8 | ......... | ......... | 7.6+0 |
| 5 | 18 | 1.040−7 | ......... | ......... | 1.9−1 | 16 | 17 | 2.202−5 | ......... | ......... | 5.6−1 |
| 5 | 21 | 3.735−6 | ......... | ......... | 9.6−1 | 16 | 23 | 5.800−1 | 5.420−1 | ......... | 9.5−1 |
| 5 | 22 | 1.850−7 | ......... | ......... | 9.6−1 | 16 | 24 | 1.163+0 | 1.090+0 | ......... | 9.5−1 |
| 5 | 24 | 1.615−7 | ......... | ......... | 1.1−1 | 16 | 25 | 3.848−9 | ......... | ......... | 1.3+0 |
| 5 | 25 | 1.158−6 | ......... | ......... | 7.2−1 | 17 | 19 | 2.94−10 | ......... | ......... | 9.2+4 |
| 5 | 26 | 2.159−5 | ......... | ......... | 7.2−1 | 17 | 20 | 3.977−6 | ......... | ......... | 7.5+0 |
| 5 | 27 | 1.044−4 | ......... | ......... | 7.2−1 | 17 | 29 | 1.063−5 | ......... | ......... | 3.0−3 |
| 6 | 10 | 4.639−2 | 4.820−2 | 3.500−2 | 3.2−1 | 17 | 30 | 2.044−5 | ......... | ......... | 5.6−1 |
| 6 | 11 | 9.235−3 | 9.630−3 | 7.000−3 | 3.2−1 | 18 | 19 | 1.304−6 | ......... | ......... | 1.8+0 |
| 6 | 17 | 1.289−3 | ......... | ......... | 4.6−1 | 18 | 20 | 1.262−7 | ......... | ......... | 1.5+2 |
| 6 | 18 | 1.522−4 | ......... | ......... | 5.1−1 | 18 | 29 | 9.960−8 | ......... | ......... | 1.4+1 |
| 6 | 22 | 1.249−1 | ......... | ......... | 9.3−1 | 18 | 30 | 2.824−6 | ......... | ......... | 4.6−1 |
| 6 | 23 | 1.084−2 | 1.030−2 | ......... | 2.9−2 | 19 | 22 | 5.851−2 | ......... | ......... | 7.4+0 |
| 6 | 24 | 2.145−3 | 2.060−3 | ......... | 2.9−2 | 19 | 23 | 1.224−1 | 1.920−1 | ......... | 1.7+0 |
| 6 | 25 | 8.624−6 | ......... | ......... | 5.2−1 | 19 | 24 | 2.482−2 | 3.870−2 | ......... | 1.7+0 |
| 6 | 26 | 8.233−7 | ......... | ......... | 2.5+0 | 19 | 25 | 7.247−9 | ......... | ......... | 1.4+2 |
| 7 | 11 | 5.554−2 | 5.790−2 | 4.000−2 | 3.2−1 | 19 | 26 | 4.360−6 | ......... | ......... | 4.8−4 |
| 7 | 17 | 1.489−4 | ......... | ......... | 5.2−1 | 20 | 21 | 5.543−2 | ......... | ......... | 7.4+0 |
| 7 | 18 | 1.426−3 | ......... | ......... | 4.8−1 | 20 | 22 | 2.772−3 | ......... | ......... | 7.4+0 |
| 7 | 21 | 1.196−1 | ......... | ......... | 9.3−1 | 20 | 24 | 1.487−1 | 2.320−1 | ......... | 1.7+0 |
| 7 | 22 | 6.010−3 | ......... | ......... | 9.3−1 | 20 | 25 | 6.19−11 | ......... | ......... | 7.4+2 |
| 7 | 24 | 1.297−2 | 1.240−2 | ......... | 3.0−2 | 20 | 26 | 1.608−7 | ......... | ......... | 3.2+0 |
| 7 | 25 | 7.271−7 | ......... | ......... | 5.2−1 | 20 | 27 | 5.636−6 | ......... | ......... | 5.4−3 |
| 7 | 26 | 5.471−6 | ......... | ......... | 6.3−1 | 21 | 30 | 1.451−2 | ......... | ......... | 3.1+0 |
| 7 | 27 | 3.039−6 | ......... | ......... | 1.5+0 | 22 | 29 | 1.356−2 | ......... | ......... | 3.1+0 |
| 8 | 10 | 4.442−1 | 3.770−1 | 2.400−1 | 9.2−1 | 22 | 30 | 9.670−4 | ......... | ......... | 3.1+0 |
| 8 | 11 | 8.912−1 | 7.570−1 | 4.900−1 | 9.2−1 | 23 | 29 | 1.113+0 | 1.140+0 | ......... | 1.0+0 |
| 8 | 17 | 7.067−7 | ......... | ......... | 2.6+0 | 24 | 29 | 1.118−1 | 1.140−1 | ......... | 1.0+0 |
| 8 | 23 | 7.247−4 | ......... | ......... | 3.3−1 | 24 | 30 | 1.006+0 | 1.030+0 | ......... | 1.0+0 |
| 8 | 24 | 1.625−3 | ......... | ......... | 3.6−1 | 25 | 29 | 1.363−9 | ......... | ......... | 3.3+2 |
| 8 | 25 | 1.69−10 | ......... | ......... | 1.7+0 | 25 | 30 | 3.612−9 | ......... | ......... | 3.5+0 |
| 9 | 10 | 9.830−5 | 1.140−3 | ......... | 3.0+0 | 26 | 29 | 3.220−6 | ......... | ......... | 1.1−1 |
| 9 | 11 | 1.999−4 | 2.290−3 | ......... | 3.1+0 | 26 | 30 | 2.671−7 | ......... | ......... | 1.5+0 |
| 9 | 17 | 1.322−7 | ......... | ......... | 5.9+0 | 27 | 30 | 4.814−6 | ......... | ......... | 1.7−1 |
| I . | J . | grasp . | mchf . | as . | R . | I . | J . | grasp . | mchf . | as . | R . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 1.700−6 | ......... | 4.500−6 | 1.8−1 | 9 | 23 | 1.715−4 | ......... | ......... | 2.5+0 |
| 1 | 4 | 1.634−8 | ......... | 2.000−9 | 4.5+0 | 9 | 24 | 3.588−4 | ......... | ......... | 2.5+0 |
| 1 | 6 | 1.051−4 | 2.500−3 | 2.400−3 | 3.2+1 | 9 | 25 | 7.61−10 | ......... | ......... | 1.3+0 |
| 1 | 8 | 1.503−1 | 1.310−1 | 1.400−1 | 5.6−1 | 10 | 12 | 9.477−2 | 1.680−2 | ......... | 4.6−1 |
| 1 | 9 | 1.012−1 | 9.210−2 | 9.100−2 | 7.8−1 | 10 | 14 | 2.559−4 | ......... | ......... | 2.3+0 |
| 1 | 12 | 1.063+0 | 1.180+0 | 1.200+0 | 8.6−1 | 10 | 15 | 2.730−4 | ......... | ......... | 1.8+0 |
| 1 | 14 | 5.616−1 | 5.780−1 | 5.400−1 | 8.7−1 | 10 | 16 | 2.392−1 | 2.370−1 | ......... | 9.3−1 |
| 1 | 15 | 2.789−1 | 2.850−1 | 2.600−1 | 8.7−1 | 10 | 19 | 8.121−1 | 9.090−1 | ......... | 1.0+0 |
| 1 | 16 | 1.942−2 | 1.490−2 | ......... | 5.5−1 | 10 | 29 | 1.665−1 | 1.060−1 | ......... | 9.9−1 |
| 1 | 19 | 3.184−1 | 1.700−1 | ......... | 6.7−1 | 11 | 12 | 9.264−3 | 3.500−3 | ......... | 4.7−1 |
| 1 | 29 | 6.900−2 | 4.170−2 | ......... | 1.0+0 | 11 | 13 | 8.404−2 | 2.070−2 | ......... | 4.7−1 |
| 2 | 3 | 1.154−6 | ......... | 1.700−6 | 2.0−1 | 11 | 14 | 1.764−5 | ......... | ......... | 5.2+0 |
| 2 | 4 | 1.174−7 | ......... | 1.000−6 | 2.1−1 | 11 | 15 | 1.661−4 | ......... | ......... | 3.2+0 |
| 2 | 5 | 4.410−7 | ......... | 2.600−6 | 1.2+0 | 11 | 16 | 2.406−1 | 2.380−1 | ......... | 9.3−1 |
| 2 | 6 | 2.771−5 | 1.700−4 | 1.800−4 | 9.9+0 | 11 | 19 | 8.158−2 | 9.110−2 | ......... | 1.0+0 |
| 2 | 7 | 1.602−4 | 1.970−3 | 1.700−3 | 1.7+1 | 11 | 20 | 7.333−1 | 8.190−1 | ......... | 1.0+0 |
| 2 | 8 | 1.503−1 | 1.300−1 | 1.300−1 | 5.6−1 | 11 | 29 | 1.663−2 | 1.040−2 | ......... | 9.9−1 |
| 2 | 9 | 9.374−2 | 8.090−2 | 8.100−2 | 7.8−1 | 11 | 30 | 1.496−1 | 9.340−2 | ......... | 9.9−1 |
| 2 | 12 | 1.025−1 | 1.110−1 | 1.000−1 | 8.6−1 | 12 | 17 | 1.447−5 | ......... | ......... | 8.4+0 |
| 2 | 13 | 9.506−1 | 1.050+0 | 1.000+0 | 8.6−1 | 12 | 18 | 8.911−6 | ......... | ......... | 8.5+0 |
| 2 | 14 | 1.437−1 | 1.510−1 | 1.400−1 | 8.7−1 | 12 | 22 | 7.344−1 | ......... | ......... | 7.6−1 |
| 2 | 15 | 7.100−1 | 7.390−1 | 4.800−1 | 8.7−1 | 12 | 23 | 2.702−2 | 6.890−3 | ......... | 2.2−1 |
| 2 | 16 | 2.097−2 | 1.520−2 | ......... | 5.6−1 | 12 | 24 | 5.313−3 | 8.140−3 | ......... | 2.2−1 |
| 2 | 19 | 3.310−2 | 1.750−2 | ......... | 6.7−1 | 12 | 25 | 1.631−8 | ......... | ......... | 1.8+1 |
| 2 | 20 | 2.878−1 | 1.520−1 | ......... | 6.7−1 | 12 | 26 | 1.204−5 | ......... | ......... | 8.7−1 |
| 2 | 29 | 7.024−3 | 4.180−3 | ......... | 1.0+0 | 13 | 17 | 4.734−9 | ......... | ......... | 7.2+3 |
| 2 | 30 | 6.214−2 | 3.740−2 | ......... | 1.0+0 | 13 | 18 | 2.262−5 | ......... | ......... | 5.3+0 |
| 3 | 10 | 1.382−7 | ......... | ......... | 4.8−1 | 13 | 21 | 6.992−1 | ......... | ......... | 7.6−1 |
| 3 | 11 | 1.885−7 | ......... | 1.500−7 | 4.4−1 | 13 | 22 | 3.495−2 | ......... | ......... | 7.6−1 |
| 3 | 17 | 4.348−6 | ......... | ......... | 8.3−1 | 13 | 24 | 3.210−2 | ......... | ......... | 2.2−1 |
| 3 | 23 | 1.774−7 | ......... | ......... | 2.9−1 | 13 | 25 | 7.97−10 | ......... | ......... | 1.8+1 |
| 3 | 24 | 8.658−8 | ......... | ......... | 9.2−2 | 13 | 26 | 4.425−7 | ......... | ......... | 2.7+0 |
| 3 | 25 | 3.017−5 | ......... | ......... | 7.2−1 | 13 | 27 | 1.509−5 | ......... | ......... | 9.5−1 |
| 4 | 10 | 1.220−7 | ......... | 3.000−7 | 2.5−1 | 14 | 17 | 7.666−5 | ......... | ......... | 1.9+1 |
| 4 | 11 | 3.396−9 | ......... | 2.900−8 | 2.0−2 | 14 | 23 | 8.043−8 | ......... | ......... | 2.0+1 |
| 4 | 17 | 7.207−7 | ......... | ......... | 9.9−1 | 14 | 24 | 8.815−5 | ......... | ......... | 2.3−1 |
| 4 | 18 | 9.915−6 | ......... | ......... | 8.2−1 | 14 | 25 | 1.628−7 | ......... | ......... | 7.2+0 |
| 4 | 22 | 6.561−7 | ......... | ......... | 9.5−1 | 15 | 17 | 5.351−6 | ......... | ......... | 6.4+0 |
| 4 | 23 | 6.962−8 | ......... | ......... | 2.7−2 | 15 | 18 | 7.031−5 | ......... | ......... | 1.5+1 |
| 4 | 24 | 4.594−8 | ......... | ......... | 1.3+0 | 15 | 22 | 4.104−5 | ......... | ......... | 9.3−1 |
| 4 | 25 | 1.898−5 | ......... | ......... | 7.2−1 | 15 | 23 | 1.158−6 | ......... | ......... | 2.3+0 |
| 4 | 26 | 7.766−5 | ......... | ......... | 7.2−1 | 15 | 24 | 4.258−5 | ......... | ......... | 1.7−1 |
| 5 | 11 | 7.569−7 | ......... | 1.800−6 | 2.1−1 | 15 | 25 | 1.861−8 | ......... | ......... | 4.0+0 |
| 5 | 17 | 1.576−9 | ......... | ......... | 4.2−3 | 15 | 26 | 5.387−8 | ......... | ......... | 7.6+0 |
| 5 | 18 | 1.040−7 | ......... | ......... | 1.9−1 | 16 | 17 | 2.202−5 | ......... | ......... | 5.6−1 |
| 5 | 21 | 3.735−6 | ......... | ......... | 9.6−1 | 16 | 23 | 5.800−1 | 5.420−1 | ......... | 9.5−1 |
| 5 | 22 | 1.850−7 | ......... | ......... | 9.6−1 | 16 | 24 | 1.163+0 | 1.090+0 | ......... | 9.5−1 |
| 5 | 24 | 1.615−7 | ......... | ......... | 1.1−1 | 16 | 25 | 3.848−9 | ......... | ......... | 1.3+0 |
| 5 | 25 | 1.158−6 | ......... | ......... | 7.2−1 | 17 | 19 | 2.94−10 | ......... | ......... | 9.2+4 |
| 5 | 26 | 2.159−5 | ......... | ......... | 7.2−1 | 17 | 20 | 3.977−6 | ......... | ......... | 7.5+0 |
| 5 | 27 | 1.044−4 | ......... | ......... | 7.2−1 | 17 | 29 | 1.063−5 | ......... | ......... | 3.0−3 |
| 6 | 10 | 4.639−2 | 4.820−2 | 3.500−2 | 3.2−1 | 17 | 30 | 2.044−5 | ......... | ......... | 5.6−1 |
| 6 | 11 | 9.235−3 | 9.630−3 | 7.000−3 | 3.2−1 | 18 | 19 | 1.304−6 | ......... | ......... | 1.8+0 |
| 6 | 17 | 1.289−3 | ......... | ......... | 4.6−1 | 18 | 20 | 1.262−7 | ......... | ......... | 1.5+2 |
| 6 | 18 | 1.522−4 | ......... | ......... | 5.1−1 | 18 | 29 | 9.960−8 | ......... | ......... | 1.4+1 |
| 6 | 22 | 1.249−1 | ......... | ......... | 9.3−1 | 18 | 30 | 2.824−6 | ......... | ......... | 4.6−1 |
| 6 | 23 | 1.084−2 | 1.030−2 | ......... | 2.9−2 | 19 | 22 | 5.851−2 | ......... | ......... | 7.4+0 |
| 6 | 24 | 2.145−3 | 2.060−3 | ......... | 2.9−2 | 19 | 23 | 1.224−1 | 1.920−1 | ......... | 1.7+0 |
| 6 | 25 | 8.624−6 | ......... | ......... | 5.2−1 | 19 | 24 | 2.482−2 | 3.870−2 | ......... | 1.7+0 |
| 6 | 26 | 8.233−7 | ......... | ......... | 2.5+0 | 19 | 25 | 7.247−9 | ......... | ......... | 1.4+2 |
| 7 | 11 | 5.554−2 | 5.790−2 | 4.000−2 | 3.2−1 | 19 | 26 | 4.360−6 | ......... | ......... | 4.8−4 |
| 7 | 17 | 1.489−4 | ......... | ......... | 5.2−1 | 20 | 21 | 5.543−2 | ......... | ......... | 7.4+0 |
| 7 | 18 | 1.426−3 | ......... | ......... | 4.8−1 | 20 | 22 | 2.772−3 | ......... | ......... | 7.4+0 |
| 7 | 21 | 1.196−1 | ......... | ......... | 9.3−1 | 20 | 24 | 1.487−1 | 2.320−1 | ......... | 1.7+0 |
| 7 | 22 | 6.010−3 | ......... | ......... | 9.3−1 | 20 | 25 | 6.19−11 | ......... | ......... | 7.4+2 |
| 7 | 24 | 1.297−2 | 1.240−2 | ......... | 3.0−2 | 20 | 26 | 1.608−7 | ......... | ......... | 3.2+0 |
| 7 | 25 | 7.271−7 | ......... | ......... | 5.2−1 | 20 | 27 | 5.636−6 | ......... | ......... | 5.4−3 |
| 7 | 26 | 5.471−6 | ......... | ......... | 6.3−1 | 21 | 30 | 1.451−2 | ......... | ......... | 3.1+0 |
| 7 | 27 | 3.039−6 | ......... | ......... | 1.5+0 | 22 | 29 | 1.356−2 | ......... | ......... | 3.1+0 |
| 8 | 10 | 4.442−1 | 3.770−1 | 2.400−1 | 9.2−1 | 22 | 30 | 9.670−4 | ......... | ......... | 3.1+0 |
| 8 | 11 | 8.912−1 | 7.570−1 | 4.900−1 | 9.2−1 | 23 | 29 | 1.113+0 | 1.140+0 | ......... | 1.0+0 |
| 8 | 17 | 7.067−7 | ......... | ......... | 2.6+0 | 24 | 29 | 1.118−1 | 1.140−1 | ......... | 1.0+0 |
| 8 | 23 | 7.247−4 | ......... | ......... | 3.3−1 | 24 | 30 | 1.006+0 | 1.030+0 | ......... | 1.0+0 |
| 8 | 24 | 1.625−3 | ......... | ......... | 3.6−1 | 25 | 29 | 1.363−9 | ......... | ......... | 3.3+2 |
| 8 | 25 | 1.69−10 | ......... | ......... | 1.7+0 | 25 | 30 | 3.612−9 | ......... | ......... | 3.5+0 |
| 9 | 10 | 9.830−5 | 1.140−3 | ......... | 3.0+0 | 26 | 29 | 3.220−6 | ......... | ......... | 1.1−1 |
| 9 | 11 | 1.999−4 | 2.290−3 | ......... | 3.1+0 | 26 | 30 | 2.671−7 | ......... | ......... | 1.5+0 |
| 9 | 17 | 1.322−7 | ......... | ......... | 5.9+0 | 27 | 30 | 4.814−6 | ......... | ......... | 1.7−1 |
Comparison of oscillator strengths (f values) for transitions among the lowest 30 levels of Si ii (a ± b ≡ a ×10±b).
| I . | J . | grasp . | mchf . | as . | R . | I . | J . | grasp . | mchf . | as . | R . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 1.700−6 | ......... | 4.500−6 | 1.8−1 | 9 | 23 | 1.715−4 | ......... | ......... | 2.5+0 |
| 1 | 4 | 1.634−8 | ......... | 2.000−9 | 4.5+0 | 9 | 24 | 3.588−4 | ......... | ......... | 2.5+0 |
| 1 | 6 | 1.051−4 | 2.500−3 | 2.400−3 | 3.2+1 | 9 | 25 | 7.61−10 | ......... | ......... | 1.3+0 |
| 1 | 8 | 1.503−1 | 1.310−1 | 1.400−1 | 5.6−1 | 10 | 12 | 9.477−2 | 1.680−2 | ......... | 4.6−1 |
| 1 | 9 | 1.012−1 | 9.210−2 | 9.100−2 | 7.8−1 | 10 | 14 | 2.559−4 | ......... | ......... | 2.3+0 |
| 1 | 12 | 1.063+0 | 1.180+0 | 1.200+0 | 8.6−1 | 10 | 15 | 2.730−4 | ......... | ......... | 1.8+0 |
| 1 | 14 | 5.616−1 | 5.780−1 | 5.400−1 | 8.7−1 | 10 | 16 | 2.392−1 | 2.370−1 | ......... | 9.3−1 |
| 1 | 15 | 2.789−1 | 2.850−1 | 2.600−1 | 8.7−1 | 10 | 19 | 8.121−1 | 9.090−1 | ......... | 1.0+0 |
| 1 | 16 | 1.942−2 | 1.490−2 | ......... | 5.5−1 | 10 | 29 | 1.665−1 | 1.060−1 | ......... | 9.9−1 |
| 1 | 19 | 3.184−1 | 1.700−1 | ......... | 6.7−1 | 11 | 12 | 9.264−3 | 3.500−3 | ......... | 4.7−1 |
| 1 | 29 | 6.900−2 | 4.170−2 | ......... | 1.0+0 | 11 | 13 | 8.404−2 | 2.070−2 | ......... | 4.7−1 |
| 2 | 3 | 1.154−6 | ......... | 1.700−6 | 2.0−1 | 11 | 14 | 1.764−5 | ......... | ......... | 5.2+0 |
| 2 | 4 | 1.174−7 | ......... | 1.000−6 | 2.1−1 | 11 | 15 | 1.661−4 | ......... | ......... | 3.2+0 |
| 2 | 5 | 4.410−7 | ......... | 2.600−6 | 1.2+0 | 11 | 16 | 2.406−1 | 2.380−1 | ......... | 9.3−1 |
| 2 | 6 | 2.771−5 | 1.700−4 | 1.800−4 | 9.9+0 | 11 | 19 | 8.158−2 | 9.110−2 | ......... | 1.0+0 |
| 2 | 7 | 1.602−4 | 1.970−3 | 1.700−3 | 1.7+1 | 11 | 20 | 7.333−1 | 8.190−1 | ......... | 1.0+0 |
| 2 | 8 | 1.503−1 | 1.300−1 | 1.300−1 | 5.6−1 | 11 | 29 | 1.663−2 | 1.040−2 | ......... | 9.9−1 |
| 2 | 9 | 9.374−2 | 8.090−2 | 8.100−2 | 7.8−1 | 11 | 30 | 1.496−1 | 9.340−2 | ......... | 9.9−1 |
| 2 | 12 | 1.025−1 | 1.110−1 | 1.000−1 | 8.6−1 | 12 | 17 | 1.447−5 | ......... | ......... | 8.4+0 |
| 2 | 13 | 9.506−1 | 1.050+0 | 1.000+0 | 8.6−1 | 12 | 18 | 8.911−6 | ......... | ......... | 8.5+0 |
| 2 | 14 | 1.437−1 | 1.510−1 | 1.400−1 | 8.7−1 | 12 | 22 | 7.344−1 | ......... | ......... | 7.6−1 |
| 2 | 15 | 7.100−1 | 7.390−1 | 4.800−1 | 8.7−1 | 12 | 23 | 2.702−2 | 6.890−3 | ......... | 2.2−1 |
| 2 | 16 | 2.097−2 | 1.520−2 | ......... | 5.6−1 | 12 | 24 | 5.313−3 | 8.140−3 | ......... | 2.2−1 |
| 2 | 19 | 3.310−2 | 1.750−2 | ......... | 6.7−1 | 12 | 25 | 1.631−8 | ......... | ......... | 1.8+1 |
| 2 | 20 | 2.878−1 | 1.520−1 | ......... | 6.7−1 | 12 | 26 | 1.204−5 | ......... | ......... | 8.7−1 |
| 2 | 29 | 7.024−3 | 4.180−3 | ......... | 1.0+0 | 13 | 17 | 4.734−9 | ......... | ......... | 7.2+3 |
| 2 | 30 | 6.214−2 | 3.740−2 | ......... | 1.0+0 | 13 | 18 | 2.262−5 | ......... | ......... | 5.3+0 |
| 3 | 10 | 1.382−7 | ......... | ......... | 4.8−1 | 13 | 21 | 6.992−1 | ......... | ......... | 7.6−1 |
| 3 | 11 | 1.885−7 | ......... | 1.500−7 | 4.4−1 | 13 | 22 | 3.495−2 | ......... | ......... | 7.6−1 |
| 3 | 17 | 4.348−6 | ......... | ......... | 8.3−1 | 13 | 24 | 3.210−2 | ......... | ......... | 2.2−1 |
| 3 | 23 | 1.774−7 | ......... | ......... | 2.9−1 | 13 | 25 | 7.97−10 | ......... | ......... | 1.8+1 |
| 3 | 24 | 8.658−8 | ......... | ......... | 9.2−2 | 13 | 26 | 4.425−7 | ......... | ......... | 2.7+0 |
| 3 | 25 | 3.017−5 | ......... | ......... | 7.2−1 | 13 | 27 | 1.509−5 | ......... | ......... | 9.5−1 |
| 4 | 10 | 1.220−7 | ......... | 3.000−7 | 2.5−1 | 14 | 17 | 7.666−5 | ......... | ......... | 1.9+1 |
| 4 | 11 | 3.396−9 | ......... | 2.900−8 | 2.0−2 | 14 | 23 | 8.043−8 | ......... | ......... | 2.0+1 |
| 4 | 17 | 7.207−7 | ......... | ......... | 9.9−1 | 14 | 24 | 8.815−5 | ......... | ......... | 2.3−1 |
| 4 | 18 | 9.915−6 | ......... | ......... | 8.2−1 | 14 | 25 | 1.628−7 | ......... | ......... | 7.2+0 |
| 4 | 22 | 6.561−7 | ......... | ......... | 9.5−1 | 15 | 17 | 5.351−6 | ......... | ......... | 6.4+0 |
| 4 | 23 | 6.962−8 | ......... | ......... | 2.7−2 | 15 | 18 | 7.031−5 | ......... | ......... | 1.5+1 |
| 4 | 24 | 4.594−8 | ......... | ......... | 1.3+0 | 15 | 22 | 4.104−5 | ......... | ......... | 9.3−1 |
| 4 | 25 | 1.898−5 | ......... | ......... | 7.2−1 | 15 | 23 | 1.158−6 | ......... | ......... | 2.3+0 |
| 4 | 26 | 7.766−5 | ......... | ......... | 7.2−1 | 15 | 24 | 4.258−5 | ......... | ......... | 1.7−1 |
| 5 | 11 | 7.569−7 | ......... | 1.800−6 | 2.1−1 | 15 | 25 | 1.861−8 | ......... | ......... | 4.0+0 |
| 5 | 17 | 1.576−9 | ......... | ......... | 4.2−3 | 15 | 26 | 5.387−8 | ......... | ......... | 7.6+0 |
| 5 | 18 | 1.040−7 | ......... | ......... | 1.9−1 | 16 | 17 | 2.202−5 | ......... | ......... | 5.6−1 |
| 5 | 21 | 3.735−6 | ......... | ......... | 9.6−1 | 16 | 23 | 5.800−1 | 5.420−1 | ......... | 9.5−1 |
| 5 | 22 | 1.850−7 | ......... | ......... | 9.6−1 | 16 | 24 | 1.163+0 | 1.090+0 | ......... | 9.5−1 |
| 5 | 24 | 1.615−7 | ......... | ......... | 1.1−1 | 16 | 25 | 3.848−9 | ......... | ......... | 1.3+0 |
| 5 | 25 | 1.158−6 | ......... | ......... | 7.2−1 | 17 | 19 | 2.94−10 | ......... | ......... | 9.2+4 |
| 5 | 26 | 2.159−5 | ......... | ......... | 7.2−1 | 17 | 20 | 3.977−6 | ......... | ......... | 7.5+0 |
| 5 | 27 | 1.044−4 | ......... | ......... | 7.2−1 | 17 | 29 | 1.063−5 | ......... | ......... | 3.0−3 |
| 6 | 10 | 4.639−2 | 4.820−2 | 3.500−2 | 3.2−1 | 17 | 30 | 2.044−5 | ......... | ......... | 5.6−1 |
| 6 | 11 | 9.235−3 | 9.630−3 | 7.000−3 | 3.2−1 | 18 | 19 | 1.304−6 | ......... | ......... | 1.8+0 |
| 6 | 17 | 1.289−3 | ......... | ......... | 4.6−1 | 18 | 20 | 1.262−7 | ......... | ......... | 1.5+2 |
| 6 | 18 | 1.522−4 | ......... | ......... | 5.1−1 | 18 | 29 | 9.960−8 | ......... | ......... | 1.4+1 |
| 6 | 22 | 1.249−1 | ......... | ......... | 9.3−1 | 18 | 30 | 2.824−6 | ......... | ......... | 4.6−1 |
| 6 | 23 | 1.084−2 | 1.030−2 | ......... | 2.9−2 | 19 | 22 | 5.851−2 | ......... | ......... | 7.4+0 |
| 6 | 24 | 2.145−3 | 2.060−3 | ......... | 2.9−2 | 19 | 23 | 1.224−1 | 1.920−1 | ......... | 1.7+0 |
| 6 | 25 | 8.624−6 | ......... | ......... | 5.2−1 | 19 | 24 | 2.482−2 | 3.870−2 | ......... | 1.7+0 |
| 6 | 26 | 8.233−7 | ......... | ......... | 2.5+0 | 19 | 25 | 7.247−9 | ......... | ......... | 1.4+2 |
| 7 | 11 | 5.554−2 | 5.790−2 | 4.000−2 | 3.2−1 | 19 | 26 | 4.360−6 | ......... | ......... | 4.8−4 |
| 7 | 17 | 1.489−4 | ......... | ......... | 5.2−1 | 20 | 21 | 5.543−2 | ......... | ......... | 7.4+0 |
| 7 | 18 | 1.426−3 | ......... | ......... | 4.8−1 | 20 | 22 | 2.772−3 | ......... | ......... | 7.4+0 |
| 7 | 21 | 1.196−1 | ......... | ......... | 9.3−1 | 20 | 24 | 1.487−1 | 2.320−1 | ......... | 1.7+0 |
| 7 | 22 | 6.010−3 | ......... | ......... | 9.3−1 | 20 | 25 | 6.19−11 | ......... | ......... | 7.4+2 |
| 7 | 24 | 1.297−2 | 1.240−2 | ......... | 3.0−2 | 20 | 26 | 1.608−7 | ......... | ......... | 3.2+0 |
| 7 | 25 | 7.271−7 | ......... | ......... | 5.2−1 | 20 | 27 | 5.636−6 | ......... | ......... | 5.4−3 |
| 7 | 26 | 5.471−6 | ......... | ......... | 6.3−1 | 21 | 30 | 1.451−2 | ......... | ......... | 3.1+0 |
| 7 | 27 | 3.039−6 | ......... | ......... | 1.5+0 | 22 | 29 | 1.356−2 | ......... | ......... | 3.1+0 |
| 8 | 10 | 4.442−1 | 3.770−1 | 2.400−1 | 9.2−1 | 22 | 30 | 9.670−4 | ......... | ......... | 3.1+0 |
| 8 | 11 | 8.912−1 | 7.570−1 | 4.900−1 | 9.2−1 | 23 | 29 | 1.113+0 | 1.140+0 | ......... | 1.0+0 |
| 8 | 17 | 7.067−7 | ......... | ......... | 2.6+0 | 24 | 29 | 1.118−1 | 1.140−1 | ......... | 1.0+0 |
| 8 | 23 | 7.247−4 | ......... | ......... | 3.3−1 | 24 | 30 | 1.006+0 | 1.030+0 | ......... | 1.0+0 |
| 8 | 24 | 1.625−3 | ......... | ......... | 3.6−1 | 25 | 29 | 1.363−9 | ......... | ......... | 3.3+2 |
| 8 | 25 | 1.69−10 | ......... | ......... | 1.7+0 | 25 | 30 | 3.612−9 | ......... | ......... | 3.5+0 |
| 9 | 10 | 9.830−5 | 1.140−3 | ......... | 3.0+0 | 26 | 29 | 3.220−6 | ......... | ......... | 1.1−1 |
| 9 | 11 | 1.999−4 | 2.290−3 | ......... | 3.1+0 | 26 | 30 | 2.671−7 | ......... | ......... | 1.5+0 |
| 9 | 17 | 1.322−7 | ......... | ......... | 5.9+0 | 27 | 30 | 4.814−6 | ......... | ......... | 1.7−1 |
| I . | J . | grasp . | mchf . | as . | R . | I . | J . | grasp . | mchf . | as . | R . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 1.700−6 | ......... | 4.500−6 | 1.8−1 | 9 | 23 | 1.715−4 | ......... | ......... | 2.5+0 |
| 1 | 4 | 1.634−8 | ......... | 2.000−9 | 4.5+0 | 9 | 24 | 3.588−4 | ......... | ......... | 2.5+0 |
| 1 | 6 | 1.051−4 | 2.500−3 | 2.400−3 | 3.2+1 | 9 | 25 | 7.61−10 | ......... | ......... | 1.3+0 |
| 1 | 8 | 1.503−1 | 1.310−1 | 1.400−1 | 5.6−1 | 10 | 12 | 9.477−2 | 1.680−2 | ......... | 4.6−1 |
| 1 | 9 | 1.012−1 | 9.210−2 | 9.100−2 | 7.8−1 | 10 | 14 | 2.559−4 | ......... | ......... | 2.3+0 |
| 1 | 12 | 1.063+0 | 1.180+0 | 1.200+0 | 8.6−1 | 10 | 15 | 2.730−4 | ......... | ......... | 1.8+0 |
| 1 | 14 | 5.616−1 | 5.780−1 | 5.400−1 | 8.7−1 | 10 | 16 | 2.392−1 | 2.370−1 | ......... | 9.3−1 |
| 1 | 15 | 2.789−1 | 2.850−1 | 2.600−1 | 8.7−1 | 10 | 19 | 8.121−1 | 9.090−1 | ......... | 1.0+0 |
| 1 | 16 | 1.942−2 | 1.490−2 | ......... | 5.5−1 | 10 | 29 | 1.665−1 | 1.060−1 | ......... | 9.9−1 |
| 1 | 19 | 3.184−1 | 1.700−1 | ......... | 6.7−1 | 11 | 12 | 9.264−3 | 3.500−3 | ......... | 4.7−1 |
| 1 | 29 | 6.900−2 | 4.170−2 | ......... | 1.0+0 | 11 | 13 | 8.404−2 | 2.070−2 | ......... | 4.7−1 |
| 2 | 3 | 1.154−6 | ......... | 1.700−6 | 2.0−1 | 11 | 14 | 1.764−5 | ......... | ......... | 5.2+0 |
| 2 | 4 | 1.174−7 | ......... | 1.000−6 | 2.1−1 | 11 | 15 | 1.661−4 | ......... | ......... | 3.2+0 |
| 2 | 5 | 4.410−7 | ......... | 2.600−6 | 1.2+0 | 11 | 16 | 2.406−1 | 2.380−1 | ......... | 9.3−1 |
| 2 | 6 | 2.771−5 | 1.700−4 | 1.800−4 | 9.9+0 | 11 | 19 | 8.158−2 | 9.110−2 | ......... | 1.0+0 |
| 2 | 7 | 1.602−4 | 1.970−3 | 1.700−3 | 1.7+1 | 11 | 20 | 7.333−1 | 8.190−1 | ......... | 1.0+0 |
| 2 | 8 | 1.503−1 | 1.300−1 | 1.300−1 | 5.6−1 | 11 | 29 | 1.663−2 | 1.040−2 | ......... | 9.9−1 |
| 2 | 9 | 9.374−2 | 8.090−2 | 8.100−2 | 7.8−1 | 11 | 30 | 1.496−1 | 9.340−2 | ......... | 9.9−1 |
| 2 | 12 | 1.025−1 | 1.110−1 | 1.000−1 | 8.6−1 | 12 | 17 | 1.447−5 | ......... | ......... | 8.4+0 |
| 2 | 13 | 9.506−1 | 1.050+0 | 1.000+0 | 8.6−1 | 12 | 18 | 8.911−6 | ......... | ......... | 8.5+0 |
| 2 | 14 | 1.437−1 | 1.510−1 | 1.400−1 | 8.7−1 | 12 | 22 | 7.344−1 | ......... | ......... | 7.6−1 |
| 2 | 15 | 7.100−1 | 7.390−1 | 4.800−1 | 8.7−1 | 12 | 23 | 2.702−2 | 6.890−3 | ......... | 2.2−1 |
| 2 | 16 | 2.097−2 | 1.520−2 | ......... | 5.6−1 | 12 | 24 | 5.313−3 | 8.140−3 | ......... | 2.2−1 |
| 2 | 19 | 3.310−2 | 1.750−2 | ......... | 6.7−1 | 12 | 25 | 1.631−8 | ......... | ......... | 1.8+1 |
| 2 | 20 | 2.878−1 | 1.520−1 | ......... | 6.7−1 | 12 | 26 | 1.204−5 | ......... | ......... | 8.7−1 |
| 2 | 29 | 7.024−3 | 4.180−3 | ......... | 1.0+0 | 13 | 17 | 4.734−9 | ......... | ......... | 7.2+3 |
| 2 | 30 | 6.214−2 | 3.740−2 | ......... | 1.0+0 | 13 | 18 | 2.262−5 | ......... | ......... | 5.3+0 |
| 3 | 10 | 1.382−7 | ......... | ......... | 4.8−1 | 13 | 21 | 6.992−1 | ......... | ......... | 7.6−1 |
| 3 | 11 | 1.885−7 | ......... | 1.500−7 | 4.4−1 | 13 | 22 | 3.495−2 | ......... | ......... | 7.6−1 |
| 3 | 17 | 4.348−6 | ......... | ......... | 8.3−1 | 13 | 24 | 3.210−2 | ......... | ......... | 2.2−1 |
| 3 | 23 | 1.774−7 | ......... | ......... | 2.9−1 | 13 | 25 | 7.97−10 | ......... | ......... | 1.8+1 |
| 3 | 24 | 8.658−8 | ......... | ......... | 9.2−2 | 13 | 26 | 4.425−7 | ......... | ......... | 2.7+0 |
| 3 | 25 | 3.017−5 | ......... | ......... | 7.2−1 | 13 | 27 | 1.509−5 | ......... | ......... | 9.5−1 |
| 4 | 10 | 1.220−7 | ......... | 3.000−7 | 2.5−1 | 14 | 17 | 7.666−5 | ......... | ......... | 1.9+1 |
| 4 | 11 | 3.396−9 | ......... | 2.900−8 | 2.0−2 | 14 | 23 | 8.043−8 | ......... | ......... | 2.0+1 |
| 4 | 17 | 7.207−7 | ......... | ......... | 9.9−1 | 14 | 24 | 8.815−5 | ......... | ......... | 2.3−1 |
| 4 | 18 | 9.915−6 | ......... | ......... | 8.2−1 | 14 | 25 | 1.628−7 | ......... | ......... | 7.2+0 |
| 4 | 22 | 6.561−7 | ......... | ......... | 9.5−1 | 15 | 17 | 5.351−6 | ......... | ......... | 6.4+0 |
| 4 | 23 | 6.962−8 | ......... | ......... | 2.7−2 | 15 | 18 | 7.031−5 | ......... | ......... | 1.5+1 |
| 4 | 24 | 4.594−8 | ......... | ......... | 1.3+0 | 15 | 22 | 4.104−5 | ......... | ......... | 9.3−1 |
| 4 | 25 | 1.898−5 | ......... | ......... | 7.2−1 | 15 | 23 | 1.158−6 | ......... | ......... | 2.3+0 |
| 4 | 26 | 7.766−5 | ......... | ......... | 7.2−1 | 15 | 24 | 4.258−5 | ......... | ......... | 1.7−1 |
| 5 | 11 | 7.569−7 | ......... | 1.800−6 | 2.1−1 | 15 | 25 | 1.861−8 | ......... | ......... | 4.0+0 |
| 5 | 17 | 1.576−9 | ......... | ......... | 4.2−3 | 15 | 26 | 5.387−8 | ......... | ......... | 7.6+0 |
| 5 | 18 | 1.040−7 | ......... | ......... | 1.9−1 | 16 | 17 | 2.202−5 | ......... | ......... | 5.6−1 |
| 5 | 21 | 3.735−6 | ......... | ......... | 9.6−1 | 16 | 23 | 5.800−1 | 5.420−1 | ......... | 9.5−1 |
| 5 | 22 | 1.850−7 | ......... | ......... | 9.6−1 | 16 | 24 | 1.163+0 | 1.090+0 | ......... | 9.5−1 |
| 5 | 24 | 1.615−7 | ......... | ......... | 1.1−1 | 16 | 25 | 3.848−9 | ......... | ......... | 1.3+0 |
| 5 | 25 | 1.158−6 | ......... | ......... | 7.2−1 | 17 | 19 | 2.94−10 | ......... | ......... | 9.2+4 |
| 5 | 26 | 2.159−5 | ......... | ......... | 7.2−1 | 17 | 20 | 3.977−6 | ......... | ......... | 7.5+0 |
| 5 | 27 | 1.044−4 | ......... | ......... | 7.2−1 | 17 | 29 | 1.063−5 | ......... | ......... | 3.0−3 |
| 6 | 10 | 4.639−2 | 4.820−2 | 3.500−2 | 3.2−1 | 17 | 30 | 2.044−5 | ......... | ......... | 5.6−1 |
| 6 | 11 | 9.235−3 | 9.630−3 | 7.000−3 | 3.2−1 | 18 | 19 | 1.304−6 | ......... | ......... | 1.8+0 |
| 6 | 17 | 1.289−3 | ......... | ......... | 4.6−1 | 18 | 20 | 1.262−7 | ......... | ......... | 1.5+2 |
| 6 | 18 | 1.522−4 | ......... | ......... | 5.1−1 | 18 | 29 | 9.960−8 | ......... | ......... | 1.4+1 |
| 6 | 22 | 1.249−1 | ......... | ......... | 9.3−1 | 18 | 30 | 2.824−6 | ......... | ......... | 4.6−1 |
| 6 | 23 | 1.084−2 | 1.030−2 | ......... | 2.9−2 | 19 | 22 | 5.851−2 | ......... | ......... | 7.4+0 |
| 6 | 24 | 2.145−3 | 2.060−3 | ......... | 2.9−2 | 19 | 23 | 1.224−1 | 1.920−1 | ......... | 1.7+0 |
| 6 | 25 | 8.624−6 | ......... | ......... | 5.2−1 | 19 | 24 | 2.482−2 | 3.870−2 | ......... | 1.7+0 |
| 6 | 26 | 8.233−7 | ......... | ......... | 2.5+0 | 19 | 25 | 7.247−9 | ......... | ......... | 1.4+2 |
| 7 | 11 | 5.554−2 | 5.790−2 | 4.000−2 | 3.2−1 | 19 | 26 | 4.360−6 | ......... | ......... | 4.8−4 |
| 7 | 17 | 1.489−4 | ......... | ......... | 5.2−1 | 20 | 21 | 5.543−2 | ......... | ......... | 7.4+0 |
| 7 | 18 | 1.426−3 | ......... | ......... | 4.8−1 | 20 | 22 | 2.772−3 | ......... | ......... | 7.4+0 |
| 7 | 21 | 1.196−1 | ......... | ......... | 9.3−1 | 20 | 24 | 1.487−1 | 2.320−1 | ......... | 1.7+0 |
| 7 | 22 | 6.010−3 | ......... | ......... | 9.3−1 | 20 | 25 | 6.19−11 | ......... | ......... | 7.4+2 |
| 7 | 24 | 1.297−2 | 1.240−2 | ......... | 3.0−2 | 20 | 26 | 1.608−7 | ......... | ......... | 3.2+0 |
| 7 | 25 | 7.271−7 | ......... | ......... | 5.2−1 | 20 | 27 | 5.636−6 | ......... | ......... | 5.4−3 |
| 7 | 26 | 5.471−6 | ......... | ......... | 6.3−1 | 21 | 30 | 1.451−2 | ......... | ......... | 3.1+0 |
| 7 | 27 | 3.039−6 | ......... | ......... | 1.5+0 | 22 | 29 | 1.356−2 | ......... | ......... | 3.1+0 |
| 8 | 10 | 4.442−1 | 3.770−1 | 2.400−1 | 9.2−1 | 22 | 30 | 9.670−4 | ......... | ......... | 3.1+0 |
| 8 | 11 | 8.912−1 | 7.570−1 | 4.900−1 | 9.2−1 | 23 | 29 | 1.113+0 | 1.140+0 | ......... | 1.0+0 |
| 8 | 17 | 7.067−7 | ......... | ......... | 2.6+0 | 24 | 29 | 1.118−1 | 1.140−1 | ......... | 1.0+0 |
| 8 | 23 | 7.247−4 | ......... | ......... | 3.3−1 | 24 | 30 | 1.006+0 | 1.030+0 | ......... | 1.0+0 |
| 8 | 24 | 1.625−3 | ......... | ......... | 3.6−1 | 25 | 29 | 1.363−9 | ......... | ......... | 3.3+2 |
| 8 | 25 | 1.69−10 | ......... | ......... | 1.7+0 | 25 | 30 | 3.612−9 | ......... | ......... | 3.5+0 |
| 9 | 10 | 9.830−5 | 1.140−3 | ......... | 3.0+0 | 26 | 29 | 3.220−6 | ......... | ......... | 1.1−1 |
| 9 | 11 | 1.999−4 | 2.290−3 | ......... | 3.1+0 | 26 | 30 | 2.671−7 | ......... | ......... | 1.5+0 |
| 9 | 17 | 1.322−7 | ......... | ......... | 5.9+0 | 27 | 30 | 4.814−6 | ......... | ......... | 1.7−1 |
Among the common transitions, f values differ by up to a factor of 2 for a few, such as 2–20, 8–10/11 and 20–24. These transitions are comparatively strong (0.15 ≤ f ≤ 0.89) and therefore better agreement is expected. However, such discrepancies do arise with varying amounts of CI (and methods/codes) as discussed in detail by Bautista et al. (2009) – see their figs 2 and 3, and particularly table 3. Similarly, discrepancies for some weak transitions (such as 1–4, 2–4/7 and 4–11) are up to an order of magnitude. Weaker transitions are more susceptible to varying amount of CI, due to cancellation or additive effects, and hence such discrepancies are very common (see also Oliver & Hibbert 2011). Overall, there is a good agreement among all calculations for most transitions.
For a few transitions, measured f values are also available (see Bautista et al. 2009 and references therein), but there is significant scatter among these. Therefore, the accuracy of the radiative data cannot be assessed by comparison with experimental results. However, another criterion normally used to assess the accuracy of f or A values is to compare the ratio (R) of their velocity and length forms. This should ideally be close to unity but often is not (Aggarwal et al. 2007), because the two formulations are not exactly the same. Similarly, different calculations with differing amount of CI may yield R closer to unity but strikingly different f values in magnitude, as already stated. Nevertheless, we include in Table 3 the ratio of the velocity and length forms obtained in our calculations with grasp.
For most (comparatively strong) transitions listed in Table 3 the ratio R is within ∼20 per cent of 1.0. However, there are exceptions. For example, for the 1–8 (3s2 3p 2P|$^o_{1/2}$|–3s2 4s 2S1/2) and 2–8 (3s2 3p 2P|$^o_{3/2}$|–3s2 4s 2S1/2) transitions, there is no discrepancy among the f values from grasp, mchf and as, but R is 0.56. On the other hand, for the 8–10/11 (3s2 4s 2S1/2–3s2 4p 2P|$^o_{1/2,3/2}$|) transitions, R is 0.92 but the f values differ by almost a factor of 2. Therefore, as explained earlier, this assessment cannot be rigorously applied, but the overall accuracy of the listed results for strong transitions appears to be satisfactory. For weak(er) transitions, R is up to 10 000, the discrepancies among f values are larger, and hence the accuracy is lower. For similar reasons, the accuracy for the E2, M1 and M2 data is also lower, because most of these are weaker in comparison to the E1 transitions. Finally, as for energy levels, we have calculated A and f values from fac also, and for most (strong) transitions the agreement with our grasp results is within ∼20 per cent.
4 LIFETIMES
Its measurement can directly lead to the assessment of accuracy of the A values, particularly if a single transition dominates. Therefore, in Table 1 we have also listed our calculated lifetimes. As already stated, A values for E1 transitions generally dominate, but for completeness we have also included the contributions from E2, M1 and M2. Their inclusion is particularly important for those levels which do not connect via E1 transitions. Schectman, Povolny & Curtis (1998) have measured τ corresponding to the 3s2 3p 2P|$^o_{3/2}$|–3s2 4s 2S1/2 transition to be 0.91 ± 0.04 ns, which compares well with our result of 0.996 ns. Correspondingly, the measured f value for this 2–8 transition is 0.130 ± 0.006 and our calculated result is 0.150. However, determination of this f value by several authors differ by up to a factor of 2, as shown in table 1 of Schectman et al. (1998). Similarly, their measured τ for the 3s2 5s 2S1/2 level is 1.99 ± 0.12 ns, in close agreement with our result of 1.865 ns and the calculation of 2.501 ns by Hibbert, Ojha & Stafford (1992). However, in a private correspondence to Schectman et al. (1998), Hibbert estimated τ to be 2.36 ns from improved calculations, and this improves the agreement between the theoretical results. Finally, we also note that for this level apart from the dominant 1–16 and 2–16 (3s2 3p 2P|$^o_{1/2,3/2}$|–3s2 5s 2S1/2) E1 transitions, the contributions of the 10–16 and 11–16 (3s2 4p 2P|$^o_{1/2,3/2}$|–3s2 5s 2S1/2) E1 are also significant, as mentioned by Schectman et al. (1998).
The other measurements of τ available are by Calamai, Smith & Bergeson (1993) for the 3s 3p24P1/2, 3/2, 5/2 levels, which are 104 ± 16, 811 ± 77 and 406 ± 33 μs, respectively. However, our corresponding theoretical results for these levels (251, 8004 and 3391 μs) are overestimated by up to an order of magnitude. The dominant contributing E1 transitions for these levels are 2–3, 2–4 and 2–5 for which the f values are 1.15 × 10−6, 1.17 × 10−7 and 4.41 × 10−7, respectively, i.e. all transitions are very weak and for these there are large variations among different calculations, as discussed in Section 3. The other partial reason for the large discrepancies is the comparative inaccuracy of our calculated energy for level 2 (3s2 3p 2P|$^o_{3/2}$|), as discussed in Section 2 and shown in Table 1. Finally, Bashkin et al. (1980) have made beam foil measurements of τ for the (3s2) 4p and 4f levels. Their measured τ of 9.1 ± 0.5 and 3.4 ± 0.3 ns compare well with our corresponding calculations of 8.9 and 3.9 ns.
5 COLLISION STRENGTHS
For the calculations of Ω, we have employed the Dirac Atomic R-matrix Code (darc) of P. H. Norrington and I. P. Grant, available at the website http://web.am.qub.ac.uk/DARC/. This is a relativistic version of the standard R-matrix code. Since the code is based on the jj coupling scheme (i.e. including fine structure) the size of the Hamiltonian increases in a calculation, but it (generally) leads to higher accuracy (for Ω and subsequently ϒ), especially for transitions among the fine-structure levels of a state, because resonances through the energies of degenerating levels are also taken into account. However, because Si ii is only moderately heavy and degeneracy among its levels is not large (see Table 1) the results obtained should be comparable with those from the standard R-matrix code (Berrington et al. 1995), provided the input parameters are similar.
The R-matrix radius adopted for Si ii is 36.8 a.u., and 56 continuum orbitals have been included for each channel angular momentum in the expansion of the wavefunction. This large expansion is computationally more demanding as the corresponding size of the Hamiltonian matrix is 15 154. However, it allows us to compute Ω up to an energy of 13 Ryd, or equivalently values of effective collision strength ϒ (see Section 6) up to Te = 6.0 × 105 K, more than an order of magnitude higher than the temperature of maximum abundance in ionization equilibrium, i.e. 20 000 K (Bryans, Landi & Savin 2009). The maximum number of channels for a partial wave is 268 and all partial waves with angular momentum J ≤ 40 are included.
Inclusion of a large range of partial waves ensures convergence of Ω for all forbidden and intercombination transitions, and at all energies. However, for some allowed transitions a larger range is preferable because Ω are not fully converged, particularly at higher energies. We demonstrate the variation of Ω in Fig. 1(a–c) at three energies (2, 6 and 10 Ryd) and for three transitions, namely 1–12 (3s2 3p 2P|$^o_{1/2}$|–3s2 3d 2D3/2), 2–13 (3s2 3p 2P|$^o_{3/2}$|–3s2 3d 2D5/2) and 2–15 (3s2 3p 2P|$^o_{3/2}$|–3s 3p22P3/2). It may be seen in these figures that Ω have (almost) converged up to an energy of 6 Ryd, but not at the higher values. To improve the accuracy of Ω at such energies, i.e. to account for higher neglected partial waves, we have included a top-up, based on the Coulomb–Bethe approximation of Burgess & Sheorey (1974). Furthermore, we have also included such contributions for forbidden transitions, based on geometric series, but these are small.
In Table 4 we list our values of Ω for transitions from the levels of the ground state (3s2 3p 2P|$^o_{1/2,3/2}$|) of Si ii at three energies of 2, 6 and 10 Ryd. The indices used to represent the levels of a transition correspond to those defined in Table 1. Similar results are not available from the work of Bautista et al. (2009), but Tayal (2008) has reported values of Ω in the 2–10 Ryd energy range. In Fig. 2 we compare our results of Ω with those of Tayal (2008) for three forbidden transitions, namely 1–10 (3s2 3p 2P|$^o_{1/2}$|–3s2 4p 2P|$^o_{1/2}$|), 1–21 (3s2 3p 2P|$^o_{1/2}$|–3s2 4f 2F|$^o_{7/2}$|) and 2–11 (3s2 3p 2P|$^o_{3/2}$|–3s2 4p 2P|$^o_{3/2}$|). For all these (and many other) transitions, Ω have fully converged within our partial waves range of J ≤ 40. Tayal (2008) included partial waves with J ≤ 36, comparable to ours and hence fully sufficient, yet his values of Ω are consistently lower by up to ∼23 per cent for all transitions. On the other hand, his Ω for allowed transitions are consistently higher by up to ∼25 per cent, as shown in Fig. 3 for three, namely 1–12 (3s2 3p 2P|$^o_{1/2}$|–3s2 3d 2D3/2), 2–13 (3s2 3p 2P|$^o_{3/2}$|–3s2 3d 2D5/2) and 2–15 (3s2 3p 2P|$^o_{3/2}$|–3s 3p22P3/2). For all these transitions, Ω have fully converged up to an energy of 6 Ryd as shown in Fig. 1, and yet the Tayal results for Ω are consistently higher at all energies. For these transitions the f values from our grasp and his mchf (Tayal 2007) calculations agree to better than 10 per cent, as shown in Table 3. However, in the scattering calculations Tayal (2008) has adopted slightly different wavefunctions, and therefore the f values obtained may not be the same as listed in Table 3. In spite of these being comparatively strong transitions, the f values do show significant variations as shown in table 3 of Bautista et al. (2009). Therefore, if the f values in the later calculations (Tayal 2008) are higher than so will be the values of Ω, but it cannot be confirmed with the limited information available.
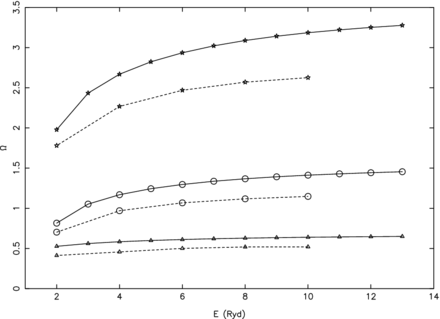
Comparison of collision strengths from our calculations from darc (continuous curves) and of Tayal (2008; broken curves) for the 1–10 (circles: 3s2 3p 2P|$^o_{1/2}$|–3s2 4p 2P|$^o_{1/2}$|), 1–21 (triangles: 3s2 3p 2P|$^o_{1/2}$|–3s2 4f 2F|$^o_{7/2}$|) and 2–11 (stars: 3s2 3p 2P|$^o_{3/2}$|–3s2 4p 2P|$^o_{3/2}$|) forbidden transitions of Si ii.
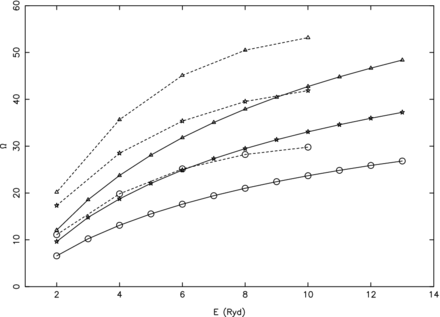
Comparison of collision strengths from our calculations from darc (continuous curves) and of Tayal (2008; broken curves) for the 1–12 (circles: 3s2 3p 2P|$^o_{1/2}$|–3s2 3d 2D3/2), 2 –13 (triangles: 3s2 3p 2P|$^o_{3/2}$|–3s2 3d 2D5/2) and 2–15 (stars: 3s2 3p 2P|$^o_{3/2}$|–3s 3p22P3/2) allowed transitions of Si ii.

Collision strengths for the 1–2 (3s2 3p 2P|$^o_{1/2}$|–3s2 3p 2P|$^o_{3/2}$|) transition of Si ii.
Collision strengths for transitions from the ground state 3s2 3p 2P|$^o_{1/2,3/2}$| levels of Si ii (a ± b ≡ a ×10±b).
| Transition . | Energy (Ryd) . | Transition . | Energy (Ryd) . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| i . | j . | 2 . | 6 . | 10 . | i . | j . | 2 . | 6 . | 10 . |
| 1 | 2 | 1.516−0 | 1.631−0 | 1.706−0 | .. | .. | ......... | ........ | ......... |
| 1 | 3 | 1.696−1 | 3.269−2 | 1.398−2 | 2 | 3 | 1.152−1 | 2.129−2 | 9.081−3 |
| 1 | 4 | 2.491−1 | 4.744−2 | 2.011−2 | 2 | 4 | 3.200−1 | 5.992−2 | 2.535−2 |
| 1 | 5 | 1.539−1 | 2.793−2 | 1.172−2 | 2 | 5 | 6.990−1 | 1.330−1 | 5.643−2 |
| 1 | 6 | 4.056−1 | 2.391−1 | 2.476−1 | 2 | 6 | 8.683−1 | 4.275−1 | 3.815−1 |
| 1 | 7 | 6.541−1 | 3.174−1 | 2.783−1 | 2 | 7 | 1.255−0 | 6.791−1 | 6.609−1 |
| 1 | 8 | 1.273−0 | 3.102−0 | 4.080−0 | 2 | 8 | 2.557−0 | 6.228−0 | 8.192−0 |
| 1 | 9 | 1.205−0 | 2.582−0 | 3.316−0 | 2 | 9 | 2.284−0 | 4.868−0 | 6.249−0 |
| 1 | 10 | 8.154−1 | 1.297−0 | 1.412−0 | 2 | 10 | 3.461−1 | 3.407−1 | 3.594−1 |
| 1 | 11 | 3.439−1 | 3.362−1 | 3.542−1 | 2 | 11 | 1.978−0 | 2.936−0 | 3.185−0 |
| 1 | 12 | 6.573−0 | 1.761+1 | 2.369+1 | 2 | 12 | 1.670−0 | 3.704−0 | 4.883−0 |
| 1 | 13 | 3.307−1 | 2.443−1 | 2.451−1 | 2 | 13 | 1.207+1 | 3.182+1 | 4.274+1 |
| 1 | 14 | 3.764−0 | 9.824−0 | 1.307+1 | 2 | 14 | 2.065−0 | 5.104−0 | 6.743−0 |
| 1 | 15 | 2.005−0 | 4.951−0 | 6.539−0 | 2 | 15 | 9.633−0 | 2.489+1 | 3.306+1 |
| 1 | 16 | 1.457−1 | 2.706−1 | 3.436−1 | 2 | 16 | 3.089−1 | 5.883−1 | 7.492−1 |
| 1 | 17 | 5.261−1 | 9.792−1 | 1.081−0 | 2 | 17 | 5.372−1 | 9.583−1 | 1.054−0 |
| 1 | 18 | 3.714−1 | 6.584−1 | 7.245−1 | 2 | 18 | 1.224−0 | 2.248−0 | 2.477−0 |
| 1 | 19 | 2.155−0 | 5.268−0 | 6.799−0 | 2 | 19 | 6.568−1 | 1.204−0 | 1.516−0 |
| 1 | 20 | 1.759−1 | 9.273−2 | 8.692−2 | 2 | 20 | 4.052−0 | 9.640−0 | 1.241+1 |
| 1 | 21 | 5.271−1 | 6.112−1 | 6.402−1 | 2 | 21 | 2.485−1 | 2.370−1 | 2.449−1 |
| 1 | 22 | 7.310−2 | 4.255−2 | 4.174−2 | 2 | 22 | 9.650−1 | 1.093−0 | 1.143−0 |
| 1 | 23 | 2.382−1 | 3.223−1 | 3.465−1 | 2 | 23 | 1.253−1 | 8.869−2 | 9.190−2 |
| 1 | 24 | 1.243−1 | 8.662−2 | 8.929−2 | 2 | 24 | 6.017−1 | 7.337−1 | 7.854−1 |
| 1 | 25 | 1.203−1 | 1.588−2 | 6.042−3 | 2 | 25 | 3.850−2 | 4.815−3 | 1.833−3 |
| 1 | 26 | 1.391−1 | 1.828−2 | 6.923−3 | 2 | 26 | 9.898−2 | 1.268−2 | 4.790−3 |
| 1 | 27 | 1.073−1 | 1.393−2 | 5.245−3 | 2 | 27 | 2.100−1 | 2.724−2 | 1.026−2 |
| 1 | 28 | 6.196−3 | 3.973−4 | 1.111−4 | 2 | 28 | 3.904−1 | 5.103−2 | 1.925−2 |
| 1 | 29 | 9.823−1 | 1.951−0 | 2.383−0 | 2 | 29 | 3.478−1 | 4.573−1 | 5.369−1 |
| 1 | 30 | 1.243−1 | 5.176−2 | 4.463−2 | 2 | 30 | 1.874−0 | 3.566−0 | 4.342−0 |
| 1 | 31 | 5.319−2 | 2.065−2 | 1.980−2 | 2 | 31 | 6.904−1 | 6.004−1 | 6.084−1 |
| 1 | 32 | 3.785−1 | 3.400−1 | 3.453−1 | 2 | 32 | 1.776−1 | 1.247−1 | 1.252−1 |
| 1 | 33 | 2.593−2 | 1.179−2 | 1.032−2 | 2 | 33 | 2.250−2 | 7.269−3 | 6.029−3 |
| 1 | 34 | 1.026−2 | 2.449−3 | 1.896−3 | 2 | 34 | 5.032−2 | 2.150−2 | 1.866−2 |
| 1 | 35 | 1.514−1 | 1.607−2 | 5.748−3 | 2 | 35 | 1.230−1 | 1.337−2 | 4.742−3 |
| 1 | 36 | 5.758−2 | 6.034−3 | 2.138−3 | 2 | 36 | 1.254−1 | 1.360−2 | 4.862−3 |
| 1 | 37 | 1.173−2 | 1.220−3 | 4.165−4 | 2 | 37 | 7.953−2 | 8.582−3 | 3.075−3 |
| 1 | 38 | 5.914−2 | 5.047−3 | 1.728−3 | 2 | 38 | 6.633−2 | 5.548−3 | 1.899−3 |
| 1 | 39 | 9.609−2 | 8.052−3 | 2.742−3 | 2 | 39 | 1.543−1 | 1.310−2 | 4.475−3 |
| 1 | 40 | 1.094−1 | 8.938−3 | 3.010−3 | 2 | 40 | 2.663−1 | 2.274−2 | 7.764−3 |
| 1 | 41 | 1.155−1 | 9.352−3 | 3.155−3 | 2 | 41 | 3.872−1 | 3.295−2 | 1.123−2 |
| 1 | 42 | 5.327−3 | 9.484−4 | 4.667−4 | 2 | 42 | 1.077−2 | 1.753−3 | 7.740−4 |
| 1 | 43 | 3.082−1 | 6.842−1 | 7.961−1 | 2 | 43 | 4.635−1 | 9.708−1 | 1.110−0 |
| 1 | 44 | 7.311−2 | 1.339−1 | 1.462−1 | 2 | 44 | 3.127−1 | 6.934−1 | 8.066−1 |
| 1 | 45 | 5.074−1 | 1.401−0 | 1.688−0 | 2 | 45 | 3.303−1 | 4.249−1 | 5.009−1 |
| 1 | 46 | 1.420−1 | 1.593−2 | 1.077−2 | 2 | 46 | 9.718−1 | 2.416−0 | 2.905−0 |
| 1 | 47 | 9.112−2 | 4.021−2 | 2.772−2 | 2 | 47 | 1.843−1 | 1.104−1 | 8.074−2 |
| 1 | 48 | 6.162−2 | 4.431−2 | 3.334−2 | 2 | 48 | 1.225−1 | 5.683−2 | 3.953−2 |
| 1 | 49 | 3.357−2 | 3.645−2 | 4.160−2 | 2 | 49 | 2.274−1 | 2.521−1 | 1.961−1 |
| 1 | 50 | 2.314−1 | 2.571−1 | 2.003−1 | 2 | 50 | 2.910−1 | 3.204−1 | 2.754−1 |
| 1 | 51 | 3.930−1 | 4.732−2 | 2.775−2 | 2 | 51 | 2.018−0 | 1.922−0 | 1.579−0 |
| 1 | 52 | 1.008−0 | 1.097−0 | 9.057−1 | 2 | 52 | 7.970−1 | 3.752−1 | 2.953−1 |
| 1 | 53 | 5.496−1 | 7.028−1 | 5.942−1 | 2 | 53 | 5.946−1 | 7.088−1 | 5.929−1 |
| 1 | 54 | 4.033−1 | 4.761−1 | 3.982−1 | 2 | 54 | 1.313−0 | 1.644−0 | 1.385−0 |
| 1 | 55 | 9.842−2 | 2.839−1 | 3.168−1 | 2 | 55 | 9.009−2 | 1.494−1 | 1.637−1 |
| 1 | 56 | 8.456−2 | 1.378−1 | 1.520−1 | 2 | 56 | 2.935−1 | 7.296−1 | 8.093−1 |
| Transition . | Energy (Ryd) . | Transition . | Energy (Ryd) . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| i . | j . | 2 . | 6 . | 10 . | i . | j . | 2 . | 6 . | 10 . |
| 1 | 2 | 1.516−0 | 1.631−0 | 1.706−0 | .. | .. | ......... | ........ | ......... |
| 1 | 3 | 1.696−1 | 3.269−2 | 1.398−2 | 2 | 3 | 1.152−1 | 2.129−2 | 9.081−3 |
| 1 | 4 | 2.491−1 | 4.744−2 | 2.011−2 | 2 | 4 | 3.200−1 | 5.992−2 | 2.535−2 |
| 1 | 5 | 1.539−1 | 2.793−2 | 1.172−2 | 2 | 5 | 6.990−1 | 1.330−1 | 5.643−2 |
| 1 | 6 | 4.056−1 | 2.391−1 | 2.476−1 | 2 | 6 | 8.683−1 | 4.275−1 | 3.815−1 |
| 1 | 7 | 6.541−1 | 3.174−1 | 2.783−1 | 2 | 7 | 1.255−0 | 6.791−1 | 6.609−1 |
| 1 | 8 | 1.273−0 | 3.102−0 | 4.080−0 | 2 | 8 | 2.557−0 | 6.228−0 | 8.192−0 |
| 1 | 9 | 1.205−0 | 2.582−0 | 3.316−0 | 2 | 9 | 2.284−0 | 4.868−0 | 6.249−0 |
| 1 | 10 | 8.154−1 | 1.297−0 | 1.412−0 | 2 | 10 | 3.461−1 | 3.407−1 | 3.594−1 |
| 1 | 11 | 3.439−1 | 3.362−1 | 3.542−1 | 2 | 11 | 1.978−0 | 2.936−0 | 3.185−0 |
| 1 | 12 | 6.573−0 | 1.761+1 | 2.369+1 | 2 | 12 | 1.670−0 | 3.704−0 | 4.883−0 |
| 1 | 13 | 3.307−1 | 2.443−1 | 2.451−1 | 2 | 13 | 1.207+1 | 3.182+1 | 4.274+1 |
| 1 | 14 | 3.764−0 | 9.824−0 | 1.307+1 | 2 | 14 | 2.065−0 | 5.104−0 | 6.743−0 |
| 1 | 15 | 2.005−0 | 4.951−0 | 6.539−0 | 2 | 15 | 9.633−0 | 2.489+1 | 3.306+1 |
| 1 | 16 | 1.457−1 | 2.706−1 | 3.436−1 | 2 | 16 | 3.089−1 | 5.883−1 | 7.492−1 |
| 1 | 17 | 5.261−1 | 9.792−1 | 1.081−0 | 2 | 17 | 5.372−1 | 9.583−1 | 1.054−0 |
| 1 | 18 | 3.714−1 | 6.584−1 | 7.245−1 | 2 | 18 | 1.224−0 | 2.248−0 | 2.477−0 |
| 1 | 19 | 2.155−0 | 5.268−0 | 6.799−0 | 2 | 19 | 6.568−1 | 1.204−0 | 1.516−0 |
| 1 | 20 | 1.759−1 | 9.273−2 | 8.692−2 | 2 | 20 | 4.052−0 | 9.640−0 | 1.241+1 |
| 1 | 21 | 5.271−1 | 6.112−1 | 6.402−1 | 2 | 21 | 2.485−1 | 2.370−1 | 2.449−1 |
| 1 | 22 | 7.310−2 | 4.255−2 | 4.174−2 | 2 | 22 | 9.650−1 | 1.093−0 | 1.143−0 |
| 1 | 23 | 2.382−1 | 3.223−1 | 3.465−1 | 2 | 23 | 1.253−1 | 8.869−2 | 9.190−2 |
| 1 | 24 | 1.243−1 | 8.662−2 | 8.929−2 | 2 | 24 | 6.017−1 | 7.337−1 | 7.854−1 |
| 1 | 25 | 1.203−1 | 1.588−2 | 6.042−3 | 2 | 25 | 3.850−2 | 4.815−3 | 1.833−3 |
| 1 | 26 | 1.391−1 | 1.828−2 | 6.923−3 | 2 | 26 | 9.898−2 | 1.268−2 | 4.790−3 |
| 1 | 27 | 1.073−1 | 1.393−2 | 5.245−3 | 2 | 27 | 2.100−1 | 2.724−2 | 1.026−2 |
| 1 | 28 | 6.196−3 | 3.973−4 | 1.111−4 | 2 | 28 | 3.904−1 | 5.103−2 | 1.925−2 |
| 1 | 29 | 9.823−1 | 1.951−0 | 2.383−0 | 2 | 29 | 3.478−1 | 4.573−1 | 5.369−1 |
| 1 | 30 | 1.243−1 | 5.176−2 | 4.463−2 | 2 | 30 | 1.874−0 | 3.566−0 | 4.342−0 |
| 1 | 31 | 5.319−2 | 2.065−2 | 1.980−2 | 2 | 31 | 6.904−1 | 6.004−1 | 6.084−1 |
| 1 | 32 | 3.785−1 | 3.400−1 | 3.453−1 | 2 | 32 | 1.776−1 | 1.247−1 | 1.252−1 |
| 1 | 33 | 2.593−2 | 1.179−2 | 1.032−2 | 2 | 33 | 2.250−2 | 7.269−3 | 6.029−3 |
| 1 | 34 | 1.026−2 | 2.449−3 | 1.896−3 | 2 | 34 | 5.032−2 | 2.150−2 | 1.866−2 |
| 1 | 35 | 1.514−1 | 1.607−2 | 5.748−3 | 2 | 35 | 1.230−1 | 1.337−2 | 4.742−3 |
| 1 | 36 | 5.758−2 | 6.034−3 | 2.138−3 | 2 | 36 | 1.254−1 | 1.360−2 | 4.862−3 |
| 1 | 37 | 1.173−2 | 1.220−3 | 4.165−4 | 2 | 37 | 7.953−2 | 8.582−3 | 3.075−3 |
| 1 | 38 | 5.914−2 | 5.047−3 | 1.728−3 | 2 | 38 | 6.633−2 | 5.548−3 | 1.899−3 |
| 1 | 39 | 9.609−2 | 8.052−3 | 2.742−3 | 2 | 39 | 1.543−1 | 1.310−2 | 4.475−3 |
| 1 | 40 | 1.094−1 | 8.938−3 | 3.010−3 | 2 | 40 | 2.663−1 | 2.274−2 | 7.764−3 |
| 1 | 41 | 1.155−1 | 9.352−3 | 3.155−3 | 2 | 41 | 3.872−1 | 3.295−2 | 1.123−2 |
| 1 | 42 | 5.327−3 | 9.484−4 | 4.667−4 | 2 | 42 | 1.077−2 | 1.753−3 | 7.740−4 |
| 1 | 43 | 3.082−1 | 6.842−1 | 7.961−1 | 2 | 43 | 4.635−1 | 9.708−1 | 1.110−0 |
| 1 | 44 | 7.311−2 | 1.339−1 | 1.462−1 | 2 | 44 | 3.127−1 | 6.934−1 | 8.066−1 |
| 1 | 45 | 5.074−1 | 1.401−0 | 1.688−0 | 2 | 45 | 3.303−1 | 4.249−1 | 5.009−1 |
| 1 | 46 | 1.420−1 | 1.593−2 | 1.077−2 | 2 | 46 | 9.718−1 | 2.416−0 | 2.905−0 |
| 1 | 47 | 9.112−2 | 4.021−2 | 2.772−2 | 2 | 47 | 1.843−1 | 1.104−1 | 8.074−2 |
| 1 | 48 | 6.162−2 | 4.431−2 | 3.334−2 | 2 | 48 | 1.225−1 | 5.683−2 | 3.953−2 |
| 1 | 49 | 3.357−2 | 3.645−2 | 4.160−2 | 2 | 49 | 2.274−1 | 2.521−1 | 1.961−1 |
| 1 | 50 | 2.314−1 | 2.571−1 | 2.003−1 | 2 | 50 | 2.910−1 | 3.204−1 | 2.754−1 |
| 1 | 51 | 3.930−1 | 4.732−2 | 2.775−2 | 2 | 51 | 2.018−0 | 1.922−0 | 1.579−0 |
| 1 | 52 | 1.008−0 | 1.097−0 | 9.057−1 | 2 | 52 | 7.970−1 | 3.752−1 | 2.953−1 |
| 1 | 53 | 5.496−1 | 7.028−1 | 5.942−1 | 2 | 53 | 5.946−1 | 7.088−1 | 5.929−1 |
| 1 | 54 | 4.033−1 | 4.761−1 | 3.982−1 | 2 | 54 | 1.313−0 | 1.644−0 | 1.385−0 |
| 1 | 55 | 9.842−2 | 2.839−1 | 3.168−1 | 2 | 55 | 9.009−2 | 1.494−1 | 1.637−1 |
| 1 | 56 | 8.456−2 | 1.378−1 | 1.520−1 | 2 | 56 | 2.935−1 | 7.296−1 | 8.093−1 |
Collision strengths for transitions from the ground state 3s2 3p 2P|$^o_{1/2,3/2}$| levels of Si ii (a ± b ≡ a ×10±b).
| Transition . | Energy (Ryd) . | Transition . | Energy (Ryd) . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| i . | j . | 2 . | 6 . | 10 . | i . | j . | 2 . | 6 . | 10 . |
| 1 | 2 | 1.516−0 | 1.631−0 | 1.706−0 | .. | .. | ......... | ........ | ......... |
| 1 | 3 | 1.696−1 | 3.269−2 | 1.398−2 | 2 | 3 | 1.152−1 | 2.129−2 | 9.081−3 |
| 1 | 4 | 2.491−1 | 4.744−2 | 2.011−2 | 2 | 4 | 3.200−1 | 5.992−2 | 2.535−2 |
| 1 | 5 | 1.539−1 | 2.793−2 | 1.172−2 | 2 | 5 | 6.990−1 | 1.330−1 | 5.643−2 |
| 1 | 6 | 4.056−1 | 2.391−1 | 2.476−1 | 2 | 6 | 8.683−1 | 4.275−1 | 3.815−1 |
| 1 | 7 | 6.541−1 | 3.174−1 | 2.783−1 | 2 | 7 | 1.255−0 | 6.791−1 | 6.609−1 |
| 1 | 8 | 1.273−0 | 3.102−0 | 4.080−0 | 2 | 8 | 2.557−0 | 6.228−0 | 8.192−0 |
| 1 | 9 | 1.205−0 | 2.582−0 | 3.316−0 | 2 | 9 | 2.284−0 | 4.868−0 | 6.249−0 |
| 1 | 10 | 8.154−1 | 1.297−0 | 1.412−0 | 2 | 10 | 3.461−1 | 3.407−1 | 3.594−1 |
| 1 | 11 | 3.439−1 | 3.362−1 | 3.542−1 | 2 | 11 | 1.978−0 | 2.936−0 | 3.185−0 |
| 1 | 12 | 6.573−0 | 1.761+1 | 2.369+1 | 2 | 12 | 1.670−0 | 3.704−0 | 4.883−0 |
| 1 | 13 | 3.307−1 | 2.443−1 | 2.451−1 | 2 | 13 | 1.207+1 | 3.182+1 | 4.274+1 |
| 1 | 14 | 3.764−0 | 9.824−0 | 1.307+1 | 2 | 14 | 2.065−0 | 5.104−0 | 6.743−0 |
| 1 | 15 | 2.005−0 | 4.951−0 | 6.539−0 | 2 | 15 | 9.633−0 | 2.489+1 | 3.306+1 |
| 1 | 16 | 1.457−1 | 2.706−1 | 3.436−1 | 2 | 16 | 3.089−1 | 5.883−1 | 7.492−1 |
| 1 | 17 | 5.261−1 | 9.792−1 | 1.081−0 | 2 | 17 | 5.372−1 | 9.583−1 | 1.054−0 |
| 1 | 18 | 3.714−1 | 6.584−1 | 7.245−1 | 2 | 18 | 1.224−0 | 2.248−0 | 2.477−0 |
| 1 | 19 | 2.155−0 | 5.268−0 | 6.799−0 | 2 | 19 | 6.568−1 | 1.204−0 | 1.516−0 |
| 1 | 20 | 1.759−1 | 9.273−2 | 8.692−2 | 2 | 20 | 4.052−0 | 9.640−0 | 1.241+1 |
| 1 | 21 | 5.271−1 | 6.112−1 | 6.402−1 | 2 | 21 | 2.485−1 | 2.370−1 | 2.449−1 |
| 1 | 22 | 7.310−2 | 4.255−2 | 4.174−2 | 2 | 22 | 9.650−1 | 1.093−0 | 1.143−0 |
| 1 | 23 | 2.382−1 | 3.223−1 | 3.465−1 | 2 | 23 | 1.253−1 | 8.869−2 | 9.190−2 |
| 1 | 24 | 1.243−1 | 8.662−2 | 8.929−2 | 2 | 24 | 6.017−1 | 7.337−1 | 7.854−1 |
| 1 | 25 | 1.203−1 | 1.588−2 | 6.042−3 | 2 | 25 | 3.850−2 | 4.815−3 | 1.833−3 |
| 1 | 26 | 1.391−1 | 1.828−2 | 6.923−3 | 2 | 26 | 9.898−2 | 1.268−2 | 4.790−3 |
| 1 | 27 | 1.073−1 | 1.393−2 | 5.245−3 | 2 | 27 | 2.100−1 | 2.724−2 | 1.026−2 |
| 1 | 28 | 6.196−3 | 3.973−4 | 1.111−4 | 2 | 28 | 3.904−1 | 5.103−2 | 1.925−2 |
| 1 | 29 | 9.823−1 | 1.951−0 | 2.383−0 | 2 | 29 | 3.478−1 | 4.573−1 | 5.369−1 |
| 1 | 30 | 1.243−1 | 5.176−2 | 4.463−2 | 2 | 30 | 1.874−0 | 3.566−0 | 4.342−0 |
| 1 | 31 | 5.319−2 | 2.065−2 | 1.980−2 | 2 | 31 | 6.904−1 | 6.004−1 | 6.084−1 |
| 1 | 32 | 3.785−1 | 3.400−1 | 3.453−1 | 2 | 32 | 1.776−1 | 1.247−1 | 1.252−1 |
| 1 | 33 | 2.593−2 | 1.179−2 | 1.032−2 | 2 | 33 | 2.250−2 | 7.269−3 | 6.029−3 |
| 1 | 34 | 1.026−2 | 2.449−3 | 1.896−3 | 2 | 34 | 5.032−2 | 2.150−2 | 1.866−2 |
| 1 | 35 | 1.514−1 | 1.607−2 | 5.748−3 | 2 | 35 | 1.230−1 | 1.337−2 | 4.742−3 |
| 1 | 36 | 5.758−2 | 6.034−3 | 2.138−3 | 2 | 36 | 1.254−1 | 1.360−2 | 4.862−3 |
| 1 | 37 | 1.173−2 | 1.220−3 | 4.165−4 | 2 | 37 | 7.953−2 | 8.582−3 | 3.075−3 |
| 1 | 38 | 5.914−2 | 5.047−3 | 1.728−3 | 2 | 38 | 6.633−2 | 5.548−3 | 1.899−3 |
| 1 | 39 | 9.609−2 | 8.052−3 | 2.742−3 | 2 | 39 | 1.543−1 | 1.310−2 | 4.475−3 |
| 1 | 40 | 1.094−1 | 8.938−3 | 3.010−3 | 2 | 40 | 2.663−1 | 2.274−2 | 7.764−3 |
| 1 | 41 | 1.155−1 | 9.352−3 | 3.155−3 | 2 | 41 | 3.872−1 | 3.295−2 | 1.123−2 |
| 1 | 42 | 5.327−3 | 9.484−4 | 4.667−4 | 2 | 42 | 1.077−2 | 1.753−3 | 7.740−4 |
| 1 | 43 | 3.082−1 | 6.842−1 | 7.961−1 | 2 | 43 | 4.635−1 | 9.708−1 | 1.110−0 |
| 1 | 44 | 7.311−2 | 1.339−1 | 1.462−1 | 2 | 44 | 3.127−1 | 6.934−1 | 8.066−1 |
| 1 | 45 | 5.074−1 | 1.401−0 | 1.688−0 | 2 | 45 | 3.303−1 | 4.249−1 | 5.009−1 |
| 1 | 46 | 1.420−1 | 1.593−2 | 1.077−2 | 2 | 46 | 9.718−1 | 2.416−0 | 2.905−0 |
| 1 | 47 | 9.112−2 | 4.021−2 | 2.772−2 | 2 | 47 | 1.843−1 | 1.104−1 | 8.074−2 |
| 1 | 48 | 6.162−2 | 4.431−2 | 3.334−2 | 2 | 48 | 1.225−1 | 5.683−2 | 3.953−2 |
| 1 | 49 | 3.357−2 | 3.645−2 | 4.160−2 | 2 | 49 | 2.274−1 | 2.521−1 | 1.961−1 |
| 1 | 50 | 2.314−1 | 2.571−1 | 2.003−1 | 2 | 50 | 2.910−1 | 3.204−1 | 2.754−1 |
| 1 | 51 | 3.930−1 | 4.732−2 | 2.775−2 | 2 | 51 | 2.018−0 | 1.922−0 | 1.579−0 |
| 1 | 52 | 1.008−0 | 1.097−0 | 9.057−1 | 2 | 52 | 7.970−1 | 3.752−1 | 2.953−1 |
| 1 | 53 | 5.496−1 | 7.028−1 | 5.942−1 | 2 | 53 | 5.946−1 | 7.088−1 | 5.929−1 |
| 1 | 54 | 4.033−1 | 4.761−1 | 3.982−1 | 2 | 54 | 1.313−0 | 1.644−0 | 1.385−0 |
| 1 | 55 | 9.842−2 | 2.839−1 | 3.168−1 | 2 | 55 | 9.009−2 | 1.494−1 | 1.637−1 |
| 1 | 56 | 8.456−2 | 1.378−1 | 1.520−1 | 2 | 56 | 2.935−1 | 7.296−1 | 8.093−1 |
| Transition . | Energy (Ryd) . | Transition . | Energy (Ryd) . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| i . | j . | 2 . | 6 . | 10 . | i . | j . | 2 . | 6 . | 10 . |
| 1 | 2 | 1.516−0 | 1.631−0 | 1.706−0 | .. | .. | ......... | ........ | ......... |
| 1 | 3 | 1.696−1 | 3.269−2 | 1.398−2 | 2 | 3 | 1.152−1 | 2.129−2 | 9.081−3 |
| 1 | 4 | 2.491−1 | 4.744−2 | 2.011−2 | 2 | 4 | 3.200−1 | 5.992−2 | 2.535−2 |
| 1 | 5 | 1.539−1 | 2.793−2 | 1.172−2 | 2 | 5 | 6.990−1 | 1.330−1 | 5.643−2 |
| 1 | 6 | 4.056−1 | 2.391−1 | 2.476−1 | 2 | 6 | 8.683−1 | 4.275−1 | 3.815−1 |
| 1 | 7 | 6.541−1 | 3.174−1 | 2.783−1 | 2 | 7 | 1.255−0 | 6.791−1 | 6.609−1 |
| 1 | 8 | 1.273−0 | 3.102−0 | 4.080−0 | 2 | 8 | 2.557−0 | 6.228−0 | 8.192−0 |
| 1 | 9 | 1.205−0 | 2.582−0 | 3.316−0 | 2 | 9 | 2.284−0 | 4.868−0 | 6.249−0 |
| 1 | 10 | 8.154−1 | 1.297−0 | 1.412−0 | 2 | 10 | 3.461−1 | 3.407−1 | 3.594−1 |
| 1 | 11 | 3.439−1 | 3.362−1 | 3.542−1 | 2 | 11 | 1.978−0 | 2.936−0 | 3.185−0 |
| 1 | 12 | 6.573−0 | 1.761+1 | 2.369+1 | 2 | 12 | 1.670−0 | 3.704−0 | 4.883−0 |
| 1 | 13 | 3.307−1 | 2.443−1 | 2.451−1 | 2 | 13 | 1.207+1 | 3.182+1 | 4.274+1 |
| 1 | 14 | 3.764−0 | 9.824−0 | 1.307+1 | 2 | 14 | 2.065−0 | 5.104−0 | 6.743−0 |
| 1 | 15 | 2.005−0 | 4.951−0 | 6.539−0 | 2 | 15 | 9.633−0 | 2.489+1 | 3.306+1 |
| 1 | 16 | 1.457−1 | 2.706−1 | 3.436−1 | 2 | 16 | 3.089−1 | 5.883−1 | 7.492−1 |
| 1 | 17 | 5.261−1 | 9.792−1 | 1.081−0 | 2 | 17 | 5.372−1 | 9.583−1 | 1.054−0 |
| 1 | 18 | 3.714−1 | 6.584−1 | 7.245−1 | 2 | 18 | 1.224−0 | 2.248−0 | 2.477−0 |
| 1 | 19 | 2.155−0 | 5.268−0 | 6.799−0 | 2 | 19 | 6.568−1 | 1.204−0 | 1.516−0 |
| 1 | 20 | 1.759−1 | 9.273−2 | 8.692−2 | 2 | 20 | 4.052−0 | 9.640−0 | 1.241+1 |
| 1 | 21 | 5.271−1 | 6.112−1 | 6.402−1 | 2 | 21 | 2.485−1 | 2.370−1 | 2.449−1 |
| 1 | 22 | 7.310−2 | 4.255−2 | 4.174−2 | 2 | 22 | 9.650−1 | 1.093−0 | 1.143−0 |
| 1 | 23 | 2.382−1 | 3.223−1 | 3.465−1 | 2 | 23 | 1.253−1 | 8.869−2 | 9.190−2 |
| 1 | 24 | 1.243−1 | 8.662−2 | 8.929−2 | 2 | 24 | 6.017−1 | 7.337−1 | 7.854−1 |
| 1 | 25 | 1.203−1 | 1.588−2 | 6.042−3 | 2 | 25 | 3.850−2 | 4.815−3 | 1.833−3 |
| 1 | 26 | 1.391−1 | 1.828−2 | 6.923−3 | 2 | 26 | 9.898−2 | 1.268−2 | 4.790−3 |
| 1 | 27 | 1.073−1 | 1.393−2 | 5.245−3 | 2 | 27 | 2.100−1 | 2.724−2 | 1.026−2 |
| 1 | 28 | 6.196−3 | 3.973−4 | 1.111−4 | 2 | 28 | 3.904−1 | 5.103−2 | 1.925−2 |
| 1 | 29 | 9.823−1 | 1.951−0 | 2.383−0 | 2 | 29 | 3.478−1 | 4.573−1 | 5.369−1 |
| 1 | 30 | 1.243−1 | 5.176−2 | 4.463−2 | 2 | 30 | 1.874−0 | 3.566−0 | 4.342−0 |
| 1 | 31 | 5.319−2 | 2.065−2 | 1.980−2 | 2 | 31 | 6.904−1 | 6.004−1 | 6.084−1 |
| 1 | 32 | 3.785−1 | 3.400−1 | 3.453−1 | 2 | 32 | 1.776−1 | 1.247−1 | 1.252−1 |
| 1 | 33 | 2.593−2 | 1.179−2 | 1.032−2 | 2 | 33 | 2.250−2 | 7.269−3 | 6.029−3 |
| 1 | 34 | 1.026−2 | 2.449−3 | 1.896−3 | 2 | 34 | 5.032−2 | 2.150−2 | 1.866−2 |
| 1 | 35 | 1.514−1 | 1.607−2 | 5.748−3 | 2 | 35 | 1.230−1 | 1.337−2 | 4.742−3 |
| 1 | 36 | 5.758−2 | 6.034−3 | 2.138−3 | 2 | 36 | 1.254−1 | 1.360−2 | 4.862−3 |
| 1 | 37 | 1.173−2 | 1.220−3 | 4.165−4 | 2 | 37 | 7.953−2 | 8.582−3 | 3.075−3 |
| 1 | 38 | 5.914−2 | 5.047−3 | 1.728−3 | 2 | 38 | 6.633−2 | 5.548−3 | 1.899−3 |
| 1 | 39 | 9.609−2 | 8.052−3 | 2.742−3 | 2 | 39 | 1.543−1 | 1.310−2 | 4.475−3 |
| 1 | 40 | 1.094−1 | 8.938−3 | 3.010−3 | 2 | 40 | 2.663−1 | 2.274−2 | 7.764−3 |
| 1 | 41 | 1.155−1 | 9.352−3 | 3.155−3 | 2 | 41 | 3.872−1 | 3.295−2 | 1.123−2 |
| 1 | 42 | 5.327−3 | 9.484−4 | 4.667−4 | 2 | 42 | 1.077−2 | 1.753−3 | 7.740−4 |
| 1 | 43 | 3.082−1 | 6.842−1 | 7.961−1 | 2 | 43 | 4.635−1 | 9.708−1 | 1.110−0 |
| 1 | 44 | 7.311−2 | 1.339−1 | 1.462−1 | 2 | 44 | 3.127−1 | 6.934−1 | 8.066−1 |
| 1 | 45 | 5.074−1 | 1.401−0 | 1.688−0 | 2 | 45 | 3.303−1 | 4.249−1 | 5.009−1 |
| 1 | 46 | 1.420−1 | 1.593−2 | 1.077−2 | 2 | 46 | 9.718−1 | 2.416−0 | 2.905−0 |
| 1 | 47 | 9.112−2 | 4.021−2 | 2.772−2 | 2 | 47 | 1.843−1 | 1.104−1 | 8.074−2 |
| 1 | 48 | 6.162−2 | 4.431−2 | 3.334−2 | 2 | 48 | 1.225−1 | 5.683−2 | 3.953−2 |
| 1 | 49 | 3.357−2 | 3.645−2 | 4.160−2 | 2 | 49 | 2.274−1 | 2.521−1 | 1.961−1 |
| 1 | 50 | 2.314−1 | 2.571−1 | 2.003−1 | 2 | 50 | 2.910−1 | 3.204−1 | 2.754−1 |
| 1 | 51 | 3.930−1 | 4.732−2 | 2.775−2 | 2 | 51 | 2.018−0 | 1.922−0 | 1.579−0 |
| 1 | 52 | 1.008−0 | 1.097−0 | 9.057−1 | 2 | 52 | 7.970−1 | 3.752−1 | 2.953−1 |
| 1 | 53 | 5.496−1 | 7.028−1 | 5.942−1 | 2 | 53 | 5.946−1 | 7.088−1 | 5.929−1 |
| 1 | 54 | 4.033−1 | 4.761−1 | 3.982−1 | 2 | 54 | 1.313−0 | 1.644−0 | 1.385−0 |
| 1 | 55 | 9.842−2 | 2.839−1 | 3.168−1 | 2 | 55 | 9.009−2 | 1.494−1 | 1.637−1 |
| 1 | 56 | 8.456−2 | 1.378−1 | 1.520−1 | 2 | 56 | 2.935−1 | 7.296−1 | 8.093−1 |
6 EFFECTIVE COLLISION STRENGTHS
To resolve resonances, we have performed our calculations of Ω in a narrow energy mesh of 0.001 Ryd (at over ∼1500 energies) in the thresholds region. In Figs 4–6 we show resonances for three transitions, namely 1–2 (3s2 3p 2P|$^o_{1/2}$|–3s2 3p 2P|$^o_{3/2}$|), 2–4 (3s2 3p 2P|$^o_{3/2}$|–3s 3p24P3/2) and 2–7 (3s2 3p 2P|$^o_{3/2}$|–3s 3p22D5/2), which are forbidden, intercombination and allowed, respectively. Furthermore, these transitions have specifically been selected because both Tayal (2008) and Bautista et al. (2009) have shown resonances for these, and hence will facilitate us in understanding the differences in the corresponding results of ϒ. For the three transitions, the resonance structures are similar in all calculations, but their magnitude and background values (ΩB) differ slightly. While the ΩB of Tayal (2008) are on the higher side, those of Bautista et al. (2009) are lower, particularly at energies below 0.8 Ryd. We would like to stress here that their lower values of Ω are not due to the lower range of included partial waves (L ≤ 16), because at these energies J ≤ 15 are sufficient for convergence, as demonstrated in Fig. 1and also confirmed with our similar plots for all three transitions with J ≤ 10 and ≤ 20.
Our calculated values of ϒ are listed in Table 5 over a wide temperature range of log Te = 3.7–5.5 K, suitable for applications to a wide range of laboratory and astrophysical plasmas. Since ϒ is a slowly varying function of Te, corresponding data at any other temperature within this range can be easily interpolated, or may be requested from the first author. In Table 6, we compare our results of ϒ with those of Bautista et al. (2009), Tayal (2008) and Dufton & Kingston (1991) for transitions from the levels of the ground state 3s2 3p 2P|$^o_{1/2,3/2}$| to higher excited levels (but only up to 3s 3p22P3/2), and at three temperatures of 5000, 10 000 and 20 000 K. These transitions are the same as reported by Dufton & Kingston (1991). For a majority of transitions, the ϒ of Tayal (2008) are the highest, although they are also lower for a few, such as 1–8/10/11 and 2–8/11. The differences between their ϒ and the other calculations are up to 50 per cent. For all these transitions, the higher values of ϒ by Tayal are because of his corresponding higher values of Ω. We would like to stress here that both ourselves and Tayal have included a comparable large range of partial waves and hence Ω for all these transitions have fully converged.
Effective collision strengths for transitions in Si ii (a ± b ≡ a × 10±b). (For complete table see Supporting Information.)
| Transition . | Temperature (log Te, K) . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| i . | j . | 3.70 . | 3.90 . | 4.10 . | 4.30 . | 4.50 . | 4.70 . | 4.900 . | 5.10 . | 5.30 . | 5.50 . |
| 1 | 2 | 5.230+0 | 5.311+0 | 5.354+0 | 5.328+0 | 5.168+0 | 4.809+0 | 4.267+0 | 3.647+0 | 3.070+0 | 2.605+0 |
| 1 | 3 | 4.582−1 | 4.699−1 | 4.706−1 | 4.667−1 | 4.568−1 | 4.334−1 | 3.937−1 | 3.419−1 | 2.842−1 | 2.264−1 |
| 1 | 4 | 7.449−1 | 7.458−1 | 7.372−1 | 7.276−1 | 7.124−1 | 6.760−1 | 6.126−1 | 5.293−1 | 4.374−1 | 3.463−1 |
| 1 | 5 | 5.558−1 | 5.535−1 | 5.476−1 | 5.495−1 | 5.522−1 | 5.337−1 | 4.845−1 | 4.135−1 | 3.347−1 | 2.591−1 |
| 1 | 6 | 1.879+0 | 1.911+0 | 1.888+0 | 1.794+0 | 1.630+0 | 1.417+0 | 1.187+0 | 9.689−1 | 7.784−1 | 6.229−1 |
| 1 | 7 | 2.161+0 | 2.262+0 | 2.305+0 | 2.252+0 | 2.096+0 | 1.865+0 | 1.601+0 | 1.340+0 | 1.101+0 | 8.937−1 |
| 1 | 8 | 1.121+0 | 1.215+0 | 1.223+0 | 1.157+0 | 1.060+0 | 9.837−1 | 9.747−1 | 1.063+0 | 1.264+0 | 1.574+0 |
| 1 | 9 | 8.780−1 | 8.984−1 | 9.064−1 | 9.053−1 | 9.048−1 | 9.185−1 | 9.654−1 | 1.065+0 | 1.233+0 | 1.472+0 |
| 1 | 10 | 6.643−1 | 6.341−1 | 6.014−1 | 5.682−1 | 5.437−1 | 5.414−1 | 5.733−1 | 6.424−1 | 7.414−1 | 8.556−1 |
| . | . | . | . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . | . | . | . |
| Transition . | Temperature (log Te, K) . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| i . | j . | 3.70 . | 3.90 . | 4.10 . | 4.30 . | 4.50 . | 4.70 . | 4.900 . | 5.10 . | 5.30 . | 5.50 . |
| 1 | 2 | 5.230+0 | 5.311+0 | 5.354+0 | 5.328+0 | 5.168+0 | 4.809+0 | 4.267+0 | 3.647+0 | 3.070+0 | 2.605+0 |
| 1 | 3 | 4.582−1 | 4.699−1 | 4.706−1 | 4.667−1 | 4.568−1 | 4.334−1 | 3.937−1 | 3.419−1 | 2.842−1 | 2.264−1 |
| 1 | 4 | 7.449−1 | 7.458−1 | 7.372−1 | 7.276−1 | 7.124−1 | 6.760−1 | 6.126−1 | 5.293−1 | 4.374−1 | 3.463−1 |
| 1 | 5 | 5.558−1 | 5.535−1 | 5.476−1 | 5.495−1 | 5.522−1 | 5.337−1 | 4.845−1 | 4.135−1 | 3.347−1 | 2.591−1 |
| 1 | 6 | 1.879+0 | 1.911+0 | 1.888+0 | 1.794+0 | 1.630+0 | 1.417+0 | 1.187+0 | 9.689−1 | 7.784−1 | 6.229−1 |
| 1 | 7 | 2.161+0 | 2.262+0 | 2.305+0 | 2.252+0 | 2.096+0 | 1.865+0 | 1.601+0 | 1.340+0 | 1.101+0 | 8.937−1 |
| 1 | 8 | 1.121+0 | 1.215+0 | 1.223+0 | 1.157+0 | 1.060+0 | 9.837−1 | 9.747−1 | 1.063+0 | 1.264+0 | 1.574+0 |
| 1 | 9 | 8.780−1 | 8.984−1 | 9.064−1 | 9.053−1 | 9.048−1 | 9.185−1 | 9.654−1 | 1.065+0 | 1.233+0 | 1.472+0 |
| 1 | 10 | 6.643−1 | 6.341−1 | 6.014−1 | 5.682−1 | 5.437−1 | 5.414−1 | 5.733−1 | 6.424−1 | 7.414−1 | 8.556−1 |
| . | . | . | . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . | . | . | . |
Effective collision strengths for transitions in Si ii (a ± b ≡ a × 10±b). (For complete table see Supporting Information.)
| Transition . | Temperature (log Te, K) . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| i . | j . | 3.70 . | 3.90 . | 4.10 . | 4.30 . | 4.50 . | 4.70 . | 4.900 . | 5.10 . | 5.30 . | 5.50 . |
| 1 | 2 | 5.230+0 | 5.311+0 | 5.354+0 | 5.328+0 | 5.168+0 | 4.809+0 | 4.267+0 | 3.647+0 | 3.070+0 | 2.605+0 |
| 1 | 3 | 4.582−1 | 4.699−1 | 4.706−1 | 4.667−1 | 4.568−1 | 4.334−1 | 3.937−1 | 3.419−1 | 2.842−1 | 2.264−1 |
| 1 | 4 | 7.449−1 | 7.458−1 | 7.372−1 | 7.276−1 | 7.124−1 | 6.760−1 | 6.126−1 | 5.293−1 | 4.374−1 | 3.463−1 |
| 1 | 5 | 5.558−1 | 5.535−1 | 5.476−1 | 5.495−1 | 5.522−1 | 5.337−1 | 4.845−1 | 4.135−1 | 3.347−1 | 2.591−1 |
| 1 | 6 | 1.879+0 | 1.911+0 | 1.888+0 | 1.794+0 | 1.630+0 | 1.417+0 | 1.187+0 | 9.689−1 | 7.784−1 | 6.229−1 |
| 1 | 7 | 2.161+0 | 2.262+0 | 2.305+0 | 2.252+0 | 2.096+0 | 1.865+0 | 1.601+0 | 1.340+0 | 1.101+0 | 8.937−1 |
| 1 | 8 | 1.121+0 | 1.215+0 | 1.223+0 | 1.157+0 | 1.060+0 | 9.837−1 | 9.747−1 | 1.063+0 | 1.264+0 | 1.574+0 |
| 1 | 9 | 8.780−1 | 8.984−1 | 9.064−1 | 9.053−1 | 9.048−1 | 9.185−1 | 9.654−1 | 1.065+0 | 1.233+0 | 1.472+0 |
| 1 | 10 | 6.643−1 | 6.341−1 | 6.014−1 | 5.682−1 | 5.437−1 | 5.414−1 | 5.733−1 | 6.424−1 | 7.414−1 | 8.556−1 |
| . | . | . | . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . | . | . | . |
| Transition . | Temperature (log Te, K) . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| i . | j . | 3.70 . | 3.90 . | 4.10 . | 4.30 . | 4.50 . | 4.70 . | 4.900 . | 5.10 . | 5.30 . | 5.50 . |
| 1 | 2 | 5.230+0 | 5.311+0 | 5.354+0 | 5.328+0 | 5.168+0 | 4.809+0 | 4.267+0 | 3.647+0 | 3.070+0 | 2.605+0 |
| 1 | 3 | 4.582−1 | 4.699−1 | 4.706−1 | 4.667−1 | 4.568−1 | 4.334−1 | 3.937−1 | 3.419−1 | 2.842−1 | 2.264−1 |
| 1 | 4 | 7.449−1 | 7.458−1 | 7.372−1 | 7.276−1 | 7.124−1 | 6.760−1 | 6.126−1 | 5.293−1 | 4.374−1 | 3.463−1 |
| 1 | 5 | 5.558−1 | 5.535−1 | 5.476−1 | 5.495−1 | 5.522−1 | 5.337−1 | 4.845−1 | 4.135−1 | 3.347−1 | 2.591−1 |
| 1 | 6 | 1.879+0 | 1.911+0 | 1.888+0 | 1.794+0 | 1.630+0 | 1.417+0 | 1.187+0 | 9.689−1 | 7.784−1 | 6.229−1 |
| 1 | 7 | 2.161+0 | 2.262+0 | 2.305+0 | 2.252+0 | 2.096+0 | 1.865+0 | 1.601+0 | 1.340+0 | 1.101+0 | 8.937−1 |
| 1 | 8 | 1.121+0 | 1.215+0 | 1.223+0 | 1.157+0 | 1.060+0 | 9.837−1 | 9.747−1 | 1.063+0 | 1.264+0 | 1.574+0 |
| 1 | 9 | 8.780−1 | 8.984−1 | 9.064−1 | 9.053−1 | 9.048−1 | 9.185−1 | 9.654−1 | 1.065+0 | 1.233+0 | 1.472+0 |
| 1 | 10 | 6.643−1 | 6.341−1 | 6.014−1 | 5.682−1 | 5.437−1 | 5.414−1 | 5.733−1 | 6.424−1 | 7.414−1 | 8.556−1 |
| . | . | . | . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . | . | . | . |
Comparison of effective collision strengths (ϒ) for transitions among the lowest 15 levels of Si ii at three temperatures of 5000, 10 000, 20 000 K.
| I . | J . | DARC . | BPRM . | BSRM . | RM . | . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Te, K . | 5K . | 10K . | 20K . | 5K . | 10K . | 20K . | 5K . | 10K . | 20K . | 5K . | 10K . | 20K . | ||
| 1 | 2 | 5.230 | 5.338 | 5.328 | 4.55 | 4.45 | 4.42 | 6.19 | 6.09 | 5.97 | 5.60 | 5.70 | 5.77 | |
| 1 | 3 | 0.458 | 0.471 | 0.467 | 0.401 | 0.398 | 0.392 | 0.512 | 0.515 | 0.502 | 0.550 | 0.516 | 0.466 | |
| 1 | 4 | 0.745 | 0.742 | 0.728 | 0.612 | 0.609 | 0.602 | 0.812 | 0.789 | 0.769 | 0.832 | 0.780 | 0.706 | |
| 1 | 5 | 0.556 | 0.550 | 0.550 | 0.441 | 0.458 | 0.477 | 0.615 | 0.595 | 0.589 | 0.571 | 0.534 | 0.488 | |
| 1 | 6 | 1.879 | 1.907 | 1.793 | 1.82 | 1.82 | 1.75 | 2.77 | 2.74 | 2.50 | 2.76 | 2.74 | 2.58 | |
| 1 | 7 | 2.161 | 2.294 | 2.252 | 2.05 | 2.14 | 2.14 | 2.94 | 2.98 | 2.80 | 2.45 | 2.44 | 2.30 | |
| 1 | 8 | 1.120 | 1.230 | 1.156 | 0.910 | 0.865 | 0.857 | 1.02 | 1.06 | 0.979 | 1.24 | 1.20 | 1.04 | |
| 1 | 9 | 0.878 | 0.904 | 0.905 | 0.887 | 0.899 | 0.916 | 1.02 | 0.988 | 0.988 | 0.716 | 0.840 | 0.902 | |
| 1 | 10 | 0.665 | 0.618 | 0.568 | ..... | ..... | ..... | 0.540 | 0.535 | 0.517 | 0.591 | 0.612 | 0.640 | |
| 1 | 11 | 0.819 | 0.737 | 0.645 | ..... | ..... | ..... | 0.561 | 0.546 | 0.509 | 0.695 | 0.682 | 0.654 | |
| 1 | 12 | 2.214 | 2.364 | 2.556 | ..... | ..... | ..... | 3.43 | 3.46 | 3.73 | 3.16 | 3.38 | 3.77 | |
| 1 | 13 | 0.796 | 0.798 | 0.736 | ..... | ..... | ..... | 1.11 | 0.993 | 0.891 | 1.19 | 1.09 | 0.981 | |
| 1 | 14 | 1.792 | 1.911 | 2.099 | ..... | ..... | ..... | 2.51 | 2.60 | 2.82 | 1.85 | 1.93 | 2.09 | |
| 1 | 15 | 1.147 | 1.209 | 1.288 | ..... | ..... | ..... | 1.64 | 1.68 | 1.76 | 1.32 | 1.35 | 1.40 | |
| 2 | 3 | 0.405 | 0.401 | 0.400 | ..... | ..... | ..... | 0.100 | 0.345 | 0.384 | 0.433 | 0.402 | 0.365 | |
| 2 | 4 | 1.049 | 1.038 | 1.025 | ..... | ..... | ..... | 0.899 | 1.07 | 1.08 | 1.13 | 1.05 | 0.956 | |
| 2 | 5 | 2.046 | 2.071 | 2.048 | ..... | ..... | ..... | 2.57 | 2.32 | 2.23 | 2.32 | 2.19 | 1.99 | |
| 2 | 6 | 2.948 | 3.119 | 3.052 | ..... | ..... | ..... | 4.03 | 4.15 | 3.88 | 3.50 | 3.48 | 3.32 | |
| 2 | 7 | 5.116 | 5.264 | 5.020 | ..... | ..... | ..... | 7.39 | 7.38 | 6.77 | 6.88 | 6.79 | 6.30 | |
| 2 | 8 | 2.239 | 2.467 | 2.325 | ..... | ..... | ..... | 1.92 | 2.14 | 1.97 | 2.49 | 2.41 | 2.15 | |
| 2 | 9 | 1.753 | 1.799 | 1.784 | ..... | ..... | ..... | 2.10 | 1.93 | 1.87 | 1.43 | 1.69 | 1.83 | |
| 2 | 10 | 0.818 | 0.740 | 0.650 | ..... | ..... | ..... | 0.545 | 0.540 | 0.507 | 0.699 | 0.687 | 0.658 | |
| 2 | 11 | 2.317 | 2.096 | 1.927 | ..... | ..... | ..... | 1.66 | 1.63 | 1.55 | 1.87 | 1.90 | 1.94 | |
| 2 | 12 | 1.352 | 1.398 | 1.371 | ..... | ..... | ..... | 1.92 | 1.80 | 1.74 | 2.13 | 2.12 | 2.21 | |
| 2 | 13 | 4.588 | 4.899 | 4.252 | ..... | ..... | ..... | 6.77 | 6.82 | 7.27 | 6.47 | 6.75 | 7.30 | |
| 2 | 14 | 1.220 | 1.258 | 1.329 | ..... | ..... | ..... | 1.91 | 1.85 | 1.89 | 1.31 | 1.34 | 1.41 | |
| 2 | 15 | 4.730 | 5.066 | 5.538 | ..... | ..... | ..... | 6.55 | 6.83 | 7.44 | 4.79 | 4.90 | 5.16 | |
| 3 | 4 | 4.371 | 3.965 | 3.612 | ..... | ..... | ..... | 3.09 | 3.28 | 3.24 | 4.92 | 4.51 | 3.94 | |
| 3 | 5 | 2.300 | 2.432 | 2.474 | ..... | ..... | ..... | 2.69 | 2.61 | 2.41 | 1.68 | 1.67 | 1.57 | |
| 3 | 6 | 1.091 | 1.019 | 0.937 | ..... | ..... | ..... | 1.26 | 1.20 | 1.08 | 1.20 | 1.20 | 1.09 | |
| 3 | 7 | 0.596 | 0.584 | 0.569 | ..... | ..... | ..... | 0.746 | 0.726 | 0.662 | 0.648 | 0.653 | 0.613 | |
| 4 | 5 | 7.446 | 7.284 | 7.041 | ..... | ..... | ..... | 7.16 | 7.07 | 6.72 | 7.36 | 6.94 | 6.31 | |
| 4 | 6 | 1.677 | 1.581 | 1.469 | ..... | ..... | ..... | 1.84 | 1.77 | 1.63 | 1.86 | 1.85 | 1.69 | |
| 4 | 7 | 1.708 | 1.632 | 1.548 | ..... | ..... | ..... | 1.70 | 1.66 | 1.57 | 1.86 | 1.86 | 1.72 | |
| 5 | 6 | 1.286 | 1.252 | 1.211 | ..... | ..... | ..... | 1.49 | 1.49 | 1.39 | 1.39 | 1.40 | 1.31 | |
| 5 | 7 | 3.813 | 3.580 | 3.314 | ..... | ..... | ..... | 4.07 | 3.86 | 3.53 | 4.17 | 4.16 | 3.80 | |
| 6 | 7 | 4.364 | 4.502 | 4.701 | ..... | ..... | ..... | 6.94 | 6.55 | 5.83 | 6.04 | 5.92 | 5.75 | |
| I . | J . | DARC . | BPRM . | BSRM . | RM . | . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Te, K . | 5K . | 10K . | 20K . | 5K . | 10K . | 20K . | 5K . | 10K . | 20K . | 5K . | 10K . | 20K . | ||
| 1 | 2 | 5.230 | 5.338 | 5.328 | 4.55 | 4.45 | 4.42 | 6.19 | 6.09 | 5.97 | 5.60 | 5.70 | 5.77 | |
| 1 | 3 | 0.458 | 0.471 | 0.467 | 0.401 | 0.398 | 0.392 | 0.512 | 0.515 | 0.502 | 0.550 | 0.516 | 0.466 | |
| 1 | 4 | 0.745 | 0.742 | 0.728 | 0.612 | 0.609 | 0.602 | 0.812 | 0.789 | 0.769 | 0.832 | 0.780 | 0.706 | |
| 1 | 5 | 0.556 | 0.550 | 0.550 | 0.441 | 0.458 | 0.477 | 0.615 | 0.595 | 0.589 | 0.571 | 0.534 | 0.488 | |
| 1 | 6 | 1.879 | 1.907 | 1.793 | 1.82 | 1.82 | 1.75 | 2.77 | 2.74 | 2.50 | 2.76 | 2.74 | 2.58 | |
| 1 | 7 | 2.161 | 2.294 | 2.252 | 2.05 | 2.14 | 2.14 | 2.94 | 2.98 | 2.80 | 2.45 | 2.44 | 2.30 | |
| 1 | 8 | 1.120 | 1.230 | 1.156 | 0.910 | 0.865 | 0.857 | 1.02 | 1.06 | 0.979 | 1.24 | 1.20 | 1.04 | |
| 1 | 9 | 0.878 | 0.904 | 0.905 | 0.887 | 0.899 | 0.916 | 1.02 | 0.988 | 0.988 | 0.716 | 0.840 | 0.902 | |
| 1 | 10 | 0.665 | 0.618 | 0.568 | ..... | ..... | ..... | 0.540 | 0.535 | 0.517 | 0.591 | 0.612 | 0.640 | |
| 1 | 11 | 0.819 | 0.737 | 0.645 | ..... | ..... | ..... | 0.561 | 0.546 | 0.509 | 0.695 | 0.682 | 0.654 | |
| 1 | 12 | 2.214 | 2.364 | 2.556 | ..... | ..... | ..... | 3.43 | 3.46 | 3.73 | 3.16 | 3.38 | 3.77 | |
| 1 | 13 | 0.796 | 0.798 | 0.736 | ..... | ..... | ..... | 1.11 | 0.993 | 0.891 | 1.19 | 1.09 | 0.981 | |
| 1 | 14 | 1.792 | 1.911 | 2.099 | ..... | ..... | ..... | 2.51 | 2.60 | 2.82 | 1.85 | 1.93 | 2.09 | |
| 1 | 15 | 1.147 | 1.209 | 1.288 | ..... | ..... | ..... | 1.64 | 1.68 | 1.76 | 1.32 | 1.35 | 1.40 | |
| 2 | 3 | 0.405 | 0.401 | 0.400 | ..... | ..... | ..... | 0.100 | 0.345 | 0.384 | 0.433 | 0.402 | 0.365 | |
| 2 | 4 | 1.049 | 1.038 | 1.025 | ..... | ..... | ..... | 0.899 | 1.07 | 1.08 | 1.13 | 1.05 | 0.956 | |
| 2 | 5 | 2.046 | 2.071 | 2.048 | ..... | ..... | ..... | 2.57 | 2.32 | 2.23 | 2.32 | 2.19 | 1.99 | |
| 2 | 6 | 2.948 | 3.119 | 3.052 | ..... | ..... | ..... | 4.03 | 4.15 | 3.88 | 3.50 | 3.48 | 3.32 | |
| 2 | 7 | 5.116 | 5.264 | 5.020 | ..... | ..... | ..... | 7.39 | 7.38 | 6.77 | 6.88 | 6.79 | 6.30 | |
| 2 | 8 | 2.239 | 2.467 | 2.325 | ..... | ..... | ..... | 1.92 | 2.14 | 1.97 | 2.49 | 2.41 | 2.15 | |
| 2 | 9 | 1.753 | 1.799 | 1.784 | ..... | ..... | ..... | 2.10 | 1.93 | 1.87 | 1.43 | 1.69 | 1.83 | |
| 2 | 10 | 0.818 | 0.740 | 0.650 | ..... | ..... | ..... | 0.545 | 0.540 | 0.507 | 0.699 | 0.687 | 0.658 | |
| 2 | 11 | 2.317 | 2.096 | 1.927 | ..... | ..... | ..... | 1.66 | 1.63 | 1.55 | 1.87 | 1.90 | 1.94 | |
| 2 | 12 | 1.352 | 1.398 | 1.371 | ..... | ..... | ..... | 1.92 | 1.80 | 1.74 | 2.13 | 2.12 | 2.21 | |
| 2 | 13 | 4.588 | 4.899 | 4.252 | ..... | ..... | ..... | 6.77 | 6.82 | 7.27 | 6.47 | 6.75 | 7.30 | |
| 2 | 14 | 1.220 | 1.258 | 1.329 | ..... | ..... | ..... | 1.91 | 1.85 | 1.89 | 1.31 | 1.34 | 1.41 | |
| 2 | 15 | 4.730 | 5.066 | 5.538 | ..... | ..... | ..... | 6.55 | 6.83 | 7.44 | 4.79 | 4.90 | 5.16 | |
| 3 | 4 | 4.371 | 3.965 | 3.612 | ..... | ..... | ..... | 3.09 | 3.28 | 3.24 | 4.92 | 4.51 | 3.94 | |
| 3 | 5 | 2.300 | 2.432 | 2.474 | ..... | ..... | ..... | 2.69 | 2.61 | 2.41 | 1.68 | 1.67 | 1.57 | |
| 3 | 6 | 1.091 | 1.019 | 0.937 | ..... | ..... | ..... | 1.26 | 1.20 | 1.08 | 1.20 | 1.20 | 1.09 | |
| 3 | 7 | 0.596 | 0.584 | 0.569 | ..... | ..... | ..... | 0.746 | 0.726 | 0.662 | 0.648 | 0.653 | 0.613 | |
| 4 | 5 | 7.446 | 7.284 | 7.041 | ..... | ..... | ..... | 7.16 | 7.07 | 6.72 | 7.36 | 6.94 | 6.31 | |
| 4 | 6 | 1.677 | 1.581 | 1.469 | ..... | ..... | ..... | 1.84 | 1.77 | 1.63 | 1.86 | 1.85 | 1.69 | |
| 4 | 7 | 1.708 | 1.632 | 1.548 | ..... | ..... | ..... | 1.70 | 1.66 | 1.57 | 1.86 | 1.86 | 1.72 | |
| 5 | 6 | 1.286 | 1.252 | 1.211 | ..... | ..... | ..... | 1.49 | 1.49 | 1.39 | 1.39 | 1.40 | 1.31 | |
| 5 | 7 | 3.813 | 3.580 | 3.314 | ..... | ..... | ..... | 4.07 | 3.86 | 3.53 | 4.17 | 4.16 | 3.80 | |
| 6 | 7 | 4.364 | 4.502 | 4.701 | ..... | ..... | ..... | 6.94 | 6.55 | 5.83 | 6.04 | 5.92 | 5.75 | |
Comparison of effective collision strengths (ϒ) for transitions among the lowest 15 levels of Si ii at three temperatures of 5000, 10 000, 20 000 K.
| I . | J . | DARC . | BPRM . | BSRM . | RM . | . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Te, K . | 5K . | 10K . | 20K . | 5K . | 10K . | 20K . | 5K . | 10K . | 20K . | 5K . | 10K . | 20K . | ||
| 1 | 2 | 5.230 | 5.338 | 5.328 | 4.55 | 4.45 | 4.42 | 6.19 | 6.09 | 5.97 | 5.60 | 5.70 | 5.77 | |
| 1 | 3 | 0.458 | 0.471 | 0.467 | 0.401 | 0.398 | 0.392 | 0.512 | 0.515 | 0.502 | 0.550 | 0.516 | 0.466 | |
| 1 | 4 | 0.745 | 0.742 | 0.728 | 0.612 | 0.609 | 0.602 | 0.812 | 0.789 | 0.769 | 0.832 | 0.780 | 0.706 | |
| 1 | 5 | 0.556 | 0.550 | 0.550 | 0.441 | 0.458 | 0.477 | 0.615 | 0.595 | 0.589 | 0.571 | 0.534 | 0.488 | |
| 1 | 6 | 1.879 | 1.907 | 1.793 | 1.82 | 1.82 | 1.75 | 2.77 | 2.74 | 2.50 | 2.76 | 2.74 | 2.58 | |
| 1 | 7 | 2.161 | 2.294 | 2.252 | 2.05 | 2.14 | 2.14 | 2.94 | 2.98 | 2.80 | 2.45 | 2.44 | 2.30 | |
| 1 | 8 | 1.120 | 1.230 | 1.156 | 0.910 | 0.865 | 0.857 | 1.02 | 1.06 | 0.979 | 1.24 | 1.20 | 1.04 | |
| 1 | 9 | 0.878 | 0.904 | 0.905 | 0.887 | 0.899 | 0.916 | 1.02 | 0.988 | 0.988 | 0.716 | 0.840 | 0.902 | |
| 1 | 10 | 0.665 | 0.618 | 0.568 | ..... | ..... | ..... | 0.540 | 0.535 | 0.517 | 0.591 | 0.612 | 0.640 | |
| 1 | 11 | 0.819 | 0.737 | 0.645 | ..... | ..... | ..... | 0.561 | 0.546 | 0.509 | 0.695 | 0.682 | 0.654 | |
| 1 | 12 | 2.214 | 2.364 | 2.556 | ..... | ..... | ..... | 3.43 | 3.46 | 3.73 | 3.16 | 3.38 | 3.77 | |
| 1 | 13 | 0.796 | 0.798 | 0.736 | ..... | ..... | ..... | 1.11 | 0.993 | 0.891 | 1.19 | 1.09 | 0.981 | |
| 1 | 14 | 1.792 | 1.911 | 2.099 | ..... | ..... | ..... | 2.51 | 2.60 | 2.82 | 1.85 | 1.93 | 2.09 | |
| 1 | 15 | 1.147 | 1.209 | 1.288 | ..... | ..... | ..... | 1.64 | 1.68 | 1.76 | 1.32 | 1.35 | 1.40 | |
| 2 | 3 | 0.405 | 0.401 | 0.400 | ..... | ..... | ..... | 0.100 | 0.345 | 0.384 | 0.433 | 0.402 | 0.365 | |
| 2 | 4 | 1.049 | 1.038 | 1.025 | ..... | ..... | ..... | 0.899 | 1.07 | 1.08 | 1.13 | 1.05 | 0.956 | |
| 2 | 5 | 2.046 | 2.071 | 2.048 | ..... | ..... | ..... | 2.57 | 2.32 | 2.23 | 2.32 | 2.19 | 1.99 | |
| 2 | 6 | 2.948 | 3.119 | 3.052 | ..... | ..... | ..... | 4.03 | 4.15 | 3.88 | 3.50 | 3.48 | 3.32 | |
| 2 | 7 | 5.116 | 5.264 | 5.020 | ..... | ..... | ..... | 7.39 | 7.38 | 6.77 | 6.88 | 6.79 | 6.30 | |
| 2 | 8 | 2.239 | 2.467 | 2.325 | ..... | ..... | ..... | 1.92 | 2.14 | 1.97 | 2.49 | 2.41 | 2.15 | |
| 2 | 9 | 1.753 | 1.799 | 1.784 | ..... | ..... | ..... | 2.10 | 1.93 | 1.87 | 1.43 | 1.69 | 1.83 | |
| 2 | 10 | 0.818 | 0.740 | 0.650 | ..... | ..... | ..... | 0.545 | 0.540 | 0.507 | 0.699 | 0.687 | 0.658 | |
| 2 | 11 | 2.317 | 2.096 | 1.927 | ..... | ..... | ..... | 1.66 | 1.63 | 1.55 | 1.87 | 1.90 | 1.94 | |
| 2 | 12 | 1.352 | 1.398 | 1.371 | ..... | ..... | ..... | 1.92 | 1.80 | 1.74 | 2.13 | 2.12 | 2.21 | |
| 2 | 13 | 4.588 | 4.899 | 4.252 | ..... | ..... | ..... | 6.77 | 6.82 | 7.27 | 6.47 | 6.75 | 7.30 | |
| 2 | 14 | 1.220 | 1.258 | 1.329 | ..... | ..... | ..... | 1.91 | 1.85 | 1.89 | 1.31 | 1.34 | 1.41 | |
| 2 | 15 | 4.730 | 5.066 | 5.538 | ..... | ..... | ..... | 6.55 | 6.83 | 7.44 | 4.79 | 4.90 | 5.16 | |
| 3 | 4 | 4.371 | 3.965 | 3.612 | ..... | ..... | ..... | 3.09 | 3.28 | 3.24 | 4.92 | 4.51 | 3.94 | |
| 3 | 5 | 2.300 | 2.432 | 2.474 | ..... | ..... | ..... | 2.69 | 2.61 | 2.41 | 1.68 | 1.67 | 1.57 | |
| 3 | 6 | 1.091 | 1.019 | 0.937 | ..... | ..... | ..... | 1.26 | 1.20 | 1.08 | 1.20 | 1.20 | 1.09 | |
| 3 | 7 | 0.596 | 0.584 | 0.569 | ..... | ..... | ..... | 0.746 | 0.726 | 0.662 | 0.648 | 0.653 | 0.613 | |
| 4 | 5 | 7.446 | 7.284 | 7.041 | ..... | ..... | ..... | 7.16 | 7.07 | 6.72 | 7.36 | 6.94 | 6.31 | |
| 4 | 6 | 1.677 | 1.581 | 1.469 | ..... | ..... | ..... | 1.84 | 1.77 | 1.63 | 1.86 | 1.85 | 1.69 | |
| 4 | 7 | 1.708 | 1.632 | 1.548 | ..... | ..... | ..... | 1.70 | 1.66 | 1.57 | 1.86 | 1.86 | 1.72 | |
| 5 | 6 | 1.286 | 1.252 | 1.211 | ..... | ..... | ..... | 1.49 | 1.49 | 1.39 | 1.39 | 1.40 | 1.31 | |
| 5 | 7 | 3.813 | 3.580 | 3.314 | ..... | ..... | ..... | 4.07 | 3.86 | 3.53 | 4.17 | 4.16 | 3.80 | |
| 6 | 7 | 4.364 | 4.502 | 4.701 | ..... | ..... | ..... | 6.94 | 6.55 | 5.83 | 6.04 | 5.92 | 5.75 | |
| I . | J . | DARC . | BPRM . | BSRM . | RM . | . | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Te, K . | 5K . | 10K . | 20K . | 5K . | 10K . | 20K . | 5K . | 10K . | 20K . | 5K . | 10K . | 20K . | ||
| 1 | 2 | 5.230 | 5.338 | 5.328 | 4.55 | 4.45 | 4.42 | 6.19 | 6.09 | 5.97 | 5.60 | 5.70 | 5.77 | |
| 1 | 3 | 0.458 | 0.471 | 0.467 | 0.401 | 0.398 | 0.392 | 0.512 | 0.515 | 0.502 | 0.550 | 0.516 | 0.466 | |
| 1 | 4 | 0.745 | 0.742 | 0.728 | 0.612 | 0.609 | 0.602 | 0.812 | 0.789 | 0.769 | 0.832 | 0.780 | 0.706 | |
| 1 | 5 | 0.556 | 0.550 | 0.550 | 0.441 | 0.458 | 0.477 | 0.615 | 0.595 | 0.589 | 0.571 | 0.534 | 0.488 | |
| 1 | 6 | 1.879 | 1.907 | 1.793 | 1.82 | 1.82 | 1.75 | 2.77 | 2.74 | 2.50 | 2.76 | 2.74 | 2.58 | |
| 1 | 7 | 2.161 | 2.294 | 2.252 | 2.05 | 2.14 | 2.14 | 2.94 | 2.98 | 2.80 | 2.45 | 2.44 | 2.30 | |
| 1 | 8 | 1.120 | 1.230 | 1.156 | 0.910 | 0.865 | 0.857 | 1.02 | 1.06 | 0.979 | 1.24 | 1.20 | 1.04 | |
| 1 | 9 | 0.878 | 0.904 | 0.905 | 0.887 | 0.899 | 0.916 | 1.02 | 0.988 | 0.988 | 0.716 | 0.840 | 0.902 | |
| 1 | 10 | 0.665 | 0.618 | 0.568 | ..... | ..... | ..... | 0.540 | 0.535 | 0.517 | 0.591 | 0.612 | 0.640 | |
| 1 | 11 | 0.819 | 0.737 | 0.645 | ..... | ..... | ..... | 0.561 | 0.546 | 0.509 | 0.695 | 0.682 | 0.654 | |
| 1 | 12 | 2.214 | 2.364 | 2.556 | ..... | ..... | ..... | 3.43 | 3.46 | 3.73 | 3.16 | 3.38 | 3.77 | |
| 1 | 13 | 0.796 | 0.798 | 0.736 | ..... | ..... | ..... | 1.11 | 0.993 | 0.891 | 1.19 | 1.09 | 0.981 | |
| 1 | 14 | 1.792 | 1.911 | 2.099 | ..... | ..... | ..... | 2.51 | 2.60 | 2.82 | 1.85 | 1.93 | 2.09 | |
| 1 | 15 | 1.147 | 1.209 | 1.288 | ..... | ..... | ..... | 1.64 | 1.68 | 1.76 | 1.32 | 1.35 | 1.40 | |
| 2 | 3 | 0.405 | 0.401 | 0.400 | ..... | ..... | ..... | 0.100 | 0.345 | 0.384 | 0.433 | 0.402 | 0.365 | |
| 2 | 4 | 1.049 | 1.038 | 1.025 | ..... | ..... | ..... | 0.899 | 1.07 | 1.08 | 1.13 | 1.05 | 0.956 | |
| 2 | 5 | 2.046 | 2.071 | 2.048 | ..... | ..... | ..... | 2.57 | 2.32 | 2.23 | 2.32 | 2.19 | 1.99 | |
| 2 | 6 | 2.948 | 3.119 | 3.052 | ..... | ..... | ..... | 4.03 | 4.15 | 3.88 | 3.50 | 3.48 | 3.32 | |
| 2 | 7 | 5.116 | 5.264 | 5.020 | ..... | ..... | ..... | 7.39 | 7.38 | 6.77 | 6.88 | 6.79 | 6.30 | |
| 2 | 8 | 2.239 | 2.467 | 2.325 | ..... | ..... | ..... | 1.92 | 2.14 | 1.97 | 2.49 | 2.41 | 2.15 | |
| 2 | 9 | 1.753 | 1.799 | 1.784 | ..... | ..... | ..... | 2.10 | 1.93 | 1.87 | 1.43 | 1.69 | 1.83 | |
| 2 | 10 | 0.818 | 0.740 | 0.650 | ..... | ..... | ..... | 0.545 | 0.540 | 0.507 | 0.699 | 0.687 | 0.658 | |
| 2 | 11 | 2.317 | 2.096 | 1.927 | ..... | ..... | ..... | 1.66 | 1.63 | 1.55 | 1.87 | 1.90 | 1.94 | |
| 2 | 12 | 1.352 | 1.398 | 1.371 | ..... | ..... | ..... | 1.92 | 1.80 | 1.74 | 2.13 | 2.12 | 2.21 | |
| 2 | 13 | 4.588 | 4.899 | 4.252 | ..... | ..... | ..... | 6.77 | 6.82 | 7.27 | 6.47 | 6.75 | 7.30 | |
| 2 | 14 | 1.220 | 1.258 | 1.329 | ..... | ..... | ..... | 1.91 | 1.85 | 1.89 | 1.31 | 1.34 | 1.41 | |
| 2 | 15 | 4.730 | 5.066 | 5.538 | ..... | ..... | ..... | 6.55 | 6.83 | 7.44 | 4.79 | 4.90 | 5.16 | |
| 3 | 4 | 4.371 | 3.965 | 3.612 | ..... | ..... | ..... | 3.09 | 3.28 | 3.24 | 4.92 | 4.51 | 3.94 | |
| 3 | 5 | 2.300 | 2.432 | 2.474 | ..... | ..... | ..... | 2.69 | 2.61 | 2.41 | 1.68 | 1.67 | 1.57 | |
| 3 | 6 | 1.091 | 1.019 | 0.937 | ..... | ..... | ..... | 1.26 | 1.20 | 1.08 | 1.20 | 1.20 | 1.09 | |
| 3 | 7 | 0.596 | 0.584 | 0.569 | ..... | ..... | ..... | 0.746 | 0.726 | 0.662 | 0.648 | 0.653 | 0.613 | |
| 4 | 5 | 7.446 | 7.284 | 7.041 | ..... | ..... | ..... | 7.16 | 7.07 | 6.72 | 7.36 | 6.94 | 6.31 | |
| 4 | 6 | 1.677 | 1.581 | 1.469 | ..... | ..... | ..... | 1.84 | 1.77 | 1.63 | 1.86 | 1.85 | 1.69 | |
| 4 | 7 | 1.708 | 1.632 | 1.548 | ..... | ..... | ..... | 1.70 | 1.66 | 1.57 | 1.86 | 1.86 | 1.72 | |
| 5 | 6 | 1.286 | 1.252 | 1.211 | ..... | ..... | ..... | 1.49 | 1.49 | 1.39 | 1.39 | 1.40 | 1.31 | |
| 5 | 7 | 3.813 | 3.580 | 3.314 | ..... | ..... | ..... | 4.07 | 3.86 | 3.53 | 4.17 | 4.16 | 3.80 | |
| 6 | 7 | 4.364 | 4.502 | 4.701 | ..... | ..... | ..... | 6.94 | 6.55 | 5.83 | 6.04 | 5.92 | 5.75 | |
Since Tayal (2008) has reported ϒ for a wider range of transitions and temperatures, we make some more comparisons with our results. Differences between the two sets of data are up to a factor of 2 (and larger for only a few) for many transitions, such as 3–8/11/12/13/14/15 and 4–8/12/13/14/15. For most cases his ϒ values are higher, but are lower for a few. In Fig. 7 we compare our ϒ with those of Tayal for three transitions, namely 3s2 3p 2P|$^o_{3/2}$|–3s 3p24P1/2, 3/2, 5/2, i.e. 2–3/4/5, which are very important for diagnostics as stated in Section 1. Towards the lower end of the temperature range his ϒ are significantly lower (by a factor of 70) for the 2–3 transition and are higher by ∼50 per cent for 2–5. Such a behaviour by the Tayal ϒ data appears to be anomalous in comparison with our results, particularly when there is a considerably closer agreement towards the higher end of the temperature range. Some differences between the two sets of data are expected at lower temperatures because of the position of resonances, a slight shift of which may alter the values of ϒ. However, large discrepancies observed for these three (and many other) transitions are not normally possible unless very high and broad resonances are present (or absent) close to the threshold, which does not appear to be the case. Tayal (2008) does not show resonances for the 2–3 transition, but our Ω are similar to that in Fig. 5 for 2–4 (see also fig. 2 of Tayal 2008), except that the magnitudes are (approximately) half for both the background as well as the peaks. This is fully expected and therefore the ϒ of Tayal (2008) are clearly anomalous for the 2–3/4/5 transitions, at temperatures below 10 000 K.
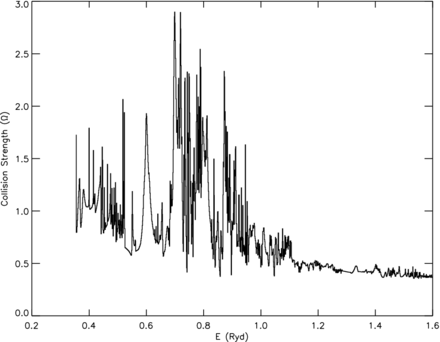
Collision strengths for the 2–4 (3s2 3p 2P|$^o_{3/2}$|–3s 3p24P3/2) transition of Si ii.
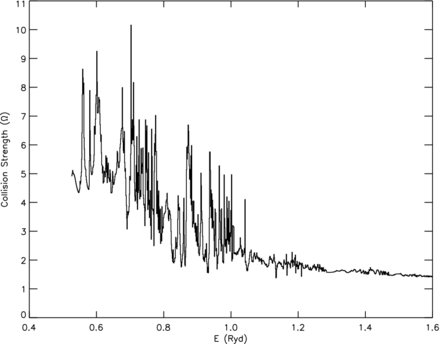
Collision strengths for the 2–7 (3s2 3p 2P|$^o_{3/2}$|–3s 3p22D5/2) transition of Si ii.
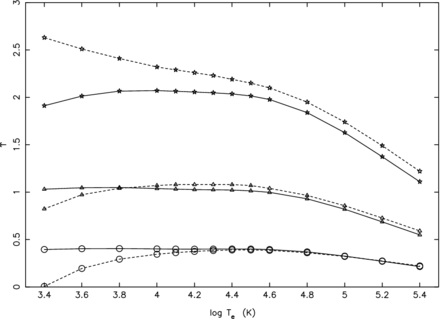
Comparison of effective collision strengths from our calculations from darc (continuous curves) and of Tayal (2008; broken curves) for the 2–3 (circles: 3s2 3p 2P|$^o_{3/2}$|–3s 3p24P1/2), 2–4 (triangles: 3s2 3p 2P|$^o_{3/2}$|–3s 3p24P3/2) and 2–5 (stars: 3s2 3p 2P|$^o_{3/2}$|–3s 3p24P5/2) transitions of Si ii.
In Fig. 8 we show one more comparison for four transitions, namely 1–12 (3s2 3p 2P|$^o_{1/2}$|–3s2 3d 2D3/2), 1–14 (3s2 3p 2P|$^o_{1/2}$|–3s 3p22P1/2), 2–13 (3s2 3p 2P|$^o_{3/2}$|–3s2 3d 2D5/2) and 2–15 (3s2 3p 2P|$^o_{3/2}$|–3s 3p22P3/2). For all these transitions the ϒ of Tayal (2008) are higher at all temperatures. Furthermore, the discrepancy with our calculations increases with the temperature, although his values of Ω differ more towards the lower end of the energy range (see Fig. 3). For the 1–14, 2–13 and 2–15 transitions the f values calculated from grasp and mchf are large and (probably) similar (see Table 3), and yet the Tayal values of ϒ are higher by ∼50 per cent. Finally, we note that comparisons shown in fig. 8 of Tayal (2008) with the ϒ of Dufton & Kingston (1991) for the 3s 3p24P1/2, 3/2–3s2 3d 2D3/2 (i.e. 3/4–12) forbidden transitions must be incorrect, because the latter did not report results for these. This is likely because Dufton & Kingston (1991) mistakenly labelled the 3s 3p22D3/2, 5/2 levels as 3s2 3d 2D3/2, 5/2, but subsequently rectified this in a later paper (Dufton & Kingston 1994). For the relevant 3s 3p24P1/2, 3/2–3s 3p22D (3/4–6) transitions there are no discrepancies between the two calculations, as already shown in Table 6. However, in comparison to our calculations, the ϒ of Tayal (2008) for the 3/4–12 transitions are overestimated by about a factor of 2 over the entire range of temperature.
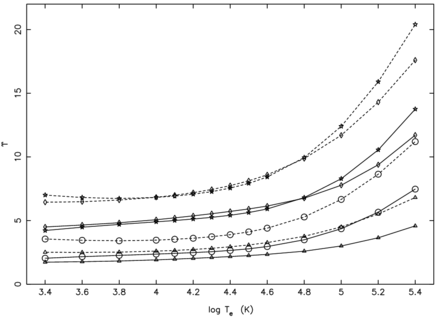
Comparison of effective collision strengths from our calculations from darc (continuous curves) and of Tayal (2008; broken curves) for the 1–12 (circles: 3s2 3p 2P|$^o_{1/2}$|–3s2 3d 2D3/2), 1–14 (triangles: 3s2 3p 2P|$^o_{1/2}$|–3s 3p22P1/2), 2–13 (stars: 3s2 3p 2P|$^o_{3/2}$|–3s2 3d 2D5/2) and 2–15 (diamonds: 3s2 3p 2P|$^o_{3/2}$|–3s 3p22P3/2) transitions of Si ii.
There is comparatively a better agreement (within 20 per cent) between our results of ϒ and those of Bautista et al. (2009). However, their data are too limited for a thorough comparison. Similarly, the earlier results of Dufton & Kingston (1991) are comparable with ours, except for a few transitions, such as 1–6/12, 2–7/12 and 6–7. Their higher ϒ values for these transitions are a direct consequence of their larger f values. Nevertheless, the limitations of their data have already been pointed in Section 1. Finally, as already noted in Section 1, Judge et al. (1991) adopted the data of Dufton & Kingston (1991) in analysing UV lines of Si ii and found discrepancies between theory and observations. Based on this, they estimated that the ϒ of Dufton & Kingston (1991) for the 3s2 3p 2Po–3s 3p24P multiplet may be overestimated by a factor of 1.5, but this is not supported by any calculations performed to date, including the present one. However, the Dufton & Kingston (1991) ϒ for the 3s2 3p 2Po–3s 3p22D multiplet do appear to be overestimated by nearly the same factor.
7 CONCLUSIONS
Energies and lifetimes for the lowest 56 levels of Si ii belonging to the n ≤ 5 configurations are reported, along with radiative rates for four types of transitions (E1, E2, M1 and M2), calculated with the grasp code. Additionally, calculations have also been performed with the fac code for comparison purposes. Based on comparisons with measurements and available theoretical results, our energy levels are estimated to be accurate to ∼0.1 Ryd. However, scope remains for improvement, although the inclusion of extensive CI is not very helpful in improving the accuracy further. Similarly, for a majority of (strong) transitions our listed A values (and other related parameters including lifetimes) are assessed to be accurate to better than 20 per cent.
For collision strengths Ω and effective collision strengths ϒ, limited previous results are available for comparison. However, Tayal (2008) has reported data over a wide range of energy and temperature, listing values of Ω and ϒ for 59 and 465 transitions, respectively. Our results are much more extensive considering 1540 transitions among 56 levels. Discrepancies of ∼25 per cent between our calculations of Ω and those of Tayal (2008) are noted for several transitions, both allowed as well as forbidden. For most transitions his results are higher, but some are lower. We have included a large range of partial waves, our results for Ω have fully converged at energies below 6 Ryd, and for higher energies the contribution of higher neglected partial waves has been taken into account. Therefore, we see no apparent deficiency in our work and estimate the accuracy of Ω to be better than 20 per cent for a majority of transitions.
For calculations of ϒ, resonances in the thresholds energy region have been resolved in a fine mesh, and are observed to be significant for many transitions. However, differences with the corresponding results of Tayal (2008) are up to a factor of 2 for many transitions, and over the entire range of temperature from 103.4 to 105.4 K. For most transitions his ϒ values are overestimated, but some are underestimated. Although Tayal included an equally large range of partial waves and energy for calculating Ω and resolved resonances to determine ϒ, the differences with our calculations are significant. In fact the energy resolution in his calculations was finer (0.00025 Ryd) in the thresholds region, but it should not make any appreciable difference in the reported results of ϒ, because the density of resonances is not very high, as seen in Figs 4–6. Nevertheless, to confirm it we have performed additional calculations with a larger resolution of 0.0005 Ryd at energies below 0.525 Ryd. These calculations affect transitions among the lowest five levels and particularly at lower temperatures. However, differences between the two sets of calculations for all transitions are less than 0.4 per cent at all temperatures. Therefore, we have confidence in our results although scope remains for improvement. We believe that the complete set of data presented here for both radiative and excitation rates for transitions in Si ii will be useful for diagnosing and modelling of astrophysical plasmas, and that some of the existing discrepancies noted by Judge et al. (1991) and Baldwin et al. (1996) will be resolved.
KMA is thankful to the Atomic Weapons Establishment, Aldermaston, for financial support.
REFERENCES
SUPPORTING INFORMATION
Additional Supporting Information may be found in the online version of this article:
Table 2. Transition wavelengths (λij in Å), radiative rates (Aji in s−1), oscillator strengths (fij, dimensionless) and line strengths (S, in atomic units) for electric dipole (E1), and Aji for E2, M1 and M2 transitions in Si ii.
Table 5. Effective collision strengths for transitions in Si ii (Supplementary Data).
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.



