-
PDF
- Split View
-
Views
-
Cite
Cite
Andrew Shannon, Cathie Clarke, Mark Wyatt, Dancing with the stars: formation of the Fomalhaut triple system and its effect on the debris discs, Monthly Notices of the Royal Astronomical Society, Volume 442, Issue 1, 21 July 2014, Pages 142–147, https://doi.org/10.1093/mnras/stu846
Close - Share Icon Share
Abstract
Fomalhaut is a triple system, with all components widely separated (∼105 au). Such widely separated binaries are thought to form during cluster dissolution, but that process is unlikely to form such a triple system. We explore an alternative scenario, where A and C form as a tighter binary from a single molecular cloud core (with semimajor axis ∼104 au), and B is captured during cluster dispersal. We use N-body simulations augmented with the Galactic tidal forces to show that such a system naturally evolves into a Fomalhaut-like system in about half of cases, on a time-scale compatible with the age of Fomalhaut. From initial non-interacting orbits, Galactic tides drive cycles in B's eccentricity that lead to a close encounter with C. After several close encounters, typically lasting tens of millions of years, one of the stars is ejected. The Fomalhaut-like case with both components at large separations is almost invariably a precursor to the ejection of one component, most commonly Fomalhaut C. By including circumstellar debris in a subset of the simulations, we also show that such an evolution usually does not disrupt the coherently eccentric debris disc around Fomalhaut A, and in some cases can even produce such a disc. We also find that the final eccentricity of the disc around A and the disc around C are correlated, which may indicate that the dynamics of the three stars stirred C's disc, explaining its unusual brightness.
1 INTRODUCTION
Fomalhaut has been suspected to be part of a widely separated binary star system for some time now (Luyten 1938). Recent analysis has confirmed that the K4V star TW PsA has both a similar proper motion and radial velocity to Fomalhaut, such that it is not an interloping field star, but forms a binary star system with Fomalhaut. The pair have a three-dimensional separation of |$5.74^{+0.04}_{-0.03}\times 10^4\,{\rm au}$|. Combining isochronal, rotational, X-ray, and lithium ages for the pair, the system is constrained to have an age of 440 ± 40 Myr, the mass of Fomalhaut A to be 1.92 ± 0.02 M⊕, and the mass of Fomalhaut B to be |$0.73^{+0.02}_{-0.01}\,{\rm M}_{\oplus }$| (Mamajek 2012). More recently, a third member of the Fomalhaut system has been recognized. The M4V star LP 876-10, or Fomalhaut C, is a 0.18 ± 0.02 M⊙ star with a three-dimensional separation from Fomalhaut A of |$1.58^{+0.02}_{-0.01}\times 10^5\,{\rm au}$| (Mamajek et al. 2013), which also has a common proper motion with Fomalhaut A and B. The uncertainty in the measured velocities of the three stars is roughly half a kilometre per second, much smaller than the relative velocities expected between field stars, allowing the inference that the system is bound. However, the escape speed for B is about a quarter kilometre per second, and C's smaller still, so little can be said about the orbital configuration.
The dynamics of the Fomalhaut system are particularly interesting as Fomalhaut A is known to harbour a debris disc (Gillett 1986), which has a coherent eccentricity of 0.11 ± 0.01 (Kalas, Graham & Clampin 2005). The origin of the debris disc's eccentricity is not known. It has been suggested that it may result from the action of one or more shepherding planet(s) (Quillen 2006; Chiang et al. 2009; Boley et al. 2012), although other possible origins have been advanced (e.g. Lyra & Kuchner 2013). Fomalhaut A is also accompanied by a point-like object dubbed ‘Fomalhaut b’ (Kalas et al. 2008). Non-detection of Fomalhaut b at thermal wavelengths led Kalas et al. (2008) to suggest that it may be the dust cloud ejected in a collision between planetesimals, or a circumplanetary ring, and Kennedy & Wyatt (2011) modelled it as a circumplanetary dust cloud created by the collisions of irregular satellites. Continuing observation has allowed for improved fits to the orbit of Fomalhaut b, which have revealed that it is not a shepherding planet, but has an eccentricity of ∼0.8, and a semimajor axis similar to the dust belt bodies (Kalas et al. 2013; Beust et al. 2014). This eccentric orbit precludes Fomalhaut b having a mass significantly above 10 M⊕, unless it was recently scattered to its highly eccentric orbit, as a more massive planet would perturb the disc to disruption (Beust et al. 2014; Tamayo 2014). The origin of the eccentricities of the dust belt's eccentricity, Fomalhaut b's eccentricity, and the nature of Fomalhaut b all remain open questions.
Moreover, Fomalhaut C has also been discovered to have a dust disc (Kennedy et al. 2014). Debris discs are rare around M stars (Gautier et al. 2007), and thus in the Fomalhaut system, which offers the possibility of additional dynamical constraints, the existence of a debris disc about an M star is of particular interest.
The formation of such a wide triple system presents some problems. The separations of both components are larger than the typical sizes of star-forming cores and thus, given that such cores rotate at far less than break-up velocity (Goodman et al. 1993), the system contains far too much angular momentum to have been created by conventional core fragmentation. The unfolding of triple stellar systems suggested by Reipurth & Mikkola (2012) appears to be inapplicable to Fomalhaut, which lacks an inner binary. Capture during cluster dispersal has also been suggested as a mechanism for wide binary formation (Kouwenhoven et al. 2010; Moeckel & Clarke 2011), but the low probability of capture makes the formation of a triple system by this method highly unlikely. The fraction of field stars with wide binaries is ∼10−2 (Dhital et al. 2010), suggesting that the chance of forming a cluster capture binary is ∼10−2, and thus forming a triple this way should have odds ∼10−4. In comparison, the chance of forming a 104 au binary is ∼10−1 (De Rosa et al. 2014). Thus, we are motivated to consider an alternative scenario, where AC form as a tighter binary from a single core, and C is moved outwards by interactions with B, which is captured as a wide binary. We describe our numerical method in Section 2, and present the results of our simulations in Section 3. We perform a subset of simulations with debris discs encircling Fomalhaut A and C in Section 4 to assess the compatibility of this scenario with the observed discs.
2 NUMERICAL METHOD
3 RESULTS
We perform a total of 1000 simulations. We define a simulation to be a match for the Fomalhaut system if the AC separation and AB separation are simultaneously between 0.5 and 1.5 times their current values. Over 500 Myr, 459 of the simulations are ever a match for the Fomalhaut system (Fig. 1). At 500 Myr, the end of our simulations, 214 systems still retain all three stars,2 191 of which have never been matches. Fig. 2 shows that the simulations where Fomalhaut B begins with lower semimajor axes and higher eccentricities were the first to go unstable, and the trend is for systems with higher semimajor axes and lower eccentricities to become unstable, and possibly pass through a Fomalhaut-like phase, at later times (Fig. 2). With a 46 per cent match rate and 19 per cent of systems remaining to become unstable at a later date, we expect 55–60 per cent of systems will eventually pass through a Fomalhaut-like phase. A similar analysis of the initial orbital parameters of the AC binary reveals no trends; the timing of the instability appears to be set only by the time taken to lower the pericentre of B's orbit enough to allow a close encounter with C.
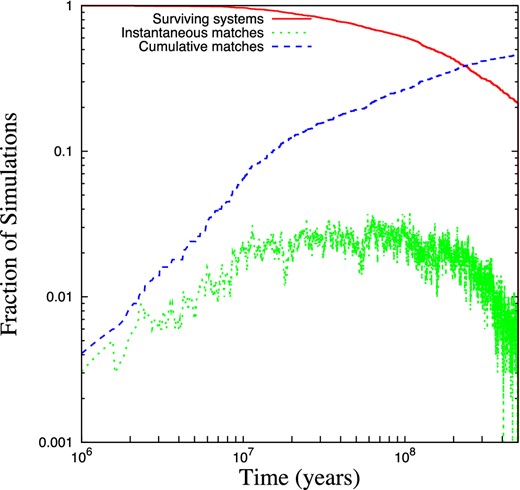
Evolution of the population, with the total number of systems still having all three stars (red solid line), the instantaneously matching systems (green dotted line), and the total number of systems that have ever matched (blue dashed line). At 500 Myr, 459 systems have ever been a match for the Fomalhaut system. In addition, 214 systems are still active, 191 of which have never been a match; these reside in roughly their original, unperturbed state.
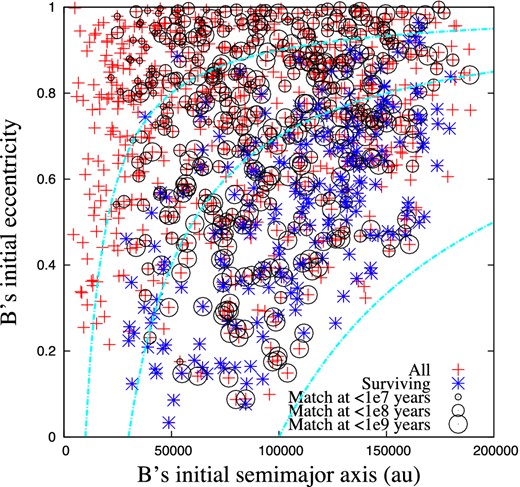
Initial semimajor axis and eccentricity of B's orbit about AC, showing if and when the system became a match, as well as those systems still active at 500 Myr. Systems with higher initial eccentricity, or lower initial semimajor axis, tend to become matches earlier. The surviving systems lie at high semimajor axis and low eccentricity, suggesting some may evolve into Fomalhaut-like systems at later times. A similar plot of C's initial orbit about A shows no significant trends. Dash–dotted lines are overplotted at initial pericentres of 104, 3 × 104, and 105 au for visualization.
The systems that are ever a match spend a mean of 17.2 Myr matching, and a median of 5.5 Myr matching (see Fig. 3). We match the simulations to the instantaneous separations in Fomalhaut (since its orbital trajectories are unknown) and thus simulated systems may move in and out of matching our criterion as the stars progress around their orbits without significant change in their orbital elements. Thus, our matching criteria may be somewhat too strict. If we instead measure the time between the first and last occasions the simulation is a match to the Fomalhaut system, the mean matching span is 47.3 Myr, and the median is 15.6 Myr (see Fig. 3), which corresponds to a few orbits of C around the AB pair.
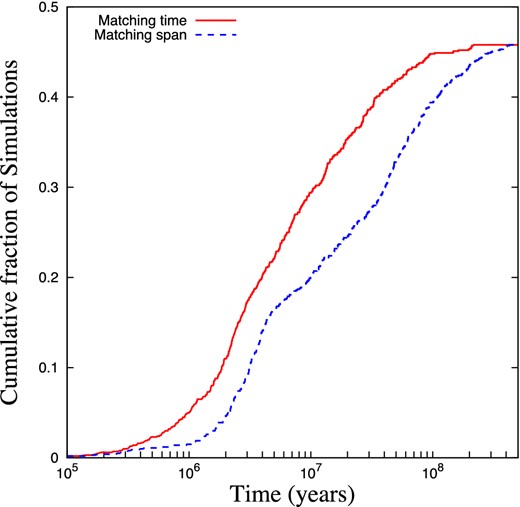
Cumulative number of simulations by the total amount of time for which they are a match to the Fomalhaut system (solid red line), and by the span of time between when they first become a match, and when they last are a match (blue dotted line).
As evidenced by the outcome that only 23 of the 459 systems which were matches for Fomalhaut persisted to 500 Myr, the matching state is a temporary one, which is typically followed by the ejection of one of the stars, most often C.3 This is perhaps not surprising – after B and C exchange places as the outer and inner binaries, respectively, their orbits will remain crossing.
We plot an example of a typical evolution in Fig. 4. This system was selected as an example because the time it spends as a match to Fomalhaut and the interval between the first and last matches, both lie between the median and mean of our distribution, and the system is a match at roughly the age of Fomalhaut. Fomalhaut B begins on a nearly circular orbit, but is driven to higher eccentricity by the action of Galactic tides. At around 380 Myr, B and C begin to interact by close encounters, leading to an exchange at 450 Myr. After a few close encounters with B, Fomalhaut C is ejected from the system. The decrease in C's eccentricity between 200 and 350 Myr is not caused by Galactic tides; rather it is caused by secular interactions between B and C. As the Galactic tide moves B to higher eccentricity, the secular interaction time-scale drops from ∼700 to ∼70 Myr (see, e.g. Ford, Kozinsky & Rasio 2000). Details such as whether the secular interactions cause an increase or decrease in eccentricity vary from simulation to simulation, but do not impact the overall character of the evolution.
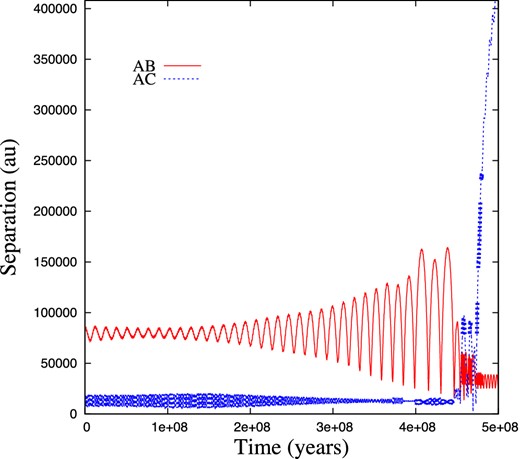
Evolution of a typical system. Fomalhauts B and C undergo several scattering encounters, during which the system resembles the actual Fomalhaut system. The thicker line segments denote where the system is identified as a match to Fomalhaut with our matching criteria.
4 DEBRIS DISCS
The presence of a coherently eccentric debris disc around Fomalhaut A provides an additional constraint on the system's history. A detailed study of how much dispersion is compatible with the observations of Fomalhaut's debris disc has not been performed (and is beyond the scope of this work), but modelling of the inner edge favours an inclination dispersion of |${\sim}2\;{\deg}$|, and the observed sharp inner edge of the debris suggests an eccentricity dispersion much less than the ring's value of 0.11 ± 0.01 (Kalas et al. 2005; Boley et al. 2012). Similarly, the dispersion in the longitude of pericentre must be small for the disc as a whole to be eccentric. Close encounters between Fomalhaut A and one or both of the other stars can disrupt the disc. In addition, the stellar dynamics may have implications for the debris disc around Fomalhaut C, as debris discs are generally rare around M stars (Lestrade et al. 2009).
To investigate this, we perform a smaller sample of 50 simulations in which we place a circular4 disc of 100 test particles around Fomalhaut A, with semimajor axis distributed randomly in a from 127 to 143 au (Boley et al. 2012). The initial conditions for the stellar orbits are the same as in Section 2. The disc is oriented randomly with respect to all system components, as well as the Galactic potential. Kennedy et al. (2014) found that Fomalhaut C also has a detectable debris disc. As debris discs are rarely detected around M stars, they speculated that the presence of a debris disc around Fomalhaut A and another around Fomalhaut C may be related. To evaluate the plausibility of this suggestion, we also included a disc of 100 test particles around Fomalhaut C in these 50 simulations. Based on constraints from the allowed temperature range of the disc detected around C, as well as size constraints from the disc being unresolved in Herschel images, we spread the disc around C with semimajor axis from 10 to 40 au, roughly the maximum allowable range. This disc, too, is oriented randomly with respect to all other system components, including A's disc.
In this sample, 19 of the systems become a match for the Fomalhaut system over 500 Myr of evolution. In Fig. 5, we plot the state of A's disc after the last instance the simulation matches the Fomalhaut system. Discs around A begin with a typical eccentricity of |$\mathcal {O}(10^{-6})$| and average apsidal alignment of |$\pm 55 \deg$|, which we measure using the standard deviation of the longitudes of pericentre of the disc particles. As the discs rise in eccentricity, they become apsidally aligned, as the eccentricity rise is driven by secular interactions with C, and the disc particles span a small range of initial semimajor axes. Close encounters can destroy the alignment, and raise eccentricities to high values, which occurs in 7 of the 19 cases (all with e ≳ 0.5). Five of the seven disrupted discs also lost disc particles.
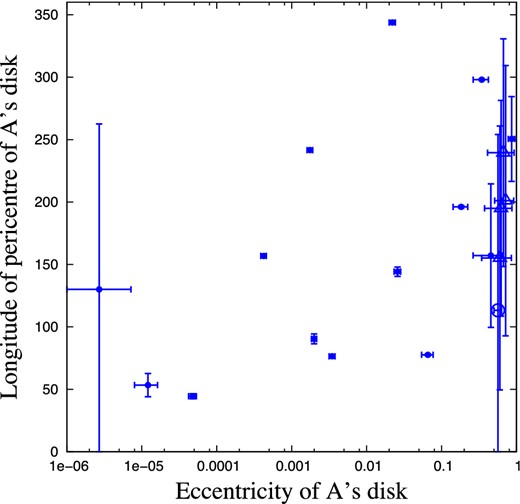
The mean eccentricity versus the mean longitude of pericentre for all the disc particles immediately after the last occasion the system was identified as a match for the Fomalhaut system. The error bars show the standard deviation among the disc particles. Discs begin with a typical eccentricity of |$\mathcal {O}(10^{-6})$| and average apsidal alignment of |$\pm 55 \deg$|. In most cases, the disc eccentricity is raised while the apsides are aligned. A few discs are significantly disrupted, with high eccentricity e ≳ 0.5 and no apsidal alignment, in five cases including the loss of disc particles (the open symbols). Thus, in 12 of the 19 cases the disc is preserved in a way compatible with the observed debris disc around Fomalhaut. Five cases develop a coherent eccentricity with a factor of 5 of Fomalhaut's e = 0.11 ± 0.01, including two with more eccentric discs.
Of particular note is that almost all of the undisrupted discs generate a coherent eccentricity. Although those cases with eccentricities of ≲10−2 are perhaps not evocative of Fomalhaut, they still represent eccentricity increases of 1–3 orders of magnitude from the initial values; such systems would require an internal mechanism to drive the eccentricity of A's disc to the high value seen today. Five discs develop coherent eccentricities between 0.02 and 0.5, evocative of Fomalhaut's disc, including two with higher eccentricities of 0.34 ± 0.08 and 0.18 ± 0.04, showing that the disc eccentricity can coherently rise as high as the value seen in Fomalhaut's disc today. The coherent eccentricity rising could similarly have produced aligned shepherding planets, as were suggested by Boley et al. (2012) to explain the ring's morphology. Previous simulations of stellar fly-bys of debris discs have shown them capable of producing eccentric rings (Larwood & Kalas 2001), but this had been rejected as an explanation for the eccentricity of Fomalhaut's ring as it was thought that repeated pericentre passages would destroy the coherence (Kalas et al. 2013). With our analysis showing the orbits of B and C evolve strongly with time, we find that repeated passages are far from assured, and thus the mechanism can be effective. Furthermore, as the time from when a system first looks like Fomalhaut to when it last looks like Fomalhaut is only a few tens of Myr, the amount of differential procession should be less than what would be expected for a system that had been evolving for 440 Myr. As seven discs are disrupted, they are incompatible with the observed disc, but represent only a minority of cases. Thus, disruption is a possible but unlikely outcome of the evolutionary model we consider here, making our model compatible with the observed disc around Fomalhaut A.
In Fig. 6, we plot the mean eccentricity of A's disc against the mean eccentricity of C's disc. We find that the mean eccentricities of the two discs are correlated. The correlation shows significant scatter, as close encounters with B may be significant source of perturbations to either disc without affecting the other. Nevertheless, this points to the possibility that the high eccentricity of A's disc may be reflected in a higher disc eccentricity for C than would normally occur for an M star. Such an externally driven eccentricity might arrest planet formation and initiate a collisional cascade by raising collision velocities (as in Kenyon & Bromley 2002), or trigger the instability of a planetary system (as in Zakamska & Tremaine 2004; Malmberg, Davies & Heggie 2011) which could subsequently stir the disc, leading to the detectability of its debris disc.
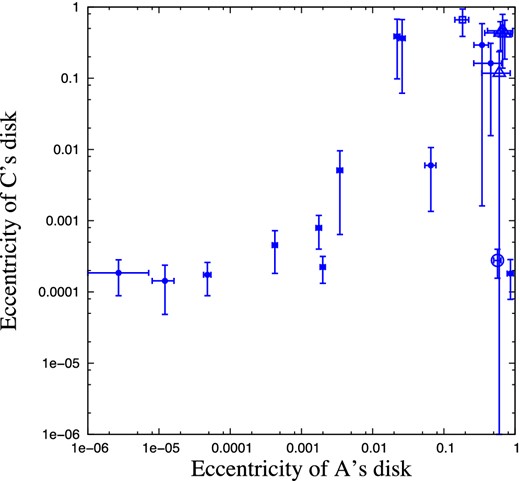
The mean eccentricity of the disc around A versus the mean eccentricity of the disc around C, from a subset of 50 simulations performed with debris discs (19 became matches). The error bars show the standard deviation among the disc particles. The mean eccentricity of disc particles around A and around C are correlated. Open symbols denote cases where disc particles were lost (squares where particles were lost from C's disc, circles for A, triangles for both). The correlation between the eccentricity of A's disc and C's disc, along with A's disc's high eccentricity today suggests C's disc may have a high eccentricity, possibly explaining the disc's unusually high brightness.
5 DISCUSSION
Formation of a weakly bound triple system like Fomalhaut is unlikely by capture of two stars during cluster dispersal. We consider an alternate scenario, where Fomalhaut A and C formed as a tighter binary (with semimajor axis 5000 ≲ a ≲ 13 600 au) and Fomalhaut B was captured into a weakly bound orbit during cluster dispersal. We simulate the evolution of such a system, and show that such a system commonly (55–60 per cent) evolves into a Fomalhaut-like system, with both components at large separations from Fomalhaut A, on time-scales compatible with the current age of the system. In this evolution, the present-day state where both components are on wide orbits is a temporary one, which typically dissociates in |$\mathcal {O}\left(10\right)$| Myr. In our simulations, systems that match Fomalhaut may be bound, or else be in the process of ejecting C from the system.
We perform an additional 50 simulations with discs of test particles around Fomalhaut A and Fomalhaut C, to ascertain whether this formation scenario is compatible with the coherent eccentric disc around Fomalhaut A, and the existence of a detectable disc around Fomalhaut C. 19 of those simulations became matches for the Fomalhaut system. In seven cases, the disc around Fomalhaut A is not significantly perturbed, and such cases would be compatible with the dynamics of A's disc being set by an internal source (see e.g., Quillen 2006). Intriguingly, five systems develop coherent eccentricities in A's disc, owing to secular interactions or close encounters with Fomalhaut C in its much tighter primordial orbit about A, with eccentricities with a factor of 5 of the present-day value. This suggests a possible origin of A's coherently eccentric disc. We also find that the final excitation of disc eccentricity around A and around C are correlated, suggesting that if A's debris disc was driven to high eccentricity by interactions with C, C's disc may be expected to have been driven to high eccentricity by A. This may explain why Fomalhaut C has a detectable debris disc, which is rarely found around an M star.
The total likelihood of the scenario presented may seem quite small, when one considers that Fomalhaut is the fourth nearest A star. However, in matching the details of any system, and focusing on the most interesting aspects, the intrinsic likelihood of that outcome will be small. The probability that the system we conjectured to be the primordial state of Fomalhaut undergoes an instability to produce a Fomalhaut-like system is ∼50 per cent. Although the probability of forming our conjectured initial state is small, 105 au binaries are an order of magnitude less common than 104 au binaries (Dhital et al. 2010; De Rosa et al. 2014), and thus given the high chance of creating a Fomalhaut-like system from an initially hierarchical system, this should be the preferred model.
There are two observational tests of this scenario. First (as noted above), we find a high likelihood (>80 per cent) that detailed orbital characterization of the Fomalhaut system will reveal that C's orbit is such that it interacts strongly with B during pericentre passage. Secondly, further circumstantial evidence in favour of this scenario would be provided if C were found to possess an eccentric disc. However, this too is not an inevitable consequence of this scenario: Fig. 6 demonstrates that there are situations where A's disc acquires an eccentricity of ≳0.1 while the eccentricity of C's disc remains substantially smaller.
We thank Grant Kennedy and Nick Moeckel for useful discussions, Dimitri Veras for providing us with the code from Veras & Evans (2013), and the anonymous referee for helpful feedback clarifying this manuscript. AS and MW are supported by the European Union through ERC grant number 279973.
In practice, most generations give an unbound B, so the precise choice of σ is not very significant, as it is the requirement the system be energetically bound which determines the initial orbit of B.
Most other simulations ejected B or C, although 12 ended in star–star collisions. We assumed radii of 1.39, 1.01, and 0.63 R⊙ to calculate collisions for Fomalhaut A, B, and C, respectively.
A total of 617 Cs were lost and 175 Bs, including simulations which were never a match to Fomalhaut.
Or rather, the orbits would be circular in the absence of the other two stars; for A's disc, C's gravitational tidal field produces typical initial eccentricities of 10−4 to 10−7, while around C, A's tidal field typically causes initial eccentricities of 10−3 to 10−6.



