Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

Abstract

The understanding of the accelerated expansion of the Universe poses one of the most fundamental questions in physics and cosmology today. Whether or not the acceleration is driven by some form of dark energy, and in the absence of a well-based theory to interpret the observations, many models have been proposed to solve this problem, both in the context of General Relativity and alternative theories of gravity. Actually, a further possibility to investigate the nature of dark energy lies in measuring the dark energy equation of state (EOS), w, and its time (or redshift) dependence at high accuracy. However, since w(z) is not directly accessible to measurement, reconstruction methods are needed to extract it reliably from observations. Here, we investigate different models of dark energy, described through several parametrizations of the EOS. Our high-redshift analysis is based on the Union2 Type Ia supernovae data set (Suzuki et al.), the Hubble diagram constructed from some gamma-ray bursts luminosity-distance indicators, and Gaussian priors on the distance from the baryon acoustic oscillations, and the Hubble constant h (these priors have been included in order to help to break the degeneracies among model parameters). To perform our statistical analysis and to explore the probability distributions of the EOS parameters, we use the Markov Chain Monte Carlo Method. It turns out that, if exact flatness is assumed, the dark energy EOS is evolving for all the parametrizations that we considered. We finally compare our results with the ones obtained by previous cosmographic analyses performed on the same astronomical data sets, showing that the latter ones are sufficient to test and compare the new parametrizations.

cosmological parameters, distance scale

1 INTRODUCTION

Since the end of the nineties, from observations on supernovae at high redshift, it is well known that the Universe is expanding. Pieces of evidence of scale temperature anisotropies in the cosmic microwave background (CMB) radiation have confirmed this result independently (Astier et al. 2006; Riess et al. 2007; Spergel et al. 2007; Kowalski et al. 2008; Planck Collaboration 2013). It is common practice to assume that the observed accelerated expansion is caused by dark energy, a presently dominant form of energy with unusual properties. The pressure of dark energy pde is negative and it is related to the positive energy density of dark energy ϵde by the equation of state (EOS) pde = wϵde, where the proportionality coefficient is such that w < 0. The nature of dark energy is still unknown, and we only know that it was estimated to be about 75 per cent of matter-energy in the Universe and that its properties are characterized by the EOS parameter, w. Extracting information on the EOS of dark energy from observational data is therefore a fundamental problem, but getting information from the observed data on such an EOS is at the same time both an issue of crucial importance and a challenging task. For probing the dynamical evolution of dark energy, under such circumstances, one can parametrize w empirically, by assuming, as usual, that this quantity evolves smoothly with redshift, so that it can be approximated by a fitting analytical expression, using two or more free parameters. Among all the possible parametrization forms of EOS, we will consider the Chevallier–Polarski–Linder (CPL) model (Chevallier & Polarski 2001; Linder 2003), which is widely used, since it presents a well-behaved and bounded behaviour for high redshifts, and a manageable two-dimensional parameter space. However, we will also introduce new parametrizations, that have been recently used by Ma & Zhang (2011) and Lazkoz, Salzano & Sendra (2010) to avoid the divergence problem inherent to the CPL parametrization, which turned out to be able to satisfy many theoretical scenarios. For constraining the parameters, which appear in the EOS, we use a large collection of cosmological data sets: the Union2 Type Ia supernovae (SNeIa) data set, the Hubble diagram constructed from some gamma-ray bursts (GRBs) luminosity-distance indicators, and in order to help break the degeneracies among model parameters, Gaussian priors on the distance from the baryon acoustic oscillations (BAOs), and the Hubble constant h. Actually, observations of the SNIa are consistent with the assumption that the observed accelerated expansion is due to a non-zero cosmological constant. However, so far the SNeIa have been observed only at redshifts z < 2, while in order to test if w is changing with redshift it is necessary to use more distant objects. New possibilities opened up when the GRBs have been discovered at higher redshifts, since this opened new avenues for cosmology, although they remain enigmatic objects. First of all, the mechanism that is responsible for releasing the incredible amounts of energy that a typical GRB emits is not yet known (see for instance Meszaros 2006 for a recent review). It is also not yet definitely known if the energy is emitted isotropically or is beamed. Despite these difficulties, GRBs are promising objects that can be used to study the expansion rate of the Universe at high redshifts (Bloom, Frail & Kulkarini 2003; Bradley 2003; Schaefer 2003, 2007; Dai, Liang & Xu 2004; Firmani et al. 2005; Amati et al. 2008; Amati, Frontera & Guidorzi 2009; Li et al. 2008; Tsutsui et al. 2009; Wang 2011a,b).

Actually, even if the huge dispersion (about four orders of magnitude) of the isotropic GRB energy makes them everything but standard candles, it has been recently empirically established that some of the directly observed parameters of GRBs are correlated with their important intrinsic parameters, such as luminosity or total radiated energy. This has allowed us to derive some correlations, which have been tested and used to calibrate those relations, and to derive their luminosity or radiated energy from one or more observables, making it possible to construct a GRBs Hubble diagram. It has also been shown that such a procedure can be implemented without specifying the cosmological model; see, for instance, Demianski & Piedipalumbo (2011), Demianski, Piedipalumbo & Rubano (2011) and references therein. In our analysis, we use a GRB HD data set consisting of 109 high-redshift GRBs, which has been constructed from the Amati Ep, i-Eiso correlation (here Ep, i is the peak photon energy of the intrinsic spectrum and Eiso the isotropic equivalent radiated energy), applying a local regression technique to estimate, in a model-independent way, the distance modulus from the recently updated Union SNeIa data set. It turns out that this and the other data sets are sufficient for our aim of testing and comparing the new parametrizations.

The scheme of the paper is as follows. In Section 2. we describe the basic elements of the parametrizations of the considered EOS, while in Section 3, we introduce the observational data sets that are used in our analysis. In Section 4, we describe some details of our statistical analysis from three sets of data. In a general discussion of our results and conclusions in Section 5, we finally present some constrains on dark energy models that can be derived from our analysis.

2 DARK ENERGY PARAMETRIZATIONS

As already said, the discovery that the expansion rate of the Universe is apparently accelerated is one of the most significant events in the modern cosmology. Although seemingly consistent with our current concordance model, in which the source of the cosmic acceleration takes the form of the Einstein cosmological constant, the precision of current data is however not sufficient to rule out the possibility of an evolving component. The fact that the Λ cold dark matter (CDM) model can be only an approximation generally leads to look for some dynamical field with a repulsive gravitational force. Moreover, this could instead be indicating that the Copernican principle is wrong, and that radial inhomogeneity is responsible for the accelerated expansion (Clarkson 2012; Valkenburg et al. 2013, Paper I; Valkenburg et al. 2013, Paper II).

Within the Friedmann–Lemaitre–Robertson–Walker (FLRW) paradigm, all possibilities can be characterized, as far as the background dynamics are concerned, by the dark energy EOS w(z). Even if, from a theoretical perspective w(z) could really be pretty much anything, a major task in cosmology today lies in searching for evidence for w(z) ≠ −1. This means in turn to find a general proper way to treat w(z), which is usually done in terms of a simple parametrization of w(z); but any such functional forms for w(z) are problematic because they are not based on a grounded theory, and flexibility is thus required, so involving a large set of parameters. However, at present the signal-to-noise ratio in the observational data is not enough to provide constraints in more than few parameters (two or three at most). To reduce the huge arbitrariness, the space of allowed w(z) models is often reduced to w ≥ −1; however, when w is an effective EOS parameterizing a modified gravity theory, as for instance a scalar–tensor or an f(R) model (Capozziello & De Laurentis 2011), then this constraint might be too restricted. An alternative procedure is to reconstruct w(z) directly from the observables without any dependence on a parametrization of w(z) or understanding of dark energy, as done, for example in Sahni et al. (2003). Some direct reconstruction methods rely, for instance, on estimating the first and second derivatives of luminosity-distance data. Actually, defining D(z) = (H0/c)(1 + z)− 1dL(z), it turns out that
(1)

Thus, given a parametrized ansatz for D(z), it is possible to reconstruct the dark energy EOS from equation (1). (See for instance Saini et al. 2000; Sahni et al. 2003, and references therein, for a review, and Rubano & Scudellaro 2002; Daly & Djorgovski 2004; Clarkson & Zunckel 2010; Lazkoz, Salzano & Sendra 2012; Sahni et al. 2013 for an overview about critical topics and alternative model-independent approaches connected to the dark energy reconstruction techniques.) New and interesting prospectives to extract information of the dark energy modelling based on a recent approach, the so-called genetic algorithms, are illustrated in Nesseris & Garcia-Bellido (2012), di Serafino et al. (2010) and di Serafino & Riccio (2010). Here, we are investigating if, by analysing a large collection of cosmological data, any indications of a deviation from the w(z) ≠ −1 come to light, as we have in fact detected in a previous cosmographic analysis, where the value of the deceleration parameter clearly confirmed the present acceleration phase, and the estimation of the jerk reflected the possibility of a deviation from the ΛCDM cosmological model. To accomplish this task, we focus on a direct and full reconstruction of the dark energy EOS through several parameterizations, widely used in the literature.

2.1 Basic equations

Within the FLRW paradigm, dark energy appears in the Friedmann equations of cosmological dynamics through its effective energy density and pressure
(2)
(3)
Here, a is the scale factor, |$H = \dot{a}/a$| the Hubble parameter, the dot denotes the derivative with respect to cosmic time, and we have assumed a spatially flat Universe in agreement with what is inferred from CMBR anisotropy spectrum (Planck Collaboration 2013). The continuity equation for any cosmological fluid is
(4)
where the energy density is ρi, the pressure pi and the EOS of each component is defined by |$\displaystyle {w=\frac{p_i}{\rho _i}}$|⁠. Ordinary non-relativistic matter has w = 0, and the cosmological constant has w = −1. If we explicitly allow the possibility that the dark energy evolves, the importance of its EOS does appear and determines the expression of the Hubble function H(z), and any derivation of it needed to obtain the observable quantities. Actually it turns out that
(5)
where |$\displaystyle {g(z)=\frac{\rho _{{\rm de}}(z)}{\rho _{{\rm de}}(0)}=\exp (3 \int _0^z \frac{w(x,\boldsymbol \theta )+1}{x+1} \, \mathrm{d}x)}$|⁠, |$w(z,{\boldsymbol \theta })$| is any dynamical form of the dark energy EOS, and |${\boldsymbol \theta }=(\theta _1, \theta _1,\ldots,\theta _n)$| are the dark energy EOS parameters. Moreover, it is
(6)
(7)
(8)
where dL(z, θ) is the luminosity distance, |$d_{\rm A}(z,{\boldsymbol \theta })$| the angular diameter distance and dV(z, θ) the volume distance defined by Eisenstein et al. (2005). All of them are needed to perform our statistical analysis. In this work, we consider three different parametrizations.
  • The so-called CPL model (Chevallier & Polarski 2001; Linder 2003).This parametrization assumes a dark energy EOS given by
    (9)
    where w0 and wa are real numbers that represent the EOS present value and its overall time evolution, respectively (Chevallier & Polarski 2001; Linder 2003). It is important to remember that for high redshifts we have the following behaviour:
    (10)
    that allows us to describe a wide variety of scalar-field dark energy models. Then, this parametrization appears to be a good compromise to construct a model-independent analysis.
  • A novel parametrization recently introduced in Ma & Zhang (2011) to avoid the future divergence problem of the CPL parametrization, and to probe the dynamics of dark energy not only in the past evolution but also in the future evolution,
    (11)
  • An oscillating dark energy EOS recently discussed in Lazkoz et al. (2010),
    (12)
    These oscillating models have been proposed to solve the so-called coincidence problem very easily, due to the sequence of different periods of acceleration, and are available in several theoretical scenarios.
It is worth noting that, it is possible to build up the link between the dark energy EOS and the cosmographic parametrization (based on the series expansion (in redshift) of the Hubble function H(z)), in order to finally cross-correlate the results obtained from such independent approaches. Actually it turns out that, at fourth order (in z)
(13)
(14)
(15)
(16)
where the function |$g(z,\boldsymbol {\theta })$| is defined above, and q0, j0, l0 are the present values of the following cosmographic functions:
(17)
(18)
(19)
(20)
It is worth noting that the deceleration parameter q(z) can be related to the EOS through the Hubble parameter H(z)
(21)

3 OBSERVATIONAL DATA SETS

As said, in our approach we use a great collection of presently available observational data sets on SNeIa and GRB Hubble Diagrams, and we set Gaussian priors on the distance from the BAOs, and the Hubble constant h.

3.1 SNeIa Hubble diagram

Over the last decade, the confidence in SNeIa as standard candles has been steadily growing, once their observations gave the first strong indication of an accelerating expansion of the Universe, since then explained by assuming the existence of some kind of dark energy or non-zero cosmological constant. Since 1995, two teams of astronomers – the High-Z Supernova Search Team and the Supernova Cosmology Project – have been discovering SNeIa at high redshifts. Here, we consider the recently updated Supernovae Cosmology Project Union 2.1 compilation (Suzuki et al. 2012), which is an update of the original Union compilation, consisting of 580 SNIa, spanning the redshift range (0.015 ≤ z ≤ 1.4). We actually compare the theoretically predicted distance modulus μ(z) with the observed one, through a Bayesian approach, based on the definition of the distance modulus,
(22)
where DL(zj, {θi}) is the Hubble free luminosity distance, expressed as a series depending on the EOS parameters, θi = (w0, …, wi, …), and μ0 encodes the Hubble constant and the absolute magnitude M.

3.2 GRBs Hubble diagram

GRBs are visible up to high z, thanks to the enormous energy that they release, and thus may be good candidates for our high-redshift cosmological investigation. Sadly, GRBs may be everything but standard candles since their peak luminosity spans a wide range, even if there have been many efforts to make them standardizable candles using some empirical correlations among distance dependent quantities and rest-frame observables (Amati et al. 2008). These empirical relations allow one to deduce the GRB rest-frame luminosity or energy from an observer frame measured quantity so that the distance modulus can be obtained with an error which depends essentially on the intrinsic scatter of the adopted correlation.

Combining the estimates from different correlations, Schaefer (2007) first derived the GRBs HD for 69 objects, which has been further enlarged using updated samples, different calibration methods and also different correlation relations, see for instance Demianski & Piedipalumbo (2011), Demianski, Piedipalumbo & Rubano (2011), showing the interest in the cosmological applications of GRBs. In this paper, we perform our cosmographic analysis using two GRBs HD data set, build up by calibrating the Amati Ep, i-Eiso relation.

3.2.1 The calibrated Amati GRBs Hubble diagram

Recently, it has been empirically established that some of the directly observed parameters of GRBs are connected with their isotropic absolute luminosity Liso or isotropic bolometric energy Eiso. These quantities appear to correlate with the GRB isotropic luminosity, its total collimation-corrected or its isotropic energy. The isotropic luminosity and energy cannot be measured directly but can be rather obtained through the knowledge of either the bolometric peak flux, denoted by Pbolo, or the bolometric fluence, denoted by Sbolo. Actually, it is
(23)
and
(24)
Therefore, Liso and Eiso depend on the GRB observables, Pbolo and Sbolo, but also on the cosmological parameters. Therefore, at a first glance it seems impossible to calibrate such GRBs empirical laws, without assuming any a priori cosmological model. This is the so-called circularity problem, which has to be overcome, in order to use GRBs as tools for cosmology. In Demianski & Piedipalumbo (2011), we have applied a local regression technique to estimate, in a model-independent way, the distance modulus from the Union SNIea sample, containing 580 SNeIa spanning the redshift range of 0.015 ≤ z ≤ 1.4. To use this large data set to estimate μ(zi), being zi any value of the redshift, we order the SNeIa sample according to the increasing value of |z − zi| and we select some fraction α of the data points, where α is a user selected value. Then, a first-order polynomial is fitted to the selected data, weighting each SNIa with an appropriate weight function. The zeroth-order term of such a linear fit is taken as the best estimate for μ(z), and the root mean square of the weighted residuals with respect to the best-fitting zeroth-order term is used as error. It is worth stressing that the value of α has to be appropriately set in order to make up a statistically valuable sample, but also to prevent the use of a low-order polynomial. Once the distance modulus at redshift z has been estimated in a model-independent way, it is possible to calibrate the Amati relation, just using the μ(z) reconstructed by the local regression technique. We consider only GRBs with z ≤ 1.414 in order to cover the same redshift range spanned by the SNeIa data. Once the Amati correlation relation has been fitted, and its parameters have been estimated, we can now use them to construct the GRBs Hubble diagram. Actually, let us remind that the luminosity distance of a GRB with the redshift z may be computed as
(25)
The uncertainty of dL(z) is then estimated through the propagation of the measurement errors on the involved quantities. We finally estimate the distance modulus for each ith GRB in our sample at redshift zi, to build the Hubble diagram plotted in Fig. 1, which we call the calibrated GRBs HD. The obvious drawback of this method is that it could suffer the systematics and uncertainties associated with SNe, as it is typical within the extragalactic distance scale techniques. In order to reduce such effects, we used the other GRBs (with z > 1.414) to construct the calibrated GRBs HD (shown in Fig. 1).
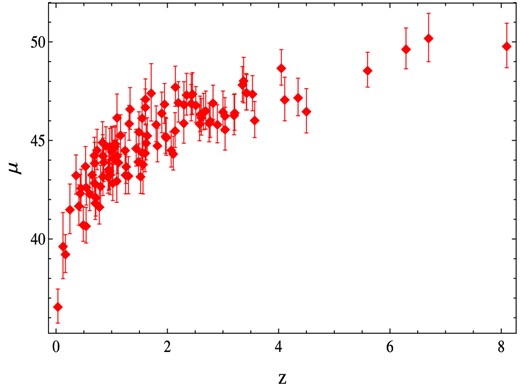
Distance modulus μ(z) for the calibrated GRBs Hubble diagram made up by fitting the Amati correlation.
Figure 1.

Distance modulus μ(z) for the calibrated GRBs Hubble diagram made up by fitting the Amati correlation.

Open in new tabDownload slide

3.3 BAOs data

While both SNIa and GRBs are based on the concept of standard candles, even if for the GRBs such a concept is generalized towards an unorthodox meaning, an alternative way to probe the background evolution of the Universe relies on the use of standard rulers. BAOs are promising standard ruler in cosmology. They are connected to density fluctuations created by acoustic waves generated by primordial perturbations: indeed, the peaks of the acoustic waves gave rise to dense regions of baryons which imprint the correlation between matter densities at the scale of the sound horizon at recombination era. Measurements of CMBR provide the absolute physical scale for these baryonic peaks, but the observed position of the peaks of the two-point correlation function of the matter distribution, compared with such absolute values, makes possible measurements of cosmological distance scales. In order to use BAOs as constraints, we follow Percival al. (2010) by first defining
(26)
with zd the drag redshift computed by using the approximated formula in Eisenstein & Hu (1998), with rs(z) the comoving sound horizon given by
(27)
and dV(z) the volume distance defined in equation (8).

4 STATISTICAL ANALYSIS

In this section, we move to our statistical analysis and present our main results on the constraints for the EOS parameters from the current observational data sets described above. In order to constrain the parameters, describing each of the dark energy EOS selected above, we perform a preliminary and standard-fitting procedure to maximize the likelihood function |${\cal {L}}({\boldsymbol p}) \propto \exp {[-\chi ^2({\boldsymbol p})/2]}$|⁠, where |${\boldsymbol p}$| is the set of cosmographic parameters and the expression for |$\chi ^2({\boldsymbol p})$| depends on the data set used. As a first test, we consider only the SNIa data, so that we define
(28)
Here, μobs and μth are the observed and theoretically predicted values of the distance modulus, while the sum is over all the SNIa in the sample. The last two terms are Gaussian priors on h and ωM = ΩMh2 and are included in order to contribute to break the degeneracies among the model parameters. We have resorted to the results of the SHOES Collaboration (Riess et al. 2009) and the WMAP7 data (Komatsu et al. 2011), respectively, to set the numbers used in equation (28). When we are using GRBs only, we define
(29)
As a next step, we combine the SNIa and GRBs HDs with other data redefining |${\cal {L}}({\boldsymbol p})$| as
(30)
The first two terms are the same as above, with |${\boldsymbol C}_{\rm SNIa/GRB}$| the SNIa/GRBs diagonal covariance matrix and (hobs, σh) = (0.742, 0.036). The third term takes into account the BAO constraints on dz = rs(zd)/DV(z), with rs(zd) the comoving sound horizon at the drag redshift zd (which we fix to be rs(zd) = 152.6 Mpc from WMAP7) and the volume distance defined as in equation (8). The values of dz at z = 0.20 and z = 0.35 have been estimated by Percival et al. (2010) using the SDSS DR7 galaxy sample, so that we define |$\chi ^2_{{\rm BAO}} = {\boldsymbol D}^T {\boldsymbol C}_{{\rm BAO}}^{-1} {\boldsymbol C}$|⁠, where |${\boldsymbol D}^T = (d_{0.2}^{{\rm obs}} - d_{0.2}^{{\rm th}}, d_{0.35}^{{\rm obs}} - d_{0.35}^{{\rm th}})$| and |${\boldsymbol C}_{{\rm BAO}}$| is the BAO covariance matrix. The next term refers to the shift parameter (Bond, Efstathiou & Tegmark 1997; Efstathiou & Bond 1999)
(31)
with z⋆ = 1090.10 the redshift of the last scattering surface. We follow again the WMAP7 data setting |$({\cal {R}}_{\rm obs}, \sigma _{{\cal {R}}}) = (1.725, 0.019)$|⁠. While all these quantities (except for the Gaussian prior on h) mainly involve the integrated E(z), the last term refers to the actual measurements of H(z) from the differential age of passively evolving elliptical galaxies. We then use the data collected by Stern et al. (2010) giving the values of the Hubble parameter for |${\cal {N}}_H = 11$| different points over the redshift range 0.10 ≤ z ≤ 1.75 with a diagonal covariance matrix. We finally perform our statistical analysis, considering a whole data set containing both the SNIa Union data set and the calibrated GBRs HD, and slightly modifying the likelihood |${\cal {L}}({\boldsymbol p})$|⁠. Actually, in order to efficiently sample the |${\cal {N}}$|-dimensional parameter space, we use the Markov Chain Monte Carlo (MCMC) method running five parallel chains and using the Gelman–Rubin convergence test. It is worth noting that the Gelman–Rubin diagnostic uses parallel chains with dispersed initial values to test whether they all converge to the same target distribution. Failure could indicate the presence of a multimode posterior distribution (different chains converge to different local modes) or the need to run a longer chain. As a test instrument it uses the reduction factor R, which is the square root of the ratio of the between-chain variance and the within-chain variance. A large R indicates that the between-chain variance is substantially greater than the within-chain variance, so that longer simulation is needed. We want that R converges to 1 for each parameter. We set R − 1 of order 0.05, which is more restrictive than the often used and recommended value R − 1 < 0.1 for standard cosmological investigations. We then test the convergence of the chains by the Gelman and Rubin criterion. Moreover, in order to reduce the uncertainties on EOS parameters, since methods like the MCMC are based on an algorithm that moves randomly in the parameter space, we a priori impose some basic consistency constraints on the positiveness of H2(z) and dL(z). We first run our chains to compute the likelihood in equations (28) and/or (29), using as starting points the best-fitting values obtained in our pre-statistical analysis, in order to select the starting points. Therefore, we perform the same MCMC calculation to evaluate the likelihood in equation (30), combining the SNIa HD, the BAO and H(z) data with the GRBs HD, respectively, as described above. We throw away first 30 per cent of the points iterations at the beginning of any MCMC run, and we thin the many times run chains. We finally extract the constraints on EOS parameters, co-adding the thinned chains. The histograms of the parameters from the merged chain are then used to infer median values and confidence ranges. Actually, the confidence levels are estimated from the final sample (the merged chain): the 15.87th and 84.13th quantiles define the 68 per cent confidence interval; the 2.28th and 97.72th quantiles define the 95 per cent confidence interval; and the 0.13th and 99.87th quantiles define the 99 per cent confidence interval. In Table 1, we present the results of our analysis. It turns out that for all the data which have been considered some indications are present for a time evolution of the dark energy EOS. 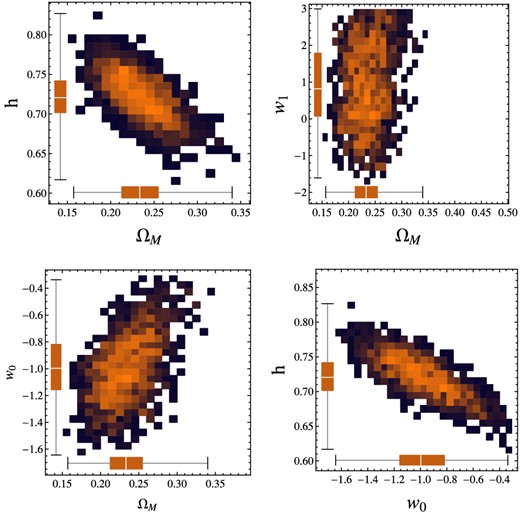The joint probability for different couples of parameters which characterize the CPL EOS, are shown in Fig. 2. Our statistical analysis has been performed introducing a parametrized redshift variable, the so-called y-redshift
(32)
which maps the z-interval [0, ∞] into the y-interval [0, 1]. This choice facilitates the comparison between the present results and the cosmographic analysis. On the other hand, it is well known that the likelihood analysis alone cannot provide an effective way to discriminate between different models. Thus, in our analysis, we use the so-called BIC as selection criterion (Schwarz 1978), defined as
(33)
where |$\mathcal {L}_{{\rm max}}$|⁠, k and N are the maximum likelihood, the number of parameters characterizing the models, and the number of data points, respectively. According to this selection criterion, a positive evidence against the model with the higher BIC is defined by a difference ΔBIC = 2 and a strong evidence is defined by ΔBIC = 6. Applying such a test to our three parametrizations for the EOS, we evaluate ΔBIC for each model, relative to the CPL model: it turns out that ΔBIC > 6, only for the 3D parametrization |$w(z)=\frac{w_1 (1-\cos (\delta \log (z+1)))}{\log (z+1)}+w_0$|⁠, pointing out a strong evidence against this model. In the case of the oscillating EOS |$w_0+w_1 (\frac{\sin (z+1)}{z+1}-\sin (1))$|⁠, we find out ΔBIC ≃ 5.9, underlying a certain (weak) positive evidence against such a parametrization. In Fig. 3, we show the redshift dependence of the CPL EOS for different values of the EOS parameters w0 and w1, and in Fig. 2 we show the joint probability for different couple of parameters for the CPL parametrization. From our investigation, we find slight indication for a non-constant EOS, w, in any considered parametrization, even if the cosmological constant is not ruled out from these observations. It turns out that the constraints on the EOS parameters can be strengthen if they are cross-checked with the results of the cosmographic analysis performed on the same data sets in Demianski et al. (2012). Without loss of generality, we can actually invert the equation (16) for the CPL parametrization, which is favourite by our analysis according to the BIC criterion, and obtain the cosmographic parameters q0 and j0, as functions of the EOS parameters
(34)
(35)
The joint probability for different couples of parameters which characterize the CPL EOS, as provided by our analysis. On the axes are plotted the box-and-whisker diagrams relatively to the different parameters: the bottom and top of the diagrams are the 25th and 75th percentile (the lower and upper quartiles, respectively), and the band near the middle of the box is the 50th percentile (the median).
Figure 2.

The joint probability for different couples of parameters which characterize the CPL EOS, as provided by our analysis. On the axes are plotted the box-and-whisker diagrams relatively to the different parameters: the bottom and top of the diagrams are the 25th and 75th percentile (the lower and upper quartiles, respectively), and the band near the middle of the box is the 50th percentile (the median).

Open in new tabDownload slide
Table 1.
Open in new tab

Constraints on the EOS parameters for different parametrization. Columns report best-fitting (xbf), mean (〈x〉) and median (⁠|$\tilde{x}$|⁠) values and the 68 and 95 per cent confidence limits.

Idxbf〈x〉|$\tilde{x}$|68% CL95% CL
w(z) = w0 + w1z(1 + z)−1
ΩM0.2250.2380.237(0.206, 0.272)(0.183, 0.305)
h0.7320.7140.713(0.68, 0.745)(0.659, 0.778)
w0−1.15−0.832−0.834(−1.17, -0.476)(−1.41, −0.36)
w1−0.99−1.06−1.05(−2.2, 0.037)(−2.8, 0.74)
|$w_0+w_1 (\frac{\sin (z+1)}{z+1}-\sin (1))$|
ΩM0.2250.2350.234(0.205, 0.264)(0.182, 0.294)
h0.7350.720.72(0.69, 0.75)(0.66, 0.78)
w0−1.01−0.96−1.0(−1.23, −0.742)(−1.43, −0.493)
w10.140.880.82(−0.27, 2.1)(−1.18, 2.8)
|$w(z)=\frac{w_1 (1-\cos (\delta \log (z+1)))}{\log (z+1)}+w_0$|
ΩM0.150.1540.153(0.15, 0.21)(0.13, 0.24)
h0.70.730.73(0.72, 0.75)(0.7, 0.78)
w0−1.55−1.54−1.55(−1.59, −1.48)(−1.66, −1.45)
w10.450.470.37(0.07, 0.78)(0.013, 1.9)
δ0.760.660.62(0.54, 0.8)(0.5, 1.1)
Idxbf〈x〉|$\tilde{x}$|68% CL95% CL
w(z) = w0 + w1z(1 + z)−1
ΩM0.2250.2380.237(0.206, 0.272)(0.183, 0.305)
h0.7320.7140.713(0.68, 0.745)(0.659, 0.778)
w0−1.15−0.832−0.834(−1.17, -0.476)(−1.41, −0.36)
w1−0.99−1.06−1.05(−2.2, 0.037)(−2.8, 0.74)
|$w_0+w_1 (\frac{\sin (z+1)}{z+1}-\sin (1))$|
ΩM0.2250.2350.234(0.205, 0.264)(0.182, 0.294)
h0.7350.720.72(0.69, 0.75)(0.66, 0.78)
w0−1.01−0.96−1.0(−1.23, −0.742)(−1.43, −0.493)
w10.140.880.82(−0.27, 2.1)(−1.18, 2.8)
|$w(z)=\frac{w_1 (1-\cos (\delta \log (z+1)))}{\log (z+1)}+w_0$|
ΩM0.150.1540.153(0.15, 0.21)(0.13, 0.24)
h0.70.730.73(0.72, 0.75)(0.7, 0.78)
w0−1.55−1.54−1.55(−1.59, −1.48)(−1.66, −1.45)
w10.450.470.37(0.07, 0.78)(0.013, 1.9)
δ0.760.660.62(0.54, 0.8)(0.5, 1.1)
Table 1.
Open in new tab

Constraints on the EOS parameters for different parametrization. Columns report best-fitting (xbf), mean (〈x〉) and median (⁠|$\tilde{x}$|⁠) values and the 68 and 95 per cent confidence limits.

Idxbf〈x〉|$\tilde{x}$|68% CL95% CL
w(z) = w0 + w1z(1 + z)−1
ΩM0.2250.2380.237(0.206, 0.272)(0.183, 0.305)
h0.7320.7140.713(0.68, 0.745)(0.659, 0.778)
w0−1.15−0.832−0.834(−1.17, -0.476)(−1.41, −0.36)
w1−0.99−1.06−1.05(−2.2, 0.037)(−2.8, 0.74)
|$w_0+w_1 (\frac{\sin (z+1)}{z+1}-\sin (1))$|
ΩM0.2250.2350.234(0.205, 0.264)(0.182, 0.294)
h0.7350.720.72(0.69, 0.75)(0.66, 0.78)
w0−1.01−0.96−1.0(−1.23, −0.742)(−1.43, −0.493)
w10.140.880.82(−0.27, 2.1)(−1.18, 2.8)
|$w(z)=\frac{w_1 (1-\cos (\delta \log (z+1)))}{\log (z+1)}+w_0$|
ΩM0.150.1540.153(0.15, 0.21)(0.13, 0.24)
h0.70.730.73(0.72, 0.75)(0.7, 0.78)
w0−1.55−1.54−1.55(−1.59, −1.48)(−1.66, −1.45)
w10.450.470.37(0.07, 0.78)(0.013, 1.9)
δ0.760.660.62(0.54, 0.8)(0.5, 1.1)
Idxbf〈x〉|$\tilde{x}$|68% CL95% CL
w(z) = w0 + w1z(1 + z)−1
ΩM0.2250.2380.237(0.206, 0.272)(0.183, 0.305)
h0.7320.7140.713(0.68, 0.745)(0.659, 0.778)
w0−1.15−0.832−0.834(−1.17, -0.476)(−1.41, −0.36)
w1−0.99−1.06−1.05(−2.2, 0.037)(−2.8, 0.74)
|$w_0+w_1 (\frac{\sin (z+1)}{z+1}-\sin (1))$|
ΩM0.2250.2350.234(0.205, 0.264)(0.182, 0.294)
h0.7350.720.72(0.69, 0.75)(0.66, 0.78)
w0−1.01−0.96−1.0(−1.23, −0.742)(−1.43, −0.493)
w10.140.880.82(−0.27, 2.1)(−1.18, 2.8)
|$w(z)=\frac{w_1 (1-\cos (\delta \log (z+1)))}{\log (z+1)}+w_0$|
ΩM0.150.1540.153(0.15, 0.21)(0.13, 0.24)
h0.70.730.73(0.72, 0.75)(0.7, 0.78)
w0−1.55−1.54−1.55(−1.59, −1.48)(−1.66, −1.45)
w10.450.470.37(0.07, 0.78)(0.013, 1.9)
δ0.760.660.62(0.54, 0.8)(0.5, 1.1)
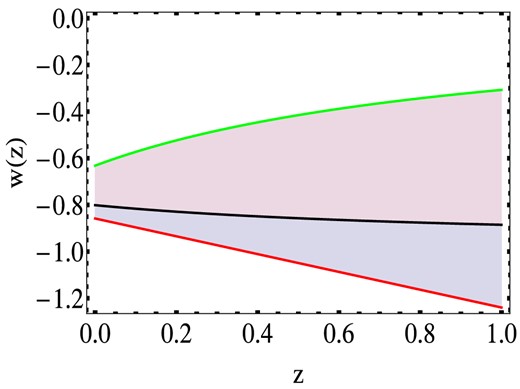
Redshift dependence of the CPL EOS for different values of the EOS parameters w0 and w1. The filled region corresponds to the allowed behaviour of the EOS, when the EOS parameters are varying within the 1σ range of confidence. Ωm is fixed and set to the best-fitting value. The solid black line corresponds to w0 = w0 bf, w1 = w1 bf.
Figure 3.

Redshift dependence of the CPL EOS for different values of the EOS parameters w0 and w1. The filled region corresponds to the allowed behaviour of the EOS, when the EOS parameters are varying within the 1σ range of confidence. Ωm is fixed and set to the best-fitting value. The solid black line corresponds to w0 = w0 bf, w1 = w1 bf.

Open in new tabDownload slide

In Figs 4 and 5, we show the behaviour of q0 as a function of w0 and the contour plots of j0 in the plane w0, w1, respectively. If we add to equations (34) and (35) the priors on the values of q0 and j0 obtained from the cosmographic analysis, it turns out that the range of confidence of the EOS parameters are squeezed at 1σ to w0 ∼ ∈(−0.87, −0.5) and w1 ∼ ∈(−0.3, 0.6). It is interesting to note, then, that the use of our large collection of present data sets, matched with the cosmographic analysis, allows us to improve the constraints on the dark energy EOS competitively with the improvements that can be achieved with future high-redshift SNeIa samples (see Salzano et al. 2013). Despite the remarkable improvements in the constraints on the EOS parameters, some caution is needed, due to the circumstance that the systems of algebraic equations in (16), and then their inverse, are highly non-linear. They admit multiple solutions for any assigned n-fold (q0, j0, s0, …), thus resulting in a strong degeneracy among the parameters, which is hard to manage. A possible strategy to ameliorate the maximum likelihood estimates could consist of incorporating the restrictions on the EOS parameters, coming from cosmography, in the likelihood itself. For this purpose, in a forthcoming paper we plan to implement at least two possibilities:

  • to use a constrained optimizer in maximizing the log-likelihood function,

  • to reparametrize the log-likelihood in such a way that the constraints are eliminated.

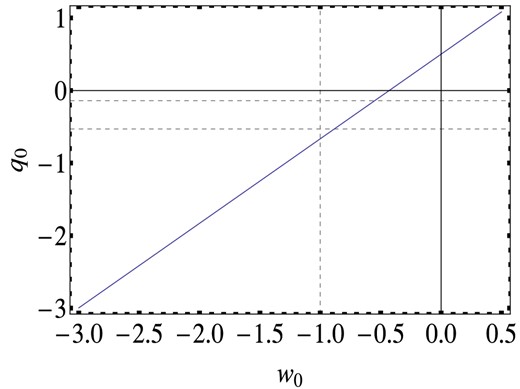
Behaviour of q0 as a function of w0 for Ωm = 0.237, as results from equation (34).The horizontal dashed lines correspond to the 2σ range of confidence for q0.
Figure 4.

Behaviour of q0 as a function of w0 for Ωm = 0.237, as results from equation (34).The horizontal dashed lines correspond to the 2σ range of confidence for q0.

Open in new tabDownload slide
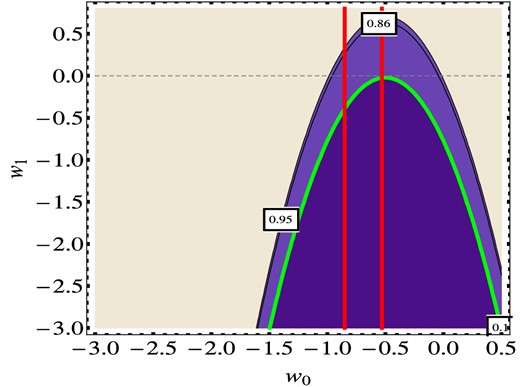
Contour plots of the jerk j0 in the plane w0, w1 for a CPL EOS parametrization, as provided by the cosmographic analysis. The value of Ωm is set at its median value Ωm = 0.237.
Figure 5.

Contour plots of the jerk j0 in the plane w0, w1 for a CPL EOS parametrization, as provided by the cosmographic analysis. The value of Ωm is set at its median value Ωm = 0.237.

Open in new tabDownload slide
On the other hand, let us note that in Daly & Djorgovski (2003, 2004, 2008) a numerical method for a direct determination, i.e. a determination from the data, of the expansion deceleration parameter, q(z), in terms of the coordinate distance |$\mathcal {Y}(z)$|⁠, has been developed (and then revised in Lazkoz et al. 2012), through the equation
(36)
valid for flat models. This expression for q(z) is valid for any homogeneous and isotropic Universe in which (1 + z) = a0/a(t), and it is therefore quite general and can be compared with any model to account for the accelerated expansion of the Universe. Using the derivation rule
(37)
we can reconstruct also q(y). This approach has the advantage to be free from any assumptions about the nature of the dark energy, but it introduces rather large errors in the estimation of q(y), since the numerical derivation is very sensitive to the size and quality of data. In Fig. 6, we compare the q(y) obtained by Daly & Djorgovski from their full data set with the q(z, θ), reconstructed by using equation (21) for any considered EOS parametrization, and also the cosmographicq(y). It is interesting to note that the cosmographically reconstructed q(y) lies completely within the region allowed by the data.
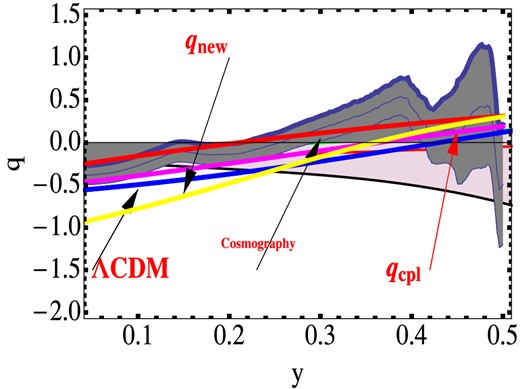
Reconstruction of deceleration history: the allowed region for q(z), obtained by Daly & Djorgovski, from the full data set is represented by the shadow area. The coloured solid line shows the deceleration function, q(z) for different EOS parametrization, as indicated by a label (the label new indicates the parametrization in equation 11). The red solid line shows the q(z) reconstruction obtained from the cosmography: it is interesting to note that it is all within the region allowed by the data.
Figure 6.

Reconstruction of deceleration history: the allowed region for q(z), obtained by Daly & Djorgovski, from the full data set is represented by the shadow area. The coloured solid line shows the deceleration function, q(z) for different EOS parametrization, as indicated by a label (the label new indicates the parametrization in equation 11). The red solid line shows the q(z) reconstruction obtained from the cosmography: it is interesting to note that it is all within the region allowed by the data.

Open in new tabDownload slide

4.1 Discussion

In the previous analysis exact flatness, i.e. Ωk = 0, has been assumed, in agreement with what is inferred from CMBR anisotropy spectrum. Indeed, the Planck analysis of the CMB is deeply consistent with a spatially flat universe. Here, however, we want to investigate whether and how strongly the constraints on the dark energy EOS change, if the curvature contribution is included in the analysis. We first forecast the sensitivity of the modulus of distance |$\mu (z, \boldsymbol { \theta })$| on Ωk as a function of both the fiducial cosmological model (with its own parameters |$\boldsymbol {\theta }$|⁠), and the redshift. To this end, we fix a flat fiducial cosmological model, constructing the corresponding |$\mu _{{\rm fid}}(z, \boldsymbol { \theta })$|⁠, and evaluate the percentage error on the modulus of distance with respect to a randomly generated high-redshift Hubble diagram, in the framework of a not flat cosmological model. As fiducial models, we consider a flat ΛCDM model and a flat CPL quintessence model. We compare both of them with a not flat CPL quintessence model. It turns out that the maximum percentage error, also considering a simulated Hubble diagram consisting of 5000 objects is about 4-5 per cent, also if non-physical values of the curvature parameters are allowed, as shown in Fig. 7. In Fig. 8, indeed, again the distribution of the percentage error provided by a simulated SNeIa data set is shown. The error on the simulated μSNeIa are estimated as
(38)
with zmax the maximum redshift of the sample, σsys an intrinsic scatter and σm is related to the measurements accuracy. In this case, zmax = 1.4, σsys = 0.15 and σm = 0.02 (Cardone et al. 2012).
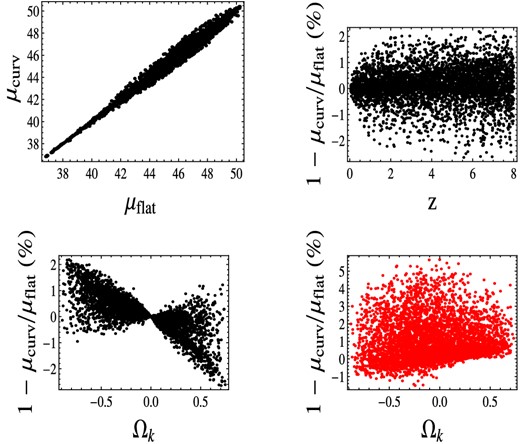
Percentage error on the modulus of distance with respect to a randomly generated Hubble diagram, in the case of a not flat cosmological model. As fiducial models, we consider a flat CPL quintessence (black points), and a flat ΛCDM (red points). In order to produce the μsimulated, ΩΛ, Ωk and the EOS parameters, w0 and w1 are variated. The Hubble constant is set at h = 0.68. The maximum relative dispersion is about 2 per cent for a flat CPL model, and reaches at most 4–5 per cent in the case of a ΛCDM model, even if unreasonable values of Ωk are allowed. It is worth noting that the GRBs Hubble diagram is ranked in the range of redshift where the dispersion reaches its own maximum (upper panel- right-hand side).
Figure 7.

Percentage error on the modulus of distance with respect to a randomly generated Hubble diagram, in the case of a not flat cosmological model. As fiducial models, we consider a flat CPL quintessence (black points), and a flat ΛCDM (red points). In order to produce the μsimulated, ΩΛ, Ωk and the EOS parameters, w0 and w1 are variated. The Hubble constant is set at h = 0.68. The maximum relative dispersion is about 2 per cent for a flat CPL model, and reaches at most 4–5 per cent in the case of a ΛCDM model, even if unreasonable values of Ωk are allowed. It is worth noting that the GRBs Hubble diagram is ranked in the range of redshift where the dispersion reaches its own maximum (upper panel- right-hand side).

Open in new tabDownload slide
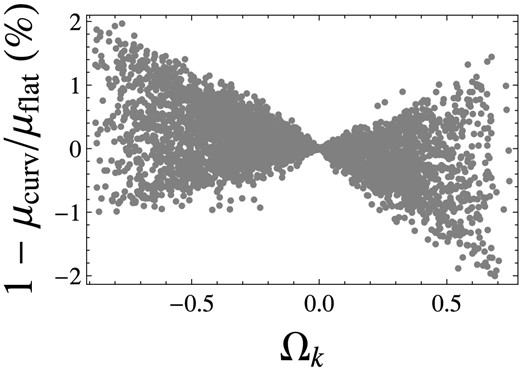
The percentage error as function of the curvature parameters in the case of a simulated SNeIa Hubble diagram for a flat CPL fiducial model.
Figure 8.

The percentage error as function of the curvature parameters in the case of a simulated SNeIa Hubble diagram for a flat CPL fiducial model.

Open in new tabDownload slide

It turns out that in the case of the simulated SNeIa Hubble diagram the scatter of the percentage error is further reduced. Moreover, we perform our analysis with the assumption of curvature included, limited to the CPL model. In order to test whether the statistical significance of our results is meaningfully overestimated by possible biases due to the GRBs calibration procedure (based on the SNeIa data set), we use GRBs only. We find that the main results of our analysis remain and

  • pieces of evidence for a time evolution of the EOS in such a parametrization are, indeed, confirmed;

  • the cosmological constant is not favourite, but is not ruled out from the analysis;

  • the very small value of Ωk is recovered.

Actually, it is worth noting that the GRBs Hubble diagram alone provides |$\Omega _{\rm k}^{{\rm median}}= -0.006$| and for the range of confidence at 1σ (−0.0073, 0.006), in agreement with the CMBR measurements. |$\Omega _{\rm m}^{{\rm median}}= 0.2465$|⁠, and the 1σ confidence range is (0.157, 0.540). Moreover, for what it concerns the parameters of the EOS parametrization, it turns out that

  • the estimated w0 is shifted with respect to the flat case, being |$w_0^{{\rm median}} = -0.71$|⁠, but the confidence range is rather stable, being (−1.05, 0.1);

  • w1 is weakly constrained, with |$w_1^{{\rm median}}=-0.24$| and the 1σ confidence range is rather stable, being (−1.05, 0.1).

This circumstance is not surprising, since the introduction of an additional dimension in the parameter space induced a strong degeneracy among Ωk, w0 and w1, as shown in Fig. 9, especially if the curvature density is restricted to the range allowed by the first cosmological Planck release, when the errors are actually dominated by the EOS.

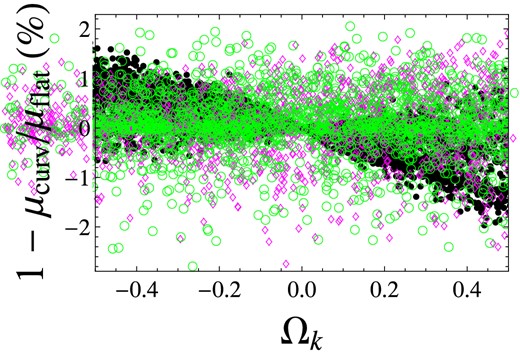
Comparison among the sensitivity of the modulus of distance $\mu (z, \boldsymbol { \theta })$ on the curvature parameters (background black points), and the EOS parameters w0 and w1 (foreground magenta and green points, respectively). It is evidence of the strong degeneracy among Ωk, w0 and w1.
Figure 9.

Comparison among the sensitivity of the modulus of distance |$\mu (z, \boldsymbol { \theta })$| on the curvature parameters (background black points), and the EOS parameters w0 and w1 (foreground magenta and green points, respectively). It is evidence of the strong degeneracy among Ωk, w0 and w1.

Open in new tabDownload slide

5 CONCLUSIONS

In this work, we have presented constraints on the dark energy EOS obtained by using an updated collection of observational data sets. In particular, we are looking for any indications of a deviation from the w(z) ≠ −1 come to light, reflecting the possibility of a deviation from the ΛCDM cosmological model. To accomplish this task, we focus on a direct and full reconstruction of the dark energy EOS through several parametrizations, widely used in the literature. We have found indications for a time evolution of the EOS in any considered parametrization, even if the cosmological constant is not ruled out from these observations. To discriminate between different models, we use the so-called BIC as selection criterion (Schwarz 1978): it turns out that the CPL parametrization is favoured by the data. Actually, we evaluated ΔBIC for each model, relative to the CPL model: it turns out that ΔBIC > 6, only for the 3D parametrization |$w(z)=\frac{w_1 (1-\cos (\delta \log (z+1)))}{\log (z+1)}+w_0$|⁠, pointing out a strong evidence against this model. In the case of the oscillating EOS |$w_0+w_1 (\frac{\sin (z+1)}{z+1}-\sin (1))$|⁠, we find out ΔBIC ≃ 5.9, underlying a certain (weak) positive evidence against such parametrization. It turns out that for the CPL parametrization |$w_0^{{\rm median}}=-0.834$|⁠, and the range of confidence at 1σ is w0 ∼ ∈(−1.17, −0.476); |$w_1^{{\rm median}}=-1.05$| and w1 ∼ ∈(−2.2, 0.037). Moreover, it turns out that if we include in the space of parameters w0 − w1 the priors on the values of q0 and j0 obtained from the cosmographic analysis, the constraints on the EOS can be improved competitively with the improvements achieved with future high-redshift SNeIa samples: the range of confidence is, indeed, squeezed at 1σ to w0 ∼ ∈(−0.87, −0.5) and w1 ∼ ∈(−0.3, 0.6). However, since the map connecting the cosmographic and the EOS parameters is highly non-linear a strong degeneracy among the parameters is observed, which is hard to manage. Finally, we reconstruct the deceleration parameter q(z) for any considered EOS parametrization, comparing it with the q(z) obtained from observational data set, and with the cosmographicqcosmographic(z). It is interesting to note that just this qcosmographic(z) lies within the region allowed by the data, thus indicating that a possible strategy to ameliorate the EOS analysis and taking into the account the cosmography results, could consist of setting up a sort of constrained maximum likelihood estimate within the MCMCs, as we intend to perform in an upcoming paper. Finally, we also investigated whether and how strongly the constraints on the dark energy EOS change, if the curvature contribution is included in the analysis. We restricted our test to the CPL EOS, as exemplum. It turns out that, the main results are confirmed, and the ranges of confidence are stable, even if unreasonable values of Ωk are allowed. The main difference consists in the appearance of a strong degeneration among the cosmological parameters Ωk, w0 and w1. It is worth noting that the GRBs Hubble diagram provides as estimate for the curvature parameter |$\Omega _{\rm k}^{{\rm median}}= -0.006$|⁠, and the 1σ confidence range is (−0.0073, 0.006), and |$\Omega _{\rm m}^{{\rm median}}=0.32$| in full agreement with the CMBR Planck measurements.

EP, MDL and PS acknowledge the support of INFN Sez. di Napoli (iniziativa Specifica CQSKY), and also EP and MDL acknowledge the support of INFN Sez. di Napoli (Iniziativa Specifica TEONGRAV). MDL is supported by MIUR (PRIN 2009).

REFERENCES

Amati
L.
Guidorzi
C.
Frontera
F.
Della Valle
M.
Finelli
F.
Landi
R.
Montanari
E.
, 
MNRAS
,
2008
, vol.
391
pg.
577
Crossref
Search ADS
 
Amati
L.
Frontera
F.
Guidorzi
C.
, 
A&A
,
2009
, vol.
508
pg.
173
Crossref
Search ADS
 
Astier
P.
et al. , 
A&A
,
2006
, vol.
447
pg.
31
Crossref
Search ADS
 
Bloom
J. S.
Frail
D. A.
Kulkarini
S. R.
, 
ApJ
,
2003
, vol.
594
pg.
674
Crossref
Search ADS
 
Bond
J. R.
Efstathiou
G.
Tegmark
M.
, 
MNRAS
,
1997
, vol.
291
pg.
L33
 
Bradley
S.
, 
ApJ
,
2003
, vol.
583
pg.
L67
Crossref
Search ADS
 
Capozziello
S.
De Laurentis
M.
, 
Phys. Rep.
,
2011
, vol.
509
pg.
167
Crossref
Search ADS
 
Cardone
V. F.
Spiro
S.
Hooki
I.
Scaramella
R.
, 
Phys. Rev. D
,
2012
, vol.
85
pg.
123510
Crossref
Search ADS
 
Chevallier
M.
Polarski
D.
, 
Int. J. Mod. Phys. D
,
2001
, vol.
10
pg.
213
Crossref
Search ADS
 
Clarkson
C.
, 
C. R. Phys.
,
2012
, vol.
13
pg.
682
Crossref
Search ADS
 
Clarkson
C.
Zunckel
C.
, 
Phys. Rev. Lett.
,
2010
, vol.
104
pg.
211301
Crossref
Search ADS
PubMed
 
Dai
Z. G.
Liang
E. W.
Xu
D.
, 
ApJ
,
2004
, vol.
612
pg.
L101
Crossref
Search ADS
 
Daly
R. A.
Djorgovski
S. G.
, 
ApJ
,
2003
, vol.
597
pg.
9
Crossref
Search ADS
 
Daly
R. A.
Djorgovski
S. G.
, 
ApJ
,
2004
, vol.
612
pg.
652
Crossref
Search ADS
 
Daly
R. A.
Djorgovski
S. G.
, 
ApJ
,
2008
, vol.
677
pg.
1
Crossref
Search ADS
 
Demianski
M.
Piedipalumbo
E.
, 
MNRAS
,
2011
, vol.
415
pg.
3580
Crossref
Search ADS
 
Demianski
M.
Piedipalumbo
E.
Rubano
C.
, 
MNRAS
,
2011
, vol.
411
pg.
1213
Crossref
Search ADS
 
Demianski
M.
Piedipalumbo
E.
Rubano
C.
Scudellaro
P.
, 
MNRAS
,
2012
, vol.
426
pg.
13961415
Crossref
Search ADS
 
di Serafino
D.
Riccio
F.
, 
18th Euromicro Int. Conf. on Parallel, Distributed and Network-Based Processing, On the Application of Multiple-Deme Parallel Genetic Algorithms in Astrophysics
,
2010
IEEE
pg.
231

Google Scholar

OpenURL Placeholder Text

 
di Serafino
D.
Gomez
S.
Milano
L.
Riccio
F.
Toraldo
G.
, 
J. Global Optim.
,
2010
, vol.
48
pg.
41
Crossref
Search ADS
 
Efstathiou
G.
Bond
J. R.
, 
MNRAS
,
1999
, vol.
304
pg.
75
Crossref
Search ADS
 
Eisenstein
D. J.
Hu
W.
, 
ApJ
,
1998
, vol.
496
pg.
605
Crossref
Search ADS
 
Eisenstein
D. J.
et al. , 
ApJ
,
2005
, vol.
633
pg.
560
Crossref
Search ADS
 
Firmani
C.
Ghisellini
G.
Ghirlanda
G.
Avila-Reese
V.
, 
MNRAS
,
2005
, vol.
360
pg.
L1
Crossref
Search ADS
 
Komatsu
E.
et al. , 
ApJS
,
2011
, vol.
192
pg.
18
Crossref
Search ADS
 
Kowalski
M.
et al. , 
ApJ
,
2008
, vol.
686
pg.
749
Crossref
Search ADS
 
Lazkoz
R.
Salzano
V.
Sendra
I.
, 
Phys. Lett. B
,
2010
, vol.
694
pg.
198
Crossref
Search ADS
 
Lazkoz
R.
Salzano
V.
Sendra
I.
, 
Eur. Phys. J. C
,
2012
, vol.
72
pg.
2130
Crossref
Search ADS
 
Li
H.
Su
M.
Fan
Z.
Dai
Z.
Zhang
X.
, 
Phys. Lett. B
,
2008
, vol.
658
pg.
95
Crossref
Search ADS
 
Linder
E. V.
, 
Phys. Rev. Lett.
,
2003
, vol.
90
pg.
091301
Crossref
Search ADS
PubMed
 
Ma
J.-Z.
Zhang
Z.
, 
Phys. Lett. B
,
2011
, vol.
699
pg.
233
Crossref
Search ADS
 
Meszaros
P.
, 
Rep. Prog. Phys.
,
2006
, vol.
69
pg.
2259
Crossref
Search ADS
 
Nesseris
S.
Garcia-Bellido
J.
, 
J. Cosmol. Astropart. Phys.
,
2012
, vol.
1211
pg.
033
Crossref
Search ADS
 
Percival
W. J.
et al. , 
MNRAS
,
2010
, vol.
401
pg.
2148
Crossref
Search ADS
 
Planck Collaboration, Planck
. ,
2013
 
results. XVI. Cosmological parameters, A&A, preprint (arXiv:1303.5076)
Riess
A. G.
et al. , 
ApJ
,
2007
, vol.
659
pg.
98
Crossref
Search ADS
 
Riess
A. G.
et al. , 
ApJ
,
2009
, vol.
699
pg.
539
Crossref
Search ADS
 
Rubano
C.
Scudellaro
P.
, 
Gen. Rel. Grav.
,
2002
, vol.
34
pg.
1931
Crossref
Search ADS
 
Sahni
V.
Saini
T. D.
Starobinsky
A. A.
Alam
U.
, 
J. Exp. Theor. Phys. Lett.
,
2003
, vol.
77
pg.
201
Crossref
Search ADS
 
Sahni
N.
Baccigalupi
C.
Martinelli
M.
Melchiorri
A.
Silvestri
A.
, 
Phys. Rev. D
,
2013
, vol.
88
pg.
043515
Crossref
Search ADS
 
Saini
T. D.
Raychaudhury
S.
Sahni
V.
Starobinsky
A. A.
, 
Phys. Rev. Lett.
,
2000
, vol.
85
pg.
6
Crossref
Search ADS
PubMed
 
Salzano
V.
Rodney
S. A.
Sendra
I.
Lazkoz
R.
Riess
A. G.
Postmann
M.
Broadhurst
T.
Coe
D.
, 
A&A
,
2013
, vol.
557
pg.
A64
Crossref
Search ADS
 
Schaefer
B. E.
, 
ApJ
,
2003
, vol.
583
pg.
L67
Crossref
Search ADS
 
Schaefer
B. E.
, 
ApJ
,
2007
, vol.
660
pg.
16
Crossref
Search ADS
 
Schwarz
G.
, 
Ann. Stat.
,
1978
, vol.
6
pg.
461
Crossref
Search ADS
 
Spergel
D. N.
et al. , 
ApJS
,
2007
, vol.
170
pg.
377
Crossref
Search ADS
 
Stern
D.
Jimenez
R.
Verde
L.
Kamionkowski
M.
Stanford
S. A.
, 
J. Cosmol. Astropart. Phys.
,
2010
, vol.
02
pg.
008
Crossref
Search ADS
 
Suzuki
et al. , 
ApJ
,
2012
, vol.
746
pg.
85
 
(The Supernova Cosmology Project)
Crossref
Search ADS
 
Tsutsui
R.
Nakamura
T.
Yonetoku
D.
Murakami
T.
Tanabe
S.
Kodama
Y.
Takahashi
K.
, 
MNRAS
,
2009
, vol.
394
pg.
L31
Crossref
Search ADS
 
Valkenburg
W.
Kunz
M.
Marra
V.
, 
Phys. Dark Univ.
,
2013
, vol.
2
pg.
219
 
(Paper II)
Crossref
Search ADS
 
Valkenburg
W.
Marra
V.
Clarkson
C.
, 
MNRAS
,
2013
 
Advanced Access, 5 (Paper I)
Wang
F. Y.
Qi
S.
Dai
Z. G.
, 
MNRAS
,
2011a
, vol.
415
pg.
3423
Crossref
Search ADS
 
Wang
F. Y.
Dai
Z. G.
, 
A&A
,
2011b
, vol.
536
pg.
96
Crossref
Search ADS
 
© 2014 The Authors Published by Oxford University Press on behalf of the Royal Astronomical Society
Issue Section:
Article
Download all slides