Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

Abstract

The dynamics of polar oscillations of compact stars are conventionally described by a set of coupled differential equations and the roles that space–time and matter play in such oscillations are consequently difficult to track. In this paper, we develop a scheme for polar oscillations in terms of one space–time and one matter variables. With our judicious choice of variables, the coupling between space–time and matter is weak, which enables the separation of these two parties. Two independent second-order ordinary differential equations are obtained, corresponding to the Cowling and inverse-Cowling approximations, and leading to accurate determination of p- and w-mode quasi-normal modes, respectively, in a unified framework.

asteroseismology, equation of state, gravitation, gravitational waves, stars: neutron, stars: oscillations

1 INTRODUCTION

Compact stars, including neutron stars (NSs) and quark stars (QSs), are notable for the high density achievable at their centres and the huge gravitational field surrounding them. Their internal structure is often the ideal test bed for the equation of state (EOS) of nuclear (or quark) matter and can provide clues to the interactions between elementary particles as well (see, e.g., Glendenning 1997; Weber 1999; Lattimer & Prakash 2007; Lattimer 2012, and references therein). Gravitational waves (GWs) emitted from oscillating NSs (or QSs) are expected to carry rich information about their internal structures and hence the physics of dense matter as well, giving rise to various efforts to infer the properties of relativistic compact stars from close examination of their oscillation spectra (see, e.g., Andersson & Kokkotas 1996, 1998; Benhar, Berti & Ferrari 1999; Kokkotas, Apostolatos & Andersson 2001; Benhar, Ferrari & Gualtieri 2004; Tsui & Leung 2005a; Tsui, Leung & Wu 2006; Lau, Leung & Lin 2010; Sotani et al. 2011; Doneva et al. 2013). Although the oscillation frequencies of NSs usually lie outside the sensitivity window of the existing GW detectors such as GEO600, LIGO I, TAMA300 and VIRGO (see, e.g., Fryer, Holz & Hughes 2002; Hughes 2003), with the advent of more sensitive third-generation GW telescopes (e.g., the proposed Einstein Telescope; see Andersson et al. 2011; Hild et al. 2011), it is probable that the structure and the composition of a compact star can be inferred from its GW signals in the coming future.

The fully relativistic formulation of stellar pulsations was first founded by Thorne & Campolattaro (1967) and since then alternative approaches to such processes have emerged in the literature (see, e.g., Lindblom & Detweiler 1983; Detweiler & Lindblom 1985; Chandrasekhar & Ferrari 1991; Lindblom, Mendell & Ipser 1997; Kokkotas & Schmidt 1999). Basically, oscillations of compact stars are classified into axial and polar types. For axial-type oscillations, the matter forming a star is essentially a spectator and only the space–time surrounding the star pulsates. For polar-type oscillations, matter motion and space–time variation are, however, coupled together. To describe such coupled motion, different forms of equations of motion have been proposed since the pioneering work of Thorne & Campolattaro (1967). For example, based on Thorne & Campolattaro (1967), Lindblom & Detweiler (1983) and Detweiler & Lindblom (1985) described the system with four coupled first-order ODEs in four variables (termed as the LD formalism in this paper), which can be readily solved numerically. Later, to draw an analogy between the oscillations of relativistic and Newtonian stars, Lindblom et al. (1997) proposed a new formalism to describe the coupled oscillation with two second-order equations (termed as the LMI formalism), which reduce directly into the corresponding Newtonian equations under the weak field limit. In another relativistic stellar pulsation formalism proposed by Allen et al. (1998) (termed as the AAKS formalism in this paper), variations in matter and space–time are described by one matter variable and two metric variables. The three variables are governed by three coupled second-order time-dependent wave equations. Allen et al. (1998) managed to evolve these three variables numerically in the time domain for certain sets of initial conditions and studied the characteristics of the GWs emitted in such cases.

Polar-type oscillations are very much involved in dynamical processes such as supernova and binary mergers of NSs. The interplay between space–time and matter in polar oscillations of compact stars, however, often poses hurdles for developing a firm grasp of these phenomena. To trace the individual roles played by matter and space–time components, different variants of the Cowling approximation (CA), where effects of metric perturbations are neglected (McDermott, Horn & Scholl 1983; Finn 1988; Lindblom & Splinter 1990; Lindblom et al. 1997), and the inverse-Cowling approximation (ICA), where fluid motion is ignored (Andersson, Kokkotas & Schutz 1996; Wu & Leung 2007), have been proposed. These approximations vary in the choice of the physical variable measuring the matter or space–time component and lead to different degrees of accuracy (see the above-mentioned references).

In this paper, we study polar oscillations with quasi-normal mode (QNM) analysis. QNMs are oscillation modes with all dynamical variables decaying exponentially in time (Press 1971; Leaver 1986; Ching et al. 1998; Kokkotas & Schmidt 1999; Berti, Cardoso & Starinets 2009; Konoplya & Zhidenko 2011). Mathematically, the perturbation variables are assumed to have the e− iωt dependence, where the eigenfrequency ω ≡ ωr − iωi is complex-valued with ωi ≥ 0 measuring the decay rate of the mode. QNMs of compact stars reveal the physical characteristics (e.g., mass, radius, moment of inertia, EOS and composition) of a star (see, e.g., Andersson & Kokkotas 1996, 1998; Benhar et al. 1999, 2004; Kokkotas et al. 2001; Tsui & Leung 2005a; Tsui et al. 2006; Lau et al. 2010). Polar QNMs of compact stars can be classified into the fluid mode, including the fundamental f mode, the pressure p mode and the gravity g mode according to the nature of respective restoring forces (Cowling 1941) and the space–time w mode which has no Newtonian counterpart.

The aim of this paper is to propose a physically more transparent picture for polar oscillations of compact stars. Two coupled second-order differential equations in the frequency domain, involving one matter field and one space–time variable used in the AAKS formalism, are derived (see Section 2 and Appendix A). Our judicious choice of the two variables enables a straightforward decoupling of the two equations, leading to two independent equations accurately describing fluid modes (especially p modes) and the w modes, respectively (see Section 3). Hence, in a unified framework, we simultaneously establish both CA and ICA, which can lead to much improved accuracies in comparison with other approximation schemes proposed previously (see Sections 4 and 5, respectively). Under the current CA, fluid motion is governed by a Sturm–Liouville eigenvalue system, where completeness and orthogonality relations hold as usual (see, e.g., Morse & Feshbach 1953). Therefore, the fluid system is a conservative one and can be studied with conventional normal-mode analysis. The mode with the lowest eigenfrequency indeed corresponds to the f mode, while the following modes are good approximations for the successive p modes. Besides, we also find that other variants of CA (McDermott et al. 1983; Finn 1988) can also be recast into a form analogous to ours, save the difference in two parameters. As regards the present ICA, to our knowledge, this is the first time that an approximate single second-order differential equation describing polar w-mode QNMs, which has been numerically verified to lead accuracies much better than one percent, has been formulated.

Geometric units in which G = c = 1 are adopted throughout this paper. We consider polar oscillations of a non-rotating compact star of perfect fluid with radius R and total mass M. Unless stated otherwise, all numerical values of frequencies are measured in units of M−1 and evaluated for the case where the angular momentum index l equals 2. Besides, we also assume that the effect of temperature on the EOS of nuclear matter is negligible, and hence g modes are omitted in our discussion. In order not to divert the reader's attention from the main physical findings achieved in the paper, we put most of the mathematical details in three appendices.

2 TWO-VARIABLE SCHEME FOR POLAR QNMs

2.1 Three-variable scheme

When a static compact star is perturbed, its fluid and space–time acquire small-amplitude, time-dependent perturbations about the equilibrium state. These perturbations are first decomposed into tensorial and vectorial spherical harmonics Ylm(θ, ψ) with angular momenta {lm} and then separated into axial and polar parts according to parity. The perturbed line element of polar parity in the Regge–Wheeler (RW) gauge is (Regge & Wheeler 1957; Thorne & Campolattaro 1967; Price & Thorne 1969; Kojima 1992)
(1)
where the convention of the metric follows that used in Kojima (1992) and eν and eλ are characteristics of the star at equilibrium (see, e.g., chapter 2, Glendenning 1997).
In the AAKS formalism (Allen et al. 1998), polar oscillations of compact stars are described by two space–time metric variables F, S and one fluid perturbation variable H, which are related to the above metric perturbations and the Eulerian change in pressure δp as follows:
(2)
The three variables S, F and H satisfy three coupled second-order differential equations and a Hamiltonian constraint (see Appendix A).
It has been shown that inside the star and in the weak field limit K and H0 are related to the perturbation in the Newtonian potential U1 by (Thorne 1969)
(3)
Therefore, following directly from equation (2), to leading orders in field strengths, S and F measure the relativistic and Newtonian effects of gravity, respectively. Hence, in order to describe generation of GWs, which is the dominant process in the space–time mode, S is the right variable to keep. On the other hand, H is proportional to the Eulerian change in pressure and describes the motion of matter. We therefore eliminate the variable F in the AAKS formalism and establish a scheme with one space–time variable S and one matter variable H.

2.2 Two-variable scheme

For QNMs, the three field variables in AAKS formalism take the time dependence e− iωt, e.g., S(r, t) = S(r)e− iωt, etc. A two-variable scheme is achievable by eliminating one of these three variables in the frequency domain. In particular, in the so-called H–S scheme, the variable F(r) and its derivative are expressed in terms of S(r), H(r) and their derivatives (see Appendix B). Two coupled second-order ODEs inside the star are then readily obtained as
(4)
(5)
where
\begin{eqnarray*} V_{S0}(r) &=& \frac{2{\rm e}^{\nu }}{r^3}\left[(n+1)r-2\pi r^3(\rho +3p)-m\right],\\ V_{H0}(r) &=& \frac{2{\rm e}^{\nu }}{r^2}\left[n+1-2\pi r^2(\rho +p)\left(3+\frac{1}{C_s^2}\right)\right],\\ V_{H1}(r) &=& \frac{{\rm e}^{(\nu +\lambda )/2}}{r^2}\left[(m+4\pi pr^3)\left(1-\frac{1}{C_s^2}\right)+2(r-2m)\right], \end{eqnarray*}
with n = (l + 2)(l − 1)/2, the tortoise coordinate |$r_*(r) = \int _0^r {\rm e}^{[\lambda (r^{\prime })-\nu (r^{\prime })]/2}{\rm d}r^{\prime }$| and Cs(r) ≡ (dp/dρ)1/2 being the sound speed in the stellar fluid. The expressions of Ui and Δi, where i = S0, S1, H0, H1, can be found in Appendix B. Their contributions are typically much smaller than those of the V terms. While Δi measure the interaction between H and S, Ui represent the effects of F on the other two fields.
Outside the star, H is identically zero and the system is described by only one second-order ODE in S:
(6)
where all potential terms appearing in equation (6) can be obtained from their corresponding terms inside the star in equation (4) by setting m(r) = M, ρ = p = 0.

2.3 Evaluation of QNMs

QNMs of vibrating compact stars are defined by the physical solutions of the proposed S and H equations with the space–time variable S satisfying the outgoing boundary condition S → exp (iωr*) at spatial infinity. In solving the S–H equation set inside the star, we numerically integrate equations (4) and (5) outwards to find S and H. First of all, the regularity boundary condition for S and H at r = 0 leads to the asymptotic behaviour |$S \approx s_0r_*^{l+1}$| and |$H \approx h_0r_*^l$| near the origin, where s0 and h0 are constants. By keeping only terms of order |$1/C_s^2$| in equation (A3) as Cs → 0 when approaching the stellar surface, one can show that (Allen et al. 1998; Ruoff 2001):
(7)
Expressing F and its derivative in terms of the other two variables, we can then impose the above boundary condition at the stellar surface to fix the ratio of s0 to h0 to obtain a unique (up to some multiplicative constant) solution of S and H inside the star. The inside and outside S function is then connected at the star surface to determine the QNM frequencies.

In the following discussion, we will show that the H–S approach achieved here naturally forms the basis of a decoupling scheme and readily leads to accurate CA and ICA for p modes and w modes, respectively.

3 SEPARATION OF SPACE–TIME AND MATTER

Dynamical processes such as supernova and binary mergers of NSs involve both space–time variation and matter motion. Likewise, when an NS is perturbed away from equilibrium, the excitation energy is initially stored partially in the space–time and partially in the matter. The energy stored in space–time is damped out rapidly through the emission of w-mode GWs owing to the short relaxation time (large imaginary part of eigenfrequency) of w modes. On the other hand, the energy in matter has to be transferred into the space–time through the coupling between matter and space–time, which is measured by the Δi terms in equations (4) and (5) and is then brought away by fluid-mode GWs. The damping of fluid modes is usually slow due to the smallness of Δi, leading to small imaginary parts of their eigenfrequencies, especially for p modes.

Our choice of space–time and matter variables provide a direct view on the weak coupling between space–time and fluid-mode oscillations. We therefore conclude that in fluid modes (especially the p modes), the associated space–time oscillations and hence GW emissions are almost negligible, whereas in the space–time w modes, fluid oscillations are hardly involved. This strongly suggests that the space–time and matter in the developed schemes can be decoupled by taking the approximation Δi = 0 in equations (4) and (5) as
(8)
(9)

4 CA FOR FLUID MODES

It is well known that the eigenfrequencies of the fluid modes, including both f and p modes, of a compact star are characterized by very small imaginary parts. The smallness of the imaginary part implies the tininess of GWs emitted in these modes, due to their weak couplings to space–time variables. The decoupled equation for the fluid variable H is given by equation (9) in Section 3. In the following, we further simplify it and develop a CA which is highly accurate for p modes and also works reasonably well for f mode.

4.1 Fluid equation

The potentials UH0 and UH1 in equation (9) have a common denominator D(ω, r) (see Appendix B),
(10)
which can drop to zero at a certain r at low frequencies, typical of f mode. On the other hand, D(ω, r) increases as ω4 at high frequencies, typical of p modes. We find that for p-mode oscillations the effects of UH0 and UH1 are pretty small (both terms decreases as 1/ω2) and further simplify equation (9) as
(11)
The above equation can also be derived by simply neglecting the S, dS/dr*, F and dF/dr* terms in H equation in AAKS formalism (see Allen et al. 1998, and also Appendix A). Unlike UH0 and UH1, which are frequency dependent, VH0 and VH1 are both frequency independent. The mathematical structure of equation (11) is more desirable than equation (9) and leads to a complete orthonormal set of eigenfunctions. Equation (9), on the other hand, properly accounts for the effects of F on the fluid motion and is found to be the best available approximation for p modes in the following discussion.

4.2 Boundary conditions

Under CA (11), p-mode oscillations are determined from equation (11) by imposing proper boundary conditions on H at r = 0 and r = R. Near the star centre, |$H \approx h_0 r_*^l$| as mentioned previously. Assuming that the EOS acquires the polytropic form p ∝ ρ1 + 1/N with the polytropic index N > 1 near the star surface, which is typical for realistic NSs, we find that |$C_s^2 \sim A_{\rm c} (R_*-r_*)$| with Ac = M/(R2N) and R* being the tortoise radius of the star. Consequently, the H-equation near the stellar surface reduces asymptotically to
\begin{equation*} \frac{{\rm d}^2 H}{{\rm d}r_*^2}-\frac{M}{R^2 A_{\rm c} (R_*-r_*)}\frac{{\rm d} H}{{\rm d}r_*}+\frac{\omega ^2}{A_{\rm c} (R_*-r_*)}H=0. \end{equation*}
There are two independent solutions for this equation. The first one is bounded and behaves as
(12)
The other one is proportional to (R* − r*)1 − N and is unbounded. As H is a physical quantity and must be finite at the stellar surface, it therefore follows equation (12).

The single H-equation (11) together with these two boundary conditions form an eigenvalue problem. The approximate eigenfrequencies of fluid modes under the CA can then be located.

4.3 Completeness and orthogonality

The eigenvalue problem of the purely matter-based H-equation (11) is actually a Sturm–Liouville eigenvalue problem, as it can be cast into the following standard form.
(13)
with
\begin{eqnarray*} P(r_*) &=& {\rm e}^{\nu }(\rho +p)r^2, \nonumber \\ Q(r_*) &=& 2{\rm e}^{2\nu }(\rho +p)\left[n+1-2\pi r^2(\rho +p)(3+{1}/{C_s^2})\right],\nonumber \\ \Lambda (r_*) &=& {\rm e}^{\nu }(\rho +p)r^2/{C_s^2}. \nonumber \end{eqnarray*}
There are a series of real eigenfrequencies {σn} and the corresponding normalized eigenfunctions {Hn(r*)}, which are defined by the boundary conditions derived above, namely (i) H is regular at r* = 0, (ii) (dH/dr*)/H = R2ω2/M at r = R*. Following straightforwardly from the standard theory of Sturm–Liouville system and the fact that Λ(r = 0) = 0 = Λ(r = R), the normalized eigenfunctions {Hn(r*)} form a complete orthogonal set obeying the completeness and orthogonality relationships (see, e.g., Morse & Feshbach 1953):
(14)
(15)

4.4 Numerical results and discussions

To gauge the accuracy of the CA developed (or ICA as discussed later) in this paper, we use EOS A (Pandharipande 1971) to construct an NS with compactness |${\cal C}=0.27$| and central density |$\rho _{\rm c}=2.227\times 10^{-3}\,{\rm km}^{-2}$| and evaluate the QNMs of the star. Table 1 shows the frequencies of the leading fluid modes obtained from exact calculation and CA (11) developed above. We see that the lowest eigenfrequency σ0 of equation (13) provides us an approximate value of the real part of f-mode frequency, ωr, f, with a percentage error of around 20 per cent. For n ≥ 1, the eigenfrequency σn yields an accurate approximation for the real part of the frequency of the nth p mode, |$\omega _{{\rm r},{\rm p}_n}$|⁠. The percentage error is usually much less than 1 per cent and decreases with increasing n (see Table 1). The improvement in accuracy from f mode to p modes of the developed CA is expected. As the imaginary part of eigenfrequency decreases from f mode to p modes, the coupling between the space–time and matter also gets weaker.

Table 1.
Open in new tab

Exact QNM frequency (ωr, ωi) and the CA frequencies σn obtained, respectively, from equations (11), (9), MVS (McDermott et al. 1983), Finn (Finn 1988) and LMI (Lindblom et al. 1997) CAs and (C2) are compared for the leading fluid modes of an EOS A star (⁠|${\cal C}=0.27$|⁠).

ModeExact(11)(9)MVSFinnLMI(C2)
(ωr, ωi)σnσnσnσnσnσn
f(0.1447, 7.5E−5)0.1163NA0.16640.17730.1665NA
p1(0.3932, 3.0E−6)0.39280.39340.44330.48060.39840.3903
p2(0.6130, 5.8E−7)0.61350.61300.64890.71020.61590.6126
p3(0.7639, 5.3E−8)0.76400.76390.78420.85250.76640.7636
ModeExact(11)(9)MVSFinnLMI(C2)
(ωr, ωi)σnσnσnσnσnσn
f(0.1447, 7.5E−5)0.1163NA0.16640.17730.1665NA
p1(0.3932, 3.0E−6)0.39280.39340.44330.48060.39840.3903
p2(0.6130, 5.8E−7)0.61350.61300.64890.71020.61590.6126
p3(0.7639, 5.3E−8)0.76400.76390.78420.85250.76640.7636
Table 1.
Open in new tab

Exact QNM frequency (ωr, ωi) and the CA frequencies σn obtained, respectively, from equations (11), (9), MVS (McDermott et al. 1983), Finn (Finn 1988) and LMI (Lindblom et al. 1997) CAs and (C2) are compared for the leading fluid modes of an EOS A star (⁠|${\cal C}=0.27$|⁠).

ModeExact(11)(9)MVSFinnLMI(C2)
(ωr, ωi)σnσnσnσnσnσn
f(0.1447, 7.5E−5)0.1163NA0.16640.17730.1665NA
p1(0.3932, 3.0E−6)0.39280.39340.44330.48060.39840.3903
p2(0.6130, 5.8E−7)0.61350.61300.64890.71020.61590.6126
p3(0.7639, 5.3E−8)0.76400.76390.78420.85250.76640.7636
ModeExact(11)(9)MVSFinnLMI(C2)
(ωr, ωi)σnσnσnσnσnσn
f(0.1447, 7.5E−5)0.1163NA0.16640.17730.1665NA
p1(0.3932, 3.0E−6)0.39280.39340.44330.48060.39840.3903
p2(0.6130, 5.8E−7)0.61350.61300.64890.71020.61590.6126
p3(0.7639, 5.3E−8)0.76400.76390.78420.85250.76640.7636
We also compare the H-function obtained from (11) and the exact H-function for the same star (EOS A, |${\cal C}=0.27$|⁠). The comparison is shown in Fig. 1. The H-functions in developed CA and the exact AAKS formalism are normalized so that
(16)
Besides, we assume that the exact H-function is real at r = R. The numerical results again confirm that the CA proposed here is very accurate for p modes. The discrepancy between the approximate and the exact wave functions grows larger for f mode, which implies that the coupling between space–time (i.e. F and S) and matter is very weak for p modes, but is not negligible for f mode.
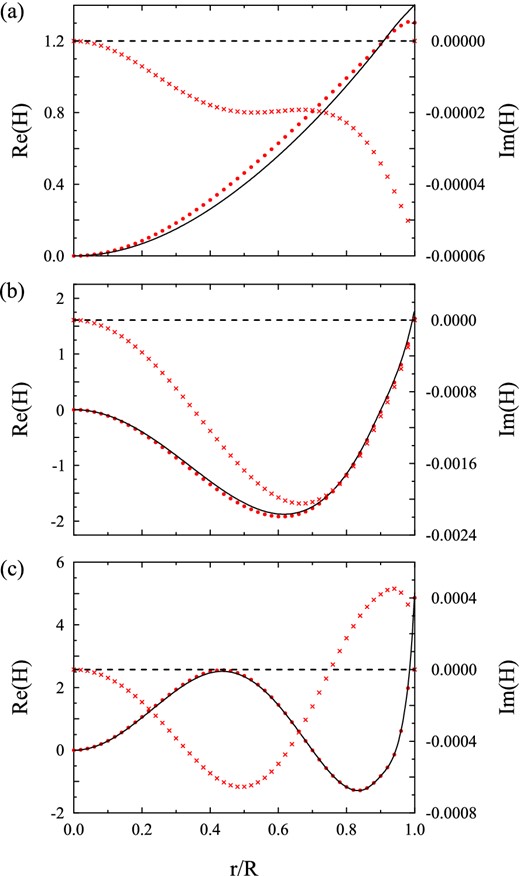
The normalized H-functions for (a) the f mode; (b) the p1 mode and (c) the p2 mode of a star constructed with EOS A (ρc = 2.227 × 10− 3 km− 2, ${\cal C}=0.27$) are plotted against the normalized radius r/R. The solid and the dashed lines are respectively, the real and the imaginary parts of H-function under CA (11). The dots and crosses, respectively, show the real and the imaginary parts of the exact H-function.
Figure 1.

The normalized H-functions for (a) the f mode; (b) the p1 mode and (c) the p2 mode of a star constructed with EOS A (ρc = 2.227 × 10− 3 km− 2, |${\cal C}=0.27$|⁠) are plotted against the normalized radius r/R. The solid and the dashed lines are respectively, the real and the imaginary parts of H-function under CA (11). The dots and crosses, respectively, show the real and the imaginary parts of the exact H-function.

Open in new tabDownload slide

Actually, as is mentioned before, the potentials Ui and couplings Δi in the exact H equation (5) have a common denominator D(ω, r) given by equation (10). It is clearly seen that the accuracy of the CA (11) would decrease if D(ω, r) is small. As is shown in Fig. 2, where D is plotted against r/R for different values of ω for the same star, D decreases with decreasing ω. In fact, for ω = σ0 (i.e. the f-mode frequency under CA), D vanishes at r/R = 0.947. Therefore, the omission of the influence of space–time (i.e. F and S) on oscillations of matter field may lead to appreciable errors at low frequencies. On the other hand, we observe that there are exactly n nodes (excluding the origin) in the wavefunction Hn, in agreement with standard theory of the Sturm–Liouville eigensystem (see, e.g., Zettl 2005).

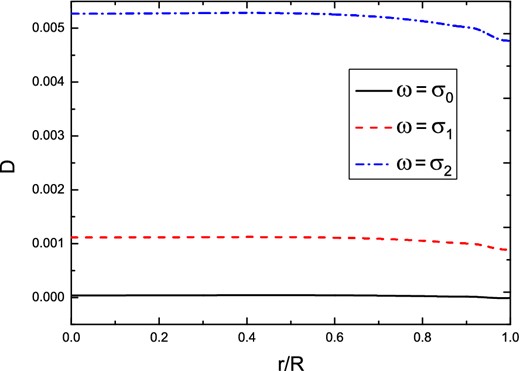
The function D(ω, r) is plotted against r/R with ω = σ0, σ1, σ2.
Figure 2.

The function D(ω, r) is plotted against r/R with ω = σ0, σ1, σ2.

Open in new tabDownload slide

For the purpose of comparison, approximate eigenfrequencies obtained from equation (9) are also listed in Tables 1 –3. While equation (9) in general can yield almost exact numerical results for p modes because it has properly taken the influence of F on H into consideration, it completely fails to locate approximate position of the f mode. As mentioned above, the inability of equation (9) to handle the f mode can be understood as a direct consequence of the fact that D could vanish at certain positions inside the star at frequencies close to the f-mode frequency.

Table 2.
Open in new tab

Exact complex eigenfrequencies (ωr, ωi) and approximate real eigenfrequencies σn obtained, respectively, from CA (11), (9) and (C2) are listed for the leading fluid modes of NSs constructed with the Sly EOS (Douchin & Haensel 2001; Haensel & Potekhin 2004) for different compactness |${\cal C}$|⁠. Entries labelled by ‘NA’ signify modes that cannot be located by a specific approximation.

|${\cal C}$|ModeExact(11)(9)(C2)
(ωr, ωi)σnσnσn
0.117f(0.0488, 1.162E−5)0.0410NANA
0.117p1(0.1654, 4.866E−7)0.16510.16540.1628
0.117p2(0.2079, 2.029E−8)0.20790.20790.2071
0.117p3(0.2390, 5.709E−9)0.23900.23900.2383
0.210f(0.1047, 5.290E−5)0.0848NANA
0.210p1(0.3281, 2.371E−6)0.32790.32830.3245
0.210p2(0.4995, 3.435E−8)0.49960.49950.4985
0.210p3(0.6154, 6.028E−9)0.61550.61540.6150
0.276f(0.1476, 7.570E−5)0.1177NANA
0.276p1(0.4074, 1.884E−6)0.40720.40750.4053
0.276p2(0.6236, 6.806E−7)0.62410.62360.6234
0.276p3(0.8192, 7.455E−8)0.81950.81920.8193
|${\cal C}$|ModeExact(11)(9)(C2)
(ωr, ωi)σnσnσn
0.117f(0.0488, 1.162E−5)0.0410NANA
0.117p1(0.1654, 4.866E−7)0.16510.16540.1628
0.117p2(0.2079, 2.029E−8)0.20790.20790.2071
0.117p3(0.2390, 5.709E−9)0.23900.23900.2383
0.210f(0.1047, 5.290E−5)0.0848NANA
0.210p1(0.3281, 2.371E−6)0.32790.32830.3245
0.210p2(0.4995, 3.435E−8)0.49960.49950.4985
0.210p3(0.6154, 6.028E−9)0.61550.61540.6150
0.276f(0.1476, 7.570E−5)0.1177NANA
0.276p1(0.4074, 1.884E−6)0.40720.40750.4053
0.276p2(0.6236, 6.806E−7)0.62410.62360.6234
0.276p3(0.8192, 7.455E−8)0.81950.81920.8193
Table 2.
Open in new tab

Exact complex eigenfrequencies (ωr, ωi) and approximate real eigenfrequencies σn obtained, respectively, from CA (11), (9) and (C2) are listed for the leading fluid modes of NSs constructed with the Sly EOS (Douchin & Haensel 2001; Haensel & Potekhin 2004) for different compactness |${\cal C}$|⁠. Entries labelled by ‘NA’ signify modes that cannot be located by a specific approximation.

|${\cal C}$|ModeExact(11)(9)(C2)
(ωr, ωi)σnσnσn
0.117f(0.0488, 1.162E−5)0.0410NANA
0.117p1(0.1654, 4.866E−7)0.16510.16540.1628
0.117p2(0.2079, 2.029E−8)0.20790.20790.2071
0.117p3(0.2390, 5.709E−9)0.23900.23900.2383
0.210f(0.1047, 5.290E−5)0.0848NANA
0.210p1(0.3281, 2.371E−6)0.32790.32830.3245
0.210p2(0.4995, 3.435E−8)0.49960.49950.4985
0.210p3(0.6154, 6.028E−9)0.61550.61540.6150
0.276f(0.1476, 7.570E−5)0.1177NANA
0.276p1(0.4074, 1.884E−6)0.40720.40750.4053
0.276p2(0.6236, 6.806E−7)0.62410.62360.6234
0.276p3(0.8192, 7.455E−8)0.81950.81920.8193
|${\cal C}$|ModeExact(11)(9)(C2)
(ωr, ωi)σnσnσn
0.117f(0.0488, 1.162E−5)0.0410NANA
0.117p1(0.1654, 4.866E−7)0.16510.16540.1628
0.117p2(0.2079, 2.029E−8)0.20790.20790.2071
0.117p3(0.2390, 5.709E−9)0.23900.23900.2383
0.210f(0.1047, 5.290E−5)0.0848NANA
0.210p1(0.3281, 2.371E−6)0.32790.32830.3245
0.210p2(0.4995, 3.435E−8)0.49960.49950.4985
0.210p3(0.6154, 6.028E−9)0.61550.61540.6150
0.276f(0.1476, 7.570E−5)0.1177NANA
0.276p1(0.4074, 1.884E−6)0.40720.40750.4053
0.276p2(0.6236, 6.806E−7)0.62410.62360.6234
0.276p3(0.8192, 7.455E−8)0.81950.81920.8193
Table 3.
Open in new tab

Exact complex eigenfrequencies (ωr, ωi) and approximate real eigenfrequencies σn obtained, respectively, from CA (11), (9) and (C2) are listed for the leading fluid modes of polytropic stars (EOS: p = 100ρ1.8) with different compactness |${\cal C}$|⁠. Entries labelled by ‘NA’ signify modes that cannot be located by a specific approximation.

|${\cal C}$|ModeExact(11)(9)(C2)
(ωr, ωi)σnσnσn
0.117f(0.0525, 1.329E−5)0.0475NANA
0.117p1(0.1160, 3.283E−6)0.11490.11640.1074
0.117p2(0.1761, 2.680E−7)0.17570.17620.1727
0.117p3(0.2338, 1.473E−8)0.23360.23380.2320
0.204f(0.1160, 5.771E−5)0.1021NANA
0.204p1(0.2337, 1.728E−5)0.23070.23430.2202
0.204p2(0.3477, 5.490E−7)0.34700.34780.3429
0.204p3(0.4584, 3.069E−8)0.45820.45840.4561
0.271f(0.1659, 5.795E−5)0.1473NANA
0.271p1(0.3012, 1.341E−5)0.29480.30200.2925
0.271p2(0.4249, 2.832E−5)0.42420.42500.4249
0.271p3(0.5496, 1.359E−5)0.54980.54950.5501
|${\cal C}$|ModeExact(11)(9)(C2)
(ωr, ωi)σnσnσn
0.117f(0.0525, 1.329E−5)0.0475NANA
0.117p1(0.1160, 3.283E−6)0.11490.11640.1074
0.117p2(0.1761, 2.680E−7)0.17570.17620.1727
0.117p3(0.2338, 1.473E−8)0.23360.23380.2320
0.204f(0.1160, 5.771E−5)0.1021NANA
0.204p1(0.2337, 1.728E−5)0.23070.23430.2202
0.204p2(0.3477, 5.490E−7)0.34700.34780.3429
0.204p3(0.4584, 3.069E−8)0.45820.45840.4561
0.271f(0.1659, 5.795E−5)0.1473NANA
0.271p1(0.3012, 1.341E−5)0.29480.30200.2925
0.271p2(0.4249, 2.832E−5)0.42420.42500.4249
0.271p3(0.5496, 1.359E−5)0.54980.54950.5501
Table 3.
Open in new tab

Exact complex eigenfrequencies (ωr, ωi) and approximate real eigenfrequencies σn obtained, respectively, from CA (11), (9) and (C2) are listed for the leading fluid modes of polytropic stars (EOS: p = 100ρ1.8) with different compactness |${\cal C}$|⁠. Entries labelled by ‘NA’ signify modes that cannot be located by a specific approximation.

|${\cal C}$|ModeExact(11)(9)(C2)
(ωr, ωi)σnσnσn
0.117f(0.0525, 1.329E−5)0.0475NANA
0.117p1(0.1160, 3.283E−6)0.11490.11640.1074
0.117p2(0.1761, 2.680E−7)0.17570.17620.1727
0.117p3(0.2338, 1.473E−8)0.23360.23380.2320
0.204f(0.1160, 5.771E−5)0.1021NANA
0.204p1(0.2337, 1.728E−5)0.23070.23430.2202
0.204p2(0.3477, 5.490E−7)0.34700.34780.3429
0.204p3(0.4584, 3.069E−8)0.45820.45840.4561
0.271f(0.1659, 5.795E−5)0.1473NANA
0.271p1(0.3012, 1.341E−5)0.29480.30200.2925
0.271p2(0.4249, 2.832E−5)0.42420.42500.4249
0.271p3(0.5496, 1.359E−5)0.54980.54950.5501
|${\cal C}$|ModeExact(11)(9)(C2)
(ωr, ωi)σnσnσn
0.117f(0.0525, 1.329E−5)0.0475NANA
0.117p1(0.1160, 3.283E−6)0.11490.11640.1074
0.117p2(0.1761, 2.680E−7)0.17570.17620.1727
0.117p3(0.2338, 1.473E−8)0.23360.23380.2320
0.204f(0.1160, 5.771E−5)0.1021NANA
0.204p1(0.2337, 1.728E−5)0.23070.23430.2202
0.204p2(0.3477, 5.490E−7)0.34700.34780.3429
0.204p3(0.4584, 3.069E−8)0.45820.45840.4561
0.271f(0.1659, 5.795E−5)0.1473NANA
0.271p1(0.3012, 1.341E−5)0.29480.30200.2925
0.271p2(0.4249, 2.832E−5)0.42420.42500.4249
0.271p3(0.5496, 1.359E−5)0.54980.54950.5501

4.5 Comparison with other CA schemes

We compare the CA developed here with other existing schemes, namely MVS (McDermott et al. 1983), Finn (Finn 1988) and LMI (Lindblom et al. 1997), and the F–S CA (C2) to be developed in Appendix C. The numerical results obtained from these approximations are shown in Table 1. It is clear that all the three CAs developed in this paper can provide more accurate results for p modes in comparison with other schemes proposed previously. While equation (9) yields the best accuracy for p modes, equation (11) successfully handles both f and p modes.

The physical origin of the high accuracy of the CA proposed here can be understood as follows. In the differential line element given by equation (1), there are three unknown metric coefficients, H0, H1 and K, which are to be determined by solving the perturbed Einstein equation. In most cases, if not all, CAs established previously the approximation H0 = K = 0 was always assumed. In the Newtonian limit, such an approximation amounts to neglecting the change in gravitational potential in stellar oscillations (Cowling 1941), which is not a good approximation for f mode and low-order p modes. In contrast, in this paper, we only take the approximation S = 0, i.e. H0 = K, which is strictly valid in the Newtonian limit. Hence, we expect that our CA can provide much improved accuracy. In fact, Table 1 and additional comparisons in Tables 2 and 3 also show that the high accuracy of the CA proposed here is generic and independent of the EOS and the compactness of the NS.

On the other hand, as an aside, we find that the CAs of (11), MVS and Finn can be unified by a single second-order differential equation in H as
(17)
where the expressions for α and β are listed in Table 4 for different approximations. Indeed, the improved accuracy of the current CA is closely tied to the choice β = 1, which originates from the non-vanishing effects due to H0 and K.
Table 4.
Open in new tab

Definition of α and β in different forms of CA.

    CA|$\hspace{14.22636pt}\alpha \hspace{14.22636pt}$||$\hspace{14.22636pt}\beta \hspace{14.22636pt}$|
(11)11
MVS10
Finn|$1-\frac{16\pi r^2(\rho +p)}{l(l+1)}$|0
    CA|$\hspace{14.22636pt}\alpha \hspace{14.22636pt}$||$\hspace{14.22636pt}\beta \hspace{14.22636pt}$|
(11)11
MVS10
Finn|$1-\frac{16\pi r^2(\rho +p)}{l(l+1)}$|0
Table 4.
Open in new tab

Definition of α and β in different forms of CA.

    CA|$\hspace{14.22636pt}\alpha \hspace{14.22636pt}$||$\hspace{14.22636pt}\beta \hspace{14.22636pt}$|
(11)11
MVS10
Finn|$1-\frac{16\pi r^2(\rho +p)}{l(l+1)}$|0
    CA|$\hspace{14.22636pt}\alpha \hspace{14.22636pt}$||$\hspace{14.22636pt}\beta \hspace{14.22636pt}$|
(11)11
MVS10
Finn|$1-\frac{16\pi r^2(\rho +p)}{l(l+1)}$|0

5 ICA FOR SPACE–TIME MODES

5.1 space–time equation

As shown by Wu & Leung (2007), in polar w-mode oscillations, the perturbation in pressure is small and accordingly the contribution of the H and dH/dr* terms in equation (4) is negligible. Hence, polar w modes can be described by equation (8), forming the ICA proposed in this paper. To our knowledge, this is the first time that a single second-order equation for polar w modes has been proposed and verified numerically (see the following discussion).

It is interesting to note that the ICA equation (8) can be further recast into a simple second-order equation
(18)
where
(19)
(20)
Here, |$\widetilde{S}$| is proportional to S as r → ∞. The above equation bears a strong resemblance to the RW equation governing the propagation of axial GWs (Chandrasekhar & Ferrari 1991), save for the frequency dependence of the potential |$\widetilde{V}(\omega , r_*)$|⁠, which, physically speaking, can be considered as the result of dispersion.

5.2 Numerical results and discussions

The space–time w modes can be located by solving equation (8) or equivalently equation (18) with the outgoing boundary condition. The numerical results of ICA proposed here (the columns labelled with ICA) are compared with the exact polar w-mode eigenfrequencies in Table 5, where the exact and approximate QNM frequencies of the leading 12 polar w modes (including two wII modes) for the above-mentioned EOS A NS (⁠|${\cal C}=0.27$|⁠) are listed. The agreement between the exact frequencies and the ICA frequencies is almost perfect, especially for ωr and higher order modes.

Table 5.
Open in new tab

QNM frequencies obtained from various ICA schemes for the leading polar w modes of an EOS A star (⁠|${\cal C}=0.27$|⁠). The first two modes are classified as the wII modes. Entries labelled by ‘NA’ signify modes that cannot be located by a specific approximation.

ExactExactICAICAHFICAHFICALMILMI
ωrωiωrωiωrωiωrωi
0.20670.79350.20650.79320.33040.8922NANA
0.45930.38910.45990.38840.50760.4980NANA
0.50960.17770.50950.17810.51020.11310.43480.0605
0.87300.30250.87300.30280.83350.27810.79240.1244
1.22660.35071.22660.35081.20060.34161.14460.1555
1.57820.38371.57820.38381.55890.37881.49610.1749
1.93020.40931.93010.40931.91480.40621.84760.1892
2.28280.43082.28280.43082.27000.42872.20040.2013
2.63590.45002.63590.45002.62500.44852.55370.2122
2.98940.46822.98940.46832.97990.46702.90790.2231
3.34290.48603.34280.48603.33440.48503.26190.2347
3.69600.50383.69600.50383.68840.50303.61580.2468
ExactExactICAICAHFICAHFICALMILMI
ωrωiωrωiωrωiωrωi
0.20670.79350.20650.79320.33040.8922NANA
0.45930.38910.45990.38840.50760.4980NANA
0.50960.17770.50950.17810.51020.11310.43480.0605
0.87300.30250.87300.30280.83350.27810.79240.1244
1.22660.35071.22660.35081.20060.34161.14460.1555
1.57820.38371.57820.38381.55890.37881.49610.1749
1.93020.40931.93010.40931.91480.40621.84760.1892
2.28280.43082.28280.43082.27000.42872.20040.2013
2.63590.45002.63590.45002.62500.44852.55370.2122
2.98940.46822.98940.46832.97990.46702.90790.2231
3.34290.48603.34280.48603.33440.48503.26190.2347
3.69600.50383.69600.50383.68840.50303.61580.2468
Table 5.
Open in new tab

QNM frequencies obtained from various ICA schemes for the leading polar w modes of an EOS A star (⁠|${\cal C}=0.27$|⁠). The first two modes are classified as the wII modes. Entries labelled by ‘NA’ signify modes that cannot be located by a specific approximation.

ExactExactICAICAHFICAHFICALMILMI
ωrωiωrωiωrωiωrωi
0.20670.79350.20650.79320.33040.8922NANA
0.45930.38910.45990.38840.50760.4980NANA
0.50960.17770.50950.17810.51020.11310.43480.0605
0.87300.30250.87300.30280.83350.27810.79240.1244
1.22660.35071.22660.35081.20060.34161.14460.1555
1.57820.38371.57820.38381.55890.37881.49610.1749
1.93020.40931.93010.40931.91480.40621.84760.1892
2.28280.43082.28280.43082.27000.42872.20040.2013
2.63590.45002.63590.45002.62500.44852.55370.2122
2.98940.46822.98940.46832.97990.46702.90790.2231
3.34290.48603.34280.48603.33440.48503.26190.2347
3.69600.50383.69600.50383.68840.50303.61580.2468
ExactExactICAICAHFICAHFICALMILMI
ωrωiωrωiωrωiωrωi
0.20670.79350.20650.79320.33040.8922NANA
0.45930.38910.45990.38840.50760.4980NANA
0.50960.17770.50950.17810.51020.11310.43480.0605
0.87300.30250.87300.30280.83350.27810.79240.1244
1.22660.35071.22660.35081.20060.34161.14460.1555
1.57820.38371.57820.38381.55890.37881.49610.1749
1.93020.40931.93010.40931.91480.40621.84760.1892
2.28280.43082.28280.43082.27000.42872.20040.2013
2.63590.45002.63590.45002.62500.44852.55370.2122
2.98940.46822.98940.46832.97990.46702.90790.2231
3.34290.48603.34280.48603.33440.48503.26190.2347
3.69600.50383.69600.50383.68840.50303.61580.2468

5.3 High-frequency ICA

As mentioned above, both US0(ω, r) and US1(ω, r) go as 1/ω2 at high frequencies. Thus, we expect that w-mode QNMs with high frequencies can be approximately located by omitting terms US0(ω, r) and US1(ω, r) in equation (8), namely
(21)
Such a scheme is termed as the high-frequency ICA (HFICA) in this paper. As shown in Table 5, HFICA works well in the high-frequency regime. In fact, HFICA can successfully explain the high-frequency asymptotic behaviour of polar w modes of compact stars (Zhang, Wu & Leung 2011).

6 CONCLUSION AND DISCUSSION

In this paper, we propose an alternative description for polar oscillations of compact stars, which consists of two coupled second-order ODEs in one metric variable (S) and one matter variable (H). The H–S approach developed here readily leads to CA (ICA) with unprecedented accuracies for polar p modes (w modes) when the two second-order ODEs are decoupled. Besides, under the CA, the wave functions Hn (n = 0, 1, 2, …) of the fluid modes (including the f mode and the p modes) are shown to form a complete orthonormal set, which paves the way for further developing perturbation schemes to improve the accuracies of the CA by including the effect of GW radiation damping.

We note that there are other theories for pulsations of compact stars which also result in two coupled second-order ODEs. For example, in the LMI formalism (Lindblom et al. 1997), the metric variable H0(r, t) and the fluid variable δU(r, t) ≡ δp(r, t)/(ρ + p) + H0(r, t)/2 are used to formulate a relativistic theory for stellar pulsations. Similar to the development of this paper, the two coupled second-order ODEs in the LMI formalism can be decoupled by adopting the approximations H0 = 0 and δU = 0, leading to the so-called LMI CA and LMI ICA, respectively. The LMI CA was applied to find the frequency of the f mode of a polytropic NS with M = 1.4 M⊙ and the percentage error was about 20 per cent for the case l = 2 (Lindblom et al. 1997), which is similar to ours. Besides, as shown in Table 1, the LMI CA can yield quite accurate frequencies for the p modes. On the other hand, the frequencies of the leading polar w modes obtained from the LMI ICA are listed in the Table 5. It is clear, from the numerical results, that the performance of the LMI ICA is not that satisfactory.

It is essential to note that the success of the CA and ICA established in this paper relies on a judicious selection of the two independent variables, namely H and S. While the former is proportional to the change in the Eulerian pressure, i.e. a proper Newtonian quantity, the latter vanishes in the weak field limit. Thus, the interplay between H and S in fluid modes and space–time modes is expected to be small, which is numerically verified in the above discussion. According to our experience, the choice of the independent variables H and S (especially the latter) is the most crucial factor leading to the high precision of the ICA scheme developed here. We note that several other schemes for CA (see, e.g., Lindblom & Splinter 1990, and references therein) and ICA (Andersson et al. 1996) based on the LD formalism have been proposed. Yet, the accuracies of these schemes are worse than that achieved in this paper. This clearly demonstrates the importance of the choice of variables in carrying out the decoupling scheme.

On the other hand, the mutual influences between space–time and matter, which are neglected in CA and ICA developed in this paper, can also be included in a perturbative manner. As supported by the accuracies of these two approximations (see numerical data shown in the paper), we expect that relevant perturbation series could converge rapidly to yield satisfactory results. For example, GWs emitted in p modes and hence the finite lifetime of these QNM could be evaluated perturbatively. Research along such direction is now underway and relevant results will be published elsewhere in due course.

Under ICA developed here, the equation of motion for |$\tilde{S}$| in equation (18), resembles the RW equation governing the motion of axial perturbations of compact stars. Such resemblance suggests that axial and polar perturbations in compact stars could be studied in a parallel way. In fact, it has recently been shown that polar w-mode QNMs can be inferred from axial w-mode QNMs asymptotically (Zhang et al. 2011). The formulation established here is likely to shed light on the related studies.

In a series of papers, Tsui & Leung (2005a,b) and Tsui et al. (2006) developed an inversion scheme to infer the internal structure and the EOS of an NS from a few of its leading axial QNMs. Despite the success in the axial case, the inversion method cannot be directly applied to the polar-type oscillations due to the complicated form of the equations of motion, which arises from the interplay between matter and space–time. The CA and ICA proposed in our paper, where both fluid modes and space–time modes are governed by second-order ODEs analogous to the RW equation, could pave the way for the generalization of the inversion scheme to include polar QNMs.

Lastly, as F is proportional to the change in the Newtonian potential in the weak field limit, it can also reveal the motion of matter indirectly and replace the role of H. In fact, one can also formulate another equivalent description for stellar pulsation using the variables F and S to develop another two-variable approach, namely the F–S approach (see Appendix C for detailed discussion). Similar to the case in the LMI formalism mentioned above, such an F–S approach can yield valid CA with accuracies worse than those obtained from equations (9) and (11), but fails to predict accurate polar w modes. The ICA in the F–S approach is identical to the HFICA in the H–S approach and hence works well only in the high frequency limit (see Appendix C and Table 5). In contrast, equation (8), or equivalently equation (18), used in the H–S approach can locate all polar w modes including the low-frequency wII modes with excellent numerical accuracies. In conclusion, the H–S approach proposed here successfully leads to feasible and accurate CA and ICA schemes in a unified framework and, in this regard, it outperforms other two-variable approaches to the best of our knowledge.

This work is supported in part by the Hong Kong Research Grants Council (Grant no.: 401807) and the direct grant (Project ID: 2060330) from the Chinese University of Hong Kong. We thank L. M. Lin, H. K. Lau and P. O. Chan for helpful discussions.

★

Present address: Department of Physics, University of California, San Diego, 9500 Gilman Drive, La Jolla, CA 92093, USA.

†

Present address: Office of University General Education, The Chinese University of Hong Kong, Shatin, Hong Kong SAR, China.

REFERENCES

Allen
G.
Andersson
N.
Kokkotas
K. D.
Schutz
B. F.
, 
Phys. Rev. D
,
1998
, vol.
58
pg.
124012
Crossref
Search ADS
 
Andersson
N.
Kokkotas
K. D.
, 
Phys. Rev. Lett.
,
1996
, vol.
77
pg.
4134
Crossref
Search ADS
PubMed
 
Andersson
N.
Kokkotas
K. D.
, 
MNRAS
,
1998
, vol.
299
pg.
1059
Crossref
Search ADS
 
Andersson
N.
Kokkotas
K. D.
Schutz
B. F.
, 
MNRAS
,
1996
, vol.
280
pg.
1230
Crossref
Search ADS
 
Andersson
N.
Ferrari
V.
Jones
D. I.
Kokkotas
K. D.
Krishnan
B.
Read
J. S.
Rezzolla
L.
Zink
B.
, 
Gen. Relativ. Gravit.
,
2011
, vol.
43
pg.
409
Crossref
Search ADS
 
Benhar
O.
Berti
E.
Ferrari
V.
, 
MNRAS
,
1999
, vol.
310
pg.
797
Crossref
Search ADS
 
Benhar
O.
Ferrari
V.
Gualtieri
L.
, 
Phys. Rev. D
,
2004
, vol.
70
pg.
124015
Crossref
Search ADS
 
Berti
E.
Cardoso
V.
Starinets
A. O.
, 
Class. Quantum Gravity
,
2009
, vol.
26
pg.
163001
Crossref
Search ADS
 
Chandrasekhar
S.
Ferrari
V.
, 
Proc. R. Soc. A
,
1991
, vol.
432
pg.
247
Crossref
Search ADS
 
Ching
E. S. C.
Leung
P. T.
van den Brink
A. M.
Suen
W. M.
Tong
S. S.
Young
K.
, 
Rev. Mod. Phys.
,
1998
, vol.
70
pg.
1545
Crossref
Search ADS
 
Cowling
T. G.
, 
MNRAS
,
1941
, vol.
101
pg.
367
Crossref
Search ADS
 
Detweiler
S.
Lindblom
L.
, 
ApJ
,
1985
, vol.
292
pg.
12
Crossref
Search ADS
 
Doneva
D. D.
Gaertig
E.
Kokkotas
K. D.
Krüger
C.
, 
Phys. Rev. D
,
2013
, vol.
88
pg.
044052
Crossref
Search ADS
 
Douchin
F.
Haensel
P.
, 
A&A
,
2001
, vol.
380
pg.
151
Crossref
Search ADS
 
Finn
L. S.
, 
MNRAS
,
1988
, vol.
232
pg.
259
Crossref
Search ADS
 
Fryer
C. L.
Holz
D. E.
Hughes
S. A.
, 
ApJ
,
2002
, vol.
565
pg.
430
Crossref
Search ADS
 
Glendenning
N. K.
, 
Compact Stars - Nuclear Physics, Particle Physics, and General Relativity
,
1997
New York
Springer-Verlag

Google Scholar

OpenURL Placeholder Text

 
Haensel
P.
Potekhin
A. Y.
, 
A&A
,
2004
, vol.
428
pg.
191
Crossref
Search ADS
 
Hild
S.
et al. , 
Class. Quantum Gravity
,
2011
, vol.
28
pg.
094013
Crossref
Search ADS
 
Hughes
S.
, 
Ann. Phys.
,
2003
, vol.
303
pg.
142
Crossref
Search ADS
 
Kojima
Y.
, 
Phys. Rev. D
,
1992
, vol.
46
pg.
4289
Crossref
Search ADS
 
Kokkotas
K. D.
Schmidt
B. G.
, 
Living Rev. Relativ.
,
1999
, vol.
2
pg.
2
Crossref
Search ADS
 
Kokkotas
K. D.
Apostolatos
T. A.
Andersson
N.
, 
MNRAS
,
2001
, vol.
320
pg.
307
Crossref
Search ADS
 
Konoplya
R. A.
Zhidenko
A.
, 
Rev. Mod. Phys.
,
2011
, vol.
83
pg.
793
Crossref
Search ADS
 
Lattimer
J. M.
, 
Ann. Rev. Nucl. Part. Sci.
,
2012
, vol.
62
pg.
485
Crossref
Search ADS
 
Lattimer
J.
Prakash
M.
, 
Phys. Rep.
,
2007
, vol.
442
pg.
109
Crossref
Search ADS
 
Lau
H. K.
Leung
P. T.
Lin
L. M.
, 
ApJ
,
2010
, vol.
714
pg.
1234
Crossref
Search ADS
 
Leaver
E. W.
, 
Phys. Rev. D
,
1986
, vol.
34
pg.
384
Crossref
Search ADS
 
Lindblom
L.
Detweiler
S. L.
, 
ApJ
,
1983
, vol.
53
pg.
73
Crossref
Search ADS
 
Lindblom
L.
Splinter
R. J.
, 
ApJ
,
1990
, vol.
348
pg.
198
Crossref
Search ADS
 
Lindblom
L.
Mendell
G.
Ipser
J. R.
, 
Phys. Rev. D
,
1997
, vol.
56
pg.
2118
Crossref
Search ADS
 
McDermott
P. N.
Horn
H. M. V.
Scholl
J. F.
, 
ApJ
,
1983
, vol.
268
pg.
837
Crossref
Search ADS
 
Morse
P. M.
Feshbach
H.
, 
Methods of Theoretical Physics
,
1953
New York
McGraw-Hill

Google Scholar

OpenURL Placeholder Text

 
Pandharipande
V.
, 
Nucl. Phys. A
,
1971
, vol.
174
pg.
641
Crossref
Search ADS
 
Press
W.
, 
ApJ
,
1971
, vol.
170
pg.
L105
Crossref
Search ADS
 
Price
R.
Thorne
K. S.
, 
ApJ
,
1969
, vol.
155
pg.
163
Crossref
Search ADS
 
Regge
T.
Wheeler
J. A.
, 
Phys. Rev.
,
1957
, vol.
108
pg.
1063
Crossref
Search ADS
 
Ruoff
J.
, 
Phys. Rev. D
,
2001
, vol.
63
pg.
064018
Crossref
Search ADS
 
Sotani
H.
Yasutake
N.
Maruyama
T.
Tatsumi
T.
, 
Phys. Rev. D
,
2011
, vol.
83
pg.
024014
Crossref
Search ADS
 
Thorne
K. S.
, 
ApJ
,
1969
, vol.
158
pg.
997
Crossref
Search ADS
 
Thorne
K. S.
Campolattaro
A.
, 
ApJ
,
1967
, vol.
149
pg.
591
Crossref
Search ADS
 
Tsui
L. K.
Leung
P. T.
, 
Phys. Rev. Lett.
,
2005a
, vol.
95
pg.
151101
Crossref
Search ADS
 
Tsui
L. K.
Leung
P. T.
, 
ApJ
,
2005b
, vol.
631
pg.
495
Crossref
Search ADS
 
Tsui
L. K.
Leung
P. T.
Wu
J.
, 
Phys. Rev. D
,
2006
, vol.
74
pg.
124025
Crossref
Search ADS
 
Weber
F.
, 
Pulsars as Astrophysical Laboratories for Nuclear and Particle Physics
,
1999
Bristol
IoP Publishing

Google Scholar

OpenURL Placeholder Text

 
Wu
J.
Leung
P. T.
, 
MNRAS
,
2007
, vol.
381
pg.
151
Crossref
Search ADS
 
Zettl
A.
, 
Sturm-Liouville Theory, Mathematical Surveys and Monographs
,
2005
Providence, RI
Am. Math. Soc.

Google Scholar

OpenURL Placeholder Text

 
Zhang
Y. J.
Wu
J.
Leung
P. T.
, 
Phys. Rev. D
,
2011
, vol.
83
pg.
064012
Crossref
Search ADS
 

APPENDIX A: AAKS FORMALISM

In the AAKS formalism (Allen et al. 1998), polar QNM oscillation of compact stars with a frequency ω are governed by the following three coupled second-order differential equations.
(A1)
(A2)
(A3)
In addition to the above three equations, S(r), F(r) and H(r) should also satisfy the Hamiltonian constraint:
(A4)
By combining equation (A2) and the Hamiltonian constraint (equation A4) together, a simple expression for H can be derived:
(A5)
which is often used to calculate the value of H, instead of integrating equation (A3), and termed as the modified Hamiltonian constraint hereafter.
As for the region outside the star, the fluid variable H vanishes identically, the two metric variables S and F evolve as
(A6)
(A7)
which can be obtained from equations (A1) and (A2) by setting p = ρ = 0 and m(r) = M.

APPENDIX B: DERIVATION OF H–S SCHEME

In the following, we eliminate the variable F from the equations of motion shown in Appendix A and establish the so-called H–S approach, which leads to accurate CA for the fluid modes (especially the p modes) and ICA for the w modes.

First of all, for the region r < R, we rewrite the modified Hamiltonian constraint (equation A5) and its derivative with respect to r* as
(B1)
(B2)
where
(B3)
(B4)
(B5)
(B6)
(B7)
(B8)
(B9)
(B10)
with ν′ = dν/dr. To arrive at equation (B2), equations (A1) and (A2) have been used to eliminate |${\rm d}^2 F/{\rm d}r^2_*$| and |${\rm d}^2 S/{\rm d}r^2_*$|⁠.
From equations (B1) and (B2), we can express F and dF/dr* in terms of S, dS/dr*, H and dH/dr* as
(B11)
(B12)
where
(B13)
(B14)
(B15)
(B16)
(B17)
(B18)
(B19)
(B20)
and D is defined in equation (10).
For r > R, the stellar pressure p and density ρ vanish and so does H, then F in equation (B11) reduces to the following form:
(B21)
which is a linear combination of S and dS/dr*. The coefficients |$\alpha _{S0}^{(\rm e)}$| and |$\alpha _{S1}^{(\rm e)}$| can be readily obtained from αS0 and αS1 by taking ρ = p = 0 and m = M:
(B22)
(B23)
with D(e) being:
(B24)
With the expressions of F and dF/dr* derived above, we manage to find equations (4) and (5) for the fields H and S inside the star. The expressions for potential Ui and coupling Δi in these two equations are as follows:
(B25)
(B26)
(B27)
(B28)
(B29)
(B30)
(B31)
(B32)
where αi and βi are defined in equations (B13)–(B20) and
(B33)
(B34)
(B35)
(B36)
(B37)
Since the functions αH1(ω, r) and αH0(ω, r) both contain a (ρ + p) factor, they vanish outside the star. Therefore, ΔH0(ω, r) and ΔH0(ω, r) vanish outside the star. The system reduces into one second-order ODE (equation 6) in S outside the star, where
(B38)
(B39)
with the α(e) coefficients defined in equations (B22) and (B23) and
(B40)
(B41)

APPENDIX C: F–S APPROACH

C1 Formalism

As both F and H could reveal the Newtonian aspect of stellar pulsations, it is natural to expect that an alternative approach using F and S to study stellar pulsations is possible. In fact, it is straightforward to make use of the Hamiltonian constraint (equation A4) to eliminate the matter field H(r*) in equation (A2) (Allen et al. 1998):
(C1)
Equations (A1) and (C1) together form two coupled second-order equations in F and S, which can be used to locate QNMs of compact stars and lead to the so-called F–S approach in this paper.

C2 Cowling approximation

Similar to the H–S approach, the S terms in equation (C1) are expected to be negligible for fluid-mode pulsations, yielding
(C2)
When subjected to suitable boundary condition (as discussed in the following), equation (C2) can give good approximation to p-mode pulsations of realistic compact stars, thereby resulting in the CA for p modes in the F–S approach. As usual, the regularity boundary condition |$F \propto r_*^l$| holds around the origin. As the fluid variable H is bounded, it can be shown that the correct boundary condition near the stellar surface is F ∼ (R* − r*)N + 1. Upon imposing the two boundary conditions mentioned above on the solution of equation (C2), we can find the approximate values of the real part of the eigenfrequencies of p modes, which are listed and compared with the exact values ωr in Tables 1–3. For p modes of NSs constructed with realistic EOSs, e.g., A and SLy (see Tables 1 and 2), the percentage error in ωr is usually less than a few per cent and decreases with the mode order and the compactness of the star. However, the accuracy of the CA scheme (equation C2) could substantially worsen for polytropic stars (especially those with large polytropic indices) in spite of the fact that it still improves with increasing compactness and mode order (see Table 3). In comparison with the two CA schemes proposed in the H–S approach, i.e. equations (11) and (9), equation (C2) is in general the least accurate one. Moreover, we cannot locate the f-mode oscillation under the CA in F–S approach.
Starting from CA (equation C2) in the F–S approach, we can also get a standard Sturm–Liouville equation in terms of the variable G ≡ F/p,
(C3)
with
(C4)
(C5)
(C6)
We note that the coefficients PG(r*) and ΛG(r*) are strictly positive, as required for a normal Sturm–Liouville equation (see, e.g., Zettl 2005). Besides, ΛG vanishes at both r = 0 and r = R. Following directly from the physical boundary condition on F as mentioned above, G tends to a finite constant at r* = R* and
(C7)
Thus, a standard Sturm–Liouville eigenvalue system is established and the normalized eigenfunctions of equation (C3), Gn(r*), where n = 1, 2, 3, …, form a complete set and satisfy the orthogonality relation (see, e.g., Zettl 2005):
(C8)
As mentioned above, in the F–S CA scheme (C2) we fail to locate the f mode. Hence, the nth eigenfunction Gn (n = 1, 2, 3, …) in fact corresponds to the nth p mode. In Fig. C1, we show the scaled eigenfunction |$\tilde{G}_n$| defined as
(C9)
which satisfies the orthonormal condition |$\int _0^{R_*} \tilde{G}_m(r_*)\tilde{G}_n(r_*)\;{\rm d}r_*=\delta _{mn}$|⁠. There are n − 1 nodes (excluding the two endpoints r = 0 and r = R) in the wavefunction |$\tilde{G}_n$| (or equivalently Gn). In particular, the wavefunction of the p1 mode is nodeless. This observation further confirms that the p1 mode is indeed the ground state of the eigenvalue equation (C3) (see, e.g., Zettl 2005) and explains why the f mode is missing in the CA scheme (C2) of the F–S approach.
The scaled function $\tilde{G}_n$ of an NS with SLy EOS (Douchin & Haensel 2001; Haensel & Potekhin 2004) and compactness ${\cal C}=0.276$ is plotted against r/R for n = 1 (solid line), 2 (dashed line), 3 (dot–dashed line), which correspond to p1, p2 and p3 modes, respectively.
Figure C1.

The scaled function |$\tilde{G}_n$| of an NS with SLy EOS (Douchin & Haensel 2001; Haensel & Potekhin 2004) and compactness |${\cal C}=0.276$| is plotted against r/R for n = 1 (solid line), 2 (dashed line), 3 (dot–dashed line), which correspond to p1, p2 and p3 modes, respectively.

Open in new tabDownload slide

C3 Inverse-Cowling approximation

We can also obtain the ICA for polar w modes within the F–S approach by neglecting the F term in equation (A1), i.e.
(C10)
Interestingly, such an ICA is merely the HFICA in the H–S approach, which works well only for w modes with high frequencies (see Table 5 for the accuracies and validity of HFICA in the H–S approach). It reflects the fact that the metric variable F also participates in the dynamics of stellar pulsations and its contribution to equation (A1) is non-negligible for w modes with low frequencies.
© 2014 The Authors Published by Oxford University Press on behalf of the Royal Astronomical Society
Issue Section:
Article
Download all slides