Star formation in the first galaxies – II. Clustered star formation and the influence of metal line cooling Free

Abstract

INTRODUCTION

The process of star formation is extremely complex, with gas thermodynamics, supersonic turbulence, self-gravity, magnetic fields and stellar feedback all playing important roles on a variety of spatial and temporal scales. It is observed that the vast majority of present-day stars form as part of small associations or clusters inside supersonically turbulent molecular clouds (e.g. Lada & Lada 2003). The stellar initial mass function (IMF) peaks around ∼0.1–0.5 M_⊙ (e.g. Kroupa 2002; Chabrier 2003) and has a power-law tail extending to larger masses (Salpeter 1955). Compared with the free-fall time evaluated at the characteristic density of the parent molecular clouds, star formation is a slow and inefficient process (e.g. Zuckerman & Evans 1974; Evans et al. 2009). Any comprehensive theory of star formation should be able to explain these characteristics in a single unified framework (see McKee & Ostriker 2007).

Supersonic turbulence, along with self-gravity, is believed to be the main process controlling star formation (Mac Low & Klessen 2004). It creates a complex, self-similar network of sheet-like and filamentary shock compressed density fluctuations. When one of these fluctuations becomes Jeans unstable it collapses and forms one, or possibly many, protostellar objects (Elmegreen 1993; Padoan & Nordlund 1999; Mac Low & Klessen 2004). This process is known as ‘gravoturbulent fragmentation’ and is pivotal for understanding how stars and stellar clusters form. The character of turbulence (Klessen, Heitsch & Mac Low 2000; Klessen 2001b; Padoan & Nordlund 2002), cloud geometry (Bonnell & Bastien 1993), rotation level and magnetic field strength (Heitsch, Mac Low & Klessen 2001; Vázquez-Semadeni, Kim & Ballesteros-Paredes 2005; Padoan & Nordlund 2011; Federrath & Klessen 2012) will all influence gas fragmentation. The thermodynamical behaviour of collapsing turbulent gas, set by various heating and cooling processes, is also crucial in moderating fragmentation (e.g. Larson 1985, 2005). In simulations utilizing a polytropic equation of state, P ∝ ρ^γ, Li, Klessen & Mac Low (2003) demonstrated that the degree of fragmentation increases with decreasing polytropic exponent γ (corresponding to an increase in the gas cooling rate). Jappsen et al. (2005) further demonstrated that the characteristic fragmentation mass scale is approximately the Jeans mass at the point where γ first exceeds unity after dipping below unity. Variations in γ have also been shown to have strong effects on gas morphology (e.g. Peters et al. 2012), the gas density probability distribution function (PDF) of supersonically turbulent gas (Scalo et al. 1998; Vázquez-Semadeni et al. 2006) and may also affect the shape of the stellar IMF (Spaans & Silk 2000).

The theory of Galactic star formation is only partially applicable to the formation of the first, so-called Population III (Pop III), stars (reviewed in Bromm 2013). These objects formed in 10^{5 − 6} M_⊙ dark matter ‘minihaloes’ at redshifts z ∼ 15-40 (Couchman & Rees 1986; Haiman, Thoul & Loeb 1996; Tegmark et al. 1997). Given the complete lack of metals, gas cooling was provided by molecular hydrogen (H₂), a relatively inefficient cooling agent. The thermalization and energy spacing of the lowest rotational levels of H₂ set a characteristic density, n ∼ 10⁴ cm⁻³, and temperature, T ∼ 200 K, where primordial gas ends its initial free-fall collapse phase. Simulations have shown the resulting star-forming clumps to have masses ≳100 M_⊙, in accord with the Jeans mass at this point (Abel, Bryan & Norman 2000; Bromm, Coppi & Larson 2002; Yoshida et al. 2006; O'Shea & Norman 2007). The final stellar mass is determined by subsequent accretion on to the initial protostellar hydrostatic core. Recent simulations revise this characteristic mass downwards by showing that the Pop III protostellar disc can fragment at high densities (Machida et al. 2008; Stacy, Greif & Bromm 2010; Clark et al. 2011a,b; Greif et al. 2011, 2012) or that prostostellar radiation can suppress gas accretion (Hosokawa et al. 2011; Stacy, Greif & Bromm 2012; Susa 2013), but still support the general conclusion that Pop III stars were typically more massive than later stellar generations.

What caused the transition from solitary, high-mass Pop III star formation to clustered, low-mass star formation is an important open question in cosmology. The introduction of metals by the first supernovae is generally thought to have driven the transition, given the enhanced cooling and thus fragmentation in metal-enriched gas. This idea was explored in Omukai (2000) who showed an increase in metallicity leads to larger cooling rates and thus lower temperatures during gaseous collapse. Bromm et al. (2001) found that when metallicity is greater than a critical metallicity of Z ≈ 10^−3.5 Z_⊙, gaseous fragmentation occurs due to metal fine-structure line emission. Later studies that explored a metal fine-structure ‘line-induced’ Pop III–II transition (e.g. Bromm & Loeb 2003; Santoro & Shull 2006; Smith & Sigurdsson 2007; Safranek-Shrader, Bromm & Milosavljević 2010) all found similar values for the metallicity needed for the star formation to transition to an efficiently fragmenting mode.

A separate set of studies suggest that the Pop III–II mode transition is not induced by metal line emission, but instead by the thermal coupling of gas and dust grains (e.g. Omukai et al. 2005; Schneider et al. 2006; Clark, Glover & Klessen 2008; Dopcke et al. 2011, 2013). This ‘dust-induced’ fragmentation occurs at a much higher density, n ∼ 10^{10 − 12} cm⁻³, than line-induced fragmentation when the thermal Jeans mass is of the order of 0.1-1 M_⊙. Studies have shown that the metallicity needed for dust–gas coupling to significantly affect the gas thermodynamical evolution and induce a star formation transition is Z ≈ 10⁻⁶ Z_⊙, much lower than the metallicity needed for a line-induced transition. This depends, though, on the creation, abundance and composition of dust at high redshifts (e.g. Dwek & Cherchneff 2011; Schneider et al. 2012a) which remains very uncertain.

More realistic three-dimensional simulations have also addressed the Pop III–II transition. Clark et al. (2008), using a piecewise equation of state, showed that dust-induced fragmentation does indeed induce solar mass scale fragmentation at high densities and emphasized the importance of angular momentum in regulating fragmentation. Dopcke et al. (2011, 2013) confirmed this finding utilizing a non-equilibrium chemical network. Starting from cosmological initial conditions, Smith et al. (2009) suggested that the interplay of metal fine-structure line cooling and the cosmic microwave background (CMB) temperature floor, T_CMB = 2.725 K(1 + z), strongly controls gas fragmentation and leads to three distinct modes of metal-enriched star formation at high redshifts. The smoothly decreasing CMB temperature sets a lower limit to which gas can radiatively cool, which may regulate the process of star formation (Clarke & Bromm 2003; Schneider & Omukai 2010) and imprint observational signatures in the chemical abundances of Galactic metal-poor stellar populations (Tumlinson 2007; Bailin et al. 2010). The CMB may also considerably increase the opacity mass limit for fragmentation given the strong temperature dependence of the mean dust opacity (Low & Lynden-Bell 1976).

Distinguishing between a dust- and line-induced star formation transition can be accomplished by observing chemical abundance patterns in metal-poor stars. Frebel, Johnson & Bromm (2007) compiled observations of metal-poor stars and showed that none has oxygen and carbon abundances smaller than the critical value needed for a line-induced transition. The recently discovered star of Caffau et al. (2011), though, has such small carbon and oxygen abundances that only dust-cooling-induced fragmentation could explain its existence (Klessen, Glover & Clark 2012; Schneider et al. 2012b), though the possibility has been raised that its true metal abundance is higher than observed (MacDonald et al. 2013). Additionally, it should be stressed that disc fragmentation into subsolar mass clumps can occur even in completely metal-free gas (Greif et al. 2011; Clark et al. 2011b), obviating the need for any sort of metal-enhanced cooling for low-mass stellar object production.

Though the level of metal enrichment in gas plays a key thermodynamic role, numerous other factors likely contributed to effecting the transition to Pop II star formation. For example, in a series of papers Jappsen et al. (2007, 2009a,b) argued that there is no metallicity threshold for a Pop III–II transition – instead, the cosmic hydrodynamic context setting the initial conditions for star formation will have the largest effect on how fragmentation proceeds. This may be especially relevant since the first metal-enriched stellar clusters likely formed in atomic cooling haloes, rather than relatively low-mass minihaloes, with potential wells deep enough to sustain supersonic turbulent motions (e.g. Wise & Abel 2007; Greif et al. 2008), though this is dependent on how exactly Pop III stars ended their lives.

The formation of stellar clusters comprised of low-mass stars, rather than solitary massive stars, has profound cosmological implications (Tornatore, Ferrara & Schneider 2007; Maio et al. 2010; Aykutalp & Spaans 2011; Latif, Schleicher & Spaans 2012; Wise et al. 2012). These earliest clusters played a key role in cosmic reionization (Bouwens et al. 2011; Finkelstein et al. 2012; Kuhlen & Faucher-Giguère 2012; Robertson et al. 2013) and may still survive today in the form of metal-poor globular clusters, as part of the recently discovered ultrafaint dwarf (UDF) Milky Way satellites (e.g. Belokurov et al. 2007; Frebel & Bromm 2012), or individually as metal-poor stars residing in the Galactic halo. If sufficiently luminous they are capable of being detected by upcoming telescopes designed to probe redshifts ≳10, such as the James Webb Space Telescope (JWST; Pawlik, Milosavljević & Bromm 2011; Zackrisson et al. 2011, 2012; Dunlop 2013). Additionally, the long-term chemical evolution of a star cluster imprints unique chemical signatures on to its members that will be useful for decoding the enrichment patterns of the first supernovae (e.g. Bland-Hawthorn et al. 2010).

This work is focused on the process of gas fragmentation, and thus star formation, in high-redshift atomic cooling haloes that have been enriched to some non-zero, but subsolar, metallicity. We present the results of three high-resolution cosmological simulations, achieving a spatial resolution of ∼0.01 physical parsecs and maximum physical density of ∼ 10^6-7 cm^{− 3}. We impose a strong Lyman–Werner (LW) radiation field that photodissociates molecular hydrogen across the computational box, delaying gaseous collapse until the assembly of a M_vir ≈ 2 × 10⁷ M_⊙ halo capable of cooling by Lyα line emission at z ≈ 16. When we identify the conditions for runaway gaseous collapse in a halo, we endow the gas in its vicinity with a non-zero metallicity and observe the subsequent metal-cooling-induced collapse. At high densities, we introduce sink particles which serve as proxies for stellar associations that would have formed at gas densities not directly resolved in the simulations. We evolve this star formation region for multiple free-fall times to observe the long-term fragmentation process, measure the efficiency with which gas is converted into stars, and study mass spectrum of high-density gaseous clumps. Using this approach, we aim to better understand the star formation properties of metal-enriched gas and the role that metal fine-structure line cooling plays in the first instances of clustered star formation in the Universe.

We organize this paper as follows. In Section 2, we describe our numerical setup and physical ingredients that enter into our study. In Section 3, we describe the results and analysis of our simulations. In Section 4, we discuss the potential limitations of our simulations. Finally, in Section 5, we discuss the implications of our findings and provide our conclusions.

Throughout this paper, we assume cosmological parameters consistent with the Wilkinson Microwave Anisotropy Probe 7 year results (Komatsu et al. 2011): Ω_Λ = 0.725, Ω_b = 0.0458, Ω_m = 0.275, h = 0.704, σ₈ = 0.810 and n_s = 0.967. Additionally, all quantities will be expressed in physical, rather than comoving, units unless explicitly stated otherwise.

NUMERICAL SETUP

Parameter choices and initial conditions

We run our simulation using the adaptive mesh refinement code flash (Fryxell et al. 2000), version 4. Our cosmological initial conditions are identical to those used in Safranek-Shrader et al. (2012). Specifically, we use a 1 Mpc³ (comoving) box initialized at z = 145 with a base grid resolution of 128³ and two nested grids for an effective resolution of 512³. This results in an effective dark matter particle mass of 230 M_⊙.

When the grid is highly refined, dark matter particles begin to become very coarsely sampled when their mass is mapped on to the grid for the purpose of the gravitational potential calculation. To alleviate this, we spatially smooth the gravitational influence of dark matter (in a manner similar to Richardson, Scannapieco & Gray 2013) above a refinement level of 12, resulting in a dark matter smoothing length of ≈ 60 comoving pc. At the redshift at which we study metal-enchanced fragmentation, this corresponds to 3.7 physical pc, roughly the radial length-scale on which baryons begin to dominate the gravitational potential.

Metal enrichment strategy

The dispersal of metals synthesized in the first stars is a complicated process moderated by the interplay of supernova ejection, gravitational reassembly and turbulent mixing with primordial gas (e.g. Karlsson, Bromm & Bland-Hawthorn 2013). The outcome of primordial metal enrichment is strongly dependent on the mass of the first stars. A non-rotating, metal-free star with a mass between 140 and 260 M_⊙ is believed to end life as a highly energetic (E_kin ∼ 10⁵² ergs) pair-instability supernova (e.g. Heger et al. 2003), though rotationally induced mixing may bring the lower limit down by nearly a factor of 2 (Chatzopoulos & Wheeler 2012). Since this explosion completely disrupts the host minihalo, the onset of metal-enriched star formation is delayed until a ∼10⁸ M_⊙ halo forms around a redshift of ∼10 (Wise & Abel 2008; Greif et al. 2010; Wise et al. 2012) where the metal ejecta would likely reassemble.

More recent simulations of Pop III star formation, though, have suggested stellar masses exceeding ∼50 M_⊙ are unlikely given radiative feedback that acts to shut off gas accretion (e.g. Hosokawa et al. 2011; Stacy et al. 2012). These more moderate mass Pop III stars end their lives as less energetic core-collapse supernovae that may not completely disrupt the host minhalo. Ritter et al. (2012) simulated the H ii region, supernova and metal transport from a 40 M_⊙ Pop III star ending its life as an E_kin = 10⁵¹ erg core-collapse supernova. While only about a half metal ejecta expanded beyond the minihalo's virial radius, within 10 Myr the ejecta began to fall back into the centre of the host minihalo, suggesting the first burst of metal-enriched star formation may have followed closely in the wake of the Pop III star formation already in cosmic minihaloes (see also Whalen et al. 2013).

With this in mind, to emulate the complex process of metal ejection and transport in the early Universe, we first run our metal-free cosmological simulation until a halo with a virial temperature of T_vir ∼ 10⁴ K capable of cooling by Lyα emission has formed in the simulation. At the point at which Lyα cooling is effective enough for gas in the centre of the halo to begin to isothermally collapse, we increase the metallicity within 1.5 R_vir of the halo to a non-zero value, either 10⁻⁴, 10⁻³ or 10⁻⁵ Z_⊙. Fig. 1 shows a slice of gas density and temperature through the selected dark matter halo at this point of virialization and denotes the spatial region where we increased the metallicity of the gas with a dashed circle.

Figure 1.

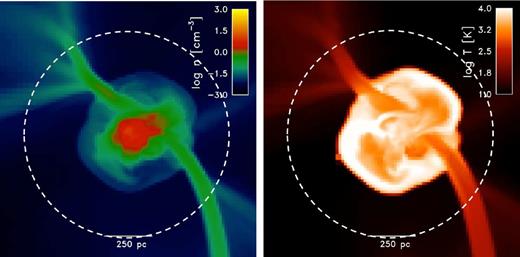
Slices of gas density (left) and temperature (right) when the metallicity of the gas was first made non-zero. The dashed circle denotes the region in which the gas metallicity was first set to a non-zero value. Cold accretion streams that penetrate the virial shock of the halo and account for most of gas accretion are readily apparent.

Open in new tabDownload slide

This idealized approach is not meant to realistically reproduce the results of simulations that track the injection and transport of metals from the first supernovae, such as Wise & Abel (2008), Greif et al. (2010) and Ritter et al. (2012). These studies have shown there to be significant metal inhomogenities on kiloparsec scales around atomic cooling haloes. Mixing between primordial and metal-enriched gas, though, is much more effective at higher densities near the centres of atomic cooling haloes. One should be aware, though, that the transport of passive scalars in grid-based codes is well known to overpredict the diffusion speed and degree of mixing (e.g. Plewa & Müller 1999; Ritter et al. 2012). The goal of this paper is to isolate the thermodynamic impact of metals on protostellar collapse and star cluster formation. Therefore, we opted to perform controlled numerical experiments separating out potential effects of inhomogeneous metal dispersal by introducing metals artificially, assuming perfect mixing. Furthermore, all gaseous fragmentation, the focus of this paper, occurs within an ∼5 parsec region in the centre of the target halo well after the metals are introduced (t ∼ 4 Myr) where turbulent motions are expected to homogenize metals of the order of a dynamical time. We discuss the possible implications of this idealized approach in Section 4.

Chemical and radiative processes

We employ a non-equilibrium chemistry solver that tracks the abundances of the following primordial chemical species: H, H⁻, H⁺, e⁻, H₂, |$\mathrm{H}_2^+$|⁠, He, He⁺, He⁺⁺, D, D⁺ and HD. We additionally include the following gas-phase metal species: C, C⁺, Si, Si⁺, O and O⁺ with the solar abundance pattern. Even a modest intergalactic ultraviolet radiation field is effective in keeping species with a first ionization potential less than 13.6 eV, such as carbon and silicon, singly ionized. Above 13.6 eV, it is a reasonable assumption that neutral hydrogen significantly attenuates the radiation field, especially before the epoch of reionization. We include this effect in our chemical network by setting the photoionization rate of neutral carbon and silicon to values corresponding to our choice of the LW background, J_{LW, 21} = 100, assuming a T = 10⁴ K blackbody spectral shape. The ionization state of oxygen is determined by collisional processes since its ionization potential is above that of neutral hydrogen's and thus does not experience a significant photoionizing flux.

In low density (n < 10⁸ cm⁻³) molecule-free gas, the most significant thermodynamic effect from heavy elements is fine-structure line emission from forbidden transitions of carbon, oxygen and silicon. To model fine-structure cooling, we follow the method of Glover & Jappsen (2007), which we briefly review here.

Sink particles

We utilize sink particles to follow the evolution of gas undergoing gravitational collapse over multiple free-fall times. Sink particles were originally introduced by Bate, Bonnell & Price (1995) in smoothed particle hydrodynamics (SPH) simulations and were first adapted into a grid-based Eulerian setting by Krumholz, McKee & Klein (2004). By accreting gas directly from the grid, sink particles effectively impose an upper limit on gas density and a lower limit on the simulation time step. Without sink particles, the time step would become prohibitively short as gas reached increasingly high densities.

The limitations of the sink particle approach have been discussed extensively in the literature (e.g. Bate, Bonnell & Bromm 2003; Bate 2009; Bate, Lodato & Pringle 2010; Federrath et al. 2010b). According to the original implementation of Bate et al. (1995), when a sink particle forms all SPH particles within its accretion radius are removed and their mass is added to the new sink particle. This results in a sharp pressure discontinuity around the sink particle and can lead to grossly overestimated accretion rates for subsonic gas flow. This problem can be overcome by imposing a boundary pressure at the sink particle accretion radius or by gradually, rather than instantaneously, accreting SPH particle mass (Hubber, Walch & Whitworth 2013). This problem is not as severe in Eulerian implementations, like ours, since sink particle formation and the subsequent gas accretion does not result in a sharp pressure discontinuity. Other limitations include the effects of treating sink particles as softened extended objects and issues concerning angular momentum conservation and viscous torques during gas accretion. Finally, it should be stressed that inside the accretion radius of a sink particle all knowledge of the flow is lost and unless sinks form at a density much greater than the opacity limit for fragmentation, which is not the case in the present simulation, there is the possibility of unresolved subfragmentation.

We evolve the systems for ∼4 Myr past the formation of the first sink particle. It is important to note that sink particles do not represent individual stars. Instead, sink particles are utilized as a computational tool making it possible evolve a self-gravitating, collapsing system for many free-fall times. In physical terms, they are approximately related to a pre-stellar core or clump that is destined to become a small stellar association (e.g. Bergin & Tafalla 2007). The properties of the sink particles, such as spatial distribution, mass and accretion rates, thus do have physical significance. Higher resolution studies are in progress that will shed light on the high-density fragmentation behaviour of the sinks.

In the simulations here we take the sink accretion radius to be the Jeans length (equation 1) at the highest level of refinement, r_acc = 4Δx = 0.06 pc ≈ 12 000 au, where Δx is the cell spacing at the highest level of refinement. The softening length for the sink–gas gravitational interaction is set to r_soft = r_acc/2 to ensure that the gravitational softening does not interfere with accretion on to the sink. Sink–sink interactions are softened when the distance between the two particles is less than Δx/2 = r_acc/8. While the density threshold ρ_J is temperature dependent, we note that at a typical temperature of 50 K ≈ T_CMB(z = 16), the threshold is ρ_J = 6.3 × 10⁻¹⁸g cm⁻³. Finally, we do not allow merging between sinks, even if the sink particles are gravitationally bound to each other. We comment on the validity of this choice in Section 4.

RESULTS

As in Safranek-Shrader et al. (2012), a spatially constant LW background with intensity J_{LW, 21} = 100 strongly suppresses the formation of H₂ and thus prevents the collapse of gas in haloes unable to cool by atomic Lyα emission. Once a halo grows massive enough so that its virial temperature is T_vir ≈ 10⁴ K, gas begins to isothermally collapse at T ∼ 8000 K. When gas reaches a density of ∼100 cm⁻³, we increase the gas metallicity within ∼500 pc of the halo's point of maximum density to a constant, non-zero value. This occurs at a redshift of z = 15.8 in a halo with virial mass M_vir = 1.4 × 10⁷ M_⊙, maximum circular velocity v_circ = 12 km s⁻¹ and virial radius r_vir ≈ 350 pc. The halo at this point is shown in the top panels of Fig. 1.

We choose three different values for this metallicity, Z = 10⁻², 10⁻³ and 10⁻⁴ Z_⊙. The limiting values bracket the metallicity needed for metal fine-structure lines to significantly alter the thermodynamic evolution of gas and promote fragmentation (e.g. Bromm et al. 2001). They are also physically reasonable given the expected generation and dispersal of metals in the first star-forming haloes (e.g. Wise & Abel 2008; Greif et al. 2010; Ritter et al. 2012), and the metallicities of local, metal-poor UDF spheroidal galaxies (e.g. Kirby et al. 2011; Frebel & Bromm 2012). The three simulations discussed here are identical except for the value of the metallicity.

Overall evolution

In all three simulations, the non-zero metallicity greatly enhances the cooling rate. The dominant cooling processes are fine-structure line emission by O and C⁺. The onset of enhanced cooling allows the gas in the halo's centre to cease its quasi-hydrostatic isothermal contraction and begin a collapse where temperature decreases with increasing density. In the 10⁻² and 10⁻³ Z_⊙ runs, the metal-cooling-induced collapse proceeds isobarically, remaining in pressure equilibrium with the surrounding warm halo gas. In the 10⁻⁴ Z_⊙ run, radiative cooling is not as efficient and the collapsing gas is overpressurized with respect to the surrounding gas. Therefore, the collapse takes longer, by roughly a factor of 2, for sink particles to form in this simulation compared with the higher metallicity runs. Gas in both the 10⁻² and 10⁻³ Z_⊙ runs reaches the CMB temperature, T_CMB ∼ 50 K, in approximately one local free-fall time, although the larger cooling rate in the 10⁻² Z_⊙ run leads to much stronger CMB coupling and nearly isothermal evolution for 10⁴ cm⁻³ < n < 10⁶ cm⁻³. In the 10⁻⁴ Z_⊙ run, the gas temperature remains above T_CMB, instead reaching a minimum temperature of T ∼ 100 K. Eventually, gas in all three simulations reaches the density for sink particle formation given in equation (13). We show density–temperature phase plots at the time of the first sink particle formation in Fig. 2. Past the formation of the first sink particle we evolve each run for ≈4 Myr. Given the characteristic density of the cold, dense regions in each run, n ∼ 10⁴ cm⁻³, this corresponds to roughly eight free-fall times. In this time period, fragmentation was widespread in the 10⁻² and 10⁻³ Z_⊙ runs which formed 11 and 9 sink particles, respectively. Only one sink particle formed in the 10⁻⁴ Z_⊙ run.

Figure 2.

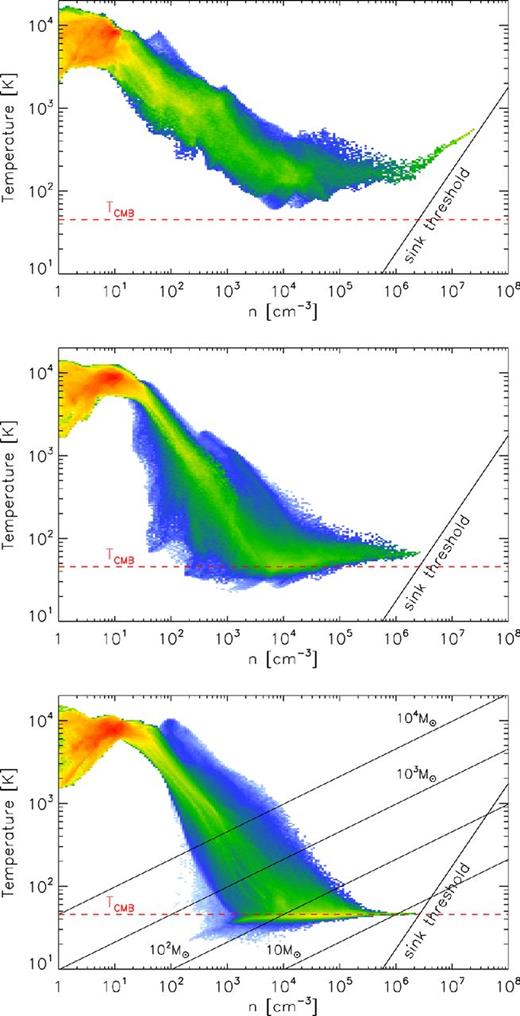
Density–temperature phase diagrams for gas within 50 pc of the densest point as the first sink particle forms for the 10⁻⁴ (top), 10⁻³ (middle) and 10⁻² Z_⊙ (bottom) runs. Colour corresponds to the gas mass at a given density and temperature. We also show the CMB temperature (red dashed horizontal line) and the temperature-dependent density threshold for sink particle creation (steep solid line; see equation 13). Additionally, in the bottom panel, we show lines of constant Jeans mass. In the higher metallicity simulations, gas first reaches T_CMB when M_J ∼ 100 M_⊙, consistent with the typical sink particle mass forming in these simulations.

Open in new tabDownload slide

Morphology and density evolution

The subsequent collapse in the 10⁻² Z_⊙ run becomes nearly isothermal at a density of n ∼ 10³-10⁴ cm^{− 3} and T = 45 K = T_CMB. The resulting structure is a cold, dense pocket of gas embedded within the turbulent, hot (T ∼ 10⁴ K) gas of the halo. This cold, dense region contains approximately 400 M_⊙ in gas and is ∼ 1-2 pc in physical size. Compression of the cold by the warm medium produces a strong, quasi-isothermal shock with Mach number |$\mathcal {M}\equiv v/c_{\mathrm{s}}\sim 3$|⁠. The morphology of the cooled region evolves from roughly spherical to sheet-like and is seeded with filamentary density perturbations. These are the well-known ‘thermal pancakes,’ an outcome of non-linear effects developing in the aftermath of thermal instability (e.g. Kritsuk & Norman 2002). We see this in projection in the top-left panel of Fig. 3 – in this view the sheet-like compressed region is seen face-on. The filamentary morphology is created entirely by the strong shock and resulting instabilities after the gas hit T_CMB. We note this is very similar to the model in which cold atomic and molecular clouds form as a result of supersonic flow convergence and thermal instability in a warm neutral medium (e.g. Hennebelle & Pérault 1999; Koyama & Inutsuka 2000; Hartmann, Ballesteros-Paredes & Bergin 2001; Heitsch et al. 2005, 2008; Vázquez-Semadeni et al. 2006; Hennebelle, Audit & Miville-Deschênes 2007).

Figure 3.

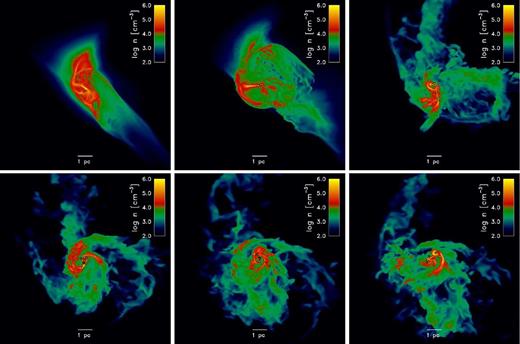
Snapshots showing mass-weighted line-of-sight density projections from the 10⁻² Z_⊙ run. Black circles represent sink particles, with the circle radius equal to the particle accretion radius. The top-left panel shows the state of the simulation just before sink particle formation. After the gas has reached the CMB temperature, thermal instability and strong, quasi-isothermal shocks produce a sheet-like morphology (seen face-on in the top-left panel) and filamentary striations. These features are transient and within ∼2 Myr the star-forming cloud becomes more disordered and has an apparent net rotation. The consecutive snapshots from left to right and top to bottom are separated by a time interval of 0.8 Myr.

Open in new tabDownload slide

The density enhancement from the isothermal shock elevates the peak gas density to ∼10⁵ cm⁻³. At this point, self-gravity becomes dominant in the highest density gas and two nearby sites of fragmentation emerge nearly concurrently, separated by ∼0.1 pc. This point in the simulation is shown in the top-middle panel of Fig. 3. These sites of fragmentation form two sink particles that rapidly create a tight binary pair. One of these sinks remains the most massive for the remainder of the simulation. We consider the onset of star formation to correspond to the time of the first sink particle formation. This occurs 4.8 Myr after the gas metallicity was assigned a non-zero value and corresponds to one free-fall time when evaluated at the density triggering metal introduction, n = 100 cm⁻³.

The morphology of the cold, dense gas changes substantially over the course of the ensuing ∼4 Myr as can be seen in the remaining panels of Fig. 3. Only the densest regions, n > 10⁴ cm⁻³ survive this subsequent hydrodynamic bounce. Over the first 3.8 Myr after the first sink particle formation, approximately 1700 M_⊙ of gas becomes incorporated into a total of 11 sink particles, a value that can also be considered a firm upper limit to the mass in stars that would have formed. Most of this mass, ∼1000 M_⊙, exists in the two most massive sink particles (the first and third to form), with masses of 460 and 510 M_⊙, respectively. The average sink particle mass is ≈145 M_⊙, though this does include two sink particles whose masses are 0.2 and 0.4 M_⊙. These sink masses are near the grid mass resolution of the simulation (ρΔx³ ∼ 0.3 M_⊙), though we argue in Section 3.2 that these are genuine gravitationally collapsed structures and not numerical artefacts. The average accretion rate on to sink particles was ≈10⁻⁴ M_⊙ yr⁻¹, consistent with a few times the characteristic accretion rate in gas clumps collapsing after Jeans instability c_s³/G (e.g. Shu 1977; Larson 2003) evaluated at T = 50 K. The sink particles are distributed in a region of approximately 1 pc in size. We stop the simulation ≈4 Myr after the formation of the first sink particle because this is roughly the time-scale at which we would expect stellar radiative feedback to significantly affect the subsequent evolution.

The 10⁻³ Z_⊙ run is qualitatively similar to the 10⁻² Z_⊙ run. We show the density evolution for that run in Fig. 4 and a representative density–temperature diagram in Fig. 2(b). At 4 Myr after the formation of the first sink particle there is a similar number of and amount of mass incorporated in sink particles as in the 10⁻² Z_⊙ run. The gas, as in the 10⁻² Z_⊙ run, hits the CMB temperature floor at a density of n ∼ 10⁴ cm⁻³, but, unlike in the higher metallicity run, because of the smaller cooling rate, begins heating up again at still higher densities. It is difficult to assess the impact of the CMB temperature floor – one-zone models would suggest that even in the absence of the CMB, gas at this metallicity would reach a minimum temperature of T ∼ 50 K (Omukai et al. 2005). Nine sink particles form within the course of 4 Myr with a total mass of 1450 M_⊙. Unlike in the 10⁻² Z_⊙ run, most of the fragmentation occurred in a disc that assembled around the first sink particle. The disc became locally gravitationally unstable and underwent pervasive fragmentation (seen in the top-middle panel of Fig. 4). This can be contrasted with fragmentation resulting from the collapse and break up of filamentary features in the 10⁻² Z_⊙ run.

Figure 4.

Same as Fig. 3 but for the 10⁻³ Z_⊙ run.

Open in new tabDownload slide

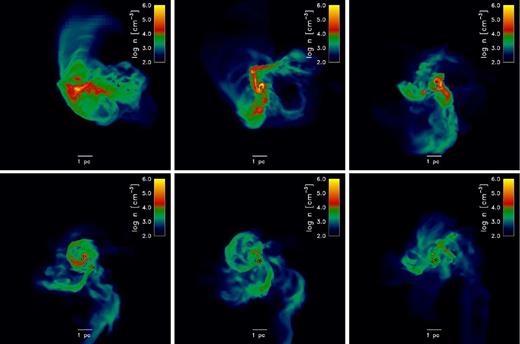
Another major difference between the 10⁻² and 10⁻³ Z_⊙ runs is the amount of cold gas available for sink particle accretion. As can be seen in the progression of the panels in Fig. 4, the dense gas supply is continually diminishing and gas above a density of n ∼ 10⁴ cm⁻³ is virtually non-existent in the last panel when sink particles have been accreting for 4 Myr. Quantitatively, after ≈4 Myr, there is 5700 M_⊙ of cold gas (defined such that n > 100 cm⁻³ and T < 1000 K) in the 10⁻² Z_⊙ run and only 1500 M_⊙ in the 10⁻³ Z_⊙ run. Either the sink particles in this run are much more effective at accreting gas, or more likely the supply of cold, dense gas from the halo is unable to meet the demand of sink particle accretion. We return to this point in Section 3.2.

We show the density evolution in the 10⁻⁴ Z_⊙ run in Fig. 5. We also show a representative density–temperature diagram in Fig. 2(a). Gas reaches a minimum temperature of T ∼ 100 K at n ∼ 10⁴ cm⁻³ where the Jeans mass is ∼1000 M_⊙. While the initial cooling that prompted the collapse was due to metal fine-structure emission, H₂ did play a significant role due to self-shielding allowing the molecular abundance to increase (see equation 3). This is identical in many respects to the thermodynamical evolution of collapsing metal-free gas and likely leads to a similar outcome (see e.g. Safranek-Shrader et al. 2012). Given the warmer temperature of the dense gas, the strong shock present in the higher metallicity simulations was absent following the collapse, the subsequent collapse remained relatively spherical, and it did not exhibit sheet-like or filamentary density perturbations. Only a single sink particle formed surrounded by a gravitationally stable, non-fragmenting gaseous disc formed in the simulation. In 4 Myr, the lone sink particle reached a mass of 520 M_⊙, had an average accretion rate of ≈10⁻⁴ M_⊙ yr⁻¹ and a peak accretion rate of ≈10⁻³ M_⊙ yr⁻¹. This is a much smaller accretion rate than the peak rate found in collapsing primordial gas (e.g. Abel, Bryan & Norman 2002; Yoshida et al. 2006; O'Shea & Norman 2007), a discrepancy predominantly due to the much higher time and spatial resolution in those studies and their ability to capture the onset of collapse at higher densities. If stellar mass scale fragmentation occurred at higher densities than resolved in the simulation, this would result in an extremely compact stellar association, or cluster, with size less than the sink particle accretion radius, 0.01 pc – this estimate, however, neglects the internal dynamical evolution of the cluster which could eject stars on to more extended orbits (e.g. Omukai, Schneider & Haiman 2008).

Figure 5.

Same as Fig. 3 but for the 10⁻⁴ Z_⊙ run. The snapshots are approximately 2 Myr apart. Differences between this and the higher metallicity runs (Figs 3 and 4) are evident. Here, only a single sink forms and is surrounded by a non-fragmenting gas disc of radius ∼0.5 pc.

Open in new tabDownload slide

The importance of following the evolution for multiple free-fall times, enabled by our use of sink particles, past the first point of collapse becomes evident from an inspection of the morphology evolution plots (Figs 3–5). This is most apparent in the 10⁻² and 10⁻³ Z_⊙ runs where the gas morphology at the point of the first sink particle formation is not at all representative of its longer term, ∼10⁶ yr, evolution. The initial isobaric cooling phase and isothermal collapse towards sink particle formation produces a dense, compact region with significant filamentary density perturbations. Within 1 Myr the region containing cold, dense gas becomes more diffuse. The further evolution, driven by the accretion of gas and sink particle dynamics produces a disordered, intermittent, filamentary flow morphology, typical of supersonic turbulence (e.g. Kritsuk et al. 2007; Federrath et al. 2010a). The majority of the sink particles, and thus stellar objects, form from density fluctuations not present at the point of first collapse. The 10⁻⁴ Z_⊙ run, though, does not experience any significant morphological evolution after sink particle creation.

Characteristic time-scales

To better understand the differences between the three runs, in Fig. 6 we show characteristic time-scales related to the dynamical and thermal evolution of the gas. We plot the free-fall time, t_ff = (3π/32Gρ)^1/2, the compression time, |$t_{\mathrm{comp}} = \rho / |{\nabla }\cdot (\rho \boldsymbol {v})|$|⁠, the sound crossing time, t_sound = λ_P/c_s, where λ_P is the pressure scalelength given by λ_P = P/|∇P| and the cooling time, t_cool = 3nk_BT/2Λ. We choose to treat the sound crossing time as a local quantity since sound waves need not propagate across an extended region to maintain isobaricity, only across one pressure scalelength. The time-scales are computed via mass weighting in logarithmically spaced density bins. For the cooling time, we additionally denote the most dominant coolant in the particular density bin (see figure).

Figure 6.

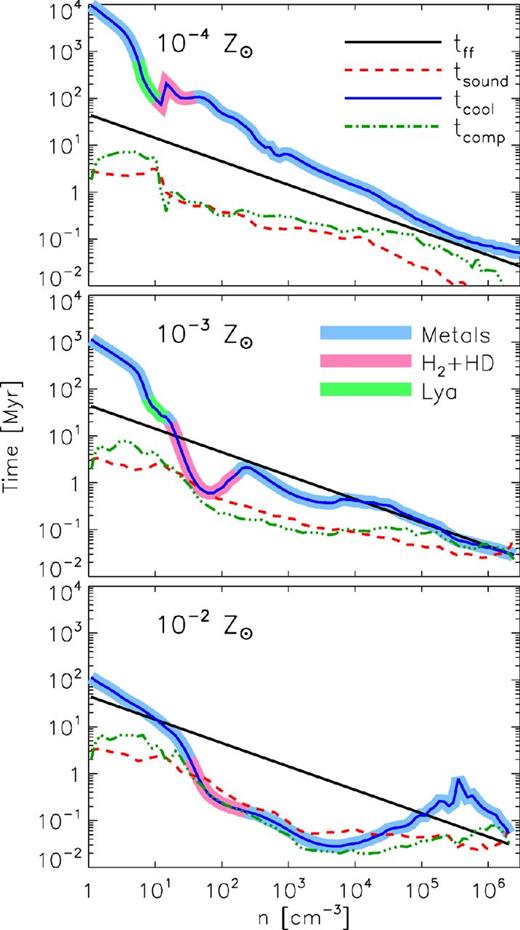
Various characteristic time-scales as a function of gas density in the 10⁻⁴ (top), 10⁻³ (middle) and 10⁻² Z_⊙ run (bottom). Shown is the free-fall time (solid black line), the sound crossing time of the pressure scaleheight (red dashed line – see the text), the compression time (green triple–dot–dashed line – see the text) and the cooling time t_cool = 3nk_BT/2Λ (blue solid line enclosed by a thicker line). The colour of the thicker line enclosing the cooling time indicates the identity of the most effective coolant. Light blue refers to metal line cooling, light red is the cooling by H₂ and HD, and green is Lyα cooling.

Open in new tabDownload slide

Gas is expected to behave quasi-isobarically when t_sound ≲ t_ff, t_cool. This is indeed the case in the 10⁻² and 10⁻³ Z_⊙ runs at densities between ∼10 and ∼10⁴ cm⁻³. As evident in Figs 2(b) and (c) the gas cooling from T ≈ 10⁴ K to T_CMB does indeed proceed quasi-isobarically. In the 10⁻⁴ Z_⊙ run, however, the ordering of time-scales is t_sound ≪ t_ff, t_cool, suggesting that the gas is overpressured with respect to its surroundings, with gravity, rather than ambient warm gas pressure, driving the compression. This is supported by the density–temperature slopes in Fig. 2(a), and by the longer time gravitational collapse took after the gas metallicity was increased in the 10⁻⁴ Z_⊙ run as compared to the higher metallicity simulations. The time-scales therefore help explain the different outcomes in the 10⁻⁴ Z_⊙ run that exhibited no fragmentation and the higher metallicity runs with pervasive fragmentation.

Fig. 6 also highlights the relative importance of molecular and metal cooling (see e.g. Glover & Clark 2014). When the gas is first endowed with a non-zero metallicity, the increased cooling rate pushes the gas past a threshold where it ceases its isothermal collapse and begins an evolution in which temperature decreases with increasing density and the adiabatic index is subisothermal, dln P/dln ρ < 1. This increases the H₂ self-shielding factor (equation 3), the H₂ abundance rapidly increases and H₂ becomes the dominant coolant in each simulation, albeit only over a small range of densities. Once the gas temperature drops below ∼200 K, however, H₂ loses its cooling efficacy and metal line cooling once again dominates. We note that when H₂ is the dominant coolant, its cooling rate is never more than a factor of ∼3 greater than the metal line cooling rate.

The metal abundance, perhaps surprisingly, plays a significant role in regulating the H₂ abundance. Our treatment of carbon and silicon as singly ionized significantly elevates the free electron abundance at densities n > 100 cm⁻³, an effect more pronounced in the higher metallicity simulations. In the 10⁻² Z_⊙ run, these additional free electrons actually set a lower limit of x_e ∼ 2 × 10⁻⁶ on the free electron abundance. Given that the formation of H₂ through the gas phase H⁻ channel depends sensitively on x_e, it is not surprising that the primordial coolant would depend on the gas metallicity.

Sink particle formation, growth and mass function

We emphasize that the sink particles here do not represent single stars, but instead are small stellar associations. We take the sink particle mass as a proxy for the stellar mass of the association. This mass is a firm upper limit as we do not include any form of stellar feedback that would likely act to reduce the gas-to-star conversion efficiency. The total mass accretion rate on to protostellar objects in one association, which is approximated by the sink particle gas accretion rate, has implications for protostellar evolution (e.g. Omukai & Palla 2003). We calculate the sink particle accretion rates by dividing the mass accreted during a time step by the length of the time step. To derive any insight on the nature of individual protostars we would need to probe higher densities up to the opacity limit for fragmentation (Low & Lynden-Bell 1976; Rees 1976).

In Fig. 7, we show the total mass in sink particles over time in the three simulations. The two higher metallicity runs reach a total sink mass of ≈1500 M_⊙ in 4 Myr. The 10⁻⁴ Z_⊙ run converts roughly a factor of 3 lower gas mass, 500 M_⊙, into one sink particle 4 Myr after its formation. In all runs, most of the sink mass is in a few large mass (>500 M_⊙) objects. The average sink accretion rate is ≈4 × 10⁻⁴ M_⊙ yr⁻¹ in the two higher metallicity simulations and ≈10⁻⁴ M_⊙ yr⁻¹ in the lowest metallicity simulation. The general trend is that the first sink particles to form remain the most massive, though there are exceptions.

Figure 7.

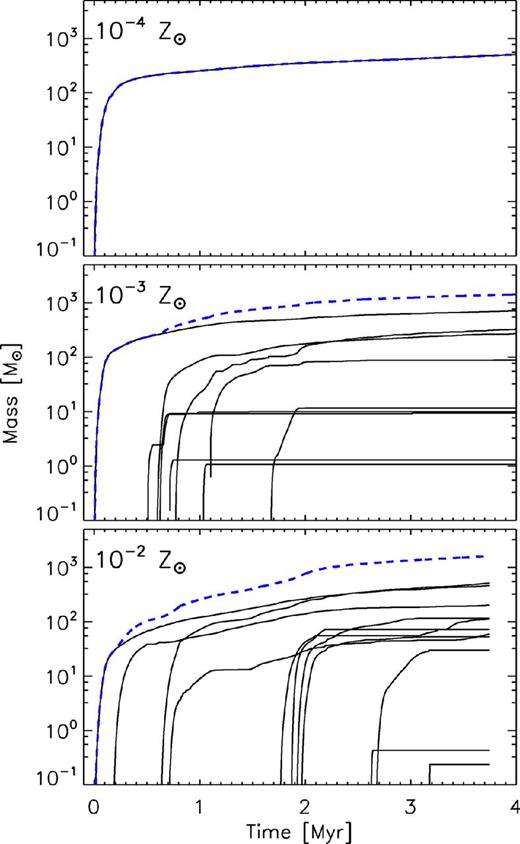
Masses of individual sink particles (black lines) and total mass in sink particles (blue dashed line) in the 10⁻⁴ (top), 10⁻³ (middle) and the 10⁻² Z_⊙ (bottom) runs. Even though the 10⁻² and 10⁻³ Z_⊙ runs formed similar numbers and total masses of sink particles, new sink particle formation in the 10⁻³ Z_⊙ run effectively ceased after ∼2 Myr.

Open in new tabDownload slide

In the 10⁻² and 10⁻³ Z_⊙ runs, many sink particles appear to permanently stop accreting after less than ∼10⁵ years of growth – this is most apparent in the middle panel of Fig. 7. It is possible that these ephemerally accreting sink particles do not represent physical gravitationally bound structures but are numerical artefacts; many of their masses lie far below the typical Jeans mass where fragmentation is likely to set in (M_J ∼ 50-100 M_⊙). These sinks, though, did pass a stringent suite of tests for creation (see Section 2.4) that includes only forming sink particles from a gravitationally bound converging gas flow. Thus, it seems that these objects are collapsed physical structures and that their mass growth was terminated by a physical mechanism, likely strong tidal interactions with more massive sink particles, though higher resolution simulations are needed to establish this conclusively.

Figure 8.

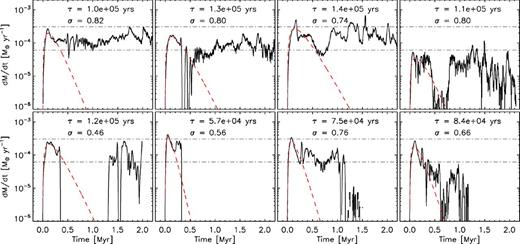
Accretion rates of the first eight sink particles to form in the 10⁻² Z_⊙ run in the first ∼2 Myr. The top and bottom horizontal dot–dashed lines show the fiducial accretion rate c_s³/G evaluated at T = 100 and 50 K, respectively. The dashed red line is a fit to the first |$0.5\,\rm {Myr}$| of accretion (equation 15) with the value of fitting parameter τ shown at the top of each panel.

Open in new tabDownload slide

Figure 9.

Same as Fig. 8, but for the 10⁻⁴ Z_⊙ run and smoothed on a |$10^4,\rm {yr}$| time-scale. Only one sink particle formed in the simulation.

Open in new tabDownload slide

Almost all the sink particle accretion rates show a similar early time (≲0.5 Myr) behaviour – a rapid rise to a peak value followed by a drop to a lower (or zero) accretion rate. It is reasonable to ask whether this general behaviour is physical or is instead a numerical artefact from instantaneous gas pressure loss following sink particle formation (e.g. Bate et al. 1995). As discussed in Section 2.4, Eulerian sink particle implementations do not suffer from this issue to the same degree that SPH implementations do. Additionally, numerous numerical studies of protostellar collapse have found rapidly peaking accretion rates followed by a decrease (e.g. Hunter 1977; Basu 1997; Whitworth & Ward-Thompson 2001; Motoyama & Yoshida 2003; Schmeja & Klessen 2004). While it is possible that the accretion rates we measure are slightly overestimated by the reduction of gas density around sink particles, this general behaviour we see is physically expected.

Beyond the first accretion rate peak, many sink particles in the 10⁻² and 10⁻³ Z_⊙ runs, especially the earliest ones formed, show sustained gas accretion over many Myr. Others do not display sustained gas accretion but instead have their accretion terminated within a few 10⁵ yr after their formation. This sharp cutoff in the accretion rates is primarily the result of these sinks experiencing a close encounter with a more massive sink particle, also seen in idealized simulations of present-day (e.g. Klessen & Burkert 2000; Klessen 2001a) and Pop III (Clark et al. 2011b) star formation. These strong dynamical encounters tend to eject less massive sinks to the outskirts of the cold gas environment where gas densities are smaller and accretion is thus lowered or completely shut off. Given the density and velocity dependence of the Bondi–Hoyle accretion rate, |$\dot{M}_{\mathrm{BH}}\propto \rho v^{-3}$|⁠, the ejected sinks effectively stop accreting.

Overall, it seems that the mode of gaseous accretion on to sink particles is a hybrid between monolithic collapse (e.g. McKee & Tan 2003), where the stellar mass (and mass function) is ultimately determined by the mass of gravitationally unstable cores, and competitive accretion (e.g. Bonnell et al. 2001), where stellar masses are the result of many cores competing for the same reservoir of gas resulting in more massive (though rarer) objects near the cluster centre accreting more such that the ‘rich get richer.’ The less massive sink particles, typically the latter ones to form, can only accrete a portion of their initial Jeans-unstable gas clumps before dynamical interactions with other sink particles terminate gas accretion. Higher mass sink particles form more massive Jeans-unstable clumps and then continue accreting from the dense gas in the central region of the cluster over many Myr.

The top panel of Fig. 10 shows the sink particle mass function at the end of each run after star formation has progressed for ≈4 Myr. The higher metallicity simulations show a preferred mass scale around ∼50 M_⊙, roughly consistent with the Jeans mass at the point at which the gas density hits the CMB temperature and fragmentation is expected to be thermodynamically suppressed. While this mass function does not represent the final stellar IMF, observations have shown there to be a connection between the pre-stellar clump mass function and the ultimate stellar IMF (e.g. Motte, Andre & Neri 1998; Beuther & Schilke 2004; André et al. 2010), suggesting that the power-law slope towards higher masses, only marginally evident in the 10⁻² Z_⊙ run, may translate directly to the slope of the ultimate stellar IMF. We caution that the inclusion of radiative feedback from accreting protostars has the potential to suppress fragmentation and thus alter the resultant mass function, particularly at the low-mass end (e.g. Krumholz, Klein & McKee 2007; Urban, Martel & Evans 2010; Bate 2012). The bottom panel of Fig. 10 shows the mass function in which sink particles located within each other's accretion radius are merged in post-processing and are only counted as a single particle. Doing this, four sink particles in the 10⁻² Z_⊙ run merge into two sinks, while in the 10⁻³ Z_⊙ run only one pair of particles merges. As is clear, this merging procedure has little effect on the resultant mass function. Finally, we emphasize that the mass function is sensitive to the resolution (which determines the sink particle formation density) and the particular choice of sink particle parameters (such as the accretion radius and the sink–gas softening length) as discovered in our initial exploratory simulations.

Figure 10.

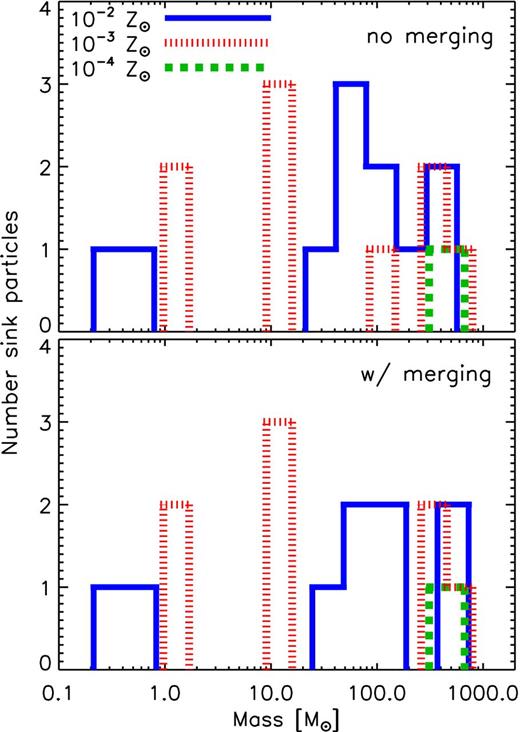
Distribution of sink particle masses in the 10⁻² (blue solid line), 10⁻³ (red short-dashed line) and 10⁻⁴ Z_⊙ (green dotted line) runs 4 Myr after the first sink particle formation. The top panel is the mass function extracted directly from the simulations. In the bottom panel, in post-processing, we merged any sink particles within each other's accretion radius. Sink merging performed in post-processing does not drastically affect the mass spectrum.

Open in new tabDownload slide

Density probability distribution function

The gas density PDF, p(ρ), is defined such that p(ρ)dρ represents the probability that a given parcel of gas has density within the range [ρ, ρ + dρ]. It is particularly sensitive to the character and strength of turbulence that imprints a specific turbulent signature on the gas density PDF. We show volume-weighted gas density PDFs for the three simulations and two different times in Fig. 11. We show the PDF for all gas within the virial radius of the halo and only for gas with temperature T < 200 K and density n > 100 cm⁻³, the latter representing the gas that has cooled and is participating in star formation.

Figure 11.

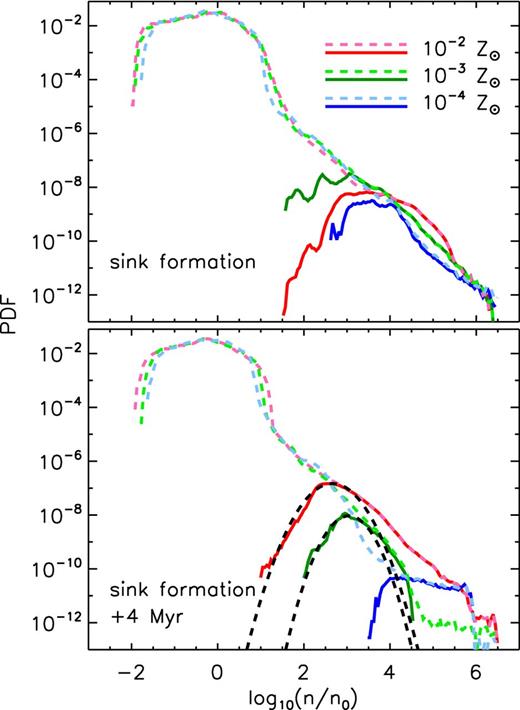
Gas density PDFs at the onset of sink particle formation (top panel) and 4 Myr later (bottom panel). We show PDFs from the 10⁻² (red lines), 10⁻³ (green lines) and 10⁻⁴ Z_⊙ (blue lines) runs. We separately plot PDFs computed using all gas within the virial radius of the halo (dashed lines) and only gas with T < 200 K and n > 100 cm⁻³ (solid lines). For the all gas PDFs, the average density is n₀ ≈ 1 cm⁻³ at both times. In the bottom panel, we show lognormal fits to the 10⁻² and 10⁻³ Z_⊙ run cold gas PDFs which have widths of σ = 0.86 and 0.71, respectively. Power-law tails, evident in the top panel and in the 10⁻⁴ Z_⊙ run in the bottom panel, are an anticipated outcome of self-gravity. In the 10⁻³ Z_⊙ run, however, this power-law tail disappears within ∼2 Myr after the first sink particle formation as the sink particles deplete the cold, dense gas.

Open in new tabDownload slide

The density PDFs in Fig. 11 exhibit a number of interesting features. The high density, cold gas PDFs peak at densities roughly three orders of magnitude higher than that of the full density PDFs. The cold gas PDFs also represent a significant ‘bump’ in the full density PDF, mainly seen in the bottom panel. This is clearly reminiscent of the density structure in thermally bistable turbulent flows (e.g. Gazol & Kim 2010; Seifried, Schmidt & Niemeyer 2011; Saury et al. 2013). The sharp increase in the peak density of the cold gas PDF in the 10⁻⁴ Z_⊙ run is due to the T < 200 K temperature cutoff which was selected with the higher metallicity simulations in mind, meant to cleanly separate the cold and hot phases that are separated by an isobarically unstable cooling phase. In the 10⁻⁴ Z_⊙ run, is it not possible to cleanly distinguish between the ambient halo gas and the cooling gas.

Star formation efficiency

Figure 12.

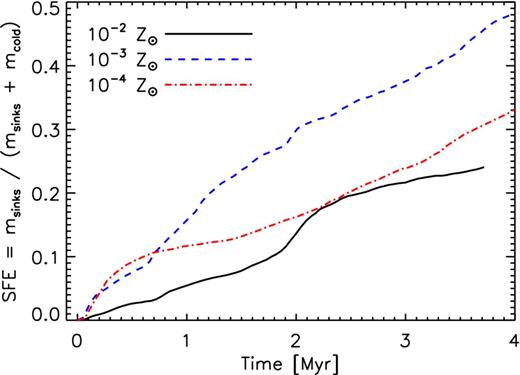
SFE as a function of time in the three different metallicity runs. We define the star formation efficiency as SFE(t) ≡ M_sinks(t)/(M_{gas, cold}(t) + M_sinks(t)) where M_{gas, cold} is the total mass of gas with temperature T < 1000 K and density n > 10 cm⁻³. This efficiency measures the efficiency with which the cold and dense gas is being incorporated in stars. Since all the curves increase with time, the sink particles are depleting the cold gas supply faster than gas is able to cool, implying that eventually, the star-forming cluster becomes gas starved.

Open in new tabDownload slide

CAVEATS AND LIMITATIONS

The most significant approximation used in the simulations is our metal enrichment strategy. Recall that when the target halo has entered the Lyα cooling-enabled isothermal collapse, we endowed gas in the vicinity of the halo with a non-zero metallicity. The metallicity was made spatially uniform, implying that metal mixing acted with perfect efficiency, which is certainly not the case. Realistically, the mixing is not instantaneous and could potentially result in concurrent Pop III and Pop II star formation (e.g. de Avillez & Mac Low 2002; Pan, Scannapieco & Scalo 2011, 2013). The process of metal mixing may begin in hydrodynamic instabilities of supernovae (e.g. Joggerst, Woosley & Heger 2009) and supernova remnants (e.g. Madau, Ferrara & Rees 2001; Ritter et al. 2012) and following turbulent transport is ultimately completed on microscopic scales via molecular diffusion. Since molecular diffusion is effective only on microscopic spatial scales (e.g. Oey 2003; Pan & Scalo 2007), turbulence is paramount for efficient mixing of primordial and metal-enriched gas. There is evidence that the process of virialization and the inflow of dark matter directed ‘cold accretion’ streams in atomic cooling haloes can be effective in driving supersonic turbulent motions (Wise & Abel 2007; Greif et al. 2008; Prieto, Jimenez & Martí 2012; Latif et al. 2013) and thus accelerating the mixing of primordial and metal-enriched gas. Frebel & Bromm (2012) suggested that a signature of incomplete mixing can be found in the chemical inhomogeneity of metal-poor stellar populations, particularly those in UDF galaxies.

The fact that metals were not present during the initial virialization process of the atomic cooling halo may also have consequences. If the high density, cold accretion streams that account for the majority of baryonic accretion into the halo had been metal enriched we would have expected them to have significantly lower temperatures than if the gas was primordial. Given the lower temperatures, the stream termination shocks would be more compressive and this could affect the virialization and star formation processes. Our choice of the time to raise the gas metallicity to a non-zero value may also directly set the characteristic fragmentation mass. In all simulations, the metals were introduced when the maximum gas density in the halo reached 100 cm⁻³. Increasing the metallicity of the gas at a lower (higher) peak density threshold would have let the gas hit the CMB floor at a smaller (larger) density, thus increasing (decreasing) the characteristic fragmentation mass scale. Our main result, though, concerning efficient fragmentation above Z = 10⁻⁴ Z_⊙ is robust in this respect, as is the typical gas accretion rate and total cluster mass. Additionally, actual protostellar fragments must ultimately emerge at higher densities in the presence of thermal gas–dust coupling and would be unaffected by this caveat.

Our simulations did not include any prescriptions for stellar feedback, processes well known to play significant roles in star formation, allowing us to isolate the process of gas collapse and fragmentation in the presence of metal cooling. We run the simulations for 4 Myr past the formation of the first sink particle, a time-scale meant to capture only the initial starburst. In this time we do not expect supernovae, stellar winds or stellar evolutionary effects to play significant roles given these processes operate on longer time-scales (∼3 − 100 Myr). Radiative feedback from accreting protostars should influence the outcome of turbulent fragmentation in the first metal-enriched star-forming regions. Detailed radiation hydrodynamic simulations (e.g. Krumholz et al. 2007; Bate 2012) have shown that the primary impact of radiative heating is the suppression of fragmentation. This results in fewer low-mass brown dwarf-like objects (e.g. Offner et al. 2009) and may enable the formation of high-mass stars in dense star-forming regions (e.g. Krumholz, Klein & McKee 2012). This suppression may be less effective in the present simulations given the much smaller metallicity and dust abundance (though see Myers et al. 2011). Simulations of metal-free star formation that include prescriptions for radiation from accreting protostars (e.g. Greif et al. 2011; Smith et al. 2011) find fragmentation to be delayed by the feedback, but not suppressed. In addition to radiative feedback, accreting protostars are known to possess energetic jets that are capable of driving turbulence and reducing the rate of star formation in actively star-forming regions (Li & Nakamura 2006; Matzner 2007; Wang et al. 2010; Cunningham et al. 2011; Krumholz et al. 2012). These jets may be especially significant in the regime considered here since our results suggest that these earliest stellar clusters formed in relatively dense environments (∼0.01–1 pc) where the effect from these outflows would be more pronounced.

We do not include dust grains in our chemical model. This eliminates dust catalysed H₂ formation and dust–gas collisional coupling that can act to heat or cool the gas. The neglect of dust–gas coupling is well justified since this does not occur at densities <∼10⁸ cm⁻³ that we resolve (e.g. Omukai et al. 2005). The dust-grain-catalysed formation of H₂ may have more significant thermal consequences. However, given that much of the star-forming gas in our simulations has temperatures below 100 K where H₂ cooling is ineffective, this would completely eliminate H₂ as an effective coolant even if it did form in much higher abundance. The formation of H₂, though, is an exothermic reaction and thus elevated H₂ formation from dust grains, while not augmenting the cooling rate, may act as a heating source.

Finally, it is worth stressing that the results of the simulations here are resolution dependent. At higher or lower resolutions, resolving higher and lower maximum densities, different physical processes will dominate the gas thermodynamics. Gas–dust coupling would have a significant thermodynamic effect on the gas at much higher densities (n ≳ 10¹⁰ cm⁻³). At lower densities (n ≲ 10³ cm⁻³) there would be almost no difference between the different metallicities considered here (see Fig. 2). Our resolution was chosen to most effectively study the effect that metal fine-structure cooling has on the fragmentation of collapsing gas concentrations. The results of the simulations are also sensitive to the sink particle parameters we used (such as the accretion radius, softening length, density for sink creation, etc.). In preparation for the production simulations presented here, exploratory simulations were performed that varied the resolution and the sink particle parameters. Modification of the gas–sink softening length and accretion radius had the largest effect on sink particle creation, growth and dynamics. Overall, the main difference between these initial simulations and the ones presented here was the number of sink particles created, though never by more than a factor of ∼1.5. The Z = 10⁻⁴ Z_⊙ simulations always produced only one sink particle independent of the resolution or sink particle parameters.

DISCUSSION AND SUMMARY

In this work, we have focused on the effect that metallic fine-structure line cooling has on the process and outcome of star formation in a high-redshift atomic cooling halo. We have run three high-resolution, zoomed cosmological simulations until the assembly of a M_vir ≈ 2 × 10⁷ M_⊙ halo at redshift ∼16 capable of atomic cooling. At this point, we endowed gas in the halo with a non-zero metallicity and observed the subsequent collapse and progression of star formation. We utilized the sink particle technique, allowing us to follow the process of star formation for many free-fall times past the first point of gravitational runaway collapse.

Theory predicts that below a metallicity of Z ∼ 10^−3.5 Z_⊙, fine-structure metal line cooling is not strong enough to significantly alter the thermodynamic and fragmentation behaviour of collapsing gas (e.g. Bromm et al. 2001). We indeed confirm this by finding a marked difference in gas morphology and fragmentation between the 10⁻³ and 10⁻⁴ Z_⊙ runs (as shown in Figs 4 and 5). In the higher metallicity runs, 10⁻² and 10⁻³ Z_⊙, the gas acquires a disordered, turbulent flow morphology. In the 10⁻⁴ Z_⊙ run, cooling was not effective enough to allow the gas to reach T_CMB, the thermal Jeans mass stayed relatively high, and no fragmentation occurred. We attribute this to two key reasons. First, the lower cooling rate in the low metallicity simulation produces gas with higher temperatures and a correspondingly higher thermal Jeans mass, decreasing the propensity for fragmentation. Additionally, the higher Mach number in the higher metallicity runs where gas was able to reach T_CMB led to larger compressibility and a greater propensity for dynamical instabilities to induce small-scale density fluctuations. This was not the case in the 10⁻⁴ Z_⊙ run where the collapse took longer (by roughly a factor of 2), maintained a large degree of spherical symmetry, and underwent no fragmentation.

The accretion rates of individual sink particles are well approximated by c_s³/G, potentially over many Myr. Quite generically, sink particle accretion rates begin low and increase to some maximum value within a few ×10⁴ yr. This first phase ends when the initial Jeans unstable gas clump is accreted by the sink. Sink particles destined to become the most massive have their accretion rate fall off by only a factor of 2-10 after this phase, but stay of the order of c_s³/G for many Myr. Lower mass sinks have their accretion terminated shortly after consuming all or a portion of the initially Jeans unstable gas clump, mainly through dynamical encounters with larger mass sinks. This suggests that protostellar accretion is a combination of relatively quick collapse (t ∼ 10⁵ yrs) and sustained accretion as the stellar association moves throughout the parent gas cloud. Sink particle masses are controlled by both the physical properties of the parent gas cloud, such as the Jeans mass when the gas hits the T_CMB, and dynamical encounters that regulate the long-term accretion rate. The creation of stellar mass fragments must predominantly occur at densities above our resolution limit, possibly as a result of dust–gas coupling (Schneider et al. 2006; Dopcke et al. 2013) or through the fragmentation of gravitationally unstable discs (Stacy et al. 2010; Greif et al. 2011). Overall, it seems most appropriate to describe the process of gaseous fragmentation and sink particle growth in the higher metallicity simulations as a hybrid between competitive accretion and monolithic collapse.

We do not detect suppression of fragmentation at high metallicities due to the CMB temperature floor suggested by Smith et al. (2009). Gas in the 10⁻² Z_⊙ run does become more strongly coupled to the CMB temperature than the 10⁻³ Z_⊙ run, but continues to fragment. In fact, both runs with metallicities above the critical value for efficient fine-structure cooling, Z_crit ≈ 10^−3.5 Z_⊙, exhibited roughly the same fragmentation behaviour as discussed in Section 3, although the primary cause of the fragmentation was different between the two runs as discussed in Section 3.1.1. Given the clump-finding approach of Smith et al. (2009) to characterize the amount of fragmentation, our differing results are unsurprising. Shown in Fig. 7, fragmentation and sink particle formation is continuous over many Myr, well after the initial runaway gravitational collapse. It is possible that another run with metallicity between 10⁻⁴ and 10⁻³ Z_⊙ would have demonstrated an elevated degree of fragmentation, but even so this would suggest that the ‘metallicity regulated’ star formation mode of Smith et al. (2009) would exist only under a very narrow range of metallicities and would not be a significant star formation pathway.

We also find disagreement with the simulations of Jappsen et al. (2007, 2009a,b) who find no metallicity threshold that distinguishes Pop III and Pop II star formation, and instead argue it is the initial conditions (e.g. level of rotation, initial temperature, degree of turbulence) that moderate the process of gas fragmentation, whereas we unambiguously identify a metallicity threshold in controlling fragmentation. Jappsen et al. (2007) argue that H₂ cooling is partly responsible for eliminating a Pop III–II metallicity threshold given that it may be a dominant coolant even in the presence of metals. In all three of the simulations presented here, H₂ was a significant coolant even given the strong LW background we included, though there was still a clear metallicity threshold for widespread fragmentation between 10⁻⁴ and 10⁻³ Z_⊙. The disagreement additionally stems from the differing redshift at which the collapse occurs. In Jappsen et al. (2009a), this redshift was 25 where the CMB temperature is ∼70 K, as opposed to a CMB temperature of T_CMB(z ≈ 16) ∼ 50 K in this work. Given Jeans mass scale fragmentation sets in when gas reaches T_CMB and the temperature dependence of the Jeans mass, M_J ∝ T^3/2, this difference in redshift can potentially be significant in suppressing fragmentation (see also Clarke & Bromm 2003).

In previous work (Safranek-Shrader et al. 2010), we presented a semi-analytical, one-zone model for fragmentation in metal-enriched atomic cooling haloes with results directly applicable to the present study. The model assumed cold-flow accretion into a M_vir = 10⁸ M_⊙ halo at z = 10. These cold flows, when shocked in the halo's interior, were heated to a temperature of T = 10⁴ K, compressed to a density n = 4 × 10³ cm⁻³, and began to isobarically cool. Continued gas accretion resulted in the compressed layer increasing in size until the sound crossing time across the fragment exceeded its free-fall time, our criteria for the onset of fragmentation. While highly simplified, it supported the conclusion, here and elsewhere, that above 10⁻⁴ Z_⊙ gas will experience fragmentation due to metal line cooling. Safranek-Shrader et al. (2010) did predict a much smaller fragmentation mass scale than found here. We attribute this discrepancy to an overestimate of the post-shock density and the lower redshift and cooler CMB temperature. We also argued that gas with metallicity 10⁻² Z_⊙ should not evolve isobarically given its short cooling time compared to the sound crossing time across the compressed post-shock layer. We find this is not the case if considering only the sound crossing time of one local pressure scaleheight. Overall, it is clear that the process of gas fragmentation in high-redshift atomic cooling haloes is complex and difficult to analyse using one-zone models.

Extrapolating beyond the results of the simulation here, it seems plausible that two different fragmentation episodes occur in low metallicity gas at high redshifts. The first occurs at relatively low densities, n ∼ 10³–10⁴ cm⁻³, when gas reaches the CMB floor as a result of metal line cooling. As shown in the simulations here, this mode is capable of forming a compact cluster of size ∼1 pc and fragment masses of the order of 50–100 M_⊙. Solar mass fragments, however, are not expected to form as a result of metal-line-induced fragmentation, especially at high redshifts, z > 10, since the CMB sets a thermodynamic lower limit on the temperature that gas can reach. The second fragmentation episode occurs at much higher densities, n ∼ 10¹⁰–10¹⁴ cm⁻³, when dust grains and gas thermally couple. This dust-induced fragmentation is capable of producing solar mass scale fragments (e.g. Clark et al. 2008; Dopcke et al. 2013) that have the potential to survive until the present day. Whether these two modes of fragmentation acted in tandem, or were individually responsible for separate stellar populations (e.g. Norris et al. 2013) is yet to be determined. An intriguing possibility, supported by the simulations presented here, is that dust-induced fragmentation is responsible for isolated solar mass Pop II stars, while the formation of a bona fide stellar cluster requires metal fine-structure line cooling operating at lower densities and larger spatial scales (e.g. Karlsson et al. 2013).

Higher resolution studies will probe densities n ≳ 10¹⁴ cm⁻³ approaching the final opacity limit for fragmentation. These future studies are crucial to fully assess the impact of metallicity and dust on the Pop III to II transition and constrain the resulting stellar IMF. Simulations that focus on the mechanical, radiative and chemical feedback from this first metal-enriched stellar generation will provide a clearer picture of stellar assembly in the first galaxies and hints to what next generation telescopes, such as the JWST, will observe.

CSS is grateful to Christoph Federrath, Jeremy Ritter and Meghann Agarwal for valuable help in technical and theoretical matters. The author also thanks Harriet Dinerstein, Steve Finkelstein, Jacob Hummel, Paul Ricker, John Scalo and Raffaella Schneider for useful comments and insights. We thank the anonymous referee for an extremely thorough and helpful critique of the original text. We acknowledge Robi Banerjee and Christopher Lindner for providing software used to produce some of the visualizations here. The flash code was in part developed by the DOE-supported Alliance Center for Astrophysical Thermonuclear Flashes (ACS) at the University of Chicago. The authors acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing HPC resources under XSEDE allocation TG-AST120024. CSS is especially grateful to generous support provided by the NASA Earth and Space Science Fellowship (NESSF) programme. This study was supported in part by National Science Foundation (NSF) under grant No. NSF PHY11-25915 through the hospitality of the Kavli Institute for Theoretical Physics to MM, NSF grant AST-1009928 and by the NASA grant NNX09AJ33G. This research has made use of NASA's Astrophysics Data System.

REFERENCES