-
PDF
- Split View
-
Views
-
Cite
Cite
Yusuke Tsukamoto, Masahiro N. Machida, Shu-ichiro Inutsuka, Formation, orbital and thermal evolution, and survival of planetary-mass clumps in the early phase of circumstellar disc evolution, Monthly Notices of the Royal Astronomical Society, Volume 436, Issue 2, 01 December 2013, Pages 1667–1673, https://doi.org/10.1093/mnras/stt1684
Close - Share Icon Share
Abstract
We report the results of our three-dimensional radiation hydrodynamics simulation of collapsing unmagnetized molecular cloud cores. We investigate the formation and evolution of the circumstellar disc and the clumps formed by disc fragmentation. Our simulation shows that disc fragmentation occurs in the early phase of circumstellar disc evolution and many clumps form. The clump can be represented by a polytrope sphere of index n ∼ 3 and n ≳ 4 at central temperature Tc ≲ 100 K and Tc ≳ 100 K, respectively. We demonstrate, numerically and theoretically, that the maximum mass of the clump, beyond which it inevitably collapses, is ∼0.03 M⊙. The entropy of the clump increases during its evolution, implying that evolution is chiefly determined by mass accretion from the disc rather than by radiative cooling. Although most of the clumps rapidly migrate inward and finally fall on to the protostar, a few clumps remain in the disc. The central density and temperature of the surviving clump rapidly increase and the clump undergoes a second collapse within 1000–2000 years after its formation. In our simulation, three second cores of masses 0.2 M⊙, 0.15 M⊙ and 0.06 M⊙ formed. These are protostars or brown dwarfs rather than protoplanets. For the clumps to survive as planetary-mass objects, the rapid mass accretion should be prevented by some mechanisms.
1 INTRODUCTION
Stars form in molecular cloud cores. When the angular momentum in the core is non-negligible, circumstellar disc formation is inevitable because most of the gas cannot directly fall on to central protostar. According to theoretical studies on the gravitational collapse of unmagnetized molecular cloud cores, the protostar is surrounded by a circumstellar disc immediately after its formation (Bate 1998, 2011; Machida, Inutsuka & Matsumoto 2010; Tsukamoto & Machida 2011).
As noted by Inutsuka, Machida & Matsumoto (2010), the resulting disc should be sufficiently massive to develop gravitational instability (GI). If Toomre's Q value of the disc is ≲1.5, the disc is gravitationally unstable to non-axisymmetric perturbation and develops spiral arms (Laughlin & Bodenheimer 1994). These spiral arms readjust the surface density (Takahashi, Inutsuka & Machida 2013) and raise the disc temperature, thereby re-stabilizing the disc. However, if radiative cooling is effective enough or the mass accretion on to the disc is sufficiently high, the disc may fragment and form clumps (Gammie 2001; Rice, Lodato & Armitage 2005; Inutsuka et al. 2010; Stamatellos, Whitworth & Hubber 2011b; Kimura & Tsuribe 2012).
Disc fragmentation is a candidate mechanism of wide-orbit planet formation (Rice et al. 2005; Vorobyov & Basu 2010; Machida, Inutsuka & Matsumoto 2011; Vorobyov, DeSouza & Basu 2013). A wide-orbit planet is a planet separated from the central star by more than 10 au (Marois et al. 2008, 2010; Lagrange et al. 2009; Thalmann et al. 2009; Lafrenière, Jayawardhana & van Kerkwijk 2010). On the other hand, it has been suggested that disc fragmentation can also explain the formation of brown dwarfs (Stamatellos & Whitworth 2009a; Stamatellos et al. 2011a) or multiple stellar systems (Machida et al. 2008; Kratter et al. 2010).
The ultimate fate of the clumps depends upon their orbital and internal evolution. If the migration time-scale is very small, the clump accretes on to the central protostar and eventually disappears. On the other hand, if the collapse time-scale of the clump is sufficiently long, dust sedimentation may cause planetary embryos to form inside the clump (Nayakshin 2010a).
Although the orbital and internal evolution of clumps in circumstellar disc is clearly important, a limited number of studies exist on the topic. Baruteau, Meru & Paardekooper (2011) investigated the orbital evolution of massive planets formed by disc fragmentation. They showed that the planets rapidly migrate inward on a type I migration time-scale (Tanaka, Takeuchi & Ward 2002). Adopting an analytical approach, Nayakshin (2010b) showed that the collapse time-scale of the clumps is ≳104 years, considerably longer than the orbital time-scale at r ∼ 100 au (approximately one thousand years). However, Nayakshin used a simplified opacity model, and he ignored further mass accretion on to the clumps from the disc. Recently, Galvagni et al. (2012) investigated the internal evolution of clumps which were extracted from three-dimensional (3D) global disc simulations. They reported a collapse time-scale of about several thousand years, shorter than the estimates of Nayakshin (2010b). However, these authors similarly neglected further mass accretion on to the clumps.
To investigate the internal evolution of clumps permitting realistic gas accretion from the disc, we must simultaneously calculate the evolution of both disc and clumps. Furthermore, appropriate treatment of radiative transfer and a realistic equation of state (EOS) are crucial in studies of both the disc fragmentation (Boley et al. 2007) and internal evolution of the clumps. Since clump evolution cannot be modelled assuming the thin disc approximation, 3D simulations are required. Two-dimensional simulations of the circumstellar disc would also overestimate the extent of disc fragmentation (T. Tsuribe, private communication). Stamatellos & Whitworth (2009b), who investigated the internal evolution of clumps in 3D radiative smoothed particle hydrodynamic (SPH) simulations, reported that clumps collapse on a time-scale of 103–104 years. However, they initially assumed a massive isolated disc and it is unclear whether such a disc can be realized during the star formation process.
To realize a self-consistent study of disc fragmentation and clump evolution, we conducted a 3D radiation hydrodynamics simulation initiated from gravitational collapse of a molecular cloud core. Using this approach, we can follow the formation of a central protostar, disc and its fragmentation. We can also follow the orbital and internal evolution of clumps with a realistic mass accretion from the disc on to them.
In this study, we ignore the magnetic field and focus on the effects of radiative cooling on the evolution of circumstellar disc and the internal structure of clumps. Note, however, that magnetic field may play an important role in the formation and evolution of the circumstellar disc, because it can efficiently transfer angular momentum (Mellon & Li 2008; Hennebelle & Ciardi 2009; Inutsuka et al. 2010; Li, Krasnopolsky & Shang 2011; Machida et al. 2011; Joos, Hennebelle & Ciardi 2012; Seifried et al. 2013). We will describe the effect of magnetic field in our subsequent paper using new numerical methods for smoothed particle magnetohydrodynamics (SPMHD; Iwasaki & Inutsuka 2011; Tsukamoto, Iwasaki & Inutsuka 2013).
This paper is organized as follows. In Section 2, we summarize the protostar formation process in a molecular cloud core and introduce the relevant terminology. The numerical method and initial condition are described in Section 3, while Section 4 presents the results. The paper concludes with a discussion in Section 5.
2 FROM CLOUD CORE TO PROTOSTAR
For later convenience, we summarize protostar formation process in the spherically symmetric cloud core and introduce the relevant terminology. The property of clumps formed in the disc is similar to the first core which is hydrostatic core formed during star formation. Thus, the internal evolution of the clump can be suitably described using the terminology of star formation (for more complete descriptions of the protostar formation process, see Larson 1969; Masunaga & Inutsuka 2000; Inutsuka 2012, and references therein).
When the gravitational energy dominates the thermal energy around the centre of the core, the cloud core begins to contract and the central density increases. While the radiative cooling due to dust thermal emissions overwhelms the compressional heating, the gas evolves isothermally, maintaining the temperature at about 10 K (isothermal collapse phase). The inner dense region collapses faster than the envelope because the time-scale of gravitational collapse is a decreasing function of density, causing runaway gravitational collapse.
At sufficiently high density (ρad ∼ 10−13 g cm−3), the compressional heating catches up with radiative cooling and the isothermal collapse terminates. The gas evolves almost adiabatically within the density range 10−13 g cm−3 ≲ ρ ≲ 10−8 g cm−3. The gas temperature rises under adiabatic contraction with the adiabatic index, γ = 5/3 for T ≲ 100 K and with γ = 7/5 for T ≳ 100 K. During this phase, thermal energy dominates over gravitational energy and a quasi-hydrostatic core forms. We refer to this quasi-hydrostatic core as the first core.
Once the central temperature of the first core reaches ∼1500 K, the hydrogen molecules begin to dissociate. This endothermic reaction promotes a second round of gravitational collapse at 10−8 g cm−3 < ρ < 10−3 g cm−3, known as the second collapse. Finally, when the molecular hydrogen is completely dissociated, the gas again evolves adiabatically with γ = 5/3 to form another hydrostatic core called as the second core. The initial mass and radius of the second core are M ∼ 10−3 M⊙ and |$r\sim 1 \text{R}_{\odot }$|, respectively. Only a small proportion of the first core collapses into the second core. Therefore, the mass of the second core is rapidly increased by mass accretion from the remnant of the first core.
3 NUMERICAL METHOD AND INITIAL CONDITION
In this study, we extend the simulation code used in our previous studies (Tsukamoto & Machida 2011, 2013) to include radiative transfer with flux-limited diffusion approximation according to Whitehouse & Bate (2004) and Whitehouse, Bate & Monaghan (2005). Unlike these works, we adopted standard explicit scheme for the gas pressure and the artificial viscosity in the gas energy equation. We adopted the EOS used in Tomida et al. (2013), which involves seven species: H2, H, H+, He, He+, He++, e−. Molecular hydrogen is assumed as a 3:1 mixture of ortho- and para-hydrogen and the translational, rotational and vibrational degrees of freedom are taken into account. The hydrogen and helium mass fractions are X = 0.7 and Y = 0.28, respectively.
We used dust opacity table provided by Semenov et al. (2003) and gas opacity table by Ferguson et al. (2005). We did not use individual time-step technique for this work and all particles were updated simultaneously. When the density exceeds the threshold density, ρthr (5 × 10−8 g cm−3), a sink particle was introduced. Around ρthr, the gas temperature reaches the dissociation temperature of molecular hydrogen (T ∼ 1500 K) and the second collapse begins in the clump. Therefore, we can follow the thermal evolution of the clump just prior to second collapse. The sink radius was set as rsink = 2 au.
The initial condition is an isothermal cloud core of uniform density, rigidly rotating with angular velocity Ω0 = 1.4 × 10−13 s−1. The mass, radius and temperature of the core are M = 1 M⊙, r = 3933 au and T = 10 K, respectively. The resultant density is ρ0 = 2.3 × 10−18 g cm−3. The initial condition was subjected to a density perturbation, δρ (= 0.01 × cos 2ϕ). The ratios of thermal to gravitational energy α0 (≡ Et/Eg) and rotational to gravitational energy β0 (≡ Er/Eg) are α0 = 0.384 and β0 = 0.01, respectively, where Et, Er and Eg denote the thermal, rotational and gravitational energy of the initial cloud core. These values are consistent with the results of recent 3D MHD simulation of molecular cloud and involved core formation (Inoue & Inutsuka 2012). The cloud core was modelled with about 530 000 SPH particles.
4 RESULTS
4.1 Overview of evolution
Starting from a prestellar core, we calculated the disc and clump evolutions to ∼6000 years following the first fragmentation. Fig. 1 shows the surface density evolution at the centre of the cloud core. This figure indicates that many clumps can form in the circumstellar disc during the early stages of disc evolution. Because the clumps connect smoothly to the disc, they are not always clearly delineated. In this paper, we defined a clump as a gaseous object whose central density, ρc, is 10−11 g cm−3 < ρc < ρthr = 5 × 10−8 g cm−3.
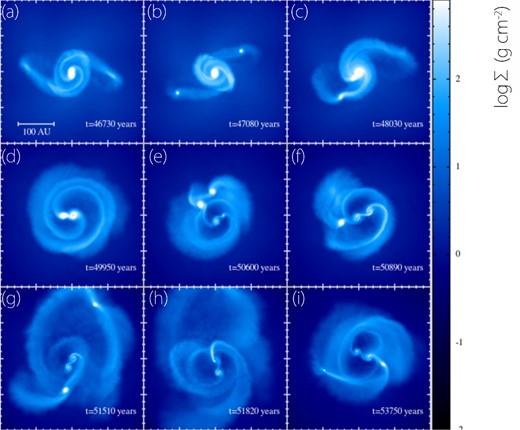
Time sequence of the surface density at the cloud centre, viewed face-on. The elapsed time after the cloud core begins to collapse is shown in each panel.
When the central density exceeds 10−11 g cm−3, the clumps are clearly distinguished from the background gas (of typical density, ρ ≲ 10−12 g cm−3). At ρc ∼ ρthr, the central temperature exceeds the dissociation temperature of the hydrogen molecule (T ∼ 1500 K) and the second collapse begins. We also defined an epoch of clump formation as the time when its central density exceeds 10−11 g cm−3, although gravitational contraction begins at lower density. Since the central first core is not formed in the disc, its thermal evolution is different from that of the other clumps. Therefore, we do not regard it as a clump. The central density of the first core exceeded ρthr at t = 47 500 years (between Figs 1b and c) and the first sink particle was introduced at this stage.
Two clumps formed (Fig. 1b) by the disc fragmentation. They rapidly migrated to the centre and accreted on to the sink particle (Fig. 1c). During this migration, a new clump formed at r ∼ 80–100 au (Fig. 1c) and similarly migrated rapidly to the centre. As it journeyed, the new clump gathered mass from the disc, increasing its central density and temperature (Fig. 1d). The central density of the clump exceeded ρthr and the second sink particle was introduced between Figs 1(d) and (e). The two sink particles were gravitationally bound and formed a binary. As seen in Figs 1(e)–(g), clump formation continued in the circumbinary disc throughout the simulation time, despite the presence of the second sink (Figs 1e–g). Most of the clumps rapidly accreted on to the sink particles and disappeared. However, one clump formed relatively far from both sink particles (see upper region of Fig. 1g) survived. The central density of this clump exceeded ρthr and a third sink particle was introduced.
Seven clumps formed within 6000 years after the first clump formation, of which five migrated to the central region and finally accreted on to the sink particles. The two clumps survived to second collapse. At the end of the calculation, the masses of the sink particles (in order of decreasing age) were 0.2 M⊙, 0.15 M⊙ and 0.06 M⊙, respectively.
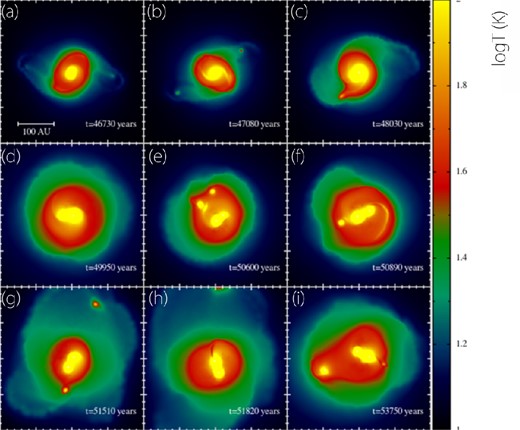
Fig. 2 shows the gas temperature at the epochs indicated in Fig. 1. Collectively, Figs 1 and 2 reveal a weak correlation between density and temperature. The gas temperature is rather determined by the gravitational potential. Therefore, EOSs that assume a polytropic relationship between pressure and density, p = p(ρ) (or the barotropic approximation), do not appropriately describe the thermal evolution of the disc. We also observe that clumps form in the outer cold regions of the disc, where the gas temperature is several tens of kelvin. Once a clump has formed, its temperature rapidly increases to higher than 100 K under compressional heating.
4.2 Orbital and internal evolution of clumps
In this subsection, we investigate the orbital and thermal evolution of the clumps. We also investigate the orbital and thermal history of the gas prior to clump formation by tracking the fluid element at the centre of each clump. To this end, we identify representative gas particles that reside at the centre of each clump. When a clump undergoes a second collapse, the representative gas particle is defined as the gas particle which has maximum density immediately before the sink particle is introduced. If a clump is tidally disrupted and accreted on to the sink particle, its central density begins to decrease at some epoch. In this case, the representative gas particle is defined as the particle which has the maximum density in the clump, at the time when the central density of clump is maximum. With this definition, the representative gas particle traces the evolution of the centre of each clump.
Fig. 3 shows the orbits of the representative gas particles. In this figure, the orbits of formed clumps (particle densities exceeding 10−11 g cm−3) are plotted with solid lines, while the preceding orbits are plotted with dashed lines. According to Fig. 3, the gas particles orbit within the disc for several orbital periods after they have accreted on to the disc. The ensuing gravitational contraction leads to clump formation. Most of the clumps are destroyed by tidal disruption and accrete on to the sink particle(s) in less than one orbital period. A notable exception is the clump shown by the cyan line. The gas was kicked out by the gravitational interaction between the binary and the clump formed relatively far from the binary. This clump was granted sufficient time for second collapse.
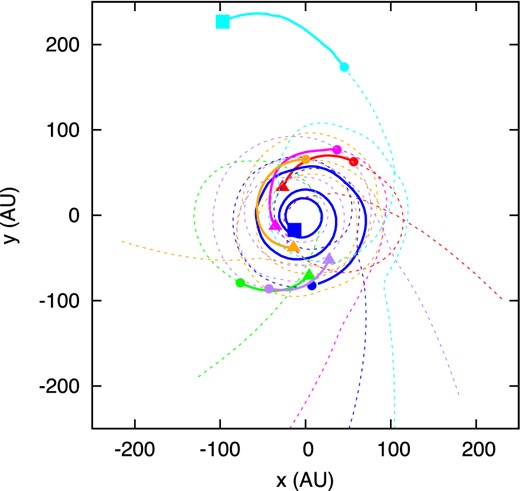
The orbits of the representative gas particles are shown. Dashed and solid lines represent the orbits before and after the clump formation (ρc > 10−11 g cm−3), respectively. Symbols mark the positions where the clumps forms (circles), where the clump central density begins to decrease (triangles), and where the second collapse begins in the clump (or the sink particles are inserted; square).
Fig. 4 shows the temperature evolution of the representative gas particles as a function of density. In this figure, a typical temperature evolution of the barotropic approximation is shown for comparison (see e.g. Bate 2011).
Unlike the barotropic approximation, the gas temperature increases to several tens kelvin at ρ = 10−15 to 10−14 g cm−3. While the gas particles orbit in the disc, they undergo the complex density and temperature evolution around ρ ∼ 10−14 to 10−12 g cm−3. The temperature of the gas can increase to 100 K due to the heating caused by the GI. Once the density exceeds ≳10−12 g cm−3, the gas becomes adiabatic and further evolution of the central temperature of the clumps consistent with adiabatic contraction. However, the complex thermal evolution at densities around ρ ∼ 10−14–10−12 g cm−3 induces the large variance of the central entropies. As described above, most of the clumps are tidally disrupted prior to the second collapse. However, in two instances (clump evolution shown by blue and cyan lines in Figs 3 and 4), the central temperature reaches the dissociation temperature of the molecular hydrogen, and second collapse is initiated. Dissociation is revealed by shallower slope at T ≳ 1500 K in Fig. 4.
The collapse time-scales of the clumps (time-scales required for second collapse) are of particular interest because some interesting planet formation scenarios assume the long collapse time-scales of the clumps (e.g. Nayakshin 2010a; Cha & Nayakshin 2011). Long collapse time-scales also enable direct observation of the clumps. Fig. 5 shows how the density of the representative gas particles evolves over time. When the gas accretes on to the disc, its density rapidly increases from ρ ∼ 10−16 to 10−13 g cm−3 and oscillates between ρ ∼ 10−14 and 10−12 g cm−3 within the disc. Gravitational contraction (occurring at ρ ≳ 10−12 g cm−3) is accompanied by a rapid increase in density. Although most of the clumps disappeared within several hundred years, two clumps survived and collapsed over a time-scale of 1000–2000 years (blue and cyan lines). This time-scale is much shorter than that estimated by Nayakshin (2010b).
4.3 Structure of clumps
In Fig. 6, for the two clumps that survived to second collapse, temperature is plotted as a function of density at different epochs (the clumps evolve from the circles to the rhombi in the figure) to investigate how the clump structure evolves. The profiles within 10 au from the centre of the clumps are shown. The clump that collapses at t = 50000 years (blue lines in Figs 3–5) is referred to as clump 1, while that collapsing at t = 52500 years (cyan lines in Figs 3–5) is denoted as clump 2. The polytropic relationship, |$T \propto \rho ^{\frac{1}{n}}$| (n = 3, 4, 5), where ρ and T are the density and temperature, respectively, is plotted for comparison.
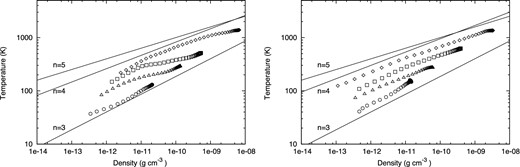
Profiles of clumps 1 (left) and 2 (right) in the density–temperature plane within 10 au of the clump centre. Symbols denote the profiles at different epochs. The central density of each epoch is ρc = 2.1 × 10−11 g cm−3 (circles), 1.3 × 10−10 g cm−3 (triangles), 1.5 × 10−9 g cm−3 (rectangles) and 6.7 × 10−9 g cm−3 (rhombi) for clump 1 and ρc = 1.6 × 10−11 g cm−3 (circles), 6.2 × 10−11 g cm−3 (triangles), 3.9 × 10−10 g cm−3 (rectangles) and 3.3 × 10−9 g cm−3 (rhombi) for clump 2. Solid lines show the polytropic relation, |$T \propto \rho ^{\frac{1}{n}}$| (n = 3, 4, 5).
The clump structures are adequately modelled by the polytrope of index n ∼ 3 at central temperatures, Tc ≲ 100 K. As the central temperature increases, the profiles become shallower, and they can be represented with the polytropes of n ≳ 4 at central temperatures exceeding 100 K. However, the structure of clump 1 is distorted and a single-index polytrope yields a poor fit at Tc > 100 K. On the other hand, the single-index polytrope sufficiently fits the structure of clump 2 at these temperature.
The structural difference between clumps 1 and 2 is attributable to the entropy of the accretion flow. The rapid inward migration of clump 1 (see Fig. 3) is accompanied by rapid entropy changes of the ambient disc gas, which distort the clump structure. On the other hand, the semi-major axis of clump 2 remains relatively constant suggesting that the entropy of the accretion flow also changes little throughout the clump evolution.
As shown in Fig. 6, the entropy of the clumps increases during their evolution. This is easily understood from the increased temperature at fixed density as the clump evolves. Entropy is introduced by mass accretion from the disc. Therefore, mass accretion plays an important role in the structural evolution of the clumps. In clumps evolving solely by radiative cooling, the entropy declines over time (see e.g. chapter 17 of Cox & Giuli 1968).
4.4 Mass evolution of clumps
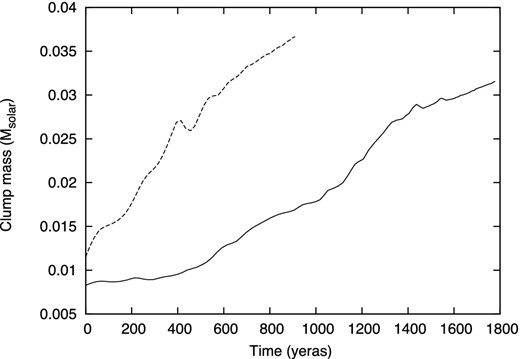
The mass of the clump 1 (solid) and clump 2 (dashed) as a function of the elapsed time after the clump formation.
The mass accretion rate on to the clump can be estimated from Fig. 7. The clump mass increases by approximately 0.01 M⊙ within 1000 years, yielding a mass accretion rate on to the clumps, |$\dot{M}_{\rm c} \sim 10^{-5} \,\mathrm{M}_{{\odot }}\ {\rm years}^{-1}$|. This result also accords with the theoretical estimate (see equation 4 in Section 5).
5 SUMMARY AND DISCUSSION
In this paper, we performed a radiation hydrodynamics simulation using a realistic EOS and investigated the orbital and internal evolution of clumps formed by disc fragmentation. Note that we investigated the formation and evolution of disc and clumps self-consistently.
According to our simulation, disc fragmentation and clump formation occur in the early evolution phase of the circumstellar disc. Disc fragmentation is induced by mass accretion from the infalling envelope. These results are consistent with previous works (Machida et al. 2011; Zhu et al. 2012). We show that most of the clumps rapidly migrate inward and accrete on to protostar(s). However, some clumps may survive to second collapse.
The disc gas and clump centres show the following evolutionary trends in their density and temperature. At densities of 10−14 ≲ ρ ≲ 10−12 g cm−3, the gas resides in the disc, where it undergoes complex thermal evolution. Heating caused by GI can raise the gas temperature to T ∼ 100 K. When the density exceeds ∼10−12 g cm−3, gravitational contraction begins and clumps form. The central gas of the clump evolves adiabatically and further evolution typifies that of first cores (Masunaga & Inutsuka 2000). However, reflecting the complex thermal history, the central entropy of the clumps has large deviation. Once gravitational contraction has begun, the central density increases rapidly towards second collapse within 1000–2000 years. We found that the clumps are adequately modelled by the polytrope spheres of index n ∼ 3 at central temperatures ≲100 K and n ≳ 4 at higher central temperature. These indices are much higher than those used in Zhu et al. (2012).
Following second collapse, the newly formed second core accumulates further mass from the disc. The final masses of the sink particles emerging from our simulation were 0.2 M⊙, 0.15 M⊙ and 0.06 M⊙ at the end of the calculation. Thus, they are rather protostars or brown dwarfs than protoplanets. This is consistent with the results of Stamatellos & Whitworth (2009a,b).
In our simulation, the formed clumps either fall on to the protostar(s) and disappear or evolve into protostars or brown dwarfs. The clump mass easily exceeds the planetary-mass range (≲0.01 M⊙). Therefore, if disc fragmentation is responsible for the wide-orbit planets found in recent observations (e.g. Marois et al. 2010), the rapid migration to the central star should be avoided, and the mass of the clumps should be kept small. Although the latter condition is little recognized, it is problematic in explaining how distant planets can emerge from disc fragmentation. To retain small mass clump and avoid rapid inward migration, an additional mechanism that decouples the disc and the clumps may be required. We will investigate such mechanisms in a more realistic setup involving magnetic fields (see Iwasaki & Inutsuka 2011; Tsukamoto et al. 2013, Iwasaki, in preparation).
We thank T. Tsuribe, K. Iwasaki, S. Okuzumi, E.I. Vorobyov and K. Tomida for their fruitful discussions. We also thank K. Tomida and Y. Hori for providing their EOS table to us. The snapshots were produced by SPLASH (Price 2007). The computations were performed on a parallel computer, XT4 system at CfCA of NAOJ and SR16000 at YITP in Kyoto University. YT is financially supported by Research Fellowships of JSPS for Young Scientists.





