-
PDF
- Split View
-
Views
-
Cite
Cite
Jun Fang, Huan Yu, Bo-Tao Zhu, Li Zhang, Gamma-ray properties of supernova remnants transporting into molecular clouds: the cases of IC 443 and W44, Monthly Notices of the Royal Astronomical Society, Volume 435, Issue 1, 11 October 2013, Pages 570–574, https://doi.org/10.1093/mnras/stt1318
Close - Share Icon Share
Abstract
Motivated by the recent report of the detailed spectra of IC 443 and W44 based on four years of observations with the Fermi Large Area Telescope, γ-rays produced via proton–proton interaction in the two supernova remnants (SNRs) have been investigated in the diffusive shock acceleration scenario. In the model, a part of the SNR shell transporting into ambient dense molecular clouds (MCs), and a shock with a relatively low Alfvén Mach number can be produced. Relativistic protons are accelerated in the shock via the diffusive acceleration process; moreover, a break in the particle distribution is induced since the damping of Alfvén waves when the shock transporting into partly ionized plasma. A spectrum of the accelerated protons in the shock can be obtained in the test-particle case, taking into account the effect of the ambient partly ionized plasma on the acceleration process. Furthermore, hadronic γ-rays with a peak around several GeVs are reproduced as the protons inelastically colliding with the ambient matter of the crushed gas. The observed γ-ray spectral distributions of the SNR IC 443 and W44 can be successfully reproduced using the static model in the test-particle scenario. It can be concluded that the observed γ-rays can be explained in the diffusive shock case as the shock waves transporting into the dense MCs for the two remnants.
1 INTRODUCTION
The Galactic cosmic rays with energies smaller than 1015 eV are widely accepted to be mainly originated from supernova remnants (SNRs), whereas direct evidence for the existence of relativistic protons in the remnants is still lacking. High-energy γ-rays from SNRs are broadly detected. The γ-rays can be produced both through the decay of neutral pions from proton–proton (pp) collisions and via inverse Compton scattering or bremsstrahlung of relativistic electrons, and it is hard to distinguish whether the hadronic process or the leptonic ones contribute mainly to the γ-rays for a SNR.
SNRs associated with molecular clouds (MCs) are ideal sources for identifying that protons can be accelerated to relativistic energies by the shocks because pp interaction can be greatly enhanced as the cosmic rays colliding with the dense clouds. The γ-rays can be produced either as relativistic protons escape from the shock waves transport into the dense clouds or as the cloud is crushed by the shock wave. Some γ-ray sources are detected to be located around SNRs, and they are interpreted as the pp interaction between the relativistic protons escaped from the SNRs and the nuclei of the clouds. However, if the projection of the γ-ray source is located within the extension of the SNR shock, it is hard to differentiate whether the cloud is crushed by the shock or not.
IC 443 and W44 are two middle-aged SNRs with dense MCs around the remnants, and the observations in γ-rays show that they are effective emitters in the GeV band (Albert et al. 2007; Acciari et al. 2009; Abdo et al. 2010a,b; Giuliani et al. 2011). Theoretically, the γ-rays from IC 443 and W44 can be explained to be produced via pp interaction crushing into the ambient clouds (Uchiyama et al. 2010; Fang & Zhang 2013). Alternatively, high-energy protons escaped from the SNRs can collide with the ambient clouds, and the γ-rays can also be produced via the pp interaction between the escaped protons and the matter in the MCs (Li & Chen 2010, 2012; Torres, Rodríguez-Marrero & de Cea Del Pozo 2010; Ohira, Murase & Yamazaki 2011; Torres et al. 2011).
γ-ray spectra with energies ranging from 60 MeV to 100 GeV of the SNRs IC 443 and W44 based on four years of observations with the Fermi Large Area Telescope (LAT) have recently been proposed (Ackermann et al. 2013). The fluxes in the sub-GeV bands are crucial to distinguish the origins of the γ-rays. Assuming that the parent spectrum of the protons has a form of a smoothly broken power law in the momentum space, the γ-ray spectra for the two remnants can be more naturally reproduced via pp interaction than through inverse Compton scattering and bremsstrahlung. Therefore, the observed characteristics of the γ-rays provide evidence to the capability of SNR accelerating protons. We focus on the γ-rays for IC 443 and W44 from the regions delineated by the radio continuum, and they are likely produced as the clouds are crushed by the shock waves (Ackermann et al. 2013).
In this paper, we investigate the properties of the hadronic γ-rays for the SNRs IC 443 and W44 in the diffusive shock acceleration regime. Diffusive shock acceleration is the most likely mechanism to accelerate charged particles to relativistic energies in SNRs. In the test-particle case, the accelerated particles has a power-law momentum distribution with an index of −3σ/(σ − 1), where σ is the compression ratio. σ is about 4 for a strong shock, and the resulting index is about 4, which is close to the observed ones derived from detections in radio bands for SNRs. However, a single power-law distribution for the accelerated particles is unable to explain the observed spectral distribution in γ-rays for IC 443 and W44.
In the model, for a remnant, a part of the shock wave transports into dense MCs with a magnetic field strength of several tens of μG, and the shock is slowed down with a velocity of ∼100 km s−1. As a result, a shock with a relatively low Alfvén Mach number can be produced, and a test-particle theory of the diffusive shock acceleration given by Kang & Ryu (2010) is used to obtain the momentum distribution of the protons accelerated by the shock. Furthermore, when the shock wave transports into a weakly ionized medium, the spectrum of the accelerated protons steepens by one power above a break energy since the Alfvén waves are heavily damped (O'C Drury, Duffy & Kirk 1996; Malkov, Diamond & Sagdeev 2012; Bykov et al. 2013). With a small Alfvén Mach number and the effect of the damping of the Alfvén waves, the particle spectrum becomes rather soft, and the detected spectra of the γ-rays for IC 443 and W44 can be successfully reproduced within this simple model.
2 MODEL AND RESULTS
IC 443 is an asymmetric SNR at a distance of about 1.5 kpc (Fesen 1984), and it remains one of the most studied remnant interacting with dense MCs. The southern part of the SNR shock is encountering with MCs based on detection of the shock-excited molecular lines (e.g. Denoyer 1979a,b; Dickman et al. 1992). Dickman et al. (1992) and Lee et al. (2008) estimated that the shocked cloud material has a mass of 500–2000 M⊙. IC 443 is an effective emitter in γ-rays. The unidentified EGRET source 3EG J0617+2238 located near the centre of the shell has a spectral index of −2.01 ± 0.06 in the band from 100 MeV to 30 GeV (Hartman et al. 1999). The γ-ray source was confirmed by AGILE (Pittori et al. 2009) and Fermi (Abdo et al. 2010b). In very high-energy γ-rays, a point-like source MAGIC J0616+225 coincident with the densest part of the MCs and the OH maser emission was detected by MAGIC (Albert et al. 2007). Moreover, Acciari et al. (2009) reported that an extended emission source coincident with the MC structure for IC 443 based on the deep observations with VERITAS. The spectrum shows a power-law shape with an index of ∼1.99 and an integral flux above 300 GeV of ∼4.63 × 10−12 cm−2 s−1.
Fig. 1 shows the resulting proton distribution for the SNRs IC 443 and W44. For IC 443, the γ-ray spectrum from pp interaction as a part of the SNR shock transporting into a dense cloud is shown in Fig. 2 with χ2/dof = 2.7. The velocity of the shock is significantly reduced when colliding with a dense matter. A low sonic Mach number or a low Alfvén Mach number is necessary to reproduce the observed γ-ray flux points in the diffusive acceleration scenario. With a number density of n1 = 200 cm−3, a temperature of T1 = 102 K, a magnetic field strength of B1 = 30 μG, η = 0.4 and a shock velocity of u1 = 70 km s−1, the sonic Mach number is 60, whereas the Alfvén Mach number is just 5.0. The spectral slope qtp of the accelerated protons in the shock is 4.36, which is mainly determined by the Alfvén Mach number in such a case. The break energy Ebr due to ion–neutral collisions as the shock transporting into the partially ionized material is 4.8 × 105 MeV, which is necessary to obtain a spectrum consistent with the obtained flux points with MAGIC and VERITAS. The average emitting volume is normalized by making the resulting flux consistent with the detection with the Fermi LAT. The accelerated protons in the shock contain an energy of 1.8 × 1049 erg, and the shocked gas has a mass of 1.6 × 103 M⊙.
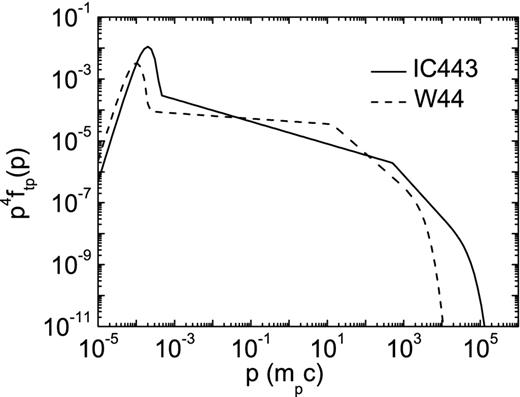
Test-particle distributions of the accelerated protons at the shock for the SNRs IC 443 (solid line) and W44 (dashed line). The parameters are n1 = 120 cm−3, T1 = 102 K, B1 = 90 μG, x0 = 1 pc, η = 0.5, d = 1.5 kpc with u1 = 70 km s−1 for IC 443; n1 = 120 cm−3, T1 = 102 K, B1 = 10 μG, x0 = 1 pc, η = 0.5, d = 2.9 kpc with u1 = 35 km s−1 for W44.
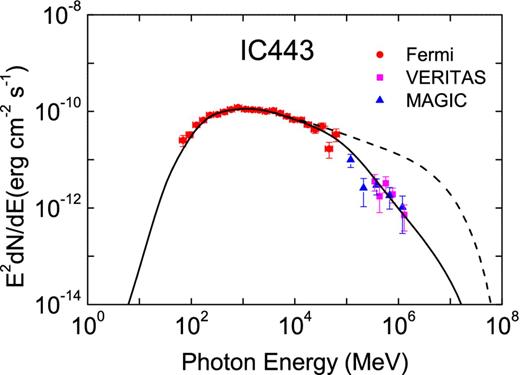
Comparison of the resulting spectrum (solid line) of pp interaction in the part of the SNR shock transporting into dense clouds with the observed γ-ray flux points for the SNR IC 443 (χ2/dof = 2.7). The dashed line represents the spectrum not taking into account the ion–neutral damping. The parameters are n1 = 200 cm−3, T1 = 102 K, B1 = 90 μG, x0 = 1 pc, η = 0.5, d = 1.5 kpc with u1 = 70 km s−1 (IC 443), and the average emitting volume is normalized by making the resulting flux consistent with the detected one with the Fermi LAT. The data points are from Ackermann et al. (2013; Fermi), Albert et al. (2007; MAGIC) and Acciari et al. (2009; VERITAS).
Fig. 3 shows the resulting spectra from pp interaction for IC 443 with different η. The spectrum is insensitive to the ratio of number density of the neutral particles to that of upstream particles (see also equation 10).
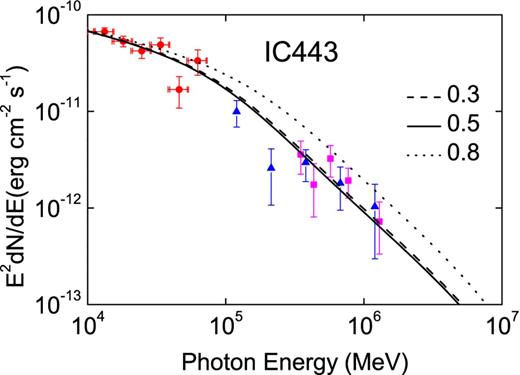
The resulting spectra from pp interaction for the SNR IC 443 with η = 0.3 (dashed line); η = 0.5 (solid line); η = 0.8 (dotted line). Others are the same as Fig. 2.
W44 locates in a complex of giant MCs with a total mass of 1 × 106 M⊙ at a distance of ∼1.9 kpc (Seta et al. 1998). Reach, Rho & Jarrett (2005) estimated that the dense radio-emitting filaments have a mass of ∼5.0 × 103 M⊙, and the number density of the cloud encountered with the SNR shock is ∼102 cm−3.
The γ-rays above 1 GeV from W44 is softer compared with IC 443. A rather smaller pbr is necessary to obtain a spectrum consistent with the detected flux points by the Fermi LAT, and then a weaker upstream magnetic field with a strength of B1 ∼ 10 μG is adopted in the calculation (see equation 10). The resulting γ-ray spectrum from the model with the detected flux points by the Fermi LAT for the SNR W44 with a distance of 2.9 kpc are shown in Fig. 4 (χ2/dof = 3.2). With an upstream number density of n1 = 120 cm−3, a temperature of T1 = 102 K, a magnetic field strength of B1 = 10 μG, η = 0.4 and a shock velocity of u1 = 35 km s−1, the sonic Mach number is 30, whereas the Alfvén Mach number is 17.6. With these parameters, the slope of the protons in the momentum space is 4.1. However, the break energy Ebr due to partially ionized material is 1.3 × 104 MeV, which is much smaller than that for IC 443 by a factor of ∼3 per cent. The accelerated protons in the shock contain an energy of 1.5 × 1049 erg, and the shocked gas has a mass of 2.5 × 103 M⊙.
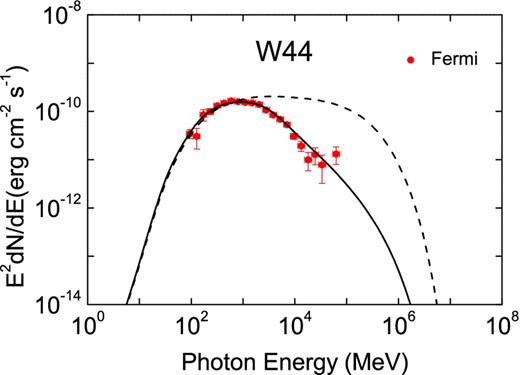
Comparison of the resulting spectra of pp interaction in the part of the SNR shock transporting into dense clouds with the observed γ-ray flux points for the SNR W44 (χ2/dof = 3.2). The dashed line represents the spectrum not take into the ion–neutral damping account. The parameters are n1 = 120 cm−3, T1 = 102 K, B1 = 10 μG, x0 = 1 pc, η = 0.4, d = 2.9 kpc with u1 = 35 km s−1. The average emitting volume is normalized by making the resulting flux consistent with the detected one with the Fermi LAT, and the data points are from Ackermann et al. (2013).
3 SUMMARY AND DISCUSSIONS
SNRs associated with MCs are effective emitters of γ-rays produced via pp interaction, and it provides evidence of the ability of the remnants accelerating ions to relativistic energies. However, it is usually unclear whether the γ-rays from a source are produced as the MCs crushed by the shock or as the accelerated protons escaped from the shock colliding with the dense clouds located around the remnant.
IC 443 and W44 are two typical sources of shock–cloud interactions with an age of ∼104 yr. Recently, Ackermann et al. (2013) reported the measured spectral energy distributions of IC 443 and W44 based on four years of observations with the Fermi LAT using an updated method for the event classification and background rejection, which can increase the effective area at 100 MeV by a factor of ∼5. The γ-rays associated with the two remnants are likely emitted from the collisions between the relativistic protons and the cloud crushed by the SNR shocks, especially a high-resolution radio continuum map for W44 provides evidence for it (Castelletti et al. 2007; Ackermann et al. 2013).
In this paper, we investigate the hadronic γ-ray properties of IC 443 and W44 in the regime of diffusive acceleration. The proton spectrum at a shock is calculated with a test-particle solution with Alfvénic drift taken into account. In the model, a part of the SNR shock transports into dense MCs, and the shock usually has a relatively low Alfvén Mach number. Furthermore, the accelerated protons steepen by one power in the particle spectrum due to the damping of Alfvén waves. The results show that the pp interaction between the relativistic protons and the gas of the crushed cloud can provide good explanation of the spectral energy distributions in γ-rays for the two remnants.
IC 443 is modelled as having a shock transporting into dense clouds with an average density of 200 cm−3, and the resulting slope of the protons is ∼4.4 due to a low Alfvén Mach number of 5. The spectral energy distribution of the pp interaction between the accelerated protons and the crushed gas is well consistent with the observed flux points by the Fermi LAT. Moreover, the break energy since ion–neutral collisions is 4.8 × 105 MeV, and, as a result, the photon spectrum show a break at ∼105 MeV, which give a natural explanation to the flux points by VERITAS and MAGIC (see Fig. 2). For W44, the γ-ray spectrum is much softer compared with IC 443. To reproduce the flux point by the Fermi LAT, a relatively weaker magnetic field strength 10 μG and a smaller shock velocity 35 km s−1 are adopted for W44 compared with IC 443. The resulting break energy is just ∼104 MeV, and the spectral energy distribution is consistent with the observations by Fermi LAT in such a scenario.
In the test-particle case of diffusive shock acceleration, a low sonic Mach number or a low Alfvén Mach number can be adopted to reproduce the observed flux points for the two remnants. The MCs around an SNR shock is usually very cold with a temperature of ≤100 K, and, as a result, the sonic Mach number is about 85 with a density of 200 cm−3 and a shock speed of 100 km s−1. However, the Alfvén Mach number is very low with a value of ∼7 with a magnetic field strength of 90 μG. In such a case, the shape of the resulting spectrum of the accelerated protons is mainly determined by the Alfvén Mach number.
The properties of γ-rays from IC 443 and W44 have been investigated based on a static and test-particle model, in which a part of the SNR shock had been impacted by the ambient dense clouds. The spectral index evolves as the shock transporting into the clouds slowed. Fig. 5 shows the resulting spectra of the accelerated protons and the spectral energy distributions of the hadronic γ-rays for IC 443 with different shock speeds. For each curve in the panel (b), the average emitting volume is normalized by making the resulting flux consistent with the detected one at 2.3 × 102 MeV detected by the Fermi LAT. For a velocity of 300 km s−1, the spectrum is extremely hard compared with the detected fluxes; moreover, more particles can be injected into the acceleration process for a faster shock, and with the velocity 300 km s−1 the shocked gas has a mass of 21 M⊙ to obtain a consistent flux at 2.3 × 102 MeV with that detected by the Fermi LAT.
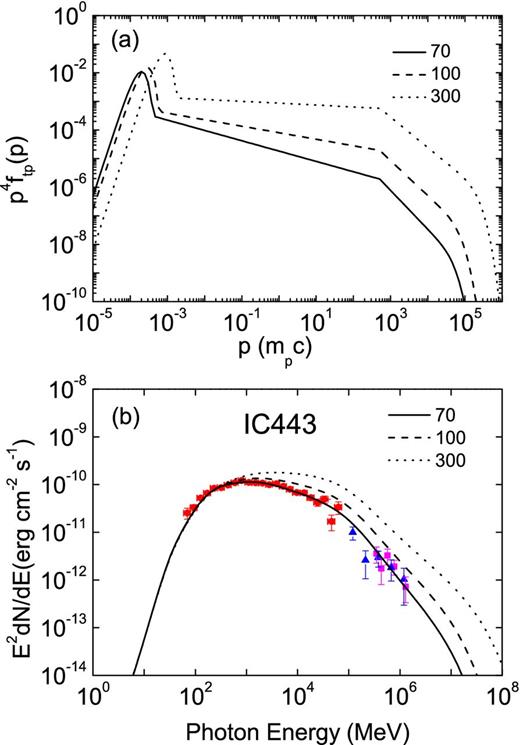
(a) Test-particle distributions of the accelerated protons at the shock for the SNRs IC 443 with u1 = 70 km s−1 (solid line); u1 = 100 km s−1 (dashed line); u1 = 300 km s−1 (dotted line). (b) The corresponding spectra of pp interaction in the parts of the SNR shocks transporting into dense clouds with the observed γ-ray flux points for the SNR IC 443. The average emitting volume is normalized by making the resulting flux consistent with the detected one at 2.3 × 102 MeV with the Fermi LAT. Others are the same as Fig. 2.
The shocked cloud has an estimated mass of ∼103 M⊙ both for IC 443 (Dickman et al. 1992; Lee et al. 2008) and for W44 (Reach et al. 2005), which can give constrains on the parameters in the model for the two remnants. To reproduce the observed fluxes in γ-rays, appropriate parameters are adopted in the calculation with that the induced masses of the crushed cloud are 1.6 × 103 and 2.5 × 103 M⊙ for IC 443 and W44, respectively. These masses are consistent with those deduced from radio observations for IC 443 and W44.
The model for the particle distribution at the shock in this paper is intrinsically static. The spectrum of the accelerated protons is mainly determined by the properties of the shock, and the acceleration history of a proton is not taken into account. Protons accelerated earlier with a faster shock can easily out produce these being produced by the slower shock.
We thank the anonymous referee for helpful comments to improving the paper. This work is partially supported by the National Natural Science Foundation of China (NSFC 11103016, 11173020), by the Yunnan Province under grant 2011FB012, by the Foundation of Yunnan University (XT412003), by the light of the western talent training project (W8090303), and by the Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences (OP201101).



