Intrinsic ellipticity correlations of galaxies: models, likelihoods and interplay with weak lensing

Capranico, Federica; Merkel, Philipp M.; Schäfer, Björn Malte

doi:10.1093/mnras/stt1269

Abstract

Subject of this paper is the statistical properties of ellipticity alignments between galaxies evoked by their coupled angular momenta. Starting from physical angular momentum models, we bridge the gap towards ellipticity correlations, ellipticity spectra and derived quantities such as aperture moments, comparing the intrinsic signals with those generated by gravitational lensing, with the projected galaxy sample of Euclid in mind. We investigate the dependence of intrinsic ellipticity correlations on cosmological parameters and show that intrinsic ellipticity correlations give rise to non-Gaussian likelihoods as a result of non-linear functional dependences. Comparing intrinsic ellipticity spectra to weak lensing spectra we quantify the magnitude of their contaminating effect on the estimation of cosmological parameters and find that biases on dark energy parameters are very small in an angular momentum-based model in contrast to the linear alignment model commonly used. Finally, we quantify whether intrinsic ellipticities can be measured in the presence of the much stronger weak lensing induced ellipticity correlations, if prior knowledge on a cosmological model is assumed.

methods: analytical, large-scale structure of Universe

1 INTRODUCTION

Weak cosmic shear, i.e. lensing by the gravitational field of the cosmic matter distribution (Blandford et al. 1991; Seitz & Schneider 1994; Seitz, Schneider & Ehlers 1994; Kamionkowski et al. 1998), is considered to be an excellent probe of structure formation processes, precision measurements of cosmological parameters (Hu 1999, 2002a,b; Takada & White 2004; Hannestad, Tu & Wong 2006) and the influence of dark energy on cosmic structure formation (Huterer & Turner 2001; Huterer 2002, 2010; Amara & Kitching 2011; Kunz 2012). The primary observables are ellipticity correlation functions or their Fourier counterparts (Jain & Seljak 1997; Hu & Tegmark 1999; Hu & White 2001; Hu & Jain 2004). These shape correlations have been first detected by a number of research groups more than 10 years ago (Bacon, Refregier & Ellis 2000; Kaiser, Wilson & Luppino 2000; Van Waerbeke et al. 2000; Wittman et al. 2000) and are now routinely used for parameter estimation. Correlations in shapes of galaxies are introduced because light rays from neighbouring galaxies experience correlation distortions due to correlations in the tidal fields through which the respective rays propagate. A common assumption is the absence of intrinsic correlations such that any positive shape correlation can be attributed to the gravitational lensing effect. This hypothesis, however, might be flawed as there are physical mechanisms by which galaxies are intrinsically shape correlated: due to the fact that neighbouring galaxies form from correlated initial conditions, their respective angular momenta are correlated (Croft & Metzler 2000; Heavens, Refregier & Heymans 2000; Crittenden et al. 2001; Mackey, White & Kamionkowski 2002). Assuming that the galactic discs are established with their symmetry axes collinear with the host haloes’ angular momentum directions one would observe galaxies at correlated angles of inclination and therefore with correlated ellipticities.

A possible consequence of this new source of ellipticity correlation is its interference with the determination of cosmological parameters from weak lensing data, in particular the properties of dark energy. This issue has been the target of a number of investigations: commonly, the description of intrinsic ellipticity correlations was based on the linear alignment model (Catelan, Kamionkowski & Blandford 2001; Hirata & Seljak 2004),

\begin{equation} \epsilon _+ = C \left(\mathrm{\partial} _x^2-\mathrm{\partial} _y^2 \right)\Phi \qquad \mathrm{and} \qquad \epsilon _{\times } = 2C\: \mathrm{\partial} _x\mathrm{\partial} _y\Phi , \end{equation}

(1)

which provides a direct modelling of the ellipticity field on the tidal shears ∂_α∂_βΦ (here, the z-axis of the coordinate system is aligned with the line of sight) and is able to give a consistent description of gradient and vorticity modes of the ellipticity field. The constant of proportionality was fixed by comparison with observations (Bridle & King 2007; Joachimi et al. 2012).

If galaxy ellipticities are in fact described by an alignment model linear in the tidal fields, then cosmological parameters, in particular the dark energy equation of state parameters would be severely biased (Bridle & King 2007; Joachimi & Bridle 2010; Kirk, Bridle & Schneider 2010; Kirk et al. 2011). Apart from ellipticity correlations themselves, ellipticity–position correlations were affected and ellipticity data would exhibit cross-correlations between intrinsic ellipticities and weak lensing (see, in particular, Hirata & Seljak 2004).

There are basically four ways of dealing with intrinsic alignments. First, they can be removed from data by using the fact that they are a small-scale phenomenon (Heymans & Heavens 2003; King & Schneider 2002, 2003; King 2005), which takes place at the cost of increasing statistical uncertainties. Secondly, one can take advantage of the fact that intrinsic alignments have different statistical properties in comparison to weak lensing ellipticity correlations (Crittenden et al. 2002; King & Schneider 2003), most notably it is possible to use the statistics of vortical excitations in the ellipticity field which are exclusively sourced by intrinsic alignments. Thirdly, one can design line-of-sight weightings that null out contributions due to intrinsic alignments (King 2005; Joachimi & Schneider 2008, 2009), which marginally increase statistical uncertainties on cosmological parameters. Parameter inference from spectra that result from data in this way still yields unbiased estimates. Finally, one can parametrize the intrinsic alignment contribution to weak lensing data and have those model parameters be determined by data alongside the cosmological parameters under consideration. Marginalization over the parameters entering the intrinsic alignment model then propagates the statistical errors of the alignment model on to the cosmological model. With a physically correct alignment model the estimates of cosmological parameters will remain unbiased. The feasibility of this approach under the assumption of Gaussian likelihoods has been demonstrated (Bridle & King 2007; Bernstein 2009; Joachimi & Bridle 2010; Kirk et al. 2010; Laszlo et al. 2012).

The motivation of this work was to explore intrinsic alignment effects and their observable properties in angular momentum-based alignment models. In these models, the ellipticity is quadratic in the tidal shear field and because they use in principle a mechanical model of angular momentum generation and ellipticity alignment, the model parameters can be constrained from information other than ellipticity data. We will need two physically meaningful variables: a parameter which is related to the angular momentum model and whose value can be measured in structure formation simulations and a disc morphology parameter which is accessible in galaxy surveys. Clearly, quadratic alignment models will differ in their prediction of ellipticity correlations compared to linear alignment models. Together with the above results employing linear alignment models we hope to complete the view on intrinsic alignments and their relevance for future weak lensing surveys.

The aim of this paper is threefold. (i) We investigate and compare two angular momentum-based alignment models in their predictions for ellipticity correlations and formulate these predictions in terms of ellipticity correlation functions, ellipticity spectra and the scale dependence of the variance of the ellipticity fields and compare these predictions with the equivalent quantities sourced by weak gravitational lensing (Sections 2 and 3). (ii) The dependence of the two ellipticity models in consideration on cosmological parameters is investigated and their likelihoods are derived. With this knowledge, we quantify the contamination of weak lensing data with an intrinsic alignment contribution and quantify how these contaminations affect the estimation of cosmological parameters (Section 4). (iii) We investigate if there is a possibility of observing intrinsic correlations in the presence of much stronger lensing induced ellipticity correlations and develop statistical methods for answering these questions (Section 5). Throughout we will focus on intrinsic ellipticity correlations caused by correlated angular momenta, which is an applicable model for spiral galaxies. Those intrinsic alignments are proportional to the squared tidal field, in contrast to the linear alignment model valid for elliptical galaxies. In this limit, we neglect cross-correlations between intrinsic ellipticity alignments with the tidal field and gravitational lensing, as those correlations are proportional to the expectation value of the tidal field cubed, which vanishes in the case of Gaussian statistics. Specifically, we consider the case of Euclid's weak lensing survey (Amendola et al. 2012).

The reference cosmological model used is a spatially flat w cold dark matter (wCDM) cosmology with Gaussian adiabatic initial perturbations in the cold dark matter (CDM) density field. The parameter choice is motivated by the Wilkinson Microwave Anisotropy Probe 7 results (Komatsu et al. 2011; Larson et al. 2011): Ω_m = 0.25, n_s = 1, σ₈ = 0.8, Ω_b = 0.04 and H₀ = 100 h km s⁻¹ Mpc⁻¹, with h = 0.72. The dark energy equation of state is set to w = −0.95.

2 COSMOLOGY

2.1 Dark energy cosmologies

In spatially flat Friedmann–Lemaître–Robertson–Walker cosmologies with the matter density parameter Ω_m and a dark energy component with equation of state w(a), the Hubble function H(a) = d ln a/dt is given by

\begin{equation} \frac{H^2(a)}{H_0^2} = \frac{\Omega _{\rm m}}{a^{3}} + (1-\Omega _{\rm m})\exp \left(3\int _a^1\mathrm{d}\ln a\,(1+w(a))\right). \end{equation}

(2)

The value w ≡ −1 corresponds to the cosmological constant Λ. The Hubble function describes the time evolution of the metric and can be used for relating comoving distance χ and scalefactor a:

\begin{equation} \chi = c\int _a^1\mathrm{d}a\,\frac{1}{a^2 H(a)}, \end{equation}

(3)

in units of the Hubble distance χ_H = c/H₀. The Hubble function also determines the critical density, |$\rho _\mathrm{crit} \equiv 3H^2 / (8\pi G)$|⁠.

2.2 CDM power spectrum

The linear CDM density power spectrum P(k) describes the fluctuation amplitude of the Gaussian homogeneous density field δ,

\begin{equation} \langle \delta (\boldsymbol {k})\delta (\boldsymbol {k}^\prime )\rangle =(2\pi )^3\delta _D(\boldsymbol {k}+\boldsymbol {k}^\prime )P(k), \end{equation}

(4)

and is given by the ansatz |$P(k)\propto k^{n_{\rm s}}T^2(k)$| with the transfer function T(k). In cosmologies with low Ω_m, T(k) is fitted by (Bardeen et al. 1986; Sugiyama 1995)

\begin{eqnarray} T(q) &=& \frac{\ln (1+2.34q)}{2.34q}\left(1+3.89q+(16.1q)^2+(5.46q)^3 \right.\nonumber\\ && \left.+\,(6.71q)^4\right)^{-{1/4}}. \end{eqnarray}

(5)

The wavenumber k is rescaled with the shape parameter Γ ≃ Ω_mh, q = k/Γ. The spectrum P(k) is normalized to the variance σ₈ of the density field on scales of R = 8 Mpc h⁻¹,

\begin{equation} \sigma ^2_R = \frac{1}{2\pi ^2}\int \mathrm{d}k\,k^2 P(k) W^2(kR) = \int \mathrm{d}\ln k\, \Delta ^2(k) W^2(kR). \end{equation}

(6)

W(x) = 3j₁(x)/x is the Fourier-transformed spherical top hat filter function. j_ℓ(x) refers to the spherical Bessel function of the first kind of order ℓ (Abramowitz & Stegun 1972; Arfken & Weber 2005) and the dimensionless variance per logarithmic wavenumber Δ²(k) = k³P(k)/(2π²) can be used instead of the CDM spectrum P(k). In computing ellipticity correlation functions and ellipticity spectra, we will employ a smoothed CDM spectrum P(k) → P(k) exp (−(kR)²) with a smoothing scale R that corresponds to a mass cutoff at a halo mass M. Those two quantities are related by |$M = 4\pi /3\,\Omega _{\rm m}\rho _\mathrm{crit}\,R^3$|⁠.

2.3 Linear structure growth

As long as the amplitudes in the cosmic density field are small, δ ≪ 1, the density field grows in a homogeneous way, |$\delta (\boldsymbol {x},a)=D_+(a)\delta (\boldsymbol {x},a=1)$|⁠. The growth function D₊(a) results from solving the growth equation (Turner & White 1997; Wang & Steinhardt 1998; Linder & Jenkins 2003),

\begin{equation} \frac{\mathrm{d}^2}{\mathrm{d}a^2}D_+(a)\! +\! \frac{1}{a}\left(3\!+\!\frac{\mathrm{d}\ln H}{\mathrm{d}\ln a}\right)\frac{\mathrm{d}}{\mathrm{d}a}D_+(a)\! =\! \frac{3}{2a^2}\Omega _{\rm m}(a) D_+(a). \end{equation}

(7)

Non-linear structure formation enhances the CDM spectrum P(k, a) on small scales by one and a half order of magnitude, which is described by the fit suggested by Smith et al. (2003).

2.4 Angular momenta from tidal shearing

Angular momenta of dark matter haloes embedded in potential flows in the large-scale structure are generated by a mechanism referred to as tidal shearing, where the differential motion of mass elements inside a protohalo gives rise to a torquing moment (Hoyle 1949; Sciama 1955; Peebles 1969; Doroshkevich 1970; White 1984):

\begin{equation} L_\alpha = a^3 H(a)\frac{\mathrm{d}D_+}{\mathrm{d}a}\epsilon _{\alpha \beta \gamma }I_{\beta \delta }\Phi _{\delta \gamma }, \end{equation}

(8)

i.e. it is the variation |$\mathrm{\partial} _\alpha \upsilon _\beta$| of the velocities |$\upsilon _\beta \sim \mathrm{\partial} _\beta \Phi$| across the protohalo and hence the tidal field Φ_αβ

\begin{equation} \Phi _{\alpha \beta }=\mathrm{\partial} _\alpha \mathrm{\partial} _\beta \Phi , \end{equation}

(9)

which is responsible for angular momentum generation. The mass distribution inside the protohalo itself is described by its inertia tensor I_αβ,

\begin{equation} I_{\alpha \beta } = \Omega _{\rm m}\rho _\mathrm{crit}\,a^3\,\int _{V_L}\mathrm{d}^3q\, (\boldsymbol {q}-\bar{\boldsymbol {q}})_\alpha (\boldsymbol {q}-\bar{\boldsymbol {q}})_\beta , \end{equation}

(10)

i.e. the second moments of the matter distribution, with the centre of mass at the position |$\bar{\boldsymbol {q}}$| and the integration comprising the Lagrangian volume of the protohalo. Throughout, we use Einstein's summation convention.

The Levi-Civita symbol in equation (8) generates the interesting misalignment property between the shear and inertia eigensystems which is required for generating angular momentum: only the antisymmetric contribution |$X^-_{\beta \gamma }$|⁠, derived from the commutator |$X^-_{\beta \gamma } = [I_{\beta \gamma }, \Phi _{\beta \gamma }]$|⁠, to the product between the tensors I_βγ and Φ_βγ is non-vanishing in contraction with the antisymmetric ϵ_αβγ and therefore relevant for angular momentum generation. The symmetric contribution |$X^+_{\beta \gamma }$|⁠, which can be isolated using the anticommutator |$X^+_{\beta \gamma } = \lbrace I_{\beta \gamma }, \Phi _{\beta \gamma }\rbrace$| cancels in the contraction. This means that for angular momentum build-up, the tidal shear and the inertia tensors are not allowed to have a common eigensystem and are skewed relative to each other (Schäfer 2009; Schäfer & Merkel 2012). Likewise, degeneracies in this relation evoked by spatial symmetries in the two tensors can prohibit the generation of angular momentum. Alternative models of galaxy angular momenta assume that the haloes are spun up by non-central, anisotropic infall in filaments (see, for instance, Pichon et al. 2010; Kimm et al. 2011; Codis et al. 2012).

2.5 Galaxy ellipticities

Ellipticity correlations between galaxies are traced back to correlated angular momenta of their host haloes. CDM haloes acquire their angular momentum by tidal shearing and due to the fact that neighbouring galaxies experience correlated tidal fields, their angular momenta are correlated in consequence. The direction of the angular momentum |$\boldsymbol {L}$| in turn determines the angle of inclination under which the galactic disc is viewed, and ultimately the ellipticity which is attributed to the galactic disc (Heavens et al. 2000; Crittenden et al. 2001, 2002; Mackey et al. 2002; Heymans & Heavens 2003): linking the angular momentum direction |$\hat{\boldsymbol {L}}= \boldsymbol {L}/L$| to the components of the complex ellipticity ϵ using the above argument yields

\begin{equation} \epsilon =\epsilon _+ +\mathrm{i}\epsilon _\times \quad \mathrm{with}\quad \epsilon _+ = \alpha \frac{\hat{L}_x^2-\hat{L}_y^2}{1+\hat{L}_z^2},\quad \epsilon _\times = 2\alpha \frac{\hat{L}_x\hat{L}_y}{1+\hat{L}_z^2}, \end{equation}

(11)

if the coordinate system is aligned with its z-axis being parallel to the line of sight. A rotation of the coordinate frame by φ causes the complex ellipticity to rotate twice as fast, ϵ → exp (2iφ)ϵ. α is a free parameter weakening the dependence between inclination angle and ellipticity for thick galactic discs and has been determined to be α ≃ 0.75 in the automatic plate-measuring machine (APM) sample (Crittenden et al. 2001) with a large uncertainty.

It should be emphasized that the assumption of a galactic disc forming perpendicularly to the host halo angular momentum direction is a very strong one, which seems suggestive but has only little support from structure formation simulations. In fact, a number of studies point at possibly large misalignments and underline the complexity of the baryonic physics on galactic scales (van den Bosch et al. 2002; Navarro, Abadi & Steinmetz 2004; Bailin & Steinmetz 2005; Bailin et al. 2005; Mayer, Governato & Kaufmann 2008; Kimm et al. 2011). The disc thickness and the degree of misalignment between the symmetry axis of the galactic disc and the angular momentum axis of the host halo therefore have a decisive role in the description of galaxy formation, and appear to be degenerate physical quantities. In our analysis, misalignments could be incorporated in choosing a smaller value for the disc thickness parameter α, which will play the role of normalizing the ellipticity spectra. The angular momentum-based alignment model is only able to capture the physics of tidal alignment of spiral galaxies. In the case of elliptical galaxies, a model which is linear in the tidal shear is more appropriate.

2.6 Weak gravitational lensing

The weak lensing convergence κ provides a weighted line-of-sight measurement of the matter density δ (for reviews, see Mellier 1999; Bartelmann & Schneider 2001; Huterer 2002; Hoekstra & Jain 2008; Bartelmann 2010):

\begin{equation} \kappa = \int _0^{\chi _H}\mathrm{d}\chi \, W_\kappa (\chi )\delta , \end{equation}

(12)

with the weak lensing efficiency W_κ(χ) as the weighting function,

\begin{eqnarray} && \!\!\!\! W_\kappa (\chi ) = \frac{3\Omega _{\rm m}}{2\chi _H^2}\frac{D_+}{a}G(\chi )\chi ,\quad \mathrm{ with }\nonumber\\ && \!\!\!\! G(\chi )= \int _\chi ^{\chi _H}\mathrm{d}\chi ^\prime \,n(z)\frac{\mathrm{d}z}{\mathrm{d}\chi ^\prime }\frac{\chi ^\prime -\chi }{\chi ^\prime }. \end{eqnarray}

(13)

n(z) denotes the redshift distribution of the lensed background galaxies (with the parametrization introduced by Smail et al. 1995),

\begin{eqnarray} n(z) = n_0\left(\frac{z}{z_0}\right)^2\exp \left(-\left(\frac{z}{z_0}\right)^\beta \right)\mathrm{d}z \quad \mathrm{with}\quad \frac{1}{n_0}=\frac{z_0}{\beta }\Gamma \left(\frac{3}{\beta }\right). \nonumber\\ \end{eqnarray}

(14)

z₀ has been chosen to be ≃0.64 such that the median of the redshift distribution is 0.9, which is anticipated for the Euclid galaxy sample (Amara & Réfrégier 2007; Amendola et al. 2012). With these definitions, one can carry out a Limber projection (Limber 1954) of the weak lensing convergence for obtaining the angular convergence spectrum C_κ(ℓ),

\begin{equation} C_\kappa (\ell ) = \int _0^{\chi _H}\frac{\mathrm{d}\chi }{\chi ^2}\,W_\kappa ^2(\chi ) P(k=\ell /\chi ), \end{equation}

(15)

which describes the fluctuation statistics of the convergence field. We will always work in the weak lensing regime, κ, γ ≪ 1, and approximate the reduced shear g ≡ γ/(1 − κ) with the lensing shear γ, which has the same statistical properties as the weak lensing convergence κ.

3 ELLIPTICITY CORRELATIONS

3.1 Angular momentum induced ellipticity correlations

The idea behind intrinsic correlations is that neighbouring galaxies build up their angular momenta with correlated tidal shears because the galaxy separation is typically smaller than the correlation length of the tidal shear field. Under the assumption that the galactic disc orients itself perpendicular to the angular momentum direction of the host halo (for a review on angular momenta of galactic discs, see Bryan et al. 2012; Romanowsky & Fall 2012), one perceives neighbouring galactic discs under correlated angles of inclination, and therefore the apparent shapes are correlated, which is measured in terms of ellipticities. We use two ellipticity correlation models in this paper, which are both constructed on the idea of correlated angular momenta, but which differ in their particular ansatz. The first model, proposed by Crittenden et al. (2001) establishes the link between the angular momentum direction to the tidal shear field in a random process in real space, whereas the second model, which is due to Mackey et al. (2002), directly formulates the ellipticity field in Fourier space, which makes it easier to quantify ellipticity spectra, but whose parametrization is not as clear as in the first case.

3.1.1 Ellipticity correlations

Correlations of the two ellipticity components ϵ₊ and ϵ_× between two points |$\boldsymbol {\theta }_1$| and |$\boldsymbol {\theta }_2$| separated by an angular distance θ can be described using two correlation functions |$C_{++}(\theta ) = \langle \epsilon _+(\boldsymbol {\theta }_1)\epsilon _+(\boldsymbol {\theta }_2)\rangle$| and |$C_{\times \times }(\theta ) = \langle \epsilon _\times (\boldsymbol {\theta }_1)\epsilon _\times (\boldsymbol {\theta }_2)\rangle$|⁠, which are conveniently combined into two correlation functions C_±(θ),

\begin{eqnarray} C_+(\theta ) & = & C_{++}(\theta ) + C_{\times \times }(\theta ) \end{eqnarray}

(16)

\begin{eqnarray} C_-(\theta ) & = & C_{++}(\theta ) - C_{\times \times }(\theta ) \end{eqnarray}

(17)

using |$C_{+\times }(\theta ) = \langle \epsilon _+(\boldsymbol {\theta }_1)\epsilon _\times (\boldsymbol {\theta }_2)\rangle = 0$|⁠. Finally, ellipticity correlation functions can be transformed to the spectra |$C_E^\epsilon (\ell )$| and |$C_B^\epsilon (\ell )$| of the gradient and vorticity modes of the ellipticity field,

\begin{eqnarray} C_E^\epsilon (\ell ) & = & \pi \int \theta\, \mathrm{d}\theta \left[C_+(\theta )J_0(\ell \theta ) + C_-(\theta )J_4(\ell \theta )\right], \end{eqnarray}

(18)

\begin{eqnarray} C_B^\epsilon (\ell ) & = & \pi \int \theta\, \mathrm{d}\theta \left[C_+(\theta )J_0(\ell \theta ) - C_-(\theta )J_4(\ell \theta )\right] \end{eqnarray}

(19)

by Fourier transform (Kaiser 1992; Schneider, van Waerbeke & Mellier 2002; Schneider & Kilbinger 2007; Fu & Kilbinger 2010). Gravitational lensing in the lowest approximation is only able to excite E modes in the ellipticity field.

3.1.2 Configuration space approach

In this work, we use the angular momentum-based ellipticity correlation model proposed by Crittenden et al. (2001) (referred to as the CNPT model), who trace ellipticity correlations back to tidal shear correlations using the conditional probability distribution |$p(\boldsymbol {L}|\Phi _{\alpha \beta })\, \mathrm{d}\boldsymbol {L}$| introduced by Lee & Pen (2001): in this model, the distribution |$p(\boldsymbol {L}|\Phi _{\alpha \beta })\, \mathrm{d}\boldsymbol {L}$| is assumed as being Gaussian which is then being marginalized over the magnitude of the angular momentum vector, retaining only its directional dependence. Writing down the ellipticity components as a function of the angular momentum direction and employing the covariance 〈L_αL_β〉 as a function of the squared tidal shear tensor, as advocated by Lee and Pen, it is possible to relate the tidal shear correlations to the spectrum of the density field.

Angular momenta |$\boldsymbol {L}$| are described as being coupled to the tidal shear by means of a Gaussian random process |$p(\boldsymbol {L}|\Phi _{\alpha \beta })\, \mathrm{d}\boldsymbol {L}$| involving tidal fields Φ_αβ shaping the covariance cov(L)_αβ of the Gaussian distribution (Lee & Pen 2001),

\begin{equation} \mathrm{cov}(L)_{\alpha \beta } = \langle L_\alpha L_\beta \rangle = \frac{\langle \boldsymbol {L}^2\rangle }{3}\left(\frac{1+a}{3}\delta _{\alpha \beta } - a\, (\hat{\Phi }^2)_{\alpha \beta }\right), \end{equation}

(20)

with the misalignment parameter a, which describes the average orientation of the protohalo's inertia to the tidal shear eigensystem. a has been measured in numerical simulation to be close to 0.25 which we will assume in this work. |$\hat{\Phi }$| is the unit normalized traceless tidal shear with the properties |$\mathrm{tr}(\hat{\Phi })=0$| and |$\mathrm{tr}(\hat{\Phi }^2)=1$|⁠. This description is valid on scales where the correlations between inertia tensors are negligible.

The conditional probability density can be used for establishing a direct relation between ellipticity ϵ and tidal shear |$\hat{\Phi }_{\alpha \beta }$| by integrating out angular momentum direction and magnitude:

\begin{equation} \epsilon (\hat{\Phi }_{\alpha \beta }) = \int \mathrm{d}\hat{\boldsymbol {L}}\, \epsilon (\hat{\boldsymbol {L}})\int L^2\, \mathrm{d}L\, p(\boldsymbol {L}|\Phi _{\alpha \beta }). \end{equation}

(21)

With this relation, one can write down the two correlation functions |$\langle \epsilon _+(\boldsymbol {x}_1)\epsilon _+(\boldsymbol {x}_2)\rangle$| and |$\langle \epsilon _\times (\boldsymbol {x}_1)\epsilon _\times (\boldsymbol {x}_2)\rangle$| of the three-dimensional ellipticity field in terms of moments ζ_n(r) (see Crittenden et al. 2001) of the tidal shear field. Those moments, in turn, are expressed as weighted integrals over the CDM spectrum, where we impose a Gaussian smoothing on a scale of 10¹¹ M_⊙ h⁻¹, which is typical for galaxies.

The correlation function of the 3D ellipticity field can then be projected on to the angular correlation function of the ellipticity components by using the configuration space Limber equation (Limber 1954):

\begin{eqnarray} C_{++}(\theta ) & = & \int \mathrm{d}\chi _1W_\epsilon (\chi _1)\,\int \mathrm{d}\chi _2W_\epsilon (\chi _2)\,\langle \epsilon _+(\boldsymbol {x}_1)\epsilon _+(\boldsymbol {x}_2)\rangle \end{eqnarray}

(22)

\begin{eqnarray} \nonumber\\ C_{\times \times }(\theta ) & = & \int \mathrm{d}\chi _1W_\epsilon (\chi _1)\,\int \mathrm{d}\chi _2W_\epsilon (\chi _2)\,\langle \epsilon _\times (\boldsymbol {x}_1)\epsilon _\times (\boldsymbol {x}_2)\rangle , \end{eqnarray}

(23)

with the distance distribution W_ϵ(χ) = n(z(χ)) dz/dχ resulting for a given cosmology from the observed redshift distribution n(z) dz of background galaxies (see equation 14). The separation distance entering the 3D correlation functions is completely determined by the two line-of-sight distances χ₁, χ₂ and the angle of separation θ. Giahi-Saravani & Schäfer (2012) have shown that distortions of the intrinsic ellipticity pattern due to the peculiar motion of galaxies is very small for multipoles up to ℓ = 1000.

3.1.3 Fourier approach

We extend our analysis by the approach of Mackey et al. (2002, hereafter MWK). Similar to Crittenden et al. (2001) they also work in the framework of tidal torque theory and relate intrinsic ellipticity to angular momentum assuming that the disc of a galaxy forms perpendicular to its spin axis. However, when computing the angular momentum the MWK model entirely neglects any correlation between the tidal field and the tensor of inertia. They argue that due to the different correlation lengths involved (while the correlations for the inertia tensor primarily arise from smaller scales the correlations in the tidal field are long ranged) a successive averaging process is permissible. First, they perform an average over inertia tensors then over the tidal field expecting the ellipticity correlation arising from long-range correlations of the latter. In contrast to this, the CNPT model takes explicitly the correlations of the inertia tensor and the tidal field via the misalignment parameter a into account.

One more simplification made by MWK is to drop the dependence of the observed ellipticity on the z-component of the angular momentum of the galaxy, i.e.

\begin{equation} \epsilon _+ = C \left(L_x^2-L_y^2 \right) \qquad \mathrm{and} \qquad \epsilon _{\times } = 2C\, L_xL_y, \end{equation}

(24)

with a constant C. Accordingly, the intrinsic ellipticity scales quadratically with the modulus of the angular momentum, leaving faster spinning galaxies more flattened. Note that by the basic structure of this relation the symmetry properties of the ellipticity field are the same ones as in equation (1).

Assuming shear and inertia being statistically independent allows us to work completely in harmonic space, which greatly facilitates the computation. Since we aim at the power spectra of the intrinsic ellipticity it is convenient to introduce the parity-conserving (E mode) and parity-violating (B mode) part of the intrinsic ellipticity field

\begin{eqnarray} E(\boldsymbol k)\, k^2 &=& \left(k_x^2 - k_y^2 \right) \epsilon _+ ({\boldsymbol k}) + 2 k_xk_y \epsilon _\times ({\boldsymbol k})\nonumber \\ B({\boldsymbol k})\, k^2 &=& -2 k_xk_y \epsilon _+ ({\boldsymbol k}) + \left(k_x^2 - k_y^2 \right) \epsilon _\times ({\boldsymbol k}). \end{eqnarray}

(25)

Focusing on modes perpendicular to the line of sight one can derive the following dimensionless ellipticity power spectra for the E and B mode, respectively,

\begin{eqnarray} \Delta _{X}^2(k) &=& \frac{C}{225} \left( \frac{3}{2}\Omega _{\rm m} H_0^2 \right)^4 \int _0^\infty \frac{\mathrm{d}\alpha }{\alpha } \Delta ^2(\alpha k)\nonumber \\ & & \times \int _{-1}^1 \mathrm{d}\mu \frac{\Delta ^2 (k\sqrt{1+\alpha ^2 - 2\alpha \mu })}{(1+\alpha ^2-2\alpha \mu )^{7/2}}g_{X}(\alpha ,\mu ). \end{eqnarray}

(26)

Here, X ∈ {E, B} and g_X is a polynomial given in equation 17 of MWK together with a detailed derivation of the expressions given above. As before, we smooth the linear power spectrum on an appropriate length-scale with a Gaussian filter function.

Finally, in order to get the corresponding angular power spectra we have to again make use of the Fourier-space variant of Limber's projection (Limber 1954):

\begin{equation} \frac{\ell (2\ell + 1)}{4\pi }\, C^\epsilon _{X}(\ell )= \frac{\pi }{\ell } \int _0^\infty \chi \,\mathrm{d}\chi \, W^2_\epsilon (\chi ) \Delta _{X}^2 (\ell / \chi ) \end{equation}

(27)

with the weighting function W_ϵ(χ) dχ = n(z) dz already introduced in equation (14).

MWK determine the constant C by computing the expectation value of the squared angular momentum modulus and adjusting C to match the mean-square source ellipticity typically observed in galaxy surveys. For our purpose, however, it makes more sense to choose C in such a way that the angular power spectra obtained with the two different approaches coincide on largest scales. This is justified by the expectation that the large-scale power will be least affected by the differences in the two approaches under consideration. Hence, we first compute the spectra using formulae (18) and (19) for appropriately chosen misalignment parameter a and galaxy thickness parameter α and subsequently determine C, so that the two models yield identical predictions for the variance of the intrinsic ellipticity field on large scales.

3.1.4 Comparison of the two ellipticity models

The ellipticity correlation functions C₊₊(θ) and C_××(θ) resulting from both models are plotted in Fig. 1 as a function of angle of separation θ, where the projection was carried out for the Euclid galaxy redshift distribution. The plot suggests correlation lengths of ∼10 arcmin for the ellipticity field and shows that under the normalizations chosen, the correlation functions resulting from the CNPT model achieves 50 per cent higher amplitudes in comparison to those predicted by the MWK model, but otherwise the general shape is in very good agreement.

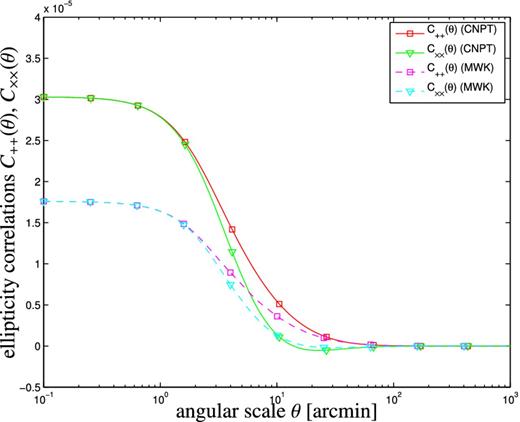
Angular ellipticity correlation functions C++(θ) (green and magenta lines) and C××(θ) (red and cyan lines), for a smoothing scale of M = 1011 M⊙ h−1, a misalignment parameter a = 0.25 and a disc thickness of α = 0.75. The correlation functions were derived using the CNPT and MWK models with the relative normalization as discussed in the text.

Figure 1.

Angular ellipticity correlation functions C₊₊(θ) (green and magenta lines) and C_××(θ) (red and cyan lines), for a smoothing scale of M = 10¹¹ M_⊙ h⁻¹, a misalignment parameter a = 0.25 and a disc thickness of α = 0.75. The correlation functions were derived using the CNPT and MWK models with the relative normalization as discussed in the text.

Open in new tab Download slide

Computing the spectra |$C_E^\epsilon (\ell )$| and |$C_B^\epsilon (\ell )$| yields Fig. 2, where for comparison the linear and non-linear spectra C_κ(ℓ) for the weak lensing convergence and the Euclid shape noise levels |$\sigma _\epsilon ^2/n$| are plotted. The shape of the ellipticity spectra shows constant amplitudes up to scales of ℓ ∼ 300, where individual ellipticities are uncorrelated, and correlations between ellipticities are present on smaller angular scales. The spectra exhibit a wide maximum on multipoles of ℓ ∼ 10³ before dropping in amplitude, which is caused by imposing the mass cutoff. For comparison and motivating our analysis, we plot predictions for the weak lensing spectrum C_κ(ℓ) for linear and non-linear CDM spectra, as well as the anticipated shot noise for Euclid. Clearly, intrinsic ellipticity correlations are subdominant compared to weak lensing induced ellipticity correlations, but can in amplitude amount to up to 30 per cent of the lensing signal on multipoles of ℓ ≃ 10³ before the shape noise makes measurements difficult. Comparing the two ellipticity models show that, if the normalization is chosen as explained, the MWK model predicts lower spectra than the model by CNPT by about 50 per cent on high multipoles as in the case of the correlation function at small separations, but both models predict similar ratios between |$C^\epsilon _E(\ell )$| and |$C^\epsilon _B(\ell )$| amounting to about a factor of 5 at high multipoles. Interestingly, intrinsic ellipticity correlations would dominate over the weak lensing signal if the lensing prediction was derived using linear structure growth only. Comparing the spectra |$C^\epsilon _E(\ell )$| and C_κ(ℓ) with the shape noise levels of Euclid clearly demonstrate the importance of intrinsic ellipticity correlations in weak lensing data.

$Ellipticity spectra $C_E^\epsilon (\ell )$ (green and magenta lines) and $C_B^\epsilon (\ell )$ (red and cyan lines) derived with the CNPT and MWK models, with weak convergence power spectrum Cκ(l), both linear and non-linear (black dashed and solid lines, respectively), and the Euclid shape noise $\sigma _\epsilon ^2/\bar{n}$, with $10^n\times \sigma _\epsilon ^2/\bar{n}$, n = 0, 1, 2 (blue dashed lines).$

Figure 2.

Ellipticity spectra |$C_E^\epsilon (\ell )$| (green and magenta lines) and |$C_B^\epsilon (\ell )$| (red and cyan lines) derived with the CNPT and MWK models, with weak convergence power spectrum C_κ(l), both linear and non-linear (black dashed and solid lines, respectively), and the Euclid shape noise |$\sigma _\epsilon ^2/\bar{n}$|⁠, with |$10^n\times \sigma _\epsilon ^2/\bar{n}$|⁠, n = 0, 1, 2 (blue dashed lines).

Open in new tab Download slide

The B-mode spectrum |$C^\epsilon _B(\ell )$|⁠, which is sourced by intrinsic alignments, is smaller by more than one order of magnitude compared to the E-mode spectrum |$C^\epsilon _E(\ell )$| at high multipoles but might dominate over other higher order lensing effects which are able to excite parity-violating modes in the ellipticity field such as source-lens clustering (Schneider et al. 2002), multiple lensing along the line of sight or violations of the Born approximation (Cooray & Hu 2002; Shapiro & Cooray 2006; Schäfer et al. 2012).

3.2 Variance in apertures

Quantities derived from the weak lensing spectrum C_κ(ℓ) are weighted variances of the convergence inside apertures of varying size θ, introduced by Schneider (1996):

\begin{equation} \langle \kappa ^2 \rangle (\theta ) = \frac{2}{\pi }\int \ell\, \mathrm{d}\ell \, W^2_1(\ell \theta )\,C_{\kappa }(\ell ), \end{equation}

(28)

and

\begin{equation} \langle M_{\kappa }^2 \rangle (\theta ) = \frac{2}{\pi }\int \ell\, \mathrm{d}\ell \,W^2_4(\ell \theta )\,C_{\kappa }(\ell ), \end{equation}

(29)

which measure the scale dependence of fluctuations’ variance in the respective field. The weighting functions W₀(x) and W₄(x), x = ℓθ, are defined as

\begin{equation} W_1(x) = \frac{J_1(x)}{x} \quad \mathrm{and}\quad W_4(x) = \frac{12J_4(x)}{x^2}, \end{equation}

(30)

respectively, for the shear variance averaged in an aperture of size θ and the aperture mass variance. The weak lensing power spectrum is substituted in the previous definitions with |$C_E^\epsilon (\ell )$| and |$C_B^\epsilon (\ell )$| in order to obtain

\begin{eqnarray} \langle \epsilon ^2_+ \rangle (\theta ) & = & \frac{2}{\pi } \int \ell\, \mathrm{d}\ell \,W^2_1(\ell \theta )C_E^\epsilon (\ell ), \end{eqnarray}

(31)

\begin{eqnarray} \langle M_\mathrm{ap}^2 \rangle (\theta ) & = & \frac{2}{\pi } \int \ell\, \mathrm{d}\ell \, W^2_4(\ell \theta )C_E^\epsilon (\ell ), \end{eqnarray}

(32)

\begin{eqnarray} \langle \epsilon ^2_\times \rangle (\theta ) & = & \frac{2}{\pi }\int \ell\, \mathrm{d}\ell \, W^2_1(\ell \theta )C_B^\epsilon (\ell ), \end{eqnarray}

(33)

\begin{eqnarray} \langle M_{\perp }^2 \rangle (\theta ) & = & \frac{2}{\pi } \int \ell\, \mathrm{d}\ell \, W^2_4(\ell \theta )C_B^\epsilon (\ell ), \end{eqnarray}

(34)

which are analogous quantites if the origin of ellipticity correlations would be purely intrinsic and generated by correlated angular momenta.

In Fig. 3 we show, how the aperture-weighted variances of the intrinsic ellipticity field should behave in the Euclid galaxy sample as a function of angular scale in comparison to that of the weak lensing field. We consider both tangential and radial shears and compare the results between the two different intrinsic ellipiticity models.

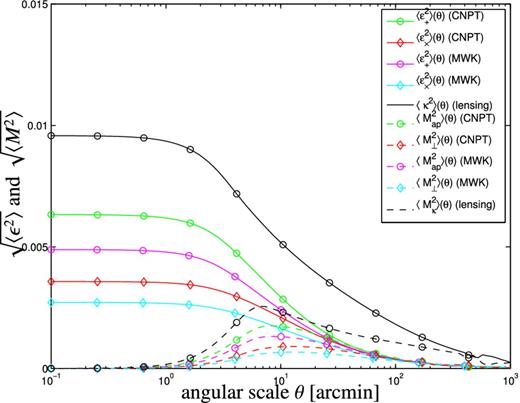
$Standard deviation of the averaged ellipticity and aperture mass as a function of aperture size θ for the CNPT and MWK models: tangential ellipticity $\langle \epsilon _+^2\rangle$ (solid green and magenta lines), radial ellipticity $\langle \epsilon _\times ^2\rangle$ (solid red and cyan lines), aperture mass $\langle M_\mathrm{ap}^2\rangle$ (dashed green and magenta lines) along with $\langle M_\perp ^2\rangle$ (dashed red and cyan lines), all for the Euclid galaxy sample in comparison to the same quantities derived from the weak lensing convergence (corresponding black lines).$

Figure 3.

Standard deviation of the averaged ellipticity and aperture mass as a function of aperture size θ for the CNPT and MWK models: tangential ellipticity |$\langle \epsilon _+^2\rangle$| (solid green and magenta lines), radial ellipticity |$\langle \epsilon _\times ^2\rangle$| (solid red and cyan lines), aperture mass |$\langle M_\mathrm{ap}^2\rangle$| (dashed green and magenta lines) along with |$\langle M_\perp ^2\rangle$| (dashed red and cyan lines), all for the Euclid galaxy sample in comparison to the same quantities derived from the weak lensing convergence (corresponding black lines).

Open in new tab Download slide

The aperture-weighted variances derived from intrinsic ellipticities decrease in magnitude which of course is a generally expected behaviour caused by the weighting functions W_n(ℓθ), and exhibit lower amplitudes compared to the lensing ones, as can be expected from the relative magnitudes of the spectra. On angular scales larger than 100 arcmin, intrinsic alignments have dropped to zero, which is compatible with them being a small-scale phenomenon, while lensing still has a considerable signal. As expected, the difference in magnitude of the variances sourced by E and B modes is smaller than the difference in spectra on small scales because of the averaging in multipole ℓ, and an analogous argument applies to the predictions by the two models under consideration.

4 PARAMETER LIKELIHOOD

In this section, the dependence of the intrinsic ellipticity spectrum on the cosmological parameter set is investigated. This is of particular relevance because of their contaminating effect in weak lensing data by introducing spurious ellipticity correlations, and because they depend on the cosmological model in a very non-linear way, much stronger than e.g. the weak lensing convergence: we point out that in our models, the angular momentum |$\boldsymbol {L}$| reflects the squared tidal shears ∂_i∂_jΦ, and the ellipticity field ϵ in turn has a very complex dependence on the angular momentum direction, which can be approximated to be quadratic for small line-of-sight components of the angular momentum direction. In the following, we keep the parameter α in our ellipticity model constant, because it can in principle be determined by analysing morphological data, as Crittenden et al. (2001) demonstrated. The misalignment parameter a replaces σ₈ because it fixes the normalization of the spectra, and is completely degenerate with α.

4.1 Parameter dependences of intrinsic alignments

When considering the angular spectra describing the ellipticity field, the parameter sensitivity of intrinsic alignments can be nicely illustrated by considering derivatives of the spectra with respect to cosmological parameters, weighted by the inverse noise. For illustration, we assume that weak lensing induced ellipticity alignments were absent from the data, and that the ellipticity shape noise would be that of Euclid. Therefore, the sensitivities, i.e. the derivative of the observables with respect to the parameters to be estimated in units of the noise,

\begin{equation} \frac{1}{\sqrt{\mathrm{cov}_{X}(\ell )}}\frac{\mathrm{\partial} C^\epsilon _X}{\mathrm{\partial} x_\mu },\quad X\in \left\lbrace E,B\right\rbrace , \end{equation}

(35)

correspond to the contributions |$\sqrt{\mathrm{d}F_{\mu \mu }/\mathrm{d}\ell }$| to the diagonal entries of a Fisher matrix F_μν, which describes the parameter dependence of the spectra |$C^\epsilon _E(\ell )$| and |$C^\epsilon _B(\ell )$| on a cosmological model. It is worth to mention that derivatives with respect to the parameter or the logarithm of the parameter are effectively equal in our case, given the fact that the parameters themselves are of the order of unity. The covariances acquire a cosmic variance error and a Poissonian shape measurement error,

\begin{equation} \mathrm{cov}_X(\ell ) = \frac{2}{2\ell +1}\frac{1}{f_\mathrm{sky}}\left(C^\epsilon _X(\ell ) + \frac{\sigma ^2_\epsilon }{n}\right)^2, \end{equation}

(36)

with σ_ϵ = 0.3, n = 30 arcmin⁻² as the number density of galaxies per square steradian and the sky fraction f_sky = 1/2.

We depict these quantities in Fig. 4 for the basic set of cosmological parameters considered here: x_μ ∈ {Ω_m, a, h, w, where n_s has been omitted due to its very weak influence on the spectra. Clearly, the E- and B-modes spectra exhibit an identical behaviour on large, cosmic variance dominated scales, where they reflect identical dependence on the physical processes of angular momentum generation and disc orientation, before differening on multipoles ℓ ≳ 300, where weaker B modes start being influenced by the noise level. The effectively non-existent dependence of the ellipticity spectra on the dark energy equation of state parameter w is particularly interesting and suggests that intrinsic alignments contaminations in weak lensing can be investigated almost independently from the dark energy model assumed. Conversely, the dependences on Ω_m and a are particularly strong, because a determines the amplitude of the spectra in much the same way as σ₈ fixes the normalization of the weak lensing spectra.

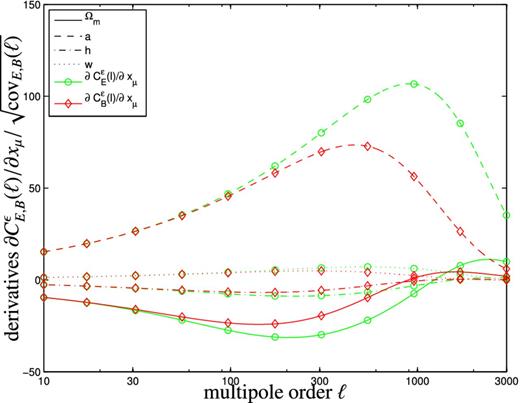
$Sensitivities $\mathrm{\partial} C_E^\epsilon (\ell )/\mathrm{\partial} x_\mu$ (green lines) and $\mathrm{\partial} C_B^\epsilon (\ell )/\mathrm{\partial} x_\mu$ (red lines) in units of $\sqrt{\mathrm{cov}_X(\ell )}$ as a function of maximum multipole order ℓ, with respect to the cosmological parameters Ωm (dashed lines), a (solid lines), h (dash-dotted lines) and w (dotted lines). The spectra were computed with the CNPT model.$

Figure 4.

Sensitivities |$\mathrm{\partial} C_E^\epsilon (\ell )/\mathrm{\partial} x_\mu$| (green lines) and |$\mathrm{\partial} C_B^\epsilon (\ell )/\mathrm{\partial} x_\mu$| (red lines) in units of |$\sqrt{\mathrm{cov}_X(\ell )}$| as a function of maximum multipole order ℓ, with respect to the cosmological parameters Ω_m (dashed lines), a (solid lines), h (dash-dotted lines) and w (dotted lines). The spectra were computed with the CNPT model.

Open in new tab Download slide

4.2 Non-Gaussian likelihoods

This section is intended to check whether our assumption of Gaussianity for the parameters likelihood is well grounded. In order to achieve this, we compare the Gaussian likelihoods derived by using the Fisher formalism,

\begin{equation} \mathcal {L}\propto \exp \left(-\frac{(x_\mu -x_\mu ^\mathrm{fid})^2}{2\sigma _\mu ^2}\right) \quad \mathrm{with}\quad \sigma _\mu ^2 = \frac{1}{F_{\mu \mu }}, \end{equation}

(37)

where the Fisher matrix is determined from the curvature of the logarithmic likelihood,

\begin{equation} F_{\mu \nu } = \sum _{\ell = \ell _\mathrm{min}}^{\ell _\mathrm{max}} \frac{\mathrm{\partial} C_E^\epsilon (\ell )}{\mathrm{\partial} x_\mu } \frac{1}{\mathrm{cov}_E(\ell )}\frac{\mathrm{\partial} C_E^\epsilon (\ell )}{\mathrm{\partial} x_\nu } \end{equation}

(38)

with a direct evaluation of the respective likelihood function, derived using the relation

\begin{equation} \mathcal {L}\propto \exp \left(-\chi ^2(x_\mu )/2\right), \end{equation}

(39)

where the χ² functional is given by

\begin{equation} \chi ^2(x_\mu ) = \sum _{\ell = \ell _\mathrm{min}}^{\ell _\mathrm{max}} \frac{1}{\mathrm{cov}_E(\ell )} \left[C_E^\epsilon (\ell |x_\mu ) - C_E^\epsilon (\ell |x_\mu ^\mathrm{fid})\right]^2 \end{equation}

(40)

and quantifies the goodness of fit of a parameter choice x_μ in the space spanned by the set of cosmological parameters {Ω_m, a, h, w, n_s}. It is important to specify that due to the weakness of the intrinsic ellipticity correlations we consider only conditional errors, i.e. we let one parameter vary at a time, keeping the remaining fixed and focus only on the stronger E-mode spectrum |$C^\epsilon _E(\ell )$|⁠. The reduced dimensionality allows us to compute the likelihood directly on a grid without having to make use of Monte Carlo sampling techniques for evaluating the likelihood.

Any deviation from a Gaussian shape of the likelihood |$\mathcal {L}$| is caused by a non-linear dependence of the spectrum |$C^\epsilon _E(\ell )$| on a model parameter x_μ, which is due to the fact that the χ² functional deviates from a parabolic shape if the model parameter is varied. The likelihood assumes an approximately Gaussian shape if it is sufficiently peaked such that a Taylor expansion of the non-linear parameter dependences is applicable in the region around the fiducial parameter choice. In our case, non-Gaussian shapes have been observed if the summation in equation (40) was restricted to the multipole range 10 ≤ ℓ ≤ 100 and quickly became Gaussian if the summation was carried out to higher multipoles.

The non-Gaussian likelihoods |$\mathcal {L}(\Omega _{\rm m})$| and |$\mathcal {L}(w)$| for the matter density and the dark energy equation of state can be seen in Fig. 5 in comparison to their Gaussian approximation. All likelihoods are centred on the fiducial model value |$x_\mu ^\mathrm{fid}$| and scaled with the width σ_μ derived with the Fisher formalism. This new normalized variable allows the curves to range in the same interval and to be comparable. Likelihoods have also been normalized to unity. Most notably, the likelihoods are more strongly peaked than their Gaussian counterparts, with slight asymmetries of |$\mathcal {L}(\Omega _{\rm m})$| towards large values and of |$\mathcal {L}(w)$| towards small parameter values. It should be noted, that the misalignment parameter a (together with the disc thickness α) is a linear parameter in our models and its likelihood |$\mathcal {L}(a)$| is always of Gaussian shape. We conclude that the amount of deviation from the ideal shape is not a serious impediment for applying the Fisher formalism for investigating intrinsic alignments, keeping in mind that in reality one observes alignments over a much wider multipole range such that the likelihoods are closer to Gaussianity.

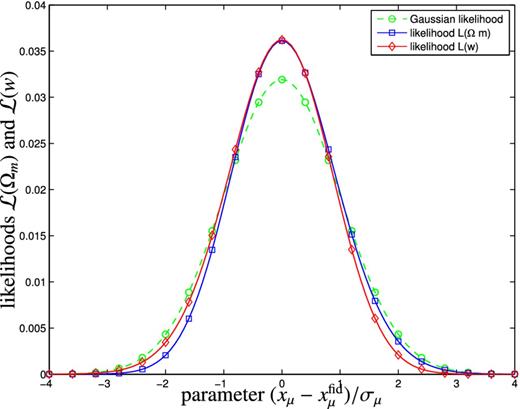
$Conditional likelihoods $\mathcal {L}(\Omega _{\rm m})$ (solid blue line) and $\mathcal {L}(w)$ (solid red line), along with their Gaussian approximations derived with the Fisher formalism ($\sigma _\mu = 1/\sqrt{F_{\mu \mu }}$, dashed green line), for an observation of ellipticity spectrum $C_E^\epsilon (\ell )$ with the Euclid survey characteristics with all other parameters fixed to their fiducial values. The multipole range was set to 10 ≤ ℓ ≤ 100 and the spectrum $C^\epsilon _E(\ell )$ entering the likelihood calculation resulted from the CNPT model.$

Figure 5.

Conditional likelihoods |$\mathcal {L}(\Omega _{\rm m})$| (solid blue line) and |$\mathcal {L}(w)$| (solid red line), along with their Gaussian approximations derived with the Fisher formalism (⁠|$\sigma _\mu = 1/\sqrt{F_{\mu \mu }}$|⁠, dashed green line), for an observation of ellipticity spectrum |$C_E^\epsilon (\ell )$| with the Euclid survey characteristics with all other parameters fixed to their fiducial values. The multipole range was set to 10 ≤ ℓ ≤ 100 and the spectrum |$C^\epsilon _E(\ell )$| entering the likelihood calculation resulted from the CNPT model.

Open in new tab Download slide

5 INTERFERENCE WITH WEAK LENSING

In this section, we show how the intrinsic alignments can affect measurements of the convergence spectrum by quantifying the parameter biases arising when trying to explain the data consisting of both weak lensing induced ellipticity correlations and intrinsic alignments by a model that only accounts for weak lensing and neglects intrinsic alignments. We consider the case of Euclid's weak lensing survey in a non-tomographic setup and give an estimation of the biases, if intrinsic alignments are not removed from data (as proposed by King 2005; Joachimi & Schneider 2008, 2009) or not properly modelled (King & Schneider 2002, 2003). We aim to supplement previous analysis of intrinsic alignment contaminations such as Hirata & Seljak (2004), Bridle & King (2007) and Kitching, Taylor & Heavens (2008) by using a physically motivated and well described alignment model for spiral galaxies with a small number of parameters which can be accessed by morphological galaxy samples (the disc thickness parameter α) and cosmological simulations (the misalignment parameter a).

5.1 Parameter constraints

Statistical errors on constraints on the cosmological parameters from the projected weak lensing power spectrum C_κ(l) when ignoring the intrinsic ellipticity spectrum can be easily obtained by using the Fisher matrix formalism, where the Fisher matrix F_μν measures the curvature of the logarithmic likelihood |$\ln \mathcal {L}$| in all parameter directions (Tegmark, Taylor & Heavens 1997):

\begin{equation} F_{\mu \nu } = \sum _{\ell = \ell _\mathrm{min}}^{\ell _\mathrm{max}} \frac{\mathrm{\partial} C_{\kappa }(\ell )}{\mathrm{\partial} x_{\mu }} \frac{1}{\mathrm{cov}_\kappa (\ell )} \frac{\mathrm{\partial} C_{\kappa }(\ell )}{\mathrm{\partial} x_{\nu }}, \end{equation}

(41)

where the covariance is given by

\begin{equation} \mathrm{cov}_\kappa (\ell ) = \frac{2}{2\ell +1}\frac{1}{f_\mathrm{sky}}\left(C_\kappa (\ell ) + \frac{\sigma ^2_{\epsilon }}{n}\right)^2. \end{equation}

(42)

In the latter expression Euclid's noise |$\sigma ^2_{\epsilon }/n$| was used as well as f_sky = 1/2 for the sky fraction, and the parameter space is spanned by the cosmological parameters x_μ ∈ {Ω_m, σ₈, h, n_s, w}. We will use the covariance cov_κ(ℓ) throughout this paper and neglect small contributions due to intrinsic alignments to the covariance of the ellipticity field, as the covariance and therefore the sampling noise is dominated by weak lensing.

The statistical nσ ellipses obtained as cross-sections through the Gaussian-approximated likelihood for all pairs of parameters are shown in Fig. 6 together with the systematical errors in parameter estimation if intrinsic alignments are not taken care of. The extent to which weak lensing parameter likelihoods are Gaussian is investigated in detail by Wolz et al. (2012).

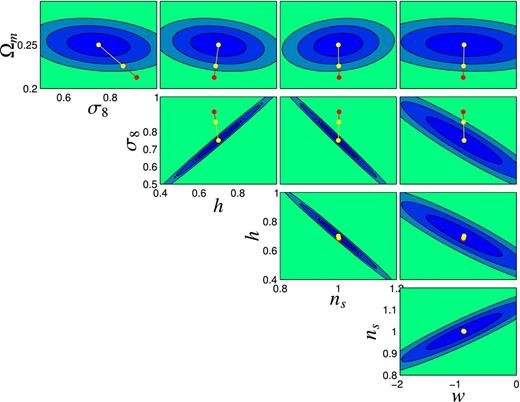
$Parameter estimation biases in Ωm, σ8, h, ns and w obtained, respectively, with the CNPT model (in red) and with the MWK model (in yellow) for Euclid's observation of the weak lensing spectrum Cκ(ℓ), which is contaminated by intrinsic alignments $C_E^\epsilon (\ell )$ on small scales. The misalignment parameter is set to a = 0.25; the disc thickness parameter is set to α = 0.75, the multipole range was 10 ≤ ℓ ≤ 3000 and as a noise amplitude we considered σϵ = 0.3. The ellipses give 1σ, 2σ and 3σ statistical uncertainties on the cosmological parameters from the weak lensing spectrum Cκ(ℓ) from the same multipole range.$

Figure 6.

Parameter estimation biases in Ω_m, σ₈, h, n_s and w obtained, respectively, with the CNPT model (in red) and with the MWK model (in yellow) for Euclid's observation of the weak lensing spectrum C_κ(ℓ), which is contaminated by intrinsic alignments |$C_E^\epsilon (\ell )$| on small scales. The misalignment parameter is set to a = 0.25; the disc thickness parameter is set to α = 0.75, the multipole range was 10 ≤ ℓ ≤ 3000 and as a noise amplitude we considered σ_ϵ = 0.3. The ellipses give 1σ, 2σ and 3σ statistical uncertainties on the cosmological parameters from the weak lensing spectrum C_κ(ℓ) from the same multipole range.

Open in new tab Download slide

5.2 Parameter estimation biases

Ultimately our analysis aims to quantify how biased the parameter estimation with Euclid data will be if intrinsic alignments as predicted from angular momentum models were present in the data, but if we were to interpret the data with a model which does not take intrinsic ellipticities into account. We therefore identify a true model which includes intrinsic alignments

\begin{equation} C_t(\ell ) = C_{\kappa }(\ell ) + C^{\epsilon }_E(\ell ) + \frac{\sigma ^2_{\epsilon }}{n} \end{equation}

(43)

and a false model, which omits intrinsic alignments and considers the ellipticities as random,

\begin{equation} C_f(\ell )= C_{\kappa }(\ell ) + \frac{\sigma ^2_{\epsilon }}{n}. \end{equation}

(44)

For both models, one can specify a goodness-of-fit parameter which in the case of Gaussian errors is the χ² functional. If the data, which follow the model C_t(ℓ), are interpreted with the wrong model C_f(ℓ), the corresponding χ² functional will exhibit its minimum at a position in parameter space shifted from the true parameter choice, because the incomplete model is forced to provide a fit to the data by detuning the parameter set away from the fiducial values. The way to achieve this goal was proposed by a number of authors (Cabré et al. 2007; Amara & Réfrégier 2008; Taburet et al. 2009; March et al. 2011; Schäfer & Heisenberg 2012) in different contexts. Taking the second-order Taylor expansion of the wrong |$\chi ^2_f$| functional around the best-fitting point |$\boldsymbol {x}_t$| of the true model one retrieves an expression involving the vector |$\boldsymbol {\delta }$|⁠:

\begin{eqnarray} \chi ^2_f(\boldsymbol {x}_f) &=& \chi ^2_f(\boldsymbol {x}_t) + \sum _{\mu }\frac{\mathrm{\partial} }{\mathrm{\partial} x_{\mu }}\chi ^2_f(\boldsymbol {x}_t)\delta _{\mu } \nonumber\\ &&+\, \frac{1}{2} \sum _{\mu ,\nu }\frac{\mathrm{\partial} ^2}{\mathrm{\partial} x_{\mu }\mathrm{\partial} x_{\nu }}\chi ^2_f(\boldsymbol {x}_t)\delta _{\mu }\delta _{\nu }, \end{eqnarray}

(45)

being |$\boldsymbol {\delta } \equiv \boldsymbol {x}_f - \boldsymbol {x}_t$|⁠. For weak systematics, this approach has been demonstrated to yield very accurate results for the estimation biases by comparison with the shift of the likelihood peak evaluated by Monte-Carlo Markov chain techniques (Taburet, Douspis & Aghanim 2010).

Now, by minimizing the ensemble-averaged |$\langle \chi ^2_f(\boldsymbol {x}_f) \rangle$| one gets the best-fitting position |$\boldsymbol {x}_f$|⁠. This operation yields a linear system of equations:

\begin{equation} \displaystyle\sum _{\nu } G_{\mu \nu } \delta _{\nu } = a_{\mu } \quad \rightarrow \quad \delta _\mu = \sum _\nu (G^{-1})_{\mu \nu }a_\nu \end{equation}

(46)

and can be inverted directly leading to the estimation bias |$\boldsymbol {\delta }$|⁠. Substitution gives expressions for the quantities G_μν and a_μ which involve derivatives of the spectra,

\begin{eqnarray} && \!\!\!\! G_{\mu \nu } \equiv \sum _{\ell = \ell _\mathrm{min}}^{\ell _\mathrm{max}}\frac{1}{\mathrm{cov}_{\kappa }} \left[ \frac{\mathrm{\partial} C_{\kappa }(\ell )}{\mathrm{\partial} x_{\mu }}\frac{\mathrm{\partial} C_{\kappa }(\ell )}{\mathrm{\partial} x_{\nu }} - C_E^\epsilon (\ell )\frac{\mathrm{\partial} ^2 C_{\kappa }(\ell )}{\mathrm{\partial} x_{\mu }\mathrm{\partial} x_{\nu }} \right], \nonumber \\ && \!\!\!\! a_{\mu } \equiv \sum _{\ell = \ell _\mathrm{min}}^{\ell _\mathrm{max}}\frac{1}{\mathrm{cov}_{\kappa }} \left[ C_E^\epsilon (\ell )\frac{\mathrm{\partial} C_{\kappa }(\ell )}{\mathrm{\partial} x_{\mu }} \right]. \end{eqnarray}

(47)

It is worth to notice that the expression for G_μν simplifies to F_μν when the correct model is used, and the bias vector is therefore zero. A consequence of this argument is that the inclusion of a Gaussian prior |$F^\mathrm{prior}_{\mu \nu }$| would reduce the parameter estimation bias due to the transformation |$G_{\mu \nu }\rightarrow G_{\mu \nu } + F^\mathrm{prior}_{\mu \nu }$|⁠, leading to smaller values for δ_μ in the inversion of the linear system equation (46).

Fig. 6 shows the biases in the estimation of the cosmological parameters induced by considering the intrinsic ellipticities. We computed the 1σ, 2σ and 3σ ellipses by means of the Fisher matrix, as explained in Section 5.1, and we considered the full range of multipoles going from ℓ_min = 10 to ℓ_max = 3000 well into the noise-dominated regime. We calculated the biases for both the CNPT and the MWK models of the intrinsic alignments: in what concerns the CNPT model we considered the value of the misalignment parameter found in n-body simulations (Lee & Pen 2000) a = 0.25, and α = 0.75 for the thickness of the disc. The biases are shown, respectively, in red for the CNPT model and in yellow for the MWK model. All parameters apart from the dark energy equation of state w and the slope n_s are significantly biased with h to a lesser degree, and in almost all cases the shift is not along the primary statistical degeneracy. The differences in the biases between the CNPT and MWK models reflect the difference in amplitude they predict, which is in our case due to the choice of normalization.

The first thing to notice is how the biases depend on the parameters. Evidently Ω_m and σ₈, parameters on which the convergence spectrum C_κ(ℓ) highly depends, seem to be mostly affected. This is in line with the fact that the presence of |$C^\epsilon _E(\ell )$| increases the normalization and adds power to the high-ℓ part of the spectrum, therefore requiring larger values of σ₈, but also causes a tilting of the spectrum which instead asks for lower Ω_m values. The other parameters are instead very weakly affected by the presence of intrinsic alignments.

5.3 Scaling of the estimation bias

It is necessary to investigate how the estimation bias scales with the normalization of the intrinsic alignment spectra, as the parameters a and α in the CNPT model and the resulting normalization C in the MWK model have a large uncertainty. It is worth recalling that the misalignment parameter a is measured in n-body simulations of structure formation, and the galaxy disc thickness α is taken from data on galaxy morphologies.

In Fig. 7, we focus on the CNPT model, by plotting the biases in units of the conditional error |$\sigma _{\mu }^2 = 1/F_{\mu \mu }$| as a function of the misalignment parameter a while keeping α fixed at 0.75. An increasing value of a means a higher misalignment between shear and inertia tensors (Lee & Pen 2000; Crittenden et al. 2001; Schäfer 2009), and hence a higher correlation between angular momenta, or, differently phrased, less randomness in their directions. This means that, within the model, the angular momenta trace the underlying tidal shear field in a tighter way. The lower limit a = 0 indicates therefore complete randomness and absence of any link of the angular momenta to the gravitational potential, as described in Lee & Pen (2000). It is visible how the biases grow fast for greater values of the parameter a, simply meaning that stronger intrinsic correlations would represent a stronger contamination to the convergence spectrum, but that for very large values of a the dependence of the parameter estimation bias with a is saturated and it evolves weaker with increasing a, and even decreases in the case of the parameter n_s. Given the fact that the estimation biases δ_μ/σ_μ change by almost two decades as a is varied, it is vitally important to determine a beforehand, either from independent observations or from simulations of structure formation.

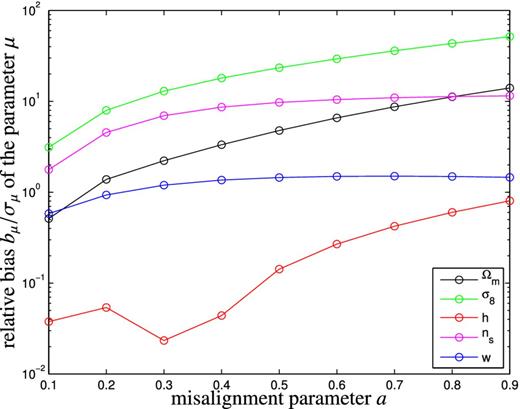
Biases bμ in units of the statistical error σμ for the cosmological parameters Ωm (black line), σ8 (green line), h (red line), ns (magenta line) and w (blue line), as a function of the misalignment parameter a of the CNPT model.

Figure 7.

Biases b_μ in units of the statistical error σ_μ for the cosmological parameters Ω_m (black line), σ₈ (green line), h (red line), n_s (magenta line) and w (blue line), as a function of the misalignment parameter a of the CNPT model.

Open in new tab Download slide

5.4 Observations of intrinsic alignments

Another approach to gain information about the intrinsic alignments relies on the subtraction of the weak lensing signal from the overall signal that is measured. This is, roughly speaking, the inverse of what is usually done with nulling techniques (for details see Joachimi & Schneider 2008, 2009, 2010), whose aim is to clear up the weak lensing signal from intrinsic alignments. The idea behind this is that if we know with high accuracy the model describing the cosmology, we can then predict how, according to this model, the weak lensing spectrum must be. By subtracting the latter from the measured spectrum, the remaining part is ascribable to intrinsic ellipticities. More precisely, if the uncertainty on the convergence power spectrum is small enough to still allow for the extraction of the intrinsic ellipticity signal, then it means that we will be able, in future surveys, to notice this weak signal in the presence of the much stronger weak lensing spectrum.

It is worth to remark, at this point, that the intrinsic alignments we consider in this work, also known as intrinsic–intrinsic alignments, are not the only contaminant to the weak lensing spectrum, usually referred to as the gravitational shear–gravitational shear signal. For instance, another source of contamination is the gravitational shear–intrinsic ellipticity (GI) correlations, which might occur when the alignment produced by a dark matter halo on a close-by galaxy correlates with the shear signal that the same halo induces on a background galaxy. This effect, first suggested by Hirata & Seljak (2004), is difficult to remove, and is not considered in our treatment. Likewise, we do not consider complications arising from the statistical uncertainty in estimating the combined spectrum |$C_\kappa (\ell )+C^\epsilon _E(\ell )$|⁠.

The problem is therefore now to understand whether the uncertainty at which the lensing spectrum can be predicted for a given cosmology is enough to attribute a high-ℓ excess in the ellipticity spectrum to intrinsic alignments. In order to quantify the uncertainty on the convergence spectrum ΔC_κ(ℓ), we consider a multivariate Gaussian likelihood for the cosmological parameters, draw from this distribution simultaneously a sample of five parameters and compute for those the weak lensing spectrum. This gives us a bundle of spectra around the fiducial spectrum |$C_\kappa (\ell |x_\mu ^\mathrm{fid})$|⁠, and allows us to define the uncertainty as the standard deviation

\begin{equation} \Delta C_\kappa (\ell )^2 = \frac{1}{n}\sum _{i=1}^{n}\left[C_\kappa \left(\ell |x_\mu ^{(i)}\right) - \left\langle C_\kappa (\ell |x_\mu ^\mathrm{fid})\right\rangle \right]^2, \end{equation}

(48)

at each multipole ℓ where the index i runs over the samples |$x_\mu ^{(i)}$| of parameter sets drawn from the multivariate Gaussian likelihood. In short, this sampling of a parameter set and measuring the variance of the resulting spectra is a method of propagating the statistical parameter uncertainty described by the likelihood to an error tube around C_κ(ℓ) reflecting the prediction uncertainty in the spectrum. This allows us now to compare the magnitude of the intrinsic ellipticity spectrum |$C^\epsilon _E(\ell )$| to this uncertainty and to quantify the significance. We have considered here, as throughout the entire paper, the semi-analytical expression for the non-linear power spectrum derived by Smith et al. (2003) without taking into account possible uncertainties in this expression, but only uncertainties on the parameters, since our goal is primarily to give a qualitative description of how the intrinsic alignment signal could be extracted from the convergence signal.

Fig. 8 shows the uncertainties n × ΔC_κ(ℓ) with n = 1, …, 5 obtained by using this technique. The likelihood from which samples on the wCDM-parameter set including Ω_m, σ₈, h, n_s and w were drawn is the one describing the knowledge on the cosmological parameters if Euclid's measurement of baryon acoustic oscillations (BAO), Euclid's weak lensing data (both in a 10-bin tomographic measurement) and Planck's cosmic microwave background (CMB) data were present, with a theoretical prior on spatial flatness. The Planck-likelihood was marginalized over the baryon density Ω_b. The error tube ΔC_κ(ℓ) can be clearly separated into two multipole ranges, the first region where the linear CDM spectrum is dominating in the generation of the weak lensing spectrum, and the second region where the non-linear enhancement of P(k) is important and where the error tube is much wider.

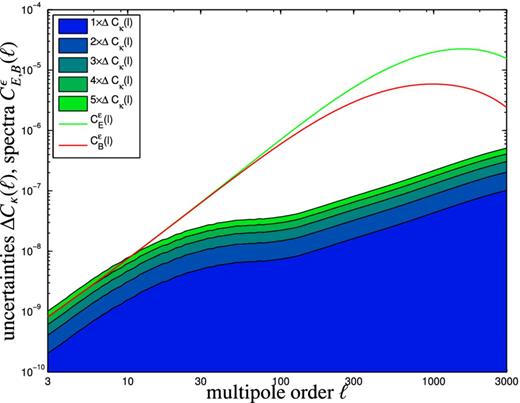
$Uncertainties ΔCκ(ℓ) (shaded area) in the prediction of the non-linear weak lensing spectra Cκ(ℓ) from drawing samples for Ωm, σ8, h, ns and w from a Gaussian parameter likelihood, for which we use a prior on the wCDM model combining BAO, lensing and the CMB (Euclid 10-bin BAO spectra, Euclid 10-bin weak lensing spectra and Planck CMB temperature and polarization spectra). The uncertainty is compared to the ellipticity spectra $C_E^\epsilon (\ell )$ (green line) and $C_B^\epsilon (\ell )$ (red line) determined with the CNPT model.$

Figure 8.

Uncertainties ΔC_κ(ℓ) (shaded area) in the prediction of the non-linear weak lensing spectra C_κ(ℓ) from drawing samples for Ω_m, σ₈, h, n_s and w from a Gaussian parameter likelihood, for which we use a prior on the wCDM model combining BAO, lensing and the CMB (Euclid 10-bin BAO spectra, Euclid 10-bin weak lensing spectra and Planck CMB temperature and polarization spectra). The uncertainty is compared to the ellipticity spectra |$C_E^\epsilon (\ell )$| (green line) and |$C_B^\epsilon (\ell )$| (red line) determined with the CNPT model.

Open in new tab Download slide

We would like to point out that for the statistical subtraction scheme to work the description of the lensing spectrum, in particular of the non-linear part, needs to be unbiased relative to the true non-linear lensing spectrum. Using an analytical formula might be simplistic and we used the analytical description because of the ease of use, while in the true application using a parametrized CDM spectrum derived from simulations might be the best way to proceed. In fact, the cosmic emulators have found a discrepancy of 5-10 per cent between the analytical formula and simulations (Heitmann et al. 2009, 2010; Lawrence et al. 2010).

With such small uncertainties and with the choice of a cosmological model with low complexity the predictive uncertainty on C_κ(ℓ) is much smaller than the amplitude of the intrinsic alignments from multipoles of ℓ ≃ 30 on, |$\Delta C_\kappa (\ell )\ll C^\epsilon _E(\ell )$|⁠. We verified that the Planck CMB likelihood alone would not be sufficient for extracting the intrinsic ellipticity spectrum. Likewise, a more complex model with a larger number of parameters would have much larger uncertainties, |$\Delta C_\kappa (\ell )\gg C^\epsilon _E(\ell )$| for most of the multipole range.

6 SUMMARY

Subject of this paper is the statistical properties of intrinsic, angular momentum induced ellipticity alignments, and their dependence on the cosmological parameter set, in comparison to ellipticity correlations induced by weak gravitational lensing. We carry out our computations with the Euclid ellipticity data sample in mind, and use the projected Euclid galaxy redshift distribution and shape noise for making forecasts.

We base our predictions for the spectra |$C_E^\epsilon (\ell )$| and |$C_B^\epsilon (\ell )$| describing fluctuations in the ellipticity field on physical models for angular momentum correlations in the large-scale structure (Crittenden et al. 2001; MWK). The two models under consideration link the angular momentum field to the tidal shear field, and model the ellipticity of a galaxy by assuming that the galactic disc is formed perpendicular to the host halo's angular momentum direction. The two models differ in describing these physical processes in configuration space versus Fourier space, and use different normalizations. For comparability, we have normalized the MWK model such that it displays the same amplitudes as the CNPT model on large angular scales. The CNPT model in turn uses three parameters, which are the mass scale of the galaxies, imposed by an Gaussian filter acting on the CDM spectrum P(k), a misalignment parameter a, which is determined to have the numerical value a ≃ 0.25 in numerical simulations (Lee & Pen 2001) and finally the disc thickness parameter α, which has been measured to be α ≃ 0.75 in the APM-galaxy sample (Crittenden et al. 2001).
Computing the ellipticity spectra |$C_E^\epsilon (\ell )$| and |$C_B^\epsilon (\ell )$| for the galaxy sample of Euclid from both models yields spectra which are constant on large angular scales and drop off exponentially on small scales, while the E-mode spectrum is larger by about an order of magnitude compared to the B-mode spectrum on multipoles of ℓ ≃ 1000. By themselves, the spectrum |$C_E^\epsilon (\ell )$| would be significantly larger than the linear weak lensing convergence spectrum C_κ(ℓ), which is comparable in amplitude to the spectrum |$C_B^\epsilon (\ell )$| on these multipoles. Non-linear structure formation, however, increases the variance of the cosmic density field strongly, such that intrinsic ellipticities contribute only ∼20 per cent to the total variance of the ellipticity field at ℓ = 1000. Aperture weighted variances give a similar impression: the averaged shear and the aperture mass of the non-linear weak lensing convergence dominate the variance on all relevant scales, and intrinsic alignments are smaller by at least a factor of 2 in this observable.
Investigating the dependence of the ellipticity spectra on cosmological parameters gives a result very different compared to other cosmological probes. Due to the dependence of the angular momentum field on the angular momentum direction and not the magnitude, σ₈ is entirely replaced by the misalignment parameter a. n_s, Ω_m and h determine the CDM spectrum P(k) (the latter two by fixing the shape parameter Γ) and Ω_m is of course appearing in the conversion between comoving distance and redshift at the stage of applying the Limber equation. Computing the derivatives |$\mathrm{\partial} C_E^\epsilon (\ell )/\mathrm{\partial} x_\mu$| and |$\mathrm{\partial} C_B^\epsilon (\ell )/\mathrm{\partial} x_\mu$| of the spectra with respect to the cosmological parameters and expressed in units of their covariance suggests that the parameters a and Ω_m are the ones most important for intrinsic alignments, with only minor dependences on the dark energy equation of state w and the Hubble parameter h. At the same time Ω_m and σ₈ are the ones best constrained by lensing, so that it is suggestive to expect the largest estimation biases in those two parameters, if the intrinsic alignments are not properly removed or modelled.
In the next step, we quantified the likelihood |$\mathcal {L}(\Omega _{\rm m},a,w)$| of the intrinsic alignment spectrum |$C_E^\epsilon (\ell )$| if lensing was not present. One could expect this likelihood to have non-Gaussian contributions because of the non-linearities present in an angular momentum-based alignment model: first, the angular momentum depends on the quadratic tidal shear and the ellipticity depends on the squared angular momentum direction. For a restricted multipole ℓ_max ≲ 100 range, one can see clear deviations from Gaussianity, which quickly vanish if the multipole range is extended. The misalignment parameter a, which describes the normalization of the spectra, is described by a Gaussian likelihood and enters as a prefactor.
We compute estimation biases on the wCDM parameter set if intrinsic alignments are not removed from the ellipticity spectrum, i.e. if the data are in reality described by |$C_\kappa (\ell )+C_E^\epsilon (\ell )$| and wrongly fitted by C_κ(ℓ) only. The strongest biases are present in Ω_m, which is measured to low and σ₈, which is estimated too high, both at the level of ∼2σ, making the estimation biases significant. Interestingly, the dark energy equation of state is almost unbiased, indicating that dark energy investigations are not directly affected by intrinsic alignments. Changing the magnitude of the intrinsic alignment contamination by increasing the misalignment parameter a shows a monotonic increase of the estimation biases for all parameters except n_s, where the estimation bias saturates at a ≃ 0.5 and drops for higher amplitudes. Clearly, these results demand a good external prior on a, either from independent measurements or from numerical simulations.
Finally, we investigate if the weak lensing convergence spectrum C_κ(ℓ) can be predicted precisely enough such that a deviation can be attributed to a contribution |$C_E^\epsilon (\ell )$|⁠. For this purpose, we develop a technique for propagating the uncertainty in the set of cosmological parameters to the variance ΔC_κ(ℓ)² around C_κ(ℓ) for the fiducial cosmology. Comparing this uncertainty with the amplitudes |$C_E^\epsilon (\ell )$| suggests that it should be measurable at high multipoles. In this process, we used a Gaussian likelihood |$\mathcal {L}$| on a standard wCDM cosmology reflecting the knowledge on the cosmological parameters from Euclid's BAO- and weak lensing spectra and from the temperature and polarization spectra of the CMB measured by Planck.

We plan to extend our research to the intrinsic alignment contamination of tomographic weak lensing data, and to include cross-correlations between the weak lensing shear and the intrinsic ellipticity field, the so-called GI alignments, which we aim to derive from angular momentum-based alignment models and which enter the ellipticity spectra at higher order. These GI-alignments are challenging to describe as they introduce ellipticity correlations across tomography bins and reduce amplitude from the spectra because of the negative cross-correlation between intrinsic ellipticity and gravitational shear. Additionally, we aim to include a linear alignment model for elliptical galaxies and to work with a proper morphological mix of ellipticities, working towards a more complete physical description of alignments in tomographic weak lensing data.

Fisher matrices for the description of parameter constraints forecast for Euclid's tomographic weak lensing survey and Euclid's BAO measurements are taken from the iCosmo resource, and the corresponding Fisher matrix for Planck's CMB spectrum has been kindly provided by Maik Weber and Youness Ayaita. We would like to thank Matthias Bartelmann, Angelos F. Kalovidouris and Vanessa M. Böhm for their suggestions, and are grateful for feedback from Anaïs Rassat and Lukas Hollenstein. FC receives funding through German Research Foundation's (DFG's) Schwerpunktprogramm SPP1177 and PMM is supported by the Graduate Academy, Heidelberg. Both FC and PMM acknowledge support from the International Max Planck Research School for Astronomy and Cosmic Physics in Heidelberg and from the Graduate School of Fundamental Physics. BMS's work was supported by the DFG within the framework of the excellence initiative through the Heidelberg Graduate School of Fundamental Physics. We thank our referee for the helpful remarks that led to significant improvement of the draft.

REFERENCES

Abramowitz

M.

Stegun

I. A.

,

Handbook of Mathematical Functions

,

1972

New York

Dover

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Amara

A.

Kitching

T. D.

,

MNRAS

,

2011

, vol.

413

pg.

1505

Crossref

Search ADS

Amara

A.

Réfrégier

A.

,

MNRAS

,

2007

, vol.

381

pg.

1018

Crossref

Search ADS

Amara

A.

Réfrégier

A.

,

MNRAS

,

2008

, vol.

391

pg.

228

Crossref

Search ADS

Amendola

L.

et al. ,

2012

preprint (arXiv:1206.1225)

Arfken

G. B.

Weber

H. J.

,

Mathematical Methods for Physicists

,

2005

6th edn

Amsterdam

Elsevier

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Bacon

D. J.

Refregier

A. R.

Ellis

R. S.

,

MNRAS

,

2000

, vol.

318

pg.

625

Crossref

Search ADS

Bailin

J.

Steinmetz

M.

,

ApJ

,

2005

, vol.

627

pg.

647

Crossref

Search ADS

Bailin

J.

et al. ,

ApJ

,

2005

, vol.

627

pg.

L17

Crossref

Search ADS

Bardeen

J. M.

Bond

J. R.

Kaiser

N.

Szalay

A. S.

,

ApJ

,

1986

, vol.

304

pg.

15

Crossref

Search ADS

Bartelmann

M.

,

Class. Quantum Grav.

,

2010

, vol.

27

pg.

233001

Crossref

Search ADS

Bartelmann

M.

Schneider

P.

,

Phys. Rep.

,

2001

, vol.

340

pg.

291

Crossref

Search ADS

Bernstein

G. M.

,

ApJ

,

2009

, vol.

695

pg.

652

Crossref

Search ADS

Blandford

R. D.

Saust

A. B.

Brainerd

T. G.

Villumsen

J. V.

,

MNRAS

,

1991

, vol.

251

pg.

600

Crossref

Search ADS

Bridle

S.

King

L.

,

New J. Phys.

,

2007

, vol.

9

pg.

444

Crossref

Search ADS

Bryan

S. E.

Kay

S. T.

Duffy

A. R.

Schaye

J.

Dalla Vecchia

C.

Booth

C. M.

,

MNRAS

,

2012

, vol.

429

pg.

3316

Crossref

Search ADS

Cabré

A.

Fosalba

P.

Gaztañaga

E.

Manera

M.

,

MNRAS

,

2007

, vol.

381

pg.

1347

Crossref

Search ADS

Catelan

P.

Kamionkowski

M.

Blandford

R. D.

,

MNRAS

,

2001

, vol.

320

pg.

L7

Crossref

Search ADS

Codis

S.

Pichon

C.

Devriendt

J.

Slyz

A.

Pogosyan

D.

Dubois

Y.

Sousbie

T.

,

MNRAS

,

2012

, vol.

427

pg.

3320

Crossref

Search ADS

Cooray

A.

Hu

W.

,

ApJ

,

2002

, vol.

574

pg.

19

Crossref

Search ADS

Crittenden

R. G.

Natarajan

P.

Pen

U.

Theuns

T.

,

ApJ

,

2001

, vol.

559

pg.

552

Crossref

Search ADS

Crittenden

R. G.

Natarajan

P.

Pen

U.

Theuns

T.

,

ApJ

,

2002

, vol.

568

pg.

20

Crossref

Search ADS

Croft

R. A. C.

Metzler

C. A.

,

ApJ

,

2000

, vol.

545

pg.

561

Crossref

Search ADS

Doroshkevich

A. G.

,

Afz.

,

1970

, vol.

6

pg.

581

Fu

L.

Kilbinger

M.

,

MNRAS

,

2010

, vol.

401

pg.

1264

Crossref

Search ADS

Giahi-Saravani

A.

Schäfer

B. M.

,

MNRAS

,

2012

, vol.

428

pg.

1312

Crossref

Search ADS

Hannestad

S.

Tu

H.

Wong

Y. Y.

,

J. Cosmol. Astropart. Phys.

,

2006

, vol.

6

pg.

25

Crossref

Search ADS

Heavens

A.

Refregier

A.

Heymans

C.

,

MNRAS

,

2000

, vol.

319

pg.

649

Crossref

Search ADS

Heitmann

K.

Higdon

D.

White

M.

Habib

S.

Williams

B. J.

Lawrence

E.

Wagner

C.

,

ApJ

,

2009

, vol.

705

pg.

156

Crossref

Search ADS

Heitmann

K.

White

M.

Wagner

C.

Habib

S.

Higdon

D.

,

ApJ

,

2010

, vol.

715

pg.

104

Crossref

Search ADS

Heymans

C.

Heavens

A.

,

MNRAS

,

2003

, vol.

339

pg.

711

Crossref

Search ADS

Hirata

C. M.

Seljak

U.

,

Phys. Rev. D

,

2004

, vol.

70

pg.

063526

Crossref

Search ADS

Hoekstra

H.

Jain

B.

,

Annu. Rev. Nucl. Part. Sci.

,

2008

, vol.

58

pg.

99

Crossref

Search ADS

Hoyle

F.

,

MNRAS

,

1949

, vol.

109

pg.

365

Crossref

Search ADS

Hu

W.

,

ApJ

,

1999

, vol.

522

pg.

L21

Crossref

Search ADS

Hu

W.

,

Phys. Rev. D

,

2002a

, vol.

66

pg.

083515

Crossref

Search ADS

Hu

W.

,

Phys. Rev. D

,

2002b

, vol.

65

pg.

023003

Crossref

Search ADS

Hu

W.

Jain

B.

,

Phys. Rev. D

,

2004

, vol.

70

pg.

043009

Crossref

Search ADS

Hu

W.

Tegmark

M.

,

ApJ

,

1999

, vol.

514

pg.

L65

Crossref

Search ADS

Hu

W.

White

M.

,

ApJ

,

2001

, vol.

554

pg.

67

Crossref

Search ADS

Huterer

D.

,

Phys. Rev. D

,

2002

, vol.

65

pg.

063001

Crossref

Search ADS

Huterer

D.

,

Gen. Relativ. Grav.

,

2010

, vol.

42

pg.

2177

Crossref

Search ADS

Huterer

D.

Turner

M. S.

,

Phys. Rev. D

,

2001

, vol.

64

pg.

123527

Crossref

Search ADS

Jain

B.

Seljak

U.

,

ApJ

,

1997

, vol.

484

pg.

560

Crossref

Search ADS

Joachimi

B.

Bridle

S. L.

,

A&A

,

2010

, vol.

523

pg.

A1

Crossref

Search ADS

Joachimi

B.

Schneider

P.

,

A&A

,

2008

, vol.

488

pg.

829

Crossref

Search ADS

Joachimi

B.

Schneider

P.

,

A&A

,

2009

, vol.

507

pg.

105

Crossref

Search ADS

Joachimi

B.

Schneider

P.

,

A&A

,

2010

, vol.

517

pg.

A4

Crossref

Search ADS

Joachimi

B.

Semboloni

E.

Bett

P. E.

Hartlap

J.

Hilbert

S.

Hoekstra

H.

Schneider

P.

Schrabback

T.

,

MNRAS

,

2012

, vol.

431

pg.

477

Crossref

Search ADS

Kaiser

N.

,

ApJ

,

1992

, vol.

388

pg.

272

Crossref

Search ADS

Kaiser

N.

Wilson

G.

Luppino

G. A.

,

2000

preprint (astro-ph/000338)

Kamionkowski

M.

Babul

A.

Cress

C. M.

Refregier

A.

,

MNRAS

,

1998

, vol.

301

pg.

1064

Crossref

Search ADS

Kimm

T.

Devriendt

J.

Slyz

A.

Pichon

C.

Kassin

S. A.

Dubois

Y.

,

2011

preprint (arXiv:1106.0538)

King

L. J.

,

A&A

,

2005

, vol.

441

pg.

47

Crossref

Search ADS

King

L.

Schneider

P.

,

A&A

,

2002

, vol.

396

pg.

411

Crossref

Search ADS

King

L. J.

Schneider

P.

,

A&A

,

2003

, vol.

398

pg.

23

Crossref

Search ADS

Kirk

D.

Bridle

S.

Schneider

M.

,

MNRAS

,

2010

, vol.

408

pg.

1502

Crossref

Search ADS

Kirk

D.

Laszlo

I.

Bridle

S.

Bean

R.

,

2011

preprint (arXiv:1109.4536)

Kitching

T. D.

Taylor

A. N.

Heavens

A. F.

,

MNRAS

,

2008

, vol.

389

pg.

173

Crossref

Search ADS

Komatsu

E.

et al. ,

ApJS

,

2011

, vol.

192

pg.

18

Crossref

Search ADS

Kunz

M.

,

C. R. Phys.

,

2012

, vol.

13

pg.

539

Crossref

Search ADS

Larson

D.

et al. ,

ApJS

,

2011

, vol.

192

pg.

16

Crossref

Search ADS

Laszlo

I.

Bean

R.

Kirk

D.

Bridle

S.

,

MNRAS

,

2012

, vol.

423

pg.

1750

Crossref

Search ADS

Lawrence

E.

Heitmann

K.

White

M.

Higdon

D.

Wagner

C.

Habib

S.

Williams

B.

,

ApJ

,

2010

, vol.

713

pg.

1322

Crossref

Search ADS

Lee

J.

Pen

U.

,

ApJ

,

2000

, vol.

532

pg.

L5

Crossref

Search ADS

Lee

J.

Pen

U.

,

ApJ

,

2001

, vol.

555

pg.

106

Crossref

Search ADS

Limber

D. N.

,

ApJ

,

1954

, vol.

119

pg.

655

Crossref

Search ADS

Linder

E. V.

Jenkins

A.

,

MNRAS

,

2003

, vol.

346

pg.

573

Crossref

Search ADS

Mackey

J.

White

M.

Kamionkowski

M.

,

MNRAS

,

2002

, vol.

332

pg.

788

(MWK)

Crossref

Search ADS

March

M. C.

Trotta

R.

Amendola

L.

Huterer

D.

,

MNRAS

,

2011

, vol.

415

pg.

143

Crossref

Search ADS

Mayer

L.

Governato

F.

Kaufmann

T.

,

Adv. Sci. Lett.

,

2008

, vol.

1

pg.

7

Crossref

Search ADS

Mellier

Y.

,

ARA&A

,

1999

, vol.

37

pg.

127

Crossref

Search ADS

Navarro

J. F.

Abadi

M. G.

Steinmetz

M.

,

ApJ

,

2004

, vol.

613

pg.

L41

Crossref

Search ADS

Peebles

P. J. E.

,

ApJ

,

1969

, vol.

155

pg.

393

Crossref

Search ADS

Pichon

C.

Gay

C.

Pogosyan

D.

Prunet

S.

Sousbie

T.

Colombi

S.

Slyz

A.

Devriendt

J.

Alimi

J.-M.

Fuözfa

A.

,

AIP Conf. Ser. Vol. 1241, The Skeleton: Connecting Large Scale Structures to Galaxy Formation

,

2010

New York

Am. Inst. Phys.

pg.

1108

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Romanowsky

A. J.

Fall

S. M.

,

ApJS

,

2012

, vol.

203

pg.

17

Crossref

Search ADS

Schäfer

B. M.

,

Int. J. Mod. Phys. D

,

2009

, vol.

18

pg.

173

Crossref

Search ADS

Schäfer

B. M.

Heisenberg

L.

,

MNRAS

,

2012

, vol.

423

pg.

3445

Crossref

Search ADS

Schäfer

B. M.

Merkel

P. M.

,

MNRAS

,

2012

, vol.

421

pg.

2751

Crossref

Search ADS

Schäfer

B. M.

Heisenberg

L.

Kalovidouris

A. F.

Bacon

D. J.

,

MNRAS

,

2012

, vol.

420

pg.

455

Crossref

Search ADS

Schneider

P.

,

MNRAS

,

1996

, vol.

283

pg.

837

Crossref

Search ADS

Schneider

P.

Kilbinger

M.

,

A&A

,

2007

, vol.

462

pg.

841

Crossref

Search ADS

Schneider

P.

van Waerbeke

L.

Mellier

Y.

,

A&A

,

2002

, vol.

389

pg.

729

Crossref

Search ADS

Sciama

D. W.

,

MNRAS

,

1955

, vol.

115

pg.

3

Crossref

Search ADS

Seitz

S.

Schneider

P.

,

A&A

,

1994

, vol.

287

pg.

349

Seitz

S.

Schneider

P.

Ehlers

J.

,

Class. Quantum Grav.

,

1994

, vol.

11

pg.

2345

Crossref

Search ADS

Shapiro

C.

Cooray

A.

,

J. Cosmol. Astropart. Phys.

,

2006

, vol.

3

pg.

7

Crossref

Search ADS

Smail

I.

Hogg

D. W.

Blandford

R.

Cohen

J. G.

Edge

A. C.

Djorgovski

S. G.

,

MNRAS

,

1995

, vol.

277

pg.

1

Smith

R. E.

et al. ,

MNRAS

,

2003

, vol.

341

pg.

1311

Crossref

Search ADS

Sugiyama

N.

,

ApJS

,

1995

, vol.

100

pg.

281

Crossref

Search ADS

Taburet

N.

Aghanim

N.

Douspis

M.

Langer

M.

,

MNRAS

,

2009

, vol.

392

pg.

1153

Crossref

Search ADS

Taburet

N.

Douspis

M.

Aghanim

N.

,

MNRAS

,

2010

, vol.

404

pg.

1197

Takada

M.

White

M.

,

ApJ

,

2004

, vol.

601

pg.

L1

Crossref

Search ADS

Tegmark

M.

Taylor

A. N.

Heavens

A. F.

,

ApJ

,

1997

, vol.

480

pg.

22

Crossref

Search ADS

Turner

M. S.

White

M.

,

Phys. Rev. D

,

1997

, vol.

56

pg.

4439

Crossref

Search ADS

van den Bosch

F. C.

Abel

T.

Croft

R. A. C.

Hernquist

L.

White

S. D. M.

,

ApJ

,

2002

, vol.

576

pg.

21

Crossref

Search ADS

Van Waerbeke

L.

et al. ,

A&A

,

2000

, vol.

358

pg.

30

Wang

L.

Steinhardt

P. J.

,

ApJ

,

1998

, vol.

508

pg.

483

Crossref

Search ADS

White

S. D. M.

,

ApJ

,

1984

, vol.

286

pg.

38

Crossref

Search ADS

Wittman

D. M.

Tyson

J. A.

Kirkman

D.

Dell'Antonio

I.

Bernstein

G.

,

Nat

,

2000

, vol.

405

pg.

143

Crossref

Search ADS

Wolz

L.

Kilbinger

M.

Weller

J.

Giannantonio

T.

,

J. Cosmol. Astropart. Phys.

,

2012

, vol.

09

pg.

009

Crossref

Search ADS

Download all slides

Month:	Total Views:
January 2017	2
February 2017	2
March 2017	2
May 2017	2
June 2017	1
July 2017	1
September 2017	2
October 2017	3
November 2017	1
December 2017	6
January 2018	2
February 2018	7
March 2018	15
April 2018	10
May 2018	14
June 2018	8
July 2018	9
August 2018	6
September 2018	4
October 2018	9
November 2018	9
December 2018	10
January 2019	3
February 2019	6
March 2019	9
April 2019	8
May 2019	14
June 2019	8
July 2019	5
August 2019	2
September 2019	8
October 2019	5
November 2019	5
December 2019	3
January 2020	11
February 2020	14
March 2020	4
April 2020	7
May 2020	2
June 2020	5
July 2020	6
August 2020	8
September 2020	7
October 2020	7
November 2020	6
December 2020	1
January 2021	3
February 2021	5
March 2021	6
April 2021	12
May 2021	4
June 2021	1
July 2021	10
August 2021	2
September 2021	3
October 2021	8
November 2021	13
December 2021	8
January 2022	6
February 2022	4
March 2022	4
April 2022	6
May 2022	4
June 2022	4
July 2022	6
August 2022	6
September 2022	3
October 2022	9
November 2022	7
December 2022	1
January 2023	6
February 2023	4
March 2023	7
April 2023	13
May 2023	8
June 2023	4
July 2023	4
August 2023	5
September 2023	7
October 2023	2
November 2023	3
December 2023	11
January 2024	7
February 2024	9
March 2024	5
April 2024	4
May 2024	9
June 2024	13
July 2024	9
August 2024	13
September 2024	8
October 2024	7
November 2024	10
December 2024	11
January 2025	5
February 2025	6
March 2025	19
April 2025	8
May 2025	2

Article Contents

Intrinsic ellipticity correlations of galaxies: models, likelihoods and interplay with weak lensing

Abstract

1 INTRODUCTION

2 COSMOLOGY

2.1 Dark energy cosmologies

2.2 CDM power spectrum

2.3 Linear structure growth

2.4 Angular momenta from tidal shearing

2.5 Galaxy ellipticities

2.6 Weak gravitational lensing

3 ELLIPTICITY CORRELATIONS

3.1 Angular momentum induced ellipticity correlations

3.1.1 Ellipticity correlations

3.1.2 Configuration space approach

3.1.3 Fourier approach

3.1.4 Comparison of the two ellipticity models

3.2 Variance in apertures

4 PARAMETER LIKELIHOOD

4.1 Parameter dependences of intrinsic alignments

4.2 Non-Gaussian likelihoods

5 INTERFERENCE WITH WEAK LENSING

5.1 Parameter constraints

5.2 Parameter estimation biases

5.3 Scaling of the estimation bias

5.4 Observations of intrinsic alignments

6 SUMMARY

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Intrinsic ellipticity correlations of galaxies: models, likelihoods and interplay with weak lensing Free

Abstract

1 INTRODUCTION

2 COSMOLOGY

2.1 Dark energy cosmologies

2.2 CDM power spectrum

2.3 Linear structure growth

2.4 Angular momenta from tidal shearing

2.5 Galaxy ellipticities

2.6 Weak gravitational lensing

3 ELLIPTICITY CORRELATIONS

3.1 Angular momentum induced ellipticity correlations

3.1.1 Ellipticity correlations

3.1.2 Configuration space approach

3.1.3 Fourier approach

3.1.4 Comparison of the two ellipticity models

3.2 Variance in apertures

4 PARAMETER LIKELIHOOD

4.1 Parameter dependences of intrinsic alignments

4.2 Non-Gaussian likelihoods

5 INTERFERENCE WITH WEAK LENSING

5.1 Parameter constraints

5.2 Parameter estimation biases

5.3 Scaling of the estimation bias

5.4 Observations of intrinsic alignments

6 SUMMARY

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Intrinsic ellipticity correlations of galaxies: models, likelihoods and interplay with weak lensing