-
PDF
- Split View
-
Views
-
Cite
Cite
A. Ferrara, F. Haardt, R. Salvaterra, Can supermassive black hole seeds form in galaxy mergers?, Monthly Notices of the Royal Astronomical Society, Volume 434, Issue 3, 21 September 2013, Pages 2600–2605, https://doi.org/10.1093/mnras/stt1350
Close - Share Icon Share
Abstract
It has been recently suggested that supermassive black holes at z ≈ 5–6 might form from superfast (Ṁ ≳ 104 M⊙ yr−1) accretion occurring in unstable, massive nuclear gas discs produced by mergers of Milky Way-sized galaxies. Interestingly, such a mechanism is claimed to work also for gas enriched to solar metallicity. These results are based on an idealized polytropic equation-of-state assumption, essentially preventing the gas from cooling. We show that under more realistic conditions, the disc rapidly (<1 yr) cools, the accretion rate drops and the central core can grow only to ≈100 M⊙. In addition, most of the disc becomes gravitationally unstable in ≈100 yr, further quenching the accretion. We conclude that this scenario encounters a number of difficulties that possibly make it untenable.
MOTIVATION
The origin of the supermassive black holes (SMBH) that we now routinely observe at epochs within the first cosmic Gyr represents one of the most intriguing puzzles in structure formation. The current paradigm implies that these objects have gathered their mass by accreting the surrounding gas on to a much smaller seed black hole (BH) (Volonteri, Haardt & Madau 2003; Volonteri & Rees 2005; Lodato & Natarajan 2006; Li et al. 2007; Di Matteo et al. 2008; Tanaka & Haiman 2009; Natarajan 2011). As massive stars end their evolution into BHs of mass m0 ≈ 10–50 M⊙, this mechanism provides the most natural route to produce the initial seeds. However, this scenario has to face at least two, partly related, serious difficulties. First, in order to reach the typical SMBH mass (≈108–9 M⊙) in the limited time (≈Gyr) available up to z = 6, the accretion must not only always proceed at the Eddington rate, but also possibly with an unusually low radiation efficiency. However, several studies (e.g. Alvarez, Wise & Abel 2009; Milosavljević et al. 2009) have now shown that stellar BHs are actually characterized by very low (|$\dot{M}\approx 10^{-12}\,\mathrm{M}_{\odot }$| yr−1) accretion rates due to radiative feedback and because they spend most of their lifetime in low-density regions.
These difficulties would be greatly smoothed out by a larger m0 ≳ 103 M⊙ seed mass. It is then worth exploring viable formation paths for these intermediate-mass SMBH seeds. Long before these problems were realized, proposals for the production of more massive (m0 ≈ 104 − 6 M⊙) seeds were made (Loeb & Rasio 1994; Eisenstein & Loeb 1995) which have now developed into more complete scenarios (Begelman, Volonteri & Rees 2006; Regan & Haehnelt 2009; Shang, Bryan & Haiman 2010; Petri, Ferrara & Salvaterra 2012; Johnson et al. 2013). This channel invokes the formation of massive black hole seeds in environments where gas gravitational collapse proceeds at very sustained rates, |$\dot{M}_{\rm g} \gtrsim 0.1{\rm -}1\,\mathrm{M}_{\odot }$| yr−1, i.e. about 100 times larger than for standard metal-free star formation; these objects are often dubbed as ‘direct collapse black holes’ (DCBH) to distinguish them from the smaller seeds of stellar origin discussed above. Where are these environments to be found? So far, the most promising candidates are dark matter haloes with virial temperature Tvir ≳ 104 K. In these haloes the primordial gas radiatively cools via collisional excitation of the hydrogen 1s → 2p transition followed by a Lyα photon emission. Given the strong temperature sensitivity of such process, the gas collapses almost isothermally, 1 + dln T/dln ρ ≡ γ ≈ 1, thermostating the temperature at T ≈ 8000 K. Under these conditions, gas fragmentation into subclumps is almost completely inhibited (Schneider et al. 2002; Omukai et al. 2005; Omukai, Schneider & Haiman 2008; Cazaux & Spaans 2009) and collapse proceeds to very high densities unimpeded.
Even this scenario is not free from concerns. In fact, it requires that a sufficiently strong Lyman–Werner UV radiation field is present to prevent H2 molecule formation and the subsequent rapid cooling. Similar enhanced cooling, leading to fragmentation of the gas, can also be produced by a non-negligible heavy element abundance; however, it is not clear if relatively large (2–3σ density fluctuations) unpolluted haloes can form.
As an alternative route to form a massive seed, Mayer et al. (2010) and Bonoli, Mayer & Callegari (2012) [but also see similar ideas put forward by Begelman, Rossi & Armitage (2008), Begelman (2010) and Ball (2012) discussing the evolution of ‘quasi-stars’] noted that merger-driven gas inflows produce an unstable, massive nuclear gas disc. Accretion from this disc feeds a central core, which according to these studies might grow up to 108 M⊙ in a very short time (≲ 105 yr). As this central core becomes Jeans unstable, it might lead to the direct formation of an SMBH even for a solar metallicity gas. Whether the extremely high accretion rates |$\dot{M} \gtrsim 10^4\,\mathrm{M}_{\odot }$| yr−1 required can be sustained is a question that needs more scrutiny. Although attractive, we show in the following that this scenario might encounter a number of difficulties that possibly make it untenable.
NUCLEAR DISc PROPERTIES
The smoothed particle hydrodynamics simulation of Mayer et al. (2010) follows the evolution of the merger of two high-redshift, still well-formed, disc galaxies embedded in a dark matter halo of mass M = 1012 M⊙. As a result of the merger a nuclear, self-gravitating disc of radius rd ≈ 40 pc and mass Md = 2 × 109 M⊙ forms. The disc gas is highly turbulent, with a velocity dispersion σ ≈ 100 km s−1; the turbulent energy is ultimately drained from the gravitational energy of the system driving the collision first, and inducing non-axisymmetric instabilities and spiral arms later on. The disc orbital period at 20 pc is 5 × 104 yr.
The simulation shows that the disc gas efficiently loses angular momentum and is transported towards the centre with astonishingly high rates, |$\dot{M} > 10^4\,\mathrm{M}_{\odot }$| yr−1, where it accumulates in a pc-sized, roughly spherical structure (the core), which therefore grows to 13 per cent of the total disc mass, 2.6 × 108 M⊙, in ≃ 0.1 Myr. Although the simulation was stopped at that time, Mayer et al. (2010) suggested that this core structure is likely to evolve into a central black hole surrounded by an accreting envelope, i.e. a quasi-star as described by Begelman et al. (2008). This guess is essentially based on the fact that the central core temperature, Tc ≈ 107 K, is too high to prevent any fragmentation and subsequent star formation in the gas on its way to the newly formed compact object.
A similar result is obtained considering a disc-like accreting flow. In this case |$\dot{M} = 3\pi \nu \Sigma$|, where |$\nu = \alpha c_{\rm s} H = \alpha c_{\rm s}^3 /\pi G \Sigma$| is the turbulent viscosity for a thin disc, H the disc scaleheight and Σ the disc surface density. We find |$\dot{M} = 3\alpha (c_{\rm s}^3/G) \approx 10^3 (T/10^7\, {\rm K})^{3/2}$| M⊙ yr−1 for the usually assumed value α = 0.1.
HOT DIScS
The DCBH scenario described by Mayer et al. (2010) relies on a very strong assumption regarding the temperature evolution of the gas in the disc and central core. In fact, the authors adopted an equation of state (EOS) based on the work of Klessen et al. (2007), who studied the interstellar medium in starburst galaxies. According to such results, an EOS T ∝ ργ − 1, with γ = 1.1–1.4 was assumed. The precise value of the adiabatic index depends on the gas density, and it was set softer by Mayer et al. (2010) in the densest regions (as, e.g., in the central core). This EOS embeds both the heat input from supernovae and the energy losses via radiative processes. Both processes were not explicitly modelled in the nuclear disc/core.
Analytical estimates
Are such thermodynamical properties of the disc gas consistent with a more realistic energy equation and, in particular, with gas cooling?
Numerical solutions
The gas cools more rapidly in the inner disc regions where the density is higher; at the same time it accretes on to the central core at a rate set by the temperature at the r0 boundary (|$\dot{M} \propto c_{\rm s}^3$|). The build-up of the central core to masses larger than the Jeans mass, MJ, leading to the final collapse to a black hole seed is however hampered by two facts. First, the core growth becomes slower as the disc gas progressively cools. Secondly, and at the same time, the inner regions of the disc become gravitationally unstable and fragment. Let us analyse these two occurrences in more detail.
The time evolution of the nuclear disc temperature as a function of the disk radius, r, obtained from the numerical solution of equation (13) is shown in Fig. 1. From there we see that in <10 yr, the central regions of the disc, within r = 5 pc, have already cooled down to ≲104 K. Due to the decreasing density of the more external regions, these remain hot for a longer time; however, after ≈103 yr the entire disk has cooled down.

Time evolution of the nuclear disc temperature as a function of the disc radius, as indicated by the colour bar.
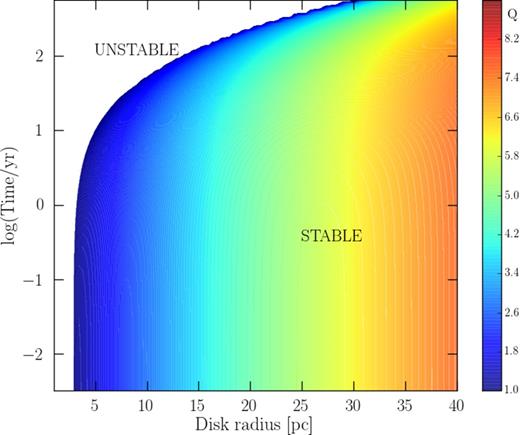
Time evolution of the nuclear disc Toomre Q parameter, as shown by the colour bar. The white areas correspond to gravitationally unstable (Q < 1) regions.
In spite of the low Q values, the role of fragmentation in quenching the accretion flow on to the core is probably subdominant. The reason is that fragmentation occurs in the free-fall time-scale. At r = r0, we find that tff = 161 yr. Such time-scale is much longer than the cooling time-scale, tc = 0.37 yr, i.e. the gas cools well before the disc fragments. Stated differently, it is the energy loss by radiation that quenches |$\dot{M}$| rather than fragmentation which appears only at a later evolutionary stage, when the gas already cooled down.
The challenge for the formation of the black hole seed as envisaged by Mayer et al. (2010) lies in forming a sufficiently massive, Jeans-unstable central core before accretion is quenched by gas cooling. Fig. 3 shows that this is extremely difficult. The central core grows rapidly as it is fed by a very high initial accretion rate (|$\dot{M} = 1{\rm -}2\times 10^3\,\mathrm{M}_{\odot }$| yr−1) and reaches a mass of about ≳100 M⊙ after about four months. Up to that point the core is still gravitationally stable, as MJ is approximately three orders of magnitude larger. However, shortly after this phase, fast gas cooling induces a sudden drop both of |$\dot{M}$| and MJ. The implication is that the core stops growing and starts to collapse. The evolution of a cold (T ≲ 100 K), collapsing, metal-enriched cloud has been subject to extensive studies in the recent years (Schneider et al. 2006; Bromm & Yoshida 2011 and references therein). All studies concur that the endpoint of the evolution is a large number of subsolar mass clumps. As suggested by Omukai et al. (2008), such low-mass clumps might eventually result in a dense cluster of low- and intermediate-mass stars.
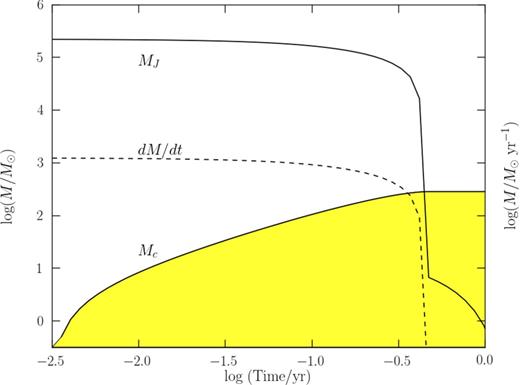
Time evolution of the central core mass, Mc, Jeans mass, MJ, and accretion rate dM/dt as indicated by the labels.
The above arguments are similar (albeit relative to larger scales) to those given by Levin (2007) and Goodman (2003), who suggested that discs in active galactic nuclei cool and fragment into stellar discs on scales much smaller than a parsec. The rapid cooling of the disc on scales of tens of pc could have consequences for gas accretion on to an SMBH already present in the galactic centre. Indeed, several studies make the assumption that accretion at the resolution limit of the simulation translates into accretion on to the central SMBH. Dotti et al. (2007) and Maio et al. (2013) ran a set of simulations including gas cooling and found that the accretion at the resolution limit (1 pc) was not significantly affected (the accretion rate would be, in any case, limited to ≲0.01 M⊙ yr−1), though this result may depend upon the details of fragmentation versus star formation.
In conclusion, in the merger+nuclear disc scenario as proposed by Mayer et al. (2010), the formation of black hole seeds as massive as 106–108 M⊙ appears problematic.
COLD DIScS
As a final possibility, we explore the case in which the disc is formed in a cold, rather than hot, state. The collapse would initially induce bulk motions and turbulence (as indeed observed in the simulations). The initial velocity dispersion of the gas is |$\sigma = v_c/\sqrt{3} =86\,{\rm {km\,s^{-1}}}$|, where vc = 150 km s−1 is the virial velocity of the 1012 M⊙ host halo at z = 7. As the gas pressure is dominated by turbulence, we can estimate the infall rate from equation (1) by substituting cs with σ. This gives a much lower accretion rate, ∼200 M⊙ yr−1.
CONCLUSIONS
The large accretion rates required to form a massive black hole by preventing fragmentation of a metal-enriched gas require that either the disc is heated at temperatures ≈107 K or that the disk can be initially set up in a cold and highly turbulent state. Both hypotheses are prone to serious problems. In the first case, the thermal energy is carried away very rapidly by cooling radiation, even considering the large optical depth of the disc. In addition, the requirements in terms of either supernova or gravitational energy to sustain such disc thermal budget are truly enormous and almost not plausible. We have shown that, under realistic thermodynamic conditions, the disc rapidly (≲1 yr) cools, the accretion rate drops and the central core can grow only to ≈100 M⊙. Previous studies of the evolution of a cold (T ≲ 100 K), collapsing, metal-enriched core have convincingly demonstrated that the final result is a large number of subsolar mass clumps that might instead eventually end up in a dense cluster of low- and intermediate-mass stars. To aggravate the situation, most of the disc becomes gravitationally unstable in ≈100 yr, further quenching the accretion. If instead the disc is born cold and turbulent, high accretion rates can be maintained only as long as turbulence can be supported. However, we find that turbulent energy is dissipated on a time-scale much shorter than the disc crossing time, thus almost completely suppressing the initially large accretion rate on to the core. These conclusions lead us to question the formation of the very hot and dense core leading to DCBH seeds, as found in the simulation of Mayer et al. (2010).
Observationally, the existence of cold discs is supported by the detection of molecular emission in the centre of Ultra Luminous Infrared Galaxies (Sanders & Mirabel 1996; Scoville, Yun & Bryant 1997; Downes & Solomon 1998; Bryant & Scoville 1999; Tacconi et al. 1999; Downes & Eckart 2007; Greve et al. 2009). The observations reveal molecular and dust disc-like structures with masses 109 − 10 M⊙ within a few tens or hundreds of parsecs from the galaxy centre (see e.g. Downes & Eckart 2007). On other hand, there is no compelling evidence for (but also against) the presence of a hot component. We have to note however that the hot-disc phase is extremely short,4 so that the probability to detect it is correspondingly low.
We suggest that the disagreement arises from the fact that either (a) the thermal structure of the disc is not properly described by the imposed polytropic EOS (radiative cooling is not included in their refined simulations) or (b) turbulence dissipation is largely underestimated. We therefore recommend that future numerical work should aim at implementing a proper treatment of the energy equation including cooling processes along with adaptive mesh refinement methods to catch the physics of the inner pc at high spatial resolution.
We acknowledge useful discussions with M. Dotti and L. Mayer.
At Z = Z⊙ cooling due to metal line emission is actually 2.5 times higher than free–free; our argument is then a conservative, valid independently of gas metallicity.
Appropriate for a standard Salpeter initial mass function extending in the mass range 0.1–100 M⊙.
Hopkins (2013) notices that in turbulent discs fragmentation can occur also for Q > 1. This is due to the broad spectrum of stochastic density fluctuations that can produce rare but extremely high-density local mass concentrations that will easily collapse.
In the original Mayer et al. (2010) simulation, the hot phases last only for a few ×104 yr, a duration decreased to ∼103 yr if cooling is considered.



