-
PDF
- Split View
-
Views
-
Cite
Cite
Angela Occhiogrosso, Serena Viti, Nadia Balucani, An improved chemical scheme for the reactions of atomic oxygen and simple unsaturated hydrocarbons – implications for star-forming regions, Monthly Notices of the Royal Astronomical Society, Volume 432, Issue 4, 11 July 2013, Pages 3423–3430, https://doi.org/10.1093/mnras/stt694
Close - Share Icon Share
Abstract
Recent laboratory experiments have demonstrated that even though contribution from other reaction channels cannot be neglected, unsaturated hydrocarbons easily break their multiple C–C bonds to form CO after their interactions with atomic oxygen. Here, we present an upgraded chemical modelling including a revision of the reactions between oxygen atoms and small unsaturated hydrocarbons for different astrochemical environments. The first conclusion is that towards hot cores/corinos atomic oxygen easily degrades unsaturated hydrocarbons directly to CO or to its precursor species (such as HCCO or HCO) and destroys the double or triple bond of alkenes and alkynes. Therefore, environments rich in atomic oxygen at a relatively high temperature are not expected to be rich in large unsaturated hydrocarbons or polycyclic aromatic hydrocarbons. In contrast, in O-poor and C-rich objects, hydrocarbon growth can occur to a large extent. In addition, new radical species, namely ketyl and vinoxy radicals, generated from other reaction channels can influence the abundances of hydrocarbons towards hot cores. We, therefore, suggest that they should be included in the available databases. Hydrocarbon column densities are calculated in the 1013–1015 cm−2 range, in good agreement with their observed values, despite the small number of data currently published in the literature.
INTRODUCTION
The interstellar medium (ISM) is extremely heterogeneous with a broad range of temperatures, densities and extinctions (Snow & Bierbaum 2008). As a consequence, a wide variety of chemical processes can occur. Oxygen is an important player in the ISM chemistry because it is the most abundant element after hydrogen and helium. Interstellar oxygen can be found in different forms and compounds, such as neutral or ionized gas, in the water of icy mantles or even in refractory materials. Its gas-phase abundances in the diffuse medium are well known (Meyer 1997), while the oxygen chemistry in denser environments seems to be poorly understood due to observational constraints (Jensen, Rachford & Snow 2005). On the other hand, oxygen chemistry has been widely investigated towards extragalactic and Galactic environments: in line with the fact that the C/O ratio determines the kind of reactions taking place in a specific region of ISM (Tsuji1973). Agúndez & Cernicharo (2006), looking at the circumstellar shells of IRC +10216, observed that carbon is locked either as CO or other O-bearing species when C/O < 1, while a higher concentration of reduced C-bearing species is present when C/O > 1. The latter condition leads to an increase in the growth of unsaturated hydrocarbons. This has been extensively confirmed by modelling and observations, and in particular Woods et al. (2012) found a large presence of unsaturated hydrocarbons, such as acetylene, by computing the physical conditions around carbon-rich asymptotic giant branch stars at subsolar metallicities.
Unsaturated hydrocarbons are organic molecules characterized by double or triple covalent bonds between adjacent carbon atoms; presently, there is no generally accepted explanation of their formation mechanisms but, as mentioned above, their abundances seem to be inversely correlated to the availability of atomic oxygen (Fortney 2012). Their most likely reactions start with the addition of atomic and radical species to their multiple bonds. In most cases, the elimination of a hydrogen atom or of a group follows, leading to more complex compounds (see, for instance, the cases of the reactions C + C2H2, C2 + C2H2, CN + C2H2; Huang et al. 2000; Kaiser 2002; Leonori et al. 2008a,b, 2010; Kaiser et al. 2003). Recent experiments in the gas phase (Capozza et al. 2004; Fu et al. 2012a,b; Leonori et al. 2012) suggest that the C–C bond breaking channel with the formation of CO is an important reaction channel for the reactions O + C2H2 and O + C2H4, while it is by far the dominant loss path for the reaction O + CH2CCH2 (allene). The fact that the reactions of atomic oxygen with unsaturated hydrocarbons lead in one step to CO can have a pivotal role in estimating the CO abundances both in the gas phase and on grain surfaces. Carbon monoxide is in turn a key species for the synthesis of organic complex molecules on grain surfaces since it can easily hydrogenate to methanol as experimentally demonstrated by Modica & Palumbo (2010). Another important aspect regarding these small hydrocarbons is their loss paths to form CH2. The latter molecular radical is indeed known to be a potential precursor of polycyclic aromatic hydrocarbons (PAHs) and many studies have been performed to stress several implications due to the presence of these aromatic hydrocarbons on the dust ( Salama 2008; Verstraete 2011); on the other hand, small unsaturated hydrocarbons are the building blocks of polyynes (organic compounds with alternating C–C single and triple bonds) and cumulenes (hydrocarbons with three or more consecutive C–C double bonds) that are also known as starting points for the synthesis of PAHs.
In the present study, we focus on the reactions between O atoms and small unsaturated hydrocarbons, namely acetylene, ethylene, methylacetylene and allene, under ISM conditions. In particular, we propose a revised chemical scheme (compared to those included in the available databases) where our reaction rates are based on new experimental branching ratios (BRs) for the different reaction channels (Capozza et al. 2004; Fu et al. 2012a,b; Leonori et al. 2012). In order to assess the effects of the recent laboratory data on the hydrocarbon abundances across different astrophysical environments, we model four typical astrochemical regions and we compare our theoretical results with the observations. The paper is organized as follows: Section 2 describes the laboratory technique used and the revised chemistry we inserted in our model; Section 3 focuses on the modelling of four different astrochemical environments; results are discussed in Section 4 and our conclusions are summarized in Section 5.
THE REACTIONS OF ATOMIC OXYGEN WITH SMALL UNSATURATED HYDROCARBONS
The following gas-phase neutral–neutral reactions have been experimentally investigated at the University of Perugia by means of the crossed molecular beam technique with mass spectrometric detection:
O + C2H4 → products
O + C2H2 → products
O + CH3CCH → products
O + CH2CCH2 → products.
In particular, the reaction mechanisms, the nature of the primary products of the different competing channels and their BRs have been determined (Capozza et al. 2004; Fu et al. 2012a,b; Leonori et al. 2012). From the analysis of the measured product's angular and velocity distributions, the product BRs are evaluated (for the detailed procedure see Balucani et al. 2006; Casavecchia et al. 2009). To derive the rate for each reaction channel, we consider the global rate constants for O + C2H2, O + C2H4, O + CH3CCH and O + CH2CCH2 scaled by the experimental BRs (see Tables 1 and 2). For reactions (i) and (ii), the rate coefficients and temperature dependence are those recommended by Baulch et al. (2005) in the range 200–2500 K and 220–2000 K for the two reactive systems, respectively. For reactions (iii) and (iv), we have considered the rate constants and temperature dependence recommended by Cvetanovic (1987) in the ranges 290–1300 K and 290–500 K, respectively. The temperatures of interest in interstellar objects are lower than those for which the temperature dependences have been determined. Therefore, we have extrapolated the trends down to 10 K, but this is an approximation and important deviations are possible.
Rate constants (at 200 K, typical of a hot core) for the different competing reaction channels for ethylene and acetylene with oxygen atoms. The last column contains the formulae [taken from National Institute of Standards & Technology (NIST) database] adopted in order to evaluate the rate constants in column 3.
| Reaction . | BRs (per cent) . | k (cm3 mol−1 s−1) . | k (T)let (cm3 mol−1 s−1) . |
|---|---|---|---|
| O + C2H2 → HCCO + H | 79 | 9.9 × 10−15 | |
| O + C2H2 → CH2 + CO | 21 | 2.6 × 10−15 | 1.89 × 10−12 (T/298)2.10 e−6535/RT |
| O + C2H2 → C2H + OH | 0 | 0 | |
| O + C2H4 → CH3 + HCO | 34 | 1.0 × 10−13 | |
| O + C2H4 → CH2CHO + H | 30 | 9.0 × 10−14 | |
| O + C2H4 → H2CO + CH2 | 20 | 6.0 × 10−14 | |
| 1.01 × 10−12(T/298)1.88 e−765/RT | |||
| O + C2H4 → CH2CO + H2 | 13 | 3.9 × 10−14 | |
| O + C2H4 → CH3CO + H | 3 | 9.0 × 10−15 | |
| O + C2H4 → C2H3 + OH | 0 | 0 |
| Reaction . | BRs (per cent) . | k (cm3 mol−1 s−1) . | k (T)let (cm3 mol−1 s−1) . |
|---|---|---|---|
| O + C2H2 → HCCO + H | 79 | 9.9 × 10−15 | |
| O + C2H2 → CH2 + CO | 21 | 2.6 × 10−15 | 1.89 × 10−12 (T/298)2.10 e−6535/RT |
| O + C2H2 → C2H + OH | 0 | 0 | |
| O + C2H4 → CH3 + HCO | 34 | 1.0 × 10−13 | |
| O + C2H4 → CH2CHO + H | 30 | 9.0 × 10−14 | |
| O + C2H4 → H2CO + CH2 | 20 | 6.0 × 10−14 | |
| 1.01 × 10−12(T/298)1.88 e−765/RT | |||
| O + C2H4 → CH2CO + H2 | 13 | 3.9 × 10−14 | |
| O + C2H4 → CH3CO + H | 3 | 9.0 × 10−15 | |
| O + C2H4 → C2H3 + OH | 0 | 0 |
Rate constants (at 200 K, typical of a hot core) for the different competing reaction channels for ethylene and acetylene with oxygen atoms. The last column contains the formulae [taken from National Institute of Standards & Technology (NIST) database] adopted in order to evaluate the rate constants in column 3.
| Reaction . | BRs (per cent) . | k (cm3 mol−1 s−1) . | k (T)let (cm3 mol−1 s−1) . |
|---|---|---|---|
| O + C2H2 → HCCO + H | 79 | 9.9 × 10−15 | |
| O + C2H2 → CH2 + CO | 21 | 2.6 × 10−15 | 1.89 × 10−12 (T/298)2.10 e−6535/RT |
| O + C2H2 → C2H + OH | 0 | 0 | |
| O + C2H4 → CH3 + HCO | 34 | 1.0 × 10−13 | |
| O + C2H4 → CH2CHO + H | 30 | 9.0 × 10−14 | |
| O + C2H4 → H2CO + CH2 | 20 | 6.0 × 10−14 | |
| 1.01 × 10−12(T/298)1.88 e−765/RT | |||
| O + C2H4 → CH2CO + H2 | 13 | 3.9 × 10−14 | |
| O + C2H4 → CH3CO + H | 3 | 9.0 × 10−15 | |
| O + C2H4 → C2H3 + OH | 0 | 0 |
| Reaction . | BRs (per cent) . | k (cm3 mol−1 s−1) . | k (T)let (cm3 mol−1 s−1) . |
|---|---|---|---|
| O + C2H2 → HCCO + H | 79 | 9.9 × 10−15 | |
| O + C2H2 → CH2 + CO | 21 | 2.6 × 10−15 | 1.89 × 10−12 (T/298)2.10 e−6535/RT |
| O + C2H2 → C2H + OH | 0 | 0 | |
| O + C2H4 → CH3 + HCO | 34 | 1.0 × 10−13 | |
| O + C2H4 → CH2CHO + H | 30 | 9.0 × 10−14 | |
| O + C2H4 → H2CO + CH2 | 20 | 6.0 × 10−14 | |
| 1.01 × 10−12(T/298)1.88 e−765/RT | |||
| O + C2H4 → CH2CO + H2 | 13 | 3.9 × 10−14 | |
| O + C2H4 → CH3CO + H | 3 | 9.0 × 10−15 | |
| O + C2H4 → C2H3 + OH | 0 | 0 |
Rate constants (at 200 K, typical of a hot core) for the different competing reaction channels. The last column contains the formulae (taken from NIST database) adopted in order to evaluate the rate constants in column 3.
| Reaction . | BRs (per cent) . | k (cm3 mol−1 s−1) . | k (T)let (cm3 mol−1 s−1) . |
|---|---|---|---|
| O + CH3CCH → C2H4 + CO | 68.0 | 5.2 × 10−13 | |
| O + CH3CCH → C2H3 + HCO | 10.0 | 7.7 × 10−14 | |
| O + CH3CCH → C2H2 + H2CO | 10.0 | 7.7 × 10−14 | 2.18 × 10−11 e−831/RT |
| O + CH3CCH → CH3CCO + H | 5.5 | 4.3 × 10−14 | |
| O + CH3CCH → CH3 + HCCO | 0.4 | 3.1 × 10−15 | |
| O + CH2CCH2 → C2H4 + CO | 81.5 | 9.8 × 10−13 | |
| O + CH2CCH2 → C2H2 + H2CO | 9.6 | 1.1 × 10−13 | |
| O + CH2CCH2 → C2H3 + HCO | 7.0 | 8.4 × 10−14 | 2.82 × 10−11 e−7732/RT |
| O + CH2CCH2 → CH2CCHO + H | 1.6 | 1.9 × 10−14 | |
| O + CH2CCH2 → CH2CO + CH2 | 0.3 | 3.6 × 10−15 |
| Reaction . | BRs (per cent) . | k (cm3 mol−1 s−1) . | k (T)let (cm3 mol−1 s−1) . |
|---|---|---|---|
| O + CH3CCH → C2H4 + CO | 68.0 | 5.2 × 10−13 | |
| O + CH3CCH → C2H3 + HCO | 10.0 | 7.7 × 10−14 | |
| O + CH3CCH → C2H2 + H2CO | 10.0 | 7.7 × 10−14 | 2.18 × 10−11 e−831/RT |
| O + CH3CCH → CH3CCO + H | 5.5 | 4.3 × 10−14 | |
| O + CH3CCH → CH3 + HCCO | 0.4 | 3.1 × 10−15 | |
| O + CH2CCH2 → C2H4 + CO | 81.5 | 9.8 × 10−13 | |
| O + CH2CCH2 → C2H2 + H2CO | 9.6 | 1.1 × 10−13 | |
| O + CH2CCH2 → C2H3 + HCO | 7.0 | 8.4 × 10−14 | 2.82 × 10−11 e−7732/RT |
| O + CH2CCH2 → CH2CCHO + H | 1.6 | 1.9 × 10−14 | |
| O + CH2CCH2 → CH2CO + CH2 | 0.3 | 3.6 × 10−15 |
Rate constants (at 200 K, typical of a hot core) for the different competing reaction channels. The last column contains the formulae (taken from NIST database) adopted in order to evaluate the rate constants in column 3.
| Reaction . | BRs (per cent) . | k (cm3 mol−1 s−1) . | k (T)let (cm3 mol−1 s−1) . |
|---|---|---|---|
| O + CH3CCH → C2H4 + CO | 68.0 | 5.2 × 10−13 | |
| O + CH3CCH → C2H3 + HCO | 10.0 | 7.7 × 10−14 | |
| O + CH3CCH → C2H2 + H2CO | 10.0 | 7.7 × 10−14 | 2.18 × 10−11 e−831/RT |
| O + CH3CCH → CH3CCO + H | 5.5 | 4.3 × 10−14 | |
| O + CH3CCH → CH3 + HCCO | 0.4 | 3.1 × 10−15 | |
| O + CH2CCH2 → C2H4 + CO | 81.5 | 9.8 × 10−13 | |
| O + CH2CCH2 → C2H2 + H2CO | 9.6 | 1.1 × 10−13 | |
| O + CH2CCH2 → C2H3 + HCO | 7.0 | 8.4 × 10−14 | 2.82 × 10−11 e−7732/RT |
| O + CH2CCH2 → CH2CCHO + H | 1.6 | 1.9 × 10−14 | |
| O + CH2CCH2 → CH2CO + CH2 | 0.3 | 3.6 × 10−15 |
| Reaction . | BRs (per cent) . | k (cm3 mol−1 s−1) . | k (T)let (cm3 mol−1 s−1) . |
|---|---|---|---|
| O + CH3CCH → C2H4 + CO | 68.0 | 5.2 × 10−13 | |
| O + CH3CCH → C2H3 + HCO | 10.0 | 7.7 × 10−14 | |
| O + CH3CCH → C2H2 + H2CO | 10.0 | 7.7 × 10−14 | 2.18 × 10−11 e−831/RT |
| O + CH3CCH → CH3CCO + H | 5.5 | 4.3 × 10−14 | |
| O + CH3CCH → CH3 + HCCO | 0.4 | 3.1 × 10−15 | |
| O + CH2CCH2 → C2H4 + CO | 81.5 | 9.8 × 10−13 | |
| O + CH2CCH2 → C2H2 + H2CO | 9.6 | 1.1 × 10−13 | |
| O + CH2CCH2 → C2H3 + HCO | 7.0 | 8.4 × 10−14 | 2.82 × 10−11 e−7732/RT |
| O + CH2CCH2 → CH2CCHO + H | 1.6 | 1.9 × 10−14 | |
| O + CH2CCH2 → CH2CO + CH2 | 0.3 | 3.6 × 10−15 |
The oxygen chemistry with hydrocarbons based on the new laboratory data was inserted in the UCL_CHEM chemical model. UCL_CHEM simulates the formation of a pre-stellar core (Phase I) and its subsequent evolution once a star is born (Phase II). During Phase I gas-grain interactions occur due to the freeze-out of atoms and molecules on the grain surfaces when temperatures drop down to 10 K. UCL_CHEM accounts for the chemistry occurring in the gas phase as well as on the grain surfaces during the free-fall collapse of a diffuse cloud. Species can also sublimate due to both non-thermal (10 K) and thermal desorption (200–300 K) (Phase II). A more detailed description of the model can be found in the literature (Occhiogrosso et al. 2011). Besides new experimental values for the reactions listed above, the new part of the chemical network contains a new species, ketyl radical (HCCO), which is produced in the reaction O + C2H2. To date, HCCO has not been detected in the ISM, but its presence was already predicted in the past by Turner & Sears (1989) who provided an upper limit for the HCCO/H2CCO ratio. We also introduce the vinoxy radical (CH2CHO), produced in the reaction O + C2H4. Furthermore, in addition to methylacetylene, its isomer CH2CCH2 (allene or propadiene) is explicitly considered. We have used either laboratory data or the rate coefficients included in the Kinetic Database for Astrochemistry (KIDA) database (Wakelam et al. 2012) for the reactions that involve these two hydrocarbon species. This distinction is not present to date in the University of Manchester Institute of Science & Technology (UMIST) database (Woodall et al. 2007).1
We have investigated how the revised part of the chemical model affects the trends in the hydrocarbon fractional abundances (relative to hydrogen nuclei) at typical densities in the ISM (Fig. 1). Then, we have run a grid of models representing (i) a diffuse cloud, (ii) a translucent cloud, (iii) a dark core and (iv) a hot core. We will analyse the contribution to the hydrocarbon abundances from their primary products formed during their interactions with oxygen atoms. We will finally compare our theoretical hydrocarbon abundances with those from the observations in the cold and warm ISM environments, where these species have been detected.
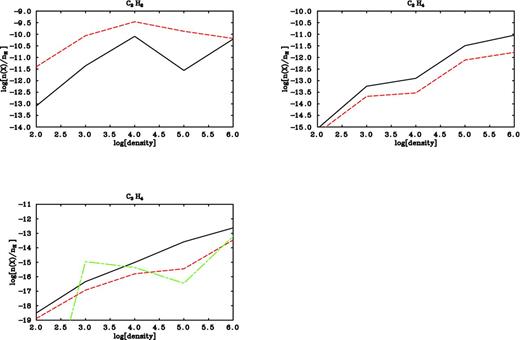
The fractional abundances (with respect to the total number of hydrogen nuclei) for selected species as a function of the density. In the top panels the solid lines represent the outputs with the same chemistry as in University of Manchester Institute of Science & Technology 2006 database and the dashed lines are the outputs after the updating; bottom panel shows the trends obtained from the revised chemistry suggested in the present study for CH3CCH (dashed line) and CH2CCH2 (dashed-dotted line), while the solid line is the trend for both C3H4 isomers resulted from the previous version of the model.
The reactions O + C2H2 and O + C2H4
Ethylene or ethene, C2H4, is the simplest alkene (alkenes are hydrocarbons with a carbon–carbon double bond), while acetylene or ethyne, C2H2, is the smallest alkyne (alkynes are hydrocarbons with a carbon–carbon triple bond). These two molecules have a similar structure, but their reactivity with oxygen atoms seems to be different (see Table 1). In particular, because of the larger number of atoms, ethylene leads to the formation of a greater number of products. According to experimental results (Capozza et al. 2004, Fu et al. 2012a,b) in both cases the channels leading to OH formation are inefficient; this was accounted for in the UMIST 2006 database (Woodall et al. 2007). The main channels of the reaction O + ethylene have been found to be those leading to CH3 + HCO (34 per cent) and CH2CHO + H (30 per cent) (Fu et al. 2012a,b). Regarding the reaction between acetylene and atomic oxygen, the dominant channel is the one leading to HCCO + H with a BR of 79 per cent while the channel leading to CH2 and CO accounts for the remaining 21 per cent (Capozza et al. 2004; Leonori, Balucani & Casavecchia 2013). We find that HCCO plays a pivotal role in the trends of C2H2 abundances (see Section 3 for more details). To date the ketyl radical has not been included in any database. We have also introduced a chemistry network for the loss processes of HCCO as shown in Table 3.
| Reaction . | k (cm3 mol−1 s−1) at 300 K . |
|---|---|
| aH + HCCO → CO + CH2 | 1.7 × 10−10 |
| aH2 + HCCO → products | 2.8 × 10−14 |
| aO + HCCO → CO + CO + H | 1.6 × 10−10 |
| Reaction . | k (cm3 mol−1 s−1) at 300 K . |
|---|---|
| aH + HCCO → CO + CH2 | 1.7 × 10−10 |
| aH2 + HCCO → products | 2.8 × 10−14 |
| aO + HCCO → CO + CO + H | 1.6 × 10−10 |
aBaulch et al. (2005) and references therein.
| Reaction . | k (cm3 mol−1 s−1) at 300 K . |
|---|---|
| aH + HCCO → CO + CH2 | 1.7 × 10−10 |
| aH2 + HCCO → products | 2.8 × 10−14 |
| aO + HCCO → CO + CO + H | 1.6 × 10−10 |
| Reaction . | k (cm3 mol−1 s−1) at 300 K . |
|---|---|
| aH + HCCO → CO + CH2 | 1.7 × 10−10 |
| aH2 + HCCO → products | 2.8 × 10−14 |
| aO + HCCO → CO + CO + H | 1.6 × 10−10 |
aBaulch et al. (2005) and references therein.
Paths of formation for C3H5, CH3CCH and CH2CCH2 based on data from KIDA database (Wakelam et al. 2012).
| Reaction . | α . | β . | γ . |
|---|---|---|---|
| H + CH3CHCH2 → C3H5 + H2 | 4.47 × 10−13 | 2.50 | 1250 |
| C2H5 + CH3CHCH2 → C3H5 + C2H6 | 2.01 × 10−11 | 0 | 0 |
| C2H3 + CH3CHCH2 → C3H5 + C2H4 | 1.72 × 10−15 | 3.50 | 2360 |
| CH2 + CH3CHCH2 → C3H5 + CH3 | 2.70 × 10−12 | 0 | 2660 |
| CH3 + C2H3 → C3H5 + H | 1.20 × 10−10 | 0 | 0 |
| CCH + CH3CHCH2 → C3H5 + C2H2 | 2.40 × 10−10 | 0 | 0 |
| C3H5+ + NH3 → CH3CCH + NH4+ | 9.00 × 10−10 | 0 | 0 |
| C2H6 + CH2CCH → CH3CCH + C2H5 | 5.83 × 10−14 | 3.30 | 9990 |
| CH4 + CH2CCH → CH3CCH + CH3 | 1.74 × 10−14 | 3.40 | 11700 |
| H2 + CH2CCH → CH3CCH + H | 1.42 × 10−13 | 2.38 | 9560 |
| C2H6 + CH2CCH → CH3CCH + C2H5 | 4.30 × 10−12 | 0 | −66 |
| C2H3 + C3H5 → CH3CCH + C2H4 | 4.00 × 10−12 | 0 | 0 |
| CH3 + C3H5 → CH3CCH + CH4 | 4.03 × 10−13 | 0.32 | −66 |
| CCH + CH3CHCH2 → CH3CCH + C2H3 | 2.00 × 10−11 | 0 | 0 |
| OH + C3H5 → CH3CCH + H2O | 1.00 × 10−11 | 0 | 0 |
| H + C3H5 → CH3CCH + H2 | 3.00 × 10−10 | 0 | 0 |
| aCH + C2H4 → CH3CCH + H | 7.80 × 10−11 | 0 | 0 |
| C3H5 + C3H5 → CH2CCH2 + CH3CHCH2 | 1.40 × 10−13 | 0 | −132 |
| C2H6 + CH2CCH → CH2CCH2 + C2H5 | 5.83 × 10−14 | 3.30 | 9990 |
| CH4 + CH2CCH → CH2CCH2 + CH3 | 1.74 × 10−14 | 3.40 | 11700 |
| H2 + CH2CCH → CH2CCH2 + H | 1.42 × 10−13 | 2.38 | 9560 |
| C2H6 + CH2CCH → CH2CCH2 + C2H5 | 1.60 × 10−12 | 0 | −66 |
| C2H3 + C3H5 → CH2CCH2 + C2H4 | 2.00 × 10−12 | 0 | 0 |
| CH3 + C3H5 → CH2CCH2 + CH4 | 4.03 × 10−13 | 0.32 | −66 |
| H + C3H5 → CH2CCH2 + H2 | 3.30 × 10−10 | 0 | 0 |
| aCH + C2H4 → CH2CCH2 + H | 3.12 × 10−10 | 0 | 0 |
| Reaction . | α . | β . | γ . |
|---|---|---|---|
| H + CH3CHCH2 → C3H5 + H2 | 4.47 × 10−13 | 2.50 | 1250 |
| C2H5 + CH3CHCH2 → C3H5 + C2H6 | 2.01 × 10−11 | 0 | 0 |
| C2H3 + CH3CHCH2 → C3H5 + C2H4 | 1.72 × 10−15 | 3.50 | 2360 |
| CH2 + CH3CHCH2 → C3H5 + CH3 | 2.70 × 10−12 | 0 | 2660 |
| CH3 + C2H3 → C3H5 + H | 1.20 × 10−10 | 0 | 0 |
| CCH + CH3CHCH2 → C3H5 + C2H2 | 2.40 × 10−10 | 0 | 0 |
| C3H5+ + NH3 → CH3CCH + NH4+ | 9.00 × 10−10 | 0 | 0 |
| C2H6 + CH2CCH → CH3CCH + C2H5 | 5.83 × 10−14 | 3.30 | 9990 |
| CH4 + CH2CCH → CH3CCH + CH3 | 1.74 × 10−14 | 3.40 | 11700 |
| H2 + CH2CCH → CH3CCH + H | 1.42 × 10−13 | 2.38 | 9560 |
| C2H6 + CH2CCH → CH3CCH + C2H5 | 4.30 × 10−12 | 0 | −66 |
| C2H3 + C3H5 → CH3CCH + C2H4 | 4.00 × 10−12 | 0 | 0 |
| CH3 + C3H5 → CH3CCH + CH4 | 4.03 × 10−13 | 0.32 | −66 |
| CCH + CH3CHCH2 → CH3CCH + C2H3 | 2.00 × 10−11 | 0 | 0 |
| OH + C3H5 → CH3CCH + H2O | 1.00 × 10−11 | 0 | 0 |
| H + C3H5 → CH3CCH + H2 | 3.00 × 10−10 | 0 | 0 |
| aCH + C2H4 → CH3CCH + H | 7.80 × 10−11 | 0 | 0 |
| C3H5 + C3H5 → CH2CCH2 + CH3CHCH2 | 1.40 × 10−13 | 0 | −132 |
| C2H6 + CH2CCH → CH2CCH2 + C2H5 | 5.83 × 10−14 | 3.30 | 9990 |
| CH4 + CH2CCH → CH2CCH2 + CH3 | 1.74 × 10−14 | 3.40 | 11700 |
| H2 + CH2CCH → CH2CCH2 + H | 1.42 × 10−13 | 2.38 | 9560 |
| C2H6 + CH2CCH → CH2CCH2 + C2H5 | 1.60 × 10−12 | 0 | −66 |
| C2H3 + C3H5 → CH2CCH2 + C2H4 | 2.00 × 10−12 | 0 | 0 |
| CH3 + C3H5 → CH2CCH2 + CH4 | 4.03 × 10−13 | 0.32 | −66 |
| H + C3H5 → CH2CCH2 + H2 | 3.30 × 10−10 | 0 | 0 |
| aCH + C2H4 → CH2CCH2 + H | 3.12 × 10−10 | 0 | 0 |
aThe α value is evaluated by the product between the ratio for each channel of reaction (Zhang et al. 2012) and the total rate constant of 3.9×10−10 cm3 mol−1 s−1.
Paths of formation for C3H5, CH3CCH and CH2CCH2 based on data from KIDA database (Wakelam et al. 2012).
| Reaction . | α . | β . | γ . |
|---|---|---|---|
| H + CH3CHCH2 → C3H5 + H2 | 4.47 × 10−13 | 2.50 | 1250 |
| C2H5 + CH3CHCH2 → C3H5 + C2H6 | 2.01 × 10−11 | 0 | 0 |
| C2H3 + CH3CHCH2 → C3H5 + C2H4 | 1.72 × 10−15 | 3.50 | 2360 |
| CH2 + CH3CHCH2 → C3H5 + CH3 | 2.70 × 10−12 | 0 | 2660 |
| CH3 + C2H3 → C3H5 + H | 1.20 × 10−10 | 0 | 0 |
| CCH + CH3CHCH2 → C3H5 + C2H2 | 2.40 × 10−10 | 0 | 0 |
| C3H5+ + NH3 → CH3CCH + NH4+ | 9.00 × 10−10 | 0 | 0 |
| C2H6 + CH2CCH → CH3CCH + C2H5 | 5.83 × 10−14 | 3.30 | 9990 |
| CH4 + CH2CCH → CH3CCH + CH3 | 1.74 × 10−14 | 3.40 | 11700 |
| H2 + CH2CCH → CH3CCH + H | 1.42 × 10−13 | 2.38 | 9560 |
| C2H6 + CH2CCH → CH3CCH + C2H5 | 4.30 × 10−12 | 0 | −66 |
| C2H3 + C3H5 → CH3CCH + C2H4 | 4.00 × 10−12 | 0 | 0 |
| CH3 + C3H5 → CH3CCH + CH4 | 4.03 × 10−13 | 0.32 | −66 |
| CCH + CH3CHCH2 → CH3CCH + C2H3 | 2.00 × 10−11 | 0 | 0 |
| OH + C3H5 → CH3CCH + H2O | 1.00 × 10−11 | 0 | 0 |
| H + C3H5 → CH3CCH + H2 | 3.00 × 10−10 | 0 | 0 |
| aCH + C2H4 → CH3CCH + H | 7.80 × 10−11 | 0 | 0 |
| C3H5 + C3H5 → CH2CCH2 + CH3CHCH2 | 1.40 × 10−13 | 0 | −132 |
| C2H6 + CH2CCH → CH2CCH2 + C2H5 | 5.83 × 10−14 | 3.30 | 9990 |
| CH4 + CH2CCH → CH2CCH2 + CH3 | 1.74 × 10−14 | 3.40 | 11700 |
| H2 + CH2CCH → CH2CCH2 + H | 1.42 × 10−13 | 2.38 | 9560 |
| C2H6 + CH2CCH → CH2CCH2 + C2H5 | 1.60 × 10−12 | 0 | −66 |
| C2H3 + C3H5 → CH2CCH2 + C2H4 | 2.00 × 10−12 | 0 | 0 |
| CH3 + C3H5 → CH2CCH2 + CH4 | 4.03 × 10−13 | 0.32 | −66 |
| H + C3H5 → CH2CCH2 + H2 | 3.30 × 10−10 | 0 | 0 |
| aCH + C2H4 → CH2CCH2 + H | 3.12 × 10−10 | 0 | 0 |
| Reaction . | α . | β . | γ . |
|---|---|---|---|
| H + CH3CHCH2 → C3H5 + H2 | 4.47 × 10−13 | 2.50 | 1250 |
| C2H5 + CH3CHCH2 → C3H5 + C2H6 | 2.01 × 10−11 | 0 | 0 |
| C2H3 + CH3CHCH2 → C3H5 + C2H4 | 1.72 × 10−15 | 3.50 | 2360 |
| CH2 + CH3CHCH2 → C3H5 + CH3 | 2.70 × 10−12 | 0 | 2660 |
| CH3 + C2H3 → C3H5 + H | 1.20 × 10−10 | 0 | 0 |
| CCH + CH3CHCH2 → C3H5 + C2H2 | 2.40 × 10−10 | 0 | 0 |
| C3H5+ + NH3 → CH3CCH + NH4+ | 9.00 × 10−10 | 0 | 0 |
| C2H6 + CH2CCH → CH3CCH + C2H5 | 5.83 × 10−14 | 3.30 | 9990 |
| CH4 + CH2CCH → CH3CCH + CH3 | 1.74 × 10−14 | 3.40 | 11700 |
| H2 + CH2CCH → CH3CCH + H | 1.42 × 10−13 | 2.38 | 9560 |
| C2H6 + CH2CCH → CH3CCH + C2H5 | 4.30 × 10−12 | 0 | −66 |
| C2H3 + C3H5 → CH3CCH + C2H4 | 4.00 × 10−12 | 0 | 0 |
| CH3 + C3H5 → CH3CCH + CH4 | 4.03 × 10−13 | 0.32 | −66 |
| CCH + CH3CHCH2 → CH3CCH + C2H3 | 2.00 × 10−11 | 0 | 0 |
| OH + C3H5 → CH3CCH + H2O | 1.00 × 10−11 | 0 | 0 |
| H + C3H5 → CH3CCH + H2 | 3.00 × 10−10 | 0 | 0 |
| aCH + C2H4 → CH3CCH + H | 7.80 × 10−11 | 0 | 0 |
| C3H5 + C3H5 → CH2CCH2 + CH3CHCH2 | 1.40 × 10−13 | 0 | −132 |
| C2H6 + CH2CCH → CH2CCH2 + C2H5 | 5.83 × 10−14 | 3.30 | 9990 |
| CH4 + CH2CCH → CH2CCH2 + CH3 | 1.74 × 10−14 | 3.40 | 11700 |
| H2 + CH2CCH → CH2CCH2 + H | 1.42 × 10−13 | 2.38 | 9560 |
| C2H6 + CH2CCH → CH2CCH2 + C2H5 | 1.60 × 10−12 | 0 | −66 |
| C2H3 + C3H5 → CH2CCH2 + C2H4 | 2.00 × 10−12 | 0 | 0 |
| CH3 + C3H5 → CH2CCH2 + CH4 | 4.03 × 10−13 | 0.32 | −66 |
| H + C3H5 → CH2CCH2 + H2 | 3.30 × 10−10 | 0 | 0 |
| aCH + C2H4 → CH2CCH2 + H | 3.12 × 10−10 | 0 | 0 |
aThe α value is evaluated by the product between the ratio for each channel of reaction (Zhang et al. 2012) and the total rate constant of 3.9×10−10 cm3 mol−1 s−1.
The reactions O + CH3CCH (methylacetylene) and O + CH2CCH2 (allene)
Since the experimental results by Leonori et al. (2012) and Balucani et al. (in preparation) have demonstrated that the reactions O + CH3CCH and O + CH2CCH2 are characterized by different BRs (and also their rate coefficients are different), we have separated the two isomeric species in our codes. The UMIST 2006 database (Woodall et al. 2007) does not distinguish between the two C3H4 isomers. Therefore, it is implicitly assumed that CH3CCH and CH2CCH2 are formed and destroyed in the same reactions and with the same efficiency. Such an assumption, however, is not warranted. For instance, it has been suggested that an important contribution to the formation of both isomers is the reaction between methylidyne radical (CH) and ethylene (Gosavi, Safarik & Strausz 1985; Wang & Huang 1998). Nevertheless, recent laboratory investigations (Zhang et al. 2012) have shown allene to be the main product with a ratio of 75–80 per cent. To account separately for CH3CCH and CH2CCH2 formation, we have inserted the main path rate coefficients as recommended by KIDA database (Wakelam et al. 2012) (see Table 4). In Table 2, the open channels for reactions (iii) and (iv) are reported with their relative yields, as experimentally determined (Leonori et al. 2012; Balucani et al., in preparation). We want to point out that, at this stage, we do not distinguish between the two C3H3O isomers, CH3CCO (for the case of methylacetylene) and CH2CCHO (for the case of allene); however, we plan to investigate their chemistry in a future work. In Table 2, the main dissimilarity is that, in the case of allene, the channel for the formation of CO dominates with a ratio of 81.5 per cent, while the BR of the reaction producing carbon monoxide from methylacetylene is only 68 per cent (Balucani et al., in preparation). The other channels contribute to a minor extent, especially in the case of the O + CH2CCH2 reaction.
CHEMICAL MODELLING
We investigated how the new reaction networks included in the model affect the hydrocarbon abundances by running simple models at typical densities for the ISM in the 102–106 cm−3 range; in particular, we simulate the case of an unphysical cloud at 10 K and constant density where we do not account for any freeze-out reaction during the collapse phase. We plot the fractional abundances obtained as outputs from these test models for C2H2, C2H4 and the two C3H4 isomers as a function of the density of the cloud at 5 × 105 yr (see Fig. 1). In order to highlight the changes in the hydrocarbon abundances, we run models with the same physical parameters as described above but including the same chemistry as in the UMIST 2006 database. In other words, the differences observed are only due to the new reaction scheme for reactions (i)–(iv) with all the other parameters kept constant. Fig. 1 shows a comparison between the hydrocarbon fractional abundances (with respect to the total number of hydrogen atoms) from the original version of the code (solid line) and the ones from the models containing the revised chemistry (dashed line). In the case of C3H4, the solid line refers to the output obtained from the UMIST 2006 database that does not distinguish between the two isomers, while the dashed line and the dotted line are the trends for CH3CCH and CH2CCH2, respectively, produced from the updated chemistry. In the absence of freeze-out, for each selected density value we observe a discrepancy between the hydrocarbon fractional abundances before and after the updating, with the exception of C2H2 at 106 cm−3. We emphasize that with this kind of comparison, we are only analyzing the effect of the new schemes on the hydrocarbon abundance prediction. We wish to stress that reactions (i)–(iv) are characterized by a certain activation energy and, therefore, their rate coefficients are very small at temperatures between 10 and 200 K. Nevertheless, they make a significant contribution in controlling the abundances of unsaturated hydrocarbons probably because of the large abundance of atomic oxygen.
In order to understand the real influence of oxygen in the hydrocarbon chemistry, we modelled four different astronomical regions: a diffuse cloud, a translucent cloud, a dark cloud and a hot core. The following section describes the models in more details.
Modelling of different astrochemical environments
Table 5 lists the physical parameters used for our modelling. For each astronomical source we run two models: we employ a rate file with the same chemistry as in the UMIST 2006 database and another one with the revised chemical network proposed in the present study.
List of the physical parameters for the case of a hot-core model: visual extinction (Av), density (nH), gas temperature (T) during Phase II, efficiency of the freeze-out (fr) during Phase I (the percentage of mantle CO given by the freeze-out parameter by the end of Phase I of the chemical model).
| . | Av (mag) . | nH (cm−3) . | T (K) . | fr (per cent) . |
|---|---|---|---|---|
| 1. Diffuse cloud | 0–1 | 1 × 102 | 100 | 0 |
| 2. Translucent cloud | 1–5 | 1 × 103 | 20 | 0 |
| 3. Dark core | 5–10 | 1 × 104 | 10 | ∼40 |
| 4. Hot core | ∼500 | 1 × 107 | 300 | ∼98 |
| . | Av (mag) . | nH (cm−3) . | T (K) . | fr (per cent) . |
|---|---|---|---|---|
| 1. Diffuse cloud | 0–1 | 1 × 102 | 100 | 0 |
| 2. Translucent cloud | 1–5 | 1 × 103 | 20 | 0 |
| 3. Dark core | 5–10 | 1 × 104 | 10 | ∼40 |
| 4. Hot core | ∼500 | 1 × 107 | 300 | ∼98 |
List of the physical parameters for the case of a hot-core model: visual extinction (Av), density (nH), gas temperature (T) during Phase II, efficiency of the freeze-out (fr) during Phase I (the percentage of mantle CO given by the freeze-out parameter by the end of Phase I of the chemical model).
| . | Av (mag) . | nH (cm−3) . | T (K) . | fr (per cent) . |
|---|---|---|---|---|
| 1. Diffuse cloud | 0–1 | 1 × 102 | 100 | 0 |
| 2. Translucent cloud | 1–5 | 1 × 103 | 20 | 0 |
| 3. Dark core | 5–10 | 1 × 104 | 10 | ∼40 |
| 4. Hot core | ∼500 | 1 × 107 | 300 | ∼98 |
| . | Av (mag) . | nH (cm−3) . | T (K) . | fr (per cent) . |
|---|---|---|---|---|
| 1. Diffuse cloud | 0–1 | 1 × 102 | 100 | 0 |
| 2. Translucent cloud | 1–5 | 1 × 103 | 20 | 0 |
| 3. Dark core | 5–10 | 1 × 104 | 10 | ∼40 |
| 4. Hot core | ∼500 | 1 × 107 | 300 | ∼98 |
We start by considering the case for a diffuse cloud (Model 1), a quite extended low density (102 cm−3) region permeated by the ultraviolet interstellar radiation field; temperatures go up to 100 K and the visual extinction is around 1 mag. Because of their relatively low-visual extinction(Av ∼ 1 mag) diffuse clouds are dominated by photodissociation reactions and there is no chemistry occurring on the grain surfaces.
As for the case of a diffuse cloud, atoms and molecules do not freeze-out on the dust for a translucent cloud (Model 2) either, an intermediate phase (in terms of physical conditions) between the diffuse and the dense medium (van Dishoeck 2000); the fact that they are called translucent is due to the presence of a bright star in their proximity that allows absorption lines to be observed. Translucent clouds are relatively cold regions (20–50 K) where densities can reach values up to 103 cm−3 although there is no evidence of a collapsing core inside these objects. Since translucent clouds can be penetrated by the radiation (their Av is between 1 and 5 mag), their chemistry is also affected by photoprocesses. Diffuse and translucent clouds are two examples of low-density interstellar regions.
We also explore the case for high-density sources, such as dark and hot cores, where a grain-surface chemistry is included in order to simulate the isothermal collapse phase during which atoms and molecules freeze on to the surfaces of dust and new species can be produced. This process is more efficient during the formation of a hot core (a very compact object characterized by densities ≥106 cm−3) (Model 4) than for the case of a dark core (Model 3) where densities increase only up to 104 cm−3; moreover, while for the case of a hot core, we need to model a second phase that describes all the heating effects that could induce molecules to thermally desorb (indeed temperatures rise up to 200–300 K), for a dark core we only account for the non-thermal desorption of species (for more details see Roberts et al. 2007) efficient already at 10 K.
RESULTS AND DISCUSSION
We discuss our results only for the case of a hot core (Model 4). Results obtained as outputs from models 1, 2, 3 show some differences in the abundances of the species involved. Nevertheless, we are not discussing those differences here since the resulting abundances are in all cases below the observational thresholds. Concerning the hot core model, in order to simulate the warm-up of icy mantles and the consequent sublimation of molecules from their surfaces, we allow a time-step desorption of species as described in Viti et al. (2004). Based on laboratory data obtained from temperature programmed desorption experiments, Viti et al. (2004) categorized a list of species along with their desorption profiles in various temperature bands. C2H2 and C2H4 were classified as intermediates between CO-like and H2O-like species. Intermediate molecules were found in the hydrogenated ice layer although they were also able to escape via monomolecular desorption because of their moderate interaction with water ice. Since the two C3H4 isomers are non-polar organic species (as well as C2H2 and C2H4), we assumed for them a similar behaviour to the one for the case of acetylene and ethylene; we therefore classified methylacetylene and allene as intermediate.
We analyse the outputs for the hydrocarbon abundances as well as the trends for the abundances of other species involved in the updated oxygen chemistry (see Fig. 2). In particular, we focus on small patterns such as CH2, CH3, HCO and H2CO that have been detected as products for all the hydrocarbon species considered. While it is difficult to determine the contribution of each reaction channel to the abundances of all hydrocarbons, UCL_CHEM provides us with an analysis of the percentage of destruction and formation pathways for any selected species and we can therefore draw some conclusions on the trends displayed in Fig. 2. For instance, CH2 is known as one of the reactants in the synthesis of hydrocarbons and its abundance is expected to decrease when hydrocarbons form; however, we observe a rise in the CH2 abundances where the trends for CH3CCH and CH2CCH2 show a peak. This behaviour could be explained in the light of the fact that HCCO drops to produce CH2 and this reaction is five orders of magnitude more efficient than the reaction between O and acetylene or methylacetylene to form ketyl radical. Another important observation concerns the decrease in the ethylene abundances in order to produce the two C3H4 isomers, meaning that the reverse reaction is more likely than the channel for the formation of CO. CH2CO is also produced by the reaction between O atoms and ethylene and as a consequence its abundances rise when the C2H4 profile drops just after 106 yr. The major contribution to the formation for CH3CCO is made by methylacetylene and, as a result, as soon as the latter species decreases, CH3CCO increases in abundance. Concerning all the other molecules, it is difficult to make predictions since they can be formed by numerous reactions, but we estimate a high fractional abundance for C2H3 and H2CO. This is in agreement with what we were expecting due to the fact that all hydrocarbons contribute to their formation.
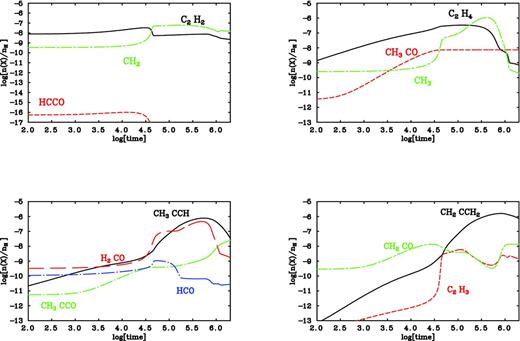
The fractional abundances (with respect to the total number of hydrogen nuclei) for selected species as a function of time.
Comparison between observational and theoretical column densities (in cm−2) for selected species. Starting from the left, the first column shows results from the original version of the code; in the second column, we report the molecular column densities calculated after our updating.
| Molecule . | UMIST 2006 . | Present work . | Observations . | Source . | References . |
|---|---|---|---|---|---|
| C2H2 | 2.70 × 1015 | 4.08 × 1014 | 5.50 × 1014 | SgrA | Lacy et al. (1989) |
| C2H4 | 1.93 × 1013 | 1.26 × 1014 | – | – | – |
| CH3CCH | 1.11 × 1015 | 6.18 × 1015 | 1.20 × 1015 | Orion-KL | Wang, Wouterloot & Wilson (1993) |
| CH2CCH2 | Not present | 1.78 × 1016 | – | – | – |
| CH2 | 2.09 × 1015 | 4.88 × 1014 | 6.60 × 1013 | Orion-KL | Hollis, Jewell & Lovas (1995) |
| CH3 | 2.70 × 1015 | 7.73 × 1013 | 8.00 × 1014 | SgrA | Feuchtgruber et al. (2000) |
| HCCO | Not present | 4.68 × 103 | – | – | – |
| CH2CO | 4.25 × 1014 | 2.55 × 1015 | 1.00 × 1014 | SgrB2 | Turner (1977) |
| HCO | 5.62 × 1012 | 5.13 × 1012 | 1.03 × 1012 | W3 | Snyder, Hollis & Ulich (1976) |
| H2CO | 6.55 × 1014 | 1.85 × 1014 | 8.32 × 1014 | Orion-KL | Wright, Plambeck & Wilner (1996) |
| CH3CO | Not present | 9.13 × 1014 | – | – | – |
| CH3CCO | Not present | 5.80 × 1015 | – | – | – |
| C2H3 | 5.44 × 1013 | 1.30 × 1013 | – | – | – |
| Molecule . | UMIST 2006 . | Present work . | Observations . | Source . | References . |
|---|---|---|---|---|---|
| C2H2 | 2.70 × 1015 | 4.08 × 1014 | 5.50 × 1014 | SgrA | Lacy et al. (1989) |
| C2H4 | 1.93 × 1013 | 1.26 × 1014 | – | – | – |
| CH3CCH | 1.11 × 1015 | 6.18 × 1015 | 1.20 × 1015 | Orion-KL | Wang, Wouterloot & Wilson (1993) |
| CH2CCH2 | Not present | 1.78 × 1016 | – | – | – |
| CH2 | 2.09 × 1015 | 4.88 × 1014 | 6.60 × 1013 | Orion-KL | Hollis, Jewell & Lovas (1995) |
| CH3 | 2.70 × 1015 | 7.73 × 1013 | 8.00 × 1014 | SgrA | Feuchtgruber et al. (2000) |
| HCCO | Not present | 4.68 × 103 | – | – | – |
| CH2CO | 4.25 × 1014 | 2.55 × 1015 | 1.00 × 1014 | SgrB2 | Turner (1977) |
| HCO | 5.62 × 1012 | 5.13 × 1012 | 1.03 × 1012 | W3 | Snyder, Hollis & Ulich (1976) |
| H2CO | 6.55 × 1014 | 1.85 × 1014 | 8.32 × 1014 | Orion-KL | Wright, Plambeck & Wilner (1996) |
| CH3CO | Not present | 9.13 × 1014 | – | – | – |
| CH3CCO | Not present | 5.80 × 1015 | – | – | – |
| C2H3 | 5.44 × 1013 | 1.30 × 1013 | – | – | – |
Comparison between observational and theoretical column densities (in cm−2) for selected species. Starting from the left, the first column shows results from the original version of the code; in the second column, we report the molecular column densities calculated after our updating.
| Molecule . | UMIST 2006 . | Present work . | Observations . | Source . | References . |
|---|---|---|---|---|---|
| C2H2 | 2.70 × 1015 | 4.08 × 1014 | 5.50 × 1014 | SgrA | Lacy et al. (1989) |
| C2H4 | 1.93 × 1013 | 1.26 × 1014 | – | – | – |
| CH3CCH | 1.11 × 1015 | 6.18 × 1015 | 1.20 × 1015 | Orion-KL | Wang, Wouterloot & Wilson (1993) |
| CH2CCH2 | Not present | 1.78 × 1016 | – | – | – |
| CH2 | 2.09 × 1015 | 4.88 × 1014 | 6.60 × 1013 | Orion-KL | Hollis, Jewell & Lovas (1995) |
| CH3 | 2.70 × 1015 | 7.73 × 1013 | 8.00 × 1014 | SgrA | Feuchtgruber et al. (2000) |
| HCCO | Not present | 4.68 × 103 | – | – | – |
| CH2CO | 4.25 × 1014 | 2.55 × 1015 | 1.00 × 1014 | SgrB2 | Turner (1977) |
| HCO | 5.62 × 1012 | 5.13 × 1012 | 1.03 × 1012 | W3 | Snyder, Hollis & Ulich (1976) |
| H2CO | 6.55 × 1014 | 1.85 × 1014 | 8.32 × 1014 | Orion-KL | Wright, Plambeck & Wilner (1996) |
| CH3CO | Not present | 9.13 × 1014 | – | – | – |
| CH3CCO | Not present | 5.80 × 1015 | – | – | – |
| C2H3 | 5.44 × 1013 | 1.30 × 1013 | – | – | – |
| Molecule . | UMIST 2006 . | Present work . | Observations . | Source . | References . |
|---|---|---|---|---|---|
| C2H2 | 2.70 × 1015 | 4.08 × 1014 | 5.50 × 1014 | SgrA | Lacy et al. (1989) |
| C2H4 | 1.93 × 1013 | 1.26 × 1014 | – | – | – |
| CH3CCH | 1.11 × 1015 | 6.18 × 1015 | 1.20 × 1015 | Orion-KL | Wang, Wouterloot & Wilson (1993) |
| CH2CCH2 | Not present | 1.78 × 1016 | – | – | – |
| CH2 | 2.09 × 1015 | 4.88 × 1014 | 6.60 × 1013 | Orion-KL | Hollis, Jewell & Lovas (1995) |
| CH3 | 2.70 × 1015 | 7.73 × 1013 | 8.00 × 1014 | SgrA | Feuchtgruber et al. (2000) |
| HCCO | Not present | 4.68 × 103 | – | – | – |
| CH2CO | 4.25 × 1014 | 2.55 × 1015 | 1.00 × 1014 | SgrB2 | Turner (1977) |
| HCO | 5.62 × 1012 | 5.13 × 1012 | 1.03 × 1012 | W3 | Snyder, Hollis & Ulich (1976) |
| H2CO | 6.55 × 1014 | 1.85 × 1014 | 8.32 × 1014 | Orion-KL | Wright, Plambeck & Wilner (1996) |
| CH3CO | Not present | 9.13 × 1014 | – | – | – |
| CH3CCO | Not present | 5.80 × 1015 | – | – | – |
| C2H3 | 5.44 × 1013 | 1.30 × 1013 | – | – | – |
Hydrocarbons have been found across different astrochemical environments, from planet atmospheres to dark clouds, in the Milky Way as well as towards other Galaxies (Pendleton 2004). One of the first hydrocarbon detections was performed by Ridgway et al. (1976), who observed CH4 and C2H2 towards the supergiant IRC + 10216, where a few years later Betz (1981) found C2H4 with a column density of 1016–1017 cm−2. Hydrocarbons were predicted to be abundant in the ISM but many of them were not observed at millimeter wavelengths because their symmetry forbids dipole rotational transitions. Some of the species listed in Table 6 have indeed not been detected towards hot cores yet, but since column densities for hydrocarbons are in the 1013–1015 cm−2 range we expect the presence of similar amounts for C2H4 and CH2CCH2. A comparison between our theoretical results and data taken from the observations highlights a general agreement within an order of magnitude; in particular, after our updates, we achieve a greater match with the observed column densities of C2H2 and CH2 than if we had used the chemistry in the UMIST 2006 database. Concerning the two C3H3O isomers, we only calculate an upper limit in their column densities since we do not account for a complete reaction network for their loss mechanisms. We would also like to stress that we have only qualitatively modelled a hot core without looking at a specific high-mass source therefore our theoretical column densities could be refined.
CONCLUSIONS
In this paper, we have presented how a more accurate chemical network representing the reactions of atomic oxygen with several unsaturated hydrocarbons affects the abundances of simple organic species in ISM. We mostly focus on the modelling of hot ISM regions where these variations were found to be more evident; however, colder regions such as diffuse and translucent clouds or a dark core have also been investigated. The first conclusion is that towards hot cores/corinos atomic oxygen easily degrades unsaturated hydrocarbons directly to CO or to its precursor species (such as HCCO or HCO) and destroys the double or triple bond of alkenes and alkynes. Therefore, environments rich in atomic oxygen at a relatively high temperature are not expected to be characterized by the presence of large unsaturated hydrocarbons or PAHs. In contrast, in O-poor and C-rich objects, hydrocarbon growth can occur to a large extent. In colder objects, the effect of the reactions of atomic oxygen with small unsaturated hydrocarbons is reduced because of the presence of small activation energy for these reactions. Moreover, we highlight the main contribution from other reaction channels that are not yet included in the databases available: ketyl and vinoxy radicals are among the new significant species that should be considered in the modelling. New attempts to detect them should be pursued and a chemical scheme for the vinoxy radical loss pathways devised. Furthermore, we have established that structural isomers, such as methylacetylene and allene, should be treated separately when they manifest a different chemical behaviour. A more general conclusion is that, if we wish to fully understand the formation of the numerous organic species detected in ISM, the intricate chemistry that leads to their formation should be treated in detail.
We finally plan to refine our theoretical results by modelling specific sources where hydrocarbons have been found. In the present study, we calculated the hydrocarbons column densities that match those from the observations within an order of magnitude although we were unable to make a comparison for all the species considered: most hydrocarbons are indeed non-polar molecules and therefore they cannot be detected. Despite this constraint, we aim to estimate the column densities for the case of symmetric hydrocarbons based on the abundances of their derivative species; for instance, as already stated by Quan & Herbst (2007), the amount of allene in a source could be related to the abundances of its derivative cyanoallene that, contrary to allene, is detectable.
The research leading to these results has received funding from the (European Community’s) Seventh Framework Program [FP7/2007–2013] under grant agreement no. 238258. We acknowledge the COST Action CM0805 – The Chemical Cosmos: Understanding Chemistry in Astronomical Environments for supporting of a short-term mission of A. Occhiogrosso from UCL to Perugia. The authors would also like to thank Paul Woods for useful discussions.
Just prior to submission of this paper a new version of the UMIST database has been announced (McElroy et al. 2013); however, UMIST 2012 database is not yet available.



