-
PDF
- Split View
-
Views
-
Cite
Cite
Santi Roca-Fàbrega, Octavio Valenzuela, Francesca Figueras, Mercè Romero-Gómez, Héctor Velázquez, Teresa Antoja, Bárbara Pichardo, On galaxy spiral arms’ nature as revealed by rotation frequencies, Monthly Notices of the Royal Astronomical Society, Volume 432, Issue 4, 11 July 2013, Pages 2878–2885, https://doi.org/10.1093/mnras/stt643
Close - Share Icon Share
Abstract
High-resolution N-body simulations using different codes and initial condition techniques reveal two different behaviours for the rotation frequency of transient spiral arms like structures. Whereas unbarred discs present spiral arms nearly corotating with disc particles, strong barred models (bulged or bulgeless) quickly develop a bar–spiral structure dominant in density, with a pattern speed almost constant in radius. As the bar strength decreases the arm departs from bar rigid rotation and behaves similar to the unbarred case. In strong barred models, we detect in the frequency space other subdominant and slower modes at large radii, in agreement with previous studies, however, we also detect them in the configuration space. We propose that the distinctive behaviour of the dominant spiral modes can be exploited in order to constraint the nature of Galactic spiral arms by the astrometric survey Gaia and by 2D spectroscopic surveys like Calar Alto Legacy Integral Field Area Survey (CALIFA) and Mapping Nearby Galaxies at APO (MANGA) in external galaxies.
INTRODUCTION
Since the early seventies, it has been suggested that the dynamics driven by bars and spirals have profound consequences on the kinematic and structural evolution of galactic discs (e.g. Miller, Prendergast & Quirk 1970; Hohl 1971; Athanassoula 1980; Sellwood & Athanassoula 1986; Friedli & Benz 1993). More recently, stellar radial migration in disc galaxies has been recognized as a critical component of disc galaxy evolution. This process may drastically alter our view of the connection between the present-day phase space and chemical distributions of stars and the processes of disc formation and evolution. Sellwood & Binney (2002) set up the dynamical framework of this process through the effects of transient spiral structure, which seems to be a crucial process to understand the solar neighbourhood observations as suggested originally by Wielen, Fuchs & Dettbarn (1996). Roskar et al. (2008), Schönrich & Binney (2009), Roskar et al. (2011) and Minchev et al. (2012), among others, revived the study of spiral arms and bars as triggers of stellar radial migration. Despite these numerous studies, fundamental questions arise such as: what is the nature of the spirals? Or, how is their pattern speed related to the motion of the stellar component? Several models have been proposed up to now, from the classical tight-winding approximation (Binney & Tremaine 2008) to the mechanisms proposed to account for self-excited spiral patterns (Toomre 1990; Bertin & Lin 1996; Sellwood 2000; D’Onghia, Vogelsberger & Hernquist 2013), or the manifold theory (Romero-Gómez et al. 2007; Tsoutsis et al. 2009; Athanassoula 2012).
In the quest of dynamical models not limited to quasi-linear approximations or steady state, N-body simulations have been used to understand the origin and evolution of spiral structures. After pioneering studies like Miller & Smith (1979), Sellwood & Sparke (1988) and Rautiainen & Salo (1999), only recently appeared another boom of papers likely as a result of progress in the computational resources and codes. This re-ignition of simulations based studies opened-up an interesting debate about the possible corotating nature of spiral patterns with disc particles (e.g. Quillen et al. 2011; Grand, Kawata & Cropper 2012a,b; Minchev et al. 2012; Baba, Saitoh & Wada 2013; D’Onghia et al. 2013). As an example, Grand et al. (2012a,b) computed collisionless N-body and smoothed particle hydrodynamics (SPH) simulations of disc galaxies and illustrated that transient spiral features appear to corotate with the disc. Comparetta & Quillen (2012) also suggested that some short-lived features arising from constructive interference between longer lived modes, i.e. fast bar and slowly moving spiral pattern modes, can be nearly corotating with the disc. This corotating nature would have consequences on the stellar radial migration mechanisms (Grand et al. 2012a).
From the observational point of view, the nature of spiral arms is also far from being clear (Sheth & Rossi 2010; Foyle et al. 2011; Ferreras et al. 2012). Nowadays, only weak observational constraints are available to answer these questions. Some constraints come out from direct measurement of the rotation frequencies radial variation in external galaxies (e.g. Meidt, Rand & Merrifield 2009), a method with a strong potential but currently applied only to a handful of galaxies, or from indirect measurements as the one proposed by Martínez-García, González-Lópezlira & Bruzual (2009). Other constraints to spiral arms’ nature are based on small-scale stellar kinematic substructure analysis in the Milky Way (MW) disc (e.g. Antoja et al. 2011, 2012). Furthermore, although it is now commonly accepted that the MW is a barred galaxy, it is not clear how the arms and bar are related or if they are connected at all. The rotation frequency of both, bar and spiral arms, seem to show different values, none in mutual corotation or in corotation with galactic disc material, leaving unclear spiral arms’ nature (Martos et al. 2004; Gerhard 2011). It is fair to say that currently, galactic arms’ pattern speed estimations are mostly model dependent (Martos et al. 2004). The situation is also not clear for external galaxies (Buta et al. 2005). The interpretation of observational results is based on previous theoretical studies and also on numerical simulations (Sellwood & Sparke 1988; Rautiainen & Salo 1999). Some of these studies adopted simplifications like 2D N-body models and a rigid halo or no halo at all. It is not clear if such assumptions may affect the generality of their conclusions as is suggested by Athanassoula (2002) for the case of bar growth. It is also not obvious if the corotating nature of spiral arms recently suggested by Grand et al. (2012a) is also valid in models with different structure (i.e. models with strong/week bar and/or bulge). Furthermore, classical methods to estimate disc modes’ rotation frequencies like time Fourier spectrograms applied to simulations, have been claimed to suffer from biases in models with multiple or week spiral arms, hampering estimations of arms’ pattern speeds (Grand et al. 2012a).
In this paper, we analyse 3D galaxy models, with different stellar/dark structure, using live haloes and with enough mass, force and time resolutions to accurately describe the internal disc kinematics. We performed some testing on the results dependence on codes and initial conditions techniques. It should be emphasized that the N-body simulations presented here are purely stellar. From the first attempt to simulate gas in barred galaxies (Sanders & Huntley 1976), it has become clear that gas influences disc stellar dynamics, by even changing the living time of bars (Bird, Kazantzidis & Weinberg 2012; Di Matteo et al. 2013). Gas makes discs to show more complicated and well-defined morphologies. As an example, inner rings, such as the Galactic molecular ring observed in our MW (Clemens, Sanders & Scoville 1988), have been the subject of numerous observational (Buta, Byrd & Freeman 2004) and theoretical investigations (e.g. Byrd, Freeman & Buta 2006; Romero-Gómez et al. 2011). The influence of the gaseous component and its subgrid physics in our simulations is now under investigation using the art code in the hydrodynamic version (Kravtsov 2003; Colín et al. 2010).
The aim of the first study presented here is to revisit the possible correlation between spiral arm kinematics and their nature using the purely stellar component. In Section 2, we describe our N-body simulations, carried out using two well-known N-body codes, art and gadget3. In Section 3, we describe the techniques used to derive the rotation frequencies, whereas the results and conclusions are presented in Sections 4 and 5, respectively.
Parameters of the simulations: column indicated by B1/5 presents the parameters for models with one million (B1) and five million (B5) star particles in the disc, simulated using art code, idem for unbarred models U1/5 in the third column and for the barred model G1, using gadget3 code, in the second column.
| Parameter . | B1/5 . | G1 . | U1/5 . |
|---|---|---|---|
| Disc mass (1010 M⊙) | 5.0 | 6.01 | 3.75 |
| Halo mass (1012 M⊙) | 1.38 | 0.66 | 1.5 |
| Disc exp. length Rd (kpc) | 3.86 | 3.0 | 4.0 |
| Disc exp. height Zd (kpc) | 0.2 | 0.2 | 0.2 |
| Halo NFW Rd (kpc) | 29.19 | 14.4 | 16.61 |
| Halo concentration | 10 | 10.4 | 18 |
| Halo DM species | 6/7 | 1 | 6/7 |
| N*disc(+N*bulge) (106) | 1.0/5.0 | 0.5(+0.5) | 1.0/5.0 |
| Neff (107) | 2.86/13.8 | 0.15 | 4.1/20.0 |
| Min. time step (104 yr) | 3.2/1.6 | 4.4 | 7.9/3.1 |
| Spatial resolution (pc) | 44.0/11.0 | 35.0 | 11.0/11.0 |
| Total integration t (Gyr) | 4.6/2.8 | 1.4 | 3.2/2.8 |
| Parameter . | B1/5 . | G1 . | U1/5 . |
|---|---|---|---|
| Disc mass (1010 M⊙) | 5.0 | 6.01 | 3.75 |
| Halo mass (1012 M⊙) | 1.38 | 0.66 | 1.5 |
| Disc exp. length Rd (kpc) | 3.86 | 3.0 | 4.0 |
| Disc exp. height Zd (kpc) | 0.2 | 0.2 | 0.2 |
| Halo NFW Rd (kpc) | 29.19 | 14.4 | 16.61 |
| Halo concentration | 10 | 10.4 | 18 |
| Halo DM species | 6/7 | 1 | 6/7 |
| N*disc(+N*bulge) (106) | 1.0/5.0 | 0.5(+0.5) | 1.0/5.0 |
| Neff (107) | 2.86/13.8 | 0.15 | 4.1/20.0 |
| Min. time step (104 yr) | 3.2/1.6 | 4.4 | 7.9/3.1 |
| Spatial resolution (pc) | 44.0/11.0 | 35.0 | 11.0/11.0 |
| Total integration t (Gyr) | 4.6/2.8 | 1.4 | 3.2/2.8 |
Parameters of the simulations: column indicated by B1/5 presents the parameters for models with one million (B1) and five million (B5) star particles in the disc, simulated using art code, idem for unbarred models U1/5 in the third column and for the barred model G1, using gadget3 code, in the second column.
| Parameter . | B1/5 . | G1 . | U1/5 . |
|---|---|---|---|
| Disc mass (1010 M⊙) | 5.0 | 6.01 | 3.75 |
| Halo mass (1012 M⊙) | 1.38 | 0.66 | 1.5 |
| Disc exp. length Rd (kpc) | 3.86 | 3.0 | 4.0 |
| Disc exp. height Zd (kpc) | 0.2 | 0.2 | 0.2 |
| Halo NFW Rd (kpc) | 29.19 | 14.4 | 16.61 |
| Halo concentration | 10 | 10.4 | 18 |
| Halo DM species | 6/7 | 1 | 6/7 |
| N*disc(+N*bulge) (106) | 1.0/5.0 | 0.5(+0.5) | 1.0/5.0 |
| Neff (107) | 2.86/13.8 | 0.15 | 4.1/20.0 |
| Min. time step (104 yr) | 3.2/1.6 | 4.4 | 7.9/3.1 |
| Spatial resolution (pc) | 44.0/11.0 | 35.0 | 11.0/11.0 |
| Total integration t (Gyr) | 4.6/2.8 | 1.4 | 3.2/2.8 |
| Parameter . | B1/5 . | G1 . | U1/5 . |
|---|---|---|---|
| Disc mass (1010 M⊙) | 5.0 | 6.01 | 3.75 |
| Halo mass (1012 M⊙) | 1.38 | 0.66 | 1.5 |
| Disc exp. length Rd (kpc) | 3.86 | 3.0 | 4.0 |
| Disc exp. height Zd (kpc) | 0.2 | 0.2 | 0.2 |
| Halo NFW Rd (kpc) | 29.19 | 14.4 | 16.61 |
| Halo concentration | 10 | 10.4 | 18 |
| Halo DM species | 6/7 | 1 | 6/7 |
| N*disc(+N*bulge) (106) | 1.0/5.0 | 0.5(+0.5) | 1.0/5.0 |
| Neff (107) | 2.86/13.8 | 0.15 | 4.1/20.0 |
| Min. time step (104 yr) | 3.2/1.6 | 4.4 | 7.9/3.1 |
| Spatial resolution (pc) | 44.0/11.0 | 35.0 | 11.0/11.0 |
| Total integration t (Gyr) | 4.6/2.8 | 1.4 | 3.2/2.8 |
MODELS AND SIMULATIONS
We have performed collisionless N-body simulations with art (Kravtsov, Klypin & Khokhlov 1997) and gadget3 (last described in Springel 2005) codes. Tests of consistency of both codes, applied to dynamics of barred galaxies can be found in Valenzuela & Klypin (2003), Colín, Valenzuela & Klypin (2006) and Klypin et al. (2009). We present here three sets of fully self-consistent models, all of them with a live exponential disc and live dark matter (DM) halo with the NFW (Navarro, Frenk & White 1997) density profile (see Table 1). The live halo ensures disc–halo angular momentum exchange, which plays an important role in the formation and evolution of bars as discussed by Athanassoula (2002). We simulated barred (B) and unbarred (U) models with the aim to compare spiral arms potentially triggered by a bar against arms triggered by other mechanisms. Models B and U were simulated using the art code. To generate initial conditions of these models we used the Jeans equation moments method as introduced by Hernquist (1993). We have also used a multimass method to sample the halo particle distribution, which allows us to obtain similar results such as using a higher number (Neff) of particles and minimizing two body scattering as discussed in Valenzuela & Klypin (2003). Barred models have a stellar disc and total mass similar to the one observed for the MW with additional initial parameters as proposed by Colín et al. (2006) (model Kcb). As discussed in Klypin, Zhao & Somerville (2002), the final properties of this model, after rescaling, can reproduce the observed quantities for the MW. This rescaling process has not been applied since it does not affect the disc kinematic properties analysed in this paper. Unbarred models have a smaller disc and a massive and highly concentrated halo. Additionally, we have used the gadget3 code to simulate barred models, labelled G, including a bulge component with a Sérsic profile (Rb = 1.75 kpc, Mb = 8.57 × 109 M⊙). For the bulged models’ initial conditions generation we have used the code described in Widrow & Dubinski (2005). The number of disc particles in our models range from one to five million particles (see Table 1).
As expected (e.g. Ostriker & Peebles 1973), the models with a relatively dominant disc (B and G) rapidly generate a bar with trailing spiral arms while unbarred models (U) do not, at least in the first ∼3 Gyr. In the first case, we have a similar halo and disc contribution to the circular velocity inside a radial exponential length and, as described in Valenzuela & Klypin (2003), the self-gravity of disc density fluctuations (disc modes) dominates making the instability grow and generate a bar (Fig. 1, left-hand and middle panels). This bar mode induces the formation of a bisymmetric spiral structure apparently connected to the bar ends (e.g. Binney & Tremaine 2008, and references therein). There is still controversy on the nature of these bisymmetric spirals (resonant coupling, manifolds, or others), but what is evident in all our models is that these structures dominate in density. For the unbarred model (Fig. 1, right) the halo contribution to the potential is higher and the disc modes cannot grow so easily. Although in both cases, the initial velocity dispersion is low (Q = 1.2), the higher halo mass concentration in the unbarred model prevents disc from having a dominant bisymmetric mode in the first Gyr of evolution, i.e. other modes grow forming a trailing three to four armed structure. Some other structures with lower density appear in the external regions of these simulations (both barred and unbarred). In the next section, we discuss their imprints on the frequency space. As expected for MW-like galaxies, we also note that rotation curves in our set of simulations are rather flat (see top panels of Fig. 1).
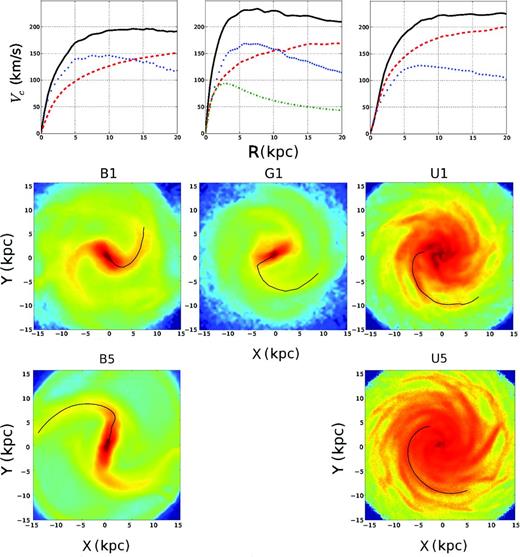
Structure of the models. Top: initial circular velocity of models B (left), G (centre) and U (right), computed from the potential field gradients using tipsy package. We show the total rotation curve (black solid), disc (blue dotted), halo (red dashed) and bulge (green dot–dashed) contributions. Center: density distribution of the models B1 (left), G1 (centre) and U1 (right) after 900 Myr of evolution. Bottom: density distribution of the models B5 (left) and U5 (right) after 900 Myr of evolution. The black solid line shows the locus of the spiral arms derived using Fourier analysis (m = 2 for B and G models, m = 4 for U). Spiral structure rotates clockwise in all models.
In all our models, spiral arm structures are observed for at least 2 to 3 Gyr. We show in Fig. 2 the temporal evolution of the spatial Fourier modes for the three models with one million particles in the disc. We see that dominant spiral modes have a recurrent nature with periodicities of less than one galactic rotation. The amplitude of the spiral arms in the unbarred case is significantly lower than in the barred models.
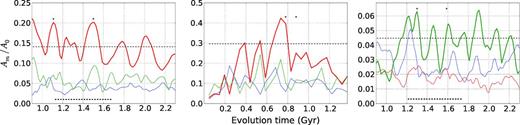
Amplitude evolution of disc modes. Fourier amplitude for modes 2 (red), 3 (blue) and 4 (green) as a function of time, averaged for radius between 4 and 10 kpc of the barred (B1, left), the bulge-barred (G1, centre) and the unbarred (U1, right) models (note change in vertical scale). The thin black dashed lines indicate a threshold in amplitude used to compute Fig. 3 using SFpFD method. The black dots indicate the snapshots for which the kinematic analysis is shown in Fig. 4 using SFpFD method, and the thick black dashed lines indicate the temporal range used to compute spectrograms in Fig. 5.
In Fig. 1, we observe that some parameters of the bar and spirals are different from B1 (one million disc particles) to B5 (five million) models. These differences are arising from the fact that the number of particles, spatial and time resolution in B5 model are much better than in B1, i.e. we are resolving smaller wavelength disc modes in the B5 case than in B1. These modes interact with the disc and then, due to the high non-linearity of the system, lead the evolution to a slightly different configuration (e.g. bar length and speed). However, global quantities like circular velocity and density profiles are more robust to such effects. The situation is well known and it has been reported in previous works (Klypin et al. 2009; Sellwood & Debattista 2009). A convergence study of this and other models will be presented in Roca-Fàbrega et al. (in preparation); however, as will be seen in next sections, the main results of our simulations are robust across changes in numerical parameters: a bar–arm structure which is dominant in density plus external and weaker arms are formed in barred discs, while in barless models low-amplitude arms are found. In the next section, we will analyse the kinematics of such spiral structures.
OVERDENSITIES AND ROTATION FREQUENCIES
We use spatial Fourier analysis azimuthally averaged in order to trace the density peak of the spirals and the bar (Valenzuela & Klypin 2003), working in cylindrical shells equally spaced in galactocentric distance. Fig. 1 shows an example of how well the spatial Fourier method traces the peak overdensities up to the end of the dominant structures (m = 2 for barred cases and m = 3, 4 for unbarred ones). We also used a density peak method as the one used in Grand et al. (2012a,b) to test that the results are method independent. Once the locus of the spiral is derived, we use both, finite differentiation among three consecutive snapshots and the classical spectrograms method (Sellwood & Athanassoula 1986) to compute the rotation frequency.
The advantages of using Spatial Fourier plus Finite Differentiation (hereafter SFpFD) are that it allows us to compute the rotation frequency of a single known mode m structure and for a single time instant. As a consequence, SFpFD is able to show us how the structures evolve with time. On the contrary, the spectrogram method (Sellwood & Athanassoula 1986) needs to be applied to a large time interval due to the Nyquist frequency limitation. Because of that, the results from spectrograms method may be contaminated by recurrent arms sequences with low or negligible spiral amplitude due to the transient nature of the structures. This drawback is already discussed by Grand et al. (2012a).
A weakness of using SFpFD, independently of having two or more spiral arms, appears when two coexisting structures of the same Fourier mode at the same radius are present. In this case, the method results in a unique structure placed at the average angle. Thus, we have to control these cases to avoid a bias in the derived rotation frequency. In contrast, spectrograms can find discrete rotation frequencies from structures coexisting at the same radius without any problem. After carefully weighting the pros and cons, we state that both methods (SFpFD and spectrograms) are complementary.
SPIRAL ARM ROTATION FREQUENCIES
We perform a first kinematical analysis on the dominant modes in density shown in Fig. 2, m = 2 for the barred (bisymmetric spiral) and m = 4 for the unbarred models (four armed structure). As can be seen in Fig. 1, the dominant density structures extend up to 10 to 11 kpc. In Fig. 3, we present the rotation frequency curves for the three models with one million disc particles computed using the SFpFD method. It includes all time steps where we can ensure the spiral arm is well formed. We empirically establish that a spiral is well formed when the amplitude of the dominant mode is above 0.7 times the maximum value of this mode in the range we study (see the thin black dashed lines in Fig. 2). These density maps are constructed from the superposition of all the rotation frequency curves at time steps when the amplitude of the mode is above the mentioned threshold. These figures show significant differences between barred and unbarred morphologies. Note how in the barred models (B1 and G1, computed using art and gadget3, respectively) the spiral pattern rotates almost as a rigid body, while in unbarred models the rotation frequency curves lie on top of the rotation of the disc particles, resulting in a spiral mode corotating with the disc.
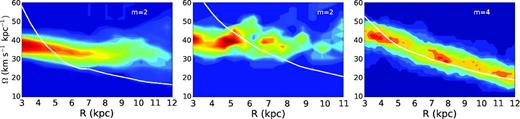
Rotation frequencies as a function of radius calculated using SFpFD method for dominant mode across time in models B1 (left, G1 (centre) and U1 (right) (see Fig. 2). Here, we plot the frequency density map of the rotation frequencies computed using all time instants when the spiral arms’ amplitude is above 70 per cent of the maximum mode amplitude (dashed line in Fig. 2). Circular frequencies of disc particles are indicated as the solid white lines and have been computed in an intermediate instant of the analysed time interval. The length of the bar is ∼4.5 kpc and ∼5 kpc for B1 and G1 models, respectively.
A more exhaustive analysis is shown in Fig. 4, considering models with a higher number of disc particles and a different technique for the detection of the spiral structure. Instead of working with density maps, here we plot single time step curves computed using SFpFD for models with both one and five million disc particles. For the B and G models we avoid the central part of the bar, for U the central complex region where the three to four armed structure converges and in both we also avoid the external regions where the number of particles is too low. The red dashed lines correspond to two instants of the one million disc particle models (included in the density plot of Fig. 3) shown as red dots in Fig. 2. More important, the blue dashed lines correspond to models with five million disc particles, both barred and unbarred, integrated using art. Furthermore, the blue dotted line corresponds to the barred art five million model for which the spirals have been detected using the density peak method (similar to the one in Grand et al. 2012a,b). Note how the conclusions reached in Fig. 3 are well corroborated. We can see spiral patterns rotating almost as a rigid body in all our barred models, both using art and gadget3, using different techniques for the spatial detection and considering a different number of particles. We have also verified that simulations with 2 × 105 disc particles show the same behaviour (not included here). A slightly decreasing rotation frequency with radius is observed only for the art model with one million disc particles (B1). Even though, this behaviour is completely different from all our art unbarred models, both using one million and five million disc particles.
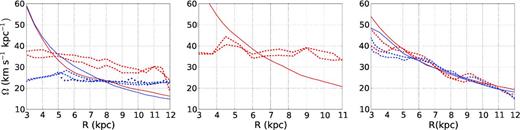
Rotation frequencies as a function of radius calculated using SFpFD method for selected time instants when the amplitude of spiral arms is maximum (black dots in Fig. 2). All the rotation frequencies analysis of the barred (B1, and B5 left), the bulge barred (G1, centre) and the unbarred (U1, right) has been computed taking cylindrical shells of 0.5 kpc width. In red dashed line, we show results obtained for models with one million disc particles. In blue dashed line, those of the art models, with five million disc particles (left- and right-hand panels, respectively, for models B5 and U5) when the amplitude of the spirals arms is maximum (0.75 and 1.12 Gyr). Circular frequencies of disc particles are indicated as the solid lines (red for models B1 and U1 and blue for models B5 and U5). Additionally, blue dots in the left-hand panel show the results of applying a density peak method similar to one used in Grand et al. (2012a) to B5 simulation, to find the spiral structure (a detailed description of this method will be included in Roca-Fàbrega et al. in preparation). The dispersion on rotation frequency profiles due to its computation at several time steps when the amplitude of the dominant mode and its behaviour can slightly change, is shown in Fig. 3. The length of the bar is ∼4.5, ∼7.0 and ∼5.0 kpc for B1, B4 and G1 models, respectively. The differences in bar properties between models B1 and B5 are discussed in Section 2.
To ensure that our results are not dependent on the method used to compute the rotation frequencies, in Fig. 5, we perform one last test using, in this case, the classical spectrogram method in B1 and U1 models with a Nyquist frequency of ∼100–150 km s−1 kpc−1. The panels framed in red correspond to the dominant modes discussed above, and they are to compare with the left- and right-hand panels of Fig. 3. Note that, again, the barred model presents a dominant mode that rotates as a rigid body, while in the unbarred case, the structures corotate with the disc particles. Two features observed in this dominant mode deserve special attention. First, in the barred model, a well-defined structure is observed at a radial range of 11–14 kpc (only the beginning of the structure is shown in the figure). It rotates slower than the disc with a frequency of about 8 km s−1 kpc−1. As mentioned in Section 3, here we note one of the advantages of the spectrograms. They are able to detect multiple spiral patterns at a given radius. Using SFpFD, we have checked that the low-frequency structure corresponds to one of the lower density structures observed in the outer radii of the centre-left panel of Fig. 1. The complex link with the dominant structure will be discussed in a forthcoming paper. As it is known, these multiple pattern speeds are common in spiral barred galaxies both in simulations and observations (e.g. Masset & Tagger 1997; Buta & Shang 2011). Secondly, and less important, we can appreciate a flat structure in the rotation frequency in the central region of the unbarred model (R < 4 kpc, bottom-right panel of Fig. 5), which could remind the signature of a weak bar mode. This is a misinterpretation since it corresponds to a m = 4 mode, and, actually, the amplitude of the m = 2 mode in this region is less than 2 per cent (see Fig. 2).
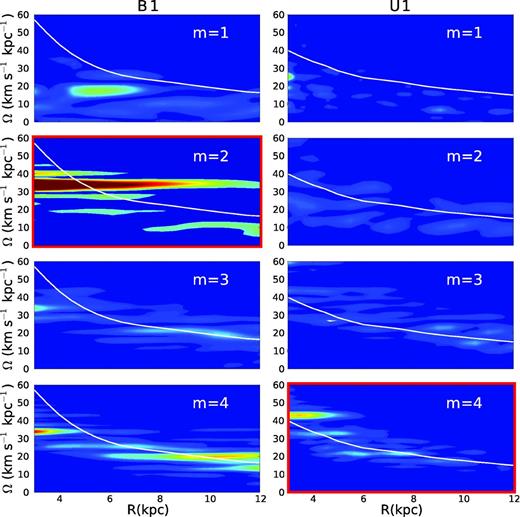
Spectrograms for the barred model B1 (left) and unbarred U1 (right) obtained using Sellwood & Athanassoula (1986) method. We show the Fourier component for the m = 1, 2, 3 and 4 modes in a window spanning 0.5 Gyr centred at 1.4 Gyr (left) and 1.45 Gyr (right), (see the dashed dark lines in top panels of Fig. 2), and with a Nyquist frequency ∼100–150 km s−1 kpc−1. The y-axis is the angular frequency in km s−1 kpc−1 and the x-axis is radius in kpc. Overplotted in white we show the rotation curve of disc particles computed for an intermediate instant of the analysed time interval.
Fig. 5 also includes the spectrograms for the subdominant modes. As in fig. 6 of Grand et al. (2012a) we find all these subdominant modes clearly corotating with the disc. This behaviour is also observed in other studies as in Minchev et al. (2012, fig. 8), although not discussed there, while they are centred on the study of resonant coupling.
DISCUSSION AND CONCLUSIONS
The rotation frequencies of the spiral modes in barred and unbarred models, integrated with different N-body codes (art and gadget), and analysed with different techniques (spectrograms and finite differences), present a well-defined different behaviour. Whereas unbarred models show transient arms corotating with disc particles, in good agreement with those recently reported by Grand et al. (2012a) and Baba et al. (2013), barred models deserve further comments. As shown in Figs 3 and 4, barred models present a spiral pattern speed almost constant in radius for all the range where the spiral structure is dominant in density. These results are consistent with those of models I, II and III in Rautiainen & Salo (1999), computed using a simplified 2D model and with rigid or no halo. We want to emphasize that whereas in those early models it is difficult to detect spiral structures in the configuration space, particularly in the external regions, in our simulations with one and five million disc particles, the spiral structure is clearly identified (see Fig. 1), allowing us to use the arm phase in order to test claimed biases in the derivation of the rotation frequencies using spectrograms (see Section 3).
It is important to compare our results with those recently obtained by Grand et al. (2012b). The authors have analysed N-body/SPH simulations of isolated barred galaxies concluding that, spiral arms’ pattern speed decreases with radius, closely in corotation with disc particles. Grand et al. (2012b) computed the rotation frequencies averaging the values obtained for several snapshots over two time intervals during spiral arm evolution, one when the bar is well defined in their images (∼1 Gyr of evolution, see their fig. 9) and the other when the bar has significantly weakened (∼1.5 Gyr, fig. 10). In both cases, the spirals pattern speed is almost corotating with disc particles. The previous result is at odds to what is obtained in our study. However, they also noted a small offset of the spiral arms’ rotation frequency profile from being corotating with disc particles, particularly when the bar is stronger, suggesting that further analysis is required. Here, we have analysed the correlation between the strength of the bar and the spiral rotation frequency in our B1 art model, a MW-like simulation. With such a purpose, we have computed arms’ rotation frequency during the first evolutionary stages, when the bar is still growing and weak (A2/A0 < 0.1) at about 0.3 Gyr of evolution. Only when the bar is weak we observe that the external m = 2 mode (bisymmetric arm) rotation frequency is close to disc corotation. After few galactic rotations, when the bar has fully formed (A2/A0 > 0.4) (as shown in Fig. 2, left-hand panel), the rotation frequency becomes almost constant, approaching the bar rigid body rotation, if any with a small decrement in radius (see Figs 3 and 4, left-hand and central panels). This result is qualitative in agreement with the statement discussed by Grand et al. (2012b), unfortunately we do not have information of bar amplitude in Grand et al. (2012b) simulations, and their models assume a gas component making harder a further comparison. We conclude that in barred models the spiral rotation frequency approaches the bar rigid body rotation with the increment of bar strength.
Furthermore, our simulations, with a high number of disc particles, allow us to analyse the behaviour at larger radii ∼12–14 kpc. As can be seen in Fig. 5 (m = 2 mode, left-hand panel second row), the spectrograms method applied to the B1 bar model shows an external structure, at radii larger than R = 11 kpc, that rotates slower than the density dominant mode. This external structure has a lower amplitude, lower rotation frequency (less than 10 km s−1 kpc−1), it is tightly wound, and it is recurrently connected/disconnected with the inner and faster spiral (see movie1). Other authors (i.e. Sellwood & Sparke 1988) have reported similar structures but apparently they detected them only in the frequency space, probably due to the statistical fluctuations given by their number of particles (see however fig. 16 in Rautiainen & Salo 1999). The lack of detection in configuration space led the authors to conclude that inner fast rotating structures correspond only to the bar structures while the slower and external ones to the entire and unique spiral mode. Here, we confirm the detection and the rotation frequency in configuration space (see Fig. 1) for all these structures, and that the inner fast rotating structure includes both: a bar and an inner spiral structure apparently connected. The slow rotating mode is an external spiral mode. We stress that we also find both structures using the SFpFD method in configuration space. In conclusion, at large radii, and for m = 2, we do see the external slow and low-amplitude arm coexisting with the dominant spiral mode which is most of the time connected to the bar.
The results presented here for the barred case are also compatible with the observations recently reported by Meidt et al. (2009). They derive rotation frequencies in four spiral galaxies: two strong barred, one unbarred and one with rings. They find that in the two strong barred cases the inner bisymmetric spirals rotate with the same frequency as the bar. Furthermore, one of the barred cases present an external armed structure rotating with a much lower frequency (see their figs 8 and 12) as it is observed in our B1 barred model. For the other cases, they find multiple pattern speeds that can be or not in a resonance coupling situation. It is important to mention that at least one of their barred galaxies is likely in interaction (M101). As discussed by the authors, the limiting observational accuracy – precision in the radial binning and frequency sampling – does not allow them to confirm or refute the small radial decrement in rotation frequency shown in our Fig. 3, therefore, they conclude that arms in their study are rigid body rotators. Further observations will be required to confirm this tendency.
From the simulations we have performed, it is clear that a difference in the spiral arm kinematics exists if they are triggered by a bar or by another mechanism, and also that barred models seem to show at least two kinds of spiral arms. Further analysis of the arm nature and numerical convergence tests will be discussed in a forthcoming paper.
As a summary we confirm that:
the dominant spiral mode (m = 2) in strong barred models is most of the time connected to the bar. Its rotation frequency is near to the bar solid body rotation, with a small decrement with radius, which is more important as the bar amplitude decreases. Arms are corotating with disc particles only for very weak bars.
Although the dominant spiral disc mode in barred simulations is the one connected with the bar, we observe at least one subdominant slow and winded mode at large radii, using either SFpFD, spectrograms (see Fig. 5) or density maps.
In unbarred models the spiral structures are corotating with disc material, in agreement with previous results (Grand et al. 2012a).
Our results are robust to changes in numerical parameters (time step, spatial resolution and number of particles), mode analysis techniques (SFpFD, spectrograms and density peak) and also to changes in numerical codes (art and gadget3).
A natural question is to ask which is the situation for the MW: do the traditional spiral arms correspond to the mode coupled with the bar? Or instead correspond to the modes we observed at larger radii? Or both? Planned and current surveys measuring stellar kinematics and distances inside our Galaxy as Gaia (ESA) or The APO Galactic Evolution Experiment (APOGEE) (SDSS) will open up the possibility of direct estimation through methods like the one proposed by Tremaine & Weinberg (1984). Spectroscopic high-resolution surveys of external galaxies like CALIFA (Sánchez et al. 2012) or MANGA (AS3/SDSSIV) will contribute to test our predictions using stellar kinematics.
We thank A. Klypin, A. Kravtsov and V. Springel for providing us the numerical codes and L. M. Widrow for providing the code to generate the initial conditions. We thank HPCC project and T. Quinn for the implementation of tipsy package. Finally, we also thank Luis Aguilar, Ivanio Puerari and Gene G. Byrd for their helpful comments on this work. This work was supported by the MINECO (Spanish Ministry of Economy) – FEDER through grants AYA2009-14648-C02-01, AYA2010-12176-E, AYA2012-39551-C02-01 and CONSOLIDER CSD2007-00050. SR-F was supported by the MECD PhD grant 2009FPU AP-2009-1636. Simulations were carried out using Pakal, Abassi2 and Atocatl at IA-UNAM and Pirineus at CESCA.
This movie (available as Supporting Information in the online version of the article) can be downloaded from http://www.am.ub.edu/∼sroca/Nbody/movies/B1.mpeg and it shows the density evolution of model B1, spanning from 0.1 to 3.1 Gyr. High-density regions (∼3.7 M⊙ pc−3) are shown in dark blue colours while zero density ones are in white.
REFERENCES
SUPPORTING INFORMATION
Additional Supporting Information may be found in the online version of this article:
Movie: Displaying the density evolution of model B1, spanning from 0.1 to 3.1 Gyr (Supplementary Data).
Please note: Oxford University Press are not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.



