-
PDF
- Split View
-
Views
-
Cite
Cite
M. Del Santo, J. Malzac, R. Belmont, L. Bouchet, G. De Cesare, The magnetic field in the X-ray corona of Cygnus X-1, Monthly Notices of the Royal Astronomical Society, Volume 430, Issue 1, 21 March 2013, Pages 209–220, https://doi.org/10.1093/mnras/sts574
Close - Share Icon Share
Abstract
The different electron distributions in the hard and soft spectral states of black hole binaries could be caused by kinetic processes and changing because of varying physical conditions in the corona. In the presence of a magnetic field in the corona, the electron distribution can appear thermal, even when acceleration mechanisms would produce non-thermal distributions. This is due to fast and efficient thermalization through synchrotron self-absorption. In this paper, we have analysed data from 6 yr of observations of Cygnus X-1 with the INTEGRAL observatory and produced 12 high-quality, stacked broad-band hard X-ray spectra representative of the whole range of spectral shapes observed in this source. We then fit these spectra with hybrid thermal/non-thermal Comptonization models and study the evolution of the physical parameters of the accretion flow across the spectral transition. In particular, we use the belm model to constrain the magnetic field in the corona through its effects on the coronal emission. Indeed, the hot electrons of the X-ray corona produce soft (optical–UV) synchrotron radiation which is then Comptonized and may affect the temperature of the electrons (and thus the slope of the X-ray spectrum) through Compton cooling. We find that in the softer states, the emission is dominated by Comptonization of the disc photons and the magnetic field is at most of the order of 106 G. In the harder states, the data are consistent with a pure synchrotron self-Compton model, although a significant contribution of Comptonization of disc photons may not be excluded. If the non-thermal excess observed above a few hundred keV in the hard state is produced in the same region as the bulk of the thermal Comptonization, we obtain an upper limit on the coronal magnetic field of about 105 G. If, on the other hand, the non-thermal excess is produced in a different location (such as the jet or a different part of the corona), the constraints on the magnetic field in the hard state are somewhat relaxed and the upper limit rises to ∼107 G. We discuss these constraints in the context of current accretion flow models.
1 INTRODUCTION
Black hole binaries (BHBs), and Cyg X-1 in particular, show dramatic spectral variability. The most dramatic variations observed in BHBs are spectral transitions which occur, for most of these sources, on the time-scales from weeks to days (Zdziarski et al. 2002). In the simplest classification, BHBs, are observed in two main spectral states: in the hard state (HS), the source emits essentially radiation peaking around 100 keV (Gierliński et al. 1997; Zdziarski & Gierliński 2004), while in the soft state (SS), the X-ray spectrum is a prominent ∼1 keV blackbody plus a power-law tail (Zdziarski 2000 and references therein). The HS spectrum is believed to originate from thermal Comptonization in a hot electron-dominated cloud (the so-called corona; Eardley, Lightman & Shapiro 1975; Sunyaev & Titarchuk 1980).
The blackbody-dominated spectrum observed in SS was associated with the optically thick accretion disc (Shakura & Sunyaev 1973), while the origin of the weak steep power-law component is still debated Zdziarski (2000). In addition, spectra with properties that are intermediate between that of the SS and HS are observed when the sources switche from one of the two stable states to the other. Terms such as ‘hard intermediate’, or ‘soft intermediate’ are often used to describe different flavours of those intermediate state (Belloni et al. 2005) but there is no unique classification (see McClintock & Remillard 2006).
The spectra of BHBs consist in several components. In the HS of Cyg X-1, the electron temperature and the Thomson optical depth of the Comptonizing plasma were found to be typically kTe = 50–100 keV and τ = 1–3 (Gierliński et al. 1997; Frontera et al. 2001). Although the scattering electrons have a predominantly Maxwellian energy distribution in the HS, there are indications that the electron distribution may have some high-energy tail, i.e. it is hybrid, thermal/non-thermal. The first evidence has been provided by CGRO/COMPTEL observations at E > 500 keV of Cyg X-1 in HS (McConnell et al. 1994, 2002). A slight indication was also inferred by CGRO/OSSE observations of GX 339−4 (Wardziński et al. 2002). Then, with the INTEGRAL mission, this feature has been observed many times during hard and/or intermediate/hard states in a number of BHBs and BH candidates (see Del Santo 2012 for a review on this topic), such as 1E 1740.7−2942 (Bouchet et al. 2009), GX 339−4 (Joinet et al. 2007; Del Santo et al. 2008; Droulans et al. 2010), Cyg X-1 (Cadolle Bel et al. 2006; Malzac et al. 2006; Jourdain, Roques & Malzac 2012; Zdziarski, Lubiński & Sikora 2012).
Alternatively, it is possible that the non-thermal excess and thermal Comptonization component are not produced by the same electron distribution but in separate regions of the corona with different physical properties (Malzac 2012). Also, radio observations of Cygnus X-1 have resolved a compact relativistic jet (Stirling et al. 2001) and it was suggested that the high-energy excess may be a component arising from it (Rahoui et al. 2011). This idea has been also proposed following the hard X-ray polarization measurements by Laurent et al. (2011) obtained with the IBIS telescope in Compton mode. These authors found that while the 250–400 keV spectrum is consistent with emission dominated by Compton scattering by thermal electrons and are weakly polarized (Pf < 20 per cent), the second spectral component seen in the 400 keV–2 MeV band is strongly polarized (Pf = 67 ± 30 per cent). They have argued that the MeV excess is likely to be produced in jet through synchrotron emission in a very coherent magnetic field. Such a high degree of polarization is indeed difficult to achieve through inverse Compton emission in the corona. Recently, Jourdain et al. (2012) reported on a similar result by using the SPI telescope. They found that above 230 keV the Cyg X-1 emission is indeed polarized, with a mean polarization fraction of 76 ± 15 per cent.
The shape of the MeV excess, however, appears difficult to reproduce in the jet scenario (Zdziarski et al. 2012). Such a scenario would also imply that the MeV excess in the HS and the non-thermal power-law emission observed in the SS have a completely different nature since the radio jet is quenched in the SS. We note that although it is very plausible that the non-thermal excess originates in the jet, it appears very unlikely that the jet emission could dominate the entire high-energy spectrum of Cyg X-1 (see e.g. Malzac, Belmont & Fabian 2009 and references therein).
The X-ray/γ-ray SS spectrum of Cyg X-1 has been studied extensively by simultaneous observations with ASCA, RXTE, BeppoSAX, and CGRO during summer 1996 (Di Salvo et al. 2001; Frontera et al. 2001). In addition to the dominating blackbody, a long power-law like tail extending up to 10 MeV was discovered (McConnell et al. 2002). The high-energy spectrum is well described by single Compton scattering off electrons having nearly a power-law distribution (Gierliński et al. 1999, hereafter G99; Frontera et al. 2001).
The different spectral states are usually understood in terms of changes in the geometry of the accretion flow. According to a popular scenario (see e.g. Done, Gierliński & Kubota 2007 for an exhaustive review), in the SS a geometrically thin accretion disc (the standard Shakura–Sunyaev disc) extends down to the last stable orbit and is responsible for the dominant blackbody emission. This disc is the source of soft seed photons for Comptonization in small active coronal regions located above and below the disc. The magnetic field lines rise above the accretion disc through magnetic buoyancy, transporting a significant fraction of the accretion power into the corona where it is then dissipated through magnetic reconnection (Galeev et al. 1979). This leads to particle acceleration in the corona. A population of high-energy electrons is formed which then cools down by up-scattering the soft photons emitted by the disc. This produces the high-energy non-thermal emission (see e.g. G99; Zdziarski et al. 2002). In the HS, the standard geometrically thin disc is truncated at distances ranging from a few tens to a few thousand gravitational radii from the BH. In its inner parts, the accretion flow takes the form of a hot geometrically thick, optically thin disc (Esin, McClintock & Narayan 1997). In this hot accretion flow, the electrons are predominantly heated by Coulomb interaction with a population of hot ions and cool down by Comptonizing their own synchrotron emission and/or soft photons from the accretion disc.
The different electron distributions in HS and SS could be caused by kinetic processes and changing because of varying physical conditions in the corona (Malzac & Belmont 2009, hereafter MB09; Poutanen & Vurm 2009, hereafter PV09). These authors showed that in presence of a magnetic field in the corona, the electron distribution can appear thermal, even when acceleration mechanisms would produce non-thermal distributions. This is due to fast and efficient thermalization through synchrotron self-absorption as first pointed out by Ghisellini, Guilbert & Svensson (1988). MB09 and PV09, presented a rough ‘fit by eye’ of the average CGRO data of Cyg X-1 with this synchrotron boiler model which already provided estimates of the magnetic field in the HS under the assumption that the non-thermal excess is produced by electrons in the same zone as the Maxwellian component. In this paper, we will use the same model to perform a statistical fit of INTEGRAL data for the whole range of observed spectral shapes and also considering the possibility that the non-thermal excess in the HS may have a different origin.
As one of the brighter galactic hard X-ray source, Cyg X-1 is a prime target for the INTEGRAL mission (Winkler et al. 2003). It was extensively observed during the performance verification (PV) phase of the mission. The onboard instruments offer an unprecedented simultaneous broad-band spectral coverage, ranging from 3 keV to several MeV. Thus, a large amount of observing time (open time and core programme for a total of about 7 Ms) have been dedicated to this target by INTEGRAL. A number of studies of the intermediate spectral states have been performed (Cadolle Bel et al. 2006; Malzac et al. 2006); an X-ray flare during the HS appears to be coincident with the TeV emission detected by MAGIC (Albert et al. 2007; Malzac et al. 2008).
Recent papers have also provided a refined estimation of the distance (d = 1.86 kpc; Reid et al. 2011) and the BH mass of Cyg X-1 (14.8 M⊙; Orosz et al. 2011).
In this work, we present the long-term behaviour and a spectral variability study of Cyg X-1 using the whole INTEGRAL data base available until Spring 2009. Rather than following the evolution of the source chronologically, the aim was to extract high-quality data representative of the source in a given ‘spectral state’. For this purpose, we stacked all the pointings with similar hardness ratios (HR) to produce 12 averaged spectra spanning the whole range of observed spectral shapes. The details of how this was done are described in Section 2. These 12 broad-band (3 keV–1 MeV) spectra were then fitted with two different hybrid thermal Comptonization models namely eqpair (Coppi 1999) and belm (Belmont, Malzac & Marcowith 2008; hereafter B08) that are described in Section 3. This allows us to constrain the physical conditions in the corona and determine how the physical parameters change during the spectral evolution. In particular, fits with belm sets quantitative constraints on the strength of the magnetic field in the corona of Cygnus X-1 for the first time. These results are described and discussed in Section 4.
2 OBSERVATIONS AND DATA ANALYSIS
We have analysed six years of Cyg X-1 observations performed by INTEGRAL until 2009 April (revolution 794) with the three coded-mask telescopes IBIS (Ubertini et al. 2003), SPI (Vedrenne et al. 2003) and JEM-X (Lund et al. 2003). We started from 2003 March (revolution 52), thus we excluded the PV phase observations (1 Ms) due to some peculiar instrument settings. Results on Cyg X-1 obtained during the calibration phase have been extensively reported (Bazzano et al. 2003; Bouchet et al. 2003; Pottschmidt et al. 2003).
For the purpose of spectral analysis, we have built our data set by selecting all IBIS observations including Cyg X-1 in a partially coded FOV of 15° × 15° where the instrument response is well known. Based on this selection, the total number of IBIS and SPI science windows (SCWs) results as 1024 (Table 1) for a total exposure time of about 3.3 Ms (a single SCW can last from 800 up to 4000 s). The total SPI exposure time is essentially the same as that of IBIS, even though a further analysis excluding SPI problematic pointings (i.e. solar flares, radiation belts) leads to a slightly lower SPI effective exposure time than IBIS. Because of the smaller FOV of the X-ray telescope JEM-X, the related selected pointings (FOV of 3|${^{\circ}_{.}}$|5 × 3|${^{\circ}_{.}}$|5 has been considered) are 364 (see Table 1). In particular, 44 SCWs for JEM-X2, operating at the beginning of the mission and 320 for JEM-X1 operating since revolution 181.
Observations log of the 12 final data set used for spectral modelling. The IBIS HR intervals, number of pointings (SCW) with IBIS and SPI and with JEM-X (within parentheses), IBIS and SPI observing exposures (Exp1), JEM-X exposure (Exp2) and the power-law slope (Γ) of the 30–100 keV IBIS/ISGRI spectra are shown.
| HR . | SCW (JEM-X) number . | Exp1 (ks) . | Exp2 (ks) . | Γ . |
|---|---|---|---|---|
| 0.37–0.41 | 7 (1) | 15.4 | 2.2 | 2.6+ 0.04− 0.03 |
| 0.43–0.48 | 12 (2) | 36.8 | 6.5 | 2.32 ± 0.02 |
| 0.48–0.50 | 35 (9) | 111.5 | 27.8 | 2.29 ± 0.01 |
| 0.50–0.53 | 59 (8) | 181.1 | 22.9 | 2.23 ± 0.02 |
| 0.53–0.56 | 82 (11) | 236.8 | 34.0 | 2.17 ± 0.02 |
| 0.56–0.58 | 38 (19) | 101.0 | 51.1 | 2.08 ± 0.02 |
| 0.58–0.61 | 113 (40) | 343.4 | 113.7 | 2.02 ± 0.02 |
| 0.61–0.64 | 97 (27) | 287.7 | 80.3 | 1.98 ± 0.02 |
| 0.64–0.66 | 114 (29) | 944.2 | 34.7 | 1.81 ± 0.02 |
| 0.66–0.68 | 340 (72) | 781.4 | 147.8 | 1.79 ± 0.02 |
| 0.68–0.70 | 157 (16) | 402.0 | 34.2 | 1.74 ± 0.02 |
| 0.70–0.72 | 9 (4) | 26.1 | 8.0 | 1.73 ± 0.02 |
| HR . | SCW (JEM-X) number . | Exp1 (ks) . | Exp2 (ks) . | Γ . |
|---|---|---|---|---|
| 0.37–0.41 | 7 (1) | 15.4 | 2.2 | 2.6+ 0.04− 0.03 |
| 0.43–0.48 | 12 (2) | 36.8 | 6.5 | 2.32 ± 0.02 |
| 0.48–0.50 | 35 (9) | 111.5 | 27.8 | 2.29 ± 0.01 |
| 0.50–0.53 | 59 (8) | 181.1 | 22.9 | 2.23 ± 0.02 |
| 0.53–0.56 | 82 (11) | 236.8 | 34.0 | 2.17 ± 0.02 |
| 0.56–0.58 | 38 (19) | 101.0 | 51.1 | 2.08 ± 0.02 |
| 0.58–0.61 | 113 (40) | 343.4 | 113.7 | 2.02 ± 0.02 |
| 0.61–0.64 | 97 (27) | 287.7 | 80.3 | 1.98 ± 0.02 |
| 0.64–0.66 | 114 (29) | 944.2 | 34.7 | 1.81 ± 0.02 |
| 0.66–0.68 | 340 (72) | 781.4 | 147.8 | 1.79 ± 0.02 |
| 0.68–0.70 | 157 (16) | 402.0 | 34.2 | 1.74 ± 0.02 |
| 0.70–0.72 | 9 (4) | 26.1 | 8.0 | 1.73 ± 0.02 |
Observations log of the 12 final data set used for spectral modelling. The IBIS HR intervals, number of pointings (SCW) with IBIS and SPI and with JEM-X (within parentheses), IBIS and SPI observing exposures (Exp1), JEM-X exposure (Exp2) and the power-law slope (Γ) of the 30–100 keV IBIS/ISGRI spectra are shown.
| HR . | SCW (JEM-X) number . | Exp1 (ks) . | Exp2 (ks) . | Γ . |
|---|---|---|---|---|
| 0.37–0.41 | 7 (1) | 15.4 | 2.2 | 2.6+ 0.04− 0.03 |
| 0.43–0.48 | 12 (2) | 36.8 | 6.5 | 2.32 ± 0.02 |
| 0.48–0.50 | 35 (9) | 111.5 | 27.8 | 2.29 ± 0.01 |
| 0.50–0.53 | 59 (8) | 181.1 | 22.9 | 2.23 ± 0.02 |
| 0.53–0.56 | 82 (11) | 236.8 | 34.0 | 2.17 ± 0.02 |
| 0.56–0.58 | 38 (19) | 101.0 | 51.1 | 2.08 ± 0.02 |
| 0.58–0.61 | 113 (40) | 343.4 | 113.7 | 2.02 ± 0.02 |
| 0.61–0.64 | 97 (27) | 287.7 | 80.3 | 1.98 ± 0.02 |
| 0.64–0.66 | 114 (29) | 944.2 | 34.7 | 1.81 ± 0.02 |
| 0.66–0.68 | 340 (72) | 781.4 | 147.8 | 1.79 ± 0.02 |
| 0.68–0.70 | 157 (16) | 402.0 | 34.2 | 1.74 ± 0.02 |
| 0.70–0.72 | 9 (4) | 26.1 | 8.0 | 1.73 ± 0.02 |
| HR . | SCW (JEM-X) number . | Exp1 (ks) . | Exp2 (ks) . | Γ . |
|---|---|---|---|---|
| 0.37–0.41 | 7 (1) | 15.4 | 2.2 | 2.6+ 0.04− 0.03 |
| 0.43–0.48 | 12 (2) | 36.8 | 6.5 | 2.32 ± 0.02 |
| 0.48–0.50 | 35 (9) | 111.5 | 27.8 | 2.29 ± 0.01 |
| 0.50–0.53 | 59 (8) | 181.1 | 22.9 | 2.23 ± 0.02 |
| 0.53–0.56 | 82 (11) | 236.8 | 34.0 | 2.17 ± 0.02 |
| 0.56–0.58 | 38 (19) | 101.0 | 51.1 | 2.08 ± 0.02 |
| 0.58–0.61 | 113 (40) | 343.4 | 113.7 | 2.02 ± 0.02 |
| 0.61–0.64 | 97 (27) | 287.7 | 80.3 | 1.98 ± 0.02 |
| 0.64–0.66 | 114 (29) | 944.2 | 34.7 | 1.81 ± 0.02 |
| 0.66–0.68 | 340 (72) | 781.4 | 147.8 | 1.79 ± 0.02 |
| 0.68–0.70 | 157 (16) | 402.0 | 34.2 | 1.74 ± 0.02 |
| 0.70–0.72 | 9 (4) | 26.1 | 8.0 | 1.73 ± 0.02 |
The IBIS scientific analysis, focused on the low-energy detector ISGRI (Lebrun et al. 2003) and the JEM-X analysis have been performed using the INTEGRAL offline analysis software, osa v.9 (Courvoisier et al. 2003; Goldwurm et al. 2003). The IBIS/ISGRI light curves (Fig. 1) have been extracted in two energy bands (20–40 keV, 40–80 keV). JEM-X and IBIS/ISGRI spectra, extracted SCW by SCW, extend from 3 to 20 keV and from 20 to 500 keV, respectively.

From top to bottom: ASM count rate in 1.5–3 keV, ASM HR (3–6 keV/1.5–3 keV), IBIS/ISGRI count rate in 20–40 keV, IBIS/ISGRI hardness (40–80 keV/20–40 keV).
To account for change over time of the energy response, IBIS is calibrated in different periods using dedicated observations of the Crab. Then for each Crab observation an ancillary response file (ARF) is estimated and associated with a given interval of revolutions in the INTEGRAL data (see IBIS User Manual). Since spectra in our data analysis (see Section 2.2) often correspond to observations collected in different periods, i.e. associated with different ARF files, we evaluated for each averaged spectrum an ARF file obtained by a weighted mean of the effective areas in the different periods involved.
2.1 SPI data treatment
The signal recorded by SPI camera is composed of contributions from sources in the FOV convolved with the instrument response function plus the background. A system of equations is to be solved to determine sources and background intensities. In order to reduce the number of uncertainties and hence to maximize the signal-to-noise ratio of each sources, a few assumptions are introduced.
The background count rates of the 19 Ge detectors (uniformity maps) are assumed to be stable on time-scale of ∼6 months, while the global normalization factor is determined on ∼6 h time-scale. For the sources, the time-scales are chosen as a function of the source intensity and temporal behaviour: the faint sources are considered as constant. More information and details on SPI data reduction can be found in Bouchet et al. (2008) and Bouchet, Roques & Jourdain (2011).
At energy around 1 MeV, high-energy particles saturate the electronics and can generate false events. The trigger signal issued by the pulse shape discriminators is used to select events between 650 keV and 2.2 MeV as explained in Jourdain & Roques (2009).
In order to maximize the signal-to-noise ratio, we used a catalogue containing sources detected above 2σ in the whole time interval spawned by the data. The catalogue contains 10, 6, 5 and 1 sources in the 25–50, 50–100, 100–300 and 300–600 keV energy bands, respectively. In addition Cyg X-1 is time-variable up to ∼400 keV, while above ∼400 keV, the signal-to-noise ratio is better when assuming Cyg X-1 as constant. Above 500 keV, we can derive a better uniformity map using high-latitude exposures (telescope pointing axis satisfying |b| > 30°) as they contain no significant source emission (Bouchet et al. 2010). Comparison of the fluxes obtained with this uniformity map and one that is determined by the fitting algorithm (Bouchet et al. 2011) shows that the difference in determined fluxes is well smaller than the error bars and hence fluxes are fully compatible. In this paper, we use SPI spectra from 22 keV up to 1 MeV (when possible because of the statistics).
2.2 Long-term behaviour and spectral variability
As a first step in characterizing the spectral variability (i.e. spectral states) of Cyg X-1, we computed the HR defined as the count rate ratio 40–80 to 20–40 keV for each one of the 1024 IBIS pointings (Fig. 1, panel 4). Cyg X-1 was most of the time in HS, so observations in HS are significantly more numerous than the ones in SS (Fig. 2). During the first three years of the INTEGRAL monitoring, Cyg X-1 showed a very variable activity in terms of both flux variation and spectral transition. Since middle of 2006, the source entered in an almost steady HS, characterized by flux variability not combined with simultaneous spectral variability (see the two flares around MJD∼540 00 and MJD∼546 00 and the corresponding flat HR in Fig. 1 panels 3 and 4, respectively). For comparison with the soft X-rays, we plot the RXTE/ASM long-term behaviour, as well as the HR (Fig. 1, panels 1 and 2).
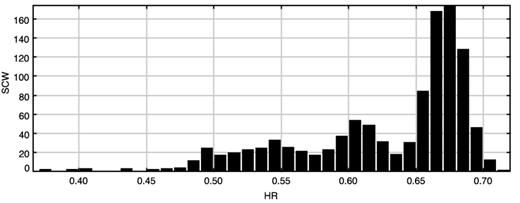
Number of the INTEGRAL pointings considered in this paper versus IBIS/ISGRI HR (40–80 keV/20–40 keV).
We have fitted individually all 1024 IBIS/ISGRI spectra from 20 to 80 keV with a simple power-law model and verified that at an SCW level IBIS spectra in this band are described by a power law with a null hypothesis probability higher than 5 per cent. Therefore, the HR we have defined can be used as a spectral state indicator.
The 1024 IBIS/ISGRI by-pointing spectra have been first averaged within each HR bin (HR bin-size = 0.01), resulting in 31 spectra covering the range HR = 0.37–0.72. These spectra have been fitted in the range 30–100 keV with a simple power law. The correlation photon index versus HR is shown in Fig. 3. Then, for the second step in averaging our IBIS spectra, in order to obtain a better statistics at high energy (above 100 keV), we have used two combined criteria. We averaged data from neighbouring HR bins with compatible (90 per cent confidence level) 30–100 keV power-law slopes (first criterium; see Fig. 3) until the error on Γ is reduced down to at least 0.02 (second criterium; Table 1). At the end, we have obtained 12 IBIS spectra collected with distinct shape spanning most of the range of observed spectral diversity of Cyg X-1.
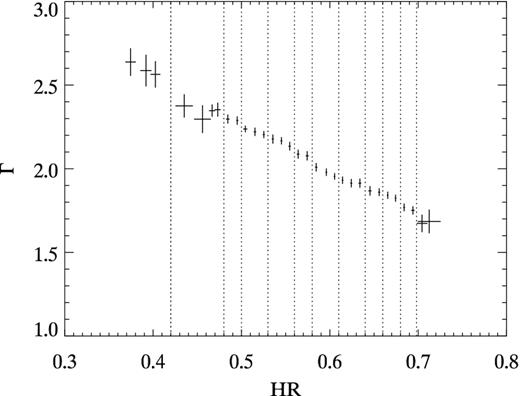
Correlation between the spectral photon index of the IBIS spectra fitted with a simple power law in the range 30–100 keV and the HR 40–80/20–40 keV. The dashed lines indicate the 12 data groups used for the final spectral analysis (see the text).
The JEM-X spectra have been then averaged following the IBIS selection. We checked the JEM-X spectral variability inside our IBIS HR bins and found that spectra inside the HR bin we have chosen are compatible with a constant slope in the JEM-X band. The SPI spectra have been extracted from the same 12 IBIS SCW groups.
3 MODELS
The 12 averaged broad-band spectra have been fitted with xspec v.11.3.2, using two Comptonization models, namely eqpair (Coppi 1999, G99) and belm (B08, MB09), plus disc reflection and relativistic iron line emission. The best-fitting parameters of the 12 averaged broad-band spectra are shown in Table 2 (eqpair) and Table 4 (belm). All quoted errors are at 90 per cent confidence level.
3.1 Coronal emission models
eqpair and belm model the emission from a homogeneous, isotropic, spherical cloud of fully ionized matter in interaction with the ambient radiation field. Not only do they compute the observed photon spectrum of the corona, but also they give the energy distributions of leptons in the corona. Those results are computed self-consistently according to the following microphysical processes: lepton–lepton Coulomb collisions, Compton scattering, photon–photon pair production, pair annihilation, self-absorbed bremsstrahlung radiation and self-absorbed synchrotron radiation (the latter for belm only). The leptons distributions are generally found to be composed of a low-energy thermal population and an additional high-energy non-thermal population, so those kind of models are usually called hybrid models. The main physical parameters that characterize such corona are its typical size, density, magnetic field, and how it is energized. However, the spectral properties depend more explicitly on non-dimensional combinations of these quantities.
For instance, the dependence on the absolute coronal size is negligible for most parameter regimes, and the radius is set to R = 5 × 107 cm, which corresponds to a region of about R ≈ 20Rg for a 15 M⊙ BH.
The proton density np is represented by the proton Thomson optical depth τp = npσTR, where σT is the Thomson cross-section. The Thomson optical depth τp provided by the two models is related to the ionization electrons only. The total optical depth (τtot) is the sum of the optical depth of e+e− pairs plus τp.
Photon escape can only be dealt with exactly by Monte Carlo or complete radiation transfer simulation. Instead, it is modelled here through an approximate escape probability formalism (e.g. Lightman, Zdziarski & Rees 1987; Lightman & Zdziarski 1987; Stern et al. 1995). eqpair uses an escape probability based on pure photon scattering, whereas the escape probability used in the present version of belm is based on both photon scattering and absorption (Sobolev 1974; Vurm & Poutanen 2009), which can lead to significant differences for low-energy photons and large optical depths. Although results with the two models can give slightly different results for a given set of parameters, the spectral dependence on parameters is identical in both models.
To compensate for losses associated with photon escape, energy can be injected in the corona (i) directly as external photons from the accretion disc, or indirectly to the leptons populations through two channels: (ii) thermal heating or (iii) non-thermal acceleration.
External photons are assumed to originate from a optically thick, multitemperature accretion disc extending from the minimal stable orbit of a non-rotating BH Rin = 6Rg out to Rout = 103Rg. The emitted multicolour blackbody spectrum is then essentially determined by the temperature Tin at the inner radius. As for the source luminosity, the power injected as soft photons is characterized by the soft compactness: ls (also named lbb in eqpair).
Thermal heating provides energy to the pool of thermal leptons with a compactness parameter lth.
Non-thermal processes such as magnetic reconnection and/or shock acceleration are expected to generate power-law like distributions of particles. This is modelled as an injection of leptons with a power-law distribution |$f(\gamma )\propto \gamma ^{-\Gamma _{\rm inj}}$| characterized by the minimal and maximal Lorentz factor γmin = 1.3 and γmax = 103 between which the acceleration takes place, the power-law index Γinj, and the total injected power described by the compactness lnth.
lh = lth + lnth corresponds to the total power supplied directly to the plasma. In steady state, all injected power goes out as photons and l = ls + lth + lnth. As far as the compactness l does not reach too large values (l < 100), the spectral shape is rather insensitive to the total compactness and to the absolute values of ls, lth and lnth. However, it depends on the channel used to injected this power, i.e. on ratios such as lh/ls and lnth/lh. For this reason, it is customary to fix ls to some reasonable value when fitting data with eqpair.
Since the shape of the spectrum depends on the ratio lB/l rather than on the absolute value of lB, we computed the belm code leaving lB/lh as free spectral parameter.
Also, in the belm code the thermalization process is treated self-consistently while in eqpair the electron distribution is assumed to be purely thermal at low energy (see MB09 for details).
The computation time with belm is comparatively longer than with eqpair and the former cannot be used for inline fitting. Instead, a table of spectra was computed and used in xspec as a table model.
3.2 Reflection on the accretion disc
Compton reflection has been modelled by using the viewing-angle-dependent Green’s functions approximation obtained by Magdziarz & Zdziarski (1995) for an isotropic point source (or equivalently an optically thin corona) above a slab. We treat Ω/2π as a free parameter, where Ω is an effective (i.e. corresponding to the observed strength of reflection) solid angle subtended by the reflector. The reflection is accompanied by an Fe fluorescence Kα line centred at an energy, Eline.
When the reflection comes from a fast rotating disc in a strong gravitational potential, Doppler and gravitational shifts become important. These effects are usually approximated by convolving both the reflected component and the Fe Kα line with the Schwarzschild disc line profile of Fabian et al. (1989; diskline in xspec).
In calculating the relativistic distortion, we consider a range of radii from Rin = 6 to Rout = 1000 gravitational radii. The disc reflection component is calculated for neutral material with standard abundances. We assumed an inclination angle of 50|${^{\circ}_{.}}$|
Due to the energy resolution and line sensitivity, the iron line study cannot be performed with JEM-X. The line energy was therefore imposed at 6.7 keV. The inclination angle, inner radius of the disc and the disc emissivity law were fixed at the same values as in the Compton reflection model. The normalization is therefore the only free parameter for the iron line emission.
4 RESULTS
4.1 Unmagnetized model
As a first study, we investigate here a model with no magnetic field (lB = 0), so we performed the analysis with EQPAIR. According to previous studies (Zdziarski et al. 2002; Wilms et al. 2006), we also have found that the bolometric luminosity of Cyg X-1 does not change significantly from SS to HS. Therefore, unless the size of the corona changes dramatically during the transition, the total compactness is not expected to vary much (Poutanen & Coppi 1998). However, the distribution of the radiation changes dramatically. In the HS, most of the luminosity comes from the corona while in SS most of the radiation is in the blackbody disc emission. We therefore fixed ls = 10 when fitting soft and intermediate/SS (States 1–4 in Table 2; G99) and ls = 1 when fitting the intermediate/hard and HS (States 5–12; Ibragimov et al. 2005).
The best-fitting parameters are shown in Table 2. We note that spectrum 1 shows spectral parameters of the canonical SS, according also to the hard X-ray power-law slope (Table 1), while spectra 9–12 show typical spectral parameters of the HS (see Zdziarski 2000; Zdziarski & Gierliński 2004). Spectra 2–8 may be defined as intermediate. In addition, we call intermediate/soft all spectra where a disc blackbody is required by the fitting procedure and intermediate/hard the spectra where it is not possible to give constraints to the inner disc temperature.
In Fig. 4, we show the relation between the best-fitting model parameters and the hard X-ray power-law slopes. Four significantly different energy spectra of Cyg X-1 are plotted in Fig. 5, while in Fig. 6 we show the total best-fitting models for each of the 12 selected spectra.
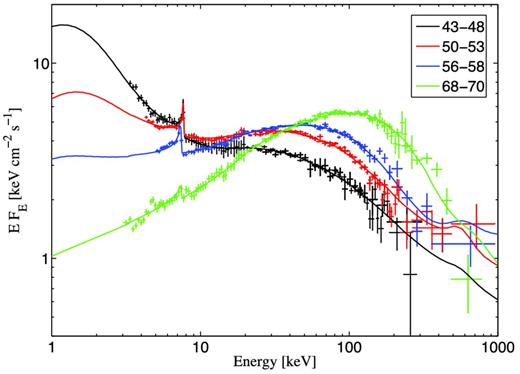
Joint JEM-X, IBIS and SPI energy spectra of Cyg X-1 during four different spectral states fitted with the thermal/non-thermal hybrid Comptonization model eqpair plus diskline (see Table 2).
In agreement with previous studies (G99), our fits show that the electron–positron pairs constitute only a small, if not negligible, fraction of the Comptonizing leptons. An interesting trend (shown in Fig. 4) is that the Thomson optical depth is lower in softest states (τp ≃ 0.2 in SS). It increases significantly from SS (spectrum 1) to intermediate states (spectra 2–8) and is approximately constant in the HS (τp ≃ 1.4, spectra 9–12). This change by a factor of 7 could be associated either to a change in electron density or in the size of the corona (since τ ∝ neR). If this is the size of the corona that changes then this would imply that the corona is larger in the HS than in the SS by a factor of ∼7. This would be in agreement with the decrease of the inner radius of the accretion disc and faster rapid variability in the SS which both suggest a smaller emitting region in the SS. But the electron density could also drive the change in Thomson depth. This could be the case if the material in the corona gradually condensates into the accretion disc when the source evolves towards softer states. Another possibility would be that the coronal material is evacuated during the ejection event (optically thin radio flare) at the spectral transition (as suggested by Rodriguez & Prat 2010). However, we see in Fig. 4 that the evolution of τp is gradual. It starts in the intermediate/hard states and continues in the SS, this appears in contradiction with a scenario in which most of the corona would be suddenly ejected at the transition. If the corona is ejected this has to be a gradual process that might be associated with the presence of strong disc winds evidenced in the SS of X-ray binaries (see e.g. Ponti et al. 2012).
We find that the inner disc temperature kTin decreases from 0.6 and 0.4 keV between spectrum 1 and 4 (SS to intermediate/soft state, see Table 2). This is combined with a decrease by a factor of 4 of the flux of the measured thermal disc component. For harder spectra, the disc temperature is so low that it cannot be constrained with our data. We therefore imposed an inner disc temperature of 0.3 keV when in intermediate/hard states (spectra 5–8) and 0.1 keV when in canonical HS (spectra 9–12). The temperature of the corona has the opposite behaviour and is larger for harder spectra, except for spectrum 1. This change of coronal temperature is driven by a change in the ratio of the electron heating rate to soft cooling photon flux in the corona (∝lh/ls) which is larger at small Γ. The fact that the temperature appears higher in the softer spectrum 1 is related to the significantly smaller optical depth in SS. In fact, even if the temperature is higher in spectrum 1, the Compton parameter y ∝ τTTe which is expected to vary approximately like lh/ls is the lowest. Then computing the absolute disc and Comptonized fluxes (respectively, |$F_{\text{bb}}$| and |$F_{\text{Compt}}$|, see Table 2) can provide indications on whether this evolution is driven by changes in the flux of soft cooling photons from the disc (∝ls) or changes in the electron heating rate (∝lh). We find that the thermal disc flux changes by more than one order of magnitude while the Comptonized radiation decreases by almost a factor of 2. The softening we observe in the states 1–4 appears to be caused by a dramatic increase in the disc thermal flux in the corona associated with a modest reduction of the electron heating rate.
Non-thermal acceleration appears to be required to fit most spectra. When trying to fit with a non-thermal compactness fraction fixed to lnth/lh = 0, only for the spectrum 12 we obtained an acceptable χ2ν (i.e. 0.98). However, for this last spectrum the statistics is very low and residuals show that an additional non-thermal component is required at high energy. For the other spectra, significant lnth/lh fractions are required. This indicates that a non-thermal electrons population may also be present in the corona (or elsewhere), together with the thermal population even during the HS. This is in agreement with previous studies performed on intermediate and hard states of BHBs, as also reported in Section 1. In soft and intermediate/soft states (1–4) though, it was not possible to constrain lnth/lh and this parameter was fixed at 0.99.
From our spectral fits, from the softest (spectrum 1) to the harder states (up to spectrum 9) Γinj parameter changes from 3.5 to 2.0. We are not able to put constraints on this parameter for spectra 10–12, so we fixed it to 2. Such a change in the slope of the injected non-thermal electrons suggests a different acceleration mechanism in SS and HS and may support the view that the non-thermal excess in the HS has a different origin (e.g. the jet). We note however that the results of MC02 suggest a different evolution (i.e. Γinj larger in the HS). It is possible that the soft injection we infer in the SS is related to the lack of photon statistic above 100 keV and to the fact that the non-thermal compactness fraction lnth/lh was fixed when fitting the softest spectra.
We checked the need for the reflection component freezing Ω/2π at 0. The results show that the χ2 are consistently worst (F-test probabilities <10−4), confirming that introducing the reflection component improves significantly the fits. Our fits suggest that the reflection component is significantly higher only in the softest state (spectrum 1) of our data set, while it is almost constant within the errors in the other states. This is a known result which can be interpreted as follows. In the HS, the reflecting disc intercepts a small fraction of the coronal radiation since the disc is truncated at a large distance from the BH; in the SS, the accretion disc extends down to the last stable orbit and is sandwiched by the illuminating corona (Done et al. 2007).
4.2 Magnetized, one-zone model with pure non-thermal acceleration
If the corona is magnetized, it must emit synchrotron emission that can add up to disc photons and be Comptonized. In this section, we aim at answering the question: How large can be the magnetic field before synchrotron emission makes the modelled spectra incompatible with the data? It was shown in MB09 and PV09 that processes such as the synchrotron boiler and Coulomb collisions can thermalize particle distribution efficiently, even when particles are accelerated through pure non-thermal mechanisms. To minimize the number of parameters, we focus here on such a model with pure non-thermal acceleration. The alternative case of thermal heating will be discussed in the next subsection.
Using belm, we have computed a table of more than 5 × 105 spectra and 5 fitting parameters: lnth/l, lB/lnth, τp, Γinj and kTin (see Table 3). This pure synchrotron self-Compton (SSC) model does not include any thermal or Coulomb heating (lth = lc = 0). As shown in MB09, the spectrum shape depends on ratios such as lB/lnth or lnth/l and not on the total compactness of the source. Therefore, the best-fitting values for these ratios are also insensitive to the exact value of l. The total compactness was thus set to the typical value l = 10, and ls was computed such as ls + lnth = l = 10.
Fitting parameters of the belm table model used in xspec and their properties (minimal and maximal values, number of interpolation values and grid style). Other parameters are set to: l = 10, ls = l − lnth, lth = 0, γmin = 1.3, γmax = 103, R = 5 × 107 cm.
| . | min . | max . | number . | grid . |
|---|---|---|---|---|
| lnth/l | 0.1 | 10 | 15 | log |
| lB/lnth | 0.001 | 10 | 15 | log |
| τp | 0.005 | 5 | 15 | log |
| Γinj | 1 | 5 | 15 | lin |
| kTin | 20 eV | 2 keV | 10 | log |
| . | min . | max . | number . | grid . |
|---|---|---|---|---|
| lnth/l | 0.1 | 10 | 15 | log |
| lB/lnth | 0.001 | 10 | 15 | log |
| τp | 0.005 | 5 | 15 | log |
| Γinj | 1 | 5 | 15 | lin |
| kTin | 20 eV | 2 keV | 10 | log |
Fitting parameters of the belm table model used in xspec and their properties (minimal and maximal values, number of interpolation values and grid style). Other parameters are set to: l = 10, ls = l − lnth, lth = 0, γmin = 1.3, γmax = 103, R = 5 × 107 cm.
| . | min . | max . | number . | grid . |
|---|---|---|---|---|
| lnth/l | 0.1 | 10 | 15 | log |
| lB/lnth | 0.001 | 10 | 15 | log |
| τp | 0.005 | 5 | 15 | log |
| Γinj | 1 | 5 | 15 | lin |
| kTin | 20 eV | 2 keV | 10 | log |
| . | min . | max . | number . | grid . |
|---|---|---|---|---|
| lnth/l | 0.1 | 10 | 15 | log |
| lB/lnth | 0.001 | 10 | 15 | log |
| τp | 0.005 | 5 | 15 | log |
| Γinj | 1 | 5 | 15 | lin |
| kTin | 20 eV | 2 keV | 10 | log |
The fitted parameters of the joint JEM-X, IBIS and SPI spectra in 12 different spectral states. Fits have been performed with eqpair combined with diskline. Values in parentheses denote parameters fixed during the fits. One of the interesting fixed parameters is ls (lbb in eqpair) which is fixed at 10 for states 1–4 and at 1 for states 5–12. The inner disc temperature is fixed at 0.3 keV in the intermediate states, while it is 0.1 keV in the harder ones. See the text for the parameters description.
| State . | HR . | lh/ls . | lnth/lh . | τp . | kTin (eV) . | Ω/2π . | Γinj . | τtot . | kTe (keV) . | χ2ν(dof) . | Flux × 10−8 (erg cm−2 s−1 ) . | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | . | . | . | . | . | . | . | . | |$\text{Bol}$| . | |$\text{bb}$| . | |$\text{Compt}$| . |
| 1 | 0.37–0.41 | 0.30+ 0.05− 0.04 | (0.99) | 0.20+ 0.18− 0.08 | 627+ 31− 108 | 0.9+ 0.3− 0.1 | 3.44+ 0.07− 0.08 | 0.20 | 48.0 | 0.82(89) | 8.1 | 5.2 | 2.4 |
| 2 | 0.43–0.48 | 0.7 ± 0.1 | (0.99) | 0.8+ 0.2− 0.4 | 416+ 144− 39 | 0.4+ 0.2− 0.1 | 2.93+ 0.04− 0.06 | 0.86 | 25.0 | 0.97(127) | 7.8 | 3.4 | 4.2 |
| 3 | 0.48–0.50 | 1.35+ 0.08− 0.20 | (0.99) | 1.21+ 0.15− 0.08 | 426+ 93− 75 | 0.41+ 0.08− 0.16 | 2.92+ 0.05− 0.02 | 1.24 | 25.7 | 0.99(129) | 7.8 | 2.1 | 5.2 |
| 4 | 0.50–0.53 | 1.63+ 0.04− 0.02 | (0.99) | 1.44+ 0.01− 0.03 | 430+ 24− 20 | 0.37+ 0.03− 0.02 | 2.80+ 0.03− 0.02 | 1.48 | 23.7 | 1.04(125) | 5.4 | 1.2 | 3.8 |
| 5 | 0.53–0.56 | 3.88+ 0.09− 0.06 | 0.75+ 0.06− 0.04 | 1.63 ± 0.02 | (300) | 0.17 ± 0.03 | 2.37+ 0.08− 0.03 | 1.7 | 37.6 | 0.98(120) | 4.6 | 0.6 | 3.8 |
| 6 | 0.56–0.58 | 4.4+ 0.2− 0.1 | 0.83 ± 0.08 | 1.61+ 0.20− 0.03 | (300) | 0.28+ 0.02− 0.04 | 2.4 ± 0.1 | 1.62 | 41.0 | 0.98(116) | 4.3 | 0.5 | 3.5 |
| 7 | 0.58–0.61 | 5.19+ 0.06− 0.15 | 0.87+ 0.05− 0.02 | 1.51+ 0.03− 0.02 | (300) | 0.29+ 0.03− 0.01 | 2.50+ 0.03− 0.17 | 1.52 | 47.2 | 0.99(118) | 4.3 | 0.4 | 3.6 |
| 8 | 0.61–0.64 | 6.1+ 0.1− 0.2 | 0.86+ 0.06− 0.05 | 1.50+ 0.07− 0.03 | (300) | 0.32 ± 0.03 | 2.33+ 0.03− 0.06 | 1.53 | 48.4 | 1.09(119) | 4.4 | 0.4 | 3.6 |
| 9 | 0.64–0.66 | 11.3+ 0.3− 0.2 | 0.55+ 0.01− 0.07 | 1.30+ 0.02− 0.06 | (100) | 0.23+ 0.04− 0.02 | 2.5+ 0.4− 0.3 | 1.34 | 67.6 | 0.91(125) | 4.2 | 0.3 | 3.8 |
| 10 | 0.66–0.68 | 16.2+ 0.2− 0.4 | 0.51 ± 0.03 | 1.38+ 0.06− 0.04 | (100) | 0.36+ 0.11− 0.02 | (2.0) | 1.53 | 64.6 | 0.96(66) | 4.7 | 0.1 | 4.0 |
| 11 | 0.68–0.70 | 16.3+ 0.8− 0.3 | 0.33+ 0.02− 0.03 | 1.30+ 0.06− 0.02 | (100) | 0.31+ 0.03− 0.02 | (2.0) | 1.41 | 76.0 | 1.04(130) | 3.5 | 0.1 | 3.1 |
| 12 | 0.70–0.72 | 15.8+ 0.7− 1.2 | 0.3+ 0.2− 0.1 | 1.3 ± 0.1 | (100) | 0.33+ 0.06− 0.04 | (2.0) | 1.39 | 77.2 | 0.95(132) | 4.9 | 0.1 | 4.3 |
| State . | HR . | lh/ls . | lnth/lh . | τp . | kTin (eV) . | Ω/2π . | Γinj . | τtot . | kTe (keV) . | χ2ν(dof) . | Flux × 10−8 (erg cm−2 s−1 ) . | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | . | . | . | . | . | . | . | . | |$\text{Bol}$| . | |$\text{bb}$| . | |$\text{Compt}$| . |
| 1 | 0.37–0.41 | 0.30+ 0.05− 0.04 | (0.99) | 0.20+ 0.18− 0.08 | 627+ 31− 108 | 0.9+ 0.3− 0.1 | 3.44+ 0.07− 0.08 | 0.20 | 48.0 | 0.82(89) | 8.1 | 5.2 | 2.4 |
| 2 | 0.43–0.48 | 0.7 ± 0.1 | (0.99) | 0.8+ 0.2− 0.4 | 416+ 144− 39 | 0.4+ 0.2− 0.1 | 2.93+ 0.04− 0.06 | 0.86 | 25.0 | 0.97(127) | 7.8 | 3.4 | 4.2 |
| 3 | 0.48–0.50 | 1.35+ 0.08− 0.20 | (0.99) | 1.21+ 0.15− 0.08 | 426+ 93− 75 | 0.41+ 0.08− 0.16 | 2.92+ 0.05− 0.02 | 1.24 | 25.7 | 0.99(129) | 7.8 | 2.1 | 5.2 |
| 4 | 0.50–0.53 | 1.63+ 0.04− 0.02 | (0.99) | 1.44+ 0.01− 0.03 | 430+ 24− 20 | 0.37+ 0.03− 0.02 | 2.80+ 0.03− 0.02 | 1.48 | 23.7 | 1.04(125) | 5.4 | 1.2 | 3.8 |
| 5 | 0.53–0.56 | 3.88+ 0.09− 0.06 | 0.75+ 0.06− 0.04 | 1.63 ± 0.02 | (300) | 0.17 ± 0.03 | 2.37+ 0.08− 0.03 | 1.7 | 37.6 | 0.98(120) | 4.6 | 0.6 | 3.8 |
| 6 | 0.56–0.58 | 4.4+ 0.2− 0.1 | 0.83 ± 0.08 | 1.61+ 0.20− 0.03 | (300) | 0.28+ 0.02− 0.04 | 2.4 ± 0.1 | 1.62 | 41.0 | 0.98(116) | 4.3 | 0.5 | 3.5 |
| 7 | 0.58–0.61 | 5.19+ 0.06− 0.15 | 0.87+ 0.05− 0.02 | 1.51+ 0.03− 0.02 | (300) | 0.29+ 0.03− 0.01 | 2.50+ 0.03− 0.17 | 1.52 | 47.2 | 0.99(118) | 4.3 | 0.4 | 3.6 |
| 8 | 0.61–0.64 | 6.1+ 0.1− 0.2 | 0.86+ 0.06− 0.05 | 1.50+ 0.07− 0.03 | (300) | 0.32 ± 0.03 | 2.33+ 0.03− 0.06 | 1.53 | 48.4 | 1.09(119) | 4.4 | 0.4 | 3.6 |
| 9 | 0.64–0.66 | 11.3+ 0.3− 0.2 | 0.55+ 0.01− 0.07 | 1.30+ 0.02− 0.06 | (100) | 0.23+ 0.04− 0.02 | 2.5+ 0.4− 0.3 | 1.34 | 67.6 | 0.91(125) | 4.2 | 0.3 | 3.8 |
| 10 | 0.66–0.68 | 16.2+ 0.2− 0.4 | 0.51 ± 0.03 | 1.38+ 0.06− 0.04 | (100) | 0.36+ 0.11− 0.02 | (2.0) | 1.53 | 64.6 | 0.96(66) | 4.7 | 0.1 | 4.0 |
| 11 | 0.68–0.70 | 16.3+ 0.8− 0.3 | 0.33+ 0.02− 0.03 | 1.30+ 0.06− 0.02 | (100) | 0.31+ 0.03− 0.02 | (2.0) | 1.41 | 76.0 | 1.04(130) | 3.5 | 0.1 | 3.1 |
| 12 | 0.70–0.72 | 15.8+ 0.7− 1.2 | 0.3+ 0.2− 0.1 | 1.3 ± 0.1 | (100) | 0.33+ 0.06− 0.04 | (2.0) | 1.39 | 77.2 | 0.95(132) | 4.9 | 0.1 | 4.3 |
The fitted parameters of the joint JEM-X, IBIS and SPI spectra in 12 different spectral states. Fits have been performed with eqpair combined with diskline. Values in parentheses denote parameters fixed during the fits. One of the interesting fixed parameters is ls (lbb in eqpair) which is fixed at 10 for states 1–4 and at 1 for states 5–12. The inner disc temperature is fixed at 0.3 keV in the intermediate states, while it is 0.1 keV in the harder ones. See the text for the parameters description.
| State . | HR . | lh/ls . | lnth/lh . | τp . | kTin (eV) . | Ω/2π . | Γinj . | τtot . | kTe (keV) . | χ2ν(dof) . | Flux × 10−8 (erg cm−2 s−1 ) . | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | . | . | . | . | . | . | . | . | |$\text{Bol}$| . | |$\text{bb}$| . | |$\text{Compt}$| . |
| 1 | 0.37–0.41 | 0.30+ 0.05− 0.04 | (0.99) | 0.20+ 0.18− 0.08 | 627+ 31− 108 | 0.9+ 0.3− 0.1 | 3.44+ 0.07− 0.08 | 0.20 | 48.0 | 0.82(89) | 8.1 | 5.2 | 2.4 |
| 2 | 0.43–0.48 | 0.7 ± 0.1 | (0.99) | 0.8+ 0.2− 0.4 | 416+ 144− 39 | 0.4+ 0.2− 0.1 | 2.93+ 0.04− 0.06 | 0.86 | 25.0 | 0.97(127) | 7.8 | 3.4 | 4.2 |
| 3 | 0.48–0.50 | 1.35+ 0.08− 0.20 | (0.99) | 1.21+ 0.15− 0.08 | 426+ 93− 75 | 0.41+ 0.08− 0.16 | 2.92+ 0.05− 0.02 | 1.24 | 25.7 | 0.99(129) | 7.8 | 2.1 | 5.2 |
| 4 | 0.50–0.53 | 1.63+ 0.04− 0.02 | (0.99) | 1.44+ 0.01− 0.03 | 430+ 24− 20 | 0.37+ 0.03− 0.02 | 2.80+ 0.03− 0.02 | 1.48 | 23.7 | 1.04(125) | 5.4 | 1.2 | 3.8 |
| 5 | 0.53–0.56 | 3.88+ 0.09− 0.06 | 0.75+ 0.06− 0.04 | 1.63 ± 0.02 | (300) | 0.17 ± 0.03 | 2.37+ 0.08− 0.03 | 1.7 | 37.6 | 0.98(120) | 4.6 | 0.6 | 3.8 |
| 6 | 0.56–0.58 | 4.4+ 0.2− 0.1 | 0.83 ± 0.08 | 1.61+ 0.20− 0.03 | (300) | 0.28+ 0.02− 0.04 | 2.4 ± 0.1 | 1.62 | 41.0 | 0.98(116) | 4.3 | 0.5 | 3.5 |
| 7 | 0.58–0.61 | 5.19+ 0.06− 0.15 | 0.87+ 0.05− 0.02 | 1.51+ 0.03− 0.02 | (300) | 0.29+ 0.03− 0.01 | 2.50+ 0.03− 0.17 | 1.52 | 47.2 | 0.99(118) | 4.3 | 0.4 | 3.6 |
| 8 | 0.61–0.64 | 6.1+ 0.1− 0.2 | 0.86+ 0.06− 0.05 | 1.50+ 0.07− 0.03 | (300) | 0.32 ± 0.03 | 2.33+ 0.03− 0.06 | 1.53 | 48.4 | 1.09(119) | 4.4 | 0.4 | 3.6 |
| 9 | 0.64–0.66 | 11.3+ 0.3− 0.2 | 0.55+ 0.01− 0.07 | 1.30+ 0.02− 0.06 | (100) | 0.23+ 0.04− 0.02 | 2.5+ 0.4− 0.3 | 1.34 | 67.6 | 0.91(125) | 4.2 | 0.3 | 3.8 |
| 10 | 0.66–0.68 | 16.2+ 0.2− 0.4 | 0.51 ± 0.03 | 1.38+ 0.06− 0.04 | (100) | 0.36+ 0.11− 0.02 | (2.0) | 1.53 | 64.6 | 0.96(66) | 4.7 | 0.1 | 4.0 |
| 11 | 0.68–0.70 | 16.3+ 0.8− 0.3 | 0.33+ 0.02− 0.03 | 1.30+ 0.06− 0.02 | (100) | 0.31+ 0.03− 0.02 | (2.0) | 1.41 | 76.0 | 1.04(130) | 3.5 | 0.1 | 3.1 |
| 12 | 0.70–0.72 | 15.8+ 0.7− 1.2 | 0.3+ 0.2− 0.1 | 1.3 ± 0.1 | (100) | 0.33+ 0.06− 0.04 | (2.0) | 1.39 | 77.2 | 0.95(132) | 4.9 | 0.1 | 4.3 |
| State . | HR . | lh/ls . | lnth/lh . | τp . | kTin (eV) . | Ω/2π . | Γinj . | τtot . | kTe (keV) . | χ2ν(dof) . | Flux × 10−8 (erg cm−2 s−1 ) . | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | . | . | . | . | . | . | . | . | |$\text{Bol}$| . | |$\text{bb}$| . | |$\text{Compt}$| . |
| 1 | 0.37–0.41 | 0.30+ 0.05− 0.04 | (0.99) | 0.20+ 0.18− 0.08 | 627+ 31− 108 | 0.9+ 0.3− 0.1 | 3.44+ 0.07− 0.08 | 0.20 | 48.0 | 0.82(89) | 8.1 | 5.2 | 2.4 |
| 2 | 0.43–0.48 | 0.7 ± 0.1 | (0.99) | 0.8+ 0.2− 0.4 | 416+ 144− 39 | 0.4+ 0.2− 0.1 | 2.93+ 0.04− 0.06 | 0.86 | 25.0 | 0.97(127) | 7.8 | 3.4 | 4.2 |
| 3 | 0.48–0.50 | 1.35+ 0.08− 0.20 | (0.99) | 1.21+ 0.15− 0.08 | 426+ 93− 75 | 0.41+ 0.08− 0.16 | 2.92+ 0.05− 0.02 | 1.24 | 25.7 | 0.99(129) | 7.8 | 2.1 | 5.2 |
| 4 | 0.50–0.53 | 1.63+ 0.04− 0.02 | (0.99) | 1.44+ 0.01− 0.03 | 430+ 24− 20 | 0.37+ 0.03− 0.02 | 2.80+ 0.03− 0.02 | 1.48 | 23.7 | 1.04(125) | 5.4 | 1.2 | 3.8 |
| 5 | 0.53–0.56 | 3.88+ 0.09− 0.06 | 0.75+ 0.06− 0.04 | 1.63 ± 0.02 | (300) | 0.17 ± 0.03 | 2.37+ 0.08− 0.03 | 1.7 | 37.6 | 0.98(120) | 4.6 | 0.6 | 3.8 |
| 6 | 0.56–0.58 | 4.4+ 0.2− 0.1 | 0.83 ± 0.08 | 1.61+ 0.20− 0.03 | (300) | 0.28+ 0.02− 0.04 | 2.4 ± 0.1 | 1.62 | 41.0 | 0.98(116) | 4.3 | 0.5 | 3.5 |
| 7 | 0.58–0.61 | 5.19+ 0.06− 0.15 | 0.87+ 0.05− 0.02 | 1.51+ 0.03− 0.02 | (300) | 0.29+ 0.03− 0.01 | 2.50+ 0.03− 0.17 | 1.52 | 47.2 | 0.99(118) | 4.3 | 0.4 | 3.6 |
| 8 | 0.61–0.64 | 6.1+ 0.1− 0.2 | 0.86+ 0.06− 0.05 | 1.50+ 0.07− 0.03 | (300) | 0.32 ± 0.03 | 2.33+ 0.03− 0.06 | 1.53 | 48.4 | 1.09(119) | 4.4 | 0.4 | 3.6 |
| 9 | 0.64–0.66 | 11.3+ 0.3− 0.2 | 0.55+ 0.01− 0.07 | 1.30+ 0.02− 0.06 | (100) | 0.23+ 0.04− 0.02 | 2.5+ 0.4− 0.3 | 1.34 | 67.6 | 0.91(125) | 4.2 | 0.3 | 3.8 |
| 10 | 0.66–0.68 | 16.2+ 0.2− 0.4 | 0.51 ± 0.03 | 1.38+ 0.06− 0.04 | (100) | 0.36+ 0.11− 0.02 | (2.0) | 1.53 | 64.6 | 0.96(66) | 4.7 | 0.1 | 4.0 |
| 11 | 0.68–0.70 | 16.3+ 0.8− 0.3 | 0.33+ 0.02− 0.03 | 1.30+ 0.06− 0.02 | (100) | 0.31+ 0.03− 0.02 | (2.0) | 1.41 | 76.0 | 1.04(130) | 3.5 | 0.1 | 3.1 |
| 12 | 0.70–0.72 | 15.8+ 0.7− 1.2 | 0.3+ 0.2− 0.1 | 1.3 ± 0.1 | (100) | 0.33+ 0.06− 0.04 | (2.0) | 1.39 | 77.2 | 0.95(132) | 4.9 | 0.1 | 4.3 |
Table 4 shows the best-fitting parameters. Fig. 8 presents a selection of four different INTEGRAL spectra fitted with belm, while Figs 9 and 10 display, respectively, the photon spectra and the particle distribution, for the corresponding models. Overall this model provides a good fit to the data (Table 4). This confirms that the data are compatible with pure non-thermal acceleration models.
Same spectra as in Table 2 fitted with the belm model with pure non-thermal acceleration plus diskline and reflect.
| HR . | lnth/l . | lB/lnth . | τp . | Γinj . | kTin (keV) . | Ω/2π . | χ2ν(dof) . | FBol × 10− 8 (erg cm−2 s−1 ) . | B (Gauss) . | |$l_{B}/l_{\text{Br}}$| . |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.37–0.41 | 0.19+ 0.05− 0.03 | <4.5 | 0.26+ 0.43− 0.08 | 3.0+ 0.4− 0.7 | 0.5 ± 0.2 | 1.1+ 0.8− 0.4 | 0.85(88) | 7.2 | 3.1 × 106 | 3.29 |
| 0.43–0.48 | 0.29+ 0.09− 0.06 | <1.4 | 1.1+ 1.1− 0.5 | 2.7+ 0.3− 0.4 | 0.21+ 0.06− 0.04 | <0.4 | 0.96(126) | 6.7 | 2.1 × 106 | 1.34 |
| 0.48–0.50 | 0.60+ 0.04− 0.05 | <0.2 | 1.9+ 0.1− 0.2 | 2.5+ 0.2− 0.1 | 0.21+ 0.06− 0.04 | 0.4 ± 0.2 | 1.05(128) | 6.3 | 1.1 × 106 | 0.31 |
| 0.50–0.53 | 0.776+ 0.008− 0.005 | <0.007 | 2.56 ± 0.07 | 2.69+ 0.13− 0.05 | (0.2) | <0.2 | 1.0(112) | 3.8 | 1.8 × 105 | 0.012 |
| 0.53–0.56 | 0.815+ 0.004− 0.002 | <0.003 | 2.45 ± 0.04 | 2.76+ 0.08− 0.04 | (0.1) | <0.1 | 1.1(120) | 3.8 | 1.2 × 105 | 0.056 |
| 0.56–0.58 | (1) | 0.09+ 0.05− 0.02 | 2.3+ 0.1− 0.2 | 2.47+ 0.12− 0.09 | − | 0.13+ 0.08− 0.06 | 0.94(117) | 3.5 | 7.1 × 105 | 0.21 |
| 0.58–0.61 | (1) | 0.050+ 0.002− 0.006 | 2.3 ± 0.1 | 2.49+ 0.01− 0.04 | − | 0.16 ± 0.01 | 0.99(119) | 3.7 | 5.4 × 105 | 0.12 |
| 0.61–0.64 | (1) | 0.025 ± 0.001 | 2.17+ 0.08− 0.10 | 2.37+ 0.02− 0.04 | − | 0.21+ 0.02− 0.03 | 0.93(117) | 3.8 | 3.9 × 105 | 0.06 |
| 0.64–0.66 | (1) | 0.03+ 0.02− 0.01 | 2.04+ 0.05− 0.03 | 2.78+ 0.02− 0.03 | − | 0.10+ 0.02− 0.06 | 0.85(126) | 3.6 | 4.2 × 105 | 0.07 |
| 0.66–0.68 | (1) | 0.004+ 0.002− 0.001 | 2.3 ± 0.1 | 2.4 ± 0.1 | − | 0.25+ 0.02− 0.05 | 1.07(67) | 4.2 | 1.6 × 105 | 0.009 |
| 0.68–0.70 | (1) | 0.012 ± 0.002 | 2.07+ 0.06− 0.04 | 2.78+ 0.03− 0.15 | − | 0.22+ 0.07− 0.08 | 0.96(118) | 3.2 | 2.5 × 105 | 0.03 |
| 0.70–0.72 | (1) | 0.0025+ 0.017− 0.001 | 2.36+ 0.08− 0.29 | 2.18+ 0.47− 0.05 | − | 0.17+ 0.08− 0.11 | 1.03(132) | 4.6 | 1.3 × 105 | 0.006 |
| HR . | lnth/l . | lB/lnth . | τp . | Γinj . | kTin (keV) . | Ω/2π . | χ2ν(dof) . | FBol × 10− 8 (erg cm−2 s−1 ) . | B (Gauss) . | |$l_{B}/l_{\text{Br}}$| . |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.37–0.41 | 0.19+ 0.05− 0.03 | <4.5 | 0.26+ 0.43− 0.08 | 3.0+ 0.4− 0.7 | 0.5 ± 0.2 | 1.1+ 0.8− 0.4 | 0.85(88) | 7.2 | 3.1 × 106 | 3.29 |
| 0.43–0.48 | 0.29+ 0.09− 0.06 | <1.4 | 1.1+ 1.1− 0.5 | 2.7+ 0.3− 0.4 | 0.21+ 0.06− 0.04 | <0.4 | 0.96(126) | 6.7 | 2.1 × 106 | 1.34 |
| 0.48–0.50 | 0.60+ 0.04− 0.05 | <0.2 | 1.9+ 0.1− 0.2 | 2.5+ 0.2− 0.1 | 0.21+ 0.06− 0.04 | 0.4 ± 0.2 | 1.05(128) | 6.3 | 1.1 × 106 | 0.31 |
| 0.50–0.53 | 0.776+ 0.008− 0.005 | <0.007 | 2.56 ± 0.07 | 2.69+ 0.13− 0.05 | (0.2) | <0.2 | 1.0(112) | 3.8 | 1.8 × 105 | 0.012 |
| 0.53–0.56 | 0.815+ 0.004− 0.002 | <0.003 | 2.45 ± 0.04 | 2.76+ 0.08− 0.04 | (0.1) | <0.1 | 1.1(120) | 3.8 | 1.2 × 105 | 0.056 |
| 0.56–0.58 | (1) | 0.09+ 0.05− 0.02 | 2.3+ 0.1− 0.2 | 2.47+ 0.12− 0.09 | − | 0.13+ 0.08− 0.06 | 0.94(117) | 3.5 | 7.1 × 105 | 0.21 |
| 0.58–0.61 | (1) | 0.050+ 0.002− 0.006 | 2.3 ± 0.1 | 2.49+ 0.01− 0.04 | − | 0.16 ± 0.01 | 0.99(119) | 3.7 | 5.4 × 105 | 0.12 |
| 0.61–0.64 | (1) | 0.025 ± 0.001 | 2.17+ 0.08− 0.10 | 2.37+ 0.02− 0.04 | − | 0.21+ 0.02− 0.03 | 0.93(117) | 3.8 | 3.9 × 105 | 0.06 |
| 0.64–0.66 | (1) | 0.03+ 0.02− 0.01 | 2.04+ 0.05− 0.03 | 2.78+ 0.02− 0.03 | − | 0.10+ 0.02− 0.06 | 0.85(126) | 3.6 | 4.2 × 105 | 0.07 |
| 0.66–0.68 | (1) | 0.004+ 0.002− 0.001 | 2.3 ± 0.1 | 2.4 ± 0.1 | − | 0.25+ 0.02− 0.05 | 1.07(67) | 4.2 | 1.6 × 105 | 0.009 |
| 0.68–0.70 | (1) | 0.012 ± 0.002 | 2.07+ 0.06− 0.04 | 2.78+ 0.03− 0.15 | − | 0.22+ 0.07− 0.08 | 0.96(118) | 3.2 | 2.5 × 105 | 0.03 |
| 0.70–0.72 | (1) | 0.0025+ 0.017− 0.001 | 2.36+ 0.08− 0.29 | 2.18+ 0.47− 0.05 | − | 0.17+ 0.08− 0.11 | 1.03(132) | 4.6 | 1.3 × 105 | 0.006 |
Same spectra as in Table 2 fitted with the belm model with pure non-thermal acceleration plus diskline and reflect.
| HR . | lnth/l . | lB/lnth . | τp . | Γinj . | kTin (keV) . | Ω/2π . | χ2ν(dof) . | FBol × 10− 8 (erg cm−2 s−1 ) . | B (Gauss) . | |$l_{B}/l_{\text{Br}}$| . |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.37–0.41 | 0.19+ 0.05− 0.03 | <4.5 | 0.26+ 0.43− 0.08 | 3.0+ 0.4− 0.7 | 0.5 ± 0.2 | 1.1+ 0.8− 0.4 | 0.85(88) | 7.2 | 3.1 × 106 | 3.29 |
| 0.43–0.48 | 0.29+ 0.09− 0.06 | <1.4 | 1.1+ 1.1− 0.5 | 2.7+ 0.3− 0.4 | 0.21+ 0.06− 0.04 | <0.4 | 0.96(126) | 6.7 | 2.1 × 106 | 1.34 |
| 0.48–0.50 | 0.60+ 0.04− 0.05 | <0.2 | 1.9+ 0.1− 0.2 | 2.5+ 0.2− 0.1 | 0.21+ 0.06− 0.04 | 0.4 ± 0.2 | 1.05(128) | 6.3 | 1.1 × 106 | 0.31 |
| 0.50–0.53 | 0.776+ 0.008− 0.005 | <0.007 | 2.56 ± 0.07 | 2.69+ 0.13− 0.05 | (0.2) | <0.2 | 1.0(112) | 3.8 | 1.8 × 105 | 0.012 |
| 0.53–0.56 | 0.815+ 0.004− 0.002 | <0.003 | 2.45 ± 0.04 | 2.76+ 0.08− 0.04 | (0.1) | <0.1 | 1.1(120) | 3.8 | 1.2 × 105 | 0.056 |
| 0.56–0.58 | (1) | 0.09+ 0.05− 0.02 | 2.3+ 0.1− 0.2 | 2.47+ 0.12− 0.09 | − | 0.13+ 0.08− 0.06 | 0.94(117) | 3.5 | 7.1 × 105 | 0.21 |
| 0.58–0.61 | (1) | 0.050+ 0.002− 0.006 | 2.3 ± 0.1 | 2.49+ 0.01− 0.04 | − | 0.16 ± 0.01 | 0.99(119) | 3.7 | 5.4 × 105 | 0.12 |
| 0.61–0.64 | (1) | 0.025 ± 0.001 | 2.17+ 0.08− 0.10 | 2.37+ 0.02− 0.04 | − | 0.21+ 0.02− 0.03 | 0.93(117) | 3.8 | 3.9 × 105 | 0.06 |
| 0.64–0.66 | (1) | 0.03+ 0.02− 0.01 | 2.04+ 0.05− 0.03 | 2.78+ 0.02− 0.03 | − | 0.10+ 0.02− 0.06 | 0.85(126) | 3.6 | 4.2 × 105 | 0.07 |
| 0.66–0.68 | (1) | 0.004+ 0.002− 0.001 | 2.3 ± 0.1 | 2.4 ± 0.1 | − | 0.25+ 0.02− 0.05 | 1.07(67) | 4.2 | 1.6 × 105 | 0.009 |
| 0.68–0.70 | (1) | 0.012 ± 0.002 | 2.07+ 0.06− 0.04 | 2.78+ 0.03− 0.15 | − | 0.22+ 0.07− 0.08 | 0.96(118) | 3.2 | 2.5 × 105 | 0.03 |
| 0.70–0.72 | (1) | 0.0025+ 0.017− 0.001 | 2.36+ 0.08− 0.29 | 2.18+ 0.47− 0.05 | − | 0.17+ 0.08− 0.11 | 1.03(132) | 4.6 | 1.3 × 105 | 0.006 |
| HR . | lnth/l . | lB/lnth . | τp . | Γinj . | kTin (keV) . | Ω/2π . | χ2ν(dof) . | FBol × 10− 8 (erg cm−2 s−1 ) . | B (Gauss) . | |$l_{B}/l_{\text{Br}}$| . |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.37–0.41 | 0.19+ 0.05− 0.03 | <4.5 | 0.26+ 0.43− 0.08 | 3.0+ 0.4− 0.7 | 0.5 ± 0.2 | 1.1+ 0.8− 0.4 | 0.85(88) | 7.2 | 3.1 × 106 | 3.29 |
| 0.43–0.48 | 0.29+ 0.09− 0.06 | <1.4 | 1.1+ 1.1− 0.5 | 2.7+ 0.3− 0.4 | 0.21+ 0.06− 0.04 | <0.4 | 0.96(126) | 6.7 | 2.1 × 106 | 1.34 |
| 0.48–0.50 | 0.60+ 0.04− 0.05 | <0.2 | 1.9+ 0.1− 0.2 | 2.5+ 0.2− 0.1 | 0.21+ 0.06− 0.04 | 0.4 ± 0.2 | 1.05(128) | 6.3 | 1.1 × 106 | 0.31 |
| 0.50–0.53 | 0.776+ 0.008− 0.005 | <0.007 | 2.56 ± 0.07 | 2.69+ 0.13− 0.05 | (0.2) | <0.2 | 1.0(112) | 3.8 | 1.8 × 105 | 0.012 |
| 0.53–0.56 | 0.815+ 0.004− 0.002 | <0.003 | 2.45 ± 0.04 | 2.76+ 0.08− 0.04 | (0.1) | <0.1 | 1.1(120) | 3.8 | 1.2 × 105 | 0.056 |
| 0.56–0.58 | (1) | 0.09+ 0.05− 0.02 | 2.3+ 0.1− 0.2 | 2.47+ 0.12− 0.09 | − | 0.13+ 0.08− 0.06 | 0.94(117) | 3.5 | 7.1 × 105 | 0.21 |
| 0.58–0.61 | (1) | 0.050+ 0.002− 0.006 | 2.3 ± 0.1 | 2.49+ 0.01− 0.04 | − | 0.16 ± 0.01 | 0.99(119) | 3.7 | 5.4 × 105 | 0.12 |
| 0.61–0.64 | (1) | 0.025 ± 0.001 | 2.17+ 0.08− 0.10 | 2.37+ 0.02− 0.04 | − | 0.21+ 0.02− 0.03 | 0.93(117) | 3.8 | 3.9 × 105 | 0.06 |
| 0.64–0.66 | (1) | 0.03+ 0.02− 0.01 | 2.04+ 0.05− 0.03 | 2.78+ 0.02− 0.03 | − | 0.10+ 0.02− 0.06 | 0.85(126) | 3.6 | 4.2 × 105 | 0.07 |
| 0.66–0.68 | (1) | 0.004+ 0.002− 0.001 | 2.3 ± 0.1 | 2.4 ± 0.1 | − | 0.25+ 0.02− 0.05 | 1.07(67) | 4.2 | 1.6 × 105 | 0.009 |
| 0.68–0.70 | (1) | 0.012 ± 0.002 | 2.07+ 0.06− 0.04 | 2.78+ 0.03− 0.15 | − | 0.22+ 0.07− 0.08 | 0.96(118) | 3.2 | 2.5 × 105 | 0.03 |
| 0.70–0.72 | (1) | 0.0025+ 0.017− 0.001 | 2.36+ 0.08− 0.29 | 2.18+ 0.47− 0.05 | − | 0.17+ 0.08− 0.11 | 1.03(132) | 4.6 | 1.3 × 105 | 0.006 |
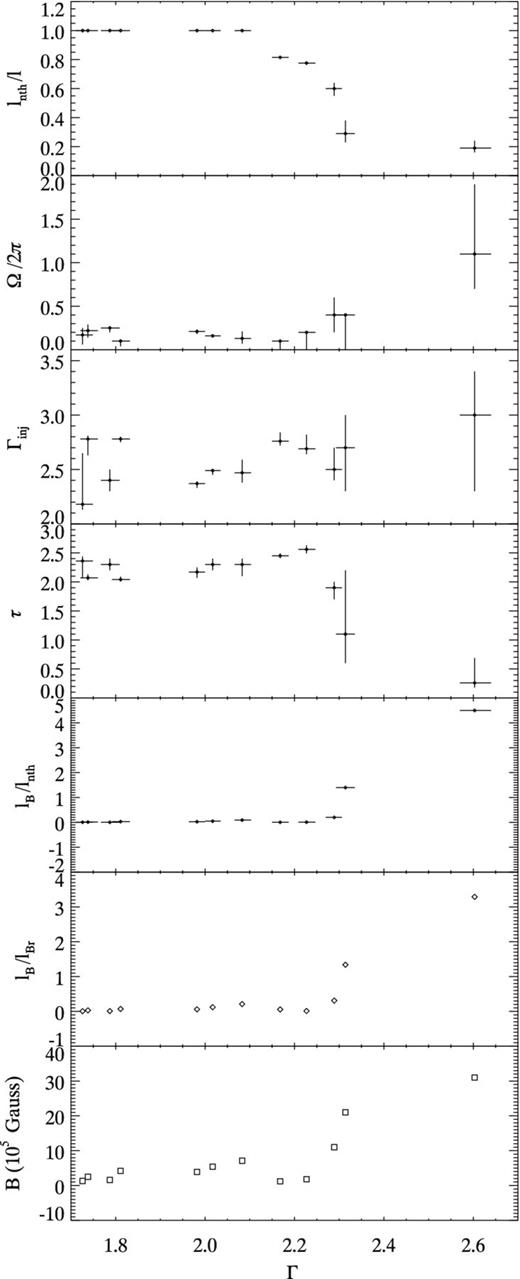
The parameters τp, kTin, lnth (or lh/ls) and the reflection amplitude have a similar behaviour as in the fits with the unmagnetized model eqair, for similar reasons (Fig. 7). The fact that lnth/l is lower in softer state is equivalent to the trend observed for the ratio lh/ls. We note that when using belm, the electron acceleration index Γinj is better constrained by the data in the magnetized model since it also affects the number of synchrotron emitting electrons which in turn controls the temperature of the Maxwellian electrons and the slope of the X-ray spectrum. The trend for a softer injection index in softer state is less clear in the fits with this magnetized model.
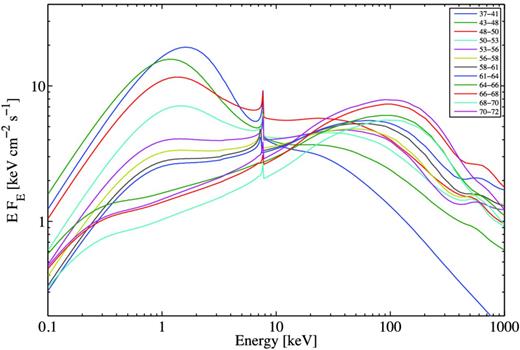
Total models obtained by fitting all 12 broad-band spectra with eqpair plus diskline (see Table 2).
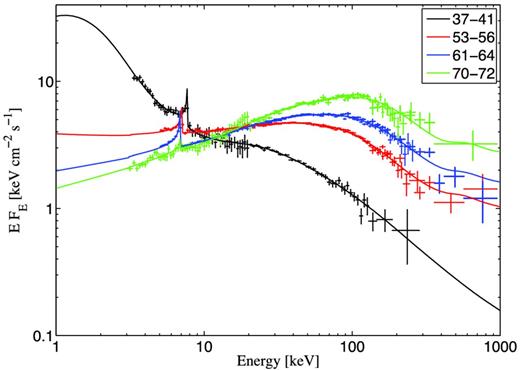
Joint JEM-X, IBIS and SPI energy spectra of Cyg X-1 during four different spectral states fitted with the belm model with pure non-thermal acceleration plus diskline and reflect (see Table 4).
From the results of our fits, it is clear that in the SS, the accretion disc photons represent the main source of soft seed photons (see Fig. 10). In the harder states (spectra 6–12), it is not possible to obtain any constraints and the synchrotron photons may dominate. We have set ls = 0 when fitting these spectra and obtained good fits. Based on the observation of correlations between X-ray flux and spectral index in several BHBs in the HS, Sobolewska et al. (2011) have argued that synchrotron seeds should dominate at luminosities below about a per cent of the Eddington limit, while disc seed photons should dominate at higher luminosities. It is interesting to note that Cyg X-1 has a stable luminosity located around this transition. It is therefore likely that both the accretion disc and the magnetic field contribute to seed the Comptonization process.
Nevertheless, since it is not possible to constrain their respective contribution from our data, assuming the extreme case of pure synchrotron seed photons allows us to set an upper limit on the magnetic compactness. Indeed, the total flux of seed photons (synchrotron+disc) determines the slope of the X-ray spectrum (via energy balance of the thermal electrons). Since the flux of synchrotron photons increases with lB, and the spectral slope is well constrained by the data, assuming that there are no disc photons is going to maximize lB. In the softer states, the spectra are consistent with lB = 0 (since they can be fitted with an unmagnetized model) but again we are able to obtain an upper limit on lB.
We note that the jump in lB/lnth and B between spectra 5 and 6 is due to the fact that we had to turn off the disc seed photon when fitting spectra 6–12. This makes the upper limit on lB less restrictive. The presence of this jump suggests that disc photons continue to play a role even in the harder spectra.
From Table 4, we see that for a corona of size R = 20Rg, these upper limits range from ≃105 G in the hardest HS to ≃3 × 106 G in the SS (see also Fig. 7). This implies strongly subequipartition magnetic fields (|$l_B/l_{B_R}<1$|) in the spectra intermediate and hard. As discussed in MB09 and Droulans et al. (2010), this has important consequences for dynamical models of the corona. Namely, this rules out any model based on an X-ray corona powered through magnetic dissipation in the HS and this may also be a problem to drive the powerful jet that is observed.
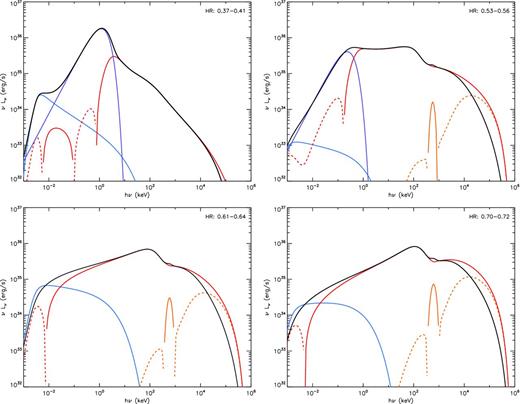
belm total models (black) corresponding to fits of the spectra shown in Fig. 8 and the components: Compton (red), pair annihilation/production (orange), synchrotron (blue), soft blackbody photons (purple). Solid lines correspond to positive contribution to the spectrum, dashed lines correspond to negative contribution.
4.3 Magnetized, two-zone model with pure thermal heating
In the previous one-zone model, we obtained upper limits on the magnetic field intensity assuming SSC and pure non-thermal acceleration. This was motivated by the overall non-thermal nature of the softer spectra and by the high-energy emission above the cutoff in the harder states (HR > 0.64), none of which is reproduced with purely thermal lepton populations. In the HS, these constraints were mostly governed by the non-thermal, highest energy data points. However, it has been suggested that the high-energy emission in the HS could originate from a different region of the accreting system, i.e. the jet (Laurent et al. 2011; Zdziarski et al. 2012) or another component of the corona (Malzac 2012). Then, the hard spectra below the cutoff could also be reproduced by SSC models with pure thermal heating. In this case, the exact heating mechanism is of little importance for spectral modelling, because whatever the heating mechanism, the resulting electron distribution is very close to a pure Maxwellian. In belm, this electron thermal heating mechanism is assumed to be Coulomb collisions with a distribution of hot thermal protons (MB09). Then, the constraints on the magnetic field are expected to be different.
To investigate this issue, we computed a new table model with pure Coulomb heating (ls = 0, lnth = 0, l = lc = lth). As before, the spectral shape does not depend on the absolute compactness of the system, and we set l = lc = 1 to prevent degeneracy issues. Then, we determined the proton temperature (kTp in Table 5) corresponding to this compactness and to the exact steady state electron distribution. The two free parameters of the table model are: lB (20 values between 0.1 and 104) and τ (20 values between 0.5 and 5). As for previous models, we also added a reflection component. We fitted the four harder spectra (HR > 0.64; see Table 5).
Spectra below 200 keV in HS fitted with a pure thermal heating model. kTp and kTp(obs) are the temperatures of the ions for lc = 1 and lc observed (lc = l), respectively.
| HR . | lB/lc . | τp . | Ω/2π . | χ2ν(dof) . | FBol × 10− 8 (erg cm−2 s−1 ) . | B (Gauss) . | lB/lBr . | kTe (keV) . | kTp (keV) . | kTp(obs) (MeV) . |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.64–0.66 | 68+ 12− 3 | 1.83+ 0.2− 0.02 | 0.12+ 0.05− 0.04 | 0.94(107) | 3.5 | 1.9 × 107 | 176.3 | 79.0 | 245 | 1.6 |
| 0.66–0.68 | 44+ 4− 8 | 2.0 ± 0.1 | 0.27+ 0.01− 0.04 | 0.94(58) | 3.9 | 1.7 × 107 | 110.3 | 70.2 | 219 | 1.5 |
| 0.68–0.70 | 48+ 12− 4 | 2.0+ 0.2− 0.06 | 0.19+ 0.05− 0.06 | 0.90(112) | 3.0 | 1.5 × 107 | 119.8 | 78.2 | 215 | 1.1 |
| 0.70–0.72 | 64+ 17− 21 | 2.1+ 0.3− 0.2 | 0.14+ 0.12− 0.06 | 0.95(113) | 4.1 | 2.0 × 107 | 157.1 | 72.3 | 183 | 1.3 |
| HR . | lB/lc . | τp . | Ω/2π . | χ2ν(dof) . | FBol × 10− 8 (erg cm−2 s−1 ) . | B (Gauss) . | lB/lBr . | kTe (keV) . | kTp (keV) . | kTp(obs) (MeV) . |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.64–0.66 | 68+ 12− 3 | 1.83+ 0.2− 0.02 | 0.12+ 0.05− 0.04 | 0.94(107) | 3.5 | 1.9 × 107 | 176.3 | 79.0 | 245 | 1.6 |
| 0.66–0.68 | 44+ 4− 8 | 2.0 ± 0.1 | 0.27+ 0.01− 0.04 | 0.94(58) | 3.9 | 1.7 × 107 | 110.3 | 70.2 | 219 | 1.5 |
| 0.68–0.70 | 48+ 12− 4 | 2.0+ 0.2− 0.06 | 0.19+ 0.05− 0.06 | 0.90(112) | 3.0 | 1.5 × 107 | 119.8 | 78.2 | 215 | 1.1 |
| 0.70–0.72 | 64+ 17− 21 | 2.1+ 0.3− 0.2 | 0.14+ 0.12− 0.06 | 0.95(113) | 4.1 | 2.0 × 107 | 157.1 | 72.3 | 183 | 1.3 |
Spectra below 200 keV in HS fitted with a pure thermal heating model. kTp and kTp(obs) are the temperatures of the ions for lc = 1 and lc observed (lc = l), respectively.
| HR . | lB/lc . | τp . | Ω/2π . | χ2ν(dof) . | FBol × 10− 8 (erg cm−2 s−1 ) . | B (Gauss) . | lB/lBr . | kTe (keV) . | kTp (keV) . | kTp(obs) (MeV) . |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.64–0.66 | 68+ 12− 3 | 1.83+ 0.2− 0.02 | 0.12+ 0.05− 0.04 | 0.94(107) | 3.5 | 1.9 × 107 | 176.3 | 79.0 | 245 | 1.6 |
| 0.66–0.68 | 44+ 4− 8 | 2.0 ± 0.1 | 0.27+ 0.01− 0.04 | 0.94(58) | 3.9 | 1.7 × 107 | 110.3 | 70.2 | 219 | 1.5 |
| 0.68–0.70 | 48+ 12− 4 | 2.0+ 0.2− 0.06 | 0.19+ 0.05− 0.06 | 0.90(112) | 3.0 | 1.5 × 107 | 119.8 | 78.2 | 215 | 1.1 |
| 0.70–0.72 | 64+ 17− 21 | 2.1+ 0.3− 0.2 | 0.14+ 0.12− 0.06 | 0.95(113) | 4.1 | 2.0 × 107 | 157.1 | 72.3 | 183 | 1.3 |
| HR . | lB/lc . | τp . | Ω/2π . | χ2ν(dof) . | FBol × 10− 8 (erg cm−2 s−1 ) . | B (Gauss) . | lB/lBr . | kTe (keV) . | kTp (keV) . | kTp(obs) (MeV) . |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.64–0.66 | 68+ 12− 3 | 1.83+ 0.2− 0.02 | 0.12+ 0.05− 0.04 | 0.94(107) | 3.5 | 1.9 × 107 | 176.3 | 79.0 | 245 | 1.6 |
| 0.66–0.68 | 44+ 4− 8 | 2.0 ± 0.1 | 0.27+ 0.01− 0.04 | 0.94(58) | 3.9 | 1.7 × 107 | 110.3 | 70.2 | 219 | 1.5 |
| 0.68–0.70 | 48+ 12− 4 | 2.0+ 0.2− 0.06 | 0.19+ 0.05− 0.06 | 0.90(112) | 3.0 | 1.5 × 107 | 119.8 | 78.2 | 215 | 1.1 |
| 0.70–0.72 | 64+ 17− 21 | 2.1+ 0.3− 0.2 | 0.14+ 0.12− 0.06 | 0.95(113) | 4.1 | 2.0 × 107 | 157.1 | 72.3 | 183 | 1.3 |
As expected, the broad-band spectrum cannot be fitted with this pure thermal model, since it does not reproduce the highest energy data, which either requires a significant level of non-thermal acceleration or must originate in a different region. When excluding data above 200 keV, we obtained good fits with χ2ν < 0.95. The results are shown in Table 5. The best-fitting Thomson optical depth and the reflection amplitude are comparable to those of the non-thermal model.
Noticeably, the ratio lB/lc is larger by about four orders of magnitude in the thermal model than in the previous non-thermal model. Indeed, the spectrum below the cutoff is essentially governed by the temperature of the thermal electron distribution. The cooling of thermal electrons is dominated by inverse Compton scattering on soft synchrotron photons. Non-thermal models produce stronger high-energy tails in the electron distribution and thus tend to provide more synchrotron seed photons than thermal models for comparable lB. Hence, the magnetic field has to be weaker in non-thermal models in order to provide the same electron temperature and reproduce the data.
Thus, by assuming that the highest energy emission originates from a different region, the constraints on the ratio lB/lc estimated in this thermal model correspond to the most conservative upper limits. Following the procedure described in the previous subsection, we obtain that the magnetic field in the HS is stronger by a factor of 100 compared to that estimated in the SSC model (Table 5). The magnetic field is now allowed to be strongly super equipartition in the HS with typical upper limits of the order of 107 G.
5 CONCLUSION
We have used data from 6 yr of observation of Cygnus X-1 with INTEGRAL, to produce 12 high-quality, stacked broad-band spectra spanning the whole range of spectral shapes observed in this source from the SS to HS. We have then fitted these spectra with hybrid thermal/non-thermal Comptonization models. We have used both a magnetized belm and an unmagnetized eqpair model. For both models, we found that the spectral changes at high energy are driven essentially by the strength of the soft seed cooling photons in the corona as the disc temperature (and inner radius of emission) changes.
During the spectral transition from HS to SS, the power of the corona decreases by less than a factor of 2 while the disc emission increases at least by a factor of ∼50. This appears to be associated with a gradual change of the Thomson depth of the corona which decreases from ≃1.5 in HS to ≃0.2 in SS, which may be caused either by a condensation of the corona into the disc or evaporation into an outflow, or compactification of the corona in the SS.
For the first time, we have performed a statistical fit of the Cyg X-1 data with the belm model. This allowed us to test the effects of the magnetic field on the coronal emission. As explained in the Section 4.2, the estimate of B depends only on our choice for R and not on the assumed fixed value of l used in the fitting procedure. Within the one-zone model the uncertainty on R is by far the main source of error on our estimate of B, and the other parameters have none or very little effects.
We found that in the SS, the emission is dominated by Comptonization of the disc photons and the upper limit on the magnetic field is at most of the order of 3 |$\times \ 10^{6} \sqrt{20 R_g/R}$| G. Such a magnetic field is energetically consistent with a magnetic dissipation process, such as reconnection, powering the corona.
In the HS, the data are consistent with a pure Comptonized synchrotron emission model, although Comptonization of disc photons cannot be excluded. We consider that a mixture of both is the most likely possibility. However, fitting in the limiting case of SSC in the HS provides upper limits on the magnetic field intensity.
If the non-thermal excess observed above a few hundred keV is produced in the same region as the bulk of the thermal Comptonization, the magnetic field is at most of a few |$10^{5} \sqrt{20 R_g/R}$| G. This is strongly subequipartition with radiation which is challenging for all dynamical accretion flow models. In this case, we also confirm the qualitative results of MB09 and PV09 that the emission in all spectral states can be modelled with pure non-thermal electron acceleration. Indeed, provided that the magnetic field is not too strong in the HS, the electrons thermalize at the observed temperature under the effects of Coulomb collisions and synchrotron self-absorption. Moreover, Wardziński et al. (2002) found analytically that if the high-energy tail observed in HS of BHBs is from the hybrid distribution, the magnetic field has to be strongly subequipartition, similar to our finding.
If, on the other hand, the non-thermal excess is produced in a different location, the constraints on the magnetic field in the HS are somewhat relaxed and we obtain an upper limit of about |$2\times 10^{7} \sqrt{20 R_g/R}$| G in the HS. Such a large magnetic field would be consistent with the magnetically dominated hot accretion flow model of Oda et al. (2010) which also appear to produce the rather large Thomson depth (τp ≃ 1.5) and low ion temperatures Tp ∼ 1010 K that we infer from the data in the HS.
MDS and GDC acknowledge financial support from the agreement ASI-INAF I/009/10/0 and from PRIN-INAF 2009 (PI: L. Sidoli). MDS and JM acknowledge financial support from Université Paul Sabatier. JM and RB acknowledge support from PNHE in France. MDS thanks IRAP/CNRS (France) for hospitality. JM thanks the Institute of Astronomy of Cambridge (UK) for hospitality. MDS and JM thank A. Zdziarski for useful scientific discussion and suggestions. MDS thanks J. Wilms and V. Grinberg for useful comments.
Based on observations with INTEGRAL, an ESA project with instruments and science data centre funded by ESA member states (especially the PI countries: Denmark, France, Germany, Italy, Switzerland, Spain), Czech Republic and Poland and with participation of Russia and the USA.





