-
PDF
- Split View
-
Views
-
Cite
Cite
David Sobral, Ian Smail, Philip N. Best, James E. Geach, Yuichi Matsuda, John P. Stott, Michele Cirasuolo, Jaron Kurk, A large Hα survey at z = 2.23, 1.47, 0.84 and 0.40: the 11 Gyr evolution of star-forming galaxies from HiZELS, Monthly Notices of the Royal Astronomical Society, Volume 428, Issue 2, 11 January 2013, Pages 1128–1146, https://doi.org/10.1093/mnras/sts096
Close - Share Icon Share
Abstract
This paper presents new deep and wide narrow-band surveys undertaken with United Kingdom Infrared Telescope (UKIRT), Subaru and the Very Large Telescope (VLT), a unique combined effort to select large, robust samples of Hα star-forming galaxies at z = 0.40, 0.84, 1.47 and 2.23 (corresponding to look-back times of 4.2, 7.0, 9.2 and 10.6 Gyr) in a uniform manner over ∼2 deg2 in the Cosmological Evolution Survey and Ultra Deep Survey fields. The deep multi-epoch Hα surveys reach a matched 3σ flux limit of ≈3 M⊙ yr−1 out to z = 2.2 for the first time, while the wide area and the coverage over two independent fields allow us to greatly overcome cosmic variance and assemble by far the largest samples of Hα emitters. Catalogues are presented for a total of 1742, 637, 515 and 807 Hα emitters, robustly selected at z = 0.40, 0.84, 1.47 and 2.23, respectively, and used to determine the Hα luminosity function and its evolution. The faint-end slope of the Hα luminosity function is found to be α = −1.60 ± 0.08 over z = 0–2.23, showing no significant evolution. The characteristic luminosity of star-forming galaxies, L*Hα, evolves significantly as log L*Hα(z) = 0.45z + log L*z = 0. This is the first time Hα has been used to trace star formation activity with a single homogeneous survey at z = 0.4–2.23. Overall, the evolution seen with Hα is in good agreement with the evolution seen using inhomogeneous compilations of other tracers of star formation, such as far-infrared and ultraviolet, jointly pointing towards the bulk of the evolution in the last 11 Gyr being driven by a statistically similar star-forming population across cosmic time, but with a strong luminosity increase from z ∼ 0 to ∼2.2. Our uniform analysis allows us to derive the Hα star formation history (SFRH) of the Universe, showing a clear rise up to z ∼ 2.2, for which the simple parametrization log10ρSFR = −2.1(1 + z)−1 is valid over 80 per cent of the age of the Universe. The results reveal that both the shape and normalization of the Hα SFRH are consistent with the measurements of the stellar mass density growth, confirming that our Hα SFRH is tracing the bulk of the formation of stars in the Universe for z < 2.23. The star formation activity over the last ∼11 Gyr is responsible for producing ∼95 per cent of the total stellar mass density observed locally, with half of that being assembled in 2 Gyr between z = 1.2 and 2.2, and the other half in 8 Gyr (since z < 1.2). If the star formation rate density continues to decline with time in the same way as seen in the past ∼11 Gyr, then the stellar mass density of the Universe will reach a maximum which is only 5 per cent higher than the present-day value.
1 INTRODUCTION
Observational studies show that star formation activity in galaxies, as measured through the star formation rate (SFR) density (ρSFR) in the Universe, has been decreasing significantly with time (e.g. Lilly et al. 1996). Nevertheless, while surveys reveal that ρSFR rises steeply out to at least z ∼ 1 (e.g. Hopkins & Beacom 2006), determining the redshift where ρSFR might have peaked at z > 1 is still an open problem. This is because the use of different techniques/indicators (affected by different biases, dust extinctions and with different sensitivities – and that can only be used over limited redshift windows) results in a very blurred and scattered understanding of the star formation history of the Universe. Other problems/limitations result from the difficulty of obtaining both large-area, large-sample, clean and deep observations (to overcome both cosmic variance and avoid large extrapolations down to faint luminosities).
One way to make significant progress in our understanding of star formation at high redshifts is through the use of narrow-band imaging techniques. These can provide sensitive wide-field surveys to select star-forming galaxies through a single emission line and track it out to high redshift as it shifts from the optical into the near-infrared (NIR). While there are a number of emission lines which are used to trace star formation, Hα is by far the best at z < 3,1 as it provides a sensitive census of star formation activity, is well calibrated and suffers only modest extinction in typical star-forming galaxies (e.g. Garn et al. 2010; Gilbank et al. 2010; Sobral et al. 2012), in contrast to shorter wavelength emission lines. Furthermore, Hα is also a much better estimate of the instantaneous SFR when compared to other widely used tracers, such as ultraviolet (UV), far-infrared (FIR) or radio, as it is sensitive to the presence of the most massive stars only, which are very short-lived. Even longer wavelength star formation tracing emission lines, such as the Paschen series lines, are less affected by dust extinction, but they are intrinsically fainter than Hα (e.g. Paα is intrinsically ∼10 × weaker than Hα for a typical star-forming galaxy) and hence provide much less sensitive surveys out to lower redshifts.
Hα surveys have been carried out by many authors (e.g. Bunker et al. 1995; Malkan, Teplitz & McLean 1996), but they initially resulted in a relatively low number of sources for z > 0.5 surveys. Fortunately, the development of wide-field NIR detectors has recently allowed a significant increase in success: at z ∼ 2, narrow-band surveys such as Moorwood et al. (2000), which could only detect a handful of emitters, have been rapidly extended by others, such as Geach et al. (2008a), increasing the sample size by more than an order of magnitude. Substantial advances have also been obtained at z ∼ 1 (e.g. Villar et al. 2008; Sobral et al. 2009a; Ly et al. 2011). Other Hα surveys have used dispersion prisms on HST to make progress (e.g. McCarthy et al. 1999; Yan et al. 1999; Hopkins, Connolly & Szalay 2000; Shim et al. 2009), and there is promising work being conducted using the upgraded WFC3 grism (e.g. WISP or 3DHST; Atek et al. 2010; Straughn et al. 2011; van Dokkum et al. 2011).
HiZELS, the High-redshift(Z) Emission Line Survey2 (Geach et al. 2008a; Sobral et al. 2009a, 2012, hereafter S09 and S12), is a campaign project using the Wide Field CAMera (WFCAM) on the United Kingdom Infrared Telescope (UKIRT), as well as the Suprime-Cam on the Subaru Telescope and the HAWK-I camera on Very Large Telescope (VLT). On UKIRT, HiZELS exploits specially designed narrow-band filters in the J and H bands (NBJ and NBH), along with the H2S(1) filter in the K band (hereafter NBK), to undertake panoramic, deep surveys for line emitters. The Subaru observations provide a comparable survey at z = 0.40 using the NB921 filter on Suprime-Cam, while the HAWK-I observations extend the UKIRT survey to fainter limits at z = 2.23 over a smaller area. The combined elements of HiZELS primarily target the Hα emission line (but also other lines; e.g. Sobral et al. 2009b) redshifted into the red or NIR at z = 0.40, 0.84, 1.47 and 2.23 (see Best et al. 2010), while the NBJ and NBH filters also detect [O ii] 3727 and [O iii] 5007 emitters at z = 2.23, matching the NBK Hα coverage at the same redshift.
One of the main aims of HiZELS is to provide measurements of the evolution of the Hα luminosity function (LF) from z = 0.0 to 2.23 (but also other properties, such as clustering, environment and mass dependences; cf. Sobral et al. 2010, 2011; Geach et al. 2012). The first results (Geach et al. 2008a; S09; S12) indicate that the Hα LF evolves significantly, mostly due to an increase of about one order of magnitude in L*Hα, the characteristic Hα luminosity, from the local Universe to z = 2.23 (S09). In addition, Sobral et al. (2011) found that at z = 0.84 the faint-end slope of the LF (α) is strongly dependent on the environment, with the Hα LF being much steeper in low-density regions and much shallower in the group/cluster environments.
However, even though the progress has been quite remarkable, significant issues remain to be robustly addressed for a variety of reasons. For example, is the faint-end slope of the Hα LF (α) becoming steeper from low to high redshift? Results from Hayes, Schaerer & Östlin (2010) point towards a steep faint-end slope at z > 2. However, Hayes et al. did not sample the bright end, and have only targeted one single field over a relatively small area, and thus cosmic variance could play a huge role. Tadaki et al. (2011) find a much shallower α at z ∼ 2 using Subaru. Furthermore, measurements so far rely on different data, obtained down to different depths and using different selection criteria. Additionally, different ways of correcting for completeness (cf. e.g. Ly et al. 2011), filter profiles or contamination by the [N ii]λλ6548, 6583.6 lines can also lead to significant differences. How much of the evolution is in fact real, and how much is a result of different ways of estimating the Hα LF? This can only be fully quantified with a completely self-consistent multi-epoch selection and analysis. Another issue which still hampers the progress is overcoming cosmic variance and probing a very wide range of environments and stellar masses at z > 1. Large samples of homogeneously selected star-forming galaxies at different epochs up to z > 2 would certainly be ideal to provide strong tests on our understanding of how galaxies form and how they evolve.
In order to clearly address the current shortcomings and provide the data that are required, we have undertaken by far the largest area, deep multi-epoch narrow-band Hα surveys over two different fields. By doing so, both faint and bright populations of equally selected Hα emitters at z = 0.4, 0.84, 1.47 and 2.23 have been obtained, using four narrow-band filters (see Fig. 1 and Table 1). This paper presents the narrow-band imaging and results obtained with the NB921, NBJ, NBH, NBK and H2 filters on Subaru, the UKIRT and the VLT, over a total of |${\sim }2\deg ^2$| in the Cosmological Evolution Survey (COSMOS; Scoville et al. 2007) and the SXDF Subaru–XMM–UKIDSS Ultra Deep Survey (UDS; Lawrence et al. 2007) fields.
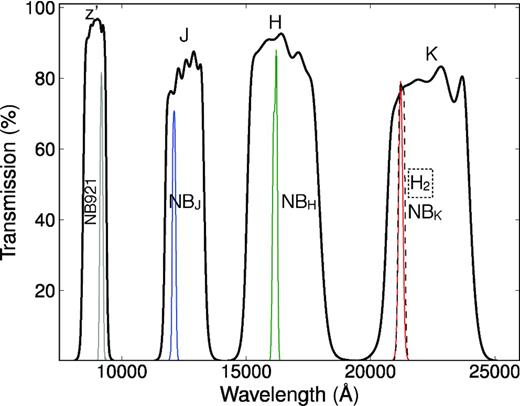
The broad- and narrow-band filter profiles used for the analysis. The narrow-band filters in the z′, J, H and K bands (typical FWHM of ≈100–200 Å) trace the redshifted Hα line at z = 0.4, 0.84, 1.47 and 2.23 very effectively, while the (scaled) broad-band imaging is used to estimate and remove the contribution from the continuum. Note that because the filters are not necessarily located at the centre of the respective broad-band transmission profile, very red/blue sources can produce narrow-band excesses which mimic emission lines; that is corrected by estimating the continuum colour of each source and correcting for it.
Narrow-band filters used to conduct the multi-epoch surveys for Hα emitters, indicating the central wavelength (μm), full width at half-maximum (FHWM), the redshift range for which the Hα line is detected over the filter FWHM and the corresponding volume (per square degree) surveyed (for the Hα line). Note that the NB921 filter provides an [O ii] survey which precisely matches the Hα z = 1.47 survey, and also an [O iii] survey which broadly matches the z = 0.84 Hα survey. The NBJ and NBH filters also provide [O ii] 3727 and [O iii] 5007 surveys, respectively, which match the z = 2.23 NBK Hα survey.
| . | λc . | FWHM . | . | Volume (Hα) . |
|---|---|---|---|---|
| NB filter . | (μm) . | (Å) . | z Hα . | (104 Mpc3 deg−2) . |
| NB921 | 0.9196 | 132 | 0.401 ± 0.010 | 5.13 |
| NBJ | 1.211 | 150 | 0.845 ± 0.015 | 14.65 |
| NBH | 1.617 | 211 | 1.466 ± 0.016 | 33.96 |
| NBK | 2.121 | 210 | 2.231 ± 0.016 | 38.31 |
| HAWK-I H2 | 2.125 | 300 | 2.237 ± 0.023 | 54.70 |
| . | λc . | FWHM . | . | Volume (Hα) . |
|---|---|---|---|---|
| NB filter . | (μm) . | (Å) . | z Hα . | (104 Mpc3 deg−2) . |
| NB921 | 0.9196 | 132 | 0.401 ± 0.010 | 5.13 |
| NBJ | 1.211 | 150 | 0.845 ± 0.015 | 14.65 |
| NBH | 1.617 | 211 | 1.466 ± 0.016 | 33.96 |
| NBK | 2.121 | 210 | 2.231 ± 0.016 | 38.31 |
| HAWK-I H2 | 2.125 | 300 | 2.237 ± 0.023 | 54.70 |
Narrow-band filters used to conduct the multi-epoch surveys for Hα emitters, indicating the central wavelength (μm), full width at half-maximum (FHWM), the redshift range for which the Hα line is detected over the filter FWHM and the corresponding volume (per square degree) surveyed (for the Hα line). Note that the NB921 filter provides an [O ii] survey which precisely matches the Hα z = 1.47 survey, and also an [O iii] survey which broadly matches the z = 0.84 Hα survey. The NBJ and NBH filters also provide [O ii] 3727 and [O iii] 5007 surveys, respectively, which match the z = 2.23 NBK Hα survey.
| . | λc . | FWHM . | . | Volume (Hα) . |
|---|---|---|---|---|
| NB filter . | (μm) . | (Å) . | z Hα . | (104 Mpc3 deg−2) . |
| NB921 | 0.9196 | 132 | 0.401 ± 0.010 | 5.13 |
| NBJ | 1.211 | 150 | 0.845 ± 0.015 | 14.65 |
| NBH | 1.617 | 211 | 1.466 ± 0.016 | 33.96 |
| NBK | 2.121 | 210 | 2.231 ± 0.016 | 38.31 |
| HAWK-I H2 | 2.125 | 300 | 2.237 ± 0.023 | 54.70 |
| . | λc . | FWHM . | . | Volume (Hα) . |
|---|---|---|---|---|
| NB filter . | (μm) . | (Å) . | z Hα . | (104 Mpc3 deg−2) . |
| NB921 | 0.9196 | 132 | 0.401 ± 0.010 | 5.13 |
| NBJ | 1.211 | 150 | 0.845 ± 0.015 | 14.65 |
| NBH | 1.617 | 211 | 1.466 ± 0.016 | 33.96 |
| NBK | 2.121 | 210 | 2.231 ± 0.016 | 38.31 |
| HAWK-I H2 | 2.125 | 300 | 2.237 ± 0.023 | 54.70 |
The paper is organized as follows. Section 2 describes the observations, data reduction, source extraction, catalogue production, selection of line emitters and the samples of Hα emitters. In Section 3, after estimating and applying the necessary corrections, the Hα LFs are derived at z = 0.4, 0.84, 1.47 and 2.23, together with an accurate measurement of their evolution at both bright and faint ends. In Section 4, the SFR density at each epoch is also evaluated and the star formation history of the Universe is presented. Section 4 also discusses the results in the context of galaxy formation and evolution in the last 11 Gyr, including the inferred stellar mass density growth. Finally, Section 5 presents the conclusions. An H0 = 70 km s−1 Mpc−1, ΩM = 0.3 and ΩΛ = 0.7 cosmology is used. Narrow-band magnitudes in the NIR and the associated broad-band magnitudes are in the Vega system, except when noted otherwise (e.g. for colour–colour selections). NB921 and z′ magnitudes are given in the AB system (except in Table 2, where they are given in Vega for direct comparison).
Observation log of all the narrow-band observations obtained over the COSMOS and UDS fields, taken using WFCAM on UKIRT, HAWK-I on the VLT and Suprime-Cam on Subaru, during 2006–2012. Limiting magnitudes (3σ, all in Vega) are the average of each field/pointing, based on the measurements of 104–106 randomly placed 2 arcsec apertures in each frame, but note that for COSMOS (NBH and NBK) the central four pointings overlap with part of the outer pointings (see Fig. 2), making the central region data up to 0.3–0.4 mag deeper, by doubling/tripling the exposure time.
| Field . | Band . | RA . | Dec. . | Int. time . | FHWM . | Dates . | mlim (Vega) . |
|---|---|---|---|---|---|---|---|
| . | (filter) . | (J2000) . | (J2000) . | (ks) . | (arcsec) . | . | (3σ) . |
| COSMOS-1 | NB921 | 09 59 23 | +02 30 29 | 2.9 | 0.9 | 2010 Dec 9 | 24.4 |
| COSMOS-2 | NB921 | 10 01 34 | +02 30 29 | 2.9 | 0.9 | 2010 Dec 9 | 24.5 |
| COSMOS-3 | NB921 | 09 59 23 | +02 04 16 | 2.9 | 0.9 | 2010 Dec 9 | 24.5 |
| COSMOS-4 | NB921 | 10 01 34 | +02 04 16 | 2.9 | 0.9 | 2010 Dec 9 | 24.5 |
| UKIDSS-UDS C | NB921 | 02 18 00 | −05 00 00 | 30.0 | 0.8 | 2005 Oct 29, Nov 1; 2007 Oct 11–12 | 26.6 |
| UKIDSS-UDS N | NB921 | 02 18 00 | −04 35 00 | 37.8 | 0.9 | 2005 Oct 30,31, Nov 1; 2006 Nov 18; 2007 Oct 11,12 | 26.7 |
| UKIDSS-UDS S | NB921 | 02 18 00 | −05 25 00 | 37.1 | 0.8 | 2005 Aug 29, Oct 29; 2006 Nov 18; 2007 Oct 12 | 26.6 |
| UKIDSS-UDS E | NB921 | 02 19 47 | −05 00 00 | 29.3 | 0.8 | 2005 Oct 31, Nov 1; 2006 Nov 18; 2007 Oct 11,12 | 26.6 |
| UKIDSS-UDS W | NB921 | 02 16 13 | −05 00 00 | 28.1 | 0.8 | 2006 Nov 18; 2007 Oct 11,12 | 26.0 |
| COSMOS-NW(1) | NBJ | 10 00 00 | +02 10 30 | 19.7 | 0.8 | 2007 Jan 14–16 | 22.0 |
| COSMOS-NE(2) | NBJ | 10 00 52 | +02 10 30 | 23.8 | 0.9 | 2006 Nov 10; 2007 Jan 13–14 | 22.0 |
| COSMOS-SW(3) | NBJ | 10 00 00 | +02 23 44 | 18.9 | 0.9 | 2007 Jan 15–17 | 22.0 |
| COSMOS-SE(4) | NBJ | 10 00 53 | +02 23 44 | 17.1 | 1.0 | 2007 Jan 15, 17, Feb 13, 14, 16 | 21.9 |
| UKIDSS-UDS NE | NBJ | 02 18 29 | −04 52 20 | 20.9 | 0.8 | 2007 Oct 21–23 | 22.0 |
| UKIDSS-UDS NW | NBJ | 02 17 36 | −04 52 20 | 22.4 | 0.9 | 2007 Oct 20–21 | 22.1 |
| UKIDSS-UDS SE | NBJ | 02 18 29 | −05 05 53 | 19.6 | 0.9 | 2007 Oct 23, 24 | 22.0 |
| UKIDSS-UDS SW | NBJ | 02 17 38 | −05 05 34 | 22.4 | 0.8 | 2007 Oct 19, 21 | 22.0 |
| COSMOS-NW(1) | NBH | 10 00 00 | +02 10 30 | 12.5 | 1.0 | 2009 Feb 27, Mar 1–2 | 21.1 |
| COSMOS-NE(2) DEEP | NBH | 10 00 52 | +02 10 30 | 107.0 | 0.9 | 2009 Feb 28, Apr 19, May 22; 2011 Jan 26–30 | 22.2 |
| COSMOS-SW(3) | NBH | 10 00 00 | +02 23 44 | 14.0 | 0.7 | 2010 Apr 2 | 21.0 |
| COSMOS-SE(4) | NBH | 10 00 53 | +02 23 44 | 18.1 | 1.0 | 2009 Mar 2, Apr 30, May 22; 2010 Apr 3 | 20.8 |
| COSMOS-A | NBH | 10 00 01 | +02 36 53 | 12.6 | 1.0 | 2010 Apr 9; 2011 Jan 25 | 21.1 |
| COSMOS-B | NBH | 10 00 54 | +02 36 30 | 12.6 | 0.9 | 2010 Apr 8–9 | 21.0 |
| COSMOS-C | NBH | 10 00 01 | +01 57 10 | 13.0 | 0.8 | 2010 Apr 6–8 | 20.8 |
| COSMOS-D | NBH | 10 00 52 | +01 57 15 | 14.2 | 0.8 | 2010 Apr 7–8 | 21.0 |
| COSMOS-E | NBH | 09 59 07 | +02 23 44 | 12.6 | 0.8 | 2010 Apr 3–6 | 20.9 |
| COSMOS-F | NBH | 09 59 07 | +02 10 30 | 12.6 | 0.7 | 2010 Apr 4 | 21.1 |
| COSMOS-G | NBH | 10 01 46 | +02 23 44 | 14.5 | 0.8 | 2010 Apr 4 and 9 | 21.0 |
| COSMOS-H | NBH | 10 01 48 | +02 10 51 | 14.0 | 0.8 | 2010 Apr 6 & 9 | 20.8 |
| UKIDSS-UDS NE | NBH | 02 18 29 | −04 52 20 | 18.2 | 0.9 | 2008 Sep 28–29; 2009 Aug 16–17; 2010 Jul 22 | 21.3 |
| UKIDSS-UDS NW | NBH | 02 17 36 | −04 52 20 | 18.0 | 0.9 | 2008 Sep 25, 29; 2010 Jul 18, 22 | 20.9 |
| UKIDSS-UDS SE | NBH | 02 18 29 | −05 05 53 | 25.2 | 0.8 | 2008 Sep 25, 28–29; 2009 Aug 16–17 | 21.5 |
| UKIDSS-UDS SW | NBH | 02 17 38 | −05 05 34 | 19.6 | 0.9 | 2008 Oct–Nov; 2009 Aug 16–17; 2010 Jul 23 and 21.3 | |
| COSMOS-NW(1) | NBK | 10 00 00 | +02 10 30 | 24.3 | 0.9 | 2006 Dec 17, 19–20; 2008 May 11; 2009 Feb 27 | 21.0 |
| COSMOS-NE(2) DEEP | NBK | 10 00 52 | +02 10 30 | 62.5 | 0.9 | 2006 May 20–21, Dec 20; 2008 Mar 6–9 | 21.3 |
| COSMOS-SW(3) | NBK | 10 00 00 | +02 23 44 | 20.0 | 0.9 | 2006 May 22, 24, Dec 20; 2009 May 20 | 20.8 |
| COSMOS-SE(4) | NBK | 10 00 53 | +02 23 44 | 19.5 | 0.9 | 2006 Nov 13–15, 30, Dec 16 | 20.9 |
| COSMOS-A | NBK | 10 00 01 | +02 36 53 | 20.0 | 1.0 | 2011 Mar 19–26, 2012 Mar 20 | 21.0 |
| COSMOS-B | NBK | 10 00 54 | +02 36 30 | 20.0 | 0.9 | 2011 Mar 25–26 | 20.8 |
| COSMOS-C | NBK | 10 00 01 | +01 57 10 | 26.7 | 0.9 | 2011 Mar 27, 30, Apr 3–5, 16–18 | 20.9 |
| COSMOS-D | NBK | 10 00 52 | +01 57 15 | 20.0 | 0.9 | 2011 Mar 30, Jun 6; 2012 Jan 5,18, Feb 26, Mar 2 | 20.9 |
| COSMOS-E | NBK | 09 59 07 | +02 23 44 | 20.0 | 0.8 | 2011 Mar 30, May 18–23, 30 | 20.7 |
| COSMOS-F | NBK | 09 59 07 | +02 10 30 | 20.0 | 0.9 | 2011 Dec 18; 2012 Mar 2, 17 | 20.8 |
| COSMOS-G | NBK | 10 01 46 | +02 23 44 | 20.0 | 0.9 | 2012 Mar 18–19 | 20.9 |
| COSMOS-H | NBK | 10 01 48 | +02 10 51 | 20.0 | 0.8 | 2012 Mar 19–20 | 20.7 |
| UKIDSS-UDS NE | NBK | 02 18 29 | −04 52 20 | 19.2 | 0.8 | 2005 Oct 18; 2006 Nov 13–14 | 20.7 |
| UKIDSS-UDS NW | NBK | 02 17 36 | −04 52 20 | 20.0 | 0.9 | 2006 Nov 11 | 20.8 |
| UKIDSS-UDS SE | NBK | 02 18 29 | −05 05 53 | 18.7 | 0.8 | 2006 Nov 15–16 | 20.7 |
| UKIDSS-UDS SW | NBK | 02 17 38 | −05 05 34 | 23.6 | 0.8 | 2007 Sep 30 | 20.9 |
| COSMOS-HAWK-I | H2 | 10 00 00 | +02 10 30 | 19.4 | 0.9 | 2009 Apr 10, 14–15, 18, May 13–14 | 21.5 |
| UKIDSS-UDS-HAWK-I | H2 | 02 17 36 | −04 52 20 | 19.1 | 1.0 | 2009 Aug 16, 19, 24, 27 | 21.7 |
| Field . | Band . | RA . | Dec. . | Int. time . | FHWM . | Dates . | mlim (Vega) . |
|---|---|---|---|---|---|---|---|
| . | (filter) . | (J2000) . | (J2000) . | (ks) . | (arcsec) . | . | (3σ) . |
| COSMOS-1 | NB921 | 09 59 23 | +02 30 29 | 2.9 | 0.9 | 2010 Dec 9 | 24.4 |
| COSMOS-2 | NB921 | 10 01 34 | +02 30 29 | 2.9 | 0.9 | 2010 Dec 9 | 24.5 |
| COSMOS-3 | NB921 | 09 59 23 | +02 04 16 | 2.9 | 0.9 | 2010 Dec 9 | 24.5 |
| COSMOS-4 | NB921 | 10 01 34 | +02 04 16 | 2.9 | 0.9 | 2010 Dec 9 | 24.5 |
| UKIDSS-UDS C | NB921 | 02 18 00 | −05 00 00 | 30.0 | 0.8 | 2005 Oct 29, Nov 1; 2007 Oct 11–12 | 26.6 |
| UKIDSS-UDS N | NB921 | 02 18 00 | −04 35 00 | 37.8 | 0.9 | 2005 Oct 30,31, Nov 1; 2006 Nov 18; 2007 Oct 11,12 | 26.7 |
| UKIDSS-UDS S | NB921 | 02 18 00 | −05 25 00 | 37.1 | 0.8 | 2005 Aug 29, Oct 29; 2006 Nov 18; 2007 Oct 12 | 26.6 |
| UKIDSS-UDS E | NB921 | 02 19 47 | −05 00 00 | 29.3 | 0.8 | 2005 Oct 31, Nov 1; 2006 Nov 18; 2007 Oct 11,12 | 26.6 |
| UKIDSS-UDS W | NB921 | 02 16 13 | −05 00 00 | 28.1 | 0.8 | 2006 Nov 18; 2007 Oct 11,12 | 26.0 |
| COSMOS-NW(1) | NBJ | 10 00 00 | +02 10 30 | 19.7 | 0.8 | 2007 Jan 14–16 | 22.0 |
| COSMOS-NE(2) | NBJ | 10 00 52 | +02 10 30 | 23.8 | 0.9 | 2006 Nov 10; 2007 Jan 13–14 | 22.0 |
| COSMOS-SW(3) | NBJ | 10 00 00 | +02 23 44 | 18.9 | 0.9 | 2007 Jan 15–17 | 22.0 |
| COSMOS-SE(4) | NBJ | 10 00 53 | +02 23 44 | 17.1 | 1.0 | 2007 Jan 15, 17, Feb 13, 14, 16 | 21.9 |
| UKIDSS-UDS NE | NBJ | 02 18 29 | −04 52 20 | 20.9 | 0.8 | 2007 Oct 21–23 | 22.0 |
| UKIDSS-UDS NW | NBJ | 02 17 36 | −04 52 20 | 22.4 | 0.9 | 2007 Oct 20–21 | 22.1 |
| UKIDSS-UDS SE | NBJ | 02 18 29 | −05 05 53 | 19.6 | 0.9 | 2007 Oct 23, 24 | 22.0 |
| UKIDSS-UDS SW | NBJ | 02 17 38 | −05 05 34 | 22.4 | 0.8 | 2007 Oct 19, 21 | 22.0 |
| COSMOS-NW(1) | NBH | 10 00 00 | +02 10 30 | 12.5 | 1.0 | 2009 Feb 27, Mar 1–2 | 21.1 |
| COSMOS-NE(2) DEEP | NBH | 10 00 52 | +02 10 30 | 107.0 | 0.9 | 2009 Feb 28, Apr 19, May 22; 2011 Jan 26–30 | 22.2 |
| COSMOS-SW(3) | NBH | 10 00 00 | +02 23 44 | 14.0 | 0.7 | 2010 Apr 2 | 21.0 |
| COSMOS-SE(4) | NBH | 10 00 53 | +02 23 44 | 18.1 | 1.0 | 2009 Mar 2, Apr 30, May 22; 2010 Apr 3 | 20.8 |
| COSMOS-A | NBH | 10 00 01 | +02 36 53 | 12.6 | 1.0 | 2010 Apr 9; 2011 Jan 25 | 21.1 |
| COSMOS-B | NBH | 10 00 54 | +02 36 30 | 12.6 | 0.9 | 2010 Apr 8–9 | 21.0 |
| COSMOS-C | NBH | 10 00 01 | +01 57 10 | 13.0 | 0.8 | 2010 Apr 6–8 | 20.8 |
| COSMOS-D | NBH | 10 00 52 | +01 57 15 | 14.2 | 0.8 | 2010 Apr 7–8 | 21.0 |
| COSMOS-E | NBH | 09 59 07 | +02 23 44 | 12.6 | 0.8 | 2010 Apr 3–6 | 20.9 |
| COSMOS-F | NBH | 09 59 07 | +02 10 30 | 12.6 | 0.7 | 2010 Apr 4 | 21.1 |
| COSMOS-G | NBH | 10 01 46 | +02 23 44 | 14.5 | 0.8 | 2010 Apr 4 and 9 | 21.0 |
| COSMOS-H | NBH | 10 01 48 | +02 10 51 | 14.0 | 0.8 | 2010 Apr 6 & 9 | 20.8 |
| UKIDSS-UDS NE | NBH | 02 18 29 | −04 52 20 | 18.2 | 0.9 | 2008 Sep 28–29; 2009 Aug 16–17; 2010 Jul 22 | 21.3 |
| UKIDSS-UDS NW | NBH | 02 17 36 | −04 52 20 | 18.0 | 0.9 | 2008 Sep 25, 29; 2010 Jul 18, 22 | 20.9 |
| UKIDSS-UDS SE | NBH | 02 18 29 | −05 05 53 | 25.2 | 0.8 | 2008 Sep 25, 28–29; 2009 Aug 16–17 | 21.5 |
| UKIDSS-UDS SW | NBH | 02 17 38 | −05 05 34 | 19.6 | 0.9 | 2008 Oct–Nov; 2009 Aug 16–17; 2010 Jul 23 and 21.3 | |
| COSMOS-NW(1) | NBK | 10 00 00 | +02 10 30 | 24.3 | 0.9 | 2006 Dec 17, 19–20; 2008 May 11; 2009 Feb 27 | 21.0 |
| COSMOS-NE(2) DEEP | NBK | 10 00 52 | +02 10 30 | 62.5 | 0.9 | 2006 May 20–21, Dec 20; 2008 Mar 6–9 | 21.3 |
| COSMOS-SW(3) | NBK | 10 00 00 | +02 23 44 | 20.0 | 0.9 | 2006 May 22, 24, Dec 20; 2009 May 20 | 20.8 |
| COSMOS-SE(4) | NBK | 10 00 53 | +02 23 44 | 19.5 | 0.9 | 2006 Nov 13–15, 30, Dec 16 | 20.9 |
| COSMOS-A | NBK | 10 00 01 | +02 36 53 | 20.0 | 1.0 | 2011 Mar 19–26, 2012 Mar 20 | 21.0 |
| COSMOS-B | NBK | 10 00 54 | +02 36 30 | 20.0 | 0.9 | 2011 Mar 25–26 | 20.8 |
| COSMOS-C | NBK | 10 00 01 | +01 57 10 | 26.7 | 0.9 | 2011 Mar 27, 30, Apr 3–5, 16–18 | 20.9 |
| COSMOS-D | NBK | 10 00 52 | +01 57 15 | 20.0 | 0.9 | 2011 Mar 30, Jun 6; 2012 Jan 5,18, Feb 26, Mar 2 | 20.9 |
| COSMOS-E | NBK | 09 59 07 | +02 23 44 | 20.0 | 0.8 | 2011 Mar 30, May 18–23, 30 | 20.7 |
| COSMOS-F | NBK | 09 59 07 | +02 10 30 | 20.0 | 0.9 | 2011 Dec 18; 2012 Mar 2, 17 | 20.8 |
| COSMOS-G | NBK | 10 01 46 | +02 23 44 | 20.0 | 0.9 | 2012 Mar 18–19 | 20.9 |
| COSMOS-H | NBK | 10 01 48 | +02 10 51 | 20.0 | 0.8 | 2012 Mar 19–20 | 20.7 |
| UKIDSS-UDS NE | NBK | 02 18 29 | −04 52 20 | 19.2 | 0.8 | 2005 Oct 18; 2006 Nov 13–14 | 20.7 |
| UKIDSS-UDS NW | NBK | 02 17 36 | −04 52 20 | 20.0 | 0.9 | 2006 Nov 11 | 20.8 |
| UKIDSS-UDS SE | NBK | 02 18 29 | −05 05 53 | 18.7 | 0.8 | 2006 Nov 15–16 | 20.7 |
| UKIDSS-UDS SW | NBK | 02 17 38 | −05 05 34 | 23.6 | 0.8 | 2007 Sep 30 | 20.9 |
| COSMOS-HAWK-I | H2 | 10 00 00 | +02 10 30 | 19.4 | 0.9 | 2009 Apr 10, 14–15, 18, May 13–14 | 21.5 |
| UKIDSS-UDS-HAWK-I | H2 | 02 17 36 | −04 52 20 | 19.1 | 1.0 | 2009 Aug 16, 19, 24, 27 | 21.7 |
Observation log of all the narrow-band observations obtained over the COSMOS and UDS fields, taken using WFCAM on UKIRT, HAWK-I on the VLT and Suprime-Cam on Subaru, during 2006–2012. Limiting magnitudes (3σ, all in Vega) are the average of each field/pointing, based on the measurements of 104–106 randomly placed 2 arcsec apertures in each frame, but note that for COSMOS (NBH and NBK) the central four pointings overlap with part of the outer pointings (see Fig. 2), making the central region data up to 0.3–0.4 mag deeper, by doubling/tripling the exposure time.
| Field . | Band . | RA . | Dec. . | Int. time . | FHWM . | Dates . | mlim (Vega) . |
|---|---|---|---|---|---|---|---|
| . | (filter) . | (J2000) . | (J2000) . | (ks) . | (arcsec) . | . | (3σ) . |
| COSMOS-1 | NB921 | 09 59 23 | +02 30 29 | 2.9 | 0.9 | 2010 Dec 9 | 24.4 |
| COSMOS-2 | NB921 | 10 01 34 | +02 30 29 | 2.9 | 0.9 | 2010 Dec 9 | 24.5 |
| COSMOS-3 | NB921 | 09 59 23 | +02 04 16 | 2.9 | 0.9 | 2010 Dec 9 | 24.5 |
| COSMOS-4 | NB921 | 10 01 34 | +02 04 16 | 2.9 | 0.9 | 2010 Dec 9 | 24.5 |
| UKIDSS-UDS C | NB921 | 02 18 00 | −05 00 00 | 30.0 | 0.8 | 2005 Oct 29, Nov 1; 2007 Oct 11–12 | 26.6 |
| UKIDSS-UDS N | NB921 | 02 18 00 | −04 35 00 | 37.8 | 0.9 | 2005 Oct 30,31, Nov 1; 2006 Nov 18; 2007 Oct 11,12 | 26.7 |
| UKIDSS-UDS S | NB921 | 02 18 00 | −05 25 00 | 37.1 | 0.8 | 2005 Aug 29, Oct 29; 2006 Nov 18; 2007 Oct 12 | 26.6 |
| UKIDSS-UDS E | NB921 | 02 19 47 | −05 00 00 | 29.3 | 0.8 | 2005 Oct 31, Nov 1; 2006 Nov 18; 2007 Oct 11,12 | 26.6 |
| UKIDSS-UDS W | NB921 | 02 16 13 | −05 00 00 | 28.1 | 0.8 | 2006 Nov 18; 2007 Oct 11,12 | 26.0 |
| COSMOS-NW(1) | NBJ | 10 00 00 | +02 10 30 | 19.7 | 0.8 | 2007 Jan 14–16 | 22.0 |
| COSMOS-NE(2) | NBJ | 10 00 52 | +02 10 30 | 23.8 | 0.9 | 2006 Nov 10; 2007 Jan 13–14 | 22.0 |
| COSMOS-SW(3) | NBJ | 10 00 00 | +02 23 44 | 18.9 | 0.9 | 2007 Jan 15–17 | 22.0 |
| COSMOS-SE(4) | NBJ | 10 00 53 | +02 23 44 | 17.1 | 1.0 | 2007 Jan 15, 17, Feb 13, 14, 16 | 21.9 |
| UKIDSS-UDS NE | NBJ | 02 18 29 | −04 52 20 | 20.9 | 0.8 | 2007 Oct 21–23 | 22.0 |
| UKIDSS-UDS NW | NBJ | 02 17 36 | −04 52 20 | 22.4 | 0.9 | 2007 Oct 20–21 | 22.1 |
| UKIDSS-UDS SE | NBJ | 02 18 29 | −05 05 53 | 19.6 | 0.9 | 2007 Oct 23, 24 | 22.0 |
| UKIDSS-UDS SW | NBJ | 02 17 38 | −05 05 34 | 22.4 | 0.8 | 2007 Oct 19, 21 | 22.0 |
| COSMOS-NW(1) | NBH | 10 00 00 | +02 10 30 | 12.5 | 1.0 | 2009 Feb 27, Mar 1–2 | 21.1 |
| COSMOS-NE(2) DEEP | NBH | 10 00 52 | +02 10 30 | 107.0 | 0.9 | 2009 Feb 28, Apr 19, May 22; 2011 Jan 26–30 | 22.2 |
| COSMOS-SW(3) | NBH | 10 00 00 | +02 23 44 | 14.0 | 0.7 | 2010 Apr 2 | 21.0 |
| COSMOS-SE(4) | NBH | 10 00 53 | +02 23 44 | 18.1 | 1.0 | 2009 Mar 2, Apr 30, May 22; 2010 Apr 3 | 20.8 |
| COSMOS-A | NBH | 10 00 01 | +02 36 53 | 12.6 | 1.0 | 2010 Apr 9; 2011 Jan 25 | 21.1 |
| COSMOS-B | NBH | 10 00 54 | +02 36 30 | 12.6 | 0.9 | 2010 Apr 8–9 | 21.0 |
| COSMOS-C | NBH | 10 00 01 | +01 57 10 | 13.0 | 0.8 | 2010 Apr 6–8 | 20.8 |
| COSMOS-D | NBH | 10 00 52 | +01 57 15 | 14.2 | 0.8 | 2010 Apr 7–8 | 21.0 |
| COSMOS-E | NBH | 09 59 07 | +02 23 44 | 12.6 | 0.8 | 2010 Apr 3–6 | 20.9 |
| COSMOS-F | NBH | 09 59 07 | +02 10 30 | 12.6 | 0.7 | 2010 Apr 4 | 21.1 |
| COSMOS-G | NBH | 10 01 46 | +02 23 44 | 14.5 | 0.8 | 2010 Apr 4 and 9 | 21.0 |
| COSMOS-H | NBH | 10 01 48 | +02 10 51 | 14.0 | 0.8 | 2010 Apr 6 & 9 | 20.8 |
| UKIDSS-UDS NE | NBH | 02 18 29 | −04 52 20 | 18.2 | 0.9 | 2008 Sep 28–29; 2009 Aug 16–17; 2010 Jul 22 | 21.3 |
| UKIDSS-UDS NW | NBH | 02 17 36 | −04 52 20 | 18.0 | 0.9 | 2008 Sep 25, 29; 2010 Jul 18, 22 | 20.9 |
| UKIDSS-UDS SE | NBH | 02 18 29 | −05 05 53 | 25.2 | 0.8 | 2008 Sep 25, 28–29; 2009 Aug 16–17 | 21.5 |
| UKIDSS-UDS SW | NBH | 02 17 38 | −05 05 34 | 19.6 | 0.9 | 2008 Oct–Nov; 2009 Aug 16–17; 2010 Jul 23 and 21.3 | |
| COSMOS-NW(1) | NBK | 10 00 00 | +02 10 30 | 24.3 | 0.9 | 2006 Dec 17, 19–20; 2008 May 11; 2009 Feb 27 | 21.0 |
| COSMOS-NE(2) DEEP | NBK | 10 00 52 | +02 10 30 | 62.5 | 0.9 | 2006 May 20–21, Dec 20; 2008 Mar 6–9 | 21.3 |
| COSMOS-SW(3) | NBK | 10 00 00 | +02 23 44 | 20.0 | 0.9 | 2006 May 22, 24, Dec 20; 2009 May 20 | 20.8 |
| COSMOS-SE(4) | NBK | 10 00 53 | +02 23 44 | 19.5 | 0.9 | 2006 Nov 13–15, 30, Dec 16 | 20.9 |
| COSMOS-A | NBK | 10 00 01 | +02 36 53 | 20.0 | 1.0 | 2011 Mar 19–26, 2012 Mar 20 | 21.0 |
| COSMOS-B | NBK | 10 00 54 | +02 36 30 | 20.0 | 0.9 | 2011 Mar 25–26 | 20.8 |
| COSMOS-C | NBK | 10 00 01 | +01 57 10 | 26.7 | 0.9 | 2011 Mar 27, 30, Apr 3–5, 16–18 | 20.9 |
| COSMOS-D | NBK | 10 00 52 | +01 57 15 | 20.0 | 0.9 | 2011 Mar 30, Jun 6; 2012 Jan 5,18, Feb 26, Mar 2 | 20.9 |
| COSMOS-E | NBK | 09 59 07 | +02 23 44 | 20.0 | 0.8 | 2011 Mar 30, May 18–23, 30 | 20.7 |
| COSMOS-F | NBK | 09 59 07 | +02 10 30 | 20.0 | 0.9 | 2011 Dec 18; 2012 Mar 2, 17 | 20.8 |
| COSMOS-G | NBK | 10 01 46 | +02 23 44 | 20.0 | 0.9 | 2012 Mar 18–19 | 20.9 |
| COSMOS-H | NBK | 10 01 48 | +02 10 51 | 20.0 | 0.8 | 2012 Mar 19–20 | 20.7 |
| UKIDSS-UDS NE | NBK | 02 18 29 | −04 52 20 | 19.2 | 0.8 | 2005 Oct 18; 2006 Nov 13–14 | 20.7 |
| UKIDSS-UDS NW | NBK | 02 17 36 | −04 52 20 | 20.0 | 0.9 | 2006 Nov 11 | 20.8 |
| UKIDSS-UDS SE | NBK | 02 18 29 | −05 05 53 | 18.7 | 0.8 | 2006 Nov 15–16 | 20.7 |
| UKIDSS-UDS SW | NBK | 02 17 38 | −05 05 34 | 23.6 | 0.8 | 2007 Sep 30 | 20.9 |
| COSMOS-HAWK-I | H2 | 10 00 00 | +02 10 30 | 19.4 | 0.9 | 2009 Apr 10, 14–15, 18, May 13–14 | 21.5 |
| UKIDSS-UDS-HAWK-I | H2 | 02 17 36 | −04 52 20 | 19.1 | 1.0 | 2009 Aug 16, 19, 24, 27 | 21.7 |
| Field . | Band . | RA . | Dec. . | Int. time . | FHWM . | Dates . | mlim (Vega) . |
|---|---|---|---|---|---|---|---|
| . | (filter) . | (J2000) . | (J2000) . | (ks) . | (arcsec) . | . | (3σ) . |
| COSMOS-1 | NB921 | 09 59 23 | +02 30 29 | 2.9 | 0.9 | 2010 Dec 9 | 24.4 |
| COSMOS-2 | NB921 | 10 01 34 | +02 30 29 | 2.9 | 0.9 | 2010 Dec 9 | 24.5 |
| COSMOS-3 | NB921 | 09 59 23 | +02 04 16 | 2.9 | 0.9 | 2010 Dec 9 | 24.5 |
| COSMOS-4 | NB921 | 10 01 34 | +02 04 16 | 2.9 | 0.9 | 2010 Dec 9 | 24.5 |
| UKIDSS-UDS C | NB921 | 02 18 00 | −05 00 00 | 30.0 | 0.8 | 2005 Oct 29, Nov 1; 2007 Oct 11–12 | 26.6 |
| UKIDSS-UDS N | NB921 | 02 18 00 | −04 35 00 | 37.8 | 0.9 | 2005 Oct 30,31, Nov 1; 2006 Nov 18; 2007 Oct 11,12 | 26.7 |
| UKIDSS-UDS S | NB921 | 02 18 00 | −05 25 00 | 37.1 | 0.8 | 2005 Aug 29, Oct 29; 2006 Nov 18; 2007 Oct 12 | 26.6 |
| UKIDSS-UDS E | NB921 | 02 19 47 | −05 00 00 | 29.3 | 0.8 | 2005 Oct 31, Nov 1; 2006 Nov 18; 2007 Oct 11,12 | 26.6 |
| UKIDSS-UDS W | NB921 | 02 16 13 | −05 00 00 | 28.1 | 0.8 | 2006 Nov 18; 2007 Oct 11,12 | 26.0 |
| COSMOS-NW(1) | NBJ | 10 00 00 | +02 10 30 | 19.7 | 0.8 | 2007 Jan 14–16 | 22.0 |
| COSMOS-NE(2) | NBJ | 10 00 52 | +02 10 30 | 23.8 | 0.9 | 2006 Nov 10; 2007 Jan 13–14 | 22.0 |
| COSMOS-SW(3) | NBJ | 10 00 00 | +02 23 44 | 18.9 | 0.9 | 2007 Jan 15–17 | 22.0 |
| COSMOS-SE(4) | NBJ | 10 00 53 | +02 23 44 | 17.1 | 1.0 | 2007 Jan 15, 17, Feb 13, 14, 16 | 21.9 |
| UKIDSS-UDS NE | NBJ | 02 18 29 | −04 52 20 | 20.9 | 0.8 | 2007 Oct 21–23 | 22.0 |
| UKIDSS-UDS NW | NBJ | 02 17 36 | −04 52 20 | 22.4 | 0.9 | 2007 Oct 20–21 | 22.1 |
| UKIDSS-UDS SE | NBJ | 02 18 29 | −05 05 53 | 19.6 | 0.9 | 2007 Oct 23, 24 | 22.0 |
| UKIDSS-UDS SW | NBJ | 02 17 38 | −05 05 34 | 22.4 | 0.8 | 2007 Oct 19, 21 | 22.0 |
| COSMOS-NW(1) | NBH | 10 00 00 | +02 10 30 | 12.5 | 1.0 | 2009 Feb 27, Mar 1–2 | 21.1 |
| COSMOS-NE(2) DEEP | NBH | 10 00 52 | +02 10 30 | 107.0 | 0.9 | 2009 Feb 28, Apr 19, May 22; 2011 Jan 26–30 | 22.2 |
| COSMOS-SW(3) | NBH | 10 00 00 | +02 23 44 | 14.0 | 0.7 | 2010 Apr 2 | 21.0 |
| COSMOS-SE(4) | NBH | 10 00 53 | +02 23 44 | 18.1 | 1.0 | 2009 Mar 2, Apr 30, May 22; 2010 Apr 3 | 20.8 |
| COSMOS-A | NBH | 10 00 01 | +02 36 53 | 12.6 | 1.0 | 2010 Apr 9; 2011 Jan 25 | 21.1 |
| COSMOS-B | NBH | 10 00 54 | +02 36 30 | 12.6 | 0.9 | 2010 Apr 8–9 | 21.0 |
| COSMOS-C | NBH | 10 00 01 | +01 57 10 | 13.0 | 0.8 | 2010 Apr 6–8 | 20.8 |
| COSMOS-D | NBH | 10 00 52 | +01 57 15 | 14.2 | 0.8 | 2010 Apr 7–8 | 21.0 |
| COSMOS-E | NBH | 09 59 07 | +02 23 44 | 12.6 | 0.8 | 2010 Apr 3–6 | 20.9 |
| COSMOS-F | NBH | 09 59 07 | +02 10 30 | 12.6 | 0.7 | 2010 Apr 4 | 21.1 |
| COSMOS-G | NBH | 10 01 46 | +02 23 44 | 14.5 | 0.8 | 2010 Apr 4 and 9 | 21.0 |
| COSMOS-H | NBH | 10 01 48 | +02 10 51 | 14.0 | 0.8 | 2010 Apr 6 & 9 | 20.8 |
| UKIDSS-UDS NE | NBH | 02 18 29 | −04 52 20 | 18.2 | 0.9 | 2008 Sep 28–29; 2009 Aug 16–17; 2010 Jul 22 | 21.3 |
| UKIDSS-UDS NW | NBH | 02 17 36 | −04 52 20 | 18.0 | 0.9 | 2008 Sep 25, 29; 2010 Jul 18, 22 | 20.9 |
| UKIDSS-UDS SE | NBH | 02 18 29 | −05 05 53 | 25.2 | 0.8 | 2008 Sep 25, 28–29; 2009 Aug 16–17 | 21.5 |
| UKIDSS-UDS SW | NBH | 02 17 38 | −05 05 34 | 19.6 | 0.9 | 2008 Oct–Nov; 2009 Aug 16–17; 2010 Jul 23 and 21.3 | |
| COSMOS-NW(1) | NBK | 10 00 00 | +02 10 30 | 24.3 | 0.9 | 2006 Dec 17, 19–20; 2008 May 11; 2009 Feb 27 | 21.0 |
| COSMOS-NE(2) DEEP | NBK | 10 00 52 | +02 10 30 | 62.5 | 0.9 | 2006 May 20–21, Dec 20; 2008 Mar 6–9 | 21.3 |
| COSMOS-SW(3) | NBK | 10 00 00 | +02 23 44 | 20.0 | 0.9 | 2006 May 22, 24, Dec 20; 2009 May 20 | 20.8 |
| COSMOS-SE(4) | NBK | 10 00 53 | +02 23 44 | 19.5 | 0.9 | 2006 Nov 13–15, 30, Dec 16 | 20.9 |
| COSMOS-A | NBK | 10 00 01 | +02 36 53 | 20.0 | 1.0 | 2011 Mar 19–26, 2012 Mar 20 | 21.0 |
| COSMOS-B | NBK | 10 00 54 | +02 36 30 | 20.0 | 0.9 | 2011 Mar 25–26 | 20.8 |
| COSMOS-C | NBK | 10 00 01 | +01 57 10 | 26.7 | 0.9 | 2011 Mar 27, 30, Apr 3–5, 16–18 | 20.9 |
| COSMOS-D | NBK | 10 00 52 | +01 57 15 | 20.0 | 0.9 | 2011 Mar 30, Jun 6; 2012 Jan 5,18, Feb 26, Mar 2 | 20.9 |
| COSMOS-E | NBK | 09 59 07 | +02 23 44 | 20.0 | 0.8 | 2011 Mar 30, May 18–23, 30 | 20.7 |
| COSMOS-F | NBK | 09 59 07 | +02 10 30 | 20.0 | 0.9 | 2011 Dec 18; 2012 Mar 2, 17 | 20.8 |
| COSMOS-G | NBK | 10 01 46 | +02 23 44 | 20.0 | 0.9 | 2012 Mar 18–19 | 20.9 |
| COSMOS-H | NBK | 10 01 48 | +02 10 51 | 20.0 | 0.8 | 2012 Mar 19–20 | 20.7 |
| UKIDSS-UDS NE | NBK | 02 18 29 | −04 52 20 | 19.2 | 0.8 | 2005 Oct 18; 2006 Nov 13–14 | 20.7 |
| UKIDSS-UDS NW | NBK | 02 17 36 | −04 52 20 | 20.0 | 0.9 | 2006 Nov 11 | 20.8 |
| UKIDSS-UDS SE | NBK | 02 18 29 | −05 05 53 | 18.7 | 0.8 | 2006 Nov 15–16 | 20.7 |
| UKIDSS-UDS SW | NBK | 02 17 38 | −05 05 34 | 23.6 | 0.8 | 2007 Sep 30 | 20.9 |
| COSMOS-HAWK-I | H2 | 10 00 00 | +02 10 30 | 19.4 | 0.9 | 2009 Apr 10, 14–15, 18, May 13–14 | 21.5 |
| UKIDSS-UDS-HAWK-I | H2 | 02 17 36 | −04 52 20 | 19.1 | 1.0 | 2009 Aug 16, 19, 24, 27 | 21.7 |
2 DATA AND SAMPLES
2.1 Optical NB921 imaging with Subaru
Optical imaging data were obtained with Suprime-Cam using the NB921 narrow-band filter. Suprime-Cam consists of 10 CCDs with a combined field of view of 34 × 27 arcmin2 and with chip gaps of ∼15 arcsec. The NB921 filter is centred at 9196 Å with an FWHM of 132 Å. The COSMOS field was observed in service mode in 2010 December with four different pointings covering the central 1.1 deg2. Total exposure times were 2.9 ks per pointing, composed of individual exposures of 360 s dithered over eight different positions. Observations are detailed in Table 2. The UDS field has also been observed with the NB921 filter (see Ouchi et al. 2010), and these data have been extracted from the archive. Full details of the data reduction and catalogue production of the UDS data were presented by S12 and the same approach was adopted for the COSMOS data. In brief, all the raw NB921 data were reduced with the Suprime-Cam Deep field REDuction (sdfred) package (Yagi et al. 2002; Ouchi et al. 2004) and iraf. The combined images were aligned to the public z′-band images of Subaru–XMM Deep Survey or the COSMOS field and point spread function (PSF) matched (FWHM=0.9 arcsec). The NB921 zero-points were determined using z′ data, so that the (z′ − NB921) colours are consistent with a median of zero for z′ between 19 and 21.5 – where both NB921 and z′ images are unsaturated and have very high signal-to-noise ratios.
Source detection and photometry were performed using SExtractor (Bertin & Arnouts 1996). Sources were detected on each individual NB921 image and magnitudes measured with 2 and 3 arcsec diameter apertures. The 3 arcsec apertures are used to select and measure Hα line fluxes: at z = 0.4 the 3 arcsec apertures measure the same physical area as 2 arcsec apertures at z = 0.8, 1.47 and 2.23 (≈16 kpc), assuring full consistency. The 2 arcsec apertures are used to measure emission lines from sources at higher redshift ([O ii] at z = 1.47, to match the NBH Hα measurement at the same redshift, and [O iii] at z = 0.84 to match the NBJ Hα survey). The average NB921 3σ limiting magnitudes (in 2 arcsec apertures) are given in Table 2.
2.2 Near-infrared imaging with UKIRT
The COSMOS and UKIDSS UDS fields were observed with WFCAM on UKIRT as summarized in Table 2, using the NBJ, NBH and NBK narrow-band filters, with central wavelengths and FWHM given in Table 1. WFCAM has four 2048 × 2048 0.4 arcsec pixel−1 detectors offset by ∼20 arcmin, resulting in a non-contiguous field of view of ∼ 27 × 27 arcmin2 which can be macro-stepped four times to cover a contiguous region of ∼ 55 × 55 arcmin2. Observations were conducted over 2006–2012, covering 1.6 deg2 (NBJ) and 2.34 deg2 (NBH and NBK) over the COSMOS and the UDS fields (see Table 2).
The coverage over UDS is a simple mosaic obtained with four different pointings, covering a contiguous region of ∼ 55 × 55 arcmin2. For the COSMOS field, an initial 0.8 deg2 coverage obtained with four WFCAM pointings was complemented in NBH and NBK by eight further WFCAM pointings, macro-jittered to obtain a combined 1.6 deg2 coverage with increasing exposure time per pixel towards the centre of the field (see Fig. 2). Part of the central region (∼0.2 deg2) benefits further from some significant extra deep data in both NBH and NBK (see Table 2), leading to a much higher total exposure time.
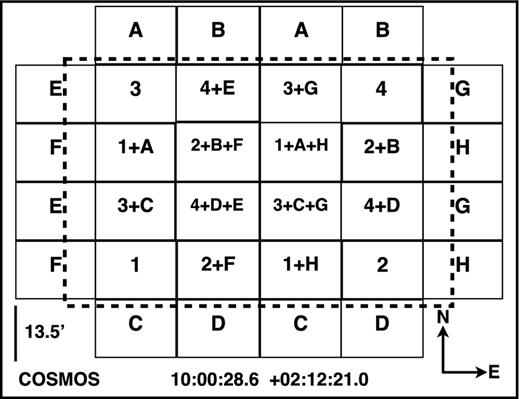
The survey strategy used to cover the COSMOS field. The central pointings (1, 2, 3 and 4; see Table 2) were complemented with further pointings (A to H) to increase both the surveyed area and the exposure time in the central area. The region delimited by the dashed line shows the NB921 coverage obtained in COSMOS. See Table 2 for details on the pointings, including exposure times.
A dedicated pipeline has been developed for HiZELS (PfHiZELS; cf. S09 for more details). The pipeline has been modified and updated since S09 mostly to (1) improve the flat-fielding3 and (2) provide more accurate astrometric solutions for each individual frame, which result in a more accurate stacking.4 The updated version of the pipeline (PfHiZELS2012) has been used to reduce all UKIRT narrow-band data (NBJ, NBH and NBK), including those already presented in previous papers. This approach guarantees a complete self-consistency and takes advantage of the improved reduction which, in some cases, is able to go deeper by ≈0.2 mag when compared to the data reduced by the previous version of the pipeline (e.g. S09).
For the COSMOS field, in order to co-add frames taken with different WFCAM cameras (due to the survey strategy; see Fig. 2), scamp is used [in combination with Sloan Digital Sky Survey (SDSS) Data Release 7] to obtain accurate astrometry solutions which account for distortions in each stack (in addition to individual frames being corrected prior to combining) before co-adding different fields. The typical rms is <0.1 arcsec, by using on average ∼500 sources per chip. By following this approach, even at the highest radial distances (r > 1000 pixel) from the centre of the images the PSF/ellipticity remains unchanged due to stacking, and the data over areas that double/triple the expose time are found to become deeper by (on average) 0.3–0.4 mag, with no radial change in the PSF.
Narrow-band images were photometrically calibrated (independently) by matching ∼100 stars per frame with J, H and K between the 12th and 16th magnitudes from the 2MASS Point Source Catalogue (Cutri et al. 2003), which are unsaturated in the narrow-band images. WFCAM images are affected by cross-talk and other artefacts caused by bright stars: accurate masks are produced in order to reject such regions. Sources were extracted using SExtractor (Bertin & Arnouts 1996), making use of the masks. Photometry was measured in apertures of 2 arcsec diameter which at z = 0.8–2.2 recover Hα fluxes over ≈16 kpc. The average 3σ depths of the entire set of narrow-band (NB) frames vary significantly, and are summarized in Table 2. The total numbers of sources detected with each filter are given in Table 3. Note that the central region of COSMOS NBH and NBK coverages benefits from a much higher total exposure time per pixel, resulting in data that are deeper by 0.3–0.4 mag (on average) than the outer regions.
A summary of the number of sources, narrow-band emitters and Hα-selected emitters for the various surveys undertaken with different narrow-band filters. Fields are C: COSMOS, U: UDS. Emitters are the narrow-band excess sources remaining after excluding artefacts and stars. Volumes are presented in units of 104 Mpc3 and correspond to the total volumes probed; deeper pointings cover relatively smaller volumes. SFRs (limiting SFRs) are presented uncorrected for dust extinction. The number of spectroscopically confirmed Hα emitters are presented in the ‘z Hα conf.’ column, while the number of Hα sources which are confirmed by an emission-line detection in another narrow-band filter are presented in ‘Conf 2lines’ column. Limiting SFRs are uncorrected for dust extinction and these represent the limit over the deepest field(s). Also, note that for all four redshifts the number of z-included sources missed by the selection is typically <10 and the z-rejected sources are typically <10 as well. Therefore, decrease of available spectroscopic redshifts with redshift does not introduce any bias.
| Filter . | Field . | Detect . | W/colours . | Emitters . | Stars . | Artefacts . | Hα . | z Hα conf. . | Conf 2lines . | Volume . | Hα SFR . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| NB . | C/U . | (3σ) . | # . | (3Σ) . | # . | # . | # . | # . | # . | (104 Mpc3) . | (M⊙ yr−1) . |
| NB921 | C | 155 542 | 148 702 | 2819 | 247 | – | 521 | 38 | – | 5.1 | 0.03 |
| NB921 | U | 236 718 | 198 256 | 6957 | 775 | – | 1221 | 8 | – | 5.1 | 0.01 |
| NBJ | C | 32 345 | 31 661 | 700 | 40 | 46 | 425 | 81 | 158 | 7.9 | 1.5 |
| NBJ | U | 21 233 | 19 916 | 551 | 49 | 30 | 212 | 14 | 79 | 11.1 | 1.5 |
| NBH | C | 65 912 | 64 453 | 723 | 60 | 63 | 327 | 28 | 158 | 49.1 | 3.0 |
| NBH | U | 26 084 | 23 503 | 418 | 23 | 5 | 188 | 18 | 188 | 22.8 | 5.0 |
| NBK | C | 99 395 | 98 085 | 1359 | 78 | 56 | 588 | 4 | 125 | 54.8 | 5.0 |
| NBK | U | 28 276 | 26 062 | 399 | 28 | 10 | 184 | 2 | 30 | 22.4 | 10.0 |
| H2 | C | 1054 | 940 | 52 | 3 | 2 | 31 | 0 | 3 | 0.9 | 3.5 |
| H2 | U | 1193 | 1059 | 33 | 7 | 1 | 14 | 0 | 0 | 0.9 | 3.5 |
| Filter . | Field . | Detect . | W/colours . | Emitters . | Stars . | Artefacts . | Hα . | z Hα conf. . | Conf 2lines . | Volume . | Hα SFR . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| NB . | C/U . | (3σ) . | # . | (3Σ) . | # . | # . | # . | # . | # . | (104 Mpc3) . | (M⊙ yr−1) . |
| NB921 | C | 155 542 | 148 702 | 2819 | 247 | – | 521 | 38 | – | 5.1 | 0.03 |
| NB921 | U | 236 718 | 198 256 | 6957 | 775 | – | 1221 | 8 | – | 5.1 | 0.01 |
| NBJ | C | 32 345 | 31 661 | 700 | 40 | 46 | 425 | 81 | 158 | 7.9 | 1.5 |
| NBJ | U | 21 233 | 19 916 | 551 | 49 | 30 | 212 | 14 | 79 | 11.1 | 1.5 |
| NBH | C | 65 912 | 64 453 | 723 | 60 | 63 | 327 | 28 | 158 | 49.1 | 3.0 |
| NBH | U | 26 084 | 23 503 | 418 | 23 | 5 | 188 | 18 | 188 | 22.8 | 5.0 |
| NBK | C | 99 395 | 98 085 | 1359 | 78 | 56 | 588 | 4 | 125 | 54.8 | 5.0 |
| NBK | U | 28 276 | 26 062 | 399 | 28 | 10 | 184 | 2 | 30 | 22.4 | 10.0 |
| H2 | C | 1054 | 940 | 52 | 3 | 2 | 31 | 0 | 3 | 0.9 | 3.5 |
| H2 | U | 1193 | 1059 | 33 | 7 | 1 | 14 | 0 | 0 | 0.9 | 3.5 |
A summary of the number of sources, narrow-band emitters and Hα-selected emitters for the various surveys undertaken with different narrow-band filters. Fields are C: COSMOS, U: UDS. Emitters are the narrow-band excess sources remaining after excluding artefacts and stars. Volumes are presented in units of 104 Mpc3 and correspond to the total volumes probed; deeper pointings cover relatively smaller volumes. SFRs (limiting SFRs) are presented uncorrected for dust extinction. The number of spectroscopically confirmed Hα emitters are presented in the ‘z Hα conf.’ column, while the number of Hα sources which are confirmed by an emission-line detection in another narrow-band filter are presented in ‘Conf 2lines’ column. Limiting SFRs are uncorrected for dust extinction and these represent the limit over the deepest field(s). Also, note that for all four redshifts the number of z-included sources missed by the selection is typically <10 and the z-rejected sources are typically <10 as well. Therefore, decrease of available spectroscopic redshifts with redshift does not introduce any bias.
| Filter . | Field . | Detect . | W/colours . | Emitters . | Stars . | Artefacts . | Hα . | z Hα conf. . | Conf 2lines . | Volume . | Hα SFR . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| NB . | C/U . | (3σ) . | # . | (3Σ) . | # . | # . | # . | # . | # . | (104 Mpc3) . | (M⊙ yr−1) . |
| NB921 | C | 155 542 | 148 702 | 2819 | 247 | – | 521 | 38 | – | 5.1 | 0.03 |
| NB921 | U | 236 718 | 198 256 | 6957 | 775 | – | 1221 | 8 | – | 5.1 | 0.01 |
| NBJ | C | 32 345 | 31 661 | 700 | 40 | 46 | 425 | 81 | 158 | 7.9 | 1.5 |
| NBJ | U | 21 233 | 19 916 | 551 | 49 | 30 | 212 | 14 | 79 | 11.1 | 1.5 |
| NBH | C | 65 912 | 64 453 | 723 | 60 | 63 | 327 | 28 | 158 | 49.1 | 3.0 |
| NBH | U | 26 084 | 23 503 | 418 | 23 | 5 | 188 | 18 | 188 | 22.8 | 5.0 |
| NBK | C | 99 395 | 98 085 | 1359 | 78 | 56 | 588 | 4 | 125 | 54.8 | 5.0 |
| NBK | U | 28 276 | 26 062 | 399 | 28 | 10 | 184 | 2 | 30 | 22.4 | 10.0 |
| H2 | C | 1054 | 940 | 52 | 3 | 2 | 31 | 0 | 3 | 0.9 | 3.5 |
| H2 | U | 1193 | 1059 | 33 | 7 | 1 | 14 | 0 | 0 | 0.9 | 3.5 |
| Filter . | Field . | Detect . | W/colours . | Emitters . | Stars . | Artefacts . | Hα . | z Hα conf. . | Conf 2lines . | Volume . | Hα SFR . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| NB . | C/U . | (3σ) . | # . | (3Σ) . | # . | # . | # . | # . | # . | (104 Mpc3) . | (M⊙ yr−1) . |
| NB921 | C | 155 542 | 148 702 | 2819 | 247 | – | 521 | 38 | – | 5.1 | 0.03 |
| NB921 | U | 236 718 | 198 256 | 6957 | 775 | – | 1221 | 8 | – | 5.1 | 0.01 |
| NBJ | C | 32 345 | 31 661 | 700 | 40 | 46 | 425 | 81 | 158 | 7.9 | 1.5 |
| NBJ | U | 21 233 | 19 916 | 551 | 49 | 30 | 212 | 14 | 79 | 11.1 | 1.5 |
| NBH | C | 65 912 | 64 453 | 723 | 60 | 63 | 327 | 28 | 158 | 49.1 | 3.0 |
| NBH | U | 26 084 | 23 503 | 418 | 23 | 5 | 188 | 18 | 188 | 22.8 | 5.0 |
| NBK | C | 99 395 | 98 085 | 1359 | 78 | 56 | 588 | 4 | 125 | 54.8 | 5.0 |
| NBK | U | 28 276 | 26 062 | 399 | 28 | 10 | 184 | 2 | 30 | 22.4 | 10.0 |
| H2 | C | 1054 | 940 | 52 | 3 | 2 | 31 | 0 | 3 | 0.9 | 3.5 |
| H2 | U | 1193 | 1059 | 33 | 7 | 1 | 14 | 0 | 0 | 0.9 | 3.5 |
2.3 Near-infrared H2 imaging with HAWK-I
The UKIDSS UDS and COSMOS fields were observed with the HAWK-I instrument (Pirard et al. 2004; Casali et al. 2006) on the VLT during 2009. A single dithered pointing was obtained in each of the fields using the H2 filter, characterized by λc = 2.124 μm and δλ = 0.030 μm (note that the filter is slightly wider than that on WFCAM). Individual exposures were of 60 s, and the total exposure time per field is 5 h. Table 2 presents the details of the observations and depth reached.
Data were reduced using the HAWK-I ESO pipeline recipes, by following an identical reduction scheme/procedure to the WFCAM data. The data have also been distortion corrected and astrometrically calibrated before combining, using the appropriate pipeline recipes. After combining all the individual reduced frames, it is possible to obtain a contiguous image of ≈7.5 × 7.5 arcmin2 in each of the fields. There are, none the less, small regions with slightly lower exposure time per pixel in regions related with chip gaps at certain positions. Because of the availability of the very wide WFCAM imaging, regions in the HAWK-I combined images for which the exposure time per pixel is <80 per cent of the total are not considered. Frames are photometrically calibrated using 2MASS as a first pass, and then using UDS and COSMOS Ks-calibrated images to guarantee a median 0 colour (K − NBK) for all magnitudes probed, as this procedure provides a larger number of sources. Similar to the procedure used for WFCAM data, sources were extracted using SExtractor and photometry was measured in apertures of 2 arcsec diameter.
2.4 Narrow-band excess selection
Here, potential line emitters are selected if Σ > 3.0 (see Fig. 3). The spread on the brighter end (narrow-band magnitudes which are not saturated, but for which the scatter is not affected by errors in the magnitude, i.e. much brighter than the limit of the images) is quantified for each data set and frame, and the minimum (BB − NB) colour limit over bright magnitudes is set by the 3 × the standard deviation of the excess colour over such magnitudes (sb). A common rest-frame equivalent width (EW) limit of EW0 = 25 Å is applied, guaranteeing a limit higher than the 3 × sb dispersion over bright magnitudes in all bands. The combined selection criteria guarantee a clean selection of line emitters and, most importantly, it ensures that the samples of Hα emitters are selected down to the same rest-frame EW, allowing one to quantify the evolution across cosmic time. An example of this selection for the full COSMOS NBK data is shown in Fig. 3 and the reader is referred to, e.g., S09 and S12 for further examples.
![Narrow-band excess as a function of narrow-band magnitude for NBK (Vega magnitudes) data over the full COSMOS coverage (1.6 deg2). These show >3σ detections in narrow-band imaging and the solid line presents the average 3.0 Σ colour significance for NBK (for the average depth, but note that the analysis is done individually for each frame, and that there are variations in depth up to 0.6 mag difference). Hα sources shown are narrow-band emitters which satisfy all the Hα selection criteria fully described in Section 2.6. The horizontal dashed line presents the EW cut used for NBK data – corresponding to a z = 2.23 rest-frame EW limit of 25 Å for Hα+[N ii]; this is the same rest-frame EW used at all redshifts.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/428/2/10.1093_mnras_sts096/2/m_sts096fig3.jpeg?Expires=1750194242&Signature=SaP8hSY877O1cvICYreHD2GL869Hrh50PADI80pun15OCaGgbziCvYFSFEV9dpi4XKa00pTKvVpkbjc7Up2~5nigbVwaKUgNjMNC8-UsnqXcoYA1bm8A45OAVrxZJOAlh3R6bw68zdfEj11cWdPB5MD8lt8TndScu5ifu2p2rMbwGMru9THY6OivIaz~kvjyotHIag2gC12z0K2-wPZH29Szexn4fXCVZnBSZtCvsgVUuxqYH1jjZMx5IFwXqpGlLY6uvBHD0Tc-As6qloB1xXKHPRSsXmQ6DXdnhS3ff751st4G2I2iiEVKyHuaEFaqIu5Qhavv1wxAdGL0P2v5gg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Narrow-band excess as a function of narrow-band magnitude for NBK (Vega magnitudes) data over the full COSMOS coverage (1.6 deg2). These show >3σ detections in narrow-band imaging and the solid line presents the average 3.0 Σ colour significance for NBK (for the average depth, but note that the analysis is done individually for each frame, and that there are variations in depth up to 0.6 mag difference). Hα sources shown are narrow-band emitters which satisfy all the Hα selection criteria fully described in Section 2.6. The horizontal dashed line presents the EW cut used for NBK data – corresponding to a z = 2.23 rest-frame EW limit of 25 Å for Hα+[N ii]; this is the same rest-frame EW used at all redshifts.
As a further check on the selection criteria, the original imaging data are used to produce BB and NB postage stamp images of all the sources. The BB is subtracted from the NB image leaving the residual flux. From visual inspection, these residual images contain obvious narrow-band sources and it is found that the remaining flux correlates well with the catalogue significance.
2.5 The samples of NB line emitters
Narrow-band detections below the estimated 3σ detection threshold were not considered. By using colour–colour diagnostics (see S12), potential stars are identified in the sample and rejected as well (the small fraction varies from band to band; see Table 3). The sample of remaining potential emitters (Σ > 3 and EW0 > 25 Å; see Table 3 for numbers) is visually checked to identify spurious sources, artefacts which might not have been masked, or sources being identified in very noisy regions (see Table 3). Sources classed as spurious/artefacts are removed from the sample of potential emitters. The final samples of line emitters are then derived.4
As a further test of the reliability of the line emitter samples, it can be noted that since the HAWK-I observations are both deeper and obtained over a larger redshift slice (due to a wider filter profile) when compared to WFCAM, they should be able to confirm all NBK emitters over the matched area. This is confirmed, as all 10 emitters which are detected with WFCAM in the matched area are recovered by HAWK-I data as well.
The catalogues, containing all narrow-band emitter candidates, are presented in Appendix . The catalogues provide IDs, coordinates, narrow-band and broad-band magnitudes, estimated fluxes and observed EWs. Further details and information are available on the HiZELS website.
The photometric redshift (photo-z from Ilbert et al. 2009; Cirasuolo et al. 2010) distributions of the sources selected with the four narrow-band filters are presented in Fig. 4. The photometric redshifts show clear peaks associated with Hα, Hβ/[O iii]λλ4959, 5007 and [O ii]λ3727 (see Fig. 4), together with further emission lines such as Paschen lines and Lyα. Spectroscopic redshifts are also available for a fraction of the selected line emitters (Yamada et al. 2005; Simpson et al. 2006; van Breukelen et al. 2007; Geach et al. 2008b; Ouchi et al. 2008; Smail et al. 2008; Lilly et al. 2009; Ono et al. 2010)6 – these will be discussed in the following sections.
![Photometric redshift distributions (peak of the probability distribution function for each source) for the NB921 line emitter candidates (upper left), NBJ (upper right), NBH (lower left) and NBK (lower right). All distributions peak at redshifts which correspond to strong emission lines, corresponding to Hα, Hβ, [O iii] and [O ii] emitters at various redshifts depending on the central wavelength of each narrow-band filter. Other populations of emitters are also found, such as Paschen lines. The dotted lines indicate the redshift for which an emission line is detectable by the narrow-band filters. Lyα emitter candidates in the NB921 data set (e.g. 18 sources in COSMOS) with photo-z of z ∼ 6–7 are not shown.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/428/2/10.1093_mnras_sts096/2/m_sts096fig4.jpeg?Expires=1750194242&Signature=dN-QnDb0FeOiKzk64pr5nsbCWVvwMC-2oU8iILTa43XcJxVp8LBO~0b4iQCPW48MTtzHsS2YDCGCZAtCL4QI1BCZVCNPmWCMQNQNuXmBEvxm32GqGAALBAYOoUK6e5VDX3oTdVs0-8fmdZwgh2-GP6Wtr5Dm0xpqZhpnWUx86mN60MkU3UxRR9y0EwSWMKbwGiWCpZ8jz~QLgMTMpt2QjjC4ol4VniQxgiEV-V0PhyAbJ5-U444NB4mDZidI9Affy8~XMiag8n2xB7ssoXarNQ6qzHX4sW9tRF-pa44OkB-zsFwal-CSmUxZvCLWqoyqyVckRBBRb5S920ssViveZg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Photometric redshift distributions (peak of the probability distribution function for each source) for the NB921 line emitter candidates (upper left), NBJ (upper right), NBH (lower left) and NBK (lower right). All distributions peak at redshifts which correspond to strong emission lines, corresponding to Hα, Hβ, [O iii] and [O ii] emitters at various redshifts depending on the central wavelength of each narrow-band filter. Other populations of emitters are also found, such as Paschen lines. The dotted lines indicate the redshift for which an emission line is detectable by the narrow-band filters. Lyα emitter candidates in the NB921 data set (e.g. 18 sources in COSMOS) with photo-z of z ∼ 6–7 are not shown.
2.6 Selecting H|$\boldsymbol {\alpha }$| emitters
Samples of Hα emitters at the various redshifts are selected using a combination of broad-band colours (colour–colour selections) and photometric redshifts (when available). Colour–colour separations of emitters are different for each redshift, and for some redshifts two sets of colour–colour separations are used to reduce contamination to a minimum. Additionally, spectroscopically confirmed sources are included, and sources confirmed to be other emission lines removed from the samples – but the reader should note that at all four redshifts the number of z-included sources missed by the selection is typically <10 and the z-rejected sources are typically <10 as well. Therefore, the decrease of available spectroscopic redshifts with redshift does not introduce any bias.5
Additionally, sources found to be line emitters in two (or three, for Hα emitters at z = 2.23) bands, making them robust Hα candidates, are also included in the samples, even if they have been missed by the colour–colour and photometric selection (although it is found that only very few real Hα sources are missed by the selection criteria). Table 3 provides the number of sources, including spectroscopically confirmed ones for each field at each redshift. Within the samples of narrow-band excess sources, 20 (NB921), 54 (NBJ), 49 (NBH) and 47 (NBK) per cent are Hα emitters at redshifts z = 0.4, 0.84, 1.47 and 2.23, respectively.
2.6.1 Hα emitters at z = 0.4
The selection of Hα emitters at z = 0.4 is primarily done by selecting sources for which 0.35 < zphot < 0.45. For further completeness, the BRiK (B − R versus i − K) colour–colour selection (see Fig. 5 and S12) is then applied to recover real Hα sources without photometric redshifts. The selection method can then be accessed by using spectroscopic redshifts (from zCOSMOS; Lilly et al. 2009), which are available for 38 sources. 36 sources are confirmed to be at z = 0.391–0.412, while two sources are [N ii] emitters. This implies a very high completeness of the sample and a contamination of ∼5 per cent over the entire sample. Contaminants have been removed and spectroscopic sources added. A total of 1742 Hα emitters at z = 0.4 are selected.
2.6.2 Hα emitters at z = 0.84
Sources are selected to be Hα emitters at z = 0.84 if 0.75 < zphot < 0.95 or if they satisfy the BRiK (see Fig. 5; S09) colour–colour selection for z ∼ 0.8 sources. Additionally, sources with 1.3 < zphot < 1.7 (likely Hβ/[O iii] z ≈ 1.4 emitters) and 2.0 < zphot < 2.5 (likely z = 2.23 [O ii] emitters) are removed to further reduce contamination from higher redshift emitters. Sources with spectroscopically confirmed redshifts are included and sources with other spectroscopically confirmed lines are removed. In practice, six Hα spectroscopic sources missed by the selection criteria are introduced in the sample; seven sources found in the sample are not Hα – a mix of [S ii], [N ii] and [O iii] emitters. A total of 95 sources are spectroscopically confirmed as Hα, while 237 sources are confirmed as dual Hα–[O iii] emitters. A total of 637 Hα emitters at z = 0.84 are selected.
2.6.3 Hα emitters at z = 1.47
Note that, as described in S12, the NBH filter can be combined with NB921 (probing the [O ii] emission line) to provide very clean, complete surveys of z = 1.47 line emitters, as the filter profiles are extremely well matched for a dual Hα–[O ii] survey. By applying the dual narrow-band selection, a total of 346 Hα–[O ii] emitters are robustly identified in COSMOS and UDS. However, the dual narrow-band selection is only complete (>98 per cent complete) if the NB921 survey probes down to [O ii]/Hα ∼0.1 (cf. S12), which is not the case for the deepest NBH COSMOS coverage. Additionally, only the central 1.1 deg2 region of the COSMOS field has been targeted with the NB921 filter.
In order to select Hα emitters in areas where the NB921 is not deep enough to provide a complete selection, or where NB921 data are not available, the following steps are taken. Sources are selected if 1.35 < zphot < 1.55, or if they satisfy the z ∼ 1.5 BzK (B − z versus z − K) criteria defined in Fig. 5, which is able to recover the bulk of the dual narrow-band emitters and sources with high-quality photometric redshifts of z ∼ 1.5. However, the z ∼ 1.5 BzK selection, although highly complete, is still contaminated by higher redshift emitters. In order to exclude likely higher redshift sources, an additional ziK (i − z versus z − K; see S12) colour–colour separation is used (see Fig. 6), in combination with rejecting sources with zphot > 1.8.
![Top panels: colour–colour separation of the different emitters in the various samples used to isolate Hα emitters at the four different redshifts. Different symbols show narrow-band emitters with different photometric redshifts and the final emitters selected to be Hα (see Section 2.6). The (B − R) versus (i − K) colour–colour separation is used to cleanly select z = 0.4 Hα emitters with the NB921 data, but also z = 0.84 Hα emitters. The z = 0.4 selection points are [0.1,0.18] and [1.24,2.01], while the selection of z = 0.84 Hα emitters is obtained with the set of points: [−0.26,0.26], [0.1,0.18], [1.01,3.21] and [1.24,2.01] (see selection regions shown in the top panels of the figure). Bottom panels: the (B − z) versus (z − K) colours are used in different ways (to maximize completeness) to obtain first-pass samples of potential z = 1.47 Hα emitters (defined by points [−0.15,0.40], [0.41,0.0], [2.31,3.6] and [2.41,2.0]) and z = 2.23 Hα emitters (z − K > B − z; Daddi et al. 2004). Note, however, that for the Hα samples at z = 1.47 and 2.23 the BzK selection is not able to differentiate effectively between Hα and higher redshift emitters, which can significantly contaminate the samples (see photometric redshift distribution). The higher redshift emitters are filtered out of the samples using another set of colours – see Fig. 6.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/428/2/10.1093_mnras_sts096/2/m_sts096fig5.jpeg?Expires=1750194242&Signature=ujP60Z6l6~GPcbsSJP7fiGD-qu9J-JIVI46VgAkDPDoolmpAnNKJI1rx2wwOJ6CkZOllJy04kAq1P7MTvzUrBB7-GjLYWvnFAW~vYX9cwRzRF7w9SzdHNwj7HrhLhVBHkcFBsu0P0ALL-PcEMp-d7662O2xxrAv9N6o8ArT1R58imECox6Oyx25M9xaEKMR~LXyxv8BmI0TKN5X-i-WM68qP--Svyqwwij56ILUtFZtB0qbP7Baeh51NHYi04b7oLxX5WvchKNYH55GwliJlYOfuSGOS79keMgPWrl7Uf5rakbfzWhtRlKEhPhBlDrcRz8JgIZ6zZgsZDuHn~LFTVA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Top panels: colour–colour separation of the different emitters in the various samples used to isolate Hα emitters at the four different redshifts. Different symbols show narrow-band emitters with different photometric redshifts and the final emitters selected to be Hα (see Section 2.6). The (B − R) versus (i − K) colour–colour separation is used to cleanly select z = 0.4 Hα emitters with the NB921 data, but also z = 0.84 Hα emitters. The z = 0.4 selection points are [0.1,0.18] and [1.24,2.01], while the selection of z = 0.84 Hα emitters is obtained with the set of points: [−0.26,0.26], [0.1,0.18], [1.01,3.21] and [1.24,2.01] (see selection regions shown in the top panels of the figure). Bottom panels: the (B − z) versus (z − K) colours are used in different ways (to maximize completeness) to obtain first-pass samples of potential z = 1.47 Hα emitters (defined by points [−0.15,0.40], [0.41,0.0], [2.31,3.6] and [2.41,2.0]) and z = 2.23 Hα emitters (z − K > B − z; Daddi et al. 2004). Note, however, that for the Hα samples at z = 1.47 and 2.23 the BzK selection is not able to differentiate effectively between Hα and higher redshift emitters, which can significantly contaminate the samples (see photometric redshift distribution). The higher redshift emitters are filtered out of the samples using another set of colours – see Fig. 6.
![Top: colour–colour separation of z = 1.47 Hα emitters and those at higher redshift (z ∼ 2.3 Hβ/[O iii], z ∼ 3.3 [O ii]); separation is obtained by (z − K) < 5(i − z) − 0.4. Bottom: colour–colour separation of z ∼ 3 Hβ/[O iii] emitters from z = 2.23 Hα emitters, given by (B − R) < −0.55(U − B) + 1.25. Using the BzK colour–colour separation only results in some contamination of the Hα sample with higher redshift emitters – the B − R versus U − B colour–colour separation allows us to greatly reduce that. The figure also indicates the location of each final Hα-selected source in the colour–colour plot. Note that sources shown as zphot ∼ 1.5 and ∼2.2 are those with photometric redshifts which are within ±0.2 of those values.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/428/2/10.1093_mnras_sts096/2/m_sts096fig6.jpeg?Expires=1750194242&Signature=lo9S9Tne2fZHKq7cRKErMwNZ704l~PLCsYHJprr62du3KiQWcbCrlBc5jpx6UjZyuMsS0dMGQEKFYCJD~nJ4dtdxkM7nLPWjoXNFGXy9RB5H4v-rkp8U-J8C4POe7yC7hL9qh07rTtX0JMyYD4-OXQT2rtyhhIBVwXEPZPI1lpYd0pZH2je8h-m-5twyYu8ASuvNbaCYhrkCkwlM5QrRLNw5J5o~-Gp-URdSeSs8qTVpdL7ovOFNK3OL6EaYZM6vibjSCdJeCl4W9qy2ktBSR3~vGjDgJUrdTBM~9x20xGz55mITQzg844YJAOu-La4uldRBb-t6vQiYUAX~JFMUqQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Top: colour–colour separation of z = 1.47 Hα emitters and those at higher redshift (z ∼ 2.3 Hβ/[O iii], z ∼ 3.3 [O ii]); separation is obtained by (z − K) < 5(i − z) − 0.4. Bottom: colour–colour separation of z ∼ 3 Hβ/[O iii] emitters from z = 2.23 Hα emitters, given by (B − R) < −0.55(U − B) + 1.25. Using the BzK colour–colour separation only results in some contamination of the Hα sample with higher redshift emitters – the B − R versus U − B colour–colour separation allows us to greatly reduce that. The figure also indicates the location of each final Hα-selected source in the colour–colour plot. Note that sources shown as zphot ∼ 1.5 and ∼2.2 are those with photometric redshifts which are within ±0.2 of those values.
The selection leads to a total sample of 515 robust Hα emitters at z = 1.47, by far the largest sample of Hα emitters at z ∼ 1.5. Comparing the double NB921 and NBH analysis with the colour and photo-z selection (for sources for which the NB921 data are deep enough to detect [O ii]) shows that the colour and photo-z selection by itself results in a contamination of ≈15 per cent and a completeness of ≈85 per cent. However, as the double NB921 and NBH analysis has been used wherever the data are available and sufficiently deep, the contamination of the entire sample is estimated to be lower (≈5 per cent) and the completeness higher (≈ 95 per cent).
2.6.4 Hα emitters at z = 2.23
As can be seen from the photometric redshift distribution in Fig. 4, the high-quality photo-z in the COSMOS and UDS fields can provide a powerful tool to select z = 2.23 sources. However, the sole use of the photometric redshifts cannot result in clean, high completeness sample of z = 2.23 Hα emitters, not only because reliable photometric redshifts are not available for 35 per cent of the NBK emitters, at the faint end, but also because the errors in the photometric redshifts will be much higher at z ∼ 2.2 than at lower redshift (particularly as one is selecting star-forming galaxies). Nevertheless, although spectroscopy only exists for a few Hα z = 2.23 sources (zCOSMOS and UDS compilation), double line detections between NBK and one of NBH ([O iii]) and/or NBJ ([O ii]) allow the identification of 155 secure Hα emitters. These can be used to optimize the selection criteria and estimate the completeness and contamination of the sample.
The selection of Hα emitters is done in the same way for both COSMOS and UDS, and for both WFCAM and HAWK-I data. An initial sample of z = 2.23 Hα emitters is obtained by selecting sources for which 1.7 < zphot < 2.8, where the limits were determined using the distribution of photometric redshifts found for confirmed Hα emitters at z = 2.23 (this selects 525 sources, of which three are spectroscopically confirmed to be contaminants and 87 are double/triple line emitters and thus robust z = 2.23 Hα emitters). Because some sources lack reliable photometric redshifts, the colour selection (z − K) > (B − z) is used to recover additional z ∼ 2 faint emitters. This colour–colour selection is a slightly modified version of the standard BzK colour–colour separation (Daddi et al. 2004).7 It selects 274 additional Hα candidates (and re-selects 90 per cent of those selected through photometric redshifts), and guarantees a high completeness of the Hα sample (see Fig. 5). However, the BzK selection also selects z ∼ 3.3 Hβ/[O iii] emitters very effectively, and the contamination by such emitters needs to be minimized. In order to do this, sources with zphot > 3.0 are excluded (121 sources). For sources for which a photometric redshift does not exist, a rest-frame UV colour–colour separation is used (B − R versus U − B; see Fig. 6, probing the rest-frame UV), capable of broadly separating z = 2.23 and ∼3.3 emitters due to their different UV colours (see Fig. 6; this removes a further 27 sources). Three sources are further removed as they are confirmed contaminants (Paβ, [S iii] and [O iii] at z = 0.65, 1.23 and 3.23, respectively).
Overall, the selection leads to a total sample of 807 Hα emitters, by far the largest sample of z = 2.23 Hα emitters ever obtained and an order of magnitude larger than the previous largest samples presented by Geach et al. (2008a) and Hayes et al. (2010). With the limited spectroscopy available, it is difficult to accurately determine the completeness and contamination of the sample, but based on the double/triple line detections (155) and the confirmed contaminants which have been removed (six), the completeness is estimated to be >90 per cent, and contamination is likely to be <10 per cent.
3 ANALYSIS AND RESULTS: Hα LF OVER 11 GYR
3.1 Removing the contamination by the [N ii] line
Due to the width of all filters in detecting the Hα line, the adjacent [N ii] lines can also be detected when the Hα line is detected at the peak transmission of the filter. A correction for the [N ii] line contamination is therefore done, following the relation given in S12. The relation has been derived to reproduce the full SDSS relation between the average log ([N ii]/Hα), f and log [EW0([N ii]+Hα)], E: f = −0.924 + 4.802E − 8.892E2 + 6.701E3 − 2.27E4 + 0.279E5. This relation is used to correct all Hα fluxes at z = 0.4, 0.84, 1.47 and 2.23. The median correction (the median [N ii]/([N ii]+Hα)) is ≈0.25.
3.2 Completeness corrections: detection and selection
It is fundamental to understand how complete the samples are as a function of line flux. This is done using simulations, as described in S09 and further detailed in S12. The simulations consider two major components driving the incompleteness: (i) the detection completeness (which depends on the actual imaging depth and the apertures used) and (ii) the incompleteness resulting from the selection (both EW and colour significance).
The detection completeness is estimated by placing sources with a given magnitude at random positions on each individual narrow-band image, and studying the recovery rate as a function of the magnitude of the source. For the large Subaru frames, 2500 sources are added for each magnitude, for WFCAM images 500, and for HAWK-I frames 100 sources are added for each realization.
The individual line completeness estimates are performed in the same way for the data at the four different redshifts. A set of galaxies is defined, which is consistent with being at the approximate redshift (applying the same photometric redshift + colour–colour selections to all NB detected sources with no significant excess) but not having emission lines above the detection limit. Emission lines are then added to the sources, and the study of the recovery fraction is undertaken. The average completeness corrections as a function of Hα flux are presented in Fig. 7. Note that the simulations include the different EW/colour cuts used in selecting line emitters in all bands, and therefore take the EW limits and colour selection into account. Also note that because of the very different distributions of magnitudes of Hα emitters from low to higher redshift, the EW/colour cut is a much more important source of incompleteness for low-redshift Hα emitters than for the highest redshift, z = 2.23.
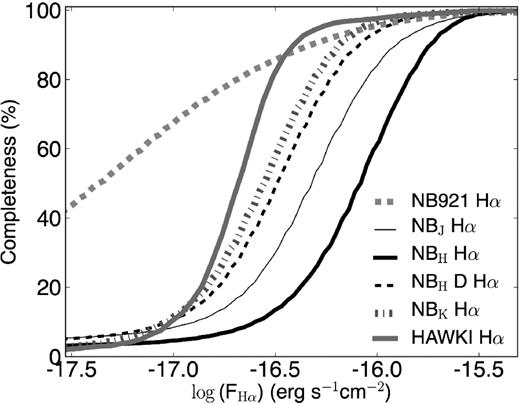
Average completeness of the various narrow-band surveys as a function of Hα flux. Note that the completeness of individual fields/frames for each band can vary significantly due to the survey strategy (e.g. see difference between one of the deep pointings in COSMOS, NBH D and the average over all NBH fields), and thus the completeness corrections are computed for each individual fields.
It should be noted that because of the differences in depth, simulations are conducted for each individual frame, and the appropriate completeness corrections applied accordingly when computing the LF. For any given completeness correction applied, an uncertainty of 20 per cent of the size of the applied correction is added in quadrature to the other uncertainties to account for the uncertainties in deriving such corrections.
3.3 Volume
At z = 0.4, the total area surveyed is 1.68 deg2. The NB921 filter, centred at 9196 Å and with an FWHM of 132 Å, can probe the Hα line [using the top-hat (TH) approximation] from zmin = 0.3907 to zmax = 0.4108. This means that the narrow-band filter surveys an Hα volume of 5.1 × 104 Mpc3 deg−2. The Hα survey therefore probes a total volume of 8.8 × 104 Mpc3.
The NBJ filter (FWHM of 140 Å) can be approximated by a TH, probing zmin = 0.8346 to zmax = 0.8559 for Hα line detections, resulting in surveying 1.5 × 105 Mpc3 deg−1. As the total survey has covered 1.3 deg2, it results in a total volume of 1.9 × 105 Mpc3. Assuming the TH model for the NBH filter (FWHM of 211.1 Å, with λTHmin = 1.606 μm and λTHmax = 1.627 μm), the Hα survey probes a (comoving) volume of 3.3 × 105 Mpc3 deg−2. Volumes are computed on a field-by-field basis as each field reaches a different depth (although the difference in volume is only important at the faintest fluxes). The total volume of the survey is 7.4 × 105 Mpc3. The volume down to the deepest depth is 3.9 × 104 Mpc3 (see Table 4 for details). The NBK filter is centred on λ = 2.121 μm, with an FWHM of 210 Å. Using the TH approximation for the filter, it can probe the Hα emission line from zmin = 2.2147 to zmax = 2.2467, so with a Δz = 0.016. The H2 filter therefore probes a volume of 3.8 × 105 Mpc3 deg−2.
The HAWK-I survey uses a slightly different H2 filter, centred on λ = 2.125 μm, with FWHM =300 Å. A TH is an even better approximation of the filter profile, with zmin = 2.2139 to zmax = 2.2596 for Hα line detections. The filter effectively probes 5.5 × 105 Mpc3 deg−2. Each HAWK-I pointing covers only about 13.08 arcmin2, and so the complete HAWK-I survey (COSMOS and UDS, 0.0156 deg2) probes a total volume of 1.7 × 104 Mpc3. Note that the survey conducted by Hayes et al. (2010) (using a narrower NB filter), although deeper, only probed 5.0 × 103 Mpc3, so a factor of 3 smaller in volume and over a single field. Table 4 presents a summary of the volumes probed as a function of Hα luminosity and the number of sources detected at each redshift.
LFs from HiZELS. LHα has been corrected for both [N ii] contamination and dust extinction (using AHα = 1 mag). Volumes assuming TH filters. ϕ corr has been corrected for both incompleteness and the fact that the filter profile is not a perfect TH.
| log LHα . | Sources . | ϕ obs . | ϕ corr . | Volume . |
|---|---|---|---|---|
| . | # . | (Mpc−3) . | (Mpc−3) . | (104 Mpc3) . |
| z = 0.40 | ||||
| 40.50 ± 0.05 | 128 | −1.84 ± 0.04 | −1.66 ± 0.04 | 8.8 |
| 40.60 ± 0.05 | 147 | −1.78 ± 0.04 | −1.70 ± 0.04 | 8.8 |
| 40.70 ± 0.05 | 118 | −1.87 ± 0.04 | −1.81 ± 0.04 | 8.8 |
| 40.80 ± 0.05 | 86 | −2.01 ± 0.05 | −1.93 ± 0.05 | 8.8 |
| 40.90 ± 0.05 | 56 | −2.20 ± 0.06 | −1.96 ± 0.07 | 8.8 |
| 41.00 ± 0.05 | 54 | −2.21 ± 0.06 | −2.03 ± 0.07 | 8.8 |
| 41.10 ± 0.05 | 34 | −2.41 ± 0.08 | −2.12 ± 0.09 | 8.8 |
| 41.20 ± 0.05 | 36 | −2.39 ± 0.08 | −2.27 ± 0.08 | 8.8 |
| 41.30 ± 0.05 | 33 | −2.43 ± 0.08 | −2.29 ± 0.09 | 8.8 |
| 41.40 ± 0.05 | 25 | −2.55 ± 0.10 | −2.42 ± 0.10 | 8.8 |
| 41.50 ± 0.05 | 25 | −2.55 ± 0.10 | −2.46 ± 0.11 | 8.8 |
| 41.60 ± 0.05 | 17 | −2.71 ± 0.12 | −2.57 ± 0.13 | 8.8 |
| 41.70 ± 0.05 | 10 | −2.94 ± 0.17 | −2.69 ± 0.19 | 8.8 |
| 41.80 ± 0.05 | 11 | −2.90 ± 0.16 | −2.73 ± 0.17 | 8.8 |
| 41.90 ± 0.05 | 8 | −3.04 ± 0.19 | −2.88 ± 0.20 | 8.8 |
| 42.00 ± 0.05 | 4 | −3.34 ± 0.30 | −3.03 ± 0.35 | 8.8 |
| 42.20 ± 0.10 | 3 | −3.45 ± 0.36 | −3.56 ± 0.51 | 8.8 |
| 42.50 ± 0.15 | 2 | −3.64 ± 0.53 | −3.71 ± 0.71 | 8.8 |
| z = 0.84 | ||||
| 41.70 ± 0.075 | 218 | −2.12 ± 0.03 | −1.93 ± 0.03 | 19.1 |
| 41.85 ± 0.075 | 222 | −2.11 ± 0.03 | −2.02 ± 0.03 | 19.1 |
| 42.00 ± 0.075 | 107 | −2.43 ± 0.04 | −2.18 ± 0.04 | 19.1 |
| 42.15 ± 0.075 | 54 | −2.72 ± 0.06 | −2.43 ± 0.06 | 19.1 |
| 42.30 ± 0.075 | 12 | −3.38 ± 0.15 | −2.73 ± 0.17 | 19.1 |
| 42.45 ± 0.075 | 10 | −3.46 ± 0.17 | −3.01 ± 0.17 | 19.1 |
| 42.60 ± 0.075 | 7 | −3.61 ± 0.21 | −3.27 ± 0.21 | 19.1 |
| 42.75 ± 0.075 | 2 | −4.16 ± 0.53 | −3.79 ± 0.55 | 19.1 |
| 42.90 ± 0.075 | 1 | −4.46 ± 0.90 | −4.13 ± 1.51 | 19.1 |
| z = 1.47 | ||||
| 42.10 ± 0.05 | 25 | −2.20 ± 0.10 | −2.13 ± 0.10 | 4.0 |
| 42.20 ± 0.05 | 32 | −2.37 ± 0.08 | −2.25 ± 0.09 | 7.5 |
| 42.30 ± 0.05 | 62 | −2.55 ± 0.06 | −2.34 ± 0.06 | 22.1 |
| 42.40 ± 0.05 | 86 | −2.67 ± 0.05 | −2.47 ± 0.05 | 40.2 |
| 42.50 ± 0.05 | 101 | −2.78 ± 0.05 | −2.62 ± 0.05 | 60.4 |
| 42.60 ± 0.05 | 106 | −2.83 ± 0.04 | −2.73 ± 0.04 | 71.4 |
| 42.70 ± 0.05 | 43 | −3.23 ± 0.07 | −2.91 ± 0.08 | 73.6 |
| 42.80 ± 0.05 | 23 | −3.50 ± 0.10 | −3.18 ± 0.11 | 73.6 |
| 42.90 ± 0.05 | 9 | −3.91 ± 0.18 | −3.55 ± 0.18 | 73.6 |
| 43.00 ± 0.05 | 5 | −4.17 ± 0.26 | −3.81 ± 0.26 | 73.6 |
| 43.10 ± 0.05 | 3 | −4.39 ± 0.37 | −4.22 ± 0.38 | 73.6 |
| 43.20 ± 0.05 | 2 | −4.57 ± 0.53 | −4.55 ± 0.55 | 73.6 |
| 43.40 ± 0.15 | 2 | −4.57 ± 0.53 | −4.86 ± 0.55 | 73.6 |
| z = 2.23 | ||||
| 42.00 ± 0.075 | 8 | −2.18 ± 0.19 | −1.93 ± 0.19 | 0.8 |
| 42.15 ± 0.075 | 11 | −2.34 ± 0.16 | −2.07 ± 0.16 | 1.6 |
| 42.30 ± 0.05 | 47 | −2.24 ± 0.07 | −2.19 ± 0.07 | 6.7 |
| 42.40 ± 0.05 | 91 | −2.36 ± 0.05 | −2.31 ± 0.05 | 20.9 |
| 42.50 ± 0.05 | 107 | −2.48 ± 0.04 | −2.41 ± 0.05 | 32.7 |
| 42.60 ± 0.05 | 158 | −2.60 ± 0.04 | −2.50 ± 0.04 | 63.3 |
| 42.70 ± 0.05 | 163 | −2.68 ± 0.04 | −2.59 ± 0.05 | 77.2 |
| 42.80 ± 0.05 | 100 | −2.89 ± 0.05 | −2.73 ± 0.06 | 77.2 |
| 42.90 ± 0.05 | 51 | −3.18 ± 0.07 | −2.88 ± 0.14 | 77.2 |
| 43.00 ± 0.05 | 30 | −3.41 ± 0.09 | −3.09 ± 0.17 | 77.2 |
| 43.10 ± 0.05 | 16 | −3.68 ± 0.12 | −3.33 ± 0.22 | 77.2 |
| 43.20 ± 0.05 | 7 | −4.04 ± 0.21 | −3.67 ± 0.31 | 77.2 |
| 43.30 ± 0.05 | 3 | −4.41 ± 0.37 | −4.01 ± 0.51 | 77.2 |
| 43.40 ± 0.05 | 2 | −4.59 ± 0.53 | −4.22 ± 0.68 | 77.2 |
| 43.60 ± 0.15 | 3 | −4.41 ± 0.37 | −4.63 ± 0.41 | 77.2 |
| log LHα . | Sources . | ϕ obs . | ϕ corr . | Volume . |
|---|---|---|---|---|
| . | # . | (Mpc−3) . | (Mpc−3) . | (104 Mpc3) . |
| z = 0.40 | ||||
| 40.50 ± 0.05 | 128 | −1.84 ± 0.04 | −1.66 ± 0.04 | 8.8 |
| 40.60 ± 0.05 | 147 | −1.78 ± 0.04 | −1.70 ± 0.04 | 8.8 |
| 40.70 ± 0.05 | 118 | −1.87 ± 0.04 | −1.81 ± 0.04 | 8.8 |
| 40.80 ± 0.05 | 86 | −2.01 ± 0.05 | −1.93 ± 0.05 | 8.8 |
| 40.90 ± 0.05 | 56 | −2.20 ± 0.06 | −1.96 ± 0.07 | 8.8 |
| 41.00 ± 0.05 | 54 | −2.21 ± 0.06 | −2.03 ± 0.07 | 8.8 |
| 41.10 ± 0.05 | 34 | −2.41 ± 0.08 | −2.12 ± 0.09 | 8.8 |
| 41.20 ± 0.05 | 36 | −2.39 ± 0.08 | −2.27 ± 0.08 | 8.8 |
| 41.30 ± 0.05 | 33 | −2.43 ± 0.08 | −2.29 ± 0.09 | 8.8 |
| 41.40 ± 0.05 | 25 | −2.55 ± 0.10 | −2.42 ± 0.10 | 8.8 |
| 41.50 ± 0.05 | 25 | −2.55 ± 0.10 | −2.46 ± 0.11 | 8.8 |
| 41.60 ± 0.05 | 17 | −2.71 ± 0.12 | −2.57 ± 0.13 | 8.8 |
| 41.70 ± 0.05 | 10 | −2.94 ± 0.17 | −2.69 ± 0.19 | 8.8 |
| 41.80 ± 0.05 | 11 | −2.90 ± 0.16 | −2.73 ± 0.17 | 8.8 |
| 41.90 ± 0.05 | 8 | −3.04 ± 0.19 | −2.88 ± 0.20 | 8.8 |
| 42.00 ± 0.05 | 4 | −3.34 ± 0.30 | −3.03 ± 0.35 | 8.8 |
| 42.20 ± 0.10 | 3 | −3.45 ± 0.36 | −3.56 ± 0.51 | 8.8 |
| 42.50 ± 0.15 | 2 | −3.64 ± 0.53 | −3.71 ± 0.71 | 8.8 |
| z = 0.84 | ||||
| 41.70 ± 0.075 | 218 | −2.12 ± 0.03 | −1.93 ± 0.03 | 19.1 |
| 41.85 ± 0.075 | 222 | −2.11 ± 0.03 | −2.02 ± 0.03 | 19.1 |
| 42.00 ± 0.075 | 107 | −2.43 ± 0.04 | −2.18 ± 0.04 | 19.1 |
| 42.15 ± 0.075 | 54 | −2.72 ± 0.06 | −2.43 ± 0.06 | 19.1 |
| 42.30 ± 0.075 | 12 | −3.38 ± 0.15 | −2.73 ± 0.17 | 19.1 |
| 42.45 ± 0.075 | 10 | −3.46 ± 0.17 | −3.01 ± 0.17 | 19.1 |
| 42.60 ± 0.075 | 7 | −3.61 ± 0.21 | −3.27 ± 0.21 | 19.1 |
| 42.75 ± 0.075 | 2 | −4.16 ± 0.53 | −3.79 ± 0.55 | 19.1 |
| 42.90 ± 0.075 | 1 | −4.46 ± 0.90 | −4.13 ± 1.51 | 19.1 |
| z = 1.47 | ||||
| 42.10 ± 0.05 | 25 | −2.20 ± 0.10 | −2.13 ± 0.10 | 4.0 |
| 42.20 ± 0.05 | 32 | −2.37 ± 0.08 | −2.25 ± 0.09 | 7.5 |
| 42.30 ± 0.05 | 62 | −2.55 ± 0.06 | −2.34 ± 0.06 | 22.1 |
| 42.40 ± 0.05 | 86 | −2.67 ± 0.05 | −2.47 ± 0.05 | 40.2 |
| 42.50 ± 0.05 | 101 | −2.78 ± 0.05 | −2.62 ± 0.05 | 60.4 |
| 42.60 ± 0.05 | 106 | −2.83 ± 0.04 | −2.73 ± 0.04 | 71.4 |
| 42.70 ± 0.05 | 43 | −3.23 ± 0.07 | −2.91 ± 0.08 | 73.6 |
| 42.80 ± 0.05 | 23 | −3.50 ± 0.10 | −3.18 ± 0.11 | 73.6 |
| 42.90 ± 0.05 | 9 | −3.91 ± 0.18 | −3.55 ± 0.18 | 73.6 |
| 43.00 ± 0.05 | 5 | −4.17 ± 0.26 | −3.81 ± 0.26 | 73.6 |
| 43.10 ± 0.05 | 3 | −4.39 ± 0.37 | −4.22 ± 0.38 | 73.6 |
| 43.20 ± 0.05 | 2 | −4.57 ± 0.53 | −4.55 ± 0.55 | 73.6 |
| 43.40 ± 0.15 | 2 | −4.57 ± 0.53 | −4.86 ± 0.55 | 73.6 |
| z = 2.23 | ||||
| 42.00 ± 0.075 | 8 | −2.18 ± 0.19 | −1.93 ± 0.19 | 0.8 |
| 42.15 ± 0.075 | 11 | −2.34 ± 0.16 | −2.07 ± 0.16 | 1.6 |
| 42.30 ± 0.05 | 47 | −2.24 ± 0.07 | −2.19 ± 0.07 | 6.7 |
| 42.40 ± 0.05 | 91 | −2.36 ± 0.05 | −2.31 ± 0.05 | 20.9 |
| 42.50 ± 0.05 | 107 | −2.48 ± 0.04 | −2.41 ± 0.05 | 32.7 |
| 42.60 ± 0.05 | 158 | −2.60 ± 0.04 | −2.50 ± 0.04 | 63.3 |
| 42.70 ± 0.05 | 163 | −2.68 ± 0.04 | −2.59 ± 0.05 | 77.2 |
| 42.80 ± 0.05 | 100 | −2.89 ± 0.05 | −2.73 ± 0.06 | 77.2 |
| 42.90 ± 0.05 | 51 | −3.18 ± 0.07 | −2.88 ± 0.14 | 77.2 |
| 43.00 ± 0.05 | 30 | −3.41 ± 0.09 | −3.09 ± 0.17 | 77.2 |
| 43.10 ± 0.05 | 16 | −3.68 ± 0.12 | −3.33 ± 0.22 | 77.2 |
| 43.20 ± 0.05 | 7 | −4.04 ± 0.21 | −3.67 ± 0.31 | 77.2 |
| 43.30 ± 0.05 | 3 | −4.41 ± 0.37 | −4.01 ± 0.51 | 77.2 |
| 43.40 ± 0.05 | 2 | −4.59 ± 0.53 | −4.22 ± 0.68 | 77.2 |
| 43.60 ± 0.15 | 3 | −4.41 ± 0.37 | −4.63 ± 0.41 | 77.2 |
LFs from HiZELS. LHα has been corrected for both [N ii] contamination and dust extinction (using AHα = 1 mag). Volumes assuming TH filters. ϕ corr has been corrected for both incompleteness and the fact that the filter profile is not a perfect TH.
| log LHα . | Sources . | ϕ obs . | ϕ corr . | Volume . |
|---|---|---|---|---|
| . | # . | (Mpc−3) . | (Mpc−3) . | (104 Mpc3) . |
| z = 0.40 | ||||
| 40.50 ± 0.05 | 128 | −1.84 ± 0.04 | −1.66 ± 0.04 | 8.8 |
| 40.60 ± 0.05 | 147 | −1.78 ± 0.04 | −1.70 ± 0.04 | 8.8 |
| 40.70 ± 0.05 | 118 | −1.87 ± 0.04 | −1.81 ± 0.04 | 8.8 |
| 40.80 ± 0.05 | 86 | −2.01 ± 0.05 | −1.93 ± 0.05 | 8.8 |
| 40.90 ± 0.05 | 56 | −2.20 ± 0.06 | −1.96 ± 0.07 | 8.8 |
| 41.00 ± 0.05 | 54 | −2.21 ± 0.06 | −2.03 ± 0.07 | 8.8 |
| 41.10 ± 0.05 | 34 | −2.41 ± 0.08 | −2.12 ± 0.09 | 8.8 |
| 41.20 ± 0.05 | 36 | −2.39 ± 0.08 | −2.27 ± 0.08 | 8.8 |
| 41.30 ± 0.05 | 33 | −2.43 ± 0.08 | −2.29 ± 0.09 | 8.8 |
| 41.40 ± 0.05 | 25 | −2.55 ± 0.10 | −2.42 ± 0.10 | 8.8 |
| 41.50 ± 0.05 | 25 | −2.55 ± 0.10 | −2.46 ± 0.11 | 8.8 |
| 41.60 ± 0.05 | 17 | −2.71 ± 0.12 | −2.57 ± 0.13 | 8.8 |
| 41.70 ± 0.05 | 10 | −2.94 ± 0.17 | −2.69 ± 0.19 | 8.8 |
| 41.80 ± 0.05 | 11 | −2.90 ± 0.16 | −2.73 ± 0.17 | 8.8 |
| 41.90 ± 0.05 | 8 | −3.04 ± 0.19 | −2.88 ± 0.20 | 8.8 |
| 42.00 ± 0.05 | 4 | −3.34 ± 0.30 | −3.03 ± 0.35 | 8.8 |
| 42.20 ± 0.10 | 3 | −3.45 ± 0.36 | −3.56 ± 0.51 | 8.8 |
| 42.50 ± 0.15 | 2 | −3.64 ± 0.53 | −3.71 ± 0.71 | 8.8 |
| z = 0.84 | ||||
| 41.70 ± 0.075 | 218 | −2.12 ± 0.03 | −1.93 ± 0.03 | 19.1 |
| 41.85 ± 0.075 | 222 | −2.11 ± 0.03 | −2.02 ± 0.03 | 19.1 |
| 42.00 ± 0.075 | 107 | −2.43 ± 0.04 | −2.18 ± 0.04 | 19.1 |
| 42.15 ± 0.075 | 54 | −2.72 ± 0.06 | −2.43 ± 0.06 | 19.1 |
| 42.30 ± 0.075 | 12 | −3.38 ± 0.15 | −2.73 ± 0.17 | 19.1 |
| 42.45 ± 0.075 | 10 | −3.46 ± 0.17 | −3.01 ± 0.17 | 19.1 |
| 42.60 ± 0.075 | 7 | −3.61 ± 0.21 | −3.27 ± 0.21 | 19.1 |
| 42.75 ± 0.075 | 2 | −4.16 ± 0.53 | −3.79 ± 0.55 | 19.1 |
| 42.90 ± 0.075 | 1 | −4.46 ± 0.90 | −4.13 ± 1.51 | 19.1 |
| z = 1.47 | ||||
| 42.10 ± 0.05 | 25 | −2.20 ± 0.10 | −2.13 ± 0.10 | 4.0 |
| 42.20 ± 0.05 | 32 | −2.37 ± 0.08 | −2.25 ± 0.09 | 7.5 |
| 42.30 ± 0.05 | 62 | −2.55 ± 0.06 | −2.34 ± 0.06 | 22.1 |
| 42.40 ± 0.05 | 86 | −2.67 ± 0.05 | −2.47 ± 0.05 | 40.2 |
| 42.50 ± 0.05 | 101 | −2.78 ± 0.05 | −2.62 ± 0.05 | 60.4 |
| 42.60 ± 0.05 | 106 | −2.83 ± 0.04 | −2.73 ± 0.04 | 71.4 |
| 42.70 ± 0.05 | 43 | −3.23 ± 0.07 | −2.91 ± 0.08 | 73.6 |
| 42.80 ± 0.05 | 23 | −3.50 ± 0.10 | −3.18 ± 0.11 | 73.6 |
| 42.90 ± 0.05 | 9 | −3.91 ± 0.18 | −3.55 ± 0.18 | 73.6 |
| 43.00 ± 0.05 | 5 | −4.17 ± 0.26 | −3.81 ± 0.26 | 73.6 |
| 43.10 ± 0.05 | 3 | −4.39 ± 0.37 | −4.22 ± 0.38 | 73.6 |
| 43.20 ± 0.05 | 2 | −4.57 ± 0.53 | −4.55 ± 0.55 | 73.6 |
| 43.40 ± 0.15 | 2 | −4.57 ± 0.53 | −4.86 ± 0.55 | 73.6 |
| z = 2.23 | ||||
| 42.00 ± 0.075 | 8 | −2.18 ± 0.19 | −1.93 ± 0.19 | 0.8 |
| 42.15 ± 0.075 | 11 | −2.34 ± 0.16 | −2.07 ± 0.16 | 1.6 |
| 42.30 ± 0.05 | 47 | −2.24 ± 0.07 | −2.19 ± 0.07 | 6.7 |
| 42.40 ± 0.05 | 91 | −2.36 ± 0.05 | −2.31 ± 0.05 | 20.9 |
| 42.50 ± 0.05 | 107 | −2.48 ± 0.04 | −2.41 ± 0.05 | 32.7 |
| 42.60 ± 0.05 | 158 | −2.60 ± 0.04 | −2.50 ± 0.04 | 63.3 |
| 42.70 ± 0.05 | 163 | −2.68 ± 0.04 | −2.59 ± 0.05 | 77.2 |
| 42.80 ± 0.05 | 100 | −2.89 ± 0.05 | −2.73 ± 0.06 | 77.2 |
| 42.90 ± 0.05 | 51 | −3.18 ± 0.07 | −2.88 ± 0.14 | 77.2 |
| 43.00 ± 0.05 | 30 | −3.41 ± 0.09 | −3.09 ± 0.17 | 77.2 |
| 43.10 ± 0.05 | 16 | −3.68 ± 0.12 | −3.33 ± 0.22 | 77.2 |
| 43.20 ± 0.05 | 7 | −4.04 ± 0.21 | −3.67 ± 0.31 | 77.2 |
| 43.30 ± 0.05 | 3 | −4.41 ± 0.37 | −4.01 ± 0.51 | 77.2 |
| 43.40 ± 0.05 | 2 | −4.59 ± 0.53 | −4.22 ± 0.68 | 77.2 |
| 43.60 ± 0.15 | 3 | −4.41 ± 0.37 | −4.63 ± 0.41 | 77.2 |
| log LHα . | Sources . | ϕ obs . | ϕ corr . | Volume . |
|---|---|---|---|---|
| . | # . | (Mpc−3) . | (Mpc−3) . | (104 Mpc3) . |
| z = 0.40 | ||||
| 40.50 ± 0.05 | 128 | −1.84 ± 0.04 | −1.66 ± 0.04 | 8.8 |
| 40.60 ± 0.05 | 147 | −1.78 ± 0.04 | −1.70 ± 0.04 | 8.8 |
| 40.70 ± 0.05 | 118 | −1.87 ± 0.04 | −1.81 ± 0.04 | 8.8 |
| 40.80 ± 0.05 | 86 | −2.01 ± 0.05 | −1.93 ± 0.05 | 8.8 |
| 40.90 ± 0.05 | 56 | −2.20 ± 0.06 | −1.96 ± 0.07 | 8.8 |
| 41.00 ± 0.05 | 54 | −2.21 ± 0.06 | −2.03 ± 0.07 | 8.8 |
| 41.10 ± 0.05 | 34 | −2.41 ± 0.08 | −2.12 ± 0.09 | 8.8 |
| 41.20 ± 0.05 | 36 | −2.39 ± 0.08 | −2.27 ± 0.08 | 8.8 |
| 41.30 ± 0.05 | 33 | −2.43 ± 0.08 | −2.29 ± 0.09 | 8.8 |
| 41.40 ± 0.05 | 25 | −2.55 ± 0.10 | −2.42 ± 0.10 | 8.8 |
| 41.50 ± 0.05 | 25 | −2.55 ± 0.10 | −2.46 ± 0.11 | 8.8 |
| 41.60 ± 0.05 | 17 | −2.71 ± 0.12 | −2.57 ± 0.13 | 8.8 |
| 41.70 ± 0.05 | 10 | −2.94 ± 0.17 | −2.69 ± 0.19 | 8.8 |
| 41.80 ± 0.05 | 11 | −2.90 ± 0.16 | −2.73 ± 0.17 | 8.8 |
| 41.90 ± 0.05 | 8 | −3.04 ± 0.19 | −2.88 ± 0.20 | 8.8 |
| 42.00 ± 0.05 | 4 | −3.34 ± 0.30 | −3.03 ± 0.35 | 8.8 |
| 42.20 ± 0.10 | 3 | −3.45 ± 0.36 | −3.56 ± 0.51 | 8.8 |
| 42.50 ± 0.15 | 2 | −3.64 ± 0.53 | −3.71 ± 0.71 | 8.8 |
| z = 0.84 | ||||
| 41.70 ± 0.075 | 218 | −2.12 ± 0.03 | −1.93 ± 0.03 | 19.1 |
| 41.85 ± 0.075 | 222 | −2.11 ± 0.03 | −2.02 ± 0.03 | 19.1 |
| 42.00 ± 0.075 | 107 | −2.43 ± 0.04 | −2.18 ± 0.04 | 19.1 |
| 42.15 ± 0.075 | 54 | −2.72 ± 0.06 | −2.43 ± 0.06 | 19.1 |
| 42.30 ± 0.075 | 12 | −3.38 ± 0.15 | −2.73 ± 0.17 | 19.1 |
| 42.45 ± 0.075 | 10 | −3.46 ± 0.17 | −3.01 ± 0.17 | 19.1 |
| 42.60 ± 0.075 | 7 | −3.61 ± 0.21 | −3.27 ± 0.21 | 19.1 |
| 42.75 ± 0.075 | 2 | −4.16 ± 0.53 | −3.79 ± 0.55 | 19.1 |
| 42.90 ± 0.075 | 1 | −4.46 ± 0.90 | −4.13 ± 1.51 | 19.1 |
| z = 1.47 | ||||
| 42.10 ± 0.05 | 25 | −2.20 ± 0.10 | −2.13 ± 0.10 | 4.0 |
| 42.20 ± 0.05 | 32 | −2.37 ± 0.08 | −2.25 ± 0.09 | 7.5 |
| 42.30 ± 0.05 | 62 | −2.55 ± 0.06 | −2.34 ± 0.06 | 22.1 |
| 42.40 ± 0.05 | 86 | −2.67 ± 0.05 | −2.47 ± 0.05 | 40.2 |
| 42.50 ± 0.05 | 101 | −2.78 ± 0.05 | −2.62 ± 0.05 | 60.4 |
| 42.60 ± 0.05 | 106 | −2.83 ± 0.04 | −2.73 ± 0.04 | 71.4 |
| 42.70 ± 0.05 | 43 | −3.23 ± 0.07 | −2.91 ± 0.08 | 73.6 |
| 42.80 ± 0.05 | 23 | −3.50 ± 0.10 | −3.18 ± 0.11 | 73.6 |
| 42.90 ± 0.05 | 9 | −3.91 ± 0.18 | −3.55 ± 0.18 | 73.6 |
| 43.00 ± 0.05 | 5 | −4.17 ± 0.26 | −3.81 ± 0.26 | 73.6 |
| 43.10 ± 0.05 | 3 | −4.39 ± 0.37 | −4.22 ± 0.38 | 73.6 |
| 43.20 ± 0.05 | 2 | −4.57 ± 0.53 | −4.55 ± 0.55 | 73.6 |
| 43.40 ± 0.15 | 2 | −4.57 ± 0.53 | −4.86 ± 0.55 | 73.6 |
| z = 2.23 | ||||
| 42.00 ± 0.075 | 8 | −2.18 ± 0.19 | −1.93 ± 0.19 | 0.8 |
| 42.15 ± 0.075 | 11 | −2.34 ± 0.16 | −2.07 ± 0.16 | 1.6 |
| 42.30 ± 0.05 | 47 | −2.24 ± 0.07 | −2.19 ± 0.07 | 6.7 |
| 42.40 ± 0.05 | 91 | −2.36 ± 0.05 | −2.31 ± 0.05 | 20.9 |
| 42.50 ± 0.05 | 107 | −2.48 ± 0.04 | −2.41 ± 0.05 | 32.7 |
| 42.60 ± 0.05 | 158 | −2.60 ± 0.04 | −2.50 ± 0.04 | 63.3 |
| 42.70 ± 0.05 | 163 | −2.68 ± 0.04 | −2.59 ± 0.05 | 77.2 |
| 42.80 ± 0.05 | 100 | −2.89 ± 0.05 | −2.73 ± 0.06 | 77.2 |
| 42.90 ± 0.05 | 51 | −3.18 ± 0.07 | −2.88 ± 0.14 | 77.2 |
| 43.00 ± 0.05 | 30 | −3.41 ± 0.09 | −3.09 ± 0.17 | 77.2 |
| 43.10 ± 0.05 | 16 | −3.68 ± 0.12 | −3.33 ± 0.22 | 77.2 |
| 43.20 ± 0.05 | 7 | −4.04 ± 0.21 | −3.67 ± 0.31 | 77.2 |
| 43.30 ± 0.05 | 3 | −4.41 ± 0.37 | −4.01 ± 0.51 | 77.2 |
| 43.40 ± 0.05 | 2 | −4.59 ± 0.53 | −4.22 ± 0.68 | 77.2 |
| 43.60 ± 0.15 | 3 | −4.41 ± 0.37 | −4.63 ± 0.41 | 77.2 |
3.4 Filter profiles: volume corrections
None of the narrow-band filters is perfect THs (see Fig. 1). In order to model the effect of this bias on estimating the volume (luminous emitters will be detectable over larger volumes – although, if seen in the filter wings, they will be detected as fainter emitters), a series of simulations is done, following S09 and S12. Briefly, a TH volume selection is used to compute a first-pass (input) LF and derive the best fit. The fit is used to generate a population of simulated Hα emitters (assuming they are distributed uniformly across redshift); these are then folded through the true filter profile, from which a recovered LF is determined. Studying the difference between the input and recovered LFs shows that the number of bright emitters is underestimated, while faint emitters can be slightly overestimated (cf. S09 for details), but the actual corrections are different for each filter and each input LF. This allows correction factors to be estimated – these are then used to obtain the corrected LF. Corrections are computed for each individual narrow-band filter.
3.5 Extinction correction
The Hα emission line is not immune to dust extinction. Measuring the extinction for each source can in principle be done by several methods, one of which is the comparison between Hα and FIR-determined SFRs (see Ibar et al., in preparation), while the spectroscopic analysis of Balmer decrements also provides a very good estimate of the extinction. As shown in S12, the median [O ii]/Hα line ratio of a large sample of galaxies can also be reasonably well calibrated (using Balmer decrement) as a dust extinction indicator (see S12 for more details). For the COSMOS z = 1.47 sample, this results in AHα = 0.8 mag (although there is a bias towards lower extinction due to the fact that the NB921 survey is not deep enough to recover sources with much higher extinctions). However, for UDS (where a sufficiently deep NB921 coverage is available) an AHα ≈ 1 mag of extinction at Hα is shown to be an appropriate median correction at z = 1.47 (see S12). A similar value has also been found at z = 0.84 (AHα ≈ 1.2; Garn et al. 2010). The dependence of extinction on observed luminosity is also relatively small (S12) at z ∼ 1.5 – therefore, for simplicity and for an easier comparison, a simple 1 mag of extinction is applied for the four redshifts and for all observed luminosities.8
Note that S12 still find a relatively mild luminosity dependence, but one which is offset to the local Universe relation (e.g. Hopkins et al. 2001) by 0.5 mag in AHα. Nevertheless, one could interpret this differently, as a single relation that holds at both z ∼ 1.5 and ∼0, provided that luminosities at both z ∼ 0 and ∼1.5 are divided by L*Hα at the corresponding epochs; this would imply that the typical extinction does not depend on SFR or Hα luminosity in an absolute manner, but rather that it depends on how star forming or luminous a source is relative to the normal star-forming galaxy at that epoch.
3.6 H|$\boldsymbol {\alpha }$| luminosity functions at |$\boldsymbol {z}$| = 0.40, 0.84, 1.47 and 2.23
By taking all Hα-selected emitters at the four different redshifts, the Hα LF is computed at four very different cosmic times, reaching a common observed luminosity limit of ≈1041.6 erg s−1 for the first time in a consistent way over ∼11 Gyr. As previously described, the method of S09 and S12 is applied to correct for the real profile (see Section 3.4). Candidate Hα emitters are assumed to be at z = 0.4, 0.84, 1.47 and 2.23 for luminosity distance calculations. Results can be found in Fig. 8 and Table 4. Errors are Poissonian, but they include a further 20 per cent of the total completeness corrections added in quadrature.
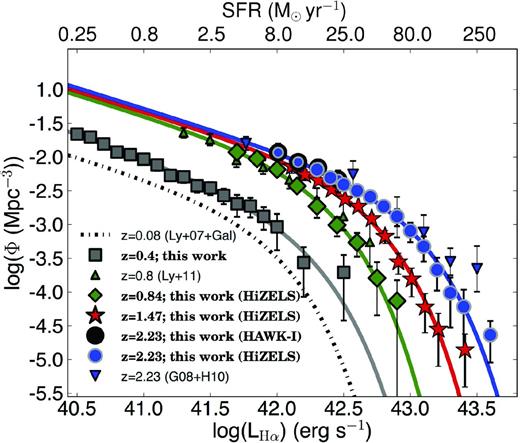
The Hα LF evolution revealed by deep and wide narrow-band surveys at z = 0.4, 0.84, 1.47 and 2.23 presented in this work. The data are combined and compared to other studies (Gallego et al. 1995; Ly et al. 2007; Geach et al. 2008a; Hayes et al. 2010), and clearly confirm the strong evolution of the LF in the last ∼11 Gyr, mostly through a continuous increase in L*Hα from z = 0 to 2.23. Note that the z = 0.4 Hα LF is constrained down to even lower luminosities which are not shown in the figure. Also, note that all Hα luminosities have been corrected by extinction with AHα = 1 mag, and that SFRs shown are based on that extinction correction. SFRs derived directly from observed Hα luminosities are a factor of 2.5 lower and Hα luminosities uncorrected for extinction are 0.4 dex lower.
The LF and SFR density evolution for 0.4 < z < 2.2, as seen through a completely self-consistent analysis using HiZELS. The measurements are obtained at z = 0.4, 0.84, 1.47 and 2.23, correcting for 1 mag extinction at Hα. Columns present the redshift, break of the LF, L*Hα, normalization (ϕ*Hα) and faint-end slope (α) of the Hα LF. The two right-hand columns present the SFR density at each redshift based on integrating the LF down to ≈3 M⊙ yr−1 or 41.6 (in log erg s−1) and for a full integration. SFR densities include a correction for AGN contamination of 10 per cent at z = 0.4 and 0.84 (see Garn et al. 2010) and 15 per cent at both z = 1.47 and 2.23. Errors on the faint-end slope α are the 1σ deviation from the best fit, when fitting the three parameters simultaneously. As α is very well constrained at all redshifts, and shown not to evolve significantly, L*Hα and ϕ*Hα are obtained by fixing α = −1.6, and the 1σ errors on L*Hα and ϕ*Hα are derived from such fits (with fixed α).
| Epoch . | L*Hα . | ϕ*Hα . | αHα . | log |$\rho _{ L_{{\rm H}\alpha }}$| (41.6) . | log |$\rho _{ L_{{\rm H}\alpha }}$| . | ρSFRHα 41.6 . | ρSFRHα (All) . |
|---|---|---|---|---|---|---|---|
| (z) . | (erg s−1) . | (Mpc−3) . | . | (erg s−1 Mpc−3) . | (erg s−1 Mpc−3) . | (M⊙ yr−1 Mpc−3) . | (M⊙ yr−1 Mpc−3) . |
| 0.40 ± 0.01 | 41.95+ 0.47− 0.12 | − 3.12+ 0.10− 0.34 | − 1.75+ 0.12− 0.08 | 38.99+ 0.19− 0.22 | 39.55+ 0.22− 0.22 | 0.008+ 0.002− 0.002 | 0.03+ 0.01− 0.01 |
| 0.84 ± 0.02 | 42.25+ 0.07− 0.05 | − 2.47+ 0.07− 0.08 | − 1.56+ 0.13− 0.14 | 39.75+ 0.12− 0.05 | 40.13+ 0.24− 0.21 | 0.040+ 0.007− 0.006 | 0.10+ 0.01− 0.02 |
| 1.47 ± 0.02 | 42.56+ 0.06− 0.05 | − 2.61+ 0.08− 0.09 | − 1.62+ 0.25− 0.29 | 40.03+ 0.08− 0.07 | 40.29+ 0.16− 0.14 | 0.07+ 0.01− 0.01 | 0.13+ 0.02− 0.02 |
| 2.23 ± 0.02 | 42.87+ 0.08− 0.06 | − 2.78+ 0.08− 0.09 | − 1.59+ 0.12− 0.13 | 40.26+ 0.01− 0.02 | 40.44+ 0.03− 0.03 | 0.13+ 0.01− 0.01 | 0.21+ 0.02− 0.03 |
| Epoch . | L*Hα . | ϕ*Hα . | αHα . | log |$\rho _{ L_{{\rm H}\alpha }}$| (41.6) . | log |$\rho _{ L_{{\rm H}\alpha }}$| . | ρSFRHα 41.6 . | ρSFRHα (All) . |
|---|---|---|---|---|---|---|---|
| (z) . | (erg s−1) . | (Mpc−3) . | . | (erg s−1 Mpc−3) . | (erg s−1 Mpc−3) . | (M⊙ yr−1 Mpc−3) . | (M⊙ yr−1 Mpc−3) . |
| 0.40 ± 0.01 | 41.95+ 0.47− 0.12 | − 3.12+ 0.10− 0.34 | − 1.75+ 0.12− 0.08 | 38.99+ 0.19− 0.22 | 39.55+ 0.22− 0.22 | 0.008+ 0.002− 0.002 | 0.03+ 0.01− 0.01 |
| 0.84 ± 0.02 | 42.25+ 0.07− 0.05 | − 2.47+ 0.07− 0.08 | − 1.56+ 0.13− 0.14 | 39.75+ 0.12− 0.05 | 40.13+ 0.24− 0.21 | 0.040+ 0.007− 0.006 | 0.10+ 0.01− 0.02 |
| 1.47 ± 0.02 | 42.56+ 0.06− 0.05 | − 2.61+ 0.08− 0.09 | − 1.62+ 0.25− 0.29 | 40.03+ 0.08− 0.07 | 40.29+ 0.16− 0.14 | 0.07+ 0.01− 0.01 | 0.13+ 0.02− 0.02 |
| 2.23 ± 0.02 | 42.87+ 0.08− 0.06 | − 2.78+ 0.08− 0.09 | − 1.59+ 0.12− 0.13 | 40.26+ 0.01− 0.02 | 40.44+ 0.03− 0.03 | 0.13+ 0.01− 0.01 | 0.21+ 0.02− 0.03 |
The LF and SFR density evolution for 0.4 < z < 2.2, as seen through a completely self-consistent analysis using HiZELS. The measurements are obtained at z = 0.4, 0.84, 1.47 and 2.23, correcting for 1 mag extinction at Hα. Columns present the redshift, break of the LF, L*Hα, normalization (ϕ*Hα) and faint-end slope (α) of the Hα LF. The two right-hand columns present the SFR density at each redshift based on integrating the LF down to ≈3 M⊙ yr−1 or 41.6 (in log erg s−1) and for a full integration. SFR densities include a correction for AGN contamination of 10 per cent at z = 0.4 and 0.84 (see Garn et al. 2010) and 15 per cent at both z = 1.47 and 2.23. Errors on the faint-end slope α are the 1σ deviation from the best fit, when fitting the three parameters simultaneously. As α is very well constrained at all redshifts, and shown not to evolve significantly, L*Hα and ϕ*Hα are obtained by fixing α = −1.6, and the 1σ errors on L*Hα and ϕ*Hα are derived from such fits (with fixed α).
| Epoch . | L*Hα . | ϕ*Hα . | αHα . | log |$\rho _{ L_{{\rm H}\alpha }}$| (41.6) . | log |$\rho _{ L_{{\rm H}\alpha }}$| . | ρSFRHα 41.6 . | ρSFRHα (All) . |
|---|---|---|---|---|---|---|---|
| (z) . | (erg s−1) . | (Mpc−3) . | . | (erg s−1 Mpc−3) . | (erg s−1 Mpc−3) . | (M⊙ yr−1 Mpc−3) . | (M⊙ yr−1 Mpc−3) . |
| 0.40 ± 0.01 | 41.95+ 0.47− 0.12 | − 3.12+ 0.10− 0.34 | − 1.75+ 0.12− 0.08 | 38.99+ 0.19− 0.22 | 39.55+ 0.22− 0.22 | 0.008+ 0.002− 0.002 | 0.03+ 0.01− 0.01 |
| 0.84 ± 0.02 | 42.25+ 0.07− 0.05 | − 2.47+ 0.07− 0.08 | − 1.56+ 0.13− 0.14 | 39.75+ 0.12− 0.05 | 40.13+ 0.24− 0.21 | 0.040+ 0.007− 0.006 | 0.10+ 0.01− 0.02 |
| 1.47 ± 0.02 | 42.56+ 0.06− 0.05 | − 2.61+ 0.08− 0.09 | − 1.62+ 0.25− 0.29 | 40.03+ 0.08− 0.07 | 40.29+ 0.16− 0.14 | 0.07+ 0.01− 0.01 | 0.13+ 0.02− 0.02 |
| 2.23 ± 0.02 | 42.87+ 0.08− 0.06 | − 2.78+ 0.08− 0.09 | − 1.59+ 0.12− 0.13 | 40.26+ 0.01− 0.02 | 40.44+ 0.03− 0.03 | 0.13+ 0.01− 0.01 | 0.21+ 0.02− 0.03 |
| Epoch . | L*Hα . | ϕ*Hα . | αHα . | log |$\rho _{ L_{{\rm H}\alpha }}$| (41.6) . | log |$\rho _{ L_{{\rm H}\alpha }}$| . | ρSFRHα 41.6 . | ρSFRHα (All) . |
|---|---|---|---|---|---|---|---|
| (z) . | (erg s−1) . | (Mpc−3) . | . | (erg s−1 Mpc−3) . | (erg s−1 Mpc−3) . | (M⊙ yr−1 Mpc−3) . | (M⊙ yr−1 Mpc−3) . |
| 0.40 ± 0.01 | 41.95+ 0.47− 0.12 | − 3.12+ 0.10− 0.34 | − 1.75+ 0.12− 0.08 | 38.99+ 0.19− 0.22 | 39.55+ 0.22− 0.22 | 0.008+ 0.002− 0.002 | 0.03+ 0.01− 0.01 |
| 0.84 ± 0.02 | 42.25+ 0.07− 0.05 | − 2.47+ 0.07− 0.08 | − 1.56+ 0.13− 0.14 | 39.75+ 0.12− 0.05 | 40.13+ 0.24− 0.21 | 0.040+ 0.007− 0.006 | 0.10+ 0.01− 0.02 |
| 1.47 ± 0.02 | 42.56+ 0.06− 0.05 | − 2.61+ 0.08− 0.09 | − 1.62+ 0.25− 0.29 | 40.03+ 0.08− 0.07 | 40.29+ 0.16− 0.14 | 0.07+ 0.01− 0.01 | 0.13+ 0.02− 0.02 |
| 2.23 ± 0.02 | 42.87+ 0.08− 0.06 | − 2.78+ 0.08− 0.09 | − 1.59+ 0.12− 0.13 | 40.26+ 0.01− 0.02 | 40.44+ 0.03− 0.03 | 0.13+ 0.01− 0.01 | 0.21+ 0.02− 0.03 |
The results not only reveal a very clear evolution of the Hα LF from z = 0 to 2.23, but also allow for a detailed investigation of exactly how the evolution occurs, in steps of ∼2–3 Gyr. The strongest evolutionary feature is the increase in L*Hα as a function of redshift from z = 0 to 2.23 (see Fig. 9), with the typical Hα luminosity at z ∼ 2 (L*Hα) being 10 times higher than locally. This is clearly demonstrated in Fig. 9, which shows the evolution of the Schechter function parameters describing the Hα LF. The L*Hα evolution from z ∼ 0 to ∼2.2 can be simply approximated as log L* = 0.45z + log L*z = 0, with log L*z = 0 = 41.87 (see Fig. 9). At the very bright end (L > 4L*), and particularly at z > 1, there seems to be a deviation from a Schechter function. Follow-up spectroscopy of such luminous Hα sources has recently been obtained for a subset of the z = 1.47 sample, and unveils a significant fraction of narrow- and broad-line active galactic nuclei (AGNs; with strong [N ii] lines as well), which become dominant at the highest luminosities (Sobral et al., in preparation). It is therefore likely that the deviation from a Schechter function is being mostly driven by the increase in the AGN activity fraction at such luminosities, particularly due to the detection of rare broad-line AGN and from very strong [N ii] emission.
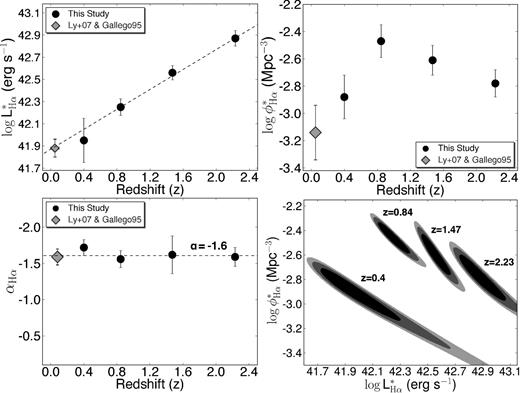
The evolution of the Schechter function parameters which best fit the Hα LF since z = 2.23. Top left: the evolution of L*Hα as a function of redshift, revealing that the break of the LF evolves significantly from z = 0 to 2.23 by a factor of 10, which can be simply parametrized by log L*Hα = 0.45z + 41.87. Top right: the evolution of ϕ*, which seems to rise mildly up to z ∼ 1 and decrease again up to z ∼ 2.2. Bottom left: the faint-end slope, however, is not found to evolve at all from z = 0.0 to 2.23 within the scatter and the errors, pointing towards α = −1.60 ± 0.08 for the faint-end slope of the Hα LF across the last 11 Gyr. Bottom right: the 1σ, 2σ and 3σ contours of the best fits to the combination of L*Hα and ϕ* fixing α = −1.6.
The normalization of the Hα LF, ϕ*, is also found to evolve, but much more mildly. There is an increase of ϕ* up to z ∼ 1 (by a factor of ∼4),9 and then this decreases again for higher redshifts by a factor of ∼2 from z ∼ 1 to 2.23 (see Fig. 9). By fitting a simple quadratic model to describe the data, one finds that the parametrization log ϕ* = −0.38z + z − 3.18 provides a good fit for z = 0–2.23, but the current data can only exclude a model with a constant ϕ* at a <2σ level. The statistical significance for evolution in ϕ* becomes even lower (1 < σ) if one restricts the analysis to z = 0.4–2.23.
The faint-end slope, α, is found to be relatively steep from z ∼ 0 up to z = 2.23 (when compared to a canonical α = −1.35), and it is not found to evolve. The median α over 0 < z < 2.23 is −1.60 ± 0.08. Very deep data from Hayes et al. (2010) and Ly et al. (2011) not only agree well with such faint-end slope, but even more importantly, their data at the faintest luminosities are also very well fitted by the best-fitting z = 2.23 and 0.84 LFs. If those data points are included and used to re-fit the LFs at those two redshifts, the resulting best-fitting faint-end slopes remain the same, but the error in α is reduced by ∼10–15 per cent.
It is therefore shown that by measuring the Hα LF in a consistent way, and using multiple fields, the faint-end slope can be very well approximated by a constant α = −1.6 at least up to z = 2.23. This shows that while the faint-end slope truly is steep at z ∼ 2, it does not become significantly steeper from z ∼ 0 to ∼2, and rather has remained relatively constant for the last 11 Gyr (our data cannot rule out weak evolution). The potential strong steepening of the faint-end slope, which has been previously reported (e.g. Hayes et al. 2010), may in part be a result of comparing different data sets which probe different ranges in luminosity, use different completeness corrections, different selection of emitters and probe a different parameter space. Furthermore, the results from Sobral et al. (2011) show that the faint-end slope depends relatively strongly on environment (α ∼ −1.1 for the densest clusters to α ∼ −1.9 for the poorest regions), which indicates that the changes in the faint-end slope measured before may also have resulted by the relatively small areas which can (by chance) probe different environments. Note that this is not the case for this paper because the multi-epoch Hα surveys cover ∼2 deg2 areas over two independent fields and are able to cover a wide range of environments. Indeed, apart from the rich, dense structures presented in Sobral et al. (2011) at z = 0.84, our Hα survey is also able to probe significantly overdense regions even at z = 2.23 (see Geach et al. 2012, for details on a significant Hα-detected overdensity in the COSMOS field). By splitting the sample in a similar way to Sobral et al. (2011) (isolating the overdensity in COSMOS and nearby regions), a variation of α with local density is clearly recovered, consistent with the results at z = 0.84, i.e. overdense regions present a much shallower α (∼− 1.3), while the general field regions have a steeper (α ∼ −1.7) faint-end slope. The dependence of α on environment since z = 2.23 will be carefully quantified in a forthcoming paper.
The steep faint-end slope of the Hα LF is in very good agreement with the UV LF at z ∼ 2 and above, and particularly consistent with a relatively non-evolving α ≈ −1.6. This can be seen by comparing the results in this paper with those presented by Treyer et al. (1998), Arnouts et al. (2005) and, more recently, Oesch et al. (2010). It is also likely that (similarly to the Hα LF) the large scatter and the different selections/corrections applied have driven studies to assume/argue for a steepening of the UV luminosity faint-end slope, just like for the Hα LF (see Oesch et al. 2010).
Overall, the results imply that the bulk of the evolution of the star-forming population from z = 0 to ∼2.2 is occurring as a strong boost in luminosity of all galaxies. The UV luminosity results also show very similar trends to the Hα LF, by revealing that the strongest evolution to z ∼ 2 is in the typical luminosity/break of the LF, which evolves significantly. However, individual measurements for the UV LF at z < 2 are still significantly affected by cosmic variance, small sample sizes and much more uncertain dust corrections, and thus the Hα analysis provides a much stronger constraint on the evolution of star-forming galaxies up to z ∼ 2.2.
4 THE STAR FORMATION HISTORY OF THE UNIVERSE: THE LAST 11 GYR WITH Hα
As detailed before, a constant 1 mag of extinction at Hα is assumed for the analysis, which is likely to be a good approach for the entire integrated star formation.
4.1 Removal of the AGN contribution
Interpreting the integral of the Hα LF as an SFR density requires a good estimation of the possible contribution of AGN to that quantity. For the z = 0.84 sample, Garn et al. (2010) conducted a detailed search for potential AGN, finding a fraction of 8 ± 3 per cent within the Hα population at z = 0.84. Similar (i.e. ∼10 per cent) AGN contaminations at lower redshift have also been found by other studies, and therefore assuming a 10 per cent contribution from AGN up to z ∼ 1 is likely to be a good approximation. At higher redshifts, and particularly for the sample at z = 1.47 and 2.23, the AGN activity could in principle be different. By looking at a range of AGN indicators – X-rays, radio and IRAC colours (and emission lines ratios for sources with such information10) – it is found that ∼15 per cent of the sources are potentially AGN at z = 1.47. Similar results are found at z = 2.23. Therefore, when converting integrated luminosities to SFR densities at each epoch, it is assumed that AGNs contribute 10 per cent of that up to z ∼ 1 and 15 per cent above that redshift. While this correction may be uncertain, the actual correction will likely be within 5 per cent of what is assumed, and in order to guarantee the robustness of the measurements, the final measurements include the error introduced by the AGN correction – this is done by adding 20 per cent of the AGN correction in quadrature to the other errors. The AGN contribution/contamination will be studied in detail in Sobral et al. (in preparation).
4.2 The Hα star formation history of the Universe
The results are shown in Table 5, both down to the approximate common survey limits and by fully integrating the LF. Fig. 10 also presents the results (fully integrating down the LFs), and includes a comparison between the consistent view on the Hα star formation history of the Universe derived in this paper with the various measurements from the literature (Hopkins & Beacom 2006; Ly et al. 2011), showing a good agreement.
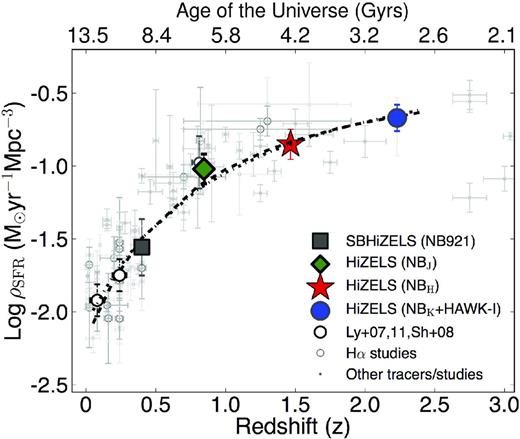
The SFR density and its evolution with redshift up to z ∼ 2.3 using Hα only, and compared to estimates at different redshifts from the literature (e.g. Hopkins 2004; Shioya et al. 2008; Ly et al. 2011, and references therein). This confirms a strong evolution in the SFR density over the last ∼11 Gyr. Overall, the simple parametrizations log ρSFR = −0.14T − 0.23, with T in Gyr (shown as a dashed line), or 2.1/(z+1), shown as a dot–dashed line, provide good approximations to the star formation history of the Universe in the last 11 Gyr. This is in very good agreement with results from Karim et al. (2011), using radio stacking over a similar redshift range in the COSMOS field.
The improvement when compared to other studies is driven by (i) the completely self-consistent determinations, (ii) the significantly larger samples and (iii) the fact that the faint-end slope is accurately measured from z ∼ 0 to ∼2.23 and LFs determined down to a much lower common luminosity limit than ever done before. A comparison with all other previous measurements (which show a large scatter) reveals a good agreement with the Hα measurements. However, the homogeneous Hα analysis provides, for the first time, a much clearer and cleaner view of the evolution. The results presented in Fig. 10 reveal the Hα star formation history of the Universe for the last ∼11 Gyr. The evolution is particularly steep up to about z ∼ 1. While the evolution is then milder, ρSFR continues to rise, up to at least z ∼ 2.
Up to z ∼ 1, the Hα star formation history is well fitted by log ρSFR = 4 × (z + 1) − 2.08. However, such parametrization is not a good fit for higher redshifts. It is possible to fit the entire Hα star formation history since z ∼ 2.2 or for the last 11 Gyr by the simple parametrization log ρSFR = −0.14T − 0.23, with T being the time since the big bang in Gyr (see Fig. 10). A power-law parametrization as a function of redshift [a × (1 + z)β] yields β = −1.0, and thus the Hα star formation history can also be simply parametrized by log ρSFR = − 2.1/(z + 1), clearly revealing that ρSFR has been declining for the last ∼11 Gyr. This parametrization is also a very good fit for results from Karim et al. (2011), using radio stacking over a similar redshift range in the COSMOS field.
4.3 The stellar mass assembled in the last 11 Gyr
The results presented in this paper can be used to provide an estimate of the stellar mass (density) which has been assembled by Hα star-forming galaxies over the last 11 Gyr. This is done in a similar way to Hopkins & Beacom (2006) or Glazebrook et al. (2004), taking into account that a significant part of the mass of newborn stars at each redshift is recycled and can be used in subsequent star formation episodes. The fraction of recycled mass depends on the IMF used. For a Salpeter IMF, which has been used for the Hα calibration, the recycling fraction is 30 per cent. Note, however, that changing the IMF does not change the qualitative results presented in this paper, in particular the agreement between the predicted and the measured stellar mass density growth. Nevertheless, changing the IMF changes both the normalization of the star formation history and the stellar mass density growth.
Here, the following approach is taken: the measured stellar mass density already in place at z ∼ 2.2 (many determinations exist; e.g. Hopkins & Beacom 2006; Pérez-González et al. 2008; Ilbert et al. 2009) is assumed to be log10 M = 7.45 M⊙ Mpc−3. By using the measured Hα star formation history derived in this paper (log ρSFR = −0.14T − 0.23), a prediction of the evolution of the stellar mass density of the Universe is computed, using the recycling fraction of the Salpeter IMF (30 per cent).
The results are presented in Fig. 11, and compared with various measurements of the stellar mass density at different redshifts available from the literature (Hopkins & Beacom 2006; Elsner, Feulner & Hopp 2008; Pérez-González et al. 2008; Marchesini et al. 2009). All literature results have been converted to a Salpeter IMF if derived with a different IMF – including those with a modified Salpeter IMF (SalA; resulting in masses a factor of 0.77 lower than Salpeter; see e.g. Hopkins & Beacom).
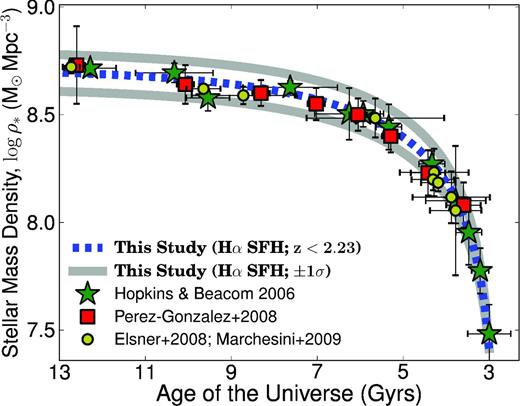
The stellar mass assembly growth inferred from the completely self-consistent Hα star formation history of the Universe over the last ∼11 Gyr, and the comparison with the observations of the stellar mass density over the same epochs. The results show a good agreement, suggesting that the Hα analysis is indeed recovering essentially all the cosmic star formation happening since z = 2.23.
The results reveal a very good agreement between the predictions based on the Hα star formation history of the Universe presented in this paper since z = 2.23 and the stellar mass density evolution of the Universe, measured directly by many authors. The results therefore indicate that at least since z = 2.23 the Hα star formation history of the Universe is a very good representation of the total star formation history of the Universe. It is possible to reconcile the observed evolution of the stellar mass density with that produced from the observed star formation history with very simple assumptions, without the need to modify the IMF or have it evolve as a function of time. The Hα analysis reveals that star formation since z = 2.23 is responsible for 95 per cent of the total stellar mass density observed today, with about half of that being assembled from z ∼ 2.2 to ∼1.2 and the other half since z ≈ 1.2. Note that the same conclusion is reached if the stellar mass density at z = 0 is adopted for the normalization (instead of that at z = 2.23) and the measured Hα star formation history is used (with appropriate recycling factor) to evolve this stellar mass density back to earlier epochs. Moreover, if the SFR density continues to decline with time in the same way as in the last ∼11 Gyr, the stellar mass density growth will become increasingly slower, with the stellar mass density of the Universe reaching a maximum which is only 5 per cent higher than its current value.
5 CONCLUSIONS
This paper presents new results from a unique combination of wide and deep narrow-band Hα surveys using UKIRT, Subaru and the VLT. It has resulted in robust and equally selected samples of several hundreds of Hα emitters in narrow redshift slices, allowing us to study and parametrize in a completely self-consistent way the evolution of the Hα LF over the last 11 Gyr of the Universe. The main results are as follows.
We robustly select a total of 1742, 637, 515 and 807 Hα emitters [Σ > 3, EW0(Hα) > 25 Å] across the COSMOS and the UDS fields at z = 0.40, 0.84, 1.47 and 2.23, respectively. These are by far the largest samples of homogeneously selected Hα emitters, while the wide area and the coverage over two independent fields allow us to greatly overcome cosmic variance and also assemble large samples of more luminous galaxies.
We find that the Hα LF evolves significantly from z ∼ 0 to ∼2.2, with the bulk of the evolution being driven by the continuous rise in L*Hα by a factor of 10 from the local Universe to z ∼ 2.2, which is well described by log L*Hα(z) = 0.45z + 41.87.
By obtaining very deep data over a wide range of epochs, it is found that the faint-end slope, α, does not evolve with redshift up to z ∼ 2.3, and is set to α = −1.60 ± 0.08 for the last 11 Gyr (0 < z < 2.2), contrarily to previous claims (based on heterogeneous samples) which argued for a steepening with redshift.
The evolution seen in the Hα LF is in good agreement with the evolution seen using inhomogeneous compilations of other tracers of star formation, such as FIR and UV, jointly pointing towards the bulk of the evolution in the last 11 Gyr being driven by a similar star-forming population across cosmic time, but with a strong luminosity increase from z ∼ 0 to ∼2.2.
This is the first time Hα has been used to trace star formation activity with a single homogeneous survey at z = 0.4–2.23. The simple parametrizations log ρSFR = −0.14T − 0.23 (with T being the age of the Universe in Gyr) or log ρSFR = − 2.1/(z + 1) are good approximations for the last 11 Gyr, showing that ρSFR has been declining since z ∼ 2.2.
The results reveal that both the shape and normalization of the Hα star formation history are consistent with the measurements of the stellar mass density growth, confirming that the Hα cosmic star formation history is tracing the bulk of the formation of stars in the Universe for z < 2.3.
The star formation activity over the last ≈11 Gyr is responsible for producing ∼95 per cent of the total stellar mass density observed locally today, with about half of that being assembled from z ∼ 2.2 to ∼1.2 and the other half at z < 1.2.
The results presented in this paper provide a self-consistent view that improves our understanding of the evolution of star-forming galaxies. Particularly, it shows that the evolution of the star-forming population in the last 11 Gyr has been mostly driven by a change in the typical SFR of the population (L*Hα), while the faint-end slope of the Hα LF has remained constant (α = −1.6), and the change in the normalization has been much more moderate. The strong evolution in L*Hα (or SFR*) may well be unveiling something very fundamental about the evolution of star-forming galaxies, as it seems to mark a transition between disc and mergers (e.g. S09) in the last 9–10 Gyr. Also, scaling SFRs by the SFR* at each epoch (or Hα luminosities by L*Hα at each epoch) seems to recover relatively non-evolving relations between scaled SFRs/luminosities and, for example, dust extinction (S12), morphological class (S09), merger rates (Stott et al., in preparation) or the typical dark matter halo in which the star-forming galaxies are likely to reside (Sobral et al. 2010).
The results presented in this paper also complement the current view on the evolution of the stellar mass function over the last 11 Gyr (e.g. Ilbert et al. 2009; Peng et al. 2010; Marchesini et al. 2012), which also reveal a non-evolving faint-end slope (of the stellar mass function) at least for z < 2, but shallower, α = −1.3. However, the typical mass of the stellar mass function, M*, is found to be roughly constant in the last 11 Gyr, with the main change being ϕ*, which continuously increases in the last ∼11 Gyr. Combining the results of the evolution of the Hα LF with those of the evolution of the stellar mass function points towards the existence of a star-forming population which is mostly evolving by an overall decrease in their SFRs/luminosity, while the overall population of galaxies evolves by a change in number density, but with a rather non-evolving typical mass (M*), a rather simple evolution scenario which is consistent with that proposed by Peng et al. (2010).
The authors would like to thank the reviewer, James Colbert, for many comments and suggestions which improved the paper significantly. DS is supported by a NOVA fellowship. IS acknowledges a Leverhulme Senior Fellowship. PNB acknowledges support from the Leverhulme Trust. YM, JPS and IS thank the UK Science and Technology Facility Council (STFC). JEG is supported by a Banting Fellowship, administered by the Natural Science and Engineering Research Council of Canada. We would like to thank Richard Ellis, Simon Lilly, Peter Capak, Adam Muzzin, Taddy Kodama, Masao Hayashi, Andy Lawrence, Joop Schaye, Marijn Franx, Huub Röttgering, Rychard Bouwens and Renske Smit for many interesting and helpful discussions. We would also like to thank Chun Ly for helpful comments. The authors wish to thank all the JAC staff for their help in conducting the observations at the UKIRT telescope and their continuous support, and we are also extremely grateful to all the Subaru staff. We also acknowledge ESO and Subaru for service observations. Finally, the authors fully acknowledge the tremendous work that has been done by both COSMOS and UKIDSS UDS/SXDF teams in assembling such large, state-of-the-art multiwavelength data sets over such wide areas, as those have been crucial for the results presented in this paper.
This work is based on observations obtained using the Wide Field CAMera (WFCAM) on the 3.8-m United Kingdom Infrared Telescope (UKIRT), as part of the High-redshift(Z) Emission Line Survey (HiZELS; U/CMP/3 and U/10B/07). It also relies on observations conducted with HAWK-I on the ESO Very Large Telescope (VLT), programme 086.7878.A, and observations obtained with Suprime-Cam on the Subaru Telescope (S10B-144S).
NOVA Fellow.
It may be possible to extend Hα studies to even higher redshifts: Shim et al. (2011) suggest that Spitzer IRAC mid-IR fluxes can be used to detect strong Hα emission at even higher redshifts (z ∼ 4). NIRCam and NIRISS on the James Webb Space Telescope will obviously significantly expand the exploration of Hα emission at such high redshifts.
For more details on the survey, progress and data releases, see http://www.roe.ac.uk/ifa/HiZELS/.
The improvements in the flat-fielding are obtained by stacking all second-pass flattened frames per field and producing source masks on the stacked images. Masks are then used to produce third-pass flats using all the frames in the jitter sequence except the frame being flattened. The third-pass flattened frames are then stacked again, and the procedure is repeated another time. This procedure is able to mask many sources which are undetected in individual frames out of the flats, but particularly to mask bright sources much more effectively, as the stacking of all images reveals a wider distribution of flux from those sources.
iraf and scamp (Bertin 2006) are used to distort correct the frames and obtain a very accurate (rms ≈ 0.1–0.2 arcsec) astrometric solution for each frame [using Two Micron All Sky Survey (2MASS)], always assuring that the flux is conserved.
Sources for which one of the broad-band colours is not available (typically 5 per cent of the sources) are assigned the median correction. The median corrections are −0.04, +0.07, +0.05 and +0.03 for NB921, NBJ, NBH and NBK, respectively.
See UKIDSS UDS website (http://www.nottingham.ac.uk/astronomy/UDS) for a redshift compilation by O. Almaini and the COSMOS data archive (http://irsa.ipac.caltech.edu/data/COSMOS) for the catalogues, spectra and information on the various instruments and spectroscopic programmes.
The selection was modified because the Daddi et al. cut was designed to select z > 1.4 sources, while here z = 2.23 emitters are targeted. The precise location of the new cut, which is 0.2 mag higher/redder in z − K than that of Daddi et al., is motivated by the confirmed Hα emitters and by the need to minimize contamination from z < 2 sources).
The correction is applied to obtain data points corrected for extinction by 1 mag at Hα.
Note that the difference in ϕ* from the Sobral et al. (2009a) Hα LF is mostly driven by ϕ*S09 reported there being ϕ*S09 = ϕ* × ln 10 (due to the fitting to d log L without taking the ln10 factor into account – see Sobral et al. 2012), which accounts for a factor of ≈2.23. The remaining difference (a factor of ∼1.5) is an actual difference driven by the improved data reduction, selection of emitters (3Σ instead of 2.5Σ), completeness and cleanness of the catalogues of Hα emitters (particularly due to the significantly improved photometric redshifts and a larger number of spectroscopic redshifts).
Follow-up spectroscopy of luminous Hα sources unveils a significant fraction of narrow- and broad-line AGN which becomes dominant at the highest luminosities (Sobral et al., in preparation), but is consistent with an overall AGN contribution to the Hα luminosity density of 15 per cent.
REFERENCES
APPENDIX A: CATALOGUES OF CANDIDATE HIZELS NARROW-BAND EMITTERS
The catalogues of potential narrow-band emitters over the COSMOS and UDS fields are presented in Tables A1 (NB921), A2 (NBJ), A3 (NBH) and A4 (NBK). It contains IDs (including field and observing band), right ascension (RA), declination (Dec.), narrow-band magnitude (NB), broad-band magnitude (BB), the significance of the narrow-band excess (Σ), estimated flux (log 10), estimated observed EW and a flag for those that are classified as Hα. Note that only the online version contains the full catalogue – here only five entries of the table are shown as examples of the entire catalogues.
A catalogue of all Σ > 3 NB921 narrow-band sources selected in the UDS and COSMOS fields from HiZELS. NB magnitudes are NB921 (AB); BB are z′ magnitudes (AB). Note that the printed version contains only five entries, in order to provide some examples contained in the full catalogue. The full catalogue is available online.
| ID . | RA . | Dec. . | NB . | BB . | Σ . | log flux . | EWobs . | Class. as Hα . |
|---|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (AB) . | (AB) . | . | (erg s−1) . | (Å) . | . |
| HiZELS-COSMOS-NB921-S12-14 | 09 58 13.57 | +02 17 15.6 | 23.86 ± 0.11 | 24.85 ± 0.08 | 13.6 | −16.255 | 418.4 | No |
| HiZELS-COSMOS-NB921-S12-105 | 09 59 57.96 | +02 17 41.5 | 23.14 ± 0.03 | 23.39 ± 0.02 | 9.9 | −16.132 | 119.8 | No |
| HiZELS-COSMOS-NB921-S12-136 | 09 58 57.55 | +02 17 45.0 | 21.64 ± 0.01 | 22.11 ± 0.01 | 56.5 | −15.636 | 105.9 | Yes |
| HiZELS-COSMOS-NB921-S12-4064 | 09 59 20.49 | +02 20 54.5 | 22.06 ± 0.01 | 22.21 ± 0.01 | 14.3 | −16.084 | 39.13 | No |
| HiZELS-UDS-NB921-S12-220582 | 02 16 19.37 | −05 13 54.2 | 22.37 ± 0.01 | 22.65 ± 0.01 | 55.6 | −16.287 | 38.22 | Yes |
| ID . | RA . | Dec. . | NB . | BB . | Σ . | log flux . | EWobs . | Class. as Hα . |
|---|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (AB) . | (AB) . | . | (erg s−1) . | (Å) . | . |
| HiZELS-COSMOS-NB921-S12-14 | 09 58 13.57 | +02 17 15.6 | 23.86 ± 0.11 | 24.85 ± 0.08 | 13.6 | −16.255 | 418.4 | No |
| HiZELS-COSMOS-NB921-S12-105 | 09 59 57.96 | +02 17 41.5 | 23.14 ± 0.03 | 23.39 ± 0.02 | 9.9 | −16.132 | 119.8 | No |
| HiZELS-COSMOS-NB921-S12-136 | 09 58 57.55 | +02 17 45.0 | 21.64 ± 0.01 | 22.11 ± 0.01 | 56.5 | −15.636 | 105.9 | Yes |
| HiZELS-COSMOS-NB921-S12-4064 | 09 59 20.49 | +02 20 54.5 | 22.06 ± 0.01 | 22.21 ± 0.01 | 14.3 | −16.084 | 39.13 | No |
| HiZELS-UDS-NB921-S12-220582 | 02 16 19.37 | −05 13 54.2 | 22.37 ± 0.01 | 22.65 ± 0.01 | 55.6 | −16.287 | 38.22 | Yes |
A catalogue of all Σ > 3 NB921 narrow-band sources selected in the UDS and COSMOS fields from HiZELS. NB magnitudes are NB921 (AB); BB are z′ magnitudes (AB). Note that the printed version contains only five entries, in order to provide some examples contained in the full catalogue. The full catalogue is available online.
| ID . | RA . | Dec. . | NB . | BB . | Σ . | log flux . | EWobs . | Class. as Hα . |
|---|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (AB) . | (AB) . | . | (erg s−1) . | (Å) . | . |
| HiZELS-COSMOS-NB921-S12-14 | 09 58 13.57 | +02 17 15.6 | 23.86 ± 0.11 | 24.85 ± 0.08 | 13.6 | −16.255 | 418.4 | No |
| HiZELS-COSMOS-NB921-S12-105 | 09 59 57.96 | +02 17 41.5 | 23.14 ± 0.03 | 23.39 ± 0.02 | 9.9 | −16.132 | 119.8 | No |
| HiZELS-COSMOS-NB921-S12-136 | 09 58 57.55 | +02 17 45.0 | 21.64 ± 0.01 | 22.11 ± 0.01 | 56.5 | −15.636 | 105.9 | Yes |
| HiZELS-COSMOS-NB921-S12-4064 | 09 59 20.49 | +02 20 54.5 | 22.06 ± 0.01 | 22.21 ± 0.01 | 14.3 | −16.084 | 39.13 | No |
| HiZELS-UDS-NB921-S12-220582 | 02 16 19.37 | −05 13 54.2 | 22.37 ± 0.01 | 22.65 ± 0.01 | 55.6 | −16.287 | 38.22 | Yes |
| ID . | RA . | Dec. . | NB . | BB . | Σ . | log flux . | EWobs . | Class. as Hα . |
|---|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (AB) . | (AB) . | . | (erg s−1) . | (Å) . | . |
| HiZELS-COSMOS-NB921-S12-14 | 09 58 13.57 | +02 17 15.6 | 23.86 ± 0.11 | 24.85 ± 0.08 | 13.6 | −16.255 | 418.4 | No |
| HiZELS-COSMOS-NB921-S12-105 | 09 59 57.96 | +02 17 41.5 | 23.14 ± 0.03 | 23.39 ± 0.02 | 9.9 | −16.132 | 119.8 | No |
| HiZELS-COSMOS-NB921-S12-136 | 09 58 57.55 | +02 17 45.0 | 21.64 ± 0.01 | 22.11 ± 0.01 | 56.5 | −15.636 | 105.9 | Yes |
| HiZELS-COSMOS-NB921-S12-4064 | 09 59 20.49 | +02 20 54.5 | 22.06 ± 0.01 | 22.21 ± 0.01 | 14.3 | −16.084 | 39.13 | No |
| HiZELS-UDS-NB921-S12-220582 | 02 16 19.37 | −05 13 54.2 | 22.37 ± 0.01 | 22.65 ± 0.01 | 55.6 | −16.287 | 38.22 | Yes |
A catalogue of all Σ > 3 NBJ narrow-band sources selected in the UDS and COSMOS fields from HiZELS. NB magnitudes are NBJ (Vega); BB are J magnitudes (Vega). Note that the printed version contains only five example entries, in order to provide some examples contained in the full catalogue. The full catalogue is available online.
| ID . | RA . | Dec. . | NB . | BB . | Σ . | log flux . | EWobs . | Class. as Hα . |
|---|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (Vega) . | (Vega) . | . | (erg s−1) . | (Å) . | . |
| HiZELS-COSMOS-NBJ-S12-206 | 09 58 42.11 | +01 58 40.5 | 21.58 ± 0.20 | 22.83 ± 0.23 | 3.5 | −16.11 | 463.5 | No |
| HiZELS-COSMOS-NBJ-S12-292 | 09 58 42.65 | +02 27 24.2 | 20.51 ± 0.08 | 20.85 ± 0.05 | 3.7 | −16.08 | 65.4 | Yes |
| HiZELS-COSMOS-NBJ-S12-293 | 09 58 42.63 | +02 19 53.2 | 20.84 ± 0.10 | 21.46 ± 0.07 | 4.4 | −16.01 | 139.3 | Yes |
| HiZELS-UDS-NBJ-S12-5 | 02 16 16.81 | −05 09 09.2 | 20.51 ± 0.08 | 20.85 ± 0.05 | 5.4 | −15.89 | 194.6 | Yes |
| HiZELS-UDS-NBJ-S12-26 | 02 16 17.15 | −05 07 42.4 | 20.84 ± 0.10 | 21.46 ± 0.07 | 4.6 | −15.96 | 79.8 | Yes |
| ID . | RA . | Dec. . | NB . | BB . | Σ . | log flux . | EWobs . | Class. as Hα . |
|---|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (Vega) . | (Vega) . | . | (erg s−1) . | (Å) . | . |
| HiZELS-COSMOS-NBJ-S12-206 | 09 58 42.11 | +01 58 40.5 | 21.58 ± 0.20 | 22.83 ± 0.23 | 3.5 | −16.11 | 463.5 | No |
| HiZELS-COSMOS-NBJ-S12-292 | 09 58 42.65 | +02 27 24.2 | 20.51 ± 0.08 | 20.85 ± 0.05 | 3.7 | −16.08 | 65.4 | Yes |
| HiZELS-COSMOS-NBJ-S12-293 | 09 58 42.63 | +02 19 53.2 | 20.84 ± 0.10 | 21.46 ± 0.07 | 4.4 | −16.01 | 139.3 | Yes |
| HiZELS-UDS-NBJ-S12-5 | 02 16 16.81 | −05 09 09.2 | 20.51 ± 0.08 | 20.85 ± 0.05 | 5.4 | −15.89 | 194.6 | Yes |
| HiZELS-UDS-NBJ-S12-26 | 02 16 17.15 | −05 07 42.4 | 20.84 ± 0.10 | 21.46 ± 0.07 | 4.6 | −15.96 | 79.8 | Yes |
A catalogue of all Σ > 3 NBJ narrow-band sources selected in the UDS and COSMOS fields from HiZELS. NB magnitudes are NBJ (Vega); BB are J magnitudes (Vega). Note that the printed version contains only five example entries, in order to provide some examples contained in the full catalogue. The full catalogue is available online.
| ID . | RA . | Dec. . | NB . | BB . | Σ . | log flux . | EWobs . | Class. as Hα . |
|---|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (Vega) . | (Vega) . | . | (erg s−1) . | (Å) . | . |
| HiZELS-COSMOS-NBJ-S12-206 | 09 58 42.11 | +01 58 40.5 | 21.58 ± 0.20 | 22.83 ± 0.23 | 3.5 | −16.11 | 463.5 | No |
| HiZELS-COSMOS-NBJ-S12-292 | 09 58 42.65 | +02 27 24.2 | 20.51 ± 0.08 | 20.85 ± 0.05 | 3.7 | −16.08 | 65.4 | Yes |
| HiZELS-COSMOS-NBJ-S12-293 | 09 58 42.63 | +02 19 53.2 | 20.84 ± 0.10 | 21.46 ± 0.07 | 4.4 | −16.01 | 139.3 | Yes |
| HiZELS-UDS-NBJ-S12-5 | 02 16 16.81 | −05 09 09.2 | 20.51 ± 0.08 | 20.85 ± 0.05 | 5.4 | −15.89 | 194.6 | Yes |
| HiZELS-UDS-NBJ-S12-26 | 02 16 17.15 | −05 07 42.4 | 20.84 ± 0.10 | 21.46 ± 0.07 | 4.6 | −15.96 | 79.8 | Yes |
| ID . | RA . | Dec. . | NB . | BB . | Σ . | log flux . | EWobs . | Class. as Hα . |
|---|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (Vega) . | (Vega) . | . | (erg s−1) . | (Å) . | . |
| HiZELS-COSMOS-NBJ-S12-206 | 09 58 42.11 | +01 58 40.5 | 21.58 ± 0.20 | 22.83 ± 0.23 | 3.5 | −16.11 | 463.5 | No |
| HiZELS-COSMOS-NBJ-S12-292 | 09 58 42.65 | +02 27 24.2 | 20.51 ± 0.08 | 20.85 ± 0.05 | 3.7 | −16.08 | 65.4 | Yes |
| HiZELS-COSMOS-NBJ-S12-293 | 09 58 42.63 | +02 19 53.2 | 20.84 ± 0.10 | 21.46 ± 0.07 | 4.4 | −16.01 | 139.3 | Yes |
| HiZELS-UDS-NBJ-S12-5 | 02 16 16.81 | −05 09 09.2 | 20.51 ± 0.08 | 20.85 ± 0.05 | 5.4 | −15.89 | 194.6 | Yes |
| HiZELS-UDS-NBJ-S12-26 | 02 16 17.15 | −05 07 42.4 | 20.84 ± 0.10 | 21.46 ± 0.07 | 4.6 | −15.96 | 79.8 | Yes |
A catalogue of all Σ > 3 NBH narrow-band sources selected in the UDS and COSMOS fields from HiZELS. NB magnitudes are NBH (Vega); BB are H magnitudes (Vega). Note that the printed version contains only five example entries, in order to provide some examples contained in the full catalogue. The full catalogue is available online.
| ID . | RA . | Dec. . | NB . | BB . | Σ . | log flux . | EWobs . | Class. as Hα . |
|---|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (Vega) . | (Vega) . | . | (erg s−1) . | (Å) . | . |
| HiZELS-COSMOS-NBH-S12-206 | 09 57 47.31 | +02 02 08.1 | 21.58 ± 0.14 | 20.99 ± 0.05 | 3.1 | −15.98 | 251.4 | No |
| HiZELS-COSMOS-NBH-S12-292 | 09 57 47.33 | +01 51 53.1 | 20.51 ± 0.02 | 18.33 ± 0.01 | 12.1 | −15.40 | 77.3 | No |
| HiZELS-COSMOS-NBH-S12-293 | 09 57 47.65 | +02 16 19.8 | 20.84 ± 0.08 | 19.80 ± 0.02 | 3.3 | −15.87 | 101.8 | No |
| HiZELS-UDS-NBH-S12-4012 | 02 16 44.17 | −04 44 53.0 | 20.04 ± 0.18 | 20.93 ± 0.04 | 3.0 | −15.87 | 308 | Yes |
| HiZELS-UDS-NBH-S12-4136 | 02 16 45.35 | −04 07 26.8 | 19.15 ± 0.08 | 19.76 ± 0.02 | 5.2 | −15.64 | 171 | Yes |
| ID . | RA . | Dec. . | NB . | BB . | Σ . | log flux . | EWobs . | Class. as Hα . |
|---|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (Vega) . | (Vega) . | . | (erg s−1) . | (Å) . | . |
| HiZELS-COSMOS-NBH-S12-206 | 09 57 47.31 | +02 02 08.1 | 21.58 ± 0.14 | 20.99 ± 0.05 | 3.1 | −15.98 | 251.4 | No |
| HiZELS-COSMOS-NBH-S12-292 | 09 57 47.33 | +01 51 53.1 | 20.51 ± 0.02 | 18.33 ± 0.01 | 12.1 | −15.40 | 77.3 | No |
| HiZELS-COSMOS-NBH-S12-293 | 09 57 47.65 | +02 16 19.8 | 20.84 ± 0.08 | 19.80 ± 0.02 | 3.3 | −15.87 | 101.8 | No |
| HiZELS-UDS-NBH-S12-4012 | 02 16 44.17 | −04 44 53.0 | 20.04 ± 0.18 | 20.93 ± 0.04 | 3.0 | −15.87 | 308 | Yes |
| HiZELS-UDS-NBH-S12-4136 | 02 16 45.35 | −04 07 26.8 | 19.15 ± 0.08 | 19.76 ± 0.02 | 5.2 | −15.64 | 171 | Yes |
A catalogue of all Σ > 3 NBH narrow-band sources selected in the UDS and COSMOS fields from HiZELS. NB magnitudes are NBH (Vega); BB are H magnitudes (Vega). Note that the printed version contains only five example entries, in order to provide some examples contained in the full catalogue. The full catalogue is available online.
| ID . | RA . | Dec. . | NB . | BB . | Σ . | log flux . | EWobs . | Class. as Hα . |
|---|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (Vega) . | (Vega) . | . | (erg s−1) . | (Å) . | . |
| HiZELS-COSMOS-NBH-S12-206 | 09 57 47.31 | +02 02 08.1 | 21.58 ± 0.14 | 20.99 ± 0.05 | 3.1 | −15.98 | 251.4 | No |
| HiZELS-COSMOS-NBH-S12-292 | 09 57 47.33 | +01 51 53.1 | 20.51 ± 0.02 | 18.33 ± 0.01 | 12.1 | −15.40 | 77.3 | No |
| HiZELS-COSMOS-NBH-S12-293 | 09 57 47.65 | +02 16 19.8 | 20.84 ± 0.08 | 19.80 ± 0.02 | 3.3 | −15.87 | 101.8 | No |
| HiZELS-UDS-NBH-S12-4012 | 02 16 44.17 | −04 44 53.0 | 20.04 ± 0.18 | 20.93 ± 0.04 | 3.0 | −15.87 | 308 | Yes |
| HiZELS-UDS-NBH-S12-4136 | 02 16 45.35 | −04 07 26.8 | 19.15 ± 0.08 | 19.76 ± 0.02 | 5.2 | −15.64 | 171 | Yes |
| ID . | RA . | Dec. . | NB . | BB . | Σ . | log flux . | EWobs . | Class. as Hα . |
|---|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (Vega) . | (Vega) . | . | (erg s−1) . | (Å) . | . |
| HiZELS-COSMOS-NBH-S12-206 | 09 57 47.31 | +02 02 08.1 | 21.58 ± 0.14 | 20.99 ± 0.05 | 3.1 | −15.98 | 251.4 | No |
| HiZELS-COSMOS-NBH-S12-292 | 09 57 47.33 | +01 51 53.1 | 20.51 ± 0.02 | 18.33 ± 0.01 | 12.1 | −15.40 | 77.3 | No |
| HiZELS-COSMOS-NBH-S12-293 | 09 57 47.65 | +02 16 19.8 | 20.84 ± 0.08 | 19.80 ± 0.02 | 3.3 | −15.87 | 101.8 | No |
| HiZELS-UDS-NBH-S12-4012 | 02 16 44.17 | −04 44 53.0 | 20.04 ± 0.18 | 20.93 ± 0.04 | 3.0 | −15.87 | 308 | Yes |
| HiZELS-UDS-NBH-S12-4136 | 02 16 45.35 | −04 07 26.8 | 19.15 ± 0.08 | 19.76 ± 0.02 | 5.2 | −15.64 | 171 | Yes |
A catalogue of all Σ > 3 NBK narrow-band sources selected in the UDS and COSMOS fields from HiZELS. NB magnitudes are NBK (Vega); BB are K magnitudes (Vega). Note that the printed version contains only five example entries, in order to provide some examples contained in the full catalogue. The full catalogue is available online.
| ID . | RA . | Dec. . | NB . | BB . | Σ . | log flux . | EWobs . | Class. as Hα . |
|---|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (Vega) . | (Vega) . | . | (erg s−1) . | (Å) . | . |
| HiZELS-COSMOS-NBK-S12-2227 | 09 58 14.05 | +02 34 05.1 | 20.26 ± 0.23 | 21.68 ± 0.16 | 3.1 | −16.31 | 728 | Yes |
| HiZELS-COSMOS-NBK-S12-45390 | 10 00 59.58 | +02 44 35.9 | 19.24 ± 0.09 | 19.92 ± 0.04 | 5.4 | −16.09 | 208 | No |
| HiZELS-COSMOS-NBKS12-44193 | 10 00 55.39 | +01 59 55.1 | 19.02 ± 0.06 | 19.68 ± 0.02 | 7.6 | −16.01 | 198 | Yes |
| HiZELS-UDS-NBK-S12-15961 | 02 18 09.03 | −04 47 49.9 | 17.47 ± 0.02 | 18.27 ± 0.01 | 30.6 | −15.33 | 262 | Yes |
| HiZELS-UDS-NBK-S12-22618 | 02 18 53.02 | −05 01 07.7 | 19.36 ± 0.10 | 20.02 ± 0.02 | 4.5 | −16.16 | 196 | No |
| ID . | RA . | Dec. . | NB . | BB . | Σ . | log flux . | EWobs . | Class. as Hα . |
|---|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (Vega) . | (Vega) . | . | (erg s−1) . | (Å) . | . |
| HiZELS-COSMOS-NBK-S12-2227 | 09 58 14.05 | +02 34 05.1 | 20.26 ± 0.23 | 21.68 ± 0.16 | 3.1 | −16.31 | 728 | Yes |
| HiZELS-COSMOS-NBK-S12-45390 | 10 00 59.58 | +02 44 35.9 | 19.24 ± 0.09 | 19.92 ± 0.04 | 5.4 | −16.09 | 208 | No |
| HiZELS-COSMOS-NBKS12-44193 | 10 00 55.39 | +01 59 55.1 | 19.02 ± 0.06 | 19.68 ± 0.02 | 7.6 | −16.01 | 198 | Yes |
| HiZELS-UDS-NBK-S12-15961 | 02 18 09.03 | −04 47 49.9 | 17.47 ± 0.02 | 18.27 ± 0.01 | 30.6 | −15.33 | 262 | Yes |
| HiZELS-UDS-NBK-S12-22618 | 02 18 53.02 | −05 01 07.7 | 19.36 ± 0.10 | 20.02 ± 0.02 | 4.5 | −16.16 | 196 | No |
A catalogue of all Σ > 3 NBK narrow-band sources selected in the UDS and COSMOS fields from HiZELS. NB magnitudes are NBK (Vega); BB are K magnitudes (Vega). Note that the printed version contains only five example entries, in order to provide some examples contained in the full catalogue. The full catalogue is available online.
| ID . | RA . | Dec. . | NB . | BB . | Σ . | log flux . | EWobs . | Class. as Hα . |
|---|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (Vega) . | (Vega) . | . | (erg s−1) . | (Å) . | . |
| HiZELS-COSMOS-NBK-S12-2227 | 09 58 14.05 | +02 34 05.1 | 20.26 ± 0.23 | 21.68 ± 0.16 | 3.1 | −16.31 | 728 | Yes |
| HiZELS-COSMOS-NBK-S12-45390 | 10 00 59.58 | +02 44 35.9 | 19.24 ± 0.09 | 19.92 ± 0.04 | 5.4 | −16.09 | 208 | No |
| HiZELS-COSMOS-NBKS12-44193 | 10 00 55.39 | +01 59 55.1 | 19.02 ± 0.06 | 19.68 ± 0.02 | 7.6 | −16.01 | 198 | Yes |
| HiZELS-UDS-NBK-S12-15961 | 02 18 09.03 | −04 47 49.9 | 17.47 ± 0.02 | 18.27 ± 0.01 | 30.6 | −15.33 | 262 | Yes |
| HiZELS-UDS-NBK-S12-22618 | 02 18 53.02 | −05 01 07.7 | 19.36 ± 0.10 | 20.02 ± 0.02 | 4.5 | −16.16 | 196 | No |
| ID . | RA . | Dec. . | NB . | BB . | Σ . | log flux . | EWobs . | Class. as Hα . |
|---|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (Vega) . | (Vega) . | . | (erg s−1) . | (Å) . | . |
| HiZELS-COSMOS-NBK-S12-2227 | 09 58 14.05 | +02 34 05.1 | 20.26 ± 0.23 | 21.68 ± 0.16 | 3.1 | −16.31 | 728 | Yes |
| HiZELS-COSMOS-NBK-S12-45390 | 10 00 59.58 | +02 44 35.9 | 19.24 ± 0.09 | 19.92 ± 0.04 | 5.4 | −16.09 | 208 | No |
| HiZELS-COSMOS-NBKS12-44193 | 10 00 55.39 | +01 59 55.1 | 19.02 ± 0.06 | 19.68 ± 0.02 | 7.6 | −16.01 | 198 | Yes |
| HiZELS-UDS-NBK-S12-15961 | 02 18 09.03 | −04 47 49.9 | 17.47 ± 0.02 | 18.27 ± 0.01 | 30.6 | −15.33 | 262 | Yes |
| HiZELS-UDS-NBK-S12-22618 | 02 18 53.02 | −05 01 07.7 | 19.36 ± 0.10 | 20.02 ± 0.02 | 4.5 | −16.16 | 196 | No |
Supporting Information
Additional Supporting Information may be found in the online version of this article:
Table A1. A catalogue of all Σ > 3 NB921 narrow-band sources selected in the UDS and COSMOS fields from HiZELS. NB magnitudes are NB921 (AB); BB are z′ magnitudes (AB).
Table A2. A catalogue of all Σ > 3 NBJ narrow-band sources selected in the UDS and COSMOS fields from HiZELS. NB magnitudes are NBJ (Vega); BB are J magnitudes (Vega).
Table A3. A catalogue of all Σ > 3 NBH narrow-band sources selected in the UDS and COSMOS fields from HiZELS. NB magnitudes are NBH (Vega); BB are H magnitudes (Vega).
Table A4. A catalogue of all Σ > 3 NBK narrow-band sources selected in the UDS and COSMOS fields from HiZELS. NB magnitudes are NBK (Vega); BB are K magnitudes (Vega) (Supplementary Data).
Please note: Oxford University Press are not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.



