Filamentary accretion cannot explain the orbital poles of the Milky Way satellites Free

Abstract

1 INTRODUCTION

The satellite galaxies of the Milky Way (MW) are distributed in a highly inclined plane around the MW disc (Lynden-Bell 1976; Kroupa, Theis & Boily 2005), termed the disc of satellites (DoS). This is true individually for the 11 ‘classical’ satellites (Metz, Kroupa & Jerjen 2007) as well as for the fainter ones detected in the Sloan Digital Sky Survey (Kroupa et al. 2010). In addition, globular clusters of the MW categorized as young halo clusters populate the same plane, and streams of stars and gas show a preference to align with it, too, thus being evidence for a vast polar structure (VPOS) around the MW (Pawlowski, Pflamm-Altenburg & Kroupa 2012).

This strong spatial anisotropy is supported by the motions of these satellite galaxies. Using proper-motion measurements, Metz, Kroupa & Libeskind (2008, M08 hereafter) have derived the orbital poles (directions of angular momenta) for eight satellite galaxies. They found a strong alignment of six orbital poles close to the normal vector to the DoS, indicating that it is rotationally supported. In addition, the Sculptor dwarf galaxy is counter-orbiting, but also within the DoS. Thus, seven of eight satellites with measured proper motions have aligned orbital axes.

Several attempts have been made to explain the aforementioned spatial and orbital anisotropy within the standard model of cosmology. Dwarf galaxies might be accreted in groups (Li & Helmi 2008; D’Onghia & Lake 2008), but Metz et al. (2009) have shown that such groups, observed extra-Galactic dwarf galaxy associations, are far too extended to explain the thin DoS structure. Comparing the orbital energy of MW satellites with dark matter subhaloes from the Via Lactea II simulation, Rocha, Peter & Bullock (2011) find a wide spread in satellite infall times. This is in conflict with a collective accretion of the satellites in a single group. A common infall of MW satellites as former satellite galaxies of the Large Magellanic Cloud (LMC) is investigated by Nichols et al. (2011), who conclude that ‘the extended disk-of-satellites cannot be explained by the dwarfs being bound to the LMC within the last two apogalacticons, and may have another origin’. Therefore, the idea of a group of galaxies centred on the LMC which was accreted is strongly disfavoured.

Libeskind et al. (2009) demonstrate that it is in principle possible that dark matter (DM) dominated satellites are similarly aligned as the most luminous MW satellites. However, this was shown to be an unsatisfactory solution, since Kroupa et al. (2010) demonstrated that their results indicate that only 0.4 per cent of all existing cold dark matter (CDM) haloes of MW mass would host a galaxy similar to the MW with a similar spatial distribution of satellites. Furthermore, Libeskind et al. (2009) only resolve very massive subhaloes (over 2.6 × 10⁹ M_⊙), which is inconsistent with the lower dynamical mass estimates of most MW satellites (Mateo 1998; Walker et al. 2007; Strigari et al. 2008). The significant overabundance of predicted bright satellites compared to observations has first been identified by Bovill & Ricotti (2011) and termed the ‘bright satellite problem’. In addition to this discrepancy in absolute numbers, Kroupa et al. (2010) have shown the inconsistency of the predicted mass functions of luminous subhaloes with that of observed MW satellite galaxies.

A series of logically incompatible conclusions have been reached by authors working in the ΛCDM framework attempting to explain the MW satellite population: Nichols & Bland-Hawthorn (2011) argue that the dwarf spheroidal (dSph) satellites had to have fallen in at a redshift of z > 3 in order for their gas content to be removed by means of tidal and ram-pressure stripping, while Deason et al. (2011) argue that the same dSph satellites must have fallen in recently in order for them to form the DoS and they discuss an example of group infall at z= 0.6. Apart from these mutually exclusive results, it has transpired that the proper motions of dSph satellites exclude infall (Angus, Diaferio & Kroupa 2011). From Via Lactea II data, Hensler & Petrov (in preparation) model the subhalo system around the MW and demonstrate that all DM subhaloes should experience star formation, do not suffer tidal disruption, but only ram-pressure gas loss, and survive as faint dSphs. The most important issues are that all satellite dSph galaxies with subhalo masses larger than 10⁶ M_⊙ have present-day surface brightnesses detectable by SDSS data and are isotropically distributed.

In one of the most recent attempts at explaining the DoS within ΛCDM, Lovell et al. (2011, L11 hereafter) have reported that CDM simulations naturally lead to satellites coherently rotating in quasi-planar distributions, such as the satellites of the MW. They calculated the directions of orbital angular momenta of DM subhaloes in six galactic high-resolution haloes taken from the Aquarius project (Springel et al. 2008). These are CDM simulations of similar halo masses to the assumed DM halo of the MW. Six different models have been analysed at resolution level 2, called Aq-A2 to Aq-F2. For details on the cosmological simulations and the method of determining subhalo angular momenta, the reader is referred to L11. In that paper, while using the results to interpret the MW data, a quantitative test showing whether or not the angular momenta of the subhaloes could feasibly represent the distribution of MW satellites was not given.1 Here we make that test, in particular because the L11 results have been used to argue that the DoS is naturally explained within ΛCDM (e.g. Keller, Mackey & Da Costa 2012).

Motivated by the DoS and the apparently coherent orbits of the satellite galaxies within it, an alternative scenario of their origin has been proposed (Lynden-Bell 1976; Kroupa et al. 2005, 2010; Metz et al. 2008). They might be tidal dwarf galaxies (TDGs), formed from the tidal debris in an encounter between the early MW and another, still gas-rich (proto-) galaxy (Zwicky 1956). Galaxy collisions can lead to perpendicularly oriented discs of debris, with aligned orbits as well as counter-orbiting material as demonstrated in Pawlowski, Kroupa & de Boer (2011, hereafter P11). Such encounters are observed even in the present epoch, for example in the interacting system VV 340 (Armus et al. 2009). TDGs are found to form both in simulated (Bournaud & Duc 2006; Wetzstein, Naab & Burkert 2007; Bournaud, Duc & Emsellem 2008) and observed (Mirabel, Dottori & Lutz 1992; Hunsberger, Charlton & Zaritsky 1996; Weilbacher, Duc & Fritze-v. Alvensleben 2003) galaxy collisions. They seem to be long-lived objects (Kroupa 1997; Recchi et al. 2007; Galianni et al. 2010; Duc et al. 2011) and share the same properties as dwarf elliptical (dE) galaxies (Dabringhausen et al., in preparation). This makes them a fundamental addition, if not even an alternative, to cosmologically formed dwarf galaxies. In fact, that TDGs may be the dominant satellite dwarf galaxy population should be a necessary outcome of ΛCDM structure formation (Okazaki & Taniguchi 2000).

Here, a new method is presented which determines how likely it is to find as strongly a clustered distribution of orbital angular momentum vectors similarly close to the equator of the MW as the MW satellite orbital poles, if the angular momenta of the satellite population were drawn from the distributions in given models. This method is then applied to the angular momentum directions of ΛCDM subhaloes as determined and published by L11, to those derived from the two Via Lactea simulations (Diemand, Kuhlen & Madau 2007; Diemand et al. 2008) and to those of tidal debris as determined from models of galaxy interactions. Section 2 describes the assumptions, the observed situation, the models and the method. In Section 3 the results are presented, followed by the conclusions in Section 4.

2 ANALYSIS

2.1 Assumed galactic disc orientation in a DM halo

It is generally assumed that the angular momentum of the baryonic disc galaxy aligns with the angular momentum of the DM halo in which it resides. This assumption seems to be supported by the alignment of the minor axis of the inner part of DM haloes with the axis of the disc galaxies in them (Bailin et al. 2005). Sharma & Steinmetz (2005) find a good correlation between baryonic gas and DM halo spin, with a mean misalignment angle of only 18.°9 at a redshift of 0. The work of Bett et al. (2010) also shows that in simulations it is most likely for a galaxy to have its spin vector aligned with the direction of angular momentum of its parent DM halo. In particular, the angular momentum of the inner halo (0.25 times the virial radius) aligns well with the galaxy spin, the median angle of misalignment being 23.°9. Taking the angular momentum of the whole halo, the median misalignment rises to 34.°4, but still the majority of galaxy spins are close to the main halo spins. Perpendicular orientations are rare (12 per cent within ±15° around the perpendicular orientation according to fig. 17 of Bett et al. 2010), just as are dark haloes in which the inner (≤0.25r_vir) and outer regions are tilted by ≈90°.

In the following, it is therefore assumed that the galaxy rotates in the same direction as the parent halo, in line with what L11 state in their paper. It is assumed that the MW disc spin and the main halo spin in the simulations are parallel. In Section 3.4 the requirement of this most likely alignment will be dropped, instead choosing an orientation of the disc galaxy which is most favourable to the formation of polar orbits, but puts the main haloes spin and disc galaxy spin at an unlikely 90° angle.

2.2 The MW satellite orbital poles

The distribution of the MW satellite orbital poles (M08) shows two characteristic properties. First of all, the orbital poles cluster close to the normal to the MW DoS. The six best-aligned orbital poles show a spherical standard distance (M08) of only ⁠. Secondly, the orbital poles preferentially fall close to the MW equator, the satellites thus move along on polar orbits. This is obvious from the direction of the average orbital pole for the six best-aligned orbital poles; it has an angular distance of only d_MW= 9.°4 from the MW equator.

New proper-motion measurements for the satellite galaxies might lead to updated orbital pole directions, which in turn might change these values. The uncertainties of the orbital poles are the projected uncertainties of the angular momenta of the satellite galaxies. They are dominated by the, often large, uncertainties in the measured proper motions. M08 have shown that the uncertainties in the distance, position and radial velocity of satellite galaxies, the distance of the Sun from the Galactic Centre and the circular velocity of the local standard of rest are negligible compared to the influence of the proper-motion uncertainties on the directions of the orbital poles. But large proper-motion uncertainties do not necessarily result in large orbital-pole uncertainties. What is important for the determination of the orbital pole of a satellite galaxy is the direction of its motion with respect to its position relative to the Galactic Centre, not its velocity.

As a result, the orbital poles of most satellites co-orbiting in the DoS are relatively well defined (directional uncertainties <15°). Only Draco and Carina show large uncertainties. However, their uncertainties fall on great circles passing close to the average orbital pole of these six best-aligned orbital poles (see fig. 1 of M08). This is why, on average, varying their orbital poles within the uncertainties cancels out when determining and d_MW.2 Within the current orbital pole uncertainties, updated proper motions can result in both larger or smaller values for and d_MW, but the changes can be expected to be small. Therefore, in the following analysis the given values for the two parameters are adopted.

Figure 1

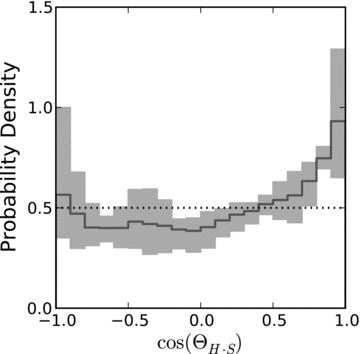
The data of fig. 1 in L11, the cosine of the angle between the main halo spin and the subhalo angular momentum vector Θ_H·S, are plotted here as a histogram (input data courtesy of Mark R. Lovell). For this plot, the subhalo orbital angular momenta of the six individual Aquarius simulations of L11 have been co-added. This results in the black, solid histogram, which gives the average probability density of the six simulations. The variation of the different simulations is illustrated by the grey shaded area. For each bin, it illustrates the maximum and the minimum of the probability density determined for the six Aquarius haloes individually. Note that the sum over all angles (of the area below the histogram) yields a probability of 1.

Open in new tabDownload slide

Fig. 1 is a remake of fig. 1 of L11 using their data. It plots the distribution of the cosine of the angle between the main halo spin and the orbital angular momenta of individual subhaloes, cos Θ_H·S. All models peak close to cos Θ_H·S= 1, so it is most likely for a subhalo to orbit in the same direction as the main halo. Three of the models also show an overabundance of counter-orbiting subhaloes close to cos Θ_H·S=−1. Overall, the probability density of the simulations lies close to the isotropic case, illustrated by the horizontal dotted line. Corotating orbits are slightly preferred in all simulations. The deviation from the isotropic value is strongest for the bins closest to the DM spin axis, where the difference in probability density is up to a factor of 2. Thus, while there is an overabundance of subhaloes with spins close to the main halo spin, all other spin directions are present in significant fractions.

In addition to the original data, in Fig. 2 we have added the orbital poles of the MW satellites. The upper panel assumes that the spin vector of the DM halo of the MW is parallel to the MW disc spin, pointing to the galactic south pole. The bottom panel assumes that the halo spin coincides with the average orbital pole of the six best-aligned MW satellites. It constitutes the most favourable orientation of the halo to explain the preferred orbital direction of the MW satellites from the simulations.

Figure 2

The same plot as shown in Fig. 1, but note the different range on the Y-axis. In addition, this plot includes the orbital poles of the eight MW satellite galaxies (dashed black histograms with error bars) from M08, generated in the same way as the model histograms. In the upper panel, it is assumed that the spin direction of the MW galaxy aligns with the main halo spin, as L11 have argued. Therefore, the histogram shows the distance of the MW satellite orbital poles measured from the MW south pole. The MW satellites are preferentially on polar orbits, perpendicular to the MW disc spin and by implication to the spin of its supposed DM halo, at odds with the L11 results. In the bottom panel the orientation of the spin of the DM halo of the MW is assumed to be aligned with the average orbital pole of the MW satellite orbital poles from M08. Therefore, the histogram shows the distance of the MW satellite orbital poles measured from Galactic coordinates (l, b) = (177.°0, −9.°4). The MW satellite orbital poles cluster much more than expected from the Aquarius simulations.

Open in new tabDownload slide

In both cases, the observed distribution differs completely from the models. In the first case, the MW satellite orbital poles peak close to cos Θ_H·S= 0, the MW equator. Most of the eight known satellite orbital poles point close to the MW equator, about 90° away from the MW pole. They therefore appear close to the centre of the plot. This is where the model distribution approaches its minimum, in contradiction to the observed distribution. In the second case, the observed orbital poles peak at the bin closest to the main halo spin by construction, which is also the maximum in the model distributions. But the peak contains 50 per cent of the orbital poles and is therefore much higher than all simulated models, which predict only about 10 per cent in this bin.

This illustrates that the observed situation does not follow the model. However, it does not rule out the possibility that the observed orbital poles are drawn from one of the model distributions. The question for which we need a quantitative answer is: How probable is this arrangement?

2.3 Models

This section describes the different models whose angular momentum direction distributions will be analysed using the method presented in the next section. For that, it is necessary to repeatedly draw eight angular momentum directions randomly from their distributions.

2.3.1 Isotropic distribution

Assuming an isotropic distribution of angular momentum directions for satellite galaxies, eight random directions are drawn from a uniform distribution on the sphere. These are used as angular momentum vectors.

2.3.2 Aquarius simulations

To test the results of L11 derived from the Aquarius cosmological simulations, the angular momentum directions are drawn from the distribution of subhalo angular momenta.3 These are shown in their fig. 4. Drawing from the whole population of subhaloes and not only from the subhaloes with the most massive progenitors should not pose a problem for this analysis, as L11 state that the latter trace the same structure of the whole subhalo sample.

Figure 4

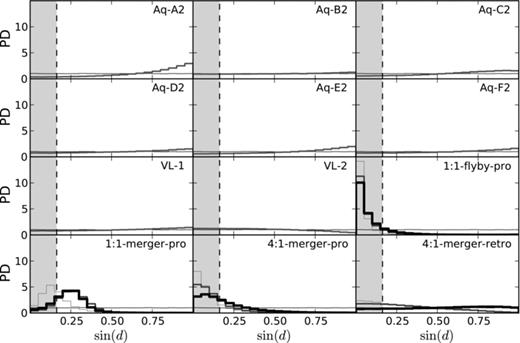
Distributions of the probability density (PD) of the angular distances of the average angular momentum vector from the equator for the six most closely angular momentum vectors out of eight different, randomly drawn angular momentum vectors. Same panels as in Fig. 3. The vertical dashed line indicates the distance of the average orbital pole of the MW satellites from the equator of the MW, d= 9.°4. To fulfil the orientation criterion, a realization has to fall to the left of this line. As in Fig. 1, the Aquarius and Via Lactea simulations produce results that make it unlikely to find a situation resembling the MW satellite orbital poles. Their subhalo angular momenta preferentially align with the main haloes spin, which is perpendicular to the equator. An exception are the Via Lactea 2 simulations, which show a slight excess at low d. All other cosmological models have a lower number of average angular momenta close to the equator than the isotropic case. Most models of galaxy interactions however naturally come up with average angular momenta of their tidal debris close to the equator, resembling the observed case of the MW satellites.

Open in new tabDownload slide

2.3.3 Via Lactea simulations

To provide a more complete picture of cosmological models, the subhalo angular momentum directions derived from the two Via Lactea simulations (Diemand et al. 2007, 2008, D07 and D08 hereafter) are also analysed. These are cosmological N-body simulations of MW-sized DM haloes with a quiet merger history. They are therefore possible hosts of a MW-type galaxy in a ΛCDM universe. The analysis is based on the data freely available on the website of the Via Lactea project4 for the two models Via Lactea 1 (VL-1; D07) and Via Lactea 2 (VL-2; D08). The subhalo angular momentum directions needed for the analysis are then determined for all subhaloes in the available data set that are within the virial radius.

The halo spin is determined from the provided random sample of 10⁵ particles at redshift zero. The sum of the angular momentum of all particles within 0.25r_vir (VL-1: r_vir= 389 kpc; VL-2: r_vir= 402 kpc; see Kuhlen, Diemand & Madau 2008) is calculated, assuming each particle to have a mass such that the total mass of the simulation is reproduced. Then the sum of the subhalo angular momenta within the same radius is subtracted from the average particle angular momentum, which only leads to a small correction in the average spin direction of 1.°8 (VL-1) and 11.°4 (VL-2). The direction of the resulting vector is then adopted as the (inner) halo spin direction, which is more closely aligned with the disc galaxy spin as discussed in Section 2.1. This procedure is less sophisticated than the analysis L11 use, but can be easily done with the freely available data of the Via Lactea simulations and should give an estimate of the spin direction of the main DM halo.

2.3.4 Tidal models

In addition to the cosmological simulations, models of a tidal origin for the MW satellites presented by P11 are analysed. In these models, a target disc galaxy collides with a perpendicularly oriented infalling disc galaxy on a polar orbit. P11 included equal-mass and 4:1 mass ratios for target-to-infalling galaxy. During the interaction, material is stripped off from the infalling galaxy and forms a disc of debris around the target galaxy, within which TDGs can form. Two populations of tidal debris form in most models, having prograde and retrograde orbits with respect to the orbit of the infalling galaxy. The models therefore not only produce orbits similar to the majority of those described by the satellite galaxy orbital poles, but can also account for the counter-orbiting direction of the Sculptor dwarf galaxy.

The distributions of angular momentum directions for these models are drawn from the tidal material, so from the angular momentum directions of individual particles. To show the evolution of the angular momentum distributions, three time steps representing 5.0, 7.5 and 10.0 Gyr after the beginning of the model calculations are considered. These are chosen to be well after the initial perigalactic passage of the two galaxies and, in the merger case, also after the final collision that happens after 2.5–4 Gyr. To include their angular momentum direction in the analysis, the particles are required to have a distance of at least 30 kpc from the central galaxy in order to avoid material from the galactic disc. If the model leads to a merger, particles with distances of up to 400 kpc are considered, while in a fly-by encounter particles can have distances from the target galaxy of up to half the distance between the two interacting galaxies.

The results of all models from P11 are compiled in Appendix A. In the following, four models will be discussed in detail. The four particular models have not been chosen to give the best results, but to show the typical range of fractions determined for the tidal models of P11. They include two 1:1 mass ratio models with the infalling galaxy-oriented prograde, one which results in a fly-by (‘1:1-flyby-pro’, called 5deg200vel in P11) and one resulting in a merger (‘1:1-merger-pro’, 7.5deg100vel in P11) of the two colliding galaxies. In addition, two 4:1 mass ratio merger models are included. One of these (‘4:1-merger-pro’, 7.5deg100vel in P11), having a prograde infalling galaxy, is one of the models with a good agreement. The other model (‘4:1-merger-retro’, 10deg100vel in P11) has an infalling galaxy in retrograde orientation and results in the worst agreement with the MW orbital poles of all tidal models. The reason is that, while the model forms a very long tidal tail of more than 300 kpc, it is dominated by a spheroid-like distribution of tidal particles out to about 50 kpc.

2.4 Method

To assess how likely it is to find a similar distribution of angular momentum directions as inferred from the eight MW satellite galaxies, it has to be estimated how often similar parameters can be produced by a given model. For this, a subsample of eight different angular momentum directions is drawn from the distribution of angular momentum directions in the model tested.

Of the eight known orbital poles of the MW satellites, six are aligned with each other and the DoS normal direction. Analogously, for each possible combination of six out of the eight angular momentum directions drawn from the models, the mean direction of the angular momenta is determined. Centred on these average directions, the spherical standard distance Δ_sph (Metz et al. 2007) of the six corresponding angular momentum directions is calculated. It is defined as

where are the angular momentum direction unit vectors, 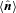is the unit vector pointing into their mean direction and ‘·’ denotes the scalar product of the vectors. Note that the formula in Metz et al. (2007) deals with axial data and therefore has to take the absolute value of the scalar product, in contrast to our case. Δ_sph is a measure for the clustering of orbital poles around their average direction. The sample of six angular momentum directions leading to the smallest Δ_sph is chosen. These are called the six best-aligned angular momenta from the sample of eight. The value for the average angular momentum direction and the spherical standard distance of these best-aligned angular momenta is stored. The spherical standard distance will be used for the clustering criterion in Section 3.1.

Finally, the angular distance d of the average angular momentum direction of the six best-aligned angular momenta to the equator of the model is computed. In the isotropic case, the ‘equator’ is an arbitrary great circle as there is no preferred direction available. The great circle 90° away from the main halo spin is referred to as the ‘equator’ in the Aquarius and Via Lactea simulations, because the main halo spin aligns with the galactic disc spin, as discussed in Section 2.1. In the case of the galaxy-interaction models, the ‘equator’ is the plane of the target galaxy which resembles the orientation of the MW disc. The angular distance to the equator is used in the orientation criterion in Section 3.2, assessing whether the average angular momentum hints at polar orbits or not.

When this algorithm is applied to the eight orbital poles of satellite galaxies of the MW, the same six satellite galaxies as reported by M08 are found to have the best-aligned orbital poles. Consequently, the algorithm gives the same parameters as reported by M08: and d_MW= 9.°4.

This process of drawing eight angular momentum directions and determining the parameters Δ_sph and d for the best-aligned subsample of six of these is called one realization. To determine the statistical properties, 10⁵ different realizations are produced for each model. The resulting distributions of the two parameters are shown in Figs 3 and 4.

Figure 3

Distributions of the probability density (PD) of the spherical standard distance Δ_sph of the six most closely aligned angular momentum vectors out of eight different, randomly drawn angular momentum vectors. In the first eight panels, the angular momentum vectors are drawn from the subhalo angular momentum vectors of the Aquarius simulations presented by L11 and from the Via Lactea simulations by D07 and D08. The last four panels show the distribution that results when drawing angular momentum vectors from the particles in calculations of galaxy interactions by P11. They each contain three distributions showing the time evolution of each model. The thin, light grey histogram illustrates the situation at 5 Gyr after the start of the calculation, the dark grey histogram at 7.5 Gyr and the thick black histogram at 10 Gyr. The case of an isotropic sample of angular momenta is included as the thin black line in all panels for comparison. The spherical standard distance for the six best-fitting orbital poles in the MW, 35.°4, is indicated by the vertical dashed lines. To fulfil the clustering criterion, a realization has to fall to the left of this line, this allowed region being highlighted by a shading. The distributions resulting from the cosmological simulations are nearly indistinguishable from the isotropic case. The vast majority of determined spherical standard distances is significantly larger than the observed one. This is completely different for the most examples of tidal material, which show very strongly concentrated distributions of angular momentum directions, in agreement with the distribution inferred from the MW satellite galaxies.

Open in new tabDownload slide

The method can be easily adjusted once more than eight satellite galaxy orbital poles become available through observations of proper motions. The number of angular momenta drawn for one realization (currently eight) would need to be increased, the number of best-aligned poles (currently six) might be changed, and the parameters and d_MW= 9.°4 adjusted to the observed situation. Note also that the analysis does not account for the alignment of the orbital poles with the DoS normal, nor does it factor in that the Sculptor satellite galaxy is counter-orbiting with respect to the six best-aligned orbital poles, but also orbiting in the DoS. If more satellite galaxies on counter-orbits are found, the analysis might need to be adjusted to account for this, e.g. by analysing not the directions of angular momenta but the orbital axes (given by the angular momentum direction and its counter direction), thus in effect combining co-orbiting and counter-orbiting poles on one half-sphere.

3 RESULTS

The results are listed in Table 1, together with the total numbers of individual angular momentum directions of each model. In addition and for completeness, the results for all tidal models of P11 are compiled in Appendix A.

Table 1

Open in new tab

Models and resulting fractions of realizations fulfilling the criteria.

Model	Reference	N			fΔ (per cent)	fd (per cent)	fboth (per cent)	findep (per cent)
Aquarius A2	L11	30 177	52.3	53.4	8.20 ± 0.09	6.00 ± 0.08	0.10 ± 0.01	0.49
Aquarius B2	L11	31 050	53.3	53.8	4.00 ± 0.06	14.83 ± 0.12	0.44 ± 0.02	0.59
Aquarius C2	L11	24 628	51.2	52.1	9.49 ± 0.10	9.28 ± 0.10	0.22 ± 0.01	0.88
Aquarius D2	L11	36 006	53.4	54.2	4.53 ± 0.07	12.39 ± 0.11	0.40 ± 0.02	0.56
Aquarius E2	L11	30 372	53.2	54.0	5.24 ± 0.07	9.68 ± 0.10	0.36 ± 0.02	0.51
Aquarius F2	L11	35 041	52.1	52.7	5.40 ± 0.07	12.16 ± 0.11	0.44 ± 0.02	0.66
Via Lactea 1	D07	2576	53.2	53.9	4.26 ± 0.07	12.86 ± 0.11	0.41 ± 0.02	0.55
Via Lactea 2	D08	9381	53.1	54.1	6.62 ± 0.08	20.28 ± 0.14	1.49 ± 0.02	1.34
Isotropic	This paper	∞	54.0	54.6	3.00 ± 0.05	16.41 ± 0.13	0.47 ± 0.02	0.49
1:1-flyby-pro (5 Gyr)	P11	5821	31.3	7.8	60.13 ± 0.25	91.12 ± 0.30	60.11 ± 0.25	54.80
1:1-flyby-pro (7.5 Gyr)	P11	5841	31.7	14.3	59.06 ± 0.24	86.79 ± 0.29	58.48 ± 0.24	51.25
1:1-flyby-pro (10 Gyr)	P11	5756	31.6	20.4	58.39 ± 0.24	84.08 ± 0.29	57.27 ± 0.24	49.09
1:1-merger-pro (5 Gyr)	P11	36 438	22.4	9.9	74.36 ± 0.27	59.10 ± 0.24	48.40 ± 0.22	43.94
1:1-merger-pro (7.5 Gyr)	P11	35 954	21.5	12.1	79.27 ± 0.28	15.06 ± 0.12	8.96 ± 0.09	11.94
1:1-merger-pro (10 Gyr)	P11	37 302	22.8	12.2	77.42 ± 0.28	20.77 ± 0.14	12.03 ± 0.11	16.08
4:1-merger-pro (5 Gyr)	P11	93 940	17.8	8.7	82.30 ± 0.29	82.84 ± 0.29	74.69 ± 0.27	68.18
4:1-merger-pro (7.5 Gyr)	P11	80 454	18.4	14.2	88.73 ± 0.30	74.52 ± 0.27	70.58 ± 0.27	66.12
4:1-merger-pro (10 Gyr)	P11	77 768	25.4	22.8	73.89 ± 0.27	53.22 ± 0.23	46.45 ± 0.22	39.33
4:1-merger-retro (5 Gyr)	P11	75 431	46.2	49.3	33.58 ± 0.18	36.17 ± 0.19	19.22 ± 0.14	12.15
4:1-merger-retro (7.5 Gyr)	P11	60 248	47.8	49.1	16.20 ± 0.13	28.92 ± 0.17	6.97 ± 0.08	4.69
4:1-merger-retro (10 Gyr)	P11	61 157	50.4	51.1	8.11 ± 0.09	13.17 ± 0.11	1.04 ± 0.03	1.07

Model	Reference	N			fΔ (per cent)	fd (per cent)	fboth (per cent)	findep (per cent)
Aquarius A2	L11	30 177	52.3	53.4	8.20 ± 0.09	6.00 ± 0.08	0.10 ± 0.01	0.49
Aquarius B2	L11	31 050	53.3	53.8	4.00 ± 0.06	14.83 ± 0.12	0.44 ± 0.02	0.59
Aquarius C2	L11	24 628	51.2	52.1	9.49 ± 0.10	9.28 ± 0.10	0.22 ± 0.01	0.88
Aquarius D2	L11	36 006	53.4	54.2	4.53 ± 0.07	12.39 ± 0.11	0.40 ± 0.02	0.56
Aquarius E2	L11	30 372	53.2	54.0	5.24 ± 0.07	9.68 ± 0.10	0.36 ± 0.02	0.51
Aquarius F2	L11	35 041	52.1	52.7	5.40 ± 0.07	12.16 ± 0.11	0.44 ± 0.02	0.66
Via Lactea 1	D07	2576	53.2	53.9	4.26 ± 0.07	12.86 ± 0.11	0.41 ± 0.02	0.55
Via Lactea 2	D08	9381	53.1	54.1	6.62 ± 0.08	20.28 ± 0.14	1.49 ± 0.02	1.34
Isotropic	This paper	∞	54.0	54.6	3.00 ± 0.05	16.41 ± 0.13	0.47 ± 0.02	0.49
1:1-flyby-pro (5 Gyr)	P11	5821	31.3	7.8	60.13 ± 0.25	91.12 ± 0.30	60.11 ± 0.25	54.80
1:1-flyby-pro (7.5 Gyr)	P11	5841	31.7	14.3	59.06 ± 0.24	86.79 ± 0.29	58.48 ± 0.24	51.25
1:1-flyby-pro (10 Gyr)	P11	5756	31.6	20.4	58.39 ± 0.24	84.08 ± 0.29	57.27 ± 0.24	49.09
1:1-merger-pro (5 Gyr)	P11	36 438	22.4	9.9	74.36 ± 0.27	59.10 ± 0.24	48.40 ± 0.22	43.94
1:1-merger-pro (7.5 Gyr)	P11	35 954	21.5	12.1	79.27 ± 0.28	15.06 ± 0.12	8.96 ± 0.09	11.94
1:1-merger-pro (10 Gyr)	P11	37 302	22.8	12.2	77.42 ± 0.28	20.77 ± 0.14	12.03 ± 0.11	16.08
4:1-merger-pro (5 Gyr)	P11	93 940	17.8	8.7	82.30 ± 0.29	82.84 ± 0.29	74.69 ± 0.27	68.18
4:1-merger-pro (7.5 Gyr)	P11	80 454	18.4	14.2	88.73 ± 0.30	74.52 ± 0.27	70.58 ± 0.27	66.12
4:1-merger-pro (10 Gyr)	P11	77 768	25.4	22.8	73.89 ± 0.27	53.22 ± 0.23	46.45 ± 0.22	39.33
4:1-merger-retro (5 Gyr)	P11	75 431	46.2	49.3	33.58 ± 0.18	36.17 ± 0.19	19.22 ± 0.14	12.15
4:1-merger-retro (7.5 Gyr)	P11	60 248	47.8	49.1	16.20 ± 0.13	28.92 ± 0.17	6.97 ± 0.08	4.69
4:1-merger-retro (10 Gyr)	P11	61 157	50.4	51.1	8.11 ± 0.09	13.17 ± 0.11	1.04 ± 0.03	1.07

Column descriptions. Model: name of the model or simulation. Reference: the original publication presenting the respective model (L11: Lovell et al. 2011; D07: Diemand et al. 2007; D08: Diemand et al. 2008; P11: Pawlowski et al. 2011). N: number of angular momentum directions from which to draw realizations. ⁠: mean of the spherical standard distance distribution. ⁠: median of the spherical standard distance distribution. f_Δ: fraction of realizations fulfilling the clustering criterion (having a spherical standard distance of no more than 35.°4, the value for the MW satellites). f_d: fraction of realizations fulfilling the direction criterion (having an average angular momentum direction pointing no further away from the equator than 9.°4, the value for the MW satellites). f_both: fraction of realizations fulfilling both criteria. f_indep=f_Δf_d: fraction fulfilling both criteria if they were independent. All uncertainties are estimated assuming Poisson statistics.

Table 1

Open in new tab

Models and resulting fractions of realizations fulfilling the criteria.

Model	Reference	N			fΔ (per cent)	fd (per cent)	fboth (per cent)	findep (per cent)
Aquarius A2	L11	30 177	52.3	53.4	8.20 ± 0.09	6.00 ± 0.08	0.10 ± 0.01	0.49
Aquarius B2	L11	31 050	53.3	53.8	4.00 ± 0.06	14.83 ± 0.12	0.44 ± 0.02	0.59
Aquarius C2	L11	24 628	51.2	52.1	9.49 ± 0.10	9.28 ± 0.10	0.22 ± 0.01	0.88
Aquarius D2	L11	36 006	53.4	54.2	4.53 ± 0.07	12.39 ± 0.11	0.40 ± 0.02	0.56
Aquarius E2	L11	30 372	53.2	54.0	5.24 ± 0.07	9.68 ± 0.10	0.36 ± 0.02	0.51
Aquarius F2	L11	35 041	52.1	52.7	5.40 ± 0.07	12.16 ± 0.11	0.44 ± 0.02	0.66
Via Lactea 1	D07	2576	53.2	53.9	4.26 ± 0.07	12.86 ± 0.11	0.41 ± 0.02	0.55
Via Lactea 2	D08	9381	53.1	54.1	6.62 ± 0.08	20.28 ± 0.14	1.49 ± 0.02	1.34
Isotropic	This paper	∞	54.0	54.6	3.00 ± 0.05	16.41 ± 0.13	0.47 ± 0.02	0.49
1:1-flyby-pro (5 Gyr)	P11	5821	31.3	7.8	60.13 ± 0.25	91.12 ± 0.30	60.11 ± 0.25	54.80
1:1-flyby-pro (7.5 Gyr)	P11	5841	31.7	14.3	59.06 ± 0.24	86.79 ± 0.29	58.48 ± 0.24	51.25
1:1-flyby-pro (10 Gyr)	P11	5756	31.6	20.4	58.39 ± 0.24	84.08 ± 0.29	57.27 ± 0.24	49.09
1:1-merger-pro (5 Gyr)	P11	36 438	22.4	9.9	74.36 ± 0.27	59.10 ± 0.24	48.40 ± 0.22	43.94
1:1-merger-pro (7.5 Gyr)	P11	35 954	21.5	12.1	79.27 ± 0.28	15.06 ± 0.12	8.96 ± 0.09	11.94
1:1-merger-pro (10 Gyr)	P11	37 302	22.8	12.2	77.42 ± 0.28	20.77 ± 0.14	12.03 ± 0.11	16.08
4:1-merger-pro (5 Gyr)	P11	93 940	17.8	8.7	82.30 ± 0.29	82.84 ± 0.29	74.69 ± 0.27	68.18
4:1-merger-pro (7.5 Gyr)	P11	80 454	18.4	14.2	88.73 ± 0.30	74.52 ± 0.27	70.58 ± 0.27	66.12
4:1-merger-pro (10 Gyr)	P11	77 768	25.4	22.8	73.89 ± 0.27	53.22 ± 0.23	46.45 ± 0.22	39.33
4:1-merger-retro (5 Gyr)	P11	75 431	46.2	49.3	33.58 ± 0.18	36.17 ± 0.19	19.22 ± 0.14	12.15
4:1-merger-retro (7.5 Gyr)	P11	60 248	47.8	49.1	16.20 ± 0.13	28.92 ± 0.17	6.97 ± 0.08	4.69
4:1-merger-retro (10 Gyr)	P11	61 157	50.4	51.1	8.11 ± 0.09	13.17 ± 0.11	1.04 ± 0.03	1.07

Model	Reference	N			fΔ (per cent)	fd (per cent)	fboth (per cent)	findep (per cent)
Aquarius A2	L11	30 177	52.3	53.4	8.20 ± 0.09	6.00 ± 0.08	0.10 ± 0.01	0.49
Aquarius B2	L11	31 050	53.3	53.8	4.00 ± 0.06	14.83 ± 0.12	0.44 ± 0.02	0.59
Aquarius C2	L11	24 628	51.2	52.1	9.49 ± 0.10	9.28 ± 0.10	0.22 ± 0.01	0.88
Aquarius D2	L11	36 006	53.4	54.2	4.53 ± 0.07	12.39 ± 0.11	0.40 ± 0.02	0.56
Aquarius E2	L11	30 372	53.2	54.0	5.24 ± 0.07	9.68 ± 0.10	0.36 ± 0.02	0.51
Aquarius F2	L11	35 041	52.1	52.7	5.40 ± 0.07	12.16 ± 0.11	0.44 ± 0.02	0.66
Via Lactea 1	D07	2576	53.2	53.9	4.26 ± 0.07	12.86 ± 0.11	0.41 ± 0.02	0.55
Via Lactea 2	D08	9381	53.1	54.1	6.62 ± 0.08	20.28 ± 0.14	1.49 ± 0.02	1.34
Isotropic	This paper	∞	54.0	54.6	3.00 ± 0.05	16.41 ± 0.13	0.47 ± 0.02	0.49
1:1-flyby-pro (5 Gyr)	P11	5821	31.3	7.8	60.13 ± 0.25	91.12 ± 0.30	60.11 ± 0.25	54.80
1:1-flyby-pro (7.5 Gyr)	P11	5841	31.7	14.3	59.06 ± 0.24	86.79 ± 0.29	58.48 ± 0.24	51.25
1:1-flyby-pro (10 Gyr)	P11	5756	31.6	20.4	58.39 ± 0.24	84.08 ± 0.29	57.27 ± 0.24	49.09
1:1-merger-pro (5 Gyr)	P11	36 438	22.4	9.9	74.36 ± 0.27	59.10 ± 0.24	48.40 ± 0.22	43.94
1:1-merger-pro (7.5 Gyr)	P11	35 954	21.5	12.1	79.27 ± 0.28	15.06 ± 0.12	8.96 ± 0.09	11.94
1:1-merger-pro (10 Gyr)	P11	37 302	22.8	12.2	77.42 ± 0.28	20.77 ± 0.14	12.03 ± 0.11	16.08
4:1-merger-pro (5 Gyr)	P11	93 940	17.8	8.7	82.30 ± 0.29	82.84 ± 0.29	74.69 ± 0.27	68.18
4:1-merger-pro (7.5 Gyr)	P11	80 454	18.4	14.2	88.73 ± 0.30	74.52 ± 0.27	70.58 ± 0.27	66.12
4:1-merger-pro (10 Gyr)	P11	77 768	25.4	22.8	73.89 ± 0.27	53.22 ± 0.23	46.45 ± 0.22	39.33
4:1-merger-retro (5 Gyr)	P11	75 431	46.2	49.3	33.58 ± 0.18	36.17 ± 0.19	19.22 ± 0.14	12.15
4:1-merger-retro (7.5 Gyr)	P11	60 248	47.8	49.1	16.20 ± 0.13	28.92 ± 0.17	6.97 ± 0.08	4.69
4:1-merger-retro (10 Gyr)	P11	61 157	50.4	51.1	8.11 ± 0.09	13.17 ± 0.11	1.04 ± 0.03	1.07

Column descriptions. Model: name of the model or simulation. Reference: the original publication presenting the respective model (L11: Lovell et al. 2011; D07: Diemand et al. 2007; D08: Diemand et al. 2008; P11: Pawlowski et al. 2011). N: number of angular momentum directions from which to draw realizations. ⁠: mean of the spherical standard distance distribution. ⁠: median of the spherical standard distance distribution. f_Δ: fraction of realizations fulfilling the clustering criterion (having a spherical standard distance of no more than 35.°4, the value for the MW satellites). f_d: fraction of realizations fulfilling the direction criterion (having an average angular momentum direction pointing no further away from the equator than 9.°4, the value for the MW satellites). f_both: fraction of realizations fulfilling both criteria. f_indep=f_Δf_d: fraction fulfilling both criteria if they were independent. All uncertainties are estimated assuming Poisson statistics.

3.1 Fulfilling the clustering criterion

Fig. 3 plots the resulting distributions of the spherical standard distances Δ_sph for the analysed models. The isotropic distribution peaks at about 55° and is spread between 30° and 75°.

The six Aquarius and the two Via Lactea simulations lead to Δ_sph-distributions that are nearly indistinguishable from the isotropic distribution. The mean value of the spherical standard distances, ⁠, is slightly lower, by up to about 3° compared to the isotropic case having ⁠.

The first three tidal models, in contrast, show a completely different behaviour in their Δ_sph-distributions. They display a very strong peak at 5°–15° in all three time steps. This peak gets lower for later time steps in all three models, showing that the angular momentum distributions widen with time. Their mean values stay relatively constant at 31° (1:1-flyby-pro), 22° (1:1-merger-pro) and 18°–25° (4:1-merger-pro). This shows that the tidal models result in much more concentrated distributions of orbital poles than the Aquarius and Via Lactea simulations. They are qualitatively very different from the isotropic case and the concentration is stable for at least half a Hubble time. The Δ_sph-distributions show tails spreading out to almost 90°. These arise from the fact that the angular momenta of the tidal debris cluster in two opposite directions, both being close to the central galaxy’s equator. In addition to the strong clustering of orbital angular momenta, this prograde and retrograde tidal debris can therefore explain the counter-orbiting direction of the Sculptor dwarf galaxy. However, this additional aspect of the tidal models being consistent with the observed situation is not considered by the present analysis.

The Δ_sph-distribution of the last tidal model (4:1-merger-retro) approaches an isotropic-like shape for the last time steps. This illustrates that the spheroid-like distribution of the merger remnant is dominating the angular momentum directions. On average, the distribution is only minimally more concentrated than those of the cosmological models.

The orbital directions of satellite galaxies can be changed by a number of processes, like scattering with other satellite galaxies (which might explain the energetic orbit of Sagittarius; see Zhao 1998), precession due to non-axisymmetric potentials or tidal torques from neighbouring galaxies. For a clustered distribution of orbital poles, these processes lead to an increase of the spherical standard distances. Therefore, the observed Δ_sph-value of the MW satellites can be interpreted as an upper limit. It might have been smaller in the past, but not larger.

To fulfil the clustering criterion, a realization has to be at least as well clustered as the MW satellite orbital poles. The Δ_sph-value of the MW satellites, 35.°4, is illustrated in Fig. 3 by the vertical dashed line. All realizations with Δ_sph≤ 35.°4 are counted as passing the clustering criterion. Their number divided by the total number of realizations per model is f_Δ, the fraction of realizations that fulfil the clustering criterion. The values of f_Δ are compiled in Table 1 for all models shown in the plot.

In the isotropic case, only 3 per cent of the realizations fulfil the clustering criterion. As can be expected from the longer tail towards lower Δ_sph-values in the Aquarius simulations, the fractions of realizations passing the clustering criterion are higher. However, this is not a strong effect; the increase compared to the value of isotropy is only a factor of 1.3 - 3.2. It might thus be concluded that filamentary accretion can account for a minor increase in the concentration of angular momenta distributions of subhaloes. The Via Lactea simulations lead to clustering results similar to those of the Aquarius simulations.

Strongly clustered distributions of angular momentum directions arise naturally in tidal interactions. The first three tidal models easily fulfil the clustering criterion, for each time step more than half of all realizations have Δ_sph≤ 35.°4: about 60 per cent in model 1:1-flyby-pro, 75 per cent in 1:1-merger-pro and 80 per cent in the 4:1-merger-pro. There is only a small variation with time: f_Δ tends to become lower with time (also compare the averages for all P11 models in Tables A1 and A2).

The last tidal model (4:1-merger-retro) starts with f_Δ of 34 per cent at 5 Gyr, but this value drops to only 8 per cent for the last time step, where it is comparable to f_Δ of the cosmological models. This shows that the initially clustered distribution of angular momentum directions in this model quickly disperses because the spheroid-like component of the merger remnant dominates over the tidal tail material. If only the tidal tail particles are included in the analysis by demanding a minimum distance from the galactic centre of 60 kpc, f_Δ becomes 28 per cent for the final time step. This fraction is still relatively small compared to that of the other tidal models.

The clustering criterion is completely independent of the orientation of the main galaxy. It alone already shows that reproducing the orbital-pole distribution of the MW satellites in the Aquarius and Via Lactea simulations is very unlikely.

3.2 Fulfilling the orientation criterion

The distribution of angular distances d of the average angular momentum from the respective equator of the model is plotted in Fig. 4. The plot in fact shows sin (d), as this results in bins representing rings of equal area measured from the equator. This gives a flat distribution for the isotropic case and therefore eases the comparison of the various distributions.

All Aquarius simulations have their maximum probability density at the poles, far away from the equator. For the bins close to the equator, their probability densities lie below the line corresponding to the isotropic case. They are therefore less likely to produce an average angular momentum vector close to the equator than the isotropic case. This results from the preferred alignment of subhalo orbits with the axis of the main halo spin, which has been illustrated in Fig. 1. For model Aq-B2, its sin (d) distribution is almost flat, mostly following the isotropic case, but with a minor increase towards the poles.

The Via Lactea models again have a behaviour similar to that of the Aquarius models; however, the VL-2 average angular momentum vectors do not peak close to the pole, but show a small increase towards the equator compared to the isotropic case.

The tidal models again behave differently. Initially (5 Gyr), the sin (d)-distributions of all four have their maximum close to the equator [sin (d) = 0]. They widen slightly for the models 1:1-flyby-pro and 4:1-merger-pro, and the peaks become lower but do not move away from the equator much. This is different for model 1:1-merger-pro, in which the distribution peaks at sin (d) ≈ 0.13 initially (5 Gyr), but moves to sin (d) ≈ 0.25 (d= 14.°5) thereafter (7.5 and 10 Gyr), indicating the precession of the angular momenta of the particles. The distributions of these three models drop to zero for sin (d) > 0.5 (d > 30°) at all time steps. The directions of their average angular momentum vectors thus all align close to the equator of the models. This is different for model 4:1-merger-retro, which has sin (d)-values spreading over the whole range. Its maximum close to the equator is the lowest initially and the sin (d)-distribution of this model approaches the isotropic case for the last time step.

The orientation of the average angular momentum vector of the six best-aligned angular momentum vectors should be close to the equator in order to resemble the case of the polar orbits of the MW satellites, which have an angular distance of the average orbital pole from the MW equator of 9.°4, represented as dashed vertical lines in Fig. 4. To fulfil the orientation criterion, the average angular distance from the equator has to be lower than or equal to this value. The fraction f_d fulfilling this criterion is calculated similar to f_Δ.

The fractions of particles fulfilling the orientation criterion are compiled in Table 1. In the isotropic case, 16 per cent of the realizations are close enough to the equator. As expected, all Aquarius simulations and Via Lactea 1 show lower fractions, by a factor of 1.1 (Aq-B2) up to 2.7 (Aq-A2) less. Only Via Lactea 2 gives a slightly higher fraction, by a factor of 1.2.

The tidal models again give the highest fractions of realizations fulfilling the orientation criterion. In model 1:1-flyby-pro, almost all (84–91 per cent) of the realizations lead to average angular momentum directions close to the equator. In model 1:1-merger-pro, this is only 15–60 per cent, because the peak of its d distribution moves further away from the equator for later time steps. For model 4:1-merger-pro, the fraction is again high (53–83 per cent). In general, the fraction drops for later time steps (see also Tables A1 and A2). The tidal model 4:1-merger-retro starts with a relatively high fraction at 5 Gyr (36 per cent), but this value drops quickly, such that at the final time step it is only 13 per cent, comparable to the cosmological models and lower than the isotropic case. Considering only particles having a distance of at least 60 kpc from the galactic centre gives a higher fraction of 29 per cent at the final time step. This is again at the lower end of the range of values for tidal models.

Doubling the accepted distance from the equator from d_MW= 9.°4 to d= 18.°8 increases f_d in the merger case, leading to 75–92 (1:1-merger-pro) and 81–96 per cent (4:1-merger-retro). It about doubles f_d for the Aquarius and Via Lactea simulations, the isotropic case and the 4:1-mass ratio retrograde merger model, and increases by up to 10 percentage points in the fly-by case.

3.3 Combining the criteria

To resemble the distribution of MW satellite orbital poles, both criteria presented before have to be met simultaneously. If the direction of the average angular momentum and the spherical standard distance would be independent, the combined fraction should simply be the product of the two fractions. If the underlying distribution of angular momentum directions is non-isotropic, this will not be the case any more. Both the actual fraction of realizations that fulfil both criteria, f_both, as well as the expected fraction if the two criteria were completely independent, f_indep, are compiled in Table 1.

As can be expected, in the isotropic model f_both and f_indep are consistent with each other, 0.5 per cent of the realizations give parameters that fulfil both criteria together. It is highly unlikely to find the observed distribution of the MW satellite orbital poles if the satellite orbits were distributed isotropically around the MW.

It has been claimed by L11 that cosmological simulations naturally give rise to ‘[...] distributions of coherently rotating satellites, such as those inferred in the Milky Way [...]’. We tested this claim by determining f_both, finding it to be falsified. All six Aquarius models result in f_both-values that are below the one for the isotropic case. The model displaying the strongest alignment of subhalo angular momenta with the main halo spin, Aq-A2, results in an MW-satellite-like distribution of orbital poles in only 0.1 per cent of the realizations. Averaging over the six Aquarius models gives a likelihood of 0.33 per cent. VL-1 is consistent with the Aquarius models, having f_both= 0.4. Only VL-2 is more likely to reproduce the observed situation than the isotropic case, but still only in 1.5 per cent of the cases. The reason is that our crudely derived halo spin direction (the sum of angular momenta of a subset of particles from the simulation) does not point into the direction in which most subhalo angular momenta point.

Most tidal models, in contrast, result in much higher fractions passing both criteria. In the equal-mass fly-by model (1:1-flyby-pro), f_both is as high as 60 per cent for the first time step. This value is only slightly reduced for the last time step, where it is 57 per cent. Therefore, this model will produce, insofar as we tested, angular momenta distributions with properties similar to that of the MW satellite orbital poles in most of the cases. The equal-mass merger case gives f_both= 48 per cent for the first time step (5 Gyr) and 12 per cent for the last (10 Gyr). While lower than in the fly-by case, this fraction is not low enough to rule out the model and is a factor of 27 larger than that of the best Aquarius simulation in this analysis and 8 times larger than the VL-2 result. The third tidal model (4:1-merger-pro) again gives very high f_both-values, also dropping with time from 75 per cent at 5 Gyr to 46 per cent at 10 Gyr.

Only the last tidal model (4:1-merger-retro) shows low f_both-values, dropping from 19 per cent (5 Gyr) to only 1 per cent (10 Gyr), a value still larger than (but only by a factor of 2–3) the average of the cosmological models. If, however, angular momenta of the particles belonging to the spheroid-like component of the merger remnant are removed by demanding a minimum distance of 60 kpc from the central galaxy, then this model still has an f_both of 13 per cent at the final time step.

As discussed in Section 3.2, doubling the allowed distance from the equator increases f_d and consequently also increases f_both. This leads to f_both= 67 per cent at the final time step for model 1:1-merger-pro and to f_both= 68 for model 4:1-merger-pro. It only slightly changes f_both for the other models, increasing the fraction by one percentage point in the fly-by model and doubling the fractions for the Aquarius and Via Lactea simulations, the isotropic case and the last tidal model (4:1-merger-retro).

Tables A1 and A2 in Appendix A compile the results for all tidal models of P11. High f_both are common; some models even show values as high as 90 per cent or more. The f_both-averages for the different model types slightly decrease with time, but the fractions can increase for some models. Overall, they remain consistent for the different time steps. The f_both-averages are highest in fly-by encounters (67–52 per cent for the investigated equal-mass and 71–41 per cent for the 4:1 mass-ratio models at time steps 5 and 10 Gyr, respectively). Retrograde mergers, on average, produce lower f_both (31–33 per cent and 20–11 per cent) than prograde mergers (41–36 per cent and 44–27 per cent). The statistical properties of the distributions of angular momentum directions in the tidal models are stable over many Gyr. In order to reproduce the observed orbital-pole distribution, it is not necessary to fine-tune the point in time after the galaxy–galaxy interaction.

Taken together, our investigations show that tidal models are capable of naturally accounting for the observed distribution of MW satellite orbital poles. In contrast to that, it can most certainly not be claimed that the Aquarius or Via Lactea models naturally produce the phase-space distribution of the MW satellites. There is no evidence in those ΛCDM models that filamentary accretion can account for the peculiar properties of the MW satellite orbits. Even an isotropic distribution of satellite angular momentum directions has a higher likelihood of accounting for the MW dSph phase-space correlation than all of the Aquarius simulations. Tidal models, however, can reproduce the observed properties with ease.

Are there structures in the Aquarius simulations that resemble the MW satellite system? An answer might be sought in the spatial distribution of the DM subhaloes, as shown in fig. 6 of L11. This figure depicts the positions of all subhaloes, but only those are coloured which have orbital angular momenta aligned close to the axis of the main halo spin (|cos (Θ_H·S)| > 0.9). As these subhaloes all move within approximately the same plane, they form a ‘quasi-planar’ distribution. However, it must not be forgotten that haloes on these orbits are only slightly overabundant, at most by a factor of about 2.3 compared to an isotropic distribution of subhalo angular momentum directions (for Aq-A2, see Fig. 1). The remaining subhaloes are the majority and do not orbit in this plane. Thus, ignoring the suggestive colouring in fig. 6 of L11, it is obvious that the spatial distribution of subhaloes does not resemble that of a disc of satellites but is much wider. The ‘quasi-planar’ distribution of L11 is, in fact, only a subset of the rather ‘quasi-spheroidal’ distribution of DM subhaloes in the Aquarius simulations. There is no mechanism to let luminous satellite galaxies only form in subhaloes selected by their final position around the host halo they end up in. The chance to reproduce the observed, well-pronounced DoS within the Aquarius models must therefore be extremely small. In addition, as discussed in Sections 2.1–2.2, the coloured subhaloes of L11 emphasize a plane most likely oriented perpendicular to the DoS.

3.4 A different equator

Relaxing the demand of the orientation criterion, one might consider the hypothetical situation that the disc galaxy axis in the DM halo does not align with the main halo spin. The most favourable situation for the cosmological simulations would then be the case in which the equator lies where most subhalo angular momentum directions cluster. Therefore, the equator can be defined as the great circle connecting the main halo spin direction and its antipole with the direction in which the highest density of subhalo angular momentum directions is found (see fig. 4 in L11). Would the Aquarius models result in satisfactory f_both-values in this case?

Even in this unlikely and extremely contrived situation for the cosmological models, their f_both values cannot compete with those of the tidal models. The highest value for f_both, 3.6 per cent, is found for Aq-C2. The other models produce lower fractions: 2.7 (Aq-A2), 2.0 (Aq-E2), 1.7 (Aq-D2), 1.5 (Aq-F2) and 0.9 (Aq-B2) per cent. Averaged over the six models, the fraction is increased by only a factor of 6, from 0.33 to 2.1 per cent.