-
PDF
- Split View
-
Views
-
Cite
Cite
A. J. Bird, M. J. Coe, V. A. McBride, A. Udalski, On the periodicities present in the optical light curves of Small Magellanic Cloud Be/X-ray binaries, Monthly Notices of the Royal Astronomical Society, Volume 423, Issue 4, July 2012, Pages 3663–3678, https://doi.org/10.1111/j.1365-2966.2012.21163.x
Close - Share Icon Share
Abstract
We present a comprehensive study of the periodic variations observed in OGLEI-band light curves of Small Magellanic Cloud (SMC) Be/X-ray binaries, discovering new optical periodicities in nine systems. We find that these periodicities are derived from a number of mechanisms, notably disturbance of the decretion disc on the orbital period of the system, and aliased non-radial pulsations. We develop metrics that allow these mechanisms to be distinguished on the basis of the shape of the folded optical light curve, and use these metrics to categorize the periodicities present in ∼50 SMC binary systems. We conclude that extreme care must be taken in the interpretation of the OGLE light curves since only around 30 per cent of the periodicities present can be unambiguously attributed to orbital periods.
1 INTRODUCTION
Be/X-ray binaries are an important subclass of high-mass X-ray binary (HMXB) that consist of a Be star and a neutron star in a binary system. Mass transfer is believed to occur initially via a semi-stable equatorial decretion disc around the Be star, some fraction of which is captured by the neutron star at, or near, its periastron passage. These episodes of mass transfer result in X-ray outbursts, during which the spin period of the neutron star can often be observed. Knowledge of the orbital period of the system is a key diagnostic tool as it allows the system to be placed on the Corbet diagram of Pspin versus Porb (Corbet 1986) that is used to identify the broad classes of HMXB systems. Orbital periods for many Be/X-ray binaries have been determined from period analysis of the X-ray light curves (driven by the spacing of the X-ray outbursts) and Doppler variations in their pulse periods, but are still unknown in many systems. For this reason, ways have been developed to try to use the optical emission as an alternative means to determine the orbital period.
The optical signature of Be/X-ray binaries is derived from a number of components: (i) the Be star itself, (ii) the Be star decretion disc and (iii) any transient accretion disc around the neutron star. The optical light curves of Be/X-ray binaries show considerable differences in the overall form, but often show long-term large variations. Similar, if not identical, effects are seen in isolated Be stars (Mennickent et al. 2002), and so these variations are typically interpreted as due to changes in the decretion disc size.
Periodicities, as opposed to aperiodic long-term variations, in the optical signature are expected from several sources on several time-scales.
Radial and non-radial pulsations of the Be star are often present in the 0.1–2.0 d period range.
Perturbation of the decretion disc by the orbiting neutron star as it passes periastron, indicating the Be-star orbital period, usually in the range 10–500 d.
Semi-stable non-uniformities of the decretion disc, such as disc warping, present on longer (years) time-scales.
The on-going OGLE1 coverage of the Small Magellanic Cloud (SMC), which effectively started with OGLE II in 1996, has provided a wealth of optical (I-band) data on the counterparts to the X-ray binary systems. With essentially daily coverage for most of each year, it has been possible to relate the optical to the X-ray data and frequently explain the characteristics of the X-ray behaviour. In addition, regular periodic behavioural patterns in optical data have, in several instances, been clearly identified with the binary period of the system – see, for example, McGowan et al. (2008) who showed correlated optical and X-ray outbursts every 138 d in SXP46.6. However, Schmidtke, Cowley & Udalski (2006) have indicated that care must be taken when interpreting all modulations as due to binary periods, since it is possible for non-radial pulsations in the Be star to beat with the daily sampling regime and produce peaks in power spectra that may be confused with binary behaviour. Furthermore, there is evidence for possible super-orbital modulation in many of these systems, a phenomenon well characterized by the behaviour of the supergiant system SMC X-1 (see, for example, Trowbridge, Nowak & Wilms 2007) that may further complicate the study of these systems. An extensive study of such possibilities is presented in Rajoelimanana, Charles & Udalski (2011).
In this paper, we present a systematic analysis of the OGLE light curves of 49 SMC Be/X-ray binary systems in which we have searched for both persistent and transient periodic behaviour. We present evidence of both pulsation-related and orbital variations visible in the OGLE light curves from a sample of SMC sources, often transient in nature, and introduce new metrics that allow some differentiation of the various periodic signals in the light curves.
2 DATA ANALYSIS
2.1 The OGLE data sets
The OGLE data sets used in this analysis provide both I-band and V-band photometry. The bulk of this work makes use of the I-band data because it is both much more comprehensive in sampling and we expect that decretion disc emission contributes a significant fraction of the I-band flux. The V-band light curves have been used as supporting data in some analyses.
Some example OGLE I-band light curves are shown in Fig. 1, illustrating various examples of optical variability in SMC binary systems. SXP0.92 shows an essentially stable I-band flux through the 12 yr of OGLE-II and OGLE-III monitoring. 1300 I-band observations were taken with a mean measurement error of δI= 9.3 mmag; the source varied by only ΔI= 85 mmag overall at a mean of I= 16.39. SXP2.37 was covered only by OGLE III, and so has only ∼700 measurement points, but varies by more than one magnitude around a mean of I= 14.88. SXP8.80 shows a similar variation, in this case covered by both OGLE-II and OGLE-III monitoring. SXP756 shows very clear periodic brightening by ΔI∼ 0.5 over a stable level of I∼ 14.6 every ∼350 d.
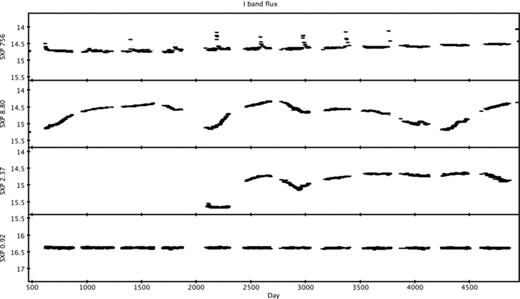
Long-term OGLE-II and OGLE-III I-band light curves for SMC sources. The light curves shown many different overall morphologies typical of Be systems – see Mennickent et al. (2002) for further examples.
Table 1 presents an overview of the data quality and coverage of the I-band and V-band photometry of the 49 objects studied. For each light curve, we indicate the date range covered, the number of data points, the mean magnitude, the average measurement error (δ) and the long-term magnitude range (Δ). Overall, a typical mean I-band magnitude is I∼ 15 with a measurement error δI∼ 7 mmag on each observation.
Basic parameters of 49 OGLE light curves for SMC Be/X-ray binaries. NI is the number of data points in the I-band light curve. I is the mean I-band magnitude. δI is the mean measurement error on the data points for each light curve. ΔI is the overall range of brightness in the light curve (in magnitudes). TJD = JD − 244 0000.5. Equivalent parameters are given for the V-band light curves.
| Source name | TJD range | NI | I (mag) | δI (mmag) | ΔI (mmag) | TJD range | NV | V (mag) | δV (mmag) | ΔV (mmag) |
| SXP2.37 | 2086.9–4868.6 | 707 | 14.89 | 6.2 | 1063 | 3326.6–4795.6 | 55 | 14.80 | 4.0 | 221 |
| SXP2.763 | 2086.9–4868.6 | 711 | 13.94 | 6.0 | 192 | 3326.6–4795.6 | 54 | 14.07 | 4.0 | 57 |
| SXP3.34 | 627.9–4953.9 | 837 | 15.57 | 6.2 | 144 | 673.8–4954.9 | 109 | 15.63 | 6.0 | 129 |
| SXP6.85 | 627.9–4862.6 | 646 | 14.70 | 4.8 | 690 | 665.9–3712.6 | 43 | 14.68 | 6.8 | 322 |
| SXP6.88 | 626.9–4954.9 | 1000 | 15.37 | 6.1 | 164 | 670.9–4954.9 | 99 | 15.56 | 5.3 | 801 |
| SXP7.78 | 2086.9–4952.9 | 762 | 14.79 | 5.1 | 196 | 3326.6–4953.9 | 89 | 14.92 | 4.0 | 75 |
| SXP7.92 | 621.9–4868.6 | 1026 | 13.82 | 4.7 | 647 | 665.9–4801.5 | 90 | 13.85 | 5.4 | 285 |
| SXP8.80 | 466.6–4952.9 | 1094 | 14.71 | 4.8 | 952 | 466.6–4953.9 | 130 | 14.71 | 4.9 | 774 |
| SXP9.13 | 466.0–4954.4 | 1077 | 16.30 | 9.1 | 284 | 466.6–4954.9 | 99 | 16.54 | 7.5 | 126 |
| SXP11.5 | 2203.6–4868.6 | 380 | 15.26 | 6.7 | 1002 | 3654.7–4801.5 | 48 | 15.25 | 4.0 | 596 |
| SXP15.3 | 466.6–4954.9 | 1075 | 14.47 | 4.7 | 250 | 466.1–4954.4 | 93 | 14.68 | 5.2 | 343 |
| SXP18.3 | 466.5–4952.9 | 1111 | 15.51 | 6.3 | 1232 | 466.6–4953.9 | 135 | 15.64 | 5.3 | 862 |
| SXP22.07 | 2104.9–4873.6 | 656 | 14.05 | 6.0 | 137 | 3315.7–4797.6 | 49 | 14.21 | 4.0 | 61 |
| SXP25.5 | 621.8–4954.9 | 1067 | 15.72 | 7.1 | 372 | 645.9–4954.9 | 94 | 15.83 | 6.3 | 400 |
| SXP31.0 | 2104.9–4873.6 | 656 | 15.31 | 6.0 | 197 | 3315.7–4797.6 | 49 | 15.49 | 4.0 | 28 |
| SXP34.08 | 2086.4–4954.4 | 724 | 16.94 | 13.3 | 105 | 3326.6–4954.9 | 69 | 16.84 | 7.6 | 48 |
| SXP46.6 | 2086.4–4954.4 | 1857 | 14.74 | 5.7 | 511 | 3326.6–4954.9 | 148 | 14.80 | 4.0 | 310 |
| SXP59.0 | 626.9–4954.9 | 1560 | 15.41 | 6.4 | 657 | 670.9–4954.9 | 140 | 15.44 | 5.0 | 365 |
| SXP65.8 | 621.9–4862.6 | 589 | 15.73 | 6.8 | 320 | 673.8–3379.6 | 39 | 15.77 | 5.9 | 118 |
| SXP74.7 | 466.5–4954.9 | 1715 | 16.68 | 11.2 | 179 | 467.1–4954.4 | 176 | 16.89 | 7.8 | 167 |
| SXP82.4 | 466.6–4952.9 | 1105 | 15.08 | 5.2 | 845 | 466.6–4953.9 | 131 | 15.21 | 4.8 | 577 |
| SXP91.1 | 2086.9–4865.6 | 713 | 14.78 | 5.3 | 126 | 3326.6–4791.6 | 50 | 15.02 | 4.0 | 86 |
| SXP101 | 2086.9–4954.9 | 737 | 15.61 | 6.9 | 127 | 3326.6–4954.9 | 71 | 15.70 | 4.3 | 67 |
| SXP138 | 2086.9–4952.9 | 762 | 16.11 | 7.8 | 294 | 3326.6–4953.9 | 89 | 16.18 | 5.2 | 125 |
| SXP140 | 2086.9–4954.9 | 724 | 15.52 | 6.6 | 550 | 3326.6–4954.9 | 67 | 15.76 | 4.6 | 371 |
| SXP152.1 | 2086.4–4954.4 | 718 | 15.43 | 6.3 | 182 | 3326.6–4954.9 | 67 | 15.69 | 5.4 | 125 |
| SXP169.3 | 2086.4–4865.1 | 712 | 15.38 | 6.0 | 192 | 3326.6–4791.6 | 50 | 15.57 | 4.7 | 96 |
| SXP172 | 466.6–4954.9 | 1075 | 14.42 | 4.7 | 484 | 466.1–4954.4 | 95 | 14.47 | 5.1 | 169 |
| SXP202A | 621.9–4954.9 | 1040 | 14.65 | 5.4 | 351 | 665.9–4954.9 | 105 | 14.75 | 4.8 | 184 |
| SXP202B | 621.4–4868.1 | 911 | 15.34 | 6.0 | 259 | 670.4–4795.1 | 88 | 15.52 | 5.5 | 181 |
| SXP214 | 466.5–4865.6 | 1060 | 15.22 | 4.2 | 447 | 673.8–4954.9 | 109 | 15.63 | 6.0 | 129 |
| SXP264 | 621.8–4954.9 | 1067 | 15.90 | 7.6 | 283 | 645.9–4954.9 | 94 | 16.09 | 6.5 | 146 |
| SXP280.4 | 2086.9–4954.9 | 728 | 15.38 | 6.1 | 244 | 3326.6–4954.9 | 69 | 15.56 | 4.8 | 198 |
| SXP293 | 621.9–4868.6 | 1037 | 14.57 | 4.7 | 288 | 665.9–4795.6 | 93 | 14.87 | 5.1 | 143 |
| SXP304 | 627.4–4954.4 | 1052 | 15.58 | 6.1 | 68 | 665.9–4954.9 | 102 | 15.75 | 5.9 | 55 |
| SXP323 | 621.3–4954.4 | 1060 | 15.24 | 5.6 | 216 | 466.6–4954.9 | 97 | 15.42 | 6.0 | 261 |
| SXP327 | 2086.9–4952.9 | 762 | 16.75 | 11.6 | 442 | 3326.6–4953.9 | 89 | 16.70 | 5.4 | 213 |
| SXP342 | 2086.4–4954.4 | 1116 | 15.12 | 6.4 | 967 | 3326.6–4954.9 | 116 | 15.16 | 4.1 | 570 |
| SXP348 | 627.9–4953.9 | 688 | 15.10 | 5.2 | 963 | 665.9–4954.9 | 62 | 15.08 | 5.9 | 629 |
| SXP455A | 627.9–4954.9 | 1762 | 15.68 | 6.5 | 718 | 665.4–4954.4 | 193 | 15.63 | 5.3 | 338 |
| SXP504 | 621.3–4868.1 | 1014 | 14.79 | 5.2 | 83 | 670.9–4795.6 | 84 | 15.01 | 5.1 | 69 |
| SXP565 | 628.4–4948.4 | 845 | 15.83 | 7.0 | 224 | 665.9–4948.9 | 78 | 16.02 | 7.0 | 110 |
| SXP645 | 621.8–4868.6 | 1030 | 14.66 | 5.7 | 916 | 670.9–4795.6 | 87 | 14.69 | 4.8 | 132 |
| SXP701 | 621.8–4868.6 | 1030 | 15.70 | 7.1 | 148 | 670.9–4795.6 | 87 | 16.02 | 6.8 | 139 |
| SXP726 | 627.4–4953.4 | 1022 | 15.49 | 5.8 | 128 | 673.8–4954.9 | 127 | 15.66 | 5.7 | 135 |
| SXP756 | 466.6–4954.9 | 1080 | 14.64 | 4.7 | 718 | 466.1–4954.4 | 98 | 14.91 | 5.1 | 402 |
| SXP893 | 466.5–4954.9 | 1080 | 15.95 | 7.7 | 128 | 466.1–4954.4 | 98 | 16.27 | 6.7 | 177 |
| SXP967 | 2104.9–4868.6 | 690 | 14.30 | 6.0 | 633 | 3326.6–4801.6 | 57 | 14.35 | 4.0 | 147 |
| SXP1323 | 627.4–4953.4 | 1021 | 14.57 | 5.7 | 153 | 673.8–4954.9 | 127 | 14.65 | 4.7 | 124 |
| Source name | TJD range | NI | I (mag) | δI (mmag) | ΔI (mmag) | TJD range | NV | V (mag) | δV (mmag) | ΔV (mmag) |
| SXP2.37 | 2086.9–4868.6 | 707 | 14.89 | 6.2 | 1063 | 3326.6–4795.6 | 55 | 14.80 | 4.0 | 221 |
| SXP2.763 | 2086.9–4868.6 | 711 | 13.94 | 6.0 | 192 | 3326.6–4795.6 | 54 | 14.07 | 4.0 | 57 |
| SXP3.34 | 627.9–4953.9 | 837 | 15.57 | 6.2 | 144 | 673.8–4954.9 | 109 | 15.63 | 6.0 | 129 |
| SXP6.85 | 627.9–4862.6 | 646 | 14.70 | 4.8 | 690 | 665.9–3712.6 | 43 | 14.68 | 6.8 | 322 |
| SXP6.88 | 626.9–4954.9 | 1000 | 15.37 | 6.1 | 164 | 670.9–4954.9 | 99 | 15.56 | 5.3 | 801 |
| SXP7.78 | 2086.9–4952.9 | 762 | 14.79 | 5.1 | 196 | 3326.6–4953.9 | 89 | 14.92 | 4.0 | 75 |
| SXP7.92 | 621.9–4868.6 | 1026 | 13.82 | 4.7 | 647 | 665.9–4801.5 | 90 | 13.85 | 5.4 | 285 |
| SXP8.80 | 466.6–4952.9 | 1094 | 14.71 | 4.8 | 952 | 466.6–4953.9 | 130 | 14.71 | 4.9 | 774 |
| SXP9.13 | 466.0–4954.4 | 1077 | 16.30 | 9.1 | 284 | 466.6–4954.9 | 99 | 16.54 | 7.5 | 126 |
| SXP11.5 | 2203.6–4868.6 | 380 | 15.26 | 6.7 | 1002 | 3654.7–4801.5 | 48 | 15.25 | 4.0 | 596 |
| SXP15.3 | 466.6–4954.9 | 1075 | 14.47 | 4.7 | 250 | 466.1–4954.4 | 93 | 14.68 | 5.2 | 343 |
| SXP18.3 | 466.5–4952.9 | 1111 | 15.51 | 6.3 | 1232 | 466.6–4953.9 | 135 | 15.64 | 5.3 | 862 |
| SXP22.07 | 2104.9–4873.6 | 656 | 14.05 | 6.0 | 137 | 3315.7–4797.6 | 49 | 14.21 | 4.0 | 61 |
| SXP25.5 | 621.8–4954.9 | 1067 | 15.72 | 7.1 | 372 | 645.9–4954.9 | 94 | 15.83 | 6.3 | 400 |
| SXP31.0 | 2104.9–4873.6 | 656 | 15.31 | 6.0 | 197 | 3315.7–4797.6 | 49 | 15.49 | 4.0 | 28 |
| SXP34.08 | 2086.4–4954.4 | 724 | 16.94 | 13.3 | 105 | 3326.6–4954.9 | 69 | 16.84 | 7.6 | 48 |
| SXP46.6 | 2086.4–4954.4 | 1857 | 14.74 | 5.7 | 511 | 3326.6–4954.9 | 148 | 14.80 | 4.0 | 310 |
| SXP59.0 | 626.9–4954.9 | 1560 | 15.41 | 6.4 | 657 | 670.9–4954.9 | 140 | 15.44 | 5.0 | 365 |
| SXP65.8 | 621.9–4862.6 | 589 | 15.73 | 6.8 | 320 | 673.8–3379.6 | 39 | 15.77 | 5.9 | 118 |
| SXP74.7 | 466.5–4954.9 | 1715 | 16.68 | 11.2 | 179 | 467.1–4954.4 | 176 | 16.89 | 7.8 | 167 |
| SXP82.4 | 466.6–4952.9 | 1105 | 15.08 | 5.2 | 845 | 466.6–4953.9 | 131 | 15.21 | 4.8 | 577 |
| SXP91.1 | 2086.9–4865.6 | 713 | 14.78 | 5.3 | 126 | 3326.6–4791.6 | 50 | 15.02 | 4.0 | 86 |
| SXP101 | 2086.9–4954.9 | 737 | 15.61 | 6.9 | 127 | 3326.6–4954.9 | 71 | 15.70 | 4.3 | 67 |
| SXP138 | 2086.9–4952.9 | 762 | 16.11 | 7.8 | 294 | 3326.6–4953.9 | 89 | 16.18 | 5.2 | 125 |
| SXP140 | 2086.9–4954.9 | 724 | 15.52 | 6.6 | 550 | 3326.6–4954.9 | 67 | 15.76 | 4.6 | 371 |
| SXP152.1 | 2086.4–4954.4 | 718 | 15.43 | 6.3 | 182 | 3326.6–4954.9 | 67 | 15.69 | 5.4 | 125 |
| SXP169.3 | 2086.4–4865.1 | 712 | 15.38 | 6.0 | 192 | 3326.6–4791.6 | 50 | 15.57 | 4.7 | 96 |
| SXP172 | 466.6–4954.9 | 1075 | 14.42 | 4.7 | 484 | 466.1–4954.4 | 95 | 14.47 | 5.1 | 169 |
| SXP202A | 621.9–4954.9 | 1040 | 14.65 | 5.4 | 351 | 665.9–4954.9 | 105 | 14.75 | 4.8 | 184 |
| SXP202B | 621.4–4868.1 | 911 | 15.34 | 6.0 | 259 | 670.4–4795.1 | 88 | 15.52 | 5.5 | 181 |
| SXP214 | 466.5–4865.6 | 1060 | 15.22 | 4.2 | 447 | 673.8–4954.9 | 109 | 15.63 | 6.0 | 129 |
| SXP264 | 621.8–4954.9 | 1067 | 15.90 | 7.6 | 283 | 645.9–4954.9 | 94 | 16.09 | 6.5 | 146 |
| SXP280.4 | 2086.9–4954.9 | 728 | 15.38 | 6.1 | 244 | 3326.6–4954.9 | 69 | 15.56 | 4.8 | 198 |
| SXP293 | 621.9–4868.6 | 1037 | 14.57 | 4.7 | 288 | 665.9–4795.6 | 93 | 14.87 | 5.1 | 143 |
| SXP304 | 627.4–4954.4 | 1052 | 15.58 | 6.1 | 68 | 665.9–4954.9 | 102 | 15.75 | 5.9 | 55 |
| SXP323 | 621.3–4954.4 | 1060 | 15.24 | 5.6 | 216 | 466.6–4954.9 | 97 | 15.42 | 6.0 | 261 |
| SXP327 | 2086.9–4952.9 | 762 | 16.75 | 11.6 | 442 | 3326.6–4953.9 | 89 | 16.70 | 5.4 | 213 |
| SXP342 | 2086.4–4954.4 | 1116 | 15.12 | 6.4 | 967 | 3326.6–4954.9 | 116 | 15.16 | 4.1 | 570 |
| SXP348 | 627.9–4953.9 | 688 | 15.10 | 5.2 | 963 | 665.9–4954.9 | 62 | 15.08 | 5.9 | 629 |
| SXP455A | 627.9–4954.9 | 1762 | 15.68 | 6.5 | 718 | 665.4–4954.4 | 193 | 15.63 | 5.3 | 338 |
| SXP504 | 621.3–4868.1 | 1014 | 14.79 | 5.2 | 83 | 670.9–4795.6 | 84 | 15.01 | 5.1 | 69 |
| SXP565 | 628.4–4948.4 | 845 | 15.83 | 7.0 | 224 | 665.9–4948.9 | 78 | 16.02 | 7.0 | 110 |
| SXP645 | 621.8–4868.6 | 1030 | 14.66 | 5.7 | 916 | 670.9–4795.6 | 87 | 14.69 | 4.8 | 132 |
| SXP701 | 621.8–4868.6 | 1030 | 15.70 | 7.1 | 148 | 670.9–4795.6 | 87 | 16.02 | 6.8 | 139 |
| SXP726 | 627.4–4953.4 | 1022 | 15.49 | 5.8 | 128 | 673.8–4954.9 | 127 | 15.66 | 5.7 | 135 |
| SXP756 | 466.6–4954.9 | 1080 | 14.64 | 4.7 | 718 | 466.1–4954.4 | 98 | 14.91 | 5.1 | 402 |
| SXP893 | 466.5–4954.9 | 1080 | 15.95 | 7.7 | 128 | 466.1–4954.4 | 98 | 16.27 | 6.7 | 177 |
| SXP967 | 2104.9–4868.6 | 690 | 14.30 | 6.0 | 633 | 3326.6–4801.6 | 57 | 14.35 | 4.0 | 147 |
| SXP1323 | 627.4–4953.4 | 1021 | 14.57 | 5.7 | 153 | 673.8–4954.9 | 127 | 14.65 | 4.7 | 124 |
Basic parameters of 49 OGLE light curves for SMC Be/X-ray binaries. NI is the number of data points in the I-band light curve. I is the mean I-band magnitude. δI is the mean measurement error on the data points for each light curve. ΔI is the overall range of brightness in the light curve (in magnitudes). TJD = JD − 244 0000.5. Equivalent parameters are given for the V-band light curves.
| Source name | TJD range | NI | I (mag) | δI (mmag) | ΔI (mmag) | TJD range | NV | V (mag) | δV (mmag) | ΔV (mmag) |
| SXP2.37 | 2086.9–4868.6 | 707 | 14.89 | 6.2 | 1063 | 3326.6–4795.6 | 55 | 14.80 | 4.0 | 221 |
| SXP2.763 | 2086.9–4868.6 | 711 | 13.94 | 6.0 | 192 | 3326.6–4795.6 | 54 | 14.07 | 4.0 | 57 |
| SXP3.34 | 627.9–4953.9 | 837 | 15.57 | 6.2 | 144 | 673.8–4954.9 | 109 | 15.63 | 6.0 | 129 |
| SXP6.85 | 627.9–4862.6 | 646 | 14.70 | 4.8 | 690 | 665.9–3712.6 | 43 | 14.68 | 6.8 | 322 |
| SXP6.88 | 626.9–4954.9 | 1000 | 15.37 | 6.1 | 164 | 670.9–4954.9 | 99 | 15.56 | 5.3 | 801 |
| SXP7.78 | 2086.9–4952.9 | 762 | 14.79 | 5.1 | 196 | 3326.6–4953.9 | 89 | 14.92 | 4.0 | 75 |
| SXP7.92 | 621.9–4868.6 | 1026 | 13.82 | 4.7 | 647 | 665.9–4801.5 | 90 | 13.85 | 5.4 | 285 |
| SXP8.80 | 466.6–4952.9 | 1094 | 14.71 | 4.8 | 952 | 466.6–4953.9 | 130 | 14.71 | 4.9 | 774 |
| SXP9.13 | 466.0–4954.4 | 1077 | 16.30 | 9.1 | 284 | 466.6–4954.9 | 99 | 16.54 | 7.5 | 126 |
| SXP11.5 | 2203.6–4868.6 | 380 | 15.26 | 6.7 | 1002 | 3654.7–4801.5 | 48 | 15.25 | 4.0 | 596 |
| SXP15.3 | 466.6–4954.9 | 1075 | 14.47 | 4.7 | 250 | 466.1–4954.4 | 93 | 14.68 | 5.2 | 343 |
| SXP18.3 | 466.5–4952.9 | 1111 | 15.51 | 6.3 | 1232 | 466.6–4953.9 | 135 | 15.64 | 5.3 | 862 |
| SXP22.07 | 2104.9–4873.6 | 656 | 14.05 | 6.0 | 137 | 3315.7–4797.6 | 49 | 14.21 | 4.0 | 61 |
| SXP25.5 | 621.8–4954.9 | 1067 | 15.72 | 7.1 | 372 | 645.9–4954.9 | 94 | 15.83 | 6.3 | 400 |
| SXP31.0 | 2104.9–4873.6 | 656 | 15.31 | 6.0 | 197 | 3315.7–4797.6 | 49 | 15.49 | 4.0 | 28 |
| SXP34.08 | 2086.4–4954.4 | 724 | 16.94 | 13.3 | 105 | 3326.6–4954.9 | 69 | 16.84 | 7.6 | 48 |
| SXP46.6 | 2086.4–4954.4 | 1857 | 14.74 | 5.7 | 511 | 3326.6–4954.9 | 148 | 14.80 | 4.0 | 310 |
| SXP59.0 | 626.9–4954.9 | 1560 | 15.41 | 6.4 | 657 | 670.9–4954.9 | 140 | 15.44 | 5.0 | 365 |
| SXP65.8 | 621.9–4862.6 | 589 | 15.73 | 6.8 | 320 | 673.8–3379.6 | 39 | 15.77 | 5.9 | 118 |
| SXP74.7 | 466.5–4954.9 | 1715 | 16.68 | 11.2 | 179 | 467.1–4954.4 | 176 | 16.89 | 7.8 | 167 |
| SXP82.4 | 466.6–4952.9 | 1105 | 15.08 | 5.2 | 845 | 466.6–4953.9 | 131 | 15.21 | 4.8 | 577 |
| SXP91.1 | 2086.9–4865.6 | 713 | 14.78 | 5.3 | 126 | 3326.6–4791.6 | 50 | 15.02 | 4.0 | 86 |
| SXP101 | 2086.9–4954.9 | 737 | 15.61 | 6.9 | 127 | 3326.6–4954.9 | 71 | 15.70 | 4.3 | 67 |
| SXP138 | 2086.9–4952.9 | 762 | 16.11 | 7.8 | 294 | 3326.6–4953.9 | 89 | 16.18 | 5.2 | 125 |
| SXP140 | 2086.9–4954.9 | 724 | 15.52 | 6.6 | 550 | 3326.6–4954.9 | 67 | 15.76 | 4.6 | 371 |
| SXP152.1 | 2086.4–4954.4 | 718 | 15.43 | 6.3 | 182 | 3326.6–4954.9 | 67 | 15.69 | 5.4 | 125 |
| SXP169.3 | 2086.4–4865.1 | 712 | 15.38 | 6.0 | 192 | 3326.6–4791.6 | 50 | 15.57 | 4.7 | 96 |
| SXP172 | 466.6–4954.9 | 1075 | 14.42 | 4.7 | 484 | 466.1–4954.4 | 95 | 14.47 | 5.1 | 169 |
| SXP202A | 621.9–4954.9 | 1040 | 14.65 | 5.4 | 351 | 665.9–4954.9 | 105 | 14.75 | 4.8 | 184 |
| SXP202B | 621.4–4868.1 | 911 | 15.34 | 6.0 | 259 | 670.4–4795.1 | 88 | 15.52 | 5.5 | 181 |
| SXP214 | 466.5–4865.6 | 1060 | 15.22 | 4.2 | 447 | 673.8–4954.9 | 109 | 15.63 | 6.0 | 129 |
| SXP264 | 621.8–4954.9 | 1067 | 15.90 | 7.6 | 283 | 645.9–4954.9 | 94 | 16.09 | 6.5 | 146 |
| SXP280.4 | 2086.9–4954.9 | 728 | 15.38 | 6.1 | 244 | 3326.6–4954.9 | 69 | 15.56 | 4.8 | 198 |
| SXP293 | 621.9–4868.6 | 1037 | 14.57 | 4.7 | 288 | 665.9–4795.6 | 93 | 14.87 | 5.1 | 143 |
| SXP304 | 627.4–4954.4 | 1052 | 15.58 | 6.1 | 68 | 665.9–4954.9 | 102 | 15.75 | 5.9 | 55 |
| SXP323 | 621.3–4954.4 | 1060 | 15.24 | 5.6 | 216 | 466.6–4954.9 | 97 | 15.42 | 6.0 | 261 |
| SXP327 | 2086.9–4952.9 | 762 | 16.75 | 11.6 | 442 | 3326.6–4953.9 | 89 | 16.70 | 5.4 | 213 |
| SXP342 | 2086.4–4954.4 | 1116 | 15.12 | 6.4 | 967 | 3326.6–4954.9 | 116 | 15.16 | 4.1 | 570 |
| SXP348 | 627.9–4953.9 | 688 | 15.10 | 5.2 | 963 | 665.9–4954.9 | 62 | 15.08 | 5.9 | 629 |
| SXP455A | 627.9–4954.9 | 1762 | 15.68 | 6.5 | 718 | 665.4–4954.4 | 193 | 15.63 | 5.3 | 338 |
| SXP504 | 621.3–4868.1 | 1014 | 14.79 | 5.2 | 83 | 670.9–4795.6 | 84 | 15.01 | 5.1 | 69 |
| SXP565 | 628.4–4948.4 | 845 | 15.83 | 7.0 | 224 | 665.9–4948.9 | 78 | 16.02 | 7.0 | 110 |
| SXP645 | 621.8–4868.6 | 1030 | 14.66 | 5.7 | 916 | 670.9–4795.6 | 87 | 14.69 | 4.8 | 132 |
| SXP701 | 621.8–4868.6 | 1030 | 15.70 | 7.1 | 148 | 670.9–4795.6 | 87 | 16.02 | 6.8 | 139 |
| SXP726 | 627.4–4953.4 | 1022 | 15.49 | 5.8 | 128 | 673.8–4954.9 | 127 | 15.66 | 5.7 | 135 |
| SXP756 | 466.6–4954.9 | 1080 | 14.64 | 4.7 | 718 | 466.1–4954.4 | 98 | 14.91 | 5.1 | 402 |
| SXP893 | 466.5–4954.9 | 1080 | 15.95 | 7.7 | 128 | 466.1–4954.4 | 98 | 16.27 | 6.7 | 177 |
| SXP967 | 2104.9–4868.6 | 690 | 14.30 | 6.0 | 633 | 3326.6–4801.6 | 57 | 14.35 | 4.0 | 147 |
| SXP1323 | 627.4–4953.4 | 1021 | 14.57 | 5.7 | 153 | 673.8–4954.9 | 127 | 14.65 | 4.7 | 124 |
| Source name | TJD range | NI | I (mag) | δI (mmag) | ΔI (mmag) | TJD range | NV | V (mag) | δV (mmag) | ΔV (mmag) |
| SXP2.37 | 2086.9–4868.6 | 707 | 14.89 | 6.2 | 1063 | 3326.6–4795.6 | 55 | 14.80 | 4.0 | 221 |
| SXP2.763 | 2086.9–4868.6 | 711 | 13.94 | 6.0 | 192 | 3326.6–4795.6 | 54 | 14.07 | 4.0 | 57 |
| SXP3.34 | 627.9–4953.9 | 837 | 15.57 | 6.2 | 144 | 673.8–4954.9 | 109 | 15.63 | 6.0 | 129 |
| SXP6.85 | 627.9–4862.6 | 646 | 14.70 | 4.8 | 690 | 665.9–3712.6 | 43 | 14.68 | 6.8 | 322 |
| SXP6.88 | 626.9–4954.9 | 1000 | 15.37 | 6.1 | 164 | 670.9–4954.9 | 99 | 15.56 | 5.3 | 801 |
| SXP7.78 | 2086.9–4952.9 | 762 | 14.79 | 5.1 | 196 | 3326.6–4953.9 | 89 | 14.92 | 4.0 | 75 |
| SXP7.92 | 621.9–4868.6 | 1026 | 13.82 | 4.7 | 647 | 665.9–4801.5 | 90 | 13.85 | 5.4 | 285 |
| SXP8.80 | 466.6–4952.9 | 1094 | 14.71 | 4.8 | 952 | 466.6–4953.9 | 130 | 14.71 | 4.9 | 774 |
| SXP9.13 | 466.0–4954.4 | 1077 | 16.30 | 9.1 | 284 | 466.6–4954.9 | 99 | 16.54 | 7.5 | 126 |
| SXP11.5 | 2203.6–4868.6 | 380 | 15.26 | 6.7 | 1002 | 3654.7–4801.5 | 48 | 15.25 | 4.0 | 596 |
| SXP15.3 | 466.6–4954.9 | 1075 | 14.47 | 4.7 | 250 | 466.1–4954.4 | 93 | 14.68 | 5.2 | 343 |
| SXP18.3 | 466.5–4952.9 | 1111 | 15.51 | 6.3 | 1232 | 466.6–4953.9 | 135 | 15.64 | 5.3 | 862 |
| SXP22.07 | 2104.9–4873.6 | 656 | 14.05 | 6.0 | 137 | 3315.7–4797.6 | 49 | 14.21 | 4.0 | 61 |
| SXP25.5 | 621.8–4954.9 | 1067 | 15.72 | 7.1 | 372 | 645.9–4954.9 | 94 | 15.83 | 6.3 | 400 |
| SXP31.0 | 2104.9–4873.6 | 656 | 15.31 | 6.0 | 197 | 3315.7–4797.6 | 49 | 15.49 | 4.0 | 28 |
| SXP34.08 | 2086.4–4954.4 | 724 | 16.94 | 13.3 | 105 | 3326.6–4954.9 | 69 | 16.84 | 7.6 | 48 |
| SXP46.6 | 2086.4–4954.4 | 1857 | 14.74 | 5.7 | 511 | 3326.6–4954.9 | 148 | 14.80 | 4.0 | 310 |
| SXP59.0 | 626.9–4954.9 | 1560 | 15.41 | 6.4 | 657 | 670.9–4954.9 | 140 | 15.44 | 5.0 | 365 |
| SXP65.8 | 621.9–4862.6 | 589 | 15.73 | 6.8 | 320 | 673.8–3379.6 | 39 | 15.77 | 5.9 | 118 |
| SXP74.7 | 466.5–4954.9 | 1715 | 16.68 | 11.2 | 179 | 467.1–4954.4 | 176 | 16.89 | 7.8 | 167 |
| SXP82.4 | 466.6–4952.9 | 1105 | 15.08 | 5.2 | 845 | 466.6–4953.9 | 131 | 15.21 | 4.8 | 577 |
| SXP91.1 | 2086.9–4865.6 | 713 | 14.78 | 5.3 | 126 | 3326.6–4791.6 | 50 | 15.02 | 4.0 | 86 |
| SXP101 | 2086.9–4954.9 | 737 | 15.61 | 6.9 | 127 | 3326.6–4954.9 | 71 | 15.70 | 4.3 | 67 |
| SXP138 | 2086.9–4952.9 | 762 | 16.11 | 7.8 | 294 | 3326.6–4953.9 | 89 | 16.18 | 5.2 | 125 |
| SXP140 | 2086.9–4954.9 | 724 | 15.52 | 6.6 | 550 | 3326.6–4954.9 | 67 | 15.76 | 4.6 | 371 |
| SXP152.1 | 2086.4–4954.4 | 718 | 15.43 | 6.3 | 182 | 3326.6–4954.9 | 67 | 15.69 | 5.4 | 125 |
| SXP169.3 | 2086.4–4865.1 | 712 | 15.38 | 6.0 | 192 | 3326.6–4791.6 | 50 | 15.57 | 4.7 | 96 |
| SXP172 | 466.6–4954.9 | 1075 | 14.42 | 4.7 | 484 | 466.1–4954.4 | 95 | 14.47 | 5.1 | 169 |
| SXP202A | 621.9–4954.9 | 1040 | 14.65 | 5.4 | 351 | 665.9–4954.9 | 105 | 14.75 | 4.8 | 184 |
| SXP202B | 621.4–4868.1 | 911 | 15.34 | 6.0 | 259 | 670.4–4795.1 | 88 | 15.52 | 5.5 | 181 |
| SXP214 | 466.5–4865.6 | 1060 | 15.22 | 4.2 | 447 | 673.8–4954.9 | 109 | 15.63 | 6.0 | 129 |
| SXP264 | 621.8–4954.9 | 1067 | 15.90 | 7.6 | 283 | 645.9–4954.9 | 94 | 16.09 | 6.5 | 146 |
| SXP280.4 | 2086.9–4954.9 | 728 | 15.38 | 6.1 | 244 | 3326.6–4954.9 | 69 | 15.56 | 4.8 | 198 |
| SXP293 | 621.9–4868.6 | 1037 | 14.57 | 4.7 | 288 | 665.9–4795.6 | 93 | 14.87 | 5.1 | 143 |
| SXP304 | 627.4–4954.4 | 1052 | 15.58 | 6.1 | 68 | 665.9–4954.9 | 102 | 15.75 | 5.9 | 55 |
| SXP323 | 621.3–4954.4 | 1060 | 15.24 | 5.6 | 216 | 466.6–4954.9 | 97 | 15.42 | 6.0 | 261 |
| SXP327 | 2086.9–4952.9 | 762 | 16.75 | 11.6 | 442 | 3326.6–4953.9 | 89 | 16.70 | 5.4 | 213 |
| SXP342 | 2086.4–4954.4 | 1116 | 15.12 | 6.4 | 967 | 3326.6–4954.9 | 116 | 15.16 | 4.1 | 570 |
| SXP348 | 627.9–4953.9 | 688 | 15.10 | 5.2 | 963 | 665.9–4954.9 | 62 | 15.08 | 5.9 | 629 |
| SXP455A | 627.9–4954.9 | 1762 | 15.68 | 6.5 | 718 | 665.4–4954.4 | 193 | 15.63 | 5.3 | 338 |
| SXP504 | 621.3–4868.1 | 1014 | 14.79 | 5.2 | 83 | 670.9–4795.6 | 84 | 15.01 | 5.1 | 69 |
| SXP565 | 628.4–4948.4 | 845 | 15.83 | 7.0 | 224 | 665.9–4948.9 | 78 | 16.02 | 7.0 | 110 |
| SXP645 | 621.8–4868.6 | 1030 | 14.66 | 5.7 | 916 | 670.9–4795.6 | 87 | 14.69 | 4.8 | 132 |
| SXP701 | 621.8–4868.6 | 1030 | 15.70 | 7.1 | 148 | 670.9–4795.6 | 87 | 16.02 | 6.8 | 139 |
| SXP726 | 627.4–4953.4 | 1022 | 15.49 | 5.8 | 128 | 673.8–4954.9 | 127 | 15.66 | 5.7 | 135 |
| SXP756 | 466.6–4954.9 | 1080 | 14.64 | 4.7 | 718 | 466.1–4954.4 | 98 | 14.91 | 5.1 | 402 |
| SXP893 | 466.5–4954.9 | 1080 | 15.95 | 7.7 | 128 | 466.1–4954.4 | 98 | 16.27 | 6.7 | 177 |
| SXP967 | 2104.9–4868.6 | 690 | 14.30 | 6.0 | 633 | 3326.6–4801.6 | 57 | 14.35 | 4.0 | 147 |
| SXP1323 | 627.4–4953.4 | 1021 | 14.57 | 5.7 | 153 | 673.8–4954.9 | 127 | 14.65 | 4.7 | 124 |
Although the observations are optimally at daily intervals, observation limits mean that a typical year of OGLE monitoring produces ∼100 usable observations spread over ∼220 d, and hence the monitoring periods are separated by ∼140 d gaps that are clearly visible in Fig. 1. A typical light curve contains ∼350 points from OGLE II (if available) and ∼800 points from OGLE III. Fig. 2 shows the separations of adjacent data points in the light curve of SXP327, which may be considered typical.
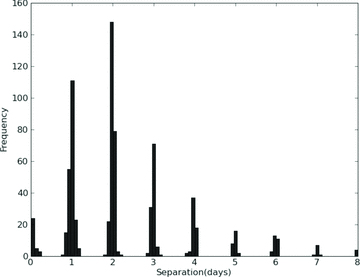
Separations of observation times of consecutive observations for SXP327 that may be considered typical of the OGLE light-curve sampling.
2.2 Analysis method
We used the fast implementation of the Lomb–Scargle (L-S) periodogram (Press & Rybicki 1989) to search for periodic signals within the data set, this method generally being preferred for data sets with unequal sampling and data gaps. Periods were searched in the range from 2 d (corresponding to the Nyquist frequency for nominally daily sampled light curves) up to 1000 d, after which sensitivity is reduced due to the finite length of the light curves. Significance levels for each periodogram were determined by using Monte Carlo simulations wherein the data points were randomized in time within the light curve, whilst maintaining the same overall time structure. A periodogram was derived for 100 000 randomized light curves, and the power level containing 99.99 per cent of the peak powers was determined. The errors on the derived periods were also derived by Monte Carlo means, using a bootstrap-with-replacement simulation performed with many iterations, the error on the period being derived from the distribution of periods recovered from typically 10 000 trials.
As the L-S method has limited sensitivity to detect high-frequency modulation in the presence of low-frequency (i.e. long-term) trends in the data, detrending of the light curves was performed to remove long-period signals. A rolling-mean calculation over a specific time window (typically 50–300 d), moved in 1 d steps, was used to determine a detrending model that was then subtracted from the light curve. Such detrending acts as a combined high-pass frequency filter and mean subtraction that should allow the L-S algorithm to work with optimum efficiency when searching for small variations on top of larger long-term variations.
The sensitivity to periodic variations will depend on a number of factors, principally the period and amplitude of the signal being searched for, the length, sampling and noise levels of the light curve being searched, and the ability of the detrending to successfully remove low-frequency noise from the light curve. We performed a number of simulations to estimate the sensitivity of our analysis to periodic variations. In each case, we created fake light curves with a known periodicity but the same sampling, mean flux and random measurement noise as real light curves. These fake light curves were then fed through the same analysis process as the true light curves to allow us to assess under what conditions the simulated periodicity is reliably reconstructed. This procedure was carried out both for 12 yr light curves, in order to assess the sensitivity to a persistent periodic signal, and for 1 yr light curves, to estimate the sensitivity to transient periodic emission.
We analysed the basic sensitivity to persistent periodic variations at a period of 50 d for four sample light curves (SXP6.88, SXP74.7, SXP214 and SXP327) representing different lengths and intrinsic measurement error levels (see Table 1). The sensitivity limit for full OGLE II + OGLE III light curves was found to vary between persistent signal amplitudes of 1.5 and 4 mmag depending on the light curve quality, and we confirmed that any signal detected above the 99.99 per cent confidence limit (at a L-S power of 20) was reconstructed at the correct period. For 1 yr data sets, the 99.99 per cent confidence limit was determined to be at a L-S power level of 14, and the sensitivity to periodicities was found to be closely related to the intrinsic measurement errors – periodic signals were correctly determined for amplitudes above ∼5 mmag in SXP6.88 and ∼4 mmag in SXP214.
We performed additional simulations to quantify the impact of the detrending employed – a series of simulations of a 10 mmag periodic signal of either 50 d or 100 d period was injected into a typical light curve, which was then detrended with windows of various widths. Only the ratio of the detrending window length to the signal period is important, and the loss of L-S power as a function of this ratio is shown in Fig. 3. As expected, the L-S power is essentially unaffected when the detrending window is significantly longer than the signal period, but the recovered L-S power is strongly reduced for periods smaller than the detrending window.
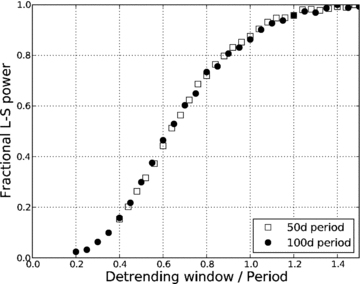
Recovered L-S power as a function of the detrending window:signal period ratio.
Finally, to quantify the effect of the sampling pattern and the length of the data set on sensitivity, we performed a set of simulations in which we created fake light curves matching the sampling of a typical composite OGLE-II and OGLE-III light curve, added a 10 mmag periodic signal of a varying period and then tested the ability of our algorithms to recover the correct period. The sensitivity was found to be very uniform over a large range of periods, with the exception of a small range around 1 yr periods where the long-term sampling pattern of the data dominated. While the correct periods were recovered at all times, the recovered L-S power, and hence sensitivity, was reduced by ∼40 per cent in narrow windows around 1 yr. This is unlikely to have a significant effect for our studies. Unsurprisingly, it also became difficult to recover the test period when it became comparable with the length of the light curve. In the case of yearly subsets of the light curves, periods beyond ∼175 d (around ∼75 per cent of the data set length) could not be reliably detected. Using the combined OGLE-II and OGLE-III light-curve lengths, this corresponds to an upper limit on the periods we can detect of ∼2000 d, but in practice the detrending windows used made this limit much lower.
3 PERIOD SEARCHING
The detrended light curves were searched for periodic signals with periods between 2 d and 1000 d looking at both the whole light curve and the annual campaigns, subject to the sensitivity limits discussed in the previous section. In the following sections, we report frequencies found in the formally acceptable region from 2 to 1000 d, and reserve any comment on the true origin of these periodicities until later sections. Table 2 indicates the periodic signals detected. We also note the periods previously published in both optical and X-ray light curves for comparison.
Sources for which significant periods have been detected. All units are in d. References for the published orbital periods are: (1) Galache et al. (2008); (2) Schmidtke et al. (2006); (3) Coe et al. (2005); (4) Edge (2005); (5) Schmidtke & Cowley (2005); (6) Schmidtke et al. (2004); (7) McGowan et al. (2007); (8) Schmidtke & Cowley (2006); (9) McGowan et al. (2008); (10) Coe et al. (2009); (12) Townsend et al. (2009); (13) Schurch et al. (2009); (14) Schmidtke & Cowley (2007); (15) Coe et al. (2008); (16) Townsend et al. (2011); (17) Schurch et al. (2011); (18) Schurch, Udalski & Coe (2008); (19) Coe & Edge (2004); (20) Rajoelimanana et al. (2011); (21) Schmidtke, Cowley & Udalski (2009a).
| Source | X-ray Porb (d) | Pub Popt (d) | Our Popt (d) | Detrend (d) |
| SXP2.37 | 18.38[16] | 18.62[18] | 9.30 ± 0.01 | 51 |
| SXP2.76 | – | 82.1[2] | 81.81 ± 0.06 | 101 |
| SXP3.34 | – | – | 10.7248 ± 0.0006 | 51 |
| SXP6.85 | 21.9[16] | 114[9] | – | – |
| SXP7.78 | 44.92[1] | 44.6[3] | 44.93 ± 0.01 | 101 |
| SXP7.92 | – | 36.8[10] | 35.61 ± 0.05 | 101 |
| SXP8.80 | 28.5[1, 16] | – | – | – |
| SXP9.13 | – | 40.17[4] | – | – |
| SXP11.5 | 36.3[12] | – | – | – |
| SXP15.3 | – | 75.1[4] | 74.32 ± 0.03 | 101 |
| SXP18.3 | 17.7[1] | 17.7[13] | 17.79 ± 0.03 | 101 |
| SXP22.1 | – | – | 83.7 ± 0.1 | 101 |
| SXP25.5 | – | 22.50[20] | 22.53 ± 0.01 | 51 |
| SXP31.0 | – | 90.4[2] | 90.53 ± 0.07 | 101 |
| SXP46.6 | 137.36[1] | 137[9] | 137.4 ± 0.2 | 165 |
| SXP59.0 | 122.25[1] | 60.2[5] | – | |
| SXP65.8 | – | 110[14] | 111.04 ± 0.15 | 201 |
| SXP74.7 | 33.38[16] | 33.4[4, 5] | 33.387 ± 0.006 | 101 |
| SXP91.1 | – | 88.2[6] | 88.37 ± 0.03 | 101 |
| SXP101 | – | 21.9[7] | 21.949 ± 0.003 | 101 |
| SXP140 | – | 197[8] | – | |
| SXP169 | 68.5[1] | 67.6[2] | 68.37 ± 0.07 | 101 |
| SXP172 | 70.4[17] | 69.9[8] | 68.78 ± 0.08 | 81 |
| SXP202B | – | 229.9[17] | 224.6 ± 0.3 | 501 |
| SXP214 | – | – | 4.5832 ± 0.0004 | 101 |
| SXP264 | – | 49.1[4] | 49.12 ± 0.03 | 101 |
| SXP280 | – | 127[2] | 127.62 ± 0.25 | 201 |
| SXP293 | – | 59.7[6] | 59.726 ± 0.006 | 101 |
| SXP304 | – | 520[8] | – | – |
| SXP323 | 116.6[1] | – | – | – |
| SXP327 | – | 45.9[15] | 45.93 ± 0.01 | 101 |
| SXP455 | – | 74.7[6] | 74.56 ± 0.05 | 101 |
| SXP455 | – | – | 209.6 ± 0.8 | 301 |
| SXP504 | 265.3[1] | 273[5] | 270.1 ± 0.5 | 501 |
| SXP565 | 151.8[1] | 95.3[6] | 152.4 ± 0.3 | 301 |
| SXP701 | – | 412[5] | – | – |
| SXP756 | – | 11.4[19] | 11.404 ± 0.001 | 31 |
| SXP756 | 389.9[1] | 394[2] | 393.6 ± 1.2 | 501 |
| SXP893 | – | – | 3.7434 ± 0.0005 | 51 |
| SXP967 | – | 101.94[21] | 101.4 ± 0.2 | 151 |
| SXP1323 | – | – | 7.9101 ± 0.0004 | 25 |
| SXP1323 | – | 26.1[8] | 26.174 ± 0.002 | 101 |
| Source | X-ray Porb (d) | Pub Popt (d) | Our Popt (d) | Detrend (d) |
| SXP2.37 | 18.38[16] | 18.62[18] | 9.30 ± 0.01 | 51 |
| SXP2.76 | – | 82.1[2] | 81.81 ± 0.06 | 101 |
| SXP3.34 | – | – | 10.7248 ± 0.0006 | 51 |
| SXP6.85 | 21.9[16] | 114[9] | – | – |
| SXP7.78 | 44.92[1] | 44.6[3] | 44.93 ± 0.01 | 101 |
| SXP7.92 | – | 36.8[10] | 35.61 ± 0.05 | 101 |
| SXP8.80 | 28.5[1, 16] | – | – | – |
| SXP9.13 | – | 40.17[4] | – | – |
| SXP11.5 | 36.3[12] | – | – | – |
| SXP15.3 | – | 75.1[4] | 74.32 ± 0.03 | 101 |
| SXP18.3 | 17.7[1] | 17.7[13] | 17.79 ± 0.03 | 101 |
| SXP22.1 | – | – | 83.7 ± 0.1 | 101 |
| SXP25.5 | – | 22.50[20] | 22.53 ± 0.01 | 51 |
| SXP31.0 | – | 90.4[2] | 90.53 ± 0.07 | 101 |
| SXP46.6 | 137.36[1] | 137[9] | 137.4 ± 0.2 | 165 |
| SXP59.0 | 122.25[1] | 60.2[5] | – | |
| SXP65.8 | – | 110[14] | 111.04 ± 0.15 | 201 |
| SXP74.7 | 33.38[16] | 33.4[4, 5] | 33.387 ± 0.006 | 101 |
| SXP91.1 | – | 88.2[6] | 88.37 ± 0.03 | 101 |
| SXP101 | – | 21.9[7] | 21.949 ± 0.003 | 101 |
| SXP140 | – | 197[8] | – | |
| SXP169 | 68.5[1] | 67.6[2] | 68.37 ± 0.07 | 101 |
| SXP172 | 70.4[17] | 69.9[8] | 68.78 ± 0.08 | 81 |
| SXP202B | – | 229.9[17] | 224.6 ± 0.3 | 501 |
| SXP214 | – | – | 4.5832 ± 0.0004 | 101 |
| SXP264 | – | 49.1[4] | 49.12 ± 0.03 | 101 |
| SXP280 | – | 127[2] | 127.62 ± 0.25 | 201 |
| SXP293 | – | 59.7[6] | 59.726 ± 0.006 | 101 |
| SXP304 | – | 520[8] | – | – |
| SXP323 | 116.6[1] | – | – | – |
| SXP327 | – | 45.9[15] | 45.93 ± 0.01 | 101 |
| SXP455 | – | 74.7[6] | 74.56 ± 0.05 | 101 |
| SXP455 | – | – | 209.6 ± 0.8 | 301 |
| SXP504 | 265.3[1] | 273[5] | 270.1 ± 0.5 | 501 |
| SXP565 | 151.8[1] | 95.3[6] | 152.4 ± 0.3 | 301 |
| SXP701 | – | 412[5] | – | – |
| SXP756 | – | 11.4[19] | 11.404 ± 0.001 | 31 |
| SXP756 | 389.9[1] | 394[2] | 393.6 ± 1.2 | 501 |
| SXP893 | – | – | 3.7434 ± 0.0005 | 51 |
| SXP967 | – | 101.94[21] | 101.4 ± 0.2 | 151 |
| SXP1323 | – | – | 7.9101 ± 0.0004 | 25 |
| SXP1323 | – | 26.1[8] | 26.174 ± 0.002 | 101 |
Sources for which significant periods have been detected. All units are in d. References for the published orbital periods are: (1) Galache et al. (2008); (2) Schmidtke et al. (2006); (3) Coe et al. (2005); (4) Edge (2005); (5) Schmidtke & Cowley (2005); (6) Schmidtke et al. (2004); (7) McGowan et al. (2007); (8) Schmidtke & Cowley (2006); (9) McGowan et al. (2008); (10) Coe et al. (2009); (12) Townsend et al. (2009); (13) Schurch et al. (2009); (14) Schmidtke & Cowley (2007); (15) Coe et al. (2008); (16) Townsend et al. (2011); (17) Schurch et al. (2011); (18) Schurch, Udalski & Coe (2008); (19) Coe & Edge (2004); (20) Rajoelimanana et al. (2011); (21) Schmidtke, Cowley & Udalski (2009a).
| Source | X-ray Porb (d) | Pub Popt (d) | Our Popt (d) | Detrend (d) |
| SXP2.37 | 18.38[16] | 18.62[18] | 9.30 ± 0.01 | 51 |
| SXP2.76 | – | 82.1[2] | 81.81 ± 0.06 | 101 |
| SXP3.34 | – | – | 10.7248 ± 0.0006 | 51 |
| SXP6.85 | 21.9[16] | 114[9] | – | – |
| SXP7.78 | 44.92[1] | 44.6[3] | 44.93 ± 0.01 | 101 |
| SXP7.92 | – | 36.8[10] | 35.61 ± 0.05 | 101 |
| SXP8.80 | 28.5[1, 16] | – | – | – |
| SXP9.13 | – | 40.17[4] | – | – |
| SXP11.5 | 36.3[12] | – | – | – |
| SXP15.3 | – | 75.1[4] | 74.32 ± 0.03 | 101 |
| SXP18.3 | 17.7[1] | 17.7[13] | 17.79 ± 0.03 | 101 |
| SXP22.1 | – | – | 83.7 ± 0.1 | 101 |
| SXP25.5 | – | 22.50[20] | 22.53 ± 0.01 | 51 |
| SXP31.0 | – | 90.4[2] | 90.53 ± 0.07 | 101 |
| SXP46.6 | 137.36[1] | 137[9] | 137.4 ± 0.2 | 165 |
| SXP59.0 | 122.25[1] | 60.2[5] | – | |
| SXP65.8 | – | 110[14] | 111.04 ± 0.15 | 201 |
| SXP74.7 | 33.38[16] | 33.4[4, 5] | 33.387 ± 0.006 | 101 |
| SXP91.1 | – | 88.2[6] | 88.37 ± 0.03 | 101 |
| SXP101 | – | 21.9[7] | 21.949 ± 0.003 | 101 |
| SXP140 | – | 197[8] | – | |
| SXP169 | 68.5[1] | 67.6[2] | 68.37 ± 0.07 | 101 |
| SXP172 | 70.4[17] | 69.9[8] | 68.78 ± 0.08 | 81 |
| SXP202B | – | 229.9[17] | 224.6 ± 0.3 | 501 |
| SXP214 | – | – | 4.5832 ± 0.0004 | 101 |
| SXP264 | – | 49.1[4] | 49.12 ± 0.03 | 101 |
| SXP280 | – | 127[2] | 127.62 ± 0.25 | 201 |
| SXP293 | – | 59.7[6] | 59.726 ± 0.006 | 101 |
| SXP304 | – | 520[8] | – | – |
| SXP323 | 116.6[1] | – | – | – |
| SXP327 | – | 45.9[15] | 45.93 ± 0.01 | 101 |
| SXP455 | – | 74.7[6] | 74.56 ± 0.05 | 101 |
| SXP455 | – | – | 209.6 ± 0.8 | 301 |
| SXP504 | 265.3[1] | 273[5] | 270.1 ± 0.5 | 501 |
| SXP565 | 151.8[1] | 95.3[6] | 152.4 ± 0.3 | 301 |
| SXP701 | – | 412[5] | – | – |
| SXP756 | – | 11.4[19] | 11.404 ± 0.001 | 31 |
| SXP756 | 389.9[1] | 394[2] | 393.6 ± 1.2 | 501 |
| SXP893 | – | – | 3.7434 ± 0.0005 | 51 |
| SXP967 | – | 101.94[21] | 101.4 ± 0.2 | 151 |
| SXP1323 | – | – | 7.9101 ± 0.0004 | 25 |
| SXP1323 | – | 26.1[8] | 26.174 ± 0.002 | 101 |
| Source | X-ray Porb (d) | Pub Popt (d) | Our Popt (d) | Detrend (d) |
| SXP2.37 | 18.38[16] | 18.62[18] | 9.30 ± 0.01 | 51 |
| SXP2.76 | – | 82.1[2] | 81.81 ± 0.06 | 101 |
| SXP3.34 | – | – | 10.7248 ± 0.0006 | 51 |
| SXP6.85 | 21.9[16] | 114[9] | – | – |
| SXP7.78 | 44.92[1] | 44.6[3] | 44.93 ± 0.01 | 101 |
| SXP7.92 | – | 36.8[10] | 35.61 ± 0.05 | 101 |
| SXP8.80 | 28.5[1, 16] | – | – | – |
| SXP9.13 | – | 40.17[4] | – | – |
| SXP11.5 | 36.3[12] | – | – | – |
| SXP15.3 | – | 75.1[4] | 74.32 ± 0.03 | 101 |
| SXP18.3 | 17.7[1] | 17.7[13] | 17.79 ± 0.03 | 101 |
| SXP22.1 | – | – | 83.7 ± 0.1 | 101 |
| SXP25.5 | – | 22.50[20] | 22.53 ± 0.01 | 51 |
| SXP31.0 | – | 90.4[2] | 90.53 ± 0.07 | 101 |
| SXP46.6 | 137.36[1] | 137[9] | 137.4 ± 0.2 | 165 |
| SXP59.0 | 122.25[1] | 60.2[5] | – | |
| SXP65.8 | – | 110[14] | 111.04 ± 0.15 | 201 |
| SXP74.7 | 33.38[16] | 33.4[4, 5] | 33.387 ± 0.006 | 101 |
| SXP91.1 | – | 88.2[6] | 88.37 ± 0.03 | 101 |
| SXP101 | – | 21.9[7] | 21.949 ± 0.003 | 101 |
| SXP140 | – | 197[8] | – | |
| SXP169 | 68.5[1] | 67.6[2] | 68.37 ± 0.07 | 101 |
| SXP172 | 70.4[17] | 69.9[8] | 68.78 ± 0.08 | 81 |
| SXP202B | – | 229.9[17] | 224.6 ± 0.3 | 501 |
| SXP214 | – | – | 4.5832 ± 0.0004 | 101 |
| SXP264 | – | 49.1[4] | 49.12 ± 0.03 | 101 |
| SXP280 | – | 127[2] | 127.62 ± 0.25 | 201 |
| SXP293 | – | 59.7[6] | 59.726 ± 0.006 | 101 |
| SXP304 | – | 520[8] | – | – |
| SXP323 | 116.6[1] | – | – | – |
| SXP327 | – | 45.9[15] | 45.93 ± 0.01 | 101 |
| SXP455 | – | 74.7[6] | 74.56 ± 0.05 | 101 |
| SXP455 | – | – | 209.6 ± 0.8 | 301 |
| SXP504 | 265.3[1] | 273[5] | 270.1 ± 0.5 | 501 |
| SXP565 | 151.8[1] | 95.3[6] | 152.4 ± 0.3 | 301 |
| SXP701 | – | 412[5] | – | – |
| SXP756 | – | 11.4[19] | 11.404 ± 0.001 | 31 |
| SXP756 | 389.9[1] | 394[2] | 393.6 ± 1.2 | 501 |
| SXP893 | – | – | 3.7434 ± 0.0005 | 51 |
| SXP967 | – | 101.94[21] | 101.4 ± 0.2 | 151 |
| SXP1323 | – | – | 7.9101 ± 0.0004 | 25 |
| SXP1323 | – | 26.1[8] | 26.174 ± 0.002 | 101 |
We emphasize here that the recovered period in the 2–1000 d region may not always represent the true period, but may result from aliasing of a periodic signal from outside the formal search range with other periodicities present in the – usually the sampling frequencies of the data. Of particular relevance in the context of this work is the effect of periods around 1 d, which when combined with the sampling pattern associated with the OGLE project data sets (Fig. 2) can produce complex aliasing patterns (often referred to as window functions). Fig. 4 shows an L-S periodogram of a simulated sine wave with a period of 0.8 d combined with a typical OGLE sampling pattern. Apart from the fundamental frequency at 1.25 cycles/day (c/d), a complex set of aliases spanning from 0 to ∼8 c/d, together with the usual reflections about the Nyquist frequencies can all be observed. The broad envelope of the peaks matches, and is clearly driven by, the data sampling shown in Fig. 2.
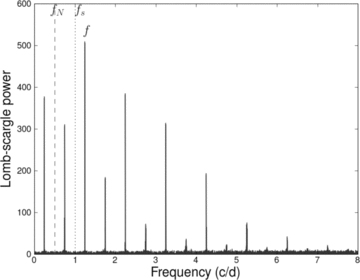
L-S periodogram for ‘fake’ sinusoid at a period of 0.8 d (f= 1.25 c/d) superimposed on the SXP1323 light-curve sampling pattern. The sampling frequency (fs) and Nyquist frequency (fN) are indicated by vertical lines.
Although the formal Nyquist frequency of the data sets with nominal daily sampling is 0.5 c/d (a 2 d period) we cannot ignore the effect of periods below 2 d when searching. Due to aliasing, periods of very near to 1 d can inject power into the periodogram far from the Nyquist frequency, and into the typical range for Be/X-ray orbital period searching. For example, a period of 0.98 d corresponds to 1.02 c/d, creating an alias at 0.02 c/d that could easily be misinterpreted as a 50 d period. This problem is illustrated in Fig. 5, which shows the detected period (in the formally useful region between 2 and 100 d) resulting from the superposition of periodic signals of various periods on to a typical OGLE-II and OGLE-III sampling pattern. There is a clear degeneracy in the solution as a recovered period could result from a number of true periods, and some a priori knowledge of the expected periods, or some other discriminator is required to break this degeneracy. A possible discriminator, the shape of the folded light curve, is discussed in the following section. One further implication of this pattern is for drifting periods (see Section 5.5) – while the alias of a drifting period will still manifest itself as a drifting period of >2 d, neither the period or rate of change of the original drifting signal can be uniquely determined as a result of this degeneracy.
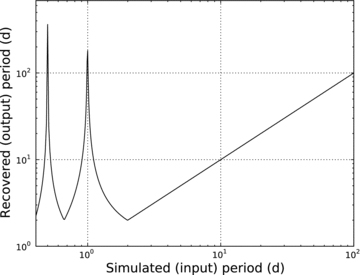
Recovered period in the 2–1000 d region for simulated periodicities in the range of 0.4–100 d.
4 FOLDED LIGHT CURVE PROFILES
Where a clear periodicity was detected in a light curve, or annual section of a light curve, we created a folded light curve for inspection. It was noted that the folded light curves fell into two broad categories and were either sinusoidal variations or sharply peaked variations often with ‘fast rise exponential decay (FRED)’-shaped profiles.
In order to quantify the shapes of the folded light curves, we defined two metrics for the folded light curves. The first is the full-width half-maximum in phase units, hereafter the phase span (PS). For a sinusoidal variation, the expected value for this metric is 0.5; values below 0.5 would be expected for sharper peaks. The second measures the asymmetry of the peak and is defined as the ratio between the distances in phase space between the peak and points at 10 per cent of maximum on the right and left sides of the peak, hereafter the phase asymmetry (PA). For a sinusoid, with a symmetric peak, the expected value is 1; values greater than 1 indicate a peak with a faster rise than fall.
The folded light-curve analysis was performed for those sources exhibiting strong persistent or quasi-persistent (seen in more than 1 yr of data) periodicities. The resulting PS and PA metrics are listed in Table 3, together with information on the subsets of data they have been extracted from.
Folded light-curve parameters for periodic sources in the SMC sample. The match parameter indicates when the X-ray and optical periods match, thus confirming an orbital period, while a ? indicates that the X-ray period is unknown. Columns indicate the detrending window (DW), the phase span (PS) and the phase asymmetry (PA) from the folded light-curve analysis – see the text for more details.
| Source | Date range (TJD) | Period (d) | Match | DW (d) | PS | PA | Amplitude (× 10−5 Jy) | Amplitude (mmag) |
| SXP2.37 | 4191–4549 | 18.60 | Y | 51.0 | 0.24 | 3.00 | 16.0 | 37.9 |
| SXP2.763 | All | 81.8 | ? | 101 | 0.35 | 1.38 | 14.1 | 16.9 |
| SXP3.34 | All | 10.72 | ? | 51 | 0.52 | 0.85 | 7.5 | 38.2 |
| SXP7.78 | All | 44.93 | Y | 101 | 0.3 | 1.5 | 14.5 | 38.4 |
| SXP7.92 | All | 35.61 | ? | 101 | 0.63 | 1.33 | 24.0 | 23.5 |
| SXP15.3 | All | 74.34 | ? | 101 | 0.53 | 0.75 | 7.2 | 15.1 |
| SXP18.3 | 3101–3824 | 17.79 | Y | 51 | 0.33 | 0.86 | 21.8 | 116.0 |
| SXP22.1 | 3101–5000 | 84.9 | ? | 121 | 0.47 | 0.88 | 11.0 | 15.0 |
| SXP25.5 | All | 22.53 | ? | 51 | 0.27 | 1.50 | 3.6 | 21.6 |
| SXP31.0 | All | 90.53 | ? | 101 | 0.33 | 5.5 | 8.8 | 39.4 |
| SXP46.6 | All excl. 3100–3800 | 137.38 | Y | 165 | 0.13 | 2.50 | 10.9 | 25.7 |
| SXP65.8 | All | 111.04 | ? | 201 | 0.33 | 2.67 | 5.1 | 29.4 |
| SXP74.7 | All | 33.38 | Y | 101 | 0.33 | 1.0 | 1.9 | 30.7 |
| SXP91.1 | All | 88.37 | ? | 101 | 0.33 | 1.1 | 20.0 | 58.6 |
| SXP101 | All | 21.95 | ? | 101 | 0.40 | 1.29 | 5.9 | 31.9 |
| SXP169.3 | All | 68.37 | Y | 101 | 0.24 | 4.0 | 7.2 | 34.4 |
| SXP172 | All | 68.785 | Y | 81 | 0.46 | 2.33 | 8.1 | 14.0 |
| SXP202B | All | 224.57 | Y | 501 | 0.23 | 2.7 | 6.3 | 28.8 |
| SXP214 | All | 4.58 | ? | 101 | 0.5 | 0.6 | 13.0 | 67.0 |
| SXP264 | All | 49.11 | ? | 101 | 0.2 | 2.5 | 4.7 | 36.3 |
| SXP280.4 | All | 127.6 | ? | 201 | 0.37 | 2.33 | 7.0 | 33.4 |
| SXP293 | All | 59.72 | ? | 101 | 0.37 | 1.63 | 41.4 | 108.0 |
| SXP327 | All | 45.9 | ? | 101 | 0.23 | 2.4 | 14.0 | 205.8 |
| SXP455 | All | 74.55 | ? | 101 | 0.3 | 0.88 | – | – |
| All | 209.7 | ? | 301 | 0.65 | 1.11 | – | – | |
| SXP504 | All | 270.1 | Y | 501 | 0.4 | 3.6 | 4.4 | 12.5 |
| SXP565 | All | 152.4 | Y | 301 | 0.2 | 1.29 | 3.4 | 24.6 |
| SXP756 | All | 393.6 | Y | 501 | 0.1 | 6.33 | 80.0 | 228.5 |
| Non-outburst | 11.404 | N | 31 | 0.57 | 1.37 | 9.7 | 25.3 | |
| SXP893 | 1283–3101 | 3.74 | ? | 51.0 | 0.59 | 1.0 | 2.9 | 26.5 |
| SXP967 | 2200–4700 | 101.37 | ? | 151 | 0.33 | 2.17 | 22.0 | 34.4 |
| SXP1323 | All | 7.91 | ? | 25 | 0.55 | 0.67 | 16.0 | 32.9 |
| All | 26.17 | ? | 101 | 0.43 | 1.08 | 24.0 | 49.8 |
| Source | Date range (TJD) | Period (d) | Match | DW (d) | PS | PA | Amplitude (× 10−5 Jy) | Amplitude (mmag) |
| SXP2.37 | 4191–4549 | 18.60 | Y | 51.0 | 0.24 | 3.00 | 16.0 | 37.9 |
| SXP2.763 | All | 81.8 | ? | 101 | 0.35 | 1.38 | 14.1 | 16.9 |
| SXP3.34 | All | 10.72 | ? | 51 | 0.52 | 0.85 | 7.5 | 38.2 |
| SXP7.78 | All | 44.93 | Y | 101 | 0.3 | 1.5 | 14.5 | 38.4 |
| SXP7.92 | All | 35.61 | ? | 101 | 0.63 | 1.33 | 24.0 | 23.5 |
| SXP15.3 | All | 74.34 | ? | 101 | 0.53 | 0.75 | 7.2 | 15.1 |
| SXP18.3 | 3101–3824 | 17.79 | Y | 51 | 0.33 | 0.86 | 21.8 | 116.0 |
| SXP22.1 | 3101–5000 | 84.9 | ? | 121 | 0.47 | 0.88 | 11.0 | 15.0 |
| SXP25.5 | All | 22.53 | ? | 51 | 0.27 | 1.50 | 3.6 | 21.6 |
| SXP31.0 | All | 90.53 | ? | 101 | 0.33 | 5.5 | 8.8 | 39.4 |
| SXP46.6 | All excl. 3100–3800 | 137.38 | Y | 165 | 0.13 | 2.50 | 10.9 | 25.7 |
| SXP65.8 | All | 111.04 | ? | 201 | 0.33 | 2.67 | 5.1 | 29.4 |
| SXP74.7 | All | 33.38 | Y | 101 | 0.33 | 1.0 | 1.9 | 30.7 |
| SXP91.1 | All | 88.37 | ? | 101 | 0.33 | 1.1 | 20.0 | 58.6 |
| SXP101 | All | 21.95 | ? | 101 | 0.40 | 1.29 | 5.9 | 31.9 |
| SXP169.3 | All | 68.37 | Y | 101 | 0.24 | 4.0 | 7.2 | 34.4 |
| SXP172 | All | 68.785 | Y | 81 | 0.46 | 2.33 | 8.1 | 14.0 |
| SXP202B | All | 224.57 | Y | 501 | 0.23 | 2.7 | 6.3 | 28.8 |
| SXP214 | All | 4.58 | ? | 101 | 0.5 | 0.6 | 13.0 | 67.0 |
| SXP264 | All | 49.11 | ? | 101 | 0.2 | 2.5 | 4.7 | 36.3 |
| SXP280.4 | All | 127.6 | ? | 201 | 0.37 | 2.33 | 7.0 | 33.4 |
| SXP293 | All | 59.72 | ? | 101 | 0.37 | 1.63 | 41.4 | 108.0 |
| SXP327 | All | 45.9 | ? | 101 | 0.23 | 2.4 | 14.0 | 205.8 |
| SXP455 | All | 74.55 | ? | 101 | 0.3 | 0.88 | – | – |
| All | 209.7 | ? | 301 | 0.65 | 1.11 | – | – | |
| SXP504 | All | 270.1 | Y | 501 | 0.4 | 3.6 | 4.4 | 12.5 |
| SXP565 | All | 152.4 | Y | 301 | 0.2 | 1.29 | 3.4 | 24.6 |
| SXP756 | All | 393.6 | Y | 501 | 0.1 | 6.33 | 80.0 | 228.5 |
| Non-outburst | 11.404 | N | 31 | 0.57 | 1.37 | 9.7 | 25.3 | |
| SXP893 | 1283–3101 | 3.74 | ? | 51.0 | 0.59 | 1.0 | 2.9 | 26.5 |
| SXP967 | 2200–4700 | 101.37 | ? | 151 | 0.33 | 2.17 | 22.0 | 34.4 |
| SXP1323 | All | 7.91 | ? | 25 | 0.55 | 0.67 | 16.0 | 32.9 |
| All | 26.17 | ? | 101 | 0.43 | 1.08 | 24.0 | 49.8 |
Folded light-curve parameters for periodic sources in the SMC sample. The match parameter indicates when the X-ray and optical periods match, thus confirming an orbital period, while a ? indicates that the X-ray period is unknown. Columns indicate the detrending window (DW), the phase span (PS) and the phase asymmetry (PA) from the folded light-curve analysis – see the text for more details.
| Source | Date range (TJD) | Period (d) | Match | DW (d) | PS | PA | Amplitude (× 10−5 Jy) | Amplitude (mmag) |
| SXP2.37 | 4191–4549 | 18.60 | Y | 51.0 | 0.24 | 3.00 | 16.0 | 37.9 |
| SXP2.763 | All | 81.8 | ? | 101 | 0.35 | 1.38 | 14.1 | 16.9 |
| SXP3.34 | All | 10.72 | ? | 51 | 0.52 | 0.85 | 7.5 | 38.2 |
| SXP7.78 | All | 44.93 | Y | 101 | 0.3 | 1.5 | 14.5 | 38.4 |
| SXP7.92 | All | 35.61 | ? | 101 | 0.63 | 1.33 | 24.0 | 23.5 |
| SXP15.3 | All | 74.34 | ? | 101 | 0.53 | 0.75 | 7.2 | 15.1 |
| SXP18.3 | 3101–3824 | 17.79 | Y | 51 | 0.33 | 0.86 | 21.8 | 116.0 |
| SXP22.1 | 3101–5000 | 84.9 | ? | 121 | 0.47 | 0.88 | 11.0 | 15.0 |
| SXP25.5 | All | 22.53 | ? | 51 | 0.27 | 1.50 | 3.6 | 21.6 |
| SXP31.0 | All | 90.53 | ? | 101 | 0.33 | 5.5 | 8.8 | 39.4 |
| SXP46.6 | All excl. 3100–3800 | 137.38 | Y | 165 | 0.13 | 2.50 | 10.9 | 25.7 |
| SXP65.8 | All | 111.04 | ? | 201 | 0.33 | 2.67 | 5.1 | 29.4 |
| SXP74.7 | All | 33.38 | Y | 101 | 0.33 | 1.0 | 1.9 | 30.7 |
| SXP91.1 | All | 88.37 | ? | 101 | 0.33 | 1.1 | 20.0 | 58.6 |
| SXP101 | All | 21.95 | ? | 101 | 0.40 | 1.29 | 5.9 | 31.9 |
| SXP169.3 | All | 68.37 | Y | 101 | 0.24 | 4.0 | 7.2 | 34.4 |
| SXP172 | All | 68.785 | Y | 81 | 0.46 | 2.33 | 8.1 | 14.0 |
| SXP202B | All | 224.57 | Y | 501 | 0.23 | 2.7 | 6.3 | 28.8 |
| SXP214 | All | 4.58 | ? | 101 | 0.5 | 0.6 | 13.0 | 67.0 |
| SXP264 | All | 49.11 | ? | 101 | 0.2 | 2.5 | 4.7 | 36.3 |
| SXP280.4 | All | 127.6 | ? | 201 | 0.37 | 2.33 | 7.0 | 33.4 |
| SXP293 | All | 59.72 | ? | 101 | 0.37 | 1.63 | 41.4 | 108.0 |
| SXP327 | All | 45.9 | ? | 101 | 0.23 | 2.4 | 14.0 | 205.8 |
| SXP455 | All | 74.55 | ? | 101 | 0.3 | 0.88 | – | – |
| All | 209.7 | ? | 301 | 0.65 | 1.11 | – | – | |
| SXP504 | All | 270.1 | Y | 501 | 0.4 | 3.6 | 4.4 | 12.5 |
| SXP565 | All | 152.4 | Y | 301 | 0.2 | 1.29 | 3.4 | 24.6 |
| SXP756 | All | 393.6 | Y | 501 | 0.1 | 6.33 | 80.0 | 228.5 |
| Non-outburst | 11.404 | N | 31 | 0.57 | 1.37 | 9.7 | 25.3 | |
| SXP893 | 1283–3101 | 3.74 | ? | 51.0 | 0.59 | 1.0 | 2.9 | 26.5 |
| SXP967 | 2200–4700 | 101.37 | ? | 151 | 0.33 | 2.17 | 22.0 | 34.4 |
| SXP1323 | All | 7.91 | ? | 25 | 0.55 | 0.67 | 16.0 | 32.9 |
| All | 26.17 | ? | 101 | 0.43 | 1.08 | 24.0 | 49.8 |
| Source | Date range (TJD) | Period (d) | Match | DW (d) | PS | PA | Amplitude (× 10−5 Jy) | Amplitude (mmag) |
| SXP2.37 | 4191–4549 | 18.60 | Y | 51.0 | 0.24 | 3.00 | 16.0 | 37.9 |
| SXP2.763 | All | 81.8 | ? | 101 | 0.35 | 1.38 | 14.1 | 16.9 |
| SXP3.34 | All | 10.72 | ? | 51 | 0.52 | 0.85 | 7.5 | 38.2 |
| SXP7.78 | All | 44.93 | Y | 101 | 0.3 | 1.5 | 14.5 | 38.4 |
| SXP7.92 | All | 35.61 | ? | 101 | 0.63 | 1.33 | 24.0 | 23.5 |
| SXP15.3 | All | 74.34 | ? | 101 | 0.53 | 0.75 | 7.2 | 15.1 |
| SXP18.3 | 3101–3824 | 17.79 | Y | 51 | 0.33 | 0.86 | 21.8 | 116.0 |
| SXP22.1 | 3101–5000 | 84.9 | ? | 121 | 0.47 | 0.88 | 11.0 | 15.0 |
| SXP25.5 | All | 22.53 | ? | 51 | 0.27 | 1.50 | 3.6 | 21.6 |
| SXP31.0 | All | 90.53 | ? | 101 | 0.33 | 5.5 | 8.8 | 39.4 |
| SXP46.6 | All excl. 3100–3800 | 137.38 | Y | 165 | 0.13 | 2.50 | 10.9 | 25.7 |
| SXP65.8 | All | 111.04 | ? | 201 | 0.33 | 2.67 | 5.1 | 29.4 |
| SXP74.7 | All | 33.38 | Y | 101 | 0.33 | 1.0 | 1.9 | 30.7 |
| SXP91.1 | All | 88.37 | ? | 101 | 0.33 | 1.1 | 20.0 | 58.6 |
| SXP101 | All | 21.95 | ? | 101 | 0.40 | 1.29 | 5.9 | 31.9 |
| SXP169.3 | All | 68.37 | Y | 101 | 0.24 | 4.0 | 7.2 | 34.4 |
| SXP172 | All | 68.785 | Y | 81 | 0.46 | 2.33 | 8.1 | 14.0 |
| SXP202B | All | 224.57 | Y | 501 | 0.23 | 2.7 | 6.3 | 28.8 |
| SXP214 | All | 4.58 | ? | 101 | 0.5 | 0.6 | 13.0 | 67.0 |
| SXP264 | All | 49.11 | ? | 101 | 0.2 | 2.5 | 4.7 | 36.3 |
| SXP280.4 | All | 127.6 | ? | 201 | 0.37 | 2.33 | 7.0 | 33.4 |
| SXP293 | All | 59.72 | ? | 101 | 0.37 | 1.63 | 41.4 | 108.0 |
| SXP327 | All | 45.9 | ? | 101 | 0.23 | 2.4 | 14.0 | 205.8 |
| SXP455 | All | 74.55 | ? | 101 | 0.3 | 0.88 | – | – |
| All | 209.7 | ? | 301 | 0.65 | 1.11 | – | – | |
| SXP504 | All | 270.1 | Y | 501 | 0.4 | 3.6 | 4.4 | 12.5 |
| SXP565 | All | 152.4 | Y | 301 | 0.2 | 1.29 | 3.4 | 24.6 |
| SXP756 | All | 393.6 | Y | 501 | 0.1 | 6.33 | 80.0 | 228.5 |
| Non-outburst | 11.404 | N | 31 | 0.57 | 1.37 | 9.7 | 25.3 | |
| SXP893 | 1283–3101 | 3.74 | ? | 51.0 | 0.59 | 1.0 | 2.9 | 26.5 |
| SXP967 | 2200–4700 | 101.37 | ? | 151 | 0.33 | 2.17 | 22.0 | 34.4 |
| SXP1323 | All | 7.91 | ? | 25 | 0.55 | 0.67 | 16.0 | 32.9 |
| All | 26.17 | ? | 101 | 0.43 | 1.08 | 24.0 | 49.8 |
Two folded light curves are shown to illustrate the principle, representing rather extreme cases. The light curve for SXP756 (Fig. 6) when folded on the orbital period shows very sharp peaks occupying a narrow phase range and showing a large asymmetry. The darker shaded region indicates the measured PS (here PS = 0.1) and the lighter shaded region indicates the region used in the calculation of the asymmetry (here PA = 6.33 indicates a very asymmetric peak).
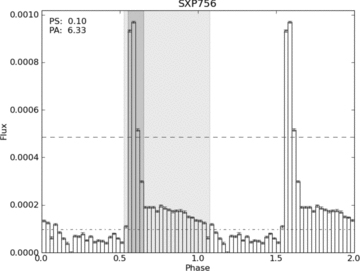
Folded light-curve analysis for SXP756 (folded on the 393.6 d period). The dashed horizontal lines indicate 10 and 50 per cent of the maximum value, where the PS (darker shaded region) and PA (lighter shaded region) are evaluated.
The folded light curve for SXP1323 folded on one of the two detected periods (Fig. 7) shows much more sinusoidal behaviour with PS = 0.43 and PA = 1.08.
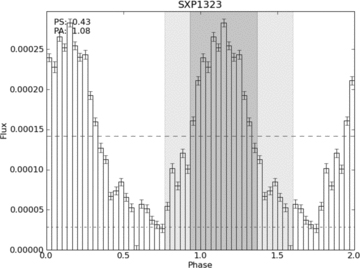
Folded light-curve analysis for SXP1323 (folded on the 26.17 d period). The dashed horizontal lines indicate 10 and 50 per cent of the maximum value, where the PS (darker shaded region) and PA (lighter shaded region) are evaluated.
The folded light-curve parameters for those SMC binaries for which the folded light-curve analysis was possible are shown in Fig. 8. It is apparent that while some of the SMC systems are clustered around the (PS,PA) = (0.5,1.0) point where sinusoids are expected to lie, others show a broad range of folded light-curve parameters.

Folded light-curve metrics for the SMC Be/X-ray binary sample. The solid lines indicate the approximate boundary between regions occupied by sinusoidal (likely aliased pulsations) and FRED-like (likely orbital) light-curve profiles.
5 DISCUSSION
The ‘Match’ column in Table 3 indicates those sources for which the period detected in optical monitoring is also seen in long-term X-ray light curves. In Be/X-ray systems, accretion and the resulting X-ray emission normally only occur when the neutron star is close to the Be star decretion disc, and there is no strong evidence for stable accretion discs forming around the neutron star. Hence, since the X-ray period can only realistically be due to orbital motion, we can use this to select a subset of sources where we believe the optical period is indicative of the orbital motion. These sources are SXP18.3, SXP46.4, SXP169.3, SXP172, SXP504, SXP565 and SXP756. There is a strong possibility that SXP280.4 also falls into this category, as the X-ray and optically derived periods are a factor of 2 different. Where the folded light curve can be parametrized, the majority of these sources fall far from the (0.5,1.0) point in Fig. 8 and so are clearly associated with FRED-like profiles.
Conversely, those sources where there is evidence that the optical period is of non-orbital origin cluster around the (0.5,1.0) point. For example, SXP1323 has two strong periods, which is difficult to explain as orbital motion. Furthermore, the two observed periods are strongly incompatible with being orbital based on the Corbet Porb - Pspin relation for a source with Pspin= 1323 s (Corbet 1986). Similarly, the 11.4 d period in SXP756 cannot be orbital, as the 393 d orbital period is established beyond doubt.
We therefore conclude that this ‘FRED-iness’ analysis and diagram is a useful tool to identify optical periods that are likely to be associated with orbital perturbations of a decretion disc based on the shape of the folded optical light curve. Both PS and asymmetry of the outbursts from disc disruption may be, to some extent, dependent on several orbital parameters – notably period and eccentricity. If we make the naive assumption that the decretion discs in Be/X-ray binary systems all recover with a similar time-scale, the PS parameter will only be effective when the disc recovery time is significantly less than the orbital period. Intuitively, more eccentric systems will show a wider range of interactions between the neutron star and decretion disc, while a completely circular system would give a much reduced optical modulation (due only to radial velocity shifts of the spectrum through a stationary filter). Overall, the method should be most sensitive for long-period, eccentric systems, but even reasonably low-eccentricity systems should provide a recognizable orbital signature in the optical light curve. In summary, then, a FRED-like folded optical light-curve profile is a strong indicator that the period is orbital. On the other hand, a very sinusoidal folded light-curve profile is often associated with non-orbital periodicities, but could still be indicative of orbital motion in a very low eccentricity system.
5.1 New orbit determinations
We have detected previously undiscovered periodicities in the OGLE II and III light curves for several sources, and confirmed previous optical modulations in many others. In some of these cases, the folded light-curve analysis gives a strong indication that the periodicity is derived from the orbit of the system, allowing us to propose them as orbital period determinations.
Specifically, the folded light-curve analyses for SXP31.0, SXP65.8, SXP264 and SXP327 provide strong evidence that the measured periods at 90.53, 111.04, 49.11 and 45.9 d, respectively, are indeed the orbital periods of these systems. Furthermore, the folded light curves of SXP280.4 and SXP967 show quite convincing evidence of non-sinusoidal (i.e. orbital) modulation at periods of 127.6 and 101.4 d, respectively (see Figs 9 and 10). The latter is a confirmation of the detection in Schmidtke et al. (2009a), but we note that this is a complex light curve, difficult to detrend and the orbital outbursts are only visible in a subset of the data.
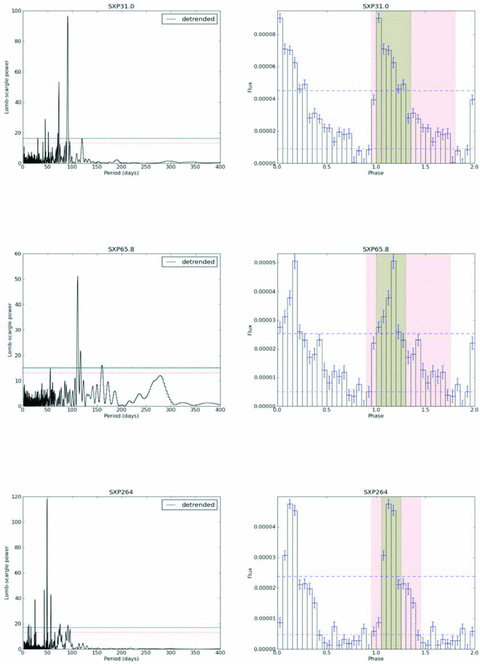
Periodograms (left) and folded light-curve analyses (right) for SXP31, SXP65.8 and SXP264, confirming previous optical periods, and strongly suggesting orbital origins for the detected periods. The dashed horizontal lines on periodograms indicate 99 and 99.9 per cent confidence limits. The dashed horizontal lines on folded light curves indicate 10 and 50 per cent of the maximum value, where PS and PA are evaluated (see the text for more details).
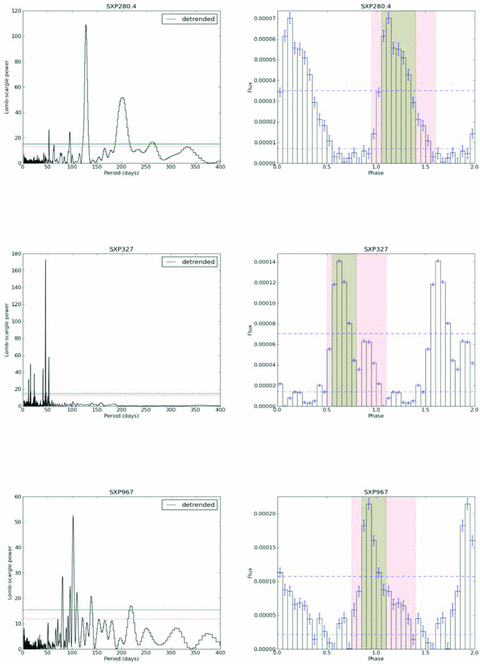
Periodograms and folded light-curve analyses for SXP280.4, SXP327 and SXP967, confirming previous optical periods, and strongly suggesting orbital origins for the detected periods. Dashed horizontal lines on periodograms indicate 99 per cent and 99.9 per cent confidence limits. Dashed horizontal lines on folded light curves indicate 10 per cent and 50 per cent of the maximum value, where PS and PA are evaluated (see the text for more details).
SXP2.37 (SMC X-2) is a particularly interesting case, which has been the cause of considerable speculation as to the origin of the periodicities seen in the light curve. Previous studies (Schurch et al. 2008) have seen periodicities at ∼6.2, 9.3 and 18.6 d, which could be interpreted as an orbital period of 18.62 d with harmonics. However, this interpretation was challenged by Schmidtke, Cowley & Udalski (2009b) who interpreted the signals as two aliased pulsations at 0.8592 d and 0.9008 d with the 18.62 d period deriving from the beat frequency between these two pulsations. However, our analysis (Fig. 11) shows that the transient 18.6 d period is firmly in the ‘orbital’ region of Fig. 8, and we thus conclude that this is by far the simplest explanation for the three periodicities seen in the periodogram. It has also now been shown independently from the X-ray data (Townsend et al. 2011) that fitting of the orbital Doppler shifts of the pulsar timing information during a long outburst yields an estimate of the orbital period of 18.38 ± 0.02 d.
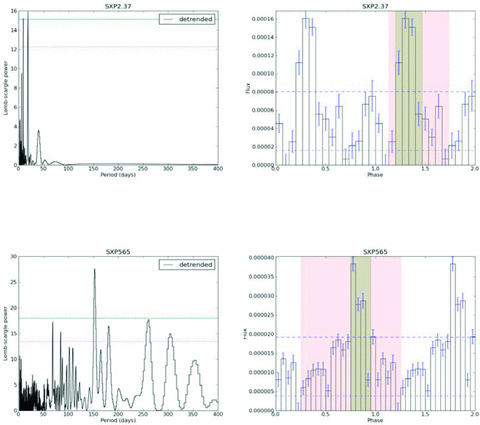
Periodograms and folded light-curve analyses for SXP2.37 and SXP565. The first indicates that the previously optical period at 18.6 d (now confirmed in the X-ray band) is of the orbital origin, and the second is the first optical detection of the previously detected X-ray period at 152.4 d. The dashed horizontal lines on periodograms indicate 99 and 99.9 per cent confidence limits. The dashed horizontal lines on folded light curves indicate 10 per cent and 50 per cent of the maximum value, where PS and PA are evaluated (see the text for more details).
For the first time, we confirm that the 152.4 d orbital period of SXP565, determined from X-ray measurements (Galache et al. 2008), can also be seen in the optical light curve (Fig. 11).
5.2 Sinusoidal variations
The periodicities observed in SXP3.34, SXP7.92, SXP15.3, SXP455 (209.7 d period), SXP893 and SXP1323 do not show the characteristics of orbital modulation of a decretion disc, but instead have folded light curves that are essentially sinusoidal in shape. Those in SXP3.34 and SXP893 (Fig. 12) are newly discovered periodicities, but for obvious reasons we do not propose them as new orbital periods. In particular, the period for SXP893, at 3.74 d, is incompatible with the usual placement of Be/X-ray binaries in the Porb - Pspin plane.
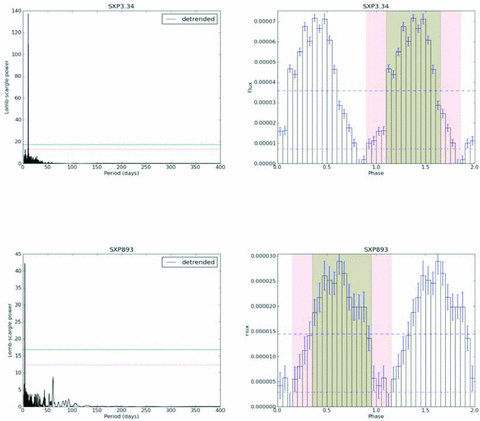
Periodograms and folded light-curve analyses for previously undetected signals in SXP3.34 and SXP893. Based on the folded light-curve analysis, these two periodicities are unlikely to be due to orbital motion. The dashed horizontal lines on periodograms indicate 99 per cent and 99.9 per cent confidence limits. The dashed horizontal lines on folded light curves indicate 10 per cent and 50 per cent of the maximum value, where PS and PA are evaluated (see the text for more details).
SXP1323 is an informative case as it shows two strong and persistent pulsations which manifest themselves as 7.91 and 26.17 d periods in the OGLE light curves. These periods have been attributed (Schmidtke & Cowley 2006) to the aliasing of non-radial pulsations at periods of 0.96 and 0.88 d in the Be star with the 1 d sampling of the data set. Thus, apparent periods at ∼8 and ∼26 d, with sinusoidal folded profiles, result from non-radial pulsations of the Be star in this system, and this is a plausible explanation for at least some of the other non-orbital periods determined.
As a further example, the second period in SXP756, of 11.4 d, is only visible outside of the sharp orbit-induced increases in brightness accompanying the Type I X-ray outbursts that are clearly separated by the 393.6 d orbital period. This secondary period has also been attributed to pulsations of the Be star or an orbiting disturbance in the outer decretion disc, and furthermore is seen to change slightly with time (Cowley & Schmidtke 2003; Coe et al. 2005).
5.3 SXP264 – a Rosetta Stone?
SXP264 is a strange but revealing object because, like SXP756, the optical light curve exhibits periods in addition to a well-established orbital modulation. Previous studies (Edge 2005) have indicated that it shows an ∼49 d orbital period in optical data. Our time-resolved analysis, however, shows a slightly different and more complex story. While the expected orbital period is stably detected for the first 10 yr of OGLE-II and OGLE-III monitoring, the peak in the time-resolved periodogram shifts significantly in the final 2 yr of OGLE-III measurements.
A deeper analysis is summarized in Fig. 13. The first 10 yr of data yield a folded light curve that shows a clear FRED-like orbital profile at the X-ray confirmed orbital period, as illustrated by a zoom on 2 yr of data in the left centre panel. Using the analysis methods of Section 4, the folded light-curve profile is parametrized by PS = 0.2 and PA = 2.5 which is entirely consistent with a FRED-like orbital modulation. The light curve for the final 2 yr however shows a much more sinusuoidal profile with a similar amplitude to that seen in the previous years, but with a visibly different period and shape (right centre panel of Fig. 13). While it is difficult to be certain with just a few cycles of the ∼80–90 d oscillations, the period of these sinusoidal variations may not be constant through the 2 yr.
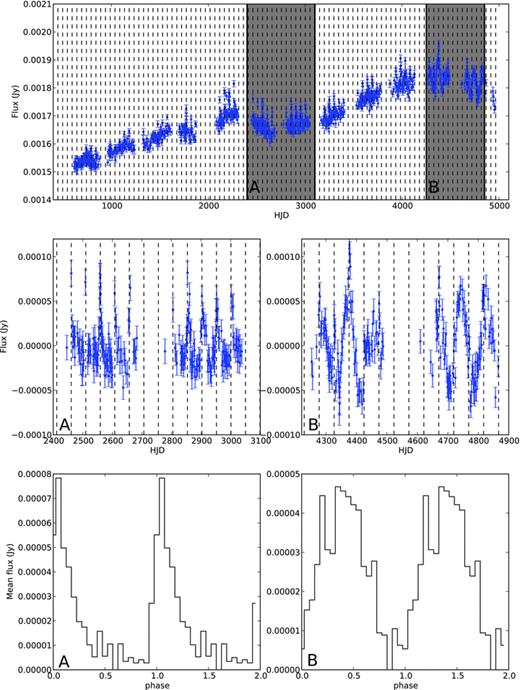
The changing shape of SXP264. Two subsections of the light curve show (A) clear orbital modulation on the 49.1 d period with a FRED-like folded shape, and (B) a strong sinusoidal modulation on a longer period, with the orbital modulation superimposed. The top panel shows the full OGLE II and III light curve, the middle panels are zoomed views of sections A and B, and the lower panels are the folded light curves – for panel A (lower), the data are folded on a 49.1 d period, while for panel B (lower), they are folded on an 80 d period. The dashed vertical lines in the top three panels indicate expected periastron passages based on the knowledge of the orbital period.
We interpret these changes in the light curve as a clear indication of both orbital-derived periodicities and non-orbital periodicities, the latter possibly being derived from aliased stellar pulsations, being visible in the same light curve, just as in SXP756. The presence of the sinusoidal variations in the last 2 yr of OGLE-III monitoring makes it more difficult to automatically detect the orbital variations, but visual inspection of the light curve of the last 2 yr around each expected periastron passage (shown by the dashed vertical lines in Fig. 13) finds clear increments in the flux at those times, showing that the orbital variations indeed continue. If the non-orbital periodicities at ∼80–90 d period do derive from aliased pulsations, we can only state that their true period is below 2 d; the degeneracy in the period reconstruction shown in Fig. 5 prevents us from unambiguously estimating the true period. There is no indication that the pulsation-derived and orbit-derived variations are mutually exclusive, as they co-exist in this light curve, but the fact that the two sections of the light curve show such clear changes indicates both the transient nature of these phenomena and the effectiveness of the light-curve shape as a way of distinguishing them.
5.4 Transient phenomena
Several of the sources discussed here display modulations that are transient in nature. In the case of orbital modulations, this is usually modelled by the growth and decline of the decretion disc around the Be star: when the disc is large, the orbital modulation is more pronounced. SXP18.3 is a good example – no periods may be detected when considering the entire light curve, but the orbital modulations are clearly detectable in a section encompassing approximately 2 yr of monitoring. Other examples may be less extreme but almost all the sources show some variability in the amplitude of the orbital modulation.
The sinusoidal modulations in systems, that we believe to be derived from aliased stellar pulsations, are also often seen to be transient in nature. While many are seen at all times throughout the OGLE II and III data sets with almost constant amplitude, others are seen to come and go, and even change in frequency (see the next section). Moreover, we sometimes see evidence of very abrupt changes in the pulsation-like behaviour – a classic example being given by SXP7.92 in Fig. 14 which shows three consecutive years of OGLE-III data. The year-to-year amplitude shows significant changes, but even more dramatic is the abrupt cessation of pulsations at TJD ≃ 2940.
Variations in the amplitude of the sinusoidal modulation of the I-band light curve of SXP7.92.
It is also appropriate to point out here a limitation of the methods used – the L-S method is insensitive to modulations superimposed on large non-periodic changes in the brightness of the underlying star. We have attempted to overcome this as far as possible by the use of detrending on appropriate time-scales in order to restore a level baseline against which the L-S method works best. However, in some systems, rapid underlying changes can dramatically reduce the sensitivity of the period searching for some parts of the data set. Thus, it is important to separate out transient phenomena intrinsic to the source itself and those introduced by changes in sensitivity to modulations.
5.5 Period drifters
One feature that has been suggested in past studies of the pulsations in Be stars in such X-ray binaries is the phenomenon of period drifting – i.e. slowly varying periods, probably associated with non-radial pulsations (NRP) from the Be star (Coe et al. 2002; Schmidtke & Cowley 2005). Though the expectation for such period changes being associated with NRP behaviour does not comfortably fit with stellar oscillation models, it is extremely unlikely that such changes could be associated with a changing orbital period on the time-scales of the OGLE data. Coe et al. (2002) discussed this possibility in the context of a possible triple system for SXP323. Since aliased non-radial pulsations are believed to be responsible for the sinusoidal modulations in many OGLE light curves, we have investigated this phenomenon of a drifting period in several systems where the periodicity is strong enough to determine the period accurately on annual time-scales.
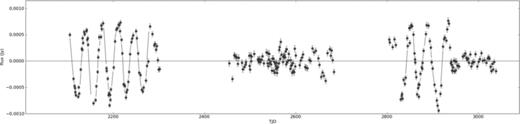
SXP214 shows a clear and steady drift in period – the first time a drifting periodicity has been determined in this system (Fig. 15). To determine the true drift rate, we assume that the measured period of around 4.55 d shown in the figure is actually the beat between the true period and the 1 d sampling of the OGLE data, but as stated previously, there is a degeneracy in this possible solution. Assuming a constant drift rate over the period of the observations, the degeneracy indicated in Fig. 5 leads to two possible solutions for the true period and drift: either a period of 0.818 d with an associated drift of +15.0 s yr−1 or a period of 1.277 d with a drift of −37 s yr−1.
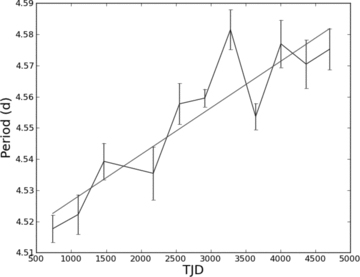
SXP323 shows a different behaviour (Fig. 16). While there is still an overall drift in period, it appears that there may not be a simple monotonic progression like that seen in SXP214. Nonetheless a simple linear fit to the data over the duration of the OGLE observations gives a change in the period of +4.92 s yr−1. Superimposed on this steady change is an apparent long-term modulation with a period of ∼2000 d, but the limited length of the data set means that the evidence for such a modulation is tentative at best.
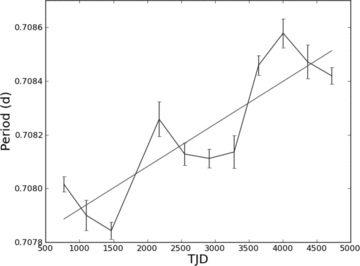
SXP701 also exhibits a convincing period drift over the duration of the OGLE observations. In this source, there is evidence for two possible observed periods (∼0.2845 and ∼0.282 d) with the main power jumping from the former to the latter after 2 yr. If a linear fit is made to the most persistent second period, then a period drift of +5.26 s yr−1 is obtained – similar to that seen in SXP323. We note that Schmidtke & Cowley (2005) obtained −2.6 s yr−1 for the period drift in this object from the shorter MACHO data set – the negative rate of change possibly arising from the misleading effect seen here in the OGLE data whereby different frequencies can take turns to dominate.
There has been some discussion in the literature as to whether the occasionally reported period drifts in Be stars (e.g. Stefl & Balona 1996) are real, or due to unresolved beating between similar periods with differently changing amplitudes. A discussion on this topic may be found in Baade (1999) but with no clear conclusions. Certainly the data presented here represent some of the longest time bases for such observations and further investigation into the OGLE archives for similar stars and periods may be profitable.
5.6 Superorbital periods
It has been suggested by Rajoelimanana et al. (2011) that these systems may exhibit optical modulation on longer time-scales than their orbital periods. Furthermore, those authors present results which indicate a possible correlation between orbital and superorbital periods (see fig. 45 in their paper). Though their plot looks convincing, care must be taken when creating such data sets. Since the total length of the OGLE data is ∼5000 d, any period longer than half of that must be treated with some scepticism. This effectively removes 6 of the 19 objects from their plot at the longer period end.
At the shorter period end, the work presented here casts doubt on the value for several periods quoted in Rajoelimanana et al. (2011) as orbital. If the shape of the modulation is strongly sinusoidal, then there is a very good chance that it arises as an alias of an underlying NRP. For example, the period of 36.4 d given for SXP7.92 appears from our work to be a strong case for being the alias of an NRP, as is also the case for SXP101 (21.9 d) and SXP3.34 (11.1 d) – the latter which Rajoelimanana et al. (2011) describe as a ‘marginal’ case anyway. If one removes these objects from their plot, together with the long-period ones, then the case for a relationship between orbital and possible superorbital periods in the remaining 10 objects is greatly reduced. There is no doubt that Be stars in the SMC (and probably elsewhere) show considerable creativity in their modes of variability (Mennickent et al. 2002), so great care must be taken when claiming actual periodicities when, instead, such observational changes may represent general long-term time-scales for change in the mass outflow from such stars. If such superorbital periods exist, then the warping of the circumstellar disc by an inclined neutron star orbital plane may provide an explanation (Martin et al. 2011).
5.7 The V-band light curves
Although the V-band data coverage is only ∼10 per cent of the I-band data, we searched the V-band data to determine if any of the types of periodicities were more systematically visible in that band. A few periodicities were significantly detectable in the V-band light curves, namely those in SXP7.78, SXP293 and SXP1323; another, SXP327, is detected but below a formally significant level. It is difficult to explain why these particular sources exhibit periodicities in the V-band while others do not. While we might expect persistent pulsations of the donor star to be easier to detect in the V-band than any decretion disc modulation, both confirmed orbital and suspected pulsation periods are included in this very small subset of detected periods. Although the amplitude of these modulations is certainly higher than average, we cannot say for sure that a large amplitude is the only reason for detection. Unfortunately, other sources that we might expect to detect on such a basis, such as SXP18.3 and SXP893, exhibit their modulation only transiently, and have only 16 and 4 V-band data points, respectively, in the relevant time periods. The data for SXP756 show only one periastron outburst, which is strong but obviously offers no basis for period detection. In all these cases then, we can state that the limited data coverage prohibits any possibility to detect the periodicities, and we should make no physical inference on the lack of detection in the V-band.
6 CONCLUSIONS
It is clear that the use of ground-based optical light curves like those in the OGLE-II and OGLE-III programs to determine the orbital periods of Be/X-ray binary systems can be an effective technique. But at the same time, it can be misleading, as other mechanisms can produce periodicities that, when combined with typical daily sampling, alias into the typical orbital period regime. This can be illustrated by the use of a  diagram (Fig. 17) in which we plot all the periodic signals detected, regardless of their suspected origin. The systems for which the modulation is known, or strongly suspected, to be of orbital origin, lie in the traditional zone of the diagram associated with the Be/X-ray binaries. However, the systems for which the origins of the periodicity may be aliased NRPs (or other sinusoidal variations of unknown origin) are outliers to this distribution, and coincidentally fall in the region traditionally associated with supergiant systems.
diagram (Fig. 17) in which we plot all the periodic signals detected, regardless of their suspected origin. The systems for which the modulation is known, or strongly suspected, to be of orbital origin, lie in the traditional zone of the diagram associated with the Be/X-ray binaries. However, the systems for which the origins of the periodicity may be aliased NRPs (or other sinusoidal variations of unknown origin) are outliers to this distribution, and coincidentally fall in the region traditionally associated with supergiant systems.
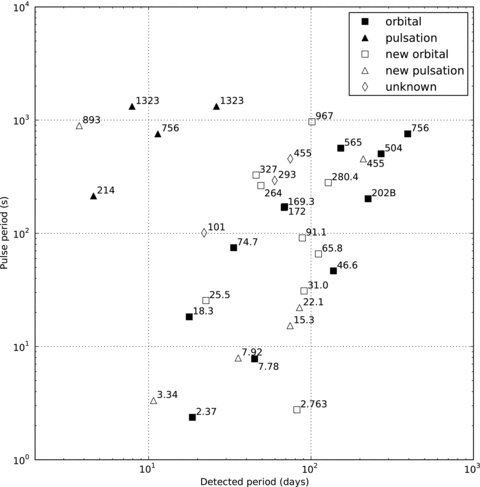
A  diagram constructed assuming all detected periodicities, coded to indicate the suspected mechanisms for the periodicities.
diagram constructed assuming all detected periodicities, coded to indicate the suspected mechanisms for the periodicities.
We present a method that allows the shape of the folded light curve to be used to distinguish between orbital periods and other mechanisms in at least some cases, but we point out that this is still not a guarantee. For now, the only unambiguous way of ascertaining the orbital periods of the Be/X-ray binaries comes from X-ray measurements, either by looking for periodic emission or using Doppler methods to fit the orbital parameters directly.
Footnotes
The OGLE project has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no. 246678 to AU. VM’s research is supported by the University of Cape Town and the National Research Foundation of South Africa.
REFERENCES



