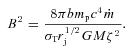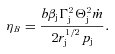-
PDF
- Split View
-
Views
-
Cite
Cite
Andrzej A. Zdziarski, Piotr Lubiński, Marek Sikora, The MeV spectral tail in Cyg X-1 and optically thin emission of jets, Monthly Notices of the Royal Astronomical Society, Volume 423, Issue 1, June 2012, Pages 663–675, https://doi.org/10.1111/j.1365-2966.2012.20903.x
Close - Share Icon Share
Abstract
We study the average X-ray and soft γ-ray spectrum of Cyg X-1 in the hard spectral state, using data from INTEGRAL. We compare these results with those from CGRO, and find a good agreement. Confirming previous studies, we find the presence of a high-energy MeV tail beyond a thermal-Comptonization spectrum; however, the tail is much softer and weaker than that recently published by Laurent et al. In spite of this difference, the observed high-energy tail could still be due to the synchrotron emission of the jet of Cyg X-1, as claimed by Laurent et al.
In order to test this possibility, we study optically thin synchrotron and self-Compton emission from partially self-absorbed jets. We develop formalisms for calculating both emission of the jet base (which we define here as the region where the jet starts its emission) and emission of the entire jet. We require the emission to match that observed at the turnover energy. The optically thin emission is dominated by that from the jet base, and it has to become self-absorbed within it at the turnover frequency. We find this implies the magnetic field strength at the jet base of  , where z0 is the distance of the base from the black hole centre. The value of B0 is then constrained from below by the condition that the self-Compton emission is below an upper limit in the GeV range, and from above by the condition that the Poynting flux does not exceed the jet kinetic power. This yields B0 of the order of ∼104 G and the location of the jet base at ∼103 gravitational radii. Using our formalism, we find the MeV tail can be due to jet synchrotron emission, but this requires the electron acceleration at a rather hard power-law index, p≃ 1.3–1.6. For acceleration indices of p≳2, the amplitude of the synchrotron component is much below that of MeV tail, and its origin is likely to be due to hybrid Comptonization in the accretion flow.
, where z0 is the distance of the base from the black hole centre. The value of B0 is then constrained from below by the condition that the self-Compton emission is below an upper limit in the GeV range, and from above by the condition that the Poynting flux does not exceed the jet kinetic power. This yields B0 of the order of ∼104 G and the location of the jet base at ∼103 gravitational radii. Using our formalism, we find the MeV tail can be due to jet synchrotron emission, but this requires the electron acceleration at a rather hard power-law index, p≃ 1.3–1.6. For acceleration indices of p≳2, the amplitude of the synchrotron component is much below that of MeV tail, and its origin is likely to be due to hybrid Comptonization in the accretion flow.
1 INTRODUCTION
Cyg X-1 is an archetypical and well-studied black hole binary. In the hard spectral state, its hard X-ray/soft γ-ray spectrum has been known to be hard below the maximum [in the EF(E) representation] at ∼100–200 keV. Above it, the spectrum shows a sharp cut-off, which then is followed by a high-energy tail, measured up to a few MeV (McConnell et al. 2002, hereafter M02).
We consider here the finding of Laurent et al. (2011, hereafter L11) of the tail at 0.4–2 MeV being very strong and hard, with the energy spectral index of α≃ 0.6 ± 0.2. The tail measured by L11 was found to be strongly polarized, which would imply it is due to synchrotron emission of the jet in this system. We calculate the average hard-state INTEGRAL spectra from the ISGRI and PICsIT detectors, and although we do find a high-energy tail above about the same energy as L11, it is weaker by about an order of magnitude as well as much softer, with α≃ 2. The weakness of the tail is also confirmed by an independent study of the average INTEGRAL SPI spectrum (Jourdain, Roques & Malzac 2012), and it is in agreement with the CGRO results of M02.
As known before, the high-energy tail can be well fitted by emission of non-thermal electrons forming a high-energy tail beyond the Maxwellian distribution, responsible for the bulk of the X-ray emission. On the other hand, the overall spectrum can also be fitted by purely thermal Comptonization (presumably in a hot accretion flow) and emission of power-law electrons with an exponential cut-off, which emission can originate in the jet.
In order to test the jet origin of the tail, we study emission of partially self-absorbed jets, such as that present in the hard state of Cyg X-1. We develop two formalisms. In one, a one-zone model of the jet base is developed. In the other, we model the emission of the entire jet (reformulating the model of Blandford & Königl 1979, hereafter BK79). We find that the optically thin emission is dominated by the jet base. In both approaches, we relate the magnetic field at the jet base to its height along the jet. We apply our model to Cyg X-1, using available measurements and upper limits. We find that the observed turnover energy, the flux at that energy, the MeV tail measurements, an upper limit on the emission in the GeV region and a measurement of the kinetic jet power allow a relatively precise determination of both the height of the jet base and its magnetic field.
2 NOTATION AND THE PARAMETERS OF CYG X-1

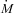 is the mass accretion rate, Pj is the sum of the total kinetic powers of the jet and counterjet,
is the mass accretion rate, Pj is the sum of the total kinetic powers of the jet and counterjet, 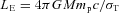 is the Eddington luminosity, σT is the Thomson cross-section, and me and mp are the electron and proton mass, respectively. We use then the symbol E for the observed photon energy.
is the Eddington luminosity, σT is the Thomson cross-section, and me and mp are the electron and proton mass, respectively. We use then the symbol E for the observed photon energy.We adopt the best-fitting values of Orosz et al. (2011) of M≃ 15 M⊙ (where M⊙ is the solar mass) and the inclination of the normal to the binary plane with respect to the line of sight of i= 27°. We assume that the jet and the disc have the same inclination. We use the best-fitting value of the distance to Cyg X-1 of Reid et al. (2011) of D= 1.86 kpc. The separation between the stars is a≃ 3 × 1012 cm, and the stellar luminosity is L*≃ 1039 erg s−1 (Caballero-Nieves et al. 2009; Orosz et al. 2011).
The opening angle of the jet in Cyg X-1 on the length scale of ∼1015 cm has been constrained by very long baseline array and Very Large Array observations to  (Stirling et al. 2001), and its velocity, to βj≃ 0.6 (Stirling et al. 2001; Gleissner et al. 2004; Malzac, Belmont & Fabian 2009), which corresponds to the Lorentz factor of
(Stirling et al. 2001), and its velocity, to βj≃ 0.6 (Stirling et al. 2001; Gleissner et al. 2004; Malzac, Belmont & Fabian 2009), which corresponds to the Lorentz factor of  . The kinetic jet power in the hard state of Cyg X-1 has been estimated as Pj≃ (1–3) × 1037 erg s−1 from the optical nebula presumably powered by the jet (Gallo et al. 2005; Russell et al. 2007). For M= 15 M⊙, LE≃ 2 × 1039 erg s−1, which gives pj∼ 10−2. On the other hand,
. The kinetic jet power in the hard state of Cyg X-1 has been estimated as Pj≃ (1–3) × 1037 erg s−1 from the optical nebula presumably powered by the jet (Gallo et al. 2005; Russell et al. 2007). For M= 15 M⊙, LE≃ 2 × 1039 erg s−1, which gives pj∼ 10−2. On the other hand,  is obtained for the observed average X-ray luminosity of LX≃ 1037 erg s−1 in the hard state of Cyg X-1 (Zdziarski et al. 2002) using an accretion efficiency of 0.05.
is obtained for the observed average X-ray luminosity of LX≃ 1037 erg s−1 in the hard state of Cyg X-1 (Zdziarski et al. 2002) using an accretion efficiency of 0.05.
The position angle of the radio jet on mas scale found by Stirling et al. (2001) (see also Rushton et al. 2011) is −(17°–24°). However, the sign of these values was misprinted as positive in Stirling et al. (2001). The actual position angle, conventionally measured from the north to the east, is negative, as stated, e.g., in Spencer et al. (2001).
A broad-band spectrum of Cyg X-1 in the hard state is shown in Fig. 1. In the radio/mm range, we show the fluxes at 2.3, 8.3, 15, 146 and 220 GHz (from table 1 of Fender et al. 2000). These fluxes can be joined by an α= 0 spectrum, which extends up to the turnover energy at Et≃ 0.1 eV in the IR. The two 0.05–0.24 eV broken power-law spectra show the fitted jet component for observations 1 and 2 (case 2, model c) of Rahoui et al. (2011, hereafter R11), with the fitted values of Et≃ 0.12 eV and 0.06 eV, respectively. The cyan crosses and error bars show the measurements of Persi et al. (1980) and Mirabel et al. (1996) of the total IR emission, which is dominated by the companion and its wind. Note that the fitted jet component represents a relatively small fraction of the total IR emission, especially at its high-energy end. The black 20 keV–5 MeV data points show the average ISGRI and PICsIT spectra obtained by us (see below), and the average 0.7–5 MeV COMPTEL spectrum from M02. The spectrum shown at 0.5–20 keV is an example of a typical hard-state spectrum, observed by BeppoSAX (Di Salvo et al. 2001). Note that this spectrum is strongly absorbed at low energies by an intervening medium; the magenta dot–dashed curve shows a model fit of the intrinsic spectrum. The 0.1–3 GeV upper limit is from AGILE (Sabatini et al. 2010), with the integral photon flux of <3 × 10−8 cm−2 s−1 (2σ). Given the large width of the energy band with a strong dependence of an implied monochromatic upper limit on the spectral shape, we use here the same EF(E) limit as that of fig. 3 of Sabatini et al. (2010). This approximately corresponds to the monochromatic flux of  cm−2 s−1 in the middle of the observed range at Eγ= 0.5 GeV. The present upper limit is a factor of a few below that of the CGRO/EGRET (given in Zdziarski & Gierliński 2004).
cm−2 s−1 in the middle of the observed range at Eγ= 0.5 GeV. The present upper limit is a factor of a few below that of the CGRO/EGRET (given in Zdziarski & Gierliński 2004).
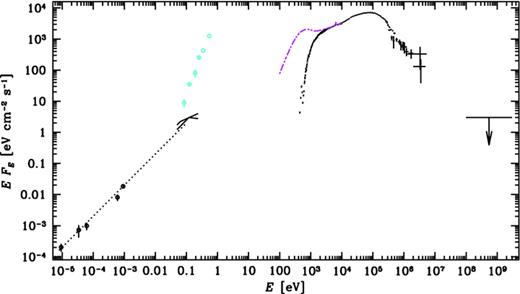
The hard-state radio to γ-ray spectrum of Cyg X-1. The five radio/mm fluxes are from Fender et al. (2000). The two IR broken power-law spectra show the jet component for observations 1 and 2 of R11. The dotted line shows an α= 0 radio spectrum extrapolated up to 0.1 eV. The cyan circles and error bars show the total IR fluxes (Persi et al. 1980; Mirabel et al. 1996), which are mostly from emission of the companion and its wind. The black X-ray and soft γ-ray data points above 20 keV show the IBIS and COMPTEL spectra. The spectrum below 20 keV, from BeppoSAX, represents a typical hard-state spectrum (which is absorbed by an intervening medium). The dot–dashed magenta curve shows a fitted model of the unabsorbed spectrum. The γ-ray upper limit is from AGILE (Sabatini et al. 2010). See Sections 2 and 3 for details.
3 THE X-RAY AND SOFT ![formula]() -RAY SPECTRA
-RAY SPECTRA
3.1 Analysis of the INTEGRAL data
We study INTEGRAL data from the IBIS instrument. We consider separately its two detectors, the ISGRI and PICsIT. We use data from the INTEGRAL revolutions from 22 to 877 (MJD 52626–55186, the years 2003–2009), which are available in the INTEGRAL Science Data Centre (ISDC). All public data with the off-axis angle <15° were selected (a <9° condition gave virtually the same spectra). The ISGRI and PICsIT data are used in the 19–500 keV and 0.25–5.4 MeV ranges, respectively.
We obtain both the average spectrum from all the above data and the average spectrum in the hard spectral state. The former is still dominated by the hard spectral state, which is due to Cyg X-1 having been mostly in it since the launch of INTEGRAL until 2010 June. Thus, the differences between the two sets are relatively minor. As the hard-state intervals, we take MJD 50350–50590, 50660–50995, 51025–51400, 51640–51840, 51960–52100, 52565–52770, 52880–52975, 53115–53174, 53540–53800, 53880–55375 following Zdziarski (2012). In addition, we also use the data from MJD 53188–53215, during which the spectra appeared typical to the hard state.
Our data analysis procedure is as follows. The ISGRI data have been reduced using the Offline Scientific Analysis (osa) 9.0 provided by the ISDC (Courvoisier et al. 2003), with the pipeline parameters set to the default values. For the spectral extraction we took into account also 22 strongest ISGRI sources in the Cyg X-1 neighbourhood. The PICsIT spectra were prepared using a non-standard software, optimized for handling Poisson-distributed data affected by a strong and variable background (Lubiński 2009). We have added a 1 per cent systematic error to each of the ISGRI and PICsIT data sets.
3.2 Average spectra
We have fitted our IBIS spectra for both all the observations and those in the hard state only with the model of hybrid Comptonization, eqpair, obtaining results similar to those of M02. The deconvolved spectra for the two data sets are shown in Figs 2(a) and (b), respectively. Since the fit results are similar for both data sets, and since the former contains also some contribution from soft/intermediate states, we describe the fit results only for the latter below. We note that the overall flux calibration for the PICsIT differs slightly from that for the ISGRI, yielding the PICsIT flux about 1.3 times higher than that of ISGRI in the overlapping energy range. In Fig. 2(a), the PICsIT spectrum is shown at its original normalization, whereas in Fig. 2(b) and 3 it is plotted renormalized to the level of ISGRI. We note that such differences between the normalization of different instruments are common, e.g. a similar difference was present for the PCA and HEXTE detectors onboard RXTE.

Comparison of average 20 keV–5 MeV spectra of Cyg X-1. (a) The spectra averaged over all INTEGRAL observations from 2003 to 2009. The black and blue spectra are from our analysis of the data from the ISGRI and PICsIT, respectively, fitted together by hybrid Comptonization. The red spectra are from the ISGRI and the Compton mode (ISGRI+PICsIT), as published by L11. The magenta and cyan crosses are the corrected ISGRI and Compton-mode spectra, respectively (Ph. Laurent, private communication). Each of those two pairs of spectra has been fitted by thermal Comptonization and a power law. The green spectra are from the SPI, fitted by two thermal-Compton components (Jourdain et al. 2012). (b) The average spectra in the hard spectral state from INTEGRAL and CGRO. The black and blue spectra are from the ISGRI and PICsIT (with the PICsIT data renormalized to the level of the ISGRI). The magenta, cyan and red symbols show the CGRO OSSE, BATSE and COMPTEL spectra, respectively, fitted together by hybrid Comptonization (M02). See Section 3 for details.
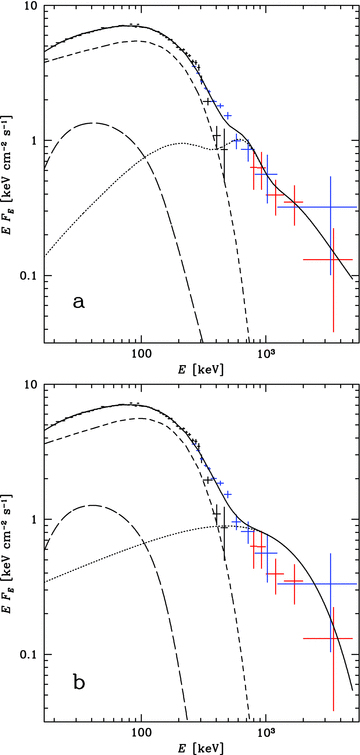
The average 20 keV–5 MeV spectra of Cyg X-1 from our analysis of the ISGRI (black) and PICsIT (blue) in the hard spectral state fitted by (a) hybrid Comptonization and reflection and (b) thermal Comptonization, reflection and an e-folded power law. For comparison, the COMPTEL spectrum from M02 (not taken into account in the fits) is shown in red. The short and long dashes and the solid curves show the thermal Compton scattering, Compton reflection and the total model, respectively. The dotted curve in (a) shows the Compton emission from the non-thermal e± plus the annihilation spectrum from the e± pairs, and in (b), the e-folded power-law component. See Section 3 for details.
Fig. 2(a) compares then our IBIS spectrum with that published in L11. The latter spectrum is from the ISGRI up to ∼400 keV, and at higher energies from the Compton mode, which utilizes both ISGRI and PICsIT. We see that those fluxes are substantially above ours, by about 30 per cent at 100 keV, and up to a factor of several above 1 MeV. However, it turns out (Ph. Laurent, private communication) that the published spectrum does not represent the average Cyg X-1 spectrum from the IBIS, and it does not correspond to the data used to calculate the polarization. The corrected average spectrum (Ph. Laurent, private communication) is shown in magenta and cyan in Fig. 2(a). Its ISGRI part agrees with our ISGRI spectrum almost perfectly. The Compton-mode spectrum still shows a disagreement with our PICsIT spectrum at ≳1 MeV, but now it is at a level of ∼(2–3)σ, compared to several σ discrepancy for the published spectrum.
In Fig. 2(a), we also show the average spectrum from the INTEGRAL SPI detector of Jourdain et al. (2012). This spectrum was obtained using all usable SPI Cyg X-1 data, which time interval spans 52797–55184, and which, similarly to our average, also includes some fraction of soft/intermediate-state data. Although there is an overall agreement with our results, the SPI spectrum is above ours at E≳30 keV, and shows a much harder decline up to 700 keV. This may be partly due to the ISGRI calibration with respect to the Crab spectrum, assuming that spectrum above 100 keV has α= 1.35, whereas current estimates give α= 1.24 ± 0.02 (Jourdain & Roques 2009). This also seems to explain our PICsIT spectrum being harder than that from ISGRI at ≳150 keV. We also see that the 2σ upper limit from SPI at 1.1–2.2 MeV is above our PICsIT flux but still somewhat below the corrected Compton-mode flux (of Ph. Laurent, private communication).
Fig. 2(b) compares then our INTEGRAL/IBIS average spectra for the hard state with the averaged ones for 1991–1994 measured by CGRO (M02). Given uncertainties in the instrument calibration, we have not applied any correcting factors to the BATSE and COMPTEL data, which were applied in M02 in order to normalize those data to the OSSE spectrum. We see that our IBIS spectrum is very similar to that from BATSE except for a slight difference in the normalization. At E≳0.4 MeV, the PICsIT, COMPTEL, BATSE and OSSE spectra all agree well.
The eqpair model is described in detail in Coppi (1999) and Gierliński et al. (1999). Our best-fitting parameters for the hard state are: the ratio of the power supplied to the Comptonizing plasma to that in the seed photons irradiating it of 6.8 ± 0.2; the fraction of the power supplied to the non-thermal electrons in the plasma of 0.16 ± 0.01; the Thomson optical depth of ionization electrons of τi= 0.79 ± 0.07; the relative strength of reflection (using the method of Magdziarz & Zdziarski 1995) of  . There is a relatively strong e± pair production in this model, with the total Thomson optical depth including pairs of 1.44, and at the equilibrium temperature of e± of kTe≃ 69 keV (note that these two quantities are not parameters of the model but instead result from the fitted and assumed parameters). We have assumed the compactness parameter of 10 of the blackbody seed photons at the temperature of 0.2 keV. The amount of pair production depends on the former, and the dependence on the latter is rather weak (see discussion in Gierliński et al. 1999). The model and its components, i.e. scattering by thermal electrons, scattering by non-thermal electrons plus pair annihilation (which is due to pairs produced by the non-thermal part of the spectrum), and Compton reflection, are shown in Fig. 3(a). An annihilation hump is seen in the second component. The decomposition of the Compton spectrum into the thermal and non-thermal components has been done using the method described in Hannikainen et al. (2005). We have assumed that the model has a 1 per cent systematic error. We have obtained a relatively good fit, χ2/dof = 94/58. The model is shown by the solid curve in Fig. 2(b). Note that although we have not fitted the COMPTEL data, our model agrees well with them.
. There is a relatively strong e± pair production in this model, with the total Thomson optical depth including pairs of 1.44, and at the equilibrium temperature of e± of kTe≃ 69 keV (note that these two quantities are not parameters of the model but instead result from the fitted and assumed parameters). We have assumed the compactness parameter of 10 of the blackbody seed photons at the temperature of 0.2 keV. The amount of pair production depends on the former, and the dependence on the latter is rather weak (see discussion in Gierliński et al. 1999). The model and its components, i.e. scattering by thermal electrons, scattering by non-thermal electrons plus pair annihilation (which is due to pairs produced by the non-thermal part of the spectrum), and Compton reflection, are shown in Fig. 3(a). An annihilation hump is seen in the second component. The decomposition of the Compton spectrum into the thermal and non-thermal components has been done using the method described in Hannikainen et al. (2005). We have assumed that the model has a 1 per cent systematic error. We have obtained a relatively good fit, χ2/dof = 94/58. The model is shown by the solid curve in Fig. 2(b). Note that although we have not fitted the COMPTEL data, our model agrees well with them.
We have then tested a two-component model in which the main part of the spectrum was fitted by thermal Comptonization without any non-thermal tail, and the observed tail was attributed to a power law with an exponential cut-off. We have found that the energy index, α, of the power law could not be constrained as the same χ2 was found in a wide range of α. However, since a possible physical interpretation of this component is a synchrotron contribution from the jet, we have fixed it at α= 0.6, for which this power law extrapolated down to the turnover energy of Et≃ 0.1 eV connects to the extrapolation of the optically thick jet emission with α≃ 0 (see Fig. 1). We have obtained the e-folding energy of Em= 1.2 ± 0.3 MeV and the 1-keV normalization of 0.11 cm−2 s−1, at χ2/dof = 96/57, i.e. only slightly worse than that of the hybrid-Compton model. The thermal plasma parameters are: the power ratio of 6.5 ± 0.2, τi= 1.52 ± 0.03 (with virtually no pair production, and with kTe= 69 keV) and  . We see that the two-component model predicts a hump at ∼2 MeV somewhat more pronounced than the hybrid-Compton model. The two components intersect at 410 keV. Thus, if the e-folded power law were strongly polarized, it could explain the polarization measured above 400 keV by L11.
. We see that the two-component model predicts a hump at ∼2 MeV somewhat more pronounced than the hybrid-Compton model. The two components intersect at 410 keV. Thus, if the e-folded power law were strongly polarized, it could explain the polarization measured above 400 keV by L11.
4 MODELS OF JET EMISSION
We study both a one-zone model of the jet base region and a jet model of the entire jet, and apply it to Cyg X-1. For our purposes, we define the jet base as the location at which the jet emission starts (assuming continuous jet emission, as in the model of BK79). This is likely to differ from the actual base where the jet is formed but the dissipation has not yet started.
As we confirm in Section 4.2, the base provides most of the optically thin jet emission. The jet base becomes optically thin at the turnover energy, Et. The value of this energy and the synchrotron flux at Et in Cyg X-1 have been measured by R11. This allows us to determine the normalization of the distribution of the emitting electrons as a function of the magnetic field. The synchrotron emission has to be self-absorbed within the jet base at Et, which imposes a relationship between the magnetic field, B0, and the location of the base, z0. Then the magnetic field strength is constrained from below by the requirement that the self-Compton emission in the γ-ray energy range does not exceed the observational upper limit. On the other hand, the magnetic energy flux cannot be greater than the observed jet kinetic energy.
4.1 One-zone model of the jet base
The radio up to far-IR emission of Cyg X-1 is flat in the dF/dE representation, ∝Eα, with α≃ 0 (see Fig. 1). This is usually interpreted as a partially synchrotron self-absorbed jet emission (BK79; Falcke & Biermann 1995). The emission at a given energy is self-absorbed from the base of the jet up to the height of z∝ν−1, and it is optically thin at higher z. The jet becomes optically thin at all z above Et. For a magnetic field of B∝z−1, conserving the magnetic energy flux (or for steeper dependencies), the optically thin emission at E > Et is dominated by the emission from the base of the jet. This follows, e.g., from the synchrotron flux, F(E) ∝B(p+ 1)/2, where p is the index of the electron power law. For B∝z−1, F(E) ∝z−(p+ 1)/2. The number of emitting electrons for a constant-velocity jet per ln z is ∝z. Thus, dF(E)/dln z∝z−α, where α= (p− 1)/2 is now the index of the optically thin synchrotron radiation. Integrating over z, we see that the first logarithmic interval of the jet length measured from its base provides about a half of the total emission for α= 0.5. Thus, in this section we adopt a one-zone approximation, with the emission region at z±z/2 (in the observer’s frame) along the jet. The validity of this approximation for optically thin emission is confirmed by our calculations of the synchrotron spectrum from the entire jet in Section 4.2.
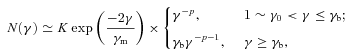
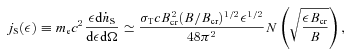
 is the critical magnetic field, h is the Planck constant, e is the electron charge and
is the critical magnetic field, h is the Planck constant, e is the electron charge and  denotes a photon production rate per unit volume. The formulation of the synchrotron coefficients in terms of σT and Bcr expresses the close correspondence between the synchrotron and Compton processes, discussed in Blumenthal & Gould (1970). The angle-integrated emissivity per unit volume is
denotes a photon production rate per unit volume. The formulation of the synchrotron coefficients in terms of σT and Bcr expresses the close correspondence between the synchrotron and Compton processes, discussed in Blumenthal & Gould (1970). The angle-integrated emissivity per unit volume is  , and the power emitted in all directions by a volume V in the jet frame is
, and the power emitted in all directions by a volume V in the jet frame is  . (We note that the similar formalism used in Z12 employed rates integrated over the source volume.) For power-law electrons, we have approximately
. (We note that the similar formalism used in Z12 employed rates integrated over the source volume.) For power-law electrons, we have approximately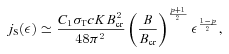

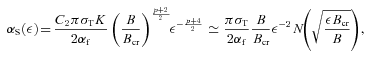
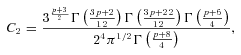
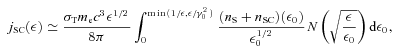
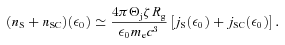
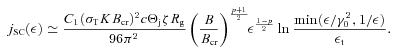
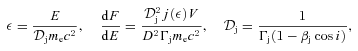
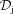 is the jet Doppler factor, and the flux transformation to the observed frame is for a steady-state source (Sikora et al. 1997). The flux component from the counterjet should be then added, for which the Doppler factor,
is the jet Doppler factor, and the flux transformation to the observed frame is for a steady-state source (Sikora et al. 1997). The flux component from the counterjet should be then added, for which the Doppler factor, 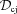 , corresponds to −βj. Hereafter, we take into account the counterjet in numerical calculations, but since the jet emission for our adopted Cyg X-1 parameters (i= 27°, βj= 0.6) is higher than that of the counterjet by
, corresponds to −βj. Hereafter, we take into account the counterjet in numerical calculations, but since the jet emission for our adopted Cyg X-1 parameters (i= 27°, βj= 0.6) is higher than that of the counterjet by 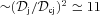 , we neglect the counterjet spectral contribution in some flux estimates. Here, the form of dF/dE above assumes the energy unit in F and E is the same, whereas they are often assumed to be different (e.g. as erg and eV, respectively), which, however, can be easily accounted for.
, we neglect the counterjet spectral contribution in some flux estimates. Here, the form of dF/dE above assumes the energy unit in F and E is the same, whereas they are often assumed to be different (e.g. as erg and eV, respectively), which, however, can be easily accounted for.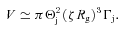
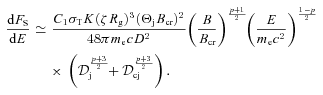
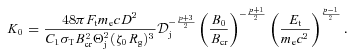
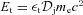 . The absorption optical depth in the observer’s direction can be approximated as
. The absorption optical depth in the observer’s direction can be approximated as 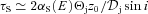 , where 2Θjz0/sin i is the path length going through the jet spine in the observer’s frame, and
, where 2Θjz0/sin i is the path length going through the jet spine in the observer’s frame, and 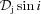 is the sine in the jet frame. Taking into account equation (14), we solve τS= 1 at Et for
is the sine in the jet frame. Taking into account equation (14), we solve τS= 1 at Et for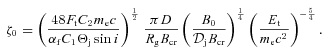
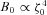 .
.4.2 The partially self-absorbed jet
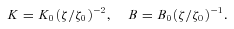
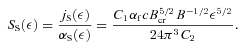
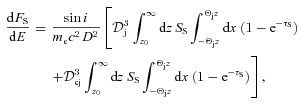
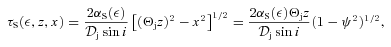
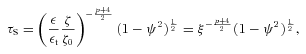
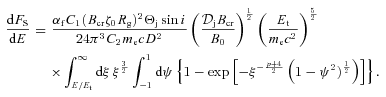
 ] needs to be added, including the turnover frequency transformed accordingly. In the optically thick case, E≪Et, and we can set the lower limit of the outer integration to 0. The resulting dimensionless double integral depends on p only, and we denote it as C3. Its values for p= 2, 3, 4 are ≃3.61, 2.10, 1.61, respectively. Then, dFS/dE in the optically thick case has α= 0,
] needs to be added, including the turnover frequency transformed accordingly. In the optically thick case, E≪Et, and we can set the lower limit of the outer integration to 0. The resulting dimensionless double integral depends on p only, and we denote it as C3. Its values for p= 2, 3, 4 are ≃3.61, 2.10, 1.61, respectively. Then, dFS/dE in the optically thick case has α= 0,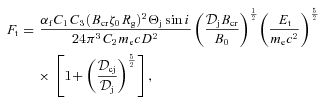
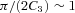 is equivalent to equation (15). This shows that the one-zone model provides a good approximation for the jet emission at Et (though, of course, the one-zone model does not yield the optically thick, α= 0, spectrum). We can also substitute
is equivalent to equation (15). This shows that the one-zone model provides a good approximation for the jet emission at Et (though, of course, the one-zone model does not yield the optically thick, α= 0, spectrum). We can also substitute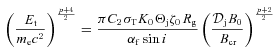
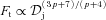 (for the jet), the optically thick emission is also beamed away from the jet axis in the jet frame, Ft∝ (sin i)(p− 1)/(p+ 4) and
(for the jet), the optically thick emission is also beamed away from the jet axis in the jet frame, Ft∝ (sin i)(p− 1)/(p+ 4) and 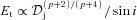 .
.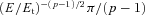 . We can then substitute Et of equation (23) to obtain the flux in the optically thin case,
. We can then substitute Et of equation (23) to obtain the flux in the optically thin case,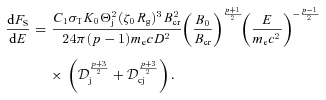
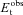 , given by
, given by
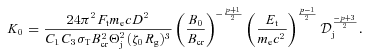
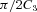 .
.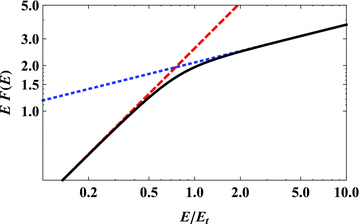
An example of the synchrotron jet spectrum (black solid curve) for p= 2.5, showing the spectral transition from the optically thick regime to the optically thin one. The normalization corresponds to the integral part of equation (21). The dashed and dotted lines show extrapolation of the optically thick and optically thin regime, respectively.
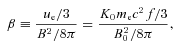
 . A contribution from ions would change the actual value of β. Here, ue is the energy density of the relativistic electrons, and f=ue/Kmec2 (see equation 42). Given the dependence of K and B on z of equation (16), the value of β is constant along the jet. We can then substitute K0 of equation (26) in equation (23), and solve it with equation (22) for B0 and ζ0. Neglecting the counterjet, we find
. A contribution from ions would change the actual value of β. Here, ue is the energy density of the relativistic electrons, and f=ue/Kmec2 (see equation 42). Given the dependence of K and B on z of equation (16), the value of β is constant along the jet. We can then substitute K0 of equation (26) in equation (23), and solve it with equation (22) for B0 and ζ0. Neglecting the counterjet, we find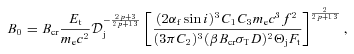
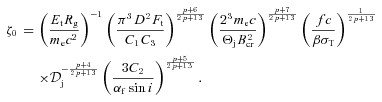
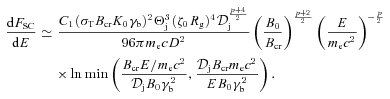
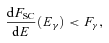
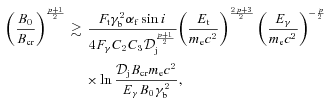
4.3 The jet parameters
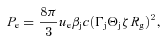
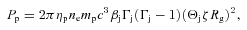
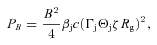
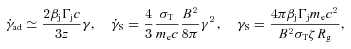
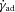 accounts for the expansion being in two dimensions only and we have assumed that the jet is conical. Appendix A considers in more detail the dependence of γS and the corresponding synchrotron photon energy on parameters of accreting sources with jets. We then define the Lorentz factor of electrons emitting at the local turnover energy, Et(ζ),
accounts for the expansion being in two dimensions only and we have assumed that the jet is conical. Appendix A considers in more detail the dependence of γS and the corresponding synchrotron photon energy on parameters of accreting sources with jets. We then define the Lorentz factor of electrons emitting at the local turnover energy, Et(ζ),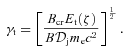
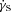 , and their adiabatic losses will dominate (neglecting Compton losses). Consequently, the cooling break energy below which adiabatic losses dominate will be approximately at
, and their adiabatic losses will dominate (neglecting Compton losses). Consequently, the cooling break energy below which adiabatic losses dominate will be approximately at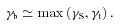
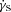 to the electron acceleration rate occurring on a gyroperiod time-scale,
to the electron acceleration rate occurring on a gyroperiod time-scale, 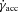 ,
,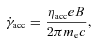

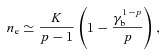
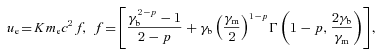
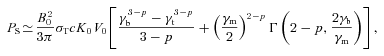
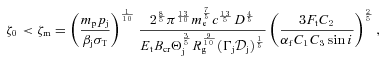
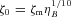 . This limit is only weakly depending on p through C2/(C1C3).
. This limit is only weakly depending on p through C2/(C1C3).4.4 Application to Cyg X-1
Here, we consider the full-jet formalism of Sections 4.2–4.3. In our model 1, we reproduce the MeV tail by the jet synchrotron emission. Given that the electrons responsible for X/γ-ray emission are cooled, γ > γb (see Appendix A), we have first considered a model with p= 1.2, at which the slope after the cooling brake is 2.2 and the X-ray energy index is α= 0.6. However, we have found that although the X-ray-emitting electrons do have γ > γb, there is a hard [α= (p− 1)/2 = 0.1] part of the spectrum above Et emitted by p= 1.2 electrons because γb≫γt. This results in the 1-MeV flux being above that observed. We have thus increased p to a value at which the model would match the 1-MeV flux. Such a model has p= 1.35, and it is shown in Fig. 5(a).
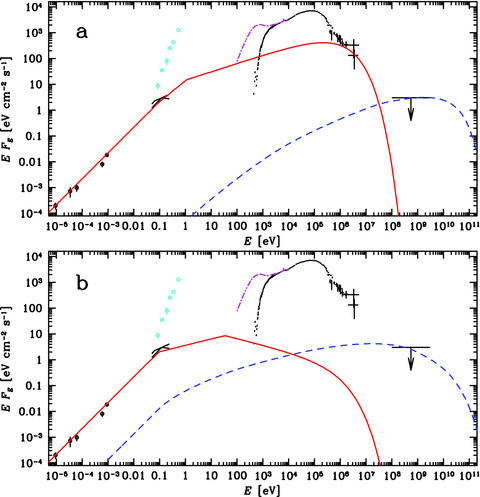
The data are the same as in Fig. 1. The red solid and blue dashed curves show the model synchrotron and Compton components, respectively. (a) Model 1 for p= 1.35, accounting for the observed MeV tail, which corresponds to the approximately maximum jet emission allowed by the data. (b) Model 2 for p= 2.5, in which case the jet emission is well below the MeV tail, which tail is then most likely emitted by hybrid plasma in the accretion flow. See Section 4.4 for details.
We have first imposed equipartition between the electron and magnetic pressure, β= 1 (see equations 28–29). This model yields the GeV flux somewhat above the observational upper limit, and a slight increase of B0, corresponding to β≃ 0.8, gives the GeV flux at that limit (see Fig. 5a). The model has ζ0≃ 860, B0≃ 8.7 × 103 G, ζm≃ 2100, γb=γS≃ 80 > γt≃ 20. The low value of p of the model results in a rather slight break at Et, from α= 0 to α= 0.175, which may not be compatible with the break found by R11. The spectrum steepens to α= 0.675 only around 1 eV.
The model has Pe≃ 8 × 1033 erg s−1, PB≃ 2 × 1033 erg s−1, Pp≃ 7ηp× 1034 erg s−1, PS≃ 1 × 1035 erg s−1. We note that Pp/ηp is much less than the estimated jet kinetic power, Pj, of Russell et al. (2007), which requires the presence of  times more protons than those corresponding to the emitting electrons. Increasing ζ0 (allowed by the GeV upper limit) decreases Pel, Pp and β, while it increases PB and it does not affect PS.
times more protons than those corresponding to the emitting electrons. Increasing ζ0 (allowed by the GeV upper limit) decreases Pel, Pp and β, while it increases PB and it does not affect PS.
In our model 2, we assume p= 2.5, motivated by p≃ 2.5 ± 0.5 found above Et in the black hole binary GX 339–4 (Gandhi et al. 2011). Imposing equipartition, β= 1, we obtain ζ0≃ 1.2 × 103, B0≃ 1.1 × 104 G, similar to those found for model 1, and Pp≃ 3ηp× 1036 erg s−1. The resulting GeV flux is >3 orders of magnitude below the observational upper limit. The model yielding the GeV flux at the upper limit, shown in Fig. 5(b), has ζ0≃ 0.8 × 103, B0≃ 3 × 103 G, β≃ 480, γS≃ 780, γt≃ 48 and ζm≃ 2600. Also, Pe≃ 3 × 1034 erg s−1, PB≃ 2 × 1032 erg s−1, Pp≃ 4ηp× 1037 erg s−1, PS≃ 1 × 1034 erg s−1. The value of Pp is only slightly above the range of Pj of Russell et al. (2007), and it can be within it for a slightly higher value of B0 (yielding a lower GeV flux). We note that the weak magnetic field of this model, with β≫ 1, is similar to that found in the γ-ray emitting region of the jet in Cyg X-3 (Z12). In both models 1 and 2, the jet in Cyg X-1 appears not dominated by e± pairs.
We note that the acceleration rate may take place only above certain minimum Lorentz factor, γ1≫ 1. In Z12, γ1∼ 103 was found necessary to explain the γ-ray spectrum of Cyg X-3 from Fermi (Fermi LAT Collaboration 2009). We have thus also considered a model with γ1= 103. The model 3 accounts for the MeV tail, and it has p= 1.6. The spectrum has an α≃ 0.5 power law above Et (due to electrons at <γ1 which are efficiently synchrotron-cooled), breaking at ∼0.5 keV to α≃ 0.8. Given the relative similarity of the spectrum to that of our model 1, we do not show it. Models with γ1≫ 1 and p > 1.6 are also possible. They do not explain the MeV tail, and are relatively similar to our model 2.
Our models 1 and 2 have γS > γt, which appears compatible with observations of relatively hard optically thin spectra above Et (Corbel & Fender 2002; Chaty et al. 2011; Gandhi et al. 2011). However, if jet magnetic fields are strong enough (which, in case of Cyg X-1, is compatible with its GeV upper limit), γS < γt is possible, which is indeed the case for our model 3. Then, the turnover region will correspond to cooled electrons. In this case, the electron index used in Sections 4.1–4.2 (which treatment is based on the synchrotron emission and absorption around Et) equals p+ 1, see equation (2), which will require certain modifications of our presented formalism.
4.5 Irradiation of the jet
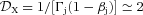 . The synchrotron losses will dominate over X-ray Compton losses (neglecting Klein–Nishina correction) for
. The synchrotron losses will dominate over X-ray Compton losses (neglecting Klein–Nishina correction) for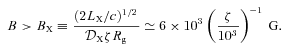
The Compton-scattered emission will be mostly directed back towards the X-ray source due to anisotropy of relativistic Compton scattering, and only a small fraction, a few per cent of the average Compton emission, will be directed towards the observer at i≃ 27° (Ghisellini et al. 1991; Dubus, Cerutti & Henri 2010; Z12). The direct emission will contribute to the high-energy soft γ-ray tail observed in Cyg X-1, and the one reflected from the accretion disc will contribute to the observed Compton reflection spectral component. On the other hand, the same kind of emission from the counterjet will be beamed along the jet axis, but it will, most likely, be blocked by the disc. Its absence may put some constraints on the outer radius of the disc (which may be relatively small in wind-fed accretion, which appears to take place in Cyg X-1).
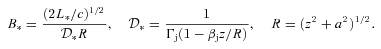
5 DISCUSSION AND CONCLUSIONS
In Section 3, we have calculated the average hard-state spectra from INTEGRAL ISGRI and PICsIT detectors over the period of 2003–2010. They are found to agree well with those from CGRO (M02). This is consistent with the long-term X-ray and radio behaviour of Cyg X-1 in the hard state being rather constant since at least 1995 (Zdziarski et al. 2011), and, in hard X-rays at >20 keV, since 1991 (Zdziarski et al. 2002).
We confirm the presence of a high-energy tail in the ≃0.5–5 MeV range. We find this tail to be very similar to that measured by CGRO, but much weaker than that claimed by L11. This has been independently confirmed by Jourdain et al. (2012), and then by the revised measurement of Ph. Laurent (private communication).
The origin of the tail is not clear. Although we find it is well fitted by hybrid Comptonization (presumably within a hot accretion flow), it can also be due to a separate spectral component, in particular synchrotron jet emission provided it has a high-energy cut-off at ∼1 MeV. If the measurement of the strong polarization above 0.4 MeV of L11 is confirmed, the latter interpretation has to hold. We note, however, that the polarization fraction of 0.67 ± 0.30 (L11) is difficult to explain even by synchrotron models, as it requires extremely well ordered magnetic fields. For example, polarization fraction of synchrotron radiation in blazars never exceeds 50 per cent, it very rarely reaches 40 per cent, and the typical values are of the order of ∼10 per cent (see e.g. Jorstad et al. 2007 and references therein). A polarization fraction of only ≃2.4 per cent was observed in the IR emission of the black hole binary XTE J1550–564 (Chaty et al. 2011), interpreted as optically thin synchrotron jet emission.
We note here that the electric vector position angle (hereafter EVPA) found by L11 is 140°± 15°. They claim it is at least 100° away from the position angle of the radio jet in Cyg X-1, implying the polarization is perpendicular to the jet. However, as we noted in Section 2, the actual position angle of the jet in Cyg X-1 is −(17°–24°) (Stirling et al. 2001; Rushton et al. 2011). Then, given that the EVPA is invariant upon adding ±180° (since the electric field of a photon oscillates, changing its sign), the EVPA of L11 can also be written as −(25°–55°), and thus it is approximately consistent with the observed jet angle. Polarization parallel to the jet can be produced if the magnetic field is dominated by the toroidal component, and/or due to compression of chaotic magnetic field in the internal shocks formed with fronts oriented (quasi-)perpendicularly to the jet axis.
In order to test whether the MeV tail may be the high-energy end of the optically thin jet synchrotron emission, we have developed a jet model allowing us to determine the parameters of its source. We noted that the synchrotron power-law spectrum begins at the turnover energy (Et), which corresponds to energy at which the base of the jet becomes optically thin. This implies that most of the optically thin emission originates in the base, which we model as a single zone. Combining the expressions for the synchrotron emission and absorption at Et, we find that the magnetic field and the height of the jet base satisfy a relation,  . Physically, it follows from the requirement of obtaining a given synchrotron flux, which yields the total number of electrons for a given B0, combined with the requirement of self-absorption at Et. The higher up the emission originates, the lower the electron density (for a conical jet) and thus the lower self-absorption optical depth for a given B0, which has to be compensated by an increase of B0.
. Physically, it follows from the requirement of obtaining a given synchrotron flux, which yields the total number of electrons for a given B0, combined with the requirement of self-absorption at Et. The higher up the emission originates, the lower the electron density (for a conical jet) and thus the lower self-absorption optical depth for a given B0, which has to be compensated by an increase of B0.
We have then developed a formalism for the synchrotron emission of the full jet (reformulating the model of BK79) at any energy. The emission is found by analytical formulae in the optically thick and thin regimes. We have confirmed the validity of the one-zone model for the optically thin emission. Our results give also detailed spectra in the transition region, near Et, as an integral. The spectra have a smooth transition between the two regimes, whereas R11 fitted the transition region as a broken power law. This may affect the accuracy of their values of Et and F(Et).
We then consider synchrotron self-Compton emission. For a given synchrotron flux at Et, a monochromatic flux from this process is  . We use the observational upper flux limit at 0.1–3 GeV from AGILE. This gives a lower limit on B0, and using the found relationship between z0 and B0, also on z0. Next, noting that the jet Poynting flux cannot exceed the total jet kinetic power estimated observationally (Gallo et al. 2005; Russell et al. 2007), we obtain upper limits on B0 and z0. We also calculate B0 and z0 from the assumption of equipartition between the magnetic field and relativistic electrons.
. We use the observational upper flux limit at 0.1–3 GeV from AGILE. This gives a lower limit on B0, and using the found relationship between z0 and B0, also on z0. Next, noting that the jet Poynting flux cannot exceed the total jet kinetic power estimated observationally (Gallo et al. 2005; Russell et al. 2007), we obtain upper limits on B0 and z0. We also calculate B0 and z0 from the assumption of equipartition between the magnetic field and relativistic electrons.
The above results are applied to Cyg X-1, using the values of Et and F(Et) of R11. This yields the location of the jet base at ∼103Rg, and B0∼ 104 G, relatively weakly dependent on the assumed value of p. We also find that in order for the observed MeV tail to be due to the jet synchrotron emission, p≃ 1.3–1.6, which are relatively low values for acceleration processes. We note that such acceleration indices are harder than that assumed before in X-ray jet models of black hole binaries, p≃ 2–2.3 (Heinz & Sunyaev 2003; Markoff et al. 2003; Merloni, Heinz & di Matteo 2003; Falcke, Körding & Markoff 2004; Heinz 2004). Low values of the acceleration index appear also to be in conflict with observations of optically thin synchrotron radio spectra (see e.g. Miller-Jones et al. 2004). On the other hand, values of p > 2 are consistent with standard acceleration models and observations of optically thin synchrotron spectra (e.g. Bednarz & Ostrowski 1998; Kirk et al. 2000). Still, our present understanding of electron acceleration appears insufficient to rule out models with p < 2.
We find that models with p > 2 can have a much higher kinetic jet power, due to a higher number of ions associated with the emitting electrons with a steep spectrum, as well as due to the magnetic field allowed then to be low by the GeV upper limit. Our model 2 has the kinetic power about equal to that determined observationally (Russell et al. 2007). This class of models, however, has the synchrotron MeV fluxes much below those of the MeV tail, and thus the tail cannot be due to that process. This, and the spectral proximity of the tail to the high energy break of the hot disc emission, may favour production of the tail in a hot accretion disc, as predicted by the hybrid Comptonization model (Poutanen & Coppi 1998; M02; Poutanen & Vurm 2009; Malzac & Belmont 2009).
These values of B0 and ζ0 are comparable to those recently obtained for XTE J1550–564 assuming a magnetic-electron equipartition in a one-zone model (Chaty et al. 2011), and for GX 339–4 (Gandhi et al. 2011). In these objects, the optically thin emission above the turnover frequency shows p≃ 2–3 (Corbel & Fender 2002; Chaty et al. 2011; Gandhi et al. 2011). Given the necessary cooling break (if those indices correspond to the un-cooled part of the electron distribution) corresponding to an energy between the IR and X-rays, the implied jet contribution to the X-rays is low. Interestingly, GX 339–4 also shows a hard X-ray tail on top of thermal Compton spectrum (Wardziński et al. 2002; Droulans et al. 2010) similar to that in Cyg X-1, which tail then has to have the origin different than synchrotron emission of the jet.
We note that the location of the jet base in Cyg X-1 at z0∼ 103Rg≃ 2 × 109 cm is in agreement with the observed large orbital modulation of the radio emission (which is due to orbital-phase dependent free–free absorption by the stellar wind from the donor), with, e.g., the depth of ≃30 per cent at 15 GHz, which requires the bulk of the radio flux to be emitted at a distance comparable to the orbital separation, z∼a≃ 3 × 1012 cm (Szostek & Zdziarski 2007; Zdziarski 2012). If the turnover frequency (emitted by the base) is νt∼ (2–3) × 1013 Hz (R11), νt/(15 GHz) ≃a/z0, in agreement with the prediction of the z∝ν−1 dependence of BK79.
On the other hand, both our estimate of the jet-base distance and the strong orbital modulation of the radio emission are not consistent with the interpretation in terms of the one-component BK79 model of ∼50 per cent of the 8.4 GHz emission observed to be resolved at the scale of ∼1014/sin i cm (Stirling et al. 2001). This interpretation yields the location of the τ= 1 region for 8.4 GHz emission at z∼ 1014 cm (Heinz 2006), which implies the jet base at z0∼ 3 × 1010 cm ∼104Rg, an order of magnitude above our estimates and implying virtually no orbital modulation at 8–15 GHz. A likely solution of this problem is an occurrence of a secondary dissipation event at a large radius [see a discussion in Zdziarski (2012)]. Then, the inner jet may still follow the BK79 model while the resolved emission is due to secondary dissipation. This also solves the problem of the Cyg X-1 jet power being much lower than the power inferred from the ring nebula. In particular, the jet power in our model 2 is about equal to that of Russell et al. (2007), and much higher than the theoretical estimate of Heinz (2006). [We note, however, that Heinz (2006) did not include in his jet power estimate the power of the ion bulk motion, which we find to be dominant (see Section 4.3).] We note that two dissipation regions at very different scales, one emitting IR to γ-rays close to the compact object, and the other emitting radio far away, are present in Cyg X-3 (Z12).
Finally, we point out that electrons in the jet base are subject to substantial irradiation by the central X-ray source. For  , its energy losses will be dominated by Compton up-scattering of X-rays. We also point out that although irradiation by the stellar photons is negligible at the jet base, it appears to dominate the synchrotron losses at distances along the jet comparable and larger than the orbital separation.
, its energy losses will be dominated by Compton up-scattering of X-rays. We also point out that although irradiation by the stellar photons is negligible at the jet base, it appears to dominate the synchrotron losses at distances along the jet comparable and larger than the orbital separation.
We thank J. Poutanen, F. Yuan and the referee for valuable comments, E. Jourdain for providing us with her published SPI spectrum in numerical form, and, especially, Ph. Laurent for his published and updated IBIS spectra and valuable discussion. This research has been supported in part by the Polish NCN grants N N203 581240, N N203 404939 and 362/1/N-INTEGRAL/2008/09/0.
Footnotes
Note that he transformed both the emission and absorption coefficients to the observer’s frame by multiplying by  (δ2 in his notation) whereas the latter should be divided by
(δ2 in his notation) whereas the latter should be divided by  , as well as transformation of the frequency should be taken into account. Consequently, the powers of δ in subsequent equations need be modified. Also, his emissivity is defined integrated over all directions and the magnetic pressure is assumed to be
, as well as transformation of the frequency should be taken into account. Consequently, the powers of δ in subsequent equations need be modified. Also, his emissivity is defined integrated over all directions and the magnetic pressure is assumed to be  .
.
Note that our β and Θj equal their 3ξ and h−1, respectively. Both the right-hand side of their equation (A2) and the term mec/3e should be multiplied by  . They neglect the relativistic effects and thus their counterjet flux equals that for the jet.
. They neglect the relativistic effects and thus their counterjet flux equals that for the jet.
REFERENCES
Appendix
APPENDIX A: Electron energy losses and the jet magnetic field
In this work, we have found that the relativistic electrons responsible for optically thin emission at E≫Et are efficiently cooled for models satisfying the observational constraints. Here, we consider the effect of synchrotron cooling more generally. The importance of the break due to the radiative losses for the electron and photon distributions in X-ray jet models (e.g. Markoff et al. 2003; Falcke et al. 2004) was earlier pointed out by Heinz & Sunyaev (2003), and then studied in detail by Heinz (2004). However, they have not calculated the possible values of this break as a function of the magnetic field in the jet.
The Lorentz factor at which the synchrotron losses equal the adiabatic losses, γS, is given by equation (36). Since B∝M−1/2 in most equipartition models (Heinz & Sunyaev 2003; Merloni et al. 2003), and z∝M for a given ζ, γS in those models is independent of M. We note that  is both the time-scale for the adiabatic losses and the characteristic time-scale a flow element of the jet spends at ∼z. Thus, for γ > γS, the loss process has enough time to significantly steepen the electron distribution. If the electrons are reaccelerated locally, their steady-state distribution steepens by unity with respect to the accelerated distribution. If the electrons are only advected from lower heights, a high-energy cut-off develops above γS.
is both the time-scale for the adiabatic losses and the characteristic time-scale a flow element of the jet spends at ∼z. Thus, for γ > γS, the loss process has enough time to significantly steepen the electron distribution. If the electrons are reaccelerated locally, their steady-state distribution steepens by unity with respect to the accelerated distribution. If the electrons are only advected from lower heights, a high-energy cut-off develops above γS.
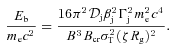


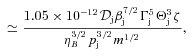
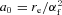 is the Bohr radius and re is the classical electron radius. We see that to achieve an un-cooled power law extending to hard X-rays, Eb∼mec2, in a jet with a moderate or high power requires a very low value of ηB.
is the Bohr radius and re is the classical electron radius. We see that to achieve an un-cooled power law extending to hard X-rays, Eb∼mec2, in a jet with a moderate or high power requires a very low value of ηB.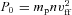 (where n is the proton density and vff is the free-fall velocity), to the pressure of the magnetic field,
(where n is the proton density and vff is the free-fall velocity), to the pressure of the magnetic field, 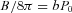 , where b is a coefficient that includes a hot-flow magnetization, a departure of the pressure in the hot flow from that of spherical accretion, and an overall scaling between the hot flow pressure and the jet pressure. The jet is launched from within a hot-flow radius, rjRg. We then assume conservation of the magnetic flux, B∝z−1. This yields
, where b is a coefficient that includes a hot-flow magnetization, a departure of the pressure in the hot flow from that of spherical accretion, and an overall scaling between the hot flow pressure and the jet pressure. The jet is launched from within a hot-flow radius, rjRg. We then assume conservation of the magnetic flux, B∝z−1. This yields