-
PDF
- Split View
-
Views
-
Cite
Cite
Dong Lai, Tidal dissipation in planet-hosting stars: damping of spin–orbit misalignment and survival of hot Jupiters, Monthly Notices of the Royal Astronomical Society, Volume 423, Issue 1, June 2012, Pages 486–492, https://doi.org/10.1111/j.1365-2966.2012.20893.x
Close - Share Icon Share
Abstract
Observations of hot Jupiters around solar-type stars with very short orbital periods (∼1 d) suggest that tidal dissipation in such stars is not too efficient so that these planets can survive against rapid orbital decay. This is consistent with recent theoretical works, which indicate that the tidal quality factor, Q★, of planet-hosting stars can indeed be much larger than the values inferred from the circularization of stellar binaries. On the other hand, recent measurements of Rossiter–McLaughlin effects in transiting hot Jupiter systems not only reveal that many such systems have misaligned stellar spin with respect to the orbital angular momentum axis, but also show that systems with cooler host stars tend to have aligned spin and orbital axes. Winn et al. suggested that this obliquity–temperature correlation may be explained by efficient damping of stellar obliquity due to tidal dissipation in the convection zone of the star. This explanation, however, is in apparent contradiction with the survival of these short-period hot Jupiters. We show that in the solar-type parent stars of close-in exoplanetary systems, the effective tidal Q★ governing the damping of stellar obliquity can be much smaller than that governing orbital decay. This is because, for misaligned systems, the tidal potential contains a Fourier component with frequency equal to the stellar spin frequency (in the rotating frame of the star) and rotating opposite to the stellar spin. This component can excite inertial waves in the convective envelope of the star, and the dissipation of inertial waves then leads to a spin–orbit alignment torque and a spin-down torque, but not orbital decay. By contrast, for aligned systems, such inertial wave excitation is forbidden since the tidal forcing frequency is much larger than the stellar spin frequency. We derive a general effective tidal evolution theory for misaligned binaries, taking account of different tidal responses and dissipation rates for different tidal forcing components.
1 INTRODUCTION
1.1 Tidal dissipation in planet-hosting stars: a conundrum
Recent measurements of stellar obliquity in transiting exoplanetary systems using the Rossiter–McLaughlin effect have shown that a significant fraction of hot Jupiter systems have misaligned stellar spin with respect to the planetary angular momentum axis (e.g. Hébrard et al. 2008; Johnson et al. 2009; Narita et al. 2009; Winn et al. 2009, 2010, 2011; Pont et al. 2010; Triaud et al. 2010; Moutou et al. 2011; Simpson et al. 2011). This suggests that a large population of hot Jupiters are formed through dynamical planet–planet scatterings (e.g. Rasio & Ford 1996; Weidenschilling & Marzari 1996; Zhou, Lin & Sun 2007; Chatterjee et al. 2008; Juric & Tremaine 2008) and, more importantly, through secular interactions between multiple planets or Kozai effect induced by a distant companion (e.g. Wu & Murray 2003; Fabrycky & Tremaine 2007; Nagasawa, Ida & Bessho 2008; Katz, Dong & Malhotra 2011; Naoz et al. 2011a,b; Wu & Lithwick 2011), although other effects involving star–disc interactions (Foucart & Lai 2011; Lai, Foucart & Lin 2011) and the assembly of protoplanetary discs (Bate, Lodato & Pringle 2010; Thies et al. 2011) may also play a role in producing spin–orbit misalignment.
Recent observations have also revealed an intriguing correlation between stellar obliquity Θ and effective temperature Teff: Winn et al. (2010) found that the misaligned systems tend to have hotter parent stars (Teff≳ 6250 K, corresponding to stellar mass M★≳ 1.3 M⊙), while the systems containing cooler stars have small obliquities. This trend was also found from a recent analysis of the stellar rotation velocities (Schlaufman 2010). Although this Θ–Teff correlation may indicate different planet formation mechanisms for stars of different masses, Winn et al. (2010) pointed out that Teff= 6250 K corresponds to the temperature below which stars contain a large subsurface convective envelope, and suggested that tidal dissipation in these stars leads to the damping of their obliquities. Indeed, the facts that effective temperature is more closely related to obliquity than stellar mass and that a few low-mass and long-period planets are exceptions to the Θ–Teff correlation (Winn et al. 2010, 2011) support the idea of tidal damping of spin–orbit misalignment in solar-type stars. Most recently, Triaud (2011) found a correlation between the obliquity and stellar age, suggesting a tidal alignment time-scale of about 2.5 Gyr.
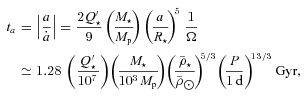
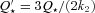 is the reduced tidal quality factor, k2 is the Love number, and
is the reduced tidal quality factor, k2 is the Love number, and 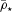 is the mean density of the star and
is the mean density of the star and  is the solar value. The inspiral time for a planet into its host star is (2/13)ta. The observations of hot Jupiters with the shortest orbital periods (such as WASP-18b, 0.94 d; WASP-19b, 0.79 d; and WASP-43b, 0.81 d; Hellier et al. 2009, 2011; Hebb et al. 2010) suggest
is the solar value. The inspiral time for a planet into its host star is (2/13)ta. The observations of hot Jupiters with the shortest orbital periods (such as WASP-18b, 0.94 d; WASP-19b, 0.79 d; and WASP-43b, 0.81 d; Hellier et al. 2009, 2011; Hebb et al. 2010) suggest 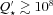 (see Brown et al. 2011). Such a large
(see Brown et al. 2011). Such a large 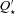 value is consistent with recent theoretical works (see Section 1.2) on the physics of tidal dissipation in planet-hosting solar-type stars (Ogilvie & Lin 2007; Barker & Ogilvie 2010, 2011; Penev & Sasselov 2011). On the other hand, in the often-used tidal evolution equations (see Section 2.5), the damping time for stellar obliquity Θ is
value is consistent with recent theoretical works (see Section 1.2) on the physics of tidal dissipation in planet-hosting solar-type stars (Ogilvie & Lin 2007; Barker & Ogilvie 2010, 2011; Penev & Sasselov 2011). On the other hand, in the often-used tidal evolution equations (see Section 2.5), the damping time for stellar obliquity Θ is 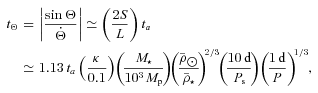
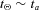 , and a tidal quality factor
, and a tidal quality factor 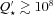 would not cause significant damping of Θ. To put it in another way, a reduction in the stellar obliquity is accompanied by a similar amount of orbital decay, Δa/a≃ (2S/L)ΔΘ/sin Θ. This poses a severe problem to the (otherwise appealing) tidal damping interpretation of the stellar obliquity–effective temperature correlation (Winn et al. 2010). One way out of this problem is to assume that the star’s convective envelope is weakly coupled to its radiative core, thus reducing the obliquity damping time for the stellar envelope (Winn et al. 2010). This assumption, however, is difficult to substantiate, as fluid instabilities may develop in the presence of large differential rotation (especially when the directions of rotation vary across the star) to quickly couple the rotations of the core and the envelope.
would not cause significant damping of Θ. To put it in another way, a reduction in the stellar obliquity is accompanied by a similar amount of orbital decay, Δa/a≃ (2S/L)ΔΘ/sin Θ. This poses a severe problem to the (otherwise appealing) tidal damping interpretation of the stellar obliquity–effective temperature correlation (Winn et al. 2010). One way out of this problem is to assume that the star’s convective envelope is weakly coupled to its radiative core, thus reducing the obliquity damping time for the stellar envelope (Winn et al. 2010). This assumption, however, is difficult to substantiate, as fluid instabilities may develop in the presence of large differential rotation (especially when the directions of rotation vary across the star) to quickly couple the rotations of the core and the envelope.To recapitulate, there is a conundrum concerning the efficiency of tidal dissipation in planet-hosting solar-type stars. On the one hand, the survival of hot Jupiters with shortest orbital periods and recent theoretical works both indicate that stellar tidal dissipation induces only modest or negligible orbital decay. On the other hand, the observed stellar obliquity–effective temperature correlation suggests that tidal dissipation is important in damping stellar obliquity.
In this paper, we show that tidal damping of spin–orbit misalignment can be much more efficient than tidal damping of the orbit. In another word, the effective tidal quality factor for the former process can be much smaller than the latter. This provides a natural resolution to the conundrum discussed above.
1.2 Basic idea
Many previous works on tidal evolution in hot Jupiter systems (e.g. Rasio et al. 1996; Sasselov 2003; Dobbs-Dixon et al. 2004; Barker & Ogilvie 2009; Jackson et al. 2009; Levrard et al. 2009; Hansen 2010; Matsumura et al. 2010) were based on the weak friction theory of equilibrium tides. This theory considers large-scale quadrupole distortion of the star, and parametrizes tidal dissipation by a dimensionless quality factor Q★ or, more generally, by a constant tidal lag time ΔtL. The theory was first formulated by Darwin (1880), and extensively applied to Solar system bodies (e.g. Goldreich & Soter 1966) and stellar binaries (see Zahn 2008, for a review). These applications have proved very useful since they provide empirical estimates or constraints on the values of Q★ for various systems. The most general (arbitrary orbital eccentricity and spin–orbit inclination angle) and correct equations for tidal evolution based on this theory were derived by Alexander (1973), and were also elaborated by others (e.g. Hut 1981; Eggleton, Kiseleva & Hut 1998; Correia & Laskar 2010).
Although it is well recognized that the equilibrium tide theory is a parametrized theory, with all the physics of tidal dissipation hidden in a single parameter Q★ or ΔtL (the Love number of the body can be absorbed into the definition of these parameters), it is not widely appreciated that the effective tidal Q★ for different processes (e.g. spin–orbit alignment and orbital decay) can be different. In another word, the widely used tidal evolution equations based on equilibrium tide theory can be incorrect even at the parametrized level. Indeed, the conundrum discussed in Section 1.1 arises because equation (2) assumes that the tidal Q★ for stellar obliquity damping is similar to the Q★ for orbital decay. In fact, this is incorrect, as we explain below.
There are three channels of tidal dissipations in solar-type stars.
Equilibrium tides. The large-scale quasi-static tidal bulge can be damped by turbulent viscosity in the star’s convective envelope (Zahn 1977, 1989). The major uncertainty involves how the effective viscosity derived from the mixing-length theory, ∼vtlt/3 (where vt and lt are the velocity and size of convective eddies, respectively), is reduced when the tidal forcing period Ptide is shorter than the convective turnover time τt=lt/vt (see Goodman & Oh 1997). Recent simulations (Penev, Barranco & Sasselov 2009, 2011) suggest that the reduction factor is about
 (for a limited range of Ptide), and the corresponding tidal Q★ well exceeds 108 (Penev & Sasselov 2011). An even larger Q★ will result if the reduction factor
(for a limited range of Ptide), and the corresponding tidal Q★ well exceeds 108 (Penev & Sasselov 2011). An even larger Q★ will result if the reduction factor  is used (see Ogilvie & Lin 2007).
is used (see Ogilvie & Lin 2007).Excitation and damping of internal gravity waves (Goodman & Dickson 1998; Ogilvie & Lin 2007; Barker & Ogilvie 2010, 2011). These waves (also called Hough waves when modified by rotation) are launched at the bottom of the star’s convective envelope and propagate towards the stellar centre. If they attain sufficient amplitudes at the centre, wave breaking will occur; this will produce significant tidal dissipation, corresponding to Q★∼ a few × 105(P/1 d)8/3 (assuming the orbital period P is much shorter than the spin period; see Barker & Ogilvie 2010). If the waves are reflected coherently at the stellar centre (e.g. by a small convective core) before non-linear breaking (Terquem et al. 1998), only weak dissipation will result (Q★≳ 108). The latest calculations by Barker & Ogilvie (2010, 2011) suggest that while the non-linear wave breaking certainly occurs for binary stars, it is probably unimportant for exoplanetary systems – this would explain the survival of short-period hot Jupiters against orbital decay (see Weinberg et al. 2011).
Excitation and damping of inertial waves. Recent theoretical works on dynamical tides in rotating planets (Ogilvie & Lin 2004, 2007; Ogilvie 2005, 2009; Papaloizou & Ivanov 2005; Wu 2005a,b; Goodman & Lackner 2009) and stars (Papaloizou & Savonije 1997; Savonije & Papaloizou 1997; Savonije & Witte 2002; Ogilvie & Lin 2007) have emphasized the importance of inertial waves driven by Coriolis force. When the tidal forcing frequency (in the rotating frame)
 is less than twice the spin frequency (Ωs), short-wavelength inertial waves can be excited. In particular, when these waves are confined to a spherical shell (as in the convection zone outside the solid core of a giant planet or in the convective envelope of a solar-type star), tidal disturbances are concentrated in very narrow regions (called ‘wave attractors’) where dissipation takes place (Ogilvie & Lin 2004; Goodman & Lackner 2009; Ogilvie 2009). It appears that this mechanism can explain the tidal Q (∼106) of giant planets and, when combined with internal gravity wave damping [see (ii) above], can also explain the dissipation required for the circularization of stellar binaries. However, for solar-type stars in hot Jupiter systems, the inertial wave dissipation mechanism is not expected to operate, since the tidal frequency
is less than twice the spin frequency (Ωs), short-wavelength inertial waves can be excited. In particular, when these waves are confined to a spherical shell (as in the convection zone outside the solid core of a giant planet or in the convective envelope of a solar-type star), tidal disturbances are concentrated in very narrow regions (called ‘wave attractors’) where dissipation takes place (Ogilvie & Lin 2004; Goodman & Lackner 2009; Ogilvie 2009). It appears that this mechanism can explain the tidal Q (∼106) of giant planets and, when combined with internal gravity wave damping [see (ii) above], can also explain the dissipation required for the circularization of stellar binaries. However, for solar-type stars in hot Jupiter systems, the inertial wave dissipation mechanism is not expected to operate, since the tidal frequency  (assuming circular orbit and aligned stellar spin) is larger than 2Ωs for typical parameters (e.g. Ps∼ 10 d and P∼ 1 d).
(assuming circular orbit and aligned stellar spin) is larger than 2Ωs for typical parameters (e.g. Ps∼ 10 d and P∼ 1 d).
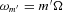 (where m′= 0, 2). As seen in the rotating frame of the star, the tidal frequencies become
(where m′= 0, 2). As seen in the rotating frame of the star, the tidal frequencies become 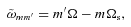
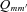 . Of particular interest is the (m, m′) = (±1, 0) components. They have
. Of particular interest is the (m, m′) = (±1, 0) components. They have 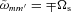 and the angular pattern frequency is
and the angular pattern frequency is 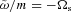 (the negative sign means it is retrograde with respect to the spin). They can generate inertial waves in the convection zone, and therefore can make a significant or dominant contribution to the tidal alignment of spin–orbit inclination. These components, however, do not contribute to orbital decay since they are static in the inertial frame and do not transfer energy (see Section 3).
(the negative sign means it is retrograde with respect to the spin). They can generate inertial waves in the convection zone, and therefore can make a significant or dominant contribution to the tidal alignment of spin–orbit inclination. These components, however, do not contribute to orbital decay since they are static in the inertial frame and do not transfer energy (see Section 3).In summary, while for aligned hot Jupiter systems, the effective stellar tidal Q★ governing orbital decay (and contributing to orbital circularization1) may be quite large (≳ 108) because channel (i) and channel (ii) (i.e. equilibrium tides and gravity waves) are ineffective and channel (iii) (inertial waves) is forbidden, for misaligned systems, inertial wave excitation becomes possible, which may provide an efficient damping mechanism for the spin–orbit misalignment.
The remainder of this paper is organized as follows. In Section 2, we develop a general effective theory for tidal evolution of misaligned binaries. It is ‘general’ because the theory takes account of the different responses (including both equilibrium and dynamical tides) of the star to different frequency components of the tidal potential. It is ‘effective’ because the responses and dissipations of different components are treated in a parametrized way. In Section 3, we present the tidal evolution equations due to inertial wave dissipation for misaligned hot Jupiter systems. We conclude in Section 4.
2 TIDAL EVOLUTION OF MISALIGNED BINARIES: A GENERAL EFFECTIVE THEORY
2.1 Tidal potential
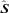 ) orbited by a companion (planet) of mass M′. The orbital semimajor axis is a and the orbital angular frequency is Ω. We allow for general spin–orbit inclination angle Θ (the angle between the spin angular momentum
) orbited by a companion (planet) of mass M′. The orbital semimajor axis is a and the orbital angular frequency is Ω. We allow for general spin–orbit inclination angle Θ (the angle between the spin angular momentum 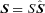 and the orbital angular momentum
and the orbital angular momentum 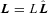 ), but consider circular orbit for simplicity. In the spherical coordinate system centred on M with the z-axis along
), but consider circular orbit for simplicity. In the spherical coordinate system centred on M with the z-axis along 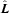 , the tidal potential produced by M′ can be expanded in terms of spherical harmonics:
, the tidal potential produced by M′ can be expanded in terms of spherical harmonics: 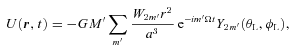
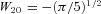 and
and 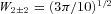 . To study the dynamical response of stellar fluid to the tidal forcing, we need to express U(r, t) in terms of Ylm(θ, φ), the spherical harmonic function defined in the inertial frame centred on M with the z-axis along
. To study the dynamical response of stellar fluid to the tidal forcing, we need to express U(r, t) in terms of Ylm(θ, φ), the spherical harmonic function defined in the inertial frame centred on M with the z-axis along 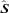 . This is achieved by the relation
. This is achieved by the relation 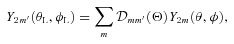
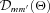 is the Wigner
is the Wigner 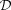 -matrix of l= 2 (e.g. Wybourne 1974), and we have chosen the y-axis along the direction
-matrix of l= 2 (e.g. Wybourne 1974), and we have chosen the y-axis along the direction 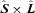 . The relevant
. The relevant 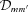 values are
values are 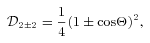
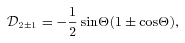
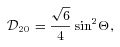
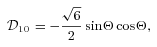
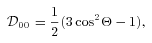
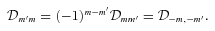
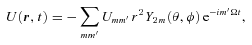
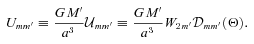
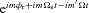 . Thus, the tidal potential is composed of various (mm′) components, each with forcing frequency m′Ω in the inertial frame. In the frame corotating with the star, the forcing frequency of the (mm′) component is
. Thus, the tidal potential is composed of various (mm′) components, each with forcing frequency m′Ω in the inertial frame. In the frame corotating with the star, the forcing frequency of the (mm′) component is 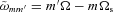 (equation 3), with the pattern rotation frequency
(equation 3), with the pattern rotation frequency 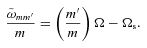
2.2 Ansatz for tidal response
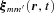 and Eulerian density perturbation
and Eulerian density perturbation 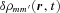 . In the absence of dissipation, these perturbations are proportional to
. In the absence of dissipation, these perturbations are proportional to 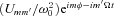 (where
(where 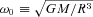 is the dynamical frequency of the star), exactly in phase with the tidal potential. When fluid dissipation is present, there will be phase shift between the fluid perturbation and the tidal potential. This phase shift, in general, depends on m, the forcing frequency (in the rotating frame)
is the dynamical frequency of the star), exactly in phase with the tidal potential. When fluid dissipation is present, there will be phase shift between the fluid perturbation and the tidal potential. This phase shift, in general, depends on m, the forcing frequency (in the rotating frame)  , as well as the intrinsic property (including the rotation rate) of the star. We write this phase shift as
, as well as the intrinsic property (including the rotation rate) of the star. We write this phase shift as 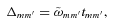
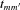 is the ‘lag time’ associated with the (mm′) perturbation. Thus, without loss of generality, we can write (mm′) component of the fluid displacement as
is the ‘lag time’ associated with the (mm′) perturbation. Thus, without loss of generality, we can write (mm′) component of the fluid displacement as 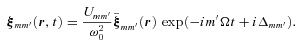
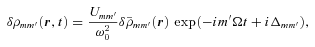
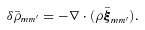
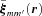 and
and 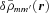 are proportional to
are proportional to 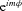 ; except for this factor, they are real functions. Also note that
; except for this factor, they are real functions. Also note that 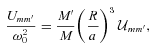
 . Thus,
. Thus, 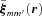 and
and  specify the amplitudes (and shapes) of the fluid perturbations after factoring out the ‘equilibrium’ dimensionless tidal distortion, (M′/M)(R/a)3.
specify the amplitudes (and shapes) of the fluid perturbations after factoring out the ‘equilibrium’ dimensionless tidal distortion, (M′/M)(R/a)3.Note that although our ansatz of the tidal responses is motivated by the weak friction theory of equilibrium tides, it is actually quite general, provided that one keeps in mind that the lag time  depends on m,
depends on m,  and the intrinsic property of the star.
and the intrinsic property of the star.
2.3 Tidal torque and energy transfer rate
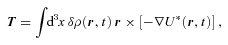
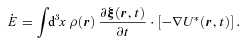
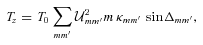
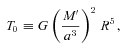
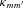 is the ‘Love coefficient’:
is the ‘Love coefficient’: 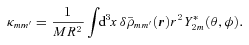
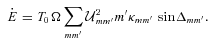
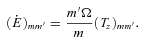
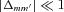 , we have
, we have 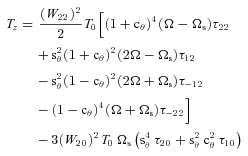
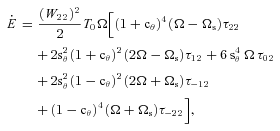
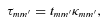
 .
.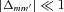 ) and contributes to the spin precession. Since Ty does change the spin–orbit elements, we will not consider it further. The x-component of T is
) and contributes to the spin precession. Since Ty does change the spin–orbit elements, we will not consider it further. The x-component of T is 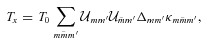
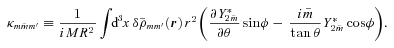
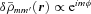 ,
, 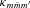 is non-zero only for
is non-zero only for 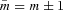 . If we define
. If we define 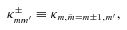
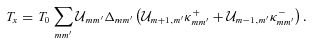
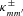 are related to the Love coefficients (equation 24) by
are related to the Love coefficients (equation 24) by 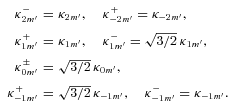
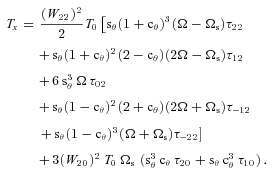
2.4 Tidal evolution equations
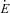 , the tidal evolution equations for the stellar spin Ωs and the orbital semimajor axis a are
, the tidal evolution equations for the stellar spin Ωs and the orbital semimajor axis a are 
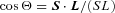 , where S=IΩs and L=μa2Ω. Using
, where S=IΩs and L=μa2Ω. Using 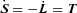 , we find
, we find 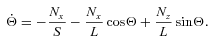
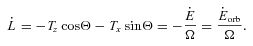
These evolution equations for  ,
,  and
and  [with
[with  and Tx given by equations (27), (28) and (35), respectively] are the most general tidal equations for circular binaries. They depend on seven independent ‘reduced’ tidal lag times
and Tx given by equations (27), (28) and (35), respectively] are the most general tidal equations for circular binaries. They depend on seven independent ‘reduced’ tidal lag times  , corresponding to the seven independent tidal forcing components. In general, each
, corresponding to the seven independent tidal forcing components. In general, each  depends on m,
depends on m,  and the intrinsic property (including Ωs) of the star.
and the intrinsic property (including Ωs) of the star.
2.5 Special case: weak friction theory of equilibrium tide
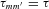 are the same for all seven tidal forcing components, we find
are the same for all seven tidal forcing components, we find 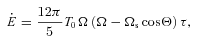
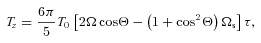
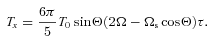
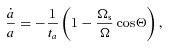
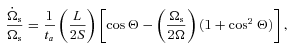

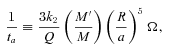
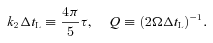
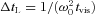 ]. These equations agree with those given in Alexander (1973) and others (Hut 1980; Eggleton et al. 1998).
]. These equations agree with those given in Alexander (1973) and others (Hut 1980; Eggleton et al. 1998).3 TIDAL TORQUE DUE TO INERTIAL WAVE DISSIPATION
 (in the rotating frame) of an inertial wave is related to its (local) wavenumber vector k by the dispersion relation (e.g. Greenspan 1968)
(in the rotating frame) of an inertial wave is related to its (local) wavenumber vector k by the dispersion relation (e.g. Greenspan 1968) 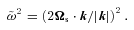
 .
. . [The (−1, 0) component has
. [The (−1, 0) component has  and is physically identical.] The tidal torque associated with this component can be read off directly from equations (27) and (35):
and is physically identical.] The tidal torque associated with this component can be read off directly from equations (27) and (35): 
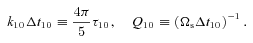
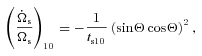
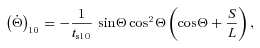
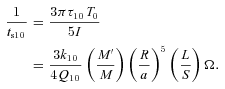
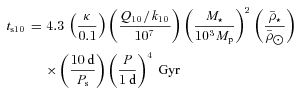
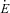 associated with this component is zero, giving
associated with this component is zero, giving 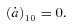
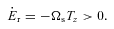
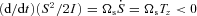 , so that
, so that 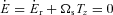 . Also note that the (1, 0) tidal force does not change the magnitude of the orbital angular momentum,
. Also note that the (1, 0) tidal force does not change the magnitude of the orbital angular momentum, 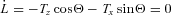 . So a circular orbit will remain circular.
. So a circular orbit will remain circular.Two interesting features of equation (52) are worth noting. First,  when Θ= 90°. Thus, if the (1, 0) tidal component is the only tidal force operating in the system, there could be many systems with the spin–orbit misalignment angle stalled around 90°. Secondly,
when Θ= 90°. Thus, if the (1, 0) tidal component is the only tidal force operating in the system, there could be many systems with the spin–orbit misalignment angle stalled around 90°. Secondly,  when cos Θ < −S/L. This implies that a retrograde system (
when cos Θ < −S/L. This implies that a retrograde system ( ) may evolve towards anti-alignment. Of course, other tidal components can also contribute to
) may evolve towards anti-alignment. Of course, other tidal components can also contribute to  (Section 2) and will weaken these features. However, with enough statistics of misaligned systems, it may be possible to test these or constrain k10/Q10.
(Section 2) and will weaken these features. However, with enough statistics of misaligned systems, it may be possible to test these or constrain k10/Q10.
A detailed calculation of Q10/k10 is beyond the scope of this paper. Previous works of tidal dissipation in rotating solar-type stars have focused on the m= 2 tide for aligned binaries (Papaloizou & Savonije 1997; Savonije & Papaloizou 1997; Savonije & Witte 2002; Ogilvie & Lin 2007) and demonstrated the importance of inertial waves. In the numerical study by Ogilvie & Lin (2007), inertial waves affect tidal dissipation in two ways: (i) short-wavelength inertial waves in the convection zone are damped by turbulent viscosity and (ii) inertial waves influence the excitation of gravity (Hough) waves in the radiative zone. Regarding (ii), they assumed that the inward-propagating Hough waves are damped near the stellar centre; this is appropriate for binary stars, but may lead to an overestimate of stellar tidal dissipation in hot Jupiter systems (Barker & Ogilvie 2010, 2011; see Section 1.2). Ogilvie & Lin (2007) found that when inertial waves are excited ( ), the tidal dissipation rate depends on
), the tidal dissipation rate depends on  in an erratic manner. On average, the energy dissipation rate in the convection zone is significantly increased (by one to three orders of magnitude, depending on the spin period) compared to equilibrium tides. For example, figs 3–6 of Ogilvie & Lin (2007) show that for a solar-type star at
in an erratic manner. On average, the energy dissipation rate in the convection zone is significantly increased (by one to three orders of magnitude, depending on the spin period) compared to equilibrium tides. For example, figs 3–6 of Ogilvie & Lin (2007) show that for a solar-type star at  , the tidal quality factor associated with inertial wave dissipation is
, the tidal quality factor associated with inertial wave dissipation is  for Ps= 10 d and
for Ps= 10 d and  for Ps= 3 d.
for Ps= 3 d.
Barker & Ogilvie (2009) reported the result of a calculation of the l= 2, m= 1 tidal dissipation for a specific F-type stellar model (appropriate for the hot Jupiter system XO-3) using the numerical method of Ogilvie & Lin (2007). Intriguingly, they found that at  , tidal dissipation is significantly enhanced, with the effective tidal Q∼ 106 (see their fig. 7). They suggested that this prominent feature arises from resonant excitation of the l=m= 1 Rossby mode. More systematic studies on the (m, m′) = (1, 0) tide for a range of stellar models (with different sizes of the convective envelope) would be useful.
, tidal dissipation is significantly enhanced, with the effective tidal Q∼ 106 (see their fig. 7). They suggested that this prominent feature arises from resonant excitation of the l=m= 1 Rossby mode. More systematic studies on the (m, m′) = (1, 0) tide for a range of stellar models (with different sizes of the convective envelope) would be useful.
4 CONCLUSION
The main point of this paper is that in close-in exoplanetary systems, when the stellar spin axis is misaligned with the orbital angular momentum axis, a new tidal dissipation channel opens up. This channel involves the excitation of inertial waves in the stellar convection zone, and is forbidden for aligned systems. Thus, tidal damping of spin–orbit misalignment can be more efficient than orbital decay. This may explain the stellar obliquity–effective temperature correlation observed by Winn et al. (2010) and the obliquity–age correlation noted by Triaud (2011), while still being consistent with the survival of hot Jupiters with very short orbital period (see Section 1.1).
On a more general level, this paper highlights the importance of treating tidal dissipation as being dependent on the tidal forcing frequency, the strength of tidal potential and the tidal processes involved (e.g. orbital decay versus spin–orbit alignment), in contrast to the equilibrium tide equations widely used in many applications and empirical works (see references in Section 1.2). Indeed, various studies of the physical mechanisms of tidal dissipation (e.g. Ogilvie & Lin 2004, 2007; Goodman & Lackner 2009; Barker & Ogilvie 2010, 2011; see also Zahn 2008, for a review of earlier works) have already made this point clear. While it is recognized that the weak friction theory of equilibrium tides (Darwin 1880; Goldreich & Soter 1966; Alexander 1973; Hut 1981; Eggleton et al. 1998) is a parametrized theory (with the tidal Q or lag time being the single parameter), we have shown in this paper that even at the parametrized level, its equations are sometimes inadequate or misleading, since different tidal processes (e.g. orbital decay versus spin–orbit alignment) may involve very different tidal dissipation mechanisms.
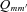 or lag times
or lag times 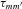 in the theory, related to the tidal responses for different Fourier components of the tidal potential. Obviously, such a system of equations with seven parameters (Section 2.4) is not convenient to use in real applications. For hot Jupiter systems, we suggest that a reduced system of equations involving two tidal Q parameters may be adopted. They are
in the theory, related to the tidal responses for different Fourier components of the tidal potential. Obviously, such a system of equations with seven parameters (Section 2.4) is not convenient to use in real applications. For hot Jupiter systems, we suggest that a reduced system of equations involving two tidal Q parameters may be adopted. They are 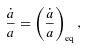
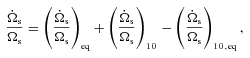
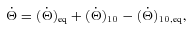
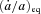 ,
, 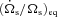 and
and 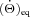 are given by equations (42)–(44) and characterized by the parameter k2/Q, while
are given by equations (42)–(44) and characterized by the parameter k2/Q, while  and
and 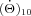 are given by equations (51) and (52) and characterized by the parameter k10/Q10. The expressions for
are given by equations (51) and (52) and characterized by the parameter k10/Q10. The expressions for 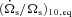 and
and 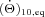 are the same as equations (51) and (52), except that the parameter k10/Q10 should be replaced by k2/Q. These equations (extended to eccentric orbits), combined with similar equations for planetary tides, can be used to assess and constrain the effects of tidal evolution in close-in exoplanetary systems.
are the same as equations (51) and (52), except that the parameter k10/Q10 should be replaced by k2/Q. These equations (extended to eccentric orbits), combined with similar equations for planetary tides, can be used to assess and constrain the effects of tidal evolution in close-in exoplanetary systems.I thank Josh Winn for update on current observations and useful discussion, and Gordon Ogilvie for helpful communication and comment. This work has been supported in part by AST-1008245.
Footnotes
Tidal dissipation in the planet also contributes to circularization.
REFERENCES



