On orbital period changes in nova outbursts

Abstract

1 INTRODUCTION

Classical novae are binary systems in which mass is transferred from a main-sequence star on to a white dwarf by Roche lobe overflow. The critical amount of mass that can be accreted on to the surface of the white dwarf prior to an outburst is a strongly decreasing function of the white dwarf mass (Truran & Livio 1986). At this mass limit, the temperature and density at the base of the accreted layer are high enough for hydrogen to ignite. The temperature then rises rapidly in a thermonuclear runaway (Starrfield, Sparks & Shaviv 1988) and the pressure at the base of the accreted layer becomes high enough that the accreted mass (and sometimes a little more) is ejected (e.g. Kovetz & Prialnik 1985).

Recurrent novae show outbursts at intervals of 10–80 yr (Webbink et al. 1987; Warner 1995). To account for the short time-scale between the outbursts, the white dwarf in a recurrent nova system must have a mass, M₁, close to the Chandrasekhar limit (e.g. Kato & Hachisu 1988, 1989). We consider in more detail the recurrent nova U Sco that most recently erupted in 2010. The evolved companion in U Sco has a mass of M₂ = 0.88 M_⊙ so the mass ratio, q=M₂/M₁ = 0.64, is relatively large.

In Section 2 we begin by re-examining all the previously proposed sources of orbital period change during a nova outburst. We first describe a simple model where the material carries away its specific angular momentum, then we include mass accretion on to the companion and frictional angular momentum losses as the binary moves through the common envelope. In Section 3 we propose a new mechanism for orbital period change involving the magnetic field on the secondary star. In Section 4 we apply our model to the outbursts in the recurrent nova U Sco.

2 OUTBURST MODEL

We consider first a simple model of the outburst where the ejected material carries away the specific angular momentum of the white dwarf. The non-degenerate mass accumulated on to the surface of the white dwarf is very thin. The envelope is ejected when the pressure at the surface of the white dwarf reaches a critical value of the order of P_crit = 10²⁰ dyn cm⁻² (e.g. Fujimoto 1982a,b; MacDonald 1983). The critical amount of mass that accumulates before a nova outburst is of the order of

1

for a white dwarf of mass M₁ and radius R₁. Both theory and observations suggest that all the material that has been accreted since the last outburst is ejected in the outburst.

The angular momentum of the binary star system is given by

2

where a is the separation of the two stars and the angular velocity, Ω, is given by Kepler’s law

3

Here the mass of the companion star is M₂ and the total mass of the system is M=M₁+M₂.

If the ejected mass carries away its specific angular momentum and all the mass is lost from the system, then the angular momentum removed from the system is

4

where a₁ is the distance of M₁ to the centre of mass of the binary

5

We neglect the spin of the white dwarf because it is not coupled to the binary orbit. By differentiating equations (2) and (3) we find the change in angular momentum of the binary

6

where Δa is the corresponding change in the separation of the system (due to mass lost) during the outburst, ΔM₁ is the change in mass of the white dwarf, ΔM₂ is the change in the mass of the secondary and ΔM is the change to the total mass of the system. For the case where all the ejected material is lost from the system, we choose ΔM₁=−Δm₁ and ΔM₂ = 0. We take the angular momentum loss from the system to be equal to that carried away by the ejected mass so that ΔJ=ΔJ_spec. With equations (2), (4) and (6) we find

7

As mass is lost from the system in the outburst the separation increases.

By differentiating equation (3) we find the period change during the outburst to be

8

and, for the case where the material carries away all of its specific angular momentum, with equation (7) we find

9

Since Δm₁ > 0 we see that the period of the system should increase during the outburst if the material carries away its specific angular momentum. In Fig. 1 we plot (ΔP/P)/(Δm₁/M) as a function of the mass ratio, q, for the different outburst models we consider. The solid constant line corresponds to this model where the mass ejected carries away its specific angular momentum.

Figure 1

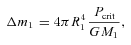
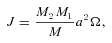
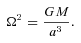
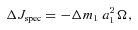
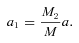
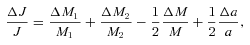
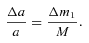
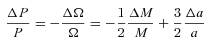
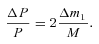
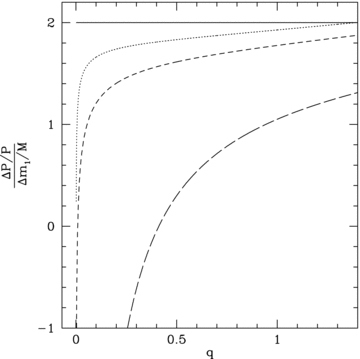
The change (ΔP/P)/(Δm₁/M) as a function of mass ratio, q=M₂/M₁. For the solid line the ejected mass just carries away its specific angular momentum (equation 9). The dotted line shows the case where accretion on to the secondary is considered (corresponding separation change in equation 11). The short-dashed line includes accretion on to the secondary and frictional angular momentum losses (corresponding separation change in equation 14). The long-dashed line takes into account the angular momentum change of the ejected material due to a magnetic field on the secondary that has R_A = 0.75 a (corresponding separation change in equation 29). We calculate the period change from the separation change with equation (8).

Open in new tabDownload slide

2.1 Mass accretion on to the companion

Now we consider the effect of a fraction of the ejected mass, β, that may be captured by the companion in the outburst. We take ΔM₁=−Δm₁ and ΔM₂=βΔm₁ so that

10

The corresponding change to the separation is then

11

(Shara et al. 1986), where q=M₂/M₁. This reduces to equation (7) with β = 0. In the absence of strong magnetic effects the maximum value of β is the fractional area of the companion’s radius. We can estimate the captured fraction of mass with

12

Because the secondary fills its Roche lobe, we can estimate the stellar radius with R₂=R_L, where

13

(Eggleton 1983). We compute the period change for this model including mass accretion on to the secondary star with equations (8) and (11). In Fig. 1 we plot (ΔP/P)/(Δm₁/M) as a function of the mass ratio for this model (dotted line). Generally, the separation change is not so large as the previous case where all the ejected mass left the binary system. However, for the largest mass ratios the period increases compared to the previous model.

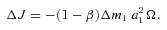
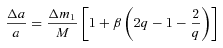
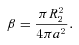
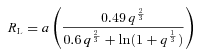
2.2 Frictional angular momentum losses

Angular momentum is lost from the binary system because of frictional angular momentum losses as the binary moves through the common envelope created by the ejected material (e.g. MacDonald 1980, 1986; Shara et al. 1986; Livio et al. 1990). This causes the separation of the system to decrease and so the period decreases too. They found that the separation change given in equation (11) becomes

14

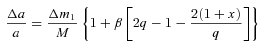
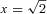(Shara et al. 1986), where for a very slow nova and x = 1 for a fast nova. We note that Livio, Govarie & Ritter (1991) suggest that assumptions made in deriving this mean that is valid only for novae with longer orbital periods. Again, we can find the period change for this model with equation (8). In Fig. 1 we plot (ΔP/P)/(Δm₁/M) as a function of the mass ratio for this model for a slow nova (short-dashed line). The separation change (and hence period change) here is, as expected, less than that for the previous case without the frictional angular momentum losses.

2.3 Magnetic braking and gravitational radiation

There are also two mechanisms that remove angular momentum from the system between outbursts that we consider briefly here. For systems with relatively long orbital periods (P≳ 3 h), magnetic braking provides the largest continual loss of angular momentum from the system. The rate of loss of angular momentum is given roughly by

15

(Rappaport, Verbunt & Joss 1983). For reasonable parameters this gives a time-scale of around a few billion years (e.g. Martin & Tout 2005).

For the closest systems (P≲ 3 h), gravitational radiation is the dominate cause of angular momentum loss from the binary system between outbursts. The rate of loss of angular momentum from two point masses in a circular orbit is

16

(Landau & Lifshitz 1951). This gives a time-scale of the order of several million years except for the very closest of systems. Neither gravitational radiation nor magnetic braking will have any effect on a system on an observable time-scale.

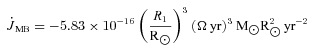
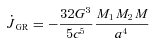
3 COROTATING EJECTED MATERIAL

In this section we consider an entirely new mechanism that can change the orbital period during a nova outburst. Suppose ejected material that moves within a critical radius (that depends on the magnetic field strength) of the secondary star couples to its magnetic field and so is forced to corotate with the binary orbit. The transfer of angular momentum between the ejected material and the binary orbit causes a change to the orbital period of the system.

The magnitude of the dipole magnetic field of the secondary is

17

where μ is the dipole moment and R is the distance to the secondary star. The magnetic field energy density is

18

The kinetic energy density of the ejected matter is

19

where ρ is the density of the ejected material. The ejection velocity, u, is in the range 300–3000 km s⁻¹ (Shara et al. 1986). From the continuity equation, close the the secondary star, we approximately have

20

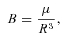
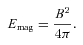
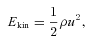
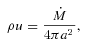
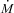where is the mass ejection rate from the primary white dwarf star. We approximate the average mass-loss rate with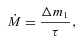

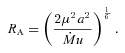
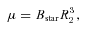
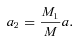
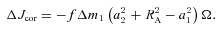
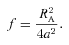
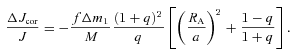
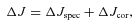
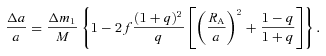
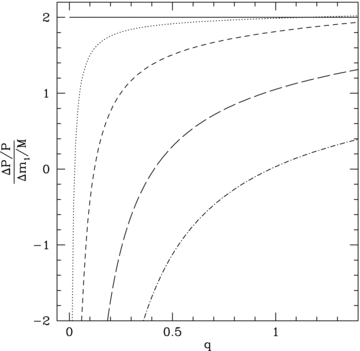
21

where τ is the time-scale over which the mass is lost.

The magnetic energy density is equal to the kinetic energy density at the Alfvén radius which we find to be

22

We consider this further in Section 4 where we apply our model to the recurrent nova U Sco. We parametrize the dipole moment with the magnetic field strength at the stellar surface, B_star, so that

23

where R₂ is the stellar radius of the companion which we find with equation (13).

The specific angular momentum of the ejected mass that is forced to corotate with the secondary is (a²₂+KR²_A) Ω assuming that the secondary is tidally locked. The distance from the centre of mass to the secondary star is

24

The constant K depends on the distribution of the material within the Alfvén radius. If it were distributed uniformly within a spherical shell, then K = 2/3. Because the density within the shell varies and the shell itself will not be perfectly spherical, we take K = 1. Thus, the angular momentum loss from the binary to the ejected material is given by

25

We estimate the fraction of the ejected mass that gains angular momentum in this way to be

26

Now with equations (2) and (25) we find

27

We substitute this into equation (6) with

28

ΔM₁=−Δm₁ and ΔM₂ = 0 to find the change in separation

29

We note that this reduces to equation (7) when there is no magnetic field. In Fig. 2 we plot (ΔP/P)/(Δm₁/M) as a function of the mass ratio for different values of the Alfvén radius. The larger magnetic fields are even capable of producing an overall decrease to the orbital period during the nova for small mass ratios.

Figure 2

The change (ΔP/P)/(Δm₁/M) as a function of mass ratio, q. For the solid line the ejected mass carries away only its specific angular momentum. All other lines take into account the angular momentum change of the ejected material due to a magnetic field on the secondary (corresponding separation change in equation 29). In order of decreasing height the lines have R_A = 0.25a (dotted line), R_A = 0.5a (short-dashed line), R_A = 0.75a (long-dashed line) and R_A = 0.9a (dot–dashed line).

Open in new tabDownload slide

In Fig. 1 we also plot (ΔP/P)/(Δm₁/M) for an Alfvén radius of 0.75a (long-dashed line) for comparison with the other models we have considered. For this strong magnetic field, the period change is smaller than with mass transfer to the secondary or frictional angular momentum losses. If a secondary star has a large magnetic field then it will significantly alter the orbital period change during a nova outburst.

There is a critical mass ratio where the additional term in equation (29) causes no change to the separation (or orbital period)

30

If q < q_crit then the ejected material that is forced to corotate with the secondary gains angular momentum, angular momentum is lost from the orbit and so the separation decreases. Similarly the orbital period change is smaller than previously predicted. However, if q > q_crit, then the material forced to corotate loses angular momentum and the orbital period increases. We plot this in the solid line in Fig. 3. We note that most observed systems have a mass ratio q≲ 1 (Ritter & Kolb 2003) because there is a critical mass ratio, that depends on M₂, above which the mass transfer becomes unstable (e.g. Smith & Vande Putte 2006). Hence in most systems the orbital period will decrease when the effects of a magnetic field are considered.

Figure 3

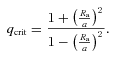
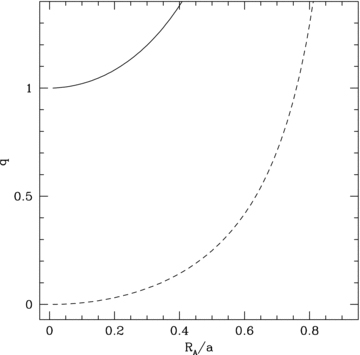
The solid line shows the critical mass ratio, q_crit, as a function of the Alfvén radius. If q < q_crit the period decreases due to the magnetic field, whereas if q > q_crit the period increases. Below the dashed line, the period change becomes negative.

Open in new tabDownload slide

We also plot the dashed line for the mass ratio below which the period change is negative. We see that for the larger magnetic fields it is possible that the orbital period may actually decrease for all mass ratios. This effect could be significant even for larger mass ratios. Frictional angular momentum losses only dominate for q≲ 0.01 (Shara et al. 1986) so this new mechanism potentially has a greater effect on the orbital period change.

4 RECURRENT NOVAE

There are now 10 recurrent novae known in our galaxy (the tenth one was discovered last year; Pagnotta et al. 2009) and one system in the LMC. In this group, U Sco has the fastest decline rate of the light curve in past outbursts, and the shortest recurrence period (11 yr since the last outburst, Schaefer 2001). It has outbursts recorded in 1863, 1906, 1917, 1936, 1945, 1969, 1979, 1987, 1999 (Schmeer 1999; Schaefer 2010) and 2010 (Schaefer et al. 2010) and others have likely been missed because of its proximity to the Sun (Schaefer 2004).

U Sco has a white dwarf with a mass M₁ = 1.55 ± 0.24 M_⊙ (Thoroughgood et al. 2001). We take the mass to be close to the upper limit for that of a white dwarf that is accreting matter before a supernova occurs, so M₁ = 1.37 M_⊙ (Hachisu et al. 2000b). This mass is consistent with the fact that U Sco has frequent outbursts. The orbital period is P = 1.230 5521 d (Schaefer 1990; Schaefer & Ringwald 1995). The radius of a non-rotating white dwarf is given approximately by

31

where M_ch = 1.44 M_⊙ is the Chandrasekhar mass (Nauenberg 1972), so the radius of the white dwarf in U Sco is R₁ = 0.003 R_⊙.

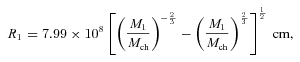
With equation (1) we find the mass accumulated before the outburst to be Δm₁ = 2.36 × 10⁻⁶ M_⊙, consistent with estimates for the 1999 outburst (Hachisu et al. 2000a) and the 2010 outburst (Banerjee et al. 2010; Diaz et al. 2010). We assume that all of this mass is ejected in the outburst. With this we find the ratio Δm₁/M = 1.05 × 10⁻⁶. The companion to the white dwarf in the system is a subgiant (Schaefer 1990) with a mass of M₂ = 0.88 M_⊙ and a radius of R₂ = 2.1 R_⊙ (Thoroughgood et al. 2001). We can take an upper limit of (the time-scale on which the optical light curve drops back to quiescence, Matsumoto, Kato & Hachisu 2003) and a lower limit of τ≈a/u (the binary crossing time). We consider a range of ejection velocities of the material between u = 300 and 3000 km s⁻¹. With this range of velocities, the lower limit to the ejection time is in the range 0.5–4 h.

In the left-hand side of Fig. 4 we plot the Alfvén radius (given in equation 22) for this system for different ejection velocities. For strong surface magnetic fields of a few thousand Gauss, it is a significant fraction of the binary separation. On the right hand side we show the fraction of mass that is ejected within the Alfvén radius (given in equation 26) of the secondary star for different mass-ejection velocities. Even for the strongest surface magnetic fields, the fraction of the ejected mass is always a small fraction of the total mass ejected.

Figure 4

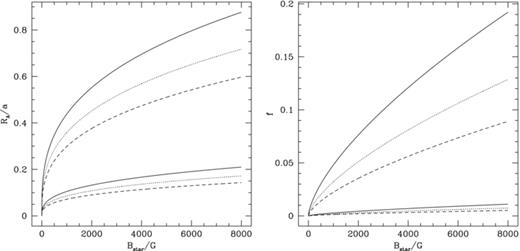
For a system with the parameters of U Sco. Left: the Alfvén radius, R_A/a, as a function of the magnetic field strength at the surface of the secondary, B_star. Right: the mass fraction, f, that is ejected within the Alfvén radius of the secondary. The upper three lines are for the upper limit on the nova time-scale, τ, and the lower three lines for the lower limit. In both plots, the solid lines are for ejection velocity u = 300 km s⁻¹, the dotted lines for u = 1000 km s⁻¹ and the dashed lines for u = 3000 km s⁻¹.

Open in new tabDownload slide

The mass ratio in U Sco is around q = 0.64. With Fig. 2 we see that with a large surface magnetic field, and hence Alfvén radius of the secondary star, the period change during an outburst in U Sco is significantly reduced. With a strong enough magnetic field the period change could even be negative (see Fig. 3). Measurements of the orbital period after the 2010 outburst are strongly encouraged in order to test this mechanism.

5 DISCUSSION AND CONCLUSIONS

We have considered the effect of a strong magnetic field on the surface of the secondary star on the orbital period change during a nova outburst. For most systems, the ejected material gains angular momentum as it couples to the magnetic field. The binary system loses angular momentum and the period change that results purely from mass loss decreases.

Our results show that, contrary to expectations, the orbital period in nova systems could decrease during outbursts, even in systems in which it would previously have been expected to increase (e.g. for P≳ 8 h, Livio et al. 1991). Very accurate determinations of pre- and post-outburst orbital periods in recurrent nova systems are therefore strongly encouraged. These could provide meaningful constraints of such quantities as the mass of the accreted envelope and the secondary’s magnetic field.

Magnetic fields of the order of a few kilogauss on the secondary star have been suggested previously (e.g. Meyer-Hofmeister, Vogt & Meyer 1996; Warner 1996). While such strong fields are typical of magnetic Ap stars, they may be less common in the secondaries of cataclysmic variables. However, high magnetic fields have been discussed for cataclysmic variables of shorter periods by Meintjes & Jurua (2006). The subgiant companion in U Sco is expected to be synchronously rotating with the orbit, with a period of 30 h, which is very fast for a subgiant. However, studies of late-type stars show that high fields can be expected for fast rotators (e.g. Noyes, Weiss & Vaughan 1984).

We thank Jim Pringle for helpful discussions.

REFERENCES