-
PDF
- Split View
-
Views
-
Cite
Cite
Baojiu Li, John D. Barrow, On the effects of coupled scalar fields on structure formation, Monthly Notices of the Royal Astronomical Society, Volume 413, Issue 1, May 2011, Pages 262–270, https://doi.org/10.1111/j.1365-2966.2010.18130.x
Close - Share Icon Share
Abstract
A coupling between a scalar field (representing the dark energy) and dark matter could produce rich phenomena in cosmology. It affects cosmic structure formation mainly through the fifth force, a velocity-dependent force that acts parallel to particle’s direction of motion and proportional to its speed, an effective rescaling of the particle masses and a modified background expansion rate. In many cases, these effects entangle and it is difficult to see which is the dominant one. Here, we perform N-body simulations to study their qualitative behaviour and relative importance in affecting the key structure formation observables, for a model with exponential scalar field coupling. We find that the fifth force, a prominent example of the scalar-coupling effects, is far less important than the rescaling of particle mass or the modified expansion rate in its effects on the matter power spectrum and mass function. In particular, the rescaling of particle masses is shown to be the key factor leading to less concentration of particles in haloes than in Λcold dark matter, a pattern which is also observed in previous independent coupled scalar field simulations.
1 INTRODUCTION
The nature of the dark energy (Copeland, Sami & Tsujikawa 2006) driving an apparent acceleration of the universe has been a cosmological puzzle for more than a decade. Models incorporating scalar fields are the most popular proposal to explain it, not only because of their mathematical simplicity and phenomenological richness, but also because the scalar field is a natural ingredient of many high-energy physics theories. A scalar field contributes a single dynamical degree of freedom which can interact indirectly with other matter species through gravity or couple directly to matter, producing a fifth force on the matter which creates violations of the Weak Equivalence Principle (WEP). This second possibility of direct coupling to matter was introduced with the hope that such a coupling could potentially alleviate the coincidence problem of dark energy (Amendola 2000) and has since then attracted a great deal of attention (see e.g. Bean & Magueijo 2001; Amendola 2004; Koivisto 2005; Lee, Liu & Ng 2006; Boehmer et al. 2008; Bean et al. 2008; Bean, Flanagan & Trodden 2008; Boehmer et al. 2010 and references therein). It was also investigated in the context of theoretical studies of the cosmological variation of the fine structure constant (Sandvik, Barrow & Magueijo 2002).
If there is a direct coupling between the scalar field and baryons, then the baryonic particles will experience a fifth force, which is severely constrained by observations, unless there is some special mechanism to suppress the fifth force effects. This happens in chameleon models, where the scalar field (the ‘chameleon’) gains mass in high-density regions (where observations and experiments are performed) whereas the fifth force effects are confined to undetectably small distances (Khoury & Weltman 2004; Mota & Shaw 2007). A common approach which avoids such complications is to assume that the scalar field couples only to the dark matter, an idea seen frequently in models with a coupled dark sector (e.g. Caldera-Cabral, Maartens & Schaefer 2009; Valiviita, Maartens & Majerotto 2010; Simpson, Jackson & Peacock 2010). In this work our scalar field will not be chameleon-like as this case has already been investigated elsewhere (Li & Zhao 2009; Zhao et al. 2010; Li & Zhao 2010).
A scalar field coupled to (dark) matter could affect cosmic structure formation in various ways. First, the background expansion rate gets modified, which will lead to faster or slower clustering of matter particles; secondly, the coupling effectively rescales the mass of the particles for the coupled matter species, changing the source term of the Poisson equation, which receives a further contribution from density perturbations of the scalar field; thirdly, the coupling to the scalar field produces a fifth force between matter particles, helping matter to cluster more strongly; finally, there is an extra velocity-dependent force on the coupled particles, which can be viewed either as a frictional force or as part of the fifth force under a frame transformation, and this force, being attractive, also promotes matter clustering.
Not all of these effects are always manifest. In fact, in some coupled-scalar-field models one or more then one of them could be negligible. An example is the model considered in Li & Zhao (2009, 2010), where only the third effect, i.e. the fifth force, is non-negligible. This situation is also assumed in some other studies of the effect of a fifth force on structure formation, e.g. the ReBEL model (Nusser, Gubser & Peebles 2005), where a Yukawa-type extra force is added while the background cosmology is taken to be the same as Λ cold dark matter (ΛCDM).
In other, more general, models, however, a coupling between scalar field (dark energy) and (dark) matter often not only produces the fifth force, but equally likely creates other effects listed above. Examples are the models investigated in Maccio et al. (2004), Baldi et al. (2010), Li & Barrow (2010), where the modified expansion rate, varying particle mass and frictional force are all non-negligible. The situation then becomes complicated here, because these could have both positive and negative effects on the structure formation, which are difficult to disentangle.
In order to clarify the importance of all these effects, we have to make detailed analysis by suppressing one or more of these effects and then comparing the results – which is our primary aim of this work, at least for the model considered (Li & Barrow 2010). In particular, we would like to see how those above effects affect the non-linear matter power spectrum, mass function and profiles of dark matter haloes. The latter is quite interesting, as it has been shown in Baldi et al. (2010) and Li & Barrow (2010) that the coupling, which is supposed to boost clustering of matter, does indeed suppress the density in the inner region of the haloes, possibly due to the frictional force and/or the varying mass effects. A clarification of the importance of these effects is also relevant to the general model tests. As we mentioned above, the majority of the investigations of the fifth force to date focus only on the fifth force itself but neglect the other effects. Yet, the same physics responsible for the fifth force will often create other associated effects, and the latter must be taken into account for the sake of consistency. If it turns out that the fifth force effects do not dominate the others, then a model-independent test of the fifth force might be difficult to obtain in cosmology, since different models predict very different background expansion and mass variation.
Since we want to investigate the non-linear regime, we will use the N-body simulation technique introduced in Li & Zhao (2010), Li & Barrow (2010) and also applied in Li (2010), Li, Mota & Barrow (2010a,b). Note that other approaches to N-body simulations for (coupled) scalar field and related models, without solving the scalar field equation of motion explicitly, have also been used in various previous work (e.g. Maccio et al. 2004; Linder & Jenkins 2003; Mainini et al. 2003; Kesden & Kamionkowski 2006; Springel & Farrar 2007; Farrar & Rosen 2007; Keselman, Nusser & Peebles 2009, 2010; Hellwing & Juszkiewicz 2009; Hellwing, Knollmann & Knebe 2010; Baldi 2010; Baldi & Pettorino 2010; Baldi & Viel 2010; Hellwing, Juszkiewicz & van de Weygaert 2010; De Boni et al. 2010; Baldi et al. 2010), while the new feature of our approach is that we solve the scalar field equation directly (in the quasi-static limit; for more details see Li & Zhao 2010; Li & Barrow 2010).
The outline of the paper is as follows. In Section 2 we introduce the basic equations needed to understand the underlying physics of the model. In Section 3 we briefly describe the simulations we have performed for the study of the different effects of a coupled scalar field on structure formation, and then display and discuss the numerical results; we summarize and conclude in Section 4.
2 BASIC EQUATIONS
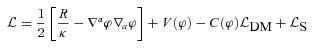
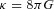 and
and 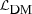 are, respectively, the Lagrangian densities for dark matter and standard model fields, φ is the scalar field and V(φ) its potential; the coupling function C(φ) characterizes the coupling between φ and dark matter. Given V(φ) and C(φ) a model is then fully specified.
are, respectively, the Lagrangian densities for dark matter and standard model fields, φ is the scalar field and V(φ) its potential; the coupling function C(φ) characterizes the coupling between φ and dark matter. Given V(φ) and C(φ) a model is then fully specified.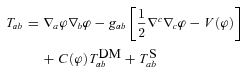
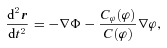
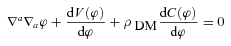
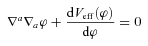
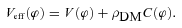
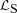 , where
, where 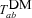 is the background value, and δφ the (not necessarily small and linear) perturbation, and subtract the background scalar-field equation of motion from the full equation to obtain the equation of motion for δφ. In the quasi-static limit where we can neglect time derivatives of δφ compared with its spatial derivatives (which turns out to be a good approximation for our simulations, because the simulation box is much smaller than the observable Universe), we get
is the background value, and δφ the (not necessarily small and linear) perturbation, and subtract the background scalar-field equation of motion from the full equation to obtain the equation of motion for δφ. In the quasi-static limit where we can neglect time derivatives of δφ compared with its spatial derivatives (which turns out to be a good approximation for our simulations, because the simulation box is much smaller than the observable Universe), we get 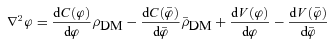
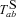 is the background dark-matter density.
is the background dark-matter density. is also known, we can then obtain the full solution of
is also known, we can then obtain the full solution of 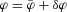 . This completes the computation of the source term for the Poisson equation:
. This completes the computation of the source term for the Poisson equation: 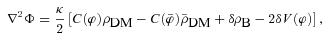
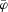 and
and 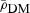 are, respectively, the density perturbations of baryons and scalar field (note that we have neglected perturbations in the kinetic energy of the scalar field because they are always very small for our model).
are, respectively, the density perturbations of baryons and scalar field (note that we have neglected perturbations in the kinetic energy of the scalar field because they are always very small for our model).We can then solve equation (8) using a linear Gauss–Seidel relaxation method on the same grid to obtain Φ. With both Φ and φ in hand, equation (3) can then be used to compute the forces on the dark matter particles, and once we have the forces, we can perform all the standard N-body operations such as momentum-kick, position-drift, time-stepping and so on.
Equations (2–8) are all what we need to complete an N-body simulation for coupled scalar field cosmology (Li & Barrow 2010), and from them we can see where the effects of the scalar-coupling enter.
The modified background expansion rate mainly affects the particle movements and time-stepping, i.e. equation (3), because in the simulations we use the cosmic scalefactor a, instead of t, as the time variable and
 .
.The varying mass effect is seen directly from equation (8), which shows that the contribution of ρDM to the source term of the Poisson equation is normalized by C(φ) which is different from 1 in general. In our model, it is not true that the mass of dark matter particles is really varying, but the net effect is just equivalent to such a variation.
The fifth force appears explicitly on the right-hand side of equation (3), but is only for coupled matter species (dark matter).
The velocity-dependent (or frictional) force hides in the fact that equations (3, 7) are given in different gauges: equation (3) is the force for a dark-matter particle and is given in that particle’s rest frame, while equation (7) is written in the fundamental observer’s frame. As a result, in order to use the δφ solved from equation (7), in equation (3), we need to perform a frame transform
 where
where  is the comoving velocity of the particle relative to the fundamental observer. This force is therefore expressed as
is the comoving velocity of the particle relative to the fundamental observer. This force is therefore expressed as  , and obviously the faster a particle travels the stronger such force it feels.
, and obviously the faster a particle travels the stronger such force it feels.
Before moving on, we should emphasize that the above separation of the four principal effects is mainly for the convenience in the numerical study. In reality, they are different consequences of the same physics, namely the scalar-field coupling, and are non-linearly coupled (one cannot simply switch off one of them in the universe). Their delineation also depends on the way in which the model is described. As an example, in our framework, the dark matter Lagrangian is independent of φ and so the mass of dark matter particles is not changed by φ[but the contribution to the Poisson equation is multiplied by C(φ)] and the varying-mass effect can be separated from other effects such as the velocity-dependent force. Maccio et al. (2004) and Baldi et al. (2010), in contrast, define the dark matter mass so that it depends on φ, and in their framework the varying-mass effect and velocity-dependent force are both consequences of the conservation of momentum. In that case it is ambiguous to separate them.
3 SIMULATIONS AND RESULTS
3.1 Model and simulation details
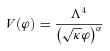
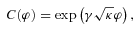
 and γ < 0 so that both V(φ) and Veff(φ) are of runaway type.1
and γ < 0 so that both V(φ) and Veff(φ) are of runaway type.1Li & Barrow (2010) have given a very detailed description of the technicalities of the N-body simulations for coupled scalar-field theories, and so we shall not repeat this methodology here. Roughly speaking, the most important distinction between our simulation and others is that we have solved the scalar field equation of motion explicitly on a grid (in the quasi-static limit). Because of this, we have been able to solve the fifth force (and the frictional force) numerically without recourse to analytical approximations. Furthermore, we have incorporated both time and the space variations of the particle mass [or more rigorously of C(φ)] because we have spatial information about the scalar field distribution.
Since our aim is to test the significance of each of the four above-named effects, we choose to suppress one of them at one time. Together with the full model, where all effects are included, and the ΛCDM model for comparison, we then have six models to simulate. Furthermore, we consider two different choices of the coupling strength γ. So in total we have 11 models, details of which are summarized in Table 1.
| Simulation no. | α | γ | Simulation description |
| L | 0.0 | 0.00 | Pure ΛCDM |
| S1 | 0.1 | −0.10 | Full coupled scalar field |
| S1a | 0.1 | −0.10 | Scalar field with the frictional force  suppressed suppressed |
| S1b | 0.1 | −0.10 | Scalar field with the fifth force  suppressed suppressed |
| S1c | 0.1 | −0.10 | Scalar field with the (time and spatial) variation of mass C(φ) removed |
| S1d | 0.1 | −0.10 | Scalar field with a ΛCDM background expansion |
| S2 | 0.1 | −0.20 | Full coupled scalar field |
| S2a | 0.1 | −0.20 | Scalar field with the frictional force  suppressed suppressed |
| S2b | 0.1 | −0.20 | Scalar field with the fifth force  suppressed suppressed |
| S2c | 0.1 | −0.20 | Scalar field with the (time and spatial) variation of mass C(φ) removed |
| S2d | 0.1 | −0.20 | Scalar field with a ΛCDM background expansion |
| Simulation no. | α | γ | Simulation description |
| L | 0.0 | 0.00 | Pure ΛCDM |
| S1 | 0.1 | −0.10 | Full coupled scalar field |
| S1a | 0.1 | −0.10 | Scalar field with the frictional force  suppressed suppressed |
| S1b | 0.1 | −0.10 | Scalar field with the fifth force  suppressed suppressed |
| S1c | 0.1 | −0.10 | Scalar field with the (time and spatial) variation of mass C(φ) removed |
| S1d | 0.1 | −0.10 | Scalar field with a ΛCDM background expansion |
| S2 | 0.1 | −0.20 | Full coupled scalar field |
| S2a | 0.1 | −0.20 | Scalar field with the frictional force  suppressed suppressed |
| S2b | 0.1 | −0.20 | Scalar field with the fifth force  suppressed suppressed |
| S2c | 0.1 | −0.20 | Scalar field with the (time and spatial) variation of mass C(φ) removed |
| S2d | 0.1 | −0.20 | Scalar field with a ΛCDM background expansion |
| Simulation no. | α | γ | Simulation description |
| L | 0.0 | 0.00 | Pure ΛCDM |
| S1 | 0.1 | −0.10 | Full coupled scalar field |
| S1a | 0.1 | −0.10 | Scalar field with the frictional force  suppressed suppressed |
| S1b | 0.1 | −0.10 | Scalar field with the fifth force  suppressed suppressed |
| S1c | 0.1 | −0.10 | Scalar field with the (time and spatial) variation of mass C(φ) removed |
| S1d | 0.1 | −0.10 | Scalar field with a ΛCDM background expansion |
| S2 | 0.1 | −0.20 | Full coupled scalar field |
| S2a | 0.1 | −0.20 | Scalar field with the frictional force  suppressed suppressed |
| S2b | 0.1 | −0.20 | Scalar field with the fifth force  suppressed suppressed |
| S2c | 0.1 | −0.20 | Scalar field with the (time and spatial) variation of mass C(φ) removed |
| S2d | 0.1 | −0.20 | Scalar field with a ΛCDM background expansion |
| Simulation no. | α | γ | Simulation description |
| L | 0.0 | 0.00 | Pure ΛCDM |
| S1 | 0.1 | −0.10 | Full coupled scalar field |
| S1a | 0.1 | −0.10 | Scalar field with the frictional force  suppressed suppressed |
| S1b | 0.1 | −0.10 | Scalar field with the fifth force  suppressed suppressed |
| S1c | 0.1 | −0.10 | Scalar field with the (time and spatial) variation of mass C(φ) removed |
| S1d | 0.1 | −0.10 | Scalar field with a ΛCDM background expansion |
| S2 | 0.1 | −0.20 | Full coupled scalar field |
| S2a | 0.1 | −0.20 | Scalar field with the frictional force  suppressed suppressed |
| S2b | 0.1 | −0.20 | Scalar field with the fifth force  suppressed suppressed |
| S2c | 0.1 | −0.20 | Scalar field with the (time and spatial) variation of mass C(φ) removed |
| S2d | 0.1 | −0.20 | Scalar field with a ΛCDM background expansion |
The physical parameters we adopt in all simulations are as follows. The present-day dark-energy fractional energy density ΩDE = 0.743 and Ωm=ΩCDM+ΩB = 0.257, H0 = 71.9 km s−1 Mpc−1, ns = 0.963, σ8 = 0.769. The size of simulation box is 64 h−1 Mpc with h=H0/(100 km s−1 Mpc−1). In all these simulations, the mass resolution is 1.114 × 109h−1 M⊙, the particle (both dark matter and baryons) number is 2563, the domain grid is a 128 × 128 × 128 cubic and the finest refined grids have 16384 cells on each side, corresponding to a force resolution of the order of 12 h−1 kpc.
3.2 Numerical results
For the numerical results, we display the matter power spectrum, mass function and halo density profiles for the 11 runs described above, and discuss how they are affected by the individual effects from the scalar coupling.
Before going to the details, it is helpful to have a quick browse about the scalar-coupling effects: (I) the velocity-dependent force  is parallel to the direction of motion
is parallel to the direction of motion  ; because
; because  and γ < 0, so it accelerates the particles. (II) The fifth force
and γ < 0, so it accelerates the particles. (II) The fifth force  in this model is found (Li & Barrow 2010) to be parallel to gravity and the ratio between the magnitudes of the two is 2γ2 to a high precision; as such the fifth force both accelerates the particles and increases their mutual attraction. (III) C(φ) < 1 because γ < 0 and φ > 0, so that the contribution of dark matter density to the source of Poisson equation gets weakened, effectively reducing the gravity force and causing less mutual attraction between particles and less clustering. (IV) For the chosen model and physical parameters, the background expansion rate decreases as |γ| increases (Li & Barrow 2010), making matter particles less diluted and cluster more. These facts are important to bear in mind for discussions below.
in this model is found (Li & Barrow 2010) to be parallel to gravity and the ratio between the magnitudes of the two is 2γ2 to a high precision; as such the fifth force both accelerates the particles and increases their mutual attraction. (III) C(φ) < 1 because γ < 0 and φ > 0, so that the contribution of dark matter density to the source of Poisson equation gets weakened, effectively reducing the gravity force and causing less mutual attraction between particles and less clustering. (IV) For the chosen model and physical parameters, the background expansion rate decreases as |γ| increases (Li & Barrow 2010), making matter particles less diluted and cluster more. These facts are important to bear in mind for discussions below.
3.2.1 Matter power spectrum
In Fig. 1, we have plotted the fractional change of the non-linear matter power spectrum with respect to ΛCDM prediction for the simulations S1 and S1a-d. Roughly, the deviation from the black solid curve (S1) indicates the importance of a given coupled-scalar effect: the larger the deviation is, the more that specific effect contributes to the full coupled scalar field result. Of least importance is the velocity-dependent force  (green dotted curves). As this force accelerates particles, it makes particles collapse faster to the regions of high density, and thus slightly enhances the clustering. Consequently, suppressing it will decrease P(k). Of the second least importance is the fifth force term
(green dotted curves). As this force accelerates particles, it makes particles collapse faster to the regions of high density, and thus slightly enhances the clustering. Consequently, suppressing it will decrease P(k). Of the second least importance is the fifth force term  (blue dashed curves). It not only accelerates particles (towards the high-density regions) but also increases the central force. As such its effect is also to enhance the clustering of matter and neglecting it leads to smaller P(k) on all scales.
(blue dashed curves). It not only accelerates particles (towards the high-density regions) but also increases the central force. As such its effect is also to enhance the clustering of matter and neglecting it leads to smaller P(k) on all scales.
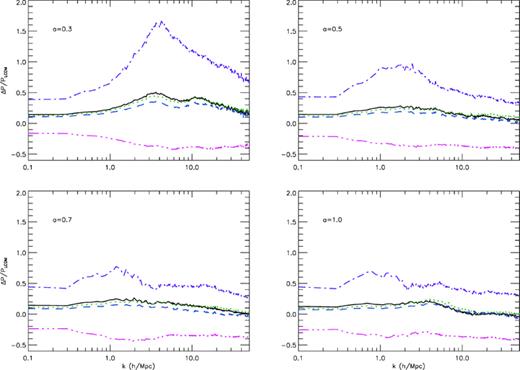
Fractional changes of the non-linear matter power spectrum with respect to the ΛCDM result at four different output times: a = 0.3 (upper-left panel), a = 0.5 (upper-right panel), a = 0.7 (lower-left panel) and a = 1.0 (lower-right panel). In each panel, the results of the simulations S1 (full coupled scalar simulation), S1a (frictional force suppressed), S1b (fifth force suppressed), S1c (mass variation removed) and S1d (ΛCDM background) are represented by the black solid, green dotted, blue dashed, purple dash–dotted and pink dash–dotted–dotted–dotted curves, respectively.
Next is the varying mass effect (purple dash–dotted curves), the presence of which reduces the source of the Poisson equation and thus weakens gravity. Obviously, its effect is to produce weaker clustering of matter particles and dropping it will increase P(k) significantly.
The most important coupled-scalar effect comes from the modified background expansion rate (pink dash–dotted–dotted–dotted curves). As mentioned above, if the universe expands more slowly [as in the case of our coupled scalar field model Li & Barrow (2010)], then particles are less diluted and have more time to cluster, resulting in a larger P(k). Changing the background expansion to ΛCDM (i.e. increasing it) simply produces a smaller P(k) than the full simulation. Note that the pink curves are consistently below zero, indicating that although simulation S1d uses the same background expansion rate as simulation L, P(k) is smaller than for the latter, a result that is again due to the fact that in S1d the varying mass effect is taken into account, weakening the matter clustering and decreasing P(k) (as discussed above, the fifth force does have the opposite effect but cannot overcome this).
In Fig. 2, we have shown the same plots, but for the models S2 and S2a-d. All the above analysis still applies but the effects just become stronger. Interestingly, the most important coupled-scalar effects (at least for our models, which are typical ones) are not those of the fifth force, but are instead the modified background expansion rate and varying mass of matter particles. This is understandable, because the magnitude of the fifth force is about 2γ2 times that of gravity, and for our S1 and S2 simulations the values are 0.02 and 0.08, respectively, while at the same time the deviations of C(φ) from 1 for these two models are ∼0.1 and ∼0.3 (Li & Barrow 2010) and so are far stronger.
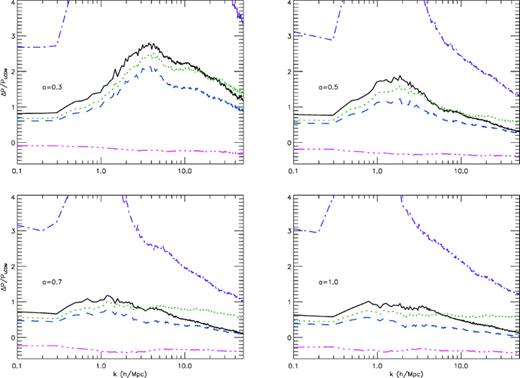
The same as Fig. 1, but for the models where  , i.e. S2 and S2a-d.
, i.e. S2 and S2a-d.
This means that one must be cautious about adding a Yukawa-type fifth force to the N-body simulation, while keeping all other things the same as in ΛCDM, because the fifth force often introduces associated effects which are more important.
3.2.2 Mass functions
Fig. 3 shows the mass functions of the simulations S1 and S1 compared with that of ΛCDM (L). Again, the deviation from the full simulation result (black solid curve) indicates the order of importance of the individual effects. The two least important factors are once more the velocity-dependent force  and the fifth force
and the fifth force  , both of which, according to our above analysis, enhance matter cluster: suppressing them causes less clustering of matter and smaller mass functions. Their influences, however, are quite weak, in particular that of the velocity-dependent force.
, both of which, according to our above analysis, enhance matter cluster: suppressing them causes less clustering of matter and smaller mass functions. Their influences, however, are quite weak, in particular that of the velocity-dependent force.
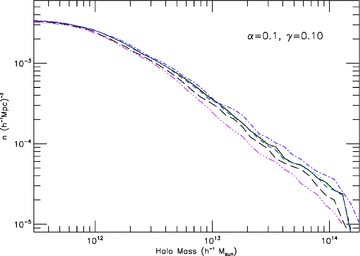
The mass functions for the models S1 (black solid curve), S1a (green dotted), S1b (blue dashed), S1c (purple dash–dotted) and S1d (pink dash–dotted–dotted–dotted) compared to the ΛCDM result (thick long dashed curve). The horizontal axis is the virial mass of haloes, in unit of h−1 M⊙; the vertical axis is the halo number density in the simulation box, in units of (h−1 Mpc)−3.
The second important effect is the variation of mass or C(φ). In case C(φ) < 1 then, as mentioned above, the mutual gravitational interaction between particles becomes weaker and particles will cluster less strongly. As a result, removing this effect enhances the matter clustering and leads to massive haloes being created in larger abundance.
The most influential effect from a coupled scalar field is the modified background expansion. Changing it to a ΛCDM background (which is faster) significantly underestimates the mass function, because particles get more diluted and have less time to clump.
The corresponding results for models S2 and S2a-d are summarized in Fig. 4, and they show the same qualitative trend as Fig. 3 but the effects are just stronger, due to the stronger coupling |γ| and thus more dramatic evolution of the scalar field φ[which means that C(φ) deviate more from unity and the expansion rate is decreased more compared to simulation L].
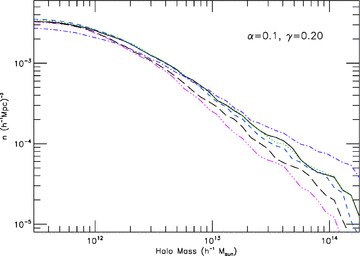
Although the mass function does show the imprint from a fifth force, this is by no means unique and could easily be dominated over by the associated coupled scalar effects like modified background expansion rate or varying particle mass.
3.2.3 Halo density profiles
Internal density profiles of the dark matter haloes are another area where the scalar field coupling could leave interesting imprints. For example, Li & Zhao (2010) showed that for a chameleon-like scalar field model the density profiles could be either increased or decreased significantly by the scalar coupling, depending on the environment of the haloes. For the models considered here, Baldi et al. (2010) and Li & Barrow (2010) have given convincing evidence that the internal density profile has similar shape to ΛCDM, but could be somewhat suppressed in the very inner parts.
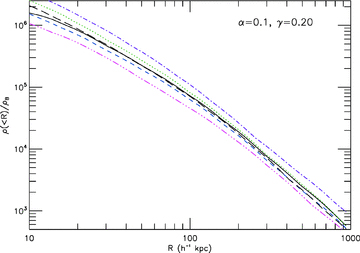
As an explicit example, Fig. 5 shows the density profiles of the most massive halo from each box for simulations L, S1 and S1a-d. The suppression of the full simulation result (black solid curve) compared with the ΛCDM prediction (thick solid dashed curve) is evident below R∼ 400 h−1 Kpc.

The internal density profile of the most massive halo in the simulation box for the models S1 (black solid curve), S1a (green dotted), S1b (blue dashed), S1c (purple dash–dotted) and S1d (pink dash–dotted–dotted–dotted) compared to the ΛCDM result (thick long dashed curve). The horizontal axis is the radius from halo centre, in unit of h−1 Kpc, and the vertical axis is the overdensity.
If the velocity-dependent force  is given up (green dotted curve), then the suppression is moderated. As discussed in Baldi et al. (2010), this is because this force effectively accelerates particles, making them travel faster and so increases the total kinetic energy of the particles inside the halo. As a result, removing this force will leave the particles with less kinetic energy, meaning that they more easily fall towards the halo centre.
is given up (green dotted curve), then the suppression is moderated. As discussed in Baldi et al. (2010), this is because this force effectively accelerates particles, making them travel faster and so increases the total kinetic energy of the particles inside the halo. As a result, removing this force will leave the particles with less kinetic energy, meaning that they more easily fall towards the halo centre.
The fifth force  is slightly more complicated. On one hand, it speeds the particles up, increasing their kinetic energy; on the other, it enhances the mutual attraction between particles, increasing the (magnitude of the) potential energy of the halo. These two effects are just opposite, as deepening the potential of a halo will pull more particles towards the centre and thus increase the concentration. For simulation S1, it seems that the former effect takes over, and dropping the fifth force (blue dashed curve) simply decreases the kinetic energy of particles and makes them more concentrated towards the halo centre.
is slightly more complicated. On one hand, it speeds the particles up, increasing their kinetic energy; on the other, it enhances the mutual attraction between particles, increasing the (magnitude of the) potential energy of the halo. These two effects are just opposite, as deepening the potential of a halo will pull more particles towards the centre and thus increase the concentration. For simulation S1, it seems that the former effect takes over, and dropping the fifth force (blue dashed curve) simply decreases the kinetic energy of particles and makes them more concentrated towards the halo centre.
The effect of the varying-mass factor C(φ) < 1 is unambiguously to suppress the overdensity inside the haloes, as it decreases the source of the Poisson equation and so weakens gravity, making the potential shallower. Dropping it simply deepens the potential and attracts more particles to the inner region of the halo (purple dash–dotted curve).
Finally, changing (increasing) the background expansion rate relative to ΛCDM again leads to less clustering of particles, and thus lower density profiles in the haloes (pink dash–dotted–dotted–dotted curves).
It is worth noting that although the velocity-dependent force, fifth force and varying mass all contribute to suppressing the internal density of the halo, the varying mass contributes most, while the fifth force contributes least. This differs from the finding of Baldi et al. (2010) that the velocity-dependence force is the determining factor, possibly due to differences in the model parameters and our detailed treatments.2 The fact that the velocity-dependent force dominates over the fifth force (which is different from what we have seen for matter power spectrum and mass function) is not surprising, for, as mentioned above, the fifth force is set to increase both the kinetic and potential energies, two effects somehow cancelling each other out.
Fig. 6 displays the same results for models S2 and S2a-d, and we can see qualitatively similar but stronger trends. The notable thing is that in this case suppressing the fifth force further lowers the inner density of the halo, an indication that here the deepening of potential dominates over the increase in kinetic energy (both are due to the fifth force).
Above we have just discussed the results for one specific halo (the most massive one), while what we are more interested in is the general behaviour. For this we have selected 10 out of the most massive haloes and computed their average density profile. The results for simulations S1 and S1a-d are shown in Fig. 7, in which we have plotted the fractional change of the averaged halo internal density with respect to the ΛCDM result. From this figure we see again that overall the internal density in the inner region of haloes is lower in (full) coupled scalar field models than in ΛCDM. Both the velocity-dependent force and varying mass tend to decrease the inner density, and both the fifth force and the modified (slower) background expansion help increase it. The effects from the varying mass and modified background expansion are dominant while the other two effects are minor, confirming our observed pattern from a single halo (Fig. 5).
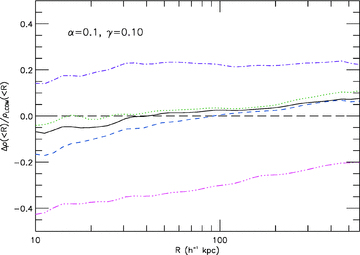
The fractional change of averaged halo density profile for the models S1 (black solid curve), S1a (green dotted), S1b (blue dashed), S1c (purple dash–dotted) and S1d (pink dash–dotted–dotted–dotted) compared to the ΛCDM result (thick long dashed curve). The horizontal axis is the distance from halo centre, in unit of h−1 Kpc, and the vertical axis is the fractional change of density with respect to the ΛCDM prediction.
We see a similar result for models S2 and S2a-d, as shown in Fig. 8. A notable difference here, however, is that the velocity-dependent force becomes more important than in S1. Indeed, it is as dominant as the varying mass effect in the inner region of the haloes, though it is still subdominant in the outer region. Note again that the fifth force is the least important amongst all the four effects, which means that using a simulation with ΛCDM plus a Yukawa-type fifth force we would be unable to catch the (probably) most significant effects from a coupled scalar field.
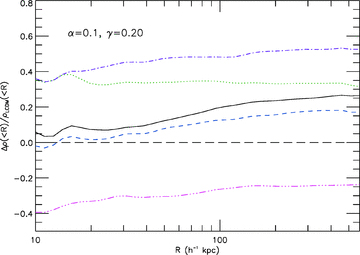
4 SUMMARY AND CONCLUSION
To summarize: in this paper, with the aid of N-body simulations, we have investigated the different impacts of a coupled scalar field on cosmic structure formation, and assessed their qualitative effects and quantitative importance. The scalar field coupling influences the structure formation mainly through a velocity-dependent force, a fifth force, a modification of the particle mass (or the source of the Poisson equation) and a modified background expansion rate. We have investigated how dropping each one of these factors leaves imprints on the key structure formation observables, like matter power spectrum, mass function and the internal density profile of dark matter haloes.
For the matter power spectrum and mass function, we find that the modified background expansion rate is by far the most important effect that the scalar-coupling can have, followed in turn by the variation of particle mass, fifth force and the velocity-dependent force. The cosmic expansion becomes slower than that in ΛCDM due to the scalar field, which means that structure has more time to form. The fifth force increases the mutual attractive force between particles, strengthening the collapse of overdense regions; both the fifth force and the velocity-dependent force could speed up particles, making the collapse faster. As a result, all these three effects help boost the growth of structure. On the other hand, the source of the Poisson equation is decreased due to the coupling function C(φ), resulting in weaker gravity and weakened structure formation.
The internal density profiles for dark matter haloes are more interesting, and as we have seen the combined effect of a scalar-coupling can be to suppress the density of the inner regions of the haloes (or to distribute particles more towards outer regions). As one might expect, the modified cosmic expansion rate is again the most important scalar-coupling effect here, and if it is dropped there will be less structure formation and lower halo density profiles. The variation of particle masses, or the modification to the source of the Poisson equation, is the second largest single effect, followed by the velocity-dependent force and fifth force. Roughly speaking, the particles tend to move towards (by a process of relaxation and virialization) the inner regions of haloes if their kinetic energy is reduced and/or the central potential gets deeper, and vice versa. In this regard, the velocity-dependent force speeds up particles and the variation of particle mass weakens the central potential, both in favour of lower central densities in haloes (cf. Figs 5–8). The fifth force has two opposite effects – to speed up particles (and so increase the kinetic energy) and to deepen the total potential. They cancel each other out to a certain extent, so making the fifth force less influential in determining the density profiles (than the velocity-dependent force).
Our results to some extent agree with previous analyses (e.g. Baldi et al. 2010) of the halo density profiles, but we stress that due to the different model specifications and treatments: a simple direct comparison cannot be made here.
It is important to bear in mind that in many cases the fifth force, which is the most well-known consequence of a coupling between matter and a scalar field, is not the most important in affecting structure formation. Such point has been made by Baldi et al. (2010), who specifically considered the effects of the varying mass and velocity-dependent force on the halo density profiles. Here, we further quantitatively study the effects due to the modified background expansion rate and find the effects on the matter power spectra and mass functions as well. The important thing is that, when we introduce such a coupling, other new effects are also brought in, and these can often be much more influential. Furthermore, the order of importance of different effects can vary from model to model, which makes model-independent studies difficult. It is in this regard that full N-body simulations, which take full account of all associated effects, are increasingly significant in the case studies of different models.
Since Veff(φ) is of runway type there is nothing to stop the scalar field rolling down Veff, so typically we shall have  today, which makes C(φ) deviate significantly from 1. Increasing |γ| will make this problem more severe, and this is why we set
today, which makes C(φ) deviate significantly from 1. Increasing |γ| will make this problem more severe, and this is why we set  rather than
rather than  .
.
There are several important differences in our treatment of the model and that of Baldi et al. (2010). First, we switch the different effects listed in Section 2 from the very beginning of the simulation (z = 49), while they do this only at very late times (i.e. in the non-linear regime only). Secondly, our simulations are all normalized at very early redshifts, which means that we use the same initial conditions for all the simulations and examine how the scalar field affects the final large-scale structure; in their simulations everything is normalized at z = 0. Thirdly, the background expansions are also different in the two works: in our model the dark matter energy density scales as ρDM ∝ a−3 while this is not true in their work because there the dark matter particle mass is varying in time [note that our ΩDM is defined using ρDM instead of C(φ)ρDM]. These differences indicate why the results of these two works cannot be compared straightforwardly.
The work described in this paper has been performed on cosmos, the UK National Cosmology Supercomputer. The matter power spectrum and halo properties are computed using powmes (Colombi et al. 2009) and mhf (Gill, Knebe & Gibson 2004), respectively. We thank Marco Baldi for comments on the draft. BL is supported by a Junior Research Fellowship at Queens’ College, Cambridge, and the Science and Technology Facility Council of the United Kingdom.
REFERENCES



