-
PDF
- Split View
-
Views
-
Cite
Cite
Emily I. Curtis, John S. Richer, A submillimetre survey of the kinematics of the Perseus molecular cloud – III. Clump kinematics, Monthly Notices of the Royal Astronomical Society, Volume 410, Issue 1, January 2011, Pages 75–93, https://doi.org/10.1111/j.1365-2966.2010.17424.x
Close - Share Icon Share
Abstract
We explore the kinematic properties of dense continuum clumps in the Perseus molecular cloud, derived from our wide-field C18O J = 3 → 2 data across four regions – NGC 1333, IC 348/HH 211, L1448 and L1455. Two distinct populations are examined, identified using the automated algorithms clfind (85 clumps) and gaussclumps (122 clumps) on existing SCUBA 850-μm data. These kinematic signatures are compared to the clumps’ dust continuum properties. We calculate each clump’s non-thermal linewidth and virial mass from the associated C18O J = 3 → 2 spectrum. The clumps have supersonic linewidths, 〈σNT/cs〉= 1.76 ± 0.09 (clfind population) and 1.71 ± 0.05 (with gaussclumps). The linewidth distributions suggest the C18O line probes a lower density ‘envelope’ rather than a dense inner core. Similar linewidth distributions for protostellar and starless clumps imply protostars do not have a significant impact on their immediate environment. The proximity to an active young stellar cluster seems to affect the linewidths: those in NGC 1333 are greater than elsewhere. In IC 348 the proximity to the old infrared cluster has little influence, with the linewidths being the smallest of all. The virial analysis suggests that the clumps are bound and close to equipartition, with virial masses similar to the masses derived from the continuum emission. In particular, the starless clumps occupy the same parameter space as the protostars, suggesting they are true stellar precursors and will go on to form stars. We also search for ordered C18O velocity gradients across the face of each core. Approximately one-third have significant detections, which we mainly interpret in terms of rotation. However, we note a correlation between the directions of the identified gradients and outflows across the protostars, indicating we may not have a purely rotational signature. The fitted gradients are in the range  to 16 km s−1 pc−1, larger than found in previous work, probably as a result of the higher resolution of our data and/or outflow contamination. These gradients, if interpreted solely in terms of rotation, suggest that the rotation is not dynamically significant: the ratios of clump rotational to gravitational energy are βrot≲ 0.02. Furthermore, derived specific angular momenta are smaller than observed in previous studies, centred around j ∼ 10−3 km s−1 pc, which indicates we have identified lower levels of rotation, or that the C18O J = 3 → 2 line probes conditions significantly denser and/or colder than n ∼ 105 cm−3 and T ∼ 10 K.
to 16 km s−1 pc−1, larger than found in previous work, probably as a result of the higher resolution of our data and/or outflow contamination. These gradients, if interpreted solely in terms of rotation, suggest that the rotation is not dynamically significant: the ratios of clump rotational to gravitational energy are βrot≲ 0.02. Furthermore, derived specific angular momenta are smaller than observed in previous studies, centred around j ∼ 10−3 km s−1 pc, which indicates we have identified lower levels of rotation, or that the C18O J = 3 → 2 line probes conditions significantly denser and/or colder than n ∼ 105 cm−3 and T ∼ 10 K.
1 INTRODUCTION
Stars form inside dense cores deep within molecular clouds. The similarity of the core mass function (CMF) to the initial mass function (IMF) of stars (see Motte, Andre & Neri 1998; Alves, Lombardi & Lada 2007) has sometimes been used (e.g. Enoch et al. 2008) as evidence against theories of core formation where no correspondence is anticipated, e.g. in the competitive accretion picture (Bonnell et al. 2001; Bate & Bonnell 2005). However, the mapping of a given CMF on to the resultant IMF is complicated by many factors (see e.g. Hatchell & Fuller 2008; Curtis & Richer 2010), such as the cores’ varying multiplicity (Goodwin et al. 2008), star-forming efficiencies (Swift & Williams 2008) and/or mass-dependent lifetimes (Clark, Klessen & Bonnell 2007). In fact, as shown by Swift & Williams (2008) and Goodwin & Kouwenhoven (2009), diverse evolutionary schemes can map the observed CMFs on to the IMF, implying the current mass function data are not sufficient to discriminate between different theoretical models by themselves.
The kinematics of star-forming cores, probed with spectral-line observations of dense molecular tracers, are arguably the best discriminator between different models of core formation (e.g. André et al. 2007; Kirk, Johnstone & Tafalla 2007, hereafter KJT07). For example, cores created by shocks in large-scale flows exhibit large velocity gradients and are located at local maxima in the line-of-sight velocity dispersion (e.g. Ballesteros-Paredes, Klessen & Vázquez-Semadeni 2003; Klessen et al. 2005). Alternatively, the magnetically controlled scenario has more quiescent velocity fields (e.g. Nakamura & Li 2005), well matched to observations of isolated starless cores with subsonic levels of turbulence (e.g. Myers 1983; Caselli et al. 2002). Such quiescent cores are in opposition to purely hydrodynamic models of gravoturbulent fragmentation (see Mac Low & Klessen 2004) which produce a majority of cores with supersonic velocity dispersions.
Offner, Klein & McKee (2008a) and Krumholz, McKee & Klein (2005) mention that the physical mechanism of star formation depends on the much debated presence (or absence) of turbulent feedback. In one view, molecular clouds are short-lived (on time-scales of order one dynamical time), non-equilibrium structures (e.g. Elmegreen et al. 2000; Hartmann 2001; Dib et al. 2007) characterized by transient turbulence, which dissipates quickly. In this scenario, stars could form by the collapse of discrete cores. Conversely, molecular clouds might form slowly and be quasi-equilibrium objects (see e.g. Shu, Adams & Lizano 1987; McKee 1999; Krumholz & Tan 2007; Nakamura & Li 2007). This would require turbulence to be constantly injected into the clouds, either externally (from e.g. supernova blast waves or H ii regions) or internally (from e.g. protostellar outflows) and cores could form through competitive accretion (Bonnell et al. 2001). Offner et al. (2008b) demonstrate that these two disparate views of star formation give rise to distinguishable kinematics in dense stellar precursors and thus the study of core kinematics potentially offers a way to probe the turbulent state of the surrounding molecular cloud.
This paper is concerned with the kinematical properties of dense clumps in the Perseus molecular cloud (hereafter simply Perseus) and compares them to theoretical models. We examine the linewidths, virial masses and ordered velocity gradients of two populations of clumps (Curtis & Richer 2010) identified across SCUBA dust continuum maps (Hatchell et al. 2005). These kinematic signatures are derived for each clump from our wide-field survey (Curtis, Richer & Buckle 2010a, hereafter Paper I) of four clusters of star-forming cores towards NGC 1333, IC 348/HH 211 (simply IC 348 hereafter), L1448 and L1455 in the J = 3 → 2 rotational lines of CO and its common isotopologues 13CO and C18O. In the preceding paper of this series (Curtis et al. 2010b, hereafter Paper II), we explored the evolution of molecular outflows across these regions. We organize this paper as follows: the remainder of the Introduction explains the naming conventions we have adopted to describe star-forming clumps/cores. Section 2 briefly describes the continuum data and associated clump catalogues alongside our spectral-line data sets, from which we derive the clump kinematics. Various clump kinematic signatures are investigated in Section 3, including the clumps’ linewidths (Section 3.1) and virial masses (Section 3.2), before we search for ordered velocity gradients across the face of the clumps in Section 3.3, which we interpret with a solid-body-rotation model. Finally, we summarize this work in Section 4.
1.1 Nomenclature and clump populations
We adhere to the clump hierarchy explained in Curtis & Richer (2010), which follows Williams, Blitz & McKee (2000). Briefly, molecular clouds contain clumps which in turn harbour cores, the direct precursors of individual or multiple stars. Clumps without embedded objects are starless, unless they are gravitationally bound when we refer to them as pre-stellar.
2 OBSERVATIONAL DATA
2.1 Dust continuum
The SCUBA 850-μm data analysed have a beam size of 14 arcsec (0.017 pc at 250 pc, our adopted distance to Perseus; see Paper I) and are sampled on a 3-arcsec grid with a typical rms noise level, σrms = 35 mJy beam−1 (Hatchell et al. 2005).
2.2 Clump catalogues
We investigate the kinematics of two populations of dust continuum clumps, which we identified in the SCUBA 850-μm data in a previous paper (Curtis & Richer 2010), using the two most popular automated algorithms: clfind (Williams, de Geus & Blitz 1994) and gaussclumps (Stutzki & Güsten 1990). Our motivation in that study was to determine which clump properties can be robustly measured and which depend on the extraction technique. We continue that approach in this work, analysing the kinematic signatures for each population in turn.
In Curtis & Richer (2010), we located 85 and 122 clumps using clfind and gaussclumps, respectively, with peak flux densities ≥4σrms = 140 mJy beam−1, across the same areas where we also have C18O J = 3 → 2 data (Paper I). The clumps were identified as starless, Class 0 or Class I protostars using the classifications of Hatchell et al. (2007, hereafter HFR07), which are based on source spectral energy distributions (SEDs) incorporating Spitzer data. We associate a clump with a HFR07 source, if the separation between the clump and HFR07 source peak positions is less than the clump’s diameter (see Curtis & Richer 2010). Given the similarities in the extraction method and resulting population, most of the clfind clumps are directly on top of the HFR07 sources and are unambiguously identified. However, three gaussclumps sources are large enough to encapsulate two HFR07 sources and their results are correspondingly included in the population statistics twice.
2.3 Spectral line
The C18O J = 3 → 2 observations used in this analysis were undertaken with the Heterodyne Array Receiver Project (HARP; Buckle et al. 2009) on the James Clerk Maxwell Telescope (JCMT) and have been described in detail previously (Paper I). Striping artefacts resulting from systematic differences in calibration between HARP channels were removed using a ‘flat-field’ procedure (fully described in Paper I). The final data sets are sampled on a 3-arcsec grid, distributed using a Gaussian gridding kernel with a 9 arcsec full width at half-maximum (FWHM), yielding an equivalent beam size of 17.7 arcsec. The median rms spectral noise values, averaged across each region’s map (measured in 0.15 km s−1 channels), are 0.18, 0.15, 0.15 and 0.14 K for NGC 1333, IC 348, L1448 and L1455, respectively.
3 THE KINEMATICS OF THE SCUBA CORES
In molecular clouds, the C18O J = 3 → 2 line is expected to be optically thin and excited in dense regions (ncrit∼ 104 cm−3). It should therefore trace material in the vicinity of or within the dense agglomerations surveyed with SCUBA. At the peak of every clump in our two catalogues (see Section 2.2), we extracted the C18O J = 3 → 2 spectrum and fitted a Gaussian profile to it using splat1 if the peak of the C18O line was ≥3σsp, where σsp is the rms spectral noise. We did not detect C18O at the 3σ level towards 4 (5 per cent) clfind and 6 (5 per cent) gaussclumps positions. Of the detections, 13 (15 per cent) clfind and 18 (15 per cent) gaussclumps spectra have double-peaked line profiles. For comparison, KJT07 made pointed N2H+J = 1 → 0 and C18O J = 2 → 1 observations on the Institut de Radio Astronomie Millimétric (IRAM) 30-m telescope (with beam sizes of 25 and 11 arcsec, respectively) towards 157 candidate cores in Perseus – 44 pointings in our fields – and found 66 (42 per cent) C18O spectra required two component Gaussian fits with three in one case. Generally, J = 2 → 1 data trace lower density (ncrit∼ 103 cm−3) and/or colder material than the 3 → 2 at lower optical depths by a factor of 2–3 in the optically thin limit. Therefore the J = 2 → 1 line is unlikely to saturate if the J = 3 → 2 data are optically thin. This suggests there are separate emitting sources along the line of sight with different temperatures and/or densities which require multiple-component fits for one transition and not the other. An alternative is simply that at our velocity resolution (0.15 km s−1 compared to KJT07’s 0.05 km s−1) many of KJT07’s separate components are blended into one, which might partly explain our larger linewidths (see Section 3.1).
3.1 Linewidths
The linewidths in molecular clouds are substantially larger than the sound speed of their constituent gas (e.g. Zuckerman & Evans 1974; Solomon et al. 1987). Such supersonic linewidths are thought to arise from chaotic and/or turbulent motions of unknown fundamental origin (see Elmegreen & Scalo 2004 and references therein). The velocity dispersion in a region scales with its size (e.g. Larson 1981) akin to the Kolmogorov law for subsonic incompressible turbulence, although turbulence in the interstellar medium is actually highly compressible and often supersonic causing shocks. However, dense star-forming cores harboured in cloud interiors possess near-thermal linewidths almost devoid of the turbulent movements that cause the broadening in their outer envelopes (e.g. Benson & Myers 1989; Barranco & Goodman 1998; Goodman et al. 1998; Pineda et al. 2010). The C18O J = 3 → 2 transition is expected to probe a region intermediate in scale between the dense core and its environment, although it is not the tracer of choice for young pre-stellar cores. In the cold (≲10 K), high-density (≥105 cm−3) centres of such objects, the conditions may result in depletion, where many molecules (including CO and its isotopologues) freeze-out on to dust grains. Such zones are better probed by molecules such as N2H+and H2D+, but in any case the CO J = 3 → 2 transitions should probe higher densities than lower J ones.
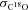 , to be the quadrature sum of its thermal and non-thermal dispersions, σT and σNT, respectively:
, to be the quadrature sum of its thermal and non-thermal dispersions, σT and σNT, respectively: 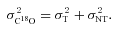
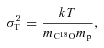
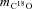 the relative molecular mass of C18O (
the relative molecular mass of C18O (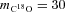 ). The clump temperature, T, is taken from the kinetic temperatures of ammonia gas (Rosolowsky et al. 2008), where available, or 10 and 15 K for identified starless and protostellar cores, respectively, where not. For those clumps without a HFR07 association we assume a temperature of 12 K. We calculate the turbulent fraction, plotted in Figs 2–5, fturb=σNT/cs, where
). The clump temperature, T, is taken from the kinetic temperatures of ammonia gas (Rosolowsky et al. 2008), where available, or 10 and 15 K for identified starless and protostellar cores, respectively, where not. For those clumps without a HFR07 association we assume a temperature of 12 K. We calculate the turbulent fraction, plotted in Figs 2–5, fturb=σNT/cs, where  is the thermal sound speed in the bulk of the gas of mean molecular mass
is the thermal sound speed in the bulk of the gas of mean molecular mass 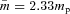 (assuming 1 He for every 5 H2) and γ the adiabatic index (∼7/5 for a diatomic molecule). For T = 10 K, cs = 0.22 km s−1 and at 15 K, cs = 0.27 km s−1. Summaries of fturb for various populations are listed in Tables 1 and 2.
(assuming 1 He for every 5 H2) and γ the adiabatic index (∼7/5 for a diatomic molecule). For T = 10 K, cs = 0.22 km s−1 and at 15 K, cs = 0.27 km s−1. Summaries of fturb for various populations are listed in Tables 1 and 2.
Spatial distribution of C18O non-thermal linewidth across NGC 1333 (upper left), IC 348 (upper right), L1448 (lower right) and L1455 (lower left). The grey-scale is SCUBA 850-μm flux density in mJy beam−1 (Hatchell et al. 2005) with contours at 100, 200, 400, 800, 1600 and 3200 mJy beam−1. Circles are positioned at the peak of every SCUBA clump in our catalogue identified using clfind (Curtis & Richer 2010) where there is a 3σ C18O detection. The circles’ size and colour reflect the linewidth as shown in the key.
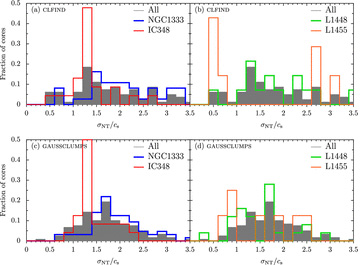
Distribution of clump turbulent fractions, fturb=σNT/cs, measured from the HARP C18O J = 3 → 2 data (see text), broken down by region for the clfind (upper panels) and gaussclumps populations (lower panels).
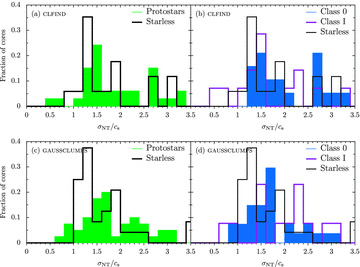
Distribution of clump turbulent fractions, fturb=σNT/cs, measured from the HARP C18O J = 3 → 2 data (see text), broken down by the different source types for the clfind (upper panels) and gaussclumps populations (lower panels).
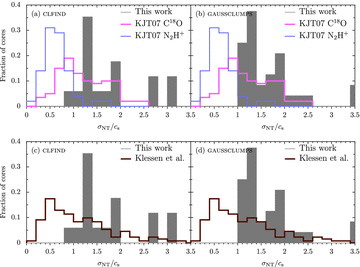
Distribution of fturb, for the starless clump populations identified with clfind (left-hand panels) or gaussclumps (right-hand panels), measured from the HARP C18O J = 3 → 2 data. Overlaid for comparison are the distributions found by KJT07 for 157 candidate cores using C18O J = 2 → 1 (upper panels, pink) and N2H+J = 1 → 0 (upper panels, blue). A prediction for cores from the gravoturbulent simulation of Klessen et al. (2005) is also shown for turbulence driven on large scales (lower panels, brown). For that simulation the turbulent fraction extends beyond 3.5 to 4.3 (not plotted), though there are small numbers of clumps in those bins (∼2 per cent).
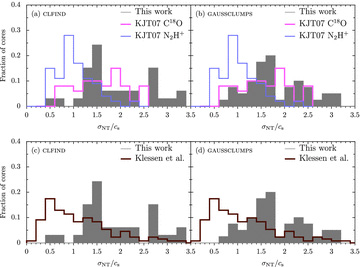
Distribution of fturb, for the protostellar clump populations identified with clfind (left-hand panels) or gaussclumps (right-hand panels), measured from the HARP C18O J = 3 → 2 data. Overlaid for comparison are the distributions found by KJT07 for 157 candidate cores using C18O J = 2 → 1 (upper panels, pink) and N2H+J = 1 → 0 (upper panels, blue). A prediction for cores from the gravoturbulent simulation of Klessen et al. (2005) is also shown for turbulence driven on large scales (lower panels, brown). For that simulation the turbulent fraction extends beyond 3.5 to 4.3 (not plotted), though there are small numbers of clumps in those bins (∼2 per cent).
Summary of the turbulent fractions, fturb, derived from Gaussian fits to the C18O J = 3 → 2 line at the peak of every SCUBA clump identified with clfind (Curtis & Richer 2010). The results are broken into either different regions in Perseus or clump classifications (see Section 2.2). The quoted errors (σ) are errors on the mean ( ) not sample deviations.
) not sample deviations.
| Population | Number | fturb | σf |
| All | 81 | 1.76 | 0.09 |
| NGC 1333 | 37 | 2.05 | 0.12 |
| IC 348 | 23 | 1.36 | 0.09 |
| L1448 | 14 | 1.8 | 0.2 |
| L1455 | 7 | 1.5 | 0.4 |
| Starless | 17 | 1.8 | 0.2 |
| Protostarsa | 33 | 1.89 | 0.12 |
| Class 0 | 19 | 2.04 | 0.16 |
| Class I | 14 | 1.7 | 0.2 |
| Population | Number | fturb | σf |
| All | 81 | 1.76 | 0.09 |
| NGC 1333 | 37 | 2.05 | 0.12 |
| IC 348 | 23 | 1.36 | 0.09 |
| L1448 | 14 | 1.8 | 0.2 |
| L1455 | 7 | 1.5 | 0.4 |
| Starless | 17 | 1.8 | 0.2 |
| Protostarsa | 33 | 1.89 | 0.12 |
| Class 0 | 19 | 2.04 | 0.16 |
| Class I | 14 | 1.7 | 0.2 |
a The Class 0 and Class I populations combined.
Summary of the turbulent fractions, fturb, derived from Gaussian fits to the C18O J = 3 → 2 line at the peak of every SCUBA clump identified with clfind (Curtis & Richer 2010). The results are broken into either different regions in Perseus or clump classifications (see Section 2.2). The quoted errors (σ) are errors on the mean ( ) not sample deviations.
) not sample deviations.
| Population | Number | fturb | σf |
| All | 81 | 1.76 | 0.09 |
| NGC 1333 | 37 | 2.05 | 0.12 |
| IC 348 | 23 | 1.36 | 0.09 |
| L1448 | 14 | 1.8 | 0.2 |
| L1455 | 7 | 1.5 | 0.4 |
| Starless | 17 | 1.8 | 0.2 |
| Protostarsa | 33 | 1.89 | 0.12 |
| Class 0 | 19 | 2.04 | 0.16 |
| Class I | 14 | 1.7 | 0.2 |
| Population | Number | fturb | σf |
| All | 81 | 1.76 | 0.09 |
| NGC 1333 | 37 | 2.05 | 0.12 |
| IC 348 | 23 | 1.36 | 0.09 |
| L1448 | 14 | 1.8 | 0.2 |
| L1455 | 7 | 1.5 | 0.4 |
| Starless | 17 | 1.8 | 0.2 |
| Protostarsa | 33 | 1.89 | 0.12 |
| Class 0 | 19 | 2.04 | 0.16 |
| Class I | 14 | 1.7 | 0.2 |
a The Class 0 and Class I populations combined.
Summary of the turbulent fractions, fturb, for the gaussclumps clump population as in Table 1.
| Population | Number | fturb | σf |
| All | 119 | 1.71 | 0.05 |
| NGC 1333 | 64 | 1.91 | 0.07 |
| IC 348 | 25 | 1.44 | 0.07 |
| L1448 | 23 | 1.52 | 0.13 |
| L1455 | 7 | 1.5 | 0.3 |
| Starless | 24 | 1.61 | 0.11 |
| Protostars | 40 | 1.80 | 0.10 |
| Class 0 | 27 | 1.73 | 0.11 |
| Class I | 13 | 2.0 | 0.2 |
| Population | Number | fturb | σf |
| All | 119 | 1.71 | 0.05 |
| NGC 1333 | 64 | 1.91 | 0.07 |
| IC 348 | 25 | 1.44 | 0.07 |
| L1448 | 23 | 1.52 | 0.13 |
| L1455 | 7 | 1.5 | 0.3 |
| Starless | 24 | 1.61 | 0.11 |
| Protostars | 40 | 1.80 | 0.10 |
| Class 0 | 27 | 1.73 | 0.11 |
| Class I | 13 | 2.0 | 0.2 |
Summary of the turbulent fractions, fturb, for the gaussclumps clump population as in Table 1.
| Population | Number | fturb | σf |
| All | 119 | 1.71 | 0.05 |
| NGC 1333 | 64 | 1.91 | 0.07 |
| IC 348 | 25 | 1.44 | 0.07 |
| L1448 | 23 | 1.52 | 0.13 |
| L1455 | 7 | 1.5 | 0.3 |
| Starless | 24 | 1.61 | 0.11 |
| Protostars | 40 | 1.80 | 0.10 |
| Class 0 | 27 | 1.73 | 0.11 |
| Class I | 13 | 2.0 | 0.2 |
| Population | Number | fturb | σf |
| All | 119 | 1.71 | 0.05 |
| NGC 1333 | 64 | 1.91 | 0.07 |
| IC 348 | 25 | 1.44 | 0.07 |
| L1448 | 23 | 1.52 | 0.13 |
| L1455 | 7 | 1.5 | 0.3 |
| Starless | 24 | 1.61 | 0.11 |
| Protostars | 40 | 1.80 | 0.10 |
| Class 0 | 27 | 1.73 | 0.11 |
| Class I | 13 | 2.0 | 0.2 |
A majority of the linewidths are supersonic with means 〈fturb〉 = 1.76 ± 0.09 2 and 1.71 ± 0.05 for the clfind and gaussclumps populations, respectively. The level of non-thermal broadening should take into account motions from both (a) the source itself, i.e. infall, rotation and outflows and (b) the source’s natal environment. Young stars can inject significant energy into their surroundings, increasing the non-thermal motions within nearby star-forming cores. For example, Caselli & Myers (1995) found an inverse relationship between a core’s NH3 linewidth and the distance to the nearest young stellar cluster in Orion B. There are three such young clusters in Perseus (see Hatchell et al. 2005): IC 348, NGC 1333 and the Per OB2 association. Therefore, of our fields, NGC 1333 and IC 348 are very near to young clusters, while L1448 and L1455 are further away (L1455 being the furthest).
The variations in fturb region-to-region (see Fig. 2), which we might attribute to each region’s distance from a young stellar cluster, are slightly different for the two populations. For the clfind clumps (see Table 1), NGC 1333 and L1448 have statistically similar fractions: 2.05 ± 0.12 and 1.8 ± 0.2, respectively. We ignore the L1455 populations in these comparisons as they are so few in number. IC 348, on the other hand, has much smaller linewidths overall: 〈fturb〉 = 1.36 ± 0.09. The gaussclumps population (see Table 2) has clumps in NGC 1333 with much larger turbulent fractions than the similar fturb means in IC 348 and L1448: 1.91 ± 0.07 compared to 1.44 ± 0.07 and 1.52 ± 0.13. Therefore, for both populations, the IC 348 linewidths are smaller than in NGC 1333, even though both regions are close to stellar clusters. This is possibly (as noted in Paper I) because the IC 348 infrared (IR) cluster is old and no longer actively forming stars, so it affects its environs much less than the NGC 1333 cluster. There is a wide range of clump fturb in L1448, which could be a result of a significant contribution to the C18O linewidth from molecular outflows. Many of the protostellar clumps in L1448 drive particularly strong flows (Paper II).
On dividing the clumps into protostellar and starless subsets (see Fig. 3), there appears to little difference between the distributions of turbulent fraction for both source types and clump populations. At the peak positions of the clfind objects, we find 〈fturb〉 = 1.8 ± 0.2 for starless clumps compared to 1.89 ± 0.12 for protostars. Similarly, 〈fturb〉 = 1.61 ± 0.11 and 1.80 ± 0.10 for starless and protostellar gaussclumps sources, respectively. Further separation of the protostars into Class 0 and I clumps does not yield statistical differences between their average fturb (see Tables 1 and 2). Unfortunately, such simple averages do not provide the whole picture we can see in the distributions (in Fig. 3). For example, if the small but significant population of high fturb starless cores were eliminated it would seem that protostars have marginally higher fturb on average. However, the large uncertainties on the average fturb do emphasize the need for larger samples of objects. For the clfind population (but not the gaussclumps sources) most of the high fturb protostars are Class 0, and all of the low fturb Class I, which is perhaps what we might expect if outflow power decreases from the Class 0 to I stage (Bontemps et al. 1996, Paper II). Overall, there are few significant differences between the starless and protostellar distributions.
We can draw interesting comparisons with the C18O (J = 2 → 1) and N2H+fturb distributions presented by KJT07 (see Figs 4 and 5). Our distributions are closer to the C18O distributions of KJT07 than their N2H+ results. The high levels of non-thermal motions, shown by some of our sources, are simply not present in N2H+ data. A striking contrast between the C18O distributions is that many of our cores have high fturb(≥3.5), which are not seen for either protostars or starless cores by KJT07. In addition, many KJT07 starless cores have subthermal linewidths (fturb < 1). These differences may be partly caused by the spectral resolution of our observations (Δv = 0.15 km s−1 compared to KJT07’s 0.05 km s−1), rather than intrinsically different results. Our slightly poorer resolution means we cannot probe as narrow linewidths and we possibly blend many of the separate components, noted in KJT07’s C18O spectra, into one. Given the similarities it seems likely our C18O J = 3 → 2 data probe the same regions as the J = 2 → 1 observations of KJT07, namely the outer parts of star-forming cores, referred to by KJT07 as their envelopes. This is probably because of C18O freeze-out in the dense, cold interiors of star-forming cores. Such regions should see an enhancement in the abundance of say N2H+ relative to C18O. KJT07 investigated this possibility for their similar population of candidate cores in Perseus by measuring the variation in the integrated C18O-to-N2H+ ratio with peak SCUBA flux density (an approximate proxy for central H2 volume density). They found high C18O-to-N2H+ ratios (i.e. little C18O depletion) occurred mainly in starless cores, which have the smallest SCUBA fluxes (i.e. lowest densities), whereas high-flux cores (mainly protostars) have low ratios suggesting high levels of C18O depletion.
Given that our starless and protostellar C18O distributions are quite similar, we may also conclude (like KJT07) that protostars do not affect their environment significantly. The starless distribution may differ from the true pre-stellar one as starless clumps with the largest linewidths are likely to be unbound, and thus the true pre-stellar turbulent fractions will be smaller. Finally, we also note little correspondence with the simulations of Klessen et al. (2005), whose results for a large-scale driven (LSD) gravoturbulent model are also plotted in Figs 4 and 5. KJT07 claim to have a good fit to the Klessen et al. data with their C18O starless population, although the model was designed to match N2H+ observations.
3.2 Virial theorem
If the C18O data trace material that will go on to form the final star and not just the ambient gas in which a young stellar object is embedded, the core linewidth can inform us about its stability, i.e. whether the cores are gravitationally bound. We can then distinguish bound, starless i.e. pre-stellar cores from unbound ones that will dissipate without forming a star.
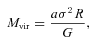
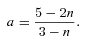
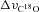 , traces the bulk of the gas with a Gaussian velocity distribution and the same non-thermal linewidth as H2, we can estimate
, traces the bulk of the gas with a Gaussian velocity distribution and the same non-thermal linewidth as H2, we can estimate 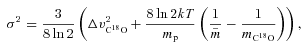
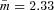 to factor in the abundance of He relative to H2 and
to factor in the abundance of He relative to H2 and 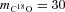 . This yields for a shallow power-law clump, n = 1.5, consistent with the shapes found by Enoch et al. (2008):
. This yields for a shallow power-law clump, n = 1.5, consistent with the shapes found by Enoch et al. (2008): 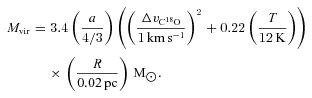
We take data on the clumps’ dust properties from Curtis & Richer (2010). Each clump’s 850-μm mass (M850) assumes the dust is optically thin, has an opacity κ = 0.012 cm2 g−1 and is at a single temperature TD. Again these temperatures are taken as the NH3 kinetic temperatures (Rosolowsky et al. 2008), where available, or 10 K (for starless cores) and 15 K (for protostars), where not. The core radius, Rdec, is the geometric mean of the two core semimajor and semiminor axis ‘sizes’ each deconvolved with the beam size. These ‘sizes’ are the standard deviation of the pixel coordinates about the core centroid, weighted by the pixel values.
There are considerable uncertainties in any dust and virial mass estimates. The errors are very difficult to quantify for individual clumps without detailed modelling. Thus, we follow complementary studies (e.g. Enoch et al. 2008; Buckle et al. 2010) and do not attempt to account for the uncertainties in our analysis, except for a discussion of their magnitude, which follows. The dust masses depend on the assumed distance to Perseus and the dust properties (temperature and opacity). We try to minimize the effects of dust temperature by using the NH3 kinetic temperature as an estimate of TD, which should be an accurate measurement at high volume densities (≳104 cm−3; e.g. Galli, Walmsley & Gonçalves 2002), where the gas and dust are thermally coupled. Nevertheless our dust temperature estimates still do not account for variations in the dust temperature across a clump. A range of distances has been used in the literature for Perseus (220 to 350 pc; see e.g. Paper I) and indeed it may not be a contiguous cloud at a single distance. These result in an uncertainty of a factor of ∼5 in the dust mass estimates. The virial masses depend on the assumed clump profile, with steeper profiles producing smaller masses, however it only varies by a factor of 1.7 between a constant density and 1/r2 profile. This combined with the uncertainties in the distance and linewidth produce again around a factor of ∼5 in uncertainty. As we previously noted (Section 3.1), it is likely that the C18O J = 3 → 2 line only traces the envelope of a clump, which could lead to an overestimate of the non-thermal H2 linewidth (compared to estimates from say NH3 or N2H+) and correspondingly the virial mass. Even if our estimates of the dust and virial masses were infallible, assuming that a clump with Mvir≫ M850 is unbound may be misleading; external pressure and/or magnetic fields may contain such a clump. For instance, KJT07 calculate that cores with external pressures consistent with their previous Bonnor–Ebert sphere modelling (Kirk, Johnstone & Di Francesco 2006), should be considered in equipartition not merely self-gravitating if Mvir∼ 2M850.
The C18O virial masses, which we plot in Fig. 6 against the 850-μm mass, lie in the range 0.8 to 22.9 M⊙ for the clfind sources and 0.4 to 17.8 M⊙ for the gaussclumps sources, reflecting their smaller radii. Most of the clumps lie scattered near the ‘equipartition’ line, Mvir= M850. The results are similar for the different algorithms, regions and evolutionary types (see Tables 3 and 4 for summaries of the population statistics). Least-squares straight-line fitting results in poorly constrained power-law exponents of 0.8–0.9 for almost all the correlations.

Virial mass versus clump dust mass for the clfind (left-hand panels, a, c and e) and gaussclumps (right-hand panels, b, d and f) populations, differentiated by region (top panels, a and b) or the classifications of HFR07 (the rest). Virial masses are estimated from the C18O J = 3 → 2 linewidth at the catalogue positions of Curtis & Richer (2010). The masses are calculated using the temperatures from Rosolowsky et al. (2008), where possible, or 10 and 15 K for starless and protostellar cores, respectively, where not. Lines denote where we expect cores to be in equipartition, i.e. Mvir= M850 (dashed) or the limit where they are self-gravitating, Mvir = 2M850 (dot–dashed), although the reader should note the considerable uncertainties in both masses. Only clumps that have a HFR07 source association are plotted.
Summary of virial mass statistics for the clfind SCUBA clumps identified in Curtis & Richer (2010), which have a HFR07 classification. All the quoted errors (σ) are errors on the mean ( ) not simple sample deviations.
) not simple sample deviations.
| Population | No | Mvir (M⊙) | σM (M⊙) | M850/Mvir | σratio |
| All | 50 | 7.8 | 0.9 | 1.32 | 0.13 |
| NGC 1333 | 24 | 8.9 | 1.2 | 0.96 | 0.15 |
| IC 348 | 16 | 4.0 | 0.8 | 1.38 | 0.22 |
| L1448 | 5 | 12.6 | 3.9 | 2.7 | 0.5 |
| L1455 | 5 | 7.9 | 1.6 | 1.4 | 0.6 |
| Starless | 17 | 4.6 | 0.8 | 1.4 | 0.2 |
| Protostars | 33 | 9.6 | 1.2 | 1.3 | 0.2 |
| Class 0 | 19 | 10.1 | 1.4 | 1.3 | 0.2 |
| Class I | 14 | 9 | 2 | 1.2 | 0.3 |
| Population | No | Mvir (M⊙) | σM (M⊙) | M850/Mvir | σratio |
| All | 50 | 7.8 | 0.9 | 1.32 | 0.13 |
| NGC 1333 | 24 | 8.9 | 1.2 | 0.96 | 0.15 |
| IC 348 | 16 | 4.0 | 0.8 | 1.38 | 0.22 |
| L1448 | 5 | 12.6 | 3.9 | 2.7 | 0.5 |
| L1455 | 5 | 7.9 | 1.6 | 1.4 | 0.6 |
| Starless | 17 | 4.6 | 0.8 | 1.4 | 0.2 |
| Protostars | 33 | 9.6 | 1.2 | 1.3 | 0.2 |
| Class 0 | 19 | 10.1 | 1.4 | 1.3 | 0.2 |
| Class I | 14 | 9 | 2 | 1.2 | 0.3 |
Summary of virial mass statistics for the clfind SCUBA clumps identified in Curtis & Richer (2010), which have a HFR07 classification. All the quoted errors (σ) are errors on the mean ( ) not simple sample deviations.
) not simple sample deviations.
| Population | No | Mvir (M⊙) | σM (M⊙) | M850/Mvir | σratio |
| All | 50 | 7.8 | 0.9 | 1.32 | 0.13 |
| NGC 1333 | 24 | 8.9 | 1.2 | 0.96 | 0.15 |
| IC 348 | 16 | 4.0 | 0.8 | 1.38 | 0.22 |
| L1448 | 5 | 12.6 | 3.9 | 2.7 | 0.5 |
| L1455 | 5 | 7.9 | 1.6 | 1.4 | 0.6 |
| Starless | 17 | 4.6 | 0.8 | 1.4 | 0.2 |
| Protostars | 33 | 9.6 | 1.2 | 1.3 | 0.2 |
| Class 0 | 19 | 10.1 | 1.4 | 1.3 | 0.2 |
| Class I | 14 | 9 | 2 | 1.2 | 0.3 |
| Population | No | Mvir (M⊙) | σM (M⊙) | M850/Mvir | σratio |
| All | 50 | 7.8 | 0.9 | 1.32 | 0.13 |
| NGC 1333 | 24 | 8.9 | 1.2 | 0.96 | 0.15 |
| IC 348 | 16 | 4.0 | 0.8 | 1.38 | 0.22 |
| L1448 | 5 | 12.6 | 3.9 | 2.7 | 0.5 |
| L1455 | 5 | 7.9 | 1.6 | 1.4 | 0.6 |
| Starless | 17 | 4.6 | 0.8 | 1.4 | 0.2 |
| Protostars | 33 | 9.6 | 1.2 | 1.3 | 0.2 |
| Class 0 | 19 | 10.1 | 1.4 | 1.3 | 0.2 |
| Class I | 14 | 9 | 2 | 1.2 | 0.3 |
Summary of virial mass statistics for the gaussclumps SCUBA clumps identified in Curtis & Richer (2010), which have a HFR07 classification. All the quoted errors (σ) are errors on the mean ( ) not simple sample deviations.
) not simple sample deviations.
| Population | No | Mvir (M⊙) | σM (M⊙) | M850/Mvir | σratio |
| All | 64 | 7.1 | 0.7 | 0.9 | 0.1 |
| NGC 1333 | 30 | 8.9 | 1.1 | 0.68 | 0.08 |
| IC 348 | 17 | 5.0 | 0.8 | 0.75 | 0.14 |
| L1448 | 12 | 6.5 | 1.5 | 2.2 | 0.4 |
| L1455 | 5 | 4.3 | 1.1 | 0.8 | 0.3 |
| Starless | 24 | 6.0 | 0.6 | 0.87 | 0.16 |
| Protostars | 40 | 7.8 | 1.0 | 0.91 | 0.13 |
| Class 0 | 27 | 8.4 | 1.1 | 1.06 | 0.18 |
| Class I | 13 | 7 | 2 | 0.67 | 0.14 |
| Population | No | Mvir (M⊙) | σM (M⊙) | M850/Mvir | σratio |
| All | 64 | 7.1 | 0.7 | 0.9 | 0.1 |
| NGC 1333 | 30 | 8.9 | 1.1 | 0.68 | 0.08 |
| IC 348 | 17 | 5.0 | 0.8 | 0.75 | 0.14 |
| L1448 | 12 | 6.5 | 1.5 | 2.2 | 0.4 |
| L1455 | 5 | 4.3 | 1.1 | 0.8 | 0.3 |
| Starless | 24 | 6.0 | 0.6 | 0.87 | 0.16 |
| Protostars | 40 | 7.8 | 1.0 | 0.91 | 0.13 |
| Class 0 | 27 | 8.4 | 1.1 | 1.06 | 0.18 |
| Class I | 13 | 7 | 2 | 0.67 | 0.14 |
Summary of virial mass statistics for the gaussclumps SCUBA clumps identified in Curtis & Richer (2010), which have a HFR07 classification. All the quoted errors (σ) are errors on the mean ( ) not simple sample deviations.
) not simple sample deviations.
| Population | No | Mvir (M⊙) | σM (M⊙) | M850/Mvir | σratio |
| All | 64 | 7.1 | 0.7 | 0.9 | 0.1 |
| NGC 1333 | 30 | 8.9 | 1.1 | 0.68 | 0.08 |
| IC 348 | 17 | 5.0 | 0.8 | 0.75 | 0.14 |
| L1448 | 12 | 6.5 | 1.5 | 2.2 | 0.4 |
| L1455 | 5 | 4.3 | 1.1 | 0.8 | 0.3 |
| Starless | 24 | 6.0 | 0.6 | 0.87 | 0.16 |
| Protostars | 40 | 7.8 | 1.0 | 0.91 | 0.13 |
| Class 0 | 27 | 8.4 | 1.1 | 1.06 | 0.18 |
| Class I | 13 | 7 | 2 | 0.67 | 0.14 |
| Population | No | Mvir (M⊙) | σM (M⊙) | M850/Mvir | σratio |
| All | 64 | 7.1 | 0.7 | 0.9 | 0.1 |
| NGC 1333 | 30 | 8.9 | 1.1 | 0.68 | 0.08 |
| IC 348 | 17 | 5.0 | 0.8 | 0.75 | 0.14 |
| L1448 | 12 | 6.5 | 1.5 | 2.2 | 0.4 |
| L1455 | 5 | 4.3 | 1.1 | 0.8 | 0.3 |
| Starless | 24 | 6.0 | 0.6 | 0.87 | 0.16 |
| Protostars | 40 | 7.8 | 1.0 | 0.91 | 0.13 |
| Class 0 | 27 | 8.4 | 1.1 | 1.06 | 0.18 |
| Class I | 13 | 7 | 2 | 0.67 | 0.14 |
Given the uncertainties in both the virial and dust mass estimates, it is not possible to draw unequivocal conclusions about the stability of individual clumps. However, we will compare distinct populations. The different regions show similar behaviour with a lot of scatter. The L1448 population is outlying for both algorithms with a high M850/Mvir ratio. L1448 is interesting as it contains large SCUBA flux densities and massive outflows but has relatively weaker C18O emission. The NGC 1333 population has a smaller M850/Mvir ratio than the others, which we might interpret as being more unbound and therefore transient, with a larger number of cores above the Mvir= M850 threshold. This could be a result of its more perturbed environment.
Protostellar clumps, by definition, should be gravitationally bound. If starless clumps occupy a similar Mvir–M850 sample space, then this suggests that they too are a gravitationally bound population. In Fig. 6, the starless and protostellar clumps occupy the same regions of the plot and their mass ratios are very similar in Tables 3 and 4. This implies that the starless population is gravitationally bound as well and truly pre-stellar in nature (as found by Enoch et al. 2008).
The clumps also seem spread around the ‘equipartition’ line Mvir= M850. Approximate equipartition was also found by Caselli et al. (2002) in a sample of 60 starless cores using N2H+ linewidths. Other studies, e.g. the C18O cores looked at by Tachihara et al. (2002), found the virial mass considerably larger than the core mass estimate. The latter result is successfully explained by the gravoturbulent models of Klessen et al. (2005), who find a large majority of starless cores with Mvir≫ M for both large and small driving-scale turbulence models, with their protostellar sources non-coincident in parameter space at M > Mvir. Our results would not favour such a model for Perseus, even in its clustered environment.
3.3 Localized velocity gradients
Systematic variations in the C18O line centre velocity are apparent across the face of many of the identified SCUBA clumps, e.g. the velocity gradually increases along a particular direction. There are a number of plausible explanations for such gradients: (i) rotation, (ii) outflows, (iii) motions between smaller unresolved constituent clumps or (iv) if gravoturbulent models are true, cores form at the stagnation points in convergent flows (e.g. Padoan et al. 2001) and velocity gradients may arise from colliding gas streams. It is difficult to distinguish between each scenario so we follow the majority of studies and focus on analysing the rotational properties of the clumps from measured velocity gradients.
A strong motivation to understand the details of rotation in star-forming cores is provided by the discs out of which most, if not all, stars are born (e.g. Shu et al. 1987). Planets are thought to originate inside such protoplanetary discs and the details of their formation crucially depend on various disc parameters, such as surface density, controlled by the detailed evolution of the angular momentum of the parent star-forming core (e.g. Lissauer 1993; Ruden 1999). Additionally, there is the classical ‘angular momentum problem’ of star formation (e.g. Spitzer 1978): the angular momentum of pre-stellar cores is orders of magnitude larger than that which can be contained within a single star, even though cores are observed to be rotating much less than originally predicted (Goodman et al. 1993, hereafter GBF93; Caselli et al. 2002).3 A plausible solution is provided by magnetic braking at the early low-density phases, where the field lines are strongly coupled to the gas and transfer angular momentum from the contracting core to the surrounding medium (e.g. Mouschovias 1987). Recent results suggest that gravitational interactions may dominate over magnetic braking. Magnetohydrodynamic (MHD) models of self-gravitating, decaying (Gammie et al. 2003) and driven (Li et al. 2004) turbulence have angular momenta consistent with each other and observations but Jappsen & Klessen (2004, hereafter JK04) and Tilley & Pudritz (2004) find similar results in purely hydrodynamic frameworks. Even if magnetic fields do dominate, they cannot indefinitely strip away angular momentum or support a core against collapse because ambipolar diffusion will eventually lead to dynamic collapse. Finally, for cores to fragment into multiple systems some angular momentum must be present and perhaps cores with the largest angular momenta will go on to form binaries (e.g. Larson 2003; Goodwin et al. 2007).
The pre-eminent observational study in this area is the search for solid-body rotation in ∼40 NH3 cores by GBF93. In all their objects the rotational energy is at most a few per cent of the gravitational and cannot provide support. An evolutionary sequence can be built using their results with others (e.g. Caselli et al. 2002), demonstrating the specific angular momentum (j = J/M) decreases with decreasing scale (JK04).
Rotational signatures become more complicated at higher resolution and once collapse has started in protostars. Belloche et al. (2002) studied a young Class 0 protostar, IRAM 04191+1522, finding two distinct regimes of collapse: the inner (r ≲ 2000–4000 au), rapidly collapsing and rotating whilst the outer (4000 ≲ r ≲ 11 000 au) has only moderate infall and rotation. The fall in rotational velocity beyond the 4000 au boundary and the flat inner profile suggests that the inner region’s angular momentum is conserved whilst it is dissipated in the outer perhaps by magnetic braking. At the distance to Perseus the r ∼ 4000 au boundary is bigger than the JCMT beam (32 arcsec diameter compared to 15 arcsec) so we may be able to probe the inner regions, although C18O will possibly freeze-out at ≲5000 au in starless and young protostellar cores.
3.3.1 Velocity gradient fitting
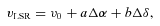
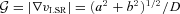 , where D is the distance to the object, at an angle (east of north),
, where D is the distance to the object, at an angle (east of north), 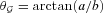 .
.We explore the C18O J = 3 → 2 velocity field of our two populations of SCUBA 850-μm clumps. At each SCUBA map pixel the corresponding spectrum in the HARP data has been fitted with a Gaussian profile to extract its centre velocity and linewidth. Fits were only performed where the spectral peak was greater than three times the rms noise, estimated on a line-free portion of the spectrum for every spatial position. L1455 was omitted, as its weak C18O emission had too few fits. We then used the Levenberg–Marquardt algorithm implemented in the scientific Python module, SciPy,4 to perform non-linear least-squares fitting of equation (7) to every clump about its SCUBA peak. GBF93 performed the same analysis on sets of randomly generated maps with no gradient and report that approximately 10 per cent of those random maps were found to have significant gradients if a ‘3σ’ criterion is used, i.e.  . Using the same significance criterion we expect similar levels of reliability.
. Using the same significance criterion we expect similar levels of reliability.
3.3.2 A signature of rotation?
We noted there are four plausible causes of velocity gradients. In this section, we look at some of the suggestions other than rotation in more detail. First, some of our clumps may be composed of smaller constituents. The gradient then might measure the velocity dispersion of the multiple cores (GBF93). If the SCUBA clumps are gravitationally bound, as suggested in Section 3.2, such dispersion in a multicore clump may signal its rotation about a common centre. HFR07 estimate within their similar core catalogue, >rsim10 per cent of clumps will break into multiple sources, by comparing the most luminous sources to higher resolution observations.
Second, the exact region that is assigned to each clump can change the fitted gradient’s magnitude, direction and level of significance. One of GBF93’s original sample, TMC-1C, a starless core in Taurus, has been mapped over a larger area at higher resolution by Schnee et al. (2007). They found a more complicated pattern of local gradients no longer consistent with solid-body or differential rotation, which had previously been noted by Caselli et al. (2002).
Finally, if the C18O line centre is affected by outflows, then this could be misinterpreted as a sign of rotation. GBF93 also fitted velocity gradients to C18O J = 1 → 0 data in a subsample of their cores – both with and without embedded objects – and found they were in the same direction as the gradients from NH3. However, they did not formally examine any outflows. Towards starless cores, outflows should not be a problem. To explore the effect on our gradients, we compare the direction of the velocity gradient to the orientation of the outflow from every protostellar source with a significant gradient in the clfind catalogue. We estimated the outflow position angle from our CO J = 3 → 2 data cubes (a full outflow analysis was presented in Paper II). For some of the protostellar clumps, the outflows are complicated and we have ignored such cases, only comparing clumps where a characteristic bipolar structure is apparent (see Table 5). In a number of these cases the velocity gradient is in the same direction as the outflow, implying we are tracing the outflow rather than solid-body rotation with the gradient. If we were viewing solid-body rotation of the core or a disc around it, we would expect the gradient and outflow to lie perpendicular to one another.
Approximate outflow orientation compared to the velocity gradient direction for clfind clumps with clear bipolar outflows. Classifications are from HFR07.
| Subregion | clfind ID | Class |  (deg E of N) (deg E of N) | Outflow orientation (deg E of N) |
| NGC 1333 | 6 | 0 | 126 | −113 |
| IC 348 | 1 | 0 | −51 | −64 |
| IC 348 | 2 | 0 | 50 | 68 |
| IC 348 | 4 | 0 | 4 | 0 |
| L1448 | 1 | 0 | 139 | 124 |
| L1448 | 2 | 0 | 78 | 165 |
| L1448 | 4 | 0 | 154 | 168 |
| Subregion | clfind ID | Class |  (deg E of N) (deg E of N) | Outflow orientation (deg E of N) |
| NGC 1333 | 6 | 0 | 126 | −113 |
| IC 348 | 1 | 0 | −51 | −64 |
| IC 348 | 2 | 0 | 50 | 68 |
| IC 348 | 4 | 0 | 4 | 0 |
| L1448 | 1 | 0 | 139 | 124 |
| L1448 | 2 | 0 | 78 | 165 |
| L1448 | 4 | 0 | 154 | 168 |
Approximate outflow orientation compared to the velocity gradient direction for clfind clumps with clear bipolar outflows. Classifications are from HFR07.
| Subregion | clfind ID | Class |  (deg E of N) (deg E of N) | Outflow orientation (deg E of N) |
| NGC 1333 | 6 | 0 | 126 | −113 |
| IC 348 | 1 | 0 | −51 | −64 |
| IC 348 | 2 | 0 | 50 | 68 |
| IC 348 | 4 | 0 | 4 | 0 |
| L1448 | 1 | 0 | 139 | 124 |
| L1448 | 2 | 0 | 78 | 165 |
| L1448 | 4 | 0 | 154 | 168 |
| Subregion | clfind ID | Class |  (deg E of N) (deg E of N) | Outflow orientation (deg E of N) |
| NGC 1333 | 6 | 0 | 126 | −113 |
| IC 348 | 1 | 0 | −51 | −64 |
| IC 348 | 2 | 0 | 50 | 68 |
| IC 348 | 4 | 0 | 4 | 0 |
| L1448 | 1 | 0 | 139 | 124 |
| L1448 | 2 | 0 | 78 | 165 |
| L1448 | 4 | 0 | 154 | 168 |
The data themselves present a more complicated picture. In Fig. 7, we overlay the outflows on top of the C18O centre velocities for the sources in Table 5. Often the higher C18O line centres (i.e. redshifted gas) correspond closely to the extent of the redshifted CO outflow lobe and similarly for the blueshifted gas. For instance, the complex outflow structure in L1448-1 is closely followed by the line centre data. Furthermore, the blueshifted outflow lobe in NGC 1333-6 is coincident with blueshifted C18O line centres. The outflow itself extends away from the clump to the west, resulting in orientations that seem very disparate in Table 5. In two cores there seems to be little outflow-gradient correspondence: IC 348-2 and L1448-4. Perhaps it is more convincing to argue that none of the cores exhibits gradients perpendicular to their outflows. Therefore, there appears to be a link between the outflow orientation and the velocity gradient, although how much this influences the gradient found in every protostar is difficult to quantify.
Outflow orientation compared to the velocity gradient direction for clumps in Table 5. The colour-scale is the C18O J = 3 → 2 line centre in km s−1 for map pixels allocated to each clump. Overlaid are contours of CO J = 3 → 2 integrated antenna temperature  for the blue- and redshifted line wings, integrated from −5 to 3 km s−1 (blue) and 12 to 18 km s−1 (red) for NGC 1333, −5 to 6 km s−1 (blue) and 11 to 15 km s−1 (red) for IC 348 and −5 to 0 km s−1 (blue) and 8 to 15 km s−1 (red) for L1448. Contours are at various heights in K km s−1(n is an integer from zero to nmax): (a) (2+4n), nmax = 4 (blue) and (4+4n), nmax = 6 (red). (b) (6+2n), nmax = 6 (blue) and (6+2n), nmax = 3 (red). (c) (8+1.5n), nmax = 6 (blue) and (4+1.5n), nmax = 8 (red). (d) (5+n), nmax = 4 (blue) and (2+n), nmax = 2 (red). (e) (2+n), nmax = 8 (blue) and (2+2n), nmax = 7 (red). (f) (2+4n), nmax = 5 (both blue and red). (g) (2+4n), nmax = 5 (both blue and red).
for the blue- and redshifted line wings, integrated from −5 to 3 km s−1 (blue) and 12 to 18 km s−1 (red) for NGC 1333, −5 to 6 km s−1 (blue) and 11 to 15 km s−1 (red) for IC 348 and −5 to 0 km s−1 (blue) and 8 to 15 km s−1 (red) for L1448. Contours are at various heights in K km s−1(n is an integer from zero to nmax): (a) (2+4n), nmax = 4 (blue) and (4+4n), nmax = 6 (red). (b) (6+2n), nmax = 6 (blue) and (6+2n), nmax = 3 (red). (c) (8+1.5n), nmax = 6 (blue) and (4+1.5n), nmax = 8 (red). (d) (5+n), nmax = 4 (blue) and (2+n), nmax = 2 (red). (e) (2+n), nmax = 8 (blue) and (2+2n), nmax = 7 (red). (f) (2+4n), nmax = 5 (both blue and red). (g) (2+4n), nmax = 5 (both blue and red).
Thus, we must view the interpretation of a linear velocity gradient as unequivocal evidence of solid-body rotation with some scepticism. However, in the absence of a strong outflow, i.e. for starless clumps and assuming we can consider each clump as a single object, rotation would seem to be a likely cause of a coherent velocity gradient and the only one we consider in the following analysis.
3.3.3 Fitted gradients
Table 6 lists the rates of detecting significant velocity gradients towards various core populations, separated by their different clump-finding algorithms, regions or types of source. They are similar for both algorithms with approximately a third of clumps displaying significant velocity gradients. The detection rate for Class 0 sources in the clfind catalogue is nearly twice as large as for the other types and Class 0s with gaussclumps. This is probably because Class 0 sources have typically stronger outflows than Class Is (e.g. Bontemps et al. 1996, Paper II). It is clear in Fig. 7 that many of the outflows extend beyond their associated clump. However, the clumps found by gaussclumps are smaller (Curtis & Richer 2010) with a definite elliptical shape, which does not necessarily follow the orientation of the outflow. The lower detection rate for Class 0 sources with gaussclumps is perhaps another example of how their velocity gradients are dominated by outflows. If the smaller gaussclumps cores trace their shape less effectively, we would expect a lower detection rate.
Number of clumps with significant velocity gradients by region, source type and algorithm. Values in parentheses are percentages which give the detection rate for the particular type of source in each region or overall.
| Source type | Region | |||
| NGC 1333 | IC 348 | L1448 | Total | |
| clfind population | ||||
| Starless | 4(67) | 2(17) | 0(0) | 6(32) |
| Class 0 | 7(64) | 3(100) | 3(75) | 13(72) |
| Class I | 4(44) | 1(50) | 0(0) | 5(45) |
| No HFR07 ID | 1(8) | 1(17) | 1(9) | 3(11) |
| All | 16(41) | 7(30) | 4(25) | 27(35) |
| gaussclumps population | ||||
| Starless | 4(50) | 6(55) | 0(0) | 10(48) |
| Class 0 | 6(50) | 1(33) | 0(0) | 7(35) |
| Class I | 3(33) | 0(0) | 0(0) | 3(35) |
| No HFR07 ID | 11(31) | 3(38) | 1(6) | 15(24) |
| All | 24(37) | 10(42) | 1(4) | 35(31) |
| Source type | Region | |||
| NGC 1333 | IC 348 | L1448 | Total | |
| clfind population | ||||
| Starless | 4(67) | 2(17) | 0(0) | 6(32) |
| Class 0 | 7(64) | 3(100) | 3(75) | 13(72) |
| Class I | 4(44) | 1(50) | 0(0) | 5(45) |
| No HFR07 ID | 1(8) | 1(17) | 1(9) | 3(11) |
| All | 16(41) | 7(30) | 4(25) | 27(35) |
| gaussclumps population | ||||
| Starless | 4(50) | 6(55) | 0(0) | 10(48) |
| Class 0 | 6(50) | 1(33) | 0(0) | 7(35) |
| Class I | 3(33) | 0(0) | 0(0) | 3(35) |
| No HFR07 ID | 11(31) | 3(38) | 1(6) | 15(24) |
| All | 24(37) | 10(42) | 1(4) | 35(31) |
Number of clumps with significant velocity gradients by region, source type and algorithm. Values in parentheses are percentages which give the detection rate for the particular type of source in each region or overall.
| Source type | Region | |||
| NGC 1333 | IC 348 | L1448 | Total | |
| clfind population | ||||
| Starless | 4(67) | 2(17) | 0(0) | 6(32) |
| Class 0 | 7(64) | 3(100) | 3(75) | 13(72) |
| Class I | 4(44) | 1(50) | 0(0) | 5(45) |
| No HFR07 ID | 1(8) | 1(17) | 1(9) | 3(11) |
| All | 16(41) | 7(30) | 4(25) | 27(35) |
| gaussclumps population | ||||
| Starless | 4(50) | 6(55) | 0(0) | 10(48) |
| Class 0 | 6(50) | 1(33) | 0(0) | 7(35) |
| Class I | 3(33) | 0(0) | 0(0) | 3(35) |
| No HFR07 ID | 11(31) | 3(38) | 1(6) | 15(24) |
| All | 24(37) | 10(42) | 1(4) | 35(31) |
| Source type | Region | |||
| NGC 1333 | IC 348 | L1448 | Total | |
| clfind population | ||||
| Starless | 4(67) | 2(17) | 0(0) | 6(32) |
| Class 0 | 7(64) | 3(100) | 3(75) | 13(72) |
| Class I | 4(44) | 1(50) | 0(0) | 5(45) |
| No HFR07 ID | 1(8) | 1(17) | 1(9) | 3(11) |
| All | 16(41) | 7(30) | 4(25) | 27(35) |
| gaussclumps population | ||||
| Starless | 4(50) | 6(55) | 0(0) | 10(48) |
| Class 0 | 6(50) | 1(33) | 0(0) | 7(35) |
| Class I | 3(33) | 0(0) | 0(0) | 3(35) |
| No HFR07 ID | 11(31) | 3(38) | 1(6) | 15(24) |
| All | 24(37) | 10(42) | 1(4) | 35(31) |
The fitted gradients are in the range 1.5 to 13.0 km s−1 pc−1 and 2.5 to 16.0 km s−1 pc−1 for clfind and gaussclumps, respectively. We provide a summary of all the different rotational properties for different categories of clumps in Tables 7 and 8. Fig. 8 is a histogram of their magnitude by region. The distributions are qualitatively similar for the different regions with the usual uncertainty due to the small sample sizes; Kolmogorov–Smirnov (K–S) tests do not conclusively reject or confirm the hypothesis that each sample is drawn from the same population. On average across all the regions, the gradients are  km s−1 pc−1 for clfind and
km s−1 pc−1 for clfind and  km s−1 pc−1 for gaussclumps. The fitted gaussclumps gradients are larger than those for clfind but may be misleading as there are only 16 clumps with detections in both. We plot the gradient found with the clfind designation versus that with gaussclumps for these common sources in Fig. 9. There is fairly good agreement on the gradient with the protostellar sources deviating the most from the line of equal gradients. This might again be because the C18O line centres are affected by outflowing gas which is not well traced by the gaussclumps outlines.
km s−1 pc−1 for gaussclumps. The fitted gaussclumps gradients are larger than those for clfind but may be misleading as there are only 16 clumps with detections in both. We plot the gradient found with the clfind designation versus that with gaussclumps for these common sources in Fig. 9. There is fairly good agreement on the gradient with the protostellar sources deviating the most from the line of equal gradients. This might again be because the C18O line centres are affected by outflowing gas which is not well traced by the gaussclumps outlines.
Average rotational properties derived from the velocity-gradient fitting for the clfind clump population. All the errors listed (σ) are errors on the mean and not sample deviations.
| Population | Number |  |  | βrot | σβ | j | σj |
| (km s−1 pc−1) | (km s−1 pc) | ||||||
| All | 27 | 5.7 | 0.5 | 0.014 | 0.003 | 0.0019 | 0.0002 |
| NGC 1333 | 16 | 5.7 | 0.7 | 0.0040 | 0.0010 | 0.0017 | 0.0002 |
| IC 348 | 7 | 5.0 | 0.6 | 0.015 | 0.006 | 0.0017 | 0.0003 |
| L1448 | 4 | 7 | 2 | 0.032 | 0.016 | 0.0032 | 0.0009 |
| Starless | 6 | 5.5 | 1.0 | 0.013 | 0.007 | 0.0021 | 0.0005 |
| Protostars | 19 | 5.8 | 0.7 | 0.008 | 0.003 | 0.0019 | 0.0003 |
| Class 0 | 14 | 6.1 | 0.8 | 0.010 | 0.004 | 0.0021 | 0.0003 |
| Class I | 5 | 4.9 | 1.5 | 0.003 | 0.001 | 0.0011 | 0.0001 |
| Population | Number |  |  | βrot | σβ | j | σj |
| (km s−1 pc−1) | (km s−1 pc) | ||||||
| All | 27 | 5.7 | 0.5 | 0.014 | 0.003 | 0.0019 | 0.0002 |
| NGC 1333 | 16 | 5.7 | 0.7 | 0.0040 | 0.0010 | 0.0017 | 0.0002 |
| IC 348 | 7 | 5.0 | 0.6 | 0.015 | 0.006 | 0.0017 | 0.0003 |
| L1448 | 4 | 7 | 2 | 0.032 | 0.016 | 0.0032 | 0.0009 |
| Starless | 6 | 5.5 | 1.0 | 0.013 | 0.007 | 0.0021 | 0.0005 |
| Protostars | 19 | 5.8 | 0.7 | 0.008 | 0.003 | 0.0019 | 0.0003 |
| Class 0 | 14 | 6.1 | 0.8 | 0.010 | 0.004 | 0.0021 | 0.0003 |
| Class I | 5 | 4.9 | 1.5 | 0.003 | 0.001 | 0.0011 | 0.0001 |
Average rotational properties derived from the velocity-gradient fitting for the clfind clump population. All the errors listed (σ) are errors on the mean and not sample deviations.
| Population | Number |  |  | βrot | σβ | j | σj |
| (km s−1 pc−1) | (km s−1 pc) | ||||||
| All | 27 | 5.7 | 0.5 | 0.014 | 0.003 | 0.0019 | 0.0002 |
| NGC 1333 | 16 | 5.7 | 0.7 | 0.0040 | 0.0010 | 0.0017 | 0.0002 |
| IC 348 | 7 | 5.0 | 0.6 | 0.015 | 0.006 | 0.0017 | 0.0003 |
| L1448 | 4 | 7 | 2 | 0.032 | 0.016 | 0.0032 | 0.0009 |
| Starless | 6 | 5.5 | 1.0 | 0.013 | 0.007 | 0.0021 | 0.0005 |
| Protostars | 19 | 5.8 | 0.7 | 0.008 | 0.003 | 0.0019 | 0.0003 |
| Class 0 | 14 | 6.1 | 0.8 | 0.010 | 0.004 | 0.0021 | 0.0003 |
| Class I | 5 | 4.9 | 1.5 | 0.003 | 0.001 | 0.0011 | 0.0001 |
| Population | Number |  |  | βrot | σβ | j | σj |
| (km s−1 pc−1) | (km s−1 pc) | ||||||
| All | 27 | 5.7 | 0.5 | 0.014 | 0.003 | 0.0019 | 0.0002 |
| NGC 1333 | 16 | 5.7 | 0.7 | 0.0040 | 0.0010 | 0.0017 | 0.0002 |
| IC 348 | 7 | 5.0 | 0.6 | 0.015 | 0.006 | 0.0017 | 0.0003 |
| L1448 | 4 | 7 | 2 | 0.032 | 0.016 | 0.0032 | 0.0009 |
| Starless | 6 | 5.5 | 1.0 | 0.013 | 0.007 | 0.0021 | 0.0005 |
| Protostars | 19 | 5.8 | 0.7 | 0.008 | 0.003 | 0.0019 | 0.0003 |
| Class 0 | 14 | 6.1 | 0.8 | 0.010 | 0.004 | 0.0021 | 0.0003 |
| Class I | 5 | 4.9 | 1.5 | 0.003 | 0.001 | 0.0011 | 0.0001 |
Average rotational properties derived from the velocity-gradient fitting for the gaussclumps clump population. All the errors listed (σ) are errors on the mean and not sample deviations.
| Population | Number |  |  | βrot | σβ | j | σj |
| (km s−1 pc−1) | (km s−1 pc) | ||||||
| All | 35 | 6.9 | 0.6 | 0.013 | 0.004 | 0.00120 | 0.00014 |
| NGC 1333 | 24 | 7.4 | 0.7 | 0.015 | 0.006 | 0.0012 | 0.0002 |
| IC 348 | 10 | 5.6 | 0.8 | 0.007 | 0.001 | 0.0011 | 0.0002 |
| Starless | 10 | 5.0 | 0.6 | 0.006 | 0.001 | 0.0010 | 0.0002 |
| Protostars | 10 | 7.0 | 1.0 | 0.009 | 0.004 | 0.0012 | 0.0002 |
| Class 0 | 7 | 6.4 | 1.0 | 0.008 | 0.005 | 0.0012 | 0.0002 |
| Class I | 3 | 8 | 3 | 0.012 | 0.010 | 0.0012 | 0.0003 |
| Population | Number |  |  | βrot | σβ | j | σj |
| (km s−1 pc−1) | (km s−1 pc) | ||||||
| All | 35 | 6.9 | 0.6 | 0.013 | 0.004 | 0.00120 | 0.00014 |
| NGC 1333 | 24 | 7.4 | 0.7 | 0.015 | 0.006 | 0.0012 | 0.0002 |
| IC 348 | 10 | 5.6 | 0.8 | 0.007 | 0.001 | 0.0011 | 0.0002 |
| Starless | 10 | 5.0 | 0.6 | 0.006 | 0.001 | 0.0010 | 0.0002 |
| Protostars | 10 | 7.0 | 1.0 | 0.009 | 0.004 | 0.0012 | 0.0002 |
| Class 0 | 7 | 6.4 | 1.0 | 0.008 | 0.005 | 0.0012 | 0.0002 |
| Class I | 3 | 8 | 3 | 0.012 | 0.010 | 0.0012 | 0.0003 |
Average rotational properties derived from the velocity-gradient fitting for the gaussclumps clump population. All the errors listed (σ) are errors on the mean and not sample deviations.
| Population | Number |  |  | βrot | σβ | j | σj |
| (km s−1 pc−1) | (km s−1 pc) | ||||||
| All | 35 | 6.9 | 0.6 | 0.013 | 0.004 | 0.00120 | 0.00014 |
| NGC 1333 | 24 | 7.4 | 0.7 | 0.015 | 0.006 | 0.0012 | 0.0002 |
| IC 348 | 10 | 5.6 | 0.8 | 0.007 | 0.001 | 0.0011 | 0.0002 |
| Starless | 10 | 5.0 | 0.6 | 0.006 | 0.001 | 0.0010 | 0.0002 |
| Protostars | 10 | 7.0 | 1.0 | 0.009 | 0.004 | 0.0012 | 0.0002 |
| Class 0 | 7 | 6.4 | 1.0 | 0.008 | 0.005 | 0.0012 | 0.0002 |
| Class I | 3 | 8 | 3 | 0.012 | 0.010 | 0.0012 | 0.0003 |
| Population | Number |  |  | βrot | σβ | j | σj |
| (km s−1 pc−1) | (km s−1 pc) | ||||||
| All | 35 | 6.9 | 0.6 | 0.013 | 0.004 | 0.00120 | 0.00014 |
| NGC 1333 | 24 | 7.4 | 0.7 | 0.015 | 0.006 | 0.0012 | 0.0002 |
| IC 348 | 10 | 5.6 | 0.8 | 0.007 | 0.001 | 0.0011 | 0.0002 |
| Starless | 10 | 5.0 | 0.6 | 0.006 | 0.001 | 0.0010 | 0.0002 |
| Protostars | 10 | 7.0 | 1.0 | 0.009 | 0.004 | 0.0012 | 0.0002 |
| Class 0 | 7 | 6.4 | 1.0 | 0.008 | 0.005 | 0.0012 | 0.0002 |
| Class I | 3 | 8 | 3 | 0.012 | 0.010 | 0.0012 | 0.0003 |
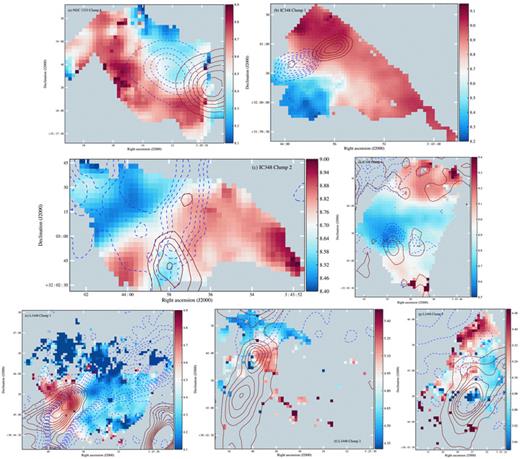
Distribution of significant ( ) velocity gradients for the clfind (top) and gaussclumps (bottom) clump populations. The L1448 distribution is not plotted for gaussclumps as it has only one significant gradient.
) velocity gradients for the clfind (top) and gaussclumps (bottom) clump populations. The L1448 distribution is not plotted for gaussclumps as it has only one significant gradient.
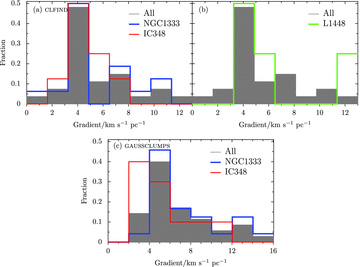
Fitted velocity gradient for gaussclumps versus clfind designations for the 16 clumps which have significant detections with both algorithms, by region (left) or by the classifications of HFR07 (right). The line marks where both gradients are equal.
There are too few sources of each classification to draw firm conclusions about any trends with age. It does seem in the distributions of Fig. 10 that the starless cores have  km s−1 pc−1 and larger gradients are protostellar. The protostellar average is larger than the starless one for the gaussclumps population:
km s−1 pc−1 and larger gradients are protostellar. The protostellar average is larger than the starless one for the gaussclumps population:  km s−1 pc−1 compared to
km s−1 pc−1 compared to  km s−1 pc−1. Although they are similar for clfind
km s−1 pc−1. Although they are similar for clfind km s−1 pc−1 compared to
km s−1 pc−1 compared to  km s−1 pc−1. This might point to an outflow contribution to the gradient.
km s−1 pc−1. This might point to an outflow contribution to the gradient.
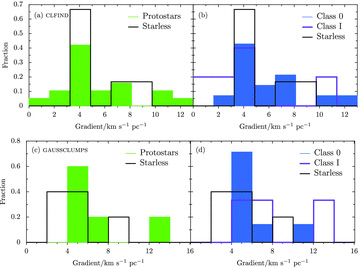
Distribution of significant ( ) velocity gradients for the classifications of HFR07 for the clfind (top) and gaussclumps (bottom) clump populations.
) velocity gradients for the classifications of HFR07 for the clfind (top) and gaussclumps (bottom) clump populations.
The gradients we find in Perseus are much greater than those originally found by GBF93 or Caselli et al. (2002) in their N2H+J = 1 → 0 survey of 60 low-mass cores: 0.3 to 3.9 km s−1 pc−1 and 0.5 to 6.0 km s−1 pc−1, respectively. Outflows cannot explain all of this difference because our starless clumps have significantly larger gradients as well. The discrepancy is reminiscent of that found by GBF93 towards B361, which was also investigated by Arquilla & Goldsmith (1985) with 13CO J = 1 → 0 data. GBF93 estimated a gradient five times smaller than the earlier study, 0.7 versus 3.3 km s−1 pc−1, which had led Arquilla & Goldsmith (1985) to conclude that rotation was dynamically significant in dark clouds. GBF93 explain the difference by emphasizing that tracers of lower critical densities can produce complicated velocity patterns dominated by outflows or clump-to-clump motions that mimic solid-body rotation. However, Olmi, Testi & Sargent (2005) fitted gradients to a number of cores in Perseus, finding similar magnitudes for the two common cores also in GBF93 and generally in the same range 0.14 to 2.32 km s−1 pc−1. Their study used C18O J = 1 → 0, CS J = 2 → 1 and N2H+J = 1 → 0 data with their C18O fitting not displaying markedly different gradients. A critical factor will undoubtedly be resolution. The angular resolution of previous surveys is worse than the 17.7 arcsec of our maps: ∼88, ∼54 and ∼46 arcsec for GBF93, Caselli et al. (2002) and Olmi et al. (2005), respectively. Hence even for their closest sources in Taurus (at 140 pc), their best linear resolution (0.037 pc) is nearly twice as large as ours (0.021 pc). A larger beam will tend to smooth out differences between regions and reduce the overall gradient magnitude. This effect may be large enough to explain the differences for cores perhaps three times as distant as Perseus,5 in a beam four times as large as ours.
3.3.4 Gradient orientation
Centrifugal stresses due to energetic rotation will flatten cores along the rotation axis. This tends to produce oblate cores (GBF93), currently the favoured shape (e.g. Jones, Basu & Dubinski 2001), which could also be caused by strong magnetic fields. If rotation dominates, we might expect the degree of core elongation to increase with increasing velocity gradient and a core’s major axis to lie parallel to the gradient, i.e. perpendicular to the rotation axis. Fig. 11 shows no relationship between the magnitude of the velocity gradient and the elongation of a clump, quantified through the axial ratio (taken from Curtis & Richer 2010). It comes as no surprise then that the angle between the clump major axis and the velocity gradient in Fig. 12 (only computed for the gaussclumps sources) seems to be distributed at random as well. Therefore, clump rotation is unlikely to be energetically significant.
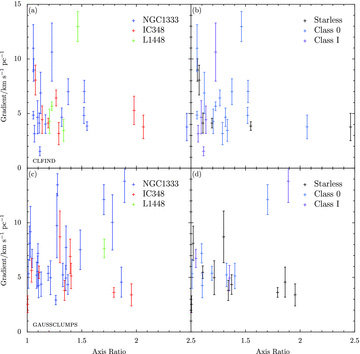
Velocity gradient versus axial ratio for clfind (top panels) and gaussclumps (bottom panels) sources broken down by region (left-hand panels) or by the classifications of HFR07 (right-hand panels).
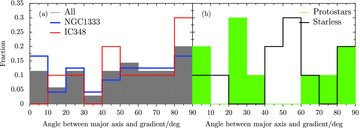
Distribution of the angle between the velocity gradient and the major axis of the gaussclumps clumps by region (left) or by the classifications of HFR07 (right). If rotational motions are elongating the clumps we would expect the gradient and axis to be in the same direction making the angle zero.
Is there a correlation between the orientation of the rotation axes of neighbouring clumps or an anticorrelation to keep the net angular momentum small? In Fig. 13, we overlay the velocity gradients on dust emission maps of the various regions. Reassuringly the directions and magnitudes of the gradients measured using both algorithms’ allocations match very well. In small patches the arrows of neighbouring clumps line up but on large scales there seems to be little correlation. This is similar to the gravoturbulent models of JK04, where shortly after collapse starts, the angular momenta in small regions are well aligned over a moderate correlation length with cores further away spinning in random directions. Their explanation is that neighbouring cores are formed from the same reservoir of material and therefore can be expected to have similar angular momenta. During subsequent accretion and evolution, the associated correlation length decreases and neighbours lose their alignment, as embedded cores are ejected and turbulence disrupts the current material or brings in new gas.
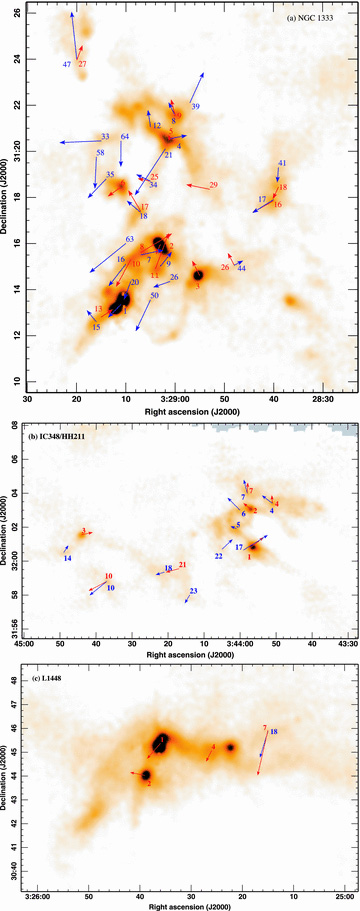
Spatial distribution of the velocity gradient detections in NGC 1333 (top), IC 348/HH 211 (middle) and L1448 (bottom). Arrows are drawn from the peak position of the associated clump for clumps where there are significant detections in either the clfind or gaussclumps catalogues. The direction and length of the arrow represent the direction and magnitude of the gradient and the detections are labelled with the reference from our SCUBA catalogues (Curtis & Richer 2010). The colour-scale is SCUBA 850-μm emission from 0 to 1600 mJy beam−1.
3.3.5 Dynamic support?
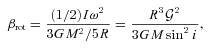
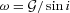 with i the angle of inclination to the line of sight. Assuming values representative of these clumps and sin i = 1, this becomes
with i the angle of inclination to the line of sight. Assuming values representative of these clumps and sin i = 1, this becomes 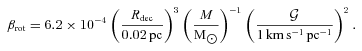
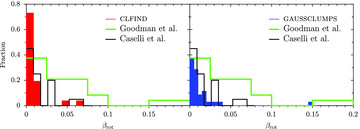
Distribution of the ratio of rotational to gravitational energies, βrot. For comparison the distributions found by GBF93 (green) and Caselli et al. (2002) (orange) are overlaid.
It would be interesting to examine how the level of support varies region-to-region and as a clump evolves. However, the numbers here are too small to draw any firm conclusions, with one or two objects heavily distorting overall averages. This is further compounded by the outflow ambiguities of the protostellar sources. Nevertheless, there are no vast differences in the populations by region or age with almost all the clumps having βrot≲ 0.02.
3.3.6 Angular momenta
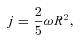
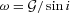 is again the angular velocity of the clump, R its radius and the factor 2/5 is for a constant density sphere. This yields for representative values
is again the angular velocity of the clump, R its radius and the factor 2/5 is for a constant density sphere. This yields for representative values 
In Fig. 15, we plot the distribution of j by region. There is little difference between the different algorithms or clumps from one region to the next. For clfind the overall average is 〈j〉 = (1.9 ± 0.2) × 10−3 km s−1 pc whilst 〈j〉 = (1.7 ± 0.2) × 10−3, (1.7 ± 0.3) × 10−3 and (3.2 ± 0.9) × 10−3 km s−1 pc in NGC 1333, IC 348 and L1448, respectively. The gaussclumps data are skewed to lower j due to their smaller clump radii but there are still few differences across the regions: 〈j〉 = (1.20 ± 0.14) × 10−3, (1.2 ± 0.2) × 10−3, (1.1 ± 0.2) × 10−3 km s−1 pc overall and in NGC 1333 and IC 348, respectively.
Distribution of j by region and algorithm: clfind on the left and gaussclumps on the right.
JK04 distinguish between starless and protostellar sources in their gravoturbulent simulations which focus particularly on rotational properties. They find wide continuous distributions for j, stretching over two orders of magnitude, as we do. Their pre-stellar cores have an order of magnitude larger j than the protostars. Fig. 16 compares our distributions of j (overall and for the starless clumps) to previously observed distributions and JK04. To match a particular set of observations, JK04 scale their code output according to the mean density, n, and temperature, T, with j depending on these as  . With appropriate scalings their data match three different observational regimes: low-mass cores mapped in the high-density tracer N2H+ (Caselli et al. 2002), low-mass cores in the slightly lower density tracer NH3 (GBF93 with Barranco & Goodman 1998; Jijina, Myers & Adams 1999) and high-mass cores in the high-density tracer N2H+ (Pirogov et al. 2003). Our observed distribution has no overlap with the high-mass cores of Pirogov et al. (2003) and little with GBF93, having much lower j. For the starless clumps only, we find 〈j〉 = (2.1 ± 0.5) × 10−3 and (1.0 ± 0.2) × 10−3 km s−1 pc for clfind and gaussclumps, respectively. The most similar distribution is that of Caselli et al. (2002), which is over twice as wide with a much larger average, 〈j〉 = 2.2 × 10−2 km s−1 pc, but does overlap with ours at low j. For our average to match that of Caselli et al. (2002), presumably our clumps would have to be considerably denser and/or colder than the values assumed by JK04 of n = 105 cm−3 and T = 10 K. In Section 3 we noted that the critical density is expected to be ncrit = 104 cm−3. However, in radiative transfer models of a free-falling protostellar envelope, we found peak H2 number densities of greater than a few times 105 cm−3 were required to reproduce the C18O J = 3 → 2 line strengths seen in our data (Curtis 2009). Alternatively or additionally, we are seeing considerably smaller angular momenta then those measured by previous authors. The narrow width of the distribution compared to previous work is likely to reflect the uniform environment of our cores in a single cloud rather then spread over many different ones as in Caselli et al. (2002) and GBF93.
. With appropriate scalings their data match three different observational regimes: low-mass cores mapped in the high-density tracer N2H+ (Caselli et al. 2002), low-mass cores in the slightly lower density tracer NH3 (GBF93 with Barranco & Goodman 1998; Jijina, Myers & Adams 1999) and high-mass cores in the high-density tracer N2H+ (Pirogov et al. 2003). Our observed distribution has no overlap with the high-mass cores of Pirogov et al. (2003) and little with GBF93, having much lower j. For the starless clumps only, we find 〈j〉 = (2.1 ± 0.5) × 10−3 and (1.0 ± 0.2) × 10−3 km s−1 pc for clfind and gaussclumps, respectively. The most similar distribution is that of Caselli et al. (2002), which is over twice as wide with a much larger average, 〈j〉 = 2.2 × 10−2 km s−1 pc, but does overlap with ours at low j. For our average to match that of Caselli et al. (2002), presumably our clumps would have to be considerably denser and/or colder than the values assumed by JK04 of n = 105 cm−3 and T = 10 K. In Section 3 we noted that the critical density is expected to be ncrit = 104 cm−3. However, in radiative transfer models of a free-falling protostellar envelope, we found peak H2 number densities of greater than a few times 105 cm−3 were required to reproduce the C18O J = 3 → 2 line strengths seen in our data (Curtis 2009). Alternatively or additionally, we are seeing considerably smaller angular momenta then those measured by previous authors. The narrow width of the distribution compared to previous work is likely to reflect the uniform environment of our cores in a single cloud rather then spread over many different ones as in Caselli et al. (2002) and GBF93.
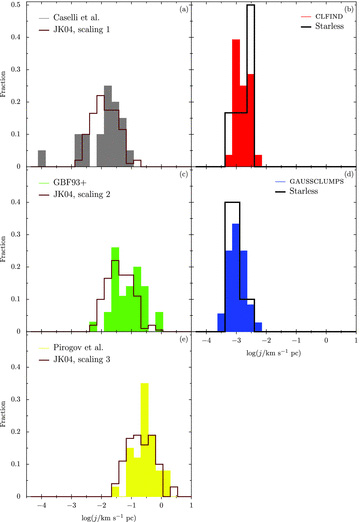
Distribution of specific angular momenta, j for starless cores. (a) N2H+J = 1 → 0 cores of Caselli et al. (2002, grey) compared to the JK04 model (brown) scaled by n = 105 cm−3 and T = 10 K. (b) All our clfind detections (red) and just those in starless clumps (black). (c) NH3 cores of GBF93, Barranco & Goodman (1998) and Jijina et al. (1999) (green) compared to the JK04 model (brown) scaled by n = 104 cm−3 and T = 10 K. (d) All our gaussclumps detections (blue) and just those in starless clumps (black). (e) N2H+J = 1 → 0 high-mass cores of Pirogov et al. (2003) compared to the JK04 model (brown) scaled by n = 104 cm−3 and T = 50 K.
On the other hand, the smaller angular momenta observed in our starless clumps may not indicate lower degrees of rotation in the clump core but may reflect a more slowly rotating outer envelope, making comparisons with tracers such as NH3 inappropriate. Redman et al. (2004) examined the asymmetric HCO+ line profiles across L1689B, a pre-stellar core in Ophiuchus, which they modelled as a rapidly rotating inner core contained within a static envelope. Again, the key diagnostics are the densities and temperatures traced by the C18O J = 3 → 2 line, which can only be properly answered with radiative transfer modelling. We would expect to probe high densities, ncrit∼ 104 cm−3, but earlier we saw the similar non-thermal linewidths for the J = 3 → 2 line compared to the J = 2 → 1, suggesting we might not be detecting very different material. A further consideration in the low-temperature environments of starless cores is CO depletion. Estimating the degree of depletion in these cores is difficult without similar observations in ‘late-depleting’ molecules, such as N2H+. However, models (e.g. Walmsley, Flower & Pineau des Forêts 2004) suggest that CO freezes-out in the central 7000 au of a pre-stellar core (this is really a temperature and density dependence). Furthermore, we noted in Section 3.1 that there is some existing evidence for considerable C18O depletion in candidate star-forming cores in Perseus (KJT07). Thus, our C18O signal in evolved starless clumps and young protostars at least should have little contribution from the dense inner core and this reasoning supports the idea we are probing a more slowly rotating envelope.
In JK04, protostars have a distribution of j that narrows with time, staying around the same average. Their distribution is also similar to that observed for binaries (see Fig. 17). Our distributions for all the sources are as narrow as those for the protostars alone in JK04’s models. For clfind there is a trend of decreasing j with protostellar age: 〈j〉 = (2.1 ± 0.3) × 10−3 and (1.1 ± 0.1) × 10−3 km s−1 pc for Class 0 and Class I clumps, which is not reproduced with gaussclumps: 〈j〉 = (1.2 ± 0.2) × 10−3 km s−1 pc (Class 0) and 〈j〉 = (1.2 ± 0.3) × 10−3 km s−1 pc (Class I). Of course in these sources there is potential confusion of the rotational signatures with outflows which is perhaps why the expected decrease in j from starless to protostellar clumps is not observed.
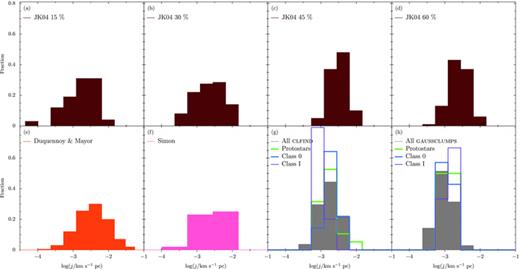
Distribution of the specific angular momenta, j, for protostars. (a)–(d) Show JK04’s model M6k2 with different star formation efficiencies: (a) 15, (b) 30, (c) 45 and (d) 60 per cent. (e) Binaries among nearby G stars of Duquennoy & Mayor (1991). (f) Binaries in Taurus (Simon 1992). (g) and (h) Show the distributions from paper for the clfind and gaussclumps designations, respectively, decomposed according to the designations of HFR07.
3.3.7 Scalings with clump size
GBF93 found that many of the derived rotation parameters scale with radius, including  (∝ R−0.4) and j(∝ R1.6) but not βrot. We plot the same parameters as a function of clump size in Fig. 18. Most of the relations found by GBF93 hold for these clumps, although there is considerable scatter. GBF93 show that the relation for the gradient is implied from a linewidth–size relation (e.g. Larson 1981), Δv = R0.6, for a core in virial equilibrium. we find βrot is independent of R as well, implying M ∝ R3 for solid body rotation (ω = constant) or for differential rotation (ω∝ R−1) that M ∝ R. The SCUBA clumps follow M ∝ R2 (Curtis & Richer 2010), so we can infer a more complicated form of rotation than pure solid body or differential to ensure βrot is independent of size.
(∝ R−0.4) and j(∝ R1.6) but not βrot. We plot the same parameters as a function of clump size in Fig. 18. Most of the relations found by GBF93 hold for these clumps, although there is considerable scatter. GBF93 show that the relation for the gradient is implied from a linewidth–size relation (e.g. Larson 1981), Δv = R0.6, for a core in virial equilibrium. we find βrot is independent of R as well, implying M ∝ R3 for solid body rotation (ω = constant) or for differential rotation (ω∝ R−1) that M ∝ R. The SCUBA clumps follow M ∝ R2 (Curtis & Richer 2010), so we can infer a more complicated form of rotation than pure solid body or differential to ensure βrot is independent of size.
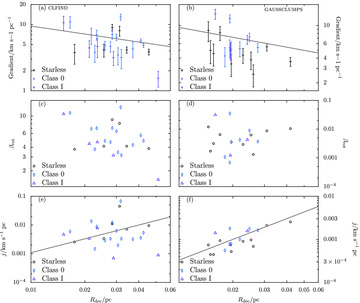
Rotational parameters as functions of clump size for clfind (left) and gaussclumps (right).  versus clump radius; βrot versus Rdec (middle panels); j versus Rdec (bottom panels). Lines mark the GBF93 relations:
versus clump radius; βrot versus Rdec (middle panels); j versus Rdec (bottom panels). Lines mark the GBF93 relations:  and j ∝ R1.6.
and j ∝ R1.6.
The scaling of j with size is of particular interest. Ohashi et al. (1997) looked at rotation in protostars in Taurus using C18O J = 1 → 0 interferometric spectra. They found at distances ≲3500 au, that j was at a constant value of ∼10−3 km s−1 pc. These findings are consistent with magnetically controlled collapse elucidated by Belloche et al. (2002), where in a dense inner core, the angular momentum is locked at a minimum value. This region could be interpreted as a magnetically supercritical core, decoupling from its subcritical environment, where j scales with R. In our data a horizontal line is almost as convincing as the slope of GBF93, indeed the spread of clump sizes is not really wide enough to constrain the trend unambiguously. Our results are therefore consistent with this magnetically controlled scenario: there is a lot of spread about j ∼ 10−3 km s−1 pc but no j much below this value. How the rotational velocity changes across a clump is less clear and is a key discriminator between different theories. Such measurements would require high-resolution interferometric observations of many cores in different stages of collapse.
4 SUMMARY
We have analysed the kinematic signatures of two populations of dust continuum clumps identified in SCUBA 850-μm data using either clfind or gaussclumps (Curtis & Richer 2010), across four regions (NGC 1333, IC 348/HH 211, L1448 and L1455) of active star formation in the Perseus molecular cloud. The kinematics were derived from our large-scale (600 arcmin2) C18O J = 3 → 2 survey (Paper I). First, the non-thermal contribution to the C18O linewidth was calculated and compared to the results of KJT07 and the gravoturbulent models of Klessen et al. (2005).
Most clumps have supersonic non-thermal linewidths, 〈σNT/cs〉 = 1.76 ± 0.09 (clfind population) or 1.71 ± 0.05 (gaussclumps), with overall distributions similar to the C18O J = 2 → 1 data of KJT07 towards dense core candidates in Perseus. This implies we are also probing the ‘envelopes’ of the star-forming clumps rather than deep within their interiors.
There is little difference in the level of the non-thermal linewidth contribution between protostars and starless clumps, implying that protostars do not affect their environment significantly. Clumps in NGC 1333 and IC 348 are in the vicinity of young stellar clusters, explaining the wider linewidths in NGC 1333 (〈σNT/cs〉 = 1.91 ± 0.07) than L1448 (1.52 ± 0.13) for the gaussclumps objects (although their linewidths are similar for clfind population: 2.05 ± 0.12 and 1.8 ± 0.2, respectively). IC 348, however, has the narrowest lines of all (1.36 ± 0.09 with clfind and 1.44 ± 0.07 with gaussclumps), possibly related to its statistically younger population (Hatchell et al. 2005), containing more starless clumps.
Second, the C18O linewidths allowed an estimate of each clump’s virial mass.
Most clumps in Perseus appear bound and close to equipartition. The ratio of the SCUBA to virial mass for clumps based on flux allocation using clfind is 〈M850/Mvir〉 = 1.32 ± 0.13, compared to 0.9 ± 0.1 for the gaussclumps decomposition.
Starless clumps occupy a similar section of M850–Mvir parameter space to the protostars suggesting that they are gravitationally bound and therefore truly pre-stellar. This has implications for our previous work investigating the starless CMF in Perseus (Curtis & Richer 2010).
These results are in contrast to the models of Klessen et al. (2005) where a majority of starless core have Mvir≫ M and occupy a different parameter space to the protostars.
Finally, we fitted a linear velocity gradient to the C18O line centres, across the face of each SCUBA clump, again identified either with clfind or gaussclumps. Significant detections were found in approximately a third of the clumps, which we interpreted in terms of solid-body rotation.
A correlation between CO J = 3 → 2 outflows and the C18O line centres is observed, implying any gradients in outflow sources, i.e. protostars, may reflect outflows rather than rotation.
The fitted gradients, in the range ∼1 to 16 km s−1 pc−1, are larger than those previously observed. This probably results from the higher angular resolution of our observations and/or outflow contamination.
There is no correlation between the gradient direction and the clump orientation nor between the gradient and clump axial ratio, implying that the rotation is not energetically significant. Furthermore, the ratio of the clump rotational to gravitational energy is typically ≲0.02, demonstrating that rotation is not dynamically important as well, with a distribution very similar to that of the N2H+ cores of Caselli et al. (2002).
The distribution of specific angular momentum is narrower and centred around lower values, j ∼ 10−3 km s−1 pc, than previous studies. Interpreting the results of JK04 this suggests a denser and/or colder environment for the Perseus clumps than seen in the Caselli et al. (2002) sample (taken to have n ∼ 105 cm−3 and T ∼ 10 K). This would seem unlikely given the large linewidths we observed towards the clumps, although radiative transfer modelling does suggest we are probing moderately high densities – peak H2 number densities of a few ×105 cm−3 for a free-falling protostellar envelope (Curtis 2009). Thus, we are probably seeing lower levels of rotation in our clumps.
There are no strong trends in the rotational parameters with radius.
The somewhat inconclusive findings of this paper motivate further work on the star-forming cores in Perseus. First, the construction of accurate radiative transfer models to determine precisely the conditions traced by the CO J = 3 → 2 transitions. Second, higher resolution or higher tracer density observations. j found in our clumps, suggestively hovers around the background value, 10−3 km s−1 pc−1, found by Ohashi et al. (1997) at radii ≲0.03 pc in Taurus’s protostellar cores. To see how exactly j varies with radius we need to probe across the clumps themselves, using higher density tracers or higher resolution observations.
Part of the starlink software collection, see http://starlink.jach.hawaii.edu
Errors quoted on averages throughout this paper are errors on the mean ( ) and not simple standard deviations (σ).
) and not simple standard deviations (σ).
Furthermore, Dib et al. (2010) point out that measurements of core angular momenta from global velocity gradient fitting tend to overestimate the intrinsic (three-dimensional) angular momenta by a factor of ∼8–10, as complicated fluctuations in the three-dimensional velocity field are smoothed out.
www.scipy.org
The most distant sources examined by Caselli et al. (2002) are L1031B at 900 pc and L1389 at 600 pc.
EIC thanks the Science and Technology Facilities Council (STFC) for studentship support while carrying out this work. We thank Jane Buckle and Gary Fuller for reading carefully an earlier version of this paper. We are grateful to the referee for comments and suggestions which improved the clarity of this paper. The JCMT is operated by The Joint Astronomy Centre (JAC) on behalf of the STFC of the United Kingdom, the Netherlands Organisation for Scientific Research and the National Research Council (NRC) of Canada. We have also made extensive use of the SIMBAD data base, operated at CDS, Strasbourg, France. We acknowledge the data analysis facilities provided by the starlink Project which is maintained by JAC with support from STFC. This research used the facilities of the Canadian Astronomy Data Centre operated by the NRC with the support of the Canadian Space Agency.
REFERENCES
Appendix
APPENDIX A: DERIVED CORE DYNAMICAL AND ROTATIONAL PROPERTIES
We list linewidths, virial masses and rotational parameters alongside other properties for every clump examined in Tables A1, A2, A3 and A4. In Figs A1 and A2, we plot the C18O J = 3 → 2 line centre velocity and best-fitting velocity gradient for every SCUBA clump with a significant detection.
Dynamical properties of SCUBA clumps found with clfind. The full version of this table is available as Supporting Information to the online version of this article.
| Subregiona | Clumpb ID | Hatchellc ID |  (K) (K) | vc(C18O) e (km s−1) |  (km s−1) (km s−1) | σNTg (km s−1) | Mvirh (M⊙) |
| NGC 1333 | 1 | 42 | 13.5 | 7.36 | 1.91 | 0.81 | 11.3 |
| NGC 1333 | 2 | 43 | 16.3 | 8.24 | 1.53 | 0.64 | 11.9 |
| NGC 1333 | 3 | 44 | 16.5 | 7.62 | 1.19 | 0.50 | 12.3 |
| NGC 1333 | 4 | 41 | 15.0 | 7.48 | 1.81 | 0.77 | 13.7 |
| NGC 1333 | 5 | 45 | 16.4 | 7.79 | 1.40 | 0.59 | 22.9 |
| … |
| Subregiona | Clumpb ID | Hatchellc ID |  (K) (K) | vc(C18O) e (km s−1) |  (km s−1) (km s−1) | σNTg (km s−1) | Mvirh (M⊙) |
| NGC 1333 | 1 | 42 | 13.5 | 7.36 | 1.91 | 0.81 | 11.3 |
| NGC 1333 | 2 | 43 | 16.3 | 8.24 | 1.53 | 0.64 | 11.9 |
| NGC 1333 | 3 | 44 | 16.5 | 7.62 | 1.19 | 0.50 | 12.3 |
| NGC 1333 | 4 | 41 | 15.0 | 7.48 | 1.81 | 0.77 | 13.7 |
| NGC 1333 | 5 | 45 | 16.4 | 7.79 | 1.40 | 0.59 | 22.9 |
| … |
a Name of subregion map.
b Clump number from Curtis & Richer (2010).
c H07 identifier.
dRosolowsky et al. (2008) NH3 kinetic temperature where they exist or 10.0, 15.0 and 12.0 K for starless clumps, protostars and clumps with no H07 identification where not, respectively.
e, f Measured C18O J = 3 → 2 line centre velocity, vc and FWHM,  from a Gaussian fit to the line profile at the clump peak.
from a Gaussian fit to the line profile at the clump peak.
g Non-thermal contribution to the linewidth estimated using the temperatures of column (d).
h Virial masses calculated using the temperatures of column (d).
Dynamical properties of SCUBA clumps found with clfind. The full version of this table is available as Supporting Information to the online version of this article.
| Subregiona | Clumpb ID | Hatchellc ID |  (K) (K) | vc(C18O) e (km s−1) |  (km s−1) (km s−1) | σNTg (km s−1) | Mvirh (M⊙) |
| NGC 1333 | 1 | 42 | 13.5 | 7.36 | 1.91 | 0.81 | 11.3 |
| NGC 1333 | 2 | 43 | 16.3 | 8.24 | 1.53 | 0.64 | 11.9 |
| NGC 1333 | 3 | 44 | 16.5 | 7.62 | 1.19 | 0.50 | 12.3 |
| NGC 1333 | 4 | 41 | 15.0 | 7.48 | 1.81 | 0.77 | 13.7 |
| NGC 1333 | 5 | 45 | 16.4 | 7.79 | 1.40 | 0.59 | 22.9 |
| … |
| Subregiona | Clumpb ID | Hatchellc ID |  (K) (K) | vc(C18O) e (km s−1) |  (km s−1) (km s−1) | σNTg (km s−1) | Mvirh (M⊙) |
| NGC 1333 | 1 | 42 | 13.5 | 7.36 | 1.91 | 0.81 | 11.3 |
| NGC 1333 | 2 | 43 | 16.3 | 8.24 | 1.53 | 0.64 | 11.9 |
| NGC 1333 | 3 | 44 | 16.5 | 7.62 | 1.19 | 0.50 | 12.3 |
| NGC 1333 | 4 | 41 | 15.0 | 7.48 | 1.81 | 0.77 | 13.7 |
| NGC 1333 | 5 | 45 | 16.4 | 7.79 | 1.40 | 0.59 | 22.9 |
| … |
a Name of subregion map.
b Clump number from Curtis & Richer (2010).
c H07 identifier.
dRosolowsky et al. (2008) NH3 kinetic temperature where they exist or 10.0, 15.0 and 12.0 K for starless clumps, protostars and clumps with no H07 identification where not, respectively.
e, f Measured C18O J = 3 → 2 line centre velocity, vc and FWHM,  from a Gaussian fit to the line profile at the clump peak.
from a Gaussian fit to the line profile at the clump peak.
g Non-thermal contribution to the linewidth estimated using the temperatures of column (d).
h Virial masses calculated using the temperatures of column (d).
Dynamical properties of SCUBA clumps found with gaussclumps. The full version of this table is available as Supporting Information to the online version of this article.
| Subregiona | Clumpb ID | Hatchellc ID |  (K) (K) | vc(C18O) e (km s−1) |  (km s−1) (km s−1) | σNTg (km s−1) | Mvirh (M⊙) |
| NGC 1333 | 1 | 41, 42 | 15.0 | 6.77 | 1.04 | 0.44 | 11.9 |
| NGC 1333 | 2 | 43 | 16.3 | 8.18 | 1.51 | 0.64 | 5.8 |
| NGC 1333 | 3 | – | 16.5 | 7.62 | 1.19 | 0.50 | |
| NGC 1333 | 4 | 45 | 16.4 | 7.82 | 1.35 | 0.57 | 8.7 |
| NGC 1333 | 5 | 46 | 14.3 | 8.40 | 1.27 | 0.54 | 4.0 |
| … |
| Subregiona | Clumpb ID | Hatchellc ID |  (K) (K) | vc(C18O) e (km s−1) |  (km s−1) (km s−1) | σNTg (km s−1) | Mvirh (M⊙) |
| NGC 1333 | 1 | 41, 42 | 15.0 | 6.77 | 1.04 | 0.44 | 11.9 |
| NGC 1333 | 2 | 43 | 16.3 | 8.18 | 1.51 | 0.64 | 5.8 |
| NGC 1333 | 3 | – | 16.5 | 7.62 | 1.19 | 0.50 | |
| NGC 1333 | 4 | 45 | 16.4 | 7.82 | 1.35 | 0.57 | 8.7 |
| NGC 1333 | 5 | 46 | 14.3 | 8.40 | 1.27 | 0.54 | 4.0 |
| … |
a Name of subregion map.
b Clump number from Curtis & Richer (2010).
c H07 identifier.
dRosolowsky et al. (2008) NH3 kinetic temperature where they exist or 10.0, 15.0 and 12.0 K for starless clumps, protostars and clumps with no H07 identification where not, respectively.
e, f Measured C18O J = 3 → 2 line centre velocity, vc and FWHM,  from a Gaussian fit to the line profile at the clump peak.
from a Gaussian fit to the line profile at the clump peak.
g Non-thermal contribution to the linewidth estimated using the temperatures of column (d).
h Virial masses calculated using the temperatures of column (d).
Dynamical properties of SCUBA clumps found with gaussclumps. The full version of this table is available as Supporting Information to the online version of this article.
| Subregiona | Clumpb ID | Hatchellc ID |  (K) (K) | vc(C18O) e (km s−1) |  (km s−1) (km s−1) | σNTg (km s−1) | Mvirh (M⊙) |
| NGC 1333 | 1 | 41, 42 | 15.0 | 6.77 | 1.04 | 0.44 | 11.9 |
| NGC 1333 | 2 | 43 | 16.3 | 8.18 | 1.51 | 0.64 | 5.8 |
| NGC 1333 | 3 | – | 16.5 | 7.62 | 1.19 | 0.50 | |
| NGC 1333 | 4 | 45 | 16.4 | 7.82 | 1.35 | 0.57 | 8.7 |
| NGC 1333 | 5 | 46 | 14.3 | 8.40 | 1.27 | 0.54 | 4.0 |
| … |
| Subregiona | Clumpb ID | Hatchellc ID |  (K) (K) | vc(C18O) e (km s−1) |  (km s−1) (km s−1) | σNTg (km s−1) | Mvirh (M⊙) |
| NGC 1333 | 1 | 41, 42 | 15.0 | 6.77 | 1.04 | 0.44 | 11.9 |
| NGC 1333 | 2 | 43 | 16.3 | 8.18 | 1.51 | 0.64 | 5.8 |
| NGC 1333 | 3 | – | 16.5 | 7.62 | 1.19 | 0.50 | |
| NGC 1333 | 4 | 45 | 16.4 | 7.82 | 1.35 | 0.57 | 8.7 |
| NGC 1333 | 5 | 46 | 14.3 | 8.40 | 1.27 | 0.54 | 4.0 |
| … |
a Name of subregion map.
b Clump number from Curtis & Richer (2010).
c H07 identifier.
dRosolowsky et al. (2008) NH3 kinetic temperature where they exist or 10.0, 15.0 and 12.0 K for starless clumps, protostars and clumps with no H07 identification where not, respectively.
e, f Measured C18O J = 3 → 2 line centre velocity, vc and FWHM,  from a Gaussian fit to the line profile at the clump peak.
from a Gaussian fit to the line profile at the clump peak.
g Non-thermal contribution to the linewidth estimated using the temperatures of column (d).
h Virial masses calculated using the temperatures of column (d).
Rotational properties of SCUBA clumps located with clfind. These properties have been found by non-linear least-squares fitting of a linear velocity gradient to the first moment of the C18O J = 3 → 2 data. Only significant detections are shown with  . The full version of this table is available as Supporting Information to the online version of this article.
. The full version of this table is available as Supporting Information to the online version of this article.
| Subregiona | Clumpb | Hatchellc | Numberd |  |  |  | βroth | ji |
| ID | class | of points | (km s−1 pc−1) | (deg E of N) | (km s−1 pc) | |||
| NGC 1333 | 2 | I | 1117 | 3.16 ± 0.76 | 155.44 | 4 | 6.98E-04 | 1.05E-03 |
| NGC 1333 | 3 | 0 | 2106 | 4.85 ± 0.35 | 26.88 | 14 | 5.39E-03 | 3.51E-03 |
| NGC 1333 | 5 | I | 2229 | 1.54 ± 0.41 | 21.10 | 4 | 8.91E-04 | 1.63E-03 |
| NGC 1333 | 6 | 0 | 978 | 4.66 ± 0.84 | 125.79 | 6 | 3.35E-03 | 1.44E-03 |
| NGC 1333 | 8 | I | 330 | 10.63 ± 2.67 | −58.59 | 4 | 4.67E-03 | 9.83E-04 |
| … |
| Subregiona | Clumpb | Hatchellc | Numberd |  |  |  | βroth | ji |
| ID | class | of points | (km s−1 pc−1) | (deg E of N) | (km s−1 pc) | |||
| NGC 1333 | 2 | I | 1117 | 3.16 ± 0.76 | 155.44 | 4 | 6.98E-04 | 1.05E-03 |
| NGC 1333 | 3 | 0 | 2106 | 4.85 ± 0.35 | 26.88 | 14 | 5.39E-03 | 3.51E-03 |
| NGC 1333 | 5 | I | 2229 | 1.54 ± 0.41 | 21.10 | 4 | 8.91E-04 | 1.63E-03 |
| NGC 1333 | 6 | 0 | 978 | 4.66 ± 0.84 | 125.79 | 6 | 3.35E-03 | 1.44E-03 |
| NGC 1333 | 8 | I | 330 | 10.63 ± 2.67 | −58.59 | 4 | 4.67E-03 | 9.83E-04 |
| … |
a Name of subregion map.
b Clump identification from Curtis & Richer (2010).
c H07 clump class, S = starless, 0 = Class 0 protostar and I = Class I protostar.
d Number of points fitted in the map.
e Fitted velocity gradient and its error.
f Angle of the fitted velocity gradient, east of north.
g Level of significance of the fit,  .
.
h Ratio of the kinetic to gravitational energy.
i Specific angular momentum.
Rotational properties of SCUBA clumps located with clfind. These properties have been found by non-linear least-squares fitting of a linear velocity gradient to the first moment of the C18O J = 3 → 2 data. Only significant detections are shown with  . The full version of this table is available as Supporting Information to the online version of this article.
. The full version of this table is available as Supporting Information to the online version of this article.
| Subregiona | Clumpb | Hatchellc | Numberd |  |  |  | βroth | ji |
| ID | class | of points | (km s−1 pc−1) | (deg E of N) | (km s−1 pc) | |||
| NGC 1333 | 2 | I | 1117 | 3.16 ± 0.76 | 155.44 | 4 | 6.98E-04 | 1.05E-03 |
| NGC 1333 | 3 | 0 | 2106 | 4.85 ± 0.35 | 26.88 | 14 | 5.39E-03 | 3.51E-03 |
| NGC 1333 | 5 | I | 2229 | 1.54 ± 0.41 | 21.10 | 4 | 8.91E-04 | 1.63E-03 |
| NGC 1333 | 6 | 0 | 978 | 4.66 ± 0.84 | 125.79 | 6 | 3.35E-03 | 1.44E-03 |
| NGC 1333 | 8 | I | 330 | 10.63 ± 2.67 | −58.59 | 4 | 4.67E-03 | 9.83E-04 |
| … |
| Subregiona | Clumpb | Hatchellc | Numberd |  |  |  | βroth | ji |
| ID | class | of points | (km s−1 pc−1) | (deg E of N) | (km s−1 pc) | |||
| NGC 1333 | 2 | I | 1117 | 3.16 ± 0.76 | 155.44 | 4 | 6.98E-04 | 1.05E-03 |
| NGC 1333 | 3 | 0 | 2106 | 4.85 ± 0.35 | 26.88 | 14 | 5.39E-03 | 3.51E-03 |
| NGC 1333 | 5 | I | 2229 | 1.54 ± 0.41 | 21.10 | 4 | 8.91E-04 | 1.63E-03 |
| NGC 1333 | 6 | 0 | 978 | 4.66 ± 0.84 | 125.79 | 6 | 3.35E-03 | 1.44E-03 |
| NGC 1333 | 8 | I | 330 | 10.63 ± 2.67 | −58.59 | 4 | 4.67E-03 | 9.83E-04 |
| … |
a Name of subregion map.
b Clump identification from Curtis & Richer (2010).
c H07 clump class, S = starless, 0 = Class 0 protostar and I = Class I protostar.
d Number of points fitted in the map.
e Fitted velocity gradient and its error.
f Angle of the fitted velocity gradient, east of north.
g Level of significance of the fit,  .
.
h Ratio of the kinetic to gravitational energy.
i Specific angular momentum.
Rotational properties of SCUBA clumps located with gaussclumps. These properties have been found by non-linear least-squares fitting of a linear velocity gradient to the first moment of the C18O J = 3 → 2 data. Only significant detections are shown with  . The full version of this table is available as Supporting Information to the online version of this article.
. The full version of this table is available as Supporting Information to the online version of this article.
| Subregiona | Clumpb | Hatchellc | Numberd |  |  |  | βroth | ji |
| ID | class | of points | (km s−1 pc−1) | (deg E of N) | (km s−1 pc) | |||
| NGC 1333 | 1 | 0 | 800 | 5.33 ± 1.33 | 135.67 | 4 | 6.90E-04 | 7.86E-04 |
| NGC 1333 | 4 | I | 922 | 4.93 ± 1.16 | −79.61 | 4 | 1.22E-03 | 7.41E-04 |
| NGC 1333 | 7 | I | 1222 | 6.73 ± 0.84 | −77.95 | 8 | 4.27E-03 | 1.56E-03 |
| NGC 1333 | 8 | 0 | 812 | 4.25 ± 1.11 | 26.44 | 4 | 1.07E-03 | 5.54E-04 |
| NGC 1333 | 9 | 0 | 1374 | 5.37 ± 0.65 | −38.35 | 8 | 3.70E-03 | 1.63E-03 |
| … |
| Subregiona | Clumpb | Hatchellc | Numberd |  |  |  | βroth | ji |
| ID | class | of points | (km s−1 pc−1) | (deg E of N) | (km s−1 pc) | |||
| NGC 1333 | 1 | 0 | 800 | 5.33 ± 1.33 | 135.67 | 4 | 6.90E-04 | 7.86E-04 |
| NGC 1333 | 4 | I | 922 | 4.93 ± 1.16 | −79.61 | 4 | 1.22E-03 | 7.41E-04 |
| NGC 1333 | 7 | I | 1222 | 6.73 ± 0.84 | −77.95 | 8 | 4.27E-03 | 1.56E-03 |
| NGC 1333 | 8 | 0 | 812 | 4.25 ± 1.11 | 26.44 | 4 | 1.07E-03 | 5.54E-04 |
| NGC 1333 | 9 | 0 | 1374 | 5.37 ± 0.65 | −38.35 | 8 | 3.70E-03 | 1.63E-03 |
| … |
a Name of subregion map.
b Clump identification from Curtis & Richer (2010).
c H07 clump class, S = starless, 0 = Class 0 protostar and I = Class I protostar.
d Number of points fitted in the map.
e Fitted velocity gradient and its error.
f Angle of the fitted velocity gradient, east of north.
g Level of significance of the fit,  .
.
h Ratio of the kinetic to gravitational energy.
i Specific angular momentum.
Rotational properties of SCUBA clumps located with gaussclumps. These properties have been found by non-linear least-squares fitting of a linear velocity gradient to the first moment of the C18O J = 3 → 2 data. Only significant detections are shown with  . The full version of this table is available as Supporting Information to the online version of this article.
. The full version of this table is available as Supporting Information to the online version of this article.
| Subregiona | Clumpb | Hatchellc | Numberd |  |  |  | βroth | ji |
| ID | class | of points | (km s−1 pc−1) | (deg E of N) | (km s−1 pc) | |||
| NGC 1333 | 1 | 0 | 800 | 5.33 ± 1.33 | 135.67 | 4 | 6.90E-04 | 7.86E-04 |
| NGC 1333 | 4 | I | 922 | 4.93 ± 1.16 | −79.61 | 4 | 1.22E-03 | 7.41E-04 |
| NGC 1333 | 7 | I | 1222 | 6.73 ± 0.84 | −77.95 | 8 | 4.27E-03 | 1.56E-03 |
| NGC 1333 | 8 | 0 | 812 | 4.25 ± 1.11 | 26.44 | 4 | 1.07E-03 | 5.54E-04 |
| NGC 1333 | 9 | 0 | 1374 | 5.37 ± 0.65 | −38.35 | 8 | 3.70E-03 | 1.63E-03 |
| … |
| Subregiona | Clumpb | Hatchellc | Numberd |  |  |  | βroth | ji |
| ID | class | of points | (km s−1 pc−1) | (deg E of N) | (km s−1 pc) | |||
| NGC 1333 | 1 | 0 | 800 | 5.33 ± 1.33 | 135.67 | 4 | 6.90E-04 | 7.86E-04 |
| NGC 1333 | 4 | I | 922 | 4.93 ± 1.16 | −79.61 | 4 | 1.22E-03 | 7.41E-04 |
| NGC 1333 | 7 | I | 1222 | 6.73 ± 0.84 | −77.95 | 8 | 4.27E-03 | 1.56E-03 |
| NGC 1333 | 8 | 0 | 812 | 4.25 ± 1.11 | 26.44 | 4 | 1.07E-03 | 5.54E-04 |
| NGC 1333 | 9 | 0 | 1374 | 5.37 ± 0.65 | −38.35 | 8 | 3.70E-03 | 1.63E-03 |
| … |
a Name of subregion map.
b Clump identification from Curtis & Richer (2010).
c H07 clump class, S = starless, 0 = Class 0 protostar and I = Class I protostar.
d Number of points fitted in the map.
e Fitted velocity gradient and its error.
f Angle of the fitted velocity gradient, east of north.
g Level of significance of the fit,  .
.
h Ratio of the kinetic to gravitational energy.
i Specific angular momentum.

SCUBA 850-μm clumps identified with clfind containing significant velocity gradients,  in NGC 1333, IC 348 and L1448. The colour-scale denotes the C18O J = 3 → 2 line centre velocity, linearly scaled from the clump minimum (blue/black) to maximum (red/white). Contours of 850-μm flux density are overlaid (black) at 100, 200, 400, 800, 1600 and 3200 mJy beam−1. A white/black circle marks the position of the clump peak emission with a white line positioned to show the direction of the fitted velocity gradient. The full version of this figure is available as Supporting Information to the online version of this article.
in NGC 1333, IC 348 and L1448. The colour-scale denotes the C18O J = 3 → 2 line centre velocity, linearly scaled from the clump minimum (blue/black) to maximum (red/white). Contours of 850-μm flux density are overlaid (black) at 100, 200, 400, 800, 1600 and 3200 mJy beam−1. A white/black circle marks the position of the clump peak emission with a white line positioned to show the direction of the fitted velocity gradient. The full version of this figure is available as Supporting Information to the online version of this article.
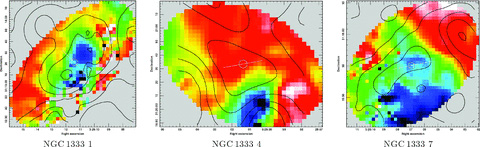
SCUBA 850 μm clumps identified with gaussclumps containing significant velocity gradients,  in NGC1333, IC 348 and L1448. The colour-scale denotes the C18O J = 3 → 2 line centre velocity, linearly scaled from the clump minimum (blue/black) to maximum (red/white). Contours of 850-μm flux density are overlaid (black) at 100, 200, 400, 800, 1600 and 3200 mJy beam−1. A white/black circle marks the position of the clump peak emission with a white line positioned to show the direction of the fitted velocity gradient. The full version of this figure is available as Supporting Information to the online version of this article.
in NGC1333, IC 348 and L1448. The colour-scale denotes the C18O J = 3 → 2 line centre velocity, linearly scaled from the clump minimum (blue/black) to maximum (red/white). Contours of 850-μm flux density are overlaid (black) at 100, 200, 400, 800, 1600 and 3200 mJy beam−1. A white/black circle marks the position of the clump peak emission with a white line positioned to show the direction of the fitted velocity gradient. The full version of this figure is available as Supporting Information to the online version of this article.
SUPPORTING INFORMATION
Additional Supporting Information may be found in the online version of this article:
Table A1. Dynamical properties of SCUBA clumps found with clfind.
Table A2. Dynamical properties of SCUBA clumps found with gaussclumps.
Table A3. Rotational properties of SCUBA clumps located with clfind.
Table A4. Rotational properties of SCUBA clumps located with gaussclumps.
Figure A1. SCUBA 850-μm clumps identified with clfind containing significant velocity gradients, σG/G≥ 3 in NGC 1333, IC 348 and L1448.
Figure A2. SCUBA 850-μm clumps identified with gaussclumps containing significant velocity gradients, σG/G≥ 3 in NGC 1333, IC 348 and L1448.
Please note: Wiley-Blackwell are not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.



