-
PDF
- Split View
-
Views
-
Cite
Cite
Ramin A. Skibba, Frank C. van den Bosch, Xiaohu Yang, Surhud More, Houjun Mo, Fabio Fontanot, Are brightest halo galaxies central galaxies?, Monthly Notices of the Royal Astronomical Society, Volume 410, Issue 1, January 2011, Pages 417–431, https://doi.org/10.1111/j.1365-2966.2010.17452.x
Close - Share Icon Share
Abstract
It is generally assumed that the central galaxy in a dark matter halo, that is the galaxy with the lowest specific potential energy, is also the brightest halo galaxy (BHG), and that it resides at rest at the centre of the dark matter potential well. This central galaxy paradigm (CGP) is an essential assumption made in various fields of astronomical research. In this paper, we test the validity of the CGP using a large galaxy group catalogue constructed from the Sloan Digital Sky Survey. For each group, we compute two statistics,  and
and  , which quantify the offsets of the line-of-sight velocities and projected positions of brightest group galaxies relative to the other group members. By comparing the cumulative distributions of
, which quantify the offsets of the line-of-sight velocities and projected positions of brightest group galaxies relative to the other group members. By comparing the cumulative distributions of  and
and  to those obtained from detailed mock group catalogues, we rule out the null hypothesis that the CGP is correct. Rather, the data indicate that in a non-zero fraction fBNC(M) of all haloes of mass M the BHG is not the central galaxy, but instead a satellite galaxy. In particular, we find that fBNC increases from ∼0.25 in low-mass haloes (1012h−1≤M≲ 2 × 1013h−1 M⊙) to ∼0.4 in massive haloes (M≳ 5 × 1013h−1 M⊙). We show that these values of fBNC are uncomfortably high compared to predictions from halo occupation statistics and from semi-analytical models of galaxy formation. We end by discussing various implications of a non-zero fBNC(M), with an emphasis on the halo masses inferred from satellite kinematics.
to those obtained from detailed mock group catalogues, we rule out the null hypothesis that the CGP is correct. Rather, the data indicate that in a non-zero fraction fBNC(M) of all haloes of mass M the BHG is not the central galaxy, but instead a satellite galaxy. In particular, we find that fBNC increases from ∼0.25 in low-mass haloes (1012h−1≤M≲ 2 × 1013h−1 M⊙) to ∼0.4 in massive haloes (M≳ 5 × 1013h−1 M⊙). We show that these values of fBNC are uncomfortably high compared to predictions from halo occupation statistics and from semi-analytical models of galaxy formation. We end by discussing various implications of a non-zero fBNC(M), with an emphasis on the halo masses inferred from satellite kinematics.
1 INTRODUCTION
According to the current paradigm of galaxy formation, all galaxies form as a result of gas cooling at the centre of the potential well of dark matter haloes. Structures form hierarchically, such that smaller haloes merge to form larger and more massive haloes. When a halo and its ‘central’ galaxy are accreted by a larger halo, it becomes a subhalo and its galaxy becomes a ‘satellite’ galaxy. In this paradigm, it is assumed that ram-pressure and tidal forces strip satellite galaxies of their gas reservoir, causing their star formation to be quenched shortly after having been accreted. The central galaxy (i.e. the galaxy with the lowest specific potential energy), however, continues to accrete new gas, and is also expected to cannibalize some of its satellites. Consequently, it is generally assumed that the central galaxy is the most luminous, most massive galaxy in a dark matter host halo, and that it resides at rest at the centre of the halo’s potential well. Following van den Bosch et al. (2005, hereafter vdB05), we will refer to this as the ‘central galaxy paradigm’ (CGP).
There are numerous areas of astronomy in which the validity of the CGP is an essential assumption, although this is rarely enunciated. Examples are various techniques to measure halo masses, such as satellite kinematics (e.g. McKay et al. 2002; van den Bosch et al. 2004; More et al. 2009), weak lensing (e.g. Mandelbaum et al. 2006; Johnston et al. 2007; Cacciato et al. 2009, hereafter C09; Sheldon et al. 2009b) and strong lensing (e.g. Kochanek 1995; Cohn et al. 2001; Koopmans & Treu 2003; Rusin et al. 2003). In addition, the CGP also features in halo occupation modelling, where assumptions have to be made regarding the distribution of galaxies within dark matter haloes in order to compute the galaxy–galaxy correlation function on small scales (e.g. Scoccimarro et al. 2001; Sheth et al. 2001; Yang, Mo & van den Bosch 2003; Zehavi et al. 2005; Zheng et al. 2005; Cooray 2005; van den Bosch et al. 2007; Tinker et al. 2008), and in algorithms developed to identify galaxy groups and clusters in photometric or spectroscopic redshift surveys (e.g. Yang et al. 2005a, 2007, hereafter Y07; Berlind et al. 2006; Koester et al. 2007).
Whether central galaxies actually comprise a special population has been debated for many years. However, recent analyses of galaxies in groups and clusters (e.g. Weinmann et al. 2006; Skibba, Sheth & Martino 2007; von der Linden et al. 2007; van den Bosch et al. 2008; Pasquali et al. 2009, 2010; Skibba 2009; Hansen et al. 2009) and halo model analyses of galaxy clustering (e.g. Skibba et al. 2006; Cooray 2006; van den Bosch et al. 2007; Skibba & Sheth 2009) have explicitly shown that central galaxies are indeed a distinct population and exhibit different properties (e.g. colour, star formation activity, AGN activity, morphology, stellar population properties) than satellite galaxies of the same stellar mass, and with different dependencies on the mass of their host halo. In addition, these studies have shown that central galaxy properties are strongly correlated with halo mass, while those of satellite galaxies only reveal a very weak dependence on the mass of the halo in which they orbit. However, it is important to realize that in virtually all of these studies, central galaxies are assumed to be the brightest (or most massive) halo galaxies. If this aspect of the CGP is not correct for a non-negligible fraction of all haloes, the differences between centrals and satellites found by these studies will have to be considered lower limits.
The validity of the CGP has been investigated by a number of authors. In particular, several recent, observational studies have shown that although most brightest halo galaxies (BHGs) are nearly at rest near the centroid of their group or cluster, or at the peak of the cluster X-ray emission, some of them are not (e.g. Beers & Geller 1983; Malumuth et al. 1992; Bird 1994; Postman & Lauer 1995; Zabludoff & Mulchaey 1998; Oegerle & Hill 2001; Yoshikawa, Jing & Börner 2003; Lin & Mohr 2004; von der Linden et al. 2007; Bildfell et al. 2008; Hwang & Lee 2008; Sanderson, Edge & Smith 2009; Coziol et al. 2009). These studies have focused on either cD galaxies in clusters or brightest cluster galaxies (BCGs) in general. It has been argued that most cD galaxies form a subpopulation of BCGs (e.g. Bernstein & Bhavsar 2001; Coziol et al. 2009) and may have grown by ‘cannibalizing’ smaller neighbouring galaxies.
In an early study, Beers & Geller (1983) analysed the spatial distribution of bright galaxies in 56 rich clusters and argue that cD galaxies tend to lie at local density peaks but not necessarily at the bottom of the potential well of the whole cluster. Oegerle & Hill (2001) found that, out of their sample of 25 Abell clusters, the cD galaxies of four of them have significant peculiar velocities relative to the cluster velocity. More recent studies have analysed the positions and velocities of BCGs. For example, in a study of 833 Sloan Digital Sky Survey (SDSS) clusters, von der Linden et al. (2007) found that 21 BCGs in their sample lie farther than 1 Mpc away from the mean galaxy in the cluster. Hwang & Lee (2008) found that the BCGs of two clusters out of a sample of 24 have significantly offset velocities and positions; these two clusters also appear to be in dynamical equilibrium. Recently, Coziol et al. (2009), using a sample of 452 Abell clusters selected for the likely presence of a dominant galaxy, estimated that the BCGs have a median peculiar velocity of 32 per cent of their host clusters’ radial velocity dispersion.
We emphasize that these results, based on large clusters, do not necessarily hold for less massive haloes. After all, in galaxy clusters, the ratio L2/L1 of the luminosities of the two brightest galaxies tends to be much smaller in a Milky Way (MW)-sized halo, on average (e.g. van den Bosch et al. 2007). For example, for the halo hosting the MW it is the ratio of the luminosities of the Large Magellanic Cloud and the MW, which is ∼0.1 (van den Bergh 1999), while this ratio is much closer to unity in Virgo, Coma and other nearby clusters (Postman & Lauer 1995). Consequently, it is only natural to expect that the CGP is more likely to be valid for low-mass haloes than for massive cluster-sized haloes. Nevertheless, vdB05 used a large sample of 3473 galaxy groups from the group catalogue of Yang et al. (2005a), and conclusively falsified the assumption that the brightest group galaxy is always at rest at the centre of the potential well. In this paper we extend the analysis of vdB05 using a larger, more accurate group catalogue, and focusing on different aspects of the CGP as a function of halo mass. In particular, we separately test two aspects of the CGP, namely (i) central galaxies reside at rest at the centre of their host halo’s potential well, and (ii) central galaxies are the brightest, most massive galaxies in their host haloes. We do so by comparing three hypotheses.
 : our null hypothesis is that the CGP is correct: central galaxies are always the brightest objects in their haloes and are at rest at the centre of the potential well.
: our null hypothesis is that the CGP is correct: central galaxies are always the brightest objects in their haloes and are at rest at the centre of the potential well. : central galaxies are the brightest objects in their haloes, but they have a velocity and spatial offset with respect to the centre of the potential well, such that the systems still obey the Jeans equations (i.e. they are still in dynamical equilibrium). We will specify the amount of offset via a velocity bias parameter, bvel, to be defined in Section 4.2.
: central galaxies are the brightest objects in their haloes, but they have a velocity and spatial offset with respect to the centre of the potential well, such that the systems still obey the Jeans equations (i.e. they are still in dynamical equilibrium). We will specify the amount of offset via a velocity bias parameter, bvel, to be defined in Section 4.2. : central galaxies reside at rest at the centre of the potential well, but they are not the brightest objects in a fraction fBNC (for ‘brightest-not-central’) of all dark matter haloes.
: central galaxies reside at rest at the centre of the potential well, but they are not the brightest objects in a fraction fBNC (for ‘brightest-not-central’) of all dark matter haloes.
In order to avoid confusion, throughout this paper we use the term ‘central galaxy’ to refer to the galaxy with the lowest specific potential energy. The central galaxy is the BHG in  and
and  , but not in
, but not in  , and its location coincides with the centre of the halo’s potential well in
, and its location coincides with the centre of the halo’s potential well in  and
and  , but not in
, but not in  .
.
We base our study on the galaxy group catalogue of Y07, extracted from the SDSS (York et al. 2000) Data Release 4 (DR4; Adelman-McCarthy et al. 2006). We analyse both the positions and velocities of BHGs relative to those of the other member galaxies, and compare the results to mock group catalogues that correspond to one of our three hypotheses. The large SDSS group catalogue, with accurate halo mass estimates, allows us to falsify  and to quantify the degree to which
and to quantify the degree to which  and
and  are valid (i.e. to constrain the values of bvel and fBNC).
are valid (i.e. to constrain the values of bvel and fBNC).
This paper is organized as follows. In Section 2, we present two statistics that quantify the offsets of BHGs, and which can be used to assess deviations from the CGP. We describe the SDSS group catalogue in Section 3 and the construction of mock group catalogues in Section 4. In Section 5, we compare these mock catalogues to the data in order to test our three hypotheses. We find that both  and
and  can be ruled out, but that
can be ruled out, but that  yields results in agreement with the data as long as 0.25 ≲fBNC≲ 0.4, with a weak dependence on halo mass. In Section 6, we discuss our results and compare them to predictions from halo occupation statistics and from two semi-analytic models of galaxy formation. We also discuss the implications for studies of satellite kinematics. Finally, we end the paper with our conclusions and a discussion of additional implications of our results.
yields results in agreement with the data as long as 0.25 ≲fBNC≲ 0.4, with a weak dependence on halo mass. In Section 6, we discuss our results and compare them to predictions from halo occupation statistics and from two semi-analytic models of galaxy formation. We also discuss the implications for studies of satellite kinematics. Finally, we end the paper with our conclusions and a discussion of additional implications of our results.
Throughout this paper, we adopt a flat Λcold dark matter (ΛCDM) cosmology with Ωm = 0.238, ΩΛ = 1 −Ωm, n = 0.951, σ8 = 0.744, and we express units that depend on the Hubble constant in terms of h≡H0/100 km s−1 Mpc−1. In addition, we use ‘log’ as shorthand for the 10-based logarithm.
2 PHASE-SPACE STATISTICS OF CENTRAL GALAXIES
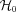 ), we use the line-of-sight velocities of galaxies obtained from their redshifts. In what follows, vBHG refers to the line-of-sight velocity of the BHG, and vsat, i refers to the line-of-sight velocity of the ith satellite galaxy. We define the difference
), we use the line-of-sight velocities of galaxies obtained from their redshifts. In what follows, vBHG refers to the line-of-sight velocity of the BHG, and vsat, i refers to the line-of-sight velocity of the ith satellite galaxy. We define the difference 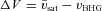 between the mean velocity of the satellite galaxies and that of the BHG. If the CGP is correct and vsat, i follows a Gaussian distribution with velocity dispersion σsat, then the probability that a halo with Nsat satellite galaxies has a value of ΔV is given by
between the mean velocity of the satellite galaxies and that of the BHG. If the CGP is correct and vsat, i follows a Gaussian distribution with velocity dispersion σsat, then the probability that a halo with Nsat satellite galaxies has a value of ΔV is given by 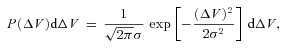
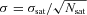 . Therefore, in principle, one could define the parameter
. Therefore, in principle, one could define the parameter 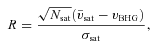
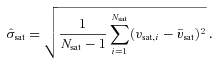
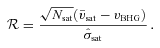
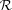 should follow a Student’s t-distribution with ν=Nsat− 1 degrees of freedom. Note that
should follow a Student’s t-distribution with ν=Nsat− 1 degrees of freedom. Note that 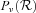 approaches a normal distribution with zero mean and unit variance in the limit Nsat→∞.
approaches a normal distribution with zero mean and unit variance in the limit Nsat→∞.In practice, although the galaxy group finder (Yang et al. 2005a; Y07) has been thoroughly tested with mock SDSS catalogues to reliably identify galaxies residing in the same dark matter halo, it is not perfect. In particular, because of redshift errors and redshift-space distortions, the group finder inevitably selects some interlopers (galaxies that are not associated with the same halo). In addition, the SDSS suffers from various incompleteness effects. If the actual BHG is missed or misidentified,  will be measured with respect to a satellite galaxy, and
will be measured with respect to a satellite galaxy, and  will tend to be overestimated. The presence of interlopers and incompleteness effects tends to create excessive wings in the
will tend to be overestimated. The presence of interlopers and incompleteness effects tends to create excessive wings in the  -distribution, and therefore a direct comparison with the Student’s t-distribution cannot be made. To circumvent these problems, we compare the
-distribution, and therefore a direct comparison with the Student’s t-distribution cannot be made. To circumvent these problems, we compare the  -distributions obtained from galaxy groups identified in the SDSS to those obtained from groups identified in mock galaxy redshift surveys (MGRSs; Section 4), which suffer from interlopers and incompleteness to the same extent as the real data.
-distributions obtained from galaxy groups identified in the SDSS to those obtained from groups identified in mock galaxy redshift surveys (MGRSs; Section 4), which suffer from interlopers and incompleteness to the same extent as the real data.
 , that quantifies the spatial separation between BHGs and satellite galaxies, using their projected angular separations perpendicular to the line-of-sight:
, that quantifies the spatial separation between BHGs and satellite galaxies, using their projected angular separations perpendicular to the line-of-sight: 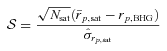
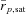 is the mean projected position of satellite galaxies in a group, in terms of the galaxies’ mean right ascensions and declinations, and
is the mean projected position of satellite galaxies in a group, in terms of the galaxies’ mean right ascensions and declinations, and 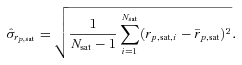
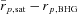 and
and 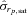 are expressed in h−1 kpc in the computation of
are expressed in h−1 kpc in the computation of 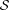 .
.For the mean and standard deviation  and
and  in the
in the  parameter (equation 4), and
parameter (equation 4), and  and
and  in the
in the  parameter (equation 5), we have tested that other estimators for these quantities, such as the biweight estimator and the gapper (Beers, Flynn & Gebhardt 1990), have an insignificant effect on our results.
parameter (equation 5), we have tested that other estimators for these quantities, such as the biweight estimator and the gapper (Beers, Flynn & Gebhardt 1990), have an insignificant effect on our results.
Note that, with these definitions, the velocity offset  and spatial offset
and spatial offset  are only valid for groups with three or more members, and are not defined for galaxy pairs or isolated galaxies.
are only valid for groups with three or more members, and are not defined for galaxy pairs or isolated galaxies.
3 APPLICATION TO THE SDSS
We first describe the SDSS galaxy group catalogue in Section 3.1 and then the subset of galaxy groups used in our analysis in Section 3.2.
3.1 Galaxy group catalogue
The analysis presented in this paper is based on the SDSS galaxy group catalogue of Y07, which is constructed by applying the halo-based group finder of Yang et al. (2005a) to the New York University Value-Added Galaxy Catalog (NYU-VAGC; see Blanton et al. 2005), which is based on the SDSS DR4 (Adelman-McCarthy et al. 2006). From this catalogue, Y07 selected all galaxies in the Main Galaxy Sample (Strauss et al. 2002) with an extinction-corrected apparent magnitude brighter than mr = 18, with redshifts in the range 0.01 ≤z≤ 0.20 and with a redshift completeness  .
.
This sample of galaxies is used to construct three group samples: Sample I, which only uses the 362 356 galaxies with measured redshifts from the SDSS, Sample II which also includes 7091 galaxies with SDSS photometry but with redshifts taken from alternative surveys1 and Sample III which includes an additional 38 672 galaxies that lack a redshift due to fibre collisions, but which we assign the redshift of its nearest neighbour. The present analysis is based on the galaxies in Sample II with mr < 17.77, which consists of 344 010 galaxies.
All the magnitudes and colours of the galaxies are Petrosian, and they have been corrected for Galactic extinction (Schlegel, Finkbeiner & Davis 1998), and have been k-corrected and evolution-corrected to z = 0.1 (Blanton & Roweis 2007). Stellar masses for all galaxies are computed using the relations between stellar mass-to-light ratio and colour of Bell et al. (2003).
The geometry of the SDSS used for the group catalogue is defined as the region on the sky that satisfies the redshift completeness criterion. To account for the effects of the survey edges, Y07 used the SDSS DR4 survey mask with MGRSs to estimate the fraction of ‘missing’ members within the halo radius for each group. The group luminosities and masses are corrected for this fraction, and groups missing 40 per cent or more of their members were excluded, which removes only 1.6 per cent of all groups.
As described in Y07, the majority of the groups in our catalogue have two estimates of their dark matter halo mass: one based on the ranking of its total characteristic luminosity, and the other based on the ranking of its total characteristic stellar mass, both determined from group galaxies more luminous than Mr− 5log h=−19.5. As shown in Y07, both halo masses agree very well with each other, with an average scatter that decreases from ∼0.1 dex at the low-mass end to ∼0.05 at the massive end. In this paper we adopt the group masses based on the stellar mass ranking, but we have checked that the luminosity ranking gives results that are almost indistinguishable. The stellar mass-based group masses are available for a total of 215 493 groups in our sample, which host a total of 277 838 galaxies. This implies that a total of 66 172 galaxies have been assigned with a group for which no reliable mass estimate is available (but see Yang, Mo & van den Bosch 2009a).
3.2 Galaxy groups used in this paper
In what follows we restrict our analyses to the 7234 galaxy groups in Sample II catalogue with three or more members, with  , and with reliable group masses greater than 1012h−1M⊙.
, and with reliable group masses greater than 1012h−1M⊙.
Because of the finite thickness of the spectroscopic fibres used, the SDSS suffers from incompleteness due to fibre collisions. No two fibres on the same SDSS plate can be closer than 55 arcsec. Although this fibre collision constraint is partially alleviated by the fact that neighbouring plates have overlap regions, ∼7 per cent of all galaxies eligible for spectroscopy do not have a measured redshift. Since fibre collisions are more frequent in regions of high (projected) density, they are more likely to occur in richer groups, thus causing a systematic bias that may need to be accounted for. Although Sample III tries to correct for this incompleteness by assigning galaxies that lack a redshift due to fibre collisions the redshift of its nearest neighbour, Zehavi et al. (2002) have shown that in roughly 40 per cent of cases, the redshift thus assigned carries a large error. Hence, although Sample II is more incomplete than Sample III, there is less of a risk of interlopers, and the redshifts are accurate, which is necessary for the analysis with galaxy line-of-sight velocities. However, if the true brightest galaxy in a group is missed due to a fibre collision, the velocity and spatial offsets  and
and  will be estimated relative to a satellite galaxy, and will tend to be overestimated, resulting in a stronger signal. To avoid this problem, we exclude groups in Sample II in which the brightest galaxy is not also a brightest group galaxy in Sample III.
will be estimated relative to a satellite galaxy, and will tend to be overestimated, resulting in a stronger signal. To avoid this problem, we exclude groups in Sample II in which the brightest galaxy is not also a brightest group galaxy in Sample III.
This results in a sample of 6760 groups with Ngal≥ 3, excluding approximately 7 per cent of the galaxy groups. This constitutes our fiducial galaxy group sample.2 To be clear, our fiducial sample simply consists of a subset of Sample II groups. We emphasize that Sample III groups are not used in our analysis; they are only used to remove those groups from Sample II that may have been affected by fibre collisions.
In Fig. 1, we show the abundance of galaxy groups as a function of richness in the catalogue, with M≥ 1012h−1 M⊙ and  . The requirement that the brightest group galaxy is also the brightest group galaxy in Sample III results in slightly fewer groups at all richnesses.
. The requirement that the brightest group galaxy is also the brightest group galaxy in Sample III results in slightly fewer groups at all richnesses.
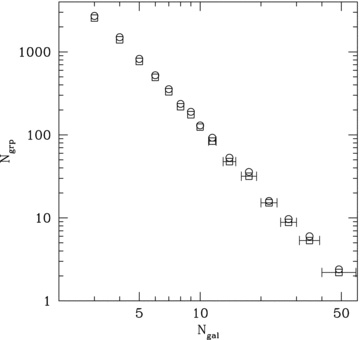
Galaxy group multiplicity function of SDSS Sample II. Circle points show the number of groups as a function of group richness, for groups with M≥ 1012h−1 M⊙ and  . Square points show Ngrp(Ngal) for groups in which we additionally require that the central galaxy is also the central galaxy of a group in Sample III. Horizontal error bars indicate the width of each bin.
. Square points show Ngrp(Ngal) for groups in which we additionally require that the central galaxy is also the central galaxy of a group in Sample III. Horizontal error bars indicate the width of each bin.
The analysis of vdB05 was done with a catalogue of 2502 groups in the 2dFGRS with four members or more; the new Y07 catalogue has nearly twice as many groups with Ngal≥ 4 (4571), which is a significant improvement. In addition, the typical rms redshift and magnitude errors of galaxies in the SDSS are 30 km s−1 and 0.035 mag (r band), respectively (Strauss et al. 2002), compared to 85 km s−1 and 0.15 mag (B band) in the 2dFGRS (Colless et al. 2001). The improved statistics of this SDSS DR4 group catalogue allow us to investigate not only the halo mass dependence of central galaxy velocity bias, but also the dependence of velocity bias on the properties of the central galaxies themselves.
4 MOCK CATALOGUES
The main goal of this paper is to use the distributions of the parameters  and
and  defined above to test our three hypotheses related to the CGP defined in Section 1. As discussed above, since the SDSS galaxy group catalogue suffers from interlopers and incompleteness effects, we require mock group catalogues constructed from MGRSs using the same halo-based galaxy group finder as used for the SDSS.
defined above to test our three hypotheses related to the CGP defined in Section 1. As discussed above, since the SDSS galaxy group catalogue suffers from interlopers and incompleteness effects, we require mock group catalogues constructed from MGRSs using the same halo-based galaxy group finder as used for the SDSS.
We construct MGRSs by populating dark matter haloes with galaxies of different luminosities. The distribution of dark matter haloes is obtained from a set of large N-body simulations (dark matter only) for the 3-yr Wilkinson Microwave Anisotropy Probe (WMAP3) ΛCDM cosmology from Macciò et al. (2007). The simulations have 5123 particles each, have periodic boundary conditions, and have box sizes of Lbox = 100 h−1 Mpc (hereafter L100) and Lbox = 300h−1 Mpc (hereafter L300). We follow Yang et al. (2004) and replicate the L300 box on a 4 × 4 × 4 grid. The central 2 × 2 × 2 boxes are replaced by a stack of 6 × 6 × 6 L100 boxes (see fig. 11 in Yang et al. 2004). This stacking geometry circumvents incompleteness problems in the mock survey due to insufficient mass resolution of the L300 simulations, and allows us to reach the desired depth of zmax = 0.20 in all directions.
Dark matter haloes are identified using the standard FOF algorithm with a linking length of 0.2 times the mean inter-particle separation. Unbound haloes and haloes with less than 10 particles are removed from the sample. The resulting halo mass functions are in excellent agreement with the analytical halo mass function of Sheth, Mo & Tormen (2001).
4.1 Assigning luminosities
We populate each halo with galaxies of different luminosities using the conditional luminosity function (CLF) model described in C09. The CLF, Φ(L|M), specifies the average number of galaxies of luminosity L in a halo of mass M, and is constrained to accurately match the SDSS r-band luminosity function (Blanton et al. 2003), the clustering strength of SDSS galaxies as a function of luminosity (Wang et al. 2007) and the galaxy–galaxy lensing data of Mandelbaum et al. (2006). The CLF assumes that the luminosity-dependent abundance, distribution and clustering of galaxies can be described as a function of halo mass. The CLF of C09 is split in two parts, Φcen(L|M) and Φsat(L|M), which describe the halo occupation statistics of central and satellite galaxies, respectively.
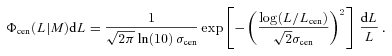

If the luminosity of the satellite is brighter than that of its central, a new luminosity is drawn until it is fainter than that of the central. Hence, in our mock universe central galaxies are always BHGs by construction.
4.2 Assigning phase-space coordinates
Having assigned all mock galaxies their luminosities, the next step is to assign them a position and velocity within their halo.
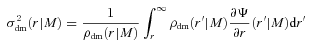
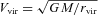 we obtain
we obtain 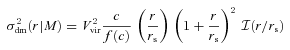
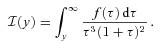
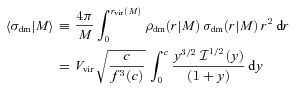
4.2.1 Central galaxies
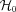 and
and 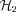 mocks, we position the central galaxy at rest at the centre of the dark matter halo (for the
mocks, we position the central galaxy at rest at the centre of the dark matter halo (for the 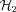 mocks, we then reshuffle the indices of central and brightest satellite, as detailed below, but we do so only after the construction of the group catalogue). In the case of the
mocks, we then reshuffle the indices of central and brightest satellite, as detailed below, but we do so only after the construction of the group catalogue). In the case of the 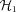 mocks, we follow the approach of vdB05, to which we refer the reader for details. Briefly, we assume that the radial coordinate of the central, r, follows a probability distribution3
mocks, we follow the approach of vdB05, to which we refer the reader for details. Briefly, we assume that the radial coordinate of the central, r, follows a probability distribution3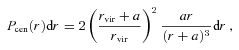
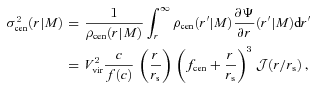
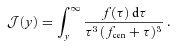
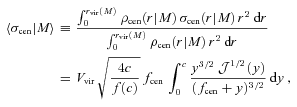
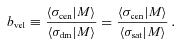
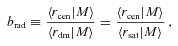
With this model, a particular value of the parameter fcen implies a particular amount of velocity and spatial bias. The relations bvel(fcen) and brad(fcen) are shown in Fig. 2. These relations only depend weakly on halo concentration (see vdB05). In the limit fcen→ 0, the probability distribution Pcen(r) becomes a delta function, implying that the central galaxy is sitting at rest at the centre of the dark matter halo (i.e. the null hypothesis  of the CGP). Larger values of fcen result in larger amounts of velocity and spatial bias. Note that bvel is always larger than brad, indicating that the signature of an off-centred central galaxy (i.e. hypothesis
of the CGP). Larger values of fcen result in larger amounts of velocity and spatial bias. Note that bvel is always larger than brad, indicating that the signature of an off-centred central galaxy (i.e. hypothesis  ) is more pronounced, and thus easier to detect, in velocity space than in configuration space.
) is more pronounced, and thus easier to detect, in velocity space than in configuration space.
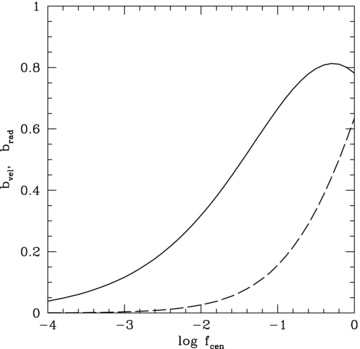
The velocity bias (solid curve) and spatial bias (dashed curve) of central galaxies as a function of the parameter fcen, which expresses the characteristic scale of the radial distribution of central galaxies in terms of the characteristic scale of the NFW density distribution. The results shown correspond to a dark matter halo with a concentration c = 10.
4.2.2 Satellite galaxies
Throughout this paper, we assume that the Nsat satellite galaxies in a halo of mass M follow a number density distribution nsat(r|M) = (Nsat/M)ρdm(r|M), so that there is no spatial bias between satellite galaxies and dark matter particles. If we further assume that the satellites are in isotropic equilibrium, it also follows that there is no velocity bias between the satellites and the dark matter, neither globally [i.e. 〈σsat|M〉=〈σdm|M〉] nor locally [i.e. σsat(r|M) =σdm(r|M)].
For simplicity, we assume that the satellites follow a spherically symmetric spatial distribution with a velocity distribution that is locally isotropic. Although this is a clear oversimplification, as some galaxy groups and clusters have anisotropic or aspherical distributions (e.g. Bailin et al. 2008; Wang et al. 2008), we do not believe that it strongly impacts our results. For example, the global velocity dispersion (i.e. obtained from all satellites) of an anisotropic system will be nearly identical to that of an isotropic system with the same gravitational potential, since both are governed by the virial equation. In other words, anisotropy changes the local line-of-sight velocity distribution (LOSVD), but leaves the second moment of the global LOSVD largely unchanged (see e.g. van den Bosch et al. 2004). Therefore, since the  parameter (equation 4) only depends on the first and second moments of the global LOSVD, our results are robust to the assumptions of isotropy and sphericity. The cumulative
parameter (equation 4) only depends on the first and second moments of the global LOSVD, our results are robust to the assumptions of isotropy and sphericity. The cumulative  -distribution is weakly dependent on higher moments of the LOSVD, but again, the effect of anisotropy is very small.
-distribution is weakly dependent on higher moments of the LOSVD, but again, the effect of anisotropy is very small.
Although there is evidence to support our assumption that satellite galaxies have number density distributions that are well fit by a NFW profile (e.g. Lin, Mohr & Stanford 2004), the corresponding concentration parameters seem to be significantly smaller than the values expected for their dark matter haloes by about a factor of 2 to 3 (e.g. Hansen et al. 2005; Yang et al. 2005b). Since we assume that satellites are unbiased with respect to the dark matter, our value for bvel will be incorrect by a factor of 〈σsat〉/〈σdm〉. Using the model described in equations (13) and (17), we estimate that this may result in an underestimating of the velocity bias by no more than 5 per cent. Given that this is a small effect compared to the other uncertainties involved in our analyses, we do not attempt to correct for it.
4.3 Mock group catalogues
Once the dark matter haloes are populated with galaxies, we construct an MGRS following the procedure described in Li et al. (2007). We place a virtual observer at the centre of the stack of simulation boxes, assign each galaxy a (α, δ)-coordinate and remove the ones that are outside the mocked SDSS survey region. For each model galaxy in the survey region, we compute its redshift (which includes the cosmological redshift due to the universal expansion, the peculiar velocity and a 35 km s−1 Gaussian line-of-sight velocity dispersion to mimic the redshift errors in the data), and its r-band apparent magnitude (based on the r-band luminosity of the galaxy).
We eliminate galaxies that are fainter than the SDSS apparent magnitude limit, and incorporate the position-dependent incompleteness by randomly eliminating galaxies according to the completeness factors obtained from the survey masks provided by the NYU-VAGC (Blanton et al. 2005). Finally, we construct group catalogues from the MGRSs, using the same halo-based group finder as used for the real SDSS DR4.
Using the method outlined above, we construct the following set of mock group catalogues. The first is a set of 10 mocks that only differ in the value of the velocity bias bvel = 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8 and 1.0. These constitute our  mocks. Note that the mock with bvel = 0 satisfies the CGP, and therefore corresponds to the null hypothesis
mocks. Note that the mock with bvel = 0 satisfies the CGP, and therefore corresponds to the null hypothesis  , while the other mocks correspond to
, while the other mocks correspond to  (i.e. BHG is a central galaxy, but is not at rest at the centre of dark matter potential well). The second set of mock group catalogues is constructed starting from the bvel = 0 mock group catalogue, in which we switch the luminosities of the central and its brightest satellite for a random fraction fBNC of all groups. We construct six mock group catalogues for fBNC = 0.1, 0.2, 0.3, 0.4, 0.5 and 0.6, respectively. These constitute our
(i.e. BHG is a central galaxy, but is not at rest at the centre of dark matter potential well). The second set of mock group catalogues is constructed starting from the bvel = 0 mock group catalogue, in which we switch the luminosities of the central and its brightest satellite for a random fraction fBNC of all groups. We construct six mock group catalogues for fBNC = 0.1, 0.2, 0.3, 0.4, 0.5 and 0.6, respectively. These constitute our  mocks.
mocks.
In order to facilitate the comparison with the SDSS galaxy group catalogue, in what follows we discard all mock groups with an assigned group mass less than 1012h−1 M⊙, and with a satellite velocity dispersion  or
or  . For the mock groups that have not been discarded, we compute the parameters
. For the mock groups that have not been discarded, we compute the parameters  and
and  . In the next section, we compare the resulting distributions
. In the next section, we compare the resulting distributions  and
and  with those obtained from the SDSS group catalogue in order to test our three hypotheses
with those obtained from the SDSS group catalogue in order to test our three hypotheses  ,
,  and
and  .
.
Finally, we note that the halo centres and central and satellite galaxies are defined only in the mock group catalogues, not in the SDSS group catalogue. The  and
and  parameters used in the following analysis are defined with respect to the BHGs in the mock and observed galaxy groups. This way, we are able to statistically analyse groups of a wide range in mass, including poor groups for which a centre or central galaxy might not be well-defined.
parameters used in the following analysis are defined with respect to the BHGs in the mock and observed galaxy groups. This way, we are able to statistically analyse groups of a wide range in mass, including poor groups for which a centre or central galaxy might not be well-defined.
5 RESULTS
Fig. 3 shows the cumulative distributions of  (left panels) and
(left panels) and  (right panels) obtained from the
(right panels) obtained from the  mocks (upper panels) and the
mocks (upper panels) and the  mocks (lower panels) for groups with four or more members (i.e. Nsat≥ 3). As expected,
mocks (lower panels) for groups with four or more members (i.e. Nsat≥ 3). As expected,  and
and  become broader for larger values of bvel (upper panels) and fBNC (lower panels). A few trends are apparent. First, note that the
become broader for larger values of bvel (upper panels) and fBNC (lower panels). A few trends are apparent. First, note that the  -distributions are all bunched together for bvel≤ 0.5. Only for bvel > 0.5 are the cumulative
-distributions are all bunched together for bvel≤ 0.5. Only for bvel > 0.5 are the cumulative  -distributions notably different. This shows that it is difficult to constrain bvel using the angular positions of galaxies, on which the
-distributions notably different. This shows that it is difficult to constrain bvel using the angular positions of galaxies, on which the  -statistic is based, vis-à-vis using the velocity-statistic
-statistic is based, vis-à-vis using the velocity-statistic  . Physically, this is a reflection of the fact that dark matter haloes have steep potential wells, so that large velocities are required even for relatively modest excursions from the centre. Secondly, and most importantly, comparing the upper and lower panels, it is clear that a non-zero value of fBNC has a different impact on
. Physically, this is a reflection of the fact that dark matter haloes have steep potential wells, so that large velocities are required even for relatively modest excursions from the centre. Secondly, and most importantly, comparing the upper and lower panels, it is clear that a non-zero value of fBNC has a different impact on  and
and  than a non-zero value of bvel. This is good news, as it implies that we will be able to discriminate between our three hypotheses.
than a non-zero value of bvel. This is good news, as it implies that we will be able to discriminate between our three hypotheses.
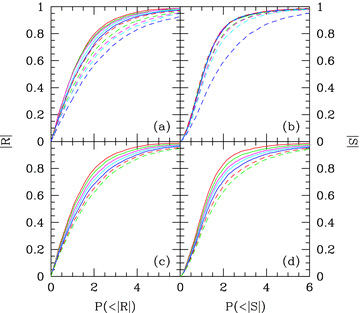
The cumulative distributions of  (left-hand panels) and
(left-hand panels) and  (right-hand panels) for the groups in mock group catalogues with four members or more. Upper panels show the distributions for mock catalogues with different amounts of bvel: the solid curves are for bvel = 0, 0.1, 0.2, 0.3 and 0.4 (red, green, magenta, cyan and blue curves, respectively, in the electronic version of this paper) and the dashed curves are for bvel = 0.5, 0.6, 0.7, 0.8 and 1 (red, green, magenta, cyan and blue curves, respectively). Lower panels show the distributions for mock catalogues with different fractions fBNC = 0, 0.1, 0.2, 0.3, 0.4, 0.5 and 0.6 (red, green, magenta, cyan, blue, dashed red and dashed green curves, respectively).
(right-hand panels) for the groups in mock group catalogues with four members or more. Upper panels show the distributions for mock catalogues with different amounts of bvel: the solid curves are for bvel = 0, 0.1, 0.2, 0.3 and 0.4 (red, green, magenta, cyan and blue curves, respectively, in the electronic version of this paper) and the dashed curves are for bvel = 0.5, 0.6, 0.7, 0.8 and 1 (red, green, magenta, cyan and blue curves, respectively). Lower panels show the distributions for mock catalogues with different fractions fBNC = 0, 0.1, 0.2, 0.3, 0.4, 0.5 and 0.6 (red, green, magenta, cyan, blue, dashed red and dashed green curves, respectively).
In what follows we will compare the cumulative  and
and  -distributions obtained from the SDSS with those obtained from our mock catalogues. Since we have a relatively large number of groups in our SDSS sample, we can perform this test for a (small) number of bins in group mass, thus giving some leverage on a possible halo mass dependence. At the massive end of the group mass distribution, the group catalogue is roughly complete, and the mass distribution closely follows the halo mass function. The constraint of four or more group members, however, cuts off the distribution at the low-mass end, leaving virtually no groups with M < 1012h−1 M⊙. We split the SDSS group catalogue in three mass bins (listed in Table 1) that contain a similar number (∼1500) of groups, and the corresponding mass cuts occur at log (M/h−1 M⊙) = 13.3 and 13.75.
-distributions obtained from the SDSS with those obtained from our mock catalogues. Since we have a relatively large number of groups in our SDSS sample, we can perform this test for a (small) number of bins in group mass, thus giving some leverage on a possible halo mass dependence. At the massive end of the group mass distribution, the group catalogue is roughly complete, and the mass distribution closely follows the halo mass function. The constraint of four or more group members, however, cuts off the distribution at the low-mass end, leaving virtually no groups with M < 1012h−1 M⊙. We split the SDSS group catalogue in three mass bins (listed in Table 1) that contain a similar number (∼1500) of groups, and the corresponding mass cuts occur at log (M/h−1 M⊙) = 13.3 and 13.75.
Halo mass bins (log (M/h−1 M⊙)) in the SDSS group catalogue, for groups with four members or more and  . The log mass ranges, mean masses, and number of groups are given.
. The log mass ranges, mean masses, and number of groups are given.
| Halo Mass Bins | log Mmin |  | log Mmax | Ngroup |
| low mass | 12 | 12.86 | 13.3 | 1434 |
| intermediate mass | 13.3 | 13.53 | 13.75 | 1540 |
| high mass | 13.75 | 14.09 | 15.2 | 1555 |
| Halo Mass Bins | log Mmin |  | log Mmax | Ngroup |
| low mass | 12 | 12.86 | 13.3 | 1434 |
| intermediate mass | 13.3 | 13.53 | 13.75 | 1540 |
| high mass | 13.75 | 14.09 | 15.2 | 1555 |
Halo mass bins (log (M/h−1 M⊙)) in the SDSS group catalogue, for groups with four members or more and  . The log mass ranges, mean masses, and number of groups are given.
. The log mass ranges, mean masses, and number of groups are given.
| Halo Mass Bins | log Mmin |  | log Mmax | Ngroup |
| low mass | 12 | 12.86 | 13.3 | 1434 |
| intermediate mass | 13.3 | 13.53 | 13.75 | 1540 |
| high mass | 13.75 | 14.09 | 15.2 | 1555 |
| Halo Mass Bins | log Mmin |  | log Mmax | Ngroup |
| low mass | 12 | 12.86 | 13.3 | 1434 |
| intermediate mass | 13.3 | 13.53 | 13.75 | 1540 |
| high mass | 13.75 | 14.09 | 15.2 | 1555 |
The results presented in Sections 5.1 and 5.2 are based on groups with at least four members (i.e. with Nsat≥ 3). We have repeated these analyses using samples of groups with three, five, six, and 10 or more members. We have also tested lower and higher halo mass thresholds. In each case we obtain constraints on bvel and fBNC that are consistent with each other at the 1σ level. Hence, our results do not depend significantly on the multiplicity and halo mass thresholds used.
5.1 Testing hypothesis ![formula]()
In order to test hypothesis  , we compare the SDSS group catalogue to mock group catalogues with different values of bvel while setting fBNC = 0. Fig. 4(a) shows the cumulative
, we compare the SDSS group catalogue to mock group catalogues with different values of bvel while setting fBNC = 0. Fig. 4(a) shows the cumulative  -distribution for different bins of halo mass obtained from the SDSS group catalogue (solid lines) and from three mock group catalogues corresponding to different values of bvel (0, 0.5 and 1). In all cases only groups with four members of more are considered. The numbers in square brackets in each panel indicate the range of log (M/h−1 M⊙) considered. Note that at fixed
-distribution for different bins of halo mass obtained from the SDSS group catalogue (solid lines) and from three mock group catalogues corresponding to different values of bvel (0, 0.5 and 1). In all cases only groups with four members of more are considered. The numbers in square brackets in each panel indicate the range of log (M/h−1 M⊙) considered. Note that at fixed  , the corresponding
, the corresponding  becomes smaller when using a bin with larger group masses. This does not necessarily imply a trend of bvel with halo mass, though. It may also be due to a mass dependence of the fraction of interlopers, or a mass dependence of the completeness of group members. Indeed, the mock group samples for a fixed value of bvel reveal the same trend, indicating that it is most likely an artefact introduced by the group finder. For each halo mass bin, the mock catalogue with bvel = 0 (i.e. the one that fulfils the null hypothesis,
becomes smaller when using a bin with larger group masses. This does not necessarily imply a trend of bvel with halo mass, though. It may also be due to a mass dependence of the fraction of interlopers, or a mass dependence of the completeness of group members. Indeed, the mock group samples for a fixed value of bvel reveal the same trend, indicating that it is most likely an artefact introduced by the group finder. For each halo mass bin, the mock catalogue with bvel = 0 (i.e. the one that fulfils the null hypothesis,  , of the CGP) predicts an
, of the CGP) predicts an  -distribution that is much narrower than that of the SDSS, while the mock catalogue with bvel = 1 yields a distribution that is too broad. Interestingly, the intermediate case, with bvel = 0.5, results in
-distribution that is much narrower than that of the SDSS, while the mock catalogue with bvel = 1 yields a distribution that is too broad. Interestingly, the intermediate case, with bvel = 0.5, results in  that are very similar to those of the SDSS, for each mass bin. This rules out the null hypothesis
that are very similar to those of the SDSS, for each mass bin. This rules out the null hypothesis  , and seems to suggest that instead central galaxies have a relatively large velocity bias with 〈σcen|M〉≃ 0.5〈σsat|M〉 with little dependence on halo mass M.
, and seems to suggest that instead central galaxies have a relatively large velocity bias with 〈σcen|M〉≃ 0.5〈σsat|M〉 with little dependence on halo mass M.
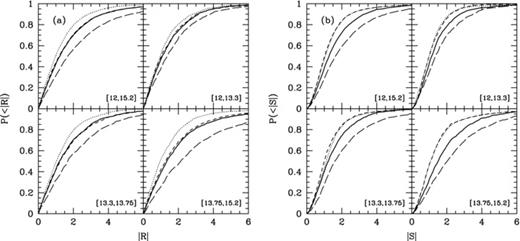
The cumulative distribution of  (left-hand figure) and
(left-hand figure) and  (right-hand figure) obtained from the SDSS group catalogue (solid black curve) compared with those obtained from three of our mocks, with bvel = 0 (red dotted curve), 0.5 (blue short-dashed curve) and 1 (green long-dashed curve), for groups with four members or more. Results are shown for four log halo mass intervals, as indicated in square brackets in each panel.
(right-hand figure) obtained from the SDSS group catalogue (solid black curve) compared with those obtained from three of our mocks, with bvel = 0 (red dotted curve), 0.5 (blue short-dashed curve) and 1 (green long-dashed curve), for groups with four members or more. Results are shown for four log halo mass intervals, as indicated in square brackets in each panel.
However, Fig. 4(b), which is similar to Fig. 4(a) except that it shows the cumulative  -distributions, paints a different picture. Both the bvel = 0.0 and bvel = 0.5 mocks predict
-distributions, paints a different picture. Both the bvel = 0.0 and bvel = 0.5 mocks predict  -distributions that are clearly too narrow, for each mass bin. Rather, the SDSS
-distributions that are clearly too narrow, for each mass bin. Rather, the SDSS  -distribution seems to require 0.5 < bvel < 1.0. Hence, it appears that no single value of bvel can simultaneously match
-distribution seems to require 0.5 < bvel < 1.0. Hence, it appears that no single value of bvel can simultaneously match  and
and  obtained from the SDSS, ruling against our hypothesis
obtained from the SDSS, ruling against our hypothesis  . In other words, although the BHGs have non-zero velocities, the velocity spread is too small to explain their displacements from the halo centres.
. In other words, although the BHGs have non-zero velocities, the velocity spread is too small to explain their displacements from the halo centres.
In order to make this more quantitative, we use the Kolmogorov–Smirnov (KS) test to compute the probabilities PKS that  and
and  of the SDSS and a particular mock are drawn from the same distribution. The results are shown in Fig. 5, which plots log (PKS) as function bvel for each of the four mass bins considered. Using the median and the 16 and 84 percentiles of PKS(bvel) for the
of the SDSS and a particular mock are drawn from the same distribution. The results are shown in Fig. 5, which plots log (PKS) as function bvel for each of the four mass bins considered. Using the median and the 16 and 84 percentiles of PKS(bvel) for the  distributions (solid lines) we obtain bvel = 0.47+0.06−0.07 for the entire mass range, and bvel = 0.44+0.09−0.07, bvel = 0.50 ± 0.05 and bvel = 0.43+0.08−0.06 for the low-, intermediate- and high-mass intervals, respectively. For the
distributions (solid lines) we obtain bvel = 0.47+0.06−0.07 for the entire mass range, and bvel = 0.44+0.09−0.07, bvel = 0.50 ± 0.05 and bvel = 0.43+0.08−0.06 for the low-, intermediate- and high-mass intervals, respectively. For the  -distributions (dashed lines) this yields bvel = 0.82+0.08−0.06 for the low-mass interval, and bvel = 0.83+0.08−0.06 for the intermediate- and high-mass intervals. Therefore, the amounts of velocity bias consistent with the
-distributions (dashed lines) this yields bvel = 0.82+0.08−0.06 for the low-mass interval, and bvel = 0.83+0.08−0.06 for the intermediate- and high-mass intervals. Therefore, the amounts of velocity bias consistent with the  and
and  -distributions of SDSS groups are significantly different, with their best-fitting values of bvel differing from each other by more than 4σ. We conclude that hypothesis
-distributions of SDSS groups are significantly different, with their best-fitting values of bvel differing from each other by more than 4σ. We conclude that hypothesis  is ruled out, since it cannot simultaneously explain the
is ruled out, since it cannot simultaneously explain the  and
and  -distributions obtained from the SDSS group catalogue.
-distributions obtained from the SDSS group catalogue.
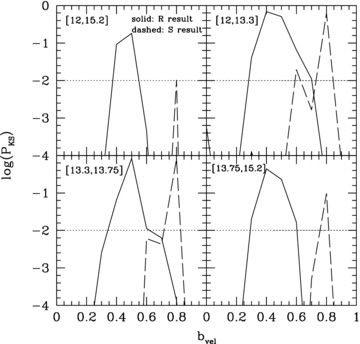
The KS-probability that the cumulative  -distribution (solid lines) and
-distribution (solid lines) and  -distribution (dashed lines) obtained from the SDSS groups is consistent with that obtained from our mocks, as a function of bvel. Results are shown for four log halo mass intervals, indicated in square brackets in each panel. The horizontal dotted line in each panel indicates PKS = 0.01: based on estimates of the scatter due to cosmic variance, we consider two distributions to be statistically equivalent when PKS > 0.01.
-distribution (dashed lines) obtained from the SDSS groups is consistent with that obtained from our mocks, as a function of bvel. Results are shown for four log halo mass intervals, indicated in square brackets in each panel. The horizontal dotted line in each panel indicates PKS = 0.01: based on estimates of the scatter due to cosmic variance, we consider two distributions to be statistically equivalent when PKS > 0.01.
5.2 Testing hypothesis ![formula]()
Having ruled out both  and
and  , we now turn our attention to hypothesis
, we now turn our attention to hypothesis  and investigate whether there is a value of fBNC for which the mock group catalogue yields
and investigate whether there is a value of fBNC for which the mock group catalogue yields  - and
- and  -distributions that are consistent with the SDSS data. To that extent we compare the SDSS group catalogue to mock catalogues with bvel = 0, but with different values of fBNC. We proceed in the same way as for
-distributions that are consistent with the SDSS data. To that extent we compare the SDSS group catalogue to mock catalogues with bvel = 0, but with different values of fBNC. We proceed in the same way as for  in the previous section: for each mock, which corresponds to a different value of fBNC, we compute
in the previous section: for each mock, which corresponds to a different value of fBNC, we compute  and
and  , which we compare to the corresponding distributions obtained from the SDSS, resulting in a value for PKS, the KS-probability that the mock and SDSS distributions are consistent with each other.
, which we compare to the corresponding distributions obtained from the SDSS, resulting in a value for PKS, the KS-probability that the mock and SDSS distributions are consistent with each other.
The results are shown in Fig. 6, where the solid and dashed lines once again correspond to the  and
and  -distributions, respectively. These KS probabilities are the means of log(PKS) for 100 realizations with different random seeds. The solid lines show that the
-distributions, respectively. These KS probabilities are the means of log(PKS) for 100 realizations with different random seeds. The solid lines show that the  -distribution of SDSS groups indicates a relatively large fraction of groups in which the central galaxy is not the BHG, with fBNC increasing from ∼0.25 in low-mass haloes (1012h−1 M⊙≤M≲ 2 × 1013h−1 M⊙) to ∼0.4 in massive haloes (M≳ 5 × 1013.75h−1 M⊙). Interestingly, the KS probabilities obtained from the
-distribution of SDSS groups indicates a relatively large fraction of groups in which the central galaxy is not the BHG, with fBNC increasing from ∼0.25 in low-mass haloes (1012h−1 M⊙≤M≲ 2 × 1013h−1 M⊙) to ∼0.4 in massive haloes (M≳ 5 × 1013.75h−1 M⊙). Interestingly, the KS probabilities obtained from the  -distributions shown by the dashed lines yield best-fitting values of fBNC that are very similar. Hence, we conclude that contrary to hypothesis
-distributions shown by the dashed lines yield best-fitting values of fBNC that are very similar. Hence, we conclude that contrary to hypothesis  , hypothesis
, hypothesis  can simultaneously match the
can simultaneously match the  and
and  obtained from the SDSS group catalogue.
obtained from the SDSS group catalogue.
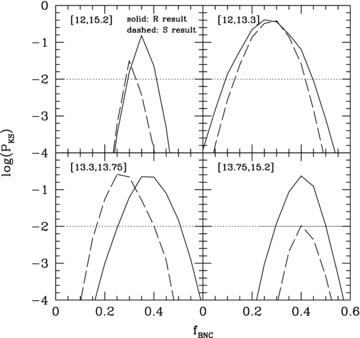
The KS-probability that the cumulative  -distribution (left-hand figure) and
-distribution (left-hand figure) and  -distribution (right-hand figure) obtained from the SDSS groups with four or more members is consistent with that obtained from MGRSs, as a function of fBNC, the fraction of groups in which the most luminous satellite is brighter than the central galaxy (see text for details). The KS probabilities here are the means of log(PKS) for 100 realizations with different random seeds.
-distribution (right-hand figure) obtained from the SDSS groups with four or more members is consistent with that obtained from MGRSs, as a function of fBNC, the fraction of groups in which the most luminous satellite is brighter than the central galaxy (see text for details). The KS probabilities here are the means of log(PKS) for 100 realizations with different random seeds.
Fig. 7 summarizes our results. It shows the best-fit values of bvel (upper panel) and fBNC (lower panel) as functions of halo mass, as inferred from the  -distributions (squares) and
-distributions (squares) and  -distributions (triangles) obtained from the SDSS galaxy group catalogue. The figure clearly shows that
-distributions (triangles) obtained from the SDSS galaxy group catalogue. The figure clearly shows that  (i.e. a non-zero fBNC) can simultaneously explain both the velocities and the positions of BHGs with respect to their satellites, while
(i.e. a non-zero fBNC) can simultaneously explain both the velocities and the positions of BHGs with respect to their satellites, while  (i.e. a non-zero bvel) is ruled out because it cannot.
(i.e. a non-zero bvel) is ruled out because it cannot.
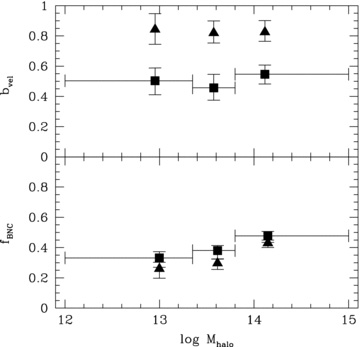
Halo mass dependence of bvel (upper panel) and fBNC (lower panel), inferred from the  -distributions (squares) and
-distributions (squares) and  -distributions (triangles) obtained from the analyses of the SDSS group catalogue (see the text for details). For the results in the upper panel, the mock catalogues had different values of bvel and fBNC = 0; for the lower panel, the mocks had different values of fBNC and bvel = 0. Points show best-fitting values of the parameters estimated from the KS probabilities; vertical error bars show 1σ uncertainties from the 16 and 84 percentiles of the PKS-distributions and horizontal error bars indicate the widths of the mass bins. Hypothesis
-distributions (triangles) obtained from the analyses of the SDSS group catalogue (see the text for details). For the results in the upper panel, the mock catalogues had different values of bvel and fBNC = 0; for the lower panel, the mocks had different values of fBNC and bvel = 0. Points show best-fitting values of the parameters estimated from the KS probabilities; vertical error bars show 1σ uncertainties from the 16 and 84 percentiles of the PKS-distributions and horizontal error bars indicate the widths of the mass bins. Hypothesis  is clearly ruled out from the fact that the
is clearly ruled out from the fact that the  -data imply a velocity bias, bvel, that is inconsistent with the value inferred from the
-data imply a velocity bias, bvel, that is inconsistent with the value inferred from the  -data.
-data.
Considering the  - and
- and  -distributions simultaneously, we infer best-fitting values for the fraction of haloes in which centrals are not BHGs of fBNC = 26+4−6 per cent for 12 ≤ log (M/h−1 M⊙) < 13.3, increasing to fBNC = 30+3−4 per cent for haloes with 13.3 ≤ log (M/h−1 M⊙) < 13.75 and fBNC = 43+2−3 per cent in the most massive haloes with log (M/h−1 M⊙) ≥ 13.75. As in Section 5.2, the best-fitting values and uncertainties are determined from the median and the 16 and 84 percentiles of the PKS(fBNC)-distributions.
-distributions simultaneously, we infer best-fitting values for the fraction of haloes in which centrals are not BHGs of fBNC = 26+4−6 per cent for 12 ≤ log (M/h−1 M⊙) < 13.3, increasing to fBNC = 30+3−4 per cent for haloes with 13.3 ≤ log (M/h−1 M⊙) < 13.75 and fBNC = 43+2−3 per cent in the most massive haloes with log (M/h−1 M⊙) ≥ 13.75. As in Section 5.2, the best-fitting values and uncertainties are determined from the median and the 16 and 84 percentiles of the PKS(fBNC)-distributions.
Before proceeding with a discussion regarding the implications of these findings, we briefly address the possibility that both  and
and  are true; BHGs are not central galaxies in a non-zero fraction fBNC of all haloes, and central galaxies have a non-zero value for their velocity bias bvel. Using mock group catalogues with non-zero values for both fBNC and bvel we estimate that the data can accommodate a small amount of velocity bias bvel≲ 0.2. We emphasize, though, that the data do not require a non-zero bvel.
are true; BHGs are not central galaxies in a non-zero fraction fBNC of all haloes, and central galaxies have a non-zero value for their velocity bias bvel. Using mock group catalogues with non-zero values for both fBNC and bvel we estimate that the data can accommodate a small amount of velocity bias bvel≲ 0.2. We emphasize, though, that the data do not require a non-zero bvel.
5.3 The impact of substructure
In the tests described above, we have always assumed that satellite galaxies follow a smooth, spherically symmetric, number density distribution, and we assigned the satellites’ peculiar velocities within its host halo under the assumption that the corresponding potential is smooth. This ignores the fact that dark matter haloes are believed to have a wealth of substructure (see Giocoli et al. 2010, and references therein; on substructure in galaxy clusters, see Richard et al. 2010). Satellite galaxies are believed to be associated with these substructures. Our treatment of the spatial and kinematic properties of satellite galaxies is only consistent with this concept of substructure if: (i) each subhalo hosts at the most one satellite, and (ii) the positions and velocities of subhaloes are not correlated with those of other subhaloes. In reality, neither of these criteria is likely to be met. Massive subhaloes are likely to host multiple satellites, and the large-scale filamentary structure is believed to introduce (weakly) correlated directions of infall for subhaloes (e.g. Vitvitska et al. 2002; Aubert, Pichon & Colombi 2004; White, Cohn & Smit 2010). Both of these effects result in correlations among the positions and/or velocities of different satellite galaxies within the same host halo, which is likely to have an impact on the  and
and  statistics.
statistics.
In order to have a crude estimate of the impact of substructure, we proceed as follows. We start by populating 1000 (virtual) dark matter haloes, all with M = 3 × 1014h−1 M⊙, with galaxies using the same CLF model as in Section 4. Similar to the  mocks, we assure that the central galaxy is always the brightest galaxy in the halo, and we position it at rest at the centre of the halo. We then compute
mocks, we assure that the central galaxy is always the brightest galaxy in the halo, and we position it at rest at the centre of the halo. We then compute  and
and  for each of these haloes. The black, solid lines in Fig. 8 indicate the corresponding
for each of these haloes. The black, solid lines in Fig. 8 indicate the corresponding  and
and  . Next we repeat this exercise, but now, in each halo, a fraction fsub of all satellites is ‘clumped’ together in a single substructure. We model this substructure as a halo of mass m=fsubM (i.e. we assign the galaxies in this subhalo phase-space coordinates in exactly the same way as we would if the halo was a ‘host’ halo of the same mass). The phase-space coordinates of the centre of the subhalo are drawn in the same way as the phase-space coordinates of the satellites that are not in a substructure. The long-dashed green curves, short-dashed blue curves and dotted red curves in Fig. 8 show the
. Next we repeat this exercise, but now, in each halo, a fraction fsub of all satellites is ‘clumped’ together in a single substructure. We model this substructure as a halo of mass m=fsubM (i.e. we assign the galaxies in this subhalo phase-space coordinates in exactly the same way as we would if the halo was a ‘host’ halo of the same mass). The phase-space coordinates of the centre of the subhalo are drawn in the same way as the phase-space coordinates of the satellites that are not in a substructure. The long-dashed green curves, short-dashed blue curves and dotted red curves in Fig. 8 show the  and
and  thus obtained for fsub = 1/3, 1/5 and 1/10, respectively. A comparison with the no-substructure case (black, solid line) shows that substructure significantly affects the
thus obtained for fsub = 1/3, 1/5 and 1/10, respectively. A comparison with the no-substructure case (black, solid line) shows that substructure significantly affects the  and
and  -distributions, and hence our conclusions, if all dark matter haloes have a most massive substructure whose mass is msub≳ 0.1M. In particular, if many haloes contain substantial substructure, then an alternative explanation for the fact that our fiducial model (which follows the CGP) does not match the data may be that the phase-space coordinates of satellite galaxies within the same dark matter host halo are correlated. In that case the fractions fBNC obtained in Section 5.2 will be significantly overestimated.
-distributions, and hence our conclusions, if all dark matter haloes have a most massive substructure whose mass is msub≳ 0.1M. In particular, if many haloes contain substantial substructure, then an alternative explanation for the fact that our fiducial model (which follows the CGP) does not match the data may be that the phase-space coordinates of satellite galaxies within the same dark matter host halo are correlated. In that case the fractions fBNC obtained in Section 5.2 will be significantly overestimated.
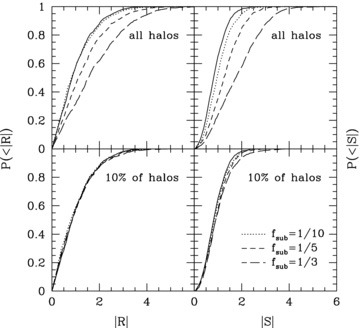
Cumulative distributions of  (left-hand panels) and
(left-hand panels) and  (right-hand panels) of 1000 mock haloes with M = 3 × 1014h−1 M⊙ populated with galaxies. Black solid curves indicate the distributions for haloes with no substructure, while the long-dashed green curves, short-dashed blue curves and dotted red curves indicate the distributions for fsub = 1/3, 1/5 and 1/10, respectively. Results are shown for the case in which all haloes have substructure (upper panels) and 10 per cent of the haloes have substructure (lower panels).
(right-hand panels) of 1000 mock haloes with M = 3 × 1014h−1 M⊙ populated with galaxies. Black solid curves indicate the distributions for haloes with no substructure, while the long-dashed green curves, short-dashed blue curves and dotted red curves indicate the distributions for fsub = 1/3, 1/5 and 1/10, respectively. Results are shown for the case in which all haloes have substructure (upper panels) and 10 per cent of the haloes have substructure (lower panels).
However, using the subhalo mass functions of Giocoli et al. (2010), we estimate that only ∼8 per cent of host haloes with M = 3 × 1014h−1 M⊙ have a most massive subhalo with fsub=m/M≥ 0.1, while only ∼0.7 per cent have a most massive subhalo with m/M≥ 0.3. Based on these estimates, and on the tests described above, we argue that ignoring substructure when populating haloes with (satellite) galaxies does not have a significant impact on the  and
and  statistics, though more sophisticated tests are required to confirm this. Therefore, we conservatively argue that the fBNC fractions obtained in this paper have to be regarded as upper limits.
statistics, though more sophisticated tests are required to confirm this. Therefore, we conservatively argue that the fBNC fractions obtained in this paper have to be regarded as upper limits.
6 DISCUSSION
The results presented in the previous section suggest that in as much as 25 to 40 per cent of all haloes, the brightest galaxy is a satellite rather than a central galaxy. In order to put these numbers in perspective, we compare them to predictions from halo occupation statistics (Section 6.1) and from two semi-analytical models (SAMs) of galaxy formation (Section 6.2). We also investigate the impact of non-zero fBNC(M) on the halo masses inferred using satellite kinematics (Section 6.3).
6.1 Comparison with halo occupation statistics
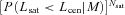 . Hence, we obtain that
. Hence, we obtain that 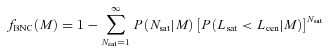
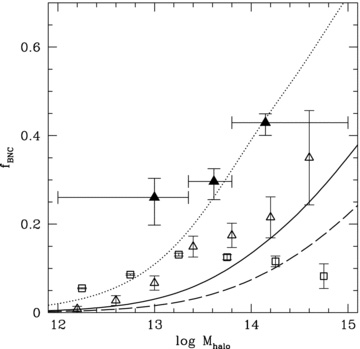
Probability that the most luminous satellite galaxy is brighter than the central galaxy in a halo, as a function of halo mass (equation 23). Result is shown for three slopes in the satellite CLF (equation 9): s = 1 (dotted curve), the fiducial s = 2 (solid curve) and s = 3 (dashed curve). For comparison, the fBNC(Mhalo) result from Fig. 7 (solid triangle points) is also shown. The predictions from the morgana semi-analytic model (open triangles) and Croton et al. (2006) semi-analytic model (open squares) are also shown, with Poisson errors.
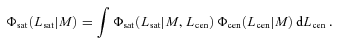
Of course, it is also possible that the discrepancy reflects an actual failure of the CLF. One possible modification, which will have little impact on the luminosity function, clustering, galaxy–galaxy lensing and mock group catalogues is a modification in the shape of Φsat(L|M) (equation 9) at the bright end. As mentioned in Section 4.1, C09 adopted a functional form for which Φsat(L|M) ∝ exp [− (L/L*sat)s] at the bright end, with s = 2. The exact value of s, though, is poorly constrained by the data, but has a significant impact on fBNC(M). This is illustrated by the dotted and dashed curves in Fig. 9, which correspond to s = 1 and s = 3, respectively. Clearly, decreasing s increases the expectation value for the luminosity of the brightest satellite, and hence the fraction of haloes for which the central galaxy is not the BHG. For s = 1 the CLF ‘predicts’ a fBNC(M) in good agreement with the data, but only for M≳ 5 × 1013h−1 M⊙. For less massive haloes, the value of fBNC inferred from the SDSS group catalogue is still too high compared to the CLF prediction, but only by about 2σ.
Another parameter that has a significant impact on fBNC(M) is the ratio Q≡L*sat/Lcen. Motivated by the CLF inferred from the SDSS group catalogue by Yang et al. (2008), C09 adopted Q = 0.562, with no dependence on halo mass. However, Hansen et al. (2009), using the maxBCG group catalogue of Koester et al. (2007), found that Q depends on halo mass and may be as small as ∼0.15 for M∼ 1014h−1 M⊙. In order for the CLF to yield fBNC(M) in rough agreement with our findings, though, we need a value of Q that is larger than 0.562 (i.e. for s = 2 we require Q∼ 0.7). These results warrant a more thorough investigation into the exact values of s and Q as function of halo mass.
Finally, we have verified that the CLF predictions for fBNC(M) do not depend significantly on our choice for the lower luminosity cut-off, Lmin.
6.2 Comparison with semi-analytical models
We now compare our results to the predictions of two SAMs of galaxy formation; the MORGANA model of Monaco, Fontanot & Taffoni (2007), as updated by Lo Faro et al. (2009), and the SAM of Croton et al. (2006).
Both SAMs adopt flat ΛCDM cosmologies, albeit with slightly different values for the cosmological parameters.4 Although both SAMs include treatments of cooling, star formation, feedback from supernovae and active galactic nuclei, mergers, starbursts and disc instabilities, the actual implementations of these physical processes are substantially different (see the original papers for details). Yet, as shown in Fig. 9 (open symbols), they predict fairly similar values for fBNC(M).5 In qualitative agreement with the data, both SAMs predict that fBNC increases with halo mass. In addition, from studying the satellite BHGs in the MORGANA model, we find that the majority of the more massive satellites represent a recently (since z∼ 0.2) accreted population, in most cases linked to the last major merger experienced by the host halo. In other words, infalling massive satellites could be a contributing cause of a non-zero fBNC.
As with the halo occupation statistics, the predictions of both models are significantly lower than the data. In both SAMs, satellite galaxies are ‘strangulated’ after being accreted by their host galaxies, so that they do not participate in the cooling flow of their parent halo. However, it has been pointed out that the standard, instantaneous implementation of this strangulation causes an overquenching of satellite galaxies (e.g. Baldry et al. 2006; Weinmann et al. 2006; Kimm et al. 2009). It has been suggested that this overquenching problem can be avoided by adopting a longer time-scale for strangulation (e.g. Kang & van den Bosch 2008; Font et al. 2008; Weinmann et al. 2009). This is likely to allow satellite galaxies to continue forming stars for some period, which will increase their stellar mass, and thus also fBNC. The effect, though, is likely to be small. Another effect that may cause the SAMs to underpredict fBNC is the fact that they often adopt dynamical friction time-scales that are too short (Boylan-Kolchin, Ma & Quataert 2008; Wetzel & White 2010). This results in (massive) satellites being accreted too rapidly, and hence in an underestimate of fBNC. Finally, the models do not take proper account of stellar mass stripping due to tidal forces, which will make satellites less massive. As emphasized in a number of recent papers, this tidal stripping of satellite galaxies is an important ingredient of galaxy formation (Monaco et al. 2006; White et al. 2007; Conroy, Ho & White 2007; Conroy, Wechsler & Kravtsov 2007; Kang & van den Bosch 2008 ; Yang, Mo & van den Bosch 2009b; Pasquali et al. 2010). It remains to be seen to what extent these additions and/or modifications of the SAMs impact fBNC(M). For the moment, we conclude that the fBNC(M) inferred from our analysis of SDSS galaxy groups is uncomfortably high compared to predictions from both halo occupation statistics and SAMs of galaxy formation.
6.3 Implication for satellite kinematics
Studies that attempt to infer the masses of dark matter haloes using the kinematics of satellite galaxies always assume that the CGP is valid (e.g. Zaritsky et al. 1993; McKay et al. 2002; van den Bosch et al. 2004; More et al. 2009). Since a typical central only has a few satellites, one normally stacks many centrals together in order to obtain sufficient signal-to-noise ratio to measure a reliable satellite velocity dispersion, σsat. With sufficiently large galaxy redshift surveys, one can measure σsat as a function of the luminosity (or stellar mass) of the central galaxies (i.e. one stacks centrals in narrow bins in luminosity or stellar mass).
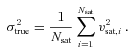
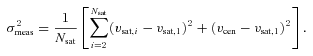
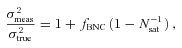
 . Since the inferred halo mass M∝σ3sat, this implies that the mass of the halo will be overestimated by a factor (1 +fBNC)3/2. Note that equation (27) is strictly valid only for stacks of systems that all have the same number of satellites. In reality, however, there will be scatter in the number of satellites per host in the stack. In what follows we assume that we do not make a large error if we adopt equation (27) but with Nsat replaced by the average number of satellites per central, 〈Nsat〉.
. Since the inferred halo mass M∝σ3sat, this implies that the mass of the halo will be overestimated by a factor (1 +fBNC)3/2. Note that equation (27) is strictly valid only for stacks of systems that all have the same number of satellites. In reality, however, there will be scatter in the number of satellites per host in the stack. In what follows we assume that we do not make a large error if we adopt equation (27) but with Nsat replaced by the average number of satellites per central, 〈Nsat〉.For relatively faint centrals, 〈Nsat〉≃ 1, and σmeas≃σtrue independent of the value of fBNC. However, at the bright end 〈Nsat〉 becomes substantially larger than unity, and a non-zero fBNC may cause a significant overestimate of the true σsat. For example, in their analysis of satellite kinematics, More et al. (2009) have 〈Nsat〉∼ 10 for their brightest host bins. If fBNC for these bins is comparable to fBNC(M) at the massive end (i.e. fBNC∼ 0.4), their inferred halo masses around bright host galaxies will be overestimated by a factor of ∼1.6.
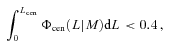
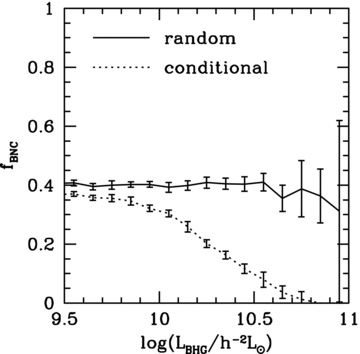
Fraction fBNC of haloes in which the brightest galaxy is not the central one, as a function of the luminosity of the BHG. The solid line shows fBNC(LBHG) for the ‘random’ mocks, and the dotted line shows the fraction for the ‘conditional’ mocks, in which whether a halo has a satellite brighter than the central is conditional on the luminosity of the central galaxy. The luminosities correspond to r-band absolute magnitudes, such that log L = 9.5 corresponds to Mr≈−19, and log L = 10.3 to Mr≈−21, etc.
We thus conclude that a proper assessment of the impact of a non-zero fBNC(M) on the halo masses inferred from satellite kinematics requires an independent assessment of the fraction fBNC as function of the luminosities of the host galaxies.
7 CONCLUSIONS
It is generally assumed that the central galaxy in a dark matter halo, that is the galaxy with the lowest specific potential energy, is also the BHG and that it resides at rest at the centre of the dark matter potential well. This CGP is an essential assumption made in various fields of astronomical research (e.g. satellite kinematics, gravitational lensing, both weak and strong, halo occupation modelling).
In this paper, we have used a large galaxy group catalogue, constructed from the SDSS DR4 by Y07, in order to test the validity of the CGP. For each group we compute two statistics,  and
and  , which quantify the offsets of the line-of-sight velocities and projected positions of brightest group galaxies relative to the other group members. By comparing the cumulative distributions of
, which quantify the offsets of the line-of-sight velocities and projected positions of brightest group galaxies relative to the other group members. By comparing the cumulative distributions of  and
and  to those obtained from detailed mock group catalogues, we have tested the null hypothesis,
to those obtained from detailed mock group catalogues, we have tested the null hypothesis,  , that the CGP is correct; hypothesis
, that the CGP is correct; hypothesis  , according to which central galaxies are BHGs but have a non-zero velocity with respect to the halo centre, parametrized by a non-zero velocity bias, bvel; and hypothesis
, according to which central galaxies are BHGs but have a non-zero velocity with respect to the halo centre, parametrized by a non-zero velocity bias, bvel; and hypothesis  , according to which central galaxies reside at rest at the centre of the halo’s potential well, but are not the BHGs in a fraction fBNC of all haloes.
, according to which central galaxies reside at rest at the centre of the halo’s potential well, but are not the BHGs in a fraction fBNC of all haloes.
In agreement with vdB05, who only used the  statistic, we show that the null hypothesis is strongly ruled out. However, contrary to vdB05, who argued that the data are consistent with a non-zero bvel, we show that
statistic, we show that the null hypothesis is strongly ruled out. However, contrary to vdB05, who argued that the data are consistent with a non-zero bvel, we show that  fails to simultaneously match the
fails to simultaneously match the  and
and  -distributions.7 Rather, we have shown that the data are consistent with hypothesis
-distributions.7 Rather, we have shown that the data are consistent with hypothesis  , indicating that BHGs are not central galaxies in a non-negligible fraction of all haloes; in particular, we find that fBNC increases from ∼0.25 in low-mass haloes (1012h−1 M⊙≤M≲ 2 × 1013h−1 M⊙) to ∼0.4 in massive haloes (M≳ 5 × 1013h−1 M⊙).
, indicating that BHGs are not central galaxies in a non-negligible fraction of all haloes; in particular, we find that fBNC increases from ∼0.25 in low-mass haloes (1012h−1 M⊙≤M≲ 2 × 1013h−1 M⊙) to ∼0.4 in massive haloes (M≳ 5 × 1013h−1 M⊙).
Considering combined models, in which BHGs are not central galaxies in a non-zero fraction fBNC of all haloes, and central galaxies have a non-zero value for their velocity bias bvel, we find that the data can at most accommodate a small amount of velocity bias (bvel≲ 0.2). We emphasize, though, that a non-zero velocity bias is not required by the data (see vdB05 for a discussion of possible physical explanations for a non-zero bvel).
Our main result is that the fraction fBNC is significant and increases with halo mass. Since some authors have assumed that the most luminous (or most massive) galaxy in a system is the central galaxy, our result that fBNC is somewhat large in galaxy groups and larger (43+2−3 per cent) in more massive clusters may seem surprising. Nevertheless, our results are consistent with other studies. For example, von der Linden et al. (2007) find that in 343 of their 625 clusters (≈55 per cent), the identified BCG is not the ‘mean’ galaxy (which lies at the centre of the cluster’s density field). Coziol et al. (2009) find that in about half of their 452 clusters, the BCGs have a median peculiar velocity greater than one third of their clusters’ velocity dispersion. Finally, in the Local Group, although the MW and Andromeda both have their own systems of satellites, they could be considered part of a single group, in which Andromeda would be identified as the BHG (van den Bergh 1999). The two galaxies are expected to eventually merge, although neither is clearly the ‘central’ galaxy.
In order to put our constraints on fBNC(M) in perspective, we have compared them to predictions from SAMs for galaxy formation and from halo occupation statistics. Both the SAM of Croton et al. (2006) and that of Lo Faro et al. (2009) predict 0.1 ≲fBNC≲ 0.2 in the halo mass range of 1013h−1≲M≲ 1015h−1 M⊙, significantly lower than the fBNC(M) inferred here from our SDSS galaxy group catalogue.
We can also use the CLF model of C09 to predict fBNC(M), if we assume that the luminosity of a satellite galaxy is independent of the luminosity of its corresponding central. Although the C09 halo occupation model accurately matches the SDSS r-band luminosity function of Blanton et al. (2003), the projected two-point correlation functions of Wang et al. (2007) and the galaxy–galaxy lensing data of Mandelbaum et al. (2006), this model also predicts a fBNC(M) that is far too low. We have shown that one can increase the predicted fBNC(M) using some small modifications of the CLF, but it remains to be seen how these modifications impact the clustering and lensing predictions. For completeness, we emphasize that halo occupation models based on the abundance-matching method (e.g. Vale & Ostriker 2004; Conroy, Wechsler & Kravtsov 2006; Conroy et al. 2007; Shankar et al. 2006; Guo et al. 2010; Moster et al. 2010) ‘predict’ that fBNC = 0, by construction, unless they assume a non-zero scatter in the relation between central galaxy luminosity and halo mass. Typically a larger amount of scatter will imply a larger fBNC. It remains to be seen whether the amount of scatter required to match the fBNC(M) inferred here is consistent with independent constraints, such as those obtained from satellite kinematics (More et al. 2009). All in all, we conclude that the constraints on fBNC(M) obtained in this paper are uncomfortably high compared to predictions from galaxy formation models and halo occupation statistics. One possible explanation may be that dark matter haloes have substructure, something that we have ignored in our analysis. Although simple tests suggest that the correlations in the phase-space parameters of satellite galaxies due to substructure are not strong enough to significantly impact our conclusions, we caution that more detailed studies are required to confirm this.
Our results have important implications for various areas in astrophysics. In particular, we have shown that a non-zero fBNC may cause an overestimate of halo masses inferred from satellite kinematics. Although the effect is expected to be negligible for faint host galaxies, because they typically only have of the order of one satellite per host, the overestimate can be significant at the bright end. The exact impact, though, depends on the fraction fBNC as function of the host luminosity, which may be very different from that as a function of halo mass. For example, if BHGs are not centrals in the fraction fBNC(M) of haloes of mass M that host the faintest centrals, then fBNC(L) drops towards zero at the bright end, and the impact on satellite kinematics is negligible.
Additional methods and analyses that may be affected by a non-zero fBNC are the following.
The inference of halo masses from weak gravitational lensing. Similar to satellite kinematics, weak lensing studies often rely on stacking the lensing signals of many clusters and groups binned by mass-correlated observables such as richness and luminosity. When interpreting such data, it is generally assumed that BHGs coincide with the centres of the dark matter haloes (e.g. Mandelbaum et al. 2006; Johnston et al. 2007; Sheldon et al. 2009a,b; Corless & King 2009; C09). Since satellite galaxies yield a different lensing signal than centrals, at least on small to intermediate scales (see e.g. Yang et al. 2006), a non-zero fBNC may have a significant impact on the lensing signal (Johnston et al. 2007), by resulting in underestimates of the richnesses and lensing profiles, for example. C09 used the CLF described in Section 4.1 to model the galaxy–galaxy lensing signal of Mandelbaum et al. (2006). As shown in Section 6.1, this CLF predicts fBNC(M) significantly lower than inferred here. It remains to be seen to what extent this may affect their interpretation of the lensing data.
Analyses of the power spectrum of luminous red galaxies (Tegmark et al. 2006; Reid et al. 2010), which can be used to constrain cosmological parameters. In tests with mock galaxy catalogues, Reid et al. (2010) find that a fraction fBNC of 0.2–0.4 results in an angle-averaged LRG power spectrum that is damped by 2–4 per cent on scales of k∼ 0.1 h Mpc−1, and the effect is larger at larger k. However, when analysing the observed power spectrum with these mock catalogues, the effect of fBNC on the recovered cosmological parameters is relatively small.
Measurements of the radial number density distribution of satellite galaxies, nsat(r|M), in haloes of mass M. Several studies that have measured nsat(r|M) using groups and clusters have assumed that the halo centre coincides with the location of the BHG (e.g. Carlberg, Yee & Ellingson 1997; Collister & Lahav 2005; Hansen et al. 2005; Yang et al. 2005b). If, instead, the BHG is a satellite galaxy, this will result in an underestimate of the concentration of nsat(r). Hence, a non-zero fBNC(M) may cast doubt on the claim, made by several of these studies, that satellite galaxies are less centrally concentrated than the dark matter. On the other hand, Lin et al. (2004) used the centre of the X-ray emission as the centre of the dark matter halo, rather than the location of the BHG, and came to a similar conclusion.
Comparisons of the properties of central and satellite galaxies. A number of recent studies have used galaxy group catalogues to split the galaxy population into centrals and satellites, and to compare their properties (e.g. Weinmann et al. 2006, 2009; Skibba et al. 2007; van den Bosch et al. 2008; Pasquali et al. 2009, 2010; Hansen et al. 2009; Kimm et al. 2009; Skibba 2009; Guo et al. 2009). Since all of these studies have assumed the brightest group galaxy to be the central galaxy, they are likely to have underestimated the true differences (i.e. a non-zero fBNC blurs the actual differences between centrals and satellites).
These redshifts are taken from the 2dFGRS (Colless et al. 2001), IRAS PSCz (Saunders et al. 2000) or RC3 (de Vaucouleurs et al. 1991). See Blanton et al. (2005) for details.
Using the additional criterion that the group masses in Samples II and III are within 0.3 dex of each other excluded another 7 per cent, but yielded results that were indistinguishable from those based on our fiducial sample.
The choice for this particular probability distribution, which corresponds to a Hernquist (1990) profile, is not motivated by any physical considerations, other than the fact that it is well behaved, both at r = 0 and at r→∞. Our results do not depend significantly on the exact shape of this probability distribution.
We do not believe that these small differences will have a significant impact on the predictions of fBNC(M).
As in our analysis of SDSS galaxy groups, the predictions of fBNC(M) from the SAMs are the fractions of haloes in which a satellite galaxy is the most luminous galaxy. The SAMs’ predictions are almost exactly the same for the fractions of haloes in which a satellite is the most massive galaxy (in terms of stellar mass).
This statement ignores the fact that a non-zero fBNC also impacts the interpretation of the stacking parameter (i.e. the luminosity of the alleged ‘centrals’) and may result in more interlopers.
Since vdB05 did not consider the spatial offsets (i.e. the  statistic), they were unable to notice this problem for the
statistic), they were unable to notice this problem for the  hypothesis.
hypothesis.
We thank Darren Croton for making the results from his SAM available to us in electronic format, and Eric Bell, Kris Blindert, Romeel Davé, Xi Kang, Tod Lauer, Alexie Leauthaud, Pierluigi Monaco, Beth Reid, Maria Pereira, Simone Weinmann and Ann Zabludoff for valuable discussions about our results and their implications. Some of the calculations were carried out on the PIA cluster of the Max-Planck-Institute für Astronomie at the Rechenzentrum Garching.
REFERENCES



