Gas dynamics of the central few parsec region of NGC 1068 fuelled by the evolving nuclear star cluster

Abstract

1 INTRODUCTION

Often challenged, but on the whole still valid, the Unified Scheme of Active Galactic Nuclei (Antonucci 1993; Urry & Padovani 1995) constitutes the standard paradigm for the composition of active galactic nuclei (AGN). Their highly energetic central activity is powered by accretion on to a supermassive black hole (10⁶– 10¹⁰ M_⊙; e.g. Shankar et al. 2004). Seeing the central engine or not in this scheme is solely determined by the orientation of a ring-like dust distribution around the galaxy centre, the so-called molecular torus. It constitutes not only the source of obscuration, but also the gas reservoir for feeding the hot accretion disc. Viewed face-on, most of the UV–optical continuum emission of the accretion disc (the so-called big blue bump) is visible in the spectral energy distribution (SED), whereas it is blocked by the dust in the case of an edge-on view. The absorbed energy is re-emitted in the infrared wavelength regime, giving rise to a pronounced peak in the SED of many AGN (Sanders et al. 1989). This scenario enables the unification of two observed classes of galaxies, namely type 1 (direct view on to the central engine) and type 2 sources (through dust). It was first proposed by Antonucci & Miller (1985), after broad emission lines– arising from fast moving gas close to the central black hole (the so-called broad-line region) – have been detected in polarized light in the Seyfert 2 galaxy NGC 1068. These photons are scattered into the line of sight and polarized by dust and free electrons above the torus opening. In unpolarized light, type 2 sources only exhibit narrow emission lines, which originate from slower gas motions further away from the black hole, in the so-called narrow-line region, stretching beyond the opening of the torus funnel.

Resolving the dusty torus was for the first time possible with the advent of the mid-infrared interferometer (MIDI) at the VLTI Very Large Telescope Interferometer (VLTI) by combining the light of two of the 8 m class VLT telescopes. This revealed geometrically thick dust structures on parsec scale in a large sample of nearby AGN (Tristram et al. 2009), but with a large variety of torus properties. Exhaustive observations of both the nearby galaxy NGC 1068 (Jaffe et al. 2004; Poncelet, Perrin & Sol 2006; Raban et al. 2009) and the Circinus galaxy (Tristram et al. 2007) found the dust to be distributed in a complex structure. The brightness distribution could be disentangled into two components: a geometrically thin disc-like structure on sub-parsec to parsec scale and a fluffy or filamentary torus-like distribution surrounding it. For the case of the Circinus galaxy, the interferometric signal even showed fine structure. This was interpreted to result from a clumpy large-scale component, which puts severe constraints on theoretical models. Not being capable of direct imaging, radiative transfer models are needed for a careful data interpretation and modelling.

From the theoretical perspective, basically three questions are of current interest:

1. What is the structure of tori?

2. What are the basic shaping processes and how do they sustain the scaleheight of the torus against gravity?

3. How are tori built up and how do they evolve and feed gas on to the central engine?

Modelling so far concentrated mainly on several aspects of the first two questions. A large number of continuous torus models have been used in radiative transfer calculations in order to compare simulated SEDs with high-resolution observations in the infrared (e.g. Pier & Krolik 1992, 1993; Granato & Danese 1994; van Bemmel & Dullemond 2003; Schartmann et al. 2005; Fritz, Franceschini & Hatziminaoglou 2006), constraining physical parameters of tori in specific galaxies or whole samples of AGN tori, such as the shape, size, luminosity etc. The most up-to-date simulations concentrate on clumpiness of the absorbing dust (e.g. Nenkova, Ivezić & Elitzur 2002; Hönig et al. 2006; Nenkova et al. 2008a,b; Schartmann et al. 2008), following a suggestion by Krolik & Begelman (1988), which helps to prolong the time-scale for the destruction of dust impacted by hot surrounding gas. Simultaneous agreement with high-resolution spectral (e.g. NACO or Spitzer) as well as interferometric data (MIDI) gives us a good idea of the possible structural properties of these tori.

Concerning the second question of the structuring agent and the stability of the vertical scaleheight against gravity, several modelling attempts have been put forward: the torus was claimed to be made up of clumps with supersonic random velocities, which are sustained by transferring orbital shear energy with the help of sufficiently elastic collisions between the clumps (e.g. Krolik & Begelman 1988; Beckert & Duschl 2004). Starburst-driven AGN tori were investigated with the help of hydrodynamical simulations of the interstellar medium (ISM), concentrating on two effects: (i) a large rate of core-collapse supernova explosions (following in situ star formation in the densest region) in a rotationally supported thin disc (Wada & Norman 2002; Wada, Papadopoulos & Spaans 2009) and (ii) feedback due to strong winds of young and massive stars (Nayakshin & Cuadra 2007). Alternative scenarios replace the torus itself by a hydromagnetic disc wind, in which dusty clouds are embedded and produce the necessary obscuration differences between type 1 and type 2 objects (Königl & Kartje 1994; Elitzur & Shlosman 2006), or by nuclear gas discs, which are warped due to an axisymmetric gravitational potential generated by discs of young stars (e.g. Nayakshin 2005). Pier & Krolik (1992) claim the importance of infrared radiation pressure in the sub-parsec to parsec-scale part of the torus or nuclear disc component. This scenario was elaborated in Krolik (2007). With the help of analytical calculations, they find good comparison of gas column densities to observations for reasonable intrinsic AGN luminosities. For a more detailed discussion of available models, see also Krolik (2007).

Despite these great successes in pinning down several aspects of physical processes in the vicinity1 of black holes, a conclusive global physical model for the build-up and evolution of gas and dust structures in the nuclear region of active galaxies as well as the origin of the dust content is still missing. The main reasons are the complexity of the physical processes, which are thought to happen in these regions, and their scalelengths, which make them invisible for direct observations in most wavebands. However, a scenario of co-evolution of nuclear starbursts and tori, based on the models of Vollmer, Beckert & Duschl (2004), Beckert & Duschl (2004) and observations of Davies et al. (2007), was suggested by Vollmer, Beckert & Davies (2008). An external mass accretion rate causes three phases as follows. (i) Massive gas infall leads to a turbulent, stellar wind-driven Q≈ 1 disc, where Q is the Toomre stability parameter. (ii) Subsequent supernova Type II explosions remove the intercloud medium, and a geometrically thick collisional clumpy disc remains. In the final phase (iii) with a low mass accretion rate, the torus gets geometrically thin and transparent. Hydrodynamical simulations of the effects of stellar feedback from a young nuclear star cluster as ubiquitously found in Seyfert galaxies (Davies et al. 2007) were investigated in an exploratory study by Schartmann et al. (2009). Turbulent mass input in combination with supernova feedback and an optically thin cooling curve yield a two-component structure, made up of a geometrically thick filamentary torus component on tens of parsec scale and a geometrically thin, but turbulent disc structure. Subsequent continuum dust radiative transfer modelling results in a good comparison with available observational data sets. Given the success of these simulations, this paper is a follow-up, concentrating more on the long-term behaviour of this scenario and justifying our assumptions with the help of further data comparison. This is enabled by treating the innermost part with a simplified effective disc model and by concentrating on the nearby and well-studied Seyfert 2 galaxy NGC 1068.

After shortly reviewing the underlying global physical model and its numerical realization, the resulting state of the gas is discussed briefly. The gas inflow of these simulations is used in a subsequent effective treatment of the resulting gas surface density of the inner disc structure for a long-term evolution study. This enables us to link the large- and the small-scale structure in these objects. The comparison of feeding parameters as well as structural parameters with observations and previous modelling is done to assess that this model is a viable option and able to explain the mass assembly in the disc, the disc properties as well as the feeding of the central supermassive black hole. Section 4 provides a critical discussion before we summarize our results in Section 5.

2 LARGE-SCALE HYDRODYNAMICAL TORUS MODEL

2.1 Model and numerical realization

In recent years, there has been growing evidence for a direct link between galactic nuclear activity and star formation on the parsec scale (Davies et al. 2007). Massive nuclear star clusters (≈10⁸ M_⊙), as ubiquitously found in Seyfert galaxies, significantly impact their environment during many stages of the evolution of their stellar population. Analytical arguments based on energy considerations (Davies et al. 2007) as well as numerical simulations (Schartmann et al. 2009) reveal that during the first phase of the evolution of the most massive stars towards core collapse supernova, most of the gas will be expelled from the region of the stellar cluster. A less violent phase follows, where the mass input is dominated by low-velocity winds during the asymptotic giant branch (AGB) phase, after approximately 50 Myr. At roughly this time, Davies et al. (2007) observationally find a switch-on process of the active nucleus, interpreted as the beginning of accretion on to the black hole of these low-velocity stellar ejecta. This is the time when our simulations start. The initial condition comprises a very low density, equilibrium distribution of matter for the given gravitational potential, which is soon washed out and is insignificant for further evolution. The injection of mass into the model space in our simulations is mimicking the process of slowly expanding planetary nebula shells: a mass of 0.5 M_⊙ is evenly distributed within a radius of 1 pc together with the equivalent of the kinetic energy of an expanding shell of 30 km s⁻¹ in the form of thermal energy and with a bulk velocity comprising the (constant) random velocity and the rotational velocity (described by a power law) of the underlying stellar distribution. The nuclear star cluster in NGC 1068 has a velocity dispersion of roughly 100 km s⁻¹ (Davies et al. 2007). Therefore, random motions are an important stabilizing mechanism and the bulk rotation must be sub-Keplerian. For the parameters of our standard model, the rotation velocity drops from approximately 70 to about 30 km s⁻¹ in the tens of parsec distance range, which corresponds well to the values derived from the SINFONI observations, which scatter around roughly 45 km s⁻¹ (Davies et al. 2007). The mass input rate is chosen according to the formalism described in Jungwiert, Combes & Palouš (2001). Gas cooling is calculated with the help of an effective cooling curve with solar metallicity, prepared with the help of the cloudy code (Plewa 1995; see also fig. 1 in Schartmann et al. 2009). The hydrodynamical evolution is then followed within the fixed gravitational potential of the nuclear stellar cluster, modelled with the help of a Plummer distribution of stars and the Newtonian potential of a central supermassive black hole with an influence radius of pc. We use outflow boundary conditions in radial as well as polar direction, not allowing for inflow. Periodic boundary conditions are applied in the azimuthal direction, where we only model a 90° fraction of the whole model space.

The hydrodynamics themselves are treated with the help of the Pluto code (Mignone et al. 2007). Being a fully Message Passing Interface (MPI)-parallelized high-resolution shock capturing scheme with a large variety of Riemann solvers, we consider it perfectly suited to treat our physical set-up. For the calculations shown in this paper, we used the two-shock Riemann solver together with a linear reconstruction method and directional splitting on a three-dimensional spherical coordinate system.

A more detailed description of the underlying physical model can be found in Schartmann et al. (2009). However, note that due to large uncertainties in the delay times and the rates of supernova Type Ia explosions (see the discussion in Schartmann et al. 2009), in this paper we solely concentrate on the effect of turbulent mass input of the nuclear star cluster. The basic physical parameters of our simulations are summarized in Table 1. They are chosen to represent the nearby – and therefore well-studied – Seyfert 2 galaxy NGC 1068.

Table 1

Open in new tab

Parameters of our standard hydro model.

Parameter	Value	Reference
MBH	8 × 106 M⊙	L03
M*	2.2 × 108 M⊙	D07
Minigas	1.0 × 102 M⊙
Rc	25 pc	G03
RT	5 pc
Rin	0.2 pc
Rout	50 pc
σ*	100 km s−1	D07
β	0.5
Tini	2.0 × 106 K
	9.1 × 10−10 M⊙/(yr M⊙)	J01
MPN	0.5 M⊙
Γ	5/3

Parameter	Value	Reference
MBH	8 × 106 M⊙	L03
M*	2.2 × 108 M⊙	D07
Minigas	1.0 × 102 M⊙
Rc	25 pc	G03
RT	5 pc
Rin	0.2 pc
Rout	50 pc
σ*	100 km s−1	D07
β	0.5
Tini	2.0 × 106 K
	9.1 × 10−10 M⊙/(yr M⊙)	J01
MPN	0.5 M⊙
Γ	5/3

Note. Mass of the black hole (M_BH), normalization constant of the stellar potential (M_*), initial gas mass (Mⁱⁿⁱ_gas), cluster core radius (R_c), torus radius (R_T), inner radius (R_in), outer radius (R_out), stellar velocity dispersion (σ_*), exponent of the angular momentum distribution of the stars (β), initial gas temperature (T_ini), normalized mass injection rate (⁠⁠), mass of a single injection (M_PN) and adiabatic exponent (Γ). The references are as follows: L03 (Lodato & Bertin 2003), D07 (Davies et al. 2007), G03 (Gallimore & Matthews 2003) and J01 Jungwiert et al. (2001). For a detailed description of the model, we refer to Schartmann et al. (2009).

Table 1

Open in new tab

Parameters of our standard hydro model.

Parameter	Value	Reference
MBH	8 × 106 M⊙	L03
M*	2.2 × 108 M⊙	D07
Minigas	1.0 × 102 M⊙
Rc	25 pc	G03
RT	5 pc
Rin	0.2 pc
Rout	50 pc
σ*	100 km s−1	D07
β	0.5
Tini	2.0 × 106 K
	9.1 × 10−10 M⊙/(yr M⊙)	J01
MPN	0.5 M⊙
Γ	5/3

Parameter	Value	Reference
MBH	8 × 106 M⊙	L03
M*	2.2 × 108 M⊙	D07
Minigas	1.0 × 102 M⊙
Rc	25 pc	G03
RT	5 pc
Rin	0.2 pc
Rout	50 pc
σ*	100 km s−1	D07
β	0.5
Tini	2.0 × 106 K
	9.1 × 10−10 M⊙/(yr M⊙)	J01
MPN	0.5 M⊙
Γ	5/3

Note. Mass of the black hole (M_BH), normalization constant of the stellar potential (M_*), initial gas mass (Mⁱⁿⁱ_gas), cluster core radius (R_c), torus radius (R_T), inner radius (R_in), outer radius (R_out), stellar velocity dispersion (σ_*), exponent of the angular momentum distribution of the stars (β), initial gas temperature (T_ini), normalized mass injection rate (⁠⁠), mass of a single injection (M_PN) and adiabatic exponent (Γ). The references are as follows: L03 (Lodato & Bertin 2003), D07 (Davies et al. 2007), G03 (Gallimore & Matthews 2003) and J01 Jungwiert et al. (2001). For a detailed description of the model, we refer to Schartmann et al. (2009).

2.2 Resulting density and temperature distribution

The resulting temporal evolution of the density distribution within a meridional plane in a three-dimensional high-resolution simulation (n_r= 250, n_θ= 133, n_φ= 70) with the parameters given in Table 1 as well as the same cut through the temperature distribution is shown in Fig. 1. In the first time-steps of the simulation, the density distribution is dominated by the original, injected mass blobs. Due to their large number density within the domain and their high randomly oriented velocities, collisions are very frequent. In our pure hydrodynamical set-up, these collisions are inelastic. Therefore, the blobs dissipate a large fraction of their kinetic energy – which is radiated away due to optically thin line and continuum cooling processes – and many of them merge to form larger complexes. As discussed in Section 2.1, the stars (and therefore also the clouds at the time of injection) possess sub-Keplerian rotation velocities at the tens of parsec distance from the centre. Therefore, the larger gas clouds no longer possess stable orbits, after losing a certain amount of kinetic energy (from the random component mainly), and tend to stream radially inwards, where they find their new equilibrium at their angular momentum barrier, after suffering some angular momentum redistribution on their way towards the centre.

Figure 1

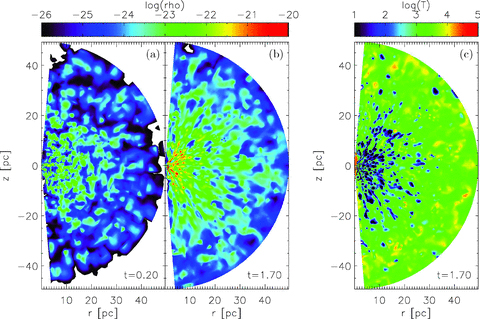
Snapshots of the density distribution in a meridional plane after (a) 0.2 orbits (corresponding to 7 × 10⁴ yr) and (b) 1.7 orbits (approximately 6 × 10⁵ yr). Panel (c) shows the temperature distribution in the same meridional plane after 1.7 orbits.

Open in new tabDownload slide

In the course of the simulation, a two-component structure builds up: a large-scale clumpy or filamentary component (mainly visible in the plots of Fig. 1) and a geometrically thin, but very dense disc on the parsec scale (not visible in the plots).2 Clumps and filaments from the outer component fall on to the thin disc and cause some amount of turbulence, triggering angular momentum transport outwards and accretion3 inwards. The corresponding temperature distribution is depicted in Fig. 1(b) and shows complementary behaviour with respect to the density distribution: the densest blobs are the coldest, whereas the tenuous gas in between is the hottest. This is due to the optically thin gas cooling, which scales quadratically with the density distribution. Fig. 2 shows the innermost part of this simulation in a cut through the equatorial plane. The main disc component in our simulation spans a radial range between roughly 0.5 and 1.1 pc. This is in approximate agreement with a disc found with the help of water maser observations with an extent between 0.65 and 1.1 pc (Greenhill & Gwinn 1997). This shows that the angular momentum distribution of the gas flowing towards the centre seems to be reasonable. Note however that the outer large-scale torus part is in equilibrium already, but mass still assembles in the disc component of our simulations. Although filling most of the volume of the model space, the obscuration properties are mostly given by the inner dense disc component. The outer fluffy torus part alone cannot account for the Seyfert 1/2 dichotomy.

Figure 2

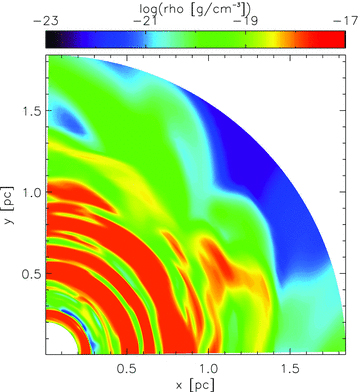
Cut through the innermost part of the equatorial plane of our three-dimensional hydrodynamical standard model after 6 × 10⁵ yr, showing the nuclear disc component.

Open in new tabDownload slide

However, it is still a matter of debate what the actual driver for angular momentum redistribution in such discs is. Due to this missing mechanism and the lack of feedback due to the formation of stars in our simulations, more and more gas from the large-scale torus component assembles in the disc, which prevents us from treating the whole Seyfert activity cycle – which is expected to be of the order of 10⁷– 10⁸ yr– in one simulation. Apart from this, these kinds of computations are very time consuming.

Therefore, we use our three-dimensional hydrodynamical simulations to describe the large-scale structure and attach an axisymmetric viscous disc model at small scales. In this paper, we are especially interested in comparing the resulting neutral hydrogen column densities, disc sizes and accretion rates through our inner boundary to various observations.

3 THE EFFECTIVE NUCLEAR DISC MODEL

3.1 Overall model and numerical realization

The idea behind these simulations is to use the gas supplied by our large-scale three-dimensional Pluto torus simulations, which is driven inwards due to dissipation of turbulent cloud motions in collisions. The resulting dense clumps cool on a small time-scale, acting as a stabilizing mechanism for the clouds and preventing them from smearing out into a continuous medium, which happens as soon as cooling is turned off. Additionally, some amount of angular momentum is transported with the help of these collisions. This inward motion stalls at the respective radius where the angular momentum barrier is reached for the corresponding gas clump and leads to the formation of a nuclear gas disc. Being restricted by the physics we are able to take into account in the large-scale simulations, this disc continuously grows in mass in our simulations, with only a very small amount being transported inwards. Simplified effective disc simulations will help us in the following to test whether a stationary state can be reached and how the physical parameters of these discs compare to observations. In this effective disc model, we calculate the viscous evolution of such discs including star formation and taking mass input from our large-scale simulations into account. Angular momentum is mediated by a turbulent viscosity [e.g. generated by magnetorotational instability (MRI) or a self-gravitating disc] and star formation happens in the densest regions of the disc.

Following Pringle (1981) and Lin & Pringle (1987), the viscous evolution of such a disc can be described by the following differential equation:

1

This equation is derived from mass and angular momentum conservation, coupled via the radial velocity (for details, see Pringle 1981). Σ(t, R) is the surface density depending on time t and radius R within the disc. The rotation is Keplerian yielding the following rotation frequency:

2

with the mass of the nuclear supermassive black hole M_BH and G being the gravitational constant. The stellar mass component is neglected here, as we are well inside the influence radius of the black hole (≈3.4 pc for NGC 1068). We assume that the viscosity is due to some turbulent process and describe it with the help of a turbulent α viscosity (Shakura & Sunyaev 1973):

3

where α_ν is a dimensionless parameter determining the strength of the angular momentum transport (α_ν∈[0, 1]), c_s is the speed of sound and H(R) is the scaleheight of the disc:

4

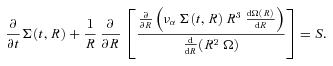
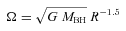
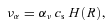
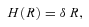
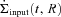with the scaling parameter δ. We added the extra terms abbreviated by S. They include a source of mass due to the input from large scale [⁠; see Section 3.2] and a sink due to star formation [⁠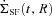; see Section 3.3]: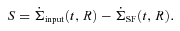

5

Equation (1) is solved with the help of Matlab's4 pdepe solver. A summary of the parameters of our effective disc standard model in addition to the ones used for the three-dimensional Pluto calculations is summarized in Table 2.

3.2 Mass input from our turbulent torus simulation

Already after the comparatively short evolution time of our three-dimensional hydrodynamical simulations, the outer part of the simulation has reached a stable equilibrium, concerning the total mass balance. This can be seen in Fig. 3, where the total gas mass outside a given radius (0.25, 2.5 and 25.0 pc) is plotted against the time. Whereas the smallest radius shown lies within the dense disc structure, we are well outside the disc further out than 2.5 pc in radius. Therefore, we use all gas, which is advected through a sphere of a radius of 2.5 pc for our effective disc simulations. This amounts to a gas mass transfer of 0.14 M_⊙ yr⁻¹ at a cluster age of 50 Myr. The temporal evolution of the accumulated mass of this gas is shown as the red dashed line in Figs 5 and 6. The change in slope is due to the decreasing mass input rate with time, according to the analytical prescription of the mass loss processes of a stellar population as described by Jungwiert et al. (2001). The radial location of input is chosen such that the angular momentum of the gas coming from the large-scale hydrodynamical simulations equals the angular momentum of a Keplerian disc at the respective radius:

6

where j_gas,input is the specific angular momentum of the gas.

Figure 3

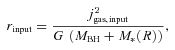
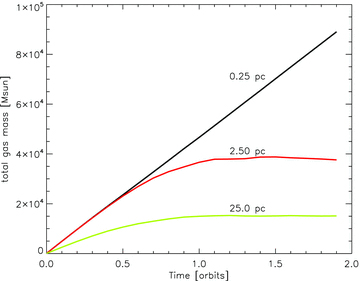
Total gas mass within the domain of our three-dimensional Pluto simulations outside a sphere of radii 0.25, 2.5 and 25 pc.

Open in new tabDownload slide

Figure 5

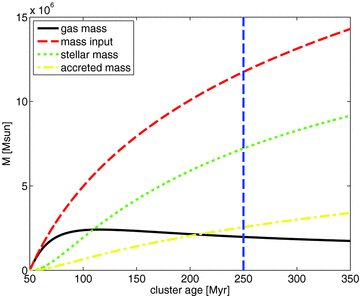
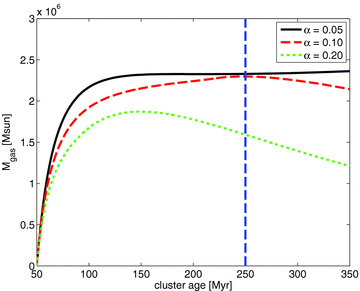
Comparison of mass contributions of the various components of our model for an α viscosity parameter of 0.05 and a gas temperature of 400 K. The blue dashed line denotes the estimated current age of the nuclear star cluster in NGC 1068.

Open in new tabDownload slide

Figure 6

Comparison of mass contributions of the various components of our model for an α viscosity parameter of 0.05 and a temperature of 50 K.

Open in new tabDownload slide

This assumes that mass inflow does not interact with disc material before settling into the disc plane (e.g. gas inflow happens from all directions and the disc is geometrically thin). Fig. 4 shows the resulting histogram of the mass flow through a sphere of a radius of 2.5 pc from the Pluto simulation. The histogram is calculated from a slightly higher resolved Pluto run with a resolution of n_r= 200, n_θ= 197 and n_φ= 103, which was restricted to a radial range between 2.5 and 50 pc. The time resolution of the gas flow derivation is approximately 3400 yr. For the histogram, a total of 100 snapshots have been used between an evolution time of 0.7 and 1.0 Myr. Colour coded is the relative frequency of a given combination of radius and surface density growth rate within the 100 snapshots. For each radial bin of this histogram, the red triangle denotes the maximum of the respective radial bin (the most frequent combination of this radius and mass input rate of the snapshots). We then fit these triangles with a parabola and renormalize to the total mass input rate. This parametrized mass input rate is given by

7

where the radius in the disc R is given in units of parsec as indicated. This function, which is also shown as the red parabola in Fig. 4, is used in the simulations of this paper. Note that a small portion of the gas at 2.5 pc possesses more angular momentum than it would have in a Keplerian disc at the same radius.

Figure 4

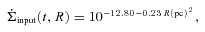
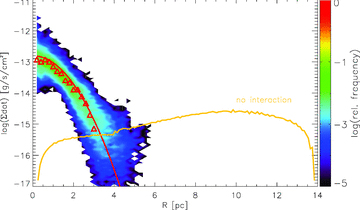
Mass input into our effective disc model, shown as the growth of the gas surface density at different radii, flowing in through a sphere with a radius of 2.5 pc from our three-dimensional Pluto turbulent torus simulation. The input radii are set according to an angular momentum distribution of a Keplerian disc. Shown is the logarithm of a histogram for 100 time-steps with a resolution of approximately 3400 yr between an evolution time of 0.7 and 1.0 Myr, where the three-dimensional hydrosimulation is already in an equilibrium state. The red triangles denote the maxima of each radial bin and the red parabola is the parametrization used as a source term in the effective disc simulations. The yellow graph denotes the growth of the gas surface density, if we directly take the angular momentum of the mass blobs, ejected from the stellar cluster and do not evolve them in a hydrodynamical simulation.

Open in new tabDownload slide

As already mentioned before, the stars in the nuclear cluster rotate with sub-Keplerian velocities. If we would use the mass injections of the stars within the nuclear star cluster directly and feed them into a Keplerian rotating disc, without hydrodynamically calculating the interaction of the blobs, then the yellow graph would result. However, during the three-dimensional Pluto simulations, turbulent motions within the large-scale torus component transport angular momentum outwards and lead to accretion of matter and therefore to a further concentration of the disc towards the centre, evident in the different shapes of the red and yellow graphs.

3.3 Treatment of star formation

Cold nuclear discs of this kind are known to be able to form stars (Nayakshin et al. 2006; Paumard et al. 2006; Alig et al. 2010). In our simulations, we convert gas into stars, wherever the Toomre stability parameter

8

is smaller than unity, where Ω is the Keplerian orbital frequency, c_s is the local speed of sound, Σ is the gas surface density and G is the gravitational constant. The amount of gas removed from the computational domain is chosen according to the Kennicutt–Schmidt star formation law (Kennicutt 1998):

9

where Σ is as usual the gas surface density within the disc. Gas which forms stars is simply removed from the simulation and will no longer participate in the viscous evolution of the disc.

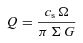
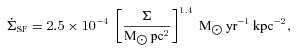
3.4 Results of the effective disc models and comparison with observations

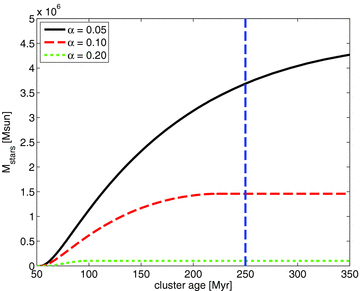
In the course of the simulation, several physical processes are competing with one another. Starting with a basically empty model space in all our simulations, the knowledge of the initial condition is lost on a very short time-scale. The mass inflow from evolving stars in our large-scale simulation first builds up the rotating disc, which is then constantly replenished over time, but with a decreasing mass input rate. The turbulent viscosity tries to move angular momentum outwards, leading to accretion of gas through the disc towards the inner edge and beyond. The residual of the newly introduced gas remains in the disc and at some point, when the Toomre stability criterion is no longer fulfilled, gravitational collapse can occur and stars will form, contributing to a stellar disc, which then coexists with the gas structure. A comparison between the various contributions for our standard model (for the parameters given in Tables 1 and 2) is shown in Fig. 5 as a function of time. The vertical dashed blue line marks the estimated current age of the nuclear star cluster in NGC 1068 of 250 Myr (Davies et al. 2007). The integrated gas mass introduced into the disc simulation is given as a red dashed line. Most of this mass then gets accreted through viscous processes, as shown with the yellow dash–dotted line. The gas residing in the disc is given as a black solid line. It rises steeply during the first few million years. By then, gas transport through the inner boundary and transformation of gas into stars get significant, leading to a turnover of the disc mass curve. In the further evolution, the disc mass stays approximately constant, whereas the slopes of the total accreted gas mass as well as the total mass in stars flatten due to the decreasing mass inflow rate.

The same comparison of contributions to the total integrated mass budget, but for the case of a lower gas temperature of only 50 K, is shown in Fig. 6. When decreasing the gas temperature, the Toomre criterion indicates instability already at lower gas densities. Therefore, star formation now dominates over the gas mass residing in the disc after roughly 110 Myr. It contributes the largest fraction of the inserted gas mass. The disc mass evolution now shows a visible decrease at later times. The dependence of star formation on the temperature of the gas in the disc can be seen directly in the comparison between Figs 5 and 6, which shows a difference of roughly a factor of 2 between the stellar mass in the 400 and the 50 K simulations. In reality, we expect the disc to consist of a multiphase medium, with regions of cold, warm and even hot gas due to gas cooling and a variety of heating processes within the disc, so that the star formation rate might be intermediate between the examples depicted here (e.g. Schartmann et al. 2009).

In the following part of this section, we study how these processes compete with one another, when changing the (generally unknown) α viscosity parameter of the disc. In this study, it takes the values 0.05, 0.1 and 0.2. Observationally, King, Pringle & Livio (2007) find for thin, fully ionized accretion discs a typical range of values between 0.1 and 0.4. Numerical studies of magnetohydrodynamical turbulence tend to derive up to an order of magnitude smaller values. For the case of circumnuclear discs, which are only partially ionized, angular momentum transport is reduced and depends strongly on the ionization fraction of the gas.

Fig. 7 shows the gas surface density distribution for the three α parameters: α_ν= 0.05 as a black solid line, α_ν= 0.10 as a red dashed line and α_ν= 0.20 as a green dotted line at an age of the nuclear star cluster of 250 Myr. The qualitative difference in the parameter study is as expected: the smaller the viscosity (scaling proportional to α_ν), the more mass is able to assemble in the disc. This is also reflected in the graph of the total gas mass in the disc (Fig. 8).

Figure 7

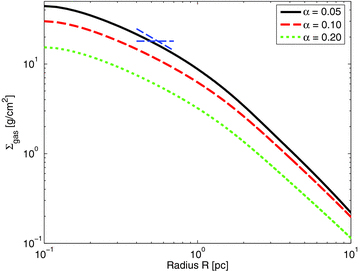
Final gas density distribution at a cluster age of 250 Myr. Superposed as blue dashed lines are the two limiting curves for the range of possible surface density distributions as determined from MIDI observations (Kishimoto et al. 2009).

Open in new tabDownload slide

Figure 8

Total gas mass of the disc.

Open in new tabDownload slide

In order to be able to compare the sizes of the discs with MIDI observations, the following procedure is applied: MIDI detects hot dust (see Section 1), which can only exist beyond the sublimation radius, which was estimated to be roughly 0.4 pc for the case of NGC 1068 (Greenhill et al. 1996; Schartmann et al. 2005). Therefore, we cut our discs at this radius, assume a constant gas-to-dust ratio and derive the half-width at half-maximum (HWHM) of the remaining structure. This then yields an HWHM of the dust disc between approximately 0.84 and 0.86 pc for the three α parameters at the current age of the nuclear star cluster in NGC 1068. Remarkably, this is very similar to the extent of the inner component as seen with MIDI. Here, an HWHM of approximately 0.7 pc is measured (Raban et al. 2009). As already mentioned before, a warped disc as seen in water maser observations of the same size was found by Greenhill & Gwinn (1997). It extends between 0.65 and 1.1 pc. Water maser emission traces warm (≈400 K), high-density (⁠⁠) molecular gas (Elitzur 1992). However, one should note that it is still unclear how the structure detected in hot dust emission with MIDI can be connected to the very dense and clumpy disc assumed from water maser emission. Nevertheless, the finding in different modes of observations as well as in physically motivated simulations suggests a common origin.

MIDI observations of a sample of nearby AGN suggest a common radial structure of AGN tori with a surface brightness distribution proportional to r⁻², which corresponds roughly to a (more or less model-independent) surface density distribution proportional to r^−1,...,0 (Kishimoto et al. 2009). Line segments with the two limiting exponents (−1 and 0) are superposed as blue dashed line segments in the radial range of the detection of a disc-like dust structure in NGC 1068 by MIDI with a size of roughly 0.7 pc in radius (Raban et al. 2009). In this radial range, the shape of the surface density distribution of our discs is well consistent with these slopes inferred from observations by Kishimoto et al. (2009), but are rather at the upper end.

The time evolution of the total gas mass within the disc (Fig. 8) shows a steep rise at the beginning of the simulation, until the gas disc is built up and a maximum is reached. Then, it is followed by a shallow decay, due to the decreasing gas mass input rate. Values are of the order of 2 × 10⁶ M_⊙ in the maximum. In good comparison to that, Kumar (1999) found a disc mass of the order of 10⁶ M_⊙ with the help of a clumpy disc model, which accounts for the observed maser emission. Furthermore, a highly inclined thin, and clumpy ring or nuclear disc with a molecular mass of 1.3 × 10⁶ M_⊙ (Montero-Castaño, Herrnstein & Ho 2009) has been found in our own galactic centre in a distance ranging from approximately 2 to 5 pc (Genzel et al. 1985; Guesten et al. 1987). This is particularly interesting, because the black hole mass in the galactic centre of 4 × 10⁶ M_⊙ (Ghez et al. 2005; Schoedel, Merritt & Eckart 2009) is very similar to the one in NGC 1068, and the mass of its circumnuclear disc is comparable to the results of our infall model.

Fig. 9 shows the total accreted mass of the parameter study. As expected, larger α_ν values lead to a larger amount of angular momentum transfer outwards and to a larger amount of gas accretion through the inner boundary, which can also be seen in the current mass transfer rate through the inner boundary (Fig. 10) in solar masses per year as a function of time. After an evolution time of 250 Myr after the cluster formation, a typical accretion rate of approximately 0.025 M_⊙ yr⁻¹ results. It is generally unknown which fraction of this mass transported through a sphere of a radius of 0.1 pc really reaches the black hole. Assuming that the efficiency is somewhere in between 10 and 100 per cent, accretion rates on to the black hole of between approximately 0.0025 and 0.025 M_⊙ yr⁻¹ result, which are well consistent with typically observed values for Seyfert galaxies of a few times 10⁻³–10⁻² M_⊙ yr⁻¹ (Jogee 2006). If we assume that all of the gas transferred through the inner boundary of our model space will reach the black hole and that the efficiency for mass energy conversion is 10 per cent, this yields a source luminosity of 1.5 × 10⁴⁴ erg s⁻¹ corresponding to 15 per cent of the Eddington luminosity. For radiative transfer calculations through a simple two-dimensional axisymmetric continuous torus model, Schartmann et al. (2005) needed a value of 20 per cent in order to obtain a good adaptation to high spatial resolution spectral energy data. In radiative transfer calculations, the source luminosity sets the scaling of the reprocessed radiation. Determining the source luminosity is a difficult task for the case of NGC 1068, it being a heavily obscured Seyfert 2 galaxy. Therefore, it can only be estimated with the help of the accretion disc radiation reflected by electrons above the dust distribution and is therefore geometry dependent. Pier et al. (1994) did a careful analysis of the geometry dependence and came up with a best estimate of

10

11

which corresponds to 35 per cent of the Eddington luminosity, including a quite large uncertainty.5 However, concerning the current mass accretion rate, our smooth disc description with an effective α parameter is an oversimplification. In reality, we expect the matter transport from the circumnuclear disc towards the inner hot accretion disc to be clumpy, as e.g. observed in the galactic centre environment (Montero-Castaño et al. 2009).

Figure 9

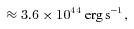
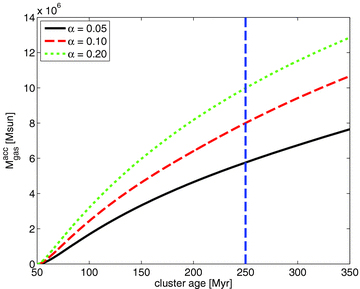
Total accreted gas mass through the inner boundary of the domain.

Open in new tabDownload slide

Figure 10

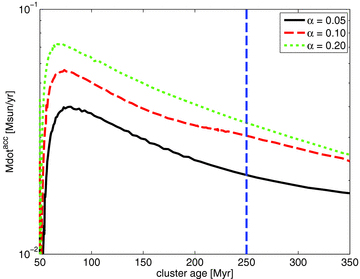
Total accretion rate of gas through the inner boundary of the domain.

Open in new tabDownload slide

The total mass of stars formed for the α parameter study is shown in Fig. 11. The star formation rate increases steeply at the beginning of the simulation, when the mass input rate is still high. Larger values of α lead to a larger mass accretion rate (see Fig. 10) and a smaller gas surface density (see Fig. 7) and in consequence to a smaller total mass in stars. A total mass of up to 4 × 10⁶ M_⊙ is reached at the current age of the nuclear star cluster. In comparison to this, Kumar (1999) estimate the stellar mass within 1 pc around the nuclear black hole in NGC 1068 to be of the order of 10⁷ M_⊙ on the basis of theoretical considerations and from observations by Thatte et al. (1997). Such a high rate of star formation will also lead to subsequent energy input into the disc by supernova Type II explosions after a few million years. This additional feedback process will stir further turbulence in the disc and might be an important driver to increase its scaleheight. However, a detailed analysis of these effects can only be done in three-dimensional, multiphase hydrodynamical simulations including the effect of gas cooling. However, using such a scenario, Wada et al. (2009) find that only on scales beyond a few parsec, a significant scaleheight can be achieved.

Figure 11

Total mass of formed stars.

Open in new tabDownload slide

A further comparison with observations can be done by calculating the neutral hydrogen column density on the line of sight. To do this, we use the gas surface density and distribute the gas homogeneously in the z-direction in a disc structure according to the scaleheight distribution assumed previously (equation 4). Many simplifications have to be assumed, concerning the geometrical distribution, the gas mixture, the ionization state etc. Therefore, only a rough estimate can be given. Assuming solar gas composition and that the disc is completely neutral, values between 4 × 10²⁵ cm⁻² for α_ν= 0.2 and 1 × 10²⁶ cm⁻² for α_ν= 0.05 result. In a compilation of observed Seyfert galaxies in Shi et al. (2006), the values spread between approximately 10²⁰ cm⁻² (which is basically the galactic foreground value) and 10²⁵ cm⁻². Seyfert 2 galaxies fill the upper part of this range starting at roughly 10²² cm⁻². This shows that our derived values lie in the upper range or even beyond the sample of Seyfert 2 galaxies. One should, however, note that a density stratification in the vertical direction of the disc is expected. In particular, Mulchaey, Myshotzky & Weaver (1992) find that the torus in NGC 1068 has a very high gas column density of the order of N_H= 10²⁵ cm⁻². An additional component on tens of parsec scale, as revealed by SINFONI, adds a column density of approximately 8.0 × 10²⁴ cm⁻² (Sánchez et al. 2009). The hydrogen column density through our outer torus component (in our three-dimensional hydrodynamical models) is only a negligible fraction of these values.

4 DISCUSSION

4.1 Keeping tori stable against gravity

One major subject in theoretical AGN torus research is the question of stability of the vertical structure. A geometrically thick torus, which is stabilized by Keplerian rotation, will soon collapse to a thin disc, when the thermal pressure is reduced by gas cooling or the turbulent pressure is dissipated, e.g. in collisions. Being a fast process happening on the order of only a few orbital periods, this contrasts with observations of geometrically thick structures. A short summary of the models proposed to circumvent this problem is given in Section 1.

In our three-dimensional hydrodynamical model, geometrically thick gas and dust structures naturally result from the fact that the emitting stars are organized in a vertically extended structure (Davies et al. 2007). These clusters are hot stellar systems, which are stabilized mainly by random motions of the stars, leading to a turbulent pressure, and rotation is only of minor importance. The turbulent motions lead only to a weak stabilization against gravity concerning the emitted gas, as the blobs merge and dissipate their random kinetic energy component on a short time-scale and are able to move radially inwards, until they find their new equilibrium radius in the Keplerian disc.

However, one should again note that the outer torus part of our model cannot account for the Seyfert 1/2 dichotomy, due to its low gas column density. This can only be done by the inner nuclear and very dense disc component. The crucial processes for puffing up this structure are still a matter of debate. Every process which is able to stir turbulence is a possible candidate. Turbulent motions within the disc will do both: puff up the disc structure to form geometrically thick tori and drive accretion as it also leads to an effective viscosity. Some ideas are discussed in Section 4.2

4.2 Origin of the turbulent viscosity

Evidence is growing that magnetic fields are most important to mediate redistribution of angular momentum in thin and ionized accretion discs. This basic idea was already coined by Shakura & Sunyaev (1973) after setting up their parametrized thin disc model (Shakura–Sunyaev disc, α disc, standard disc). The first numerical realization of this MRI was given by Balbus & Hawley (1991) showing that a weak magnetic field together with a shear flow is able to maintain a magnetic dynamo in accretion discs and lead to an accretion flow. This scenario still forms the basis of the most up-to-date simulations. In our case, this might be relevant only for the innermost region of the disc and a boundary layer, which can be directly ionized by the central source (e.g. Blaes & Balbus 1994). However, there is still contradiction between theoretically derived α values and those measured in observations (King et al. 2007).

Furthermore, any kind of turbulent process will lead to an effective viscosity and thereby drives angular momentum redistribution. Relevant for our simulations is first the merging of blobs and streams of gas into the nuclear disc. Possessing a range of various momenta coming from different directions, this leads to enhanced turbulence within the disc. Detailed hydrodynamical simulations of these processes are planned and will give us an estimate of the relevance for angular momentum transfer in the disc.

Rice & Armitage (2009) proposed self-gravity to be the dominant transport mechanism of angular momentum for the case of discs, which are too weakly ionized to sustain MHD turbulence (Blaes & Balbus 1994). This might be the situation within some radial extent of cold and dense protoplanetary accretion discs and might be relevant for the case of our nuclear discs as well. Furthermore, it has been shown that fragmentation is equivalent to α≤ 0.06 (Rice, Lodato & Armitage 2005).

Due to the large amount of star formation in some of our simulations, secondary feedback processes such as supernova Type II explosions might contribute significantly during some phases of the evolution. Interaction with wind and ultraviolet radiation pressure will play a role in the part of the central region with direct lines of sight towards the nucleus.

4.3 Dependence on the cluster rotation profile

For the case of this paper, a simple power law is assumed for the radial dependence of the rotation velocity of the underlying nuclear stellar cluster. On the tens of parsec scale, this is a fair representation of the flat rotation curve observed with SINFONI (Davies et al. 2007) for NGC 1068. Given the good comparison of our results with observations as discussed in Section 3.4, we think that our model is a possible solution. A different rotation velocity distribution of the stars – as has been observed for other nearby Seyfert galaxies – will lead to a change in the radial dependence of the mass input rate, used as a source term for the effective disc simulations. Test calculations with several analytic input rates showed only slightly different results. However, a detailed analysis of various dynamical initial conditions necessitates an extensive parameter study and a detailed understanding of the angular momentum redistribution, which is beyond the scope of this paper and will be discussed in subsequent publications. It will finally enable us to make statistical statements and compare our results to observations of samples of galaxies.

5 CONCLUSIONS

In this paper, we show that evolving stars from a massive and young nuclear star cluster, as found in nearby Seyfert galaxies, provide enough gas to assemble a parsec-sized nuclear gas disc. To this end, we combine an enhanced version of the Schartmann et al. (2009) models with a simplified treatment of the innermost parsec-scale region, where a nuclear disc builds up. As far as possible, we derive input parameters of our models from observations of the nearby and well-studied Seyfert 2 galaxy NGC 1068. This two-stage analysis enables us to (i) do a long-term evolution study, (ii) link the tens of parsec-scale region of galactic nuclei (observed with the SINFONI instrument) to the sub-parsec scales (probed by MIDI and in water maser emission) and (iii) test our model directly with a large number of observational results. Such comparisons show that the total mass and surface density distribution of these nuclear discs are compatible with recent observations. Our three-dimensional hydrodynamic simulations are based upon the observations of young and massive nuclear star clusters in the centres of nearby Seyfert galaxies. In our global scenario, the gas ejection of their stars provides both, material for the obscuration within the so-called unified scheme of AGN and a reservoir to fuel the central, active region. Gas is injected in the form of blobs formed by emissions of single intermediate mass stars with low expansion velocities. In contrast to this, turbulent velocities as taken over from the hot stellar system are high and contribute significantly to the clumping of the gas distribution as a whole, through interaction between gas blobs, transforming kinetic energy into heat. Cooling instability further confines these clouds and filaments, which then tend to move towards the minimum of the effective potential. After only a few orbital periods, this represents a clumpy and filamentary flow of gas towards the inner region, where it opens out into a disc structure and sets into a stationary state in the large-scale part. As we currently cannot treat the physics of the inner part correctly in our three-dimensional hydrodynamical simulations, we feed the mass inflow into our viscous disc model, in order to be able to estimate observable quantities. At the current age of the nuclear starburst in NGC 1068 of 250 yr, our simulations yield disc sizes of the order of 0.8–0.9 pc, which compare well to the observed maser disc extent and disc sizes as inferred from interferometric observations in the mid-infrared. The gas mass of a few times 10⁶ M_⊙ in the disc is in good comparison to models of discs, tuned to reproduce these maser observations. The resulting mass transfer rate of 0.025 M_⊙ yr⁻¹ through the inner rim of our disc compares well to typical Seyfert galaxies. However, NGC 1068 seems to be in a heavily accreting state, which can be accommodated in our model only, when assuming e.g. clumpy accretion. Furthermore, rough estimates of gas column densities of our model are in agreement with NGC 1068 being a Compton thick source. On the basis of these comparisons, we conclude that the proposed scenario seems to be a reasonable model and shows that nuclear star formation and subsequent AGN activity are intimately related.

We thank the referee, Keichi Wada, for useful comments to improve the clarity of the paper and Volker Gaibler for helpful discussions. Part of the numerical simulations has been carried out on the SGI Altix 4700 HLRB II of the Leibniz Computing Centre in Munich (Germany).

REFERENCES

Author notes