-
PDF
- Split View
-
Views
-
Cite
Cite
Elisabetta Majerotto, Jussi Väliviita, Roy Maartens, Adiabatic initial conditions for perturbations in interacting dark energy models, Monthly Notices of the Royal Astronomical Society, Volume 402, Issue 4, March 2010, Pages 2344–2354, https://doi.org/10.1111/j.1365-2966.2009.16140.x
Close - Share Icon Share
Abstract
We present a new systematic analysis of the early radiation era solution in an interacting dark energy model to find the adiabatic initial conditions for the Boltzmann integration. In a model where the interaction is proportional to the dark matter density, adiabatic initial conditions and viable cosmologies are possible if the early-time dark energy equation of state parameter is we > −4/5. We find that when adiabaticity between cold dark matter, baryons, neutrinos and photons is demanded, the dark energy component satisfies automatically the adiabaticity condition. As Type Ia supernovae or baryon acoustic oscillation data require the recent-time equation of state parameter to be more negative, we consider a time-varying equation of state in our model. In a companion paper, we apply the initial conditions derived here and perform a full Monte Carlo Markov Chain likelihood analysis of this model.
1 INTERACTING DARK ENERGY


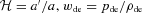 is the DE equation of state parameter, a prime indicates derivative with respect to conformal time τ, and Qc is the rate of transfer of dark matter density due to the interaction. Various forms for Qc have been investigated (see e.g. Wetterich 1995; Amendola 1999; Billyard & Coley 2000; Zimdahl & Pavon 2001; Chimento et al. 2003; Farrar & Peebles 2004; Koivisto 2005; Olivares, Atrio-Barandela & Pavon 2005; Sadjadi & Alimohammadi 2006; Guo, Ohta & Tsujikawa 2007; Bean et al. 2008a; Boehmer et al. 2008; Corasaniti 2008; He & Wang 2008; Quartin et al. 2008; Quercellini et al. 2008; Valiviita, Majerotto & Maartens 2008; Caldera-Cabral, Maartens & Urena-Lopez 2009b; Chongchitnan 2009; Gavela et al. 2009; He, Wang & Abdalla 2009a; Jackson, Taylor & Berera 2009; Pereira & Jesus 2009). We consider models where the interaction has the form of a decay of one species into another – as in simple models of reheating and curvaton decay (Malik, Wands & Ungarelli 2003; Sasaki, Valiviita & Wands 2006; Assadullahi, Valiviita & Wands 2007). Such a model was introduced by Boehmer et al. (2008) and Valiviita et al. (2008). It is not derived from a Lagrangian (in contrast with, e.g., Wetterich 1995; Amendola 1999), but it is motivated physically as a simple phenomenological model for decay of dark matter particles into DE. In this sense, it improves on most other phenomenological models, which are typically designed for mathematical simplicity, rather than as models of interaction. The methods that we use here and in the companion paper (Valiviita, Maartens & Majerotto 2009) may readily be extended to other interactions, including those based on a Lagrangian. We assume that in the background, the interaction takes the form (Boehmer et al. 2008; Valiviita et al. 2008)
is the DE equation of state parameter, a prime indicates derivative with respect to conformal time τ, and Qc is the rate of transfer of dark matter density due to the interaction. Various forms for Qc have been investigated (see e.g. Wetterich 1995; Amendola 1999; Billyard & Coley 2000; Zimdahl & Pavon 2001; Chimento et al. 2003; Farrar & Peebles 2004; Koivisto 2005; Olivares, Atrio-Barandela & Pavon 2005; Sadjadi & Alimohammadi 2006; Guo, Ohta & Tsujikawa 2007; Bean et al. 2008a; Boehmer et al. 2008; Corasaniti 2008; He & Wang 2008; Quartin et al. 2008; Quercellini et al. 2008; Valiviita, Majerotto & Maartens 2008; Caldera-Cabral, Maartens & Urena-Lopez 2009b; Chongchitnan 2009; Gavela et al. 2009; He, Wang & Abdalla 2009a; Jackson, Taylor & Berera 2009; Pereira & Jesus 2009). We consider models where the interaction has the form of a decay of one species into another – as in simple models of reheating and curvaton decay (Malik, Wands & Ungarelli 2003; Sasaki, Valiviita & Wands 2006; Assadullahi, Valiviita & Wands 2007). Such a model was introduced by Boehmer et al. (2008) and Valiviita et al. (2008). It is not derived from a Lagrangian (in contrast with, e.g., Wetterich 1995; Amendola 1999), but it is motivated physically as a simple phenomenological model for decay of dark matter particles into DE. In this sense, it improves on most other phenomenological models, which are typically designed for mathematical simplicity, rather than as models of interaction. The methods that we use here and in the companion paper (Valiviita, Maartens & Majerotto 2009) may readily be extended to other interactions, including those based on a Lagrangian. We assume that in the background, the interaction takes the form (Boehmer et al. 2008; Valiviita et al. 2008) 
In Valiviita et al. (2008), we considered the case of fluid DE with a constant equation of state parameter −1 < wde≤−4/5 and found a serious large-scale non-adiabatic instability in the early radiation era. This instability grows stronger as wde approaches −1. Phantom models, wde < −1, do not suffer from this instability, but we consider them to be unphysical.

There are two critical features of the analysis of interacting models, which are not always properly accounted for in the literature.
- The background energy transfer rate Qc does not in itself determine the interaction in the perturbed universe. One should also specify the momentum transfer rate, preferably via a physical assumption. We make the physical assumption that the momentum transfer vanishes in the dark matter rest frame; this requires that the energy–momentum transfer rate is given covariantly by (Kodama & Sasaki 1984; Valiviita et al. 2008)where uμc is the dark matter four-velocity and δc=δρc/ρc is the cold dark matter (CDM) density contrast.5

Adiabatic initial conditions in the presence of a dark sector interaction require a very careful analysis of the early radiation solution, both in the background and in the perturbations. We derive these initial conditions by generalizing the methods of Doran et al. (2003) to the interacting case, thereby extending our previous results (Valiviita et al. 2008).
We give here the first systematic analysis of the initial conditions for perturbations in the interacting model given by equation (5)– and our methods can be adjusted to deal with other forms of interaction. In the companion paper Valiviita et al. (2009), we report the results of our full Monte Carlo Markov Chain likelihood scans for this model. Cosmological perturbations of other interacting models have been investigated, e.g., in Amendola et al. (2003); Koivisto (2005); Olivares, Atrio-Barandela & Pavon (2006); Mainini & Bonometto (2007); Bean, Flanagan & Trodden (2008b); Bean et al. (2008a); Corasaniti (2008); La Vacca & Colombo (2008); Pettorino & Baccigalupi (2008); Schäfer (2008); Schaefer, Caldera-Cabral & Maartens (2008); Caldera-Cabral, Maartens & Schaefer (2009a),Chongchitnan (2009); Gavela et al. (2009); He et al. (2009a); He, Wang & Jing (2009b); He, Wang & Zhang (2009c); Jackson et al. (2009); Koyama, Maartens & Song (2009); Kristiansen et al. (2009); La Vacca et al. (2009) and Vergani et al. (2009).
2 PERTURBATION EQUATIONS


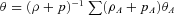 is the total velocity perturbation (θ=−k2v). The evolution equations for density perturbations and velocity perturbations for a generic fluid are (Valiviita et al. 2008; Kodama & Sasaki 1984)
is the total velocity perturbation (θ=−k2v). The evolution equations for density perturbations and velocity perturbations for a generic fluid are (Valiviita et al. 2008; Kodama & Sasaki 1984) 






3 BACKGROUND SOLUTION IN EARLY RADIATION ERA
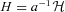 instead of the conformal Hubble parameter
instead of the conformal Hubble parameter  . In the radiation era we have
. In the radiation era we have 
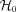 is the conformal Hubble parameter today and Ωr0=ρr0/ρcrit0≈ 2.47 × 10−5h−2 is the radiation energy density parameter today. Here h is defined by H0=h× 100 km s−1 Mpc−1, and as a0= 1, we have
is the conformal Hubble parameter today and Ωr0=ρr0/ρcrit0≈ 2.47 × 10−5h−2 is the radiation energy density parameter today. Here h is defined by H0=h× 100 km s−1 Mpc−1, and as a0= 1, we have  . Furthermore, we have H= (2t)−1 and
. Furthermore, we have H= (2t)−1 and 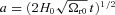 where t is the cosmic time. By equation (15) we find
where t is the cosmic time. By equation (15) we find 

 , and we can neglect the term in square brackets, so that the solution is
, and we can neglect the term in square brackets, so that the solution is 



 . For these times, ρc∝a−3. In typical models that provide a good fit to cosmic microwave background (CMB) data,
. For these times, ρc∝a−3. In typical models that provide a good fit to cosmic microwave background (CMB) data,  , and the conformal time at matter-radiation equality is
, and the conformal time at matter-radiation equality is  . If we demand that the evolution of ρc is effectively standard during the whole RD era, i.e. τswitch > τeq, we require
. If we demand that the evolution of ρc is effectively standard during the whole RD era, i.e. τswitch > τeq, we require 


4 SUPERHORIZON INITIAL CONDITIONS FOR PERTURBATIONS




The evolution of perturbations on super-Hubble scales with various values of the early DE equation of state parameter in the RD and MD eras.
| wde in the RD or MD era | RD era | MD era | Viable? |
| wde < −1 | Adiabatic | Adiabatic | Viable, but phantom |
| −1 < wde < −4/5 | ‘Blow-up’ isocurvature growth | ‘Blow-up’ isocurvature growth | Non-viable |
| −4/5 ≤wde < −2/3 | Adiabatic | Isocurvature growth | Viable, if Γ small enough |
| −2/3 ≤wde < −1/2 | Adiabatic (standard) | Adiabatic | Viable |
| −1/2 ≤wde < +1/3 | Adiabatic (standard) | Adiabatic (standard) | Viable |
| wde in the RD or MD era | RD era | MD era | Viable? |
| wde < −1 | Adiabatic | Adiabatic | Viable, but phantom |
| −1 < wde < −4/5 | ‘Blow-up’ isocurvature growth | ‘Blow-up’ isocurvature growth | Non-viable |
| −4/5 ≤wde < −2/3 | Adiabatic | Isocurvature growth | Viable, if Γ small enough |
| −2/3 ≤wde < −1/2 | Adiabatic (standard) | Adiabatic | Viable |
| −1/2 ≤wde < +1/3 | Adiabatic (standard) | Adiabatic (standard) | Viable |
Note. ‘Adiabatic’ means that it is possible to specify adiabatic initial conditions so that the total gauge-invariant curvature perturbation ζ stays constant on super-Hubble scales. ‘Adiabatic (standard)’ means that the behaviour of perturbations at early times on super-Hubble scales is the same as in the non-interacting model.
The evolution of perturbations on super-Hubble scales with various values of the early DE equation of state parameter in the RD and MD eras.
| wde in the RD or MD era | RD era | MD era | Viable? |
| wde < −1 | Adiabatic | Adiabatic | Viable, but phantom |
| −1 < wde < −4/5 | ‘Blow-up’ isocurvature growth | ‘Blow-up’ isocurvature growth | Non-viable |
| −4/5 ≤wde < −2/3 | Adiabatic | Isocurvature growth | Viable, if Γ small enough |
| −2/3 ≤wde < −1/2 | Adiabatic (standard) | Adiabatic | Viable |
| −1/2 ≤wde < +1/3 | Adiabatic (standard) | Adiabatic (standard) | Viable |
| wde in the RD or MD era | RD era | MD era | Viable? |
| wde < −1 | Adiabatic | Adiabatic | Viable, but phantom |
| −1 < wde < −4/5 | ‘Blow-up’ isocurvature growth | ‘Blow-up’ isocurvature growth | Non-viable |
| −4/5 ≤wde < −2/3 | Adiabatic | Isocurvature growth | Viable, if Γ small enough |
| −2/3 ≤wde < −1/2 | Adiabatic (standard) | Adiabatic | Viable |
| −1/2 ≤wde < +1/3 | Adiabatic (standard) | Adiabatic (standard) | Viable |
Note. ‘Adiabatic’ means that it is possible to specify adiabatic initial conditions so that the total gauge-invariant curvature perturbation ζ stays constant on super-Hubble scales. ‘Adiabatic (standard)’ means that the behaviour of perturbations at early times on super-Hubble scales is the same as in the non-interacting model.
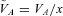 and a rescaled anisotropic stress
and a rescaled anisotropic stress  , as in Doran et al. (2003), we obtain the following evolution equations:
, as in Doran et al. (2003), we obtain the following evolution equations: 









 , and we used the Einstein equations
, and we used the Einstein equations 




 and
and  , we then see that equations (29)–(38) form a set of 10 linear differential equations for 10 perturbation variables
, we then see that equations (29)–(38) form a set of 10 linear differential equations for 10 perturbation variables  and
and  . (Note that ΠA= 0 for A≠ν.)
. (Note that ΠA= 0 for A≠ν.)


 can be read from equations (29)–(38) after substituting equations (42)–(44) and the background evolution of ρc/ρde from (19) or (20), depending on the value of we.
can be read from equations (29)–(38) after substituting equations (42)–(44) and the background evolution of ρc/ρde from (19) or (20), depending on the value of we.The initial conditions are specified for modes well outside the horizon, i.e. for x≪ 1. There will be several independent solution vectors to equation (45), that we write as  . If no term of
. If no term of  diverges for x→ 0, then we can approximate
diverges for x→ 0, then we can approximate  by a constant matrix
by a constant matrix  . If we require more accuracy, we can expand
. If we require more accuracy, we can expand  up to a desired order in x. For example, up to order x3 the matrix
up to a desired order in x. For example, up to order x3 the matrix  contains the constant term
contains the constant term  as well as terms proportional to x, x2 and x3 in the case where we≤−2/3. However, in the case
as well as terms proportional to x, x2 and x3 in the case where we≤−2/3. However, in the case  contains in addition to integer powers of x also non-integer powers 1 − 3we, 2 − 3we, 3 − 3we, etc. and 2 + 3we, 3 + 3we, 4 + 3we, etc. The listed ones and possibly their multiples can fall in the range (0, 3). For a given we, however, one should drop those which turn out to be of higher order than x3.
contains in addition to integer powers of x also non-integer powers 1 − 3we, 2 − 3we, 3 − 3we, etc. and 2 + 3we, 3 + 3we, 4 + 3we, etc. The listed ones and possibly their multiples can fall in the range (0, 3). For a given we, however, one should drop those which turn out to be of higher order than x3.
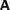 and each solution
and each solution 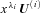 as
as 

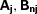 and
and 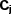 are constant (not depending on the time variable x) matrices and U(i)j are constant vectors. Note that for we≤−2/3 all
are constant (not depending on the time variable x) matrices and U(i)j are constant vectors. Note that for we≤−2/3 all 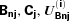 and U(i)Cj terms vanish. For simplicity, we demonstrate this case below, which leads to only integer powers. Substituting equations (47) and (48) into the evolution equation (45) and equating order by order, we obtain
and U(i)Cj terms vanish. For simplicity, we demonstrate this case below, which leads to only integer powers. Substituting equations (47) and (48) into the evolution equation (45) and equating order by order, we obtain 



 :
: 
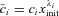 represent the initial contribution of the vector U(i) to the total perturbation vector U(xinit). The imaginary part of λi represents oscillations of
represent the initial contribution of the vector U(i) to the total perturbation vector U(xinit). The imaginary part of λi represents oscillations of  , while the real part gives its power-law behaviour:
, while the real part gives its power-law behaviour:  . The contribution corresponding to the eigenvalue(s) with largest real part, Re(λi), will dominate as time goes by, while initial contributions from eigenvectors corresponding to λi with smaller real part will become negligible compared to the dominant mode. Hence, to set initial conditions deep in the radiation era but well after inflation, it is sufficient to specify the contribution coming from mode(s) with largest Re(λi).
. The contribution corresponding to the eigenvalue(s) with largest real part, Re(λi), will dominate as time goes by, while initial contributions from eigenvectors corresponding to λi with smaller real part will become negligible compared to the dominant mode. Hence, to set initial conditions deep in the radiation era but well after inflation, it is sufficient to specify the contribution coming from mode(s) with largest Re(λi).From now on, we divide the treatment into two cases −2/3 < we < 1/3 and we≤−2/3. Before proceeding, we should point out that the matrix method presented in Doran et al. (2003) and applied to non-interacting constant-wde DE, represents a systematic and efficient approach for finding initial conditions. Once the matrix  has been read from the set of first order differential equations (29)–(38), one can feed it into a symbolic mathematical program such as maple or mathematica and easily extract the constant part
has been read from the set of first order differential equations (29)–(38), one can feed it into a symbolic mathematical program such as maple or mathematica and easily extract the constant part  as well as the other parts (such as
as well as the other parts (such as  , …,
, …,  ) up to any desired order. Then it is simple linear algebra to find the eigenvalues λi and eigenvectors U(i)0 of
) up to any desired order. Then it is simple linear algebra to find the eigenvalues λi and eigenvectors U(i)0 of  and, if higher order solutions in kτ are needed, to substitute these step by step into equations (50)–(52) etc. in order to find the solutions
and, if higher order solutions in kτ are needed, to substitute these step by step into equations (50)–(52) etc. in order to find the solutions  .
.
4.1 Case − 2/3 < we < 1/3
 from equation (43) and the energy density parameters from equation (44) into equations (29)–(38). Then, using equation (20) for ρc/ρde in the last two of them, and taking the limit x→ 0, we find the
from equation (43) and the energy density parameters from equation (44) into equations (29)–(38). Then, using equation (20) for ρc/ρde in the last two of them, and taking the limit x→ 0, we find the  matrix:
matrix: 
 .
.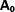 are
are 







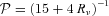 and C1 is a dimensionless normalization constant corresponding to, e.g., Δγ and Δν at the initial time.
and C1 is a dimensionless normalization constant corresponding to, e.g., Δγ and Δν at the initial time.The vector (62) is identical to the standard adiabatic initial condition vector (see Doran et al. 2003). In particular, it should be noted that although we did not require adiabaticity of DE, (62) automatically satisfies the condition Sde,A= 0 for all A=γ, ν, c, b. In Doran et al. (2003), this result was found for non-interacting DE. Here we have now shown that also interacting DE is automatically adiabatic, once CDM, baryons, photons and neutrinos are set to be adiabatic.
Finally, since all components of the vector (62) are different from zero, it is not necessary to compute terms to higher order in x, and we use equation (62) as our adiabatic initial condition for the computation of the CMB power spectrum for models with −2/3 < we < 1/3.
Lee, Liu & Ng (2006) have reported that the quintessence isocurvature mode decays away (in an interacting quintessence model which is quite similar to our setup). After our systematic derivation of initial conditions, this decay can be tracked down to the fact that Re(λ±d) in equation (55) are negative. The reason for this is that in quintessence models the early-time equation of state parameter is typically larger than −2/3, indeed positive [but in Lee et al. (2006) less than +2/3]. So Re(λ±d) is negative, and hence the isocurvature mode decays. In the next subsection, we will see that also in the range −4/5 ≤we≤−2/3 (or we < −1) the DE isocurvature mode decays (although in this case the interaction affects the evolution of DE perturbations), whereas in the range −1 < we < −4/5 the DE isocurvature mode is a rapidly growing mode as recently realized by Valiviita et al. (2008).
4.2 Case we≤−2/3
Since at early times the equation of state can be approximated as a constant, we=w0+wa, this case has already been studied in Valiviita et al. (2008), where a constant −1 < wde≤−2/3 was analysed. A serious non-adiabatic large-scale instability that excludes these models was found whenever −1 < wde < −4/5, no matter how weak the interaction was. However, we notice that there is a limited region of parameter space, −4/5 ≤wde≤−2/3, where the instability can possibly be avoided. In the case of a constant DE equation of state parameter, this range would be observationally disfavoured, since, for example, supernova data require that wde is closer to −1 at recent times. In the case of time-varying wde(a), we do not have this problem as w0 can be close to −1 while −4/5 < we≤−2/3. In the following, we repeat the analysis of initial conditions done in Valiviita et al. (2008), but using the matrix method of Doran et al. (2003), extended to include the interaction, and give the conditions for a viable cosmology.
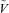 from equation (43) and the energy density parameters from equation (44) into equations (29)–(38), as well as ρc/ρde from equation (19) into the last two of them, and taking the limit x→ 0, we find the
from equation (43) and the energy density parameters from equation (44) into equations (29)–(38), as well as ρc/ρde from equation (19) into the last two of them, and taking the limit x→ 0, we find the 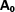 matrix, which is very similar to our previous result (equation 54). This happens because everything remains unchanged, except that we must replace in equations (37) and (38) the evolution of ρc/ρde with equation (19), and whenever Ωde appears we must now substitute the ∝x3 behaviour from (44), instead of the
matrix, which is very similar to our previous result (equation 54). This happens because everything remains unchanged, except that we must replace in equations (37) and (38) the evolution of ρc/ρde with equation (19), and whenever Ωde appears we must now substitute the ∝x3 behaviour from (44), instead of the 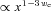 behaviour. Therefore, only the last two rows in (54) are modified, and will now read
behaviour. Therefore, only the last two rows in (54) are modified, and will now read 
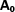 are
are 

 . In addition to this, Re(λ+g) is positive also in the small range
. In addition to this, Re(λ+g) is positive also in the small range  . Therefore, Re(λ+g) > 0 for −1 < we < −4/5. This corresponds to the blow-up solution found in Valiviita et al. (2008); λ+g is larger, the closer we is to −1. There is no blowup of perturbations for −4/5 ≤we≤−2/3, because then the largest Re(λi) are zero.
. Therefore, Re(λ+g) > 0 for −1 < we < −4/5. This corresponds to the blow-up solution found in Valiviita et al. (2008); λ+g is larger, the closer we is to −1. There is no blowup of perturbations for −4/5 ≤we≤−2/3, because then the largest Re(λi) are zero.4.2.1 Case −1 < we < −4/5; non-adiabatic blowup
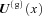 corresponding to the fastest growing mode, λ+g. At zeroth order in x, it is given by
corresponding to the fastest growing mode, λ+g. At zeroth order in x, it is given by 


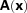 and
and 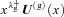 into the evolution equation (45) and equating order by order, we obtain
into the evolution equation (45) and equating order by order, we obtain 



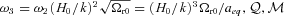 and
and 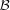 are
are 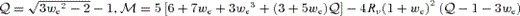 and
and  . This solution coincides with equations (63)–(70) of Valiviita et al. (2008), after substituting nψ=λ+g+ 3, J= 1 − 16Rν[5(nψ+ 2)(nψ+ 1) + 8Rν]−1, converting into Newtonian gauge (by using equations (25) with B=E= 0) and conveniently renormalizing the vector. Equation (72) is the initial condition vector for the case −1 < we≤−4/5, when the dominant eigenvector is that corresponding to λ+g.
. This solution coincides with equations (63)–(70) of Valiviita et al. (2008), after substituting nψ=λ+g+ 3, J= 1 − 16Rν[5(nψ+ 2)(nψ+ 1) + 8Rν]−1, converting into Newtonian gauge (by using equations (25) with B=E= 0) and conveniently renormalizing the vector. Equation (72) is the initial condition vector for the case −1 < we≤−4/5, when the dominant eigenvector is that corresponding to λ+g.

4.2.2 Cases we < −1 or −4/5 ≤ we≤−2/3; adiabatic initial conditions

 . This corresponds to equations (59)–(61) of Valiviita et al. (2008). All components except Δde are equal to the initial conditions for −2/3 < we < 1/3 (equation (62)). However, as pointed out in Valiviita et al. (2008), Δde=Δγ/4 corresponds exactly to the adiabaticity condition for DE: Sde A= 0. Namely, substituting the result (73) into definition (57), we find
. This corresponds to equations (59)–(61) of Valiviita et al. (2008). All components except Δde are equal to the initial conditions for −2/3 < we < 1/3 (equation (62)). However, as pointed out in Valiviita et al. (2008), Δde=Δγ/4 corresponds exactly to the adiabaticity condition for DE: Sde A= 0. Namely, substituting the result (73) into definition (57), we find 
5 CONCLUSION
We have presented, for the first time, a systematic derivation of initial conditions for perturbations in a model of interacting dark matter–DE fluids, in the early radiation era. These initial conditions are essential for studying the further evolution of perturbations up to today's observables. They are the initial values for perturbations in any Boltzmann integrator which solves the multipole hierarchy and produces the theoretical predictions for the CMB temperature and polarization angular power spectrum, as well as the matter power spectrum. We have focused on the interaction Qμc=−Γρc(1 +δc)uμc, where Γ is a constant rate of energy density transfer [see equations (1) and (2)]. Generalizing a previous result for non-interacting DE in Doran et al. (2003), we find that, in our interacting model, requiring adiabaticity between all the other constituents (photons, neutrinos, baryons and CDM) leads automatically also to DE adiabaticity, if its early-time equation of state parameter is we < −1 or −4/5 ≤we≤ 1/3. In our previous work (Valiviita et al. 2008), we showed that if the equation of state parameter for DE is −1 < wde < −4/5 in the radiation or matter eras, the model suffers from a serious non-adiabatic instability on large scales. In this paper, the systematic derivation of initial conditions confirms that result. However, in this paper we have shown that the instability can easily be avoided, if we allow for suitably time-varying DE equation of state. The main results are verbally summarized in Table 1.
In the companion paper (Valiviita et al. 2009), we modified the Code for Anisotropies in the Microwave Background (CAMB) Boltzmann integrator1 (Lewis, Challinor & Lasenby 2000), using the adiabatic initial conditions derived here for the interacting model, and performed full Monte Carlo Markov Chain likelihood scans for this model as well as for the non-interacting (Γ= 0) model for a reference, with various combinations of publicly available data sets: WMAP (Komatsu et al. 2009), WMAP and Arcminute Cosmology Bolometer Array Receiver (ACBAR; Reichardt et al. 2009), SN (Kowalski et al. 2008), BAO (Percival et al. 2007), WMAP and SN, WMAP and BAO, WMAP and SN and BAO.
With the parametrization wde=w0a+we(1 −a), viable interacting cosmologies result for w0 close to −1 and we < −1 or −4/5 < we≤ 1/3, as long as w0+ 1 and we+ 1 have the same sign (Valiviita et al. 2009). These particular conclusions apply exclusively to the interaction model we considered in this paper.
However, the method can be easily adapted for studying different interactions: one only needs to modify the background evolution and interaction terms in equations (29), (30), (37) and (38), before reading a new matrix  from them. Based on section IV of Valiviita et al. (2008), the other interacting fluid models [
from them. Based on section IV of Valiviita et al. (2008), the other interacting fluid models [ or
or  , where α, β≲ 1 are dimensionless constants], that are common in the literature, behave in a very similar way to the model studied here, i.e. for −1 < we < wcrit the models are not viable due to the early-time large-scale blowup of perturbations, for wcrit < we < wadi the models can be viable and non-standard adiabatic initial conditions may be found and for we > wadi (or we < −1) the models are viable and standard (non-interacting) adiabatic initial conditions can be found. The critical value wcrit is determined by demanding that the ‘blow-up’ mode is actually a decaying mode and the fastest ‘growing’ curvature perturbation mode is a constant, i.e. the largest real part of the eigenvalues λi is zero, which with the notation of Valiviita et al. (2008) is guaranteed whenever Re(n+) ≤ 3. In our model the critical value, wcrit=−4/5, is independent of the strength of interaction, but in the above-mentioned models it depends on α or β, as indicated by equations (85) and (98) in Valiviita et al. (2008). In general, our results show that the (early-time) DE equation of state plays, together with the interaction model, an important role in the (in)stability of perturbations.
, where α, β≲ 1 are dimensionless constants], that are common in the literature, behave in a very similar way to the model studied here, i.e. for −1 < we < wcrit the models are not viable due to the early-time large-scale blowup of perturbations, for wcrit < we < wadi the models can be viable and non-standard adiabatic initial conditions may be found and for we > wadi (or we < −1) the models are viable and standard (non-interacting) adiabatic initial conditions can be found. The critical value wcrit is determined by demanding that the ‘blow-up’ mode is actually a decaying mode and the fastest ‘growing’ curvature perturbation mode is a constant, i.e. the largest real part of the eigenvalues λi is zero, which with the notation of Valiviita et al. (2008) is guaranteed whenever Re(n+) ≤ 3. In our model the critical value, wcrit=−4/5, is independent of the strength of interaction, but in the above-mentioned models it depends on α or β, as indicated by equations (85) and (98) in Valiviita et al. (2008). In general, our results show that the (early-time) DE equation of state plays, together with the interaction model, an important role in the (in)stability of perturbations.
JV and RM are supported by STFC. During this work JV received support also from the Academy of Finland.
REFERENCES



