-
PDF
- Split View
-
Views
-
Cite
Cite
F. Marinacci, F. Fraternali, L. Ciotti, C. Nipoti, Stationary models for the extraplanar gas in disc galaxies, Monthly Notices of the Royal Astronomical Society, Volume 401, Issue 4, February 2010, Pages 2451–2462, https://doi.org/10.1111/j.1365-2966.2009.15821.x
Close - Share Icon Share
Abstract
The kinematics of the extraplanar neutral and ionized gas in disc galaxies show a systematic decline of the rotational velocity with height from the plane (vertical gradient). This feature is not expected for a barotropic gas, whilst it is well reproduced by baroclinic fluid homogeneous models. The problem with the latter is that they require gas temperatures (above 105 K) much higher than the temperatures of the cold and warm components of the extraplanar gas layer. In this paper, we attempt to overcome this problem by describing the extraplanar gas as a system of gas clouds obeying the Jeans equations. In particular, we consider models having the observed extraplanar gas distribution and gravitational potential of the disc galaxy NGC 891: for each model, we construct pseudo-data cubes and compare them with the H i data cube of NGC 891. In all cases, the rotational velocity gradients are in qualitative agreement with the observations, but the synthetic and the observed data cubes of NGC 891 show systematic differences that cannot be accommodated by any of the explored models. We conclude that the extraplanar gas in disc galaxies cannot be satisfactorily described by a stationary Jeans-like system of gas clouds.
1 INTRODUCTION
Observations of several spiral galaxies at various wavelengths have revealed massive gaseous haloes surrounding the galactic discs. This extraplanar gas is multiphase: it is detected in H i (e.g. Swaters, Sancisi & van der Hulst 1997), in Hα (Rand 2000; Rossa et al. 2004) and in X-ray observations (Wang et al. 2001; Strickland et al. 2004). Thanks to high-sensitivity H i observations of some edge-on galaxies, like NGC 891 (Oosterloo, Fraternali & Sancisi 2007), we can trace these haloes up to 10–20 kpc from the plane and we can study their kinematics in detail. A remarkable feature of the extraplanar gas is its regularly decreasing rotational velocity uϕ at increasing distances from the Galactic plane (vertical gradient). Fraternali et al. (2005) found that in NGC 891 the vertical gradient is ∼−15 km s−1 kpc−1 (see also Heald et al. 2007). For other galaxies (e.g. NGC 2403), gradients of the same order have been estimated (see Fraternali 2009).
The dynamical state of the extraplanar gas can provide useful insights to understand its origin. Two main frameworks have been proposed: the galactic fountain (Shapiro & Field 1976; Bregman 1980) and the cosmological accretion (Oort 1970; Binney 2005). In the galactic fountain model, partially ionized gas is ejected from the disc by supernova explosions and stellar winds, it travels through the halo and eventually falls back to the disc. Due to difficulties in running high-resolution hydrodynamical simulations of the whole galactic disc (see e.g. Melioli et al. 2008), the gas in the galactic fountain model is often treated ballistically, i.e. as a collection of non-interacting clouds subject to the gravitational field of the galaxy (Collins, Benjamin & Rand 2002). The ballistic galactic fountain is able to reproduce the gas distribution observed in spiral galaxies, but in general the predicted vertical gradient of uϕ is significantly lower than observed (Fraternali & Binney 2006). In the accretion models, the extraplanar gas is the result of the infall of cool intergalactic gas. The two scenarios are not mutually exclusive: in fact, it has been argued that the contribution of accretion is limited to only 10–20 per cent of the total mass of extraplanar gas (Fraternali & Binney 2008).
In a complementary approach, some authors (Benjamin 2002; Barnabè et al. 2006) have focused on the construction of models for the extraplanar gas under the assumption of stationarity. In this approach, the problem of the origin of the extraplanar gas is not addressed, and the main effort is to clarify the global dynamical state of the gas. Usually, in the stationary approach, the extraplanar gas is described as a homogeneous fluid in permanent rotation. In the simplest of fluid homogeneous models, vertical and radial motions of the gas are neglected and therefore the vertical gravitational field of the galaxy is balanced only by the pressure gradient of the gas. In other studies, turbulence has also been added as an extrapressure term (e.g. Koyama & Ostriker 2008). According to the Poincaré–Wavre theorem (Lebovitz 1967; Tassoul 1978), a vertical gradient in the rotational velocity can be present only if the pressure of the medium is not stratified on the density, therefore in fluid homogeneous models the gas distribution is necessarily baroclinic (Barnabè et al. 2006; see also Waxman 1978). Remarkably, in their study of NGC 891, Barnabè et al. (2006) found that if the baroclinic configuration is built from general physical arguments, the model rotational velocity well reproduces the observed rotation curves at different heights over the galactic disc and for a large radial range. However, the temperature predicted for the system is >105 K, well above that of the neutral gas.
Here, we investigate if and how this ‘temperature problem’ can be solved. We make use of the fact that stationary fluid equations for a gaseous system in permanent rotation are, from a formal point of view, identical to the stationary Jeans equations for an axisymmetric system with isotropic velocity dispersion. Thus, also in this case, a decrease of rotational velocities with increasing distances from the mid-plane is obtained when the density field is built using the approach described by Barnabè et al. (2006). In this paper, we analyse this alternative interpretation of the baroclinic fluid homogeneous models. In practice, we consider a ‘gas’ of cold H i clouds described by the stationary Jeans equations, where the thermal pressure, needed for the vertical balance of the galaxy gravitational field, is replaced by the velocity dispersion of the clouds.
In the present approach, some preliminary consideration on the physical state of the clouds is important. In fact, H i halo clouds are often assumed to be embedded in, and in pressure equilibrium with, a hot medium (corona) that is about a thousand times less dense and provides the pressure required to confine them (Spitzer 1956; Wolfire et al. 1995). In the Milky Way, there is plenty of evidence for the existence of this medium, such as emission from highly ionized metals (e.g. Sembach et al. 2003) and the head–tail morphology of individual high-velocity clouds (HVCs; e.g. Brüns et al. 2000). Due to the high-density contrast, the pressure-confined clouds cannot be supported by the pressure of the external medium and must be moving more or less ballistically in a way akin to water drops in the air (Bregman 1980). This assumption is commonly employed in galactic fountain models (e.g. Collins et al. 2002). On the time-scale taken for a cloud to move about 1000 times its length, the trajectory may deviate significantly from the ballistic one due to the interactions with the external medium. This time-scale depends on the cloud mass but it is longer than a dynamical time for the larger clouds (Fraternali & Binney 2008). The typical mass of an halo cloud is difficult to estimate. In the Milky Way, the new determinations of distances for the HVCs give masses from a few ×104 to 106 M⊙ (e.g. Wakker et al. 2008), for external galaxies the mass resolution is often above 106 M⊙ but in M31 several clouds with masses down to ∼1 × 105 M⊙ have been observed (Thilker et al. 2004). We estimate that for a cloud of 105 M⊙, the drag time-scale is more than 10 times the dynamical time and it is therefore fair to treat the system as purely dynamical. Moreover, if the H i halo of a galaxy like NGC 891 is made up of clouds with this mass and radii of 100 pc, the collision time between clouds turns out to be about five times the dynamical time and the system can be considered collisionless.
The substitution of a fluid system with a gas of clouds is also not trivial from the point of view of the comparison with the observations, as several delicate issues arise when considering H i observations (see Section 3.3). To overcome these problems, we follow Fraternali & Binney (2006, 2008) and construct, as an output for each of the models investigated, a pseudo-data cube with the same resolution and total flux as the data cube of the H i observations. This procedure assures a full control of projection and resolution effects. Moreover, the comparison with the raw data removes all the intermediate stages of data analysis and the associated uncertainties. For completeness, we also investigate some phenomenological anisotropic models.
The paper is organized as follows. In Section 2, we illustrate the Jeans-based interpretation of the baroclinic solutions, introducing the anisotropic case which has no analogous fluid counterpart, and we discuss the conditions required for these solutions to have a negative vertical velocity gradient. In Section 3, we present the method adopted to construct isotropic and anisotropic models for the edge-on galaxy NGC 891, whilst in Section 4 we compare their predictions with the H i observations. Section 5 is devoted to the discussion of the results, and Section 6 concludes.
2 Jeans-based description of fluid baroclinic solutions
2.1 Isotropic Jeans solutions

 , and we are assuming that uR=uz= 0, i.e. no net motion in the radial and the vertical directions is considered. Under these assumptions, the streaming velocity of the clouds is given by
, and we are assuming that uR=uz= 0, i.e. no net motion in the radial and the vertical directions is considered. Under these assumptions, the streaming velocity of the clouds is given by 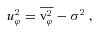


The expression above reveals that the existence of physically acceptable solutions with u2ϕ≥ 0 everywhere is not guaranteed for independent choices of ρ and Φ. In Barnabè et al. (2006), general rules for constructing physically acceptable baroclinic solutions are illustrated. For example, in the usual case in which ∂Φ/∂R≥ 0 and ∂Φ/∂z≥ 0, a sufficient condition to ensure the positivity of u2ϕ is that ∂ρ/∂z≤ 0 and ∂ρ/∂R≥ 0. The same rules apply also here suggesting the use of centrally depressed density distributions. This implies that in the central regions the density is radially increasing moving outwards, which is consistent with the radial H i distribution observed in spiral galaxies such as NGC 891 (Oosterloo et al. 2007).
2.2 Anisotropic Jeans solutions


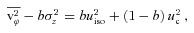

 into the streaming motion u2ϕ and the azimuthal velocity dispersion σ2ϕ. Following the widely used Satoh (1980),k-decomposition, we have
into the streaming motion u2ϕ and the azimuthal velocity dispersion σ2ϕ. Following the widely used Satoh (1980),k-decomposition, we have 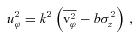

 , so k and b are not fully independent. Note that if the corresponding isotropic model leads to a physically acceptable solution then a sufficient condition to ensure the positivity of u2ϕ is b≤ 1: if u2iso≥ 0, the left-hand side of equation (7) can be negative only if b > 1, so the use of the Satoh decomposition is consistent with the assumption σR≤σz. This requirement is in agreement with the observations that show large vertical motions of the order of 50–100 km s−1 and velocity dispersion along R and ϕ of the extraplanar gas of approximately 20 km s−1 (Oosterloo et al. 2007; Boomsma et al. 2008). Summarizing, this simple parametrization of the velocity dispersion anisotropy is consistent with physically acceptable solutions provided that: (i) b≤ 1 and (ii) the corresponding isotropic model has u2ϕ≥ 0 everywhere.
, so k and b are not fully independent. Note that if the corresponding isotropic model leads to a physically acceptable solution then a sufficient condition to ensure the positivity of u2ϕ is b≤ 1: if u2iso≥ 0, the left-hand side of equation (7) can be negative only if b > 1, so the use of the Satoh decomposition is consistent with the assumption σR≤σz. This requirement is in agreement with the observations that show large vertical motions of the order of 50–100 km s−1 and velocity dispersion along R and ϕ of the extraplanar gas of approximately 20 km s−1 (Oosterloo et al. 2007; Boomsma et al. 2008). Summarizing, this simple parametrization of the velocity dispersion anisotropy is consistent with physically acceptable solutions provided that: (i) b≤ 1 and (ii) the corresponding isotropic model has u2ϕ≥ 0 everywhere.2.3 Conditions to have negative vertical gradient
An important property of the extraplanar gas is the decrease of its rotational velocity with the distance from the galactic plane. To study the kinematics of the extraplanar gas in the models it is helpful to have general expressions (such as equation 2 of Waxman 1978) relating the vertical gradient of the rotational velocity to other physical quantities in stationary configurations.


3 Application to NGC 891
The general rules of Section 2 are now applied to the specific case of the extraplanar gas of NGC 891, to explore whether the proposed models reproduce the observed decrease of the rotational velocity for increasing z. We note that the resulting models can directly describe the extraplanar H i gas seen in the observations because the vertical ‘pressure’ support, needed against the galaxy gravitational field, is now provided by the velocity dispersion of the clouds, rather than by the thermodynamic temperature as in the homogeneous baroclinic models of Barnabè et al. (2006). The present investigation differs from that of Barnabè et al. (2006) also because we adopt an observationally justified density distribution for the extraplanar gas and perform the comparison of the models with the observational data by constructing a pseudo-data cube for each model with the same resolution and total flux as the observations.
3.1 The galaxy model



3.2 The cloud distribution


Total H i emission map of NGC 891 as obtained by the observations (red contours and colour scale) and by the cloud density distribution of Section 3.2 (black contours). The map has a spatial resolution of 25 arcsec (∼1.2 kpc) with contour levels, starting from the outermost, of 0.15, 0.3, 0.6, 1.2, 2.4, 4.8, 9.6 × 1020 cm−2. The shaded area delimits the emission expected from the disc.
We now verify that the density distribution guarantees the existence of physically acceptable solutions (i.e. u2ϕ≥ 0 everywhere). It can be easily shown that ∂ρ/∂z≤ 0 for the density distribution (16), whilst the radial density profile presents, for each z, a maximum at some value Rmax(z): the positivity of u2ϕ is then guaranteed in the region R≤Rmax, where ∂ρ/∂R > 0, whilst it has to be investigated in the external region, where ∂ρ/∂R < 0 (see Section 2.1), by numerical inspection. We found that, with the adopted parameters, the density distribution (16) produces physically acceptable solutions for all the models investigated. For what concerns, the vertical velocity gradient, the considerations made in Section 2.3 are valid: in particular, we expect that the rotational velocities of the models are lower than the circular velocity (8) for R≥Rmax, if the vertical velocity gradient is negative.
In our models, we are only aiming to reproduce the extraplanar gas and therefore neglect the region where emission from the disc is expected. Such a region is covered by shaded areas in all the figures where the comparison with the data is shown (Figs 1, 3, 5 and 6). The size of this region (|z| < 1.64 kpc) is calculated as ± 3σ × (spatial resolution of the data) assuming that the galactic disc is perfectly co-planar. In fact, the resolution of the observations (half power beam width = 0.64 kpc) is much larger than the expected intrinsic scaleheight of the H i disc (100–200 pc), i.e. the disc is not resolved. The exclusion of the disc is necessary to avoid the complication of a region where the gas is almost certainly not described by the considered Jeans equations. The implicit assumption is that, in a real galaxy, at the lower halo boundaries the velocity dispersion, induced by some (unspecified) physical process in the disc, is the same as the one provided by our density distribution (see Figs 2 and 4). This requirement is necessary for the system to be stationary.

Comparison of representative velocity channels of the H i data cube of NGC 891 and the predictions of three stationary models: the isotropic (first column), the k= 0.9 and b= 1 (second column) and the b= 1 maximally rotating (third column) models. The shaded area in each channel delimits the emission expected from the disc. The contour levels, starting from the outermost, are 0.25, 0.5, 1, 2, 5, 10, 20, 50 mJy beam−1; the beam size is 28 arcsec = 1.3 kpc.

Comparison of five representative velocity channels of the H i data cube of NGC 891 and the predictions of three three-integral anisotropic models: b= 0.1 and k= 1 (first column), b= 0.3 and k= 1 (second column) and b= 0.1 and k= 0.9 (third column). The shaded area in each channel delimits the emission expected from the disc and the contour levels are the same as in Fig. 3.

Comparison between two position–velocity cuts perpendicular to the plane of NGC 891 and some representative models. In the first row, the cut is made at R= 7.5 kpc on side of the galaxy where the gas is moving towards the observer, and the corresponding residuals, are presented in the second row. In the third row, the cut is on the same side of the galaxy but at R= 2.8 kpc and the residuals are shown in the fourth row. The shaded area in each plot delimits the emission expected from the disc and the contour levels are the same as in Fig. 3. For the residuals, computed subtracting the model to the data, the black contours represents positive values whilst the white contours are the negative ones; also in this case the contour levels (absolute value) are the same as in Fig. 3.

Intrinsic rotational velocities and velocity dispersion for system of clouds that can be described by a classical two-integral phase-space distribution function, at z= 1.7 kpc and z= 5.1 kpc. From left to right: isotropic model, k= 0.9 model and maximally rotating model (σϕ= 0). Velocity panels: the dotted lines represent the circular velocity uc whilst the solid lines are the model rotational velocities uϕ. Dispersion panels: the dashed lines indicate σz and the solid lines σϕ. In the isotropic case, all the components of the dispersion are the same, whilst in the other two models σz=σR.

Intrinsic rotational velocities and velocity dispersion for the anisotropic model b= 0.1 and k= 1 (left-hand column), the model b= 0.3 and k= 1 (central column) and the model b= 0.1 and k= 0.9 (right-hand column) at z= 1.7 and 5.1 kpc. Rotational velocity panels: the dotted lines represent the circular velocity uc whilst the solid lines are the rotational velocities uϕ. Dispersion panels: the dashed lines indicate σz, the solid lines σϕ and the dash–dotted lines σR; in the first two cases, σϕ=σR.
3.3 Construction of the model
Having fixed the galaxy gravitational field and the cloud density distribution, for each model we first compute σz by integrating numerically equation (3) with a finite-difference scheme. In the isotropic case, we then compute the rotational field from equation (4) using the same numerical scheme. In the anisotropic cases, we can integrate equation (6) or just use (7). The rotation velocity and the azimuthal component of the velocity dispersion are then evaluated on the numerical grid by means of equations (9) and (10). We verified that equations (6) and (7) give the same results in all explored anisotropic models.
As an output for the models a pseudo-data cube, with the same spectral and spatial resolutions and total flux as the data cube of H i observations, is generated as follows. In each grid point, the cloud density, the rotational velocity and the velocity dispersion are projected numerically along the line of sight for the inclination of the galaxy, which is assumed to be seen exactly edge-on. From the projected velocity, we construct a first data cube and, to account for the effect of the velocity dispersion, we convolve the projected density in each cell of this cube with a normalized Gaussian profile with a dispersion equal to the projected velocity dispersion. Finally, for a more realistic comparison, the cube is smoothed to the same spatial resolution as the data (full power beam width = 28 arcsec ≈ 1.3 kpc). We remind that the construction of a pseudo-data cube is crucial because it bypasses all the intermediate stages of data analysis, and the assumptions made in these stages. A critical case is the comparison of the data rotation curves with the rotational velocities predicted by the models. The rotation curves of the extraplanar gas (and of edge-on galaxies in general) are usually derived by fixing a certain amount of line-of-sight velocity dispersion and using the so-called ‘envelope tracing’ method (see Sancisi & Allen 1979; Fraternali et al. 2005). Clearly, if a model has velocity dispersions inconsistent with that adopted to derive the rotation curves from the data (as it happens here; see Section 4), a direct comparison between the two cannot be done (see Section 5).
4 RESULTS
We now present the most important features of some of the considered stationary models for the extraplanar gas of NGC 891, and compare them with the observations.
4.1 Isotropic model
We start by describing the main intrinsic features of the isotropic model, i.e. the analogue of a stationary baroclinic fluid model where the thermal pressure of the gas is replaced by a globally isotropic velocity dispersion tensor. It is then expected that the behaviour of the isotropic model is similar to the baroclinic solutions of Barnabè et al. (2006). However, there is an important difference between these two models in the choice of the density distribution. In our model, the density is chosen to match the observed H i emission (see Fig. 1), whilst the density distribution of Barnabè et al. (2006) was just chosen to satisfy the general rules that guarantee a physically acceptable rotational velocity field. In other words, our density distribution is fixed by the H i observations, and not by the requirement u2ϕ≥ 0. Using this cloud distribution, the resulting σz=σR=σϕ has values ranging from 160 (in the centre) to 35 km s−1 (at R∼ 20 kpc) with mean values between 50 and 100 km s−1 (Fig. 2, bottom-left panel).
In the left-hand panels of Fig. 2, we present the rotation curves (top panel) and the radial velocity dispersion profiles (bottom panel) at distances from the plane z= 1.7 kpc (lower halo boundary) and z= 5.1 kpc; the dashed lines show the circular velocities uc. As expected from the considerations of Section 2.3, in the external regions of the galaxy the rotational velocity is below the circular velocity because of the negative vertical gradient in uϕ. The radial profile of the velocity dispersion shows a monotonic decrease with R but the values of the dispersion are everywhere greater than the mean observed value of ∼20 km s−1. This latter is also the value adopted to derive the rotation curves above the plane from the H i observations of NGC 891 (Fraternali et al. 2005, here shown in Fig. 7). As a consequence, a direct comparison between these curves and the circular velocities of our models is not possible. We stress again that these problems are overcome by comparing directly the models with the raw data cubes, where all the kinematical and density effects are fully taken into account.

Rotational velocities of the model b= 0.1 and k= 1 (solid line) and rotation curves in the H i by Fraternali et al. (2005) (points with error bars) at z= 3.9 kpc (top panel) and z= 5.2 kpc (bottom panel). For each plot, the long-dashed line represents the rotational velocity on the mid-plane.
Fig. 3 (first column from the left) shows the pseudo-data cube constructed from this Jeans model, while each panel in the rightmost column represents the observed emission of H i gas in a particular velocity channel. The numbers on the top-right corners of the data column represent the deviations of the line-of-sight velocities from the systemic one (528 km s−1), whilst the shaded area on each map delimits the emission expected from the disc (±3σ spatial resolution), which we are not attempting to reproduce with this model. We can see that the observed H i emission at higher rotational velocity (corresponding to the channel at vlos=−236.0 km s−1) is fully due to the mid-plane, i.e. the halo is not visible. This is not surprising because the halo gas rotates more slowly than the gas in the disc and in fact, as we move towards the bottom panels, the halo emission becomes important. Due to its high-velocity dispersion, in the isotropic Jeans model some emission in the halo region is present also in the upper two velocity channels; only in the middle channel, the agreement is good whilst in the bottom channels the emission is too horizontally elongated.
Summarizing, it is possible to construct an isotropic Jeans model with a realistic halo density distribution, in which a negative vertical gradient in the rotational velocity is present. However, the predicted velocity dispersions along the line of sight are much higher than those observed, so that a number of features of the data cube are not reproduced. In order to solve these problems, in the next section we consider different models with anisotropic velocity dispersion tensors.
4.2 Anisotropic models
The assumption of anisotropy in the velocity dispersion can overcome, at least in principle the problems originated by the high values of σ obtained in the isotropic models. In Section 4.2.1, we focus on the classical Satoh decomposition in a two-integral distribution function (i.e. σR=σz everywhere), and in Section 4.2.2 we discuss the case of a three-integral phase-space distribution function for the cloud system. In the following, we indicate with σlos the component of the velocity dispersion along the line of sight on each place in the galaxy.
4.2.1 Two-integral anisotropic systems
We examine here cloud systems described by a two-integral phase-space distribution function, for which σz=σR. The relevant equations are obtained by taking b= 1 in equations (5), and adopting a Satoh decomposition in the azimuthal direction. When k= 0 σ2ϕ is maximal, while when k= 1 the system is isotropic. Allowing for k=k(R, z), more rotationally supported models can be constructed, up to the maximally rotating one where σ2ϕ= 0 (Ciotti & Pellegrini 1996). First of all, we investigate a model with constant k and assume k= 0.9; for lower values, the disagreement with the data increases. We expect that the model is not better than the isotropic (k= 1) case in reproducing the observations, because σlos is increased by the adopted anisotropy; in particular, as can be inferred from equation (10), σϕ≥σz=σR. The central column of Fig. 2 (bottom panel) clearly illustrates this fact, showing a difference among σϕ and the other two components of approximately 30 km s−1, on average. For what concerns, the properties of the rotation curves, the considerations carried out in the isotropic case are still valid, because from equations (7) and (9) it follows that uϕ=kuiso so that in the external regions of the galaxy uϕ < uc. The pseudo-data cube of the model presented in Fig. 3 (second column) shows that in the channels close to the systemic velocity (bottom) the emission of this model is even more elongated than in the isotropic case, in complete disagreement with the data.
In two-integral systems, the line-of-sight velocity dispersion can be reduced only if k > 1. As a limit case, we present the results for the maximally rotating model in which k=kmax(R, z) ≥ 1 such that the rotational velocity has its maximum value everywhere and σϕ= 0. The corresponding intrinsic rotation curves are presented in Fig. 2 (top-right panel) and their peculiarity is the steep rise in the central regions. The reduced value of σlos improves the agreement with the data, as it can be seen from the pseudo-data cube of the model in Fig. 3, especially in the channels near the systemic velocity. This agreement is not so good in the channel at vlos=−236.0 km s−1 and in general in all the channels between −236.0 and −161.8 km s−1 (not shown here) where, due to the steep rise in the rotational velocity at small R, there is emission in the central halo regions not seen in the data.
4.2.2 Three-integral anisotropic systems
We now turn the attention to the models with b≤ 1 (therefore supported by a three-integral phase-space distribution function) and we first discuss the case σR=σϕ (i.e. k= 1). The best fit to the data is obtained by an anisotropic model with b∼ 0.1, which limits the line-of-sight velocity dispersion to about 20 km s−1 for a large interval of R (Fig. 4, bottom-left panel). The rotation curves for this model (top-left panel) are very similar to the circular velocity curves, in accordance with equation (7) which states that, in the limiting case b= 0, the curves coincide. The pseudo-data cube of the model is presented in Fig. 5 (leftmost column). In the high-velocity channels (top panels), the halo emission is still present but, at variance with the isotropic case, this is due to the fact that the rotational velocities of the model are slightly higher than those observed. In the low-velocity channels (bottom panels), the halo emission is narrower than the data along the horizontal axis, due to a rapid decrease of the velocity dispersion in the outer parts. We discuss these discrepancies more in detail in Section 5.
An important issue regarding the anisotropic models is the effect that the choice of the parameters b and k may have on the properties of the solutions. We analyse this aspect by fixing the value of one of the two parameters and by varying the other. The results of this comparison, for representative values of b and k, are shown in Fig. 4, where the model with b= 0.1 and k= 1 (which, hereafter, we will also refer to as the ‘high-σz model’) has been taken as a reference case. In particular, increasing the value of b at fixed k has the net result of increasing the line-of-sight velocity dispersion (i.e. σR and σϕ) whilst the rotational velocity is decreased; the decrease in rotational velocity is also obtained when the value of k is decreased at fixed b, but in this case only the value of σϕ is affected. In Fig. 5, we present the pseudo-data cubes of the models just described. The emission of the reference model (b= 0.1, k= 1) in all the velocity channels is less horizontally extended than that of the model with b= 0.3, due to the smaller values of σlos. Although the b= 0.3 model seems to agree better with the data in the channel maps close to systemic velocity, the top panels of Fig. 5 show substantial halo emission, due to the now increased line-of-sight velocity dispersion. The interpretation of the differences between the reference model and the model with k≠ 1 is complicated by the fact that σϕ≠σR so that the extension of the emission strongly depends on their relative contribution to the velocity dispersion along the line-of-sight. In particular, the importance of σϕ is maximum in the high-velocity channels (top panels), and then it progressively diminishes in the channels near the systemic velocity in favour of σR.
In short, three-integral models with b < 1 and k= 1 perform better than the isotropic and the two-integral models because σlos can be reduced to values comparable to the observed one. However, a number of features of the data cubes are still not reproduced revealing intrinsic problems with all these stationary models that we discuss more in detail in the next sections.
4.3 Position–velocity plots
Among the models presented above, we select the three most representative and compare them further with the H i data. Fig. 6 shows two cuts of data cube of NGC 891 (rightmost column) taken perpendicularly to the plane of the galaxy at R= 7.5 kpc (first row) and R= 2.8 kpc (third row) from the centre, towards north-east. These plots are analogous to those shown in fig. 16 of Oosterloo et al. (2007). The position–velocity diagrams are compared with the prediction of three models: the isotropic model, the maximum rotation model and the three-integral high-σz model. Also the corresponding residuals are shown (second and fourth rows) computed as the difference between the data and the models; the shaded area in each position–velocity plot delimits the emission expected from the disc.
The characteristic triangular shape of the data diagrams (rightmost column) is due to the negative vertical gradient in the rotational velocity of the halo and is the key feature that the models should reproduce. Clearly, this is not the case for the isotropic model as the high-velocity dispersion makes the emission very elongated, although a negative vertical gradient in the rotational velocity is visible. In the 2.8-kpc cut (third row), the emission is so elongated that a substantial amount of gas is apparently ‘counter-rotating’ (upper part of the plot). The maximally rotating model (second column) also does not reproduce the shape of the emission especially at R= 2.8 kpc from the centre of the galaxy (third row). Also in this case the predicted line-of sight velocity dispersion is too high. The position–velocity diagrams for the high-σz model (third column) show a qualitative agreement with the data as the triangular shape is reproduced. However, the velocity dispersion in the upper halo |z| > 5 kpc is clearly not matched and there is a downward shift of the emission especially visible in the 7.5 kpc cut. These features are also apparent in the residual maps and in particular the high-σz model, despite reproducing well the shape of the data, shows substantial residuals. In addition, the residuals also reveal the intrinsic asymmetric distribution of the extraplanar gas with respect to the mid-plane of NGC 891.
Fig. 6 gives a different view of the discrepancies already noted in Figs 3 and 5. The advantage of a cut perpendicular to the plane of the galaxy is that it captures in one diagram the kinematics of the extraplanar gas at different heights and, as mentioned, its characteristic triangular shape is the evidence of the gradient in rotational velocity with height. The only model that reproduces at least qualitatively this shape is the anisotropic b= 0.1, k= 1 model.
5 DISCUSSION
In this paper, we have explored an alternative interpretation of the baroclinic fluid homogeneous models for extraplanar gas, i.e. that of a ‘gas’ of H i clouds described by the stationary Jeans equations. Due to the formal equivalence of the equations describing the two systems, a similarity in the behaviour of the isotropic Jeans model and that of the baroclinic solutions of Barnabè et al. (2006) is expected. The present investigation is not just a re-interpretation of the results of Barnabè et al. (2006): even in the isotropic case, our models differ from theirs in the choice of galaxy mass and cloud density distributions. We find that the choice of the mass model has a little impact on the properties of the solutions, but the form of the density distribution is critical. Barnabè et al. (2006) adopted a very flat density distribution, in order to reproduce the off-plane rotation curves. A flat density distribution requires less pressure support against the vertical gravitational field of the galaxy which results in a low temperature of the gas, typically 105 K. For such a temperature, the expected velocity dispersion in a Jeans isotropic model would have been of the order of 30 km s−1, close to the mean observed value (Oosterloo et al. 2007). Instead, in the present model the parameters of the density distribution are tuned to reproduce the observed H i distribution which has a greater scaleheight than that used by Barnabè et al. (2006, see equation 17). Thus, the typical values of the velocity dispersion necessary to sustain the halo are of a factor ∼3 higher than the above. As we have seen, this high-velocity dispersion has a large impact on the observable kinematics of the extraplanar gas and it is the main reason why the isotropic model fails to reproduce the data. The higher values of the velocity dispersion also influence the rotational velocities: indeed the rotation curves of our Jeans model are about 20 km s−1 lower than those obtained by Barnabè et al. (2006).
The high values of the velocity dispersion of the H i halo clouds may appear, at first sight, unphysical. However, we note that these velocities are unavoidable in any model attempting to reproduce gaseous haloes with such large scaleheights (e.g. Fraternali & Binney 2006). The source of kinetic energy for these clouds must come from supernovae, indeed hydrodynamical simulations of superbubble expansion in galactic discs predict these kinds of blowout velocities (e.g. Mac Low & McCray 1988). Finally, we also note that velocities of the order of 100 km s−1 are in fact typical for halo clouds in the Milky Way (Wakker & van Woerden 1997) and have been observed in external galaxies whenever the inclination of the disc along the line of sight is favourable (e.g. van der Hulst & Sancisi 1988; Boomsma et al. 2008).
As already mentioned in Section 4.3, the most satisfactory model is the anisotropic b= 0.1, k= 1 model (or high-σz model), which has been constructed in order to have σR=σϕ < σz. These requirements are roughly in agreement with the prescriptions for a galactic fountain where the material is ejected mostly vertically from the disc and falls back also vertically. Fraternali & Binney (2006, 2008) have built galactic fountain models for NGC 891 and compared them with the data cube in the same way we did here. They found that the halo gas distribution is well reproduced by fountain clouds that are kicked out of the disc with a Gaussian distribution of initial velocities and dispersion of about 80 km s−1, which is a value very similar to the average σz predicted by our stationary models (Fig. 4). Moreover, Fraternali & Binney (2006) investigated the opening angles about the normal to the plane of the ejected clouds finding that it has to be lower than 15°, in other words the clouds are ejected almost vertically. Therefore, the b= 0.1, k= 1 model is quantitatively similar to the fountain models. What makes the difference between the two is the lack of non-circular (inflow and outflow) ordered motions in our stationary model that, instead, in fountain models are always present.
The most problematic discrepancy between the high-σz model and the data is visible in the channel map close to the systemic velocity (see channel at −5.2 km s−1 in Fig. 5). This map shows the gas that has a null velocity component along the line of sight (once the systemic velocity has been removed). Much of this gas is located in the outer parts (in R) of the galaxy both in the disc and in the halo. The width of the channel (along the horizontal axis) is mostly due to the velocity dispersion of this gas. The high-σz model fails to reproduce the data in two ways: (1) the channel map is too narrow and (2) the width (in the x-axis) of the emission decreases with height contrary to what seen in the data. These differences are caused by the fact that the velocity dispersion in the model decreases both with R and with z, whilst in the data the two behaviours seem reverse. The fact that the velocity dispersion increases with height has been clearly shown by Oosterloo et al. (2007) who built artificial cubes with different parameters and compared them with the NGC 891 data cubes. These authors also kept the dispersion constant with R and reproduced much better the shape of the channel maps close to the systemic velocity (see their fig. 14). The decrease of the velocity dispersion with R and z is a common problem of all our stationary models and may be related to the lack of (ordered) non-circular motions mentioned above.
In the high-σz model, the rotational velocities can be directly compared with those obtained from the data because the line-of-sight velocity dispersion has values comparable with the observed one. In Fig. 7, we show the rotation curves of NGC 891 at distances from the plane of 3.9 kpc (top panel) and 5.2 kpc (from Fraternali et al. 2005). The rotational velocities predicted by the b= 0.1, k= 1 model are shown as solid lines, the dashed line shows the rotation curve in the plane. In the derivation of these rotation curves from the data, it has been assumed a constant value of the velocity dispersion2(20 km s−1). The curves have been derived using the envelope tracing method, which is such that the larger is the velocity dispersion one assumes the lower is the obtained rotational velocity. In our high-σz model, the velocity dispersion is not constant along R and it is exactly 20 km s−1 only at ∼10 kpc (Fig. 4). Ideally, one should correct the data points for this effect obtaining slightly lower velocities for R < 10 kpc and higher for R > 10 kpc but the effect is minimal. Overall, for what concerns the rotation curves of NGC 891 we can say that the high-σz stationary model predicts a gradient that is quite close to (although slightly lower than) the observed one.
The stationary models presented here do not aim to explain the origin of the extraplanar gas. Instead, their goal is to find a stationary description for the extraplanar gas phenomenon whatever physical mechanism is producing it, assuming that it can be considered roughly stationary. This assumption should be reasonably valid if the extraplanar gas is produced for instance by a galactic fountain and the star formation rate of the galaxy does not vary considerably with time as it seems to be the case for galaxies like the Milky Way (e.g. Twarog 1980). The investigation presented by Fraternali & Binney (2006) shows that the rotational velocities predicted by a galactic fountain model are systematically higher than the one derived from the data and also higher than those predicted by the stationary high-σz model shown in Fig. 7. This latter result is not surprising given that in the fountain model the gas clouds move outwards for a large fraction of their trajectories and thus tend to be at vϕ > uc for most of their time (uc is the circular speed at that position). On the contrary, in the high-σz model the gas has basically uϕ≃uc (Fig. 4). Fraternali & Binney (2008) revised the fountain model by including interactions of the fountain clouds with the surrounding ambient medium (see also Barnabè et al. 2006 for a similar suggestion). These interactions cause the fountain clouds to lose part of their angular momentum and to decrease their rotation velocities. Such a model is to date the best description for the dynamics of the extraplanar gas. In addition to the rotational velocities, this latter model reproduces the data cube in detail including the channel maps close to the systemic velocity (see fig. 2 of Fraternali & Binney 2008). Kaufmann et al. (2006) also reproduced the rotation curves of NGC 891 fairly well with a model in which the extraplanar gas forms by condensation of the extended warm–hot corona, but they did not attempt to build pseudo-data cubes to compare directly with the observations. However, the thermal instability on which such a model is based is unlikely to occur in galactic coronae, because of the combined effect of buoyancy and thermal conduction (Binney, Nipoti & Fraternali 2009).
Whatever the origin of the extraplanar gas, it is important to investigate whether or not it is in a stationary state. If so, it should be possible to find stationary models that reproduce these data in detail. This paper has been the second attempt of this sort after Barnabè et al. (2006). In both these attempts, non-circular motions of the gas clouds have been neglected for simplicity, but in the kinematics of the extraplanar gas this kind of motions are clearly present (e.g. Boomsma et al. 2008; Fraternali et al. 2001) and they could affect substantially the observed kinematics of the halo. More likely, the cause of the discrepancy between our treatment and the observations lies on the assumptions of a Jeans-based model and in particular on the ballistic nature of the cloud motion. Not only the drag between the H i halo clouds and the corona may have an important dynamical effect but also at the turbulent cloud/corona interface there may be a considerable exchange of mass. Modelling this interface is a very challenging numerical problem (e.g. Vieser & Hensler 2007a,b and a secure estimate of the rate of mass exchange is not yet available. This issue will be studied in a forthcoming paper (Marinacci et al., in preparation).
6 Summary and conclusions
In this paper, motivated by the results of Barnabè et al. (2006), we investigated the possibility that the extraplanar gas in spiral galaxies can be modelled as a ‘gas’ composed by cold H i clouds that follows the stationary Jeans equations. In doing this, we are assuming that the pressure-bound clouds are moving almost ballistically in the halo. This assumption is valid in the limit of massive clouds having negligible rates of mass exchange with the corona.
In this alternative interpretation of fluid baroclinic models, the thermal pressure is replaced by an isotropic velocity dispersion tensor, so that the problem of high temperature of gaseous homogeneous models is eliminated. We have also extended the discussion to simple phenomenological models with anisotropic velocity dispersion tensors. We constructed both isotropic and anisotropic models in the well-constrained gravitational field of the spiral galaxy NGC 891, and compared their predictions to the observed kinematics of the extraplanar gas in that galaxy. For each model, we built a pseudo-data cube with the same resolution and total flux as the observations. The main results of our analysis can be summarized as follows.
The adopted functional form of the cloud density distribution, taken by the observations, leads to physically acceptable solutions in all the models investigated. The cloud density distribution is centrally depressed, and, in order to match the vertical extension of the H i halo of NGC 891, it has higher scaleheight than that used by Barnabè et al. (2006).
All the models computed show a negative vertical gradient in the rotational velocity, the distinctive feature of the kinematics of the extraplanar gas.
The support against the vertical gravitational field of the galaxy requires a σz≃ 50−100 km s−1 and therefore the line-of-sight velocity dispersion of the isotropic model is a factor ∼ 3−4 higher than that observed.
With the introduction of the anisotropy, it is possible to restrict the line-of-sight velocity dispersion to the observed values, but the predicted vertical gradient in the rotational velocity is somewhat too shallow and other features of the data cube are not fully reproduced.
We conclude that the dynamics of extraplanar gas in a galaxy like NGC 891 is not fully described by any of the stationary models considered here. However, a model with an anisotropic velocity dispersion tensor, which mimics a galactic fountain is the preferable among all. The fact that none of the stationary Jeans models analysed here can reproduce all the features of the observed (extraplanar) gas kinematics might suggest that the cloud motion is not purely ballistic, and that the interaction between the clouds and the coronal gas, perhaps in the form of mass exchange, plays an important dynamical role.
Note that this anisotropy cannot be realized (except for b= 1) under the common assumption of a two-integral distribution function depending on energy and angular momentum along the z-axis, as in this case σR=σz.
Fraternali et al. (2005) assumed σgas∼ 8 km s−1, for the disc and the halo. Oosterloo et al. (2007) found that the velocity dispersion in the halo is actually larger and about 20 km s−1, thus it is appropriate to shift the data points of Fraternali et al. (2005) down by 11 km s−1 (see Fraternali & Binney 2008 for details). This is equivalent to derive the rotation curves assuming a constant σgas∼ 20 km s−1 for the halo region.
We thank G. Bertin for helpful discussions and J.J. Binney for reading the manuscript and providing precious suggestions to improve the presentation of the paper. We also thank an anonymous referee for his/her valuable comments.
REFERENCES



