Interpreting the Kustaanheimo–Stiefel transform in gravitational dynamics

Abstract

1 INTRODUCTION

The Kustaanheimo–Stiefel (KS) transform is a remarkable relation between the two most important elementary problems in dynamics: under a transformation of coordinates and time, a Kepler problem changes into a harmonic oscillator. Especially noteworthy is that the collision singularity in the Kepler problem is transformed into a regular point. The name comes from the works by Kustaanheimo (1964) and Kustaanheimo & Stiefel (1965), while the book by Stiefel & Scheifele (1971), which is largely devoted to the KS transform and its consequences, is perhaps the best-known source. For a very short summary, see ‘regularization’ in Binney & Tremaine (2008). An important application of the KS transformation is in numerical orbit integration, where the singularity removal is used to great advantage for simulating dense stellar systems with near collisions (Aarseth & Zare 1974a,b; Jernigan & Porter 1989; Mikkola & Aarseth 1990, 1993). Some recent papers also re-examine the formalism itself (Bartsch 2003; Waldvogel 2006).

In two dimensions there is a much simpler version of the KS transform going back to Levi-Civita (1920). In the Levi-Civita transform, the coordinate plane is read as the complex plane, and the complex square root of the coordinate becomes the transformed coordinate. The geometrical interpretation is clear: the complex phase gets halved. The KS transform is also a kind of square root, but in four dimensions. One wonders how the geometrical interpretation generalizes.

It turns out that slewing a telescope is a convenient geometrical analogy. Suppose the telescope is at zenith and we want to slew it to a particular star in one rotation. Normally we would simply move along a great circle from the zenith to the star. However, we might prefer a different rotation (to avoid crossing the moon, say). For example, we could choose the mid-point on the above great circle and rotate about it by 180°. In any case, the chosen rotation axis and the rotation angle are effectively the KS transform of the star. This idea of rotation in three dimensions about a non-unique axis generalizes the idea of halving the phase in a complex square root.

This paper attempts to provide some new insight into the KS transform by providing some reformulations and new derivations of known results, and especially to make the geometrical interpretation evident.

2 QUATERNIONS AND ROTATION

Before considering KS theory, it is useful to review a concise algebraic way of specifying rotations in three dimensions, not often used in astrophysics but standard in computer graphics: quaternions.

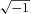Quaternions are a generalization of complex numbers. The of complex numbers is replaced by three unit quaternions i, j, k, such that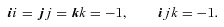

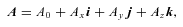
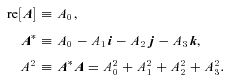
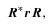
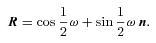
1

From (1) it follows that ij=k=−ji and so on. In other words, quaternions are like a combination of dot and cross products in vector algebra. (Although historically quaternions came before, having been invented by none other than W. R. Hamilton of Hamilton's equations.)

A general quaternion has the form

2

where we will call A₀ the real part. A quaternion with no real part is effectively a vector in three dimensions.

In analogy with complex numbers, we will use the following notation for quaternion conjugates and absolute values:

3

It is easy to see that re [A*]= re[A] and (AB)*=B*A*, and as a result

4

Rotation in quaternion notation is beautifully concise. Say we want to rotate a vector r by angle ω about a unit vector n. Using quaternion algebra the rotation is simply

5

where

6

Unlike the equivalent expression using Euler angles, the expression (5) has no coordinate singularities (or ‘gimbal lock’) and as a result is numerically more stable, which explains its popularity in computer graphics.

For an arbitrary (i.e. non-unit) quaternion R, the expression (5) amounts to a rotation combined with scalar multiplication.

It is possible to represent quaternions as matrices (though not necessary, even for numerical work). A familiar representation is in terms of Pauli matrices:

7

or

8

Pauli matrices are most important as operators on quantum two-state systems (being Hermitian, whereas quaternions are anti-Hermitian). In recent years, the most exciting two-state quantum systems have been Qbits in quantum computing. It turns out that expressions of the type (5) appear in the description of quantum-computing gates (see Mermin 2007, who also provides a derivation of essentially the above three-dimensional rotation formula).

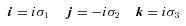
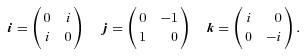
3 THE KUSTAANHEIMO–STIEFEL TRANSFORM

Let

9

denote a point in space. The KS transform of q is the quaternion

10

the transformation formula being

11

A solution for Q is

12

as is easily verified by multiplication, following the quaternion rules. However, Q^I is not unique, because changing to

13

leaves equation (11) invariant. Thus ψ behaves like a gauge.

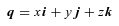
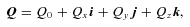
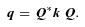
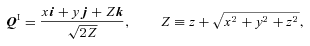
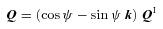
Everything so far is already in the literature. The new result in this paper is that we can readily visualize Q, including its non-uniqueness.

Comparing (11) and (5), it is evident that Q is a rotator that takes the z-axis to q. To visualize Q, let us rewrite q as

14

where r, θ and φ are the usual polar coordinates. Rewriting Q^I in the solution (12) and simplifying, we have

15

In other words, the zenith distance of Q^I is half-way along the great circle from k to q. From (6) we see the rotation angle ω would be π. Now let us apply the gauge transformation (13) with ψ=π/2 to Q^I. This gives

16

Now the implied rotation is by θ, about an axis perpendicular to both k and q. In general, we can write

17

which is to say, Q could be anywhere on the great circle joining Q^I and Q^II. The telescope-slewing analogy given above is simply a description of the preceding three formulas.

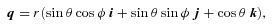
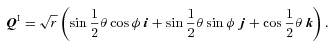
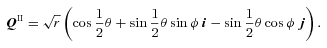
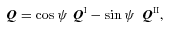
An interesting special case is φ= 0, which gives q=r(cos θ k+ sin θ i) and ⁠. Then Q^I is effectively the complex square root of q (we need to read k as the real axis and i as the imaginary axis). In other words, the planar case can be reduced to the Levi-Civita transform by a suitable gauge.

Quaternion formulations of the KS transform have been discussed by several authors: Stiefel & Scheifele (1971) mention quaternions but appear to dislike them, while later authors (for example Vivarelli 1994; Waldvogel 2006) are more favourable. The precise definition adopted for the transform varies, but is equivalent to equation (11). That Q represents a rotation and shrinking/stretching of q is also known. Bartsch (2003) specifically notes that the rotation axis is unique in two dimensions but not in three. However, the explicit description of the implied rotations, as above, appears to be new.

4 THE CANONICAL MOMENTUM

So far we have just discussed geometry, but of course the real significance of the KS transform is dynamics, which we now consider. Let

18

be the canonical momentum conjugate to q. We seek

19

that will be canonically conjugate to Q. Let us write

20

Using the identity (4), we can rewrite the middle term as re[p (dQ*kQ)*]. Since p=−p* and (dQ*kQ)*=Q*(−k)dQ the term becomes becomes re[p*Q*k dQ]. Thus we have

21

Now if we define

22

we have

23

which is to say, p· dq=P· dQ. Provided the Hamiltonian depends on P, Q only through p, q and not on the gauge ψ, the transformation (P, Q) → (p, q) is canonical.

To get an explicit expression for p, we multiply (22) on the left by Q*k, obtaining

24

Note that while we have to be careful about the order of multiplication when i, j, k are involved, real numbers like Q² commute with everything. Since p has no real part, re[Q*kP]= 0 identically. We can think of it as a formal constant of motion resulting from invariance with respect to ψ.

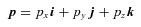
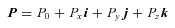
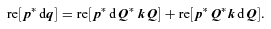
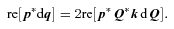
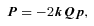
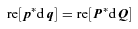
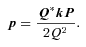
That P (as defined in equation 22, or equivalently) completes a canonical transformation is a standard part of KS theory, but the derivation of the canonical condition using quaternion identities appears to be new.

5 THE TWO-BODY PROBLEM AND THE HARMONIC OSCILLATOR

Let us now write the Kepler Hamiltonian

25

in terms of KS variables. Multiplying each of (11) and (22) by its quaternion conjugate, we have

26

and substituting these gives

27

We now use a device known in Hamiltonian dynamics as a Poincaré time transformation. This involves introducing a fictitious time variable s, whose relation to t we choose to be

28

Since Q² is the radial distance in the Kepler problem, (28) is in fact Kepler's equation, and s is the eccentric anomaly. In the fictitious time variable s, the equations of motion are given by a new Hamiltonian

29

with E being the constant initial value of H. The time-transformed Γ Hamiltonian is zero along a trajectory, but its partial derivatives are not zero.

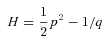
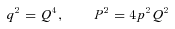
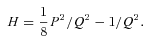
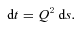
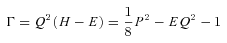
The Hamiltonian Γ is remarkable indeed. For E < 0 (bound orbits) it is a harmonic oscillator. Since Q has four components, Γ is like a mass on an isotropic spring in four Euclidean dimensions. Thus the well-known fact that the bound Kepler problem has a dynamical O(4) symmetry. For the unbound case, the symmetry group is different: formally the Lorentz group, but with a physical meaning completely different from special relativity. And – perhaps most importantly – Hamilton's equations for Γ are well behaved even at Q= 0 (a collision). This is known as regularization and was the original motivation for KS theory.

The effect of an external force F is simple. From (22) it follows immediately that F will add an extra contribution of −2kQF to dP/dt, which amounts to a contribution of −2Q²kQF to dP/ds. Provided the external force is non-singular, the equations of motion in s remain regular.

6 REGULARIZING THE THREE-BODY PROBLEM

Application of KS regularization to N-body simulations involves expressing the gravitating system either as a tree-like hierarchy of coupled two-body systems (Jernigan & Porter 1989) or as a chain (Mikkola & Aarseth 1990, 1993). The basic idea can be described using the three-body problem with all masses unity. Here again, quaternions enable a concise formulation.

In relative coordinates, the Hamiltonian for three unit gravitating masses can be written (cf. equation 12 in Aarseth & Zare 1974a) as

30

plus an additional potential V(q₁, q₂). Here q₁, q₂ expresses the position of the first and second body relative to the zeroth body, while p₁, p₂ express the momenta of the first and second bodies in the barycentric frame. Meanwhile, V(q₁, q₂) expresses the mutual interaction of the first and second bodies, plus any external potential. We can regard V(q₁, q₂) as an external potential, and since we already know how to deal with external forces, we set V aside and concentrate on H.

Now we introduce KS variables q₁=Q*₁kQ₁ and so on. Defining

31

we can write p₁·p₂ as Π/(4Q²₁Q²₂). Applying a Poincaré time transformation

32

gives

33

where E is the value of H. The Γ Hamiltonian has no denominators,and is thus regular for collisions with the zeroth body. (We assume V remains regular, that is to say, the first and second bodies do not collide with each other or any other bodies than the zeroth. In practice, simulations redefine the relative coordinates whenever necessary, according to who is close to whom.)

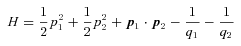
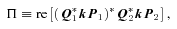
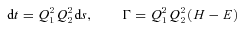
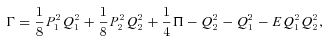
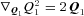For the equations of motion, we need derivatives with respect to quaternion components. First we have ⁠. Slightly more subtle is 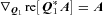if A is independent of Q₁. Using this last identity, together with the definition (31) of Π, we derive

34

Hamilton's equations are then

35

and similarly for P₂, Q₂.

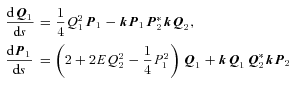
7 DISCUSSION

In dynamical astronomy the KS transformation is profound, but may appear mysterious. This paper attempts to make it less mysterious, and hopefully therefore more useful, by explaining it in three-dimensional geometric terms. There are several possible directions in which the KS transformation may turn out to be useful.

First, one can imagine new orbit integrators specialized to nearly Keplerian problems. Work on dense stellar systems with near collisions has already been mentioned (for reviews see the books Aarseth 2003; Heggie & Hut 2003). In the planetary regime, which differs from the dense-stellar case in having few bodies but many more orbital times, time transformations reminiscent of (28) used for KS regularization have proved useful for highly eccentric orbits (Mikkola 1997; Emel'yanenko 2002), while some integration algorithms (Mikkola & Tanikawa 1999; Preto & Tremaine 1999) apply the time transformation (28) implicitly. Could the KS transformation itself be exploited here?Fukushima (2005) has some further ideas.

Secondly, it is conceivable that KS variables could simplify perturbation theory. Perturbation theory in classical celestial mechanics (see for example Murray & Dermott 2000) is algebraically frighteningly complicated, basically because the natural variables for the unperturbed and perturbed parts (being the Keplerian action-angles and real-space coordinate) are related through an implicit equation. On the other hand, the action-angles of the KS-transformed Kepler problem are explicitly related to space coordinates – the implicit equation is transferred to the time variable. Could some major simplification be achieved through KS variables? Some progress has been made by Vrbik (2006).

Thirdly, the KS transformation might provide new insight into analogous quantum problem. Bander & Itzykson (1966a,b) derive the symmetry groups of the bound and unbound Coulomb problems. These turn out to be the same four-dimensional symmetries as in KS theory. Is the KS transformation implicit in that work?

I am grateful to Seppo Mikkola for introducing me to KS theory, and to Marcel Zemp, Scott Tremaine and the referee, Jörg Waldvogel, for suggesting improvements in the manuscript.

REFERENCES