Heating of near-Earth objects and meteoroids due to close approaches to the Sun Free

Abstract

1 INTRODUCTION

It is well known that the physical properties of most asteroids (and their fragments, the meteorites) have been affected by heating processes. The analysis of the available meteorite collections shows that meteorites and their asteroidal parent bodies have been thermally altered to some degree. The alteration ranges from low-temperature aqueous processes (<300 K) up to partial or complete melting, differentiation and fractional crystallization (>1150 K) (Keil 2000). The main source of heating has been identified as internal heating induced by decay of short-lived radionuclides, notably ²⁶Al (Grimm & McSween 1993). The effects of heating processes have also been identified on the surfaces of asteroids by remote sensing spectroscopy of primitive main-belt asteroids (Vilas & Gaffey 1989; Hiroi et al. 1993). Despite the general consensus on radionuclides heating, other processes have been suggested to occur: for instance, heating during the pre-accretion phase or due to collisions. The latter may produce high temperatures in the regions involved in high-energy impacts, often causing the partial melting of the involved bodies (see discussion in Rivkin et al. 2002).

In this paper, we discuss a new heating process, which has been neglected so far, namely the heating due to close approaches to the Sun. This effect may be relevant for bodies such as near-Earth objects (NEOs), whose perihelia are sometimes very close to the Sun, and significant temperatures can be attained.

In the present NEO population, the fraction of bodies with relatively small perihelion (q) is very small. However, this is by no means representative of the past (and future) dynamical tracks. Detailed simulations show that a large fraction of NEOs may have had small perihelion distances for some time, hence experiencing episodes of strong heating. Moreover, since meteoroids have an orbital evolution similar to that of NEOs, this process may also affect the meteorite samples.

The detailed effects of the heating during Sun-close approaches depend on the thermal properties of the bodies. Albedo, emissivity, macroscopic surface roughness and thermal inertia are the physical parameters that determine the surface temperature. The latter parameter measures the resistance of a material to temperature changes, for example, due to the varying day/night illumination caused by the rotation of the body. The rotation state of the body also affects its temperature profile. For instance, for given set of thermophysical parameters, a rapid rotating asteroid has a temperature distribution more smoothed out in longitude than a slower rotating one. The direction of the body's spin vector causes also seasonal effects.

In this work, we estimate the amount of heating due to the Sun that NEOs and meteorites are likely to have experienced. We do this by studying their dynamical history. We then use thermal models to correlate their dynamical history with surface temperatures. Finally, some possible consequences of the heating are discussed.

2 ORBITAL PROPERTIES OF NEOS

NEOs evolve rapidly in the Keplerian orbital elements space (a, e, i) due to a combination of close encounters with the terrestrial planets and resonances with the giant planets. Two aspects of this orbital evolution are relevant for the analysis of the heating process: (i) the probability that each NEO attained a q below a given limit (q_s) during the evolution; (ii) the cumulative time spent at distances below q_s. In the following sections, we first explain how we estimated these quantities and then present and discuss the results that we have obtained.

2.1 Estimating the past dynamical histories of NEOs

The most complete model of the orbital distribution of NEOs is that developed by Bottke et al. (2000, 2002). This model assumes that NEOs come primarily from five intermediate sources: the 3:1 mean-motion resonance with Jupiter; the ν₆ secular resonance; the Mars-crossing population (IMC); the collection of resonances crossing the outer asteroid belt (OB) and the trans-Neptunian region [as dormant Jupiter family comets (JFC)]. In the NEO orbital space (q < 1.3 au), the steady state orbital distribution of the bodies coming from each of these sources [R_source(a, e, i)] was computed using a large number of numerical simulations. The orbital distribution of the NEO population was then constructed as a linear combination of the distributions related to each source, i.e.

The coefficients N_source for this combination were determined by fitting the distribution of the NEOs discovered or accidentally recovered by the Spacewatch survey, once observational biases had been taken into account. This model was later shown to reproduce adequately also the orbital distributions of NEOs discovered by the LINEAR and Catalina Sky surveys (Zavodny et al. 2008).

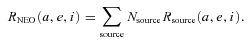
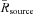Given a specific NEO, using the Bottke et al. model we estimate the probability that it comes from each of the considered intermediate sources, as follows. We first define a box in (a, e, i) orbital space in which the NEO currently resides. Then, for each source, we compute ⁠, as the integral of R_source(a, e, i) over the box; we also compute 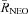in an equivalent manner. Then, the probability that the NEO comes from a given source is given by

In our calculation, we use boxes of size ⁠. The probability P(q_s) that the considered NEO achieved in the past an orbit q < q_s is

where P_source(q) is the probability that objects coming from the source achieved q < q_sbefore entering the (a, e, i) box. Similarly, the mean time T(q_s) spent on orbits with q < q_s can be computed as

where T_source(q_s) is the mean time spent on orbits with q < q_s by the particles reaching these kinds of orbits from the source, before entering the (a, e, i) box. To compute P_source(q_s) and T_source(q_ss), we went back to the original simulations used by Bottke et al. to construct the R_source(a, e, i) distributions. The computation is just a matter of book-keeping, while the outputs of these simulations are read sequentially in time. For simplicity (and availability of the original simulations), we did this only for the 3:1, ν₆ and OB sources. We then assumed that the objects coming from the IMC population behave statistically as a 1:1 combination of the objects coming from the 3:1 and ν₆ sources; similarly we assumed that the objects coming from the JFC source share the same statistical properties of those coming from the OB source. These assumptions are of course not exact, but are relatively close to reality. By doing this, the equations defining P(q_s) and T(q_s) are effectively restricted to three sources (3:1, ν₆, OB) with new coefficients

1

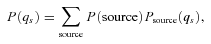
2.2 Results

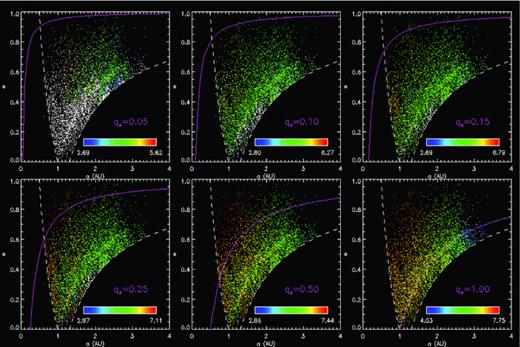
In Fig. 1, we report the a−e scatter plot of the NEO population for several values of q_s. For each panel, the colour of NEOs is coded according to the probability of experiencing q < q_s. The curve q=q_s is also overplotted. The figure clearly shows that the orbital paths followed by each NEO very often have led to small perihelion distances, much shorter than their present q. In particular, this is evident for q_s= 0.05, 0.1 au: only few NEOs are presently below those values, but a significant fraction of the NEO population spent some time, during the evolution, with a smaller perihelion. The average probability versus q_s is shown in Fig. 2 (left-hand panel).

Figure 1

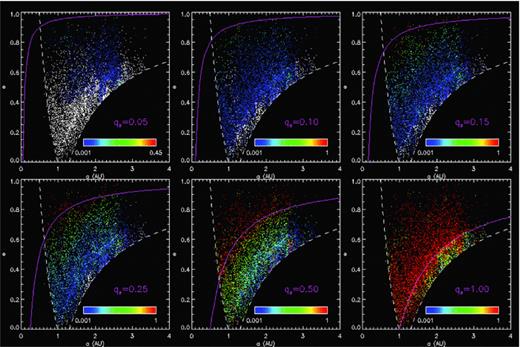
Semimajor axis versus eccentricity scatter plot of the present NEO population for several values of q_s. NEOs are plotted with colours coded according to their probability of staying below q_s (white dots indicate zero probability). For each panel, the corresponding q=q_s curve is also shown.

Open in new tabDownload slide

Figure 2

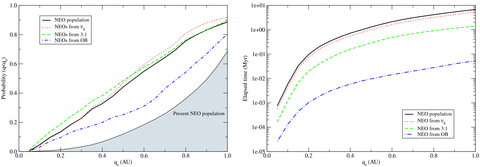
Left-hand panel: average NEO probability of q < q_s. The curves for the three source regions have been normalized to the number of NEOs coming from each region. Right-hand panel: average NEO cumulative time spent at q < q_s. The curves for the three main source regions are also shown.

Open in new tabDownload slide

It is obvious that the present orbit and the past history are correlated (this is the rationale of our computations); however, the correlation is not trivial. As a general trend, P(q_s) decreases for objects with increasing value of their current perihelion distance q. Only bodies with semimajor axes in the region of the main resonances ν₆ and 3:1 (a= 2 − 2.5 au) can have large P(q_s) even if they currently have a large value of q (see Fig. 1). This happens because these resonances entail large oscillations of the eccentricity. Moreover, we remark that the bodies with the smallest value of P(q_s) are those with large semimajor axis (beyond 2.5 au), mostly coming from the OB source. We may thus expect that a significant percentage of NEOs, originating in the inner part of the main belt and delivered through the ν₆ resonance, have been affected by the consequences of the heating process, and thus possibly physically altered (see also the discussion in the following). The other bodies should have kept more systematically their original properties, at least for what concerns the alterations due to heating. Another interesting result concerns the time spent at distances smaller than q_s. In Fig. 3, we show the NEO population with colours coded according to the cumulative time elapsed for q < q_s. We found that, even for small q_s, the time elapsed by NEOs at close distances to the Sun can be considerably high, reaching the 10 per cent of the typical lifetimes (10 Myr) or, in a few cases, even more. The average cumulative time spent below q_s is shown in Fig. 2 (right panel).

Figure 3

Same as Fig. 1, with colours coded according to the logarithm of cumulative time spent below q_s (white dots indicate T_s= 0).

Open in new tabDownload slide

A closer look at the results of our simulations in order to identify the most heated NEOs shows that 1 per cent of NEOs have a 50 per cent probability of having been at q < 0.1 au. Such probability becomes 5 per cent at 0.2 au. Their cumulative time spent below such distances can vary considerably, from several 10³ yr to several Myr. Interestingly, one of the objects predicted to be highly processed is the peculiar 3200 Phaethon, whose probability of having been at q < 0.1 au is 56 per cent for a cumulative time of 0.3 Myr.

On the other hand, there are NEOs that never went close to the Sun, and therefore they represent the least processed bodies. For instance, 2 per cent of NEOs have a probability of less than 10 per cent to have spent time below q_s= 0.8 au. These two extreme samples of NEOs – the hot and cool bodies – show interesting features in the a−e plot (see Fig. 4).

Figure 4

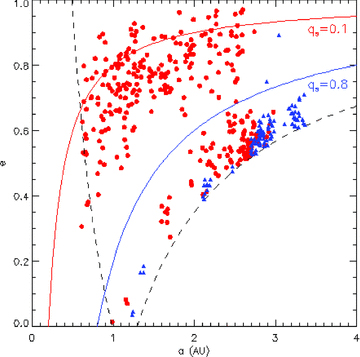
The disposition of the ‘hot’ and ‘cool’ NEOs. The hot NEOs (red circles) are defined as those having a probability of at least 50 per cent to fall below 0.1 au. The ‘cool’ (blue triangles) are those having a probability of less than 10 per cent to fall below 0.8 au.

Open in new tabDownload slide

3 THERMAL PROPERTIES OF NEOS

In the previous section, we have shown that a fraction of the NEO population has experienced small perihelion distances; some of these bodies had q < q_s also for a long cumulative time. For these objects the effects of the solar heating may have altered their surface properties. In this section, we use asteroid thermal and thermophysical models (TPMs) to investigate in more detail the dependence of the surface temperature of a body on its heliocentric distance and thermophysical properties. Obviously the presence of surface regolith, and its continuous mixing, due to microcollisions or tidal mixing (Marchi et al. 2006a) or YORP reshaping (Harris, Fahnestock & Pravec 2009), may – at least partially – mask the above mentioned alterations.

The surface temperature depends on the body's thermal and rotational properties. However, rough estimate of surface temperatures at perihelion can be obtained from the equation of instantaneous thermal equilibrium with sunlight:

2

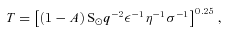
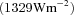where A is the bolometric Bond albedo, S_⊙ is the solar constant at 1 au ⁠, ε is the infrared emissivity, σ is the Stefan–Boltzmann constant and η is the so-called beaming parameter (see Harris & Lagerros 2002, and references therein). The latter can be seen as a measure of the departure of the asteroid temperature distribution from that of a spherical, smooth body with all surface points in instantaneous thermal equilibrium with sunlight (which would have η= 1). The value of η is a strong function of the macroscopic roughness and the thermal inertia of the surface (Spencer, Lebofsky & Sykes 1989; Harris 1998; Delbo' et al. 2007). The latter parameter, which measures the resistance of a material to temperature changes, is defined as ⁠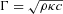, where Γ is the thermal inertia, ρ is the density of the material, c is its specific heat content and κ is the thermal conductivity. In particular, η > 1 indicates a surface with a temperature cooler than one of the instantaneous thermal equilibrium, whereas η < 1 is expected for a surface with low thermal inertia and significant roughness.

An upper limit for the NEO surface temperature can be obtained by setting in equation (2) a very low bolometric albedo (A= 0.01, corresponding to a geometric visible albedo, p_V, of 0.03 and the default phase integral −G= 0.15, Bowell et al. (1989); p_V= 0.03 is at present the lowest geometric albedo measured for NEAs), a zero thermal inertia and a strong infrared beaming (η= 0.57; Wolters et al. 2005). For an infrared emissivity of 0.9 – commonly adopted for the mineralogy of NEOs (Lim et al. 2005; Salisbury et al. 1991; Mustard & Hays 1997) – we find temperatures of 1968 and 1391 K at 0.05 and 0.10 au, respectively. Average parameter values for NEOs [i.e. A= 0.05 from p_V= 0.14 (Stuart & Binzel 2004) and G= 0.15; η= 1.0] yields subsolar temperatures of 1782 and 1260 K at 0.05 and 0.10 au, respectively. A lower limit for the surface temperature can be obtained for a small body with instantaneous redistribution of the heat in the whole volume,with no difference between the temperature of day and night: namely an isothermal object. This latter case can be obtained using η= 4 in equation (2). We obtain 1343 K at 0.05 au and 949 K at 0.10 au for A= 0.05. We note that the largest ever measured η-value for a NEO is 3.1 (3671 Dionysus; Harris & Davies 1999). Fig. 5 shows the surface temperature as function of the heliocentric distances for the three cases described above.

Figure 5

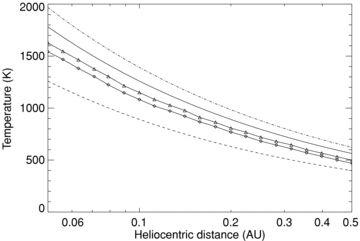
Temperature of NEOs as function of their heliocentric distances. In particular, continuous line: temperature of the subsolar point for a flat surface in instantaneous thermal equilibrium with sunlight (physical parameters are A= 0.05, η= 1.0 and ε= 0.9). Dashed–dotted line: temperature of the subsolar point for a rough, low-albedo surface in instantaneous thermal equilibrium with sunlight (physical parameters are A= 0.01, η= 0.6 and ε= 0.9). Dashed line: temperature of an isothermal smooth-surface body (physical parameters are A= 0.05 η= 4.0, ε= 0.9). This curve can represent the temperature of the meteorites. Dotted lines with symbols: temperature above which a 70 per cent (diamonds) and 50 per cent (triangles) fraction of the surface area of an NEO is heated to. See Section 3 for further details.

Open in new tabDownload slide

However, observable consequences of heating can come out if and only if the whole surface (or a large amount of it) has been involved, and thus altered. In order to estimate the fraction of the surface above a certain temperature threshold, more accurate knowledge of the temperature distribution on the surface of asteroids is needed. Thermophysical modelling is required to obtain this information. A TPM (see Spencer et al. 1989; Lagerros 1996; Emery et al. 1998; Harris & Lagerros 2002; Delbo' & Tanga 2009 and references therein) describes an asteroid as a polyhedron made by a mesh of planar facets. The temperature of each facet is determined by numerically solving the one-dimensional heat diffusion equation into the subsurface with boundary conditions given by the diurnal variable illumination and by the energy irradiated away by each facet at the surface, and by setting the heat flow at the deepest subsurface element equal to zero. In our implementation of the TPM, the subsurface is divided into 32 slabs of thickness 0.25 times the diurnal heat penetration depth ⁠, where ω= 2π/P with P the rotation period of the asteroid; the deepest subsurface element is therefore 8 l_s beneath the surface. Surface and subsurface temperatures are controlled by a number of physical parameters including the heliocentric distance q, A, ε, Γ, P, the direction of the rotation axis with respect to the Sun and the shape of the body.

In the following, we assume a spherical asteroid with the spin vector perpendicular to its orbital plane, P= 6 h, ε= 0.9, A= 0.1 and Γ= 200 J m⁻² s^−0.5 K⁻¹. The latter is the average value of the thermal inertia for km-sized NEAs (Delbo' et al. 2007). The TPM was run on circular orbits with heliocentric distances ranging from 0.05 to 0.5 au. At the beginning of each run, a complete rotation of the body is performed and the average temperature of each facet is recorded. The temperature at each rotation step (usually 360 steps per rotation are performed) is calculated assuming instantaneous thermal equilibrium between thermal infrared emission and absorption of solar energy {i.e. T_i= [(1 −A) S_⊙q⁻² cos θ_i(t) ε⁻¹σ⁻¹]^0.25}, where T_i is the temperature of the i_th surface element of the mesh, q is the heliocentric distance of the body and θ_i is the angle formed by the normal of the i_th surface element of the mesh with the direction to the Sun, and it varies with the time t. The average temperature of each facet is then used as the initial temperature of all 32 subsurface slabs including the one at the surface. The temperature profile as a function of time, i.e. the asteroid rotational phase, is monitored on each facet during the warm-up phase, which can take up to 50–100 (depending on the value of q) full rotations until the temperature profile stabilizes and the initial temperature conditions are forgotten. A final rotation is then performed and the maximum temperature of each facet is stored. The areas of those facets whose maximum temperatures are found above a given temperature threshold (T_s) are added up, and the ratio of this area to the total area of the body surface is calculated for a range of values of T_s from 0 up to 2000 K. The value of T_s for which the ratio of the surface whose maximum temperature is above T_s is equal to 0.7 and 0.5 is found by interpolation. Fig. 5 shows these values of T_s for different heliocentric distances: these values represent the temperature above which a 70 and 50 per cent fraction of the surface area of the body was heated to.

We also note that the temperature above was calculated using a TPM with smooth surface. However, it is well known that roughness increases the average surface temperatures by a maximum of 20–30 per cent with respect to those of a smooth surface. Running the TPM on orbits with substantial eccentricity does not significantly affect the final result.

4 DIFFERENCE BETWEEN NEOS AND METEORITES

Meteorites are collected on the Earth surface after having passed some time in a NEO-like orbit. Their history may be various: some may be relatively young fragments from cratering or catastrophic collisions, or from tidal shattering of NEOs, others may have a longer independent history, maybe a long orbital evolution as NEOs. Despite the different size, observed NEOs and meteorites are believed to share a common origin; moreover the orbital evolution of meteorites is typically dominated by the same dynamical processes as NEOs.

However, for what concerns the alterations due to heating, we expect some important differences with respect to NEOs. (i) Meteorites might have spent in near-Earth space a shorter time than the average NEO, because of their short collisional lifetime. This is suggested by the fact that the statistics of fall times (in the afternoon versus in the morning) is skewed towards afternoon falls with respect to that of the expected NEO impacts (Morbidelli & Gladman 1998). As a result the time spent might have not been enough for considerable heating. (ii) Meteorites are systematically by far smaller than NEOs. Thus, the thermal history is also likely different. (iii) Bodies that collide with the Earth (like meteorites) have preferentially q∼ 1 au. This introduces a further bias with respect to the observed NEO population, where many of the bodies have a very low probability of collision with the Earth. Indeed, since P(q_s) decreases with increasing q, this implies that meteorites are likely less heated than NEOs.

In the limit of a very small body, we can imagine an almost instantaneous redistribution of the heat in the whole volume, no day–night difference, a quasi-isothermal object. If we use the same formulas and basic assumptions to explore this extreme case, the factor of 4 between the surface of a spherical body and its cross-section introduces a factor of 4^−1/4 in the attainable temperature, which consequently decreases by ∼30 per cent (see equation 2 and the discussion in the previous section). Real meteorites may behave in a more complex way, but somehow similar to the above scenario. In fact, an accurate thermal model suggests that a thin layer, in the region close to the subsolar point, may attain large temperatures, similar to those estimated for asteroids. However, we expect that those thin layers are systematically erased during the approach of the meteorite to the Earth, mainly due to atmospheric friction. Thus the meteorite ‘as we see it’, i.e. after we recover it on the ground, retains no effect of the strong surface heating, and its thermal evolution can be analysed in terms of the ‘isothermal’ approximation. Thus, the thermal history of NEO and meteorites can be considerably different. We must take this consideration into account when attempting to compare laboratory measured quantities on meteorites with analogue quantities derived from the remote sensing of asteroids.

5 DISCUSSION: CONSEQUENCES OF THE HEATING

The purpose of the present paper is to point out the importance of the heating history of NEOs and meteoroids, due to very close passes to the Sun. Even if the general ideas seem rather robust, the physical consequences have to be explored in deeper detail. In fact, a number of interesting phenomena can be caused by the mentioned heating. Generally speaking, the heating can drive volatile release, therefore the surface composition of NEOs and, to a lesser extent, meteoroids become progressively depleted of volatiles. In the case of temperature higher than 1200 K, silicate sublimation is expected.

For temperatures below the melting points of the different silicates known to be present on asteroid surfaces, it is worth to note that thermal heating can cause annealing: this is in general a transition from an amorphous to a crystalline structure. The total time that an object spent with q < q_s is extremely important in this kind of process. This is because the rate, k, at which a material is transformed from amorphous to crystalline is a function of temperature via an equation of the form: k=a exp (−E_a/bT), where a and b are constants determined from experiments (see e.g. Brucato et al. 2003, and references therein) and E_a is the activation energy for the transition. The latter depends on the chemical nature of the silicate.

Concerning the most ‘primitive’ NEOs, i.e. those belonging to the C types, more severe effects are foreseen. For instance the aqueous altered carbonaceous chondrites are strongly affected by moderately high temperatures (Hiroi et al. 1996). We note that the percentage of C-type NEOs with aqueous alteration features (in particular the 0.7 μm feature) is rather high among main belt asteroids, of about 50 per cent (Bus & Binzel 2002; Carvano, Mothé-Diniz & Lazzaro 2003). This percentage drops below 10 per cent for NEOs: only three objects over more than 30 C-type NEOs having visible spectroscopic measurements show subtle absorption features at 0.7 μm. These results have been also found by Vilas (2005) on the basis of ECAS photometry. On the other hand, the hydration is a common feature in the meteorite collection, in agreement with what our considerations predict. However, the data are too few and probably not unambiguous enough to support the explanation of the difference of the NEOs hydration properties solely in terms of heating. For instance, one (2002 NX18) of the C-type NEOs with hydration features is probably coming from the Outer Belt, thus has presumably been poorly exposed to heating. A similar result holds also for 162173, while the dynamical history of 2002 DH2 is less clear. An alternative explanation can be that NEOs sample peculiar source regions.

Similar considerations apply also to the cometary objects, namely those NEOs coming from the JFC source region (about 70 NEOs are estimated to originate in this way). The very close passages to the Sun and high-temperature heating should have produced a rapid release of all volatiles, leading to the stage of depleted cometary nuclei.

Another interesting aspect is related to the space weathering, which is expected to be much more efficient in proximity to the Sun (Marchi et al. 2006b; Paolicchi et al. 2007). Changing from 1 to 0.1 au increases the space weathering rate by two orders of magnitude. Similar considerations might also apply to other effects depending on the solar radiation, such as Yarkovsky and YORP.

Moreover, we find that the thermal histories of NEOs and meteorites may be considerably different, therefore the above mentioned processes may introduce systematic differences in their physical properties. A future analysis of these points will be worthwhile; in general, we remark that the effects of close passages to the Sun, in terms of heating, but also as concerns other processes, should not be neglected, especially when evaluating the targets for future space missions to NEOs, such as the European/Japanese Marco Polo mission or the USA Osiris mission.

We thank J. Brucato for helpful comments and the referee A. R. Dobrovolskis for carefully reading the paper. PP thanks ASI funds.

REFERENCES