-
PDF
- Split View
-
Views
-
Cite
Cite
K. K. Nandi, A. I. Filippov, F. Rahaman, Saibal Ray, A. A. Usmani, M. Kalam, A. DeBenedictis, Features of galactic halo in a brane world model and observational constraints, Monthly Notices of the Royal Astronomical Society, Volume 399, Issue 4, November 2009, Pages 2079–2087, https://doi.org/10.1111/j.1365-2966.2009.15399.x
Close - Share Icon Share
Abstract
Several aspects of the 4d imprint of the 5d bulk Weyl radiation are investigated within a recently proposed model solution. It is shown that the solution has a number of physically interesting properties. The constraints on the model imposed by combined measurements of rotation curve and lensing are discussed. A brief comparison with a well-known scalar field model is also given.
1 INTRODUCTION
Early observations led to the hypothesis that there could be large amounts of non-luminous matter hidden in the galactic haloes (Oort 1930; Zwicky 1933, 1937). Later observations of flat rotation curves of spiral galaxies confirmed the hypothesis (Freeman 1970; Roberts & Rots 1973; Ostriker, Peebles & Yahill 1974; Einasto, Kaasik & Saar 1974; Rubin, Thonnard & Ford 1978; Rubin, Roberts & Ford 1979; Sofue & Rubin 2001; Kochanek et al. 2005). Doppler emissions from stable circular orbits of neutral hydrogen clouds in the halo allow the measurement of tangential velocity vtg(r) of the clouds treated as probe particles. According to Newton's laws, centrifugal acceleration v2tg/r should balance the gravitational attraction GM(r)/r2, which immediately gives v2tg=GM(r)/r. That is, one would expect a fall-off of v2tg(r) with r. However, observations indicate that this is not the case: vtg approximately levels off with r in the halo region. The only way to reconcile this result of observation is to hypothesize that the mass M(r) increases linearly with distance r. Luminous mass distribution in the galaxy does not follow this behaviour. Hence, we conclude that there must be huge amounts of non-luminous matter hidden in the halo. This unseen matter is given a technical name, dark matter. Gravitational lensing measurements have further confirmed the presence of dark matter (Maoz 1994; Barnes et al. 1999; Cheng & Krauss 1999; Sofue & Rubin 2001; Trott & Webster 2002; Weinberg & Kamionkowski 2002; Kochanek & Schechter 2004; Smith et al. 2005; Faber & Visser 2006; Metcalf & Silk 2007). Current estimates suggest that about 23 per cent of matter in the whole Universe consists of dark matter residing in the galactic haloes.
Although the exact nature of the dark matter is as yet unknown, several candidates for it have been proposed in the literature. One of the favoured candidates is the standard cold dark matter of the so-called SCDM paradigm (Efstathiou, Sutherland & Madox 1990; Pope et al., 2004). Despite its initial success, the current consensus seems to converge on the Lambda CDM or ΛCDM model that is related to the accelerating expansion of the Universe (Tegmark 2004a,b).
Analytic halo models include the framework provided by scalar–tensor theories. Scalar fields are important because they are predicted by supersymmetric unification theories (see e.g. Ellis et al. 1998). In particular, a prototype of scalar–tensor theories, namely the Brans–Dicke theory with scalar field φ, has the potentiality to explain a wide range of effects, from those in Solar system (Weinberg 1972; Bhadra, Sarkar & Nandi 2007) and gravitational lensing (Bhadra 2003; Nandi, Zhang & Zakharov 2006; Sarkar & Bhadra 2006) to those arising from objects as exotic as wormholes (Agnese & La Camera 1995; Nandi, Islam & Evans 1997; Nandi et al. 1998; Bhadra & Sarkar 2005). Fay (2004) considered a larger class of scalar–tensor theories with a potential V(φ), and with coupling parameter ω=ω(φ), for the investigation of galactic dynamics. Many other halo models including suitable variants of scalar field theories also exist in the literature (see e.g. Bekenstein & Milgrom 1984, Sanders 1984, 1986, Soleng 1995, Matos, Guzmán & Nuñez 2000, Peebles 2000; Nucamendi, Salgado & Sudarsky 2001, Mielke & Schunck 2002, Cabral-Rosetti et al. 2002, Lidsey, Matos & Ureña-Lopez 2002; Bharadwaj & Kar 2003; Arbey, Lesgourgues & Salati 2003). Substantial halo models are provided by the brane world theory (Mak & Harko 2004; Rahaman et al. 2008).
The motivation for the brane world model, which we are considering in this article, comes from an entirely different but important direction. It comes from the consideration of higher dimensional space–time because it can be argued that 4d is not big enough to fully accommodate the self-interaction dynamics of gravity. In a recent article, Dadhich (2009) has given persuasive arguments based on flat space imbedding, self-interaction and charge neutrality. But why only 5d and not higher? The reason is that the conformally flat Friedmann-Robertson-Walker (FRW) universe is embeddable only in 5d flat space–time, which means that free gravity does not propagate farther than 4d because the Weyl curvature vanishes for this FRW universe. The Randall & Sundrum (1999a,b) model provides the following setting: the three-brane (i.e. our 4d space–time which confines matter and other gauge fields) has zero Weyl curvature, and it bounds the 5d constant curvature bulk space–time. To probe into fifth dimension, one cannot rely on light signals as they do not propagate there. Therefore, a possible probe has to rely only on the propagation of gravity off the brane in an unfamiliar non-free manner (Dadhich 2009). For this, one needs to devise a purely gravity experiment and a method to fathom gravity propagation in higher dimension. This being a formidable task, the usual approach is to look for measurable imprints coming from 5d into known gravitational configurations. The galactic halo, where gravity is the king, provides a natural large-scale arena for this observation. It is quite probable that the effect of unseen dark matter is due to such imprints which contribute to the source term of Einstein's 4d field equations. Solving Einstein's equations, one then tries to work out the details of higher-dimensional non-local effects.
Static spherically symmetric exterior solutions of the brane world model have been derived in the literature (Dadhich et al. 2000; Germani & Maartens 2001; Casadio, Fabbri & Mazzacurati 2002; Visser & Wiltshire 2003; Harko & Mak 2004; Mak & Harko 2004; Creek et al. 2006; Viznyuk & Shtanov 2007). While all of these works are motivated by one or the other relevant considerations, the solution by Rahaman et al. (2008) is based on the simplest supposition of rotation curves that connects dark matter with the brane world model in a straightforward way. Whatever be the analytic model, there must be a way to contrast its predictions with actual measurements. The key point is that one does not directly measure the metric functions but indirectly measures gravitational potentials and masses from rotation curve and lensing observations. Bharadwaj & Kar (2003) advocated that a combination of rotation curves and lensing measurements could be used to determine the equation of state of the halo fluid, although their model was restricted to specific form of flat rotation curve as well as guesses on equations of state. Faber & Visser (2006) have shown how; in the first post-Newtonian approximation, the combined measurements of rotation curves and gravitational lensing allow inferences about the mass and pressure profile of the galactic halo as well as its equation of state.
In this paper, we wish to explore various features of the brane world solution by Rahaman et al. (2008) focusing in particular on the constraints imposed by combined measurements. Our general conclusion is that the model has a number of interesting properties. Nevertheless, it is too premature to say if the model is observationally supported. The relevant measurement constraints on the model are worked out. This paper is organized as follows. In this section, we have already delineated the motivation for the brane world model. In Section 2, we briefly outline the field equations and the solution under consideration for later use. Section 3 discusses the nature of the galactic fluid while Section 4 shows stability of circular orbits. In Section 5, we establish the attractive nature of gravity in the halo arguing from two different viewpoints, and in Section 6 we discuss observational constraints. In Section 7 we make a brief comparison with the central features of a scalar field model. Section 8 contains the conclusions.
2 FIELD EQUATIONS AND THE SOLUTION
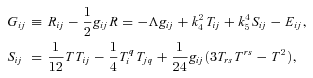
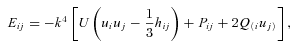
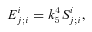
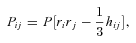
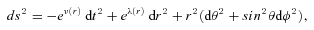
 . In static vacuum (Tij= 0, Qi= 0) with the trace-free source term Eii= 0 ⇒Rii= 0, and with the unit radial vector ri= (0, 1, 0, 0), the field equations (1) yield the following (Mak & Harko 2004):
. In static vacuum (Tij= 0, Qi= 0) with the trace-free source term Eii= 0 ⇒Rii= 0, and with the unit radial vector ri= (0, 1, 0, 0), the field equations (1) yield the following (Mak & Harko 2004): 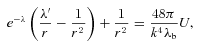
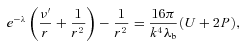
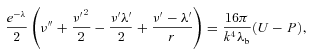

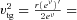 constant (Chandrasekhar 1983), Rahaman et al. (2008) obtained a solution as follows:
constant (Chandrasekhar 1983), Rahaman et al. (2008) obtained a solution as follows: 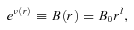
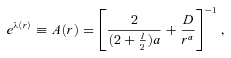
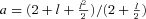 . They showed that the mass function
. They showed that the mass function 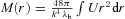 increases linearly with r, which agrees with observation (Begeman 1989). However, this expression for mass is Newtonian and is applicable only so long as one can neglect pressure contributions although as yet there is no observational ground for such a neglect. To see the expressions for various types of mass distributions in terms of observational parameters, we wait till Section 6. Meanwhile, there are several other facets of the solution that need attention, which are addressed below.
increases linearly with r, which agrees with observation (Begeman 1989). However, this expression for mass is Newtonian and is applicable only so long as one can neglect pressure contributions although as yet there is no observational ground for such a neglect. To see the expressions for various types of mass distributions in terms of observational parameters, we wait till Section 6. Meanwhile, there are several other facets of the solution that need attention, which are addressed below.3 NATURE OF DARK RADIATION
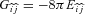 in the observer's orthonormal rest frame
in the observer's orthonormal rest frame 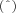 . Using equations (10) and (11) in (6)–(8), we get
. Using equations (10) and (11) in (6)–(8), we get 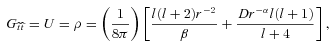
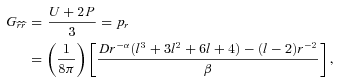
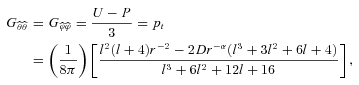
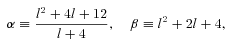
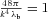 and redefined the fluid stresses (ρ, pr, pt, pt) in terms of U and P. Eliminating U from equations (13), (14), one can easily find the expression for P(r) as given in Rahaman et al. (2008) after their arbitrary constant of integration is set to zero. There is actually no room for a non-zero constant because once the metric functions are known, U and P follow from equations (6)–(8).
and redefined the fluid stresses (ρ, pr, pt, pt) in terms of U and P. Eliminating U from equations (13), (14), one can easily find the expression for P(r) as given in Rahaman et al. (2008) after their arbitrary constant of integration is set to zero. There is actually no room for a non-zero constant because once the metric functions are known, U and P follow from equations (6)–(8).The interesting results we find are the following: while U is the same as ρ, the dark pressure P(r) is equal to neither pr nor pt but P(r) =pr(r) −pt(r) ≠ 0. This indicates that the dark Weyl radiation imprint cannot be characterized in the rest frame by a perfect fluid which requires pr(r) =pt(r). So the perfect fluid version of dark radiation is that U(r) ≠ 0 but P(r) = 0. Looking at equation (2), we see that the imprint radiation in 4d vacuum is a dust-like fluid where  . This is not the case with the solution under consideration since pr(r) ≠pt(r). This pressure anisotropy is a good feature of the solution from the point of view of exterior matching. Note that the solution cannot be matched to the Schwarzschild exterior metric at the boundary of the halo if the pressures were isotropic (Bharadwaj & Kar 2003). The Schwarzschild solution, although not the unique spherically symmetric vacuum when considering the brane world model, is desirable for mimicking the far region (vacuum) of true 4d gravity, as supported by observation. We further see that the dark radiation fluid is not of exotic nature. The minimal condition for exoticity is that the Null Energy Condition (NEC) should be violated (Hochberg & Visser 1998). We find that the NEC is satisfied at all radii because ρ+pr≥ 0 (Fig. 1). Transverse pressures are not included as they refer only to normal matter (Visser, Kar & Dadhich 2003). Even if we include them, we find ρ+pr+ 2pt≥ 0 for all r.
. This is not the case with the solution under consideration since pr(r) ≠pt(r). This pressure anisotropy is a good feature of the solution from the point of view of exterior matching. Note that the solution cannot be matched to the Schwarzschild exterior metric at the boundary of the halo if the pressures were isotropic (Bharadwaj & Kar 2003). The Schwarzschild solution, although not the unique spherically symmetric vacuum when considering the brane world model, is desirable for mimicking the far region (vacuum) of true 4d gravity, as supported by observation. We further see that the dark radiation fluid is not of exotic nature. The minimal condition for exoticity is that the Null Energy Condition (NEC) should be violated (Hochberg & Visser 1998). We find that the NEC is satisfied at all radii because ρ+pr≥ 0 (Fig. 1). Transverse pressures are not included as they refer only to normal matter (Visser, Kar & Dadhich 2003). Even if we include them, we find ρ+pr+ 2pt≥ 0 for all r.
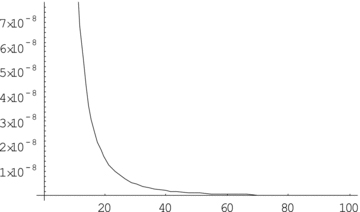
Plot of ρ+pr with distance r in kpc. We find that ρ+pr≥ 0 and that it rapidly decreases with distance, indicating that the pointwise NEC is satisfied. As mentioned in the text, in all the figures, the values of the constants are chosen as l= 0.000001 and D= 0.00001. The distances are shown along the abscissa.
In the rest of the article, we assume the following numerical values for constants. Observations of the frequency shifts in the H i radiation show that, in the halo region, vtg/c is nearly constant at a value 7 × 10−4 (Binney & Tremaine 1987; Persic, Salucci & Stel 1996; Boriello & Salucci 2001). Thus l∼ 10−6. We also note that the solution is not used for small r, the inner core of the galaxy. Accordingly, to be consistent with observational facts, in all the figures in this paper we shall take B0= 1, l= 0.000001, D= 0.00001 and fairly large distances in kpc.
4 STABILITY OF CIRCULAR ORBITS
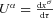 of a test particle moving solely in the subspace of the brane (and restricting ourselves to θ=π/2), the equation gνσUνUσ=−m20 can be cast in a Newtonian form
of a test particle moving solely in the subspace of the brane (and restricting ourselves to θ=π/2), the equation gνσUνUσ=−m20 can be cast in a Newtonian form 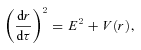

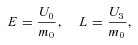
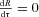 and, additionally,
and, additionally, 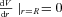 . From these two conditions follow the conserved parameters:
. From these two conditions follow the conserved parameters: 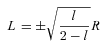
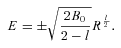
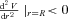 and unstable if
and unstable if 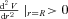 . Putting the expressions for L and E in
. Putting the expressions for L and E in 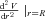 , we obtain, after straightforward calculations, the final result, viz.,
, we obtain, after straightforward calculations, the final result, viz., 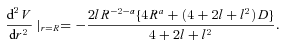
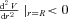 so that circular orbits are stable in the model under consideration when D > 0. The latter condition is always satisfied since, from equation (11), we see that D has a dimension proportional to a power of radius R. The radius is always positive and so is D.
so that circular orbits are stable in the model under consideration when D > 0. The latter condition is always satisfied since, from equation (11), we see that D has a dimension proportional to a power of radius R. The radius is always positive and so is D.5 ATTRACTION IN DARK RADIATION
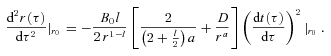
The quantity in square brackets is grr and must therefore be positive. Therefore, this expression is negative and it can be deduced that particles are attracted towards the centre. Detailed discussions on this quantity may be found in Ford & Roman (1996) and Lobo (2008). A related issue is the following. In the Newtonian limit, the gravitational energy of a spherically symmetric, gravitationally attractive system, with sufficient fall-off properties, is negative. One could potentially argue that the 4d gravitational effects due to higher dimensional Weyl stresses on the brane should not be subject to the same criteria as in true four-dimensional gravity. However, from the point of view of the Newtonian limit on the 3d brane, as well as CMB studies, it is desirable that the contribution from the Weyl stresses be not too large away from the galaxy. The question then becomes one of how to quantify such an effect in the relativistic case.
We choose as our quantifier the following: the total gravitational energy EG in the halo region must be negative (Misner, Thorne & Wheeler 1973; Lynden-Bell, Katz & Bičák 2007), where by gravitational energy we mean the quantity defined below. It is necessary to explicitly verify it because a positive energy density does not always lead to attractive gravity (Nandi et al. 2009).
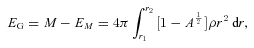
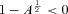 by definition (proper radial length is larger than the Euclidean length) and
by definition (proper radial length is larger than the Euclidean length) and 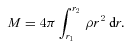
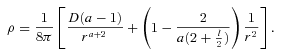
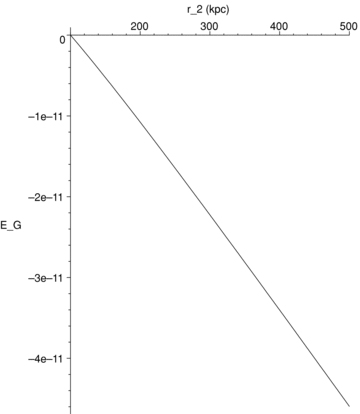
Plot of EG(r2) versus r2. The lower limit of integration in equation (23) fixed at, say, r1= 100 kpc while r2 is varied from 100 to 500 Kpc. The value of EG is very small but negative.
6 OBSERVATIONAL CONSTRAINTS
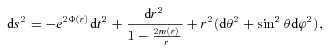
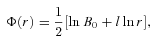
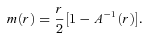
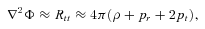
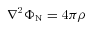
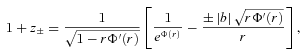
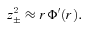
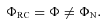
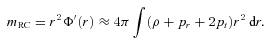
Photons can also be regarded as probe particles as they sense the gravitational field in the halo during their travel to the observer. The effect of gravity on photon motion can be calculated in terms of a refractive index n(r) (see also Boonserm et al. 2005). For the Schwarzschild gravity, the exact geodesic equation, including the equation for Shapiro time delay, of massless particles was expressed in terms of n(r) by Nandi & Islam (1995) via the idea of optical–mechanical analogy. This idea has been further extended by Evans et al. (2001) to arbitrary spherically symmetric space–times and by Alsing (1998) to rotating space–times. The geodesic motion of both massless and massive particles could be expressed exactly in terms of a single generalized refractive index N=n2V/c where V is the three-velocity of the particle. For light motion, V=c/n.
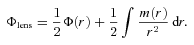
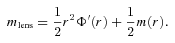
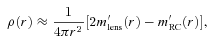
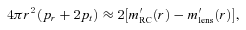
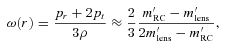
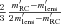 to be expected from combined observations.
to be expected from combined observations.Note that pseudo-quantities are the observable quantities. The general procedure to determine the metric can be stated as follows: once one is able to observationally determine the profiles of pseudo-quantities, one can work backwards to find the corresponding metric functions. This is a kind of reverse technique observational astrophysicists use. If the observed pseudo-profiles fit (up to experimental error) with the analytic profiles of a priori given metric functions, one can say that the solution is physically substantiated. Otherwise, it has to be ruled out as non-viable. In this sense, the observed pseudo-profiles play the role of constraints on the possible metric solutions.
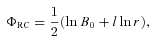
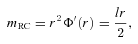
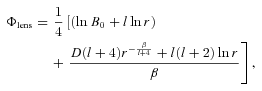
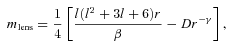
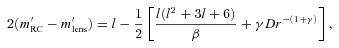
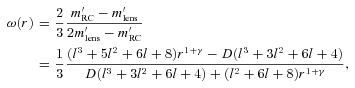
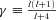 .
.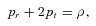
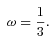
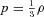 , the usual equation of state for radiation. Noting that U=ρ and using equation (45) in equation (34) we find that the mass in the first post-Newtonian approximation becomes
, the usual equation of state for radiation. Noting that U=ρ and using equation (45) in equation (34) we find that the mass in the first post-Newtonian approximation becomes 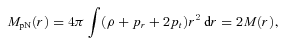
Upper curve represents the function Φlens and the lower curve ΦRC. Although the functions differ nearer to the centre, the difference becomes only of the order of 10−6 as one moves away from the centre. Scalar field model provides the same behaviour.
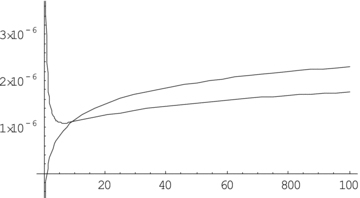
Upper line represents mRC(r), the middle one mlens(r) and the lower one MpN(r). All the masses increase with distance, though they diverge in values in the far field because of varying pressure contributions.
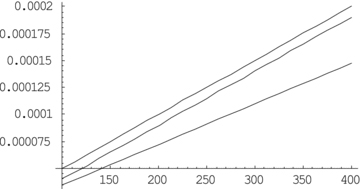
Plot of 2(m′RC−m′lens) versus r. We see that the numerical value of pressure is of the order of ∼10−7 like in the scalar field model. But this is of the same order as the energy density ρ (see equation 46), which indicates that pressure contributions are not altogether negligible in comparison to energy density. The solution thus can be said to describe a mild non-Newtonian system.
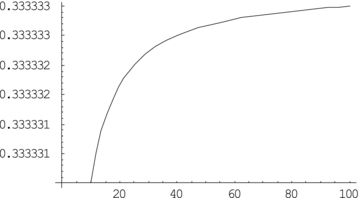
Plot of ω(r) versus r. We can clearly see that the equation of state predicted by the considered solution is ω= 1/3. One expects this radiation equation of state to be supported by combined observations. Scalar field model differs exactly here (see equation 61).
7 COMPARISON WITH A SCALAR FIELD MODEL
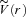 proposed by Matos et al. (2000) and compare it with the present brane world model. Using the flat rotation curve condition, they obtain the full solution as (we distinguish their quantities by tilde)
proposed by Matos et al. (2000) and compare it with the present brane world model. Using the flat rotation curve condition, they obtain the full solution as (we distinguish their quantities by tilde) 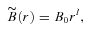
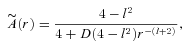
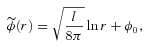
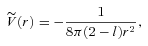
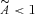 (see equation 28). Because of this, their expressions for density and pressures lead to different conclusions than those in the brane world model considered here. For example, the expression for density exhibit
(see equation 28). Because of this, their expressions for density and pressures lead to different conclusions than those in the brane world model considered here. For example, the expression for density exhibit 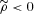 , meaning violation of weak energy condition (WEC) and furthermore it leads to
, meaning violation of weak energy condition (WEC) and furthermore it leads to 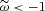 , implying repulsive gravity in the halo, which may not be as desirable as the attractive gravity scenario in the brane world model discussed here. Therefore, it is necessary to re-calculate the relevant quantities with D≠ 0.
, implying repulsive gravity in the halo, which may not be as desirable as the attractive gravity scenario in the brane world model discussed here. Therefore, it is necessary to re-calculate the relevant quantities with D≠ 0.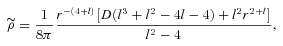
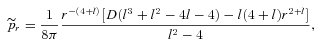
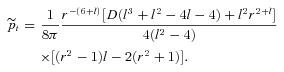
We wish to emphasize here that the role of non-zero value of D is crucial not only for avoiding repulsive gravity but also for arriving at a correct conclusion about the relative strengths between pressure and density. For instance, let us take D= 1. In the distant halo region, we can take, say, r∼ 100–300 kpc, and with l∼ 10−6, we find the numerical values to be  and
and  , which means that they are of the same order. But
, which means that they are of the same order. But  , which indicates that total pressure is roughly one hundred times less than the density. However, if we take D= 0.00001, we find that
, which indicates that total pressure is roughly one hundred times less than the density. However, if we take D= 0.00001, we find that  . If we keep on decreasing the value of D further (but never exactly to zero for reasons stated above), we see that the total pressure dominates more and more over density so that the system becomes indeed non-Newtonian as claimed by Matos, Guzmán & Nuñez (2000). Such minuscule values of D are remarkably similar to those recommended for our solution (see Section 5).
. If we keep on decreasing the value of D further (but never exactly to zero for reasons stated above), we see that the total pressure dominates more and more over density so that the system becomes indeed non-Newtonian as claimed by Matos, Guzmán & Nuñez (2000). Such minuscule values of D are remarkably similar to those recommended for our solution (see Section 5).
The next question is how far can we decrease D? We note the following interesting scenario: when D= 10−7, we find  , which leads to
, which leads to  . This is the extreme non-Newtonian model possible in the scalar field model. On the other hand, if D= 10−8, we find that
. This is the extreme non-Newtonian model possible in the scalar field model. On the other hand, if D= 10−8, we find that  up to r=r0= 200 kpc (attractive gravity) and becomes
up to r=r0= 200 kpc (attractive gravity) and becomes  after r=r0 (repulsive gravity). At r=r0, there is a singularity in
after r=r0 (repulsive gravity). At r=r0, there is a singularity in  . When D= 10−9, we find that
. When D= 10−9, we find that  , exhibiting the characteristics that follow from the same choice D= 0. Therefore, we conclude that the limiting value of D is 10−7.
, exhibiting the characteristics that follow from the same choice D= 0. Therefore, we conclude that the limiting value of D is 10−7.
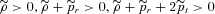 for D≥ 10−7, so we can say that the halo matter is not exotic because the WEC and NEC are satisfied everywhere. Therefore, we expect an attractive halo. To confirm it, again we follow the prescription in Lynden-Bell et al. (2007), and find that the total gravitational energy is indeed negative:
for D≥ 10−7, so we can say that the halo matter is not exotic because the WEC and NEC are satisfied everywhere. Therefore, we expect an attractive halo. To confirm it, again we follow the prescription in Lynden-Bell et al. (2007), and find that the total gravitational energy is indeed negative: 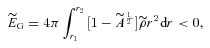
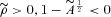 and r2 > r1.
and r2 > r1.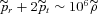 . As a result, equation (30) leading to a purely Newtonian definition of mass M(r) as in equation (24) does not apply. However, incorporating the pressure contribution, the dynamical mass in the first post-Newtonian order is
. As a result, equation (30) leading to a purely Newtonian definition of mass M(r) as in equation (24) does not apply. However, incorporating the pressure contribution, the dynamical mass in the first post-Newtonian order is 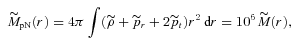
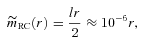
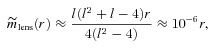
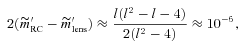
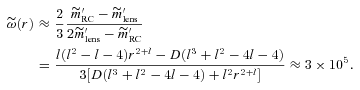
Note that if we straightaway put D= 0 in equation (61), we get  , conveying a completely different conclusion. Thus, while the numerical values of observable potentials and masses behave like those in the brane solution, it is only the equation of state (61) that differs widely because
, conveying a completely different conclusion. Thus, while the numerical values of observable potentials and masses behave like those in the brane solution, it is only the equation of state (61) that differs widely because  has a value ∼105 compared to
has a value ∼105 compared to  (cf. equation 47). Therefore, we conclude that, with the suggested small non-zero values of D, the interesting model proposed by Matos et al. (2000) can also be a viable alternative.
(cf. equation 47). Therefore, we conclude that, with the suggested small non-zero values of D, the interesting model proposed by Matos et al. (2000) can also be a viable alternative.
8 CONCLUSIONS
In the foregoing, we first discussed the motivation for considering higher dimensions, which probably distinguishes the solution (27, 28) as a more interesting search for the halo model. It is the three-brane that we experience, and therefore the bulk contributions U and P are translated into brane quantities via Einstein equations, which provide a way to have insights into the nature of the galactic fluid. The present model shows that the halo does not have a perfect fluid equation of state but NEC is preserved, meaning that the fluid is not exotic. It was shown that circular orbits in the halo are stable and that the dark radiation is attractive in nature, as it must be. Thus, the solution satisfies two crucial physical requirements: circular orbit stability and attractive gravity in the halo. The next task was to derive the constraints on the solution imposed by combined observations of rotation curve and lensing.
The analyses by Nucamendi et al. (2001), Lake (2004) and Faber & Visser (2006) have been carried out without reference to any specific form of metric functions. The specific functions (27, 28) yielded the right-hand sides of equations (40)–(44) in terms of parameters to be measured by a combination of rotation curve and lensing measurements. These are effectively the constraint equations on the chosen solution. If combined observations turn out to tally with the behaviour predicted by equations (40)–(44), then the brane world solution (27, 28) can be said to be supported by observation. Until that happens, the solution would remain largely an academic curiosity.
As discussed in the Introduction, the increase of mass linearly with r comes from an elementary Newtonian argument to explain the observed fact of flat rotation curves. A key question still remains: how much of pressure contribution is there in the making of that mass; that is, is it just the Newtonian M(r) of equation (24) or MpN(r) of equation (34)? The solution by Rahaman et al. (2008) does exhibit a linear increase of the Newtonian mass M(r). Fortunately, even if pressures are included, we find MpN(r) = 2M(r) (cf. equation 48), that is they are of the same order showing that the theoretical linear mass increase is pretty consistent with both the definitions within the present model. Such an increase is also supported by observable pseudo-masses, as expected. However, this is just one aspect of the solution shared by many other models too. The distinguishing features lie elsewhere. For instance, we saw that in the scalar field model  (cf. equation 57). As emphasized earlier, such distinguishing features will have to be determined only by the detailed analyses of data profiles of potential, pressure and, most importantly, the equation of state obtained through the combined rotation curve and lensing measurements. The bottom line is that the present solution depicts the halo as a mildly non-Newtonian model (pressure contribution is of the same order as energy density) in contrast to the highly non-Newtonian scalar field model. Although both the models share many properties including an anisotropic non-perfect fluid equation of state, sharp differences appear in the computation of MpN(r) and in the equation of state characterized by ω(r). Observations to date do not seem yet conclusive enough (for a discussion, see Faber & Visser 2006) to tell us which one, if any, is closer to reality among all the competitive halo models.
(cf. equation 57). As emphasized earlier, such distinguishing features will have to be determined only by the detailed analyses of data profiles of potential, pressure and, most importantly, the equation of state obtained through the combined rotation curve and lensing measurements. The bottom line is that the present solution depicts the halo as a mildly non-Newtonian model (pressure contribution is of the same order as energy density) in contrast to the highly non-Newtonian scalar field model. Although both the models share many properties including an anisotropic non-perfect fluid equation of state, sharp differences appear in the computation of MpN(r) and in the equation of state characterized by ω(r). Observations to date do not seem yet conclusive enough (for a discussion, see Faber & Visser 2006) to tell us which one, if any, is closer to reality among all the competitive halo models.
We thank Arunava Bhadra for several enlightening discussions. KKN thanks Guzel N. Kutdusova for her assistance at BSPU and SSPA where part of the work was carried out.
REFERENCES



