-
PDF
- Split View
-
Views
-
Cite
Cite
R. Fares, J.-F. Donati, C. Moutou, D. Bohlender, C. Catala, M. Deleuil, E. Shkolnik, A. C. Cameron, M. M. Jardine, G. A. H. Walker, Magnetic cycles of the planet-hosting star τ Bootis – II. A second magnetic polarity reversal, Monthly Notices of the Royal Astronomical Society, Volume 398, Issue 3, September 2009, Pages 1383–1391, https://doi.org/10.1111/j.1365-2966.2009.15303.x
Close - Share Icon Share
Abstract
In this paper, we present new spectropolarimetric observations of the planet-hosting star τ Bootis, using ESPaDOnS and Narval spectropolarimeters at Canada–France–Hawaii Telescope and Telescope Bernard Lyot, respectively.
We detected the magnetic field of the star at three epochs in 2008. It has a weak magnetic field of only a few gauss, oscillating between a predominant toroidal component in January and a dominant poloidal component in June and July. A magnetic polarity reversal was observed relative to the magnetic topology in 2007 June. This is the second such reversal observed in 2 years on this star, suggesting that τ Boo has a magnetic cycle of about 2 years. This is the first detection of a magnetic cycle for a star other than the Sun. The role of the close-in massive planet in the short activity cycle of the star is questioned.
τ Boo has a strong differential rotation, a common trend for stars with shallow convective envelope. At latitude 40°, the surface layer of the star rotates in 3.31 d, equal to the orbital period. Synchronization suggests that the tidal effects induced by the planet may be strong enough to force at least the thin convective envelope into corotation.
τ Boo shows variability in the Ca ii H & K and Hα throughout the night and on a night-to-night time-scale. We do not detect enhancement in the activity of the star that may be related to the conjunction of the planet. Further data are needed to conclude about the activity enhancement due to the planet.
1 INTRODUCTION
Hot Jupiters (HJ) are giant planets orbiting their stars with very short orbital period (less than 10 d), having masses comparable to or larger than that of Jupiter. They represent about 25 per cent of all discovered extrasolar planets. Their proximity to their parent stars likely influences their orbital evolution and internal structure; a variety of interactions (generically called star–planet interactions or SPI) are also expected to occur.
Observations suggest that some HJ systems undergo episodes of enhanced variability in their activity (e.g. central emission in Ca ii H & K or Balmer lines) (Shkolnik, Walker & Bohlender 2003; Shkolnik et al. 2005) or in their mean optical brightness (Walker et al. 2008). These SPI episodes are apparently phase shifted with orbital conjunctions (Shkolnik et al. 2005); they are also reported to exhibit longer term fluctuations, suggesting an intermittent (‘on–off’) nature of SPI (Shkolnik et al. 2008).
Two types of interactions were proposed to qualitatively explain the observations: magnetic and tidal interactions (Cuntz, Saar & Musielak 2000). Magnetic SPI can induce reconnection events between the magnetic field lines of the star and those of the planet; the result is a modulation of the stellar activity with the orbital period. Tidal interactions result in two tidal bulges on the star, and thus enhanced activity will be modulated by half the orbital period. Potential phase lags (between the orbital conjunction and the epochs of activity variability enhancement) may result from the tilt of the magnetic axis relative to the rotational one (McIvor, Jardine & Holzwarth 2006); other scenarios of interaction may also explain this, as adopting the Alfvén wing model (Preusse et al. 2006) or considering a non-potential magnetic field configuration for the closed corona of the star (Lanza 2008). Simulations of Ca ii H & K light curves of an HJ hosting star also show that the interactions depend on the configuration of the magnetic field which the planet crosses, and thus disappearance of the SPI may be explained by a change of the stellar magnetic field (Cranmer & Saar 2007).
The magnetic field of the star is therefore expected to play a key role in these interactions, either by triggering them directly (magnetic interactions) or by tracing them indirectly (tidal interactions influencing the generation of the magnetic field, for example, by enhancing the shear at the base of the convective envelope). The study of the global magnetic field of HJ hosting stars thus appears as a promising tool to quantitatively investigate these SPIs.
With a massive HJ orbiting in 3.31 d at 0.049 au (Butler et al. 1997; Leigh et al. 2003), the F7 star τ Boo is a good candidate for our study. It has a shallow outer convective envelope of about  , while the mass of the planet is about
, while the mass of the planet is about  . This star has moderate-intrinsic activity (Shkolnik et al. 2005, 2008), suggesting that it may be a good candidate for detecting any planet-induced activity signatures (of presumably very low amplitude). τ Boo has a weak magnetic field of a few gauss (Catala et al. 2007; Donati et al. 2008), that switched its polarity in an year, which makes the study of the magnetic field of this star interesting.
. This star has moderate-intrinsic activity (Shkolnik et al. 2005, 2008), suggesting that it may be a good candidate for detecting any planet-induced activity signatures (of presumably very low amplitude). τ Boo has a weak magnetic field of a few gauss (Catala et al. 2007; Donati et al. 2008), that switched its polarity in an year, which makes the study of the magnetic field of this star interesting.
We present in this paper a new multi-epoch spectropolarimetric study of τ Bootis. The modelling of the large-scale magnetic field of the star, its differential rotation and its activity is presented in Sections 3, 4 and 5. We draw some conclusions in Section 6.
2 OBSERVATIONS
Spectropolarimetric data of τ Bootis were collected using ESPaDOnS and Narval. ESPaDOnS is a high-resolution spectropolarimeter installed at the 3.6-m Canada–France–Hawaii Telescope (CFHT) in Hawaii. Narval is a twin instrument, installed at the 2-m Telescope Bernard Lyot (TBL) in France. The spectra obtained using both instruments span the whole optical domain (370 to 1048 nm), having a resolution of about 65 000. Each spectrum consists of four subexposures taken in different configurations of the polarimeter waveplates, in order to perform a full circular polarization analysis. Data were reduced using a fully automatic reduction tool Libre-Esprit, installed at the CFHT and the TBL. It extracts unpolarized (Stokes I) and circular polarized (Stokes V) spectra of the stellar light. A null spectrum (labelled N) is also produced to confirm that the detected polarization is real and not due to spurious instrumental or reduction effects (Donati et al. 1997).
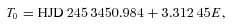
Maximum-entropy fits (thin red line) to the observed Stokes V LSD profiles (thick black line) of τ Boo for 2008 January (top), 2008 June (bottom left) and 2008 July (bottom right) are displayed. The orbital cycle of each observation (as listed in Tables 1 and 2) and 1σ error bars are also shown next to each profile.
Journal of 2008 January observations obtained with ESPaDOnS. Columns 1–8 sequentially list the ut date, the heliocentric Julian date and ut time (both at mid-exposure), the complete exposure time, the peak S/N (per 2.6 km s−1 velocity bin) of each observation (around 700 nm), the orbital cycle (using the ephemeris given by equation 1), the RV associated with each exposure and the rms noise level (relative to the unpolarized continuum level Ic and per 1.8 km s−1 velocity bin) in the circular polarization profile produced by LSD.
| Date (2008) | HJD (245 4000+) | ut (h:m:s) | texp (s) | S/N | Cycle (312+) | vrad (km s−1) | σLSD(10−4Ic) |
| 19 Jan | 486.084820 | 14:01:58 | 4×100 | 1404 | 0.4880 | −16.325 | 0.27 |
| 19 Jan | 486.092120 | 14:12:28 | 4×100 | 1420 | 0.4902 | −16.331 | 0.26 |
| 20 Jan | 487.070470 | 13:41:10 | 4×160 | 1500 | 0.7855 | −16.807 | 0.26 |
| 20 Jan | 487.080380 | 13:55:26 | 4×160 | 1590 | 0.7885 | −16.801 | 0.24 |
| 20 Jan | 487.090870 | 14:10:33 | 4×160 | 1685 | 0.7917 | −16.798 | 0.23 |
| 21 Jan | 488.036410 | 12:52:00 | 4×235 | 1826 | 1.0772 | −16.156 | 0.21 |
| 21 Jan | 488.050970 | 13:12:59 | 4×235 | 1808 | 1.0815 | −16.143 | 0.21 |
| 21 Jan | 488.064370 | 13:32:16 | 4×235 | 1850 | 1.0856 | −16.135 | 0.21 |
| 21 Jan | 488.160300 | 15:50:23 | 4×235 | 1871 | 1.1146 | −16.063 | 0.20 |
| 21 Jan | 488.173630 | 16:09:35 | 4×235 | 1704 | 1.1186 | −16.054 | 0.23 |
| 21 Jan | 488.184770 | 16:25:38 | 4×125 | 1245 | 1.1219 | −16.046 | 0.31 |
| 22 Jan | 489.040310 | 12:57:31 | 4×240 | 1767 | 1.3802 | −16.083 | 0.22 |
| 22 Jan | 489.053420 | 13:16:23 | 4×240 | 1869 | 1.3842 | −16.092 | 0.21 |
| 22 Jan | 489.067010 | 13:35:57 | 4×240 | 1972 | 1.3883 | −16.101 | 0.19 |
| 22 Jan | 489.160330 | 15:50:19 | 4×240 | 2064 | 1.4165 | −16.160 | 0.18 |
| 22 Jan | 489.173410 | 16:09:09 | 4×240 | 2088 | 1.4204 | −16.171 | 0.18 |
| 22 Jan | 489.186580 | 16:28:07 | 4×240 | 1979 | 1.4244 | −16.176 | 0.19 |
| 23 Jan | 490.046950 | 13:06:57 | 4×260 | 1855 | 1.6841 | −16.808 | 0.21 |
| 23 Jan | 490.061030 | 13:27:13 | 4×260 | 1864 | 1.6884 | −16.809 | 0.21 |
| 23 Jan | 490.075200 | 13:47:38 | 4×260 | 1848 | 1.6926 | −16.810 | 0.21 |
| 23 Jan | 490.159790 | 15:49:25 | 4×230 | 1823 | 1.7182 | −16.825 | 0.21 |
| 23 Jan | 490.172450 | 16:07:39 | 4×230 | 1830 | 1.7220 | −16.824 | 0.21 |
| 23 Jan | 490.185120 | 16:25:54 | 4×230 | 1760 | 1.7258 | −16.826 | 0.22 |
| 24 Jan | 491.062630 | 13:29:24 | 4×230 | 2160 | 1.9907 | −16.362 | 0.17 |
| 24 Jan | 491.104600 | 14:29:50 | 4×180 | 1830 | 2.0034 | −16.317 | 0.21 |
| 26 Jan | 493.046930 | 13:06:33 | 4×240 | 1685 | 2.5898 | −16.593 | 0.21 |
| 26 Jan | 493.060120 | 13:25:33 | 4×240 | 1686 | 2.5938 | −16.609 | 0.20 |
| 26 Jan | 493.073290 | 13:44:31 | 4×240 | 1704 | 2.5977 | −16.615 | 0.20 |
| 26 Jan | 493.161890 | 15:52: 5 | 4×220 | 1698 | 2.6245 | −16.708 | 0.22 |
| 26 Jan | 493.174080 | 16:09:38 | 4×220 | 1748 | 2.6282 | −16.724 | 0.21 |
| 26 Jan | 493.186500 | 16:27:31 | 4×220 | 1689 | 2.6319 | −16.728 | 0.22 |
| 27 Jan | 494.046290 | 13:05:31 | 4×240 | 1264 | 2.8915 | −16.677 | 0.26 |
| 27 Jan | 494.059860 | 13:25:03 | 4×240 | 1410 | 2.8956 | −16.657 | 0.22 |
| 27 Jan | 494.072960 | 13:43:55 | 4×240 | 1367 | 2.8995 | −16.650 | 0.23 |
| 27 Jan | 494.160790 | 15:50:23 | 4×220 | 1502 | 2.9260 | −16.579 | 0.24 |
| 27 Jan | 494.173120 | 16:08:09 | 4×220 | 1430 | 2.9298 | −16.579 | 0.26 |
| 27 Jan | 494.185340 | 16:25:44 | 4×220 | 1573 | 2.9335 | −16.569 | 0.25 |
| 29 Jan | 496.118430 | 14:49:09 | 4×300 | 1461 | 3.5170 | −16.412 | 0.23 |
| 29 Jan | 496.134930 | 15:12:54 | 4×300 | 1426 | 3.5220 | −16.420 | 0.23 |
| 29 Jan | 496.150890 | 15:35:54 | 4×300 | 1847 | 3.5268 | −16.452 | 0.19 |
| Date (2008) | HJD (245 4000+) | ut (h:m:s) | texp (s) | S/N | Cycle (312+) | vrad (km s−1) | σLSD(10−4Ic) |
| 19 Jan | 486.084820 | 14:01:58 | 4×100 | 1404 | 0.4880 | −16.325 | 0.27 |
| 19 Jan | 486.092120 | 14:12:28 | 4×100 | 1420 | 0.4902 | −16.331 | 0.26 |
| 20 Jan | 487.070470 | 13:41:10 | 4×160 | 1500 | 0.7855 | −16.807 | 0.26 |
| 20 Jan | 487.080380 | 13:55:26 | 4×160 | 1590 | 0.7885 | −16.801 | 0.24 |
| 20 Jan | 487.090870 | 14:10:33 | 4×160 | 1685 | 0.7917 | −16.798 | 0.23 |
| 21 Jan | 488.036410 | 12:52:00 | 4×235 | 1826 | 1.0772 | −16.156 | 0.21 |
| 21 Jan | 488.050970 | 13:12:59 | 4×235 | 1808 | 1.0815 | −16.143 | 0.21 |
| 21 Jan | 488.064370 | 13:32:16 | 4×235 | 1850 | 1.0856 | −16.135 | 0.21 |
| 21 Jan | 488.160300 | 15:50:23 | 4×235 | 1871 | 1.1146 | −16.063 | 0.20 |
| 21 Jan | 488.173630 | 16:09:35 | 4×235 | 1704 | 1.1186 | −16.054 | 0.23 |
| 21 Jan | 488.184770 | 16:25:38 | 4×125 | 1245 | 1.1219 | −16.046 | 0.31 |
| 22 Jan | 489.040310 | 12:57:31 | 4×240 | 1767 | 1.3802 | −16.083 | 0.22 |
| 22 Jan | 489.053420 | 13:16:23 | 4×240 | 1869 | 1.3842 | −16.092 | 0.21 |
| 22 Jan | 489.067010 | 13:35:57 | 4×240 | 1972 | 1.3883 | −16.101 | 0.19 |
| 22 Jan | 489.160330 | 15:50:19 | 4×240 | 2064 | 1.4165 | −16.160 | 0.18 |
| 22 Jan | 489.173410 | 16:09:09 | 4×240 | 2088 | 1.4204 | −16.171 | 0.18 |
| 22 Jan | 489.186580 | 16:28:07 | 4×240 | 1979 | 1.4244 | −16.176 | 0.19 |
| 23 Jan | 490.046950 | 13:06:57 | 4×260 | 1855 | 1.6841 | −16.808 | 0.21 |
| 23 Jan | 490.061030 | 13:27:13 | 4×260 | 1864 | 1.6884 | −16.809 | 0.21 |
| 23 Jan | 490.075200 | 13:47:38 | 4×260 | 1848 | 1.6926 | −16.810 | 0.21 |
| 23 Jan | 490.159790 | 15:49:25 | 4×230 | 1823 | 1.7182 | −16.825 | 0.21 |
| 23 Jan | 490.172450 | 16:07:39 | 4×230 | 1830 | 1.7220 | −16.824 | 0.21 |
| 23 Jan | 490.185120 | 16:25:54 | 4×230 | 1760 | 1.7258 | −16.826 | 0.22 |
| 24 Jan | 491.062630 | 13:29:24 | 4×230 | 2160 | 1.9907 | −16.362 | 0.17 |
| 24 Jan | 491.104600 | 14:29:50 | 4×180 | 1830 | 2.0034 | −16.317 | 0.21 |
| 26 Jan | 493.046930 | 13:06:33 | 4×240 | 1685 | 2.5898 | −16.593 | 0.21 |
| 26 Jan | 493.060120 | 13:25:33 | 4×240 | 1686 | 2.5938 | −16.609 | 0.20 |
| 26 Jan | 493.073290 | 13:44:31 | 4×240 | 1704 | 2.5977 | −16.615 | 0.20 |
| 26 Jan | 493.161890 | 15:52: 5 | 4×220 | 1698 | 2.6245 | −16.708 | 0.22 |
| 26 Jan | 493.174080 | 16:09:38 | 4×220 | 1748 | 2.6282 | −16.724 | 0.21 |
| 26 Jan | 493.186500 | 16:27:31 | 4×220 | 1689 | 2.6319 | −16.728 | 0.22 |
| 27 Jan | 494.046290 | 13:05:31 | 4×240 | 1264 | 2.8915 | −16.677 | 0.26 |
| 27 Jan | 494.059860 | 13:25:03 | 4×240 | 1410 | 2.8956 | −16.657 | 0.22 |
| 27 Jan | 494.072960 | 13:43:55 | 4×240 | 1367 | 2.8995 | −16.650 | 0.23 |
| 27 Jan | 494.160790 | 15:50:23 | 4×220 | 1502 | 2.9260 | −16.579 | 0.24 |
| 27 Jan | 494.173120 | 16:08:09 | 4×220 | 1430 | 2.9298 | −16.579 | 0.26 |
| 27 Jan | 494.185340 | 16:25:44 | 4×220 | 1573 | 2.9335 | −16.569 | 0.25 |
| 29 Jan | 496.118430 | 14:49:09 | 4×300 | 1461 | 3.5170 | −16.412 | 0.23 |
| 29 Jan | 496.134930 | 15:12:54 | 4×300 | 1426 | 3.5220 | −16.420 | 0.23 |
| 29 Jan | 496.150890 | 15:35:54 | 4×300 | 1847 | 3.5268 | −16.452 | 0.19 |
Journal of 2008 January observations obtained with ESPaDOnS. Columns 1–8 sequentially list the ut date, the heliocentric Julian date and ut time (both at mid-exposure), the complete exposure time, the peak S/N (per 2.6 km s−1 velocity bin) of each observation (around 700 nm), the orbital cycle (using the ephemeris given by equation 1), the RV associated with each exposure and the rms noise level (relative to the unpolarized continuum level Ic and per 1.8 km s−1 velocity bin) in the circular polarization profile produced by LSD.
| Date (2008) | HJD (245 4000+) | ut (h:m:s) | texp (s) | S/N | Cycle (312+) | vrad (km s−1) | σLSD(10−4Ic) |
| 19 Jan | 486.084820 | 14:01:58 | 4×100 | 1404 | 0.4880 | −16.325 | 0.27 |
| 19 Jan | 486.092120 | 14:12:28 | 4×100 | 1420 | 0.4902 | −16.331 | 0.26 |
| 20 Jan | 487.070470 | 13:41:10 | 4×160 | 1500 | 0.7855 | −16.807 | 0.26 |
| 20 Jan | 487.080380 | 13:55:26 | 4×160 | 1590 | 0.7885 | −16.801 | 0.24 |
| 20 Jan | 487.090870 | 14:10:33 | 4×160 | 1685 | 0.7917 | −16.798 | 0.23 |
| 21 Jan | 488.036410 | 12:52:00 | 4×235 | 1826 | 1.0772 | −16.156 | 0.21 |
| 21 Jan | 488.050970 | 13:12:59 | 4×235 | 1808 | 1.0815 | −16.143 | 0.21 |
| 21 Jan | 488.064370 | 13:32:16 | 4×235 | 1850 | 1.0856 | −16.135 | 0.21 |
| 21 Jan | 488.160300 | 15:50:23 | 4×235 | 1871 | 1.1146 | −16.063 | 0.20 |
| 21 Jan | 488.173630 | 16:09:35 | 4×235 | 1704 | 1.1186 | −16.054 | 0.23 |
| 21 Jan | 488.184770 | 16:25:38 | 4×125 | 1245 | 1.1219 | −16.046 | 0.31 |
| 22 Jan | 489.040310 | 12:57:31 | 4×240 | 1767 | 1.3802 | −16.083 | 0.22 |
| 22 Jan | 489.053420 | 13:16:23 | 4×240 | 1869 | 1.3842 | −16.092 | 0.21 |
| 22 Jan | 489.067010 | 13:35:57 | 4×240 | 1972 | 1.3883 | −16.101 | 0.19 |
| 22 Jan | 489.160330 | 15:50:19 | 4×240 | 2064 | 1.4165 | −16.160 | 0.18 |
| 22 Jan | 489.173410 | 16:09:09 | 4×240 | 2088 | 1.4204 | −16.171 | 0.18 |
| 22 Jan | 489.186580 | 16:28:07 | 4×240 | 1979 | 1.4244 | −16.176 | 0.19 |
| 23 Jan | 490.046950 | 13:06:57 | 4×260 | 1855 | 1.6841 | −16.808 | 0.21 |
| 23 Jan | 490.061030 | 13:27:13 | 4×260 | 1864 | 1.6884 | −16.809 | 0.21 |
| 23 Jan | 490.075200 | 13:47:38 | 4×260 | 1848 | 1.6926 | −16.810 | 0.21 |
| 23 Jan | 490.159790 | 15:49:25 | 4×230 | 1823 | 1.7182 | −16.825 | 0.21 |
| 23 Jan | 490.172450 | 16:07:39 | 4×230 | 1830 | 1.7220 | −16.824 | 0.21 |
| 23 Jan | 490.185120 | 16:25:54 | 4×230 | 1760 | 1.7258 | −16.826 | 0.22 |
| 24 Jan | 491.062630 | 13:29:24 | 4×230 | 2160 | 1.9907 | −16.362 | 0.17 |
| 24 Jan | 491.104600 | 14:29:50 | 4×180 | 1830 | 2.0034 | −16.317 | 0.21 |
| 26 Jan | 493.046930 | 13:06:33 | 4×240 | 1685 | 2.5898 | −16.593 | 0.21 |
| 26 Jan | 493.060120 | 13:25:33 | 4×240 | 1686 | 2.5938 | −16.609 | 0.20 |
| 26 Jan | 493.073290 | 13:44:31 | 4×240 | 1704 | 2.5977 | −16.615 | 0.20 |
| 26 Jan | 493.161890 | 15:52: 5 | 4×220 | 1698 | 2.6245 | −16.708 | 0.22 |
| 26 Jan | 493.174080 | 16:09:38 | 4×220 | 1748 | 2.6282 | −16.724 | 0.21 |
| 26 Jan | 493.186500 | 16:27:31 | 4×220 | 1689 | 2.6319 | −16.728 | 0.22 |
| 27 Jan | 494.046290 | 13:05:31 | 4×240 | 1264 | 2.8915 | −16.677 | 0.26 |
| 27 Jan | 494.059860 | 13:25:03 | 4×240 | 1410 | 2.8956 | −16.657 | 0.22 |
| 27 Jan | 494.072960 | 13:43:55 | 4×240 | 1367 | 2.8995 | −16.650 | 0.23 |
| 27 Jan | 494.160790 | 15:50:23 | 4×220 | 1502 | 2.9260 | −16.579 | 0.24 |
| 27 Jan | 494.173120 | 16:08:09 | 4×220 | 1430 | 2.9298 | −16.579 | 0.26 |
| 27 Jan | 494.185340 | 16:25:44 | 4×220 | 1573 | 2.9335 | −16.569 | 0.25 |
| 29 Jan | 496.118430 | 14:49:09 | 4×300 | 1461 | 3.5170 | −16.412 | 0.23 |
| 29 Jan | 496.134930 | 15:12:54 | 4×300 | 1426 | 3.5220 | −16.420 | 0.23 |
| 29 Jan | 496.150890 | 15:35:54 | 4×300 | 1847 | 3.5268 | −16.452 | 0.19 |
| Date (2008) | HJD (245 4000+) | ut (h:m:s) | texp (s) | S/N | Cycle (312+) | vrad (km s−1) | σLSD(10−4Ic) |
| 19 Jan | 486.084820 | 14:01:58 | 4×100 | 1404 | 0.4880 | −16.325 | 0.27 |
| 19 Jan | 486.092120 | 14:12:28 | 4×100 | 1420 | 0.4902 | −16.331 | 0.26 |
| 20 Jan | 487.070470 | 13:41:10 | 4×160 | 1500 | 0.7855 | −16.807 | 0.26 |
| 20 Jan | 487.080380 | 13:55:26 | 4×160 | 1590 | 0.7885 | −16.801 | 0.24 |
| 20 Jan | 487.090870 | 14:10:33 | 4×160 | 1685 | 0.7917 | −16.798 | 0.23 |
| 21 Jan | 488.036410 | 12:52:00 | 4×235 | 1826 | 1.0772 | −16.156 | 0.21 |
| 21 Jan | 488.050970 | 13:12:59 | 4×235 | 1808 | 1.0815 | −16.143 | 0.21 |
| 21 Jan | 488.064370 | 13:32:16 | 4×235 | 1850 | 1.0856 | −16.135 | 0.21 |
| 21 Jan | 488.160300 | 15:50:23 | 4×235 | 1871 | 1.1146 | −16.063 | 0.20 |
| 21 Jan | 488.173630 | 16:09:35 | 4×235 | 1704 | 1.1186 | −16.054 | 0.23 |
| 21 Jan | 488.184770 | 16:25:38 | 4×125 | 1245 | 1.1219 | −16.046 | 0.31 |
| 22 Jan | 489.040310 | 12:57:31 | 4×240 | 1767 | 1.3802 | −16.083 | 0.22 |
| 22 Jan | 489.053420 | 13:16:23 | 4×240 | 1869 | 1.3842 | −16.092 | 0.21 |
| 22 Jan | 489.067010 | 13:35:57 | 4×240 | 1972 | 1.3883 | −16.101 | 0.19 |
| 22 Jan | 489.160330 | 15:50:19 | 4×240 | 2064 | 1.4165 | −16.160 | 0.18 |
| 22 Jan | 489.173410 | 16:09:09 | 4×240 | 2088 | 1.4204 | −16.171 | 0.18 |
| 22 Jan | 489.186580 | 16:28:07 | 4×240 | 1979 | 1.4244 | −16.176 | 0.19 |
| 23 Jan | 490.046950 | 13:06:57 | 4×260 | 1855 | 1.6841 | −16.808 | 0.21 |
| 23 Jan | 490.061030 | 13:27:13 | 4×260 | 1864 | 1.6884 | −16.809 | 0.21 |
| 23 Jan | 490.075200 | 13:47:38 | 4×260 | 1848 | 1.6926 | −16.810 | 0.21 |
| 23 Jan | 490.159790 | 15:49:25 | 4×230 | 1823 | 1.7182 | −16.825 | 0.21 |
| 23 Jan | 490.172450 | 16:07:39 | 4×230 | 1830 | 1.7220 | −16.824 | 0.21 |
| 23 Jan | 490.185120 | 16:25:54 | 4×230 | 1760 | 1.7258 | −16.826 | 0.22 |
| 24 Jan | 491.062630 | 13:29:24 | 4×230 | 2160 | 1.9907 | −16.362 | 0.17 |
| 24 Jan | 491.104600 | 14:29:50 | 4×180 | 1830 | 2.0034 | −16.317 | 0.21 |
| 26 Jan | 493.046930 | 13:06:33 | 4×240 | 1685 | 2.5898 | −16.593 | 0.21 |
| 26 Jan | 493.060120 | 13:25:33 | 4×240 | 1686 | 2.5938 | −16.609 | 0.20 |
| 26 Jan | 493.073290 | 13:44:31 | 4×240 | 1704 | 2.5977 | −16.615 | 0.20 |
| 26 Jan | 493.161890 | 15:52: 5 | 4×220 | 1698 | 2.6245 | −16.708 | 0.22 |
| 26 Jan | 493.174080 | 16:09:38 | 4×220 | 1748 | 2.6282 | −16.724 | 0.21 |
| 26 Jan | 493.186500 | 16:27:31 | 4×220 | 1689 | 2.6319 | −16.728 | 0.22 |
| 27 Jan | 494.046290 | 13:05:31 | 4×240 | 1264 | 2.8915 | −16.677 | 0.26 |
| 27 Jan | 494.059860 | 13:25:03 | 4×240 | 1410 | 2.8956 | −16.657 | 0.22 |
| 27 Jan | 494.072960 | 13:43:55 | 4×240 | 1367 | 2.8995 | −16.650 | 0.23 |
| 27 Jan | 494.160790 | 15:50:23 | 4×220 | 1502 | 2.9260 | −16.579 | 0.24 |
| 27 Jan | 494.173120 | 16:08:09 | 4×220 | 1430 | 2.9298 | −16.579 | 0.26 |
| 27 Jan | 494.185340 | 16:25:44 | 4×220 | 1573 | 2.9335 | −16.569 | 0.25 |
| 29 Jan | 496.118430 | 14:49:09 | 4×300 | 1461 | 3.5170 | −16.412 | 0.23 |
| 29 Jan | 496.134930 | 15:12:54 | 4×300 | 1426 | 3.5220 | −16.420 | 0.23 |
| 29 Jan | 496.150890 | 15:35:54 | 4×300 | 1847 | 3.5268 | −16.452 | 0.19 |
Journal of June and July observations obtained with Narval. Columns 1–8 indicate the same parameters as in Table 1.
| Date (2008) | HJD (245 4000+) | ut (h:m:s) | texp (s) | S/N | Cycle (+358) | vrad (km s−1) | σLSD(10−4Ic) |
| 21 June | 639.358680 | 20:33:14 | 4×300 | 858 | 0.7600 | −16.868 | 0.45 |
| 21 June | 639.381310 | 21: 5:49 | 4×600 | 1200 | 0.7669 | −16.843 | 0.32 |
| 21 June | 639.411470 | 21:49:16 | 4×600 | 1359 | 0.7760 | −16.832 | 0.28 |
| 22 June | 640.362370 | 20:38:39 | 4×300 | 1471 | 1.0630 | −16.179 | 0.24 |
| 22 June | 640.384990 | 21:11:14 | 4×600 | 1997 | 1.0699 | −16.154 | 0.18 |
| 22 June | 640.415150 | 21:54:39 | 4×600 | 2118 | 1.0790 | −16.132 | 0.17 |
| 25 June | 643.375010 | 20:57:10 | 4×600 | 1660 | 1.9725 | −16.397 | 0.22 |
| 27 June | 645.358100 | 20:33: 2 | 4×300 | 1374 | 2.5712 | −16.538 | 0.25 |
| 28 June | 646.351660 | 20:23:53 | 4×300 | 1363 | 2.8712 | −16.704 | 0.25 |
| 10 July | 658.351740 | 20:25:20 | 4×600 | 1873 | 6.4939 | −16.368 | 0.19 |
| 14 July | 662.352640 | 20:27: 6 | 4×600 | 1355 | 7.7017 | −16.914 | 0.28 |
| 15 July | 663.348890 | 20:21:49 | 4×600 | 1810 | 8.0025 | −16.432 | 0.20 |
| 17 July | 665.352950 | 20:27:54 | 4×450 | 1880 | 8.6075 | −16.666 | 0.20 |
| 17 July | 665.376170 | 21: 1:20 | 4×450 | 1843 | 8.6145 | −16.673 | 0.20 |
| 18 July | 666.347980 | 20:20:52 | 4×450 | 1901 | 8.9079 | −16.635 | 0.19 |
| 18 July | 666.371210 | 20:54:18 | 4×450 | 1854 | 8.9149 | −16.585 | 0.19 |
| 19 July | 667.374180 | 20:58:42 | 4×450 | 1492 | 9.2177 | −15.925 | 0.26 |
| 19 July | 667.397390 | 21:32: 8 | 4×450 | 1196 | 9.2247 | −15.912 | 0.33 |
| 20 July | 668.373790 | 20:58:15 | 4×450 | 1050 | 9.5194 | −16.390 | 0.36 |
| 20 July | 668.397020 | 21:31:43 | 4×450 | 1229 | 9.5265 | −16.427 | 0.32 |
| 21 July | 669.349580 | 20:23:31 | 4×450 | 1172 | 9.8140 | −16.843 | 0.32 |
| 21 July | 669.372800 | 20:56:57 | 4×450 | 1259 | 9.8210 | −16.814 | 0.30 |
| 22 July | 670.348550 | 20:22: 9 | 4×450 | 1846 | 10.1156 | −16.081 | 0.19 |
| 22 July | 670.371770 | 20:55:35 | 4×450 | 1791 | 10.1226 | −16.047 | 0.20 |
| 23 July | 671.348660 | 20:22:25 | 4×450 | 898 | 10.4175 | −16.156 | 0.49 |
| 23 July | 671.371890 | 20:55:53 | 4×450 | 571 | 10.4245 | −16.141 | 1.03 |
| 24 July | 672.352850 | 20:28:34 | 4×450 | 1717 | 10.7207 | −16.832 | 0.21 |
| 24 July | 672.376080 | 21: 2: 2 | 4×450 | 1649 | 10.7277 | −16.825 | 0.23 |
| Date (2008) | HJD (245 4000+) | ut (h:m:s) | texp (s) | S/N | Cycle (+358) | vrad (km s−1) | σLSD(10−4Ic) |
| 21 June | 639.358680 | 20:33:14 | 4×300 | 858 | 0.7600 | −16.868 | 0.45 |
| 21 June | 639.381310 | 21: 5:49 | 4×600 | 1200 | 0.7669 | −16.843 | 0.32 |
| 21 June | 639.411470 | 21:49:16 | 4×600 | 1359 | 0.7760 | −16.832 | 0.28 |
| 22 June | 640.362370 | 20:38:39 | 4×300 | 1471 | 1.0630 | −16.179 | 0.24 |
| 22 June | 640.384990 | 21:11:14 | 4×600 | 1997 | 1.0699 | −16.154 | 0.18 |
| 22 June | 640.415150 | 21:54:39 | 4×600 | 2118 | 1.0790 | −16.132 | 0.17 |
| 25 June | 643.375010 | 20:57:10 | 4×600 | 1660 | 1.9725 | −16.397 | 0.22 |
| 27 June | 645.358100 | 20:33: 2 | 4×300 | 1374 | 2.5712 | −16.538 | 0.25 |
| 28 June | 646.351660 | 20:23:53 | 4×300 | 1363 | 2.8712 | −16.704 | 0.25 |
| 10 July | 658.351740 | 20:25:20 | 4×600 | 1873 | 6.4939 | −16.368 | 0.19 |
| 14 July | 662.352640 | 20:27: 6 | 4×600 | 1355 | 7.7017 | −16.914 | 0.28 |
| 15 July | 663.348890 | 20:21:49 | 4×600 | 1810 | 8.0025 | −16.432 | 0.20 |
| 17 July | 665.352950 | 20:27:54 | 4×450 | 1880 | 8.6075 | −16.666 | 0.20 |
| 17 July | 665.376170 | 21: 1:20 | 4×450 | 1843 | 8.6145 | −16.673 | 0.20 |
| 18 July | 666.347980 | 20:20:52 | 4×450 | 1901 | 8.9079 | −16.635 | 0.19 |
| 18 July | 666.371210 | 20:54:18 | 4×450 | 1854 | 8.9149 | −16.585 | 0.19 |
| 19 July | 667.374180 | 20:58:42 | 4×450 | 1492 | 9.2177 | −15.925 | 0.26 |
| 19 July | 667.397390 | 21:32: 8 | 4×450 | 1196 | 9.2247 | −15.912 | 0.33 |
| 20 July | 668.373790 | 20:58:15 | 4×450 | 1050 | 9.5194 | −16.390 | 0.36 |
| 20 July | 668.397020 | 21:31:43 | 4×450 | 1229 | 9.5265 | −16.427 | 0.32 |
| 21 July | 669.349580 | 20:23:31 | 4×450 | 1172 | 9.8140 | −16.843 | 0.32 |
| 21 July | 669.372800 | 20:56:57 | 4×450 | 1259 | 9.8210 | −16.814 | 0.30 |
| 22 July | 670.348550 | 20:22: 9 | 4×450 | 1846 | 10.1156 | −16.081 | 0.19 |
| 22 July | 670.371770 | 20:55:35 | 4×450 | 1791 | 10.1226 | −16.047 | 0.20 |
| 23 July | 671.348660 | 20:22:25 | 4×450 | 898 | 10.4175 | −16.156 | 0.49 |
| 23 July | 671.371890 | 20:55:53 | 4×450 | 571 | 10.4245 | −16.141 | 1.03 |
| 24 July | 672.352850 | 20:28:34 | 4×450 | 1717 | 10.7207 | −16.832 | 0.21 |
| 24 July | 672.376080 | 21: 2: 2 | 4×450 | 1649 | 10.7277 | −16.825 | 0.23 |
Journal of June and July observations obtained with Narval. Columns 1–8 indicate the same parameters as in Table 1.
| Date (2008) | HJD (245 4000+) | ut (h:m:s) | texp (s) | S/N | Cycle (+358) | vrad (km s−1) | σLSD(10−4Ic) |
| 21 June | 639.358680 | 20:33:14 | 4×300 | 858 | 0.7600 | −16.868 | 0.45 |
| 21 June | 639.381310 | 21: 5:49 | 4×600 | 1200 | 0.7669 | −16.843 | 0.32 |
| 21 June | 639.411470 | 21:49:16 | 4×600 | 1359 | 0.7760 | −16.832 | 0.28 |
| 22 June | 640.362370 | 20:38:39 | 4×300 | 1471 | 1.0630 | −16.179 | 0.24 |
| 22 June | 640.384990 | 21:11:14 | 4×600 | 1997 | 1.0699 | −16.154 | 0.18 |
| 22 June | 640.415150 | 21:54:39 | 4×600 | 2118 | 1.0790 | −16.132 | 0.17 |
| 25 June | 643.375010 | 20:57:10 | 4×600 | 1660 | 1.9725 | −16.397 | 0.22 |
| 27 June | 645.358100 | 20:33: 2 | 4×300 | 1374 | 2.5712 | −16.538 | 0.25 |
| 28 June | 646.351660 | 20:23:53 | 4×300 | 1363 | 2.8712 | −16.704 | 0.25 |
| 10 July | 658.351740 | 20:25:20 | 4×600 | 1873 | 6.4939 | −16.368 | 0.19 |
| 14 July | 662.352640 | 20:27: 6 | 4×600 | 1355 | 7.7017 | −16.914 | 0.28 |
| 15 July | 663.348890 | 20:21:49 | 4×600 | 1810 | 8.0025 | −16.432 | 0.20 |
| 17 July | 665.352950 | 20:27:54 | 4×450 | 1880 | 8.6075 | −16.666 | 0.20 |
| 17 July | 665.376170 | 21: 1:20 | 4×450 | 1843 | 8.6145 | −16.673 | 0.20 |
| 18 July | 666.347980 | 20:20:52 | 4×450 | 1901 | 8.9079 | −16.635 | 0.19 |
| 18 July | 666.371210 | 20:54:18 | 4×450 | 1854 | 8.9149 | −16.585 | 0.19 |
| 19 July | 667.374180 | 20:58:42 | 4×450 | 1492 | 9.2177 | −15.925 | 0.26 |
| 19 July | 667.397390 | 21:32: 8 | 4×450 | 1196 | 9.2247 | −15.912 | 0.33 |
| 20 July | 668.373790 | 20:58:15 | 4×450 | 1050 | 9.5194 | −16.390 | 0.36 |
| 20 July | 668.397020 | 21:31:43 | 4×450 | 1229 | 9.5265 | −16.427 | 0.32 |
| 21 July | 669.349580 | 20:23:31 | 4×450 | 1172 | 9.8140 | −16.843 | 0.32 |
| 21 July | 669.372800 | 20:56:57 | 4×450 | 1259 | 9.8210 | −16.814 | 0.30 |
| 22 July | 670.348550 | 20:22: 9 | 4×450 | 1846 | 10.1156 | −16.081 | 0.19 |
| 22 July | 670.371770 | 20:55:35 | 4×450 | 1791 | 10.1226 | −16.047 | 0.20 |
| 23 July | 671.348660 | 20:22:25 | 4×450 | 898 | 10.4175 | −16.156 | 0.49 |
| 23 July | 671.371890 | 20:55:53 | 4×450 | 571 | 10.4245 | −16.141 | 1.03 |
| 24 July | 672.352850 | 20:28:34 | 4×450 | 1717 | 10.7207 | −16.832 | 0.21 |
| 24 July | 672.376080 | 21: 2: 2 | 4×450 | 1649 | 10.7277 | −16.825 | 0.23 |
| Date (2008) | HJD (245 4000+) | ut (h:m:s) | texp (s) | S/N | Cycle (+358) | vrad (km s−1) | σLSD(10−4Ic) |
| 21 June | 639.358680 | 20:33:14 | 4×300 | 858 | 0.7600 | −16.868 | 0.45 |
| 21 June | 639.381310 | 21: 5:49 | 4×600 | 1200 | 0.7669 | −16.843 | 0.32 |
| 21 June | 639.411470 | 21:49:16 | 4×600 | 1359 | 0.7760 | −16.832 | 0.28 |
| 22 June | 640.362370 | 20:38:39 | 4×300 | 1471 | 1.0630 | −16.179 | 0.24 |
| 22 June | 640.384990 | 21:11:14 | 4×600 | 1997 | 1.0699 | −16.154 | 0.18 |
| 22 June | 640.415150 | 21:54:39 | 4×600 | 2118 | 1.0790 | −16.132 | 0.17 |
| 25 June | 643.375010 | 20:57:10 | 4×600 | 1660 | 1.9725 | −16.397 | 0.22 |
| 27 June | 645.358100 | 20:33: 2 | 4×300 | 1374 | 2.5712 | −16.538 | 0.25 |
| 28 June | 646.351660 | 20:23:53 | 4×300 | 1363 | 2.8712 | −16.704 | 0.25 |
| 10 July | 658.351740 | 20:25:20 | 4×600 | 1873 | 6.4939 | −16.368 | 0.19 |
| 14 July | 662.352640 | 20:27: 6 | 4×600 | 1355 | 7.7017 | −16.914 | 0.28 |
| 15 July | 663.348890 | 20:21:49 | 4×600 | 1810 | 8.0025 | −16.432 | 0.20 |
| 17 July | 665.352950 | 20:27:54 | 4×450 | 1880 | 8.6075 | −16.666 | 0.20 |
| 17 July | 665.376170 | 21: 1:20 | 4×450 | 1843 | 8.6145 | −16.673 | 0.20 |
| 18 July | 666.347980 | 20:20:52 | 4×450 | 1901 | 8.9079 | −16.635 | 0.19 |
| 18 July | 666.371210 | 20:54:18 | 4×450 | 1854 | 8.9149 | −16.585 | 0.19 |
| 19 July | 667.374180 | 20:58:42 | 4×450 | 1492 | 9.2177 | −15.925 | 0.26 |
| 19 July | 667.397390 | 21:32: 8 | 4×450 | 1196 | 9.2247 | −15.912 | 0.33 |
| 20 July | 668.373790 | 20:58:15 | 4×450 | 1050 | 9.5194 | −16.390 | 0.36 |
| 20 July | 668.397020 | 21:31:43 | 4×450 | 1229 | 9.5265 | −16.427 | 0.32 |
| 21 July | 669.349580 | 20:23:31 | 4×450 | 1172 | 9.8140 | −16.843 | 0.32 |
| 21 July | 669.372800 | 20:56:57 | 4×450 | 1259 | 9.8210 | −16.814 | 0.30 |
| 22 July | 670.348550 | 20:22: 9 | 4×450 | 1846 | 10.1156 | −16.081 | 0.19 |
| 22 July | 670.371770 | 20:55:35 | 4×450 | 1791 | 10.1226 | −16.047 | 0.20 |
| 23 July | 671.348660 | 20:22:25 | 4×450 | 898 | 10.4175 | −16.156 | 0.49 |
| 23 July | 671.371890 | 20:55:53 | 4×450 | 571 | 10.4245 | −16.141 | 1.03 |
| 24 July | 672.352850 | 20:28:34 | 4×450 | 1717 | 10.7207 | −16.832 | 0.21 |
| 24 July | 672.376080 | 21: 2: 2 | 4×450 | 1649 | 10.7277 | −16.825 | 0.23 |
The Zeeman signatures of τ Boo are extremely small. We use least-squares deconvolution (LSD) to improve the S/N of our data. This technique consists of deconvolving the observed spectra using a line mask. The line mask was computed using a Kurucz model atmosphere with solar abundances; effective temperature and logarithmic gravity (in cm s−2) are set to 6250 K and 4.0, respectively. The line mask includes most moderate to strong lines present in the optical domain (those featuring central depths larger than 40 per cent of the local continuum, before any macro turbulent or rotational broadening, about 4000 lines throughout the whole spectral range) but excludes the strongest, broadest features, such as Balmer lines, whose Zeeman signature is strongly smeared out compared to those of narrow lines. The typical multiplex gain for the polarization profiles is between 25 and 30, implying noise levels in LSD polarization profiles as low as 20 parts per million (ppm).
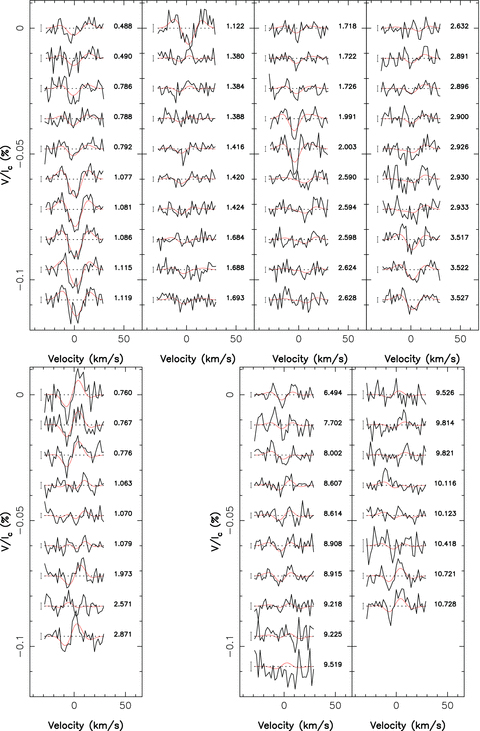
Radial velocities (RV) of the star can be obtained by fitting the Stokes I profiles (unpolarized profiles) with a Gaussian to each profile. The values we obtain are in good agreement with the expectations (Fig. 1), when using the orbital ephemeris of Catala et al. (2007). All spectra are automatically corrected from spectral shifts resulting from instrumental effects (e.g. mechanical flexures, temperature or pressure variations) using telluric lines as a reference. Though not perfect, this procedure allows spectra to be secured with RV precision of better than 30 m s−1 (Moutou et al. 2007; Morin et al. 2008b). All spectra are corrected from the orbital motion.
RV of τ Boo derived from our Narval (red dots) and ESPaDOnS (green dots) spectra as a function of orbital phase, with their error bars (20–30 m s−1). The RV model plotted here (blue full line) corresponds to our fit of the data, giving orbital solution compatible with those in the literature (Butler et al. 2006).
3 MAGNETIC MODELLING
3.1 Model description
We use Zeeman Doppler Imaging (ZDI) to get magnetic maps of τ Boo and an estimation of its differential rotation. ZDI is a tomographic imaging technique; it consists of inverting series of Stokes V profiles into a map of the parent magnetic topology, i.e. both the location of magnetic spots and the orientation of the field lines. We use the most recent version of the code (Donati et al. 2006), which describes the field by its poloidal and toroidal components, both expressed in terms of spherical harmonic expansions. This has the advantage that both simple and complex magnetic topologies can be reconstructed. The energy of axisymmetric (l < m/2) and non-axisymmetric modes is easily calculated from the coefficients of the spherical harmonics.
The surface of the star is decomposed into 50 000 small cells of similar area. The procedure takes into account the contribution of each cell to the reconstructed profile. This is done by iteratively comparing the synthetic profile to the observed one, until they match within the error bars (i.e. reduced chi-square χ2r∼ 1). Since the inversion problem is ill-posed, we use Maximum Entropy as a criterion that ensures a unique solution.
The models we use for computing the local Stokes I and V profiles associated with each grid cell are quite simple. Stokes I is modelled by a Gaussian with a full width at half-maximum (FWHM) of 11 km s−1. Stokes V is modelled assuming the weak field approximation, i.e. V∝g Blos dI/dv where Blos is the line-of-sight projected magnetic field at a selected point at the surface of the star and g is the mean landé factor (set to 1.2). The magnetic field detected on τ Boo (5–10 G; Catala et al. 2007; Donati et al. 2008) demonstrates that this approximation is valid.
3.2 Magnetic maps
Given the projected equatorial velocity of τ Boo (vesin i= 15.9 km s−1) and the FWHM of the local profile intensity of 11 km s−1, there are approximately nine spatial resolution elements around the equator. In practice, the information added to the maps when considering a degree of spherical harmonics greater than 8 is of little significance; we therefore use lmax= 8. As in Catala et al. (2007), the inclination angle of the rotation axis of the star with respect to the line-of-sight is assumed to be i= 40°. Fitting the N (null) profiles (instead of Stokes V profiles) assuming no magnetic field at the surface of the star gives a χ2r level varying between 0.85 and 0.9 depending on the epoch (indicating that our error bars are slightly overestimated by about 5 per cent). We therefore fit all our Stokes V data to a level of χ2r= 0.9.
3.2.1 2008 January
The observed and reconstructed Stokes V profiles of 2008 January are shown in Fig. 2 (top panel). The signatures vary strongly in shape and amplitudes over rotational phases (e.g. signatures of January 20 compared to those of January 22), which suggests a complex magnetic topology. Reconstructed profiles fit the observed ones within the error bars. The corresponding magnetic map is shown in Fig. 3 (second column).
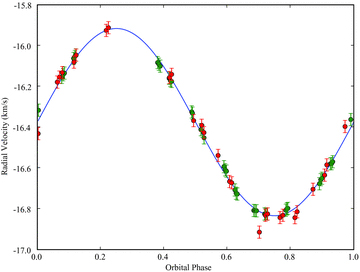
Maximum-entropy reconstructions of the large-scale magnetic topology of τ Boo as derived from our 2008 January (second column), 2008 June (third column) and 2008 July (right-hand column) data sets are displayed. The radial, azimuthal and meridional components of the field (with magnetic flux values labelled in G). The star is shown in flattened polar projection down to latitudes of −30°, with the equator depicted as a bold circle and parallels as dashed circles. Radial ticks around each plot indicate orbital phases of observations. The 2007 June magnetic map of τ Boo (Donati et al. 2008) is added in the left-hand column to ease comparison.
τ Boo has a weak surface magnetic field of just a few gauss, reaching a maximum strength at the surface of the star of about 5 to 10 G. The toroidal field dominates (contributing to 62 per cent of the total magnetic energy) in the form of a ring of mainly axisymmetric azimuthal field encircling the whole star. The radial poloidal field shows a more complex topology, with two regions of negative polarity at intermediate latitudes, and a positive one. None of those magnetic regions dominates the others, contrary to 2007 June (when the positive polarity contributes more than the negative polarity). Axisymmetric modes enclose 20 per cent of the poloidal field energy (see Table 3).
Average magnetic field on the surface of the star, percentage of the toroidal energy relative to the total one, percentage of the energy contained in the axisymmetric modes of the poloidal component and percentage of the energy contained in the modes of l≤ 2 of the poloidal component for each epoch of observation. Data for June 2007 are taken from Donati et al. (2008).
| B (G) | % toroidal | % axisymmetric modes in poloidal | %l≤ 2 in poloidal | |
| 2007 June | 3.7 | 17 | 60 | 52 |
| 2008 January | 3.1 | 62 | 20 | 50 |
| 2008 June | 2.3 | 13 | 36 | 36 |
| 2008 July | 1.7 | 9 | 62 | 47 |
| B (G) | % toroidal | % axisymmetric modes in poloidal | %l≤ 2 in poloidal | |
| 2007 June | 3.7 | 17 | 60 | 52 |
| 2008 January | 3.1 | 62 | 20 | 50 |
| 2008 June | 2.3 | 13 | 36 | 36 |
| 2008 July | 1.7 | 9 | 62 | 47 |
Average magnetic field on the surface of the star, percentage of the toroidal energy relative to the total one, percentage of the energy contained in the axisymmetric modes of the poloidal component and percentage of the energy contained in the modes of l≤ 2 of the poloidal component for each epoch of observation. Data for June 2007 are taken from Donati et al. (2008).
| B (G) | % toroidal | % axisymmetric modes in poloidal | %l≤ 2 in poloidal | |
| 2007 June | 3.7 | 17 | 60 | 52 |
| 2008 January | 3.1 | 62 | 20 | 50 |
| 2008 June | 2.3 | 13 | 36 | 36 |
| 2008 July | 1.7 | 9 | 62 | 47 |
| B (G) | % toroidal | % axisymmetric modes in poloidal | %l≤ 2 in poloidal | |
| 2007 June | 3.7 | 17 | 60 | 52 |
| 2008 January | 3.1 | 62 | 20 | 50 |
| 2008 June | 2.3 | 13 | 36 | 36 |
| 2008 July | 1.7 | 9 | 62 | 47 |
3.2.2 2008 June
Figs 2 and 3 show the reconstructed Stokes V profiles and map of τ Boo for 2008 June data (left-bottom panel in Fig. 2 and third column in Fig. 3).
Phase coverage is poor. Unlike in 2008 January, the dominant component of the field is the poloidal one, enclosing 87 per cent of the total magnetic energy: the reconstructed map shows, for the radial field, three regions of positive polarity at low and intermediate latitudes and two dominant regions of negative polarity at intermediate and high latitudes. The absence of any reconstructed feature in the interval of phases 0.10 to 0.55 is an effect of the poor phase coverage at this epoch. For the poloidal field, axisymmetric and non-axisymmetric modes have almost the same contribution to the poloidal energy (∼33 per cent), while axisymmetric modes dominate the toroidal field (enclosing 68 per cent of the toroidal field energy).
3.2.3 2008 July
The reconstructed profiles for 2008 July fit the observations at χ2r of 0.9 (see the right-bottom panel of Fig. 2). The data cover four rotation periods, and are well sampled over the rotational cycle. The reconstructed map shows a field of a few gauss, mainly poloidal (91 per cent of the energy), with a weak toroidal component (right-hand column of Fig. 3). The radial field shows a net negative polarity region around the pole, another one at low latitudes and three positive regions at intermediate latitudes.
4 DIFFERENTIAL ROTATION
4.1 Method
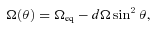
4.2 Results
For 2008 January, our data covered about three rotations. The differential rotation parameters we find are Ωeq= 1.86 ± 0.02 rad d−1 and dΩ=− 0.18 ± 0.07 rad d−1, implying apparently an anti-solar differential rotation (very scarcely or never observed in F stars; Reiners 2007). The field for 2008 January is mainly toroidal, i.e. the component providing the strongest contribution to the energy is the azimuthal one; being mostly axisymmetric, this component does not carry much information about the differential rotation. We therefore decided to estimate the parameters of differential rotation using the radial field map only. The parameters we obtain for this second fit are Ωeq= 1.93 ± 0.02 rad d−1 and dΩ= 0.28 ± 0.10 rad d−1, more compatible with the results of Donati et al. (2008).
For 2008 June and July, the paraboloids are well defined, giving approximately the same parameters for the differential rotation. Ωeq= 2.05 ± 0.04 rad d−1 and dΩ= 0.42 ± 0.10 rad d−1 for 2008 June, and Ωeq= 2.12 ± 0.12 rad d−1 and dΩ= 0.5 ± 0.15 rad d−1 for 2008 July. It implies that τ Boo rotates in 3 d at the equator while in 3.9 d at the poles. The orbital period being 3.31 d, we infer that latitude ∼ 38° is rotating synchronously with the planet orbital motion, in agreement with the results of Donati et al. (2008).
5 ACTIVITY INDICATORS
We also studied the variation of the residual emission of various activity proxies (in particular Hα, Ca ii H & K). This is done for our three runs by calculating a mean profile (per spectral line) for all the spectra, subtracting it from each spectrum, and then calculating the equivalent width of the residual emission by fitting this residual with a Gaussian profile (we find that this procedure minimizes the error bar on the estimated flux). The signatures of the residual emission for Ca ii H & K are extremely small (smaller than 0.5 per cent of the unpolarized continuum). Thanks to the better quality of the spectra around 700 nm, Hα shows more accurate signatures. The activity variations show similar trends in Ca ii H & K and Hα (see Fig. 4); a clear positive correlation is observed between both activity indicators.
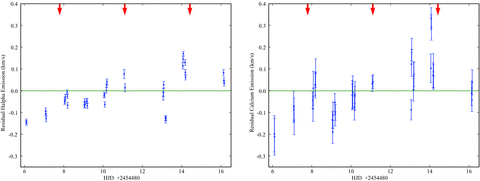
Residual signature of Hα (left-hand panel) and calcium (right-hand panel) as a function of the Heliocentric Julian Date for the ESPaDOnS run 2008 January. Red arrows mark the time of opposition. The activity variations show similar trends in Ca ii H & K and Hα.
τ Boo shows intrinsic variability during each night and a night-to-night variability. The clearest trend of January data is a long-term evolution over 10 d unrelated to either the rotational period or the orbital period. To investigate the period on which the activity varies, we fitted the activity residuals using a single sine wave. The fit for all the observed epochs is poor. A small enhancement is observed around the orbital phase 0.8, but it is not significant because of the high intrinsic variability of the star. This enhancement is no longer visible once the long-term trend is removed.
6 DISCUSSION AND CONCLUSION
We observed τ Boo during three epochs in 2008: January, June and July and reconstructed the corresponding magnetic maps. A weak magnetic field (maximum intensity 5–10 G) is present at the surface of the star, whose configuration varies from epoch to epoch (i.e. on a time-scale of months). As for 2006 June (Catala et al. 2007) and 2007 June (Donati et al. 2008), the field shows a dominant poloidal component in 2008 June and July, but it is predominantly toroidal in 2008 January. Table 3 lists the main field properties at each epoch.
Our observations reveal a new global magnetic polarity reversal between 2007 June and 2008 June [following the one reported in Donati et al. (2008) that occurred between 2006 June and 2007 June]. This switch is observed for the three components of the field. In 2008 June, radial field shows positive magnetic regions near the pole and negative ones at lower latitudes, while the opposite is observed for 2007 June (Donati et al. 2008). The change in polarity is also observed for both azimuthal and meridional fields. The 2008 July map confirms this conclusion.
Our observation in 2008 January shows that the field has evolved compared to 2007 June, but features no global polarity switch. This suggests that the magnetic cycle of τ Boo is of about 2 yr, much shorter than that of the Sun (∼22 yr). Comparing 2007 June and 2008 January maps, the azimuthal field becomes stronger in the latter and the radial field weaker, showing a dephasing between the poloidal and toroidal fields, as for the Sun (Charbonneau 2005).
To carry out a slightly more quantitative analysis, we calculated the (signed) magnetic flux for the radial and azimuthal components on the Northern hemisphere of the star. In the particular case of Br, the magnetic flux is counted positive for latitudes higher than 30° and negative for latitudes between 0° and 30° to take into account the contribution of both dipolar and quadrupolar terms of the poloidal field. We simultaneously fitted the two fluxes with sine waves of equal period, the period being varied over a range of 100–900 d. We find that the best fit is obtained at 800 d (2.2 yr) (Fig. 5) and at 250 d (8 months); the 800 d minimum is broader and potentially more likely. This analysis also suggests that the toroidal field is shifted (by 18 per cent of the period of 250 d and 28 per cent of the period of 800 d) with respect to the poloidal field. A phase shift between the poloidal and toroidal components is also observed for the Sun (of 25 per cent of the cycle length; Charbonneau & MacGregor 1997; Jouve & Brun 2007). We can safely conclude that the cycle of τ Boo is at least 10 times shorter than that of the Sun. We caution that this result needs confirmation from additional data, e.g. obtaining a denser monitoring of the magnetic topology over several successive cycles.
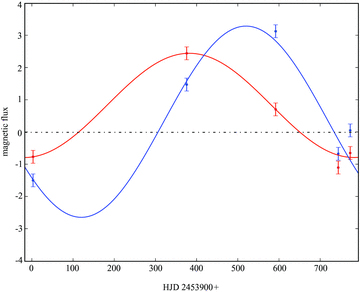
Fluxes of the radial field (red) and azimuthal field (blue) versus HJD, calculated for the Northern hemisphere of the star. In the particular case of Br, the magnetic flux is counted positive for latitudes higher than 30° and negative for latitudes between 0° and 30° to take into account the contribution of both dipolar and quadrupolar terms of the poloidal field. The best sinusoidal fit for P= 800 d is plotted (see text for more details), using the same colours.
We measured the differential rotation of the star for our three observed epochs. τ Boo has a strong one, the latitudinal angular rotation shear being dΩ= 0.46 ± 0.08 rad d−1. Our results are in good agreement with Donati et al. (2008). Catala et al. (2007) and Reiners (2006) also found similar results, using the Fourier Transform Method described by Reiners & Schmitt (2002). τ Boo's equator rotates in 3 d, while its pole rotates in 3.9 d. This means that a latitude at ∼ 40° is synchronized with the planet. In contrast to the magnetic field, the differential rotation of τ Boo has not changed over 2 years of observations. This is similar to what is observed for the Sun. The average differential rotation calculated from four runs is dΩ= 0.43 ± 0.12 rad d−1. We note that in 2008 January run, the differential rotation measured from the radial component is only slightly weaker than (though still compatible with) the average differential rotation.
We find that activity signatures in usual spectral indexes are very weak (0.5 per cent of the unpolarized continuum). The star shows variability during the night, and from one night to another. The night-to-night variability shows the same trend in Ca ii H & K and Hα. We do not see a clear correlation of the residual emission with any sensible period. Our data do not allow us to detect potential activity enhancement due to the planet; such enhancement (if any) is smaller than the short- and long-term intrinsic variability that we see in the spectra.
τ Boo is nevertheless a good candidate to study SPI. This is the first star where a magnetic cycle is observed. The generation of the magnetic field of F-type stars is due to dynamo mechanisms, thought to be operating at the base of the convective envelope (the tachocline). τ Boo's observed magnetic cycle is accelerated compared to that of the Sun. Is it a result of the very shallow convection of τ Boo  To answer this question, one has to compare this result to other studies on similar stars (having shallow convective envelope). Marsden et al. (2006) and Jeffers & Donati (2008) studied the magnetic field of the G0 star HD 171488, which also features a shallow convective envelope and a strong level of differential rotation. They, however, did not notice any global changes in its magnetic field over 2 years; no magnetic polarity switch is observed over 4 years (Donati, private communication) which means that its magnetic cycle is longer than 8 years. One difference between τ Boo and HD 171488 is that the former is orbited by an HJ. The presence of the HJ at small orbital distance may be responsible for the accelerated cycle of τ Boo, by synchronizing the outer convective envelope of the star (due to tidal interactions) and enhancing the shear at the tachocline. Such a scenario should, however, be studied in details. The synchronicity of the outer envelope and its decoupling with the stellar interior are still not well understood. Simulations of the effect of a perturbation due to the planet in the dynamo generation will be attempted; observing more F stars, with and without HJ, and studying their magnetic cycles would permit us to give constraints to the models and draw conclusions on the effect of the planet.
To answer this question, one has to compare this result to other studies on similar stars (having shallow convective envelope). Marsden et al. (2006) and Jeffers & Donati (2008) studied the magnetic field of the G0 star HD 171488, which also features a shallow convective envelope and a strong level of differential rotation. They, however, did not notice any global changes in its magnetic field over 2 years; no magnetic polarity switch is observed over 4 years (Donati, private communication) which means that its magnetic cycle is longer than 8 years. One difference between τ Boo and HD 171488 is that the former is orbited by an HJ. The presence of the HJ at small orbital distance may be responsible for the accelerated cycle of τ Boo, by synchronizing the outer convective envelope of the star (due to tidal interactions) and enhancing the shear at the tachocline. Such a scenario should, however, be studied in details. The synchronicity of the outer envelope and its decoupling with the stellar interior are still not well understood. Simulations of the effect of a perturbation due to the planet in the dynamo generation will be attempted; observing more F stars, with and without HJ, and studying their magnetic cycles would permit us to give constraints to the models and draw conclusions on the effect of the planet.
This work is based on observations obtained with ESPaDOnS at the CFHT and with NARVAL at the TBL. CFHT/ESPaDOnS are operated by the National Research Council of Canada, the Institut National des Sciences de l'Univers of the Centre National de la Recherche Scientifique (INSU/CNRS) of France and the University of Hawaii, while TBL/NARVAL are operated by INSU/CNRS. We thank J. Morin, V. Petit and G. Wade for collecting some of the ESPaDOnS data for us, and the CFHT and TBL staff for their help during the observations. We also thank the referee, A. Lanza, for valuable comments on the manuscript.
REFERENCES



