Formation of the resonant populations in the Kuiper belt: gas-drag-induced resonant capture Free

Abstract

1 INTRODUCTION

Present-day Kuiper belt objects (KBOs) have most of their orbits within a relatively thick disc outside that of Neptune as they are located around heliocentric distances in the range 35–50 au, where the whole Kuiper belt seems to have an abrupt end (Luu & Jewitt 2002; Morbidelli, Brown & Levison 2003; Chiang et al. 2007; Cruikshank et al. 2007; Morbidelli et al. 2008a,b).1Kenyon & Luu (1999) have described planetesimal accretion calculations in the Kuiper belt that include fragmentation and velocity evolution. The number of objects larger than 1 km may exceed 10⁸, more than 70 000 objects over 100 km in diameter are believed to reside there and the current mass of the Kuiper belt is near 0.1 M_⊕. The size distribution of KBOs was studied by Fraser & Kavelaars (2009). On the basis of their orbital elements, KBOs can be grouped into distinct dynamical classes, namely the classical, the resonant and the scattered ones (Jewitt, Luu & Trujillo 1998; Morbidelli & Brown 2004; Jewitt, Moro-Martín & Lacerda 2008).2 We investigate hereafter the formation of the resonant populations.

As is known, resonant KBOs are trapped in mean motion resonances with Neptune, mainly 3:2 orbital period resonance at 39.4 au. Approximately one-third of all known KBOs are engaged into the 3:2 resonance (Chiang et al. 2007). The same resonance is also occupied by Pluto. In contrast, only a few objects are claimed to be associated with the inner 5:4 and 4:3 resonances (34.9 and 36.4 au, respectively) and the outer 2:1 resonance (47.7 au). Some other weak resonances are also clearly observed, for instance 5:3 and 7:4 Neptunian mean motion resonances (42 and 44 au) (Chiang et al. 2003; Lykawka & Mukai 2007; de la Fuente Marcos & de la Fuente Marcos 2008; Jewitt et al. 2008).

Malhotra (1995) has proposed a mechanism of resonance sweeping to explain the origin of resonantly captured KBOs. Accordingly, as Neptune radially migrates outwards, its mean motion resonance is swept ahead of it through the Kuiper belt and captures resonant objects (see also Tiscareno & Malhotra 2008 for a discussion). The radial migration of Neptune is assumed to be smooth and continuous. This theory predicted that the populations of the 3:2 and 2:1 resonances should be of the same order. Zhou et al. (2002) improved this by introducing a stochastic term to make this outward migration more realistic. Chiang & Jordan (2002) analysed a series of numerical integrations to measure the efficiencies of KBOs' capture into the 3:2 and 2:1 resonances considering the model of resonant capture and migration. The discovered occupation of the 1:1 and 5:2 mean motion resonances is not easily understood within the model of resonance sweeping by a migratory Neptune over an initially dynamically cold belt (Chiang et al. 2003). Gomes (2003) argued that most high-inclination 3:2 resonant objects were captured during Neptune's migration from the scattered disc population rather than from an originally cold Kuiper belt as in the Malhotra (1995) scenario. Tsiganis (2005) also suggested that planetary migration produced the observed orbital distribution of KBOs. Yeh & Jiang (2001) showed, however, that the scattered planet shall move on an eccentric orbit and thus the pure radial migration is too naive, although it could be an approximation. One also has to understand how the migration stops, and thus explain Neptune's current orbital radius and how the orbit becomes nearly circular finally (see, however, Levison et al. 2008). Levison & Morbidelli (2003) also argued that the objects currently observed in the dynamically cold Kuiper belt were most probably formed within ∼35 au and were transported outwards during Neptune's final phase of migration. Contrary, Lykawka & Mukai (2008) proposed that the orbital history of an outer planet beyond Pluto with tenths of the Earth's mass can explain the trans-Neptunian belt orbital structure.

As a complementary study, Jiang & Yeh (2004, 2007 investigated the effect of a protostellar gaseous disc analogous to the primordial solar nebula on the resonance capture of solid particles, or ‘proto-KBOs’, ∼4 Gyr ago when the dynamical structure of the Kuiper belt was presumably established.3de la Fuente Marcos & de la Fuente Marcos (2008) further investigated this mechanism. [de la Fuente Marcos & de la Fuente Marcos (2001) already studied the orbital evolution of proto-KBOs due to gas drag. That paper tries to demonstrate that stellar encounters lead to significant modification of the primordial orbital distribution in a population of proto-KBOs.] Recently, Chanut, Winter & Tsuchida (2008) studied trajectories of solid particles whose orbits decay due to gas drag in a solar nebula and are perturbed by the gravity of the secondary body on an eccentric orbit. Muto & Inutsuka (2009) numerically considered the orbital evolution of a particle interacting with a single planet in a protoplanetary disc. Their paper is not just numerical but includes a number of purely theoretical analyses and approximations. As was pointed out to the authors by the referee of this paper, the work by Muto & Inutsuka (2009) shares some background with our paper. Like Muto & Inutsuka (2009), we consider a two-dimensional model by viscosity terms replaced by friction. Unlike Muto & Inutsuka (2009), however, in this work a more specific application to the case of KBO populations is intended. In addition, in sharp contrast to our study, Muto & Inutsuka (2009) did not obtain a condition when planet's gravitational torque at the Lindblad resonance exceeds the viscous torque, equation (23) below, which is the main result of this study.

It was shown numerically by Jiang & Yeh (2004, 2007 and de la Fuente Marcos & de la Fuente Marcos (2008) that the gaseous drag of a protostellar disc can trap proto-KBOs into resonances rather easily, and the resonant populations are correlated with the gaseous drag strength. Here, we present an analytical study intended to describe Jiang & Yeh's (2004, 2007) and de la Fuente Marcos & de la Fuente Marcos' (2008) drag-induced mechanism of resonant capture for proto-KBOs when gas was still around.

2 THE MODEL

An annulus of solid particles with inner radius R and radial extent ΔR in a Sun–planet–gas disc system is studied, with M_Sun being the mass of the Sun, M_Nep being the mass of Neptune, M_disc being the mass of the gaseous disc, M_KBO being the mass of the proto-KBO belt, M_Nep∼M_disc∼M_KBO∼ 10⁻⁵M_Sun, 2h is the effective thickness of the belt and 2h/R≪ 1. These are shown schematically in Fig. 1. The fact that 2h/R is small means that the annulus is considered by us as rather dynamically cold and that the pressure gradient in it is much smaller than both the gravitational and the centrifugal forces. In such a centrally condensed, disc-shaped solar nebula, there is a systematic difference between the velocity of the gas, which is pressure-supported, and that of the solid component, which is not. In a laminar disc with density and pressure decreasing radially and vertically outwards, solids tend to orbit with Keplerian speeds. Gas in protoplanetary nebulae rotates at speeds lower than the Keplerian speed, V_rot, by an amount ∼ηV_rot; typical models of a standard reference model of a disc, known as the ‘minimum mass solar nebula’, are characterized by

1

where r is the distance from the Sun (Youdin & Chiang 2004). The resulting relative motions of the gas and solids induce drag forces that produce radially inward and vertically downward drifts of the particles relative to the gas. Thus, drag forces cause the orbits of solid particles larger than dust grains to decay. Radial velocities depend strongly on particle size, reaching inward values of the order of 10⁴ cm s⁻¹ for metre-sized objects at about 5 au for the standard solar nebula; kilometric bodies are not affected by gas drag (Weidenschilling 1977, figs 2–5 therein; Völk et al. 1978; Weidenschilling 1980; Cuzzi, Dovrovolskis & Champney 1993; de la Fuente Marcos & de la Fuente Marcos 2000).

Figure 1

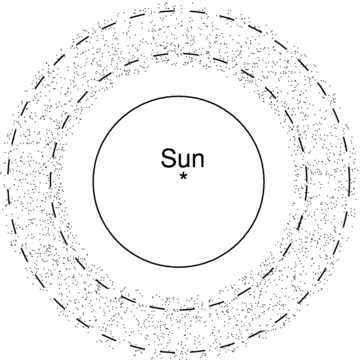
A schematic model of a Sun–planet–proto-KBO disc. The solid line is the orbit of Neptune, and the dashed lines are the positions of the 3:2 outer Lindblad resonance (inner line) and the 2:1 outer Lindblad resonance (outer line) with Neptune. Dots denote proto-KBOs.

Open in new tabDownload slide

Consider a free gaseous or proto-KBO element orbiting in a circle of radius r with angular speed Ω(r) in the equatorial plane z= 0 of the Sun with an associated gravitational potential Φ_Sun(r, z), where (r, ϕ, z) are cylindrical coordinates and the axis of the disc rotation is taken oriented along the z-axis. In a plane perpendicular to the rotation axis, the equilibrium motion is described by the following equation:

2

where Ω=Ω(r) is the angular rotation velocity at the distance r from the Sun, ρ₀(r, z) is the mean volume mass density of the gaseous (proto-KBO) disc, c_⊥ is the speed of sound in the z= 0 equatorial plane and the term ∝c²_⊥ is a small correction motion. As is seen, planar equilibrium is established in a simple manner in such a disc, i.e. it is governed mainly by the balance between the centrifugal and gravitational forces. The unperturbed disc has velocity v₀= (0, rΩ, 0), where the angular velocity Ω(r) is taken to be a function of r alone (Binney & Tremaine 2008). The equation of hydrostatic equilibrium along the z coordinate (for z≪r) is obviously

3

where c_z is the sound speed in the normal to the plane direction. The disc is geometrically thin if 2h≪r, which from the equation h≈c_z/Ω, where c_z∼c_⊥, is equivalent to the disc being dynamically cold, c_⊥≪rΩ, i.e. the sound speed of the disc is much less than the orbital speed rΩ.

By considering the geometrically thin annulus, 2h≪R where R is the outer radius of the system, in equation (3) one can expand ∂Φ_Sun/∂z about the orbit plane as

4

and μ²= (∂²Φ₀/∂z²)|_z=0 is the squared frequency of natural vertical oscillations. Equations (3) and (4) then imply that

5

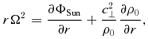
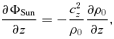
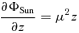
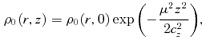
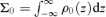where ρ₀(r, 0) is the density on the equatorial plane and is the surface density of the unperturbed annulus. It is this equilibrium model that is to be examined for stability in this investigation.

If this test element is displaced by an arbitrary small amount, it will oscillate freely in the horizontal and vertical directions about the reference circular orbit with epicyclic frequency κ(r) and vertical frequency μ(r) given by Lindblad's theory of epicyclic motion; generally, μ≈Ω≈κ (Goldreich & Tremaine 1982; Shu 1984; Borderies & Longaretti 1994; Griv, Yuan & Gedalin 1999).4 In our model, proto-KBOs move in an annulus around the Sun performing almost circular, i.e. epicyclic motions, and a gaseous disc and Neptune provide additional weak drag and tidal forces (disturbances) on solid particles. Proto-KBOs in the annulus can be considered as two-dimensional forced oscillators with eigenfrequencies κ(r) and μ(r). Neptune with its gravitational field Φ_Nep(r, z) is a driving force with frequency Ω_Nep.

To reiterate, Malhotra (1995), as well as Tsiganis (2005), Tsiganis et al. (2005), Murray-Clay & Chiang (2006), Terquem & Papaloizou (2007), Chambers (2008), Levison et al. (2007, 2008), Ida & Lin (2008), Morbidelli et al. (2008), Morbidelli & Levison (2008), Kirsh et al. (2009) and others, has suggested that the planets would continue to migrate for at least several tens of Myr after their formation, due to their interaction with the disc of planetesimals. This idea is still a subject to some debate. In contrast and following Boss (1997, 2001, 2002, 2003, 2008), Mayer et al. (2002, 2004), Griv & Gedalin (2005), Griv (2006) and Durisen et al. (2007), we suggest that all the planets around the Sun were created simultaneously by the disc's gravitational instability, assuming no migration of planets. The gravitational instability can create the protoplanet very rapidly, on dynamical (orbital) time-scales ∼10⁴ yr, provided that the disc-cooling time is similarly shot (Rice, Lodato & Armitage 2005; Clarke, Harper-Clark & Lodato 2007: Griv 2007). The instability can give rise to torques that can help to clear cooled discs around stars on time-scales of ∼10⁶ yr (Griv 2006, 2007; Griv, Liverts & Mond 2008), in accord with astronomical requirements (Greaves 2005; Hillenbrand 2008).

3 BASIC EQUATIONS

To proceed in a more quantitative manner, we must first derive the equations of motion of solid material. We use here a fluid dynamic approach. It may be shown that most features of the process can be revealed by this simple model. An infinitesimally thin, spatially homogeneous, isothermal and non-self-gravitating fluid annulus in equilibrium is considered, whose evolution is described by the momentum and continuity equations. As we only consider the two-dimensional coplanar orbits, the equations of motion are similar to the ones used in Goldreich & Tremaine (1982), Meyer-Vernet & Sicardy (1987), Griv (2006, 2007) and Griv et al. (2008). The linearized equations of motion read (written with respect to a rotating frame with angular velocity Ω_Nep)

6

7

8

where v_r, v_ϕ and Σ₁ are, respectively, the perturbations of the radial velocity, azimuthal velocity and surface density of the proto-KBO subsystem, Σ=Σ₀+Σ₁(r, t), Σ₀ is the equilibrium surface density, |Σ₁/Σ₀| ≪ 1, c_s is the local speed of sound, ω_*=m(Ω−Ω_Nep), Ω(r) is the angular velocity at a distance r from the Sun and Ω_Nep= (M_SunG/r³)^1/2. The force field per unit mass

where ν_drag > 0 is a constant that depends on the properties of the fluid and the dimensions of the object and v is the velocity of the object, is used to incorporate the effect of viscous resistance or drag into the model. Goldreich & Tremaine (1981) and Greenberg (1983) have used a similar simple damping model, applied to the particle's orbital parameters. The drag force is proportional to the local gas density and also the difference between the velocity of the object and the local rotating velocity of the gaseous disc (Murray & Dermott 1999). This equation for linear drag is appropriate for objects moving through a fluid at relatively slow speeds. The validity of such a simple model is very limited since it does not account for detailed mechanisms of the drag force: the particle size distribution, spin degrees of freedom, etc.

In equations (6)–(8), the total gravitational potential Φ is decomposed into two parts: Φ(r, ϕ) =Φ_Sun(r) +Φ_Nep(r, ϕ) and Φ_Nep is considered to impose small non-axisymmetric perturbations on an otherwise axisymmetric disc, |∇Φ_Sun| ≪ |∇Φ_Nep|,

and

(d_s denotes the separation of the Sun and Neptune centres). The orbit of Neptune is taken as circular, so that in the rotating frame any perturbation is selected in the form

9

where X_m is the real amplitude, m is the non-negative number, c.c. denotes the complex conjugate; and in the linear approximation in equation (9), one can select one of the Fourier harmonics,

Here, X(r, t) stands for any of the above-mentioned physical variables. Of course, the stationary X₀(r) value of some quantity may be equal to zero, as is, for instance, the case for the radial component of the velocity in a dissipationless disc. Evidently, X is a periodic function of ϕ, and hence m must be an integer, m= 0, 1, 2, … Neptune's orbital frequency Ω_Nep= (M_SunG/a³_Nep)^1/2 and a_Nep is Neptune's orbit radius. Neptune's potential amplitude Φ_m(r) may be written in the form (e.g. Goldreich & Tremaine 1982; Shu 1984)

10

where b^(m)_1/2 is the classical Laplace coefficient,

11

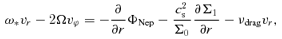
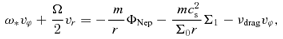
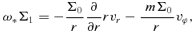
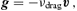
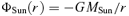
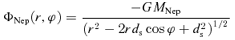
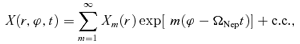
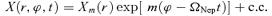
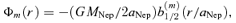
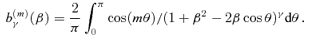
3.1 Unperturbed motion

To repeat ourselves, the equilibrium in the (r, ϕ) plane is established in a simple manner in such an annulus, i.e. it is governed mainly by the balance between the centrifugal ∝ rΩ² and gravitational ∝ ∇Φ_Sun forces,

Unperturbed proto-KBOs have velocities v₀= (0, rΩ), where the angular velocity Ω=Ω(r) is taken to be a function of r alone (Binney & Tremaine 2008).

In the absence of any perturbing gravity, Φ_Nep=Σ₁=ν_drag= 0, equations (6) and (7) yield the ordinary epicyclic velocities of solid particles

12

13

where K and φ₀ are constants of integration,

is the epicyclic frequency and 2Ω/κ≈ 2. The values of r and ϕ coordinates of the element as functions of time are readily obtained by direct integration of equations (12) and (13).

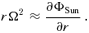
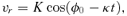
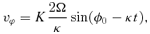
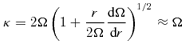
4 PERTURBED MOTION

If now Φ_Nep, Σ₁ and ν_drag≠ 0, equations (6) and (7) yield (Goldreich & Tremaine 1979, 1982; Meyer-Vernet & Sicardy 1987; Griv 2006; Griv et al. 2008)

14

15

where D(r) =Ω²−ω²_*, ω_*=m(Ω−Ω_Nep−ıν_drag/m) and ıν_drag/m is a small imaginary part of Ω_Nep. These expressions and equation (8) describe the spiral density wave caused by a mean motion resonance with Neptune. The importance of the parameter ω_* can be seen from the fact that the coefficients of equations (14) and (15) have singularities and other special features at

These are usually designated as the corotation resonance, the outer Lindblad resonance and the inner Lindblad resonance. Thus, the condition D(r) = 0 defines horizontal Lindblad resonance radii a_m at which Ω_m=±m(Ω_m−Ω_Nep). Below, only the outer Lindblad resonances are considered at which Ω_m=−m(Ω_m−Ω_Nep)[or Ω_m=m/(m+ 1)Ω_Nep and m≥ 1] (Goldreich & Tremaine 1982; Shu 1984).

Close enough to the outer Lindblad resonance, D→ 0, the system of equations (14) and (15) is degenerate:

16

and in the vicinity of the resonance (r=a_m)

17

where A(a_m) plays the role of the effective Neptune's potential amplitude at a resonance position (Goldreich & Tremaine 1979; Meyer-Vernet & Sicardy 1987). A natural width of resonances at the heliocentric distance a∼ 40 au,

18

is about 0.2 au. In equation (18), q is the non-dimensional correction factor; q≈ 0.5 for m > 1 (Goldreich, Rappaport & Sicardy 1995). As is seen, the typical width of resonances is much smaller than the radial extent of the annulus ΔR∼ 15 au.

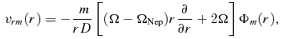
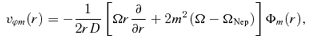
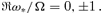
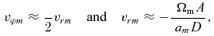
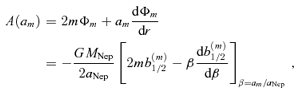
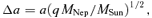
5 TORQUES

5.1 Gravitational torque

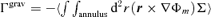From its definition, the torque exerted by Neptune on the annulus is ⁠, where 〈⋯〉 denotes the space average. Regions in which the torque is positive tend to expand. Using Parseval's theorem and equations (16) and (17), it is straightforward to show that in terms of the Fourier components defined in equation (9)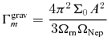

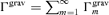19

and (Meyer-Vernet & Sicardy 1987). The gravitational torque is therefore positive, and Neptune's orbital momentum is transferred outwards to solid particles at the outer Lindblad resonances. An applied gravitational torque increases the angular momentum of the resonant proto-KBO element and thus leads to the motion of the element at a larger radius and thus tends to decrease its Ω.5 As a result, proto-KBOs drift outwards from the planet at these resonances; simultaneously the planet is repulsed. So narrow ∼0.2 au gaps in the annulus near each orbital resonance with Neptune may be created.

5.2 Viscous torque

On the other hand, the difference in mean flow velocities causes solid material rotating about the central star to be frictionally dragged by gas: the action of drag on solids is to induce orbital decay, i.e. to decrease the major semi-axis. An applied viscous torque decreases the angular momentum of the proto-KBO element and thus leads to motion of the element at a smaller radius and thus the rotation velocity of the element increases as a result of damping. Proto-KBOs move inwards losing energy and angular momentum; the speed of inward migration shall be proportional to the strength of the drag force. Assuming that relative velocities, v_rel, between solids and surrounding gas are less than the gas sound speed and the object radius, r_KBO, is smaller than the gaseous mean free path λ, one can apply Epstein's aerodynamic drag law to proto-KBOs:

20

where ρ_g is the mass density of gas.6 The Epstein drag force is equal to the classical Stokes drag force,

where η is the dynamic viscosity of gas, when λ/r_KBO= 4/9 (Weidenschilling 1977). The conditions v_rel < c_s and r_KBO < λ are satisfied for particles having r_KBO≲ 1 (r/au)^2.75 cm in the minimum mass solar nebula (Youdin & Chiang 2004). The latter conditions hold for all cases of interest (Weidenschilling 1977). Thus, small <1 km objects are considered. Using equation (1) and considering the two-dimensional disc (2ρ_gr_KBO→Σ₀), we rewrite equation (20) in the form

21

The viscous (negative) torque which is exerted by gas on solid particles at the resonance position a_m due to the drag interaction is therefore

22

In general, the action of viscosity on the annulus is to spread it out (Pringle 1981).

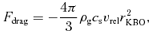
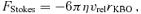
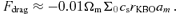
6 FORMATION OF RESONANT POPULATIONS

We suggest that the resonant KBO populations are connected to cases where Neptune's gravitational torque exceeds the viscous torque, i.e. the negative drift of solid particles due to the drag is counteracted by the positive drift due to the orbital Neptunian resonances,

or, by using equations (19) and (22), finally

23

Given the geometry of the problem, many proto-KBOs can get captured into the 3:2 resonance but not into the 2:1 resonance. This is because more solid particles with initial distances from the Sun r > a_m may be trapped in the 3:2 resonances (Fig. 1, inner dashed line) than in the 2:1 resonance (Fig. 1, outer dashed line) (and a_m denotes the corresponding resonance radius). As a result and in agreement with observations, the inner 3:2 resonance may become much more distinct. Clearly, these analytical results should be regarded merely as approximate estimates, in the order of magnitude. A deeper quantitative study would be desired.

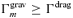
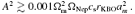
7 SUMMARY

It is likely that a residual gas disc, with a mass compared to that of the giant planets, was present when formation of the Kuiper belt occurred. Our analysis suggests the gas-drag-induced resonant capture as a mechanism able to explain the observed resonant population of the Kuiper belt. The torque exerted by Neptune on the proto-KBO annulus is positive at the outer Lindblad resonances. As angular momentum is transferred outwards from the planet, solid particles in the close vicinity of the resonances drift outwards to the outer part of the system under study. On the other hand, in an unperturbed viscous gas–solids annulus, most of the proto-KBO mass is accreted on to the central region losing energy and angular momentum. If the condition (23) is satisfied, the latter processes may lead to the formation of relatively narrow, ≲0.2 au, rings of solid material. The number of proto-KBOs captured into the 3:2 resonance may become a very large fraction of all objects, consistent with the observational results.

A separate investigation based on simulations should be done to confirm (or deny!) our suggestion. In particular, the hypothesis advocated in the article should be checked by measurement of the criterion given by equation (23). Also, simulations appear to indicate that the relative strength of the resonances depends strongly on the particle size distribution (de la Fuente Marcos & de la Fuente Marcos 2008). This also has to be explained. Future works may target physical collisions between both proto-KBOs and present-day KBOs as well. The work is in progress.

The authors would like to thank Irena Zlatopolsky for useful discussions. The suggestions of David Eichler, Michael Gedalin, Edward Liverts and Yury Lyubarsky were very helpful in revising and clarifying the results in this work. Thanks to an anonymous referee for the critical reading of the manuscript and his/her numerous comments which helped to improve this paper. This work was funded through the Israel Science Foundation, the Israeli Ministry of Immigrant Absorption in the framework of the programme ‘KAMEA’ and by the Theoretical Institute for Advanced Research in Astrophysics in Taiwan.

REFERENCES