-
PDF
- Split View
-
Views
-
Cite
Cite
S. L. Casewell, P. D. Dobbie, R. Napiwotzki, M. R. Burleigh, M. A. Barstow, R. F. Jameson, High-resolution optical spectroscopy of Praesepe white dwarfs, Monthly Notices of the Royal Astronomical Society, Volume 395, Issue 4, June 2009, Pages 1795–1804, https://doi.org/10.1111/j.1365-2966.2009.14593.x
Close - Share Icon Share
Abstract
We present the results of a high-resolution optical spectroscopic study of nine white dwarf candidate members of Praesepe undertaken with the VLT and Ultraviolet and Visual Echelle Spectrograph. We find, contrary to a number of previous studies, that WD0836+201 (LB390, EG59) and WD0837+199 (LB393, EG61) are magnetic and non-magnetic white dwarfs, respectively. Subsequently, we determine the radial velocities for the eight non-magnetic degenerates and provide compelling evidence that WD0837+185 is a radial velocity variable and possibly a double-degenerate system. We also find that our result for WD0837+218, in conjunction with its projected spatial location and position in initial mass–final mass space, argues it is more likely to be a field star than a cluster member. After eliminating these two white dwarfs, and WD0836+199 which has no clean Sloan Digital Sky Survey photometry, we use the remaining five stars to substantiate modern theoretical mass–radius relations for white dwarfs. In light of our new results, we re-examine the white dwarf members of Praesepe and use them to further constrain the initial mass–final mass relation (IFMR). We find a near-monotonic IFMR, which can still be adequately represented by simple linear function with only one outlier which may have formed from a blue straggler star.
1 INTRODUCTION
The initial mass–final mass relation (IFMR) is a theoretically predicted positive correlation between the main-sequence mass of a star with M≲ 10 M⊙ and the mass of the white dwarf remnant left behind after it has expired (e.g. Iben & Renzini 1983). Understanding the form of this relation is important since it provides a handle on the total amount of gas enriched with He, N and other metals that low or intermediate mass stars, which account for 95 per cent of all stars, return to the interstellar medium at the end of their life cycles. Moreover, the form of the upper end of the IFMR is relevant to the studies of Type II supernovae as it can provide a constraint on the minimum mass of star that will experience this fate.
The form of the IFMR is extremely difficult to predict from theory alone due to the many complex processes occurring during the final phases of stellar evolution (e.g. third dredge-up, thermal pulses, mass loss; Iben & Renzini 1983). This means that robust empirical data are essential for constraining its form. However, these are by no means simple to obtain, a significant difficulty being the determination of the main-sequence mass of a star that has long since ceased to exist. This difficulty can be alleviated by using white dwarf members of open star clusters (Bergeron, Saumon & Wesemael 1995a; Claver et al. 2001; Dobbie et al. 2004; Williams, Bolte & Koester 2004; Kalirai et al. 2005; Dobbie et al. 2006a,b; Kalirai et al. 2007; Williams & Bolte 2007) to define the IFMR (e.g.Weidemann 1977, 2000; Ferrario et al. 2005; Dobbie et al. 2006a; Williams & Bolte 2007; Kalirai et al. 2008). Here, since the age of the population can be determined from the location of the main-sequence turn-off (e.g. Sandage 1956; King & Schuler 2005 in Ursa Major), the lifetime, and ultimately the mass, of the progenitor star of any degenerate member can be estimated by calculating the difference between the cooling time of the white dwarf and the cluster age.
None the less, until relatively recently, rather few white dwarf members of open star clusters had been identified. Dobbie et al. (2006a) suggest ∼30 associated with 14 clusters, while the IFMR derived by Ferrario et al. (2005) used 40 DA white dwarfs from seven open star clusters, including NGC 2099. The uncertainties in membership status, cluster ages and the relatively large distances of these scarce, faint objects resulted in large scatter in the IFMR (Claver et al. 2001; Ferrario et al. 2005). To begin to address this issue and gauge the level of intrinsic scatter in the IFMR, we recently investigated the white dwarf members of the moderately rich nearby Praesepe open cluster. At a distance of 177+10.3−9.2 pc (as determined from Hipparcos measurements; Mermilliod et al. 1997), it is one of the closest star clusters. It is slightly metal rich with respect to the Sun ([Fe/H]=+0.11; An et al. 2007). Indeed, as both the metallicity and the kinematics of Praesepe are similar to those of the Hyades, the former is often touted as a member of the Hyades moving group and therefore is assumed to have an age comparable to the latter, τ= 625 ± 50 Myr (e.g. Claver et al. 2001). We note that this age for the Hyades was derived by comparing model isochrones generated from slightly metal-enhanced (Z= 0.024) stellar models which included moderate convective overshooting to the colours and magnitudes of a sample of cluster members selected using Hipparcos astrometric data (Perryman et al. 1998).
In Dobbie et al. (2004, 2006a), we increased the number of probable white dwarf members of Praesepe from five to 11. All these candidate members share the proper motion of the cluster (e.g. Claver et al. 2001; Dobbie et al. 2004). We used estimates from the literature and our own measurements of the effective temperature and the surface gravity of these white dwarfs to determine their masses and the masses of their progenitor stars so that we could study their locations in initial mass–final mass space. Combining these with data from a number of other open clusters with comparatively well-constrained ages and the Sirius binary system, we concluded that most stars follow rather closely a monotonically increasing IFMR, which can be approximately described by a simple linear function over the initial mass range 2.7 M⊙ to 6 M⊙. Nevertheless, there existed a small number of outliers, all attributable to the Praesepe cluster.
Here, we present the results of a high-resolution optical spectroscopic study of nine out of 11 candidate Praesepe degenerates. In the next section, we describe the data acquisition and analysis, including the measurement of line core velocity shifts and the redetermination of effective temperatures and surface gravities. We then utilize the five most appropriate Praesepe degenerates to re-examine the theoretical white dwarf mass–radius relation. Subsequently, we determine the radial velocities for all eight non-magnetic white dwarfs and use these to confirm their membership status. Finally, we examine our new results in the context of the IFMR.
2 ACQUISITION AND REDUCTION OF DATA
High-resolution spectroscopy of nine of the 11 DA white dwarf candidate members of Praesepe was obtained using the Ultraviolet and Visual Echelle Spectrograph (UVES) on the UT2 facility of the European Southern Observatory's (ESO) Very Large Telescope at Cerro Paranal, Chile. The data were acquired in service mode within the period 2005 November 16 and 2006 January 19 and using 45-min exposure times. As only relaxed constraints were specified for the sky conditions, these data were generally obtained through thin cirrus and in mediocre seeing (≲1.4 arcsec).
The observations utilized the UVES parallel mode, where cross dispersers CD2 and CD3, in conjunction with dichroic1 (390+580) and the HER5 and SHP700 filters provided simultaneous wavelength coverage over 370–500 and 420–680 nm in the blue and red arms, respectively. The 1.5-arcsec slit resulted in a nominal spectral resolution of λ/Δλ∼ 20 000.
The data were reduced using the UVES pipeline which is based on the midas software supplied by ESO (Ballester & Hensberge 1995). The pipeline was run in OPTIMAL mode and an additional custom routine written by R. Napiwotzki applied to reduce the magnitude of the ripples which are sometimes apparent in these spectra. Calibration frames were taken every night the science data were acquired. These include format-check frames, bias frames, flat fields, an order definition template and a ThAr arc lamp spectrum. In addition to these calibrations, a spectrally featureless DC white dwarf (WD0000-345) was observed with the same instrument set-up on 2006 July 3. The spectrum of this star was used to remove remaining UVES instrumental signature from the data. The completed spectra, each of which has a signal-to-noise ratio ∼25 per resolution element, can be seen in Fig. 1. These spectra have been median filtered, smoothed and co-added for the purpose of this figure.
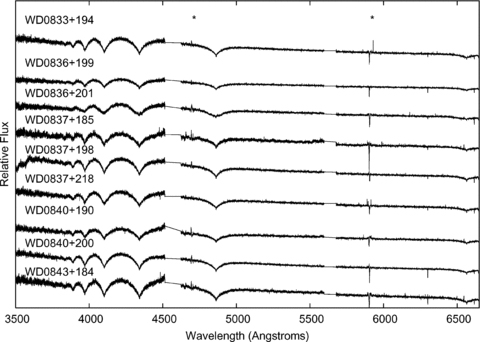
The full median filtered, smoothed, stacked UVES spectra for the nine white dwarfs included in this study. Note the Zeeman-shifted components of the Balmer lines in the spectrum of WD0836+201 (see Fig. 5 for more detail). The asterisks mark artefacts caused by dead pixels in the array. There are also two breaks in the data of width ∼80 Å at 4580 and 5640 Å caused by the edges of the CCDs.
2.1 Data analysis
Our first step in analysing these echelle data was to remove the signature of telluric water vapour from around Hα using an absorption template constructed from numerous UVES spectra of white dwarfs obtained at Paranal Observatory as part of the SpY programme (Napiwotzki et al. 2001). Next, the data were compared to the predictions of white dwarf model atmospheres using the spectral fitting programme FITSB2 (v2.04; Napiwotzki et al. 2004).
The grid of pure-H model spectra was calculated using the plane-parallel, hydrostatic, non-local thermodynamic equilibrium (non-LTE) atmosphere code tlusty, v200 (Hubeny 1988; Hubeny & Lanz 1995) and the spectral synthesis code synspec v48 (Hubeny & Lanz 2001). tlusty assumes plane-parallel geometry and hydrostatic equilibrium. The models include a treatment for convective energy transport according to the ML2 prescription of Bergeron, Wesemael & Fontaine (1992), adopting a mixing length parameter, α= 0.6. These calculations utilized a model H-atom which incorporates explicitly the eight lowest energy levels and represents levels n= 9 to 80 by a single superlevel. The dissolution of the high-lying levels was treated by means of the occupation probability formalism of Hummer & Mihalas (1988) generalized to the non-LTE atmosphere situation by Hubeny, Hummer & Lanz (1994). All calculations include the bound-free and free–free opacities of the H− ion and incorporate a full treatment for the blanketing effects of H i lines and the Lyman −α, −β and −γ satellite opacities as computed by N. Allard (Allard et al. 2004). During the calculation of the model structure, the lines of the Lyman and Balmer series were treated by means of an approximate Stark profile but in the spectral synthesis step detailed profiles for the Balmer lines were calculated from the Stark broadening tables of Lemke (1997). The grid of model spectra covered the Teff range of 13 000–20 000 K in steps of 1000 K and log g between 7.5 and 8.5 in steps of 0.1 dex.
2.2 Determination of effective temperature and gravity
Each white dwarf has been observed at least three times. We used FITSB2 to fit our grid of model spectra to the eight Balmer absorption lines ranging from Hα to H10 in each exposure. So as to match the instrument resolution, the models were convolved with a Gaussian with a full width at half-maximum of 0.2 Å. In addition, points in the observed data lying more than 3σ from the model were clipped from subsequent iterations of the fitting process. Both the starting values and the new values derived here for Teff and log g for each white dwarf are given in Table 1. The errors given in Table 1 for Teff and log g are formal fitting errors and are unrealistically small as they neglect systematic uncertainties, e.g. flat fielding errors and model shortcomings. In subsequent discussion here, we follow Napiwotzki, Green & Saffer (1999) and assume an uncertainty of 2.3 per cent in Teff and 0.07 dex in log g.
ID, effective temperature, log g, mass and cooling time for the Praesepe white dwarfs with UVES spectroscopy. The previous effective temperature and surface gravity estimates are from Dobbie et al. (2006a) and Claver et al. (2001), where the values shown are as listed in this literature. The FITSB2 data are shown with the formal fitting errors. An uncertainty of 2.3 per cent and 0.07 dex are more realistic for Teff and log g. Additionally, for Praesepe members, we list our estimate of the progenitor mass. The magnetic white dwarf WD0836+201 has been omitted as our models do not include a treatment for magnetism. Additionally, no initial mass has been given for WD0837+218 as it is believed more likely to be a field star than a cluster member.
| ID | Teff K | log g | FITSB2 Teff K | FITSB2 logg | M M⊙ | R ×10−2 R⊙ | τcool Myrs | MinitM⊙ |
| WD0833+194 | 14999+208−258 | 8.18+0.04−0.03 | 14852±41 | 8.182±0.005 | 0.721±0.043 | 1.143±0.103 | 270+32−28 | 3.32+0.33−0.22 |
| WD0836+199 | 14060 ±630 | 8.34±0.06 | 14571±60 | 8.233±0.010 | 0.752±0.044 | 1.102±0.099 | 308+37−32 | 3.46+0.43−0.27 |
| WD0837+185 | 14748+396−404 | 8.24+0.06−0.05 | 15076±60 | 8.306±0.010 | 0.804±0.044 | 1.039±0.094 | 319+39−35 | 3.50+0.48−0.29 |
| WD0837+199 | 17098±350 | 8.32±0.05 | 17240±38 | 8.195±0.006 | 0.737±0.043 | 1.130±0.102 | 179+23−20 | 3.07+0.20−0.15 |
| WD0837+218 | 16833+236−272 | 8.39+0.04−0.02 | 16875±44 | 8.473±0.008 | 0.909±0.044 | 0.919±0.083 | 305+40−35 | - |
| WD0840+190 | 14765+264−277 | 8.21+0.03−0.03 | 14935±68 | 8.381±0.010 | 0.849±0.045 | 0.985±0.089 | 368+46−40 | 3.73+0.71−0.39 |
| WD0840+200 | 14178±350 | 8.23±0.05 | 14983±42 | 8.176±0.005 | 0.721±0.043 | 1.143±0.103 | 263+31−28 | 3.30+0.32−0.21 |
| WD0843+184 | 14498+199−206 | 8.22+0.04−0.04 | 15018±50 | 8.340±0.008 | 0.823±0.045 | 1.016±0.092 | 339+42−37 | 3.59+0.55−0.33 |
| ID | Teff K | log g | FITSB2 Teff K | FITSB2 logg | M M⊙ | R ×10−2 R⊙ | τcool Myrs | MinitM⊙ |
| WD0833+194 | 14999+208−258 | 8.18+0.04−0.03 | 14852±41 | 8.182±0.005 | 0.721±0.043 | 1.143±0.103 | 270+32−28 | 3.32+0.33−0.22 |
| WD0836+199 | 14060 ±630 | 8.34±0.06 | 14571±60 | 8.233±0.010 | 0.752±0.044 | 1.102±0.099 | 308+37−32 | 3.46+0.43−0.27 |
| WD0837+185 | 14748+396−404 | 8.24+0.06−0.05 | 15076±60 | 8.306±0.010 | 0.804±0.044 | 1.039±0.094 | 319+39−35 | 3.50+0.48−0.29 |
| WD0837+199 | 17098±350 | 8.32±0.05 | 17240±38 | 8.195±0.006 | 0.737±0.043 | 1.130±0.102 | 179+23−20 | 3.07+0.20−0.15 |
| WD0837+218 | 16833+236−272 | 8.39+0.04−0.02 | 16875±44 | 8.473±0.008 | 0.909±0.044 | 0.919±0.083 | 305+40−35 | - |
| WD0840+190 | 14765+264−277 | 8.21+0.03−0.03 | 14935±68 | 8.381±0.010 | 0.849±0.045 | 0.985±0.089 | 368+46−40 | 3.73+0.71−0.39 |
| WD0840+200 | 14178±350 | 8.23±0.05 | 14983±42 | 8.176±0.005 | 0.721±0.043 | 1.143±0.103 | 263+31−28 | 3.30+0.32−0.21 |
| WD0843+184 | 14498+199−206 | 8.22+0.04−0.04 | 15018±50 | 8.340±0.008 | 0.823±0.045 | 1.016±0.092 | 339+42−37 | 3.59+0.55−0.33 |
ID, effective temperature, log g, mass and cooling time for the Praesepe white dwarfs with UVES spectroscopy. The previous effective temperature and surface gravity estimates are from Dobbie et al. (2006a) and Claver et al. (2001), where the values shown are as listed in this literature. The FITSB2 data are shown with the formal fitting errors. An uncertainty of 2.3 per cent and 0.07 dex are more realistic for Teff and log g. Additionally, for Praesepe members, we list our estimate of the progenitor mass. The magnetic white dwarf WD0836+201 has been omitted as our models do not include a treatment for magnetism. Additionally, no initial mass has been given for WD0837+218 as it is believed more likely to be a field star than a cluster member.
| ID | Teff K | log g | FITSB2 Teff K | FITSB2 logg | M M⊙ | R ×10−2 R⊙ | τcool Myrs | MinitM⊙ |
| WD0833+194 | 14999+208−258 | 8.18+0.04−0.03 | 14852±41 | 8.182±0.005 | 0.721±0.043 | 1.143±0.103 | 270+32−28 | 3.32+0.33−0.22 |
| WD0836+199 | 14060 ±630 | 8.34±0.06 | 14571±60 | 8.233±0.010 | 0.752±0.044 | 1.102±0.099 | 308+37−32 | 3.46+0.43−0.27 |
| WD0837+185 | 14748+396−404 | 8.24+0.06−0.05 | 15076±60 | 8.306±0.010 | 0.804±0.044 | 1.039±0.094 | 319+39−35 | 3.50+0.48−0.29 |
| WD0837+199 | 17098±350 | 8.32±0.05 | 17240±38 | 8.195±0.006 | 0.737±0.043 | 1.130±0.102 | 179+23−20 | 3.07+0.20−0.15 |
| WD0837+218 | 16833+236−272 | 8.39+0.04−0.02 | 16875±44 | 8.473±0.008 | 0.909±0.044 | 0.919±0.083 | 305+40−35 | - |
| WD0840+190 | 14765+264−277 | 8.21+0.03−0.03 | 14935±68 | 8.381±0.010 | 0.849±0.045 | 0.985±0.089 | 368+46−40 | 3.73+0.71−0.39 |
| WD0840+200 | 14178±350 | 8.23±0.05 | 14983±42 | 8.176±0.005 | 0.721±0.043 | 1.143±0.103 | 263+31−28 | 3.30+0.32−0.21 |
| WD0843+184 | 14498+199−206 | 8.22+0.04−0.04 | 15018±50 | 8.340±0.008 | 0.823±0.045 | 1.016±0.092 | 339+42−37 | 3.59+0.55−0.33 |
| ID | Teff K | log g | FITSB2 Teff K | FITSB2 logg | M M⊙ | R ×10−2 R⊙ | τcool Myrs | MinitM⊙ |
| WD0833+194 | 14999+208−258 | 8.18+0.04−0.03 | 14852±41 | 8.182±0.005 | 0.721±0.043 | 1.143±0.103 | 270+32−28 | 3.32+0.33−0.22 |
| WD0836+199 | 14060 ±630 | 8.34±0.06 | 14571±60 | 8.233±0.010 | 0.752±0.044 | 1.102±0.099 | 308+37−32 | 3.46+0.43−0.27 |
| WD0837+185 | 14748+396−404 | 8.24+0.06−0.05 | 15076±60 | 8.306±0.010 | 0.804±0.044 | 1.039±0.094 | 319+39−35 | 3.50+0.48−0.29 |
| WD0837+199 | 17098±350 | 8.32±0.05 | 17240±38 | 8.195±0.006 | 0.737±0.043 | 1.130±0.102 | 179+23−20 | 3.07+0.20−0.15 |
| WD0837+218 | 16833+236−272 | 8.39+0.04−0.02 | 16875±44 | 8.473±0.008 | 0.909±0.044 | 0.919±0.083 | 305+40−35 | - |
| WD0840+190 | 14765+264−277 | 8.21+0.03−0.03 | 14935±68 | 8.381±0.010 | 0.849±0.045 | 0.985±0.089 | 368+46−40 | 3.73+0.71−0.39 |
| WD0840+200 | 14178±350 | 8.23±0.05 | 14983±42 | 8.176±0.005 | 0.721±0.043 | 1.143±0.103 | 263+31−28 | 3.30+0.32−0.21 |
| WD0843+184 | 14498+199−206 | 8.22+0.04−0.04 | 15018±50 | 8.340±0.008 | 0.823±0.045 | 1.016±0.092 | 339+42−37 | 3.59+0.55−0.33 |
2.3 Determination of line core velocity shifts
Using our new determinations for the values of Teff and log g (with the exception of WD0836+201) as input parameters, a model grid which was more finely sampled in wavelength space than the first (0.05 Å) was used in conjunction with FITSB2 to measure the velocity shift of the line cores of the Hα and Hβ lines in the spectra of each white dwarf. Crude estimates for the line core velocity shifts were obtained initially, taking into account the heliocentric correction. The line fitting was then re-run using these as starting values for the final fit, to minimize the errors and ensure that each result was robust. We made reliable estimates of the uncertainties on the line shift measurements based on the bootstrapping method of statistical resampling (Efron 1982). We note that a detailed study of the wavelengths of prominent water absorption lines in a large number of UVES spectra obtained as part of the SpY project, which uses an identical instrumental set-up to this study, indicates that error in the external calibration of the wavelength scale of UVES from spectrum to spectrum is at the 0.7 km s−1 level. As an independent check of our results, we also performed these fits using a different set of synthetic spectra (the LTE model atmospheres of Koester et al. 2001). Fortunately, no systematic discrepancies were found between the results derived using the two sets of models and the differences for any object were well within the measurement uncertainties. The line core velocity measurements for each observation may be found in Table 2.
ID, line core shift measurements for each data set (RV1,RV2, RV3, RV4, χ2 and log10 probability of the white dwarf being a radial velocity variable, for the eight non-magnetic Praesepe white dwarfs investigated). The errors take into account the 0.7 km s−1 uncertainty in the UVES wavelength calibration.
| ID | RV1 (km s−1) | RV2 (km s−1) | RV3 (km s−1) | RV4 (km s−1) | χ2 | log10 prob |
| WD0833+194 | 77.13±2.09 | 79.60±2.15 | 83.54±2.86 | 75.69±2.77 | 4.788321 | −0.726 |
| WD0836+199 | 75.11±4.88 | 85.86±3.72 | 84.66±2.49 | 94.57±3.49 | 11.29552 | −1.990 |
| WD0837+185 | 70.39±4.08 | 83.44±1.98 | 90.89±2.51 | - | 18.70493 | −4.062 |
| WD0837+199 | 75.47±1.94 | 76.71±2.51 | 71.25±2.76 | 70.09±2.12 | 5.920174 | −0.937 |
| WD0837+218 | 80.18±1.79 | 81.95±2.44 | 83.66±1.88 | - | 1.955053 | −0.425 |
| WD0840+190 | 91.32±7.64 | 84.66±3.10 | 82.77±3.54 | - | 1.037816 | −0.225 |
| WD0840+200 | 73.76±3.27 | 75.42±1.83 | 74.82±2.19 | 74.64±2.24 | 0.2153261 | −0.011 |
| WD0843+184 | 93.40±3.08 | 86.10±1.99 | 87.66±3.10 | 87.80±2.06 | 4.008115 | −0.584 |
| ID | RV1 (km s−1) | RV2 (km s−1) | RV3 (km s−1) | RV4 (km s−1) | χ2 | log10 prob |
| WD0833+194 | 77.13±2.09 | 79.60±2.15 | 83.54±2.86 | 75.69±2.77 | 4.788321 | −0.726 |
| WD0836+199 | 75.11±4.88 | 85.86±3.72 | 84.66±2.49 | 94.57±3.49 | 11.29552 | −1.990 |
| WD0837+185 | 70.39±4.08 | 83.44±1.98 | 90.89±2.51 | - | 18.70493 | −4.062 |
| WD0837+199 | 75.47±1.94 | 76.71±2.51 | 71.25±2.76 | 70.09±2.12 | 5.920174 | −0.937 |
| WD0837+218 | 80.18±1.79 | 81.95±2.44 | 83.66±1.88 | - | 1.955053 | −0.425 |
| WD0840+190 | 91.32±7.64 | 84.66±3.10 | 82.77±3.54 | - | 1.037816 | −0.225 |
| WD0840+200 | 73.76±3.27 | 75.42±1.83 | 74.82±2.19 | 74.64±2.24 | 0.2153261 | −0.011 |
| WD0843+184 | 93.40±3.08 | 86.10±1.99 | 87.66±3.10 | 87.80±2.06 | 4.008115 | −0.584 |
ID, line core shift measurements for each data set (RV1,RV2, RV3, RV4, χ2 and log10 probability of the white dwarf being a radial velocity variable, for the eight non-magnetic Praesepe white dwarfs investigated). The errors take into account the 0.7 km s−1 uncertainty in the UVES wavelength calibration.
| ID | RV1 (km s−1) | RV2 (km s−1) | RV3 (km s−1) | RV4 (km s−1) | χ2 | log10 prob |
| WD0833+194 | 77.13±2.09 | 79.60±2.15 | 83.54±2.86 | 75.69±2.77 | 4.788321 | −0.726 |
| WD0836+199 | 75.11±4.88 | 85.86±3.72 | 84.66±2.49 | 94.57±3.49 | 11.29552 | −1.990 |
| WD0837+185 | 70.39±4.08 | 83.44±1.98 | 90.89±2.51 | - | 18.70493 | −4.062 |
| WD0837+199 | 75.47±1.94 | 76.71±2.51 | 71.25±2.76 | 70.09±2.12 | 5.920174 | −0.937 |
| WD0837+218 | 80.18±1.79 | 81.95±2.44 | 83.66±1.88 | - | 1.955053 | −0.425 |
| WD0840+190 | 91.32±7.64 | 84.66±3.10 | 82.77±3.54 | - | 1.037816 | −0.225 |
| WD0840+200 | 73.76±3.27 | 75.42±1.83 | 74.82±2.19 | 74.64±2.24 | 0.2153261 | −0.011 |
| WD0843+184 | 93.40±3.08 | 86.10±1.99 | 87.66±3.10 | 87.80±2.06 | 4.008115 | −0.584 |
| ID | RV1 (km s−1) | RV2 (km s−1) | RV3 (km s−1) | RV4 (km s−1) | χ2 | log10 prob |
| WD0833+194 | 77.13±2.09 | 79.60±2.15 | 83.54±2.86 | 75.69±2.77 | 4.788321 | −0.726 |
| WD0836+199 | 75.11±4.88 | 85.86±3.72 | 84.66±2.49 | 94.57±3.49 | 11.29552 | −1.990 |
| WD0837+185 | 70.39±4.08 | 83.44±1.98 | 90.89±2.51 | - | 18.70493 | −4.062 |
| WD0837+199 | 75.47±1.94 | 76.71±2.51 | 71.25±2.76 | 70.09±2.12 | 5.920174 | −0.937 |
| WD0837+218 | 80.18±1.79 | 81.95±2.44 | 83.66±1.88 | - | 1.955053 | −0.425 |
| WD0840+190 | 91.32±7.64 | 84.66±3.10 | 82.77±3.54 | - | 1.037816 | −0.225 |
| WD0840+200 | 73.76±3.27 | 75.42±1.83 | 74.82±2.19 | 74.64±2.24 | 0.2153261 | −0.011 |
| WD0843+184 | 93.40±3.08 | 86.10±1.99 | 87.66±3.10 | 87.80±2.06 | 4.008115 | −0.584 |
In order to describe the statistical likelihood that a given target's velocity is constant or otherwise between each observation, we calculated a χ2 statistic for each star based on the prior assumption that the velocities are stable with time, i.e. any object with a χ2 below 10 can be considered to have a constant radial velocity. It can be seen from Table 2 that while the measurements for most objects are consistent with a constant velocity, there is evidence that the wavelengths of the line cores in the spectra of WD0837+185 change from exposure to exposure. We note that in the SpY project where velocity measurements have been obtained for a sample of 1000 white dwarfs, objects with a probability of less than 10−3, corresponding to one false ‘detection’ due to chance statistical fluctuations, are flagged as potential variables. Given our assessment of the probability of obtaining the tabled radial measurements for WD0837+185 by chance (< 10−4), we are led to conclude that this white dwarf is a radial velocity variable.
3 RESULTS
3.1 A possible double degenerate?
A cursory glance at Figs 2 and 3 appears to substantiate the above conclusion that WD0837+185 is a radial velocity variable. However, we find no compelling direct evidence of any cool companion within either the UVES or the Sloan Digital Sky Survey (SDSS) spectrum of WD0837+185, the latter extending to 9200Å. There is also no detection of this object in the 2MASS Point Source Catalogue (Skrutskie et al. 2006), although it is listed in the UKIRT Infrared Deep Sky Survey Large Area Survey (UKIDSS LAS; Warren et al. 2007), with magnitudes Z= 18.29 ± 0.03, Y= 18.49 ± 0.04 and H= 18.50 ± 0.14 (on a Vega system). Taken in conjunction with the SDSS optical photometry (u= 18.35 ± 0.03, g= 18.02 ± 0.02, r= 18.32 ± 0.01, i= 18.56 ± 0.02, z= 18.76 ± 0.04, on approximately an AB magnitude system), these also provide no evidence for the presence of a cool companion (see Fig. 4). Indeed, based on the DUSTY models of Chabrier et al. (2000), we set a limit of Mcool≲ 0.05 M⊙, at the distance and age of this cluster. Given the rarity of brown dwarf + white dwarf binaries (e.g. Farihi, Becklin & Zuckerman 2005 estimate the fraction of L dwarf companions to white dwarfs to be at <0.5 per cent), this suggests that any companion is more likely to be another white dwarf.
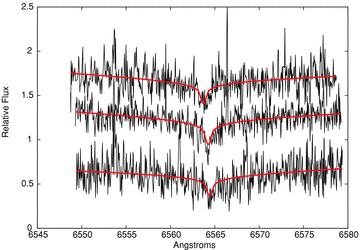
The Hα line profile in the three sets of spectra observed for WD0837+185. The red lines are the FITSB2 model fits to the data. The core of the lines can be seen moving. These observations were taken on 2005 November 16 (UT1) and December 14 (UT2 + UT3). The observations are plotted in chronological order with the earliest observation at the top of the plot.
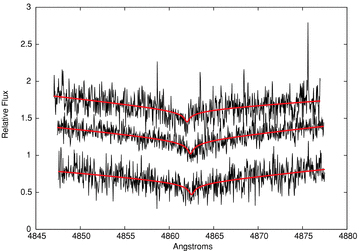
As for Fig. 2, but for the Hβ line profile from the three sets of spectra observed for WD0837+185.
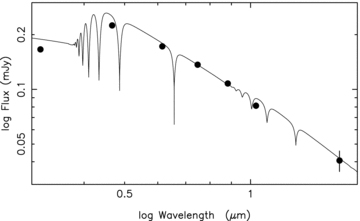
Sloan u, g, r and i, and UKIDSS Z, Y and H band photometry of WD0837 + 185, compared to a synthetic DA white dwarf spectrum for Teff= 15076 K and log g= 8.306. There is no evidence for excess emission due to a cool companion. At an age of 625 Myr, these data suggest that such an object, if present, must have a mass < 0.05 M⊙.
However, there is no evidence in the UVES spectrum which would indicate the presence of a He-atmosphere DB companion and the observed Balmer line profiles are relatively well matched by a synthetic spectrum for a single DA white dwarf. Moreover, at the spectroscopically determined effective temperature and surface gravity, the SDSS magnitudes of WD0837+185 are consistent with those of a single degenerate at the distance of Praesepe. The models of Holberg & Bergeron (2006) indicate an isolated DA of this effective temperature and surface gravity to have Mg∼ 11.6. If we were to assume that WD0837+185 had a degenerate companion with Mg≲ 12.5, the absolute magnitude of this hypothetical binary would be Mg≲ 11.2. Since the observed magnitude of this object is g= 18.02 ± 0.02, this would infer a double degenerate lying well beyond the back of the cluster (d ≳ 220 pc). So, if this is a binary, the likelihood of Praesepe membership, as indicated by the proper motion and the mean radial velocity, would appear to favour a putative white dwarf companion which is significantly less luminous than WD0837+185.
For a cooling time ≲625 Myr (i.e. the age of the cluster), the available data suggest that any degenerate companion must be massive (M≳ 1.2 M⊙; Mg≳ 12.5; Holberg & Bergeron 2006; Althaus et al. 2007), with a low intrinsic luminosity due to its small radius. If this is the case, the total mass of this system would be larger than the Chandrasekhar limit (≈1.4 M⊙) and this binary has the potential to be a progenitor for a Type Ia supernova (Iben & Tutukov 1984; Livio 2000; Napiwotzki et al. 2001, 2003). Further study of this system is warranted to better constrain the masses of the components, and to determine if the system is close enough that it will merge within a Hubble time. We note that WD0837+185 sits on the IFMR defined by the bulk of the other objects (see Fig. 7), so there is nothing in terms of the mass of this white dwarf to suggest that this system has experienced close binary evolution.
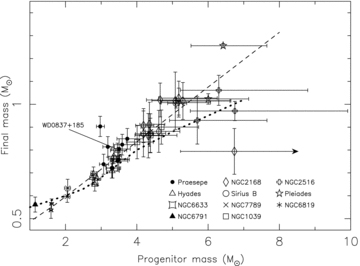
A plot showing the revised locations of the Praesepe white dwarfs in initial mass–final mass space (filled circles). The locations of the degenerate members of the NGC 6633 (square star), NGC 7789 (cross), NGC 6819 (asterisk), Hyades (open triangles), Sirius binary system (open circle), the Pleiades (open stars), NGC 2168 (open diamonds), NGC 1039 (open squares), NGC 6791 (filled triangles) and NGC 2516 (open ‘+’ signs) are also shown. The relation of Weidemann (2000) (dotted line) and a revised linear fit to 41 white dwarfs (dashed line) are overplotted. The radial velocity variable, WD0837+185 is labelled.
3.2 Magnetic white dwarf
We note here that the identities of WD0837+199 and WD0836+201 have been confused in some previous studies, e.g. Claver et al. (2001), Dobbie et al. (2004) and Dobbie et al. (2006a). The UVES spectrum of WD0836+201 (LB390, EG59) clearly shows Zeeman-shifted components (see Fig. 5). This is consistent with Reid (1996) who notes his fit to the Hα line core in the spectrum of WD0836+201 (LB390) is particularly poor, as would be expected if trying to fit Zeeman-shifted components with non-magnetic synthetic spectra. Claver et al. (2001) also find a magnetic white dwarf in Praesepe, and in fig. 8 of Claver et al. (2001) present the fit to the spectrum, but label it as EG61 (i.e. WD0837+199, LB393) for which they determine Teff= 17 098 K and log g= 8.32. Moreover, table 3 of Claver et al. (2001) erroneously labels EG61 as WD0836+201. We believe from our data that the magnetic white dwarf is EG59 and this object has been mislabelled in Claver et al. (2001). Dobbie et al. (2006a) and Dobbie et al. (2004) never observed WD0836+201 or WD0837+199 but refer to EG61 as the magnetic white dwarf as identified by Claver et al. (2001). The Zeeman-shifted Balmer lines in the UVES spectrum of WD0836+201 due to the substantial magnetic field (B≈ 3 MG) prevent us from obtaining a meaningful result via fitting the absorption lines with our non-magnetic models.
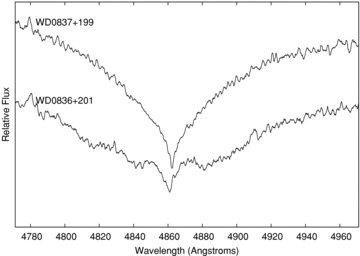
The full median filtered, smoothed, stacked UVES spectra for WD0837+199 and WD0836+201 covering the Hβ line profile. The Zeeman-shifted components can be seen for WD0836+201.
3.3 Constraints on the white dwarf mass–radius relation
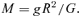
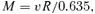
In light of this, we have assumed that the candidate Praesepe white dwarfs which are consistent with the general trend of the IFMR, as defined by data points from other systems, are robust cluster members. In this case, the distance to each degenerate has been taken to be that to the centre of the Praesepe, but with an uncertainty associated with the intracluster spatial distribution of the white dwarfs. Here, we adopt D= 184.5 ± 6 pc as the distance to the cluster centre, which is the weighted mean of the Hipparcos-based measurement, (m−M)0= 6.24 ± 0.12 (Mermilliod et al. 1997), the ground-based parallax measurement, (m−M)0= 6.42 ± 0.33 (Gatewood & de Jonge 1994) and a recent photometric determination which takes into account a new spectroscopic determination of the cluster metallicity, (m−M)0= 6.33 ± 0.04 (An et al. 2007). All white dwarf candidate members of Praesepe identified in the survey of Dobbie et al. (2004), which extended beyond 2.5° of the cluster, are found to lie within 2° of the cluster centre, corresponding to 6.5 pc at D= 184.5 pc. If the distribution of the white dwarfs is spherically symmetric about the cluster centre then all are likely to lie within the distance range D=184.5±8.5 pc.
The radius of each degenerate has been determined by scaling the distance (D) by the square root of the estimated flux ratio, (f/F)0.5, where f is the observed flux at the Earth's surface and F is the flux at the surface of the white dwarf. The surface flux in the SDSS filters (r, i and z; e.g. Fukugita et al. 1996) for each star has been obtained from the pure-H model atmospheres of Holberg & Bergeron (2006), where cubic splines have been used to interpolate between points in the grid. The uncertainty in the surface flux due to the error in the surface gravity determination for each object was calculated to be 0.3–0.4 per cent, assuming a generous uncertainty of ±0.1 in the log g measurement, and so was assumed negligible. However, in the temperature range of interest, the error in the effective temperature determination for each object was found to introduce an uncertainty of ∼3.5 per cent in F (r, i and z). We note that this uncertainty would have been larger if the u or g bands were used. The observed SDSS fluxes (Table 4) are believed to have absolute uncertainties at the 2 per cent level (Adelman-McCarthy et al. 2008). Thus, the estimated total combined uncertainty in our white dwarf radius determinations is ∼5 per cent, where contributions from errors in the white dwarf distances, the predicted fluxes and the observed fluxes are 4.6, 1.75 and 1 per cent, respectively, and have been added quadratically.
The SDSS magnitudes, the model independent masses and radii for the white dwarf members of Praesepe with UVES spectroscopy. The magnetic white dwarf, WD0836+201, the possible double-degenerate system, WD0837+185, WD0836+199 which has no clean SDSS photometry and WD0837+218, which sits above the bulk of white dwarfs in the IFMR, have been omitted from these calculations.
| Name | r | i | z | M M⊙ | R ×10−2 R⊙ |
| WD0833+194 | 18.09±0.02 | 18.34±0.02 | 18.65±0.04 | 0.78±0.05 | 1.133±0.057 |
| WD0837+199 | 17.81±0.01 | 18.08±0.02 | 18.34±0.04 | 0.71±0.04 | 1.160±0.059 |
| WD0840+190 | 18.44±0.01 | 18.70±0.02 | 18.98±0.04 | 0.75±0.05 | 0.954±0.049 |
| WD0840+200 | 18.01±0.01 | 18.21±0.02 | 18.57±0.05 | 0.75±0.05 | 1.175±0.060 |
| WD0843+184 | 18.36±0.01 | 18.61±0.02 | 18.85±0.04 | 0.84±0.05 | 0.993±0.050 |
| Name | r | i | z | M M⊙ | R ×10−2 R⊙ |
| WD0833+194 | 18.09±0.02 | 18.34±0.02 | 18.65±0.04 | 0.78±0.05 | 1.133±0.057 |
| WD0837+199 | 17.81±0.01 | 18.08±0.02 | 18.34±0.04 | 0.71±0.04 | 1.160±0.059 |
| WD0840+190 | 18.44±0.01 | 18.70±0.02 | 18.98±0.04 | 0.75±0.05 | 0.954±0.049 |
| WD0840+200 | 18.01±0.01 | 18.21±0.02 | 18.57±0.05 | 0.75±0.05 | 1.175±0.060 |
| WD0843+184 | 18.36±0.01 | 18.61±0.02 | 18.85±0.04 | 0.84±0.05 | 0.993±0.050 |
The SDSS magnitudes, the model independent masses and radii for the white dwarf members of Praesepe with UVES spectroscopy. The magnetic white dwarf, WD0836+201, the possible double-degenerate system, WD0837+185, WD0836+199 which has no clean SDSS photometry and WD0837+218, which sits above the bulk of white dwarfs in the IFMR, have been omitted from these calculations.
| Name | r | i | z | M M⊙ | R ×10−2 R⊙ |
| WD0833+194 | 18.09±0.02 | 18.34±0.02 | 18.65±0.04 | 0.78±0.05 | 1.133±0.057 |
| WD0837+199 | 17.81±0.01 | 18.08±0.02 | 18.34±0.04 | 0.71±0.04 | 1.160±0.059 |
| WD0840+190 | 18.44±0.01 | 18.70±0.02 | 18.98±0.04 | 0.75±0.05 | 0.954±0.049 |
| WD0840+200 | 18.01±0.01 | 18.21±0.02 | 18.57±0.05 | 0.75±0.05 | 1.175±0.060 |
| WD0843+184 | 18.36±0.01 | 18.61±0.02 | 18.85±0.04 | 0.84±0.05 | 0.993±0.050 |
| Name | r | i | z | M M⊙ | R ×10−2 R⊙ |
| WD0833+194 | 18.09±0.02 | 18.34±0.02 | 18.65±0.04 | 0.78±0.05 | 1.133±0.057 |
| WD0837+199 | 17.81±0.01 | 18.08±0.02 | 18.34±0.04 | 0.71±0.04 | 1.160±0.059 |
| WD0840+190 | 18.44±0.01 | 18.70±0.02 | 18.98±0.04 | 0.75±0.05 | 0.954±0.049 |
| WD0840+200 | 18.01±0.01 | 18.21±0.02 | 18.57±0.05 | 0.75±0.05 | 1.175±0.060 |
| WD0843+184 | 18.36±0.01 | 18.61±0.02 | 18.85±0.04 | 0.84±0.05 | 0.993±0.050 |
Subsequently, the mass for each star has been re-calculated using equation (2), this time using a gravitational redshift determined by subtracting the predicted line-of-sight velocity (RVC in Table 3), assuming each white dwarf shares the cluster motion, from the weighted mean measured shift of the non-LTE cores of the Hα and Hβ lines (Table 4). As open cluster escape velocities are typically low, approximately twice the velocity dispersion (e.g. Fellhauer et al. 2003), any object that has a space velocity substantially different from the cluster mean will be rapidly lost from the system. We note in this context that as the white dwarf members of Praesepe have cooling ages of τcool∼ 200–300 Myr, it is unlikely that putative point asymmetries in mass loss during the later stages of AGB evolution have displaced their space velocities greatly from the cluster mean. Moreover, the velocity dispersion of ∼1 M⊙ cluster members as determined by Mermilliod & Mayor (1999) is only 0.8 km s−1. Propagating these uncertainties, we estimate that the mass determination for each white dwarf using the gravitational redshift should be robust to ∼6 per cent.
ID, name, coordinates, expected line-of-sight velocity assuming cluster membership (RVC), weighted mean line core shift, gravitational redshift based on UVES Teff and log g, line-of-sight velocity (RVO) and estimated deviation from cluster velocity [(RVO-RVC)/(ΔRV2O+ 0.82)0.5], for the eight non-magnetic white dwarfs included in this work.
| ID | Name | RA | Dec. | RVC | H-α,H-β shift | GR. | RVO±ΔRVO | (RVO-RVC)/(ΔRV2O+ 0.82)0.5 |
| J2000.0 | km s−1 | |||||||
| WD0833+194 | – | 08:36:10.01 | +19:38:19.1 | 35.0 | 78.6±1.2 | 40.1±4.4 | 38.5±4.6 | +0.74 |
| WD0836+199 | LB1847,EG60 | 08:39:47.20 | +19:46:12.1 | 34.5 | 86.1±1.7 | 43.4±4.7 | 42.7±5.0 | +1.61 |
| WD0837+185 | LB5959 | 08:40:13.30 | +18:43:26.4 | 34.8 | 84.3±1.5 | 49.2±5.2 | 35.1±5.4 | +0.05 |
| WD0837+199 | LB393, EG61 | 08:40:28.09 | +19:43:34.8 | 34.5 | 73.5±1.1 | 41.5±4.5 | 32.0±4.6 | −0.53 |
| WD0837+218 | 08:40:31.47 | +21:40:43.1 | 33.9 | 81.9±1.1 | 62.8±6.5 | 19.1±6.6 | −2.24 | |
| WD0840+190 | 08:42:58.03 | +18:54:35.5 | 34.4 | 84.5±2.2 | 54.7±5.7 | 29.8±6.1 | −0.74 | |
| WD0840+200 | LB1876 | 08:42:52.32 | +19:51:11.3 | 34.2 | 74.9±1.1 | 40.1±4.4 | 34.8±4.5 | +0.13 |
| WD0843+184 | LB8648 | 08:46:01.91 | +18:30:48.5 | 34.2 | 88.0±1.2 | 51.5±5.4 | 36.5±5.5 | +0.41 |
| ID | Name | RA | Dec. | RVC | H-α,H-β shift | GR. | RVO±ΔRVO | (RVO-RVC)/(ΔRV2O+ 0.82)0.5 |
| J2000.0 | km s−1 | |||||||
| WD0833+194 | – | 08:36:10.01 | +19:38:19.1 | 35.0 | 78.6±1.2 | 40.1±4.4 | 38.5±4.6 | +0.74 |
| WD0836+199 | LB1847,EG60 | 08:39:47.20 | +19:46:12.1 | 34.5 | 86.1±1.7 | 43.4±4.7 | 42.7±5.0 | +1.61 |
| WD0837+185 | LB5959 | 08:40:13.30 | +18:43:26.4 | 34.8 | 84.3±1.5 | 49.2±5.2 | 35.1±5.4 | +0.05 |
| WD0837+199 | LB393, EG61 | 08:40:28.09 | +19:43:34.8 | 34.5 | 73.5±1.1 | 41.5±4.5 | 32.0±4.6 | −0.53 |
| WD0837+218 | 08:40:31.47 | +21:40:43.1 | 33.9 | 81.9±1.1 | 62.8±6.5 | 19.1±6.6 | −2.24 | |
| WD0840+190 | 08:42:58.03 | +18:54:35.5 | 34.4 | 84.5±2.2 | 54.7±5.7 | 29.8±6.1 | −0.74 | |
| WD0840+200 | LB1876 | 08:42:52.32 | +19:51:11.3 | 34.2 | 74.9±1.1 | 40.1±4.4 | 34.8±4.5 | +0.13 |
| WD0843+184 | LB8648 | 08:46:01.91 | +18:30:48.5 | 34.2 | 88.0±1.2 | 51.5±5.4 | 36.5±5.5 | +0.41 |
ID, name, coordinates, expected line-of-sight velocity assuming cluster membership (RVC), weighted mean line core shift, gravitational redshift based on UVES Teff and log g, line-of-sight velocity (RVO) and estimated deviation from cluster velocity [(RVO-RVC)/(ΔRV2O+ 0.82)0.5], for the eight non-magnetic white dwarfs included in this work.
| ID | Name | RA | Dec. | RVC | H-α,H-β shift | GR. | RVO±ΔRVO | (RVO-RVC)/(ΔRV2O+ 0.82)0.5 |
| J2000.0 | km s−1 | |||||||
| WD0833+194 | – | 08:36:10.01 | +19:38:19.1 | 35.0 | 78.6±1.2 | 40.1±4.4 | 38.5±4.6 | +0.74 |
| WD0836+199 | LB1847,EG60 | 08:39:47.20 | +19:46:12.1 | 34.5 | 86.1±1.7 | 43.4±4.7 | 42.7±5.0 | +1.61 |
| WD0837+185 | LB5959 | 08:40:13.30 | +18:43:26.4 | 34.8 | 84.3±1.5 | 49.2±5.2 | 35.1±5.4 | +0.05 |
| WD0837+199 | LB393, EG61 | 08:40:28.09 | +19:43:34.8 | 34.5 | 73.5±1.1 | 41.5±4.5 | 32.0±4.6 | −0.53 |
| WD0837+218 | 08:40:31.47 | +21:40:43.1 | 33.9 | 81.9±1.1 | 62.8±6.5 | 19.1±6.6 | −2.24 | |
| WD0840+190 | 08:42:58.03 | +18:54:35.5 | 34.4 | 84.5±2.2 | 54.7±5.7 | 29.8±6.1 | −0.74 | |
| WD0840+200 | LB1876 | 08:42:52.32 | +19:51:11.3 | 34.2 | 74.9±1.1 | 40.1±4.4 | 34.8±4.5 | +0.13 |
| WD0843+184 | LB8648 | 08:46:01.91 | +18:30:48.5 | 34.2 | 88.0±1.2 | 51.5±5.4 | 36.5±5.5 | +0.41 |
| ID | Name | RA | Dec. | RVC | H-α,H-β shift | GR. | RVO±ΔRVO | (RVO-RVC)/(ΔRV2O+ 0.82)0.5 |
| J2000.0 | km s−1 | |||||||
| WD0833+194 | – | 08:36:10.01 | +19:38:19.1 | 35.0 | 78.6±1.2 | 40.1±4.4 | 38.5±4.6 | +0.74 |
| WD0836+199 | LB1847,EG60 | 08:39:47.20 | +19:46:12.1 | 34.5 | 86.1±1.7 | 43.4±4.7 | 42.7±5.0 | +1.61 |
| WD0837+185 | LB5959 | 08:40:13.30 | +18:43:26.4 | 34.8 | 84.3±1.5 | 49.2±5.2 | 35.1±5.4 | +0.05 |
| WD0837+199 | LB393, EG61 | 08:40:28.09 | +19:43:34.8 | 34.5 | 73.5±1.1 | 41.5±4.5 | 32.0±4.6 | −0.53 |
| WD0837+218 | 08:40:31.47 | +21:40:43.1 | 33.9 | 81.9±1.1 | 62.8±6.5 | 19.1±6.6 | −2.24 | |
| WD0840+190 | 08:42:58.03 | +18:54:35.5 | 34.4 | 84.5±2.2 | 54.7±5.7 | 29.8±6.1 | −0.74 | |
| WD0840+200 | LB1876 | 08:42:52.32 | +19:51:11.3 | 34.2 | 74.9±1.1 | 40.1±4.4 | 34.8±4.5 | +0.13 |
| WD0843+184 | LB8648 | 08:46:01.91 | +18:30:48.5 | 34.2 | 88.0±1.2 | 51.5±5.4 | 36.5±5.5 | +0.41 |
The magnetic white dwarf, WD0836+201, the possible double-degenerate system, WD0837+185, WD0836+199 which has no clean SDSS photometry and WD0837+218 which sits well above the bulk of objects in the IFMR have been omitted from these calculations. Our estimates of the masses and radii of the remaining five white dwarfs are given in Table 4.
These masses and radii are plotted in Fig. 6 (light grey points with error bars) together with the most robust points currently available in the literature (small points with error bars). The masses of Procyon B (Teff≈ 7700 K), 40 Eri B (Teff≈ 16 700 K) and Sirius B (Teff≈ 25000 K) have been determined precisely using dynamical methods since these white dwarfs are members of visual binaries. Moreover, the distances to these three systems are well constrained by Hipparcos parallax measurements (ESA 1997). Theoretical mass–radius relations for Teff= 5000, 15 000 and 30 000 K, based on the CO core, thick H-layer evolutionary models of Fontaine, Brassard & Bergeron (2001), are also shown (black lines). Four out of the five Praesepe stars are located within 1σ of the Teff= 15 000 K track. WD0840+190 lies somewhat below this (∼2σ). It is possible that the radius of this object has been underestimated perhaps because it resides on the very back edge of the cluster. However, there is good agreement between the spectroscopic and flux-based radius estimates for all five white dwarfs. Alternatively, the radial velocity of this object may be overestimated by ∼ 4–5 km s−1, resulting in a marginally low gravitational redshift determination. WD0840+190 may have very recently received a velocity kick through an interaction with a binary system near the centre of the cluster and be in the process of leaving Praesepe. A remaining possibility is that the low-level ripple in some of our UVES spectra could have adversely affected our determination of the shift of the line cores. Given that the slope of the IFMR is not expected to change significantly within the comparatively narrow mass window in which our objects reside, the impact of a number of uncertainties, e.g. the velocity dispersion, the intracluster distribution of the white dwarfs and the random errors in our line core shift measurements, can be reduced if we take the weighted mean of the masses and the radii of the five stars. In this case, we determine the Mmean= 0.760 ± 0.021 M⊙ and Rmean= 0.01067 ± 0.00024 R⊙ (large filled circle in Fig. 6).
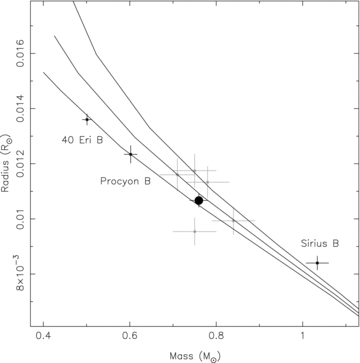
The mass–radius relation for white dwarfs. The locations of the five individual Praesepe white dwarfs for which we were able to estimate radius and mass are shown (light grey points) together with their weighted mean (large black circle). Three degenerate components of visual binary systems for which the most robust estimates of mass and radius are currently available (black squares) and theoretical mass–radius relations for white dwarfs with CO cores with thick H layers at effective temperatures of Teff= 5000 (bottom), 15 000 (middle) and 30 000 K (top) are also shown (solid black lines).
Given that the mean effective temperature of these five objects is Teff≈ 15 400 K, we find the location of this point in mass–radius space to be entirely consistent with the theoretical relation. Indeed, the proximity of all four robust data points to the model tracks strongly supports the theoretical white dwarf mass–radius relation and confirms the veracity of the prediction that white dwarfs with larger masses have smaller radii.
3.4 Radial velocities and the membership status of WD0837+218
As has been discussed in the introduction, the white dwarf members of open clusters are extremely useful for constraining the form of the IFMR. However, to assess the level of intrinsic scatter in this relation it is crucial that field white dwarf interlopers are eliminated from samples. An excellent way to adjudge cluster membership is via the measurement of radial velocities. Open star clusters typically have small velocity dispersions. For example, Mermilliod & Mayor (1999) determine a velocity dispersion of only 0.8 km s−1 for a sample of single F5-K0 members of Praesepe. Moreover, as discussed previously, it is unlikely that these white dwarfs will have velocities which differ substantially from the mean cluster velocity due to evolutionary effects (e.g. asymmetric mass loss) since they have remained within the projected tidal radius of Praesepe despite having formed 200–300 Myr ago. While the gravitational redshift component to the velocity shift of the absorption line cores in the spectra of white dwarfs is appreciable, given the robustness of evolutionary models as demonstrated above, if the effective temperature and surface gravity of a star is known, then the magnitude of this effect can be calculated straightforwardly using equation 2.
Hence, the radial velocity for each candidate Praesepe degenerate has been obtained by taking the difference between the measured shift of the line cores and the gravitational redshift as determined from evolutionary models and the measured gravity and effective temperature. It can be seen from Table 3 that, as expected, the radial velocities of the bulk of the white dwarfs, including the mean velocity of our candidate double-degenerate system, lie within 1σ of that expected if they are members of Praesepe. These latter values have been estimated assuming a total cluster space velocity of VTOT= 47.5 km s−1, a convergent point of  , J2000.0 (e.g. Mermilliod et al. 1990; Mermilliod & Mayor 1999) and the method detailed in Reid (1996). We find that the measured radial velocity of only one star, WD0837+218, is notably different (14.8 ± 6.6 km s−1 or 2.24σ below), from the velocity predicted on the assumption of cluster membership. There is no evidence in the available data that this object is a radial velocity variable. As this white dwarf has the largest projected separation from the cluster centre of those identified by Dobbie et al. (2004), and appears to be an outlier in the IFMR of Dobbie et al. (2006a), we are led to conclude that it is more likely a field star interloper than a member of Praesepe. Assuming this to be correct, it should not be used for constraining the form of the IFMR.
, J2000.0 (e.g. Mermilliod et al. 1990; Mermilliod & Mayor 1999) and the method detailed in Reid (1996). We find that the measured radial velocity of only one star, WD0837+218, is notably different (14.8 ± 6.6 km s−1 or 2.24σ below), from the velocity predicted on the assumption of cluster membership. There is no evidence in the available data that this object is a radial velocity variable. As this white dwarf has the largest projected separation from the cluster centre of those identified by Dobbie et al. (2004), and appears to be an outlier in the IFMR of Dobbie et al. (2006a), we are led to conclude that it is more likely a field star interloper than a member of Praesepe. Assuming this to be correct, it should not be used for constraining the form of the IFMR.
3.5 Minor revision to the initial mass–final mass relation
These new UVES data for eight white dwarf members of Praesepe are only of moderate signal-to-noise ratio per pixel but are homogeneous in nature and of much higher resolution than previously published spectra. The line shift measurements suggest that previous studies of these stars may have been systematically underestimated by a small amount (∼0.1) of their surface gravities. For example, for WD0843+184 we derive a radial velocity of 45.2 km s−1 based on the surface gravity (and effective temperature) of Dobbie et al. (2006a). Additionally, we estimate a radial velocity of 42.9 km s−1 for WD0837+199 adopting the surface gravity (and effective temperature) erroneously assigned to WD0836+201 in Claver et al. (2001). On this basis, we argue that our measurements of effective temperature and surface gravity are, except in the case of the magnetic white dwarf WD0836+201, to be preferred to those obtained previously.
As in our earlier work (e.g. Dobbie et al. 2006a), we have utilized a grid of evolutionary models based on a mixed CO core composition and a thick H surface layer (e.g. Fontaine et al. 2001) to estimate the mass and cooling time of each white dwarf from our measurements of effective temperature and surface gravity (see Table 1). Cubic splines have been used to interpolate between the points within this grid. The lifetime of the progenitor star of each white dwarf has then been calculated by subtracting the cooling time from the age of the cluster (625±50 Myr). Subsequently, to constrain the mass of the progenitor star, as in our earlier work we have used the stellar evolution models of Girardi et al. (2000), here for solar metallicity (Z⊙= 0.019, which is close to the value favoured by Anders & Grevesse 1989). Again cubic splines were used to interpolate between the points in the grid. We find that these model grids indicate that the difference between the lifetimes of 3–4 M⊙ stars with Z= 0.019 and 0.030 compositions is only ≈1 per cent. As the metallicity of Praesepe is midway between these values, the use of calculations for solar composition to estimate initial masses here appears adequate. Our estimates of the masses, cooling times and progenitor masses for each of the white dwarfs are shown in Table 1.
The revised locations of the Praesepe white dwarfs are plotted in Fig. 7, where the cooling times, masses and initial masses for WD0836+197 (LB5893), WD0840+205 and WD0836+201 are based on effective temperature and surface gravity estimates from the literature (Claver et al. 2001; Dobbie et al. 2006a). WD0837+218 has been excluded since based on the arguments presented above it appears more likely to be a field star. We also include in this plot the hydrogen-rich white dwarf members of a number of other systems where, for a given initial mass range, parameters such as cluster age are relatively well constrained – namely NGC 6819 and NGC 7789 (Kalirai et al. 2008), NGC 6791 (Kalirai et al. 2007), NGC 6633 (Williams & Bolte 2007), the Hyades (Bergeron, Liebert & Fulbright 1995b), NGC 2168 (M35; Williams, Bolte & Koester 2004, 2009), NGC 2516 (Koester & Reimers 1996) and the Pleiades (Bergeron et al. 1995a; Dobbie et al. 2006a,b) and the Sirius binary (Liebert et al. 2005). For the degenerate members of the Hyades, NGC 2168, NGC 2516, the Pleiades and the Sirius binary, we have made the same assumptions regarding white dwarf effective temperatures and surface gravities and cluster ages and metallicities as we did in Dobbie et al. (2006a,b). For NGC 6819, NGC 7789 and NGC 6633 we have assumed solar metallicity and have adopted the cluster ages and white dwarf effective temperatures and surface gravities given in the referenced literature. We have excluded the three lower mass white dwarf candidate members of NGC 1039 (Rubin et al. 2008) and NGC 7063 LAWDS 1 (Williams & Bolte 2007) since proper motion measurements indicate these are probably field stars (Dobbie et al. 2009). For the super-solar metallicity NGC 6791, we have used the [Fe/H]=+0.18 models of Girardi et al. (2000) since this is the most metal-rich composition available in their grid. We have included only the white dwarfs with a mass indicative of a CO core. The lower mass helium white dwarfs in this cluster could be the products of close binary evolution (e.g. Bedin et al. 2008; van Loon, Boyer & McDonald 2008) or the products of a metallicity-enhanced mass loss mechanism (Kalirai et al. 2007). Note that as in Dobbie et al. (2006a,b), the NGC 2168 white dwarf candidate member LAWDS 22 was not included here as Williams et al. (2004) were unable to obtain a satisfactory model fit to the observed Balmer lines.
As has been shown by a number of authors (e.g. Ferrario et al. 2005; Dobbie et al. 2006a; Williams & Bolte 2007; Kalirai et al. 2008), the IFMR as defined by the vast majority of current semi-empirical data (Fig. 7) can be reasonably approximated by a simple linear function (dashed line). Interestingly, WD0837+185, the radial velocity variable, does not appear to be an outlier. If the system experienced a common envelope phase then it may well have occurred during the later stages of the AGB. In this case, the evolution would approximate that of a single star. Indeed, there is only one star, WD0836+197, which deviates substantially from the general trend. Intriguingly, there appears to be nothing else untoward about this star. For example, Dobbie et al. (2006a) confirmed it to be a proper motion member, while the spectroscopy of Claver et al. (2001) reveals no evidence of Zeeman shifts in the Balmer line cores. The line-of-sight velocity as derived from the line core velocity shift measurement of Reid (1996) and the spectroscopic effective temperature and surface gravity estimates of Claver et al. (2001) is extremely close to the value expected on the basis of cluster membership. This argues against, but does not rule out, it being a radial velocity variable. Furthermore, Karl et al. (2005) found no evidence for rapid rotation, the shape of the Hα line core setting a limit of v sin i < 22 km s−1.
The magnetic white dwarf, WD0836+201, sits marginally above the bulk of white dwarfs in Fig. 7. However, Teff and log g from line fitting are likely to be less robust here than for non-magnetic degenerates. Indeed, the SDSS photometry (g−i, u−r) is more consistent with a slightly lower effective temperature (Teff∼ 15 000 K). We note that despite a gravitational redshift-based mass estimate (Heber, Napiwotzki & Reid 1997) appearing to be consistent with the spectroscopic mass determination of Claver et al. (2001), this result is void due to the confusion between WD0836+201 and WD0837+199. In any case, it is not obvious that a strongly magnetic white dwarf should be expected to follow an IFMR delineated by non-magnetic stars. Magnetism may hinder mass loss during post-main-sequence evolution (Wickramasinghe & Ferrario 2000). Alternatively, all strongly magnetic white dwarfs (B≳ 1 MG) might be produced through close binary interaction. Tout et al. (2008) propose that isolated high field magnetic white dwarfs form via the merging of two stellar cores within a common envelope environment. This unusual evolutionary history would presumably result in a higher than expected white dwarf mass for the estimated progenitor mass.
Thus, the location of WD0836+197 in initial mass–final mass space may represent the best evidence for strong differential mass loss. However, the lack of other comparatively deviant points in Fig. 7 and the sharply peaked form of the white dwarf mass distribution leads us to still prefer an evolutionary scenario in which it has formed from a blue straggler star. Praesepe is known to contain a number of blue straggler stars (e.g. 40 Cancri and Epsilon Cancri; Ahumada & Lapasset 2007).
A revised linear least squares fit to the 41 white dwarfs in this plot, which excludes the magnetic white dwarf WD0836+201 and the outlier WD0836+197, between progenitor masses of 1.15 M⊙ and 7 M⊙, gives parameters m= 0.1197 ± 0.0074 and c= 0.3569 ± 0.0220. These parameters are not greatly different from our original estimates of m= 0.133 ± 0.015 and c= 0.289 ± 0.051 (Dobbie et al. 2006a) or those from the recent work of other groups, e.g. Kalirai et al. (2008) determine m= 0.109 ± 0.007 and c= 0.394 ± 0.025.
4 SUMMARY
We have presented an analysis of high-resolution VLT and UVES spectroscopy of nine white dwarf candidate members of Praesepe. For the eight non-magnetic stars, we have measured the velocity shift of the Hα and Hβ line cores and obtained revised estimates of their effective temperatures and surface gravities. We have shown that contrary to the conclusions of a number of previous studies, WD0836+201 is the magnetic white dwarf. We have also provided evidence that WD0837+185 is a radial velocity variable and possibly a double-degenerate system. Additionally, we have used the five most appropriate Praesepe stars to obtain a new robust constraint on the white dwarf mass–radius relation. This new data point and the three most robust existing data points have been shown to lie in close proximity to the theoretical tracks. This result confirms the veracity of modern theoretical white dwarfs mass–radius relations. In light of this, we have determined the radial velocities of all eight non-magnetic degenerates. We have found that the line-of-sight velocity of WD0837+218, when examined in conjunction with its projected position with respect to the cluster centre and its location in initial mass–final mass space, argues that it is more likely to be a field star than a cluster member. It should thus be discounted from investigations concerned with the form of the IFMR. We have employed our new parameters for the Praesepe white dwarf members, in conjunction with comparatively robust data from other open clusters, to re-assess the form of the IFMR. We find that there is only one substantial outlier, WD0836+197, from a near-monotonic IFMR, which can still be adequately represented by simple linear function. The location of this star in initial mass–final mass space may be evidence of strong differential mass loss but given the lack of other outlying stars and the sharply peaked nature of the white dwarf mass distribution, we still favour an evolutionary scenario in which it has formed from a blue straggler star.
SLC acknowledges the financial support of STFC. RN and MRB are supported by STFC Advanced Fellowships. This research has made use of NASA's Astrophysics Data System. Funding for the creation and distribution of the SDSS Archive has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Aeronautics and Space Administration, the National Science Foundation, the US Department of Energy, the Japanese Monbukagakusho and the Max Planck Society. The SDSS Web site is http://www.sdss.org/.he. SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory and the University of Washington. This work is based in part on data obtained as part of the UKIRT Infrared Deep Sky Survey.
REFERENCES
Author notes
Based on observations made with ESO telescopes at the La Silla Paranal Observatory under programme ID 076.D-0751.



