Time-dependent simulations of steady C-type shocks Free

Abstract

1 INTRODUCTION

Molecular outflows associated with protostellar objects (e.g. Bally & Lada 1983) drive shocks into dark molecular clouds where the fractional ionization χ is low (χ < 10⁻⁶). The low values of χ cause the gas and the magnetic field to be weakly coupled. Charged particles are then pushed through the neutral gas by Lorentz forces, giving rise to ambipolar diffusion (Mestel & Spitzer 1956). Collisions between the charged and neutral particles accelerate, compress and heat the neutral gas ahead of the shock front and a magnetic precursor forms. If the shock speed is low enough for the gas to cool efficiently, the flow becomes continuous in all fluids (e.g. Mullan 1971). Such shocks are referred to as C-type shocks (Draine 1980).

Draine, Roberge & Dalgarno (1983, hereafter DRD) calculated the structures of steady perpendicular C-type shocks in diffuse and dense molecular media using a steady-state multifluid magnetohydrodynamic (MHD) description. They included a detailed treatment for energy and momentum transfer between different particles, oxygen-based chemistry and radiative cooling. They also assumed that the ion and electron densities exceed the grain charge density. However, for a fractional ionization below 10⁻⁷, grains play an important role in governing the electromagnetic forces (Draine 1980). In the densest regions of molecular clouds where n_H≥ 10⁶ cm⁻³, the fractional ionization constraint is usually fulfilled.

Pilipp, Hartquist & Havnes (1990) included the effect of dust grains on the structure of perpendicular steady C-type shocks more rigorously than previous authors (e.g. DRD). Their four-fluid models predict different shock widths than obtained in similar models of DRD. This model was extended to oblique shocks by Pilipp & Hartquist (1994) who found that in such shocks the transverse component of the magnetic field rotates about the propagation direction of the shock as long as there is a non-negligible Hall conductivity. This happens for a wide range of conditions, but Pilipp & Hartquist were unable to find solutions for fast-mode shocks.

Wardle (1998) pointed out that, to find a stable shock structure for steady oblique fast-mode shocks, one needs to integrate the steady-state equations backwards in time from the downstream boundary. However, such a method requires an exact thermal, chemical and ionization equilibrium. Such equilibrium does not obtain in most shocks of interest. For instance, the abundance of water, an important coolant, is out of equilibrium for about 10⁵ yr or more from the time the gas cools below several hundred degrees. This highlights the necessity for time-dependent simulations to calculate the C-type shock structure. Ciolek & Roberge (2002) were the first to include a fluid description of grain dynamics in multifluid MHD simulations. However, their study is restricted to perpendicular shocks. The multifluid approach developed by Falle (2003) overcomes this limitation.

In this paper, we study the structures of steady fast-mode C-type shocks using time-dependent multifluid MHD simulations. In Section 2, we describe the numerical code and the physical processes that we include. Then, we apply the code to perpendicular and oblique shocks with parameters similar to those of DRD including a single-sized grain fluid (Section 3) or multiple-sized grain fluids (Section 4). Finally, we discuss the results and give our conclusions in Section 5.

2 THE MODEL

2.1 Numerical code

As the ionization fraction within molecular clouds is low, the plasma needs to be treated as a multicomponent fluid consisting of neutrals, ions, electrons and N dust grain species. The governing equations for the neutral fluid are given by

1

2

3

where e_n=p_n/(γ− 1) +ρ_nv²_n/2 is the internal energy per unit mass, s_jn is the mass transfer rate between the charged fluid j and the neutral fluid, H_j is the energy sinks or sources for the different fluids, B is the magnetic field, E is the electric field and J is the current given by ⁠.

In the limit of small mass densities for the charged fluids, their inertia can be neglected. Also, the charged fluids are in thermal balance as their heat capacities are small. For the charged fluid j, the equations then reduce to

4

5

6

where α_j is the charge to mass ratio, K_jn is the collision rate coefficient of the charged fluid j with the neutrals and G_jn is the energy transfer rate per unit volume between the charged fluid and the neutral fluid. The expressions for K_jn and G_jn are given by Draine (1986). We use the reduced energy equation to calculate the temperatures of the ion and electron fluids. For the grain fluids, a hydrodynamic approximation with zero pressure is appropriate as the thermal velocity dispersion of the dust grains is small compared to the drift velocity with the neutrals.

The collisions of the charged particles with the neutral particles affect the evolution of the magnetic field. Using the reduced momentum equations for the charged fluids (equation 5) and the expression for the current J, the electric field can be expressed as (Cowling 1956)

where r_// is the resistivity along the magnetic field, r_H is the Hall resistivity and r_AD is the ambipolar resistivity. The expressions of the resistivities are given by, for example, Falle (2003) and depend strongly on the Hall parameter, β_i=α_i|B|/K_niρ_n, which is the ratio between the gyrofrequency of the charged fluid and collision frequency of the charged fluid with the neutrals. Substitution of the above expression into the Maxwell–Faraday equation then gives the magnetic induction equation:

7

where M=v_n×B is the hyperbolic magnetic flux and R is the resistance matrix which depends on the Hall resistivity, the ambipolar resistivity and the resistivity along the magnetic field. (For an expression for R, see Falle 2003.)

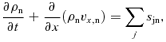
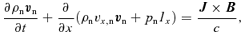
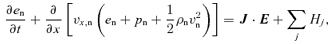
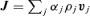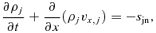
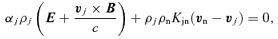
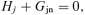
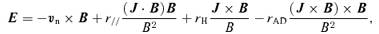
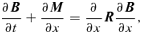
Equations (1–7) are solved using the numerical scheme described by Falle (2003). This scheme uses a second-order hydrodynamic Godunov solver for the neutral fluid equations (equations 1–3). The charged fluid densities are calculated using an explicit upwind approximation to the mass conservation equation (equation 4), while the velocities and temperatures are calculated from the reduced momentum and energy equations (equations 5 and 6). The magnetic field is advanced explicitly, even though this implies a restriction on the stable time-step at high numerical resolution (Falle 2003).

2.2 Physical processes

The numerical code described in the previous section is quite general. In order to investigate the effects of dust grains in fast-mode shocks, it is necessary to specify the source terms, i.e. the mass, momentum and energy transfer coefficients and the energy sources and sinks, to describe the relevant physics. The chemical network that we adopted is the one used by Pilipp et al. (1990) and Pilipp & Hartquist (1994).

Mass transfer between the ion and electron fluids and the neutral fluid is due to cosmic ray ionization at a rate of 10⁻¹⁷ s⁻¹, electron recombination with Mg⁺, dissociative recombination with HCO⁺ and recombination of ions on charged grains. Here, we have assumed that the main gas phase ions are Mg⁺ and HCO⁺ (Oppenheimer & Dalgarno 1974). The cross-section for these recombination reactions is taken from Pilipp et al. (1990).

Mass is also transferred between the ion and electron fluids and the grain fluids due to ion neutralization on grain surfaces. Ions and electrons stick to dust grains upon colliding with them. Also, they pass on their charge with unit efficiency. The grain charge then critically depends on the electron-grain and ion-grain collision rates (which themselves depends on the electron density and temperature, the ion density and temperature and the ion-grain relative streaming speed). The average grain charge is evaluated following Havnes, Hartquist & Pilipp (1987). Individual grains can have a charge that differs from the average value, but it is mostly within one unit of the average (Elmegreen 1979).

Different radiative cooling processes for the neutral and electron fluids are included in the code. The electron gas is cooled by the excitation and subsequent de-excitation of molecular hydrogen (e.g. DRD). This process only becomes important when the electron fluid temperature exceeds ≈ 1000 K. In the neutral gas, the dominant cooling processes are associated with O, CO, H₂ and H₂O. The radiative transitions for atomic oxygen, i.e. O i lines, are calculated using the procedure of DRD. The radiative losses from excited rotational-vibrational states of molecular hydrogen are a fit to the data presented by Hartquist, Dalgarno & Oppenheimer (1980), while those of CO are calculated by using Hollenbach & McKee (1979). Finally, we use Neufeld & Melnick (1987) to calculate the losses due to rotational transitions in H₂O. The heating rate of the neutral gas by cosmic rays is from DRD. We have not included any radiative losses for the ion fluid. From equation (6) and using the expression for G_i (Draine 1986), we find that the ion temperature, T_i, is given by

8

where T_n is the neutral temperature, m_n is the neutral particle mass and k_B is the Boltzmann constant.

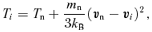
2.3 Initial conditions

The initial conditions of our simulations are adopted from DRD and similar studies such as Wardle (1998) and Chapman & Wardle (2006). This allows a comparison of our results with those of these studies.

The neutral fluid has a number density of n_H= 10⁴ or 10⁶ cm⁻³ and is composed mainly of molecular hydrogen so that m_n≈ 2 m_H. Small amounts of other neutral species such as O, CO and H₂O are also present. The initial abundances of O, CO and H₂O are taken to be 4.25 × 10⁻⁴n_H, 5 × 10⁻⁵n_H and 0, respectively. However, as the abundances of O and H₂O evolve substantially as gas is heated, the abundances of the important coolants are recalculated at every time-step. The dominant ions within the gas are assumed, as mentioned above, to be HCO⁺ and Mg⁺. The ion mass is then m_i≈ 30 m_H. Also, we assume that the ions are only singly ionized.

The dust grains are all assumed to be spherical with a radius of a_g= 0.4 μm and a mass of 8.04 × 10⁻¹³ g (where the density of the grains is taken 3 g cm⁻³). The grain to hydrogen mass ratio in the unshocked region has the canonical value of 0.01. The densities of the ion and electron fluids and the average grain charge are calculated from ionization equilibrium. For the temperatures that we adopt, i.e. T_n= 8.4 K for n_H= 10⁴ cm⁻³ and T_n= 26.7 K for n_H= 10⁶ cm⁻³, the average grain charge is quite close to −e and the electron and ion number densities are roughly the same, i.e. n_e≈n_i.

In the interstellar medium, the magnitude of the magnetic field scales roughly as B≈ 1 μG (n_H/cm⁻³)^−1/2 (see DRD) so that B= 10⁻⁴ G for n_H= 10⁴ cm⁻³ and B= 10⁻³ G for n_H= 10⁶ cm⁻³. The Alfvén speed of the gas is then the same at both densities, i.e. v_A= 2.2 km s⁻¹. In the far upstream region, the magnetic field lies in the x, y plane and makes an angle of 30°, 45°, 60° or 90° (perpendicular shock) with the x-axis. We assume that a shock is propagating in the positive x-direction with a speed of 25 km s ⁻¹. Such a shock is a strong fast-mode shock with an Alfvénic Mach number of M_A≈ 11.5.

Using the upstream fluid properties, the properties far downstream of the shock are calculated from the Rankine–Hugionot relations for an isothermal, magnetized shock. For our initial shock structure, we assume that the shock is a discontinuity at x= 0 separating the upstream and downstream properties. We follow the evolution of the shock to steady state within the shock frame.

2.4 Computational details

The size of the computational box is assumed to be a few times the shock width. By balancing the ion-neutral drag force with the Lorentz force, we can estimate the shock thickness: (e.g. Draine & McKee 1993)

9

where v_s is the shock speed. However, the grain-neutral friction is comparable to the ion-neutral friction for

or

where we substituted the expressions for the collision rates with the neutrals (Draine 1986) and assumed the relative speed between the neutrals and the grains to be of the order of v_s/2. This constraint is fulfilled in the heated precursor for both densities, and the shock thickness is determined by the grain-neutral drag. The expression for the shock width is similar to equation (9) and given by

10

Values of χ appropriate for the precursor must be used. Flower, Pineau des Forêts & Hartquist (1985) first pointed out that chemistry leads to a large drop in χ in the precursor of many shocks. The numerical domain is then chosen to be −10L_g≤x≤ 10L_g with a free-flow boundary condition at the downstream side and fixed inflow at the upstream boundary. We use a uniform grid with 400 cells.

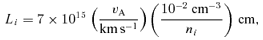
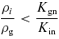
As our initial conditions are discontinuous, the inertia of the charged fluid, even the ions, cannot be neglected during the initial stages of the evolution. However, the inertial phase of the charged fluid is short compared to the time to approach a steady configuration (e.g. Roberge & Ciolek 2007). Although the inertial phase does not affect the final steady shock structure here, this effect should not be ignored for some other time-dependent models.

3 C-TYPE SHOCK MODELS

In this section, we present steady C-type shock structures for large single-sized grains. First, we discuss perpendicular shocks and then shocks propagating at an oblique angle with the magnetic field.

3.1 Perpendicular shocks

Fig. 1 shows the structures in multiple flow variables for perpendicular shocks at different densities. It is clear that both shock structures represent C-type shocks. As our models are similar to DRD, we can compare our results with Figs 2 and 3 of DRD. Although the shapes of the shocks are qualitatively similar, our shock widths are about four times larger than in DRD. This is due to a lower fractional ionization in our models which is a consequence of including the chemistry governing the ionization rather than assuming a constant ion flux as DRD did. The drag force of the charged particles on the neutrals is then lower as well and is balanced by the magnetic pressure over a larger length-scale. A consequence of the larger shock widths is that the gas has more time to radiate away its energy. The maximum temperature of the neutrals within the shock front is only 530 K for n_H= 10⁴ cm⁻³ and 905 K for n_H= 10⁶ cm⁻³, while DRD found 1223 and 1334 K, respectively.

Figure 1

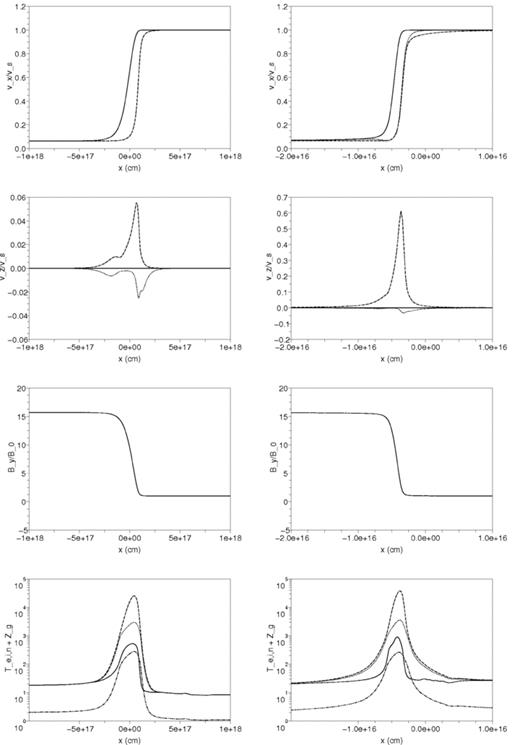
The shock structure for a perpendicular shock propagating in a quiescent region with n_H= 10⁴ cm⁻³ (left-hand panel) and n_H= 10⁶ cm⁻³ (right-hand panel). From top to bottom panels, we plot the velocity in the x- and z-direction for the neutrals (solid line), ions/electrons (dashed line) and grains (dotted line), the tangential magnetic field and the temperatures of the ions (dashed line), electrons (dotted line) and neutrals (solid line) as well as the absolute value of the grain charge (dash–dotted line). The velocities are normalized with respect to the shock speed and the magnetic field to the total upstream magnetic field.

Open in new tabDownload slide

Figure 2

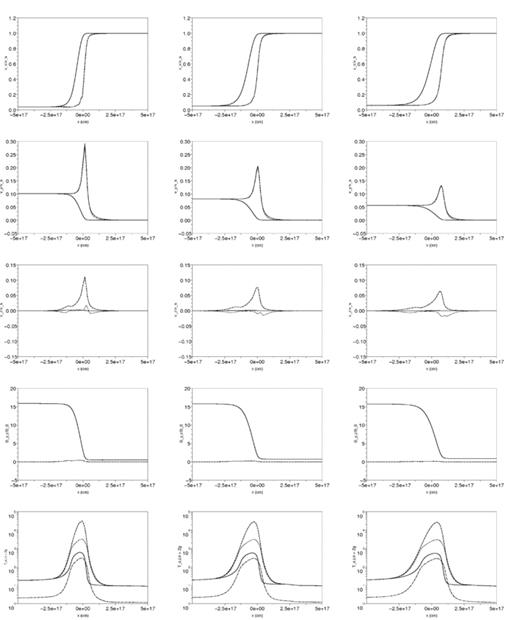
The shock structure for an oblique shock propagating at an angle of 30° (left-hand panel), 45° (middle panel) and 60° (right-hand panel) with the magnetic field in a quiescent region with n_H= 10⁴ cm⁻³. From top to bottom panels, we plot the velocity in the x-, y- and z-direction for the neutrals (solid line), ions/electrons (dashed line) and grains (dotted line), the tangential magnetic field in the y-direction (solid line) and z-direction (dashed line) and the temperatures of the ions (dashed line), electrons (dotted line) and neutrals (solid line) as well as the absolute value of the grain charge (dash–dotted line). The velocities are normalized with respect to the shock speed and the magnetic field to the total upstream magnetic field.

Open in new tabDownload slide

Figure 3

Same as in Fig. 2, but with an upstream density of n_H= 10⁶ cm⁻³.

Open in new tabDownload slide

Fig. 1 shows that the speed of the grains relative to the neutrals is less than the speed of the ions relative to the neutrals. The difference in relative speeds is due to the different response of the charged fluids to the Pedersen along E′ (=E+v_n×B) and Hall current along E′×B within the shock front. From equation (5), we find

11

where β_j is the Hall parameter of the charged fluid. For electrons and ions with |β_e,i| ≫ 1, the particles are tied to the magnetic field and

At the other extreme, |β_j| ≪ 1, the charged particles move with the neutrals. For the n_H= 10⁶ cm⁻³ models, the grains have a Hall parameter ranging from −0.1 (the upstream value) to a minimum of −1.5 within the shock front. For these values, the E′ term has a non-negligible contribution to the drift velocity. For the x-component of the velocity of the grains, this term only becomes important when the grains switch from moving with the neutrals to moving with the ions and electrons (see Fig. 1). The z-component of the E′ term, however, has a larger contribution to the drift forcing the grains to move with the neutrals. The lower density model exhibits this effect to a lesser extent as the grain Hall parameter lies between −1 and −20. Then, the E′ term is less important and provides only a small contribution to the drift.

The velocity difference between the ions and electrons with the neutrals determines the temperature of the charged particles through collisional heating. The maximum velocity difference in the models is ≈v_s giving a maximum ion temperature of a few times 10⁴ K. Electron cooling becomes important at temperatures of about 1000 K reflected in a considerably lower electron temperature at roughly 3 × 10³K. The electron temperature within the shock front is important for the dynamics of the shock as the average grain charge is

12

for |Z_g| ≫ 1 and n_g|Z_g| ≪n_e (e.g. Draine 1980). Otherwise, the average grain charge is roughly −1. From Fig. 1, we find that the average grain charge follows this dependence on the electron temperature with the average grain charge reaching maximum values of about −250.

3.2 Oblique shocks

For a finite magnetic field component parallel to the shock propagation and a non-zero Hall conductivity, the Hall current along E′×B has a component parallel to the propagation direction of the shock. As the total current in that direction is zero if the shock is steady, the Hall current needs to be balanced by the Pedersen current (along E′). This Pedersen current gives rise to the rotation of the magnetic field around the shock propagation (Pilipp & Hartquist 1994). Significant rotation occurs when the Hall conductivity is larger than the Pedersen conductivity (Wardle 1998).

For the n_H= 10⁴ cm⁻³ models, the Hall conductivity is always smaller than the Pedersen conductivity and there is no significant rotation of the magnetic field (see z-component of magnetic field in Fig. 2). The rotation increases marginally as the angle, θ, between the direction of shock propagation and the magnetic field decreases. The other shock properties, also, do not change significantly with θ. The temperatures of the different fluids and the average grain charge are similar to the ones found for the perpendicular shock. These results agree well with the θ-dependence of the steady shock structure found by Chapman & Wardle (2006). The similarity of the shock structure for different values of θ results from the minor contribution of the grains to the drag force on the neutrals. The grains do not determine the dynamics and drift with the other charged species.

Significant differences, however, are seen in the n_H= 10⁶ cm⁻³ models. Here, the grains are the dominant contributors to the drag force on the neutrals. Furthermore, there is a significant charge separation giving rise to a large Hall conductivity. In Fig. 3, we see that there is a substantial rotation of the magnetic field. Also the magnetic field upstream is no longer a stable node, but a spiral node as the Hall conductivity changes wave propagation upstream (Wardle 1998; Falle 2003). As for n_H= 10⁴ cm⁻³, the rotation decreases for larger θ, while the shock width increases.

The rotation of the magnetic field has large consequences for the drift velocity of the charged particles. Fig. 3 shows that the velocity structure changes considerably with θ. Also, the grains move significantly differently than the ions and electrons, especially in the θ= 30° model (see Fig. 3). Along the propagation direction, electrons and ions are decelerated immediately. The grains, however, are initially accelerated before being decelerated. Furthermore, they lag the ions and electrons. To drift in the direction opposite to the ions and electrons, the grains motion must be dominated by the E′ term in equation (11) and E′_x must be in the same direction as the x-component of E′×B. The large differences in drift velocity are expected as the rotation of the magnetic field is induced by a charge separation (and thus large Hall conductivity). For larger θ, the Hall conductivity and rotation decrease, so that the ions, electrons and grains move more together. As expected, the velocity profile converges to the perpendicular shock structure (see Figs 1 and 3).

4 MULTIPLE GRAIN SPECIES

In Section 3, we have assumed a single-sized grain fluid. In molecular clouds, however, the dust has a grain-sized distribution given by (Mathis, Rumpl & Nordsieck 1977)

13

where dn is the number density of grains with radii between a and a+ da. To take into account the effect of multiple dust species, we include an additional small-grain fluid with a_s= 0.04 μm (i.e. a_s=a_g/10) and m_s= 8.03 × 10⁻¹⁶ g (or m_s=m_g/1000). The total mass density of the grain fluid, ρ_s+ρ_g, is assumed to be 1 per cent of the neutral mass density (as in our previous models). With the adopted grain-sized distribution, most of the mass is in the small grain fluid. Furthermore, the small grains dominate the grain-neutral friction and, thus, the shock dynamics as the collision coefficient between grains and neutrals is proportional to a²_{g, s}/m_{g, s} (see Draine 1986). From Fig. 4, we see that the shock width is indeed, as expected from equation (10), an order of magnitude smaller than for the model with single-sized large grains.

Figure 4

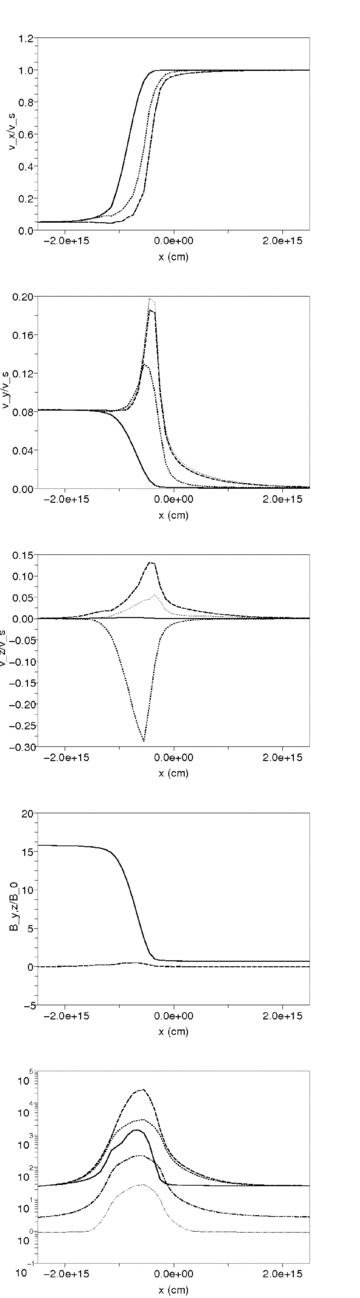
Similar to the 45° model of Fig. 3, but for two grain fluids. The small grains are indicated on the velocity component figures with a thin-dotted line, while their average charge is given by a thin-dash–dotted line.

Open in new tabDownload slide

Although the small grains have an average charge about an order of magnitude smaller than the large grains (see equation 12), the small grains have a larger Hall parameter and are strongly coupled to the magnetic field. The velocity plots in Fig. 4 show that the small grains move with the electrons and ions, while the large grains move with velocities between those of the neutrals and the other charged particles. The grain charge density is dominated by the small grains and free electrons are depleted from the gas phase (i.e. n_i≫n_e). The charge separation between the charged particles is thus small and the Hall conductivity is too. The rotation of the magnetic field out of the plane is then negligible. Also, the upstream magnetic field is no longer a spiral node, but a stable node.

The inclusion of a second grain species thus changes the shock structure considerably. Including additional grain species will further affect the shock structure as more dust grains are loading the magnetic field lines. Then, the signal speed at which disturbances propagate through the charged fluid decreases. For small polycyclic aromatic hydrocarbon abundances, the signal speed is close to 25 km s⁻¹ (Flower & Pineau des Forêts 2003) leading to the possibility that the resulting shock is a J-type shock in which the grain inertia cannot be neglected.

5 SUMMARY AND DISCUSSIONS

In this paper, we have presented 1D time-dependent multifluid MHD simulations of perpendicular and oblique C-type shocks in dusty plasmas. We have included in our numerical code relevant mass transfer processes, such as electron recombination with Mg⁺ and dissociative recombination with HCO⁺, and radiative cooling by O, CO, H₂ and H₂O. Also, the mass and charge transfer from ions and electrons to the dust grains is taken into account to calculate the average grain charge. Our models are the first of oblique fast-mode shocks in dense molecular clouds in which a fluid treatment of grain dynamics has been combined with a self-consistent calculation of the thermal and ionization balances including appropriate microphysics. We have performed simulations with single-sized and two dust grains species in plasmas of different density.

Dust grains do not change the shock dynamics much at n_H= 10⁴ cm⁻³ and the shock structures for oblique and perpendicular shocks are quite similar. Grains, however, dominate the shock dynamics at high densities (n_H= 10⁶ cm⁻³). For oblique shocks, the magnetic field in the shock front is not confined to the upstream magnetic field plane. The amount of rotation obtained depends on the Hall and Pedersen conductivities. For single-sized grains, the rotation is significant and increases with smaller θ as the Hall conductivity in these models is comparable to the Pedersen conductivity. For some models, the magnetic field at the upstream side of the shock even spirals around the direction of shock propagation. When we include an additional small grain species, the rotation mostly disappears. The small grains which carry most of the charge move with the ions and electrons reducing the Hall conductivity. Our models corroborate the main qualitative conclusions of previous studies (DRD; Pilipp & Hartquist 1994; Wardle 1998; Chapman & Wardle 2006; Guillet, Pineau des Forêts & Jones 2007), showing that our numerical method is efficient, rigorous and robust. In addition, we have succeeded in taking a significant step by developing the first oblique shock code capable of producing reliable results for comparisons with observations. Previous oblique shock models were restricted by less rigorous treatments of either the grain dynamics or the thermal and ionization balances.

However, our model does have some restrictions. First, we determine the drift velocities of the grains solely by balancing the grain-neutral friction with the Lorentz force and neglect their inertia. While small dust grains can be considered inertialess, large grains have a drag length, i.e. the length-scale for gas drag to decelerate the grains, that in some cases is comparable to the length-scale for magnetic field compression (Ciolek & Roberge 2002). Therefore, large grain inertia cannot always be neglected. Secondly, for small grains, the average grain charge is close to the elementary charge. As there is some fluctuation around the average, a fraction of the small grains has a zero or even positive charge. The neutral grains decouple from the magnetic field, while the positive grains drift in a different direction to the negative grains. Although this fluctuation around the average grain charge changes the shock structure, its effect is only minimal (Guillet et al. 2007).

A time-dependent method is not only robust (even for non-equilibrium conditions) for finding steady-state shock structures but also vital for modelling transient phenomena. In the vicinity of protostellar objects, the abundance of SiO is significantly enhanced (e.g. Martin-Pintado, Bachiller & Fuente 1992; Jiménez-Serra et al. 2004). It is thought that the SiO emission arises from the interaction of a protostellar jet with local dense clumps (Lefloch et al. 1998). Grain sputtering within C-type shocks releases the SiO depleted on the grains back into the gas phase (Caselli, Hartquist & Havnes 1997; Schilke et al. 1997). Numerical models using steady C-type shocks indeed show good agreement with recent observations of SiO line intensities in the L1157 and L1448 molecular outflows (Gusdorf et al. 2008a,b). However, it is doubtful that shocks interaction with dense clumps has reached steady state. In subsequent papers, we will study the interaction of C-type shocks with dense clumps and include grain sputtering to calculate the SiO emission.

We thank the anonymous referee for a report that helped to improve the manuscript. SVL gratefully acknowledges STFC for the financial support.

REFERENCES