-
PDF
- Split View
-
Views
-
Cite
Cite
Paul S. Cally, Mausumi Dikpati, Peter A. Gilman, Three-dimensional magneto-shear instabilities in the solar tachocline – II. Axisymmetric case, Monthly Notices of the Royal Astronomical Society, Volume 391, Issue 2, December 2008, Pages 891–900, https://doi.org/10.1111/j.1365-2966.2008.13934.x
Close - Share Icon Share
Abstract
A Boussinesq model of the development of non-axisymmetric (in particular m= 1) three-dimensional magneto-shear instabilities in the solar tachocline was presented in Paper I. However, there it was erroneously concluded that the axisymmetric (m= 0) modes are stable, and they were not discussed further. Here it is shown that, although m= 0 modes are indeed stable for broad magnetic profiles, they are strongly unstable to radial shredding (high radial wavenumber) instabilities on the poleward shoulders of toroidal magnetic bands at high field strengths (roughly 40–100 kG depending on bandwidth and latitude). These instabilities have growth rates comparable to or greater than those for tipping instabilities (m= 1) in many cases, but both are strongly stabilized by gravitational stratification characteristic of the upper radiative core. Weaker fields are m= 0 stable (though weakly m= 1 unstable), even in neutral gravitational stratification (convection zone).
1 INTRODUCTION
The solar tachocline is a thin shear layer straddling the base of the convection zone (e.g. Charbonneau et al. 1999). It was discovered helioseismically at the beginning of the 1990s along with the result that the internal differential rotation is roughly independent of latitude through the bulk of the convection zone. Based on several considerations, the tachocline has come to be regarded as the most likely seat for the solar dynamo (Tobias & Weiss 2007). As it contains both the convective overshoot region and the top of the radiative core, it is presumably able to store toroidal magnetic flux long enough to be amplified by dynamo action. The neutral buoyancy of the convection zone would make such flux buoyantly unstable on much shorter time-scales (Hughes 2007).
However, this raises the issue of stability to other effects, notably the latitudinal shear from equator to pole. A very nice result of Watson (1981), obtained years before the tachocline was discovered, suggests that it is stable to purely hydrodynamic two-dimensional (2D) motions in spherical shells. However, a long line of development beginning with Gilman & Fox (1997) indicates that 2D magneto-shear instabilities abound.
In Cally (2003, hereafter Paper I), the three-dimensional (3D) linear magneto-shear instabilities of a Boussinesq solar tachocline model were explored by numerically calculating complex eigenvalues representing the longitudinal phase speed c, where exp[im(φ−ct)] is the assumed dependence on longitude φ and time t. For the most part, only non-axisymmetric modes m= 1, 2, 3, … were considered. However, in Section 2.1, it was erroneously concluded that there are no axisymmetric (m= 0) instabilities. We correct that result here.
The Boussinesq model is one natural extension of the original 2D spherical shell analyses of tachocline magneto-shear instabilities, which began with Gilman & Fox (1997) in the linear regime and Cally (2001) for the non-linear case. In 2D, it is easily shown that m= 0 modes are always stable, primarily because mass cannot cross toroidal field lines. There is a wide array of 2D non-axisymmetric instabilities ( ) though, especially for m= 1, affecting both broad and banded magnetic profiles and which persist into 3D. However, there are also new instabilities, manifesting in the development of very fine radial structure, that are not present in 2D, but can dominate in 3D. An example is the ‘polar kink’ instability (Paper I). Growth rates comparable to the solar rotation frequency are common, indicating dynamically important processes. A detailed summary of these various instabilities is given in Gilman & Cally (2007). Based on an analysis of broad toroidal magnetic field profiles, Kitchatinov & Rüdiger (2008) argue that 3D shredding instabilities place stringent upper limits on the toroidal magnetic field that the top layers of the radiative core can support, but we find that this is not the case for banded profiles, where buoyancy can stabilize them.
) though, especially for m= 1, affecting both broad and banded magnetic profiles and which persist into 3D. However, there are also new instabilities, manifesting in the development of very fine radial structure, that are not present in 2D, but can dominate in 3D. An example is the ‘polar kink’ instability (Paper I). Growth rates comparable to the solar rotation frequency are common, indicating dynamically important processes. A detailed summary of these various instabilities is given in Gilman & Cally (2007). Based on an analysis of broad toroidal magnetic field profiles, Kitchatinov & Rüdiger (2008) argue that 3D shredding instabilities place stringent upper limits on the toroidal magnetic field that the top layers of the radiative core can support, but we find that this is not the case for banded profiles, where buoyancy can stabilize them.
In this paper we will demonstrate that vigorous radially shredding instabilities also develop in axisymmetric modes m= 0, at least on the poleward shoulders of banded magnetic profiles. On the other hand, the broad magnetic profiles previously examined in many papers (e.g. Gilman & Fox 1997; Cally 2001) are stable at m= 0. These instabilities may have important consequences for the dynamo and the structure of tachocline magnetic flux, though, being axisymmetric, they cannot supply dynamo action themselves (by the antidynamo theorem of Cowling 1933).
An alternative approximate model of 3D instabilities is based on the non-Boussinesq hydrostatic primitive equations (HPE) of Gilman, Dikpati & Miesch (2007), an extension of the so-called ‘shallow water’ magnetohydrodynamic (MHD) theory of Gilman (2000). An analysis of the current problem using this approach (Dikpati et al. 2008) obtains very similar results to those described here, despite the differences in the model.
2 EQUATIONS FOR m=0
We recall the fundamental linearized Boussinesq equations from Paper I:
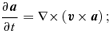
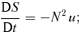
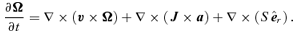
Here a and v= (u, v, w) are the Alfvén and plasma velocities, respectively [in spherical coordinates (r, θ, φ)], S=g s/cp is the scaled entropy density, N is the Brunt–Väisälä frequency (assumed constant), Ω=∇×v is the vorticity and J=∇×a is the current density. Lengths are scaled to make the tachocline radius unity and times so that the equatorial rotation frequency ω0[θ= (π/2)]= 1. All zeroth-order terms are assumed independent of r. Perturbed quantities are taken to depend on time as exp [−iσt].
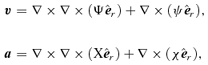
In Paper I it was claimed that there is no non-trivial non-stationary m= 0 solution for linear 3D tachocline instabilities. This conclusion is based on an algebraic error. The linearized equations set out in (I-14) and (I-15) are in part incorrect, and should instead be
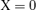
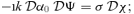
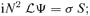
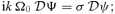
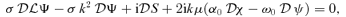
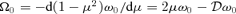 ,
, 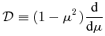
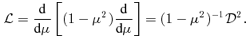
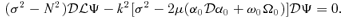
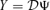 , we have the second-order ordinary differential eigenproblem:
, we have the second-order ordinary differential eigenproblem: 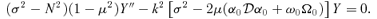
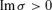 and in particular if σ2 < 0.
and in particular if σ2 < 0.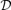 and
and 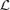 commute and
commute and 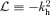 . Here kh is the horizontal wavenumber. Then we recover the usual gravity wave dispersion relation
. Here kh is the horizontal wavenumber. Then we recover the usual gravity wave dispersion relation 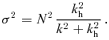
3 INTEGRAL THEOREMS
Several useful exact results follow directly from equation (13).
Theorem 1
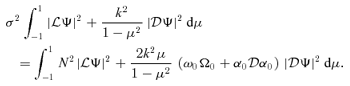
Proof.
Multiply equation (12) by  and integrate over (−1, 1). Since
and integrate over (−1, 1). Since  at the poles [recall
at the poles [recall  ], integration by parts proves the result. □
], integration by parts proves the result. □
Corollary 1.
σ2 is real, so either σ is real (indicating stability) or pure imaginary (exponential instability). There is no overstability.
Corollary 2.
A sufficient condition for stability σ2 > 0 is that N2≥ 0 and  everywhere.
everywhere.
Remark 1
If (1 −μ2)ω0 > 0 decreases monotonically from equator to poles (as expected) then μΩ0=−μ∂[(1 −μ2)ω0]/∂μ≥ 0, in which case rotation is a stabilizing influence. Moreover,  is clearly positive everywhere for a simple monotonic magnetic profile such as α0=aμ, which is therefore also stabilizing. However, it can be destabilizing on the poleward side of bands where α20 decreases.
is clearly positive everywhere for a simple monotonic magnetic profile such as α0=aμ, which is therefore also stabilizing. However, it can be destabilizing on the poleward side of bands where α20 decreases.
Corollary 3
The usual broad magnetic profile α0=aμ combined with the standard quadratic differential rotation ω0= 1 −sμ2 (0 ≤s≤ 1) is stable to axisymmetric disturbances.

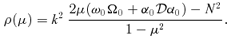
In terms of Y, the Integral Theorem 1 takes the equivalent form.
Theorem 2
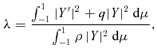
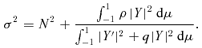
Proof.
Multiply equation (13) by Y* and integrate over (−1, 1). □
Corollary 4
σ2 < N2 if ρ is negative everywhere. This is relevant to the radiative core, where the buoyancy frequency greatly exceeds rotational and Alfvénic frequencies.
4 EIGENFUNCTION EXPANSION
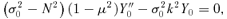
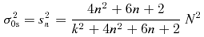
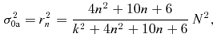
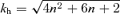 in the symmetric case and
in the symmetric case and  for the antisymmetric modes.
for the antisymmetric modes.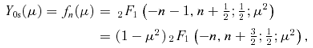
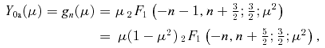
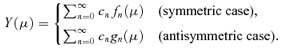
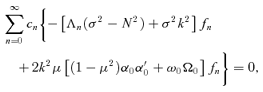
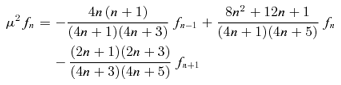
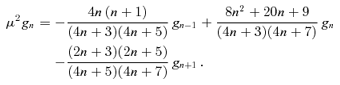
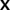 , where the (n− 1, n) (superdiagonal) element is the coefficient of fn−1 in equation (26), the (n, n) element is the coefficient of fn above and the (n+ 1, n) element is the fn+1 coefficient, and if we let
, where the (n− 1, n) (superdiagonal) element is the coefficient of fn−1 in equation (26), the (n, n) element is the coefficient of fn above and the (n+ 1, n) element is the fn+1 coefficient, and if we let 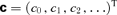 represent the (column) vector of coefficients in Y, then
represent the (column) vector of coefficients in Y, then 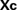 gives the coefficients of μ2Y. The coefficients of
gives the coefficients of μ2Y. The coefficients of 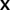 for the antisymmetric case are defined analogously by the terms in equation (28). Multiplication of Y by a function h(μ2) then corresponds to
for the antisymmetric case are defined analogously by the terms in equation (28). Multiplication of Y by a function h(μ2) then corresponds to  , where
, where 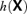 is the matrix function h of
is the matrix function h of 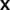 . It is defined and calculated trivially if h is a polynomial function, but otherwise may be constructed using eigenvector decomposition.
. It is defined and calculated trivially if h is a polynomial function, but otherwise may be constructed using eigenvector decomposition.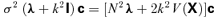
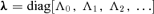 and the profiles are specified by V(μ2) ≡μ[(1 −μ2)α0(μ)α′0(μ) +ω0(μ)Ω0(μ)].
and the profiles are specified by V(μ2) ≡μ[(1 −μ2)α0(μ)α′0(μ) +ω0(μ)Ω0(μ)].In practice, the mode set is truncated to  and equation (29) is readily solved using a standard numerical routine, even with an
and equation (29) is readily solved using a standard numerical routine, even with an  of several hundred. Comparison with the shooting method reveals exquisite accuracy.1 This Galerkin method has the great advantage of yielding a large number of eigenvalues at once. Eigenfunctions are also easily generated if desired.
of several hundred. Comparison with the shooting method reveals exquisite accuracy.1 This Galerkin method has the great advantage of yielding a large number of eigenvalues at once. Eigenfunctions are also easily generated if desired.
5 MAGNETIC FIELD BANDS: EXAMPLE SOLUTIONS
We now explore the effects of varying k, N and various magnetic parameters on the eigenfrequencies σ, with particular reference to the unstable modes σ2 < 0. For simplicity, the solar-like differential rotation profile ω0= 1 − 0.18 μ2 is adopted throughout, except where otherwise noted.
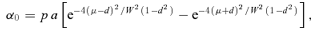
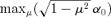 is a/2, corresponding to that in the broad α0=aμ configuration. Values of a around unity (approximate peak field strength 105G) or less are of solar interest, though higher values may be relevant to other stars.
is a/2, corresponding to that in the broad α0=aμ configuration. Values of a around unity (approximate peak field strength 105G) or less are of solar interest, though higher values may be relevant to other stars.Fig. 1 indicates the values of a and W for which  is somewhere negative in −1 < μ < 1. Assuming N2≥ 0, Corollary 2 states that a necessary condition for instability is that (a, W) be to the right-hand side of the relevant curve for its latitude (the three curves are for three different band latitudes). In fact, if N2= 0, instability will result at sufficiently high k everywhere to the right-hand side of these curves, as the eigenfunction
is somewhere negative in −1 < μ < 1. Assuming N2≥ 0, Corollary 2 states that a necessary condition for instability is that (a, W) be to the right-hand side of the relevant curve for its latitude (the three curves are for three different band latitudes). In fact, if N2= 0, instability will result at sufficiently high k everywhere to the right-hand side of these curves, as the eigenfunction  can become sufficiently restricted to the unstable region to make the right-hand side of equation (15) negative.
can become sufficiently restricted to the unstable region to make the right-hand side of equation (15) negative.
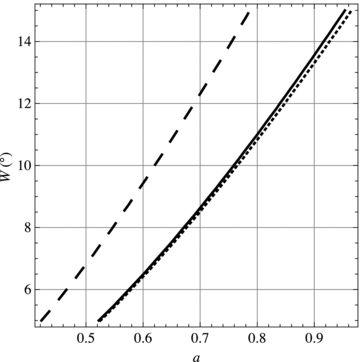
Banded magnetic field stability diagram. For banded profiles of the form (equation 29), with strength a, width W and central position μ=d= sin(latitude), instability can only occur at points (a, W) to the right-hand side of the relevant curve for each latitude. Full curve: 30° latitude bands; dashed curve: 15° latitude; dotted curve: 45° latitude.
5.1 Role of k
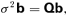
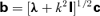 and
and 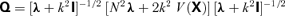 . In the k→∞ limit,
. In the k→∞ limit, 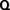 reduces to
reduces to 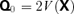 .
.Clearly, σ2=N2 at k= 0. But what happens to the eigenvalues as k increases from 0 to ∞ or as the magnetic field or rotation strengthens? We perform an analysis which makes it clear that how σ asymptotically approach the eigenvalues of  as k→∞.
as k→∞.
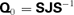 . In the usual case where there are no degenerate eigenvalues,
. In the usual case where there are no degenerate eigenvalues, 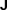 is diagonal and contains those eigenvalues as its elements. Irrespective of this,
is diagonal and contains those eigenvalues as its elements. Irrespective of this, 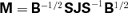 may be substituted into equation (31), which is then re-arranged to yield
may be substituted into equation (31), which is then re-arranged to yield 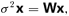

 is the identity matrix and
is the identity matrix and 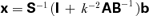 . Clearly,
. Clearly, 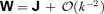 as k→∞, indicating diagonal dominance for large k, and similar quadratic convergence to the eigenvalues of
as k→∞, indicating diagonal dominance for large k, and similar quadratic convergence to the eigenvalues of 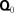 (elements of the diagonal matrix
(elements of the diagonal matrix 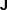 ). This follows from Gerschgorin's theorem, as the off-diagonal terms are all
). This follows from Gerschgorin's theorem, as the off-diagonal terms are all 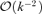 .
.In Fig. 2, we address the k dependence of a banded profile. The unstable eigenvalues are apparent. Interestingly, there appear to be two distinct families of eigenmode; one closely bound to the buoyancy frequency and one (much sparser) which seems independent of it once k becomes large enough.
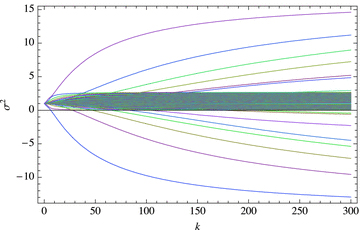
Symmetric eigenvalues σ2 as functions of k for the banded case ω0= 1 −0.18μ2, a= 2 magnetic bands of width 5° centred at μ= 0.5, N= 1. Here, 201 expansion modes are used to adequately resolve the narrow magnetic band.
Fig. 3 illustrates the eigenfunctions of unstable modes as k increases. We see that they become much more narrowly confined to the unstable region on the poleward shoulder of the band. We conclude that magnetic bands in the radiative zone, and also perhaps in an overshoot layer, are extremely susceptible to axisymmetric instabilities sharply localized on their poleward shoulders. This illustrates how the right-hand side of equation (15) becomes negative by concentrating the eigenfunction where  . Experiment suggests that, irrespective of N, instability always results at sufficiently large k if
. Experiment suggests that, irrespective of N, instability always results at sufficiently large k if  is negative somewhere.
is negative somewhere.
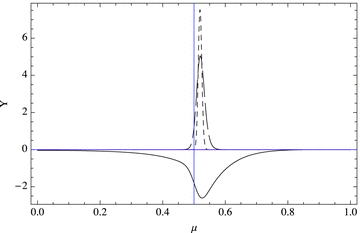
The eigenfunctions, calculated using the expansion method, corresponding to the most unstable eigenvalues σ= 0.875505 ı, 3.12112 ı and 3.70786 ı for k= 10 (full curve), 100 (long-dashed) and 500 (dashed), respectively, in the symmetric case for the banded profile of Fig. 2. The 5° magnetic band is centred on μ= 0.5, indicated by the vertical line. N= 1 throughout.
5.2 Role of N
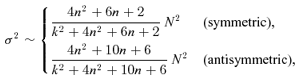
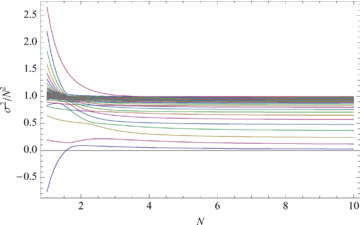
σ2/N2 as a function of Brunt–Väisälä frequency N for symmetric perturbations with ω0= 1 − 0.18μ2, k= 10 and an a= 2 magnetic band at 30° latitude of width 5°. (Eigenexpansion calculation with 201 modes.)
Examination of the important case, N= 0 (convection zone), not addressed in Fig. 4 is deferred till Figs 5,10 and 11 (top panels).
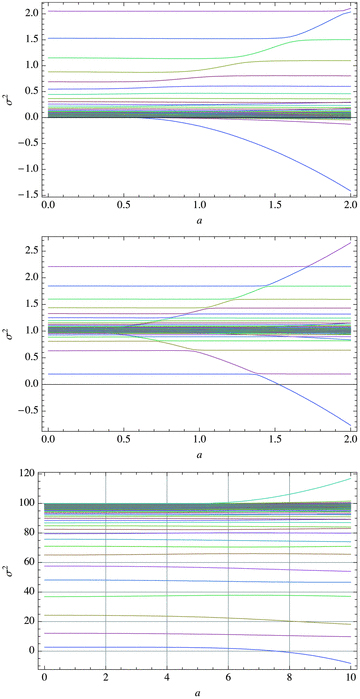
Symmetric eigenvalues σ2 (k= 10) as functions of field strength parameter a for the magnetic band at 30° latitude of width 5°. Top panel: N= 0; centre panel: N= 1; bottom panel: N= 10. Note the extended range in a in the bottom panel.
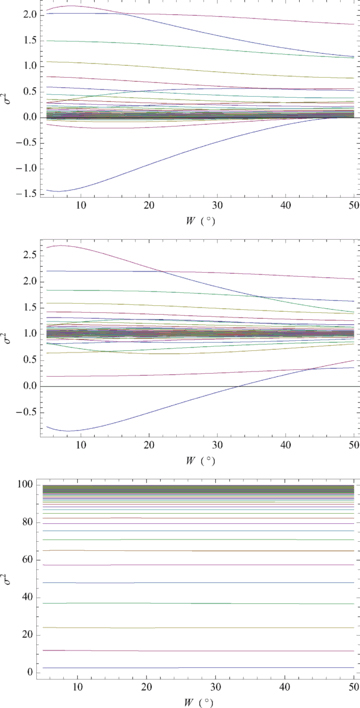
Symmetric eigenvalues σ2 (k= 10) as functions of bandwidth W for the magnetic band at 30° latitude and strength a= 2. Top panel: N= 0; centre panel: N= 1; bottom panel: N= 10.
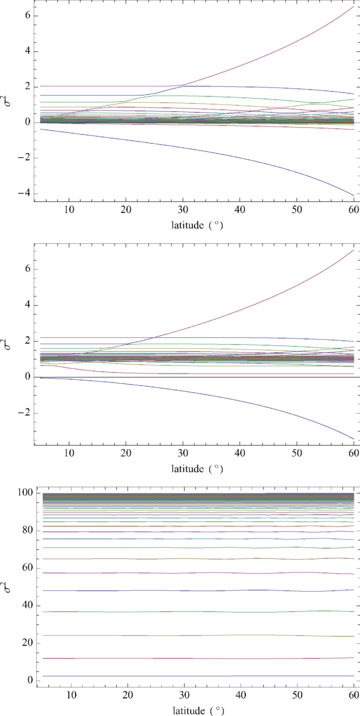
Symmetric eigenvalues σ2 (k= 10) as functions of band latitude for the magnetic band of width 5° and strength a= 2. Top: N= 0; centre: N= 1; bottom: N= 10.
5.3 Role of field strength a
How do the frequencies vary with field strength a? We examine our standard 5° band at ±30°, but vary the field strength parameter a (Fig. 5). If N is small enough, increasing a gives rise to unstable eigenvalues (note the avoided crossings). However, once N becomes even moderately large (10 in the bottom panel), it suppresses all instability up till very high values of a (7.57 in this case).
5.4 Varying a, k and N: the marginal stability equation
In the radiative zone, the Brunt–Väisälä frequency is very large compared to the rotational frequency, N≫ω0. Rotation is therefore unimportant. For the magnetic field to destabilize, the system requires a similarly large a. Fig. 7 (symmetric) indicates that instability increases linearly with a at fixed N, and that stability ensues as N increases at fixed a.
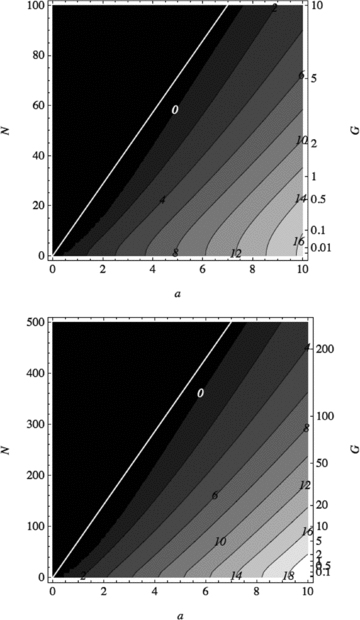
The growth rate  of symmetric instabilities of the 5° band at 30° latitude with n= 1 (top panel) and n= 5 (bottom panel) as a function of field strength a and dimensionless Brunt–Väisälä frequency N (or effective gravity G). The differential rotation ω0= 1 − 0.18μ2 has been re-introduced. The black region corresponds to stability and the white line to the asymptotic curve
of symmetric instabilities of the 5° band at 30° latitude with n= 1 (top panel) and n= 5 (bottom panel) as a function of field strength a and dimensionless Brunt–Väisälä frequency N (or effective gravity G). The differential rotation ω0= 1 − 0.18μ2 has been re-introduced. The black region corresponds to stability and the white line to the asymptotic curve  (see text). For this magnetic profile,
(see text). For this magnetic profile,  .
.
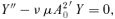
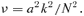
Theorem 3
In the ω0≪N limit, any triple (a, k, N) corresponding to marginal stability σ= 0 remains marginally stable as a, k and N are adjusted, provided ak/N stays fixed. Furthermore, for a given a and N, the minimum unstable k is  .
.
Fig. 6 confirms this. It shows that  is correct; the stability margin of a case without rotation lies exactly on the expected line.
is correct; the stability margin of a case without rotation lies exactly on the expected line.
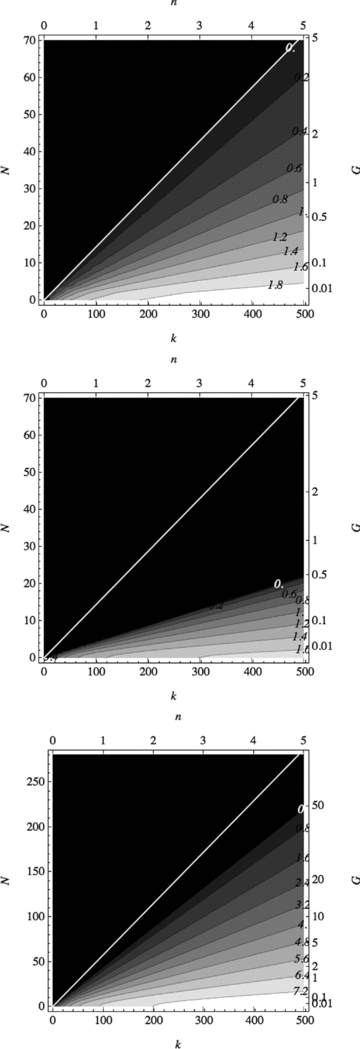
The growth rate  (labelled contours) of symmetric instabilities of the 5° band at 30° latitude with n= 1 (k= 99.3459) in the absence of rotation, presented as a function of field strength a and Brunt–Väisälä frequency N. The asymptotic marginal stability curve (in white), corresponding to
(labelled contours) of symmetric instabilities of the 5° band at 30° latitude with n= 1 (k= 99.3459) in the absence of rotation, presented as a function of field strength a and Brunt–Väisälä frequency N. The asymptotic marginal stability curve (in white), corresponding to  , is exact in this instance. The black region is stable.
, is exact in this instance. The black region is stable.
For future comparison with the HPE approach of Dikpati et al. (in preparation), we set k=nπ/H, where  is the layer thickness (recall that the Boussinesq shell has radius r= 1). Here, n is an integer specifying the number of half wavelengths which fit across the layer. With this H, our Brunt–Väisälä frequency N and their ‘effective gravity’G are related by G=N2H2= 10−3N2. We look at both n= 1 (k= 99.3459) and n= 5 (k= 496.729).
is the layer thickness (recall that the Boussinesq shell has radius r= 1). Here, n is an integer specifying the number of half wavelengths which fit across the layer. With this H, our Brunt–Väisälä frequency N and their ‘effective gravity’G are related by G=N2H2= 10−3N2. We look at both n= 1 (k= 99.3459) and n= 5 (k= 496.729).
Fig. 7 (top panel) adds rotation. As expected, its stabilizing influence shifts the marginal stability curve slightly to the right-hand side. In the bottom panel, k is increased by a factor of 5, but the theoretical marginal stability line remains equally valid.
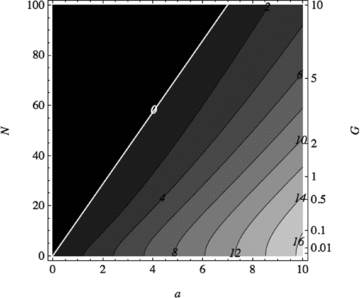
Fig. 8 similarly plots  as a function of k (or n) and N for a fixed. The top panel has no rotation, and again, the marginal stability line is exact. The bottom panels re-introduce our standard differential rotation for a= 1 and 4. Note that the rotationless marginal stability curve again provides a good estimate of where instability turns on with rotation present, provided a is large. For smaller a, where rotation is more important (recall we are comparing
as a function of k (or n) and N for a fixed. The top panel has no rotation, and again, the marginal stability line is exact. The bottom panels re-introduce our standard differential rotation for a= 1 and 4. Note that the rotationless marginal stability curve again provides a good estimate of where instability turns on with rotation present, provided a is large. For smaller a, where rotation is more important (recall we are comparing  with ω0Ω0), the discrepancy is large.
with ω0Ω0), the discrepancy is large.
The growth rate  of symmetric instabilities of the 5° band at 30° latitude. Top panel: a= 1, no rotation; middle panel: a= 1 with rotation; bottom panel: a= 4 with rotation, all as functions of k (or n) and N (or G). Note the higher growth rate at higher a. The differential rotation ω0= 1 − 0.18μ2 is employed for the bottom panels. The black region corresponds to stability and the white line to the asymptotic exchange of stability curve
of symmetric instabilities of the 5° band at 30° latitude. Top panel: a= 1, no rotation; middle panel: a= 1 with rotation; bottom panel: a= 4 with rotation, all as functions of k (or n) and N (or G). Note the higher growth rate at higher a. The differential rotation ω0= 1 − 0.18μ2 is employed for the bottom panels. The black region corresponds to stability and the white line to the asymptotic exchange of stability curve  , which is exact in the non-rotating case. For this magnetic profile,
, which is exact in the non-rotating case. For this magnetic profile,  .
.
Fig. 9 plots  as a function of bandwidth and latitude. In both the symmetric and the antisymmetric cases, the minimum
as a function of bandwidth and latitude. In both the symmetric and the antisymmetric cases, the minimum  is around 5, though this occurs for wide low-latitude bands in the symmetric case, and for narrower high-latitude bands in the antisymmetric case. The minimum
is around 5, though this occurs for wide low-latitude bands in the symmetric case, and for narrower high-latitude bands in the antisymmetric case. The minimum  in the symmetric case is 4.976 at W= 35.1° and latitude 16.7°. The antisymmetric case has a minimum within the domain displayed in Fig. 9 of 5.312 at W= 11° and latitude 60°, but continues to decrease at higher latitudes.
in the symmetric case is 4.976 at W= 35.1° and latitude 16.7°. The antisymmetric case has a minimum within the domain displayed in Fig. 9 of 5.312 at W= 11° and latitude 60°, but continues to decrease at higher latitudes.
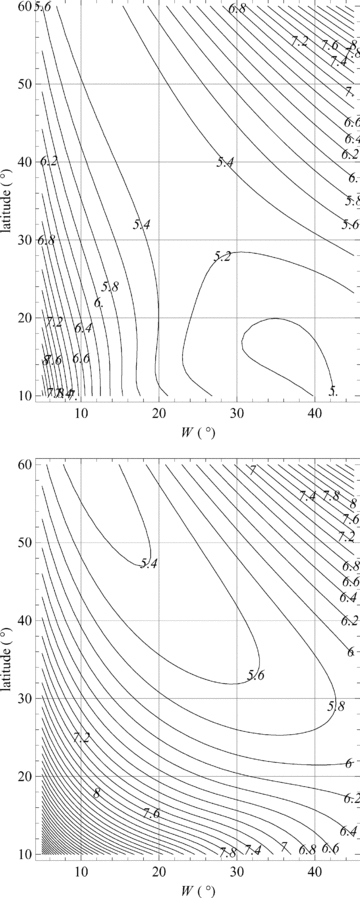
The asymptotic factor  (labelled contours) determining the minimum unstable radial wavenumber
(labelled contours) determining the minimum unstable radial wavenumber  for given N and a in the absence of rotation for bands of width W and a range of latitudes. Top panel: symmetric case; bottom panel: antisymmetric case.
for given N and a in the absence of rotation for bands of width W and a range of latitudes. Top panel: symmetric case; bottom panel: antisymmetric case.
5.5 Role of bandwidth W
Fig. 10 shows reducing instability with increasing bandwidth at fixed a and latitude, as expected because of the increase in  on the poleward shoulders (Corollary 2). Again, σ < N when N is large (see Corollary 4).
on the poleward shoulders (Corollary 2). Again, σ < N when N is large (see Corollary 4).
5.6 Role of band latitude
Fig. 11 shows increasing instability with increasing band latitude at a= 2 and small N. This is again expected: Fig. 12(a) shows how  attains larger and larger negative values on the poleward shoulder as band latitude is increased (cf. Corollary 2). The lower panels of Fig. 12 demonstrate that the bands are stable at even slightly lower field strengths a, as previously seen in Fig. 5 and as predicted in Fig. 1.
attains larger and larger negative values on the poleward shoulder as band latitude is increased (cf. Corollary 2). The lower panels of Fig. 12 demonstrate that the bands are stable at even slightly lower field strengths a, as previously seen in Fig. 5 and as predicted in Fig. 1.
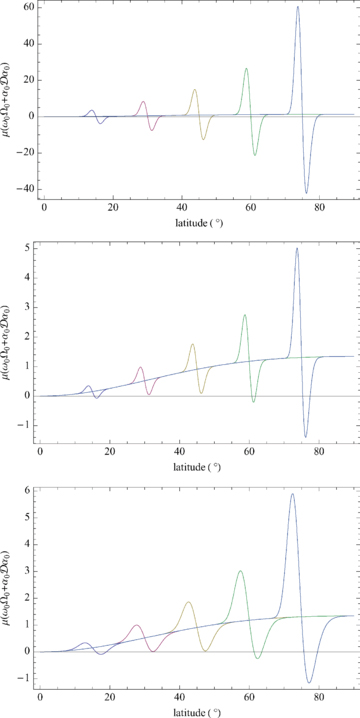
 as a function of latitude for bands at 15°, 30°, 45°, 60° and 75°. Top panel: a= 2, W= 5°; centre panel: a= 0.5, W= 5°; bottom panel: a= 0.75, W= 10°. Negative values (on the poleward shoulders) are a destabilizing influence (Corollary 2). The rotational angular velocity is ω0= 1 − 0.18μ2 as usual. The relative roles of rotation (the slow rise) and magnetic field (the banded differentiated Gaussians) are readily distinguished. Corollary 2 indicates stability of 5° mid-latitude bands for a≲ 0.5 and N2≥ 0 and of 10° mid-latitude bands for a≲ 0.75 and N2≥ 0.
as a function of latitude for bands at 15°, 30°, 45°, 60° and 75°. Top panel: a= 2, W= 5°; centre panel: a= 0.5, W= 5°; bottom panel: a= 0.75, W= 10°. Negative values (on the poleward shoulders) are a destabilizing influence (Corollary 2). The rotational angular velocity is ω0= 1 − 0.18μ2 as usual. The relative roles of rotation (the slow rise) and magnetic field (the banded differentiated Gaussians) are readily distinguished. Corollary 2 indicates stability of 5° mid-latitude bands for a≲ 0.5 and N2≥ 0 and of 10° mid-latitude bands for a≲ 0.75 and N2≥ 0.
5.7 Visualization
Fig. 13 depicts the development of an m= 0 band instability at k= 30. Of course, arbitrarily higher k are even more unstable (slightly) and result in finer kinked structure in r, unless dissipative effects limit them. As expected, the effect is predominantly on the poleward shoulder of the band.
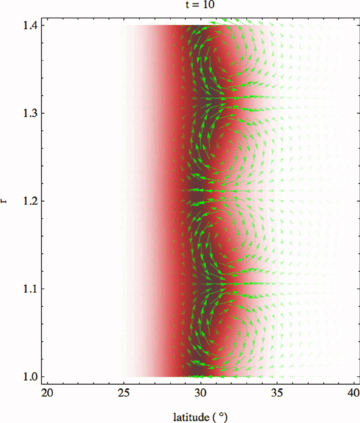
Linear development of the k= 30 symmetric instability in latitude–radius space of the 5°, a= 1 band at 30° latitude with N= 1. The shading represents (toroidal) magnetic field strength (field direction into the page) and the arrows represent velocity (by both their length and colour saturation). The eigenvalue is σ= 0.538 ı. The eigenfunction is displayed at time t= 10, given an initial perturbation of 0.1 per cent at t= 0.
Figs 14 and 15 illustrate symmetric and antisymmetric instabilities, respectively, in 10° bands at 15° latitude. In the symmetric case with a= 4, the eigenfunction ties together strongly across the equator, resulting in a significantly different eigenvalue for the symmetric (0.955 ı) and antisymmetric (0.708 ı) cases. Although the magnetic bands remain distinctly confined to their respective hemispheres at the epoch shown, the velocity clearly crosses the equator vigorously. Note also that the high Brunt–Väisälä frequency causes the velocity cells to be almost entirely latitudinal, as radial motion against the stratification is very difficult. In the antisymmetric case, the velocity equatorward of the band is weak.
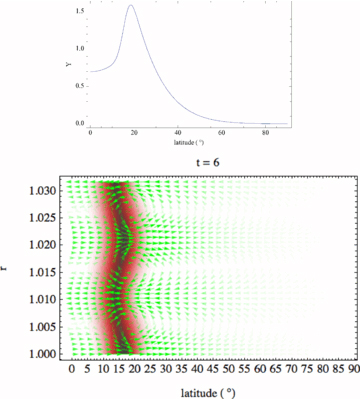
High stratification case N= 100 and n= 3 (k= 3π/H with  ) for an a= 4, 10° band at 15° latitude. Symmetric case. Top panel: the eigenfunction. Note the large value at the equator. Bottom panel: linear development of the instability (note that the vertical axis has been expanded to aid visibility). The eigenvalue is σ= 0.955 ı.
) for an a= 4, 10° band at 15° latitude. Symmetric case. Top panel: the eigenfunction. Note the large value at the equator. Bottom panel: linear development of the instability (note that the vertical axis has been expanded to aid visibility). The eigenvalue is σ= 0.955 ı.
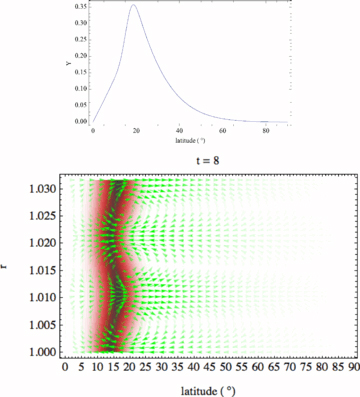
Same as Fig. 14, except for the antisymmetric case. The eigenvalue is σ= 0.708 ı.
For a high latitude (45°) band (not shown), the eigenfunction indicates that the coupling across the equator is much reduced. This is also suggested by the fact that the symmetric and antisymmetric eigenvalues are the same to seven decimal places, and by greatly reduced equatorial velocities.
6 CONCLUSIONS
We draw the following conclusions about m= 0 instabilities in the Boussinesq approximation.
σ2 is real, so there is no overstability.
Stratification is a stabilizing influence if N2 > 0 and destabilizing if N2 < 0.
Standard solar differential rotation ω0= 1 −sμ2, 0 < s < 1, is a stabilizing influence.
Classical broad magnetic profiles are stabilizing, but banded profiles are destabilizing on their poleward shoulders, where μα0α′0 < 0.
Banded magnetic profiles are stable up to some magnetic field threshold a≈ 0.4–1 which depends on bandwidth and latitude (Fig. 1).
If
 anywhere, there will always be unstable modes at sufficiently high k. Increasing N2 delays but does not ultimately suppress this. Diffusive effects could limit high-k instability, but we have not explored these (though see Paper I for a discussion of how thermal conduction affects the non-axisymmetric instabilities).
anywhere, there will always be unstable modes at sufficiently high k. Increasing N2 delays but does not ultimately suppress this. Diffusive effects could limit high-k instability, but we have not explored these (though see Paper I for a discussion of how thermal conduction affects the non-axisymmetric instabilities).The eigenfunctions of unstable modes in banded magnetic cases are more sharply confined to the poleward shoulder of the bands as k increases, but less tightly confined as N increases.
In the absence of rotation, the marginal stability case σ= 0 corresponds to
 , where ν0 depends only on the shape of the band and not its strength. For the classical Gaussian bands discussed here, Fig. 9 presents contour plots of
, where ν0 depends only on the shape of the band and not its strength. For the classical Gaussian bands discussed here, Fig. 9 presents contour plots of  for a range of bandwidth W and band latitude. Typically,
for a range of bandwidth W and band latitude. Typically,  is around 5–7 for cases of solar interest. Re-introducing rotation slightly stabilizes this, moving the critical wavenumber slightly above kmin (assuming a is large; the effect of rotation is more significant if a≲ 1; see Fig. 8).
is around 5–7 for cases of solar interest. Re-introducing rotation slightly stabilizes this, moving the critical wavenumber slightly above kmin (assuming a is large; the effect of rotation is more significant if a≲ 1; see Fig. 8). is an important quantity for band instability: the larger it is (above
is an important quantity for band instability: the larger it is (above  ), the larger the growth rate.
), the larger the growth rate.The velocity produced by axisymmetric instabilities at large N in low-latitude bands couples across the equator, setting up shallow meridional flows extending well beyond the bands.
7 DISCUSSION ON THE SIGNIFICANCE OF INSTABILITY IN BANDS
At first sight, the prevalence and vigour of both m= 0 and m= 1 high radial wavenumber instabilities present a challenge to the idea that sufficient toroidal magnetic flux can be stored and amplified in the tachocline to supply the solar cycle. As noted in Paper I, it would appear that toroidal fields of the order of 10 T (105G) are needed for this purpose if storage is entirely in the convective overshoot layer, or somewhat less if the magnetic field extends deeper into the radiative zone proper. Such high field strengths are also required to maintain the integrity of rising flux tubes destined to form active regions at the surface (e.g. Moreno-Insertis, Caligari & Schüssler 1995) and to ensure that they do not appear at too high latitudes (Choudhuri & Gilman 1987). The axisymmetric stability limits on field strength in banded toroidal fields are summarized in Fig. 1, and at least approach these required values.
However, non-axisymmetric instabilities can set in at much lower field strengths. This is illustrated in Fig. 16, where both the m= 0 and 1 growth rates  are plotted as a function of a for a typical banded profile (see caption for details) at k= 1000 (the large k delivers a near maximal growth rate).3 The axisymmetric case is strictly stable up to a= 0.76 for N= 0, but the m= 1 modes are weakly unstable throughout. With mild stabilizing stratification (N= 10), both m= 0 and 1 growth rates are significantly reduced. N= 100 (quite modest for the upper radiative region), corresponding to a buoyancy period of about 6 h, completely stabilizes the m= 0 modes up to a= 1.52 and reduces the m= 1 growth rates to negligible values (even at a= 1, the e-folding time is almost 4 yr). Of course, large N does nothing to stabilize the 2D tipping instabilities k= 0 and m= 1, but these typically saturate at tipping angles of 10°–20° (Cally, Dikpati & Gilman 2003) and do not disrupt the band.
are plotted as a function of a for a typical banded profile (see caption for details) at k= 1000 (the large k delivers a near maximal growth rate).3 The axisymmetric case is strictly stable up to a= 0.76 for N= 0, but the m= 1 modes are weakly unstable throughout. With mild stabilizing stratification (N= 10), both m= 0 and 1 growth rates are significantly reduced. N= 100 (quite modest for the upper radiative region), corresponding to a buoyancy period of about 6 h, completely stabilizes the m= 0 modes up to a= 1.52 and reduces the m= 1 growth rates to negligible values (even at a= 1, the e-folding time is almost 4 yr). Of course, large N does nothing to stabilize the 2D tipping instabilities k= 0 and m= 1, but these typically saturate at tipping angles of 10°–20° (Cally, Dikpati & Gilman 2003) and do not disrupt the band.
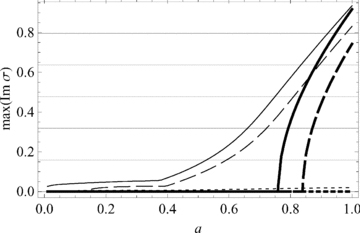
Comparison of the growth rates as a function of field strength a of the most unstable antisymmetric modes at k= 1000, and m= 0 (thick curves) and m= 1 (thin) in the case of W= 10° bands at ±30° latitude. The horizontal grid represents growth rates which produce amplitude increases of e, e2, e3, …, in one equatorial rotation period (month). Full lines: N= 0; dashed: N= 10; dotted: N= 100.
Based on an analysis of instabilities in the broad magnetic profile α0=aμ, Kitchatinov & Rüdiger (2008) argue that the high-k shredding instabilities limit radiation zone field strengths to a mere 600 G, at which point diffusive effects are able to stop them. However, as we have just seen, banded profiles are easily stabilized up to high field strengths by the stable stratification of the radiative core. Diffusive effects will limit the most unstable (high-k) instabilities further. We therefore see little impediment to storing  G fields below the convection zone. It is also likely that significant twist in the flux ropes stabilizes them, as happens in rising tubes (Moreno-Insertis et al. 1996).
G fields below the convection zone. It is also likely that significant twist in the flux ropes stabilizes them, as happens in rising tubes (Moreno-Insertis et al. 1996).
For example, the numerical values for the most unstable symmetric eigenvalue of a typical banded profile case,  , calculated with 201 and 401 expansion modes, respectively, are identical to 12 decimal places, indicating the extreme accuracy of the spectral method. In the latter case, the matrices are set up and all 401 eigenvalues are calculated on a 2.16 GHz macbook Pro laptop computer by Mathematica in 2.5 s.
, calculated with 201 and 401 expansion modes, respectively, are identical to 12 decimal places, indicating the extreme accuracy of the spectral method. In the latter case, the matrices are set up and all 401 eigenvalues are calculated on a 2.16 GHz macbook Pro laptop computer by Mathematica in 2.5 s.
We assume μA20′ < 0 somewhere, as in the banded profiles.
The m= 1 growth rates are calculated using the spectral method of Paper I with 200 modes.
M.D. acknowledges partial support from NASA grants NNH05AB521 and NNX08AQ34G.
REFERENCES



