-
PDF
- Split View
-
Views
-
Cite
Cite
Arthur B. Congdon, Charles R. Keeton, C. Erik Nordgren, Analytic relations for magnifications and time delays in gravitational lenses with fold and cusp configurations, Monthly Notices of the Royal Astronomical Society, Volume 389, Issue 1, September 2008, Pages 398–406, https://doi.org/10.1111/j.1365-2966.2008.13604.x
Close - Share Icon Share
Abstract
Gravitational lensing provides a unique and powerful probe of the mass distributions of distant galaxies. Four-image lens systems with fold and cusp configurations have two or three bright images near a critical point. Within the framework of singularity theory, we derive analytic relations that are satisfied for a light source that lies a small but finite distance from the astroid caustic of a four-image lens. Using a perturbative expansion of the image positions, we show that the time delay between the close pair of images in a fold lens scales with the cube of the image separation, with a constant of proportionality that depends on a particular third derivative of the lens potential. We also apply our formalism to cusp lenses, where we develop perturbative expressions for the image positions, magnifications and time delays of the images in a cusp triplet. Some of these results were derived previously for a source asymptotically close to a cusp point, but using a simplified form of the lens equation whose validity may be in doubt for sources that lie at astrophysically relevant distances from the caustic. Along with the work of Keeton, Gaudi & Petters, this paper demonstrates that perturbation theory plays an important role in theoretical lensing studies.
1 INTRODUCTION

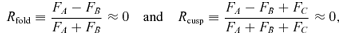
The curves show the caustic (top) and critical curve (bottom) for a SIE lens with minor-to-major axis ratio q= 0.5. The local orthogonal coordinates defined by the rotation matrix  are indicated for a fold point (left-hand panel) and a cusp point (right-hand panel). In the top two panels, a source (triangle) with position (y1, y2) measured from the centre of the caustic (astroid) has position (u1, u2) in the rotated coordinates centred on a fold point (left-hand panel) or a cusp (right-hand panel). In the bottom two panels, the four images (triangles) have positions (x1, x2) measured from the centre of the critical curve (ellipse) and positions (θ1, θ2) in the rotated coordinates.
are indicated for a fold point (left-hand panel) and a cusp point (right-hand panel). In the top two panels, a source (triangle) with position (y1, y2) measured from the centre of the caustic (astroid) has position (u1, u2) in the rotated coordinates centred on a fold point (left-hand panel) or a cusp (right-hand panel). In the bottom two panels, the four images (triangles) have positions (x1, x2) measured from the centre of the critical curve (ellipse) and positions (θ1, θ2) in the rotated coordinates.
Observationally, the fold and cusp relations are violated in several lens systems (e.g. Hogg & Blandford 1994; Falco, Lehar & Shapiro 1997; Keeton, Kochanek & Seljak 1997; Keeton et al. 2003,2005). These so-called ‘flux-ratio anomalies’ are taken as strong evidence that lens galaxies contain significant small-scale structure (e.g. Mao & Schneider 1998; Metcalf & Madau 2001; Chiba 2002). Since global modifications of the lens potential (modelled with multipole terms, for example) cannot explain the anomalous flux ratios (Evans & Witt 2003; Congdon & Keeton 2005; Yoo et al. 2005,2006), it is generally believed that lens galaxies must contain substructure in the form of mass clumps on a scale ≳106M⊙ (Dobler & Keeton 2006). Indeed, substructure is observed in at least two lens systems, in the form of a dwarf galaxy near the main lens galaxy (Schechter & Moore 1993; McKean et al. 2007). The substructure could well be invisible, though; numerical simulations of structure formation in the cold dark matter (CDM) paradigm predict that galaxy dark matter haloes are filled with hundreds of dark subhaloes (e.g. Klypin et al. 1999; Moore et al. 1999). The abundance of flux-ratio anomalies in lensed radio sources implies that lens galaxies contain ∼2 per cent (0.6–7 per cent at 90 per cent confidence) of their mass in substructure (Dalal & Kochanek 2002). This may be somewhat higher than the amount of CDM substructure (e.g. Mao et al. 2004), although new higher-resolution simulations are attempting to refine the theoretical predictions and make more direct comparisons with lensing observations (e.g. Gao et al. 2004; Diemand, Kuhlen & Madau 2007; Strigari et al. 2007). While there is still work to be done along these lines, it is clear that violations of the ideal fold and cusp relations provide important constraints on the small-scale distribution of matter in distant lens galaxies.
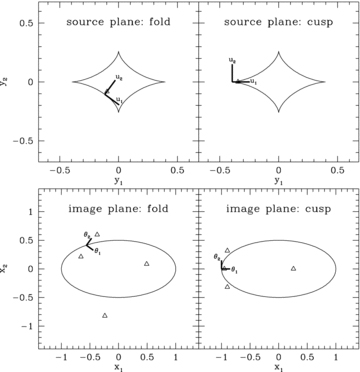
Keeton et al. (2003,2005) pointed out that the ideal fold and cusp relations only hold for a source asymptotically close to the caustic. If we want to use flux-ratio anomalies to study small-scale structure in lens galaxies, it is vital that we understand how much Rfold and Rcusp can deviate from zero for realistic smooth lenses just because the source lies a small but finite distance from the caustic. To that end, Keeton et al. (2003) used a Taylor series approach to demonstrate that Rcusp= 0 to lowest order, and used Monte Carlo simulations to suggest that Rcusp∝d2, where d is the distance between the two most widely separated cusp images. In order to derive the leading non-vanishing term in Rcusp analytically, it would be necessary to extend the Taylor series to a higher order of approximation. This has not been done before, since including higher-order terms substantially complicates the analysis. Instead, previous authors have made assumptions about which terms are important and which terms can be neglected, in order to obtain an analytically manageable problem.
As we will see, perturbation theory provides a natural way to overcome the difficulties of the Taylor series approach. Keeton et al. (2005) used perturbation theory to show that for fold lenses, Rfold is proportional to the image separation d1 of the fold pair. We extend their analysis in several important ways. We derive the leading-order non-vanishing expression for Rcusp using perturbation theory. We also show, for the first time, how the combination of singularity theory and perturbation theory can be used to study time delays between lensed images for both fold and cusp systems. Working in analogy to flux ratios, we derive time-delay relations for fold and cusp lenses, which we will apply (in a forthcoming paper) to observed lenses in order to identify ‘time-delay anomalies’. As time delays join flux ratios in probing small-scale structure in lens galaxies (see Keeton & Moustakas 2008), singularity theory and perturbation theory once again provide the rigorous mathematical foundation.
2 MATHEMATICAL PRELIMINARIES
To study lensing of a source near a caustic, it is convenient to work in coordinates centred at a point on the caustic. Non-spherical lenses typically have two caustics. The ‘radial’ caustic separates regions in the source plane for which one (outside) and two (inside) images are produced. 1 Within the radial caustic is the ‘tangential’ caustic or astroid, which separates regions in the source plane for which two (between the two caustics) and four (inside the astroid) images are produced. We are interested in four-image lenses, where the source is within the astroid. We therefore make no further reference to the radial caustic. A typical astroid is shown in Fig. 1 for a lens galaxy modelled by a singular isothermal ellipsoid (SIE), which is commonly used in the literature (e.g. Kormann, Schneider & Bartelmann 1994) and appears to be quite a good model for real lens galaxies (e.g. Rusin & Kochanek 2005; Koopmans et al. 2006). It is customary to define source-plane coordinates (y1, y2) centred on the caustic and aligned with its symmetry axes. However, for fold and cusp configurations, where the source is a small distance from the caustic, it is more natural to work in coordinates (u1, u2) centred on the fold or cusp point. For convenience, we define the u1 axis tangent to (and the u2 axis orthogonal to) the caustic at that point. Transforming from the (y1, y2) plane to the (u1, u2) plane requires a translation plus a rotation. To derive this coordinate transformation, we follow the discussion in appendix A1 in Keeton et al. (2005), which summarizes the results of Petters et al. (2001).
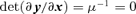 , where ∂y/∂x is the Jacobian of y, and is known as the inverse magnification matrix. We choose coordinates such that the origin of the source plane (y= 0) is on the caustic. In addition, we require that the origin of the lens plane (x= 0) maps to the origin of the source plane. We are interested in sources that lie near the caustic point (y= 0), which give rise to lensed images near the critical point (x= 0). In this case, we may expand the lens potential in a Taylor series about the point x= 0. We then find that the inverse magnification matrix at x= 0 is given by
, where ∂y/∂x is the Jacobian of y, and is known as the inverse magnification matrix. We choose coordinates such that the origin of the source plane (y= 0) is on the caustic. In addition, we require that the origin of the lens plane (x= 0) maps to the origin of the source plane. We are interested in sources that lie near the caustic point (y= 0), which give rise to lensed images near the critical point (x= 0). In this case, we may expand the lens potential in a Taylor series about the point x= 0. We then find that the inverse magnification matrix at x= 0 is given by 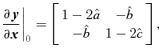
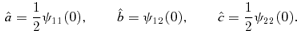
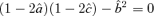 . In addition, at least one of
. In addition, at least one of 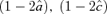 and
and 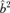 must be non-zero (Petters et al. 2001, p. 349). Consequently,
must be non-zero (Petters et al. 2001, p. 349). Consequently, 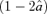 and
and 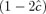 cannot both vanish. Without loss of generality, we assume that
cannot both vanish. Without loss of generality, we assume that 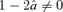 .
.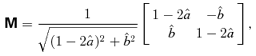

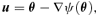
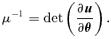
 , and is not necessarily related to the tangent to the critical curve.
, and is not necessarily related to the tangent to the critical curve.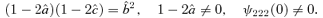
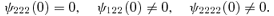
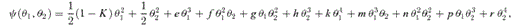
3 THE FOLD CASE
In this section, we use perturbation theory (e.g. Bellman 1966) to derive an analytic relation between the time delays in a fold pair. To derive this expression, we must first obtain the image positions at which the time delay is evaluated. These results were derived by Keeton et al. (2005). We offer a summary of their analysis in Section 3.1 and present our new results for the time delay in Section 3.2.
3.1 Image positions
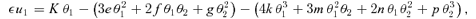
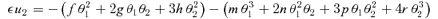
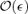 , the right-hand sides must be accurate to the same order. Noting that the lowest-order terms on the right-hand side are linear or quadratic in θ, we write
, the right-hand sides must be accurate to the same order. Noting that the lowest-order terms on the right-hand side are linear or quadratic in θ, we write 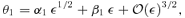

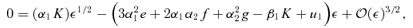

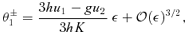
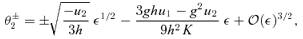
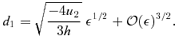
3.2 Time delays
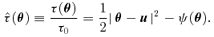
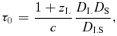
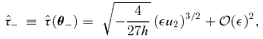
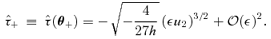
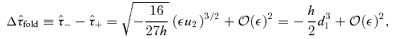
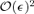 , while these same terms enter at
, while these same terms enter at 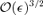 in quantities involving derivatives.
in quantities involving derivatives.To summarize,  . For comparison, Rfold∝d1. Since d1 is small, a violation of the ideal relation
. For comparison, Rfold∝d1. Since d1 is small, a violation of the ideal relation  is more likely to indicate the presence of small-scale structure in the lens galaxy than would be indicated by a non-zero value of Rfold.
is more likely to indicate the presence of small-scale structure in the lens galaxy than would be indicated by a non-zero value of Rfold.
Our analytic expression for  is only valid for sources sufficiently close to the caustic that higher-order terms are negligible. To quantify this statement, we compare our analytic approximation with the differential time delay computed numerically from the exact form of the lens equation. The numerical analysis requires a specific lens model, so we consider a SIE with axis ratio q= 0.5 as a representative example. We use the software of Keeton (2001) to compute the astroid caustic, and then choose a point on the caustic, far from a cusp, to serve as the origin of the (u1, u2) frame. For a given value of u2, we solve the exact lens equation to obtain the image positions and time delay for the fold doublet. The top left panel of Fig. 2 shows
is only valid for sources sufficiently close to the caustic that higher-order terms are negligible. To quantify this statement, we compare our analytic approximation with the differential time delay computed numerically from the exact form of the lens equation. The numerical analysis requires a specific lens model, so we consider a SIE with axis ratio q= 0.5 as a representative example. We use the software of Keeton (2001) to compute the astroid caustic, and then choose a point on the caustic, far from a cusp, to serve as the origin of the (u1, u2) frame. For a given value of u2, we solve the exact lens equation to obtain the image positions and time delay for the fold doublet. The top left panel of Fig. 2 shows  in units of θ2E as a function of u2 in units of θE, where θE is the Einstein angle of the lens. The analytic and numerical results are in good agreement for sources within 0.05θE of the caustic, although the curves do begin to diverge as u2 increases. The difference between the numerical and analytic curves (which represents the error in the analytic approximation, denoted by ɛ) is shown in the middle left panel. The bottom left panel shows the logarithmic slope of the error curve, d(ln ɛ)/d(ln u2). Together, the middle and the bottom left panels verify that our analytic approximation is accurate at the order of ε3/2. Furthermore, these panels suggest that the next non-vanishing term is of the order of ε5/2 and has a positive coefficient. The interesting implication is that the coefficient of the ε2 term seems to vanish. At our current order of approximation, we are not able to determine whether this is rigorously true, and if so, how general it is; we merely offer the remark in the hope that it may be useful for future analytic studies. For now, we focus on the verification that our analytic approximation is accurate at the order to which we work.
in units of θ2E as a function of u2 in units of θE, where θE is the Einstein angle of the lens. The analytic and numerical results are in good agreement for sources within 0.05θE of the caustic, although the curves do begin to diverge as u2 increases. The difference between the numerical and analytic curves (which represents the error in the analytic approximation, denoted by ɛ) is shown in the middle left panel. The bottom left panel shows the logarithmic slope of the error curve, d(ln ɛ)/d(ln u2). Together, the middle and the bottom left panels verify that our analytic approximation is accurate at the order of ε3/2. Furthermore, these panels suggest that the next non-vanishing term is of the order of ε5/2 and has a positive coefficient. The interesting implication is that the coefficient of the ε2 term seems to vanish. At our current order of approximation, we are not able to determine whether this is rigorously true, and if so, how general it is; we merely offer the remark in the hope that it may be useful for future analytic studies. For now, we focus on the verification that our analytic approximation is accurate at the order to which we work.
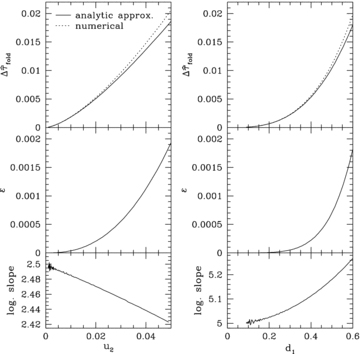
The top panels show the time delay for a fold pair as a function of source position (left-hand panel) and image separation (right-hand panel), for a SIE lens with axis ratio q= 0.5. The solid line shows our analytic approximation while the dotted line shows the exact result obtained by solving the lens equation numerically. The quantities u2 and d1 are defined in the text, and are shown here in units of the Einstein angle, θE. The time delay is given in units of θ2E. The middle panels show the error in the analytic approximation,  , due to our neglect of higher-order terms. The bottom panels show the logarithmic slope of the error curve, d(ln ɛ)/d(ln u2) on the left-hand side and d(ln ɛ)/d(ln d1) on the right-hand side. There is some numerical noise in the logarithmic slope due to numerical differentiation. Together, the middle and bottom panels verify that our analytic expression is accurate at order ε3/2 (cf. equation 25).
, due to our neglect of higher-order terms. The bottom panels show the logarithmic slope of the error curve, d(ln ɛ)/d(ln u2) on the left-hand side and d(ln ɛ)/d(ln d1) on the right-hand side. There is some numerical noise in the logarithmic slope due to numerical differentiation. Together, the middle and bottom panels verify that our analytic expression is accurate at order ε3/2 (cf. equation 25).
Since the source position u2 is not observable, we compare the analytic and numerical time delays as a function of the image separation d1 in the right-hand panels of Fig. 2. The range of d1 corresponds to that used for u2 in the left-hand panels. For a canonical fold lens with d1= 0.46θE (Keeton et al. 2005), our analytic expression gives a very good approximation, indicating that our analysis can be applied in astrophysically relevant situations – not just when the source is asymptotically close to the caustic, but even when it lies some small but finite distance away.
4 THE CUSP CASE
We now apply our perturbative method to the case of a source near a cusp point. This approach has not been applied to cusp lenses before. Appendix A of Keeton et al. (2003) derives the image positions and magnifications for a cusp triplet assuming a simplified form of the lens equation. As we noted in Section 1, this simplified lens equation assumes that certain terms may be set to zero, using criteria that are less than rigorous. We use the lens equation derived from the fourth-order lens potential, and use perturbation theory to verify the results of Keeton et al. (2003) and extend the analysis to a higher order of approximation. We also study time delays for a cusp lens for the first time. Our analysis does not involve simplifying assumptions, and indicates that perturbation theory is a powerful method in the study of lensing.
4.1 Image positions
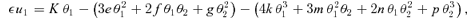
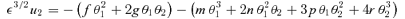
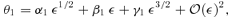
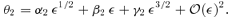
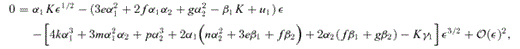
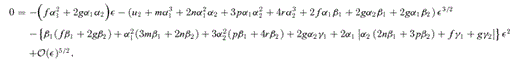

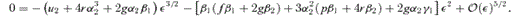
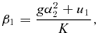
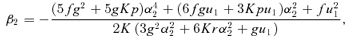
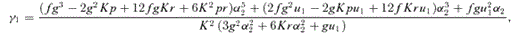
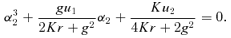
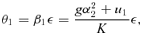
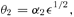
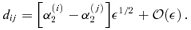
4.2 Magnifications
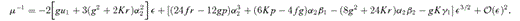
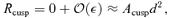
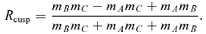
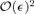 in the numerator, since the leading-order term in the denominator is
in the numerator, since the leading-order term in the denominator is 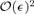 . By substituting the solutions for α2 into the numerator, we find that Rcusp= 0 to lowest order, in agreement with Keeton et al. (2003). We repeat this procedure for the next-leading term of
. By substituting the solutions for α2 into the numerator, we find that Rcusp= 0 to lowest order, in agreement with Keeton et al. (2003). We repeat this procedure for the next-leading term of 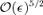 in the numerator, and find that Rcusp= 0 at linear order in d[i.e.
in the numerator, and find that Rcusp= 0 at linear order in d[i.e. 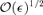 ] as well; this result was unattainable using the formalism of Keeton et al. (2003). To proceed to higher order, we must extend our perturbative analysis by including terms of the form δiε2 in equations (28) and (29) for the image positions. We denote the coefficient of d2 by Acusp, which we do not write down here, since that would require several pages. Given the complexity of this term, it is not practical to evaluate Acusp analytically. However, we have numerically computed Rcusp for the case of a SIE model with q= 0.5 (see Fig. 3) and find that Rcusp∝u1∝d2. While it is conceivable that Acusp might be zero for some specific lens model, this is clearly not the case in general. We have thus analytically demonstrated that Rcusp vanishes through linear order in d, placing the numerical result of Keeton et al. (2003) on solid mathematical ground.
] as well; this result was unattainable using the formalism of Keeton et al. (2003). To proceed to higher order, we must extend our perturbative analysis by including terms of the form δiε2 in equations (28) and (29) for the image positions. We denote the coefficient of d2 by Acusp, which we do not write down here, since that would require several pages. Given the complexity of this term, it is not practical to evaluate Acusp analytically. However, we have numerically computed Rcusp for the case of a SIE model with q= 0.5 (see Fig. 3) and find that Rcusp∝u1∝d2. While it is conceivable that Acusp might be zero for some specific lens model, this is clearly not the case in general. We have thus analytically demonstrated that Rcusp vanishes through linear order in d, placing the numerical result of Keeton et al. (2003) on solid mathematical ground.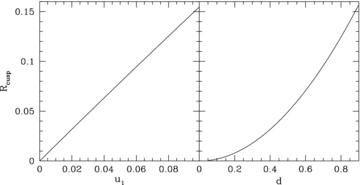
Rcusp as a function of u1 (left-hand panel) and d (right-hand panel) for a SIE with q= 0.5, obtained by solving the lens equation numerically.
4.3 Time delays
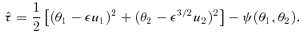
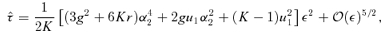
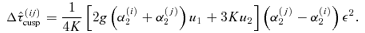
In the fold case, we found that the time delay scales as ε3/2 and only depends on the lens potential through the parameter h. For a cusp, however, h= 0, so it is not surprising that the lowest-order term in the time delay is of  . Furthermore, if we had not included the γi ε3/2 terms in our expansions of the image positions for a cusp (equations 28 and 29), it would not have been possible to obtain a perturbative expression for the time delay; instead, we would simply have found
. Furthermore, if we had not included the γi ε3/2 terms in our expansions of the image positions for a cusp (equations 28 and 29), it would not have been possible to obtain a perturbative expression for the time delay; instead, we would simply have found  .
.
5 SUMMARY
We have developed a unified, rigorous framework for studying lensing near fold and cusp critical points, which can (in principle) be extended to arbitrary order. We have found that the differential time delay of a fold pair assumes a particularly simple form, depending only on the image separation and the Taylor coefficient h=ψ222(0)/6. This result is astrophysically relevant, since it is quite accurate even for sources that are not asymptotically close to the caustic. We have also obtained perturbative expressions for the image positions, magnifications and time delays of a cusp triplet. These results rest on the key insight that a source at a given distance ε from a cusp along the relevant symmetry axis of the caustic can only move a perpendicular distance of ε3/2 in order to remain inside the caustic (Blandford & Narayan 1986). We have shown rigorously that the distance dependence of the magnification ratio Rcusp conjectured by Keeton et al. (2003) is correct. We have also demonstrated that the leading-order expression for the image positions is given by the relations presented by Keeton et al. (2003), and have provided the necessary framework for deriving the image positions corresponding to a Taylor expansion of the lens potential at arbitrary truncation order. Finally, we have derived cusp time delays analytically for the first time. Our results provide a rigorous foundation for identifying anomalous flux ratios and time delays in gravitational lens systems, and for using them to study small-scale structure in the mass distributions of distant galaxies.
We are neglecting faint images predicted to form near the centres of lens galaxies because they are highly demagnified and difficult to detect.
We thank A. O. Petters and Peter Schneider for helpful discussions and suggestions, and for their careful reading of the manuscript. We also thank the anonymous referee for useful comments.
REFERENCES



