-
PDF
- Split View
-
Views
-
Cite
Cite
F. Rahaman, M. Kalam, A. DeBenedictis, A. A. Usmani, Saibal Ray, Galactic rotation curves and brane-world models, Monthly Notices of the Royal Astronomical Society, Volume 389, Issue 1, September 2008, Pages 27–33, https://doi.org/10.1111/j.1365-2966.2008.13559.x
Close - Share Icon Share
Abstract
In the present investigation, flat rotational curves of the galaxies are considered under the framework of brane-world models where the four-dimensional effective Einstein equation has extra terms which arise from the embedding of the 3-brane in the five-dimensional bulk. It has been shown here that these long-range bulk gravitational degrees of freedom can act as a mechanism to yield the observed galactic rotation curves without the need for dark matter. The present model has the advantage that the observed rotation curves result solely from well-established non-local effects of gravitation, such as dark radiation and dark pressure under a direct use of the condition of flat rotation curves and does not invoke any exotic matter field.
1 INTRODUCTION
The presence of dark matter was suspected for the first time by Oort (1930a,b,c) while carrying out his observations of stellar motions in the local galactic neighbourhood. On the other hand, Zwicky (1933,1937) discovered the presence of dark matter on a much larger scale through his studies of galactic clusters. He, by comparing the virial mass and luminous mass of galactic clusters, concluded that a large amount of matter remains hidden in the galactic haloes. Afterwards, observation of the flatness of galactic rotation curves (Roberts & Rots 1973; Einasto, Kaasik & Saar 1974; Ostriker, Peebles & Yahill 1974; Rubin, Thonnard & Ford 1978; Rubin, Roberts & Ford 1979) supported Zwicky's suggestion regarding the presence of non-luminous matter. The flatness of the galactic rotation curves is indicative of the presence of much more matter within the galaxy than the visible material. Best estimates support a spherical distribution of matter thus leading to the picture of a visible galaxy surrounded by a dark-matter halo. It can be observed that dark-matter gravitational effects are more manifest at larger radius (Begeman 1989).
It is seen that inside the optical radius the shapes of the rotation curves probably correlate with the light distribution (Kent 1987) whereas some degree of velocity variation has been observed in the outer regions which might be related to the overall mass distribution (van Albada & Sancisi 1986). The velocity decrease may be even more than 50 km s−1 on both sides of some of the galaxies (Casertano & van Gorkom 1991). However, the measurements on rotation curves in spiral galaxies show that the coplanar orbital motion of gas in the outer parts of these galaxies keeps more or less a constant value up to several luminous radii (Persic, Salucci & Stel 1996). Another important feature is that the rotation curve profile of a spiral galaxy is flat outside a central galactic region (Rubin et al. 1979) and this flatness of the rotation curves might be due to the energy density of dark matter which varies as 1/r2 (Matos, Guzman & Nunez 2000b).
In subsequent years, gravitational lensing of objects like bullet clusters and the temperature distribution of hot gas in galaxies and galactic clusters as well as some other approaches have further confirmed the existence of dark matter (Maoz 1994; Cheng & Krauss 1999; Weinberg & Kamionkowski 2002; Faber & Visser 2006; Metcalf & Silk 2007).
Now, observation of anisotropy in the cosmic microwave background (CMB) (Spergel 2003) suggests that the total energy density of the Universe is 1.02 ± 0.02. On the other hand, observations of CMB and deuterium abundance (Sahni 2004) as well as theoretical predictions (Olive, Steigman & Walker 2000) confirm that the baryon density of the Universe cannot be more than 4 per cent of the total energy density. These results hinted at a huge discrepancy between Ωtotal and Ωbaryons. The introduction of Inflationary Theory by Guth (1981) and others (Linde 1982; Albrecht & Steinhardt 1982) enabled theoreticians to conclude that the Universe must appear to be flat and the total energy density of the Universe is close to the critical value. Since it was well established that visible matter could not contribute more than 4–5 per cent of the total energy density, it was initially speculated that 90–96 per cent of the total energy density must be hidden matter, that is dark matter (Guzman et al. 2003). But, in spite of intense searches, the requisite amount of dark matter was not found. So, a crisis developed in the cosmological arena. However, the emergence of the idea of dark energy which is thought to be responsible for accelerating the Universe (Perlmutter et al. 1998; Riess et al. 1998) seems to have, ultimately, removed that crisis. It is now known that about two-thirds of the total energy density comes in terms of this dark energy while the remaining one-third is contributed by matter, both visible and dark (Sahni 2004). Thus, at present, the dynamics of the Universe is governed by two components, the exact nature of both of which are unknown, one is dark matter and another is dark energy.
It has been argued that dark matter played a significant role during structure formation in sub-megaparsec scales of the early Universe. However, though the exact composition of dark matter is still unknown, it is thought that most probably this is of non-baryonic type. The reason behind this is that it is difficult to reconcile baryonic dark matter with the small density perturbations (δρ/ρ∼ 10−5 at z≃ 1100) measured by COBE and CMB experiments (Sahni 2004). Moreover, it is now quite established that the hot dark matter – like light neutrinos cannot contribute significantly to the large amount of dark matter residing in the Universe, because in that case galactic clusters with huge masses (∼ 1015M⊙) were the first objects to form. However, this is not supported by the observational constraint regarding neutrino mass and their density (Elgaroy et al. 2002; Ellis 2003; Minakata & Sugiyama 2003; Spergel 2003). On the other hand, cold dark matter, which does not contain any appreciable internal thermal motion, can cluster on small scales (Sahni 2004). This supports the well-known hierarchical structure formation and suggests that most of the dark matter must be cold and non-baryonic. The previous cold dark-matter models, introduced in the early 1980's, assumed that ΩCDM= 1 and were known as Standard Cold Dark Matter (SCDM) models. In spite of initial success SCDM models have fallen out of grace (Efstathiou, Sutherland & Madox 1990; Pope et al. 2004). Particularly, after the introduction of the idea of an accelerating Universe, the SCDM model is replaced by Λ-CDM model for including dark energy as a part of the total energy density of the Universe. This Λ-CDM model is found to be in nice agreement with various sets of observations (Tegmark et al. 2004a,b).
However, it is to be noted that not only the neutrino, as mentioned earlier, but also many other candidates exist for dark matter. Literature surveys reveal that Guzman et al. (2003) considered quintessence-like dark matter in spiral galaxies whereas Nukamendi and others (Matos, Guzman & Lopez 2000a; Matos et al. 2000b; Nukamendi, Salgado & Surarsky 2000, 2001; Lee & Lee 2004) have suggested that monopoles could be the galactic dark matter whose energy density varies as 1/r2. However, Nukamendi et al. (2000,2001); Lee & Lee (2004); Rahaman et al. (2007) studied global monopoles as a candidate for galactic dark matter in the framework of the scalar tensor theory of gravity. In this line of investigations Matos et al. (2000a,b) have examined the possibility and hence the type of dark matter that determines the geometry of a space–time where the flat rotational curves could be explained. Cembranos, Dobado & Maroto (2003) have shown that in the context of brane-world scenarios with low-tension massive brane fluctuations, that is branons, are natural dark-matter candidates and they could make up the galactic halo. There are also examples where the neutralino (Nihei, Okada & Seto 2005) and axino (Panotopoulos 2005) dark matter have been studied in brane-world cosmology. Under the same brane-world scenario it has been concluded that the neutral hydrogen clouds at large distances from the galactic centre may be explained by postulating the existence of dark matter (Harko & Mak 2005; Harko & Cheng 2006). On the other hand, it is found by Panotopoulos (2007) that the gravitino can play the role of dark matter in the Randall–Sundrum type II brane model (Randall & Sundrum 1999b) and determined what the gravitino mass should be for different values of the five-dimensional Planck mass. Interestingly, Viznyuk & Shtanov (2007) have discussed the subject in frames of the brane-world with induced curvature, which can explain not only dark matter in galaxies but also dark matter effects on the cosmological scale.
Therefore, it can be observed that in the framework of brane cosmology researchers have made several attempts to understand various features of galactic dark matter with different approaches (Mukohyama 2000; Langlois, Sorbo & Rodriguez-Martinez 2002; Cembranos et al. 2003; Gumjudpai, Maartens & Gordon 2003; Harko & Mak 2005; Harko & Cheng 2006; Böhmer & Harko 2007; Panotopoulos 2007; Viznyuk & Shtanov 2007).
Here, we will study a five-dimensional brane-world model and show that the long-range bulk gravitational degrees of freedom can act as a mechanism to yield the observed galactic rotation curves without the need for dark matter. This model has the advantage that the observed rotation curves result solely from well-established non-local gravitational effects, such as dark radiation and dark pressure, due to the five-dimensional bulk and does not rely on the introduction of an unknown and unseen matter field.
The above result that the dark radiation and its associated mass, known as dark mass, being a linearly increasing function of the distance has a similar behaviour as the dark matter at the galactic scale have also been obtained by Böhmer & Harko (2007). However, the approach of Harko and his collaborators is quite different from us as their method is either involved in the conformally symmetric space–times (Mak & Harko 2004; Harko & Mak 2005) or although they also consider constant rotational velocity with different approach, their emphasis is on the qualitative analysis of varied physical parameters in terms of observable quantities (Harko & Cheng 2006; Böhmer & Harko 2007). Unlike the previous studies the motivation in the present study is primarily concerned with the condition for flat rotation curves (which arises from the demand that the considered test particles should have constant tangential velocity) which has been exploited as a key to our entire investigation. This simple supposition provides us the required connection between dark matter and brane-world model in a very straightforward way.
The scheme of the present investigation is as follows. In Section 2, we present the relevant vacuum field equations for five-dimensional brane-world models whereas solutions will be sought for and utilised to provide acceptable galactic rotation curves on the brane in Section 3. We discuss, in Section 4, how different features of non-local effects of the brane-world scenarios are relevant for dark matter and hence may be responsible for the flatness of rotation curves which are in agreement with observations.
2 FIELD EQUATIONS FOR FIVE-DIMENSIONAL BRANE-WORLD MODELS
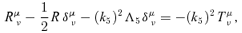
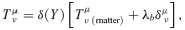
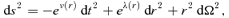
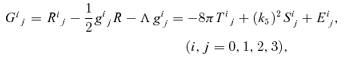
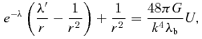
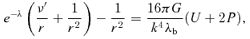
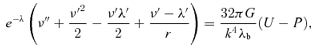
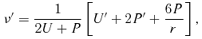
3 SOLUTIONS FOR DARK-MATTER PARAMETERS ON BRANE-WORLD MODELS
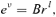
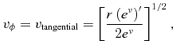
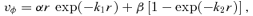
![A sample rotation curve utilising an ansatz for vφ of the form vφ=αr exp (−k1r) +β[1 − exp (−k2r)].](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/389/1/10.1111_j.1365-2966.2008.13559.x/1/m_mnras0389-0027-f1.jpeg?Expires=1750249414&Signature=mO-NGL~GrtHWVUq-gq1e6tpVoD6DJBq9t1yYKK97ljKbWwoY2THVGXg6JQWy4TTV~N537oqlwCzewtvKdtUvW~ME0WOUGnImMvP4fgHXGXpur~Jm96KUB5zEQyCIdARhbFFEUn8deSqyezK2P3b9CetrvoTRfvc-fymVGEAHi-o8CiOJjTRlat8Olj28VDJ5rkHfeOXU7Lxuo4f8ReI9vEalNzH-Ja-3ebiYqioviIZyT3BMBAycFtBq8GuvKARZqwQJnYlpXunbkLPbyVhT6de1bBZhSwl59nVwGapzcRQudpbgBCQZz2uFMViSDsqtJdPiI~9rFeADFlTCQkqZgg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
A sample rotation curve utilising an ansatz for vφ of the form vφ=αr exp (−k1r) +β[1 − exp (−k2r)].
In the inner regions, it is expected that the mass due to the concentration of stars will dominate the dynamics. A typical galactic star will, however, be moving in what to a reasonable approximation is vacuum, so that the vacuum equations are valid. To make the analysis tractable we will assume a test-particle star, located at some radius r*, moving under the influence of the spherically symmetric gravitational field due to stars located inside its orbit (r < r*) in the brane-world scenario. Without detailed knowledge of the Weyl stresses one does not know the exact form of the spherically symmetric vacuum equations. However, given the form of the rotation curve as given by equation (11), we can study the properties the metric must possess. Equation (10), utilising equation (11), may actually be integrated to yield an analytic expression for ν(r). The analytic result is rather unwieldy and not very perspicuous so instead a plot of eν(r) is provided in Fig. 2 from which it may be verified that we have the asymptotic form of equation (9) for appropriate l.
![The metric function exp [ν(r)] generated by the ansatz (11).](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/389/1/10.1111_j.1365-2966.2008.13559.x/1/m_mnras0389-0027-f2.jpeg?Expires=1750249414&Signature=LRaujriicPj1TCh0hlYCqbyuByDdUZ84oigOyYjPdoaLnDAek5aUWUdrA4YuSjZX3GDzRBXenS6yzhCItoOvSVX7QPhtVUCKEFwJx6pxrFK~LputCG8VVN05U0t5SafDYYU8f5dNksyWvIvncjUimhZPKTHQkCaG~xC2caiABHE4wjZd9XW8IZZm-F-XaHUJpRcYOSc1CaDS2XhFjIE4tK6FAia5bFoCTJ-rbg0SwBL~SsYMKxJGIr51F~oKkr7GCQAhTazM6YmSrUPiriJAkRdtSU7ljyUuv0vj3sxxPvVN4poKvBQbtdGoFvKIhfoi7e89HqUCf8MBBlvUj6dy~Q__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
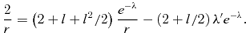
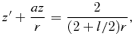
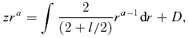
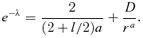
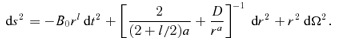
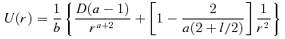
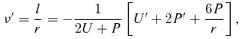
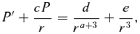
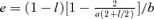 .
.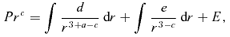
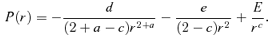
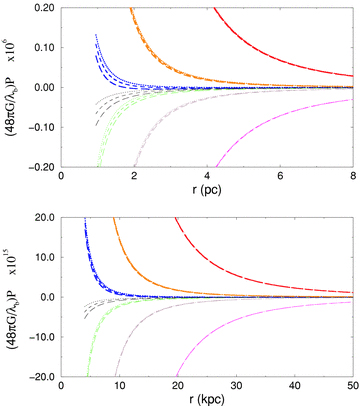
Variation of P versus r. The upper and lower panels correspond to short and long r behaviours. The black curves represent D= 0.0 for both the panel. For the upper panel, blue, orange and red colours represent D= 0.0000001, 0.000001 and 0.00001, and green, brown and pink colours represent D=−0.0000001, −0.000001 and −0.00001, respectively. For the lower panel, blue, orange and red colours represent D= 0.001, 0.01 and 0.1, and green, brown and pink colours represent D=−0.001, − 0.01 and −0.1, respectively. For all the colours, dotted, dashed and long-dashed curves correspond to vφ= 200, 250 and 300 Km s−1, respectively.
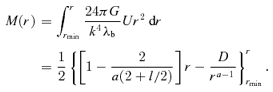
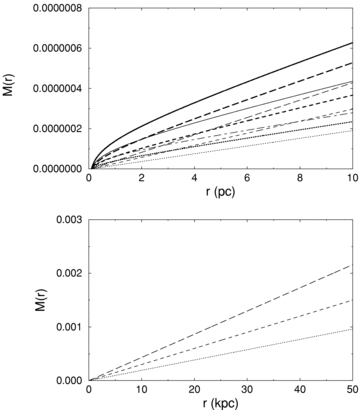
Plot for the variation of M(r) versus r. The upper and lower panels correspond to short and long r behaviours. The dotted, dashed and long-dashed curves represent vφ= 200, 250 and 300 Km s−1, respectively. For all these, thin curves and thick curves correspond to D= 0.0 and 1.0, respectively. The chain, solid and thick solid curves, respectively, represent vφ= 200, 250 and 300 Km s−1 but for D= 2.0. In the lower panel, plots represent the case for D= 1.0 only because of results are not found significantly sensitive to D at long distances. As equation for M is singular at r= 0, the minimum value of r is taken to be 0.1 (pc).
4 DISCUSSIONS AND CONCLUSIONS
In this paper, we have investigated the possibility of the existence of dark matter via galactic rotation curves under the framework of brane-world models. It has been observed that the non-local effects of the bulk as manifested through dark radiation and hence dark mass acts as the so-called dark matter which is thought to be responsible for the flatness of rotation curves around galaxies. From equation (22), it can easily be seen that M is linearly increasing with the radial distance of the galaxy. This is also clearly evident from the graphical plots (Fig. 4 and also Figs 5–7) of the different physical quantities. However, to get this connection we have employed a very simple supposition as expressed in equation (9) which arises from the demand that test particles under consideration will have constant tangential velocity. Note that this constant tangential velocity actually refers to the flatness of the galactic rotation curves.
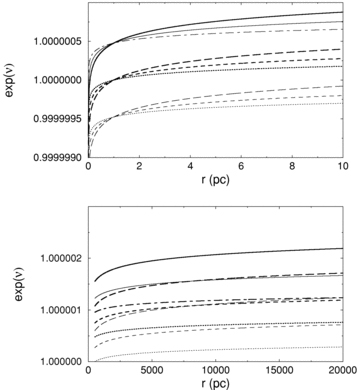
Plot for the variation of eν versus r. The upper and lower panels correspond to short and long r behaviours. The dotted, dashed and long-dashed curves represent vφ= 200, 250 and 300 Km s−1, respectively. For all these, thin curves and thick curves represent B= 0.9999995 and B= 1.0, respectively. The chain, solid and thick solid curves, respectively, represent vφ= 200, 250 and 300 Km s−1 but for B= 1.0000005.
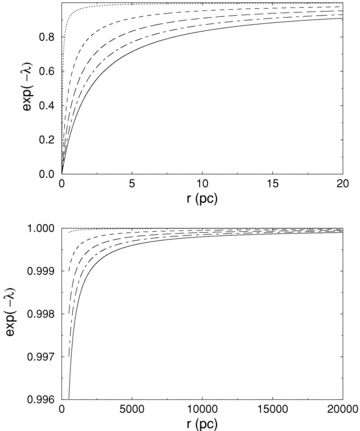
Plot for the variation of e−λ versus r. The upper and lower panels correspond to short and long r behaviours. The dotted, dashed, long-dashed, chain and solid curves represent D= 0.05, 0.5, 1.0, 1.5 and 2.0, respectively.
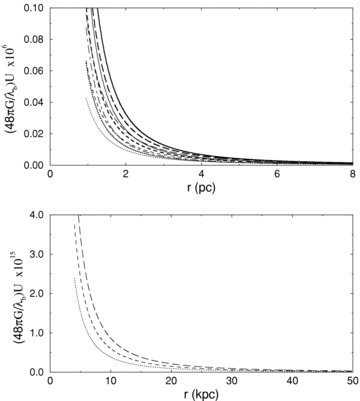
Plot for the variation of U versus r. The upper and lower panels correspond to short and long r behaviours. The dotted, dashed and long-dashed curves represent vφ= 200, 250 and 300 Km s−1, respectively. For all these, thin curves and thick curves correspond to D= 0.0 and D= 1.0, respectively. The chain, solid and thick solid curves, respectively, represent vφ= 200, 250 and 300 Km s−1 but for D= 2.0. In the lower panel, plots represent the case for D= 1.0 only because of results are not found significantly sensitive to D at long distances.
In this context, it can be observed that there is a striking similarity between Figs 5 and 6 of the present work under brane-world models with those of Rahaman et al. (2007) drawn for a global monopole field in the Brans–Dicke theory under the same equation (9). Actually, Rahaman et al. (2007) have shown by using Brans–Dicke theory that monopole could be the galactic dark matter in the spiral galaxies whereas, Guzman & Matos (2000) have proposed scalar fields as dark matter in the spiral galaxies.2 This immediately indicates the global monopole as one of the candidates for galactic dark
matter irrespective of the underlying theories. At the same time it seems that we get confirmation of dark matter not only from the brane-world model but also from Brans–Dicke theory. In this connection, it is asserted by Harko & Mak (2005) that ‘… despite more than 20 yr of intense experimental and observational effort, up to now no non-gravitational evidence for dark matter has ever been found …’.
We would like to put some comments on the properties of Weyl tensor which might be relevant here. It is already mentioned in the field theoretical part that Eij is due to the long-range gravitational degrees of freedom and is a projection of the bulk Weyl tensor on to the brane via Eμν=Cμανβnαnβ with C the five-dimensional Weyl tensor and the n vectors are five-dimensional unit normal vectors of the brane. It is also mentioned in connection to equation (4) that on the brane, we experience standard four-dimensional general relativity with the exception that the source of the four-dimensional Einstein tensor is augmented by higher order stress-energy effects and five-dimensional Weyl tensor gravitational terms. It is therefore highly probable, that if Randall–Sundrum models (Randall & Sundrum 1999a,b) are correct, the physical effects we attribute to unseen material (for example, dark matter and dark energy) are actually due to these extra source terms. Another point regarding the Weyl tensor is that the presence of Weyl stresses means that the matching conditions do not have a unique solution on the brane and hence knowledge of five-dimensional Weyl tensor is needed as a minimum condition for uniqueness. It is shown by Dadhich et al. (2000) that in the five-dimensional brane, the high-energy corrections to the energy density, together with the Weyl stresses from bulk gravitons, imply that on the brane the exterior metric of a static source is no longer the Schwarzschild metric.
There have been several studies addressing the issue of acceptable spherically symmetric vacuum solutions in brane-world scenarios (Visser & Wiltshire 2003; Harko & Mak 2004; Creek et al. 2006; Ponce de Leon 2007; Viznyuk & Shtanov 2007). It was explicitly demonstrated in these references how the brane-world equations provide a weaker requirement on the four-dimensional brane metric than the Einstein equations in four dimensions. Therefore, a more general class of solutions may be admitted in the brane-world picture than the Schwarzschild solution. Ponce de Leon demonstrated that the non-static situation differs from the static one by the extra requirement that T00=T11 at the matter-vacuum boundary. This requirement is sufficient to close the system of equations, yielding a Schwarzschild or Reissner–Nordström-like metric (where the ‘charge’ term arises from an integration constant) as possible exteriors for non-static systems. For the static system, he showed that no such restriction occurs at the boundary and therefore the vacuum solutions admit a much wider (infinitely many) possible vacua.
Here, we are not concerned with the form of the full five-dimensional metric and therefore it is not specified. Given a well-behaved four-dimensional metric, the bulk metric's existence as a solution of the bulk field equations is guaranteed by the Campbell–Maagard embedding theorem (Seahra & Wesson 2003; Wesson 2005).
However, in this context, we would like to make a point that global monopoles are a dark-matter candidate (with very strong restrictions) different to scalar fields.
AAU and SR are thankful to the authority of Inter-University Centre for Astronomy and Astrophysics, Pune, India for providing the Associateship programme under which a part of this work was carried out. We also thank the referee for his valuable suggestions, which have enabled us to improve the manuscript substantially.
REFERENCES



