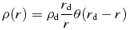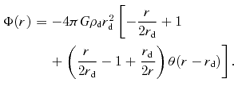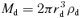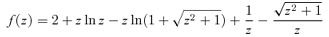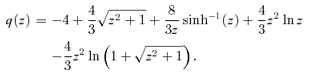Dynamical response to supernova-induced gas removal in spiral galaxies with dark matter halo Free

Abstract

1 INTRODUCTION

It is well known that the luminosity L of luminous spiral galaxies correlates tightly with their rotation velocity V_rot, as called the Tully–Fisher relation (hereafter TFR; Tully & Fisher 1977). The TFR is usually described as a power-law scaling relation L∝V^γ_rot, and the rms scatter of the TFR is smaller for optical passbands of longer wavelengths. In particular, the I-band TFR is significantly tight and its scatter is approximately as small as 0.4 mag (Willick et al. 1997; Kannappan, Fabricant & Franx 2002), with a power-law index γ≃ 3–3.5 (e.g. Pierce & Tully 1988; Sakai et al. 2000). Light at longer wavelengths from galaxies traces old late-type stars, unaffected by sporadic formation of young stars, and represents the mass of luminous matter. Thus, the tightness of the I-band TFR suggests the existence of some driving mechanism that depends on mass of galaxies in processes of their formation.

The current standard model of cosmology is the cold dark matter (CDM) model. Since the initial spectrum of density fluctuations has larger amplitudes for smaller scales in this model, the scenario of structure formation is hierarchical clustering, in the sense that smaller dark haloes cluster to form larger dark haloes hierarchically, thereby creating a scaling relation between mass M and circular velocity V_circ of dark haloes (Faber 1982; Blumenthal et al. 1984). High-resolution N-body simulations, based on a power spectrum P(k) ∝kⁿ with an index n=−2.5 appropriate for galaxy scales or reciprocal of wavenumber k⁻¹, have provided M∝V³_cir, reminiscent of the TFR if a constant mass-to-light ratio (M/L) is assumed (e.g. Navarro, Frenk & White 1997). Consequently, the CDM model naturally involves a TFR-like scaling relation as observed for luminous spiral galaxies, because a constant M/L is indeed known to be a good approximation to such galaxies (e.g. Faber & Gallagher 1979).

When studying the formation of galaxies originated from the growth of density fluctuations in the early Universe, however, it is also necessary to take into account the effects of star formation and supernova (SN) explosions in individual galaxies. In particular, dwarf galaxies have shallow gravitational potential wells, so that energy feedback from SN explosions significantly affects their evolution and hence scaling relations that follow. In a framework of monolithic collapse scenario of galaxy formation, several authors studied scaling relations for dwarf galaxies in two extreme cases, i.e. the dark matter dominated case in which dark halo dominates the gravitational potential (Dekel & Silk 1986), and the baryon-dominated case of self-gravitating galaxies without dark matter (Yoshii & Arimoto 1987).

Steinmetz & Navarro (1999) derived, for the first time by numerical simulations, the TFR for luminous spiral galaxies in the CDM model, using a method of N body and smoothed particle hydrodynamics (SPH) combined with star formation and SN feedback explicitly. They also showed that the star formation rate is regulated for M/L to be almost constant. However, the zero-point of the TFR turned out to differ from that observed, so that the simulated spiral galaxies were too faint to be consistent with observations at the same circular velocity. It was therefore pointed out that processes of star formation and SN feedback in current N-body/SPH simulations have to be improved (see also Governato et al. 2007; Portinari & Sommer-Larsen 2007).

Semi-analytic (SA) models of galaxy formation have been invented as a complementary approach to numerical simulations, in which complex processes such as star formation and SN feedback are simply modelled on galaxy scales. SA models have indeed succeeded in reproducing many observational results, for example, the luminosity function of galaxies as well as the TFR, by suppressing the formation of dwarf galaxies owing to SN feedback (Somerville & Primack 1999; Cole et al. 2000; De Lucia, Kauffmann & White 2004; Nagashima & Yoshii 2004; Kang et al. 2005; Croton et al. 2006).

Recent progress in observational techniques has enabled us to see much more properties of distant galaxies and faint dwarf galaxies beyond the limit of magnitude attained so far. In contrast to the success of SA models in accounting for luminous galaxies, they came to face a serious discrepancy between predicted and observed dynamical properties of dwarf galaxies, while reproducing their photometric properties quite well (e.g. Cole et al. 2000; van den Bosch 2002).

Here we would like to stress that the dynamical response to gas removal induced by SN explosions, which has been overlooked in most SA models, is unavoidable in dwarf, less massive galaxies. Nagashima & Yoshii (2003) formulated how the structure of spherical galaxies responds to SN-induced gas removal in a gravitational potential of dark halo, and Nagashima & Yoshii (2004) incorporated this effect into an SA model to show that many properties of elliptical galaxies, including the Faber–Jackson relation (Faber & Jackson 1976), can be reproduced to faint magnitudes of dwarf ellipticals. A more sophisticated SA model associated with high-resolution N-body cosmological simulations also provides a good agreement between predicted and observed properties of galaxies (Nagashima et al. 2005). Accordingly, as a natural extension of Nagashima & Yoshii's trial, it is worth investigating whether such a dynamical effect could also reproduce the observed TFR down to faint magnitudes in spiral galaxies.

In this paper, using the Kuzmin disc (Kuzmin 1952,1956) as a galaxy disc embedded in a spherical dark halo, we present in Section 2 the general formulation for the dynamical response in size and rotation velocity of discs. In Section 3 we examine such effect for several choices of density distribution of dark halo. In Section 4 we derive the resulting TFRs and disc size versus magnitude relations. In Section 5 we summarize the results of this paper. Detailed derivations of analytic expressions are given in Appendix A.

2 DYNAMICAL RESPONSE OF GALACTIC DISC IN DARK MATTER HALO

In this section, we formulate the dynamical response accompanied by SN feedback to a spiral galaxy consisting of baryons and dark matter. We consider a thin baryonic disc or the Kuzmin disc embedded in a non-rotating spherical dark halo whose density profile is either NFW, homogeneous or r⁻¹. We assume that the thin disc is axisymmetrical and rotation dominated with negligible velocity dispersions. Note that the density profile of the Kuzmin disc is more or less similar to the exponential disc except for the central region.

The gas of low angular momentum in an extended halo collapses towards the galaxy centre on a dynamical time-scale and dissipates the energy to cause a burst of star formation in the central region. On the other hand, the gas of higher angular momentum gradually falls on to a disc plane on a longer time-scale and settle on a circular annulus of the disc at the radius according to the value of angular momentum of the gas. This fallen gas is converted into stars to form a stellar disc.

If the kinetic energy, which is released by SNe following the star formation, exceeds the binding energy of the disc, the remaining gas is removed out of the disc. This disc dynamically recovers a final equilibrium. In general, the final state could be either a puffed-up disc where velocity dispersions dominate over the rotation, or a thin disc where the rotation remains to dominate with negligible velocity dispersions (Biermann & Shapiro 1979). In this paper, it is enough to consider only the latter, because we are primarily interested in scaling relations in spiral galaxies.

First, we consider that the gas removal occurs after all the material falls in to form the disc. In this case, the disc achieves a centrifugal equilibrium with the mass M_i and the angular momentum J_i as an initial state. Since the gas removal accompanies the simultaneous losses of mass and angular momentum, the disc should newly recover a centrifugal equilibrium with the mass M_f and the angular momentum J_f as a final state, depending not only on the amount of such losses ΔM (M_i−M_f) and ΔJ (J_i−J_f), but also on whether the time-scale of such losses is longer or shorter than the dynamical scale (Biermann & Shapiro 1979).

On the other hand, the gas removal may well occur while the material is still falling into the disc. In this case, only a part of the material falls in to form the disc and almost no gas removal occurs afterwards. The disc would then be settled in centrifugal equilibrium with the mass M_f and the angular momentum J_f throughout from the beginning. This situation is formally equivalent to the case such that the gas removal occurs on much shorter time-scale compared to the dynamical time-scale. Therefore, the related formula below in this section could also apply to the situation considered here.

2.1 Formulation

The kinetic energy T due to rotation, the gravitational self plus interaction potential energy W and the total angular momentum J of the Kuzmin disc of baryons in a dark halo are given by

1

2

and

3

respectively, where G is the gravitational constant and g is the constant dependent on density distribution, M is the mass, V is the characteristic rotation velocity and r is the characteristic radius. The subscripts ‘b’ and ‘d’ refer to the baryonic and dark matter components, respectively. The function f(z) has a form dependent on density distribution, and the argument z is a radius r_b normalized by r_d or z=r_b/r_d.

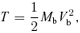
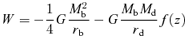
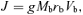
Hereafter, the quantities of baryons with the subscript ‘i’ in place of ‘b’ are designated as an initial state before the gas removal, and those with the subscript ‘f’ as a final state after the gas removal. Note that the quantities of dark matter with the subscript ‘d’ are assumed not to change throughout the gas removal.

First, we describe the initial state expressing the total energy of the disc as

4

provided that the virial equilibrium 2T_i=−W_i holds, and the angular momentum as

5

Next, assuming that the disc profile does not change just after the gas removal, we express the total energy as

6

Then, conserving this energy, the disc dynamically responds towards recovering a virial equilibrium as the final state:

7

and

8

We here consider an extreme approximation of impulsive mass-loss such that the gas removal is faster than the dynamical relaxation. From equations (4) and (7), we express the final quantities in terms of the initial quantities as

9

and

10

where z_i,f=r_i,f/r_d and m_i,f=M_i,f/M_d.

We consider another extreme approximation of adiabatic mass-loss such that the gas removal is slower than the dynamical relaxation. The total change from the initial to final states is a sum of consecutive infinitesimal changes. Substituting m_f=m_i+ dm and z_f=z_i+ dz in equation (9) and linearizing it, we obtain

11

where the subscript ‘i’ is omitted for simplicity. The first term comes from the self-gravitating baryons alone, and the second term from the gravitational interaction of baryons with dark halo. Solving this differential equation, we obtain

12

where

13

and C is an integration constant or an adiabatic invariant here. Then we express the final quantities in terms of the initial quantities for the adiabatic mass-loss:

14

together with the same form of equation (10) for the rotation velocity.

It is apparent from equations (9),(10) and (14) that the ratios of dynamical quantities r_f/r_i(=z_f) and V_f/V_i are obtained when the ratios of m_i(=M_i/M_d), z_i(=r_i/r_d) and m_f/m_i(=M_f/M_i) are given. In other words, given m_i and z_i, the ratios of r_f/r_i and V_f/V_i are formally written as a function of M_f/M_i:

15

and

16

For the impulsive and adiabatic approximations of mass-loss, the change of specific angular momentum is given by

17

from equations (5) and (8). When the gas removal occurs from the central region of the disc where the mass is concentrated but the rotation velocity is small, (J/M)_f/(J/M)_i should exceed unity. On the other hand, when the gas removal occurs from the outer region of the disc where the mass is small but the rotation velocity is large, (J/M)_f/(J/M)_i is less than unity. Therefore we use the value of (J/M)_f/(J/M)_i to discuss where in the disc the site of efficient gas removal is located.

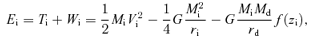
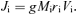
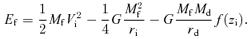
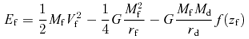
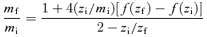
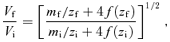
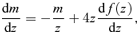
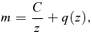
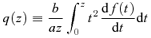
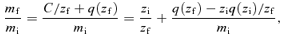
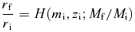
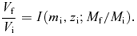
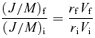
2.2 Limiting cases

In this subsection, before studying more general gas removal, we examine two limiting cases of M_i/M_d≫ 1 and M_i/M_d≪ 1.

In the baryon-dominated case of M_i/M_d≫ 1, we have for the impulsive mass-loss

18

and for the adiabatic mass-loss

19

The fact that the value of (J/M)_f/(J/M)_i is always larger than unity for the impulsive mass-loss suggests that the gas removal should preferentially occurs from the central region of the disc, whereas the fact of (J/M)_f/(J/M)_i= 1 for the adiabatic mass-loss yields that the same fraction of mass is lost across the disc over its entire radial range.

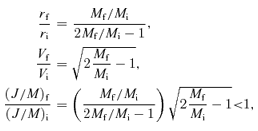
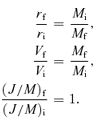
In the dark matter dominated case of M_b/M_d≪ 1, the disc size and rotation velocity of the initial disc hardly change during the gas removal, because the dominant gravitational potential of dark halo allows almost no response in structure and dynamics of the disc.

3 DYNAMICAL RESPONSE ON DISC SIZE AND ROTATION VELOCITY

In this section, based on the analytic expression of f(z) for the Kuzmin disc embedded in a dark halo with the NFW, homogeneous and 1/r density distributions, we calculate the strength of dynamical response for r_f/r_i, V_f/V_i and (J/M)_f/(J/M)_i as a function of M_f/M_i for several combinations of m_i= 0.05–0.2 and z_i= 0.05–0.2.

The range of m_i explored is based on the following consideration. We assume that all the baryonic matter is distributed in the same way as the dark matter initially and falls in to make up the disc. Then the upper bound of m_i is set by the current estimate of density ratio ρ_b/ρ_d≃ 0.2 in the Universe. Considering a possibility that not all of the baryonic matter falls into the initial disc, we rather arbitrarily adopt a range of m_i= 0.05–0.2 for the initial mass ratio.

The range of z_i=r_i/r_d is based on the following consideration. From the observed luminosity profile and rotation curve of dwarf spirals, the scale radius of dark halo of 10⁹–10¹⁰M_⊙ is estimated as (1.5–4) h⁻¹kpc, and the corresponding rotation velocity is estimated as 40–70 km s⁻¹ (Burkert 1995), where h is the Hubble constant H₀ defined as h=H₀/100 km s⁻¹Mpc⁻¹. In addition, the radial exponential scalelength of such dwarf spirals is estimated as (0.5–2) h⁻¹kpc (Pildis et al. 1997; Schombert et al. 1997), thus giving the scale ratio of 0.3–0.5 as observed in the local universe. Regarding this ratio as obtained after the initial disc expands by a factor of several due to the gas removal (see below), we adopt a range of z_i= 0.05–0.2 for the initial scale ratio.

3.1 Kuzmin disc in the NFW halo

We examine the dynamical response to the Kuzmin disc embedded in the NFW halo. The surface mass density distribution of the Kuzmin disc is given by

20

with the gravitational potential

21

As for the NFW halo, the density distribution is given by

22

with the gravitational potential

23

where c is a concentration parameter. Since the essential characteristic length of the NFW halo is r_d/c instead of r_d, we hereafter define z=r_b/(r_d/c).

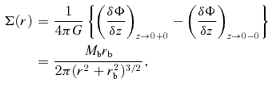
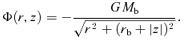
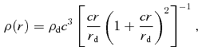
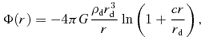
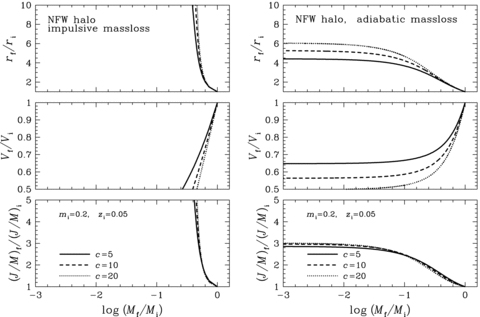
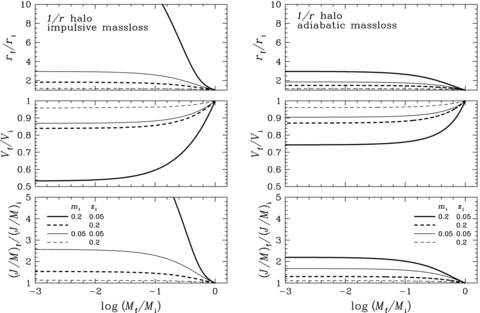
Fig. 1 shows the dependence of dynamical response on m_i and z_i with c= 10 for the impulsive mass-loss in the left-hand column, and for the adiabatic mass-loss in the right-hand column. In each of the columns, the strength of dynamical response for r_f/r_i, V_f/V_i and (J/M)_f/(J/M)_i is shown in order from top to bottom panels as a function of M_f/M_i for several combinations of m_i and z_i.

Figure 1

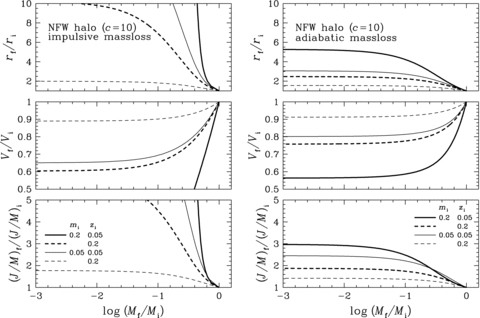
Dynamical response of the Kuzmin disc embedded in the NFW halo. The results shown are the dependence of dynamical response on m_i=M_i/M_d and z_i=r_i/(r_d/c) with c= 10 for the impulsive mass-loss in the left-hand column, and for the adiabatic mass-loss in the right-hand column. In each of the columns, the strength of dynamical response for r_f/r_i (top panel), V_f/V_i (middle panel) and (J/M)_f/(J/M)_i (bottom panel) is plotted against the final to initial disc mass ratio M_f/M_i for various combinations of m_i and z_i.

Open in new tabDownload slide

It is clear from this figure that the dynamical response monotonically increases as M_f/M_i decreases and asymptotically reaches a constant level at M_f/M_i≤ 0.1. Furthermore, given M_f/M_i, the dynamical response is stronger for increasing the ratio of surface mass densities of initial disc and dark halo projected on to the disc plane or m_i/z²_i. Such a tendency holds irrespective of either the impulsive or adiabatic mass-loss. However, comparing the left- and right-hand columns, we find that the dynamical response is greatly suppressed for the adiabatic mass-loss, in particular, even by a factor of 10 or so within the range of m_i/z²_i and M_i/M_d considered.

Fig. 2 shows the dependence of dynamical response on c with m_i= 0.2 and z_i= 0.05. There is a tendency such that the dynamical response is stronger for increasing c, or equivalently decreasing r_i/r_d because z_i=r_i/(r_d/c) is fixed here.

Figure 2

Dynamical response of the Kuzmin disc embedded in the NFW halo. Same as in Fig. 1, but for the dependence of dynamical response on the concentration parameter c with m_i= 0.2 and z_i=r_i/(r_d/c) = 0.05.

Open in new tabDownload slide

The specific angular momentum after the gas removal (J/M)_f is always larger than that before the gas removal (J/M)_i, which suggests that the gas removal occurs from the central region of the disc where specific angular momentum is small. This is the condition that the disc should remain thin and rotation dominated before and after the gas removal.

3.2 Dependence on dark matter distribution

We examine how the Kuzmin disc responds depending on the density distribution of dark halo. Here we consider the homogeneous and 1/r density distributions in a spherical halo truncated at r=r_d:

24

and

25

respectively, where θ(x) is the Heaviside step function.

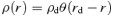
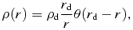
The results for these two distributions are shown in Figs 3 and 4, respectively. We see from these figures that, given m_i and z_i, the dynamical response for the homogeneous density distribution is stronger than that for the 1/r density distribution with which dark matter is more confined inside the characteristic radius of the initial disc r_i.

Figure 3

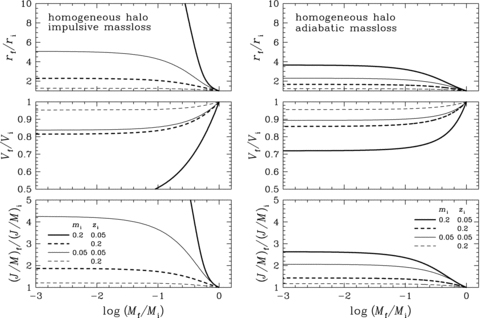
Dynamical response of the Kuzmin disc embedded in the dark halo. Same as in Fig. 1, but for the truncated spherical halo with the homogeneous density distribution.

Open in new tabDownload slide

Figure 4

Dynamical response of the Kuzmin disc embedded in the dark halo. Same as in Fig. 1, but for the truncated spherical halo with the 1/r density distribution.

Open in new tabDownload slide

We also see that, given m_i and z_i, the dynamical response for the NFW halo (Fig. 1) is even stronger than those considered here. This is because, adopting c= 10 in the definition of z_i=r_i/(r_d/c), the NFW halo is more extended beyond the truncation radius r_d, thereby dark matter is less confined inside the initial disc radius r_i as far as the value of m_i is fixed.

Furthermore, the dynamical response for the impulsive mass-loss is much stronger than that for the adiabatic mass-loss, which is also the case of the NFW halo (Figs 1 and 2).

3.3 Dependence on baryonic matter distribution

It is instructive here to additionally examine the dynamical response of an exponential disc for which the surface mass density distribution is given by

26

where r_s is the scalelength of the disc. This choice of Σ(r), which allows no analytic expression of W, is known to be more appropriate to spiral galaxies than the Kuzmin disc.

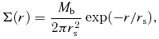
For the purpose of comparison, we equate the effective radius of the exponential disc to that of the Kuzmin disc, or ⁠. Then, the dynamical response of the exponential disc embedded in the NFW halo is calculated by numerically integrating W, and the result is shown in Fig. 5 in the same way as in Fig. 1.

Figure 5

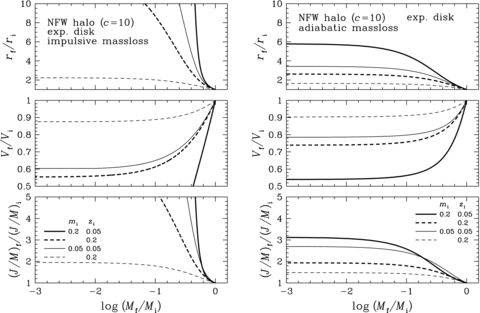
Dynamical response of the exponential disc embedded in the NFW halo. The results are shown in the same way as in Fig. 1, for direct comparison with the results for the Kuzmin disc. We note that the scalelength r_s of the exponential disc is related to r_b in z via ⁠.

Open in new tabDownload slide

It is evident from these figures that, given m_i and z_i, the dynamical response of the exponential disc is only slightly stronger than that of the Kuzmin disc. Namely the difference is very small for the impulsive mass-loss and is much smaller for the adiabatic mass-loss. This is understood, because the Kuzmin disc is more or less similar to the exponential disc except for the central region. Therefore, without loss of generality, we use the Kuzmin disc in Section 4 for the study of dynamical response in spiral galaxies over a full range of magnitude observed.

4 SCALING RELATIONS MODIFIED BY DYNAMICAL RESPONSE

In this section, using the Kuzmin disc, we investigate the effects of dynamical response in predicting the rotation velocity versus magnitude relation (TFR) and the disc size versus magnitude relation.

We begin with the assumption that dark matter haloes in the CDM universe obey the scaling relations (e.g. Navarro et al. 1997)

27

The baryonic matter in an individual halo falls in to form the galaxy disc and a part of such fallen gas goes back to the halo region owing to the gas removal induced by SNe in the disc. Cosmological N-body/SPH simulations have shown that along this scheme of galaxy formation the above scaling relations of dark matter haloes almost hold in bright spiral galaxies where the effect of SN feedback is minimal (e.g. Steinmetz & Navarro 1999). Consequently, in this paper, we assume that initial discs before the gas removal obey the same scaling relations as dark matter haloes, instead of entering into detailed discussions of physical processes involved. This assumption accords with our use of m_i=M_i/M_d and z_i=r_i/r_d as constant parameters, yielding

28

where the subscript ‘i’ stands for the quantities of initial discs before the gas removal as in previous section.

Next, we express the quantities of final discs after the gas removal, to which the subscript ‘f’ is attached. Considering that disc mass is a sum of remaining gas and stars M_i=M_gas+M_* before the gas removal and is left with stars M_f=M_* after the gas removal, and introducing the strength parameter for SN feedback β≡M_gas/M_* for which β≪ 1 for massive and normal galaxies and β≫ 1 for dwarf galaxies, we obtain

29

Following the definition in equation (10) of Nagashima et al. (2005), we set

30

where V_hot is an effective SN-feedback strength in units of velocity, and α_hot is a constant power index.

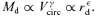
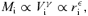
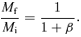
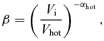
Our analysis below confines to the NFW halo, because the homogeneous and 1/r density distributions are of academic interest only. Values of the parameters used are V_hot= 150 km s⁻¹ and α_hot= 2 and 4 for the SN-feedback strength, while m_i= 0.2 and z_i= 0.05, 0.1 and 0.2 for the initial disc.

4.1 Tully–Fisher relation

Theoretical TFR or the V_f–M_f relation is obtained by a set of the following equations:

31

and

32

where I(a,b;x) is given in equation (16).

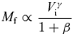
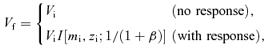
This relation is compared with the data of rotation velocity V_rot and absolute magnitude M_I of spiral galaxies in the I band taken from the table of Mathewson, Ford & Buchhorn (1992), and the results are shown in Fig. 6 for α_hot= 2 and in Fig. 7 for α_hot= 4, together with the data. In each of these figures the left- and right-hand panels are for the impulsive and adiabatic mass-losses, respectively.

Figure 6

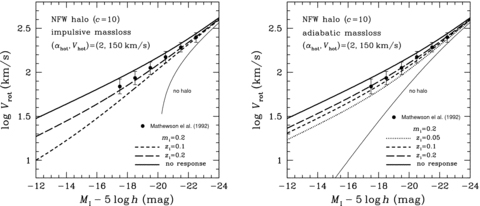
Theoretical I-band Tully–Fisher relations with and without dynamical response of the Kuzmin disc embedded in the NFW halo. The results with α_hot= 2 are shown by various thick lines in the left-hand panel for the impulsive mass-loss and in the right-hand panel for the adiabatic mass-loss, while the result with no halo is shown by thin line only for the academic purpose of comparison. Filled circles represent the data taken from the table of Mathewson et al. (1992). V_rot is the rotation velocity, M_I is the absolute I magnitude and h is the Hubble constant H₀ defined as h=H₀/100 km s⁻¹Mpc⁻¹.

Open in new tabDownload slide

Figure 7

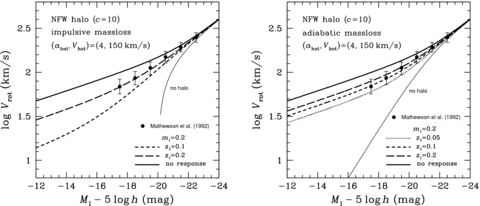
Theoretical I-band Tully–Fisher relations with and without dynamical response of the Kuzmin disc embedded in the NFW halo. Same as in Fig. 6, but for α_hot= 4.

Open in new tabDownload slide

Here, assuming a constant baryonic mass to I-band light ratio M_i/L_I and equating V_i to the observed rotation velocity V_rot for bright galaxies, we have set the power index γ= 3 in equation (31) by adjusting the V_f–M_f relation along the horizontal axis in Figs 6 and 7 to fit to the observed TFR in the bright end. Our setting of γ= 3 is consistent with the scaling relation of dark haloes obtained by N-body CDM simulations (Navarro et al. 1997) as well as the scaling relation of spiral galaxies obtained by N-body/SPH CDM simulations (Steinmetz & Navarro 1999).

We see from these figures that the V_f–M_f relations with no dynamical response and with no dark halo deviate significantly from the faint data, while the dynamical response with dark halo improves the fit to the data. In particular, the V_f–M_f relations that well agree with the data over the full range of M_I observed are those of z_i= 0.2 and α_hot= 2–4 for the impulsive mass-loss, and those of z_i= 0.1–0.2 and α_hot= 2 as well as z_i= 0.2 and α_hot= 4 for the adiabatic mass-loss.

4.2 Disc size versus magnitude relation

Theoretical disc size versus magnitude relation or the r_f–M_f relation is obtained by a set of the following equations:

33

and

34

where H(a,b;x) is given in equation (15). Here, V_i(r_i) is obtained from the relation of (V_i/V_hot)^γ= (r_i/r_hot)^ε according to equation (28), where r_hot corresponding to V_hot is obtained from the rotation velocity versus magnitude relation and the disc size versus magnitude relation. So far we have used the characteristic radius r_b to represent the disc size. 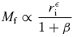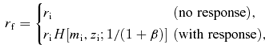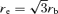However, we hereafter use the effective radius of the Kuzmin disc to be consistent with the usual observational definition.

This relation is then compared with the data of effective disc radius r_e and absolute magnitude M_B of spiral galaxies in the B band taken from the table of Impey et al. (1996), and the results are shown in Fig. 8 for α_hot= 2 and in Fig. 9 for α_hot= 4, together with the data. In each of these figures the left- and right-hand panels are for the impulsive and adiabatic mass-losses, respectively.

Figure 8

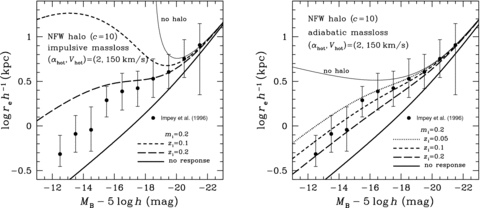
Theoretical B-band disc size versus absolute magnitude relations with and without dynamical response of the Kuzmin disc embedded in the NFW halo. The results with α_hot= 2 are shown by various thick lines in the left-hand panel for the impulsive mass-loss and in the right-hand panel for the adiabatic mass-loss, while the result with no halo is shown by thin line only for the academic purpose of comparison. Filled circles represent the data taken from the table of Impey et al. (1996). r_e is the effective disc radius, M_B is the absolute B magnitude and h is the Hubble constant H₀ defined as h=H₀/100 km s⁻¹Mpc⁻¹.

Open in new tabDownload slide

Figure 9

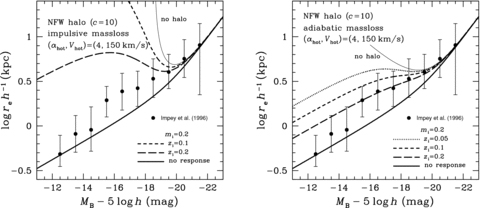
Theoretical B-band disc size versus absolute magnitude relations with and without dynamical response of the Kuzmin disc embedded in the NFW halo. Same as in Fig. 8, but for α_hot= 4.

Open in new tabDownload slide

In order to avoid any systematics arising from our use of the velocity data in the I band and the size data in the B band, we first transform the theoretical relation from the I band to the B band by applying the empirical formula M_B= 0.86M_I−1.31, then we compare it with the data of r_e and M_B in the B band. Such a transformation formula is obtained by eliminating V_rot from the observed TFRs in the B and I bands (Pierce & Tully 1988), and gives B−I≃ 1.2 for dwarf galaxies with M_I≃−18 + 5 log h, and B−I≃ 1.6 for bright galaxies with M_I≃−21 + 5 log h. These colours agree well with the observed colours 〈B−V〉= 0.4–0.5 and 〈V−I〉= 0.7–0.8 for dwarf galaxies (Schombert et al. 1995,1997; Makarova 1999; O'Neil, Bothun & Schombert 2000), and with the synthetic colours of 〈B−V〉= 0.5–0.6 and 〈V−I〉= 1.0–1.1 for bright Sb and Sc galaxies from table 3a of Fukugita, Shimasaku & Ichikawa (1995).

Here, applying the above transformation formula and allowing a small, constant offset of log r_e(B) − log r_e(I) between the effective radii in the B and I bands, we have set the power index ε= 2 in equation (33) by adjusting the r_f–M_f relation along the horizontal and vertical axes in Figs 8 and 9 to fit to the observed disc size versus magnitude relation in the bright end. Our setting of ε= 2 is consistent with the scaling relation of dark haloes predicted by a power-law spectrum of initial density fluctuations with an index n=−2 which is a reasonable approximation to the CDM spectrum on galaxy scales (Navarro et al. 1997).

We find that the r_f–M_f relation is much more sensitive to the parameters than the V_f–M_f relation, and many of the predicted relations cannot reproduce the faint data at all. In particular, all the relations considered for the impulsive mass-loss should be rejected by the data. On the other hand, for the adiabatic mass-loss, the relations of z_i= 0.1–0.2 and α_hot= 2 agree with the data over the full range of M_B observed, and the relation of z_i= 0.2 and α_hot= 4 agrees with the data brighter than M_B=−16 only.

5 RESULTS

Current SA models, where the mass-loss from individual galaxies by SN feedback is taken into account without considering dynamical response, are known to overpredict the rotation velocity of dwarf spiral galaxies (thick solid lines in Figs 6 and 7) and at the same time underpredict their disc size (thick solid lines in Figs 8 and 9). We could easily imagine that such discrepancies are resolved by the dynamical response of a virialized system associated with weakening of the gravitational potential, most likely owing to the mass-loss that we consider in this paper.

In fact, there exist several solutions with dynamical response that account for the observed relation between rotation velocity and absolute I magnitude (Section 4.1) and the observed relation between disc size and absolute B magnitude (Section 4.2). However, these two relations can only be reproduced simultaneously in a limited range of parameter space for the adiabatic mass-loss, namely m_i= 0.2 and z_i= 0.1–0.2. For the SN feedback, the weak case of α_hot= 2 is preferable to the strong case of α_hot= 4.

Such an almost unique solution with α_hot= 2 for the adiabatic mass-loss gives the final ratio of z_f= 0.3–0.4 for dwarf galaxies. This value of z_f agrees with observations in the local universe (see Section. 3). The value of (J/M)_f/(J/M)_i beyond unity suggests that the mass-loss does not accompany the loss of angular momentum.

The results above are obtained for dark haloes with a concentration parameter of c= 10, but it is known that c is predicted to vary from 10 for large haloes to significantly larger values of 20–30 for small haloes (Bullock et al. 2001b; Macció et al. 2007). It is then worth examining this dependence with other parameters fixed. The results by varying c for the TFR and the disc size versus magnitude relation are shown in Figs 10 and 11, respectively. As seen from these figures, contrary to the case of impulsive mass-loss, the variation in c does not make much difference in the results for the adiabatic mass-loss, which validates our conclusion in favour of adiabatic mass-loss, irrespective of concentration of the mass included in dark haloes.

Figure 10

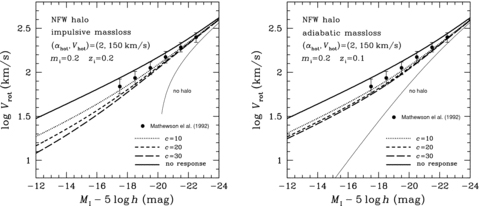
Theoretical I-band Tully–Fisher relations with and without dynamical response of the Kuzmin disc embedded in the NFW halo. Same as in Fig. 6, but for the dependence on the concentration parameter c. The results are shown by various thick lines in the left-hand panel for the impulsive mass-loss and in the right-hand panel for the adiabatic mass-loss.

Open in new tabDownload slide

Figure 11

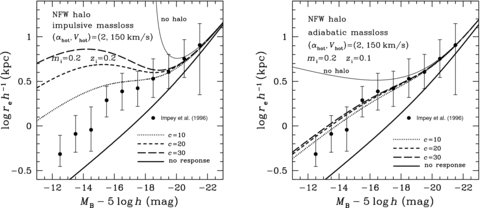
Theoretical B-band disc size versus absolute magnitude relations with and without dynamical response of the Kuzmin disc embedded in the NFW halo. Same as in Fig. 8, but for the dependence on the concentration parameter c. The results are shown by various thick lines in the left-hand panel for the impulsive mass-loss and in the right-hand panel for the adiabatic mass-loss.

Open in new tabDownload slide

6 DISCUSSION

6.1 Losses of mass and angular momentum

The angular momentum distribution in dark haloes is well established theoretically based on the CDM model (e.g. Catelan & Theuns 1996; Nagashima & Gouda 1998). It is natural to assume that the baryonic components acquire the same amount of specific angular momentum as that of their host haloes, because the cosmic tidal field provides the angular momentum to dark matter and baryons in the same manner (White 1984). This assumption has been a basis of most theories of galaxy formation.

From observations of dwarf spiral galaxies, van den Bosch, Burkert & Swaters (2001) found that their mean (or total) specific angular momenta are very similar to those of their host haloes predicted by those theories. Moreover they found that the disc to halo mass ratio is smaller than the baryon fraction in the Universe. This means that only a part of baryons forms discs whereas it keeps an amount of specific angular momentum similar to that of host haloes. They also examined the specific angular momentum distribution in individual haloes, and surprisingly found that it is inconsistent with theoretical prediction by Bullock et al. (2001a) based on high-resolution N-body simulations.

Secondly, the observed surface density distribution of dwarf spiral galaxies is described as an exponential distribution (e.g. Mathewson et al. 1992), different from that expected from the CDM model which provides much more centrally concentrated discs when compared with the exponential distribution. This cannot be solved even if SN feedback is simply considered (van den Bosch 2001).

One possible solution to the above discrepancies should be obtained by considering the mass-loss from the central region of discs, where the gas should have the specific angular momentum lower than that in the outer region. SN feedback driving the mass-loss without the loss of angular momentum leads discs to increasing their specific angular momentum, i.e. (J/M)_f/(J/M)_i > 1. This situation is consistent with that considered in this paper, as shown in the previous section.

So far we have assumed rotation-dominated discs throughout gas removal. With this assumption, the specific angular momentum always increases after the mass-loss, yielding (J/M)_f/(J/M)_i > 1. On the other hand, the transformation of rotation-dominated discs to velocity dispersion dominated discs, which is the puff-up transformation, leads discs to decreasing the specific angular momentum, yielding (J/M)_f/(J/M)_i < 1 (Biermann & Shapiro 1979). This situation should occur when the gas in the outer region is removed where the specific angular momentum is large. Such a way of gas removal would be caused by the tidal stripping in clusters of galaxies (e.g. Gunn & Gott 1972; Fujita & Nagashima 1999; Okamoto & Nagashima 2003). Biermann & Shapiro (1979) proposed that this mechanism should be of lenticular galaxy formation. If so, the fraction of S0 galaxies in clusters will be higher than that in fields, and the rotation velocity of dwarf galaxies in clusters will be systematically lower than that in fields. This should be observationally clarified in future.

6.2 Density profiles of dark haloes

We have assumed three types of density profiles of dark haloes, such as the NFW profile with an inner slope of −1 and an outer slope of −3 (equation 22), and two power-law profiles with a slope of 0 (homogeneous) and −1 (r⁻¹).

The NFW profile is suggested by N-body simulations, and many authors claim that the inner slope will become even steeper after the condensation of baryons owing to the cooling (Blumenthal et al. 1986), which is called as the adiabatic contraction (but see Sellwood & McGaugh (2005) for the effects of random motions). In fact, this implicitly assumes that the cooling time-scale is longer than the relaxation time-scale for dark haloes to settle into the NFW profile, i.e. baryons cool and shrink after virialization. On galaxy scales, however, this would not be the case. The cooling time-scale is much shorter than the dynamical time-scale, and the relaxation time-scale is similar to or longer than the dynamical time-scale. Thus it is not unnatural to assume that a mixture of dark matter and cooled baryons virializes. In this case, there would be galaxy discs within dark haloes with the NFW profile, without undergoing the adiabatic contraction. This might be an opposite limiting case to the adiabatic contraction, but recent X-ray observation of the intracluster medium has found that there is no evidence of contraction of the dark halo (Zappacosta et al. 2006). Since the central cD galaxy is massive enough to suppress the SN feedback, we do not need to expect the expansion due to dynamical response to SN-induced gas removal. Thus it is possible to say that a simple assumption of adiabatic contraction does not work in reality. This should justify our use of the NFW profile for dark haloes that surround galaxy discs. To clarify this, of course, high-resolution hydrodynamical simulations including the gas cooling processes are required (e.g. Gnedin et al. 2004).

6.3 Hierarchical formation of galaxies

In Section 4, our results of dynamical response to SN-induced gas removal within dark haloes are applied to scaling relations for galaxies, under the assumption that simple scalings among mass, velocity and size of baryonic components have been set up before the gas removal. It is reasonable to consider that these are inferred from observations of scaling relations for massive galaxies where SN feedback is not effective owing to their deep gravitational potential wells.

This seems to be somewhat in contrast to the approach of e.g. van den Bosch (2001), in which the direction of angular momentum vector is assumed to be invariant. However, it has been shown that the direction can be moved by contiguous accretion of dark matter (Nagashima & Gouda 1998; Saitoh & Wada 2004). Therefore, it is not assured that the specific angular momentum of discs is similar to that of host haloes averaged over whole regions.

We thus believe that it is reasonable to use the scaling relations for massive galaxies as the initial state for the dynamical response to gas removal.

7 SUMMARY

We have analysed the dynamical response to SN-induced gas removal on rotation velocity and disc size of spiral galaxies, explicitly taking into account the underlying gravitational potential wells made by dark matter. This is an extension of Nagashima & Yoshii (2003) in which spherical galaxies were considered, but for thin discs in spherical dark haloes to describe spiral galaxies realistically. Similarly, expansion of discs decreases their rotation velocity and increases their size owing to the dynamical response to gas removal even within dark haloes. As shown in Section 3, the dynamical response provides unavoidable effects on the evolution of spiral galaxies, particularly on dwarf spiral galaxies because of their shallow gravitational potential wells.

We have examined the effects of dynamical response on scaling relations among mass, rotation velocity and disc size of spiral galaxies. Since it is complicated to make such relations within a framework of hierarchical formation scenario of galaxies as discussed in Section 6, we use scaling relations which massive galaxies satisfy as the initial state before the gas removal. The SN-induced gas removal decreases the mass particularly of dwarf galaxies, thus distorting their scaling relations significantly. Such a distortion in the TFR as well as the disc size versus magnitude relation has been pointed out by many papers working on SA models of galaxy formation (e.g. Cole et al. 2000; Nagashima & Yoshii 2004; Nagashima et al. 2005), in which the dynamical response on spiral galaxies is not taken into account. We have shown that the dynamical response considered in this paper is able to reproduce the scaling relations as observed.

The hierarchical clustering scenario provides complicated galaxy formation processes. There are many physical processes such as radiative gas cooling, star formation and SN feedback, within merging dark haloes. Furthermore, while the gas removal occurs mostly due to SN feedback in massive galaxies, other processes including photoheating by the UV background may unlikely scale the same way in dwarf galaxies (Nagashima, Gouda & Sugiura 1999; Sommerville 2002; Benson et al. 2003; Hoeft et al. 2006). In addition, the formation history is also complicated. For example, discs accrete the gas which is once expelled from galaxies. It means that discs get bigger even after the dynamical response has exerted upon them. Then, luminous discs tend to cause large extinction by dust, which would bend the TFR. To investigate the observed properties of galaxies, therefore, we need to fully incorporate the effects of dynamical response into realistic models of galaxy formation like our SA models. We will study the physical origin of scaling relations including the TFR in more realistic situations in a forthcoming paper.

This work was supported in part by the Grant-in-Aid for the Scientific Research Fund (17104002 and 18749007) of the Ministry of Education, Culture, Sports, Science and Technology of Japan, and by a Nagasaki University president's Fund grant. HK is supported by the Japan Society for the Promotion of Science for Young Scientists (1589).

REFERENCES

Appendix

APPENDIX A: GRAVITATIONAL POTENTIAL ENERGY OF TWO-COMPONENT SYSTEM

In this section we provide analytic expressions of f(z) and q(z) for the gravitational interaction potential energy of the Kuzmin disc of baryons embedded in various density distributions of dark matter halo.

A1 The NFW dark halo

The NFW density distribution and the corresponding gravitational potential are given, respectively, by

(A1)

and

(A2)

Then, we obtain the total mass of dark halo

(A3)

and the analytic expression of the following function:

(A4)

For this case, we cannot obtain the exact analytic expression of q(z). Instead, we obtain an approximate expression of q(z) around z= 0 as follows:

(A5)

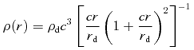
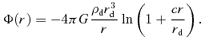
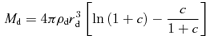
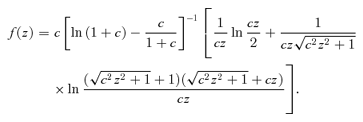
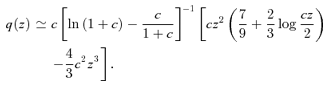
A2 The homogeneous dark halo

The homogeneous density distribution and the corresponding gravitational potential are given, respectively, by

(A6)

and

(A7)

Then, we obtain the total mass of dark halo

(A8)

and the analytic expressions of the following functions:

(A9)

and

(A10)

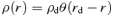
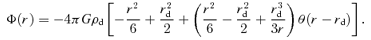
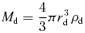
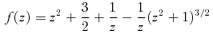
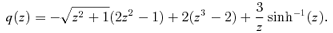
A3 The r⁻¹ profile dark halo

The 1/r density distribution and the corresponding gravitational potential are given, respectively, by

(A11)

and

(A12)

Then, we obtain the total mass of dark halo

(A13)

and the analytic expressions of the following functions:

(A14)

and

(A15)