-
PDF
- Split View
-
Views
-
Cite
Cite
D. Lynden-Bell, S. Jin, Analytic central orbits and their transformation group, Monthly Notices of the Royal Astronomical Society, Volume 386, Issue 1, 1 May 2008, Pages 245–260, https://doi.org/10.1111/j.1365-2966.2008.13018.x
Close - Share Icon Share
Abstract
A useful crude approximation for Abelian functions is developed and applied to orbits. The bound orbits in the power-law potentials A r−α take the simple form (ℓ/r)k= 1 +e cos (mφ), where k= 2 −α > 0 and ℓ and e are generalizations of the semi-latus-rectum and the eccentricity. m is given as a function of ‘eccentricity’. For nearly circular orbits m is  , while the above orbit becomes exact at the energy of escape where e is 1 and m is k. Orbits in the logarithmic potential that gives rise to a constant circular velocity are derived via the limit α→ 0. For such orbits, r2 vibrates almost harmonically whatever the ‘eccentricity’. Unbound orbits in power-law potentials are given in an appendix. The transformation of orbits in one potential to give orbits in a different potential is used to determine orbits in potentials that are positive powers of r. These transformations are extended to form a group which associates orbits in sets of six potentials, e.g. there are corresponding orbits in the potentials proportional to r, r−2/3, r−3, r−6, r−4/3 and r4. A degeneracy reduces this to three, which are r−1, r2 and r−4 for the Keplerian case. A generalization of this group includes the isochrone with the Kepler set.
, while the above orbit becomes exact at the energy of escape where e is 1 and m is k. Orbits in the logarithmic potential that gives rise to a constant circular velocity are derived via the limit α→ 0. For such orbits, r2 vibrates almost harmonically whatever the ‘eccentricity’. Unbound orbits in power-law potentials are given in an appendix. The transformation of orbits in one potential to give orbits in a different potential is used to determine orbits in potentials that are positive powers of r. These transformations are extended to form a group which associates orbits in sets of six potentials, e.g. there are corresponding orbits in the potentials proportional to r, r−2/3, r−3, r−6, r−4/3 and r4. A degeneracy reduces this to three, which are r−1, r2 and r−4 for the Keplerian case. A generalization of this group includes the isochrone with the Kepler set.
1 INTRODUCTION
Since schooldays when we encountered the rigid pendulum, most of us have been frustrated by our inability to integrate in elementary terms Abelian expressions of the form  , where S(u) has simple zeros at ua and up≥ua but is not quadratic. In practice S usually depends linearly or quadratically on parameters which we shall call ɛ and h, and its zeros up and ua depend on ɛ and h often in quite complicated ways. In Appendix A we relieve this frustration by showing how for each pair of ua and up, S may be replaced at lowest order by a quadratic function with the same zeros and the integral may be approximately evaluated parametrically via perturbation theory.
, where S(u) has simple zeros at ua and up≥ua but is not quadratic. In practice S usually depends linearly or quadratically on parameters which we shall call ɛ and h, and its zeros up and ua depend on ɛ and h often in quite complicated ways. In Appendix A we relieve this frustration by showing how for each pair of ua and up, S may be replaced at lowest order by a quadratic function with the same zeros and the integral may be approximately evaluated parametrically via perturbation theory.
We do not have to solve S(ɛ, h, u) for its zeros up and ua. Instead we regard up and ua as parameters and then easily find the ɛ(ua, up) and h(ua, up) to which they correspond. The process of replacing S by a different quadratic function for each pair of zeros up and ua we call quadrating (after the old verb ‘to quadrate’ which means ‘to make square’). Surely using ‘quadrate’ to mean ‘to make quadratic’ is not too great an extension! As the simple, though crude, method developed can be applied to a far wider class of problems than those encountered here, we have mentioned it first in Section 1.
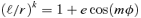
 , then r=r(mφ) is an orbit of angular momentum m h under the central force
, then r=r(mφ) is an orbit of angular momentum m h under the central force 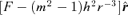 . Newton also pointed out that r(t) was the same for both orbits, so, if the new orbit were viewed from axes revolving at the rate
. Newton also pointed out that r(t) was the same for both orbits, so, if the new orbit were viewed from axes revolving at the rate  , then the two orbits would have the same shape. But note that
, then the two orbits would have the same shape. But note that  is not a constant rotation rate, but speeds up when r is small and slows down when r is large. When we view the orbit from axes that rotate uniformly at the same mean rate
is not a constant rotation rate, but speeds up when r is small and slows down when r is large. When we view the orbit from axes that rotate uniformly at the same mean rate 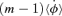 , the orbits can have very different shapes involving figures of eight for the more eccentric ones (Lynden-Bell & Lynden-Bell 1995).
, the orbits can have very different shapes involving figures of eight for the more eccentric ones (Lynden-Bell & Lynden-Bell 1995).Recently in a fine paper, Struck (2006) showed that orbits of moderate or low eccentricity in logarithmic or power-law potentials with or without cores were well approximated by analytic orbits of the form (1). His approximate orbits are surprisingly accurate. Struck was, in part, stimulated to find this result by a paper by Touma & Tremaine (1997) that demonstrated the richness of the resonances in the perturbation theory of these systems. Valluri et al. (2005) have emphasized that the apsidal precession found in non-inverse-square orbits is significantly dependent on the eccentricity of the orbit involved.
Surprisingly, we have been led to orbits of the form (1) by looking at orbits of extreme eccentricity e= 1, where Struck's methods did not give accurate results. Standard works on orbits, Boccaletti & Pucacco (1996), Contopoulos (2002) and Binney & Tremaine (1987), do not point out that the orbits of zero energy in power-law potentials can be exactly solved analytically. The same variables can be used to solve the nearly circular orbits. Since both highly eccentric and small eccentricity orbits can be so solved, it would be surprising if there were not a good approximation, based on the same variables, that interpolated between e= 1 and 0. Struck's methods do this well for small and moderate eccentricities. Here we show that all orbits are well approximated by analytic orbits of the form (1) for 0 ≤e≤ 1.
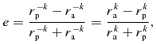
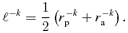
We note that for the Kepler case k= 1 and the above formulae all reduce to the usual ones. We write ℓ=Lrc, where rc(h) is the radius of the circular orbit of angular momentum h. We have rkc= (2 −k)−1h2/A. The dimensionless parameters L and m are functions of e. Orbits of small eccentricity have  , while those with e= 1 have m=k. We find the orbits in the −V2 ln r potential from the limiting case k→ 2.
, while those with e= 1 have m=k. We find the orbits in the −V2 ln r potential from the limiting case k→ 2.
In Appendix A we show how to improve the accuracy of our orbits via perturbation theory; however, for most purposes the simplicity of the initial approximation (1) outweighs the extra complication that accompanies greater accuracy. Our methods can be applied to non-power-law potentials (see Kalnajs 1979) but here, for simplicity, we limit ourselves to power laws.
While our methods can be extended to unbound orbits, the results are less pleasing so they are consigned to Appendix B.
In Section 3 we use the transformation theory of Newton, Bohlin, Arnold and others to transform our orbits for 0 < k < 2 into orbits in potentials with positive powers of r. We show how that theory can be extended naturally to give a set of transformations that form a group. We develop the subgroup of switch transformations and show that orbits in the potentials ψ∝rk−2 are conjugate to orbits in the potentials r2(2−k)/k, r−k, r2k/(2−k), r−4/k and r−4/(2−k). These transformations are not restricted to power laws, although special simplifications occur for them. Applications are made to Plummer's law.
It is shown that the full group has a transformation that connects the Keplerian potential to the isochrone.
2 ANALYTIC ORBITS
2.1 General orbits in potentials with 0 < k < 2
Those looking for orbits in potentials with powers k outside the above range should consult Section 3.
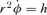 and
and 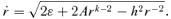
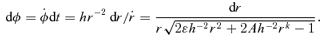
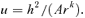
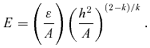
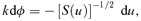
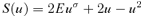
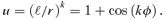
Our analytic strategy for integrating equation (7) more generally is to replace S(u) with a quadratic function SQ(u), which has precisely the same zeros, ua and up, corresponding to the apocentre and pericentre of the orbit. Thus SQ=q2(up−u)(u−ua) whose q2, the coefficient of −u2 in SQ, is to be determined so that in some average sense SQ(u) is a good approximation to S(u) in the radial range up≥u≥ua occupied by the orbit. For example, we find that choosing q2 so that  gives a q that is good to 2 per cent accuracy. A better choice, given later, is the natural starting point for the perturbation theory of Appendix A.
gives a q that is good to 2 per cent accuracy. A better choice, given later, is the natural starting point for the perturbation theory of Appendix A.
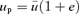 and it follows that
and it follows that 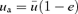 so
so 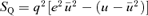 . If we make the substitution
. If we make the substitution 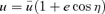 , we find that the integration of (7) gives qkφ=η, so the orbit is
, we find that the integration of (7) gives qkφ=η, so the orbit is 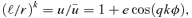
Crucial to this method of solving for the orbits is the knowledge of up and ua. A critical step in finding them is to regard the rp and ra of an orbit as given, in place of its energy and angular momentum. Those can easily be found if rp and ra are given, but solving the other way around is usually difficult. Once the orbit has been found, this approximation allows us to determine the radial action and hence the time from pericentre to a given point on the orbit.
Having outlined our general procedure, we now turn to solving the circular and nearly circular orbits using u, rather than r, as the variable.
2.2 Nearly circular orbits
 is zero for them their energy is ɛc where
is zero for them their energy is ɛc where 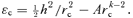
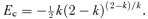
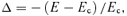
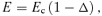
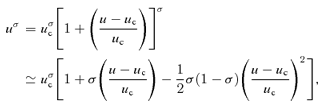

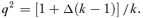
 , we have
, we have 
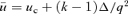 and
and 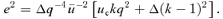
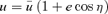 yields
yields 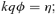
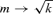 .
.Whereas these formulae have been derived by neglecting the (u−uc)3 and higher terms in the expansion of uσ, it should be realized that the coefficient of the uσ term itself vanishes at the energy of escape. Thus, despite this neglect, our formulae are exact, not just for Δ small, but also at Δ= 1. Indeed at Δ= 1 we see that  and e= 1. However, even such partial reassurance should not deceive us into believing that formulae (11) and (13) are good enough at intermediate values of e.
and e= 1. However, even such partial reassurance should not deceive us into believing that formulae (11) and (13) are good enough at intermediate values of e.
2.3 Analysis of general orbits
In the non-linear regime, we see from the e= 1 orbits that u has its mean at 1 rather than at 2 −k. It makes little sense to expand uσ about uc= 2 −k when Δ is not small. Nevertheless we would like to quadrate S, that is, approximate S(u) by some quadratic function. We adopt a very different procedure in the non-linear case. In place of fixing the energy and the angular momentum of an orbit and then determining its shape and size, we choose, instead, a pericentric distance rp and an apocentric distance ra. From these it is simple to find exactly what energy and angular momentum are needed. Equivalently we can fix the values of ℓ and e so then rp=ℓ/(1 +e)1/k and ra=ℓ/(1 −e)1/k, as can be seen from (1) with mφ equal to first 0 and then π.
 at both rp and ra, we have for ɛ < 0
at both rp and ra, we have for ɛ < 0
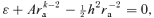
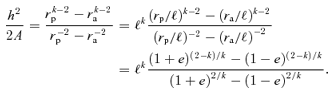
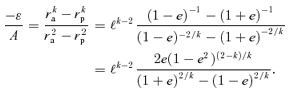
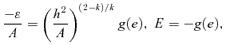
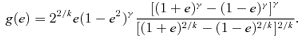
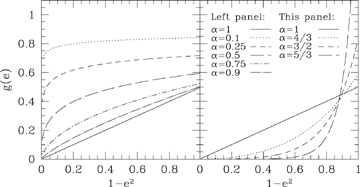
The function g(e) for various values of α= 2 −k. g(e) is minus the dimensionless energy E. As α→ 0, the graph tends to the line g(e) ≡ 1.
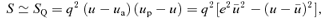
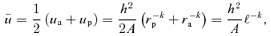
 is twice the final expression in (17) but without the ℓk. The ‘eccentricity’e is (up−ua)/(up+ua) as always. Using (20) for S(u) with the substitution
is twice the final expression in (17) but without the ℓk. The ‘eccentricity’e is (up−ua)/(up+ua) as always. Using (20) for S(u) with the substitution 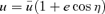 , we readily integrate equation (7) to obtain qkφ=η as before. So the solution is still equation (1) with m=qk, but we must still determine q2.
, we readily integrate equation (7) to obtain qkφ=η as before. So the solution is still equation (1) with m=qk, but we must still determine q2.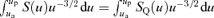 . This gives, for σ≠ 1/2 (i.e. α≠ 2/3),
. This gives, for σ≠ 1/2 (i.e. α≠ 2/3), 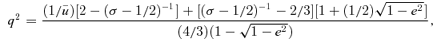
 can be expressed as a function of k and e only, via (17) and (21). We have chosen this power of u in the integrals we equate above, as it gives the best agreement to the true m without compromising on the simplicity of the expression for q. We note that choosing u−1 in the integrals gives as good an agreement as using u−3/2, but with the resulting m becoming overestimates on the true value for α < 1 and vice versa for α > 1. Choosing an exponent between −1 and −1.5 results in better agreement still, but we lose the simplicity of the resulting analytic expression for q. The exponent of −4/3 is as good as any, but gives the following somewhat awkward result:
can be expressed as a function of k and e only, via (17) and (21). We have chosen this power of u in the integrals we equate above, as it gives the best agreement to the true m without compromising on the simplicity of the expression for q. We note that choosing u−1 in the integrals gives as good an agreement as using u−3/2, but with the resulting m becoming overestimates on the true value for α < 1 and vice versa for α > 1. Choosing an exponent between −1 and −1.5 results in better agreement still, but we lose the simplicity of the resulting analytic expression for q. The exponent of −4/3 is as good as any, but gives the following somewhat awkward result: 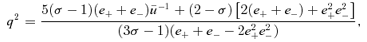
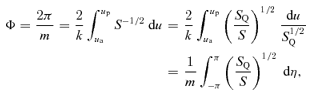
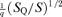 is
is 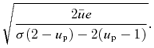
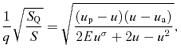
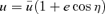 , at the other seven points ±π/4, ±π/2, ±3π/4 and cos η=−0.990. For convenience, we label the values of u at ±π/4 and ± 3π/4 as
, at the other seven points ±π/4, ±π/2, ±3π/4 and cos η=−0.990. For convenience, we label the values of u at ±π/4 and ± 3π/4 as 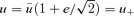 and
and 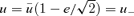 , respectively. Our estimate of 1/q is the average over the eight values that result:
, respectively. Our estimate of 1/q is the average over the eight values that result: 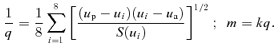
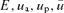 are all functions of e.
are all functions of e.2.4 Comparisons with computed orbits
Orbits were computed in the xy plane from the Cartesian form of the equations of motion for potentials with α= 0.25, 0.55, 0.75, 1.5 and 1.0. The last provides a valuable check that we get m= 1 in the Newtonian case, even at very high eccentricities of order 0.999. We also checked that  for nearly circular orbits and that m→k as e→ 1 for all the values of α. As m varies quite rapidly with eccentricity as e→ 1, accurate computations are required at high eccentricities. Orbits in the logarithmic potential which gives a constant circular velocity are considered later, in Section 2.6; the approximation adopted there is somewhat different.
for nearly circular orbits and that m→k as e→ 1 for all the values of α. As m varies quite rapidly with eccentricity as e→ 1, accurate computations are required at high eccentricities. Orbits in the logarithmic potential which gives a constant circular velocity are considered later, in Section 2.6; the approximation adopted there is somewhat different.
Fig. 2 shows a comparison between our estimated values of m and the computed values of m for potentials with α= 0.25, 0.55, 0.75 and 1.5. For all values of α shown, the deviation of m calculated from the analytical formula (23) is only a fraction of a per cent. Note that both plots are against  so that high eccentricities are on the left-hand side and low eccentricities are on the right-hand side. It is, of course, possible to read off m as a function of
so that high eccentricities are on the left-hand side and low eccentricities are on the right-hand side. It is, of course, possible to read off m as a function of  or of e from the computed points in this figure.
or of e from the computed points in this figure.
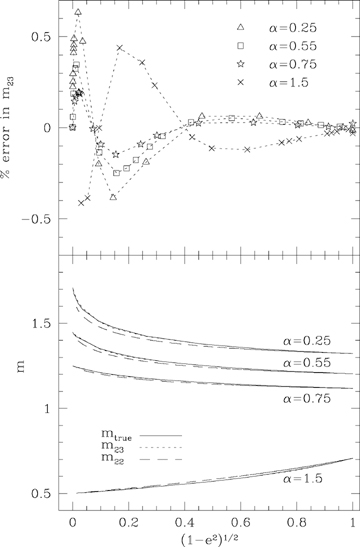
The top panel shows the percentage difference between the true value of m from computed orbits and m23 calculated from the analytical formula (23), plotted as functions of  for different values of 2 −k=α. The largest deviations occur at high eccentricities; the region 0.1–0.3 in
for different values of 2 −k=α. The largest deviations occur at high eccentricities; the region 0.1–0.3 in  corresponds to 0.995 > e > 0.954. The bottom panel shows the values of m, estimated using (22) and (23), along with the true values, again for four values of α.
corresponds to 0.995 > e > 0.954. The bottom panel shows the values of m, estimated using (22) and (23), along with the true values, again for four values of α.
Panel (a) of Fig. 3 shows a computed orbit in the potential with α= 0.25 together with an orbit of the same m, ra and rp but calculated from the equation (ℓ/r)k= 1 +e cos (mφ). This demonstrates how the shape given by equation (1) fits the computed orbit. A better fit is obtained using the perturbation theory of Appendix A. The dotted orbit in panel (b) is (ℓ/r)k= 1 +e cos(m23φ) and the gradual precession due to the error in the estimated m23 is readily seen.
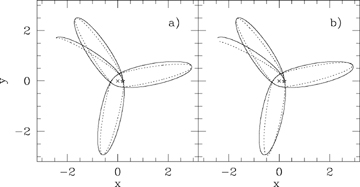
An orbit in the 2 −k=α= 0.25 potential, chosen to be in the high-eccentricity region where the approximation is least good. The full line is the computed true orbit. In panel (a), it is compared to (ℓ/r)k= 1 +e cos(mφ) (dotted line) with m chosen to agree with the computed orbit. This shows the deviation in the shape of the lobes. In panel (b), the value of m is estimated by the 8-point average of equation (23) and the error in m is readily seen from the different precession of the solid and dotted orbits. The difference in the true value of m and that estimated from the 8-point average is less than 0.5 per cent. All orbits start at the starred location.
Fig. 4 shows two orbits with the same ratio of ra/rp but in the potentials with α= 0.55 and α= 0.75. Because the definition of ‘eccentricity’ we gave in equation (2) depends on α (through k), these orbits have eccentricities of 0.662 and 0.596, respectively. Note that the two drawings have the same number of apsides but these have precessed much less for the α= 0.75 orbit as the potential is closer to the Keplerian α= 1.
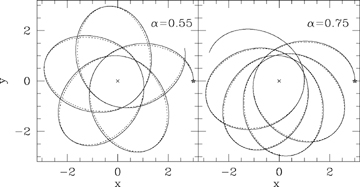
Two computed orbits with the same rmin/rmax in potentials with different 2 −k=α are compared with the analytic orbits (ℓ/r)k= 1 +e cos (mtrueφ) (dotted lines). The α= 0.55 orbit has e= 0.662 while the α= 0.75 orbit has e= 0.596 and precesses much less rapidly. Both the shapes and the precession rates of these orbits are well represented by the analytic formula.
Fig. 5 shows two orbits in the α= 1.5 potential for which the precession is forwards because α > 1 whereas the other illustrations all have a backward precession. Under the transformation ζ=zk/2 considered in Section 3, these orbits transform into ones in the potentials ψ∝r2α/k=r6. For orbits with α > 1, the straight perturbation theory giving m=kq with q given by (23) yields m to better than 0.5 per cent.
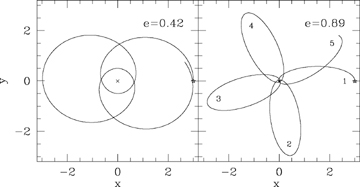
Two orbits in the 2 −k=α= 1.5 potential. The orbit on the left-hand side has a forward precession by nearly 180° whilst that on the right-hand side has a forward precession by a little over 270°. The turn close to the origin in the latter cannot be seen but is a more rapidly turning version of that seen on the left-hand side. The lobes are numbered in sequential order for the higher eccentricity orbit.
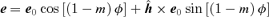 . This e obeys
. This e obeys 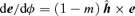 . The angle between the radius vector to the particle and the eccentricity vector is then mφ and the equation of the orbit (1) can be rewritten as
. The angle between the radius vector to the particle and the eccentricity vector is then mφ and the equation of the orbit (1) can be rewritten as 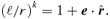
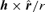 and the radial velocity can be obtained from the orbit and the energy equation. Using our approximations quadrating the latter, we find
and the radial velocity can be obtained from the orbit and the energy equation. Using our approximations quadrating the latter, we find 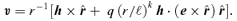
Given v and r at one time one might wish to use these equations at a later time. Then one needs to find e, h, ℓ, q and m from the initial v and r together with the known potential ψ=Ar−α. From v and r it is easy to construct ɛ=½v2−Ar−α and h=r×v, from these E is found. For given E and α, e may be found from Fig. 1. ℓ then follows from (17) and m, q from (23). The direction of e within the plane perpendicular to h then follows from  with the ambiguity in angle resolved from
with the ambiguity in angle resolved from  which follows from the v equation above. Thus all the orbital parameters are determined.
which follows from the v equation above. Thus all the orbital parameters are determined.
2.5 Action, adiabatic invariants and time
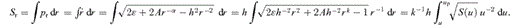
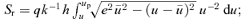
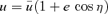 , this becomes, setting f= 1/e,
, this becomes, setting f= 1/e, 
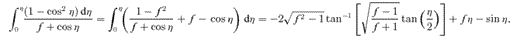
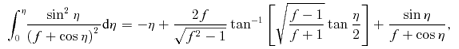
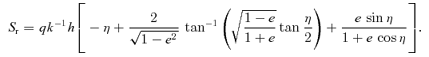
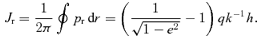
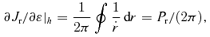
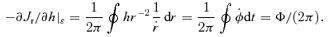
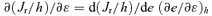
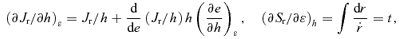
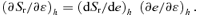
In the general case, use of 1/u∝rk as a variable does not lead to a prettier equation for t, such as the one Kepler derived for k= 1, but see the next section for logarithmic potentials.
In the equatorial plane the total action is SA=Sr+hzφ. The action variables are Jr and hz=h. The angle variables are the phases of the oscillations in r and φ and are given by wr=∂SA/∂Jr and wφ=∂SA/∂h. For general orbits, the action variables are most often employed when the potential is of the more general separable form ψ=Ar−α−B(θ)/r2; h2 is no longer conserved but I=h2− 2B(θ) is. The general action is then SA=Sr+Sθ+hzφ with  and Jθ= 1/(2π)∮∂Sθ/∂θdθ. The angle variables are wθ=∂SA/∂Jθ and wφ=∂SA/∂hz.
and Jθ= 1/(2π)∮∂Sθ/∂θdθ. The angle variables are wθ=∂SA/∂Jθ and wφ=∂SA/∂hz.
2.6 Logarithmic potentials α→ 0
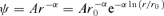 and expand to obtain ψ=Arα0 [1 −α ln (r/r0) + 0 (α2)]. We set A=V2/α and consider taking the limit as α→ 0 while keeping V2 fixed so A tends to infinity. To keep a finite potential, we have to subtract the constant Ar−α0 from ψ, so we obtain a new potential
and expand to obtain ψ=Arα0 [1 −α ln (r/r0) + 0 (α2)]. We set A=V2/α and consider taking the limit as α→ 0 while keeping V2 fixed so A tends to infinity. To keep a finite potential, we have to subtract the constant Ar−α0 from ψ, so we obtain a new potential 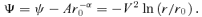
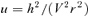
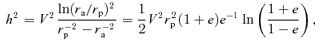
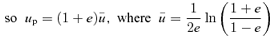

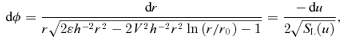
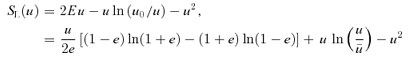
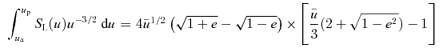
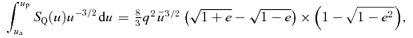
 is given by (32). This yields
is given by (32). This yields 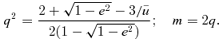
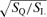 over η, where
over η, where 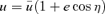 . At up,
. At up, 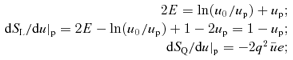
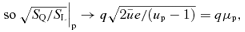
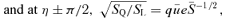
 . As found in Section 2.3, the apocentre once again poses a problem and we evaluate
. As found in Section 2.3, the apocentre once again poses a problem and we evaluate 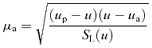
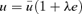 where λ=−0.990, as before, and where SL(u) is given by (34). So a 4-point estimate of q is given by
where λ=−0.990, as before, and where SL(u) is given by (34). So a 4-point estimate of q is given by 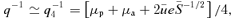
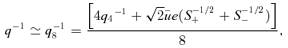
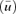 and
and 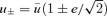 . Fig. 6 shows the contribution of each point in (39) and (40) along with a comparison of the true m and the value derived from the 8-point estimate via m40=q8k. Fig. 7 compares an approximate orbit to a computed one.
. Fig. 6 shows the contribution of each point in (39) and (40) along with a comparison of the true m and the value derived from the 8-point estimate via m40=q8k. Fig. 7 compares an approximate orbit to a computed one.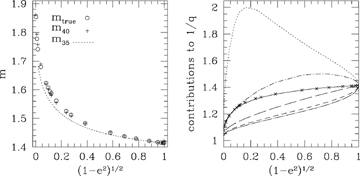
The left-hand panel shows a comparison between the true value of m (open circles) and that estimated from equation (35), which gives m to better than 2 per cent, and the 8-point average in equation (40), which gives m to better than 1 per cent. The right-hand panel shows (in thick solid) the true value of 1/q=k/m overlaid (in crosses) with that derived from the 8-point average. The agreement is clearly good to a fraction of a per cent. The individual contributions made by each of the points given in the terms of equations (39) and (40) are also shown. From the top, the various lines correspond to ua (dotted), u+ (dot–short-dashed),  (long-dashed), u− (short-dashed) and up (dot–long-dashed).
(long-dashed), u− (short-dashed) and up (dot–long-dashed).
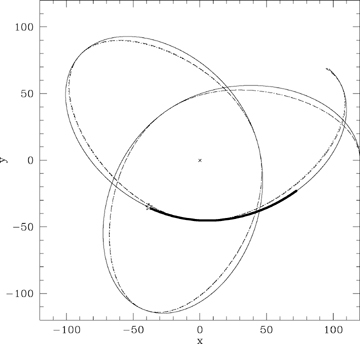
An orbit in the logarithmic potential. The solid line is the computed orbit, and the dotted line shows the approximate orbit (ℓ/r)2= 1 +e cos(mtrueφ). Overlaid (and hardly visible) is a dashed line showing an orbit with the estimated m, calculated from (40), instead of mtrue. The error in this value of m is less than 0.1 per cent. The heavy line shows the piece of such an orbit for the trailing Magellanic Stream, with the location of the Magellanic Clouds indicated by the open star.
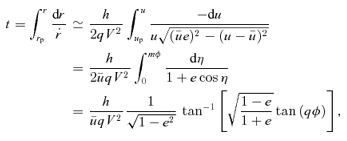
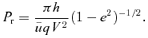
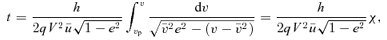
 and
and 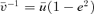 ; setting
; setting 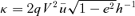 we see that
we see that 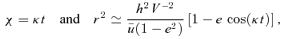
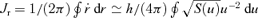 . This integral was evaluated in equation (28), so for this case k= 2 and
. This integral was evaluated in equation (28), so for this case k= 2 and 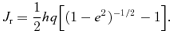
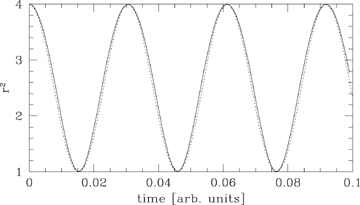
The almost simple harmonic variation of r2 as a function of time in an orbit with ra/rp= 2 in the logarithmic potential. The dotted line is a sinusoid of the same period.
It should be emphasized that while we have set ourselves the target of getting analytical formulae that give m to 1 per cent or better for all eccentricities, we have not paid attention to minimizing errors in the temporal periods. We find that such errors are indeed higher and no doubt our formulae could be improved upon by a study of such errors.
3 TRANSFORMATION THEORY
Newton (1687) realized that the ellipse was a possible orbit both in a harmonic central potential and in an inverse-square law. In the first case the centre of force is at the centre of the ellipse, while in the latter case it is at the focus. This led him to pose the question under what circumstances can the same curve be the trajectory of a particle under a force from one of two different centres. Newton's (1714) discussion of this is well described in Chandrasekhar's (1995) book, as well as in later work by Bohlin (1911), Levi-Cìvita (1924) and Arnold (1990). All demonstrate the transformation that converts the harmonic ellipse into the Kepler ellipse and vice versa. Collas (1981) gave the relationship between equivalent potentials. Here we show that this transformation, S1, can be embedded into a larger set of transformations that form a group. We mainly concentrate on the subgroup of switch transformations which have six members but which give just three related potentials r−1, r2 and r−4 in the Kepler case, since r−1 is self-conjugate under one of the transformations. In the complete group, these potentials are also related to the isochrone (Henon 1959).
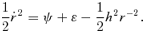
 . Setting F=ρ′τ we find
. Setting F=ρ′τ we find 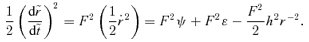
For this to be an orbital equation like (45), the three terms on the right-hand side must be  and
and  , but not necessarily in that order.
, but not necessarily in that order.
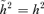 , identifying the last terms but switching the roles of the other two. Thus for S1 we set
, identifying the last terms but switching the roles of the other two. Thus for S1 we set 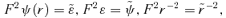
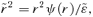
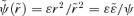 . Applying this to the power-law potential ψ=Ar−α yields
. Applying this to the power-law potential ψ=Ar−α yields 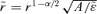 so
so 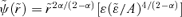 (note: α= 1 gives
(note: α= 1 gives 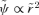 ) the quantity in square brackets is, of course, constant. However, we could alternatively leave the first term on the right-hand side of (46), identifying it with
) the quantity in square brackets is, of course, constant. However, we could alternatively leave the first term on the right-hand side of (46), identifying it with 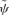 but switching the roles of the other two terms. This leads us to the transformation S2 in which
but switching the roles of the other two terms. This leads us to the transformation S2 in which 
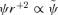 and
and 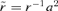 , where
, where 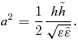
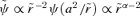 (for power laws). More generally we may ask that
(for power laws). More generally we may ask that 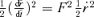 but that the three terms
but that the three terms 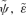 and
and 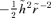 that constitute this quantity are independent linear combinations of F2ψ, F2ɛ and
that constitute this quantity are independent linear combinations of F2ψ, F2ɛ and 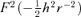 . If one applies two of this more general class of transformations one after the other, it is simple to see that the net result is a transformation of this class, that the identity transformation belongs to the class and that every transformation has a unique inverse in the class. These transformations form a group in the sense of group theory, since they clearly obey the associative law
. If one applies two of this more general class of transformations one after the other, it is simple to see that the net result is a transformation of this class, that the identity transformation belongs to the class and that every transformation has a unique inverse in the class. These transformations form a group in the sense of group theory, since they clearly obey the associative law 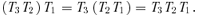
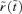 in the new potential
in the new potential 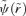 that corresponds to the old r(t) in the old potential ψ. To get the transformation of φ we remember that
that corresponds to the old r(t) in the old potential ψ. To get the transformation of φ we remember that 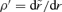 and for
and for 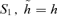 so under the transformation S1 using (46) and (47)
so under the transformation S1 using (46) and (47)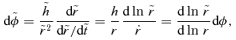
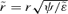 so
so 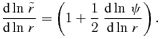
 is a power of r, for then
is a power of r, for then 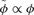 . Furthermore, this occurs if and only if ψ follows a power law in r; so
. Furthermore, this occurs if and only if ψ follows a power law in r; so 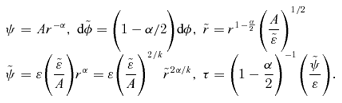
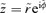 then, from the above, the S1 mapping is of the form
then, from the above, the S1 mapping is of the form 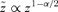 , i.e. a conformal map in the complex plane. In general, a closed orbit will map into an unclosed Lissajoux rosette, but when 1 −α/2 =N1/N2 where N1 and N2 are relatively prime integers, then the transformation of an orbit that closes after one turn will be an orbit that closes after N2 turns which has N1 times as many apsides.
, i.e. a conformal map in the complex plane. In general, a closed orbit will map into an unclosed Lissajoux rosette, but when 1 −α/2 =N1/N2 where N1 and N2 are relatively prime integers, then the transformation of an orbit that closes after one turn will be an orbit that closes after N2 turns which has N1 times as many apsides.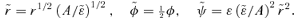
 we find
we find 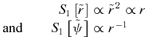
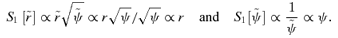
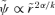 , which will be a positive power of
, which will be a positive power of  and the transformed orbit takes the form
and the transformed orbit takes the form 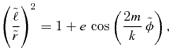
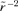 on the left-hand side whatever α we start from, but the values of 2m/k vary with α.
on the left-hand side whatever α we start from, but the values of 2m/k vary with α.S1 is the basis for the regularization of the close encounters of two bodies carried out in three dimensions by Kustaanheimo & Stiefel (1965).
3.1 The switch subgroup
If we try to find a transformation that switches the angular momentum and potential terms in (46) while leaving the energy term unchanged, we fail because  and with F constant we are unable to accomplish the desired switch.
and with F constant we are unable to accomplish the desired switch.
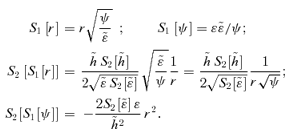
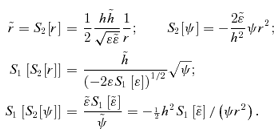
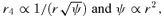
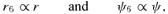
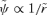 , so Newton's law is invariant under S2. However, S2 acting on r2 leads to
, so Newton's law is invariant under S2. However, S2 acting on r2 leads to 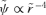 , but a further application of S1 leaves r−4 invariant. Thus under the transformations considered so far, there are conjugate orbits in the r−1, r2 and r−4 potentials. More generally, if we start with ψ∝r−α, then S1 gets us to ψ∝r2α/(2−α) (where we have dropped the tildes), while S2 brings us to ψ∝rα−2. The double transformations S2S1 and S1S2 give ψ∝r−4/(2−α) and r2(2−α)/α, respectively, while S1S2S1 leads to ψ∝r−4/α. Further applications only bring us back to potentials already included. In fact, there are six transformations in this subgroup, yielding a conjugacy of orbits in the six potentials r−α, r2α/(2−α), rα−2, r−4/(2−α), r2(2−α)/α and r−4/α. For α=−1, these are r, r−2/3, r−3, r−4/3, r−6 and r4. For α= 1/2, they are r−1/2, r2/3, r−3/2, r−8/3, r6 and r−8. These powers become somewhat bizarre for small α.
, but a further application of S1 leaves r−4 invariant. Thus under the transformations considered so far, there are conjugate orbits in the r−1, r2 and r−4 potentials. More generally, if we start with ψ∝r−α, then S1 gets us to ψ∝r2α/(2−α) (where we have dropped the tildes), while S2 brings us to ψ∝rα−2. The double transformations S2S1 and S1S2 give ψ∝r−4/(2−α) and r2(2−α)/α, respectively, while S1S2S1 leads to ψ∝r−4/α. Further applications only bring us back to potentials already included. In fact, there are six transformations in this subgroup, yielding a conjugacy of orbits in the six potentials r−α, r2α/(2−α), rα−2, r−4/(2−α), r2(2−α)/α and r−4/α. For α=−1, these are r, r−2/3, r−3, r−4/3, r−6 and r4. For α= 1/2, they are r−1/2, r2/3, r−3/2, r−8/3, r6 and r−8. These powers become somewhat bizarre for small α. 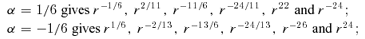
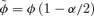 holds only for power-law potentials under the S1 transformation. Under S2 we find
holds only for power-law potentials under the S1 transformation. Under S2 we find 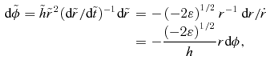
 to φ. However,
to φ. However, 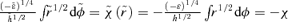 , so if χ(r) is known for the first orbit then, with
, so if χ(r) is known for the first orbit then, with 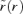 known,
known, 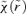 is known for the second.
is known for the second.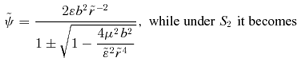
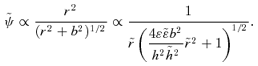
3.2 The larger group
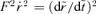 but in place of merely switching the terms on the right-hand side of (46) we ask that those terms are linear combinations of
but in place of merely switching the terms on the right-hand side of (46) we ask that those terms are linear combinations of 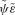 and
and 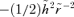 , we obtain the full group of transformations. A general transformation of the group is then
, we obtain the full group of transformations. A general transformation of the group is then 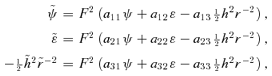
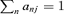 for j= 1, 2, 3.
for j= 1, 2, 3.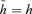 without loss of generality,
without loss of generality, 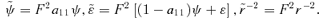
 to r when the value of F2 is taken from the third:
to r when the value of F2 is taken from the third: 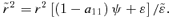
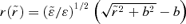 ,
, 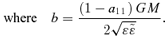
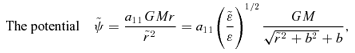
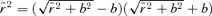 .
.The potential  is the isochrone, see Henon (1959). This is the most general potential in which all orbits can be found using only elementary functions (trigonometric etc.) as stated by Eggen, Lynden-Bell & Sandage (1962); the detailed proof of this was only published many years later in Evans, de Zeeuw & Lynden-Bell (1990).
is the isochrone, see Henon (1959). This is the most general potential in which all orbits can be found using only elementary functions (trigonometric etc.) as stated by Eggen, Lynden-Bell & Sandage (1962); the detailed proof of this was only published many years later in Evans, de Zeeuw & Lynden-Bell (1990).
4 CONCLUSIONS
We have found crude, but useful, approximations to Abelian functions by quadrating the expression under the surd while keeping the end points as the constant parameters. For our problem, these methods give accuracies to better than 1 per cent.
We have shown that the e= 1‘parabolic’ orbits at the energy of escape can be solved exactly, and we have given analytic expressions for m(e) which hold for all eccentricities 0 ≤e≤ 1. We have thus illuminated why Struck found these orbits to be such good approximations at low and moderate eccentricities.
The transformation theory has allowed us to extend these results to orbits in potentials which are positive powers of r and we have extended the transformations to form a group.
Our thanks are due to the Rijksuniversity of Groningen where this work began while Donald Lynden-Bell was Blaauw Professor. Contact with Jihad Touma when this work was being prepared for publication informed us of Struck's work and so changed Section 1 substantially. Greater clarity was infused by the referee Professor Boccaletti.
REFERENCES
Appendices
APPENDIX A: PERTURBATION THEORY
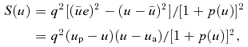
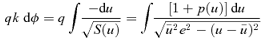
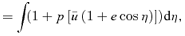
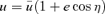 .
.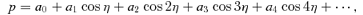
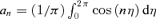 for n≠ 0. We chose q so that the average of
for n≠ 0. We chose q so that the average of 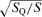 over η is 1. This ensures that the average 〈p〉= 0, so a0= 0.
over η is 1. This ensures that the average 〈p〉= 0, so a0= 0.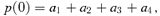
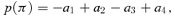
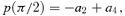
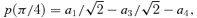
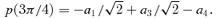
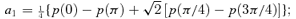
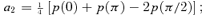
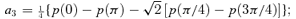
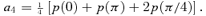
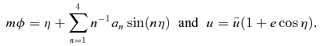
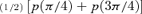 because the condition 〈p〉= 0 ensures its consistency and we replace p(π) by p(φ) with φ= cos−1(−0.990).
because the condition 〈p〉= 0 ensures its consistency and we replace p(π) by p(φ) with φ= cos−1(−0.990).APPENDIX B: UNBOUND ORBITS
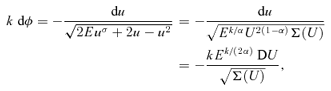
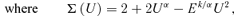
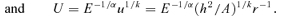
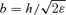 and the value of the perihelion distance rp. The energy equation at rp is
and the value of the perihelion distance rp. The energy equation at rp is 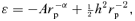
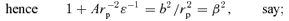
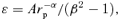
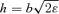 .
.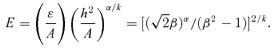
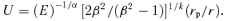
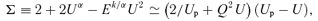

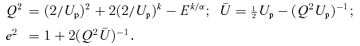
Thus for E > 1 we may integrate, using this quadratic approximation to obtain  , where m2*=Q2E−k/α and
, where m2*=Q2E−k/α and  .
.
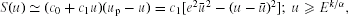
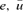 follow them.
follow them.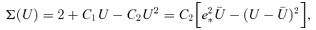
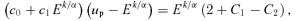
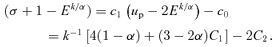


The four equations (B4), (B5 i), (B5 ii) and (B6), in whichever form is relevant, are readily solved for the four constants c0, c1, C1 and C2.
Our orbits can now be found in the form, (ℓ/r)k= 1 +e cos(mφ) for h2/Ark≥Ek/2 where m2=k2c1, but for larger r, we get ℓ*/r= 1 +e* cos [m*(φ+φ*)].



