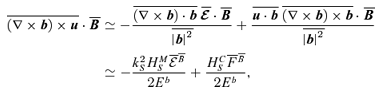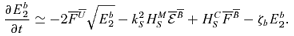-
PDF
- Split View
-
Views
-
Cite
Cite
Alejandra Kandus, Analysis of the effect of a mean velocity field on a mean field dynamo, Monthly Notices of the Royal Astronomical Society, Volume 378, Issue 4, June 2007, Pages 1356–1364, https://doi.org/10.1111/j.1365-2966.2007.11863.x
Close - Share Icon Share
Abstract
We study semi-analytically and in a consistent manner the generation of a mean velocity field  by helical magnetohydrodynamical (MHD) turbulence, and the effect that this field can have on a mean field dynamo. Assuming a prescribed, maximally helical small-scale velocity field, we show that large-scale flows can be generated in MHD turbulent flows via small-scale Lorentz force. These flows back-react on the mean electromotive force of a mean field dynamo through new terms, leaving the original α and β terms explicitly unmodified. Cross-helicity plays the key role in interconnecting all the effects. In the minimal τ closure that we chose to work with, the effects are stronger for large relaxation times.
by helical magnetohydrodynamical (MHD) turbulence, and the effect that this field can have on a mean field dynamo. Assuming a prescribed, maximally helical small-scale velocity field, we show that large-scale flows can be generated in MHD turbulent flows via small-scale Lorentz force. These flows back-react on the mean electromotive force of a mean field dynamo through new terms, leaving the original α and β terms explicitly unmodified. Cross-helicity plays the key role in interconnecting all the effects. In the minimal τ closure that we chose to work with, the effects are stronger for large relaxation times.
1 INTRODUCTION
Magnetohydrodynamical (MHD) turbulence seems to be a major physical process to generate and maintain the magnetic fields observed in most of the structures of the Universe (Zel'dovich et al. 1983; Brandenburg & Subramanian 2005a). When addressing the problem of the generation of large-scale magnetic fields by small-scale turbulent flows, a model known as mean field dynamo (MFD) is usually considered (Moffatt 1978). Despite its simplicity and lack of broad applicability, it proved to be a very useful tool in studying qualitatively conceptual issues of large-scale magnetic field generation. The mechanism is based on decomposing the fields into large-scale, or mean fields,  , and small-scale, turbulent ones u, b, a. These small-scale fields have very small coherence length, but their intensities can be higher than that of the mean fields. In this mechanism, the evolution equation for
, and small-scale, turbulent ones u, b, a. These small-scale fields have very small coherence length, but their intensities can be higher than that of the mean fields. In this mechanism, the evolution equation for  is written as
is written as  , where
, where  is the Ohmic resistivity and
is the Ohmic resistivity and  the turbulent electromotive force (TEMF).1 The term
the turbulent electromotive force (TEMF).1 The term  is usually disregarded in the studies of MFD as the focus of most of them is to understand the generation of large-scale quantities due to small-scale effects. If homogeneous and isotropic turbulence is considered, the TEMF can be written as
is usually disregarded in the studies of MFD as the focus of most of them is to understand the generation of large-scale quantities due to small-scale effects. If homogeneous and isotropic turbulence is considered, the TEMF can be written as  , with
, with  and
and  being a correlation time (Moffatt 1972; Rudiger 1974; Pouquet, Frisch & Leorat 1976; Zel'dovich et al. 1983). The dependencies on
being a correlation time (Moffatt 1972; Rudiger 1974; Pouquet, Frisch & Leorat 1976; Zel'dovich et al. 1983). The dependencies on  and b are due to the back-reaction of those induced fields on the dynamo (Moffatt 1978; Brandenburg & Subramanian 2005a). In the kinematically driven dynamo considered here, the features of the generated fields crucially depend on the helicity of the flows: helical flows are at the base of the mechanisms to generate large-scale fields, while non-helical flows would only produce small-scale fields. This separation, however, is somewhat artificial, as small-scale fields are also produced by helical turbulence (Brandenburg & Subramanian 2005a).
and b are due to the back-reaction of those induced fields on the dynamo (Moffatt 1978; Brandenburg & Subramanian 2005a). In the kinematically driven dynamo considered here, the features of the generated fields crucially depend on the helicity of the flows: helical flows are at the base of the mechanisms to generate large-scale fields, while non-helical flows would only produce small-scale fields. This separation, however, is somewhat artificial, as small-scale fields are also produced by helical turbulence (Brandenburg & Subramanian 2005a).
In this paper, we want to address an issue not (or very seldom) considered in the literature up to now, namely, the induction of large-scale flows  , also named shear flows, by the small-scale turbulent fields, and how these induced flows back-react on the turbulent electromotive force
, also named shear flows, by the small-scale turbulent fields, and how these induced flows back-react on the turbulent electromotive force  of a MFD. On one side, we mean that the expression
of a MFD. On one side, we mean that the expression  would be valid only during the time interval in which
would be valid only during the time interval in which  , and on the other, even if this condition is satisfied,
, and on the other, even if this condition is satisfied,  could be affected by the generation of
could be affected by the generation of  and consequently its functional form should be modified to incorporate this effect. The generation of magnetic fields due to the action of these large-scale velocity flows instead of by
and consequently its functional form should be modified to incorporate this effect. The generation of magnetic fields due to the action of these large-scale velocity flows instead of by  was recently addressed analytically by several authors (Rogachevskii & Kleeorin 2003, 2004; Rädler & Stepanov 2006), and was also studied numerically by Brandenburg (2001) and semi-analytically by Blackman & Brandenburg (2002). However, none of those works specifically addressed the issue we want to analyse here.
was recently addressed analytically by several authors (Rogachevskii & Kleeorin 2003, 2004; Rädler & Stepanov 2006), and was also studied numerically by Brandenburg (2001) and semi-analytically by Blackman & Brandenburg (2002). However, none of those works specifically addressed the issue we want to analyse here.
We work in the framework of the two-scale approximation that consists of assuming that mean fields peak at a scale k−1L while turbulent ones do so at k−1S≪k−1L, and also consider homogenous and isotropic turbulence. Although this kind of turbulence is of dubious validity when dealing with large-scale fields, it serves well for initial, qualitative studies of the sought effects. Another assumption we will make is that  is force-free, i.e. of maximal current helicity. Although fields with this feature can be observed in certain astrophysical environments, they are not a generality, and also they are not seen in some numerical simulations. The main reason to use them here is to simplify the (heavy) mathematics, while maintaining a physically meaningful scenario.
is force-free, i.e. of maximal current helicity. Although fields with this feature can be observed in certain astrophysical environments, they are not a generality, and also they are not seen in some numerical simulations. The main reason to use them here is to simplify the (heavy) mathematics, while maintaining a physically meaningful scenario.
In order to find  when Lorentz force acts on the plasma, we must solve a differential equation that contains terms with one-point triple correlations, i.e. averages of products of three stochastic fields evaluated at the same point. This means that instead of dealing with only one equation to solve for
when Lorentz force acts on the plasma, we must solve a differential equation that contains terms with one-point triple correlations, i.e. averages of products of three stochastic fields evaluated at the same point. This means that instead of dealing with only one equation to solve for  , we have to solve a hierarchy of them. In order to break this hierarchy and thus simplify the mathematical treatment of the problem, we must choose a closure prescription, which consists of writing the high-order correlations as functions of the lower order ones, but maintaining the physical features of the problem under study. In MHD, the intensity of the non-linearities is measured by the magnetic Reynolds number, which is defined in the induction equation for the magnetic field, ∂B/∂t=∇(U×B) +η∇2B, as Rm∼ (UB/l) /(ηB/l2) =Ul/η, where U is a characteristic velocity of the plasma, l is a characteristic length and η is the ohmic resistivity. Thus, for Rm≪ 1 the non-linear terms can be neglected in front of the resistive ones, and therefore the equations become linear, while for Rm≫ 1 the resistive terms should be dropped off in front of the non-linear ones. The intermediate regime is more difficult to analyse. In this paper, we will consider Rm≫ 1, i.e. the non-linearities must be maintained and, consequently, a closure scheme must be selected to deal with them. We choose to work with the so-called minimal τ approximation (Blackman & Field 2002; Brandenburg & Subramanian 2005a), whereby the triple moments in the equation for
, we have to solve a hierarchy of them. In order to break this hierarchy and thus simplify the mathematical treatment of the problem, we must choose a closure prescription, which consists of writing the high-order correlations as functions of the lower order ones, but maintaining the physical features of the problem under study. In MHD, the intensity of the non-linearities is measured by the magnetic Reynolds number, which is defined in the induction equation for the magnetic field, ∂B/∂t=∇(U×B) +η∇2B, as Rm∼ (UB/l) /(ηB/l2) =Ul/η, where U is a characteristic velocity of the plasma, l is a characteristic length and η is the ohmic resistivity. Thus, for Rm≪ 1 the non-linear terms can be neglected in front of the resistive ones, and therefore the equations become linear, while for Rm≫ 1 the resistive terms should be dropped off in front of the non-linear ones. The intermediate regime is more difficult to analyse. In this paper, we will consider Rm≫ 1, i.e. the non-linearities must be maintained and, consequently, a closure scheme must be selected to deal with them. We choose to work with the so-called minimal τ approximation (Blackman & Field 2002; Brandenburg & Subramanian 2005a), whereby the triple moments in the equation for  will be considered as proportional to quadratic moments, and written in the form
will be considered as proportional to quadratic moments, and written in the form  , with the proportionality factor ζ∼τ−1rel, where τrel is a relaxation time that can in principle be scale, and/or Rm, dependent. The validity of this closure was checked numerically (Brandenburg & Subramanian 2005b) for low Reynolds numbers, and was also verified for the case of passive scalar diffusion. We will assume that it is also valid for all the triple correlations that may appear throughout this work. We consider boundary conditions such that all total divergencies vanish. These conditions may be a bit unrealistic for astrophysical systems, but they have two advantages: magnetic helicity becomes a gauge-invariant quantity (Berger & Field 1984) and the obtained results can be compared with numerical simulation, as to perform them it is customary to use those conditions. We consider fully helical, prescribed, u fields.
, with the proportionality factor ζ∼τ−1rel, where τrel is a relaxation time that can in principle be scale, and/or Rm, dependent. The validity of this closure was checked numerically (Brandenburg & Subramanian 2005b) for low Reynolds numbers, and was also verified for the case of passive scalar diffusion. We will assume that it is also valid for all the triple correlations that may appear throughout this work. We consider boundary conditions such that all total divergencies vanish. These conditions may be a bit unrealistic for astrophysical systems, but they have two advantages: magnetic helicity becomes a gauge-invariant quantity (Berger & Field 1984) and the obtained results can be compared with numerical simulation, as to perform them it is customary to use those conditions. We consider fully helical, prescribed, u fields.
Our starting points are the evolution equations for  and for the magnetic helicities HML,S, as the evolution of these quantities is tightly interlinked (Blackman & Field 2002; Brandenburg & Subramanian 2005a) in the absence of shear flows. When including
and for the magnetic helicities HML,S, as the evolution of these quantities is tightly interlinked (Blackman & Field 2002; Brandenburg & Subramanian 2005a) in the absence of shear flows. When including  new terms appear in the equation for
new terms appear in the equation for  , but the ones that drive the evolution of
, but the ones that drive the evolution of  in the absence of
in the absence of  , i.e. the α and β terms (Moffatt 1972; Rudiger 1974; Pouquet et al. 1976; Blackman & Field 2002), are not explicitly modified. For those new terms, further equations must be derived, which in turn show the subtleties of the interplay among
, i.e. the α and β terms (Moffatt 1972; Rudiger 1974; Pouquet et al. 1976; Blackman & Field 2002), are not explicitly modified. For those new terms, further equations must be derived, which in turn show the subtleties of the interplay among  and
and  . Due to the chosen boundary conditions, the evolution equations for HML and HMS do not explicitly depend on
. Due to the chosen boundary conditions, the evolution equations for HML and HMS do not explicitly depend on  ; they will do so implicitly through
; they will do so implicitly through  . We consider fully helical
. We consider fully helical  fields, so we study their growth through its associated kinetic helicity,
fields, so we study their growth through its associated kinetic helicity,  and show that, for fully helical, prescribed u, large-scale flows will be always generated, as long as the small-scale Lorentz force is not null, i.e. if
and show that, for fully helical, prescribed u, large-scale flows will be always generated, as long as the small-scale Lorentz force is not null, i.e. if  . We will consider two values for the magnetic Reynolds number, Rm= 200 and 2000, and for each case analyse the effect of short and large τrel. In general, we find that for short τrel (large ζ), i.e. strong non-linearities, the effect of large-scale flow is negligible, thus producing results that practically do not differ from the ones in the absence of large-scale flows. For large τrel (small ζ), the general effect is an enhancement of the electromotive force and the inverse cascade of magnetic helicity, this enhancement being stronger for Rm= 2000 than for Rm= 200.
. We will consider two values for the magnetic Reynolds number, Rm= 200 and 2000, and for each case analyse the effect of short and large τrel. In general, we find that for short τrel (large ζ), i.e. strong non-linearities, the effect of large-scale flow is negligible, thus producing results that practically do not differ from the ones in the absence of large-scale flows. For large τrel (small ζ), the general effect is an enhancement of the electromotive force and the inverse cascade of magnetic helicity, this enhancement being stronger for Rm= 2000 than for Rm= 200.
2 MAIN EQUATIONS
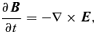
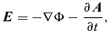
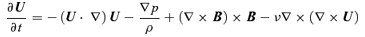
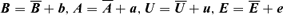 and
and  , where any mean value of stochastic quantities vanishes. The derivation of the evolution equations for the mean and stochastic fields is a standard procedure, already described in the literature (Zel'dovich et al. 1983; Blackman & Field 2002). Consequently, we only write here the results. Assuming incompressibility of the large- and small-scale flows, considering that
, where any mean value of stochastic quantities vanishes. The derivation of the evolution equations for the mean and stochastic fields is a standard procedure, already described in the literature (Zel'dovich et al. 1983; Blackman & Field 2002). Consequently, we only write here the results. Assuming incompressibility of the large- and small-scale flows, considering that 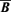 is force-free and working with Coulomb gauge for the vector potential, i.e.
is force-free and working with Coulomb gauge for the vector potential, i.e. 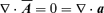 , we obtain the following equations for the mean fields:
, we obtain the following equations for the mean fields: 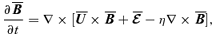
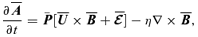
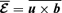 is the TEMF and
is the TEMF and 
 is the projector that selects the subspace of solutions of equation (2) that satisfy the Coulomb gauge condition and the subspace of solutions of (3) that satisfy the incompressibility condition. Observe that equation (6) shows that a large-scale velocity field can be induced from an initially zero value, as long as
is the projector that selects the subspace of solutions of equation (2) that satisfy the Coulomb gauge condition and the subspace of solutions of (3) that satisfy the incompressibility condition. Observe that equation (6) shows that a large-scale velocity field can be induced from an initially zero value, as long as 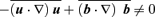 . The equations for the small-scale fields read
. The equations for the small-scale fields read 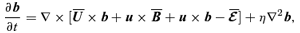
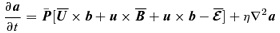
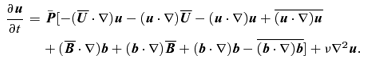
2.1 Evolution equation for derived quantities: magnetic helicity, large-scale kinetic helicities and the stochastic electromotive force
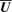 can grow due to the action of a MFD, and back-react on it and on the magnetic helicity. This last quantity is defined as the average over the entire volume of the dot product A·B (Biskamp 1997). In this way, we write the magnetic helicity associated to the large- and small-scale fields, respectively, as
can grow due to the action of a MFD, and back-react on it and on the magnetic helicity. This last quantity is defined as the average over the entire volume of the dot product A·B (Biskamp 1997). In this way, we write the magnetic helicity associated to the large- and small-scale fields, respectively, as 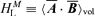 and HMS≡〈a·b〉vol, and by definition they can only depend on time. The evolution equations for HML and HMS, for the chosen boundary conditions, read as (Blackman & Field 2002)
and HMS≡〈a·b〉vol, and by definition they can only depend on time. The evolution equations for HML and HMS, for the chosen boundary conditions, read as (Blackman & Field 2002) 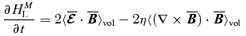
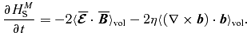
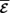 .
.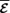 given above, the evolution equation for the TEMF is
given above, the evolution equation for the TEMF is  . Proceeding similarly to Blackman & Field (2002) and Kandus, Vasconcelos & Cerqueira (2006), it now reads
. Proceeding similarly to Blackman & Field (2002) and Kandus, Vasconcelos & Cerqueira (2006), it now reads 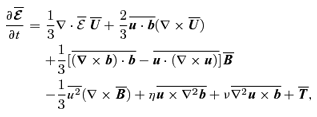
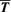 are the triple correlations for which a closure must be applied. Observe that the presence of
are the triple correlations for which a closure must be applied. Observe that the presence of 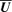 adds two new terms to the equation for
adds two new terms to the equation for 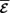 but does not explicitly modify the ones found in the absence of those flows. The influence of
but does not explicitly modify the ones found in the absence of those flows. The influence of 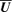 on the terms proportional to
on the terms proportional to 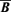 will be through the dependence of those terms with the magnetic helicities (cf. Blackman & Field 2002). To gain conceptual clearness, we will make further physical hypotheses on our systems, which will also help to simplify the mathematics. One of them is to consider that large-scale flows
will be through the dependence of those terms with the magnetic helicities (cf. Blackman & Field 2002). To gain conceptual clearness, we will make further physical hypotheses on our systems, which will also help to simplify the mathematics. One of them is to consider that large-scale flows 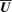 are fully helical. This is consistent with the concept of MFD and with the chosen boundary conditions. Therefore, to track the evolution of the large-scale velocity flow, we will study its associated kinetic helicity, defined as
are fully helical. This is consistent with the concept of MFD and with the chosen boundary conditions. Therefore, to track the evolution of the large-scale velocity flow, we will study its associated kinetic helicity, defined as  , where
, where  is the vorticity. The derivation of the equation for
is the vorticity. The derivation of the equation for 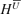 is explained in the Appendix and the result is
is explained in the Appendix and the result is 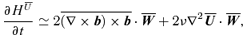
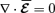 which, besides being consistent with the chosen boundary conditions, means that the induction of large-scale magnetic fields is maximal for
which, besides being consistent with the chosen boundary conditions, means that the induction of large-scale magnetic fields is maximal for 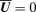 (cf. equation 4). Observe that by imposing Coulomb gauge on equation (5),2 we obtain a further constraint on the mean fields, namely
(cf. equation 4). Observe that by imposing Coulomb gauge on equation (5),2 we obtain a further constraint on the mean fields, namely 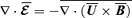 , and the fact that we consider it equal to zero allows us to replace
, and the fact that we consider it equal to zero allows us to replace 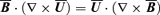 .
.3 IMPLEMENTING THE TWO-SCALE APPROXIMATION
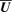 and
and 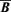 derived from
derived from 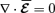 , and the fact that we are considering
, and the fact that we are considering 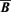 as force-free, we can write
as force-free, we can write 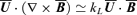 , where the last semi-equality stems from the fact that
, where the last semi-equality stems from the fact that 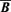 is considered to be force-free. From equations (10) and (11), we see that the dot product of
is considered to be force-free. From equations (10) and (11), we see that the dot product of 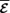 with
with 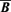 is responsible for magnetic helicity transport. Let us write
is responsible for magnetic helicity transport. Let us write 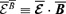 .3 Its evolution equation is
.3 Its evolution equation is 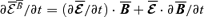 . Proceeding similarly as in Blackman & Field (2002) and Kandus et al. (2006), we obtain the following full form for the evolution equation for
. Proceeding similarly as in Blackman & Field (2002) and Kandus et al. (2006), we obtain the following full form for the evolution equation for 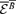 in the two-scale approximation:
in the two-scale approximation: 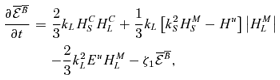
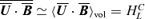 , the large-scale cross-helicity;
, the large-scale cross-helicity; 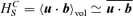 , the small-scale cross-helicity;
, the small-scale cross-helicity; 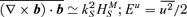 and
and 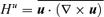 where these two last quantities are considered prescribed. Since we are considering
where these two last quantities are considered prescribed. Since we are considering 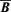 to be force-free, we replaced
to be force-free, we replaced 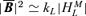 and
and 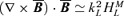 . The last term in equation (14),
. The last term in equation (14), 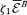 , includes the effect of viscosity, resistivity, the term
, includes the effect of viscosity, resistivity, the term 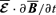 and, more importantly, the three-point correlations denoted by
and, more importantly, the three-point correlations denoted by 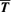 in equation (12). We see that besides the equations derived until now, we need the ones for HCL,S. The derivation of these equations is sketched in the Appendix and, although being a straightforward procedure, it is a rather tedious one and we end up with a system of seven equations, besides the four ones already shown above: the two equations for HCL,S, the ones for
in equation (12). We see that besides the equations derived until now, we need the ones for HCL,S. The derivation of these equations is sketched in the Appendix and, although being a straightforward procedure, it is a rather tedious one and we end up with a system of seven equations, besides the four ones already shown above: the two equations for HCL,S, the ones for 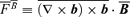 , i.e. the dot product of the small-scale Lorentz force with
, i.e. the dot product of the small-scale Lorentz force with  , for
, for 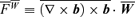 , for
, for  , for
, for 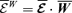 , i.e. the scalar product of the TEMF with the large-scale vorticity, and for
, i.e. the scalar product of the TEMF with the large-scale vorticity, and for 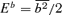 , i.e. the small-scale magnetic energy. Equation (14) is already expressed in the two-scale form. The other 10 equations read as
, i.e. the small-scale magnetic energy. Equation (14) is already expressed in the two-scale form. The other 10 equations read as 
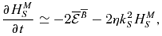
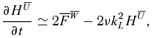
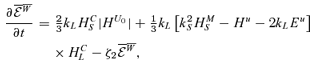
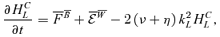
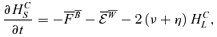
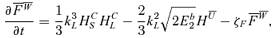
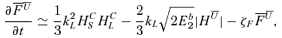
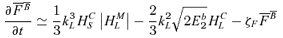

4 MAKING THE EQUATIONS NON-DIMENSIONAL
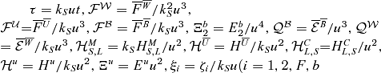 ), Re=νkS/u, Rm=ηkS/u, with Re the Reynolds number, Rm the magnetic Reynolds number and r=kL/kS. The non-dimensional equations then read as
), Re=νkS/u, Rm=ηkS/u, with Re the Reynolds number, Rm the magnetic Reynolds number and r=kL/kS. The non-dimensional equations then read as 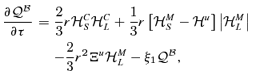
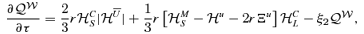

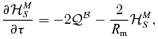
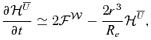
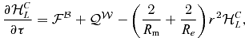
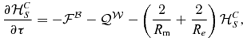
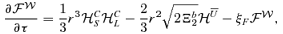
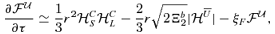
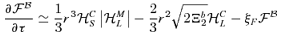
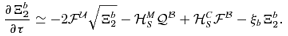
5 NUMERICAL RESULTS AND DISCUSSION
We numerically integrated equations (25)–(35) using the following parameters and initial conditions:  ,
,  and 2000 (i.e. magnetic Prandtl number Pm= 1), ξi= 1/2 (strong non-linearities) and ξi= 1/Rm (weak non-linearities).4 A comment about the chosen values for ξi is in order: in principle, this parameter can depend on Rm; however, results of numerical simulations show that it is of the order of unity for Rm < 100. In this sense, the value ξ= 1/2 would be in accordance with those results. As we are working here with larger values of Rm for which, to our knowledge, there is a lack of numerical estimations of ξi, we chose two values that might represent the two extreme behaviours of this parameter. Nevertheless, we must stress that the validity of this choice should be checked by direct numerical simulations. In Fig. 1, we plotted
and 2000 (i.e. magnetic Prandtl number Pm= 1), ξi= 1/2 (strong non-linearities) and ξi= 1/Rm (weak non-linearities).4 A comment about the chosen values for ξi is in order: in principle, this parameter can depend on Rm; however, results of numerical simulations show that it is of the order of unity for Rm < 100. In this sense, the value ξ= 1/2 would be in accordance with those results. As we are working here with larger values of Rm for which, to our knowledge, there is a lack of numerical estimations of ξi, we chose two values that might represent the two extreme behaviours of this parameter. Nevertheless, we must stress that the validity of this choice should be checked by direct numerical simulations. In Fig. 1, we plotted  as a function of τ for ξi= 1/2. The long dashed line corresponds to Rm= 200, while the short dashed one corresponds to Rm= 2000. We see that the generation of
as a function of τ for ξi= 1/2. The long dashed line corresponds to Rm= 200, while the short dashed one corresponds to Rm= 2000. We see that the generation of  is rather weak, but the effect seems to be stronger for Rm= 2000 as time passes. In Fig. 2, we plotted
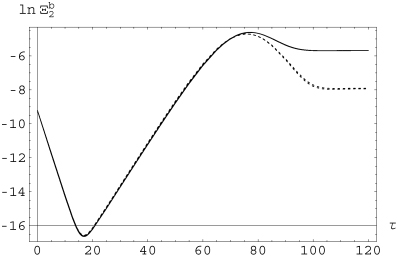
is rather weak, but the effect seems to be stronger for Rm= 2000 as time passes. In Fig. 2, we plotted  as a function of τ for ξi= 1/Rm. The full line corresponds to Rm= 200 while the dotted one corresponds to Rm= 2000. In this case, there is a strong production of large-scale kinetic helicity, it being stronger for Rm= 2000 at the beginning of the integration, while for later times there seems to be no difference between the outcomes for the two Rm considered. In Fig. 3, we plotted the logarithm of the small-scale magnetic energy, ln(Ξb2) as a function of τ, for ξi= 1/2. Each curve consists of two curves: one with the effect of
as a function of τ for ξi= 1/Rm. The full line corresponds to Rm= 200 while the dotted one corresponds to Rm= 2000. In this case, there is a strong production of large-scale kinetic helicity, it being stronger for Rm= 2000 at the beginning of the integration, while for later times there seems to be no difference between the outcomes for the two Rm considered. In Fig. 3, we plotted the logarithm of the small-scale magnetic energy, ln(Ξb2) as a function of τ, for ξi= 1/2. Each curve consists of two curves: one with the effect of  and the other without this field. This superposition of curves means that for the chosen value of ξi the effect of
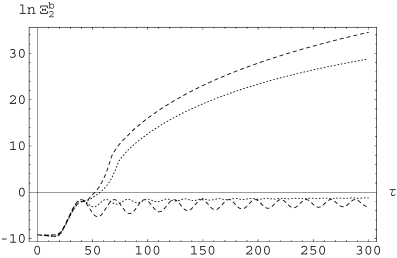
and the other without this field. This superposition of curves means that for the chosen value of ξi the effect of  on the evolution of small-scale magnetic energy is negligible. The upper curve corresponds to the largest value of Rm, and we see that in this case a saturation value for Ξb2 larger than for Rm= 200 is attained. In Fig. 4, we plotted the logarithm of the small-scale magnetic energy ln(Ξb) for ξi= 1/Rm. Long dashed curves correspond to Rm= 2000: upper curve contains the effect of
on the evolution of small-scale magnetic energy is negligible. The upper curve corresponds to the largest value of Rm, and we see that in this case a saturation value for Ξb2 larger than for Rm= 200 is attained. In Fig. 4, we plotted the logarithm of the small-scale magnetic energy ln(Ξb) for ξi= 1/Rm. Long dashed curves correspond to Rm= 2000: upper curve contains the effect of  , while the lower oscillating curve is without the action of those fields. Short dashed curves correspond to Rm= 200, with the same features for the presence and absence of
, while the lower oscillating curve is without the action of those fields. Short dashed curves correspond to Rm= 200, with the same features for the presence and absence of  . We see that the action of
. We see that the action of  strongly enhances the generation of small-scale magnetic energy, and again this effect is stronger for larger Rm. In Fig. 5, we plotted
strongly enhances the generation of small-scale magnetic energy, and again this effect is stronger for larger Rm. In Fig. 5, we plotted  as a function of τ for ξi= 1/2. Here, again each curve consists of two curves, one with the effect of
as a function of τ for ξi= 1/2. Here, again each curve consists of two curves, one with the effect of  and the other without, showing again that for strong non-linearities the effect of those flows is negligible, consistent with previous figures. The upper curve corresponds to Rm= 2000 while the lower curve corresponds to Rm= 200. We see that again for larger Rm there is an enhancement of
and the other without, showing again that for strong non-linearities the effect of those flows is negligible, consistent with previous figures. The upper curve corresponds to Rm= 2000 while the lower curve corresponds to Rm= 200. We see that again for larger Rm there is an enhancement of  . In Fig. 6, we plotted
. In Fig. 6, we plotted  as a function of τ for ξi= 1/Rm. We see here again that the action of large-scale flows enhances the mean electromotive force
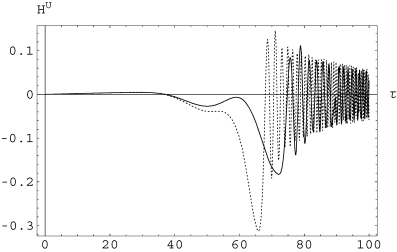
as a function of τ for ξi= 1/Rm. We see here again that the action of large-scale flows enhances the mean electromotive force  , and this enhancement is stronger for larger Rm. The oscillating, dotted-line curve corresponds to Rm= 2000, and the full-line curve to Rm= 200. The curves corresponding to the absence of the effect of those flows are almost indistinguishable from the τ-axis. In Fig. 7, we plotted
, and this enhancement is stronger for larger Rm. The oscillating, dotted-line curve corresponds to Rm= 2000, and the full-line curve to Rm= 200. The curves corresponding to the absence of the effect of those flows are almost indistinguishable from the τ-axis. In Fig. 7, we plotted  as a function of τ for ξ= 1/2. Here, again each curve consists of two curves, one with the effect of
as a function of τ for ξ= 1/2. Here, again each curve consists of two curves, one with the effect of  and the other without, showing again that for strong non-linearities the effect of those flows is negligible. The fast growing curve corresponds to Rm= 200 while the lower one corresponds to Rm= 2000. The coincidence of the two curves for short times corresponds to the kinematic regime, where back-reaction of the induced magnetic fields b did not take place yet. In Fig. 8, we plotted
and the other without, showing again that for strong non-linearities the effect of those flows is negligible. The fast growing curve corresponds to Rm= 200 while the lower one corresponds to Rm= 2000. The coincidence of the two curves for short times corresponds to the kinematic regime, where back-reaction of the induced magnetic fields b did not take place yet. In Fig. 8, we plotted  as a function of τ for ξ= 1/Rm. We see here again that the action of large-scale flows enhances the mean electromotive force
as a function of τ for ξ= 1/Rm. We see here again that the action of large-scale flows enhances the mean electromotive force  and this enhancement is stronger for larger Rm. Dashed curves correspond to Rm= 2000: the ones with the largest amplitude correspond to the action of
and this enhancement is stronger for larger Rm. Dashed curves correspond to Rm= 2000: the ones with the largest amplitude correspond to the action of  , while the lower amplitude corresponds to the absence of this effect. The full line corresponds to Rm= 200 and the features with respect to the presence and absence of large-scale flows are the same as for Rm= 200. The coincidence of all four curves at the beginning of the evolution corresponds to the kinematic regime. In Fig. 9, we plotted
, while the lower amplitude corresponds to the absence of this effect. The full line corresponds to Rm= 200 and the features with respect to the presence and absence of large-scale flows are the same as for Rm= 200. The coincidence of all four curves at the beginning of the evolution corresponds to the kinematic regime. In Fig. 9, we plotted  as a function of τ for ξi= 1/2. The dashed line curve corresponds to Rm= 2000 while the full line corresponds to Rm= 200. Consistently with Fig. 1, we see that
as a function of τ for ξi= 1/2. The dashed line curve corresponds to Rm= 2000 while the full line corresponds to Rm= 200. Consistently with Fig. 1, we see that  is larger for larger Rm. In Fig. 10, we plotted
is larger for larger Rm. In Fig. 10, we plotted  as a function of τ for ξi= 1/Rm. The dotted line corresponds to Rm= 2000 while the full corresponds line to Rm= 200. Consistently with Fig. 2, we see that
as a function of τ for ξi= 1/Rm. The dotted line corresponds to Rm= 2000 while the full corresponds line to Rm= 200. Consistently with Fig. 2, we see that  is larger for Rm= 2000 than for Rm= 200, with the difference in amplitudes between both quantities getting smaller with time.
is larger for Rm= 2000 than for Rm= 200, with the difference in amplitudes between both quantities getting smaller with time.
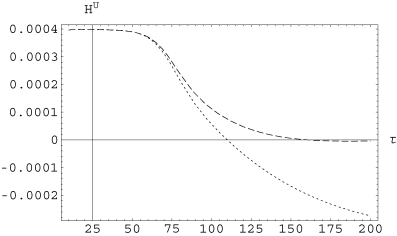
Large-scale kinetic helicity  as a function of τ for ξi= 1/2. The long dashed line corresponds to Rm= 200, and the dotted line to Rm= 2000. The generation of
as a function of τ for ξi= 1/2. The long dashed line corresponds to Rm= 200, and the dotted line to Rm= 2000. The generation of  is stronger for the largest value of Rm.
is stronger for the largest value of Rm.
Large-scale kinetic helicity  as a function of τ for ξi= 1/Rm. The full line corresponds to Rm= 200, and the dotted one to Rm= 200. At the beginning, the induction of
as a function of τ for ξi= 1/Rm. The full line corresponds to Rm= 200, and the dotted one to Rm= 200. At the beginning, the induction of  is stronger for the largest value of Rm.
is stronger for the largest value of Rm.
Logarithm of the small-scale magnetic energy Ξb2 as a function of τ, for ξi= 1/2. Each curve is in fact two curves, with and without the effect of  , which means that in this case the effect of those flows is negligible. The upper curve corresponds to Rm= 2000 and the lower one to Rm= 200. The small-scale magnetic energy density is very small although larger for Rm= 2000.
, which means that in this case the effect of those flows is negligible. The upper curve corresponds to Rm= 2000 and the lower one to Rm= 200. The small-scale magnetic energy density is very small although larger for Rm= 2000.
Logarithm of the small-scale magnetic energy Ξb2 as a function of τ for ξi= 1/Rm. The upper, long dashed curve corresponds to the presence of  , while the lower, oscillating one corresponds to the absence of those flows, both of them for Rm= 2000. Short dashed curves represent the same quantities but for Rm= 200. In this case, large-scale flows strongly enhance the production of small-scale magnetic energy, and this effect is again stronger for larger values of Rm.
, while the lower, oscillating one corresponds to the absence of those flows, both of them for Rm= 2000. Short dashed curves represent the same quantities but for Rm= 200. In this case, large-scale flows strongly enhance the production of small-scale magnetic energy, and this effect is again stronger for larger values of Rm.
Mean electromotive force  as a function of τ for ξi= 1/2. Each curve is two curves, one with the effect of
as a function of τ for ξi= 1/2. Each curve is two curves, one with the effect of  and the other without those fields, showing that for this value of ξ the effect of those fields is negligible. The upper curve corresponds to Rm= 2000 and the lower curve to Rm= 200, which shows that for the largest
and the other without those fields, showing that for this value of ξ the effect of those fields is negligible. The upper curve corresponds to Rm= 2000 and the lower curve to Rm= 200, which shows that for the largest  is slightly stronger.
is slightly stronger.
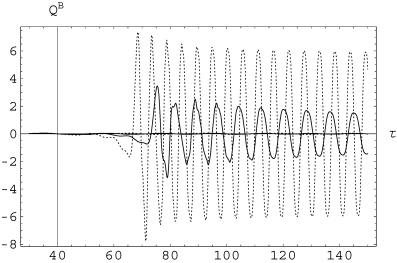
Mean electromotive force  as a function of τ for ξi= 1/Rm. The dotted line corresponds to Rm= 2000 and the full line to Rm= 200. The curves corresponding to the absence of large-scale flows are of negligible amplitude and almost indistinguishable from the τ-axis, showing that in this case the enhancement of the TEMF by the shear fields is very strong.
as a function of τ for ξi= 1/Rm. The dotted line corresponds to Rm= 2000 and the full line to Rm= 200. The curves corresponding to the absence of large-scale flows are of negligible amplitude and almost indistinguishable from the τ-axis, showing that in this case the enhancement of the TEMF by the shear fields is very strong.
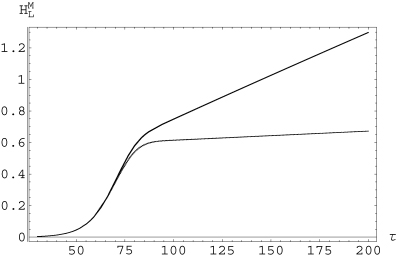
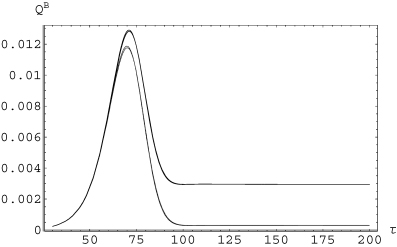
Large-scale magnetic helicity  as a function of τ, for ξi= 1/2. Again, in this figure, each curve is two curves, one with the effect of
as a function of τ, for ξi= 1/2. Again, in this figure, each curve is two curves, one with the effect of  and the other without, showing that the effect of those flows on the evolution of magnetic helicity is negligible for the chosen value of ξi. The growing curve corresponds to Rm= 200, while the slowly growing, lower curve corresponds to Rm= 2000.
and the other without, showing that the effect of those flows on the evolution of magnetic helicity is negligible for the chosen value of ξi. The growing curve corresponds to Rm= 200, while the slowly growing, lower curve corresponds to Rm= 2000.
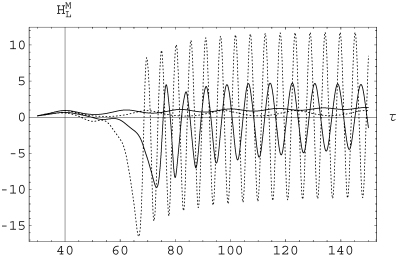
Large-scale magnetic helicity  as a function of τ, for ξi= 1/Rm. Dotted curves correspond to Rm= 2000, while continuous curves correspond to Rm= 200. In each case, the strongly oscillating curves correspond to the action of large-scale flows, while the slow oscillations correspond to their absence. Consistently with what was shown in Fig. 6, the action of
as a function of τ, for ξi= 1/Rm. Dotted curves correspond to Rm= 2000, while continuous curves correspond to Rm= 200. In each case, the strongly oscillating curves correspond to the action of large-scale flows, while the slow oscillations correspond to their absence. Consistently with what was shown in Fig. 6, the action of  enhances the cascade of magnetic helicity.
enhances the cascade of magnetic helicity.
Large-scale cross-helicity  as a function of τ for ξi= 1/2. Consistently with Fig. 1, the generation of large-scale cross-helicity is stronger for Rm= 2000 (dashed line) than for Rm= 200 (full line).
as a function of τ for ξi= 1/2. Consistently with Fig. 1, the generation of large-scale cross-helicity is stronger for Rm= 2000 (dashed line) than for Rm= 200 (full line).
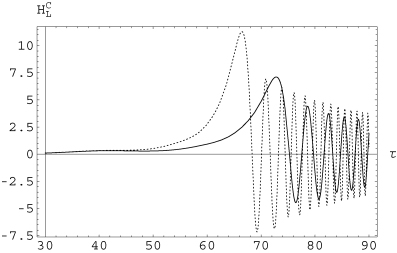
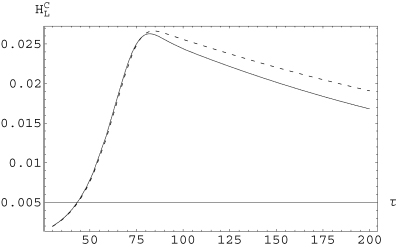
Large-scale cross-helicity  as a function of τ, for ξi= 1/Rm. Consistently with Fig. 2, the generation of large-scale cross-helicity is stronger for Rm= 2000 (dotted line) than for Rm= 200 (continuous line).
as a function of τ, for ξi= 1/Rm. Consistently with Fig. 2, the generation of large-scale cross-helicity is stronger for Rm= 2000 (dotted line) than for Rm= 200 (continuous line).
6 CONCLUSIONS
In this paper, we studied semi-analytically and qualitatively the generation of large-scale flows by the action of a turbulent MFD, and the back-reaction of those flows on the turbulent electromotive force for two values of magnetic Reynolds number, Rm= 200 and 2000, and magnetic Prandtl number Pm= 1. We considered a system in which small-scale turbulent flows are fully helical and prescribed by a given external mechanism, i.e. a kinematically driven dynamo, and that this system possesses boundary conditions such that all total divergencies vanish. The turbulence was considered to be homogeneous and isotropic, which, although being of limited applicability to obtain quantitative results for real systems, serves to study many conceptual aspects of large-scale magnetic field generation, besides enormously simplifying the mathematics. We followed the evolution of large-scale flows through their associated kinetic helicity  , as one of the suppositions we made was that those flows were fully helical too. One crucial assumption we made was that
, as one of the suppositions we made was that those flows were fully helical too. One crucial assumption we made was that  , which, due to the Coulomb gauge, imposed a further constraint on
, which, due to the Coulomb gauge, imposed a further constraint on  and
and  that allowed us to express several terms as large-scale cross-helicity. Another one was to assume that
that allowed us to express several terms as large-scale cross-helicity. Another one was to assume that  is force-free and the main reason to adopt it is that it helped to simplify the mathematics. Although this condition can be fulfilled in certain astrophysical environments, this is not a general situation; therefore it should be dropped off in future works that aim at generalizing this work.
is force-free and the main reason to adopt it is that it helped to simplify the mathematics. Although this condition can be fulfilled in certain astrophysical environments, this is not a general situation; therefore it should be dropped off in future works that aim at generalizing this work.
We found that large-scale flows act on the TEMF  through large- and small-scale cross-helicities and that for the minimal τ closure considered here, the effect of those fields is stronger for large relaxation times (ξi= 1/Rm). For short relaxation time (ξi= 1/2), the effect of those fields seems to be negligible. The choice of the values for ξi was arbitrary, in the sense that, to our present knowledge, it is not known how that parameter depends on the magnetic Reynolds number for Rm > 100. For Rm < 100, it seems to be confirmed that ξi is of the order of unity. Here, we chose to work with two values that may be considered as representative of two extreme possibilities: ξi= 1/2 would be consistent with the predictions of the numerical simulations (although they were made for a different Rm interval), while ξ= 1/Rm would represent a resistive case. In any case, more reliable values should be given by numerical simulations performed for Rm > 100.
through large- and small-scale cross-helicities and that for the minimal τ closure considered here, the effect of those fields is stronger for large relaxation times (ξi= 1/Rm). For short relaxation time (ξi= 1/2), the effect of those fields seems to be negligible. The choice of the values for ξi was arbitrary, in the sense that, to our present knowledge, it is not known how that parameter depends on the magnetic Reynolds number for Rm > 100. For Rm < 100, it seems to be confirmed that ξi is of the order of unity. Here, we chose to work with two values that may be considered as representative of two extreme possibilities: ξi= 1/2 would be consistent with the predictions of the numerical simulations (although they were made for a different Rm interval), while ξ= 1/Rm would represent a resistive case. In any case, more reliable values should be given by numerical simulations performed for Rm > 100.
Due to the simple system considered and the approximations we made, we do not intend to find quantitative results, such as for example estimate the time interval during which  is valid, nor do we extract more conceptual and qualitative conclusions. We end this work stressing on the importance of studying this problem via numerical simulations, which will show us the next paths to follow in a further analytical study, besides confirming or contesting the results presented here. The semi-analytical study of the anisotropic case is also of most importance, as well as the consideration of other boundary conditions.
is valid, nor do we extract more conceptual and qualitative conclusions. We end this work stressing on the importance of studying this problem via numerical simulations, which will show us the next paths to follow in a further analytical study, besides confirming or contesting the results presented here. The semi-analytical study of the anisotropic case is also of most importance, as well as the consideration of other boundary conditions.
Overlines denote local spatial averages: they represent vector quantities whose intensities may vary in space, but whose direction and sense are uniform or vary smoothly. 〈〉vol denote volume averages, i.e. quantities that can depend only on time.
We cannot use equation (8) for a to calculate  as it is trivially zero.
as it is trivially zero.
Observe that in contrast to previous works, here  is the dot product of the TEMF with
is the dot product of the TEMF with  , and not the component of that force along the mean magnetic field. We chose to work with this function because it facilitates the numerical integration of the equations, while preserving the generic behaviour of the projections.
, and not the component of that force along the mean magnetic field. We chose to work with this function because it facilitates the numerical integration of the equations, while preserving the generic behaviour of the projections.
As before, subindex ‘i’ denotes 1, 2, F and b. In each integration, we assume that all ξi are the same for all ‘i’.
∇·〈 (∇×b) ×b〉=−b·∇2b− | ∇×b|2≃k2S| b|2−k2S| b|2= 0.
We thank P. Mininni for suggesting the idea of this work and the referee for many suggestions and comments that helped to improve it. Financial support from FAPESB, grant APR205/2005, is acknowledged. The present work was done under project PROPP-UESC 00220.1300.489.
REFERENCES
Appendices
APPENDIX A: DEDUCTION OF THE COMPLEMENTARY EVOLUTION EQUATIONS
Here, we sketch the derivation of the evolution equation for the large-scale kinetic helicity as well as the set of extra equations needed to study the problem considered in this article.
A1 Evolution equation for the large-scale vorticity
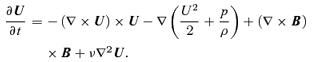
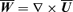 is obtained by simply taking the curl of equation (A1), after replacing the decomposition in mean and stochastic fields, and using the hypothesis that u is fully helical. We have
is obtained by simply taking the curl of equation (A1), after replacing the decomposition in mean and stochastic fields, and using the hypothesis that u is fully helical. We have 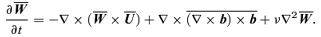
A2 Evolution equation for the large-scale kinetic helicity
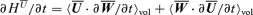 . Replacing the corresponding equations, we obtain
. Replacing the corresponding equations, we obtain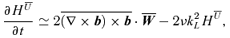
 . We define
. We define 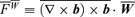 , and thus equation (A3) reads
, and thus equation (A3) reads 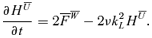
A3 Evolution equation for ![formula]() and its projections
and its projections
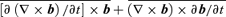 . After a somewhat lengthy, but straightforward, calculation, where it is assumed that for the two-scale approximation
. After a somewhat lengthy, but straightforward, calculation, where it is assumed that for the two-scale approximation 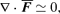 5 we obtain
5 we obtain 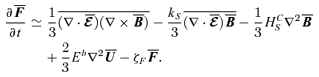
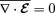 , so equation (A5) reduces to
, so equation (A5) reduces to 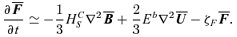
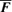 with
with 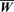 and
and 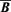 , we use the above defined expression
, we use the above defined expression 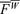 , and an analogous expression for
, and an analogous expression for 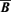 . Again, the evolution equation is found by taking the time derivative of the complete expression. In the two-scale approximation, we have
. Again, the evolution equation is found by taking the time derivative of the complete expression. In the two-scale approximation, we have 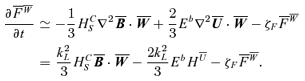
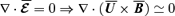 , we can write
, we can write 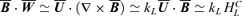 . Using the fact that for a fully helical
. Using the fact that for a fully helical 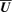 field we can write
field we can write 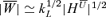 , we obtain
, we obtain 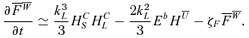
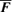 along
along  and along
and along 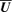 we proceed analogously as for
we proceed analogously as for 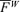 . Using the fact that for a large-scale force-free field we can write | B0| =k1/2L| HML|1/2, we obtain
. Using the fact that for a large-scale force-free field we can write | B0| =k1/2L| HML|1/2, we obtain 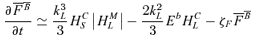
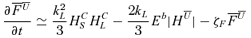
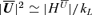 .
.A4 Evolution equation for the cross-helicity
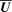 and u and using equation (4) and (7), we obtain the following equation for the large-scale cross-helicity, HCL, and the small-scale cross-helicity HCS:
and u and using equation (4) and (7), we obtain the following equation for the large-scale cross-helicity, HCL, and the small-scale cross-helicity HCS: 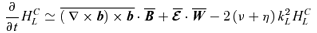
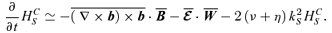
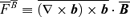 , defining
, defining 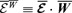 , and using the fact that for fully helical
, and using the fact that for fully helical 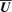 we can write
we can write 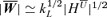 , in the two-scale approximation we have
, in the two-scale approximation we have 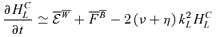
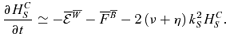
A5 Evolution equation for ![formula]()
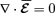 , we obtain
, we obtain 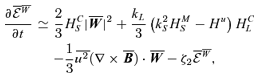
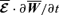 , and the three-point correlations. Performing
, and the three-point correlations. Performing 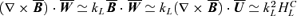 , where the semi-equality before the last stems from the fact that
, where the semi-equality before the last stems from the fact that 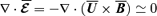 , we obtain
, we obtain 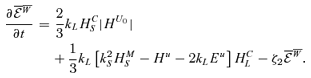
A6 Evolution equation for Eb
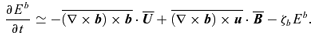
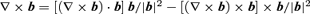 and thus
and thus