Abstract
We have performed two-dimensional (2D) hydromagnetic simulations with an adaptive mesh refinement code to examine the response of a pre-existing initially spherical dense core to a non-linear fast-mode wave. One key parameter is the ratio of the wavelength to the initial core radius. If that ratio is large and the wave amplitude is sufficient, significant compression of the core occurs, as envisaged by Myers & Lazarian in their ‘turbulent cooling flow’ picture. For smaller values of that ratio, an initial value of the ratio of the thermal pressure to magnetic pressure of 0.2, and sufficiently large wave amplitude, the scattering induces the production of dense substructure in the core. This substructure may be related to that detected in the dense core associated with the cyanopolyyne peak in TMC-1. Our simulations also show that short-wavelength waves, contrary to large-wavelength waves, do not confine dense cores.
1 INTRODUCTION
Ballesteros-Paredes & MacLow (2002), Padoan & Nordlund (2002), Gammie et al. (2003), Li et al. (2004), Nakamura & Li (2005) and Vázquez-Semadeni et al. (2005) are amongst the authors who have performed three-dimensional (3D) simulations to investigate the formation of clumps in media in which the value of β, the ratio of the thermal pressure to magnetic pressure, is initially small everywhere but in which velocity perturbations exist. These calculations have included many ingredients.
In three previous papers, we have carried out one-dimensional (1D) (Falle & Hartquist 2002, hereafter FH02; Lim, Falle & Hartquist 2005, hereafter LFH05) and two-dimensional (2D) (Van Loo, Falle & Hartquist 2006, hereafter VFH06) numerical studies of magnetohydrodynamic (MHD) waves in low-β plasma to elucidate the mechanism by which clumps form. We consider the results of particular relevance to the formation of dense cores (e.g. Caselli et al. 2002) within translucent clumps like those discovered in CO maps of the Rosette Molecular Cloud (Williams, Blitz & Stark 1995). The FH02 and VFH06 studies concerned small-amplitude waves and involved 1D and 2D calculations, respectively. A significant difference in the results of the two studies is that dense core-like structures persisted longer in the 2D simulations than in the 1D simulations. In 2D, such a structure survived as long as the amplitude that might be loosely associated with the fast-mode component of the large-scale perturbation remained a significant fraction of its initial value.
The interaction of fast-mode waves with large-scale density inhomogeneities produced substructure within the large-scale clumps. The large-scale structures themselves arise due to the non-linear steepening of the fast-mode waves. The present paper is concerned with a related but somewhat different problem: the response of a pre-existing dense core-like structure to a background wave. The effect of large-amplitude hydromagnetic waves has already been studied analytically by McKee & Zweibel (1992). Using a time-averaged form of the virial theorem, they showed that a turbulent medium can pressure-confine a dense clump. A limitation of their analysis is that it does not describe the effect of large-wavelength perturbations. With our numerical model, we can study the effect of both large and small wavelength perturbations.
Numerical simulations of this problem are limited, as most studies (e.g. Mac Low, McKee & Klein 1994) only describe the effect of a shock hitting an inhomogeneity. The flow initially compresses the dense core, but eventually destroys and fragments the core. A similar behaviour can also be expected for non-linear waves. Our simulations can be considered a natural extension and generalization of work on shocks interacting with inhomogeneities.
The response of a dense core to a background wave may well be relevant to the detection of substructure in Core D, which coincides with the cyanopolyyne peak, in the TMC-1 by Peng et al. (1998). TMC-1 is a ridge of dense cores, each of which has a size of 0.1–0.2 pc and a mass of one to several solar masses (e.g. Hirahara et al. 1992). The substructures studied by Peng et al. (1998) have sizes of 0.03–0.06 pc and masses of 0.01–0.15 M⊙. Most are not bound by self-gravity and are too small to produce brown dwarfs. Since many of these substructures have masses below the Jeans mass, they must have formed by some mechanism other than gravitational instability.
A possible mechanism for forming the substructure may be the same as or related to the mechanism giving rise to dense core formation in the picture that we have pursued in FH02, LFH05 and VFH06 and which is, no doubt, contributing to dense core formation in the other numerical simulations referenced above. However, that mechanism ceases to give large density contrast structures if β≥ 1 unless the amplitude of the wave is hyper-Alfvénic (FH02; LFH02). Some dense cores may have values of β as low as 0.1 (e.g. Ward-Thompson et al. 2000; Ward-Thompson 2002) but some may have values of β greater than unity (e.g. Kirk, Ward-Thompson & Crutcher 2006). The lines emitted by species such as CS, NH3 and CO in dense cores show substantial non-thermal components to their broadening, which are, however, usually not highly supersonic with respect to the thermal sound speed in H2 (e.g. Fuller & Myers 1992). For the substructure in Core D of TMC-1, the non-thermal line broadening component is important but in most substructures markedly subsonic in the above sense. The fact that dense cores possess substantial non-thermal internal velocities and, in some cases, have values of β somewhat below unity supports the possibility that wave scattering on a dense core may lead to substructure like that of TMC-1's Core D.
In the present paper we examine the effect of MHD waves on dense cores. Additionally, we derive the properties of the waves that produce substructures within dense cores. The paper is structured as follows. In Section 2 we describe the numerical model. We then describe how the dense core evolves in the absence of MHD waves (Section 3) in order to understand the effect of the waves (Section 4). Finally, we summarize and discuss these results in Section 5.
2 NUMERICAL MODEL
We can use different approaches to study the effect of MHD waves on a dense core. One way is to continuously excite a wave at the boundary of the computational domain. The wave then propagates to the core and interacts with it. Another option is to embed a dense core in a wave. In our calculations we use the latter as dense cores arise where the waves are.
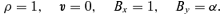
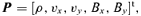
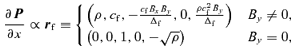
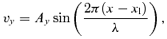
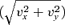is equal to a given amplitude A. The initial state at a position x+Δx and y can then be calculated using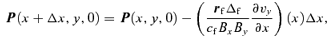 
We still need to embed a dense core in the fast-mode wave. We represent the core by a uniformly dense region of radius r at the centre of the computational box. The density ρ0 of the core is taken such that β within the core is between 0.1 and 1 as polarization observations suggest (Ward-Thompson et al. 2000; Ward-Thompson 2002) for some dense cores. As β= 2ρa2/B2, the core density must lie between 5 and 50 for a= 0.1. Note that there is a small variation of β within a dense core as the magnetic pressure changes across the core.
Our model can then be specified by the isothermal sound speed a, the value α for background By field, the wave properties (i.e. the wavelength λ and the amplitude A) and the core properties (i.e. the density ρ0 and radius r). However, as we use dimensionless units, the radius of the core and the wavelength of the fast-mode wave are not independent parameters. The relevant free parameter is λ/r. Therefore, we assume a fixed core radius of r= 2 in all our calculations and only vary λ.
To solve the 2D MHD equations we use an adaptive mesh refinement code. The basic algorithm is a second-order Godunov scheme which uses a linear Riemann solver (Falle 1991). We included the divergence cleaning algorithm of Dedner et al. (2002) to stabilize the numerical scheme. The code uses a hierarchy of grids such that the grid spacing of level n is Δx/2n, where Δx the grid spacing of the coarsest level. A refinement criterion determines where in the computational domain a finer grid is needed. The computational domain is −10 < x < 10 and −10 < y < 10 and we use periodic boundary conditions. The finest grid has a resolution of 800 × 800.
3 EVOLUTION OF A DENSE CORE IN THE ABSENCE OF MHD WAVES
In an isothermal gas a dense core is overpressured, which means that the core expands. As this introduces waves and shocks into the background medium even when the core is not embedded in a wave, it is convenient to discuss this expansion in the absence of an embedding wave. This problem is the magnetic version of the 2D isothermal Riemann problem.
In a purely hydrodynamical case, a shock develops and propagates outward into the rarefied gas. At the same time, a rarefaction wave reduces the density inside the core by travelling inward. As there is no preferred direction, the expansion is isotropic. However, this is no longer true in a magnetized medium because waves (and, thus, also shocks) have a propagation speed which depends on the angle between the magnetic field and the direction of propagation. Fig. 1 shows the expansion of a dense core in a magnetic field.
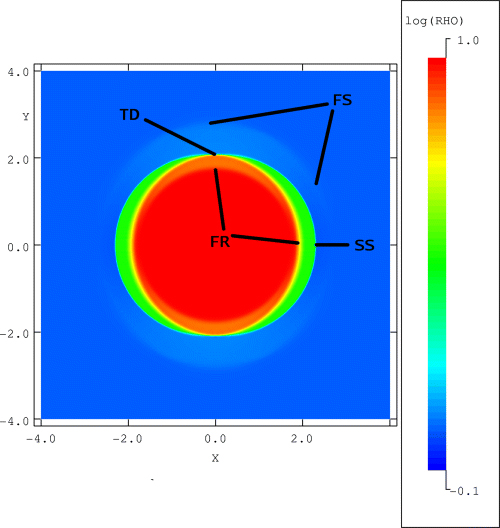
The density structure of an expanding dense core. The expansion depends strongly on the angle between the propagation direction and the magnetic field. Perpendicular to the field a fast-mode shock (FS) propagates outward and a fast-mode rarefaction (FR) inward. These waves are separated by a tangential discontinuity (TD). For expansion at oblique angles the TD breaks up into a slow-mode shock (SS) and a slow-mode rarefaction (SR). Parallel to the field the FS disappears. The model parameters are ρ0= 10, a= 0.316 and α= 0. The core is not embedded in a wave.
Slow-mode waves or Alfvén waves cannot propagate perpendicular to the magnetic field. Thus, only fast-mode features develop in those directions. A weak fast-mode shock is propagating outward into the background medium, while a fast-mode rarefaction wave propagates into the dense core. The magnetic pressure increases in material through which the shock and rarefaction wave have passed. A tangential discontinuity1 exists between the material that has passed through the front of the rarefaction wave and the material that has passed through the shock. The total pressure (pg+B2/2) is continuous at the tangential discontinuity but neither pg nor B2/2 is. The fast-mode shock is sufficiently weak that it does not produce a large density discontinuity. Hence, the largest jump in density is at the tangential discontinuity. As it coincides with the edge of the expanding dense core, the tangential discontinuity moves outward with the gas swept up by the fast-mode shock.
Slow-mode waves do exist for directions oblique and parallel to the magnetic field. A slow-mode shock moves outward and a slow-mode rarefaction wave propagates inward. These slow-mode features lie between the fast-mode shock and rarefaction wave. Although the tangential discontinuity disappears, there is still a sheet in between the slow-mode shock and rarefaction wave separating the initial core material and the shocked background material.
The density of the material within a region bounded by the slow-mode shock is comparable to that of the dense core material that has passed through the slow-mode rarefaction wave, which would make the observational identification of the dense-core boundary difficult. Since the slow magnetosonic speed increases when the angle with the magnetic field decreases, the expansion of the core is faster along the magnetic field lines than perpendicular to it.
In our calculation the fast-mode shock weakens when the angle between its direction of propagation and the magnetic field decreases. For parallel expansion the fast-mode shock even turns into a linearized wave. Also, the slow-mode rarefaction wave merges with the fast-mode rarefaction (see Fig. 1).
Finally, the core disperses as there is no force holding it together. The dispersal is faster for higher initial densities of the core. Also, when the thermal gas pressure becomes more dominant in the background gas (i.e. β increases), the dense core disappears more quickly.
4 A DENSE CORE EMBEDDED IN AN MHD WAVE
When a dense core is embedded in a fast-mode wave, density substructures can be generated by the interaction between the wave and the core. The analysis in FH02 shows that high-density contrasts are associated with slow-mode waves when β is small. They also showed that non-linear steepening of a fast-mode wave can readily excite these slow-mode components.
To produce substructures, slow-mode waves must be excited within the core itself (as their propagation speed is low). This means that the time-scale for non-linear steepening tns≈λ/2 A must be smaller or comparable to the Alfvén crossing time tA=r/cA. We immediately see that for large wavelengths tns≫tA even if their amplitude is comparable to the Alfvén speed. Short-wavelength waves, however, steepen within the core itself as long as their amplitude is not too small.
The interplay between MHD waves and a dense core is, thus, wavelength dependent. Therefore, it is convenient to discuss the results for long and short waves separately. We typically take λ= 20 and λ= 2 in our calculations.
4.1 Results for large wavelengths
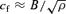(for a < ca). This means that a part of the wave – i.e. the part within the core – moves slower than the rest of the wavefront. Consequently, the velocity of the gas must change at the boundary of the core. However, more importantly, this induces a change in the magnetic field at the boundary of the core, which follows directly from the induction equation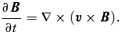 
Thus, the interaction with the wave causes an increase of the magnetic pressure. While there is initially no discontinuity in the total pressure perpendicular to the magnetic field (see Section 3), the total pressure outside the core can be much higher than inside the core. The magnitude of this change depends on the amplitude of the fast-mode wave. Small-amplitude waves are too weak to produce any significant change and the core then disperses as though no fast-mode wave is present in the background gas (see Fig. 2). However, when the amplitude of the fast-mode wave is large, the magnetic pressure increases significantly. Now the region outside the core is overpressured compared to the core itself. A fast-mode shock arises and propagates into the core. This shock is weak and, therefore, compresses the gas by a small factor as can be seen in Fig. 3(a).
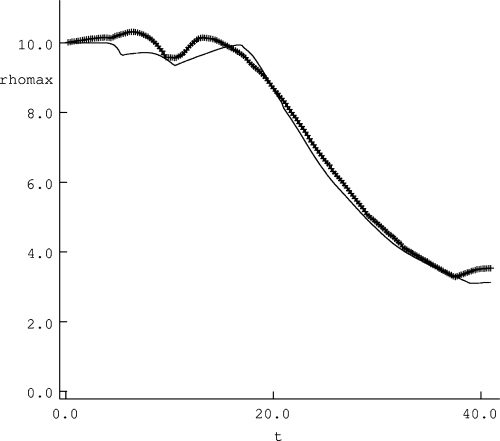
The temporal evolution of the maximum density within the dense core. The thin solid line shows the evolution in a homogeneous background gas (i.e. A= 0), while the thick solid line represents a model with a small-amplitude wave. The model parameters are ρ0= 10, α= 0.25, λ= 20, A= 0.05 and a= 0.1. Initially, β= 0.2 in the dense core.
(a) Similar to Fig. 2, but now for a large-amplitude fast wave. (b) The plasma β associated with the fluid element that has the highest density. The model parameters are given by ρ0= 10, α= 0.25, λ= 20, A= 0.5 and a= 0.1.
Although the expected increase in density from the motion of the wave across the core is small, Fig. 3(a) shows that the maximum density increases significantly for t > 20. We also find that most mass is concentrated within a single region. As the time-scale corresponds to the time for a wave to steepen into a shock (tns≈ 20 for λ= 20 and A= 0.5), we expect that this high-density structure is generated by the interaction between the fast-mode shock and the core exciting slow-mode waves. However, β needs to smaller than unity for this process to be effective (see the analysis in FH02). Fig. 3(b) shows that β for the fluid element associated with the maximum density obeys this constraint reasonably well.
We can now examine how the model parameters influence the wave–core interaction. Of all parameters the wave amplitude is perhaps the most important. The wave amplitude determines how much the magnetic pressure changes at the boundary. Small-amplitude waves do not affect the evolution of the core, while large-amplitude waves modify the entire core structure. In the latter case, a core can be compressed to a density considerably higher than the initial one. The maximum density is limited by the β≲ 1 constraint. Because of this constraint, it is also more difficult to produce high-density contrasts in models where ρ0 and a are high. Then β is already close to unity or higher.
When the wavelength is larger than the radius of the core, the initial position of the core centre with respect to a wave node becomes an additional free parameter. However, the fast-mode wave still propagates with a lower speed inside the core. The variations described above always occur. Hence, the results are essentially independent of the initial position.
4.2 Results for small wavelengths
A small-wavelength wave steepens much faster into a shock than one with a large wavelength. If the amplitude of the small-wavelength wave is not too small, the time-scale for non-linear steepening is shorter than the Alfvén crossing time. This means that a shock arises before the wave leaves the dense core. Then the generation of density substructures can be readily described with the models of FH02 and VFH06.
When a fast-mode wave steepens into a shock, slow-mode waves are excited. This produces persistent perturbations with large density contrasts. The fast-mode wave is most efficient in exciting the slow-mode components for modest values of α, which is the tangent of the angle between its direction of propagation and the magnetic field. Steepening is slower for very small values of α and the shock does not produce slow-mode waves, when α is too large (FH02).
Similar to Fig. 3, but now for λ= 2.
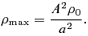
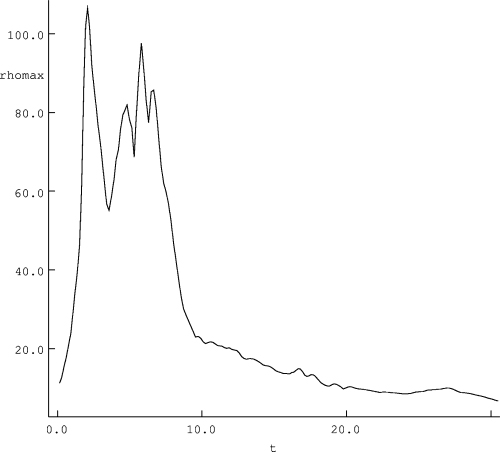
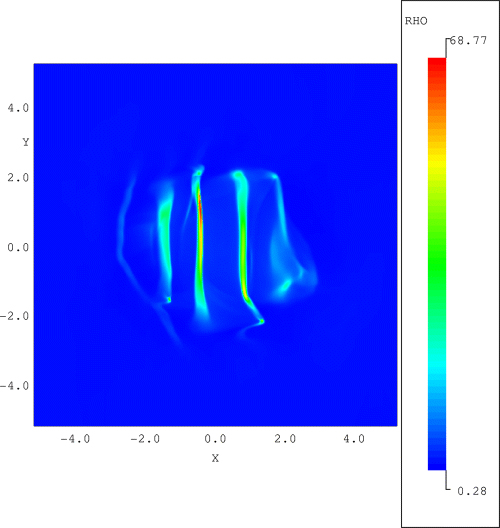
The density structure at t= 3 inside the dense core. The high-density regions are produced due to non-linear steepening of the fast-mode wave. The initial state is given by λ= 2, A= 0.5, te= 0.01, α= 0.25 and ρ0= 10.
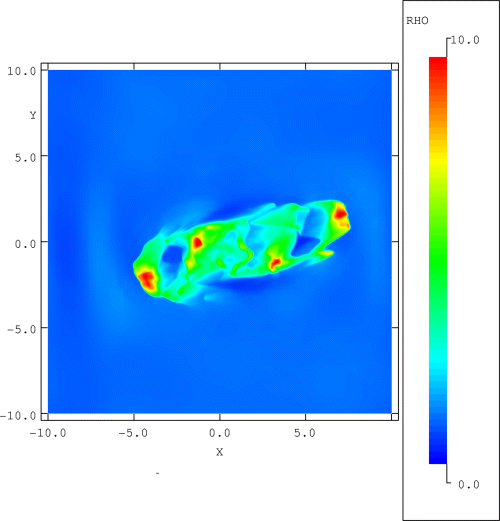
Similar to Fig. 5, but now for t= 18. Dense substructures form within the expanding core due to the interaction between dense regions and the initial fast mode.
High-density structures do not only arise inside the core, but also at the boundary. In the explanation above, we neglected the effects occurring at the boundary of the core. In a similar way as for the large-wavelength waves, overpressured regions arise producing fast-mode shocks which move into the core. Because of the compression caused by the fast-mode shock, dense substructures, thus, not only form inside the core but also at the boundary of the core.
5 SUMMARY AND DISCUSSIONS
We have studied the interaction between magnetosonic waves and dense cores for which the ratio, β, of thermal gas pressure to magnetic pressure is initially 0.2. We follow the evolution of a core embedded in a fast-mode wave. We find that large-amplitude waves can change the evolution of the core considerably.
The interaction between the fast-mode wave and a dense core depends strongly on the relative size of the core to the wavelength. When the core radius is smaller than the wavelength, the strongest effects are induced near the boundary of the core. Eventually, these effects disrupt the global structure of the core, but confine it. Furthermore, we find that a core can be compressed significantly. This result suggests that a large-wavelength fast-mode wave can trigger the collapse of a gravitationally unbound dense core, which is of relevance to the turbulent cooling flow picture of Myers & Lazarian (1998). However, additional calculations which include self-gravity are required to confirm this.
Short-wavelength waves, on the other hand, play an important role in the generation of substructure in a core without breaking up the core. However, contrary to the large-wavelength waves, the dense core expands faster than without the scattering wave. The wave thus does not confine the core. Although β is close to unity in our simulations, slow-mode waves excited by the non-linear steepening of the fast-mode wave produce high-density contrasts within the core. Such small-scale features have been observed in the cores of cold dense clouds such as TMC-1 (Peng et al. 1998). We do not find the large number of microclumps inferred from observations of Core D, but this can be readily explained by the limitations of our model. The most important limitation is perhaps that we only studied the effect of a single wave. A real velocity field is more accurately described as a superposition of an ensemble of waves. Because of wave–wave interactions, large structures then break up into smaller ones.
Hartquist, Williams & Viti (2001) showed that the substructures in Core D need to be about 0.1 Myr old to comply with the observed molecular variety and abundances. If the substructures are being generated due to slow-mode excitation, the time-scales should be of the same order. For a core radius of R= 0.1 pc and a= 0.3 km s−1 and a somewhat larger Alfvén speed, the substructures in our simulations arise on time-scales of a few 105 yr (a few times R/ca which is the relevant time-scale in our simulations). As both time-scales are of the same order, the microstructure in dense cold core can indeed be generated by small-wavelength magnetosonic waves.
A discontinuity is a tangential discontinuity if there is neither magnetic flux nor mass flux across it, i.e. un= 0 and Bn= 0 (Burgess 1995).
SVL gratefully acknowledges the financial support of PPARC.
REFERENCES
