-
PDF
- Split View
-
Views
-
Cite
Cite
Volker Springel, Lars Hernquist, Cosmological smoothed particle hydrodynamics simulations: the entropy equation, Monthly Notices of the Royal Astronomical Society, Volume 333, Issue 3, July 2002, Pages 649–664, https://doi.org/10.1046/j.1365-8711.2002.05445.x
Close - Share Icon Share
Abstract
We discuss differences in simulation results that arise between the use of either the thermal energy or the entropy as an independent variable in smoothed particle hydrodynamics (SPH). In this context, we derive a new version of SPH that, when appropriate, manifestly conserves both energy and entropy if smoothing lengths are allowed to adapt freely to the local mass resolution. To test various formulations of SPH, we consider point-like energy injection, as in certain models of supernova feedback, and find that powerful explosions are well represented by SPH even when the energy is deposited into a single particle, provided that the entropy equation is integrated. If the thermal energy is instead used as an independent variable, unphysical solutions can be obtained for this problem.
We also examine the radiative cooling of gas spheres that collapse and virialize in isolation, and of haloes that form in cosmological simulations of structure formation. When applied to these problems, the thermal energy version of SPH leads to substantial overcooling in haloes that are resolved with up to a few thousand particles, while the entropy formulation is biased only moderately low for these haloes under the same circumstances. For objects resolved with much larger particle numbers, the two approaches yield consistent results. We trace the origin of the differences to systematic resolution effects in the outer parts of cooling flows. When the thermal energy equation is integrated and the resolution is low, the compressional heating of the gas in the inflow region is underestimated, violating entropy conservation and improperly accelerating cooling.
The cumulative effect of this overcooling can be significant. In cosmological simulations of moderate size, we find that the fraction of baryons which cool and condense can be reduced by up to a factor ∼2 if the entropy equation is employed rather than the thermal energy equation, partly explaining discrepancies with semi-analytic treatments of galaxy formation. We also demonstrate that the entropy method leads to a greatly reduced scatter in the density–temperature relation of the low-density Lyα forest relative to the thermal energy approach, in accord with theoretical expectations.
1 Introduction
Smoothed particle hydrodynamics (SPH) was introduced by Gingold & Monaghan (1977) and Lucy (1977) as an alternative to grid-based fluid solvers, and has developed into a mature and popular simulation technique. The Lagrangian nature of SPH enables it to adjust to the large dynamic range posed by problems such as the formation of galaxies and large-scale structure in a manner that is difficult to match with non-adaptive Eulerian methods. It has been shown that SPH can produce accurate results in many situations (e.g. Steinmetz & Müller 1993), albeit at the expense of an artificial viscosity which broadens shocks over several smoothing lengths.
The use of SPH to study the formation and evolution of galaxies was pioneered more than a decade ago by a number of researchers (Evrard 1988, 1990; Hernquist 1989; Hernquist & Katz 1989; Barnes & Hernquist 1991; Hiotelis & Voglis 1991; Katz & Gunn 1991; Navarro & Benz 1991; Katz, Hernquist & Weinberg 1992; Thomas & Couchman 1992, among others). Together with subsequent applications, these works demonstrated the reliability of the approach, and ultimately influenced our understanding of, e.g., quasar absorption-line systems, the intracluster medium, and galaxy interactions. While cosmological SPH simulations have also provided a successful instrument for exploring galaxy formation, it has recently become clear that subtle numerical properties of existing algorithms severely influence characteristics of model galaxies, such as their luminosities and colours.
These numerical complications follow once radiative cooling of the gas is included. Cooling is critically important in the conventional paradigm of galaxy formation, because it enables baryons to accumulate in the centres of haloes, where they act as a reservoir of cold, dense gas for forming stars. Thus, cosmological hydrodynamic simulations must incorporate these dissipative effects to determine the formation sites and stellar masses of galaxies. Ultimately, an appropriate treatment of star formation and associated feedback processes is also required. However, it is clear that reliable cooling rates, uncompromised by numerical effects, are essential if the simulations are to predict accurate galaxy properties.
Unfortunately, calculating the proper amount of gas that can radiatively cool is a difficult problem, especially in hierarchical cosmologies where the most abundant objects are of low mass and hence will invariably be relatively poorly resolved. Naively, it is expected that coarse resolution will tend to inhibit cooling, because the radiative cooling rate per unit volume is a sensitive function of local density, and high-density peaks will be washed out by smoothing. Near the resolution limit of SPH, this effect will suppress cooling entirely, since haloes will not harbour sufficient quantities of high-density gas if they contain ∼Nsph gas particles, where Nsph is the number of SPH smoothing neighbours. When the mass resolution is poor, gas particles can also be heated by two-body interactions with heavy dark matter particles (Steinmetz & White 1997), which further reduces the effective cooling rates.
However, inadequate resolution can also act in the opposite sense and enhance the cooling rate in haloes. This can arise from, e.g., ‘in-shock cooling’ (Hutchings & Thomas 2000). In SPH, shock fronts are broadened and gas passing through them is heated only ‘slowly’ to post-shock temperatures. During this transition, gas can radiate energy, artificially depressing post-shock temperatures and reducing the cooling time of post-shock gas. This effect is particularly severe when the functional dependence of the cooling rate on temperature exhibits a peak between pre- and post-shock temperatures (Martel & Shapiro 2001). The gas can then cool severely in a broadened shock, in extreme cases converting it incorrectly into an isothermal shock. Additional problems can develop in density discontinuities between the hot phase of a halo and the condensed cold gas that has already cooled. Owing to limited resolution, SPH estimates of the density for hot particles passing close to cold particles will be biased high if they sample the dense cold phase, leading to accelerated cooling (Pearce et al. 1999, Thacker et al. 2000, Croft et al. 2001).
Given these complications, and the highly non-linear nature of radiative cooling, it is unclear whether or not cooling rates obtained by existing cosmological SPH codes are reliable, in particular with respect to the majority of haloes which are resolved with relatively few particles. However, despite the fundamental importance of this issue, only limited attempts have been made to examine the systematic dependence of the results on numerical resolution or technique (among others, Thacker et al. 2000). Abadi, Bower & Navarro (2000) found good agreement between SPH predictions and a variant of the self-similar cooling wave solution derived by Bertschinger (1989). While self-similar tests are useful, it is difficult to validate codes in typical cosmological settings from them, because in reality the cooling function is not self-similar, and the objects forming early on contain few particles. The latter is a particularly important restriction, because for sufficiently large particle numbers SPH yields the proper continuum limit.
In this study, we are especially interested in deviations from the correct behaviour when the resolution is coarse. To examine this issue, we compare entropy formulations of SPH (Hernquist 1993) with variants of the standard algorithm in which the thermal energy equation is integrated. By appealing to a variational principle, we also derive a novel version of SPH which manifestly conserves both the energy and the entropy (under appropriate conditions) even when the smoothing lengths are fully adaptive. In order to investigate the numerical properties of these formulations of SPH in situations where cooling is important, we study collapsing and virializing gas spheres in isolation, and we compute a set of full cosmological simulations of structure formation.
We also explore the behaviour of SPH when feedback scenarios are invoked that deposit large quantities of energy into single particles, as in the method proposed recently by Springel & Hernquist (2001) for modelling starbursts and associated galactic winds and outflows. Benz & Thielemann (1990) have argued that in explosive outbursts, energy must be deposited in a smooth manner for SPH to produce reasonable results, and a similar concern has been raised by Klypin (private communication). We show that singular point explosions do indeed present severe difficulties for some of the standard formulations of SPH, but also demonstrate that reasonable solutions are obtained when the entropy equation is integrated, thereby justifying the numerical validity of feedback schemes that make use of point-like energy injection.
The outline of our paper is as follows. In Section 2 we briefly review several common treatments of SPH. We then derive a new conservative formulation in terms of the entropy equation in Section 3. In Section 4 we start our comparisons by considering strong explosions in a uniform background. In Section 5 we analyse systematic differences between various formulations of SPH in a series of collapse simulations of gas spheres that undergo radiative cooling. We then extend this analysis to small cosmological simulations of structure formation in Section 6. Finally, we conclude and summarize in Section 7.
2 Entropy formulation of SPH
In the conventional implementation of SPH (e.g. Monaghan 1992), the density of each particle is computed according to

where rij≡ri-rj, and W(r, h) is the SPH kernel.1 Commonly, variable smoothing lengths are employed so that the number of neighbours for each particle with ∣rij∣≤hi is maintained at a nearly fixed value Nsph. This adaptive kernel estimation implicitly obeys the continuity equation. The thermal energy and momentum equations can then be integrated in time according to
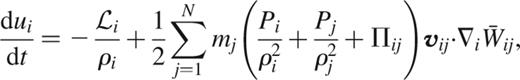
and
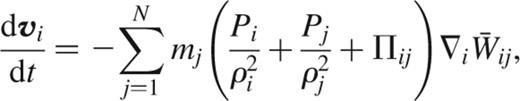
respectively (Monaghan & Gingold 1983, Monaghan 1992, Hernquist 1993, Springel, Yoshida & White 2001). Here,
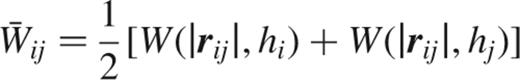
is a symmetrized kernel (Hernquist & Katz 1989), and Πij denotes the artificial viscosity, for which we adopt a standard form as in Steinmetz (1996). Note that we have also included an emissivity per unit volume ℒi=ℒ(ρi,ui) to describe external sinks or sources of energy due to radiative cooling or heating.
Some authors prefer to employ Wij=W(∣rij∣,[hi+hj]/2) in the above equations, so that smoothing lengths are symmetrized rather than the kernels. It is also possible to apply a similar procedure to the estimation of the local density (Hernquist & Katz 1989). However, of larger importance are the choices made for the symmetrization of the pressure terms in the equations of motion and in the energy equation.
As a variant of pair-wise symmetrization with arithmetic means, Hernquist & Katz (1989) suggested the use of geometric means instead, which appeared to provide better integration stability for the thermal energy in their numerical tests. In this case, the SPH equations read
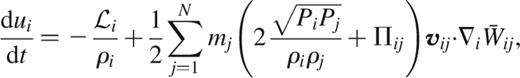
and
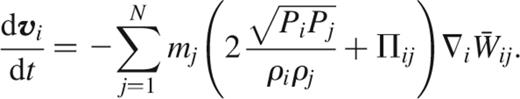
A number of SPH codes have employed this formulation (among others, Hernquist & Katz 1989; Katz, Weinberg & Hernquist 1996; Davé, Dubinski & Hernquist 1997; Carraro, Lia & Chiosi 1998; Springel et al. 2001).
While both of the above formulations are pleasingly symmetric between particles i and j, there is actually no compelling need to distribute the pressure work done by a particle pair equally between them. In fact, if one simply uses the SPH estimate for the local velocity divergence to derive the energy equation, one obtains
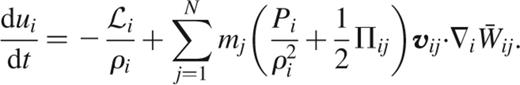
This form of the thermal energy equation has frequently been used in SPH computations instead of a symmetrized form (Evrard 1988; Rasio & Shapiro 1991; Navarro & White 1993; Nelson & Papaloizou 1993; Steinmetz & Müller 1993; Couchman, Thomas & Pearce 1995; Hultman & Källander 1997; Thacker et al. 2000). It conserves energy just as well, but as Couchman et al. (1995) pointed out, it produces less scatter in the entropy. Note that this formulation cannot give rise to negative temperatures, as can occur for other formulations of the energy equation in certain situations.
In principle, there are many other forms that the dynamical equations can take in SPH. It is clear, however, that differences between various implementations will in general be small in the limit of relatively smooth flows. However, this need not be true for extreme cases, such as point explosions and cooling flows, as we discuss in what follows. In our tests, we are especially interested in how well different versions of SPH perform when physical conditions are unusual and numerical resolution is only poor or moderate, as is often the case in cosmological simulations of galaxy formation.
A somewhat more fundamental change in the numerical scheme is to formulate SPH in terms of dynamical equations for the entropy (Lucy 1977, Benz & Hills 1987, Hernquist 1993), rather than the internal energy. We can characterize the specific entropy s of a fluid element in terms of an entropic function A(s), defined by
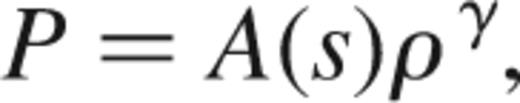
where γ is the adiabatic index. Rather than following the evolution of the internal energy, we can integrate
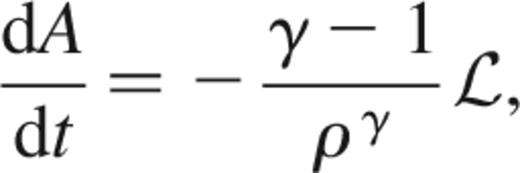
for an inviscid fluid. Note that a convective time derivative is used here, so that A(s) is conserved for each fluid element in an adiabatic flow (ℒ=0). In this approach, the temperature is inferred from
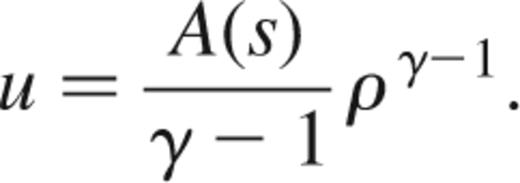
If shocks occur, the entropic function A(s) can vary with time even in the absence of other sources or sinks of entropy. In order to allow for this possibility, an artificial viscosity needs to be introduced into SPH. For example, a suitable SPH discretization of equation (9) is given by
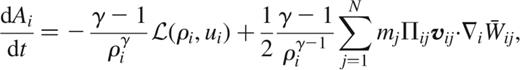
which shows that entropy is generated only by the artificial viscosity in shocks, and by external sources of heat, if they are present. In the entropy formulation of SPH, this expression is integrated in place of equation (2). Note that this approach provides tight control on sources of entropy and, in particular, it is possible to manifestly guarantee that the specific entropy of a particle can only grow in time (assuming for the moment that external sources of entropy are unimportant). This property can be exploited to obtain sharper shock profiles, or to devise shock detection algorithms.
In the continuum limit, employing equation (9) is equivalent to solving the gas dynamics by means of the equation for the internal energy. However, when the number of neighbours defining smoothed estimates in SPH is finite, as is always the case in practice, the two formulations exhibit differences, with one or the other yielding a better approximation to the continuum solution. In particular, Hernquist (1993) has shown that while integrating the internal energy in SPH results in good energy conservation, entropy is not conserved even for purely adiabatic flows. On the other hand, if the entropy is integrated, the total energy is not necessarily conserved. Hernquist (1993) also showed that these errors are primarily caused by the use of variable smoothing and the neglect of relevant terms in the dynamical equations. However, even for fixed smoothing lengths, simultaneous conservation of energy and entropy is not manifest in the above formulations of SPH, but is guaranteed only in the continuum limit; i.e., for a very fine sampling of the fluid.
There is perhaps a tendency to take violations of entropy conservation less seriously than those of total energy, which may explain why most SPH implementations have been made by integrating the thermal energy equation together with the equations of motion, resulting in good energy conservation. However, as we demonstrate below, this choice can lead to significant violations of entropy conservation in certain situations which are important for cosmological simulations of galaxy formation.
3 A fully conservative formulation of SPH
In principle, it is possible to construct Lagrangian treatments of hydrodynamics that behave better in their conservation properties, for example based on spatial Voronoi tesselations (Serrano & Espanol 2001). Alternatively, for SPH, one can explicitly account for terms arising from the variation of the smoothing lengths; the so-called ∇h terms. Nelson & Papaloizou (1993, 1994) have shown that conservation of energy and entropy can be improved substantially if such ∇h terms are included (see also Serna, Alimi & Chieze 1996). However, this approach leads to somewhat cumbersome forms for the dynamical equations and introduces noise into smoothed estimates owing to the dependence of the correction terms on the single most distant neighbour. Consequently, this version of SPH has not found widespread usage in astrophysical applications.
With this in mind, we now derive a new formulation of SPH which employs variable smoothing lengths and which conserves energy and entropy (when appropriate) by construction. To this end, consider the Lagrangian

in the independent variables q=(r1,…,rN,h1,…,hN), where the thermal energy acts as the potential generating the motion of SPH particles. The densities ρi are functions of q, as defined by equation (1). The quantities Ai are treated as constants; i.e., the flow is assumed to be strictly adiabatic for now.
We select smoothing lengths by requiring that a fixed mass is contained within a smoothing volume, viz.  , where Msph=mNsph relates the mass Msph to the typical number Nsph of smoothing neighbours for an average particle mass m. These equations provide N constraints
, where Msph=mNsph relates the mass Msph to the typical number Nsph of smoothing neighbours for an average particle mass m. These equations provide N constraints

on the coordinates of the Lagrangian.
We now obtain the equations of motion from
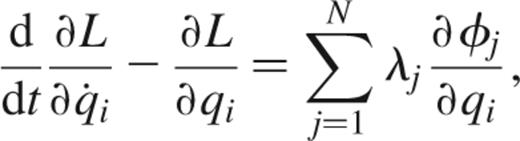
where N Lagrange multipliers λi have been introduced. The second half of these 2N equations gives the Lagrange multipliers as
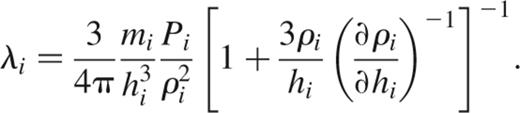
With this result, the first half of the equations then yields
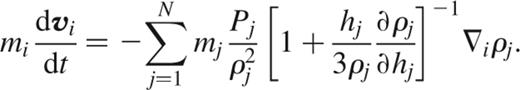
Using
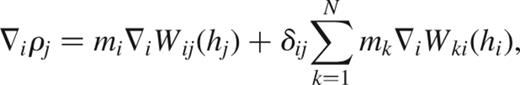
we finally obtain the equations of motion
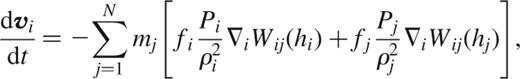
where the fi are defined by
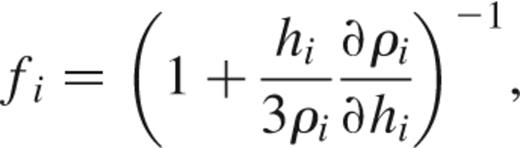
and the abbreviation Wij(h)=W(∣ri-rj∣,h) has been used.
Note that because the potential (thermal) energy of the Lagrangian depends only on coordinate differences, the pairwise force in equation (18) is automatically antisymmetric. Total energy, entropy, momentum, and angular momentum are therefore all manifestly conserved, provided that the smoothing lengths are adjusted locally to ensure constant mass resolution as defined by equation (13). Though not explicitly present, the ∇h terms are thus consistently included to all orders.
Moreover, the equations of motion (18) are remarkably similar to some prior implementations of SPH. In fact, our equations of motion reduce to those employed by Thomas & Couchman (1992) if one sets fi=fj=1. Hence the modifications needed to realize the benefits noted above in existing SPH codes are minor, necessitating only a few additional computations. In particular, the quantities ∂ρi/∂hi can be easily computed along with the densities themselves. A slightly more involved alteration is required for the algorithm which updates smoothing lengths, since it is now necessary to ensure that a ‘constant mass’ resides within a smoothing volume rather than a constant number of neighbours. The requisite changes are minimal, however, if an iterative bisection algorithm is used to determine the hi and ρi, as for example in the parallel version of gadget (Springel et al. 2001).
In order to complete our derivation, we now incorporate an artificial viscosity to allow for the handling of shocks. We invoke a viscous force
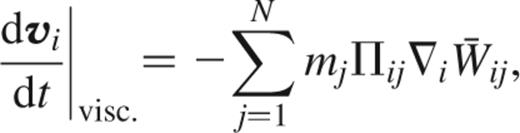
just as in the standard formulation of SPH, and add it to the acceleration given by equation (18). The resulting dissipation of kinetic energy is exactly balanced by a corresponding increase in thermal energy if the entropy is evolved according to equation (11).
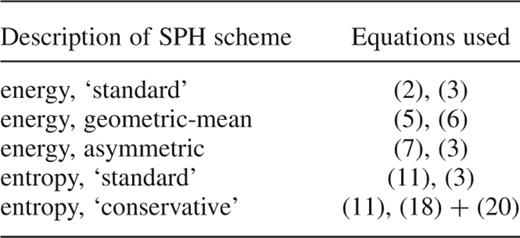
In the following sections we describe detailed tests of various implementations of SPH. In this context, we distinguish between ‘energy’ formulations of SPH, where the thermal energy equation is integrated, and ‘entropy’ formulations, where the entropic function is integrated. We will consider three variants of the energy approach: a ‘standard’ one described by equations (2) and (3), one where the symmetrization is done using a geometric mean, and one where the standard form for the equations of motion is combined with the asymmetric form of the energy equation. We contrast these schemes with a ‘standard’ entropy formulation, where equation (2) is replaced by the entropy equation (11), and we finally investigate the performance of our new SPH formulation given by equations (11) and (18), together with (20), which we refer to as the ‘conservative entropy approach’. The different combinations of SPH equations used are summarized in Table 1.
4 Point-like energy injection
In the feedback model of Springel & Hernquist (2001), starbursts are accompanied by the release of substantial amounts of thermal energy, injected into individual SPH particles which represent the hot ISM left behind by starbursts. These particles can be sufficiently energetic to entirely escape from galactic haloes.
As we now discuss, the standard formulation of SPH is not well-suited for dealing with ‘delta-function’ energy distributions such as this. For definiteness, we consider the propagation of spherical Taylor–Sedov blast waves, which describe the gas dynamics resulting from the point-like injection of energy into a homogeneous medium of negligible pressure. This problem thus serves as a test case for the numerical behaviour of a code when starburst-‘explosions’ are produced. The analytic similarity solution for a strong explosion is well known (e.g. Landau & Lifshitz 1966). After a time t, the blast wave propagates a distance
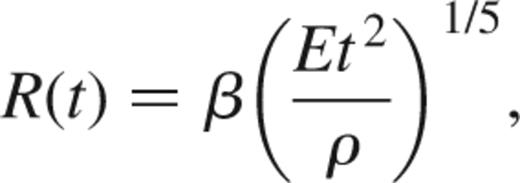
where the constant β depends on the adiabatic index γ(β=1.15 for γ=5/3), E is the explosion energy, and ρ describes the initial density of the ambient gas. Directly at the spherical shock front, the gas density jumps to a maximum compression of ρ′/ρ=(γ+1)/(γ-1), with most of the mass inside the sphere being swept up into a thin radial shell. Behind the shock, the density rapidly declines and ultimately vanishes towards the explosion centre. Modelling this problem accurately in 3D is a challenge for any hydrodynamical code.
In the following, we describe explosions set up in periodic boxes of unit length per side and unit density, using a Cartesian grid to initialize particle distributions. At time t=0, we inject an explosion energy E=1 into a single particle, and compute the subsequent 3D evolution using the parallel SPH-code gadget (Springel et al. 2001).
In the ‘standard’ formulation of SPH (integration of the thermal energy equation and arithmetic mean for the pressure terms), a perhaps surprising phenomenon is observed: The direct neighbours of the explosion seed are quickly driven to unphysical negative temperatures. This is a result of the pair-wise symmetrization of the pressure terms in the energy equation. First, the neighbouring particles of the explosion seed are pushed away. Once they gain velocity, the pressure work done by the particle pairs needs to be supplied by a corresponding decline of thermal energy. Due to the symmetrization, the (large) rate of decline of thermal energy is equally distributed between the particles of each pair. For a strong explosion, this quickly consumes any thermal energy the neighbouring particles of the explosion seed might have had previously, and drives them towards negative temperatures. Formally, total energy would still be conserved in this case, but our code suppresses unphysical negative temperatures and enforces a minimum value of zero for the thermal energy, thereby leading to an unavoidable, strong violation of energy conservation in this case. Note that this behaviour is not a consequence of time integration errors, but is a result of the initial conditions and the particular set of equations used to evolve them. In our tests, we observe energy violations of up to ∼25 per cent, generated entirely in the initial phase. After a short time, however, the energy distribution of the central particles becomes sufficiently ‘smooth’ that a successful explosion still develops. Of course, the initial ‘cooling’ of the neighbouring particles and the error in the explosion energy are substantial artefacts of the solution. These problems can be avoided completely if the asymmetric form of the thermal energy equation is used, in which case energy is conserved accurately for these point explosions.
If a geometric mean is instead used to symmetrize the pressure terms, it is clear that the maximum rate of decline of internal energy in particle pairs that involve the explosion seed becomes smaller. However, for the problem of a single point explosion, this damping leads to a completely unphysical solution: No explosion takes place. This is because the geometric mean (nearly) vanishes if the background is (nearly) pressureless.
However, integrating the entropy equation leads to a solution that is as physically well-behaved as the one for the asymmetric form of the thermal energy equation. As before, the explosion seed pushes particles away, but because they are compressed, their temperatures increase, as they should, because their entropy is required to increase monotonically. Unphysical negative temperatures cannot result from the dynamics, regardless of how the energy is initially distributed. However, the total energy is not conserved as well with this approach. We observe a characteristic pattern of fluctuations in the total energy, as shown in Fig. 1. There is a maximum deviation of ∼4 per cent occurring in the early phase of the expansion of the blast wave, but there is no long-term secular trend, indicating that the entropy-method conserves energy quite well unless the conditions are extreme. The initial fluctuation is related to the strong variations of the smoothing lengths near the beginning of the simulation. However, if our new conservative formulation of the entropy approach is used, the variations of the smoothing lengths are properly accounted for in the equations of motion, and so energy is conserved at all times.
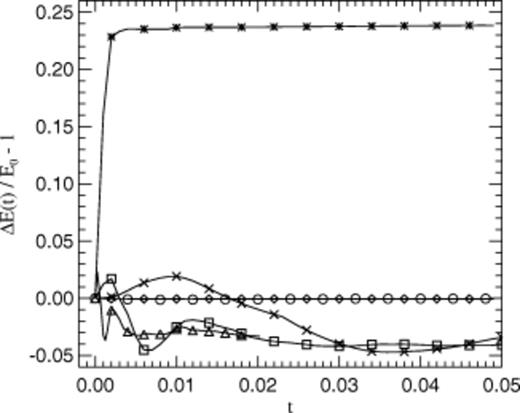
Deviation of the total energy from the initial explosion energy as a function of time for a number of different simulations. The large positive deviation that reaches a maximum error of ∼24 per cent is for a 323 run where the initial energy is added to a single particle and the thermal energy equation is integrated in the standard form. In this case, energy conservation is violated, because the code prevents the occurrence of unphysical negative temperatures in the early phase of the evolution. When the initial energy is deposited smoothly instead, this is prevented, and energy is well conserved (diamonds). Crosses, boxes, and triangles indicate results for 163, 323 and 643 single point explosions where the code instead integrates the entropy equation and the equations of motion in a standard form. Initially, a fluctuation with a characteristic pattern is observed. The maximum error is about ∼4 per cent, but at later times, energy conservation is reasonable. However, when our new conservative entropy formulation is employed, energy is again well conserved (circles).
In Fig. 2 we show an example of the time evolution of an explosion set up in a 323 grid by injecting the energy into a single particle, and by using the conservative entropy-method for SPH. The explosion is not exactly spherical, but is slightly modulated by effects due to the geometric pattern of the Cartesian grid seen around the exploding particle. Note that the resolution available for following the self-similar evolution of the blast wave effectively grows with time. At a given time, the resolution can be assessed by the ratio of the radius that the blast wave has reached to the initial mean interparticle separation. For example, at time t=0.04, the effective resolution is 10.17 for the 323 grid, with about 4405 particles contained inside the spherical shock front.
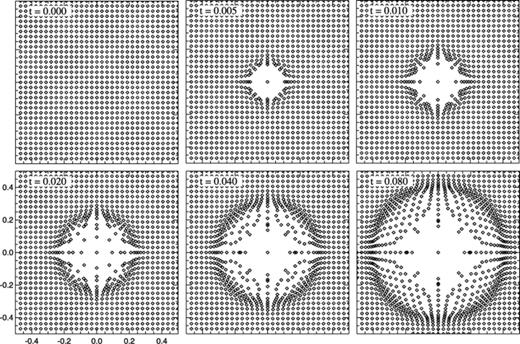
Point explosion triggered by the injection of an energy E=1 into a single particle in a pressureless medium of unit density. Initially, the particles were distributed on a 323 Cartesian grid; the mid-plane is shown in all panels. The evolution was computed in terms of the entropy equation, using our new conservative formulation.
In Fig. 3 we show radial density profiles for different 323 simulations at a time t=0.04 after the explosion, computed with all five variants of SPH discussed above, but with the initial explosion energy smoothed according to the SPH kernel. Due to the more regular initial conditions, the spherical symmetry of the explosions is now nearly perfect. The results for integrating the entropy, or the thermal energy in its standard or asymmetric form, are similar, but notice that our new conservative entropy-method produces the smallest amount of scatter in the density estimates for particles in the blast wave. However, it is obvious that the variant of SPH where pressure terms are symmetrized with a geometric mean gives a considerably worse match to the analytic Sedov solution than the other methods. The shock wave appears to be delayed in time with this technique.
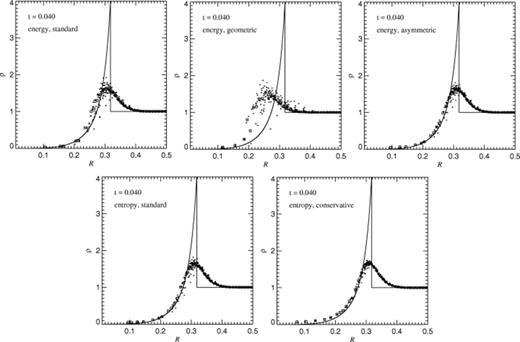
Radial density distribution at a time t=0.04 after the triggering of an explosion in a 323 particle distribution, with the initial explosion energy smoothed by the SPH kernel. Results for different formulations of SPH are shown. Top: Integration of the thermal energy, from left to right: in its standard form, with geometric mean symmetrization, and with the asymmetric form of the energy equation. Bottom: Integration of the entropy equation in the standard form (left) and with the new conservative formulation (right). Small points indicate distances and densities measured from individual particles, while boxes denote spherically averaged values. Solid lines show the analytical Sedov solution (adiabatic index γ=5/3).
Finally, in Fig. 4 we show radial density profiles for 163, 323, and 643 simulations at a time t=0.02 after the explosion. In these tests, the explosion energy was deposited into a single particle, and the entropy equation was integrated. This resolution test makes it clear that it is difficult to resolve the internal structure of a thin shock wave in 3D accurately, and that it is challenging to obtain the expected maximum value of the density compression, albeit increasing the number of particles drastically improves the solution. It is also possible to improve resolution by modifying the smoothing algorithm of SPH so that it locally adjusts to properties of the flow (Shapiro et al. 1996, Owen et al. 1998). Note, however, that the propagation of the shock front in time is described quite accurately in all cases, as well as the density structure behind the blast wave. This is true even for the very low resolution of 163, and it illustrates the remarkable robustness of SPH in three dimensions. The 323 result shown also compares very well to the one in Fig. 3, where the energy had been deposited in a smoothed fashion.
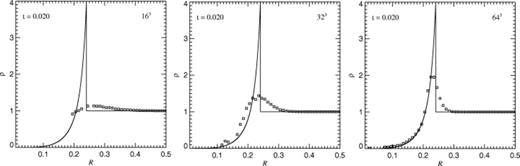
Radial density distribution at a time t=0.02 after the triggering of an explosion in particle distributions of varying mean interparticle separation. From left to right, 163, 323, and 643 particles are used in a box of unit side length. The effective resolutions at time t (taken to be the mean interparticle separation in units of the radius of the blast wave) are 3.86, 7.71, and 15.42, respectively, corresponding to roughly 240, 1921, and 15 370 particles inside the spherical shock wave. Boxes mark spherically averaged density values, and solid lines indicate the analytical Sedov solution.
From these experiments we conclude that formulations of SPH in terms of entropy or in terms of the asymmetric form of the energy equation are able to produce quite reasonable results for the explosive release of energy into a single particle. It has been argued (Benz & Thielemann 1990, Owen et al. 1998) that SPH can treat a strong explosion only if the energy is initially deposited sufficiently smoothly, i.e., if the explosion energy is distributed according to the smoothing kernel into a group of particles. We think that this argument really only applies when the thermal energy is integrated in its symmetrized form, where neighbouring particles of a single explosion seed can suffer from an unphysical decline in temperature and entropy. While an initial smoothing of the explosion energy can cure this problem, certain starburst algorithms rely on the possibility of locally releasing a large amount of energy in a single particle. Note that using the geometric mean to symmetrize the pressure terms does increase the robustness of the thermal energy method, but yields noticeably worse or even unphysical solutions for the explosion problem.
5 Cooling within haloes
Radiative cooling within haloes is a highly non-linear process that can be severely influenced by numerical resolution. In order to straightforwardly examine such systematic effects, we consider a series of idealized test problems consisting of gas spheres that collapse and virialize under their own self-gravity. We parametrize the models by a ‘virial velocity’V. Each gas sphere has a total mass M=V3/(10GH0) and is initially at rest with a density profile ρ(r)∝1/r, a radius R=V/(5H0), and a thermal energy per unit mass of u=5.0×10-4V2. After being released, these gas spheres collapse to their centres, bounce back, and virialize through a strong outgoing shock. As such, this problem is a version of the ‘Evrard’ collapse (Evrard 1988), a common test problem for SPH, except that we allow the gas to cool radiatively like a plasma composed of a primordial mix of helium and hydrogen. The actual cooling rates are computed as in Katz et al. (1996). In order to arrive at a clean inner boundary condition to allow for well-defined resolution studies, we set the gravitational softening to a fixed value of ε=1.5×10-3V/H0 in all the tests, and we turn cold gas within a distance of less than 0.25ε from the origin and with a density higher than 7.2×107ρcrit into stationary sink particles that only gravitationally interact with the remainder of the gas. This ensures that once it can cool efficiently, the gas at the origin will essentially be fixed at a density 7.2×107ρcrit, allowing a meaningful attempt to achieve convergence for the entire density profile as the mass resolution is increased. For the particle numbers employed here, the SPH smoothing lengths of particles in the sink region will be smaller than 0.5ε; hence they are no longer interacting with particles in the actual cooling flow once they are converted into sink particles.
While this test problem is highly idealized, it is nevertheless relevant for simulations of galaxy formation, because in that case the virialization of haloes and the subsequent cooling of their gas happens in an analogous, yet dynamically more complicated manner. Note that we deliberately excluded dark matter from this test to highlight gas-dynamical effects without introducing complexities arising from collisionless dynamics. An interesting alternative test would be to examine self-similar cooling wave solutions (Bertschinger 1989). While having an analytic solution is an advantage, we prefer to use a set-up that is closer to actual cosmological simulations with respect to particle number, to collapse scenario, and to the cooling function. This simplifies the interpretation of numerical effects.
Because the cooling function for primordial gas introduces characteristic temperatures, the evolution depends on the mass-scale of the collapsing sphere. We here consider spheres of mass M=1015h-1 M⊙, where h=0.7 parameterizes the Hubble constant H0=100 h-1 km s-1 Mpc-1. These gas spheres thus have the mass of a rich cluster of galaxies, and a virial temperature of ≃5×107 K. Note that because these ‘clusters’ consist of only gas, their cooling times will be shorter than those of real, dark-matter-dominated clusters of comparable mass.
In Fig. 5 we show the deposition rate of cold gas in the halo centre as a function of time, computed for mass resolutions ranging from 552 to 92 096 particles, and for the five variants of SPH listed in Table 1. The deposition rate is given in units of total mass per unit time, where unit time is 1/(10H0)=0.98 h-1 Gyr. A value of 0.5 thus means an accretion rate such that 50 per cent of the gas cools within 1.4 Gyr for h=0.7.
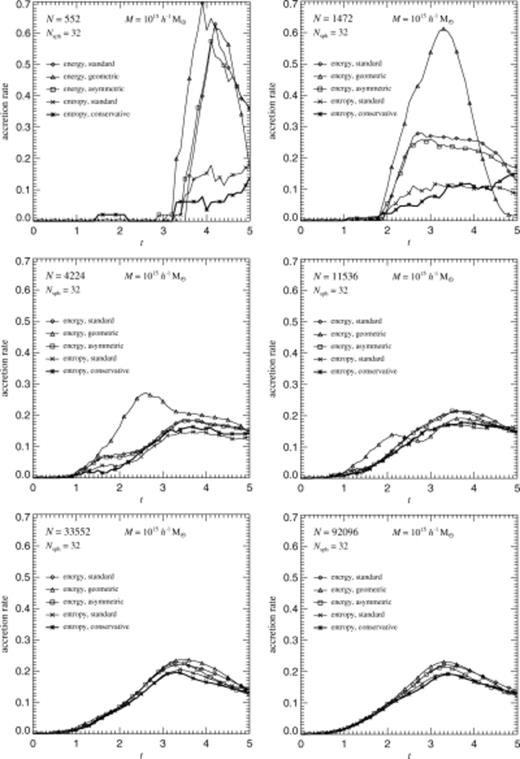
Rate at which cold gas accumulates in the centres of collapsing and virializing gas spheres of mass M=1015h-1 M⊙. Each panel compares results obtained for a given particle number with the five formulations of SPH listed in Table 1. Symbols are used to mark the lines drawn for each of the SPH variants, and the result for our new version of SPH is highlighted by a bold line. The accretion rates are given in units of the total mass per unit time, where unit time is 1 h−1 Gyr.
From Fig. 5 it is evident that at low resolution there are strong systematic differences between the energy and entropy formulations of SPH. When the thermal energy equation is integrated, cooling rates are substantially overestimated, while with the entropy equation, they are slightly underestimated compared to the ‘converged’ values measured at very high resolution. As the particle number is increased, the various treatments yield results that are in better and better agreement. In itself, this is reassuring, but it is unsettling that the cooling rate can be as dramatically overestimated, as is seen in the 552 and 1472 particle runs which integrated the thermal energy equation. After all, many haloes in cosmological simulations are resolved with far fewer particles. Therefore all of these haloes are likely subject to strong overcooling. Moreover, in hierarchical scenarios of structure formation, larger systems will inherit this problem if their progenitors suffered from overcooling. Such behaviour may well explain why cosmological SPH simulations predict more gas cooling than is expected based on simple analytic models (Benson et al. 2001, Pearce et al. 2001; Yoshida et al., in preparation).
Note from Fig. 5 that the low-resolution results for the geometric symmetrization of the pressure terms are particularly discrepant compared to the high-resolution solutions. Even the simulation with 1472 particles cools all the gas in the initial collapse in this case, and for 4224 and 11 536 particles there are still strong ‘shoulders’ in the accretion rate at early times around t≃2. Such a shoulder is also present for the other energy-based methods in the 4224 runs, but it is absent for the conservative entropy formulation.
To determine the cause of the difference in the low-resolution behaviour between the entropy and energy formulations of SPH, it is instructive to examine the radial structure of the cooling flows in the simulations. In Fig. 6 we show profiles of the density, the temperature, the radial velocity, and the radial mass flux for one of our runs at time t=4.0, when the cooling flow has been operative for some time and the accretion is almost stationary. It is seen that there is an inflow region in the radial range ∼20–300 h−1 kpc, where the gas is moving inwards at nearly constant radial velocity, and the density profile is steeply rising with slope ≃−2. It is important to note that this inflow is essentially adiabatic; the gas is not yet radiating efficiently, hence the temperature is strongly rising as the gas is compressed on its inbound path. Close to the very centre, the gas begins to cool efficiently, leading to an accelerated inflow, and eventually to a rapid drop in the temperature to around 104 K. It is clear that an underestimate of the compressional heating of the gas in the extended inflow region will artificially boost the overall accretion rate. In fact, we believe that it is this effect which is responsible for the overcooling in the thermal energy runs at low resolution, as we now demonstrate.

Radial profiles of density (top left), temperature (top right), mean radial velocity (bottom left), and mean radial mass flux (bottom right). The profiles are shown for the collapse of a 1015h−1 M⊙ gas sphere, at time t=4.0 after the start of the simulation. The particular model shown here was evolved with the new conservative entropy formulation, using 92 096 particles for the initial conditions. In all panels, symbols represent averages obtained for logarithmic bins in the radial coordinates, while the lines are boxcar averages of these points.
In the left-hand panel of Fig. 7 we show the change ΔA(s) in the entropy of individual SPH particles between two subsequent simulation outputs of the 1472 particle runs, for both the standard energy and entropy methods. Recall that A(s) should change only as a result of radiative losses, or owing to generation of entropy by the artificial viscosity in shocks. We plot ΔA(s) as a function of ρ4/3u1/2, which is the relevant dependence of the entropy loss rate due to cooling in this temperature range. When we compare particles from the thermal energy and the entropy runs in this way, we see that A(s) for the particles in the energy run decreases faster than expected based on the cooling rate, where this expectation is given by the locus of particles from the entropy run. This may be expressed differently by saying that the entropy of these particles is violated – it decreases faster than can be accounted for by the external sinks of entropy. It should be noted that in spite of this, the total energy is well conserved for these particles, i.e., the total energy declines at exactly the rate at which energy is radiated.
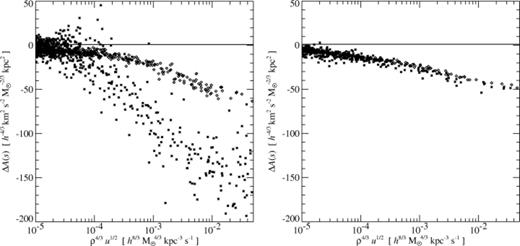
Decline of entropy of individual particles between two subsequent output times from the gas sphere simulations, spaced Δt=0.1 apart, and measured at t=3.4. The left-hand panel compares particles from the N=1472 simulation computed either using the standard energy formulation (stars) or using the entropy formulation (diamonds). The particles are plotted versus ρ4/3u1/2, because the rate of decline of entropy due to cooling is expected to be approximately proportional to this quantity. The range of ρ4/3u1/2 shown corresponds to the region of the cooling flow where the gas begins to cool rapidly. It is seen that the particles in the thermal energy run lose entropy faster than can be explained by cooling alone. This error arises because the adiabatic flow is not sufficiently well resolved, ultimately leading to overcooling. In the right-hand panel, we show the same measurement for the N=11 536 runs. Here the two formulations of SPH show a consistent rate of entropy decline due to cooling.
What we observe in Fig. 7 is a discreteness effect arising from insufficient resolution in the cooling flow, where the adiabatic heating of the inflow is not adequately resolved. If the particle number is increased, the resulting false loss of entropy is avoided, as can be seen in the right-hand panel of Fig. 7, where we show the equivalent plot for the 11 536 particle simulations. We note that the geometric symmetrization of the thermal energy equation is particularly prone to this effect. At low resolution, an infalling particle that interacts with particles that are already much colder will not be heated sufficiently despite its strong compression, because the geometric mean heavily suppresses adiabatic work done between particle pairs at different temperatures.
In fact, we have found that this relative suppression of pair-wise forces in the geometric symmetrization technique can be strong enough to render density discontinuities unstable. In order to highlight this effect, we have considered a test problem where two ‘phases’ of gas of equal pressure are brought into contact along a planar intersection, with the density of one of the phases being substantially higher than that of the other. Since we take the gas to be initially at rest in this problem, the resulting density discontinuity should remain stable for all times.
However, as a result of its inherent smoothing, it is clear that SPH will not be able to precisely maintain the sharpness of the initial density discontinuity. Instead, we expect that the gas at the intersection will undergo some small transient motion before it settles into a relaxed state, such that the phase boundary ends up being slightly washed out. We investigate this relaxation process with a three-dimensional realisation of a density discontinuity of strength ρ2/ρ1=125. For definiteness, we consider a periodic box of size 4×1×1 where one half is filled with a 2×73 particle grid at a fiducial density ρ1=1, and the other half is filled with a 2×353 grid. All particles are taken to have equal mass, such that the density in the latter half is ρ2=125. Temperatures are assigned such that an equal pressure of P=1 in both phases (using γ=5/3) is obtained.
In Fig. 8 we show a comparison of the time evolution of the resulting particle system obtained for three different SPH formulations, using Nsph=32 smoothing neighbours in each case. In the top three panels we show the evolution when the new conservative entropy formulation is used. The system shows the expected behaviour. Low-density particles adjacent to the high-density phase ‘see’ some of the dense particles, and are hence estimated slightly high in density. Likewise, the density estimates of particles close to the edge of the high-density phase become biased low, such that the phase transition is slightly washed out. However, the phase boundary remains reasonably sharp, and its stability is maintained for arbitrarily long times.

Time evolution of a strong density discontinuity when evolved with three different SPH variants, as indicated in the panels. The simulations follow two phases of gas that are brought into contact at time t=0 in a three-dimensional, periodic box of dimension 4×1×1. Initially, the gas is at rest and has equal pressure of P=1, with the region ∣x∣>1 being filled with gas at density ρ1=1, and the region ∣x∣<1 being filled with gas at density ρ2=125. The symbols show individual particle densities, with triangles marking particles that were originally in the low-density phase, while those that were in the high-density phase are plotted as diamonds.
In comparison, the behaviour resulting for the standard energy formulation of SPH is quite similar, but the sharpness of the initial density discontinuity is not preserved quite as well. In particular, a larger number of particles from the original low-density phase are affected by higher density estimates attained in the new equilibrium. If the system was subject to density-dependent cooling, this may cause an overestimate of the cooling rates of particles close to the boundary.
This may, however, be seen as a small effect compared to the relative performance of the geometric symmetrization technique, which gives a solution that is drastically worse than the ones obtained for the other two methods. In fact, as the lower row of panels in Fig. 8 shows that the phase boundary behaves in an unstable way in this case, resulting in an unphysical evolution of the system. Particles from the low-density phase are literally pressed into the high-density phase. This happens because the geometric symmetrization renders the repulsive forces between particle pairs of very different temperature largely ineffective. As a result, each of the 7×7 columns of low-density particles orthogonal to the boundary penetrates as a finger into the high-density phase, causing a partial overlap of the fluids, and the gradual decay of the initial density discontinuity. Clearly, if the system was subject to cooling, the hot low-density phase would suffer from a substantial increase of its cooling rate because it would tend to overlap with the dense cold phase, thereby becoming subject to overestimates of density.
6 Cosmological results
Based on the results presented above, we expect a significant difference in the fraction of gas that can cool in haloes of a given size in full cosmological simulations when SPH is formulated either in terms of the thermal energy equation or the entropy equation. We examine this further using moderate-sized test simulations at two different mass resolutions, containing a total of 2×503 and 2×1003 dark matter and SPH particles, respectively. We consider a canonical ΛCDM cosmology with parameters Ω0=0.3, ΩΛ=0.7, Ωb=0.04, h=0.67, and σ8=0.9 within a periodic box of length 11.3 h−1 Mpc per side. We include radiative heating and cooling processes for a primordial mix of helium and hydrogen in the way described by Katz et al. (1996). An external UV background field similar to that advocated by Haardt & Madau (1996) photoionizes the gas, and reionization takes place at redshift z≃6 (for details, see Davé et al. 1999). For the purposes of the present study, we have not renormalized the ionizing background to match, e.g., the redshift evolution of the mean opacity of the Lyman-α forest, as is commonly done (see, e.g., Hernquist et al. 1996). While boxes of this size are too small to be representative of the Universe at low redshifts, they suffice to investigate systematic differences arising from different formulations of SPH.
In Fig. 9 we show the fraction of baryons residing in different phases as a function of redshift. These phases are defined as in Davé et al. (2001). Gas with temperatures above 107 K is referred to as ‘hot’, gas with temperatures between 105 and 107 K is ‘warm’, and at lower temperatures gas is either labelled ‘diffuse’ if it is at overdensities ρ<1000ρ, or ‘condensed’ (cold) for ρ>1000ρ. The left-hand panel of Fig. 9 shows the result when the thermal energy equation is integrated with geometric mean symmetrization, while the right-hand panel is for our new conservative entropy method. In each panel, we show the results obtained for the 2×503 resolution as thick lines, while thin lines give the results for the 2×1003 simulations.
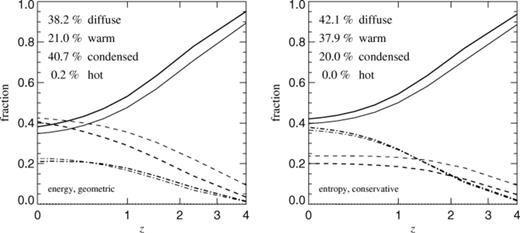
Mass fractions of gas in different phases as a function of redshift. Gas with temperatures below 105 K is considered to be either ‘diffuse’ (solid), if it is at low density (ρ<1000ρ), or ‘condensed’ (dashed) otherwise. Gas with intermediate temperatures 105–107 K is labelled ‘warm’ (dot-dashed), and for T>107 K‘hot’ (dotted). The left-hand panel shows simulations where the thermal energy equation with geometric symmetrization was integrated, while the right-hand panel gives results for our new conservative entropy method. In both panels, thick lines refer to a resolution of 2×503, and thin lines to 2×1003. Note that the entropy method cools substantially less gas, which is also reflected in the differing fractions of condensed and warm gas.
When the two SPH methods are compared, it is obvious that there is a very large difference in the amount of gas that becomes cold and dense. The entropy method predicts almost a factor of 2 less cold gas for these simulations, which is reflected in a corresponding difference in the amounts of gas in the warm phase. The fraction of gas in the diffuse phase is nearly unaffected, however. There is virtually no hot gas in these simulations, because the box size is too small to contain massive galaxy clusters. Note that the fraction of cold gas keeps growing for the geometric method by a large amount even at low redshifts, while it stays nearly constant for the entropy method for redshifts below z≃2. This is probably related to the instability of density discontinuities in the geometric symmetrization technique, as discussed at the end of Section 5. At low redshifts, this allows large haloes to keep cooling efficiently, because their gas easily ‘overlaps’ with the phase of cold dense gas that has accumulated at the centres of these haloes.
As far as convergence is concerned, the total amount of cold gas becomes slightly larger in both SPH variants when better mass resolution is employed. For example, the fraction of cold gas goes up from 20.0 to 23.7 per cent in the entropy method when moving from the 2×503 to the 2×1003 resolution. Note, however, that the higher resolution runs are able to probe haloes of smaller mass than were previously resolved. The gas that cools in these newly seen objects can possibly account to a large extent for the difference in the total amount of cold gas. A better assessment of convergence is therefore obtained if we compare the content of cold gas in individual haloes as a function of their mass. To this end, we find haloes in the simulations as follows. We first construct a catalogue of group candidates using a friends-of-friends algorithm with linking length of 0.2, applied to the dark matter only. For each dark matter group that contains at least 64 particles, we define a group centre as the position of the particle with the minimum gravitational potential. We then determine a spherical ‘virial radius’ around this centre such that the enclosed ‘virial mass’ of gas and dark matter has an overdensity of 180 with respect to the background. For each of the resulting haloes, we also compute its fractional content of gas, (Mgas/Mvir)×(Ω0/Ωb), normalized to the universal baryon fraction. Similarly, we define a fraction of cold gas, where cold is here taken to be gas colder than 5×104 K, and we define a ‘hot’ gas content simply as the difference of the total and cold gas fractions.
In Fig. 10 we show these gas fractions as a function of virial mass, comparing results for the 2×503 and 2×1003 simulations when the geometric symmetrization is used, or the new entropy formulation is employed. In the top two panels we have used logarithmic bins in mass to compute mean gas fractions for haloes in each mass bin. This suppresses the scatter, which we separately illustrate for the entropy runs in the bottom three panels by plotting individual haloes as symbols.
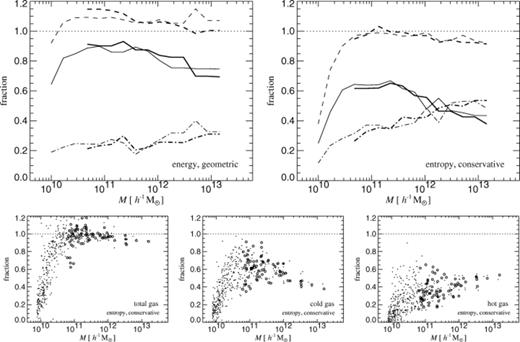
Fraction of gas mass in haloes as a function of virial mass, measured at z=0. The top two panels compare results at obtained for two different formulations of SPH at resolutions of 2×503 (thick lines) and 2×1003 (thin lines). In each case, we show fractions of total (dashed lines), cold (solid lines), and hot (dot-dashed lines) gas within the virial radius, normalized to the universal baryon fraction. The plotted values are averages obtained for groups of haloes in logarithmic bins of size Δlog M=0.226 in mass. The bottom three panels show directly the gas fractions of individual haloes in the entropy simulations. Hollow and filled circles give results for the 2×503 and 2×1003 resolutions, respectively.
Overall, the agreement between the low- and high-resolution runs is gratifyingly good for the entropy method, as seen in the top right-hand panel of Fig. 10. Even at the resolution limit of 6.15×1010h-1 M⊙ of our 2×503 halo catalogue, the fraction of cold gas is well reproduced, apart perhaps from a small bias towards a lower amount of cold gas, which is, however, expected on the basis of our earlier results for the cooling in isolated gas spheres. Interestingly, at the low-mass end, the high-resolution catalogue shows a drop of the total gas fraction below the universal value, while a similar effect is not observed for the low-resolution run. This depletion of the total gas content is presumably caused by the UV background that we included (Gnedin 2000). At redshift z=0, this effect appears to be strong enough to start reducing the gas content in objects with virial temperatures below T∼8×104 K.
When the cold gas fractions for the geometric symmetrization technique are considered, it again becomes clear that this method cools gas too efficiently. Here the low-resolution run actually tends to produce more cold gas at a given mass scale than the high-resolution run, again in agreement with the trends seen in the collapse simulations of isolated gas spheres discussed earlier. Note that the difference in the cold and total gas fractions between the two different resolutions is also markedly larger than seen for the entropy runs. Interestingly, the total baryon fraction is also pushed beyond the universal value in this method, indicating that the strong cooling also affects the accretion flow into the haloes.
The difference in the phase-space distributions of the gas between the different SPH techniques may also be shown directly in a density–temperature diagram. In Fig. 11 we show where the SPH particles lie in the overdensity–temperature plane. Compared to the simulation that integrates the entropy, the plume of shock heated gas is clearly less populated in the run that evolved the energy equation. This gas has cooled and moved to the locus of dense gas at T≃104 K. The amount of diffuse, low-density gas is the same in the two simulations. However, the entropy run clearly exhibits much less scatter in the density–temperature relation of the photoionized IGM. Hui & Gnedin (1997) have studied the expected density–temperature relation of the photoionized intergalactic medium. At low overdensities (δ<5), the gas is expected to follow a power-law ‘equation of state’

Phase-space diagrams of the density–temperature plane at z=0 for two 2×503 cosmological simulations with cooling. The number density of SPH particles is shown in grey-scale. The left-hand panel gives the result for an integration of the thermal energy, using geometric symmetrization, while the right-hand panel shows the result for an integration of the entropy equation with our new conservative approach.

where δb is the baryonic overdensity. The amplitude T0 and the slope α at a given epoch depend on the details of the reionization history, and on cosmology. Because gas with density around or below the mean is not expected to have been shocked, very little scatter is expected around this relation, as long as the ionizing radiation field is homogeneous.
We examine the scatter in the equation of state of the IGM in Fig. 12. In the top panels we compare the temperature–density relation for the two runs at redshift z=4, and in the bottom panels at redshift z=0. While at redshift z=4 the scatter in the thermal energy equation run is only marginally larger than that in the entropy run, it has grown substantially by redshift z=0. This happens because the adiabatic cooling of the particles due to the expansion of the Universe is perturbed by noise in the SPH estimates. The particles see only a finite number of neighbours that move away from them and generate the adiabatic cooling. While they cool at nearly the correct rate on average, some of them will do so more rapidly or more slowly than average and, as a result, particles tend to diffuse away from the adiabat they are expected to follow. In addition, for a small number of smoothing neighbours and a nearly homogeneous particle distribution, there can be a small bias in the mean of the estimates of the local velocity divergences, resulting in a mean temperature that does not decline exactly in proportion to a−2, where a is the scalefactor. In fact, this happens for the thermal energy run, which arrives at an IGM equation of state with a slightly higher value of T0. This is a result of a small systematic underestimate of the cooling rate due to the adiabatic expansion of the universe. Ultimately, this is again a manifestation of the violation of entropy conservation in this approach. Note that our code computes the rate of change of thermal energy for each SPH particle in physical coordinates; thus the situation can be compared to a homogeneously expanding polytrope where the smoothing lengths increase with the expansion. As Hernquist (1993) has shown, the entropy will be violated under these circumstances. On the other hand, if the entropy is integrated, the adiabatic cooling is automatically exact. Particles will move to higher temperatures only if they are shocked. The entropy computation thus proceeds essentially as in the ‘semi-analytic’ method outlined by Hui & Gnedin (1997), and should represent the more accurate result.
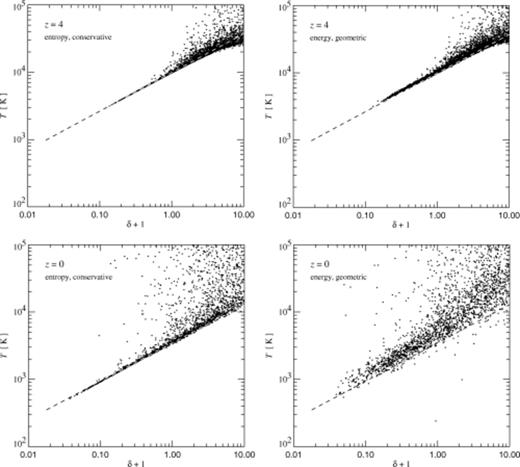
Temperature-density relations for the photoionized IGM at two different redshifts, and for two different methods of solving the SPH equations. For graphical clarity, only a random subset of 5 per cent of the particles is shown in each case. In the top panels at z=4, a line has been fitted to the particles in the entropy run (conservative formulation), marking the equation of state of unshocked IGM gas. It has amplitude T0=9925 K and slope α=0.57. The same line is also plotted in the corresponding thermal energy run (geometric symmetrization employed). In the bottom panels, the fit to the entropy run is described by T0=3550 K, α=0.58, and again, the same line is drawn for the z=0 thermal energy run.
7 Discussion
We have derived a new formulation of SPH that, when appropriate, manifestly conserves both entropy and energy if the smoothing lengths are adjusted to a constant local mass resolution. Unlike previous attempts to include ∇h-terms, the equations of motion retain a remarkably simple form. In our approach, ∇h-terms do not have to be evaluated explicitly, mitigating additional sources of noise. This improves on previous schemes where these terms depend on the single particle with the maximum distance among the set of neighbours.
We have investigated the robustness of several formulations of SPH when applied to the problem of cooling in haloes under conditions of poor resolution, and when dealing with strong explosions triggered by local energy injection, as in certain feedback scenarios. As such, these test problems are highly relevant for current attempts to model galaxy formation in cosmological SPH simulations.
We find that the standard formulations of SPH in terms of the thermal energy can lead to substantial overcooling in poorly resolved haloes when cooling flows are not adequately resolved. This can lead to insufficient compressional heating in the accretion flow or, expressed differently, to a violation of entropy conservation in the adiabatic region of the flow. In the cooling problem, this leads to an accelerated accretion, an effect that becomes more substantial for haloes resolved with few particles, and for temperatures in a range where the cooling function declines with temperature. The effect is particularly severe for a geometric symmetrization of the pressure terms, which can also cause unstable behaviour of strong density discontinuities.
Point-like energy injection can lead to unphysical negative temperatures in the standard formulation of SPH. When the temperatures of these particles are prevented from becoming negative, a reasonable explosion still takes place once the initial energy has spread over a smoothing volume, but a substantial violation of total energy conservation results. When the pressure terms are symmetrized with a geometric mean, the integration of the thermal energy equation is more stable, but then unphysical behaviour may result for very strong gradients in energy density. A better alternative is to use the asymmetric form of the thermal energy equation, which avoids such artefacts.
On the other hand, when the entropy equation is integrated, point explosions are also treated very well. Even when the initial explosion energy is deposited in a smooth way, the blast waves exhibit less scatter than for an integration of the thermal energy equation. However, the total energy is not conserved well in this case, and shows fluctuations of order several per cent, although there are no secular trends of energy violation. This is not surprising. Hernquist (1993) has shown that for standard formulations of SPH, simultaneous conservation of energy and entropy is not manifest. Depending on whether SPH is solved in terms of energy or entropy, one of the conservation laws is only strictly fulfilled in the continuum limit. However, in this paper we have derived a new formulation of SPH that solves this problem and conserves both energy and entropy. In addition, this new method is nearly as easy to implement numerically as the standard approach.
We believe that the results presented in this study clearly favour the entropy formulation of SPH for cosmological simulations of galaxy formation. It provides the best technique among the ones we have tested for modelling the process of point-like energy injection, which is relevant for certain feedback algorithms. It also avoids artificial overcooling in poorly resolved haloes and reduces the scatter in the density–temperature relation of the gas in the low density Lyα forest.
Acknowledgments
We thank Simon White and Simone Marri for instructive discussions and critical comments that were helpful for the work on this paper. We are indebted to David Weinberg for useful suggestions, and to the anonymous referee for providing a highly useful report that helped to improve the paper. This work was supported in part by NSF grants ACI96-19019, AST-9803137, and PHY 9507695.
References
1 We assume that the kernel drops to zero at r=h.



