Episodic accretion in magnetically layered protoplanetary discs

Abstract

1 Introduction

The structure and evolution of protoplanetary discs depend upon the rate at which gas can shed its angular momentum and thereby flow inwards. Two widely applicable physical mechanisms are known to lead to the required outward angular momentum transport. If the gas is coupled to a magnetic field, instabilities that inevitably arise in differentially rotating discs (Velikhov 1959; Chandrasekhar 1961; Balbus & Hawley 1991) lead to turbulence and angular momentum transport (Brandenburg et al. 1995; Stone et al. 1996; for a review see e.g. Hawley & Balbus 1999). If the disc is massive enough, gravitational instability leads to additional transport (Toomre 1964; Laughlin & Bodenheimer 1994; Nelson et al. 1998; Pickett et al. 2000).

Applying these findings to the construction of protoplanetary disc models leads to the structure shown schematically in Fig. 1 (after Gammie 1996). In the inner disc, MHD turbulence transports angular momentum. However, at larger radii of r∼1 where the temperature is typically a few hundred kelvin, magnetic field instabilities are suppressed by the low ionization fraction (Matsumoto & Tajima 1995; Gammie 1996; Gammie & Menou 1998; Livio 1999; Wardle 1999; Sano & Miyama 1999; Sano et al. 2000). This leads (Gammie 1996) to the formation of a layered disc structure, in which the gas near the disc mid-plane is cold, shielded from ionizing high-energy radiation, and quiescent (non-turbulent). Turbulence and accretion occur only in a thin surface layer that is ionized by cosmic rays. Moving still further outwards, the entire thickness of the disc again becomes viscous, either at the radius where the surface density is small enough for cosmic rays to penetrate to the mid-plane, or where the onset of disc self-gravity provides an alternative non-magnetic source of angular momentum transport.

Figure 1.

Illustration of the radial structure of the disc in the layered disc model (after Gammie 1996). At small radii, the central temperature exceeds T_crit, the temperature above which MHD turbulence provides an efficient source of angular momentum transport. In the intermediate, layered region, the central temperature is too low for the disc to support MHD turbulence. Accretion occurs through a surface layer which is kept ionized by cosmic rays, while the disc near the mid-plane is quiescent. At larger radii, the entire thickness of the disc is again viscous, with angular momentum transport being driven by self-gravity.

Open in new tabDownload slide

The predictions of a static layered disc model for the accretion rate and spectral energy distribution of T Tauri stars were discussed by Gammie (1996), and are broadly consistent with observations [e.g. with the accretion rate for classical T Tauri stars measured by Gullbring et al. (1998)]. In this paper we consider the evolution of the layered disc, which cannot be in a steady state (Gammie 1996, 1999; Stepinski 1999), and examine the implications for the outflow history of young stars and for the predicted disc mass. The most significant changes to the disc structure occur at the radii of greatest interest for planet formation (Reyes-Ruiz & Stepinski 1995), and we discuss the implications for the migration of low-mass planets, and for the eccentricity of massive planets interacting with the disc.

2 Layered protoplanetary disc evolution

2.1 Equations

Describing the evolution of the surface density Σ(r,t) and mid-plane temperature T_c(r,t) of a layered disc requires only minor modifications to the usual time-dependent equations for thin accretion discs. We denote the surface density of the ‘active’ (viscous) disc by Σ_a. if

(1)

or

(2)

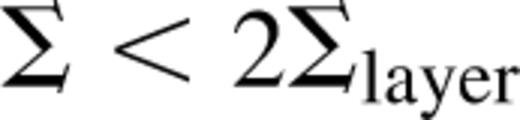
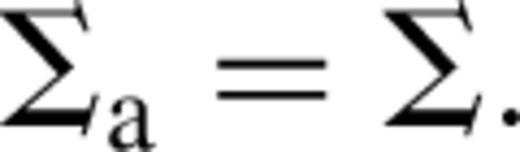then the disc is viscous throughout its thickness and Otherwise only the surface layers are viscous and 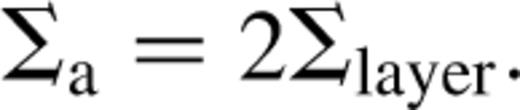The values of these parameters are determined by the requirement that the disc be sufficiently ionized to support MHD turbulence (Gammie 1996). We adopt 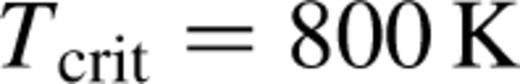and 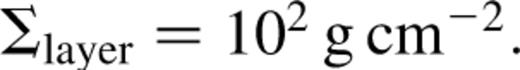For a Keplerian disc, the angular velocity is 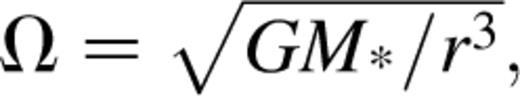where M_* is the stellar mass. The surface density evolution is then described by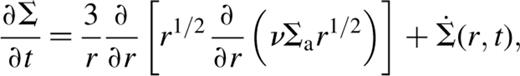

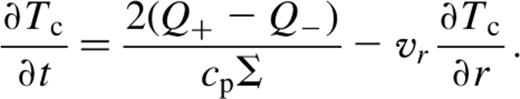
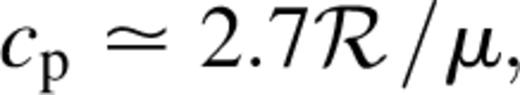(3)

where ν is the kinematic viscosity and Σ˙(r,t) is the rate of change of the surface density owing to infall on to the disc.

For the energy equation, we adopt a simplified form of that used by Cannizzo (1993),

(4)

Here c_p is the disc specific heat, which for temperatures T_c∼10³ K is given by where ℛ is the gas constant and μ=2.3 is the mean molecular weight. Q₊ represents local heating owing to viscous dissipation, given by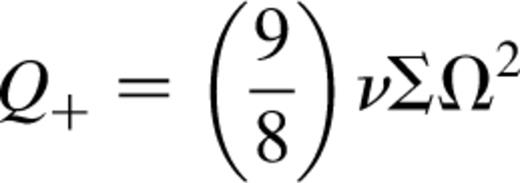

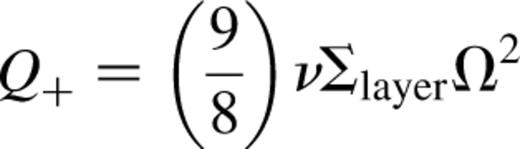
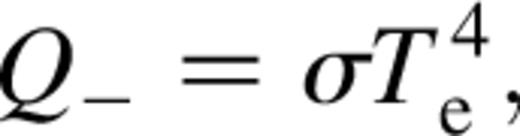
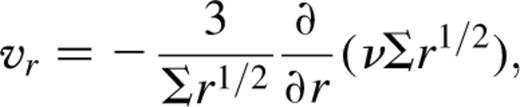
(5)

if the entire disc is viscous and

(6)

otherwise. For Q₋, the local cooling rate, we assume that each annulus of the disc radiates as a blackbody at temperature T_e, so that

(7)

where σ is the Stefan–Boltzmann constant. Finally, we include an advective term in the energy equation, which depends on the vertically averaged radial velocity,

(8)

and the radial temperature gradient.

2.2 Vertical structure

Completing the model requires specification of both the viscosity ν and the vertical structure, which sets the relation between the central temperature T_c and the surface temperature T_e. We adopt the simplest, vertically averaged approach, for which

(9)

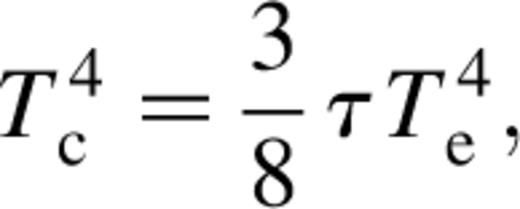
where is the optical depth for a given opacity κ(ρ_c,T_c). When an annulus makes the transition to the layered state, we crudely account for this by replacing (Σ/2) in the expression for τ by Σ_layer. Note that this means that we do not attempt to treat the vertical structure during the transition consistently.

Analytic expressions for low-temperature Rosseland mean opacities are given by Bell et al. (1997). The behaviour of the disc depends primarily on the opacity near the transition temperature T_crit, for which the fit is

(10)

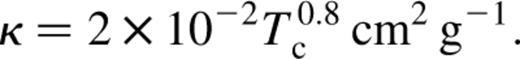
The full list of opacities used is quoted in Table 1. These fits have been taken from Bell & Lin (1994), with the modifications for low temperatures quoted in Bell et al. (1997).

Table 1.

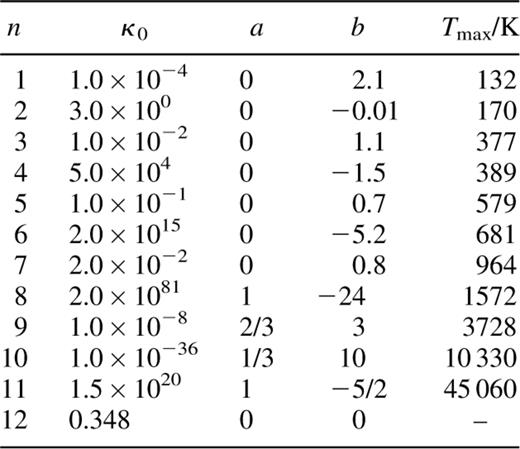
Opacity regimes in ascending order of temperature, fitted by analytic functions of the form We have used fits provided by Bell & Lin (1994), as modified for low temperatures by Bell et al. (1997). The maximum temperature T_max for each regime is quoted for a typical disc density of 10⁻⁹ g cm2⁻³ (where specification of the density is necessary).

Open in new tabDownload slide

2.3 Viscosity

We adopt an alpha prescription (Shakura & Sunyaev 1973) for the viscosity,

(11)

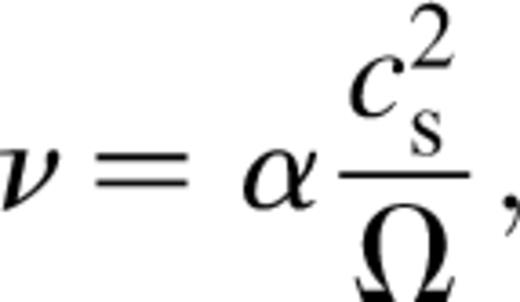
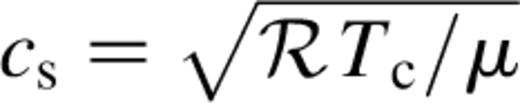where is the mid-plane sound speed and α is a dimensionless parameter measuring the efficiency of angular momentum transport. Numerical simulations of MHD turbulence in discs suggest that α≈10⁻² (Brandenburg et al. 1995; Stone et al. 1996).

2.4 Self-gravity

An immediate consequence of the layered disc structure is that the accretion rate through the surface layer is a fixed, increasing function of radius (Gammie 1996). Inevitably, therefore, material builds up in the quiescent layer over time, until the surface density becomes high enough that self-gravity of the disc becomes important. The condition for this is that the Toomre Q parameter (Toomre 1964), given by

(12)

is less than some critical value Q_crit, which is of the order of unity. Here, we adopt Q_crit=2. When Q<Q_crit non-axisymmetric instabilities set in and act to transport angular momentum outwards. In doing so, the surface density evolves in such a way that the stability of the disc generally increases, thereby self-regulating the violence of the instability.

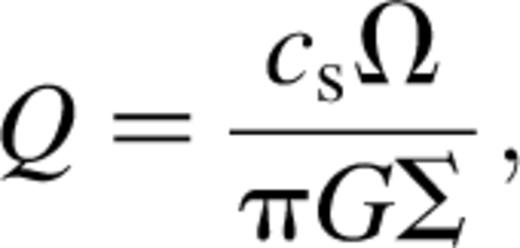
In a local approximation, the efficiency of angular momentum transport owing to self-gravity can be determined by the requirement that viscous heating balances radiative losses (Gammie 1999). This approach, in which the cooling time directly determines α, is most appropriate for discs for which the thermal balance is determined by viscous heating. Even in this limit, global effects may be important (Balbus & Papaloizou 1999). A global redistribution of surface density, driven by self-gravity, can also occur even if the disc temperature is set externally (for example by irradiation). This is the limit that has been studied extensively using isothermal or polytropic simulations (e.g. Laughlin & Bodenheimer 1994). For protoplanetary discs, models suggest that both viscous heating and irradiation can be important at different epochs and radii (Bell et al. 1997).

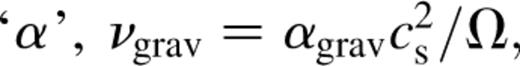Given the above complications, it is evident that attempts to include the effects of self-gravity into one-dimensional disc models can only be approximate. We adopt the form suggested by Lin & Pringle (1987, 1990), and use a variant of equation (11) along with an effective gravitational ‘α’, with

(13)

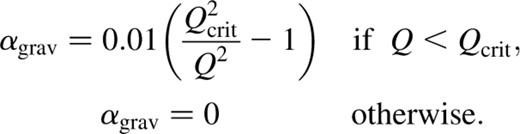
Operationally, we solve equations (3) and (4) using an explicit finite difference method, and include the self-gravity as an additional sweep over the grid using ν_grav and the full surface density Σ in the diffusive part of equation (3), and as an additional heating term in the energy equation.

3 Results

For our numerical calculations we adopt an inner disc radius r_in=3.5×10¹¹ (5 R_⊙), and an outer disc radius (40 au). The computational grid of 120 radial mesh-points is uniform in a scaled radial variable A zero-torque boundary condition is imposed at r_in, while at r_out we prevent outflow by setting the radial velocity, v_r, to zero. When mass is added to the disc (representing infall of further material from the molecular cloud), we take Σ˙ to be a Gaussian centred at 10 au with a width of 1 au. This is exterior to the layered section of the disc that we are interested in studying, so the details of how mass is added are unimportant here. We add mass assuming that it has the same specific angular momentum and temperature as the local disc material.

3.1 Steady infall models

To demonstrate the evolution of the layered disc model, we first take the infall rate on to the outer disc &#x004d;̇_infall to be a constant. We take as suggested by numerical simulations of MHD disc turbulence, and allow the disc to evolve from an initially low mass (10⁻² M_⊙) until either a steady state or a limit cycle has developed.

Fig. 2 shows the accretion rate on to the star for a range of mass infall rates between 5×10⁻⁷ and 3×10⁻⁶M_⊙yr⁻¹ for the highest infall rate, the disc is able to transport gas steadily on to the star. The inner region, in which is able to be supplied by an outer disc in which Q<Q_crit and the angular momentum is transported by self-gravity. Q is typically around 1.5 in this region, with the transition occurring at a radius of ≈3 au.

Figure 2.

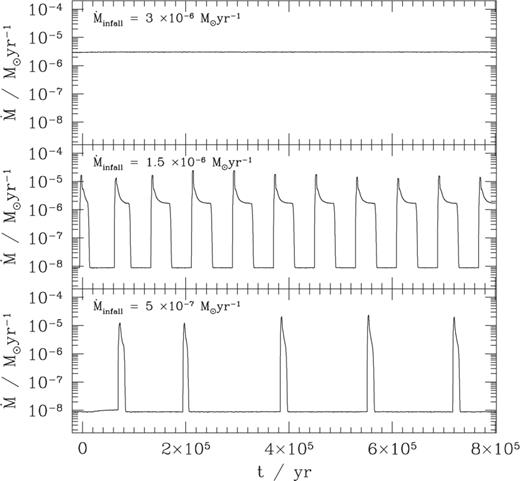
Protostellar accretion for models with a constant rate of infall on to the outer disc. From top down, the panels show models with M˙_infall= and respectively. All models are shown after initial transients have decayed. Steady accretion occurs for sufficiently high accretion rates through the outer disc. At lower accretion rates, the mass flow on to the star is strongly time-dependent.

Open in new tabDownload slide

For lower infall rates such steady accretion is not possible. After an initial phase in which the disc mass increases steadily, a limit cycle is obtained in which outbursts, with a peak accretion rate alternate with quiescent intervals where Both the duration of the outbursts and the recurrence time vary with the rate at which gas is supplied to the outer disc. However, to order of magnitude, for we find and

The mechanism for these outbursts is shown in Fig. 3, which plots the central temperature during the quiescent interval leading up to an outburst. Following the end of one outburst, there is an extended layered region of the disc between ≈0.3 and ≈3 au. This region is stable against gravitational instability, and supports only the small quiescent accretion rate. Gas flowing inwards from the more active self-gravitating region of the disc thus accumulates in the quiescent region, and the transition radius where the disc becomes self-gravitating moves inward. At the same time, the greater dissipation rate in the self-gravitating disc creates a local peak in the disc temperature, which also moves inwards. A new outburst is triggered when this peak first exceeds T_crit, thereby satisfying the condition for MHD turbulence to be restarted. Once the outburst begins, thermal energy is rapidly advected inwards, triggering a transition of the entire inner disc into a hot turbulent state with high accretion rate. This continues until the reservoir of accumulated mass has been depleted, whereupon a cooling wave sweeps through the disc and returns it to the quiescent, layered state.

Figure 3.

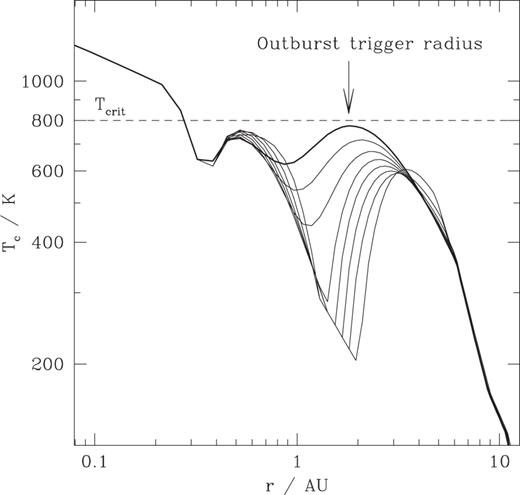
Evolution of the disc central temperature during quiescence. An outburst is triggered when the central temperature in the layered region first exceeds T_crit (dashed line), the temperature at which the disc is well enough ionized to support MHD turbulence. The curves show temperature profiles plotted at intervals of 10⁴ yr, with the earliest time-slice having the lowest temperature at 2 au. The final time-slice, shown as the upper, bold curve, immediately precedes the start of an outburst.

Open in new tabDownload slide

The derived outburst durations are consistent with the expected viscous time-scale in protoplanetary discs at radii of a few au. For an outburst triggered at a radius of approximately 2 au, the viscous time-scale once the disc is in outburst, given by

(14)

where h is the disc scaleheight, is approximately

(15)

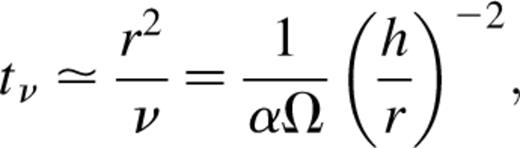
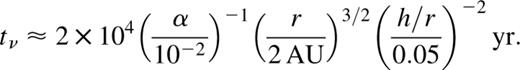
This is only a rough estimate, but it is of the correct order of magnitude to match the numerical model.

The involvement of disc self-gravity means that relatively large disc masses are required for the limit cycle to operate. In our models, M_disc fluctuates between 0.2 and 0.3 M_⊙. During an outburst, only a small fraction of the disc mass — around 20 per cent — is accreted. In more realistic evolutionary models, in which the mass infall rate declines with time, the disc will therefore be able to produce a handful of outbursts, with a few hundredths of a solar mass of gas accreted during each, before settling into a permanent quiescent state.

3.2 Relation to FU Orionis events

The most striking variability observed in pre-main-sequence stars occurs in FU Orionis events (e.g. Kenyon 1995; Hartmann & Kenyon 1996), which are large-amplitude outbursts in the system luminosity originating in the accretion disc. The statistics of these events are subject to considerable uncertainty, but the peak accretion rate during outbursts is of the order of 10⁻⁴ M_⊙ yr⁻¹, while the duration is generally thought to be around 10² yr.

The most popular explanation for FU Orionis events is in terms of a disc thermal instability (e.g. Bell & Lin 1994; Kley & Lin 1999, and references therein), akin to that used to model dwarf novae (e.g. Cannizzo 1993). In the protostellar case, a thermal instability can only operate at extremely small disc radii, typically at less than 0.1 au. Matching the observed time-scales then requires small values of α (10⁻³ to 10⁻⁴), with correspondingly large values for the disc surface density. As noted by Gammie (1999), it would be attractive to dispense with the need for a thermal instability by invoking an alternative limit cycle of a layered disc. This might be possible if the transition to the outburst state was triggered at the extreme inner edge of the layered region. Whether this happens depends on where in the quiescent layer mass preferentially accumulates, and the outcome is therefore sensitive to the detailed, and rather uncertain, physics of the layered disc. In our model, in which matter is being added to the layered region primarily at large radius, the triggering occurs at the outer edge of the layered region, and the time-scales are inconsistent with those of FU Orionis events. We note, however, that the accretion rates of approximately that we obtain during our outbursts fall into the thermally unstable regime. The long outbursts obtained here could then feed shorter FU Orionis events of the sort calculated by Bell & Lin (1994).

3.3 Protostellar accretion history

Continuous replenishment of the disc mass from infall is not a realistic model for protostellar accretion. To explore how the accretion rate on to the star may evolve with time, we adopt a simple model for the infall of gas on to the disc. The details are model-dependent (see e.g. Larson 1969; Shu 1977; Basu 1998), but at early times the infall rate is expected to be of the order of where c_s is the sound speed in the collapsing cloud. For cloud temperatures T∼10 K this implies an infall rate of ∼10⁻⁵ M_⊙ yr⁻¹. We take an initial infall rate of 2×10⁻⁵ M_⊙yr⁻¹ and assume that this declines exponentially on the freefall time-scale, where ρ_cloud is the cloud density. We take Other input parameters are as described earlier.

With these parameters, Fig. 4 shows the accretion rate for the layered disc model. For comparison, we also show the results from a viscous disc model that has identical parameters, but which has no layered region. This control model would be appropriate, for example, if angular momentum transport were driven by a purely hydrodynamic mechanism the efficiency of which was independent of the disc temperature. We compute the control model by using the same code and infall history, but with T_crit set to zero.

Figure 4.

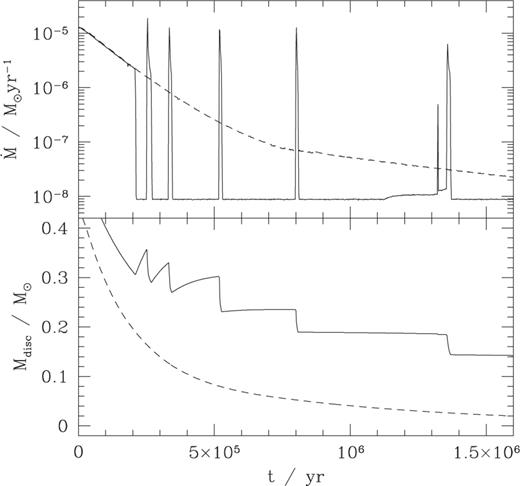
Accretion rate and disc mass as a function of time. The solid curves are for layered disc models in which the mass infall rate on to the outer disc declines exponentially. For comparison with these, the dashed curves show the evolution of a model without a layered structure. This model has identical parameters, except that the disc is assumed to be viscous at all radii and central temperatures.

Open in new tabDownload slide

Initially, when the infall rate is higher than around both models support an accretion rate on to the star which tracks that with which matter is being added to the disc. Subsequently, accretion through the layered disc occurs in outbursts with properties similar to those described earlier, but with increasing intervals between events. For this model, the last outburst before the disc became permanently quiescent occurred after 2 Myr. The accretion rate on to the star in the control model, on the other hand, declines smoothly with time. Similar results are obtained using other functional forms for the mass infall rate as a function of time.

The time-scales of variability predicted by the model are much longer than any direct observational record. Indirect evidence for long-time-scale variability of young stars, however, is provided by studies of protostellar outflows, since the rate of mass outflow via jets is widely believed to track the accretion rate. For example, observations by Reipurth, Bally & Devine (1997) suggest that large-amplitude variations in the outflow rate occur not only on the 10²-yr time-scales characteristic of FU Orionis events, but also on much longer time-scales of 10⁴ yr or greater. These longer time-scales are characteristic of processes occurring at larger disc radii than thermal instabilities, and are consistent with instabilities, of the kind discussed here, originating in the layered disc region.

The outburst accretion rate in the layered disc model is several orders of magnitude higher than that in the equivalent fully viscous disc model at However, the time-averaged accretion rate is substantially lower, so that at late times the disc mass in the layered model substantially exceeds that in the viscous model. We find that after By this time the mass of the fully viscous disc has dropped to only 10⁻² M_⊙. As shown in Fig. 5, most of this extra mass is tied up in the quiescent layer at radii of the order of 1 au, where the surface density exceeds the minimum-mass solar nebula estimate (Hayashi, Nakazawa & Nakagawa 1985) by about two orders of magnitude.

Figure 5.

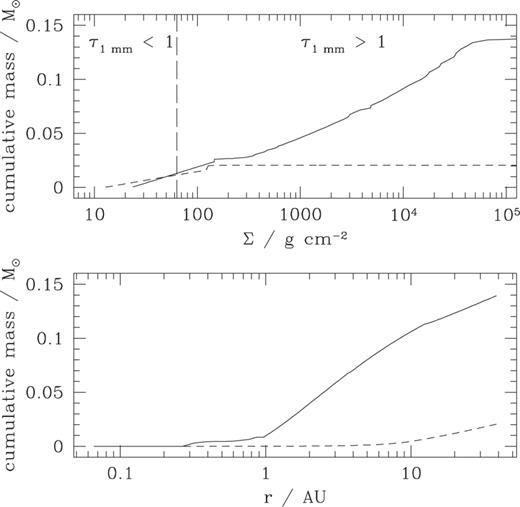
Cumulative disc mass as a function of (upper panel) surface density Σ and (lower panel) radius. The solid curve shows the layered disc model at For comparison, the dashed curve shows results for the fully viscous model at the same time. The vertical dashed line in the upper panel shows the approximate surface density below which the disc would be optically thin at Essentially all the additional mass present in the layered disc is locked up in highly optically thick regions at small radii. The amount of mass at is comparable in both the layered and the fully viscous models.

Open in new tabDownload slide

3.4 Compatibility with observations of protoplanetary discs

A disc mass of a few tenths of a solar mass at early times is consistent with the upper end of the disc mass distribution inferred from millimetre-wavelength observations (Beckwith et al. 1990; Osterloh & Beckwith 1995). However, the layered disc model predicts that a substantial mass — at least a few hundredths of a solar mass — remains in the disc throughout most of the typical classical T Tauri disc lifetime (Strom 1995). Although recent measurements of the mass of H₂ in debris discs indicate that several Jupiter masses of gas can persist beyond 10 Myr (Thi et al. 2001), our predicted disc masses are in apparent contradiction with millimetre observations of many systems with disc masses estimated at 10⁻³ M_⊙ or smaller.

To check whether this is a serious problem for the layered disc model, we plot in Fig. 5 the cumulative distribution of disc mass as a function of surface density. Most of the ‘additional’ mass in the layered disc, compared with the equivalent fully viscous control model, is locked up in the quiescent layer at small radii and high surface density. This material is highly optically thick, and thus would not contribute to the observed emission at millimetre wavelengths. For a range of dust models, the opacity of dust at is thought (Menśhchikov & Henning 1997; Beckwith et al. 1990) to be in the range (note that this is per gram of dust). For a gas-to-dust ratio of 100, this implies that an optical depth of unity at 1 mm is attained for At this surface density threshold, the masses of optically thin gas in the layered and non-layered disc models are very similar. The masses of protoplanetary discs inferred from millimetre-wavelength measurements could thus substantially underestimate the true disc masses.

The accretion rates inferred for classical T Tauri stars can also provide a test. In the simplest version of the layered disc model, the accretion rate during quiescence does not change over the lifetime of the protostellar phase. This rate is consistent with the order of magnitude inferred for accreting classical T Tauri stars (Gullbring et al. 1998). There have also been suggestions that the observationally inferred accretion rate declines with increasing stellar age (Hartmann et al. 1998). Although currently the scatter in measured accretion rates at a given assumed age is very large, and the age estimates themselves are subject to substantial uncertainties (Tout, Livio & Bonnell 1999), this observation poses difficulties for the simplest layered disc model (Stepinski 1998). We note, however, that changes in the quiescent accretion rate with time would be expected in more complete models, for example if the opacity from dust decreased with time as a result of grain growth. Including heating of the disc from the changing stellar radiation would also lead to a decline in the quiescent accretion rate.

4 Planet formation

The environment which a layered disc presents for planet formation differs in several respects both from previous viscous disc models (e.g. Lin & Pringle 1990), and from static models such as the minimum-mass solar nebula. At radii between a few tenths of an au and several au, the gas near the disc mid-plane is almost always quiescent, unless the settling of centimetre-sized particles itself drives additional instabilities (Goldreich & Ward 1973; Cuzzi, Dobrovolskis & Champney 1993). The low viscosity of the disc in this region would reduce the rate at which massive planets migrate inwards, and may allow planet–disc interactions to excite significant eccentricity (Papaloizou, Nelson & Masset 2001).

Other differences include the disc at large radii remaining mildly unstable to gravitational instability for a relatively long time — around a Myr — because the reduced time-averaged accretion rate leads to a larger disc mass at late times when compared with viscous disc models. Outbursts, which persist for a substantial fraction of the disc lifetime, mean that much of the inner disc is expected to be subject to rapid heating and cooling episodes. However, we find no evidence that these cooling waves drive the disc into a state where gravitational collapse would occur.

The survival of solid bodies in protoplanetary discs is limited by the rate at which they migrate inwards relative to the gas. Migration can be rapid for centimetre-sized bodies (e.g. Godon & Livio 1999, and references therein), and is particularly problematic for low-mass planets, for which migration occurs because of the influence of gravitational torques (Goldreich & Tremaine 1979). In standard disc models, the migration time-scale for Earth-mass planets at a few au can be as short as which leaves little time to assemble the cores of giant planets before the putative building blocks are consumed by the star. The rate of migration depends only very weakly upon the surface density profile (Ward 1997), but is sensitive to the gradient of the central temperature, and can be halted if there exists a region of the disc where During the quiescent phase, the models that we have discussed here possess such a non-monotonic central temperature profile at radii of (Fig. 3), leading to the possibility of an enhanced probability of giant planet formation at those radii (Papaloizou & Terquem 1999). Current radial velocity surveys are sensitive to massive planets at radii i.e. within this region. If migration is as rapid as currently suspected, a consequence of the layered disc model would probably be fewer planets at larger radii than would be expected from an extrapolation from the current data.

5 Summary

In this paper, we have presented models for the evolution of magnetically layered protoplanetary discs. Given our present understanding of angular momentum transport in discs, this model represents the best guess for the structure of protoplanetary discs at radii of the order of 1 au, where the gas is cool and poorly coupled to the magnetic field. The evolutionary models presented here suggest a number of important differences with non-layered viscous disc models.

• (i)

  The disc cannot be in a steady state for outer disc accretion rates in the range A limit cycle is obtained, in which heating when the layered region of the disc becomes self-gravitating periodically restarts MHD turbulence, leading to outbursts of accretion on to the star. All calculations to date of layered discs obtain strongly episodic accretion, despite variations in the physical processes included in the models (Gammie 1999; Stepinski 1999). This is the most robust prediction of the model.

• (ii)

  The duration of outbursts depends on where in the quiescent disc they are triggered. In our model, the outbursts are long, with duration ∼10⁴ yr. They could drive repeated strong episodes of mass outflow from the inner disc, resulting in ‘pulsing’ of the observed jets.

• (iii)

  The time-averaged accretion rate is reduced because of the bottleneck created by the layered region of the disc. As a result, the disc mass at late times is large, typically ≈0.1 M_⊙ at Most of this mass is locked up in the quiescent layer of the disc at small radii.

• (iv)

  The central temperature is strongly modified, and often increases with radius, near the transition between the layered disc and the outer self-gravitating region. This could slow the otherwise rapid rate of low-mass planetary migration at radii

• (v)

  A low viscosity in the layered region of the disc affects the migration rate and eccentricity evolution of massive planets at the radii currently probed by radial velocity surveys.

Current observations provide only very limited constraints on the properties of protoplanetary discs at the radii of greatest interest for planet formation. As a result, there remains substantial uncertainty in our knowledge of how these discs evolve. Models, such as this one, that attempt to include more realistic disc physics can lead to very different environments for planet formation and migration than the highly simplified models usually considered. The most obvious observational predictions of the model are that some very young stars should be accreting at the low ‘quiescent’ rate of the order of 10⁻⁸ M_⊙ yr⁻¹, and that high accretion rate outbursts should continue, albeit with lesser frequency, during a substantial fraction of the classical T Tauri phase.

Acknowledgments

PJA thanks the Institute of Astronomy for their hospitality during the course of part of this work, and Charles Gammie, John Papaloizou and Henk Spruit for helpful discussions. This work was partially supported by the Training and Mobility of Researchers (TMR) programme of the European Commission. ML acknowledges support from NASA Grant NAG5-6857. JEP is grateful to STScI for continuing support under their Visitors Program.

References

Author notes