Hydrodynamical winds from two-temperature plasma in X-ray binaries

Abstract

1 Introduction

X-ray binary systems containing a black hole candidate are typically found to be in two different spectral states. In the hard state, the broad-band X-ray spectrum can be described as a power law (photon spectral index ≈1. 5) with a high-energy cut-off around 100 keV. In the soft state, the spectrum consists of two components. There is usually an extended power law (with spectral index ≈2. 5) and a soft X-ray emission which has a spectral shape similar to that of a blackbody. For a recent review of the observations and phenomenological description of these sources see Tanaka & Shibazaki (1996).

The modelling of the hard-state spectra can be described in terms of an unsaturated Comptonization process of soft photons in a region with hot electrons kT ≈ 50 ke V) and electron scattering optical depths of the order of unity. In a pioneering study, Shapiro, Lightman & Eardley (1976) identified this hot region with a geometrically thick, optically thin, hot accretion disc. In this model, the gravitational energy dissipates in the disc, heating the ions which in turn transfer the energy to electrons by Coulomb interactions. However, the electron—ion Coulomb interaction rate is inefficient in such an environment of low density and high electron temperature, and this leads to a large difference in temperature between the electrons and ions, with the ion temperature reaching nearly virial values (10¹¹ K). The importance of radial advection of energy in such a disc was noted by Ichimaru (1977). Taking advection into account, Narayan & Yi (1994) constructed self-similar solutions for the disc equations, called advection-dominated accreting flows (ADAF), showing not only that the proton temperatures approach their virial values, but also that the radiative efficiency of accretion can be significantly reduced as a result of the advection of energy into the black hole. In an alternative description, Chakrabarti & Titarchuk (1995) argued that under certain conditions a shock may arise in such accretion discs, and identified the hot Comptonizing region with the post-shock flow. Despite the differences in the geometry, radiative processes and detailed disc structure, both these models have in common the presence of a two-temperature plasma.

Such a plasma is a natural outcome of any accretion disc model which (i) identifies the hard state X-ray spectrum as a result of the unsaturated Comptonization process of soft photons, (ii) assumes that the viscous energy dissipated heats the ions and (iii) assumes that the only mechanism for energy transfer between the ions and electrons is Coulomb interaction. We note here that these assumptions may not be valid because the viscous energy dissipated may heat the electrons preferentially if a strong equipartition magnetic field is present in the disc (Bisnovatyi-Kogan & Lovelace 2000). In addition, there could be unknown mechanisms which transfer energy between ions and electrons more efficiently than the Coulomb interaction. Thus, it will be useful to have an independent observational signature which could confirm the existence of two-temperature plasmas in black hole candidate systems.

The nearly virial proton temperature of this plasma suggests the possibility of a strong hydrodynamical wind arising from these systems (e. g. Piran 1977; Takahara, Rosner & Kusunose 1989; Kusonose 1991). Such an outflow could transport away a significant fraction of mass, energy and/or angular momentum, thereby affecting the structure and stability of the disc, and the radiative efficiency of accretion for a given mass transfer rate. Chakrabarti (1999) and Das (1999) have studied the possibility of outflows in the context of the shock/centrifugal barrier models. They find that for certain values of the disc parameters (e. g. accretion rate and specific entropy) a hydrodynamical wind occurs. For the ADAF disc solutions, Blandford & Begelman (1999) argued that only a small fraction (<1 per cent) of the gas actually falls into the black hole and the rest is driven away as a wind (in an advection-dominated inflow—outflow solution – ADIOS), thereby effectively reducing the radiative efficiency. Beckert (2000) confirmed this result for different viscosity laws, while Quataert & Narayan (1999) showed that the X-ray spectra from such a wind-driven accretion process can explain the observed spectra of some black hole candidate systems in quiescence. These calculations were undertaken for low mass-accretion rates, and it is not clear how the system will behave in the high-accretion rate regime inferred for black hole candidate systems in the hard state.

The formation of hydrodynamical winds from accretion discs depends on the structure and geometry of the discs. Thus, detailed calculations of the outflow are intrinsically model dependent. Furthermore, reliable calculations of the structure of such discs are difficult because uncertainties exist in the vertical distribution of energy dissipation in the disc that are associated with our lack of detailed understanding of the viscosity. We note that internal magnetic fields in the disc could also facilitate (or inhibit) the formation of winds. Here, electromagnetic forces may accelerate and collimate the wind to form high-velocity jets, as observed in microquasar systems (Mirabel & Rodriguez 1999). Considering these uncertainties, a prudent approach would be to estimate the wind characteristics using only those parameters that can be directly constrained by the fitting of spectral energy distributions. Such an analysis would allow a rough estimation of the magnitude of the mass and energy lost in the form of a wind for a system in question. With such an objective in mind, we report in this paper on calculations of the structure of an hydrodynamical wind similar to those found by Takahara et al. (1989), but in the context of a uniform spherical two-temperature plasma around an accreting black hole. Rather than treating the entire disc/wind configuration with detailed heating and cooling processes as in Kusunose (1991), the calculations are parametrized in terms of the electron temperature of the cloud, T_e, the optical depth, τ, and the total luminosity of the source. We adopt this approach as these parameters are constrained by spectral fitting analyses.

In the next section, the formulation of the problem and the numerical results are presented. The application of these results to observed systems is given in Section 3 and discussed in the last section.

2 Hydrodynamical winds

The mass-loss rate due to a hydrodynamical wind depends sensitively on the ion temperature. This allows a system to be defined as wind-dominated if the ion temperature is greater than some critical value (T_c), while for temperatures less than this value the mass- and energy-loss rates are small enough not to affect the dynamics of the system. This critical temperature will scale as the virial one, i. e. 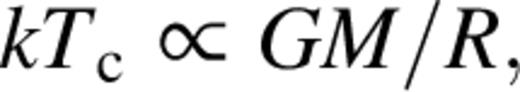where R is the size of the region and M is the mass of the black hole. For a two-temperature plasma the power output is mediated by electron—proton Coulomb interactions, and the luminosity, L, is given by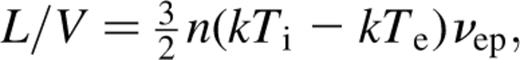

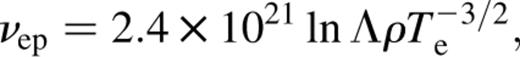
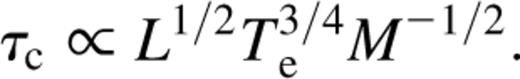
(1)

where V = 4/3πR³ is the volume of the sphere, n is the average number density, T_i and T_e are the ion and electron temperatures, and ν_ep is the frequency of the electron—ion Coulomb interaction. A critical optical depth τ_c (= nσ_TR) may be defined for the system, wherein for systems with τ < τ_c, the ion temperature is larger than T_c (see below). Taking the above relationships into account, with the Coulomb exchange rate given as (Spitzer 1962)

(2)

where lnλ(≈15) is the Coulomb logarithm and ρ is the mass density, it follows that

(3)

As L and T_e are parameters that can be constrained by spectral fitting, τ_c can be directly estimated for a black hole of a given mass. Spectral fitting can also give information about the optical depth of the system, which can then be compared with τ_c to determine whether the system could be wind-dominated or not. The above analysis shows that τ_c does not depend on the size R of the system. This is fortunate as R is not constrained well by observations.

To quantify the above analysis, we solve for the hydrodynamical wind structure from a spherical two-temperature plasma with an optical depth (τ), electron temperature T_e and luminosity L. The central mass is taken to be M = 10 M_⊙, and the radius of the sphere is fixed at R = 20 GM/c². We use the basic equations of the hydrodynamical theory of stellar winds (Parker 1958), which are the conservation of radial momentum

(4)

and the conservation of mass, i. e. the mass outflow,

(5)

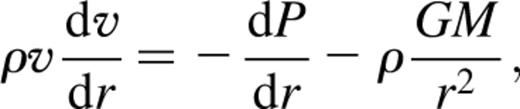
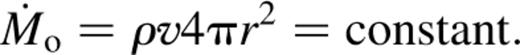
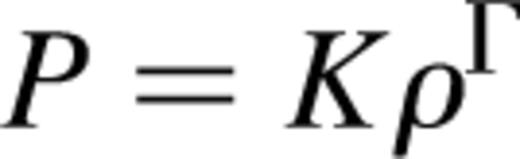Here v is the radial velocity, is the pressure and Γ is the adiabatic index. These equations can be combined to give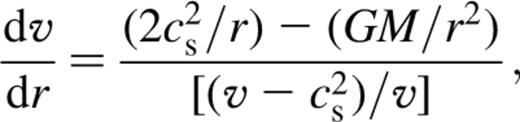

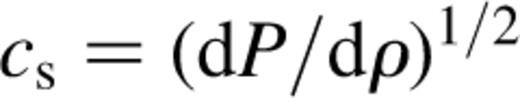(6)

where is the sound speed. At the sonic point, both the numerator and denominator vanish. Wind solutions were constructed by integrating from the sonic point. The inner boundary is taken at R, where the number density 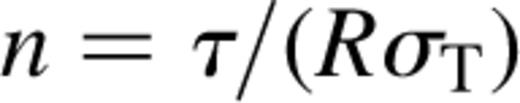and the ion temperature is calculated using equation (1). The solution is constructed such that at infinity both the density and the pressure tend to zero. 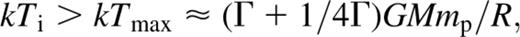A wind solution does not exist if the ion temperature at the surface For high values of the flow is supersonic at the surface, i. e. the sonic point is actually located at a radius smaller than R. Thus we restrict this analysis only to those values of Γ such that 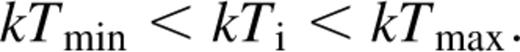Note that for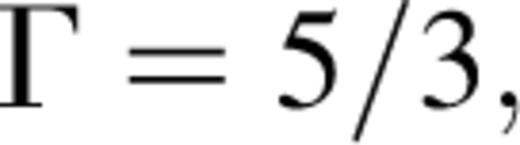 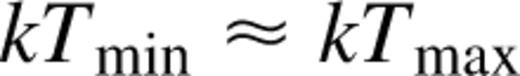and a wind solution with a sonic radius greater than R does not exist for any kT_i. Thus this analysis is restricted to values of 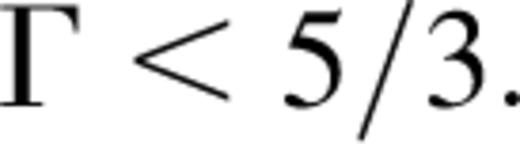Such regimes have also been studied by Chakrabarti (1999). For example, in the limit of efficient conduction of heat an isothermal wind flow results corresponding to 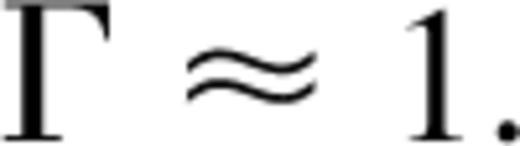. Radiative processes can also lead to redistrubution of energy in the wind leading to 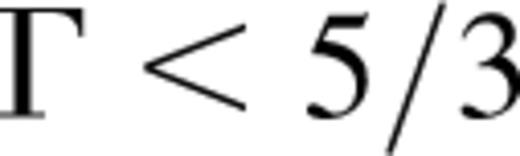(Chakrabarti 1999).

In Fig. 1, the calculated mass-loss rate as a function of ion temperature is illustrated for a fixed optical depth (τ = 1). The virial temperature T_v ≡ GMm_p/kR for the sphere is ≈5 × 10¹¹ K. As expected, &#x004d;̇_o is sensitive to the ion temperature; a factor of 2 increase in T_i causes an increase of &#x004d;̇_o by two orders of magnitude. This justifies defining a critical temperature beyond which the system is wind-dominated and below which it is not. For comparison, we note that the ion temperatures in ADAF-type solutions correspond to T_i ∼ T_v, which is lowered in the presence of winds (Misra & Taam 2001). The mass-loss rate can be expressed in terms of luminosity, optical depth and electron temperature. For a typical luminosity (L = 10³⁸ erg s⁻¹) and electron temperature (T_e = 50 ke V), the variation of the mass-loss rate with optical depth is shown in Fig. 2. Here, the sensitivity of &#x004d;̇_o with τ is apparent; a factor of 2 increase in τ decreases &#x004d;̇_o by at least three orders of magnitude. We show the con tour plots of &#x004d;̇_o for the τ, T_e and τ, L planes in Figs 3 and 4 respectively. These plots highlight the steep variation of &#x004d;̇_o with all three parameters.

Figure 1.

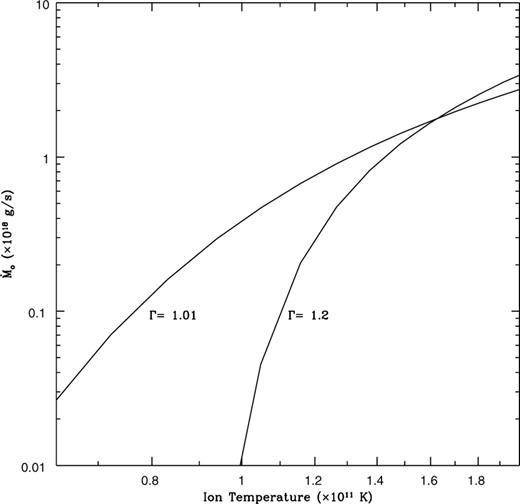
The variation of the mass outflow rate with ion temperature for adiabatic indices Γ = 1.2. (nearly isothermal) and The other parameters are: and

Open in new tabDownload slide

Figure 2.

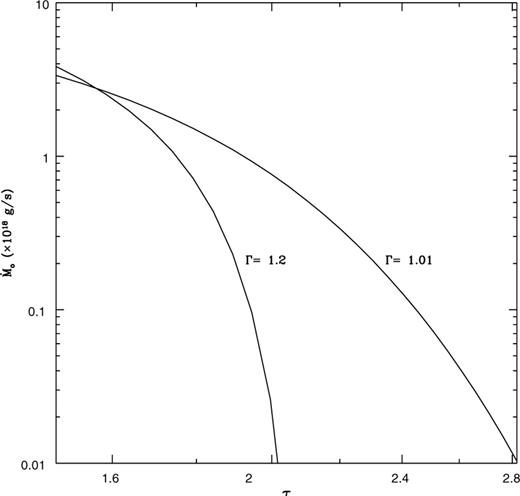
The variation of the mass outflow rate with optical depth for adiabatic indices Γ = 1.01 (nearly isothermal) and Γ = 1.2. The other parameters are: M = 10 M_⊙, R = 20 GM/c², kT_e = 50 ke V and L = 10³⁸ erg s⁻¹.

Open in new tabDownload slide

Figure 3.

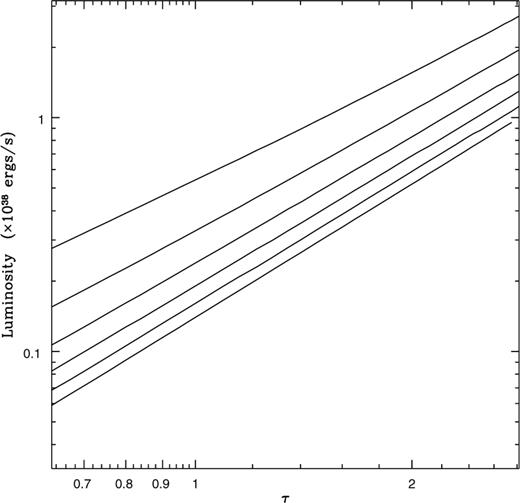
Contours of mass outflow rate (M˙_o) for luminosity and optical depth. The con tours correspond to from top to bottom . The other parameters are:

Open in new tabDownload slide

Figure 4.

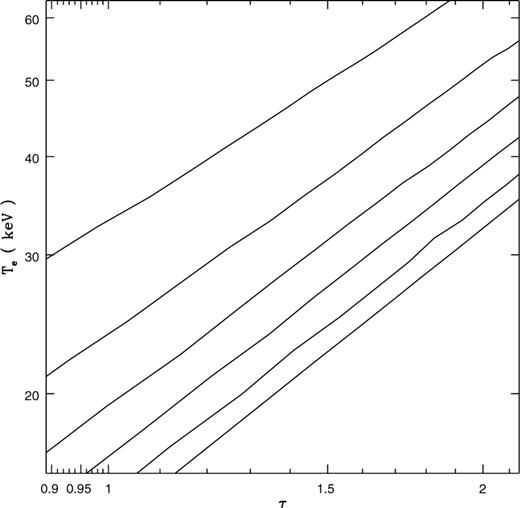
Same as in Fig. 3, except that the con tours are for electron temperature and optical depth for a luminosity of L = 10³⁸ erg s⁻¹

Open in new tabDownload slide

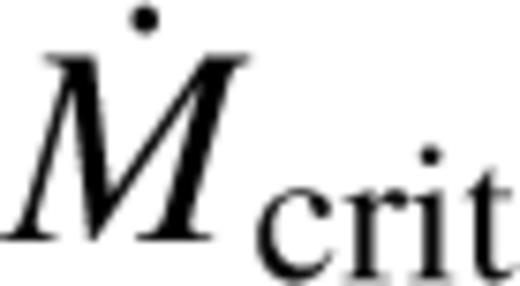The τ, T_e and L parameter space can then be divided into two regions corresponding to high and low values of &#x004d;̇_o. In particular, we define the wind dominated region as corresponding to and the complementary region as the non-wind-dominated one. The choice of &#x004d;̇_crit is ad hoc and is chosen to be 10¹⁸ g s⁻¹. Since the dependence of &#x004d;̇_o on the parameters is steep, choosing &#x004d;̇_crit to be 10¹⁷ g s⁻¹ still leads to a division of the parameter space into nearly similar regions. A critical optical depth τ_c can be defined as a function of L and T_e for which 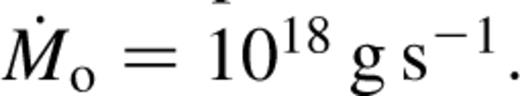The topology of Figs 3 and 4 and the qualitative analysis described in the beginning of this section (equation 3) suggest that τ_c can be represented as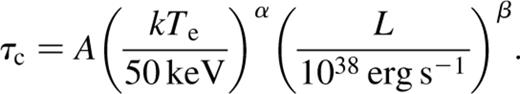

(7)

We constrain A, α and β for different values of &#x004d;̇_crit, Γ, M and R, and present the results in Table 1.

Table 1.

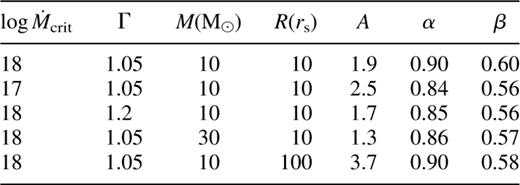
Values of A. β and α in equation (7). Here M₀ is in units of gs^Ȓ1 and R is in units of r_s = 2 GM/c².

Open in new tabDownload slide

From these results it can be seen that A, α and β do not vary greatly with changes in &#x004d;̇_crit, Γ, M or R. Thus to within a factor of 2, the critical optical depth can be represented as

(8)

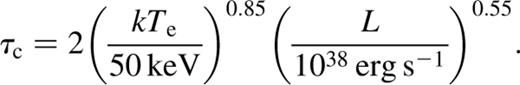
We can now use equation (8) to determine from observations if a particular system is wind-dominated or not.

3 Application to X-ray binaries

Assuming that a two-temperature plasma configuration is established subject to the conditions described in Section 2, we discuss the possible applications of hydrodynamical winds to binary systems that contain compact objects. In the following we first discuss the results for the black hole candidate systems Cyg X-1, GX 339−4, and Nova Muscae. For convenience, the results are summarized in Table 2.

Table 2.

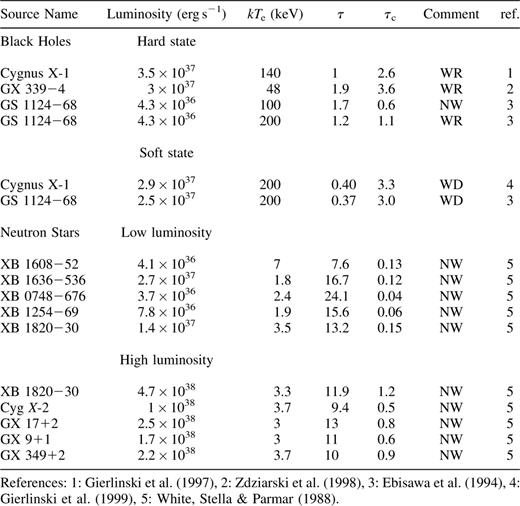
Comparison of interred and critical optical depth for various X-ray binaries. The luminosity, electron temperature (T_e) and optical depth (τ) have been quoted from the references. The symbols WD. WR and NW stand for wind-dominated, wind-regulated and no wind, respectively. For GS 1124–68 (Nova Muscae) and Cygnus X-l (soft state), the electron temperature is assumed and the optical depth has been estimated using equation (9). Note that for the soft state, the assumptions used in this analysis may not be valid (see text).

Open in new tabDownload slide

The hard-state spectrum of Cyg X-1 has been fitted by Gierlinski et al. (1997) with a Comptonization model, and they obtained the following parameters: τ ≈ 1,kT_e ≈ 140 ke V L = 3.5 × 10³⁷ erg s⁻¹ and (for a distance of 2. 5 kpc). Using these values we find from equation (8) that τ_c=2. 6 for a black hole of 10 M_⊙, which is of the order of the observed σ ≈ 1. Similarly, for another black hole system, GX 339 –4 in the low state, Zdziarski (1998) obtained σ = 1.93 kT_e = 48 ke V and L = 3 ×10³⁷ erg s⁻¹. For these values τ_c = 3.6 which is again of the order of the observed τ. Thus, our analysis of both Cygnus X-1 and GX in their hard states indicates that these systems are on the borderline between having a strong or a weak wind. This may point to the existence of a feedback mechanism wherein the energy and mass loss from the wind regulate the hot disc structure.

Unlike the persistent systems discussed above, black hole X-ray novae are transients. In these sources, the luminosity increases by several orders of magnitude in ≈10 d and then decays exponentially in a time-scale of ≈1 month. During the peak of the outburst the system is usually in the soft spectral state and makes a transition to the hard state in months (see Tanaka & Shibazaki 1996). Observations of the X-ray transient source Nova Muscae (GS 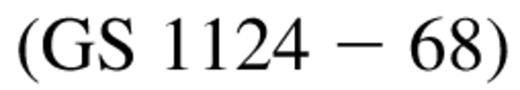by the Ginga satellite throughout most of its evolution were reported in Ebisawa et al. (1994). Since the Ginga energy band is restricted to <20 keV, the roll-over of the spectrum at high energies was not observed. Thus, a Comptonization fit does not constrain both T_e and τ. In particular, only a low-energy spectral index (α_s) (during different times of the evolution) was measured. For a Comptonized spectrum, α_s is approximately related to T_e and τ by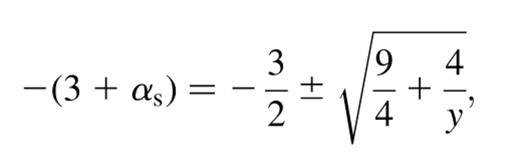

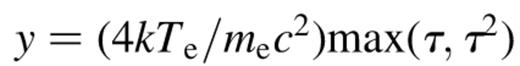(9)

where is the Compton y-parameter. For Nova Muscae in the hard state, α_s was observed to ≈0. 5 at a luminosity 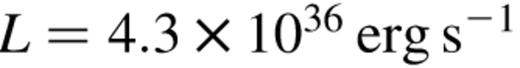(Ebisawa et al. 1994). If we now assume that 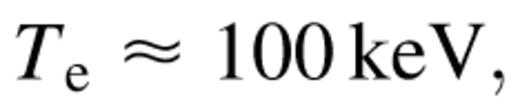one obtains 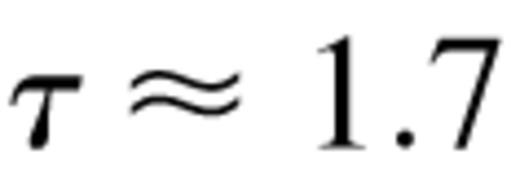from equation (9). The critical optical depth for such a system is then 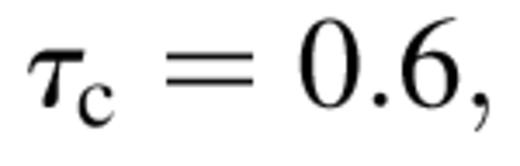which is less than the inferred τ, indicating the absence of a strong wind. However, a strong wind is indicated if one assumes 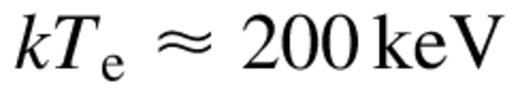instead, as the inferred 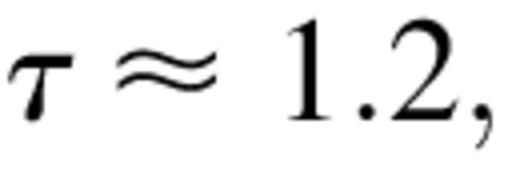which is close to the critical value of 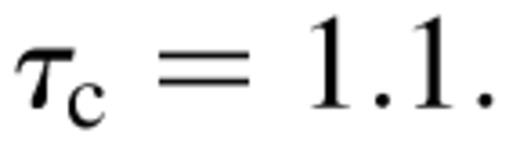Thus, hydrodynamical winds can be important in the hard state of Nova Muscae, provided that the electron temperatures are ≳150 keV.

In the soft state of black hole candidate systems, the power-law spectrum is steeper than in the hard state. Gierlinski et al. (1997) analysed the soft-state Cygnus X-1 data and found that the energy spectral index and the power law extends up to ≈200 keV with no apparent cut-off. They argued that thermal Comptonization does not describe the spectra well. Instead, the power law is probably due to non-thermal Comptonization. In this case, the presence of non-thermal electrons indicates that the electrons are probably heated directly, instead of mediated by processes involving protons. Thus, the basic assumption underlying this study is probably not valid for the soft spectral state of Cygnus X-1. Nevertheless, from the observed and assuming that one would infer using equation (9) that This is much smaller than the critical value of perhaps indicating the presence of a strong wind. A similar result is obtained from the soft state of Nova Muscae (see Table 2).

In addition to black hole candidates, the spectra from X-ray binary systems that contain a neutron star can also be described as being due to Comptonization. Hot two-temperature accretion flows around neutron stars have recently been constructed by Medvedev & Narayan (2001). On the other hand, the hot region may not be the accretion disc itself, but instead could be an extended corona surrounding the boundary layer between the disc and the surface of the star. This analysis can still be applied to these systems as long as the assumption that the total luminosity of the source is channelled by the protons to the electrons remains valid. 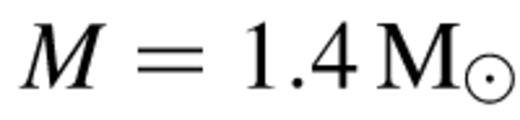The critical optical depth when and 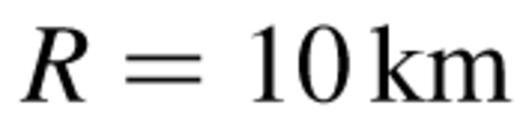is found to be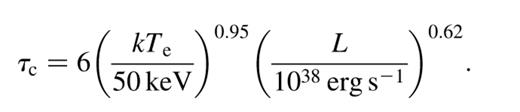

(10)

Spectral fitting of EXOSAT data from several neutron star binaries has been undertaken by White, Stella & Parmar (1988), and is summarized in Table 2. For Cygnus X-2, they constrain and (for a distance of 8 kpc). Using equation (10), we find that which is significantly less than the observed value. Similar results were obtained for other neutron star systems in both the high- and low-luminosity levels (Table 2). This implies that unlike black hole candidate X-ray binary systems, their neutron star counterparts are not dominated by a hydrodynamic wind. This result is further supported by the analysis undertaken by Medvedev & Narayan (2000), who constructed self-similar accretion flows on to neutron stars and found that hydrodynamic winds are not important in these systems.

4 Summary and discussion

The possible occurrence of hydrodynamical winds in X-ray binary systems has been investigated. From simple considerations, the conditions under which these winds can be important have been identified. It is found that the mass-loss rate in such winds depends sensitively on the luminosity of the source, as well as the electron temperature and optical depth of the coronal region. The steep dependence of the mass-loss rate on these parameters facilitates the use of a critical optical depth to indicate whether or not a given system can support such a wind. Application of the theory indicates that winds can exist in the hard state of the black hole candidates Cyg X-1, GX 339−4 and GS 1124−68.

Strong winds in these systems may decrease the radiative efficiency where &#x004d;̇_i is the mass-inflow rate) by carrying away a substantial amount of matter and energy. For Nova Muscae, the radiative efficiency has been estimated to be for the soft state and for the hard state (Misra 1999). These values are lower than that expected from an Keplerian disc which could be caused by the presence of a strong wind rather than energy advection into the black hole. Winds may also affect the thermal stability of accretion discs by introducing an additional channel for energy loss (e. g., Piran 1977).

We reiterate that the analysis undertaken in this paper is based on the assumption that the gravitational energy dissipated in the system is transferred to the electrons by the ions via Coulomb interactions. This naturally restricts the analysis to only certain systems where this is valid. As mentioned earlier, the soft-state spectrum of black hole candidate systems is probably of a non-thermal origin, and hence the analysis performed in this study cannot be applied. Even for the hard spectral states of compact X-ray binaries considered here, alternative models to a two-temperature plasma description have been proposed. For example, the X-ray spectra could be due to magnetic flare activity above a cold disc (Poutanen & Fabian 1999) or produced by a disc with a rapidly varying radial temperature profile (Misra, Chitnis & Melia 1998). Thus, it should be emphasized that the results presented here are specifically discussed within the framework of a two-temperature plasma model.

The spherical geometry assumed here is simplistic even though two-temperature discs are geometrically thick. Furthermore, the effect of angular momentum or of convection on the dynamics of accretion and the wind outflow have not been taken into account. The former effect can increase the mass-outflow rate as a result of centrifugal support, whereas the latter effect can affect the thermal structure of the underlying disc and hence the existence of a wind. In this context, the thermal structure is dependent on the direction in which angular momentum is radially transported by convection, and the magnitude of the viscosity parameter (see Narayan, Igumenshchev & Abramowicz 2000). A more detailed analysis should take these effects and radiative heating/cooling of the wind into account in at least two spatial dimensions (e. g., Chakrabarti & Molteni 1993). However, such analyses will, by necessity, be model dependent and limited by the uncertainties in the vertical structure and geometry of the hot disc.

The hydrodynamical winds described in this paper may be confined to form a jet-like structure by the geometry of the disc and magnetic fields. Furthermore, if they are accelerated to relativistic speeds by electromagnetic forces, they may provide the origin of the radio jets observed in the black hole candidate systems known as microquasars (Mirabel & Rodriguez 1998). On the other hand, the radio jets may be a different phenomenon that is unrelated to hydrodynamical winds. In that case it is desirable to have direct observational signatures of these outflows. Since the Thomson optical depth of the winds calculated here (i. e. the optical depth from the surface of the sphere R to infinity) is typically <0. 1, column densities of the order of 10²³ cm⁻² are indicated. Although the X-ray continuum spectra are not expected to be altered by the outflow, a significant fraction of the column density may not be highly ionized, giving rise to observable absorption and/or emission lines. The detection of P Cygni type profiles by high-resolution X-ray satellites Chandra and Newton-XMM may provide evidence for the existence of such winds and serve as a useful diagnostic not only of the wind structure, but also the of physics underlying the disc.

Acknowledgments

RM acknowledges support from the Lindheimer Fellowship at Northwestern University.

References