Evolution of the X-ray luminosity and metallicity of starburst blown superbubbles Free

Abstract

1 Introduction

The formation and evolution of galaxies is one of the most captivating problems of modern astrophysics. With present-day techniques, young starbursts can be observed at large look-back times and much work has been devoted to the detailed studies of the optical and near-UV properties of such systems at intermediate and high redshifts. The defining characteristic of starburst galaxies is that their optical spectrum is dominated by strong permitted emission lines from H and He and forbidden lines from O, Ne, N and S on top of a weak continuum characteristic of the H ii region associated with young (≤10 Myr) star-forming regions. While the UV radiation from the massive stars excites and ionizes the associated H ii regions, the stellar winds and supernova explosions lead to giant hot bubbles in the interstellar medium (ISM) that will emit mainly in the X-ray regime.

Most of the information about the properties of the ‘warm ISM’ (T ~ _E K) in young giant star-forming regions comes from the analysis of their optical emission lines. Such observations indicate, perhaps surprisingly, that the warm ISM in starburst galaxies is not yet contaminated by the metals ejected by the present burst. In contrast, little is known about the ‘hot ISM’(T_E ~ 10⁶⁻⁷ K) where most of the newly produced metals are presumably located. Data from ROSAT, ASCA and BeppoSAX, although inconclusive, seem to suggest subsolar iron abundance and about solar abundances for the α elements (Bauer & Bregman 1996; Persic et al. 1998; Ptak et al. 1999; but see Dahlem, Weaver & Heckman 1998 and Weaver et al. 2000).

Here we report an attempt to explain this apparent discrepancy by combining a realistic estimate of the metal content evolution of the hot ISM with two-dimensional hydrodynamical simulations of evolving superbubbles.

2 Superbubbles in Starbursts

The mechanical energy from evolving starbursts is known to lead to the formation of superbubbles in their ISM. This happens as the violently ejected matter from winds and supernovae becomes thermalized at a reverse shock providing both a high temperature (T ≥ 10⁷−10⁸ K) and a high-thermal-pressure plasma that in turn drives a strong shock (the so-called outer shock) into the surrounding ISM. The outer shock is responsible for sweeping and accelerating the surrounding ISM into a large-scale shell, while the hot thermalized ejecta fills most of the volume formerly occupied by the swept-up gas. The two gases, the ejecta and the swept-up ISM, are separated by a contact discontinuity and there is little enrichment, at this time, of the ISM at large (Tenorio-Tagle 1996).

Several calculations (see Tenorio-Tagle & Bodenheimer 1988; Silich & Tenorio-Tagle 1998 and references therein) have shown how the expanding structures acquire a variety of shapes, depending on how the ISM is distributed. Fairly round and figure-of-eight shaped remnants are expected for a constant-density medium and plane stratified atmospheres, respectively. Superbubbles are also known to blow out upon the sudden acceleration experienced when crossing supersonically a large negative density gradient. At that moment, the accelerated section of the shell of swept-up matter becomes Rayleigh–Taylor unstable and fragments, while the hot superbubble interior is vented into the low-density surrounding gas. The escaping material then pushes again an outer shock to build a new and even larger shell evolving into the halo of the galaxy. If the shock reaches the outskirts of the galaxy with a speed larger than the escape velocity of the system, it may also establish a galactic wind. This is in fact detected in the case of some nuclear starbursts (e.g. Heckman et al. 1996; Tenorio-Tagle & Muñoz Tuñón 1998). The latter event is expected to have drastic consequences as all the newly processed starburst elements, originally found in the hot superbubble interior, will be channelled out of their parent galaxy into the intergalactic medium.

Superbubbles have been recognized for their large-scale expanding H i shells (Heiles 1979; Brinks & Bajaja 1986; Maschenko, Thilker & Broun 1999). Some of the youngest ones are detected at optical frequencies emanating from giant H ii regions (Meaburn 1980; Heckman, Armus & Miley 1990; Martin 1996; Oey 1996), and many have been identified by the X-rays emitted from their hot interiors (Wang & Helfand 1991; Heckman et al. 1995; Wang 1999).

Current predictions of the X-ray luminosity are based on the fact that, in the temperature range of ∼10⁷−10⁸ K the X-ray emissivity can be approximated by a linear function of the gas metallicity. For the 0.1–2.4 keV energy band, the emissivity is, very nearly, ∧_x = 3Z × 10⁻²³ erg cm³ s⁻¹ where Z is the metallicity in solar units. A simple analytic model may then be used to estimate the X-ray luminosity from a spherically symmetric, energy-dominated bubble bound by a cold radiative shell, and presenting self-similar temperature and density distributions (see Chu & Mac Low 1990 for a constant energy input rate, and Silich 1995 for a power-law energy deposition). For a constant ambient gas density, and constant-energy input rate, the X-ray luminosity over the energy band 0.1–2.4 keV is given by is given by

(1)

where L₃₈ is the mechanical luminosity of the starburst in units of 10³⁸ erg s⁻¹, n₀ is the ambient gas number density, and t₇ is the evolutionary time in units of 10⁷ yr. I(τ) is a dimensionless integral:

(2)

and τ = T_cut/T_c is the ratio of the X-ray cut-off temperature (the lowest limit considered for the gas temperature to lead to an important X-ray emission; T_cut≈ 5×10⁵ K) to the bubble central temperature T_c.

This simple model has been applied to a number of objects, from stellar wind bubbles to starburst galaxies. In most cases, the observed X-ray luminosities exceed the simple model predictions greatly (e.g. Chu & Mac Low 1990 for Large Magellanic Cloud bubbles; Walter et al. 1998 for a superbubble in the nearby dwarf galaxy IC 2574; Martin & Kennicutt 1995 for diffuse X-ray emission from the central region of the starburst galaxy NGC 5253). There are several proposed solutions to this discrepancy. Chu & Mac Low (1990) have proposed off-centred supernova explosions. Franco et al. (1993) included the interaction of a fragmented ejecta with the outer shell and Martin & Kennicutt (1995) concluded that cloud evaporation may be a dominant mechanism to increase the X-ray emission.

In what follows we will show that the injection of energy and mass from an ageing stellar cluster not only leads to the large-scale evolving superbubbles detected at a variety of frequencies, but also to a time-dependent enhanced metallicity of their hot interior that has important consequences for the evolution of the X-ray luminosity and observed metal content of the hot superbubble. Section 3 discusses the time-dependent production of metals. Section 4 presents the model results regarding the energy deposited by massive coeval starbursts, the mixing of the enriched material and the cooling of the gas. The resultant time-dependent X-ray luminosity is given in Section 5 and the conclusions are drawn in Section 6.

3 Time-Dependent Metal Production in Starbursts

Our central aim is to explore the changes in the evolution of the X-ray luminosity of starburst superbubbles associated with the expected change in the chemical composition of the hot bubble interior.

In this first exploration we have decided to follow in detail the evolution of the iron and oxygen abundances, iron because it is the element that is easiest to measure from X-ray spectroscopy and oxygen because it, comprising almost half of the mass of all the metals, is the best tracer of metallicity and has a dominant effect in the cooling function dependence on metal content.

We have to indicate that one major uncertainty in this analysis is given by the metal yields, i.e. the metal production rates per unit mass of long-lived stars (e.g. Renzini et al. 1993). We have adopted the approach of including in our computations the EXTREME theoretical yields for both oxygen and iron with the hope that the ‘true’ solution will be bound by these extreme cases.

We assume that the gas ejected by stellar winds and supernovae (SNe) includes all the newly synthesized oxygen and iron. For a power-law initial mass function (IMF) the total ejected mass as a function of the cluster age t is

(3)

where we have assumed that massive stars lose all their mass as they explode as SNe (Pilyugin 1993; Pilyugin & Edmunds 1996), a Salpeter IMF with upper M_up = 100M_⊙ and lower M_low = 1M_⊙ cut-off masses and a slope of α = 235. The normalization constant f₀ is determined by the total mass of the star cluster M_SB,

(4)

The mass of the stars exploding after an evolutionary time t, [M∗(t)], has been found using Chiosi, Nasi & Sreenivasan (1978) and Stothers (1972) approximations to the main-sequence lifetime of massive stars:

(5)

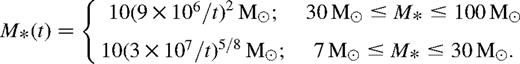
Heavy element yields from massive stars have been considered in a number of papers (Renzini et al. 1993). The theoretical yields depend strongly on the adopted stellar evolution models; therefore we have decided to consider the extreme cases as detailed in the following paragraphs.

3.1 Oxygen yields

For the oxygen yield, we express its dependence with stellar mass (M∗) using two extreme tracks.

• (1)
  The ‘no wind’ (NW) Pilyugin & Edmunds (1996) analytic approximation to Maeder (1992) and Thielemann, Nomoto & Hashimoto (1993) models for the yield

  

  (6)

  which neglects the oxygen yield for stars with a mass smaller than 10.5 M_⊙, and
• (2)

  The ‘with wind’ (WW) track that uses stellar evolution models with stellar winds (Maeder 1992; Woosley, Langer & Weaver 1993). In this case equation (6) applies to the mass range 10.5 M_⊙ ≤ M_* ≤25 M_⊙, and a constant yield is then assumed up to the upper mass limit M_up = 100 M_⊙

3.2 Iron yields

For a normal stellar population most of the iron production comes from SNe Ia, which produce 0.5–0.7 M_⊙ of iron per SN after the ⁵⁶Ni decay. However, as we are interested here in the earlier stages of the starburst evolution, i.e. stellar clusters with ages less than about 20–30 Myr, only the iron yield from SNe II is included in our calculations.

The theoretical iron production from type II SNe is highly uncertain (see Renzini et al. 1993), so we consider here the two extreme estimates, Arnett (1991) where the iron yield increases with increasing progenitor mass and Thielemann et al. (1992) where the iron yield decreases with increasing progenitor mass.

• (1)
  Arnett's (1991) iron yield dependence on stellar mass can be approximated by a linear function for stars in range 10 M_⊙ ≤M_* 40 M_⊙:

  

  (7)

  For stellar masses outside the above range we have assumed constant values of Y_Fe: Y_Fe = 0.02 M_⊙ for M_* ≤ 10 M_⊙ and Y_Fe = 0.02 M_⊙ for M_* > 40 M_⊙. We will refer to these iron yields as A91.

• (2)
  Thielemann et al. (1992) iron yield dependence on stellar mass can be approximated by an exponential function,

  

  (8)

  within the 13–25 M_⊙ range. Outside this range the yield is assumed constant and equal to Y_Fe(M_*) = 0.24 M_⊙ for low-mass stars and Y_Fe(M_*) = 0.05 M_⊙ for stars with an initial mass larger than 25 M_⊙. We will refer to these iron yields as T92.

Fig. 1 displays the adopted oxygen and iron yields as functions of the initial star mass M∗. Note that the yields in equations (7) and (8) have been calculated for solar metallicity stars (and are the only ones available) while the stars and the initial ISM in all but one of our models have an initial metallicity of 0.1 Z_⊙ both in oxygen and in iron.

Figure 1.

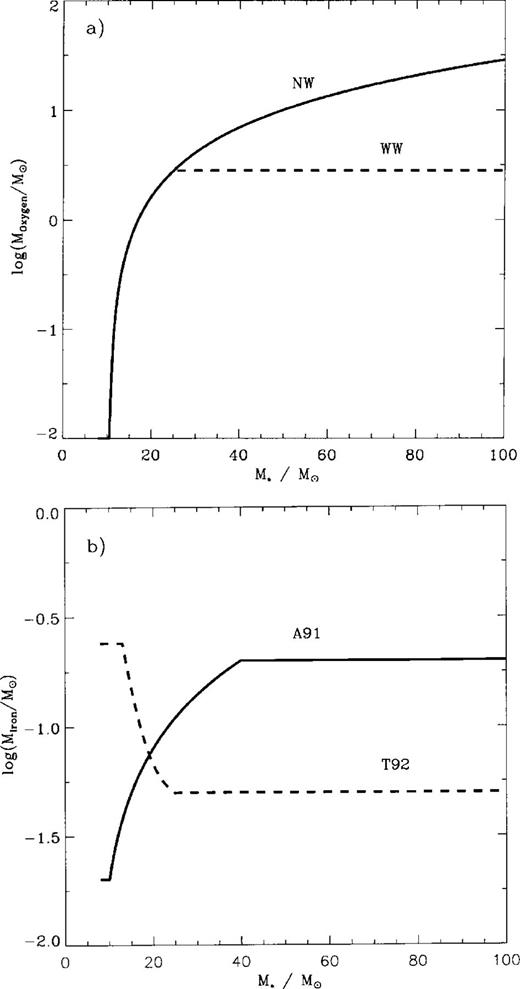
The adopted approximations for the oxygen (panel a) and the iron (panel b) yields of massive stars with the initial mass M∗.

Open in new tabDownload slide

4 Superbubble Evolution with Time-Dependent Metallicity

The Fe and O abundances of the hot bubble interior relative to solar are given by

(9)

(10)

where M_ev is the mass added to the shocked wind region resulting from the cold outer shell evaporation. In what follows, the metallicities are given in solar units, for which we adopt Z_O = 0.0083 and Z_Fe = 0.00126Z (Grevesse, Noels & Sauval 1996).

Fig. 2 shows the time evolution of the total amount of matter injected into the superbubble interior (M_ejecta) for the NW case for oxygen and A91 yields for iron (top panel) and the WW case for oxygen and T92 yields for iron (bottom panel). A clear difference in the rate of production of oxygen and iron is apparent. While oxygen rapidly climbs to an asymptotic value in less than 10 Myr, iron remains at a low level and it is still increasing at 40 Myr in the T92 case (Fig. 2b). Note that at this time the amount of iron has not yet reached its final value, as the most important contribution to iron production is expected later on from type I SNe that have progenitors with masses below 10 M_⊙.

Figure 2.

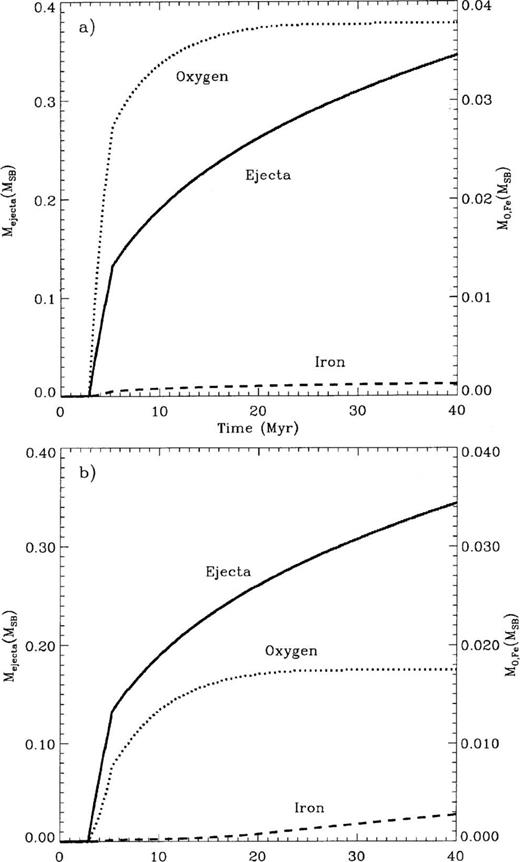
Time-dependent metal production from 10⁶ M_⊙ starbursts. The panels display the cumulative amount of mass fraction (in units of the starburst mass M_SB) ejected as the coeval starburst evolves in time (solid line). Also shown are the oxygen (dotted lines) and iron (dashed lines) mass fractions. The top panel (a) shows the oxygen production under the ‘no wind’ (NW) approximation and the iron production for the A91 prescription. The bottom panel (b) illustrates the ‘with wind’ (WW) oxygen production together with the T92 yields for iron. The right -hand side scale indicates the mass of O or Fe in units of the starburst mass.

Open in new tabDownload slide

We have included the evolution of the metal content of the hot bubble interior in our hydrodynamical calculations of the evolution of the superbubble associated with a 10⁶ M_⊙ coeval starburst of initial abundance Z ~ 0.1 Z_⊙. The computations were carried out with our three-dimensional Lagrangian code, based on the thin layer approximation (Bisnovatyi-Kogan & Silich 1995; Silich & Tenorio-Tagle 1998). In all cases the total mass of the host galaxy is 10¹⁰ M_⊙, while the gas mass is 10⁹ M_⊙. The galaxy model is similar to that used by Li & Ikeuchi (1992), Tomisaka & Bregman (1993), Silich & Tenorio-Tagle (1998) and Tenorio-Tagle et al. (1999; hereafter Paper I). The gas density distribution includes two isothermal components. One represents a central dense molecular disc with a mass of 5×10⁷M_⊙ and the second describes a low density and extended halo. Both components are in a quasi-equilibrium state supported by rotation and random gas motions with a velocity dispersion of 20 and 80 km s⁻¹, respectively. The temperature of both components is ∼1000 K.

The assumed initial density distribution of the model (Fig. 3) is similar to that of case A1 in Paper I (hereinafter reference model: RM). The 10⁶ M_⊙ starburst was assumed to produce a constant mechanical energy at a rate of ∼3.2×10⁴⁰ erg s⁻¹ (see Leitherer & Heckman 1995) for the first 40 Myr of its evolution.

Figure 3.

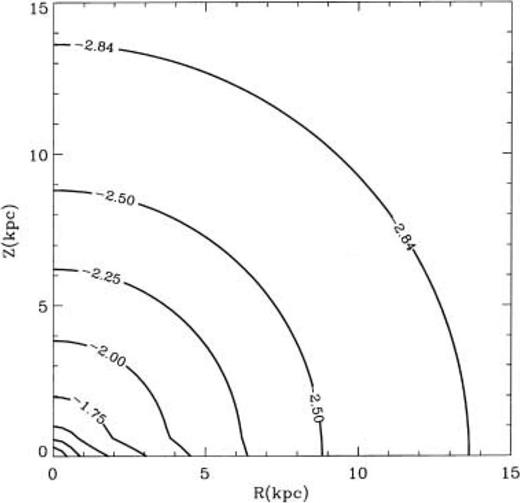
The logarithmic density distribution for a 10⁹ M_⊙ ISM model. Labels correspond to the logarithmic number density and the outer contour represents the edge of the galaxy.

Open in new tabDownload slide

Four different cases were calculated (1, 2, 3 and RM). In all we assume that the supernova products rapidly mix with all the gas within the superbubble interior. The main differences among them are the effects of evaporation of mass from the cold shell, the metal production rates both for oxygen (with wind and no wind) and iron (Thieleman's or Arnett's), and the energy input from the central star cluster. The model input parameters are summarized in Table 1.

Table 1.

Model parameters.

Open in new tabDownload slide

Case 1 includes the thermal evaporation from the cold shell segments and considers its mixing with the ejecta from type II supernovae. The no-wind and A91 approximations were used for case 1NW, and the with-wind and T92 approximations for case 1WW.

Case 2 neglects the process of thermal evaporation and thus the metals are allowed to mix only with the ejected stellar envelopes, the latter assumed to have the same metallicity as the ISM in the host galaxy. As in case 1, case 2NW includes the no-wind and A91 approximations while case 2WW includes the with-wind and T92 approximations.

Case 3 is similar to case 1NW except that the mechanical energy input rate is 10 times larger i.e. 3.2×10⁴¹ erg s⁻¹). Case 3A corresponds to an initial metallicity of the ISM of 0.1 Z_⊙, whereas case 3B assumes solar initial metallicity.

The calculations follow the change with time of the metallicity in the superbubble interior and apply the correspondingly modified cooling rates. For the outer shell we assumed that its metallicity remains constant in time and equal to Z_ISM. The results are compared with our reference model RM which assumed that the cooling function, scaled to the initial metallicity of the host galaxy, remained unchanged with time. Furthermore, for our comparison case RM we have also assumed, as in most calculations in the literature, that the same cooling function could be applied throughout the flow.

Figs 4(a) and (b) show the evolution with time of the size and expansion velocity of the superbubble for cases 1NW and 3A, respectively. The figure displays values of the fastest expansion velocity measured along the symmetry axis, as well as of the largest radius reached by the superbubble during the first 40 Myr of evolution. The maximum expansion velocity shows an initial deceleration, followed by a strong acceleration that leads to several hundreds of km s⁻¹ immediately after blow-out from the central disc. This short phase is abruptly interrupted once sufficient halo matter has been swept into the expanding shell causing, once again, a steady deceleration of the remnants. By comparing the maximum expansion speed with the escape velocity from the host galaxy (V_esc), we can discern whether the decelerating remnant remains bound (as in case 1) or is able to reach the galaxy outer boundary and eject its contents into the intracluster medium (as in the more energetic case 3). In this respect, the results for cases 1, 2 and RM are identical, as all three assumed the same mechanical energy injection and the same parent galaxy. The generated remnants, in all three, have identical size, expansion speed and total amount of swept-up mass. On the other hand, the total luminosity and the metal content inside the superbubble are different for the different models, as discussed below.

Figure 4.

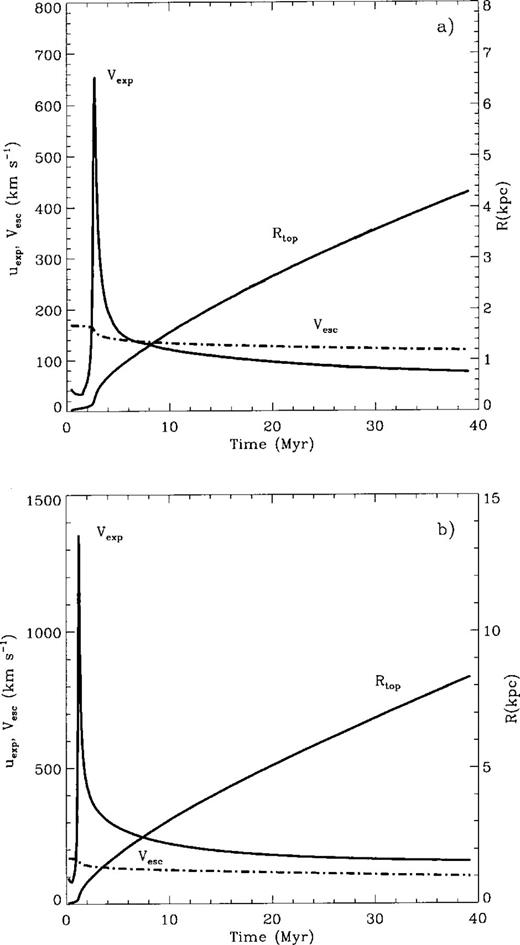
Evolution of the superbubbles. (a) Case 1NW and (b) case 3A; shown as a function of time are the maximum expansion speed (km s⁻¹) measured along the symmetry axis (solid lines), the galaxy escape velocity (dash–dotted lines) and the radius (in kpc) reached by the superbubble.

Open in new tabDownload slide

Fig. 5 shows, for cases 1NW and 2NW, the amount of matter swept by the outer shock (M_shell) and the total mass (M_interior) inside the cavity, which includes both the matter thermally evaporated from the shell and the mass ejected by SNe, as functions of time. Note that in both case 2 models (without shell evaporation) all the mass within the cavity is produced by SNe and M_interior = M_ejecta. Also shown are the cumulative amounts of matter ejected by SNe (M_ejecta) and the corresponding masses of oxygen (M_O) and iron (M_Fe). The sharp M_shell decrease observed at about 5 Myr results from the outer shock merging at the mid-plane of the galaxy (see Silich & Tenorio-Tagle 1998).

Figure 5.

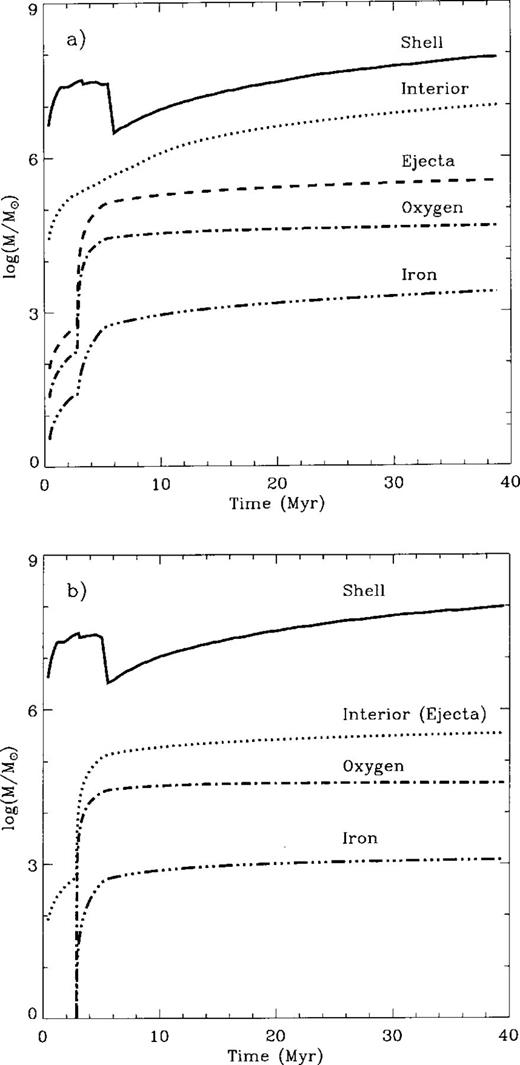
The log of the swept up mass (in M_⊙) and that inside the superbubbles for cases (a) 1NW and (b) 2NW, as a function of time. The curves represent the log of total swept-up mass (solid lines), and total mass inside the superbubbles (dotted lines labelled ‘Interior’). The latter includes both the amount of matter thermally evaporated from the shell (not shown) and the mass ejected by SNe (dashed lines labelled ‘ejecta’, coinciding with M_interior in panel b). Also shown are the log of the total oxygen and iron mass (dash–dotted lines). In both cases these were calculated following the NW and A91 approximations (see Section 3).

Open in new tabDownload slide

In case 1 (Fig. 5a), the injected metals were allowed to mix thoroughly with the matter evaporated from the expanding shell. Note that for such a massive starburst, the amount of hot matter evaporated from the shell reaches a large fraction of the total mass of the shell (M_interior ∼ 10 per cent of M_shell per cent of M_shell). The total oxygen mass surpasses 10⁴ M_⊙ while the total mass in iron reaches ∼10³ M_⊙.

Case 2 assumes no mass evaporation from the shell, and thus, apart from the small contribution arising from the early wind phase, the mass of the hot bubble M_hot is very similar to the matter ejected by supernovae (M_ejecta). Thus the amount of oxygen and iron are very close to the values expected from the synthesis by the massive starburst (Fig. 5b for case 2NW).

Fig. 6 shows the evolution of metallicity of the superbubble interior as a function of time for the different model assumptions regarding the yields, the mixing of heavy elements and the mass evaporation. Case 1NW (using the NW and A91 approximations) rapidly (between 4 and 5 Myr) reaches supersolar metallicities Z_O ∼ 8Z_⊙ for oxygen, and solar values for iron (Z_Fe) (Fig. 6a). Z_O then slowly decays to about 3 Z_⊙ after 10 Myr of evolution, to solar after 20 Myr and to under solar (∼0.5 Z_⊙) at the end of the calculation. Z_Fe becomes under solar after 6 Myr and slowly approaches the metallicity of the host galaxy (0.1 Z_⊙).

Figure 6.

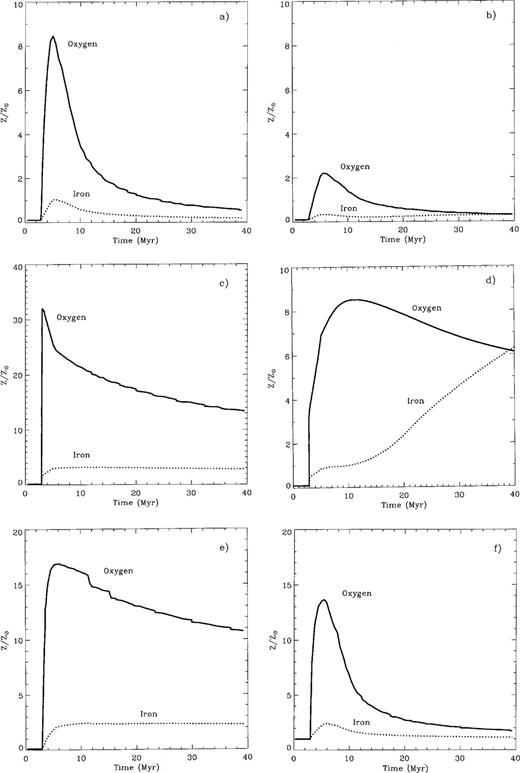
The panels display the oxygen and iron content of superbubbles (in solar units: Z_O=0.0083 and Z_Fe = 0.00126 from Grevesse et al. 1996) for the models (a) 1NW (with thermal evaporation of the cold outer shell segments) no mass loss and A91 approximations; (b) 1WW with mass loss and T92 approximations; (c) 2NW (no shell evaporation, no mass loss and A91 approximations); (d) 2WW, (no shell evaporation, with mass loss and T92 approximations); (e) 3A, a 10⁷ M_⊙ starburst within a 0.1 Z_⊙ ISM, and (f) 3B, a 10⁷ M_⊙ starburst within a Z_⊙ ISM.

Open in new tabDownload slide

The maximum abundances (both of O and Fe) that result from the more realistic stellar evolution models allowing massive stars to lose their mass via stellar winds (cases WW) are below the above values. The metallicity that results from case 1WW, assuming T92 approximations for the production of metals (Fig. 6b), reaches Z_O ∼ 2Z_⊙ that is four times below the value obtained for stellar evolution without mass loss. Z_O reaches its maximum after 6 Myr of evolution, and then falls continuously down to the solar value just after 10 Myr and slowly approaches 0.1 Z_⊙ at the end of the calculation. Z_Fe on the other hand, remains subsolar throughout the calculation. However, because Thielemann et al. (1992) model predicts the iron yield to be larger for the low-mass stars, Z_Fe begins to grow with time after 10 Myr of the starburst evolution, when the lower mass stars become SNe. Z_Fe is comparable to Z_O at the end of the calculation.

The difference between the mass-conserving (NW) and the wind-dominated (WW; Arnett 1991, Thielemann et al. 1992) models is more notorious in cases 2 (without shell evaporation), when hot gas metallicity is directly defined by the chemical composition of the SN ejected matter.

For the case 2NW (stellar models without mass loss), oxygen metallicity exceeds 30 Z_⊙ after about 3 Myr of evolution (Fig. 6c). Even after 40 Myr this case remains with Z_O > 13 Z_⊙. In this case (with iron yields from A91), Z_Fe ∼ 3 Z_⊙ after 6 Myr of evolution and remains almost constant throughout the calculation.

Case 2WW (using the stellar models with mass loss and Thielemann et al. 1992 results for the Fe production rate) also presents a rapid early rise in Z_O. However, the maximum metallicity Z_O = 8Z_⊙, reached at 10 Myr, is about four times lower than the value found for stellar models without mass loss. After the maximum, Z_O declines slowly to reach 6 Z_⊙ after 40 Myr of evolution (Fig. 6d). Z_Fe, on the other hand, remains subsolar for the first 12 Myr, but then rises, reaching 6 Z_⊙ at the end of the SN II phase. This rise is a direct consequence of Thielemann et al. (1992) models having most of the Fe production in low-mass SNe II.

For the most energetic starburst with Z_ISM=0.1Z_⊙ (case 3A), large values of Z_O ≥ 10Z_⊙ are found within the first 15 Myr (Fig. 6e). The enhanced metallicities, however, are not diluted in this case, as the fast and hot quasi-adiabatic outer shell has inhibited mass evaporation.

The effect of increasing the initial ISM metallicity from 0.1 Z_⊙ to Z_⊙ is illustrated in model 3B. Unexpectedly, the interior bubble metallicity is lower and more peaked with time (Fig. 6f). This results from a much faster shell cooling because of the higher initial metallicity, and consequently an earlier shell evaporation because of a steep temperature gradient between the cold shell material and the hot bubble interior. This in turn leads to a more effective dilution of the freshly produced metals by the evaporated gas from the shell.

5 The X-ray Luminosity of Superbubbles

The X-ray emission from superbubbles arise from two different physical regions: the dense outer shell of accelerated ISM and the hot superbubble interior (Suchkov et al. 1994; Silich & Tenorio-Tagle 1998; Strickland & Stevens 1998; D'Ercole & Brighenti 1999). Our description of the inner bubble structure is based on the Weaver et al. (1977) similarity solution. It is assumed that the bubble interior density is dominated by mass evaporated from the low-temperature shell. The mass loss rate from the shell, Ṁ_shell, is defined by classical evaporation theory and reads as (Mac Low & McCray 1988)

(11)

where thermal conductivity is given by κ = CT^5/2, C = 6 × 10⁻⁷ egr s⁻¹ cm⁻¹ K^−7/2, μ is the mean mass per particle, T is the hot gas temperature and R_shell is the shell radius. The density n and temperature T profiles then can be approximated by (Mac Low & McCray 1988)

(12)

(13)

where n_c and T_c are the central hot gas number density and temperature, and x= r/R_shell is the dimensionless distance from the bubble centre. To account for the expected difference in density and temperature distributions for adiabatic and radiative shell segments, we approximate the inner bubble luminosity as

(14)

where ε is the ratio of the radiative surface segments to the total remnant surface area, and L_R and L_A are the X-ray emissions from the interior of the fully radiative and adiabatic bubbles, respectively (Silich & Tenorio-Tagle 1998)

(15)

Here I(T_c,λ) is a dimensionless integral given by

(16)

R_cut and T_cut are the X-ray cut-off radius and temperature respectively. We used a self-similar power index λ = 2/5 for L_R, and λ = 1/20 for a more homogeneous gas distribution within a bubble with an adiabatic hot shell. The X-ray luminosity from the adiabatic shell segments is taken to be

(17)

where dσ is the adiabatic segment surface area, and ΔR is the segment thickness.

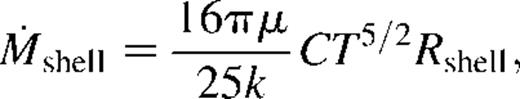
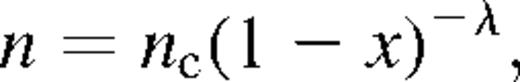
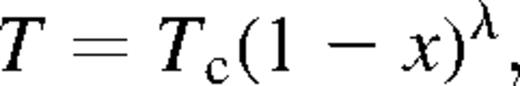
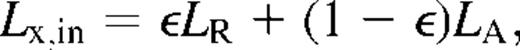
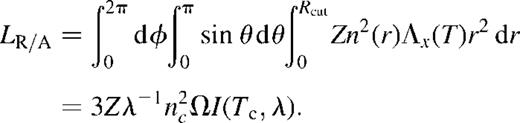
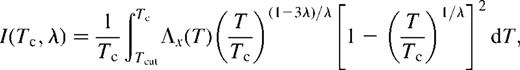
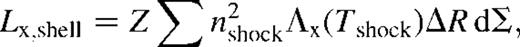
Fig. 7(a) shows the total and the shell contribution to the X-ray emissivity of case 1NW, using the hot gas metallicities shown in Fig. 6(a). The contribution of the shell to the total emission becomes most important immediately after blow-out of the remnant from the central gas distribution into the extended halo of the host galaxy. During blow-out the shock reaches speeds of several hundreds of km s⁻¹, leading to high temperatures where v_shock is the shock velocity in units of 10³ km s⁻¹) which allow the shocked gas to radiate in the X-ray regime. The shell contribution becomes rapidly less important as the shock slows down and the shell cools below the X-ray cut-off temperature (∼5×10⁵) and condenses into a narrow and dense outer boundary of the superbubble. On the other hand, the luminosity of the superbubble interior is found to remain within the range of observed values (10³⁸−5×10³⁹ erg s⁻¹) throughout the evolution. Fig. 7(b) compares the time-dependent X-ray luminosity for our case 1 under the two assumptions for metal production rate. Clearly, the lower metallicities reached in the WW model lead to a smaller X-ray emission, although the difference never amounts to more than a factor of 5.

Figure 7.

The log X-ray luminosity, as a function of time, for case 1NW under A91 approximation for the yields. (a) shows the outer shell contribution (dotted line) and the total luminosity (solid line); (b) compares the above total luminosity with that derived for case 1WW under the T92 assumptions (dotted line); and (c) shows the X-ray luminosity in the two indicated X-ray bands for case 1NW.

Open in new tabDownload slide

Fig. 7(c) gives the contribution to the X-ray luminosity of case 1NW in two different energy bands, as a function of time. The two energy bands considered are from 0.1 to 2.2, and from 1.6 to 8.3 keV (X-ray emissivities from Suchkov et al. 1994). Clearly, most of the X-ray luminosity arises from the soft X-ray component. The high-energy X-rays are caused mostly by the larger central temperatures in the superbubble interior.

Fig. 8 shows the time evolution of L_x, per unit mass, in models 1NW, 2NW, 3A and 3B, as well as the same quantity for the reference model RM which did not include changes in metallicity arising from the injection of new metals into the cavity. The main difference between cases 1NW and RM comes from the hot superbubble interior and can amount to more than an order of magnitude, particularly after 10 Myr, once the shell contribution has become negligible in both cases. Note that the X-ray luminosity of the reference case (RM) is in fact rather similar to that of case 2NW (without thermal evaporation). However, in case 2 the reduced X-ray emissivity from the interior is a result of the fact that, without the substantial extra mass input, the amount of matter able to radiate is orders of magnitude too small. Case 3, our most powerful starburst, leads to the largest luminosities of all cases.

Figure 8.

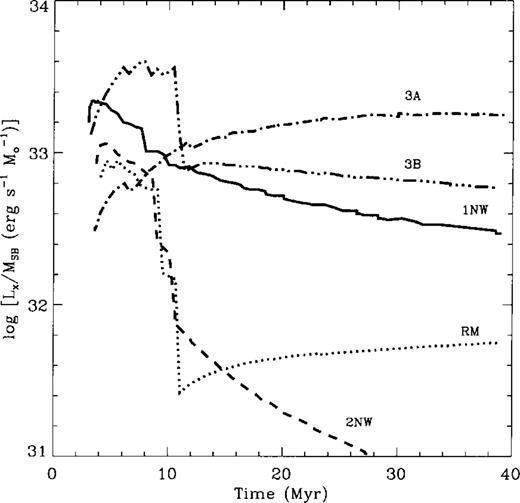
The log of the X-ray luminosity of superbubbles per unit mass as a function of time for cases 1NW (low Z), RM (low Z), 2NW (low Z), and massive starburst 3A (low Z) and 3B (solar abundance), as labelled.

Open in new tabDownload slide

It is interesting to notice an important difference between the bubble evolution in low (case 3A) and high (case 3B) metallicity ISMs. Up to 10 Myr, the X-ray luminosity of the bubble in the metal-rich galaxy is almost an order of magnitude larger than that for the low-metallicity one. However, as the high-metallicity bubble reaches the radiative phase much earlier than the low-metallicity one, the metal-rich shell (3B) cools rapidly around 11 Myr, whereas in the metal-poor case (3A) it remains adiabatic and hot. This results in a rapid decrease of L_x in the high-metallicity model, which, after 12 Myr, drops below the X-ray emission from the low-metallicity one, and declines more slowly afterwards. The plot indicates that similar X-ray luminosities per unit mass (∼10³³ erg s⁻¹ M_⊙⁻¹) arise from cases that allow mass evaporation from the outer shell, irrespective of the mass of the starburst causing the superbubble. This is very different from the calculations that do not account for the change in metallicity of the superbubble interior (RM), and also from those that do not account for shell evaporation (cases 2).

6 Conclusions

The calculations presented here, with the exception of those for the more massive starburst (case 3), differ only slightly in their final outcome regarding the size, expansion velocity and amount of matter swept by evolving superbubbles. However, they show enormous differences in the metallicity of the hot interior, and thus produce largely different X-ray emissivities.

The effects of injection of new metals into the superbubble interior are most noticeable during the H ii region lifetime (the first 10 Myr). If oxygen is used as a tracer, the metallicity reaches, immediately after the start of the SN phase, values well above solar metallicity. The maximum value is achieved 3 to 5 Myr after the beginning of this phase. Later, mixing with the evaporated mass slowly reduces the impact of SNe. Note, however, that if massive stars are assumed not to have strong winds, large values of Z_O≥ Z_⊙ would remain present inside the superbubble for at least the time required to reach the end of the type II SN phase (40 Myr). This is true even in the extreme case where the host galaxy initial metal abundance is well below solar. On the other hand, if iron is used as the tracer of metallicity, values of Z_Fe≤ Z_⊙ are always predicted, regardless of the assumed iron production scheme. All of the cases without mass evaporation, on the contrary, lead to metallicities larger than solar throughout the evolution, regardless of the assumed tracer.

More massive starbursts result in very strong shocks and a long-lasting hot, quasi-adiabatic outer shell from which thermal evaporation is strongly inhibited. Such starbursts show over solar metallicity throughout their evolution, regardless of the tracer.

Finally, we comment on the present-day abundance determination of X-ray gas. ROSAT observations allow us, in principle, to derive the metal abundance of a (T ∼ 1–30 × 10⁶ K) plasma, by X-ray spectral fittings. However, the process is problematic, because of the poor energy resolution of the ROSAT PSPC detector, and the derived ISM metallicities disagree, in many cases, with those deduced from optical observations (Trinchieri et al. 1994; Saraccco & Ciliegi 1995; Bauer & Bregman 1996). The situation has somewhat improved with the ASCA and BeppoSAX observations, yet the X-ray measurements still suggest significantly subsolar abundance for Fe combined with somewhat subsolar abundances for α elements (Bauer & Bregman 1996; Persic et al. 1998; Ptak et al. 1999). At this stage it is very difficult (and possibly not relevant) to compare the metallicities derived from emission optical lines with those derived from X-ray observations, as we are probing different phases of the ISM with them.

The complexity of the X-ray spectra of starburst galaxies, combined with the poor spectral resolution of the pre-Chandra and pre-XMM observations, makes the determination of metallicities very model-dependent (e.g. Strickland & Stevens 1998; Netzer 1999). Dahlem et al. (1998) and Weaver Heckman & Dahlem (2000) have discussed the difficulties in deriving metallicities from X-ray data, and, by combining ROSAT and ASCA data for nearby edge-on starbursts like NGC 253 and M82, they concluded that the fitting is consistent with near-solar abundances, and therefore extremely low metallicities as derived by only ROSAT or ASCA data are no longer required.

Our most important conclusions are that supersolar CNO products in superbubble interiors can strongly influence their X-ray luminosity while at the same time Fe abundances remain subsolar.

In any case, X-ray spectroscopy of starbursts with the new facilities, Chandra and XMM, combined with models of the type described here, will undoubtedly be the best tool to determine empirically the yields of massive stars and type II SNe in stellar systems over a wide range of metallicities.

Acknowledgments

The authors acknowledge fruitful conversations with Andy Fabian, and with Michael Dahlem and Kim Weaver, who kindly provided us with their results prior to publication. We specially acknowledge the useful remarks of the referee that helped to improve the clarity of the paper. SAS acknowledges support from a Royal Society grant for joint projects with countries of the former Soviet Union. SAS, GTT and ET also thank the IoA in Cambridge for support and hospitality during a visit to the United Kingdom where the calculations were performed. HN acknowledges the hospitality of the IoA, where this collaboration was initiated, and financial support by the Israel Science Foundation. Research Grants from CONACYT (Mexican Research Council) are thankfully acknowledged by GTT and ET.

References

Author notes