-
PDF
- Split View
-
Views
-
Cite
Cite
K. L. Bell, A. Matthews, C. A. Ramsbottom, Electron collisional excitation of Si VIII: (
,
,
) fine-structure transitions, Monthly Notices of the Royal Astronomical Society, Volume 322, Issue 4, April 2001, Pages 779–784, https://doi.org/10.1046/j.1365-8711.2001.04183.x
Close - Share Icon Share
Abstract
Effective collision strengths for electron-impact excitation of the N-like ion Si viii are calculated in the close-coupling approximation using the ab initioR-matrix method. The 22 fine-structure levels arising from the 11 lowest LS target states: 2s22p3, 2s2p4, 2p5 and 2s22p23s are retained in the present calculation. The effective collision strengths for all forbidden transitions within the 1s22s22p34S3/2o,2D3/2,5/2o,2P1/2,3/2o ground configuration levels are obtained by averaging the electron collision strengths, for a wide range of incident electron energies, over a Maxwellian distribution of velocities. Results are presented for electron temperatures in the range log T(K) = 3.3 to log T(K) = 6.5, applicable to many laboratory plasmas and in particular to astrophysical plasmas. We believe that the results are the most accurate to date and, indeed, the only data available which take account of resonance effects.
1 Introduction
Emission lines from nitrogen-like ions with 2s22p3 ground configurations have long been known to be useful as density diagnostics of solar and nebular plasmas. The intensity ratio of forbidden lines that arise from transitions within the ground configuration of O ii was first suggested by Aller, Ufford & Van Vleck (1949) as a diagnostic for gaseous nebulae. Feldman et al. (1978) pointed out that the O ii ratio is not a useful diagnostic for the solar atmosphere, but that forbidden lines of the ions Mg vi, Si viii, S x, and Ar xii that belong to the same isoelectronic sequence as O ii could be used to determine electron densities in the inner corona. More recently, Doschek et al. (1997) have derived electron densities in the solar polar coronal holes from a forbidden spectral line ratio of Si viii. They employed lines corresponding to transitions  and
and  It is noted however that this ratio, whilst primarily depending on the electron density, may also have some sensitivity to the electron temperature. Recent work by Keenan et al. (1999), in employing the same ratio in a study of the emission lines of [O ii] in the optical and ultraviolet spectra of planetary nebulae, clearly shows that the ratio has sensitivity to the electron temperature. In this paper we extend our earlier work for Mg vi (Ramsbottom & Bell 1997) and S x (Bell & Ramsbottom 1999) to consider electron-impact excitation for all forbidden transitions within the ground configuration levels of Si viii.
It is noted however that this ratio, whilst primarily depending on the electron density, may also have some sensitivity to the electron temperature. Recent work by Keenan et al. (1999), in employing the same ratio in a study of the emission lines of [O ii] in the optical and ultraviolet spectra of planetary nebulae, clearly shows that the ratio has sensitivity to the electron temperature. In this paper we extend our earlier work for Mg vi (Ramsbottom & Bell 1997) and S x (Bell & Ramsbottom 1999) to consider electron-impact excitation for all forbidden transitions within the ground configuration levels of Si viii.
Surprisingly little attention has been paid to this ion. Davis, Kepple & Blaha (1976) and (1977) used the distorted wave approximation, neglecting exchange, for a few dipole allowed transitions from the 2s22p34So, 2Do levels and parametrized their effective collision strengths. The only calculation, to the best knowledge of the present authors, which has been performed for the fine-structure forbidden transitions considered in this paper is that of Bhatia & Mason (1980). They also employed the distorted wave method, together with a transformation of the K-matrices obtained in LS-coupling, into pair-coupling using algebraic re-coupling coefficients, which allow for spin-orbit interaction and other relativistic effects. 13 fine-structure levels were considered, namely those arising from the seven LS-coupling states associated with the 2s22p3 and 2s2p4 configurations, and limited configuration-interaction was included in the target state representation. They presented collision strengths only at three values of the electron energy: 10, 15 and 20 Ryd. In their review article, Pradhan & Gallagher (1992) gave a percentage uncertainty to these collision strengths of less than 30 per cent. However, a more significant error can arise in calculating the effective collision strength. The distorted wave method neglects resonances and it has been shown that even the inclusion of additional resonances can affect fine-structure forbidden transitions by as much as a factor of two (Ramsbottom, Bell & Keenan 1997).
Clearly there is a need for a large and sophisticated close-coupling calculation, which includes extensive configuration-interation wavefunctions to represent the target states and which takes full account of resonance effects.
2 Method
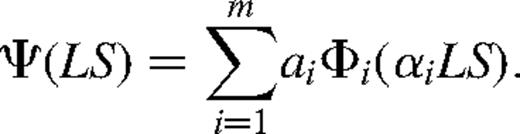
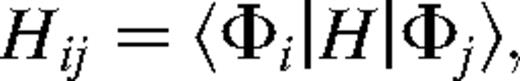
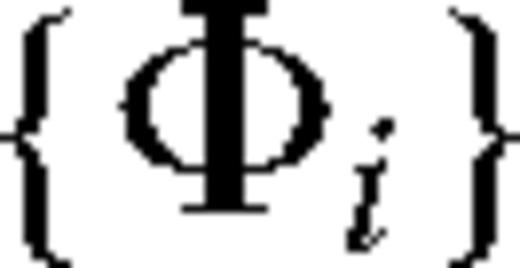 are built from a set of one-electron functions, each consisting of a product of a radial function, a spherical harmonic and a spin function
are built from a set of one-electron functions, each consisting of a product of a radial function, a spherical harmonic and a spin function 
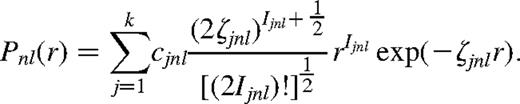
The powers of r, {Ijnl}, are held constant, but the coefficients {cjnl} and the exponents {ζjnl} are treated as variational parameters when determining the radial functions. Nine orthogonal orbitals were used in the calculation, five ‘spectroscopic’ (1s, 2s, 2p, 3s, 3d) and four pseudo-orbitals (3p, 4s, 4d, 4f). The parameters cjnl, Ijnl, ζjnl for the 1s, 2s and 2p functions were taken to be the Hartree—Fock values obtained by Clementi & Roetti (1974) for the 2s22p34So Si viii ground state. For the remaining orbitals, Table 1 gives the configurations used, together with the state employed to obtain the orbital parameters by the minimization of the associated energy level. The pseudo-orbitals are included to represent the effects of electron correlation omitted by, for example, the Hartree—Fock method. The coefficients for all of the orbitals are given in Table 2.
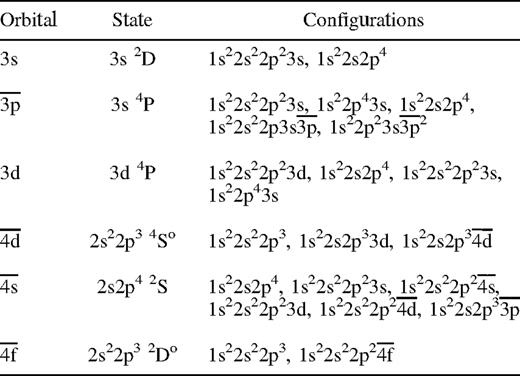
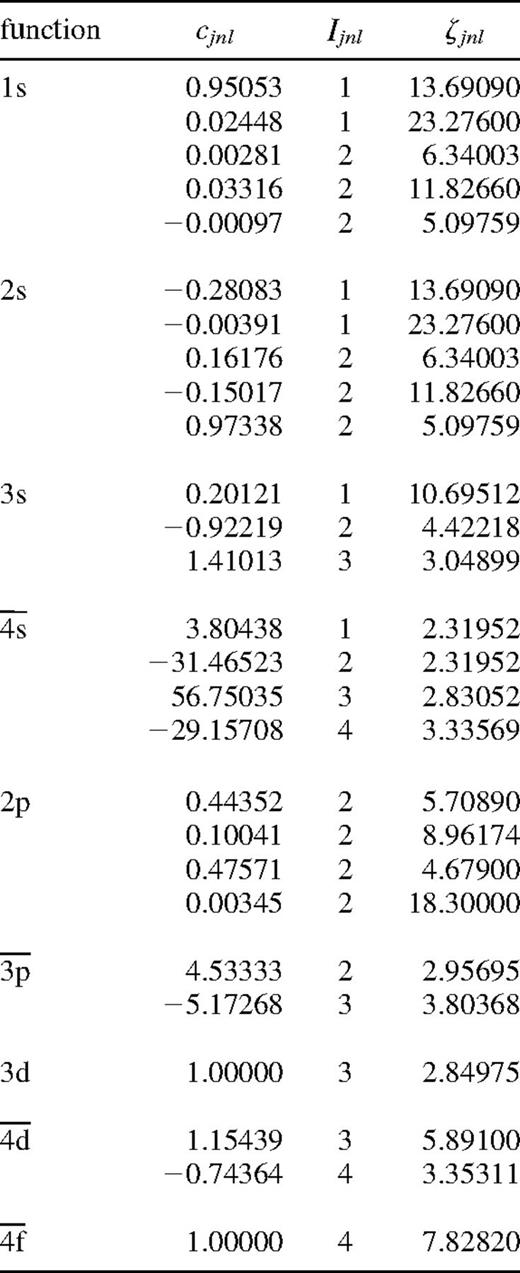
The configuration-interaction wavefunctions of the Si viii target states were then constructed from this orbital set using configurations obtained from one electron replacement in the basis reference set 1s22s22p3, 1s22s2p4, 1s22p5 and 1s22s22p23s, the 1s-shell being kept closed, together with the configurations 1s22s22p3p2, 1s22s22p4s2, 1s22s22p4d2, 1s22p33s3p, 1s22p33p4s, 1s22p33p3d and 1s22p33p4d. A total of 330 configurations formed in this way were retained in the wavefunction expansion for both odd and even parity states. Table 3 presents the calculated energy levels in Ryd relative to the 2s22p34So ground state. Comparisons are made with the observed data of Martin & Zalubas (1983), and the SSTRUCT intermediate coupling calculations of Bhatia & Mason (1980). The agreement between the present results and experiment is excellent with the largest difference of 3 per cent occurring for the odd parity states.
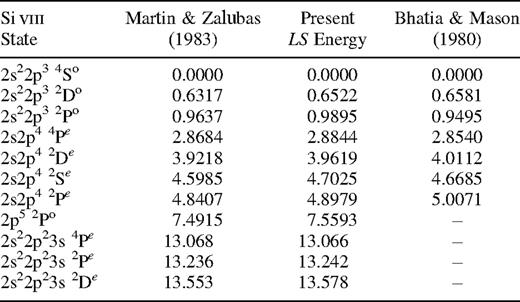
Target state energies (in Ryd) relative to the 2s22p34So groundstate of Si VIII.
The electron scattering calculations were performed using the established R-matrix approach. The theory has been described by Burke & Robb (1975), and Seaton (1987), and the associated codes given by Berrington et al. (1987). 35 Schmidt-orthogonalized continuum orbitals were included, so that a converged R-matrix was obtained up to the highest electron energy considered, namely, 160 Ryd. The R-matrix radius was taken to be 6 atomic units. The LS-coupled Hamiltonian diagonal matrices were adjusted so that the theoretical term energies matched the recommended values of Martin & Zalubas (1983). We note that this energy adjustment ensures the correct positioning of resonances relative to all thresholds included in the calculation. All total angular momenta up to and including  were included together with all possible total spin, so that for the forbidden transitions considered in this paper, convergence of the collision strengths was fully achieved. Having obtained the scattering K-matrices within the framework of the LS-coupling scheme, we utilize the program of Saraph (1978) to transform to LSJ intermediate-coupling including fine-structure mixing of the target terms and thus produce collision strengths, Ω, between the J-resolved levels [McLaughlin & Bell (2000) provide fuller details of the transformation].
were included together with all possible total spin, so that for the forbidden transitions considered in this paper, convergence of the collision strengths was fully achieved. Having obtained the scattering K-matrices within the framework of the LS-coupling scheme, we utilize the program of Saraph (1978) to transform to LSJ intermediate-coupling including fine-structure mixing of the target terms and thus produce collision strengths, Ω, between the J-resolved levels [McLaughlin & Bell (2000) provide fuller details of the transformation].
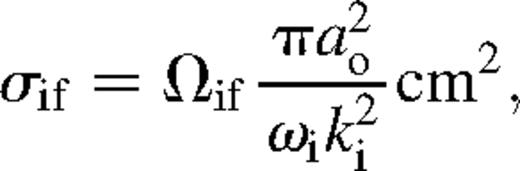
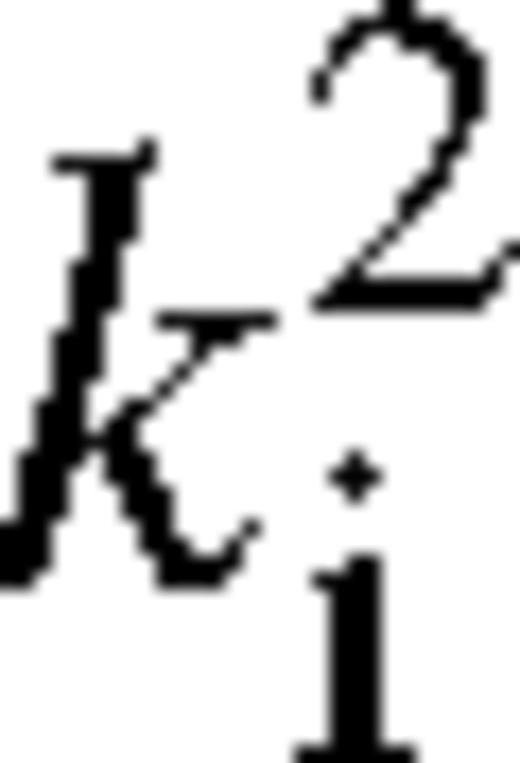 the incident electron energy in Ryd and ao the Bohr radius. While the collision strength is often useful in its own right, more frequently in application it is assumed that the scattering electrons have a Maxwellian velocity distribution. The effective collision strength is then the appropriate quantity. For excitation from level i to level f, the (dimensionless) effective collision strength, ϒif, at electron temperature Te (in K) is given by
the incident electron energy in Ryd and ao the Bohr radius. While the collision strength is often useful in its own right, more frequently in application it is assumed that the scattering electrons have a Maxwellian velocity distribution. The effective collision strength is then the appropriate quantity. For excitation from level i to level f, the (dimensionless) effective collision strength, ϒif, at electron temperature Te (in K) is given by 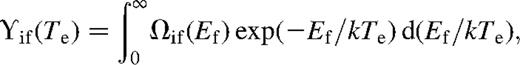
3 Results and discussion
In order to evaluate accurately the effective collision strengths, it is imperative to know the energy dependence of the collision strength over a wide energy region and for a large number of energies. Therefore, to properly delineate the complex autoionizing resonances in the cross-sections, we have utilized a sufficiently fine mesh of incident impact energies (typically 0.005 Ryd) across the range 0–160 Ryd. Pseudo-resonances arising from our inclusion of pseudo-orbitals in the wavefunction representation (Burke, Sukumar & Berrington 1981) have been smoothed out for energies above the highest lying threshold included (2s22p23s 2De).
Figs 1–5 graphically present the collision strength for all 10 fine-structure forbidden transitions between the 2s22p3 levels in Si viii and comparison is made with the earlier results of Bhatia & Mason (1980). For most transitions the agreement between the present results and the distorted wave data is at least as good as the 30 per cent accuracy indicated by Pradhan & Gallagher (1992) as the accuracy for the Bhatia & Mason calculation; indeed, for the two transitions  and
and  the accord is excellent. However, more significant differences are found for the two transitions
the accord is excellent. However, more significant differences are found for the two transitions  and
and  and therefore significant differences will be found for any effective collision strength calculated by the two sets of data, even ignoring the resonance structure in the present calculation. The present work reveals, for all transitions, a wealth of resonance structure dominating the collision strength in the low-energy region. The effect of these resonances converging to the target state thresholds is to enhance the corresponding effective collision strengths, particularly in the low-temperature region. Such resonant enhancement has been consistently found (cf. Bell & Ramsbottom 1999 and references therein) and is a common characteristic for forbidden transitions of this kind.
and therefore significant differences will be found for any effective collision strength calculated by the two sets of data, even ignoring the resonance structure in the present calculation. The present work reveals, for all transitions, a wealth of resonance structure dominating the collision strength in the low-energy region. The effect of these resonances converging to the target state thresholds is to enhance the corresponding effective collision strengths, particularly in the low-temperature region. Such resonant enhancement has been consistently found (cf. Bell & Ramsbottom 1999 and references therein) and is a common characteristic for forbidden transitions of this kind.
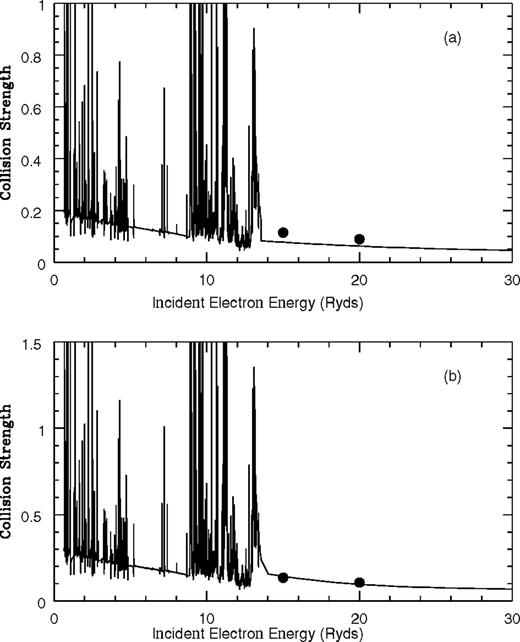
Collision strength as a function of incident electron energy in Ryd for the fine-structure transitions: (a) 2s22p3
 and (b) 2s22p3
and (b) 2s22p3
 Present results are lines while the dots represent Bhatia & Mason (1980).
Present results are lines while the dots represent Bhatia & Mason (1980).
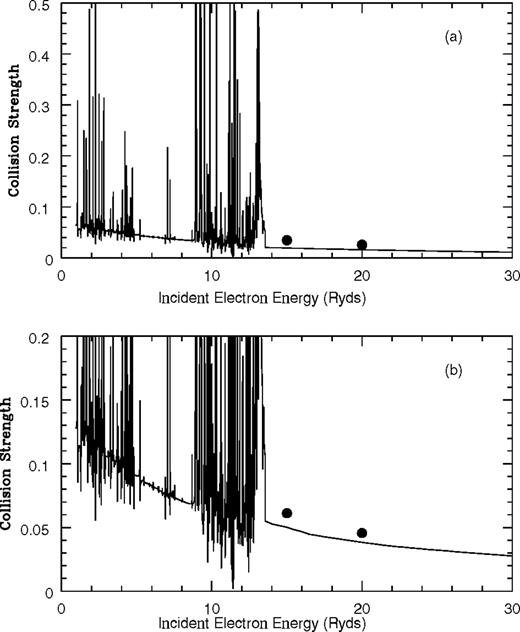
Collision strength as a function of incident electron energy in Ryd for the fine-structure transitions: (a) 2s22p3
 and (b) 2s22p3
and (b) 2s22p3
 Present results are lines while the dots represent Bhatia & Mason (1980).
Present results are lines while the dots represent Bhatia & Mason (1980).
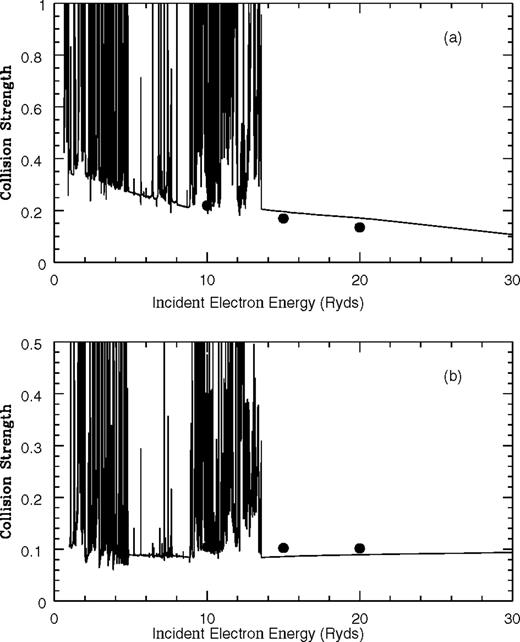
Collision strength as a function of incident electron energy in Ryd for the fine-structure transitions: (a) 2s22p3
 and (b) 2s22p3
and (b) 2s22p3
 Present results are lines while the dots represent Bhatia & Mason (1980).
Present results are lines while the dots represent Bhatia & Mason (1980).
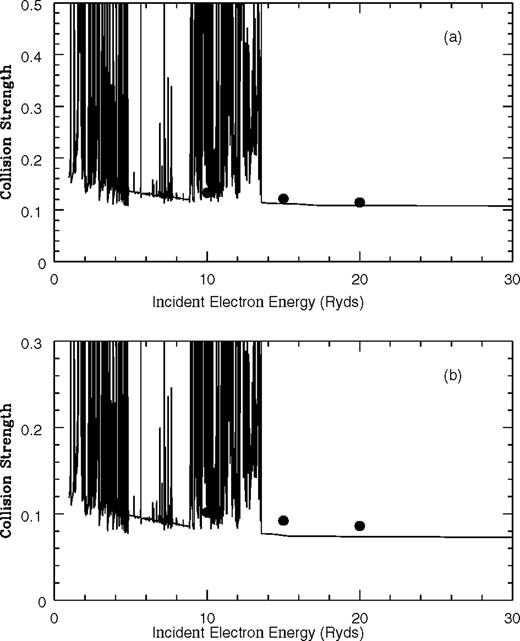
Collision strength as a function of incident electron energy in Ryd for the fine-structure transitions: (a) 2s22p3
 and (b) 2s22p3
and (b) 2s22p3
 Present results are lines while the dots represent Bhatia & Mason (1980).
Present results are lines while the dots represent Bhatia & Mason (1980).
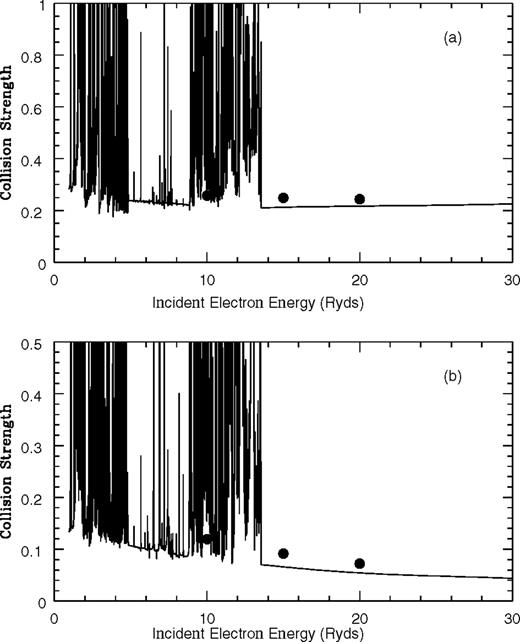
Collision strength as a function of incident electron energy in Ryd for the fine-structure transitions: (a) 2s22p3
 and (b) 2s22p3
and (b) 2s22p3
 Present results are lines while the dots represent Bhatia & Mason (1980).
Present results are lines while the dots represent Bhatia & Mason (1980).
To illustrate the effect of resonances on the effective collision strength and to help in assessing the accuracy of the results we consider two examples in Figs 6 and 7. In both figures we plot the effective collision strength using the full (including resonances) calculated collision strength data as well as the effective collision strength obtained by extracting a non-resonant background (equivalent to the distorted wave approximation) from the collision strength. In both cases the effect of including resonances is clear and, in Fig. 7 for the  transition, the shape of the effective collision strength plotted against log(T) changes with a factor of about 4 increase at the maximum owing to the inclusion of resonances. For log(T) less than about 5.7, the increase comes entirely from the resonance structure lying below the 2s2p42P state, while at higher temperatures a further increase of less than 10 per cent comes from the resonance structure lying at higher incident electron energies.
transition, the shape of the effective collision strength plotted against log(T) changes with a factor of about 4 increase at the maximum owing to the inclusion of resonances. For log(T) less than about 5.7, the increase comes entirely from the resonance structure lying below the 2s2p42P state, while at higher temperatures a further increase of less than 10 per cent comes from the resonance structure lying at higher incident electron energies.
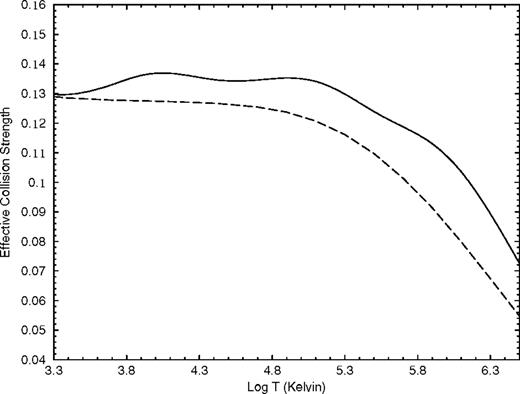
Effective collision strength as a function of log temperature in K, for the 2s22p3
 fine-structure transition. Solid line: present results including all resonant structure; dashed line: present results using non-resonant background collision strength.
fine-structure transition. Solid line: present results including all resonant structure; dashed line: present results using non-resonant background collision strength.
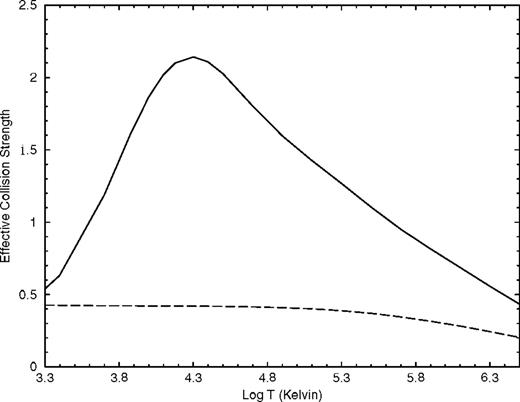
Effective collision strength as a function of log temperature in K, for the 2s22p3
 fine-structure transition. Solid line: present results including all resonant structure; dashed line: present results using non-resonant background collision strength.
fine-structure transition. Solid line: present results including all resonant structure; dashed line: present results using non-resonant background collision strength.
Table 4 presents the effective collision strengths for all 10 forbidden fine-structure transitions for electron temperatures in the range  to
to  applicable to many laboratory plasmas and in particular to astrophysical plasmas. The accuracy of the present data for the effective collision strengths is difficult to predict and can only properly be assessed by comparison with more sophisticated calculations and/or through application to the interpretation of astrophysical plasma data. However, from the discussion above and from our experience from similar and other calculations (Bell & Ramsbottom 1999 and references therein) would suggest that an accuracy in the region of
applicable to many laboratory plasmas and in particular to astrophysical plasmas. The accuracy of the present data for the effective collision strengths is difficult to predict and can only properly be assessed by comparison with more sophisticated calculations and/or through application to the interpretation of astrophysical plasma data. However, from the discussion above and from our experience from similar and other calculations (Bell & Ramsbottom 1999 and references therein) would suggest that an accuracy in the region of  per cent can be anticipated in the low-temperature region where all the open channels are included in the close-coupling calculation. However, a lower accuracy will certainly be the case for the high-temperature results. The most serious error in the present data arises for the omission of higher-lying target states in the wavefunction representation of the Si viii ion. The present calculation is the most elaborate to date and to include higher-lying target states with extensive configuration-interaction wavefunctions poses considerable problems. We are confident that the accuracy of the present data will meet the requirements of most plasma diagnostics.
per cent can be anticipated in the low-temperature region where all the open channels are included in the close-coupling calculation. However, a lower accuracy will certainly be the case for the high-temperature results. The most serious error in the present data arises for the omission of higher-lying target states in the wavefunction representation of the Si viii ion. The present calculation is the most elaborate to date and to include higher-lying target states with extensive configuration-interaction wavefunctions poses considerable problems. We are confident that the accuracy of the present data will meet the requirements of most plasma diagnostics.
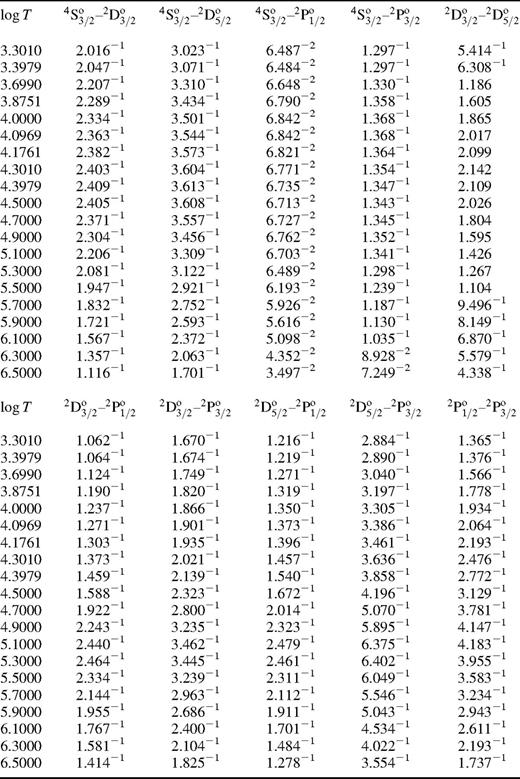
Effective collision strengths for Si viii as a function of the decimal logarithm of the electron temperature in K.
Acknowledgments
The work reported in this paper has been supported by PPARC, under the auspices of a Rolling Grant PPA/G/O/1997/00693. Our thanks are also due to the referee, J. Dubau, for comments which contributed to the improvement of this paper.
References



 ,
, 