-
PDF
- Split View
-
Views
-
Cite
Cite
K. L. Bell, C. A. Ramsbottom, Effective collision strengths for fine-structure forbidden transitions among the 2s22p3 levels of S x, Monthly Notices of the Royal Astronomical Society, Volume 308, Issue 3, September 1999, Pages 677–682, https://doi.org/10.1046/j.1365-8711.1999.02732.x
Close - Share Icon Share
Abstract
Effective collision strengths for electron-impact excitation of the N-like ion S x are calculated in the close-coupling approximation using the multichannel R-matrix method. Specific attention is given to the 10 astrophysically important fine-structure forbidden transitions among the 4So, 2Do and 2Po levels in the 2s22p3 ground configuration. The total (e−+ion) wavefunction is expanded in terms of the 11 lowest LS eigenstates of S x, and each eigenstate is represented by extensive configuration-interaction wavefunctions. The collision strengths obtained are thermally averaged over a Maxwellian distribution of velocities, for all 10 fine-structure transitions, over the range of electron temperatures log T(K)=4.6–6.7 (the range appropriate for astrophysical applications). The present effective collision strengths are the only results currently available for these fine-structure transition rates.
1 Introduction
Emission lines from nitrogen-like ions with 2s22p3 ground configurations have long been known to be useful as density diagnostics of solar and nebular plasmas. Aller, Uffer & Van Vleck (1949) suggested using the intensity ratio of forbidden lines that arise from transitions within the ground state of O ii as density diagnostics for gaseous nebulae. The lines that they considered corresponded to the transitions  and
and  Since then there have been numerous applications of the technique to planetary nebulae and other astrophysical objects, and the necessary electron collision atomic data have recently been calculated to high accuracy by McLaughlin & Bell (1998). However, the O ii ratio is not a useful diagnostic for the solar atmosphere, and instead other nitrogen-like ions can be used to determine electron densities; in particular, Wilhelm et al. (1995) have suggested that the 1213 Å/1196 Å line pair in S x is useful for electron density or temperature diagnostic studies with SUMER (Solar Ultraviolet Measurements of Emitted Radiation) flown on the Solar and Heliospheric Observatory. Indeed, Feldman et al. (1997), in a coronal spectrum of the solar high-temperature atmosphere, have detected the above S x lines as well as the
Since then there have been numerous applications of the technique to planetary nebulae and other astrophysical objects, and the necessary electron collision atomic data have recently been calculated to high accuracy by McLaughlin & Bell (1998). However, the O ii ratio is not a useful diagnostic for the solar atmosphere, and instead other nitrogen-like ions can be used to determine electron densities; in particular, Wilhelm et al. (1995) have suggested that the 1213 Å/1196 Å line pair in S x is useful for electron density or temperature diagnostic studies with SUMER (Solar Ultraviolet Measurements of Emitted Radiation) flown on the Solar and Heliospheric Observatory. Indeed, Feldman et al. (1997), in a coronal spectrum of the solar high-temperature atmosphere, have detected the above S x lines as well as the  1552-Å line and the
1552-Å line and the  1575-Å line.
1575-Å line.
Surprisingly little attention has been paid to this ion. Blaha (1969) used a weak coupling approximation, with exchange, but only considered the transition  He tabulated the collision strength at a single energy value and suggested that the result could be in error by as much as a factor of 2. The only other investigation is that carried out by Bhatia & Mason (1980). They employed the distorted wave method, together with a transformation of the R-matrices obtained in LS coupling, into pair coupling using algebraic re-coupling coefficients which allow for spin—orbit interaction and other relativistic effects. 13 fine-structure levels were considered, namely those arising from the seven LS-coupling states associated with the 2s22p3 and 2s2p4 configurations, and limited configuration-interaction was included in the target state representation. They presented collision strengths only at three values of the electron energy between 15 and 30 Ryd(where 1 Ryd = 2.180 × 10−18 J).
He tabulated the collision strength at a single energy value and suggested that the result could be in error by as much as a factor of 2. The only other investigation is that carried out by Bhatia & Mason (1980). They employed the distorted wave method, together with a transformation of the R-matrices obtained in LS coupling, into pair coupling using algebraic re-coupling coefficients which allow for spin—orbit interaction and other relativistic effects. 13 fine-structure levels were considered, namely those arising from the seven LS-coupling states associated with the 2s22p3 and 2s2p4 configurations, and limited configuration-interaction was included in the target state representation. They presented collision strengths only at three values of the electron energy between 15 and 30 Ryd(where 1 Ryd = 2.180 × 10−18 J).
Clearly there is a need for a large and sophisticated close-coupling calculation that includes extensive configuration-interation wavefunctions to represent the target states and which takes full account of resonance effects.
2 Methods
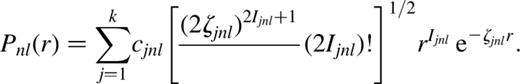
The parameters cjnl, Ijnl and ζjnl for the 1s, 2s and 2p functions were taken to be the Hartree—Fock values obtained by Clementi & Roetti (1974) for the 2s22p34So S x ground state. Spectroscopic 3s and 3d functions were obtained by optimizing the energies of the 2s22p2(1D)3s 2D and 2s22p23d 4P states, respectively, using the configuration-interaction code civ3 (Hibbert 1975). A 3p pseudo-orbital was included to allow for the different 2p functions occurring in the different target states, and the parameters were obtained by optimizing the energy of the 2s22p23s 4P state. Further correlation orbitals, 4s, 4d and 4f, were obtained by optimization of the energies of the 2s2p42S, 2s22p34So and 2s22p32Do states, respectively. The parameters for the orbitals are given in Table 1.
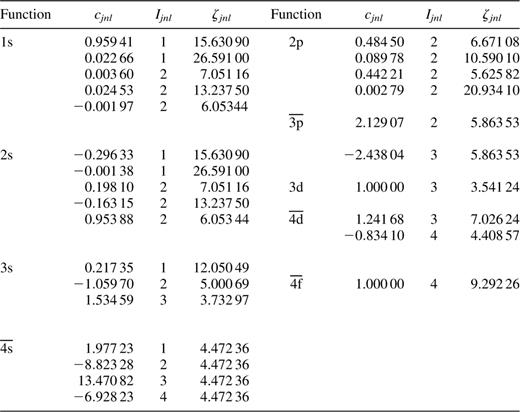
The configuration-interaction wavefunctions of the S x target states were then constructed from this orbital set using configurations obtained from one electron replacement in the basis reference set 1s22s22p3, 1s22s2p4, 1s22p5 and 1s22s22p23s, the 1s shell being kept close, together with the configurations 2s22p3p2, 2s22p4s2, 2s22p4d2, 2p33s3p, 2p33s4s, 2p33p3d and 2p33p4d. A total of 330 configurations formed in this way were retained in the wavefunction expansion for both odd and even parity states. Table 2 presents the calculated energy levels in rydbergs relative to the 2s22p34So ground state. Comparisons are made with the observed data of Martin, Zalubas & Musgrove (1990), the theoretical predictions of the Opacity Project (obtained from the TOPbase data bank: Cunto et al. 1993), the stationary second-order many-body perturbation theory (MBPT) results of Merkelis et al. (1997) and the intermediate-coupling calculations of Bhatia & Mason (1980) using the code sstruct. The agreement between the present results and experiment is excellent with the largest difference of 3 per cent occurring for the 2s22p32Do state. A significant improvement over the work of Bhatia & Mason (1980) is apparent, particularly for the highest state considered by them, namely the 2s2p42P state. Similarly, it is seen that the present data agree better in general with experiment than do the Opacity Project data, but not quite so well as the results of Merkelis et al. (1997).
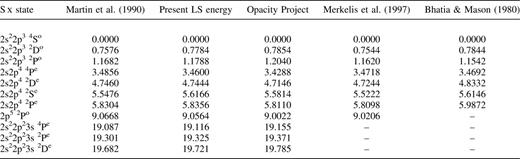
Target state energies (in rydbergs) relative to the 2s22p34So ground state of S x.
Although the agreement of the present energy levels with experiment is excellent, when calculating effective collision strengths for use in astrophysical applications it is essential to utilize experimental energy differences (Martin et al. 1990) to ensure that the thresholds lie in their exact positions. Hence the present R-matrix calculation has been carried out with the energies shifted to the experimental values of Martin et al. (1990).
The calculation of the collision strength, Ωif, between an initial target state i and a final state f was then performed using the R-matrix close-coupling codes (Berrington et al. 1987). The (N+1)-electron configurations were generated by allowing one electron excitation from the two basis distributions 1s22s2p4 and 1s22s22p23s, with the restrictions that the 1s shell remains closed, that the 2p shell retains at least one electron and that there is a maximum of only one electron in the 4f shell. Experience has shown that this achieves a correct balance in the various correlations. In constructing the total wavefunction in the R-matrix internal region, 20 continuum orbitals were used for each incident electron orbital angular momentum. The R-matrix boundary was found to be 7.6 Ryd. We included all partial waves with total angular momentum  , for both even and odd parities and singlet, triplet and quintet multiplicities, which was found to be sufficient to ensure convergence of the cross-sections for the forbidden transitions considered in this paper.
, for both even and odd parities and singlet, triplet and quintet multiplicities, which was found to be sufficient to ensure convergence of the cross-sections for the forbidden transitions considered in this paper.
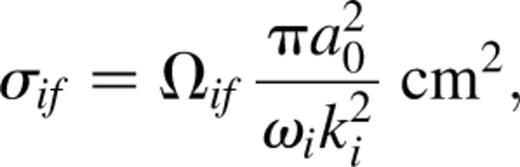
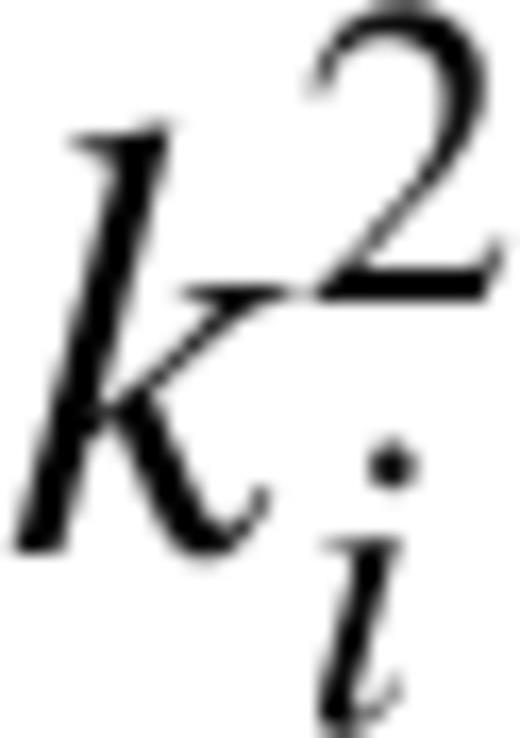 the incident electron energy in rydbergs and a0 the Bohr radius. Having obtained collision strengths within the framework of the LS-coupling scheme, we utilized the program of Saraph (1978) to transform to a jj-coupling scheme and thus produced the collision strengths between the j-resolved levels.
the incident electron energy in rydbergs and a0 the Bohr radius. Having obtained collision strengths within the framework of the LS-coupling scheme, we utilized the program of Saraph (1978) to transform to a jj-coupling scheme and thus produced the collision strengths between the j-resolved levels.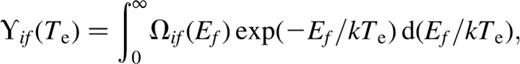
3 Results and discussion
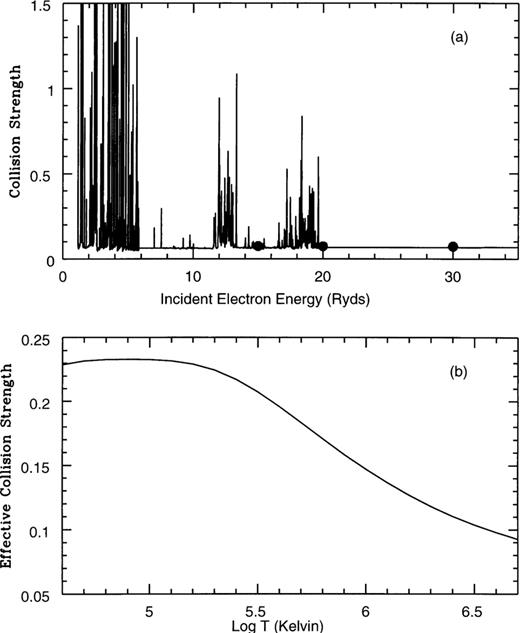
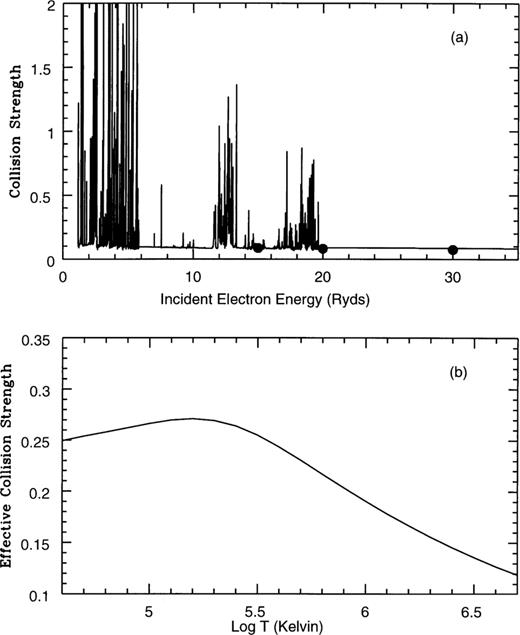
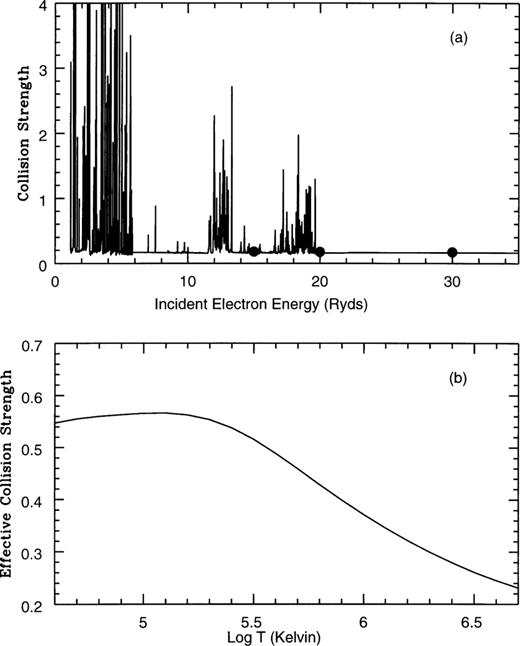
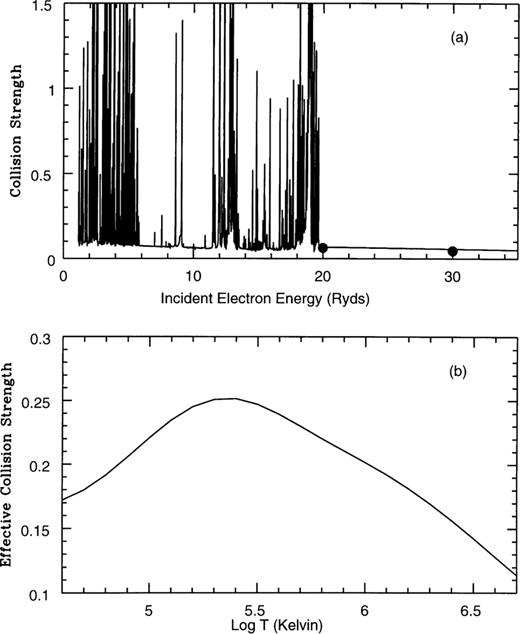
In order to evaluate accurately the effective collision strengths, it is imperative to know the energy dependence of the collision strength over a wide energy region and for a large number of energies. Therefore, to delineate properly the complex autoionizing resonances in the cross-sections, we have utilized a sufficiently fine mesh of incident impact energies (typically 0.005 Ryd) across the range 0-129.6 Ryd. Pseudo-resonances arising from our inclusion of pseudo-orbitals in the wavefunction representation (Burke, Sukumar & Berrington 1981) have been smoothed out for energies above the highest lying threshold included (2s22p23s 2De). Figs 1–10 graphically present the collision strength and the corresponding Maxwellian averaged effective collision strength for the forbidden fine-structure transitions of interest. Comparison is made with the earlier results of Bhatia & Mason (1980) for the collision strengths.
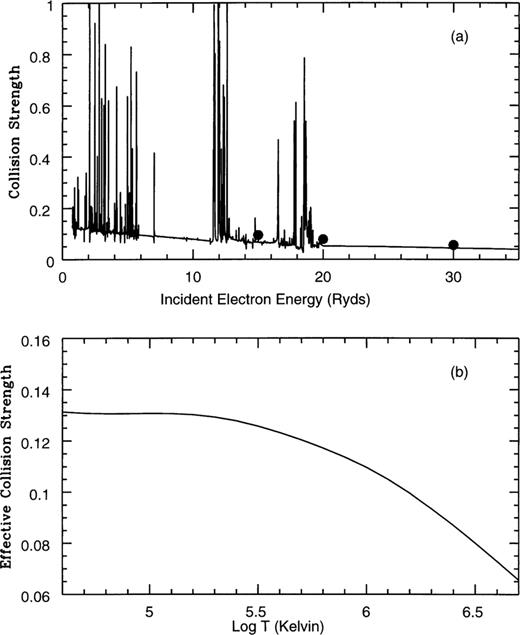
The collision strength as a function of incident electron energy in rydbergs (a), and the effective collision strength as a function of log temperature in kelvin (b), for the  fine-structure transition. Solid line: present results; filled circles: Bhatia & Mason (1980).
fine-structure transition. Solid line: present results; filled circles: Bhatia & Mason (1980).
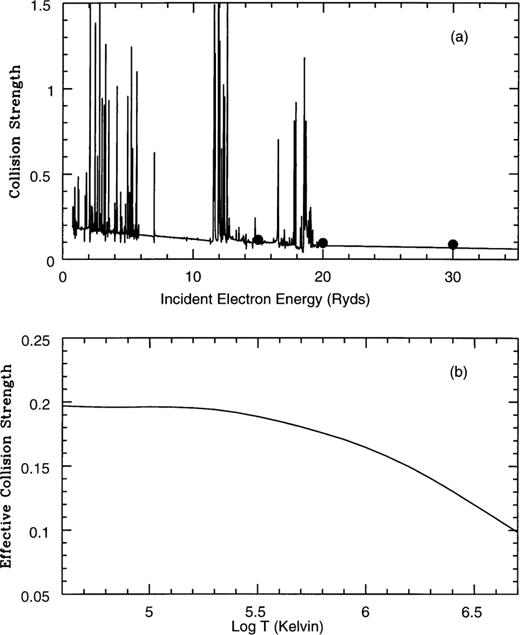
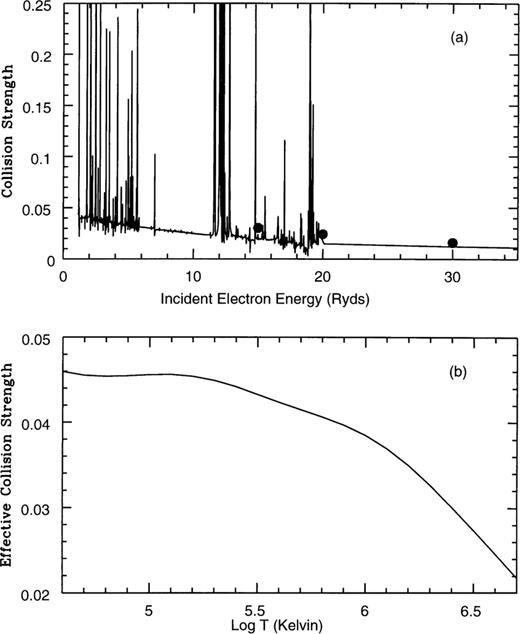
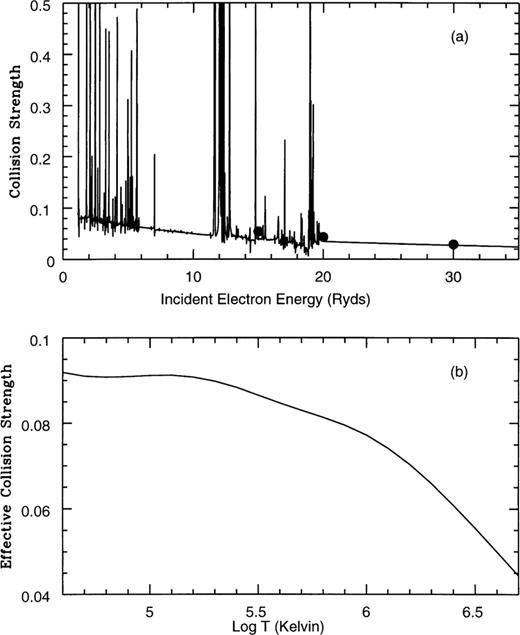

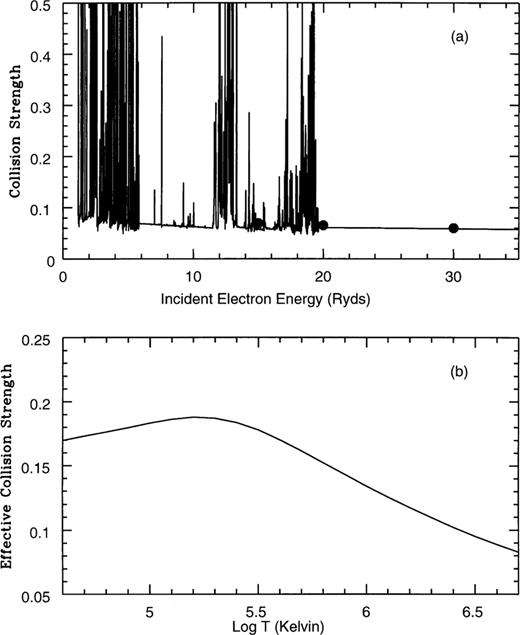
In Figs 1(a) and 2(a) we present the collision strengths for the spin-forbidden  transitions respectively. In both cases the complex resonances converging to the target state thresholds are shown to be properly resolved and located primarily in the low-energy region. Comparison is made with the distorted wave results of Bhatia & Mason (1980). The agreement for both transitions is excellent and suggests that the background cross-section is probably accurate to within a few per cent. The corresponding Maxwellian averaged effective collision strengths are shown in Figs 1(b) and 2(b), where it is seen that they decrease with increasing temperature — a behaviour commonly found for forbidden transitions.
transitions respectively. In both cases the complex resonances converging to the target state thresholds are shown to be properly resolved and located primarily in the low-energy region. Comparison is made with the distorted wave results of Bhatia & Mason (1980). The agreement for both transitions is excellent and suggests that the background cross-section is probably accurate to within a few per cent. The corresponding Maxwellian averaged effective collision strengths are shown in Figs 1(b) and 2(b), where it is seen that they decrease with increasing temperature — a behaviour commonly found for forbidden transitions.
The results for the  transitions are represented in Figs 3 and 4 respectively, with a similar behaviour predicted for both. The presence of autoionizing resonances in the near-threshold collision strengths leads to some resonant enhancement of the effective collision strengths for very low temperatures. It is, however, difficult to assess by how much the effective collision strengths have been enhanced owing to lack of data available for comparison. Again, excellent agreement is found in comparison with the three values calculated by Bhatia & Mason (1980) for the collision strengths.
transitions are represented in Figs 3 and 4 respectively, with a similar behaviour predicted for both. The presence of autoionizing resonances in the near-threshold collision strengths leads to some resonant enhancement of the effective collision strengths for very low temperatures. It is, however, difficult to assess by how much the effective collision strengths have been enhanced owing to lack of data available for comparison. Again, excellent agreement is found in comparison with the three values calculated by Bhatia & Mason (1980) for the collision strengths.
The collision strengths for the  ,
,  and
and  forbidden transitions presented in Figs 5–10 reveal a mass of resonance structure dominating the collision cross-section in the low-energy region. The effect of these resonances converging to the target state thresholds is clearly to enhance the corresponding effective collision strengths, particularly in the low-temperature region. Such resonant enhancement has consistently been found, for example, by Ramsbottom et al. (1994); Ramsbottom, Berrington & Bell (1995), Ramsbottom, Bell & Stafford (1996), Ramsbottom, Bell & Keenan (1997); Ramsbottom & Bell (1998), and is a common characteristic for forbidden transitions of this kind. Again excellent agreement is found with the collision strength data of Bhatia & Mason (1980), with the exception of the
forbidden transitions presented in Figs 5–10 reveal a mass of resonance structure dominating the collision cross-section in the low-energy region. The effect of these resonances converging to the target state thresholds is clearly to enhance the corresponding effective collision strengths, particularly in the low-temperature region. Such resonant enhancement has consistently been found, for example, by Ramsbottom et al. (1994); Ramsbottom, Berrington & Bell (1995), Ramsbottom, Bell & Stafford (1996), Ramsbottom, Bell & Keenan (1997); Ramsbottom & Bell (1998), and is a common characteristic for forbidden transitions of this kind. Again excellent agreement is found with the collision strength data of Bhatia & Mason (1980), with the exception of the  transition, where the present results at 20- and 30-Ryd incident electron energy are somewhat larger.
transition, where the present results at 20- and 30-Ryd incident electron energy are somewhat larger.
The accuracy of the present data for the effective collision strengths is difficult to predict, and can only properly be assessed by comparison with more sophisticated calculations and/or through application to the interpretation of astrophysical plasma data. However, our experience from similar and other calculations (Ramsbottom et al. 1994, 1995, 1996, 1997; Ramsbottom & Bell 1998) would suggest that an accuracy in the region of  10 per cent can be anticipated in the low-temperature region where all the open channels are included in the close-coupling calculation. However, a lower accuracy will certainly be the case for the high-temperature results. The most serious error in the present data arises for the omission of higher lying target states in the wavefunction representation of the S x ion. The present calculation is the most elaborate to date, and to include higher lying target states with extensive configuration-interaction wavefunctions poses considerable problems. We are confident that the accuracy of the present data will meet the requirements of most plasma diagnostics.
10 per cent can be anticipated in the low-temperature region where all the open channels are included in the close-coupling calculation. However, a lower accuracy will certainly be the case for the high-temperature results. The most serious error in the present data arises for the omission of higher lying target states in the wavefunction representation of the S x ion. The present calculation is the most elaborate to date, and to include higher lying target states with extensive configuration-interaction wavefunctions poses considerable problems. We are confident that the accuracy of the present data will meet the requirements of most plasma diagnostics.
Acknowledgments
The work reported in this paper has been supported by PPARC, under the auspices of Rolling Grant PPA/G/O/1997/00693, and the computations were carried out on the CRAY J932-SN9522 at Rutherford Appleton Laboratory.
References



 fine-structure transition.
fine-structure transition. fine-structure transition.
fine-structure transition. fine-structure transition.
fine-structure transition. fine-structure transition.
fine-structure transition. fine-structure transition.
fine-structure transition. fine-structure transition.
fine-structure transition. fine-structure transition.
fine-structure transition. fine-structure transition.
fine-structure transition. fine-structure transition.
fine-structure transition.